
この章では、データ圧縮法の一つである「ハフマン符号化 ( Huffman Coding )」について説明します。
画像に限らず、たいていのデータ列というものは程度の差はあるものの「冗長さ(規則性)」を持っています。データ圧縮とは、このような「冗長さ」を減らす処理であり、データ列の持つ規則性の傾向によって、効果的な方法も変わります。
ランレングス法では、要素の並び方に対する規則性に着目してデータを圧縮していました。これは局所的な冗長さに対するものであり、データ列全体に対する冗長さとしては、他に要素の出現頻度というものがあります。ハフマン符号化は、データの出現頻度に対する規則性に着目してデータ圧縮を行う手法の一つです。
通常、各ピクセルの色コードは固定長のビット列が割り当てられています。例えば「True Color」の場合、各成分はどれも 8 ビット長で表わされることになります。しかし色の成分が全て均等に使用されるわけではなく、その出現頻度にはばらつきがあるため、よく使用される成分に短いビット列、あまり使用されない成分に長いビット列をそれぞれ割り当てることを考えることにします。
このような可変長の符号を使用する場合、区切りをどのように表現するかが大きな問題となります。すぐに思いつくのが終端符号の導入ですが、終端符号を含むビット列は符号として扱えなくなるため、圧縮効果に対して悪影響を及ぼします。例えば、終端符号を 1 ビットの '0' で表わした場合、符号としては "1", "11", "111", ... のような、ビット '1' だけからなるビット列しか扱えなくなり、よほど使用頻度にばらつきがない限り、ほとんど圧縮できない ( 逆にサイズが大きくなってしまう ) ことになります。だからといって、終端符号を長くすると、それだけで大きな無駄になってしまいます。
ここで利用できるのが電話番号の割り当て方法です。電話番号は 10 進の可変長符号ですが、番号を最後までダイアルすれば、末尾を明示しなくても電話は自動的に繋がります。これは、どの電話番号も他の電話番号の先頭部分に重複しないように番号が割り当てられているためであり、例えば "0123456" という電話番号がある場合、その末尾にさらに数字をつなげた "01234567" などの番号は使用しないようにしています。このように構成された可変長符号を「接頭符号 ( Prefix Code)」といいます。
一般的に、 n 進の接頭符号系は n 分木の形で表わすことができ、根から葉までたどる道筋で一つの接頭符号を表現することになります。ニ進の場合はニ分木で表現できるので、適当にニ分木を描いて葉の位置にデータを一つずつ割り当てると接頭符号系ができあがります。あるデータに対する接頭符号は、根から辿る道筋から左の枝を通ったら '0'、右の枝なら '1' と読むことで得ることができます。
以下に、ニ分木で表現した接頭符号系の例を示します。
| データ番号 | 接頭符号 |
|---|---|
| 1 | 0 |
| 2 | 10 |
| 3 | 110 |
| 4 | 1110 |
| 5 | 1111 |
どのデータ番号に割り当てられた符号も、他の番号の先頭部分と重複していないことが、上の例からもわかると思います。
あるデータが、データ列全体中に占める割合は
で表わせます。上記例の接頭符号系において、データ番号 1 - 5 の出現回数をそれぞれ 50 , 25, 15, 5, 5 回とした場合、変換前のデータの大きさが 8 ビットならば
変換前 : 8 x ( 50 + 25 + 15 + 5 + 5 ) = 800 ビット
変換後 : 1 * 50 + 2 * 25 + 3 * 15 + 4 * ( 5 + 5 ) = 185 ビット
となり、185 / 800 x 100 = 23.125 % まで圧縮されるのに対し、出現回数がそれぞれ 5, 5, 15, 25, 50 回だった場合、
で 360 / 800 x 100 = 45 % にまで変換後のデータ列は大きくなってしまいます。
このように、ただニ分木の葉にデータを適当に並べただけでは最適な圧縮効果が望めないため、圧縮後のデータサイズを最小にするためのアルゴリズムを考える必要があります。
「デビッド・ハフマン( David A. Huffman )」は、上記条件を満たす接頭符号系を生成するためのアルゴリズムを 1952 年に発表しました。そのアルゴリズムは以下のようになります。
| 1 | 2 |
|---|---|
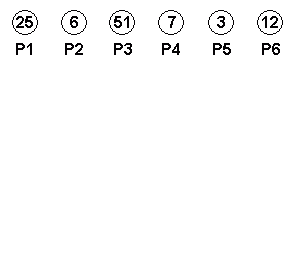 |  |
| 3 | 4 |
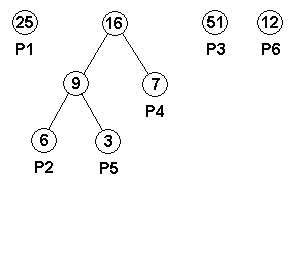 | 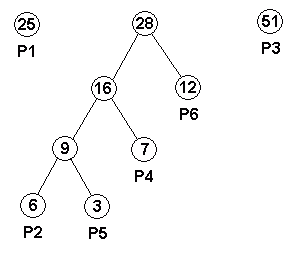 |
| 5 | 6 |
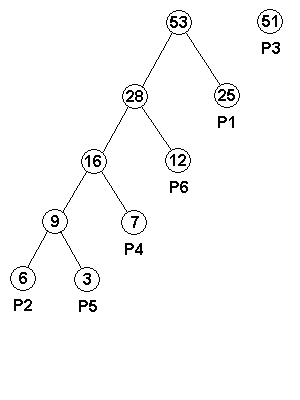 | 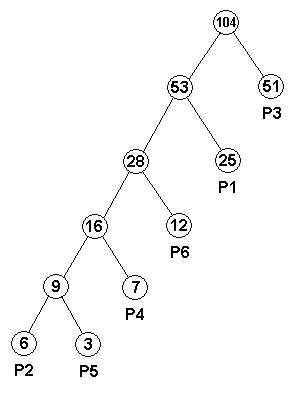 |
| パレット番号 | 出現頻度 | 接頭符号 |
|---|---|---|
| P1 | 25 | 01 |
| P2 | 6 | 00000 |
| P3 | 51 | 1 |
| P4 | 7 | 0001 |
| P5 | 3 | 00001 |
| P6 | 12 | 001 |
このアルゴリズムは、考案者の名をとって「ハフマン符号化 ( Huffman Coding )」と呼ばれます。以下に、このアルゴリズムを用いたハフマン木作成のサンプルを示します。
/// ハフマン木の節を表す構造体 template<typename T> struct HuffmanTreeNode { /// 子の節の添字(節番号)に対する型 typedef typename std::vector< HuffmanTreeNode<T> >::size_type size_type; T value; /// 値 size_t count; /// 出現頻度 size_type left; /// 左の子の節番号 size_type right; /// 右の子の節番号 /* コンストラクタ */ /// 全要素を指定して構築 /// /// t 値 /// c 出現頻度 /// l,r 左右の子の節番号 HuffmanTreeNode( T t, size_t c, size_type l, size_type r ) : value( t ), count( c ), left( l ), right( r ) {} /* メンバ関数 */ /// 節の大小関係を評価する /// /// 自分自身が引数の節よりも小さければ true を返す。 /// 大小関係は出現頻度 count で評価する。 /// /// dest 比較対象の節 bool operator<( const HuffmanTreeNode& dest ) const { return( count < dest.count ); } }; /* MakeHuffmanTree : forest を森としてハフマン木を作成する 各節ははじめから子を持たない状態になっているものとする 戻り値として根の位置(先頭要素からの距離)を返す */ template<typename T> typename std::vector< HuffmanTreeNode<T> >::difference_type MakeHuffmanTree( typename std::vector< HuffmanTreeNode<T> >* forest ) { // 発生頻度によりソートする std::sort( forest->begin(), forest->end() ); // 根の位置 typename std::vector< HuffmanTreeNode<T> >::difference_type root = 0; // 木にする節の位置 typename std::vector< HuffmanTreeNode<T> >::size_type sz = 0; while ( sz + 1 < forest->size() ) { // 木にする節の位置を示す反復子 typename std::vector< HuffmanTreeNode<T> >::iterator s = forest->begin() + sz; // 木にする二つの節を連結する親の節(これが根の節となる) HuffmanTreeNode<T> node( T(), s->count + ( s + 1 )->count, sz, sz + 1 ); // 挿入位置を決めて親の節を登録する typename std::vector< HuffmanTreeNode<T> >::iterator p = std::upper_bound( s + 2, forest->end(), node ); root = std::distance( forest->begin(), p ); // insert前に根の節の位置を登録しておく forest->insert( p, node ); sz += 2; } return( root ); } typedef HuffmanTreeNode<unsigned char> UCharNode; // ハフマン木の要素 typedef std::vector<UCharNode> HuffmanTree; // ハフマン木 /* CountPalet : 画像 draw 上のピクセルに対し、各パレットの出現頻度をカウントして palet に登録する RGB 各成分はまとめてカウンタへ登録する。 */ void CountPalet( const DrawingArea_IF& draw, std::vector<size_t>* palet ) { // 出現頻度の初期化 palet->assign( RGB::MAX + 1, 0 ); Coord<int> c; RGB rgb; for ( c.y = 0 ; c.y < draw.size().y ; ++( c.y ) ) { for ( c.x = 0 ; c.x < draw.size().x ; ++( c.x ) ) { draw.point( c, &rgb ); for ( RGB::size_type st = RGB::RED ; st < RGB::RGB_SIZE ; ++st ) ++( ( *palet )[rgb[st]] ); } } } /* MakeForest : パレットの出現頻度 counter から、ハフマン木作成用の森 forest を作成する */ void MakeForest( const std::vector<size_t>& counter, HuffmanTree* forest ) { forest->clear(); for ( std::vector<size_t>::const_iterator cit = counter.begin() ; cit != counter.end() ; ++cit ) { if ( *cit == 0 ) continue; forest->push_back( UCharNode( std::distance( counter.begin(), cit ), *cit, forest->max_size(), forest->max_size() ) ); } }
サンプルのプログラムは、主にパレット毎の頻度をカウントするルーチン ( CountPalet ) とハフマン木を作成するルーチン ( MakeHuffmanTree ) の二つに分けられます。符号化は RGB 成分単位で行っています。これは、色コード全体を使ってハフマン木を作成すると、自然画の場合は一致する色コードが少なくなり過ぎて圧縮率が悪くなると判断したためです。
ハフマン木は、構造体 HuffmanTreeNode を要素とする可変長配列で表現します。HuffmanTreeNode は値 value と頻度情報(カウンタ) count、左右の子の節がある配列上の添字 ( 節番号 ) left, right をそれぞれ保持し、節番号 left, right を使って各要素を連結する構成になります。以前紹介した「二分探索木」によく似ており、実際どちらも二分木の構造を持っています。しかし、二分探索木は節の値との大小関係から左右の節をたどるため、右の節にある部分木の節は全て、自身より大きな値を持ち、左の節にある部分木の節は逆により小さな値を持つ構成を取るのに対し、ハフマン木は子の節の頻度の和が親の節の頻度と等しくなり値の大小関係はまったく無関係になります。またハフマン木の場合、値は葉の部分だけが持つことになります。
画像に対して RGB 成分の頻度を CountPalet でカウントし、その結果を可変長配列 palet に保持します。palet は、RGB 成分 ( 0 - 255 ) の数だけ要素を確保して、添字が RGB 成分に等しくなるカウンタを加算する方法で頻度を求めています。従って、画像に存在しない RGB 成分の要素はゼロのままとなります。次に MakeForest を使って、palet の内容をハフマン木 forest にコピーします。このとき頻度がゼロの要素は無視して、画像内に存在する RGB 成分だけを取得します。また、子の節は全てない状態 ( ここでは vector の領域確保可能な要素数 max_size() で子の節がないことを表現しています ) とし、全ての節が終端である状態とします。この "森" を使って、MakeHuffmanTree にて前述の方法でハフマン木を作成していきます。最初に STL ( Standard Template Library ) にある関数 sort を使って配列を昇順に並べ替えます。HuffmanTreeNode は大小比較用叙述関数 "operator<" を持ち、頻度を使って大小判定をしているため、ソート後は頻度の小さいものから順に並べ替えられることになります。その後、先頭にある二つの節を子とする新たな節を作成し、そのカウンタを子の節のカウンタの和としておきます。これをソート済みの配列に順序が崩れないように挿入するわけですが、この時 STL の関数 upper_bound を使っています (*2-1)。この関数は、配列がソートされていることを前提に、指定した値を二分探索して最後に見つかった要素 ( これが指定値より大きな要素列の先頭を表します ) の反復子を返します。その前の位置に要素を挿入すれば、大小関係は崩れません。なお、この挿入した節は現在の根の節を表すことになります。
節を挿入する前に、その反復子から、distance 関数 ( 二つの反復子の間の添字の差を求める関数 ) を使って根の位置の節番号を求めています。これは、節を挿入した時に配列全体のメモリ上の位置が変更され、保持した反復子が意味を持たなくなる場合があるためです。そのため、挿入前に添字に戻し、配列全体の移動に影響を受けないようにしています。
ハフマン符号化による圧縮効率は、データの ( ここではパレットコードの ) 使用頻度のばらつきによって左右されます。ハフマン符号化のような可変長符号化の場合、この圧縮効率は、情報理論の中の「エントロピー(平均情報量)」という概念を使って表わすことができます。
事象 x が配列中で出現する確率を P( x ) としたとき、エントロピーは以下の式で計算することができます。
Σx{x∈Ω}( -P( x ) log2P( x ) )
Ω は全事象を表し、その中の全ての要素に対して発生確率から中の式を計算してその和を求めた結果がエントロピーであるということになります。これで得られる数値は、一つのデータあたり平均で何ビットに収まるかを表わす理論限界値となります。上で示したハフマン木の例の場合、
| データ | P(x) | -P(x) log2P(x) |
|---|---|---|
| P1 | 0.240 | 0.494 |
| P2 | 0.0577 | 0.237 |
| P3 | 0.490 | 0.504 |
| P4 | 0.0673 | 0.262 |
| P5 | 0.0288 | 0.147 |
| P6 | 0.115 | 0.359 |
でエントロピーは
となり、理論的には平均 2 ビット程度まで圧縮できることになります。それに対し、圧縮後の実際の平均ビット数は
で、理論値にほぼ一致することがわかります。
*2-1) 「検索アルゴリズム (2) 二分探索/二分探索木」の「1) 二分探索(Binary Search)」にある表 1-6 の中でも紹介しています。
ハフマン符号化により圧縮したデータを復元するとき、圧縮前のデータとその符号との対応表が必要になります。この対応表の大きさによっては逆にデータサイズを増加させてしまうことになるため、なるべく小さなサイズで表現できるような工夫が必要になります。
一番簡単な対応表としては、各パレットコードに対応する符号を単純に配列上に並べる方法ですが、ハフマン符号は最長で ( データの種類 - 1 ) になるため ( ハフマン木が完全に退化して線形リストと同じ状態となり、かつ全てのデータが使用されていた場合に最長のハフマン符号を持つデータが現れます )、256 通りの値を持ちうるパレットコードの場合は 255 ビットが最長となります。この場合、一つの符号に 32 バイトものエリアが必要となり、符号表は 8 KB もの大きさになります。
しかし、最大の符号長はたいてい 10 数ビット程度に収まるので、符号の長さを適当なビット数に制限することで配列の大きさを小さくすることができます。例えば、符号長を 4 バイト ( = 通常 32 ビット ) にすれば符号表は 1 KB にまで小さくすることができます。もしこの符号長を超える符号が現れたら処理をあきらめるか、制限を可変にして最大符号長をより大きくするという手があります。
ハフマン符号表とハフマン木を相互変換するためのサンプル・プログラムを以下に示します。
/// ハフマン符号の型 typedef unsigned int HuffmanCode; /* ハフマン符号型変数のビット構成 ハフマン符号型変数の上位側にハフマン符号、下位側にその長さを保持する。 ハフマン符号長を保持するビット列の長さは HUFFMAN_LENGTH_SIZE、 ハフマン符号のビット長は HUFFMAN_CODE_SIZE で保持する。 ハフマン符号は右詰めとする。 */ /// ハフマン符号長を保持するビット列の長さ const unsigned int HUFFMAN_LENGTH_SIZE = 5; /// ハフマン符号を保持するビット列の長さ const unsigned int HUFFMAN_CODE_SIZE = CHAR_BIT * sizeof( HuffmanCode ) / sizeof( char ) - HUFFMAN_LENGTH_SIZE; /// ハフマン符号長を得るためのマスク const HuffmanCode HUFFMAN_LENGTH_MASK = ~( ~0 << HUFFMAN_LENGTH_SIZE ); /* MakeHuffmanCodeFromTree : ハフマン木 huffmanTree の要素を符号化して配列表 huffmanCode に登録する 処理は再帰的に行い、nodeIdx は次に処理する節の位置を表す。それまでに符号化した結果は code が持ち、 level は node の高さ ( ハフマン符号長と等しい ) を表す。 */ template<class T> bool MakeHuffmanCodeFromTree ( const typename std::vector< HuffmanTreeNode<T> >& huffmanTree, typename std::vector< HuffmanTreeNode<T> >::difference_type nodeIdx, HuffmanCode code, HuffmanCode level, std::map<T,HuffmanCode>* huffmanCode ) { if ( level > HUFFMAN_CODE_SIZE ) return( false ); if ( static_cast<typename std::vector< HuffmanTreeNode<T> >::size_type>( nodeIdx ) >= huffmanTree.size() ) return( false ); typename std::vector< HuffmanTreeNode<T> >::const_iterator node = huffmanTree.begin() + nodeIdx; if ( node->right != huffmanTree.max_size() ) if ( ! MakeHuffmanCodeFromTree( huffmanTree, node->right, code * 2 + 1, level + 1, huffmanCode ) ) return( false ); if ( node->left != huffmanTree.max_size() ) if ( ! MakeHuffmanCodeFromTree( huffmanTree, node->left, code * 2, level + 1, huffmanCode ) ) return( false ); if ( node->left == huffmanTree.max_size() && node->right == huffmanTree.max_size() ) ( *huffmanCode )[node->value] = ( code << HUFFMAN_LENGTH_SIZE ) | level; return( true ); } /* AddNodeToHuffmanTree : ハフマン符号をハフマン木 huffmanTree に追加する cit->first は値、cit->second は値に対するハフマン符号をそれぞれ表す。 */ template<class T> void AddNodeToHuffmanTree ( typename std::map<T,HuffmanCode>::const_iterator cit, typename std::vector< HuffmanTreeNode<T> >* huffmanTree ) { HuffmanCode code = cit->second >> HUFFMAN_LENGTH_SIZE; HuffmanCode level = cit->second & HUFFMAN_LENGTH_MASK; HuffmanTreeNode<T> leaf( T(), 0, huffmanTree->max_size(), huffmanTree->max_size() ); typename std::vector< HuffmanTreeNode<T> >::size_type nodeIdx = 0; for ( ; level > 0 ; --level ) { // 符号ビットが 1 なら右、0 なら左の子の節を選択 if ( ( ( code >> ( level - 1 ) ) & 1 ) != 0 ) { if ( (*huffmanTree)[nodeIdx].right == huffmanTree->max_size() ) { huffmanTree->push_back( leaf ); (*huffmanTree)[nodeIdx].right = huffmanTree->size() - 1; } nodeIdx = (*huffmanTree)[nodeIdx].right; } else { if ( (*huffmanTree)[nodeIdx].left == huffmanTree->max_size() ) { huffmanTree->push_back( leaf ); (*huffmanTree)[nodeIdx].left = huffmanTree->size() - 1; } nodeIdx = (*huffmanTree)[nodeIdx].left; } } (*huffmanTree)[nodeIdx].value = cit->first; } /* MakeTreeFromHuffmanCode : ハフマン符号の配列表 huffmanCode からハフマン木 huffmanTree を作成する */ template<class T> void MakeTreeFromHuffmanCode ( const std::map<T,HuffmanCode>& huffmanCode, std::vector< HuffmanTreeNode<T> >* huffmanTree ) { HuffmanTreeNode<T> leaf( T(), 0, huffmanTree->max_size(), huffmanTree->max_size() ); huffmanTree->clear(); huffmanTree->push_back( leaf ); // 根の節を初期化 for ( typename std::map<T,HuffmanCode>::const_iterator cit = huffmanCode.begin() ; cit != huffmanCode.end() ; ++cit ) AddNodeToHuffmanTree( cit, huffmanTree ); }
ハフマン符号の型は符号なし整数型 unsigned int として定義しています。通常は 4 バイト 32 ビットであり、先頭の 27 ビットを符号そのものに、末尾の 5 ビットを符号長に割り当てます。よって、符号長は最大 32 - 5 = 27 ビットまでとなります。
関数 MakeHuffmanCodeFromTree は、ハフマン木からハフマン符号を取り出して、配列表に格納するための関数です。はじめに符号長が最大長を超えていないかを確認し、もし超えていたらすぐに false を返すようにしています。つまりここでは符号長が制限を越えたら処理をあきらめているわけですが、どのようなデータ列にも対応したい場合は、ここで符号長を拡張する処理を加える必要があります。
次に、着目している節の左右それぞれにつながった節がある場合、符号列と符号長を更新してから、その節を新たな引数にして自分自身を呼び出します。符号列は 2 倍 ( つまり左側へ 1 ビットシフト )した後、右側の節に対しては 1 を加えて末尾のビットを 1 とし、左側に対しては何もせずに末尾のビットを 0 のままにすることで更新することができます。もし左右どちらの子も存在しなければ、その節は葉であることになるのでその値と作成した符号列を配列表に登録します。
配列表には STL のコンテナ・クラスである map を利用しています。このクラスは "キー" と "値" のペアを保持するときに便利な連想配列であり、ここでは "キー" に HaffmanTreeNode のメンバ変数 value を、"値" にハフマン符号をペアで登録しています。
関数 MakeTreeFromHuffmanCode は、逆にハフマン符号配列表からハフマン木を再構築するための関数です。実際に処理するのは AddNodeToHuffmanTree で、符号列の先頭から順にビットを読んで、1 ならば右の、0 ならば左の子をたどります。もし子がなければ新たな節を追加してつないでいき、符号列の全てのビットを読み終えたら、最後にたどり着いた節に値を代入して処理を終了します。
各値に対するハフマン符号が求められれば、あとはデータ列を符号化して圧縮を行うだけです。ハフマン符号化とその復号化処理を行うサンプル・プログラムを以下に示します。
typedef std::map<unsigned char,HuffmanCode> HuffmanCodeMap; // バイトデータとハフマンコードのマップ /* WriteToArray : huffmanCode を encdata へ書き込む bitData は一時的にビット列を保持するキャッシュで、bitLen がバッファサイズをオー バーしたら encData へ出力する */ void WriteToArray( HuffmanCode huffmanCode, HuffmanCode* bitData, unsigned int* bitLen, std::vector<HuffmanCode>* encData ) { // HaffmanCode のビット数 const unsigned int szHuffmanCode = sizeof( HuffmanCode ) * CHAR_BIT / sizeof( char ); // huffmanCode をコードと長さに分解 HuffmanCode code = huffmanCode >> HUFFMAN_LENGTH_SIZE; HuffmanCode length = huffmanCode & HUFFMAN_LENGTH_MASK; *bitLen += length; if ( *bitLen >= szHuffmanCode ) { // キャッシュがいっぱいになったら encdata へ出力 *bitLen -= szHuffmanCode; encData->push_back( ( *bitData << ( length - *bitLen ) ) | ( code >> *bitLen ) ); *bitData = code & ~( ~0 << *bitLen ); } else { *bitData = ( *bitData << length ) | code; } } /* EncodeToHuffmanCode : 画像データ draw に対してハフマン符号化を行う パレットコードに対するハフマン符号列は huffmanCode にあり、符号化した結果は encData へ書き込まれる 対象画像データが持つ全てのパレットコードが huffmanCode にあることを前提とする。そうでないデータが あった場合は処理を中断して false を返す */ bool EncodeToHuffmanCode ( const DrawingArea_IF& draw, const HuffmanCodeMap& huffmanCode, std::vector<HuffmanCode>* encData ) { if ( &draw == 0 || &huffmanCode == 0 || encData == 0 ) return( false ); // HaffmanCode のビット数 const unsigned int szHuffmanCode = sizeof( HuffmanCode ) * CHAR_BIT / sizeof( char ); encData->clear(); Coord<int> c; RGB rgb; HuffmanCode bitData = 0; // 符号化ビットのキャッシュ unsigned int bitLen = 0; // キャッシュしたビット列の長さ for ( c.y = 0 ; c.y < draw.size().y ; ++( c.y ) ) { for ( c.x = 0 ; c.x < draw.size().x ; ++( c.x ) ) { draw.point( c, &rgb ); for ( RGB::size_type st = 0 ; st < RGB::RGB_SIZE ; ++st ) { HuffmanCodeMap::const_iterator cit = huffmanCode.find( rgb[st] ); if ( cit == huffmanCode.end() ) return( false ); // 取得できないことはありえない WriteToArray( cit->second, &bitData, &bitLen, encData ); } } } if ( bitLen > 0 ) encData->push_back( bitData << ( szHuffmanCode - bitLen ) ); return( true ); } /* ReadFromTree : ハフマン符号列を cit で始まる反復子から読み取りながら、ハフマン木 huffmanTree をたどって値を rgb に取得する root はハフマン木の根を表し、encEnd はハフマン符号列のある配列の末尾の次を表す。 bitData は cit から読み込んだビット列を保持するキャッシュで、bitLen が残りのビット長を保持する。 */ bool ReadFromTree ( const HuffmanTree& huffmanTree, HuffmanTree::difference_type root, std::vector<HuffmanCode>::const_iterator* cit, std::vector<HuffmanCode>::const_iterator encEnd, RGB* rgb, HuffmanCode* bitData, unsigned int* bitLen ) { // HaffmanCode のビット数 const unsigned int szHuffmanCode = sizeof( HuffmanCode ) * CHAR_BIT / sizeof( char ); for ( RGB::size_type st = 0 ; st < RGB::RGB_SIZE ; ++st ) { HuffmanTree::const_iterator tree = huffmanTree.begin() + root; // たどる開始位置は root から while ( tree->left != huffmanTree.max_size() || tree->right != huffmanTree.max_size() ) { // キャッシュの再読み込み if ( *bitLen == 0 ) { if ( *cit == encEnd ) return( false ); *bitData = *( ( *cit )++ ); *bitLen = szHuffmanCode; } if ( ( ( *bitData >> ( *bitLen - 1 ) ) & 1 ) == 1 ) { if ( tree->right == huffmanTree.max_size() ) return( false ); // 右側がたどれない tree = huffmanTree.begin() + tree->right; } else { if ( tree->left == huffmanTree.max_size() ) return( false ); // 右側がたどれない tree = huffmanTree.begin() + tree->left; } --( *bitLen ); } ( *rgb )[st] = tree->value; } return( true ); } /* DecodeFromHuffmanCode : ハフマン符号列 encData から、ハフマン木 huffmanTree を使って複合化を行い、結果を画像領域 draw に描画する root は huffmanTree の根を表す。 */ bool DecodeFromHuffmanCode ( const std::vector<HuffmanCode>& encData, const HuffmanTree& huffmanTree, HuffmanTree::difference_type root, DrawingArea_IF* draw ) { if ( &encData == 0 || &huffmanTree == 0 || draw == 0 ) return( false ); Coord<int> c; RGB rgb; HuffmanCode bitData = 0; // encData から取り出したビット列を一時的に保持するキャッシュ unsigned int bitLen = 0; // キャッシュにある残りビット数 std::vector<HuffmanCode>::const_iterator cit = encData.begin(); for ( c.y = 0 ; c.y < ( draw->size() ).y ; ++( c.y ) ) { for ( c.x = 0 ; c.x < ( draw->size() ).x ; ++( c.x ) ) { if ( ! ReadFromTree( huffmanTree, root, &cit, encData.end(), &rgb, &bitData, &bitLen ) ) return( false ); draw->pset( c, rgb ); } } return( true ); }
EncodeToHuffmanCode 関数は画像データをハフマン符号に変換するための関数です。ハフマン符号表 huffmanCode から画像データ draw の RGB 成分をキーにハフマン符号を取り出し、符号データ列 encData へ書き込みます。draw は画像領域 DrawingArea_IF 型のデータで、各座標値の RGB 成分を、メンバ関数 point で取得したり、pset でセットすることができる抽象オブジェクトと考えて下さい。また、huffmanCode には draw が持つ全ての RGB 成分があらかじめ保持されていることを前提に処理しているため、対象のハフマン符号が見つからなかった場合は処理を中断するようになっています。
encData への書き込みはビット単位で行われるため、途中まで書き込まれたビット列はいったんキャッシュに保持して、満杯になったら配列へ書き込むようにしています。そのための関数が WriteToArray になります。
DecodeFromHuffmanCode は、符号化したデータ列 encData を復号化して画像オブジェクト draw に描画するための関数ですが、ハフマン符号から再構築したハフマン木をあらかじめ用意しておく必要があります。ここでもビット単位での処理が必要なことから途中まで読み込まれたビット列をキャッシュに保持する形式を取り、読み込み用の関数として ReadFromTree を用意しています。また、encData にある符号は全てハフマン木に存在していることを前提としているので、値が見つからない場合は処理を中断するようになっています。
復号化するときには必ずハフマン木を再構築する必要があります。この処理を省略する手段として木構造そのままの形でハフマン符号を保持する方法もあります。ハフマン符号とそれに対する値とペアで保持した場合、一つの要素のサイズは ( 値のサイズ + 符号のサイズ ) であり、RGB 成分 1 バイトと符号 4 バイトの構成なら 5 バイト必要となります。また、要素数は画像が持つ RGB 成分の個数と等しくなります。それに対し、ハフマン木をそのまま保持した場合は節の総個数が ( 要素数 x 2 - 1 ) になり (*3-1)、一つの節のサイズは葉のとき値のサイズそのもの、そうでないとき二つの添字 ( 節番号 ) のサイズになります。葉とそれ以外を区別しない場合は ( 値のサイズ + 二つの節番号のサイズ ) なので、RGB 成分が値で、添字が unsigned short int などの(通常) 2 バイト整数値となる型だった場合は符号をそのまま保持した時と変わらないことになり、総個数が増える分、表のサイズは大きくなってしまいます。
RGB 成分は最大 256 個の要素があるので、節の個数は 256 x 2 - 1 = 511 個になります。節番号としては 9 ビットが必要で値が 8 ビットなので、ビット列を詰めてギリギリまで小さなサイズにしたときの最大サイズは 511 x ( 8 + 9 x 2 ) = 13286 ビット ≅ 1661 バイトとなります。符号を保持する場合の最大サイズが 256 x 5 = 1280 バイトであることを考えると、ビット処理してまでハフマン木のままで符号を保持するメリットはありません。しかし、節番号の部分に RGB 成分を保持して葉は作らないことにし、節番号は 9 ビットめを 1 にした 256 からスタートするようにすれば ( つまり実際の節番号は 9 ビットめを 0 にした値になります )、節の個数は葉の部分を除いた 255 個となり、値を保持する変数も不要になるので全体のサイズは最大で 255 x 9 x 2 = 4590 ビット ≅ 574 バイトに収まります ( ビット処理をせずに節番号を 2 バイトとしても、最大サイズは 255 x 2 x 2 = 1020 バイトで符号そのものを保持するより少しだけ小さくなります )。
ハフマン木をそのまま符号表にするためのサンプル・プログラムを以下に示します。
typedef std::pair<unsigned short int, unsigned short int> ChildNodeIndex; /* TransHT_CopyChild : ハフマン木 srcTree から配列表 destTree への要素のコピー p は destTree 上にある親の節の left, right いずれかへのポインタで、そのコピー元が srcTree[childIndex] になる。 */ void TransHT_CopyChild( const HuffmanTree& srcTree, HuffmanTree::size_type childIndex, std::vector<ChildNodeIndex>* destTree, unsigned short int* p ) { const unsigned short int PADDING = 0x100; // 節番号に加える定数 ( 9 ビットめを 1 にする ) if ( childIndex == srcTree.max_size() ) return; // 子の節が葉だった場合、色コードをセット if ( srcTree[childIndex].left == srcTree.max_size() && srcTree[childIndex].right == srcTree.max_size() ) *p = srcTree[childIndex].value; // そうでなかったら新たな要素を配列表に追加してその節番号をセット else { *p = destTree->size() + PADDING; TransHuffmanTree( srcTree, childIndex, destTree ); } } /* TransHuffmanTree : ハフマン木 srcTree の srcIndex 番目の要素をそのまま配列表 destTree に収める 処理の開始は srcIndex に根の節の番号を渡す。この時 destTree の先頭の要素は根の節となる */ void TransHuffmanTree( const HuffmanTree& srcTree, HuffmanTree::size_type srcIndex, std::vector<ChildNodeIndex>* destTree ) { if ( srcIndex >= srcTree.size() ) return; destTree->push_back( ChildNodeIndex( 0, 0 ) ); std::vector<ChildNodeIndex>::size_type destIndex = destTree->size() - 1; // 左側の節をチェック TransHT_CopyChild( srcTree, srcTree[srcIndex].left, destTree, &( (*destTree)[destIndex].first ) ); // 右側の節をチェック TransHT_CopyChild( srcTree, srcTree[srcIndex].right, destTree, &( (*destTree)[destIndex].second ) ); } /* InverseHT_CheckChild : ハフマン木 destTree の子 child が節番号か RGB 成分かをチェックする */ void InverseHT_CheckChild( HuffmanTree* destTree, UCharNode::size_type* child ) { const unsigned short int PADDING = 0x100; // 節番号から減算する定数 ( 9 ビットめを 0 にする ) // 節番号ならば 9 ビットめを 0 にする if ( *child > RGB::MAX ) { *child -= PADDING; // RGB 成分なら葉の節として追加・結合する } else { RGB::primary_type value = *child; *child = destTree->size(); destTree->push_back( UCharNode( value, 0, destTree->max_size(), destTree->max_size() ) ); } } /* InverseHuffmanTree : 配列表 srcTree をハフマン木 destTree に逆変換する srcTree の先頭の要素が根の節であることを前提とする。 */ void InverseHuffmanTree( const std::vector<ChildNodeIndex>& srcTree, HuffmanTree* destTree ) { destTree->clear(); // srcTree からそのまま destTree へ内容をコピー for ( std::vector<ChildNodeIndex>::const_iterator cit = srcTree.begin() ; cit != srcTree.end() ; ++cit ) destTree->push_back( UCharNode( 0, 0, cit->first, cit->second ) ); HuffmanTree::size_type sz = destTree->size(); for ( HuffmanTree::size_type i = 0 ; i < sz ; ++i ) { // 左の節を逆変換 InverseHT_CheckChild( destTree, &( (*destTree)[i].left ) ); // 右の節を逆変換 InverseHT_CheckChild( destTree, &( (*destTree)[i].right ) ); } }
ハフマン木を符号表にする関数は TransHuffmanTree です。コピー先の配列表 destTree は ChildNodeIndex 型の要素からなる可変長配列で、ChildNodeIndex 型の実体は unsigned short int 型の要素二つからなる構造体 ( STL の pair 型 ) です。これらの要素は first, second 二つのメンバ変数としてアクセスすることができるので、first に左、second に右の子の節番号または RGB 成分を保持するようにします。最初に destTree へデフォルト状態の要素を一つ追加しておいて、左右の子に対して TransHT_CopyChild 関数を使って正しい要素になるように内容を書き換えます。
TransHT_CopyChild 関数へは、コピー元のハフマン木 srcTree への参照と、左右いずれかの子の節の節番号 srcIndex、配列表 destTree、最後に destTree にある左右いずれかの子の節へのポインタ p を渡します。p は、ハフマン木の子の節 srcTree[srcIndex] をコピーする対象となります。前述の通り、子の節が葉であれば RGB 成分そのものを p の示す先に書き込み、そうでなければ destTree へ srcTree[srcIndex] のコピー先となる節を、再度 TransHuffmanTree を呼び出して作成します。TransHuffmanTree では最初に新たな節を destTree の末尾に追加してコピーを行うため、p へは destTree の現在のサイズ ( 要素が追加されればこれが末尾の要素への添字になります ) を登録しています。また同時に、節番号であることが分かるように、9 ビットめを 1 にします。
InverseHuffmanTree は逆に、配列表からハフマン木へ戻すための関数です。基本的には TransHuffmanTree とあまり変わらず、子の節への節番号が RGB 成分へ変換されたものかどうかをチェックして、もし RGB 成分であれば新たな節を追加して結合する処理を繰り返しています。実際の処理は InverseHT_CheckChild へ左右それぞれの子の節番号へのポインタを渡して行います。
*3-1) 何故そうなるかは帰納法で考えるとわかりやすいと思います。データが一つの時は明らか。N 個のデータに 2N - 1 個の節が使われているとき、さらに一つのデータを加えると、データを格納する葉とつなぐための節の計二つが必要で節の総計は 2N + 1 = 2(N + 1) - 1 になります。
前章で使ったテスト用の画像を使い、ハフマン符号化による圧縮率を検証してみます。まずは、前章で利用した「風景」画像 10 枚を使った結果を以下に示します。
| 画像 | 符号サイズ (Bytes) | 圧縮率 (%) |
|---|---|---|
| 画像 1 | 2202552 | 93.36 |
| 画像 2 | 2313704 | 98.07 |
| 画像 3 | 2270524 | 96.24 |
| 画像 4 | 2292740 | 97.18 |
| 画像 5 | 2345188 | 99.40 |
| 画像 6 | 2316912 | 98.20 |
| 画像 7 | 2316604 | 98.19 |
| 画像 8 | 2310320 | 97.92 |
| 画像 9 | 2277032 | 96.51 |
| 画像 10 | 2336908 | 99.05 |
テスト画像は全て 1024 x 768 のサイズなので、1 ピクセルあたり 3 バイトとすれば 2359296 バイトのデータ量になります。圧縮率は、符号サイズをこのデータ量で割った比率です。結果としてはほとんど圧縮されていません。これらの画像はどれも RGB 成分全てが使われているので、ハフマン符号表の大きさは 256 x 5 = 1280 バイトとなりました。ハフマン木の形で保持したとしても、255 x 4 = 1020 のデータ量が必要となります。
次は、「アニメ調」の画像での検証結果です。
| 画像 | 符号サイズ (Bytes) | 圧縮率(%) | ||
|---|---|---|---|---|
| ハフマン符号 | RLE 法 | PIC 圧縮法 | ||
| 画像 1 | 1781536 | 75.51 | 76.65 | 83.90 |
| 画像 2 | 2026120 | 85.88 | 81.88 | 74.24 |
| 画像 3 | 1607240 | 68.12 | 85.16 | 77.17 |
| 画像 4 | 1916812 | 81.25 | 71.97 | 66.58 |
| 画像 5 | 945192 | 40.06 | 35.82 | 34.41 |
| 画像 6 | 2313912 | 98.08 | 100.60 | 99.37 |
| 画像 7 | 2004736 | 84.97 | 97.10 | 103.19 |
| 画像 8 | 2020492 | 85.64 | 94.51 | 108.74 |
| 画像 9 | 1246972 | 52.85 | 55.29 | 58.48 |
| 画像 10 | 2223492 | 94.24 | 89.59 | 88.28 |
これらのテスト画像も全て 1024 x 768 のサイズであり、RGB 成分全てが使用されたため、「風景」の場合と画像や符号表などの大きさは変わりません。比較として「(1) ランレングス法」で検証した「ランレングス法」と「PIC 圧縮法」での圧縮率も示してあります。
それぞれの圧縮法を比較すると、「ランレングス法」や「PIC 圧縮法」で圧縮率が高かったものはハフマン符号化でも高い圧縮率が得られていることがわかります。「ハフマン符号化」は、画像全体に対する各成分の発生頻度の偏りを利用して圧縮していると考えることができますが、対して「ランレングス法」や「PIC 圧縮法」は局所的に同じデータがあればそれをまとめるという圧縮法です。「風景」の場合、「ランレングス法」や「PIC 圧縮法」では逆にサイズが大きくなる傾向がありましたが、「ハフマン符号」では多少サイズを小さくすることができました。局所的には異なる色が使われていても、全体的に見れば偏りがあることがその理由であると考えられますが、「アニメ調」の場合、全体に対して偏りが大きい画像に局所的でも似た色を使う傾向があるのかもしれません。
最後は、「ランレングス法」や「PIC 圧縮法」で最も圧縮率の高かった「アニメ調」GIF 画像での検証結果です。
| 画像 | 符号サイズ (Bytes) | 圧縮率 (%) | 符号表サイズ (Bytes) | 木構造符号表サイズ (Bytes) | 圧縮率(%) | |
|---|---|---|---|---|---|---|
| RLE 法 | PIC 圧縮法 | |||||
| 画像 1 | 1039256 | 44.05 | 1030 | 820 | 6.83 | 4.95 |
| 画像 2 | 1210788 | 51.32 | 835 | 664 | 30.08 | 25.84 |
| 画像 3 | 613224 | 25.99 | 1225 | 976 | 7.86 | 5.97 |
| 画像 4 | 987364 | 41.85 | 1185 | 944 | 16.65 | 11.01 |
| 画像 5 | 1222364 | 51.81 | 565 | 448 | 7.45 | 4.70 |
| 画像 6 | 958320 | 40.62 | 875 | 696 | 11.24 | 8.20 |
| 画像 7 | 648060 | 27.47 | 1015 | 808 | 6.46 | 5.16 |
| 画像 8 | 850436 | 36.05 | 525 | 416 | 15.41 | 11.85 |
| 画像 9 | 977524 | 41.43 | 1205 | 960 | 17.90 | 13.72 |
| 画像 10 | 953200 | 40.40 | 1045 | 832 | 13.30 | 10.08 |
GIF 画像の場合、色数が少ないため符号表のサイズが今までよりも小さく、画像によってバラバラです。ここでも「ランレングス法」と「PIC 圧縮法」での圧縮率を示してありますが、比較すると「ハフマン符号化」の圧縮率はあまり高くない傾向にあります。「ハフマン符号化」を単体で利用するのはあまり意味がないように見えますが、ハフマン符号化はどのようなデータ列にも適用が可能なので、「ランレングス法」と「PIC 圧縮法」などで圧縮したバイト列をさらに「ハフマン符号化」で圧縮してしまうようなことは簡単にできます。実際、他の圧縮アルゴリズムと組み合わせて使うということが多く、JPEG, MP3, zip, gzip などでも利用されています。
今回は、ハフマン木とその符号表の作成方法について紹介しましたが、次の章ではこの続きとして「ハフマン木の正規化」と「動的ハフマン圧縮」を紹介したいと思います。今回のハフマン圧縮法は「静的ハフマン圧縮」と呼ばれ、はじめにハフマン木を作成してからデータの変換を行う手法になるのですが、「動的ハフマン圧縮」ではデータの処理とハフマン木の更新を並行して行うため、符号表が不要になります。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |