曲線描画

(2) ベジェ曲線

前回は、多項式を使って曲線を描画する方法を検討し、最終的にスプライン曲線を利用した描画処理までを実装してみました。今回は、より洗練された手法として「ベジェ曲線(Bézier Curve)」を紹介したいと思います。

(注) 数式などの記法について (ドキュメントの中で使用している数式の表現方法に関する注意点です)

1) ブレンディング関数 (Blending Function)

前回、パラメトリック方程式を利用した曲線の描画方法を紹介しました。X, Y 座標それぞれを変数 t の関数として別々に定義して、t の値を変化させながら座標値を求めるという手法です。この時は、与えられた点を通る多項式を連立方程式によって求めていましたが、関数の決め方には他にもいろいろな方法が考えられます。そこで、「ブレンディング関数 (Blending Function)」というパラメトリック方程式を定義して、その種類を変えることによって、与えられた点に対する様々な曲線を描画するようにします。点列 Pk ( k = 0, 1, ... N ) に対し、ブレンディング関数を fk(t) として、曲線の軌跡 P(t) を以下の式で求めます。

P(t) = Σk{0→N}( fk(t)・Pk )

Pk は通常、二次元か三次元です。各成分に対し、ブレンディング関数は同じものが使用されます。fk(t) が滑らかな関数なら、得られる軌跡も滑らかな曲線になり、不連続な関数を使えば描画結果も通常は不連続になります。さらに、この関数に対して様々な特性を持たせることで、得られる曲線の特性も変化します。

■ 単位元分割 (Partition Of Unity)

「1 の分割」などの呼ばれ方もありますが、日本語での名称が正確に決まっているわけではないようなので「単位元分割」としています。これは、ブレンディング関数の各 t における和が必ず単位元 1 になるというものです。式で表すと

Σk{0→N}( fk(t) ) = 1

となります。これが成り立つとき、座標系を変換しても曲線の形状が変化しないという特性が得られます。この特性は「アフィン不変性 (Affine Invariance)」と呼ばれています。

P(t) = Σk{0→N}( fk(t)・Pk )

に対し、P'k = MPk + c と変換を行います。M は任意の行列で、回転や拡大・縮小などの座標変換が行われます。また、c は定数ベクトルで平行移動を表します。このような変換を「アフィン変換 (Affine Transformation)」といいます。この時のブレンディング関数による和を P'(t) とすると

P'(t)=Σk{0→N}( fk(t)・P'k )
=Σk{0→N}( fk(t)・( MPk + c ) )
=MΣk{0→N}( fk(t)・Pk ) + Σk{0→N}( fk(t)・c )
=MP(t) + cΣk{0→N}( fk(t) )

と計算できます。Σk{0→N}( fk(t) ) は通常 t を変数とする関数となるので、変換後の曲線の形状はこの関数によって変化します。しかし Σk{0→N}( fk(t) ) = 1 が成り立てば

P'(t) = MP(t) + c

となり、アフィン変換後の点列から求めた曲線と、曲線を求めてからアフィン変換を行った結果は等しくなります。

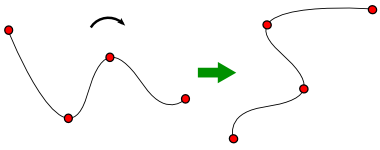アフィン不変性
図 1-1. アフィン不変性

この特性は、特にベクタ・グラフィック (座標でグラフィックを管理するタイプの画像) 用のエディタなどで、点列を指定して曲線を表現する場合に重要になります。点列を指定した後、その全体をアフィン変換したい時、元の曲線の形状から変化しないことは必須の条件となるからです。

■ 凸閉包性 (Convex Hull Property)

単位元分割の性質を持ったブレンディング関数に対し、各関数が任意の t に対しゼロまたは正値である場合、曲線は「凸閉包性 (Convex Hull Property)」を持ちます。凸閉包性とは、各点を頂点とする多角形(ポリゴン)が凸多角形 (内角が 180 度を超える頂点がない多角形) ならば、その内部に必ず曲線が入るという特性です。

まず、各点の X 座標を Xk ( k = 0, 1, ... N ) とし、その最小値を mx とします。ブレンディング関数 fk(t) が単位元分割で、任意の t に対して fk(t) ≥ 0 のとき、曲線上の X 座標 X(t) は、

P(t)=Σk{0→N}( fk(t)・Xk )
≥Σk{0→N}( fk(t)・mx )
=mxΣk{0→N}( fk(t) )
=mx

となります。これは Y 座標も同様に成りたちます。また、同じ考え方によって、曲線の座標が点列の中の最大値以下になることも示すことができます。つまり、点列の最小値と最大値によって囲まれる矩形の内部に曲線が入ることになります。ブレンディング関数が単位元分割ならばアフィン不変性が成り立つので、特に回転に対して曲線の形状が変化することはありません。そこで、点列から成る多角形のある一辺が、X 座標が等しくなるように (つまり垂直な辺になるように)、さらに X 座標が一番小さくなるように回転すると、この場合も先程の内容は成り立つので、その辺を曲線が超えることはありません。各辺に対しても同様なことが成り立つので、多角形の内部から曲線が外側にはみ出てしまうことはないことになります。但し、内角が 180 度を超えるような頂点がある場合は成り立たない場合が生じます。この時は、凹になったところをスキップして点を結んだ時の多角形の内部に曲線が入る形になります。

凸閉包性
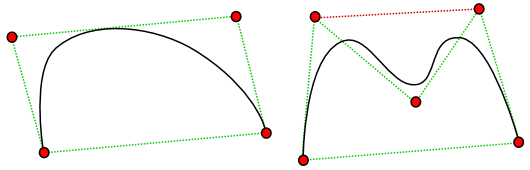図 1-2. 凸閉包性

凸閉包性が成り立つ場合、点列が直線上にあれば、曲線がその直線からはみ出ることがないことを意味するので、直線に変換されることになります。実際、点列 { ( xk, yk ) } ( k = 0, 1, ... N ) が直線 y = px + q 上にあるとき、曲線 ( X(t), Y(t) ) の Y 座標成分 Y(t) は

Y(t)=Σk{0→N}( yk・fk(t) )
=Σk{0→N}( ( pxk + q )・fk(t) )
=pΣk{0→N}( xk・fk(t) ) + qΣk{0→N}( fk(t) )
=pX(t) + q

なので、直線になることが示されます。ここでは単位元分割の性質だけを使って示しているので、ブレンディング関数が常に正値でなくとも直線になることは成り立ちますが、点列からなる線分の中に収まるためには正値である必要があります。

■ 対称性 (Symmetry)

次の式が成り立つ場合、点列を逆側からたどっても曲線の形状は変わりません。但し、変数 t の定義域は 0 ≤ t ≤ 1 としています。

fk(t) = fN-k( 1 - t )

パラメトリック方程式

P(t) = Σk{0→N}( fk(t)・Pk )

に対し、先ほどの等式が成り立つとすれば、

P(t)=Σk{0→N}( fN-k( 1 - t )・Pk )
=Σk{0→N}( fk( 1 - t )・PN-k )

となります。つまり、点列と t をどちらも逆順にたどっても (但し、ブレンディング関数の添字はそのままです) 曲線に変化はないことを意味するので、結果として曲線は対称性を持つことになります。定義域が t0 ≤ t ≤ t1 ならば、

fk(t) = fN-k( t0 + t1 - t )

を満たせば対称性が得られます。ここで注意点ですが、曲線自体が対称になるわけではありません。点列を逆からたどっても曲線が変化しないという意味であることに注意してください。

■ 変動減少特性 (Variation Diminishing Property)

「変動減少特性 (Variation Diminishing Property)」とは、点列をその順番に線分で結んで得られる折れ線と、その点列から得られた曲線に対して、任意の直線との交点を数えた時、曲線との交点数が必ず折れ線との交点数以下になる性質のことを意味します。この条件を満たす曲線は非常に少なく、今回紹介するベジェ曲線や、B-スプライン曲線などが該当します。

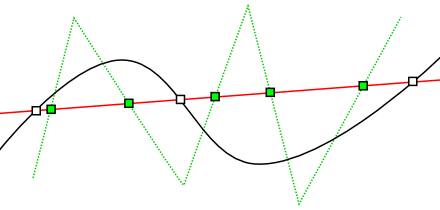変動減少特性
図 1-3. 変動減少特性

変動減少特性は、平たく言えば点列が激しく変動していてもそれを抑えこむことができることを意味します。多項式を利用した曲線描画のときのように意図しない方向へ曲線が描画されてしまうことが少なくなり、激しい凸凹があってもそれを綺麗にならすことができるので、これは非常に有用な性質の一つです。

■ 線形独立 (Linear Independence)

ブレンディング関数が線形独立の関係にあるとき、この関数は「基底関数」と考えることができます。曲線の軌跡は、各点列を係数としたブレンディング関数による線形結合の形で表現されています。ブレンディング関数が線形独立でない場合、ある曲線を表現するための点列の組は無数に存在することになります。例えば、ブレンディング関数を

f0(t) = t + 1
f1(t) = 2t + 2

の二種類とした時、この二つは線形独立ではありません。この二式を使って b(t) = 4t + 4 を表したい場合、

b(t)=af0(t) + bf1(t)
=a( t + 1 ) + b( 2t + 2 )
=( a + 2b )t + ( a + 2b )
=4t + 4

より a + 2b = 4 という式がただ一つだけ得られます。このような数の組 ( a, b ) は無数にあり、一つに決めることはできません。しかし、f0(t) = t とすれば二式は線形独立となり、a, b を求める連立方程式は

a + 2b = 4
2b = 4

なので、解は ( a, b ) = ( 0, 2 ) の一つだけが得られます。この例において、a, b が点列の座標を意味するので、ある式を決める点列が無数にあるということがこれで理解できると思います。

基底関数については、次の章でもう少し詳しく説明します。

■ 端点通過 (Endpoint Interpolation)

点列の始点と終点を曲線が必ず通るという特性です。曲線の軌跡は、ブレンディング関数を各点で重み付けして和を計算した結果に過ぎないので、各点を曲線が通るという保証はありません。t の定義域が 0 ≤ t ≤ 1 のとき、曲線が各点を通ることを保証するためには、

fk( k / N ) = 1
fj( k / N ) = 0 ( j ≠ k )

である必要があります。しかし、これは条件としては厳しすぎるので、端点のみに限定をすれば、

f0( 0 ) = 1
fj( 0 ) = 0 ( j > 0 )

fN( 1 ) = 1
fj( 1 ) = 0 ( j < N )

を満たせば成り立ちます。定義域を任意 ( t0 ≤ t ≤ t1 ) とした場合は、

f0( t0 ) = 1
fj( t0 ) = 0 ( j > 0 )

fN( t1 ) = 1
fj( t1 ) = 0 ( j < N )

がその条件になります。

2) バーンスタイン多項式 (Bernstein Polynomial)

多項式 f(t) = Σk{0→N}( aktk ) = a0 + a1t + ... + aNtN は、係数 a = ( a0, a1, a2, ... aN ) を変化させることによって様々な形にすることができます。任意の t に対して f(t) = 0 が成り立つためには、全ての係数 ak がゼロでなければなりません。また、その逆も明らかに成り立ちます。このような関係にあるベクトルは「線形独立」であると言いますが、f(t) を係数 a と t = { 1, t, t2, ... tN } を使った線形結合であると考えれば、t は互いに線形独立なので「基底(Basis)」の一種であると考えることができます。この基底のことを「累乗基底(Power Basis)」といいます。ベクトルではなく変数が基底と考えると変な感じがしますが、全ての実数が並んだ無限の要素を持つベクトルだと考えれば同じようにイメージすることができると思います。その線形結合である f(t) もとうぜん無限の要素を持ち、それぞれがある t の値(要素)に対応していると考えるわけです。

多項式を表現することができる基底としては他にも存在し、その中の一つに「バーンスタイン基底関数(Bernstein Basis Polynomials)」というものがあります。この基底は、次のような関数です。

bk,N(t) = C( N, k )・tk( 1 - t )N-k

但し、k は 0 から N までの範囲の整数値で、それ以外に対しては bk,N(t) = 0 とします。

C( N, k ) は「二項係数 (Binomial Coefficient)」で、下式で表されます。

C( N, k ) = N! / k!( N - k )!

N 個の中から k 個の要素を選択する組み合わせの数はこの値になり、一般的には N と k を縦に並べて括弧で括る形で表されますが、HTML 形式で縦に並べて書くのは非常に大変なので、このような表現方法にしています。

なお、b0,N(0), bN,N(1) は、0 の 0 乗を含みます。この値は不定ですが、00 = 1 としておくと不連続とならず都合がいいので、ここではそのように表します。k や N - k をゼロ固定にして、lim{t→0}( t0 ), lim{t→1}( ( 1 - t )0 ) と考えるわけです。

以下に、N = 1, 2, 3 の場合の bk,N(t) の形を示します。

Nkbk,N(t)
101 - t
1t
20( 1 - t )2
12t( 1 - t )
2t2
30( 1 - t )3
13t( 1 - t )2
23t2( 1 - t )
3t3

この例からも明らかなように、k > 0 ならば bk,N(0) = 0 ( b0,N(0) = 1 ) であり、k < N ならば bk,N(1) = 0 ( bN,N(1) = 1 ) になります。

t を 0 から 1 までの固定値としたとき、バーンスタイン基底関数は「二項分布 (Binomial Distribution)」そのものになります。「二項定理 (Binomial Theorem)」より、

( a + b )N = Σk{0→N}( C( N, k )・akbN-k )

が成り立ち、a = t, b = 1 - t とすれば右辺の和の各項はバーンスタイン基底関数 bk,N(t) そのものになるので、

Σk{0→N}( C( N, k )・tk( 1 - t )N-k ) = [ t + ( 1 - t ) ]N = 1

つまり、任意の t に対し、Σk{0→N}( bk,N(t) ) = 1 が成り立つことになります。また、0 < t < 1 ならば C( N, k ) > 0, t > 0, 1 - t > 0 なので bk,N(t) > 0 が成り立ちます。したがって、bk,N(t) は 0 < t < 1 のとき確率密度関数として成り立つことになるわけです。

二項係数については、以下の関係式が成り立つのでした。

C( N, k ) = C( N - 1, k - 1 ) + C( N - 1, k )

この式をバーンスタイン基底関数の定義式に代入すると、

bk,N(t)=C( N, k )・tk( 1 - t )N-k
=[ C( N - 1, k - 1 ) + C( N - 1, k ) ]・tk( 1 - t )N-k
=t・C( N - 1, k - 1 )・tk-1( 1 - t )(N-1)-(k-1) + ( 1 - t )・C( N - 1, k )・tk( 1 - t )(N-1)-k
=t・bk-1,N-1(t) + ( 1 - t )・bk,N-1(t)

という関係式が得られ、この式を使って再帰的にバーンスタイン基底関数を求めることができます。また、

t・bk,N-1(t)=C( N - 1, k )・tk+1( 1 - t )(N-1)-k
={ ( N - 1 )! / k!・[ ( N - 1 ) - k ]! }・tk+1( 1 - t )N-(k+1)
=[ ( k + 1 ) / N ]・{ N! / ( k + 1 )!・[ N - ( k + 1 ) ]! }・tk+1( 1 - t )N-(k+1)
=[ ( k + 1 ) / N ]・C( N, k + 1 )・tk+1( 1 - t )N-(k+1)
=[ ( k + 1 ) / N ]・bk+1,N(t)
( 1 - t )・bk,N-1(t)=C( N - 1, k )・tk( 1 - t )(N-1)-k+1
={ ( N - 1 )! / k!・[ ( N - 1 ) - k ]! }・tk( 1 - t )N-k
=[ ( N - k ) / N ]・[ N! / k!・( N - k )! ]・tk( 1 - t )N-k
=[ ( N - k ) / N ]・C( N, k )・tk( 1 - t )N-k
=[ ( N - k ) / N ]・bk,N(t)

より、二式を辺々加えると

t・bk,N-1(t) + ( 1 - t )・bk,N-1(t)=bk,N-1(t)
=[ ( k + 1 ) / N ]・bk+1,N(t) + [ ( N - k ) / N ]・bk,N(t)

となって、最大次数 N を下げる方向へバーンスタイン基底関数を再帰的に求めることも可能です。この式は、

tk( 1 - t )N-k + tk+1( 1 - t )N-(k+1)=tk( 1 - t )N-(k+1)[ ( 1 - t ) + t ]
=tk( 1 - t )(N-1)-k

より、左辺の第一項が bk,N(t) / C( N, k )、第二項が bk+1,N(t) / C( N, k + 1 )、右辺が bk,N-1(t) / C( N - 1, k ) であることを利用して、

bk,N(t) / C( N, k ) + bk+1,N(t) / C( N, k + 1 ) = bk,N-1(t) / C( N - 1, k )

という形で表すこともできます。

バーンスタイン基底関数 bk,N(t) は明らかに最大次数 N の多項式です。bk,N(t) を累乗基底の形に変換した時、係数がどのようになるかを求めてみます。

bk,N(t)=C( N, k )tk( 1 - t )N-k
=C( N, k )tkΣi{0→N-k}( C( N - k, i )・(-t)i )
=C( N, k )tkΣi{k→N}( (-1)i-k・C( N - k, i - k )・ti-k )
=Σi{k→N}( (-1)i-k・C( N, k )・C( N - k, i - k )・ti )

ここで、

C( N, k )・C( N - k, i - k )=[ N! / k!・( N - k )! ][ ( N - k )! / ( i - k )!・( N - i )! ]
=N! / k!・( i - k )!・( N - i )!
=N!・i! / k!・( i - k )!・i!・( N - i )!
=[ N! / i!・( N - i )! ][ i! / k!・( i - k )! ]
=C( N, i )・C( i, k )

なので、

bk,N(t) = Σi{k→N}( (-1)i-k・C( N, i )・C( i, k )・ti )

となって、k より低次項の係数はゼロ、それ以上の次数の項の係数は (-1)i-k・C( N, i )・C( i, k ) で表されます。逆に、累乗基底 ti ( i ≤ N ) を bk,N(t) の線形結合を使って表すとどのようになるでしょうか。例えば N = 3 のときの t の表し方を考えると、一次項 t は、高次側から見て b1,3(t) で初めて発生するので ( bk,N(t) が tk を掛けた形になっているので、各項の次数は必ず k 以上になります )、b3,3(t), b2,3(t), b1,3(t) に適当な係数を掛けて和を計算すると、

Ab3,3(t) + Bb2,3(t) + Cb1,3(t)
=At3 + 3Bt2( 1 - t ) + 3Ct( 1 - t )2
=( A - 3B + 3C )t3 + ( 3B - 6C )t2 + 3Ct

になります。C = 1 / 3 とすれば、t の係数は 1 となり、B = 2 / 3, A = 1 で他の項の係数はゼロになるので、

t = b3,3(t) + ( 2 / 3 )b2,3(t) + ( 1 / 3 )b1,3(t)

になります。累乗基底の形に表した時、一番次数の低い項は係数が一つのみ、次に次数の低い項は係数二つ、という具合に未知数は一つずつ増えていくので ( これも、bk,N(t) が k 以上の項しか持たないことから明らかです )、全ての係数は一意に決めることができます。この結果を見ると、ti は bi,N(t) から bN,N(t) までの線形結合で表すことができて、bi,N(t) の係数を ai とすると ai = 1 / C( N, i ) である ( bi,N(t) = C( N, i )・ti( 1 - t )N-i の ti の係数は明らかに C( N, i ) です ) ことは簡単に理解できます。bi+1,N(t) の係数 ai+1 は、bi+1,N(t) の ti+1 成分に対する係数が C( N, i + 1 ) であり、bi,N(t) の ti+1 成分に対する係数が ( -1 )・C( N, i )・C( N - i, 1 ) であることから

C( N, i + 1 )ai+1 - C( N, i )・C( N - i, 1 )ai = 0

から求められて

ai+1 = [ C( N, i )・C( N - i, 1 )ai ] / C( N, i + 1 ) = C( N - i, 1 ) / C( N, i + 1 )

になります。これを繰り返すと全ての係数を求めることができます。この一般式は

ti = Σk{i→N}( [ C( k, i ) / C( N, i ) ]bk,N(t) )

であり、実際にこれが成り立つとすると、

ti+1=t・Σk{i→N}( [ C( k, i ) / C( N, i ) ]bk,N(t) )
=Σk{i→N}( [ C( k, i ) / C( N, i ) ]・C( N, k )・tk+1( 1 - t )N-k )
=Σk{i→N}( [ C( k, i ) / C( N, i ) ]・[ ( k + 1 ) / ( N + 1 ) ]・C( N + 1, k + 1 )・tk+1( 1 - t )(N+1)-(k+1) )
=Σk{i→N}( [ C( k, i ) / C( N, i ) ]・[ ( k + 1 ) / ( N + 1 ) ]・bk+1,N+1(t) )

ここで、

[ C( k, i ) / C( N, i ) ]・[ ( k + 1 ) / ( N + 1 ) ]=[ k!・( k + 1 ) / i!・( k - i )! ] / [ N!・( N + 1 ) / i!・( N - i )! ]
=[ ( k + 1 )! / i!・( i + 1 )・( k - i )! ] / [ ( N + 1 )! / i!・( i + 1 )・( N - i )! ]
={ ( k + 1 )! / ( i + 1 )!・[ ( k + 1 ) - ( i + 1 ) ]! }
 / { ( N + 1 )! / ( i + 1 )!・[ ( N + 1 ) - ( i + 1 ) ]! }
=C( k + 1, i + 1 ) / C( N + 1, i + 1 )

なので、

ti+1 = Σk{i→N}( [ C( k + 1, i + 1 ) / C( N + 1, i + 1 ) ]・bk+1,N+1(t) )

になります。よって、Σk{i→N}( [ C( k, i ) / C( N, i ) ]bk,N(t) ) に対して i → i + 1, N → N + 1、つまり和を計算する初期・末尾の添字を一つ多くすればよいことになります。t0 = 1 = Σk{0→N}( [ C( k, 0 ) / C( N, 0 ) ]・bk,N(t) ) は任意の N に対して常に成り立つので、帰納法によって、先ほど示した式が正しいことが証明されます。ちなみに、例で示した係数が異なるように見えますが、

C( N - i, 1 ) / C( N, i + 1 )=[ ( N - i )! / 1!・( N - i - 1 )! ] / [ N! / ( i + 1 )!・( N - i - 1 )! ]
=[ ( i + 1 )! / 1! ] / [ N! / ( N - i )! ]
=[ ( i + 1 )! / i!・1! ] / [ N! / i!・( N - i )! ]
=C( i + 1, i ) / C( N, i )

となるので内容は等しくなっています。

最後に、バーンスタイン基底関数の導関数を計算してみます。

dbk,N(t) / dt=C( N, k )[ ktk-1( 1 - t )N-k - ( N - k )tk( 1 - t )N-k-1 ]
=[ N!・k / k!・( N - k )! ]tk-1( 1 - t )N-k - [ N!・( N - k ) / k!・( N - k )! ]tk( 1 - t )N-k-1
=[ ( N - 1 )!・N / ( k - 1 )!・( N - k )! ]tk-1( 1 - t )N-k - [ ( N - 1 )!・N / k!・( N - k - 1 )! ]tk( 1 - t )N-k-1
=N・C( N - 1, k - 1 )・tk-1( 1 - t )N-k - N・C( N - 1, k )・tk( 1 - t )N-k-1
=N・[ bk-1,N-1(t) - bk,N-1(t) ]

この結果からわかるように、バーンスタイン基底関数の導関数は次数を一つ下げたバーンスタイン基底関数の線形結合で表されます。さらに二階導関数を求めると

d2bk,N(t) / dt2=N・[ dbk-1,N-1(t) / dt - dbk,N-1(t) / dt ]
=N・{ ( N - 1 )[ bk-2,N-2(t) - bk-1,N-2(t) ] - ( N - 1 )[ bk-1,N-2(t) - bk,N-2(t) ] }
=N( N - 1 )[ bk-2,N-2(t) - 2bk-1,N-2(t) + bk,N-2(t) ]

となります。三階導関数は

d3bk,N(t) / dt3=N( N - 1 )[ dbk-2,N-2(t) / dt - 2dbk-1,N-2(t) / dt + dbk,N-2(t) / dt ]
=N( N - 1 )( N - 2 ){ [ bk-3,N-3(t) - bk-2,N-3(t) ] - 2[ bk-2,N-3(t) - bk-1,N-3(t) ] + [ bk-1,N-3(t) - bk,N-3(t) ] }
=N( N - 1 )( N - 2 )[ bk-3,N-3(t) - 3bk-2,N-3(t) + 3bk-1,N-3(t) - bk,N-3(t) ]

となって、ちょうど二項定理によく似た形を得ることができます。この結果から、m 階導関数は

dmbk,N(t) / dtm = [ N! / ( N - m )! ]Σi{0→m}( ( -1 )m-iC( m, i )bk-i,N-m(t) )

であることが予想できて、これが成り立つ場合、m + 1 階導関数は

dm+1bk,N(t) / dtm+1=[ N! / ( N - m )! ]Σi{0→m}( ( -1 )m-iC( m, i )dbk-i,N-m(t) / dt )
=[ N! / ( N - m )! ]( N - m )Σi{0→m}( ( -1 )m-iC( m, i )[ bk-i-1,N-m-1(t) - bk-i,N-m-1(t) ] )
=[ N! / ( N - m - 1 )! ]{ Σi{0→m}( ( -1 )m-iC( m, i )bk-(i+1),N-m-1(t) ) - Σi{0→m}( ( -1 )m-iC( m, i )bk-i,N-m-1(t) ) }
=[ N! / ( N - m - 1 )! ]{ Σi{1→m+1}( ( -1 )m-i+1C( m, i - 1 )bk-i,N-m-1(t) ) + Σi{0→m}( ( -1 )m-i+1C( m, i )bk-i,N-m-1(t) ) }
=[ N! / ( N - m - 1 )! ]{ Σi{1→m}( ( -1 )m-i+1[ C( m, i - 1 ) + C( m, i ) ]bk-i,N-m-1(t) ) + ( -1 )m+1C( m, m )bk-m-1,N-m-1(t) + ( -1 )0C( m, 0 )bk,N-m-1(t) }

ここで、

C( m, i - 1 ) + C( m, i )=m! / ( i - 1 )!( m - i + 1 )! + m! / i!( m - i )!
=[ i・m! + ( m - i + 1 )・m! ] / i!( m - i + 1 )!
=( m + 1 )! / i!( m + 1 - i )!
=C( m + 1, i )

が成り立ち、C( m, m ) = C( m + 1, m + 1 ) = 1、C( m, 0 ) = C( m + 1, 0 ) = 1 なので、

dm+1bk,N(t) / dtm+1 =[ N! / ( N - m - 1 )! ]Σi{0→m+1}( ( -1 )m-i+1C( m + 1, i )bk-i,N-m-1(t) )

となって、帰納法により成り立つことが証明できます。

以上、バーンスタイン基底関数の特徴をまとめておきます。

■ バーンスタイン基底関数の定義
bk,N(t) = C( N, k )・tk( 1 - t )N-k
■ bk,N(0)=0( k > 0 )
=1( k = 0 )
bk,N(1)=0( k < N )
=1( k = N )
■ バーンスタイン基底関数の和
Σk{0→N}( bk,N(t) ) = 1
■ 正値性
0 < t < 1 ならば bk,N(t) > 0
■ 次数の繰り上げ(漸化式)
bk,N(t) = t・bk-1,N-1(t) + ( 1 - t )・bk,N-1(t)
■ 次数の繰り下げ
bk,N-1(t) = [ ( k + 1 ) / N ]・bk+1,N(t) + [ ( N - k ) / N ]・bk,N(t)
■ バーンスタイン基底関数の累乗基底による表現
bk,N(t) = Σi{k→N}( (-1)i-k・C( N, i )・C( i, k )・ti )
■ 累乗基底のバーンスタイン基底関数による表現
ti = Σk{i→N}( [ C( k, i ) / C( N, i ) ]bk,N(t) )
■ 導関数
dbk,N(t) / dt = N( bk-1,N-1(t) - bk,N-1(t) ) (一階導関数)
dmbk,N(t) / dtm = [ N! / ( N - m )! ]Σi{0→m}( ( -1 )m-iC( m, i )bk-i,N-m(t) ) (高階導関数)

累乗基底が互いに線形独立であるように、バーンスタイン基底関数も線形独立の関係にあり、基底としての条件を満たしています。

BN(t) = Σk{0→N}( ak・bk,N(t) )

としたとき、これを累乗基底の線形結合の形に表すと、

BN(t)=Σk{0→N}( ak・bk,N(t) )
=Σk{0→N}( ak・Σi{k→N}( (-1)i-k・C( N, i )・C( i, k )・ti ) )
=a0 + Σk{0→1}( ak・(-1)1-k・C( N, 1 )・C( 1, k )・t ) + ...
 + Σk{0→N}( ak・(-1)N-k・C( N, N )・C( N, k )・tN )

となります。任意の t に対して BN(t) = 0 が成り立つためには

a0 = 0
Σk{0→1}( ak・(-1)1-k・C( N, 1 )・C( 1, k )・t ) = 0
 :
Σk{0→N}( ak・(-1)N-k・C( N, N )・C( N, k )・tN ) = 0

となる必要があり、最初の式 a0 = 0 をその下に代入することで a1 = 0 が得られ、その操作を繰り返すことで最終的に 0 ≤ k ≤ N において ak = 0 であることが示され、バーンスタイン基底関数も基底として利用できるという事になります。この関数を「バーンスタイン多項式 ( Bernstein Polynomial )」といいます。以下、バーンスタイン基底関数を累乗基底と同じような形で表すため bNk と表す場合があります。

t を 0 ≤ t ≤ 1 の範囲で固定した時、バーンスタイン多項式は二項分布による各係数の期待値と同じ意味になります。係数の最大値を M、最小値を m とした時、

BN(t) ≤ MΣk{0→N}( bNk ) = M

BN(t) ≥ mΣk{0→N}( bNk ) = m

より m ≤ B(t) ≤ M となります (これは任意の k に対して bNk ≥ 0 ( 0 ≤ t ≤ 1 ) なので成り立つということに注意が必要です)。

係数を、0 ≤ u ≤ 1 の定義域の関数 f(u) とします。u = k / N における N 個の関数値に対する期待値は

Σk{0→N}( f( k / N )・bNk )

と表されます。このような計算は「加重和・重み付け和 ( Weighted Sum )」という操作になり、bk,N(t) を「加重関数・重み付け関数 ( Weight Function )」と呼ばれる、各関数値に重み付けをする関数とみなして積和を求めることを意味しています。こうして求められる和が f( k / N ) の最大・最小値を超えないことは先ほど示したとおりです。よって、N を大きくするほど f(t) の値域に近い値が f( k / N ) に含まれる可能性は大きくなり、f(t) の値域から大きく外れる部分が含まれる可能性は小さくなります。以下、この加重和を BNf(t) と表します。

bk,N(t) は、t を固定して k を確率変数とすると二項分布そのものなので、その期待値は Nt になります。t が 0 から 1 まで変化するとき、期待値も 0 から N まで変化します。t = k / N のとき期待値は k になり、そのときの BNf(t) は f( k / N ) 付近の値の重み付けが大きいことになります。BNf(0) = f(0)、BNf(1) = f(1) であることは簡単に示すことができるので、100% f(0) で重み付けされた状態から始まり、徐々に値の大きな t に対する f(t) に対する比率を増やしながら推移して、t = 1 において 100% f(1) で重み付けされた状態になります。

ここで注意しなければならないのは、BNf(t) が f(t) の補間関数となるわけではないということです。すなわち、サンプル点 k / N において BNf( k / N ) = f( k / N ) が成り立つわけではありません。これは、t = k / N において f( k / N ) によって 100% 重み付けされるわけではないことから容易に理解できます。また、f(t) が多項式であったとしても、次数が異なれば常に BNf(t) = f(t) となるわけでもありません。例えば、f(t) = t2 に対して N = 3 のバーンスタイン基底関数を使って加重和を計算すると、

B3f(t)=Σk{0→3}( ( k / 3 )2・b3k )
=( 1 / 9 )b31 + ( 4 / 9 )b32 + b33
=t( 1 - t )2 / 3 + 4t2( 1 - t ) / 3 + t3
=t[ ( 1 - 2t + t2 ) + 4( t - t2 ) + 3t2 ] / 3
=t( 1 + 2t ) / 3

となって一致しません。しかし、N を任意としたとき、

BNf(t)=Σk{0→N}( ( k / N )2・bNk )
=Σk{1→N}( ( k / N )2・C( N, k )tk( 1 - t )N-k )
=Σk{0→N-1}( [ ( k + 1 ) / N ]2・C( N, k + 1 )tk+1( 1 - t )N-k-1 )
=tΣk{0→N-1}( [ ( k + 1 ) / N ]・C( N - 1, k )tk( 1 - t )N-k-1 )
=( t / N ){ Σk{0→N-1}( k・bN-1k ) + Σk{0→N-1}( bN-1k ) }
=( t / N )[ ( N - 1 )t + 1 ]
=t2 + t( 1 - t ) / N

となります。但し、Σk{0→N-1}( k・bN-1k ) = ( N - 1 )t は、bN-1k が t を固定したとき二項分布そのものであり、左辺がその平均を表すことから成り立ちます。N を大きくすると二項めはどんどんと小さくなり、N → ∞ ではゼロに収束するため、極限においては lim{N→∞}( BNf(t) ) = t2 が成り立ちます。実際には、0 ≤ t ≤ 1 を定義域とする任意の f(t) に対し、lim{N→∞}( BNf(t) ) = f(t) が成り立ちます。つまり、BNf(t) は N を大きくすることでいくらでも任意の f(t) に近づけることができることになります(補足 1)。

バーンスタイン基底関数を使って、任意の数列から多項式を求めるサンプル・プログラムを以下に示します。

/**********************************************************
  BernsteinPolynomial : Bernstein多項式
**********************************************************/
class BernsteinPolynomial
{
  unsigned int n_;          // 次数
  vector<double> binCoeff_; // 二項係数 ( 0-n_ までの n_+1 個 )

  // 階乗 k! を求める
  static double fact( unsigned int k );
  // 二項係数 C( n, k ) を求める
  static double calcBinCoeff( unsigned int k, unsigned int n );

 public:

  /*
    コンストラクタ

    unsigned int n : 次数
  */
  BernsteinPolynomial( unsigned int n )
  { reset( n ); }

  // 二項係数の再計算
  void reset( unsigned int n );

  /*
    Bernstein基底関数 b( t; k, n_ ) の値を求める

    unsigned int k : パラメータ k
    double t : 変数 t

    戻り値 : 計算結果
  */
  double operator()( unsigned int k, double t )
  { return( ( k > n_ ) ? 0 : binCoeff_[k] * pow( t, k ) * pow( 1 - t, n_ - k ) ); }
};

/*
  BernsteinPolynomial::reset : 二項係数の再計算

  unsigned int n : 次数
*/
void BernsteinPolynomial::reset( unsigned int n )
{
  n_ = n;
  binCoeff_.resize( n_ + 1 );
  for ( unsigned int k = 0 ; k <= n_ ; ++k )
    binCoeff_[k] = calcBinCoeff( k, n_ );
}

/*
  BernsteinPolynomial::fact : 階乗 k! を求める

  計算には Stirling の公式を利用

  k! = sqrt( 2πk )・pow( k / e, k )・exp( 1 / 12k - 1 / 360pow( k, 3 ) + 1 / 1260pow( k, 5 ) )

  unsigned int k : k の値

  戻り値 : 階乗 k!
*/
double BernsteinPolynomial::fact( unsigned int k )
{
  if ( k == 0 ) return( 1 ); // 0! = 1
  if ( k <= 2 ) return( k ); // 1! = 1, 2! = 2

  double d = k;
  double ne = sqrt( 2 * M_PI * d ) * pow( ( d / exp( 1 ) ), d );

  return( ne * exp( 1 / ( 12 * d ) - 1 / ( 360 * pow( d, 3 ) ) + 1 / ( 1260 * pow( d, 5 ) ) ) );
}

/*
  BernsteinPolynomial::calcBinCoeff : 二項係数 C( n, k ) を求める

  unsigned int k : k の値
  unsigned int n : n の値

  戻り値 : 二項係数 C( n, k )
*/
double BernsteinPolynomial::calcBinCoeff( unsigned int k, unsigned int n )
{
  if ( n < k ) return( 0 );    // n < k なら C( n, k ) = 0
  if ( k == 0 ) return( 1 );    // C( n, 0 ) = 1
  if ( k == 1 ) return( n );   // C( n, 1 ) = n

  return( fact( n ) / ( fact( k ) * fact( n - k ) ) );
}

/*
  CalcBernsteinPolynomial : バーンスタイン多項式の値を計算する

  const vector<double>& x : バーンスタイン係数
  double t : 関数に代入する値

  戻り値 : 計算結果
*/
double CalcBernsteinPolynomial( const vector<double>& x, double t )
{
  if ( x.size() == 0 ) return( 0 );

  // バーンスタイン基底関数の次数 n は、区間の数 (数列の数 - 1)
  unsigned int n = x.size() - 1;

  BernsteinPolynomial bp( n );

  double d = 0; // 計算結果
  for ( unsigned int k = 0 ; k <= n ; ++k )
    d += bp( k, t ) * x[k];

  return( d );
}

BernsteinPolynomial はバーンスタイン多項式 ( 正確にはバーンスタイン基底関数 ) の値を計算するためのクラスです。オブジェクト構築時に次数を指定することで先に二項係数の部分を計算しておき、t から基底関数の値を求めるときに毎回計算し直す必要がないようにしています。メンバ関数の fact は階乗を計算するために利用しますが、この計算には「スターリングの公式 (Stirling's Formula)」を利用して近似値計算を行っています。CalcBernsteinPolynomial 関数は、BernsteinPolynomial オブジェクトを利用して、与えられた数列を係数とするバーンスタイン多項式の値を求めるためのもので、t を変化させながら逐次計算させることで多項式のグラフを得ることができます。

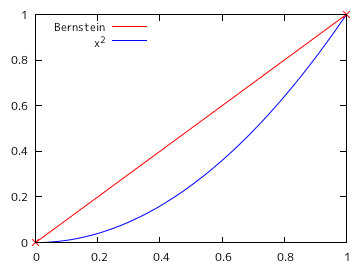
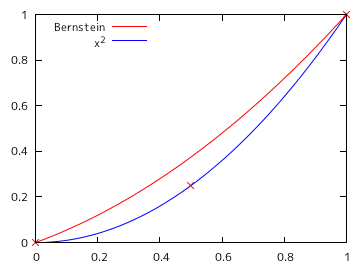
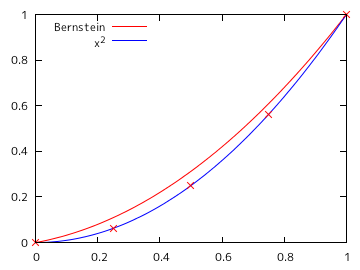
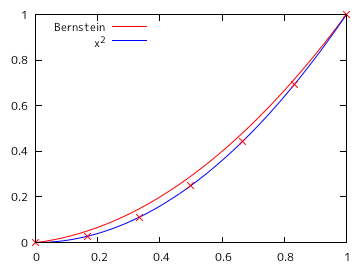
サンプル・プログラムを使って、f(x) = x2 から等間隔に N 個 ( N = 2, 3, 5, 7, 10, 20 ) の点列を抽出し、その値を係数にバーンスタイン多項式を求めた時のグラフを以下に示します。横軸の定義域は 0 から 1 までとし、0.01 刻みで値を計算しています。グラフの赤線はバーンスタイン多項式、青線は x2 を表し、×で示された点は抽出したポイントを示しています。

図 2-1. バーンスタイン多項式のグラフ
N = 2N = 3
N=2N=3
N = 5N = 7
N=5N=7
N = 10N = 20
N=10N=20

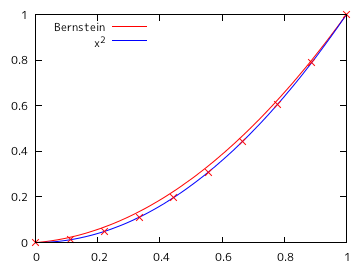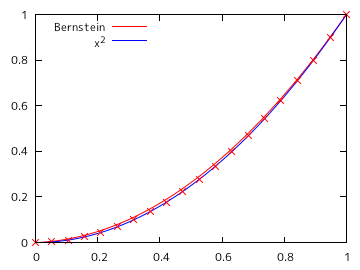N = 2 の時は、多項式は直線になっています。また、次数を大きくすると、元の曲線に近づく様子がこの結果からわかります。

3) ベジェ曲線 (Bézier Curve)

自動車などの工業製品をデザインする際、コンピュータを用いて設計を行うためのソフトウェアとして「CAD (Computer Aided Design)」が誕生しました。工業製品のデザインには任意の曲線や曲面を描画する必要があり、その研究は 1950 年代頃から始まったと言われています。その中で誕生したのが「ベジェ曲線 (Bézier Curve)」で、ブレンディング関数としてバーンスタイン基底関数を使った曲線です。

自動車メーカーのシトロエン社とルノー社は、それぞれ独立にベジェ曲線を考案しましたが、それが公表されたのは 1960 年代後半になってからで、それまでは企業秘密とされていたようです。シトロエン社でベジェ曲線を考案したのはフランスの物理数学者「ド・カステリョ (Paul de Casteljau)」で、その発案はルノー社よりも早かったのですが、公表したのはルノー社の方が先だったために、曲線の名前はルノー社のエンジニア「ピエール・ベジェ (Pierre Bézier)」から付けられています。ベジェによってベジェ曲線が公表されたのは 1962 年ですが、ド・カステリョは 1959 年に発案をしています。しかし、それがルノー社によって公表されたのは 1974 年で、発案から 15 年も後のことでした。

N + 1 個の点列 { Pk } ( k = 0, 1, ... N ) に対し、ベジェ曲線 P(t) は以下の式で表されます。

P(t) = Σk{0→N}( Pk・bk,N(t) )

ここで、bk,N(t) はバーンスタイン基底関数を表します。バーンスタイン基底関数の性質から、ベジェ曲線は以下の特性を持っています。

  1. アフィン不変性である
  2. 凸閉包性である
  3. 点列を逆からたどっても曲線は変化しない
  4. 変動減少特性がある
  5. 点列が直線上にあればベジェ曲線も直線になる
  6. 端点を必ず通過する
  7. 端点で接線となる

「アフィン不変性」と「凸閉包性」は、バーンスタイン基底関数が単位元分割であり正値であることから導かれます。また、点列を逆からたどっても曲線が変化しないことは、バーンスタイン基底関数の対称性から得られる特性です。

bN-k,N(1 - t)=C( N, N - k )・( 1 - t )N-ktN-(N-k)
=C( N, k )・tk( 1 - t )N-k
=bk,N(t)

より、バーンスタイン基底関数の対称性が証明できます。但し、ここで C( N, N - k ) = C( N, k ) を利用しています (*3-1)。

「端点で接線となる」というのは、点列からなるベクトル P1 - P0 と PN - PN-1 が、それぞれベジェ曲線の始点・終点の接線方向を指すことを意味します。バーンスタイン基底関数の導関数は

dbk,N(t) / dt=N・C( N - 1, k - 1 )・tk-1( 1 - t )N-k - N・C( N - 1, k )・tk( 1 - t )N-k-1( 0 < k < N )
=-N( 1 - t )N-1( k = 0 )
=NtN-1( k = N )

なので、t = 0 のとき

dbk,N(0) / dt=0( 1 < k ≤ N )
=N( k = 1 )
=-N( k = 0 )

であり、t = 1 のとき、

dbk,N(1) / dt=0( 0 ≤ k < N - 1 )
=-N( k = N - 1 )
=N( k = N )

です。従って、t = 0, 1 でのベジェ関数の導関数の値は

dP(0) / dt=Σk{0→N}( Pk・dbk,N(0) / dt )
=N( P1 - P0 )
dP(1) / dt=Σk{0→N}( Pk・dbk,N(1) / dt )
=N( PN - PN-1 )

になります。dP(0) / dt, dP(1) / dt はそれぞれ P1 - P0, PN - PN-1 の N 倍なので、向きは等しいことになります。

ベジェ曲線の軌跡を計算するためのサンプル・プログラムを以下に示します。

/**********************************************************
  BezierCurveBase : ベジェ曲線描画用基底クラス
**********************************************************/
class BezierCurveBase : public ParametricEquation
{
  unsigned int size_;        // 点列のサイズ
  vector<double> x_; // 点列の x 座標
  vector<double> y_; // 点列の y 座標

  // calc : 曲線の X/Y 座標値を計算する(純粋仮想関数)
  virtual double calc( const vector<double>& p, double t ) = 0;

 public:

  /*
    BezierCurveBase コンストラクタ
  */

  /*
    点列の数を指定

    unsigned int n : 点列の数
  */
  BezierCurveBase( unsigned int n )
    : size_( n ), x_( size() ), y_( size() ) {}

  /*
    配列の範囲を指定

    vector< Coord<double> >::const_iterator it0, it1 : 配列の範囲
    (it1 は末尾の次を表すため含まれない)
  */
  BezierCurveBase( vector< Coord<double> >::const_iterator it0,
                   vector< Coord<double> >::const_iterator it1 )
    : size_( it1 - it0 ), x_( size() ), y_( size() )
  { set( it0, it1 ); }

  /*
    配列全体を指定

    const vector< Coord<double> >& p : 対象の点列
  */
  BezierCurveBase( const vector< Coord<double> >& p )
    : size_( p.size() ), x_( size() ), y_( size() )
  { set( p.begin(), p.end() ); }

  /*
    set : 点列の座標をセットする
  */

  /*
    点列の座標を一つ指定する

    unsigned int k : セットする位置
    const Coord<double>& p : 対象の点の座標
  */
  void set( unsigned int k, const Coord<double>& p )
  { if ( k < size() ) { x_[k] = p.x; y_[k] = p.y; } }

  /*
    配列の範囲とセットする開始位置を指定する

    unsigned int k : セットする位置
    vector< Coord<double> >::const_iterator it0, it1 : 対象の点列の範囲
  */
  void set( unsigned int k,
            vector< Coord<double> >::const_iterator it0,
            vector< Coord<double> >::const_iterator it1 );

  /*
    配列の範囲を指定して(点列が充分にあれば)全要素をセットする

    vector< Coord<double> >::const_iterator it0, it1 : 対象の点列の範囲
  */
  void set( vector< Coord<double> >::const_iterator it0,
            vector< Coord<double> >::const_iterator it1 )
  { set( 0, it0, it1 ); }

  // 点列のサイズを返す
  unsigned int size() const
  { return( size_ ); }

  // x, y の値を求める
  virtual double x( double t )
  { return( calc( x_, t ) ); }
  virtual double y( double t )
  { return( calc( y_, t ) ); }

  // 仮想デストラクタ
  virtual ~BezierCurveBase() {}
};

/*
  BezierCurveBase::set : 点列の座標を取得する

  unsigned int k : セットする位置
  vector< Coord<double> >::const_iterator it0, it1 : 描画対象の点列の開始と終了
*/
void BezierCurveBase::set( unsigned int k,
                           vector< Coord<double> >::const_iterator it0,
                           vector< Coord<double> >::const_iterator it1 )
{
  while ( it0 != it1 ) {
    if ( k >= size_ ) break;
    set( k, *it0 );
    ++it0;
    ++k;
  }
}

/**********************************************************
  BezierCurve : バーンスタイン多項式を使ったベジェ曲線
**********************************************************/
class BezierCurve : public BezierCurveBase
{
  BernsteinPolynomial func_; // Bernstein多項式

  // calc : バーンスタイン多項式の値を計算する
  virtual double calc( const vector<double>& p, double t );

 public:

  /*
    BezierCurve コンストラクタ

    BezierCurveBaseコンストラクタをそのまま利用
  */

  BezierCurve( unsigned int n )
    : BezierCurveBase( n ), func_( ( size() == 0 ) ? 0 : size() - 1 ) {}
  BezierCurve( vector< Coord<double> >::const_iterator it0,
               vector< Coord<double> >::const_iterator it1 )
    : BezierCurveBase( it0, it1 ), func_( ( size() == 0 ) ? 0 : size() - 1 ) {}
  BezierCurve( const vector< Coord<double> >& p )
    : BezierCurveBase( p ), func_( ( size() == 0 ) ? 0 : size() - 1 ) {}
};

/*
  BezierCurve::calc : バーンスタイン多項式の値を計算する

  const vector<double>& p : 点列の座標成分(多項式の係数)
  double t : 関数に代入する値

  戻り値 : 計算結果
*/
double BezierCurve::calc( const vector<double>& p, double t )
{
  unsigned int n = size(); // 点列のサイズ
  double d = 0;            // 計算結果

  for ( unsigned int k = 0 ; k < n ; ++k )
    d += func_( k, t ) * p[k];

  return( d );
}

BezierCurveBase は、前回作成した ParametricEquation からの派生クラスです。このようにすることで、曲線描画用のプログラムをそのまま流用することができます。しかし、曲線の座標を求めるためのメンバ関数 calc が純粋仮想関数なので、このままではまだインスタンス化して利用することはできません。その後にある BezierCurve が BezierCurveBase の派生クラスで、ここで calc が実装されています。calc での座標計算の内容は先ほど示した関数 CalcBernsteinPolynomial と同じですが、多項式はあらかじめメンバ変数 func_ として用意しておくので、BernsteinPolynomial オブジェクトの生成はコンストラクタ時の一回のみになります。なぜ、わざわざ BezierCurveBase を基底クラスとして用意したかについては後ほど明らかになります。

サンプル・プログラムを使って、放物線上に並べた点列によるベジェ曲線を描画した結果を以下に示します。N が点列の数を表し、点列は X 軸方向に対して等間隔になるように並べています。

図 3-1. ベジェ曲線による放物線の表現
N = 3N = 5
N=3N=5
N = 10N = 20
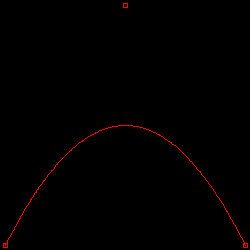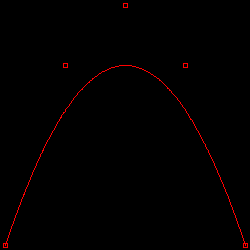N=10N=20

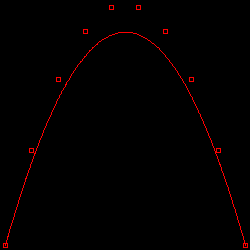点列の数が増えると、曲線が放物線に近づく様子がここでも確認できます。この結果を見ると、点列が多いほど、点列の並びにより近い理想的な曲線が描画できるように見えますが、実際には全く意図しない曲線となる場合もあります。

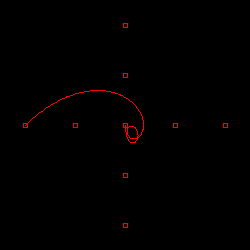渦巻状の点列に対するベジェ曲線(BezierCurve)
図 3-2. ベジェ曲線による渦巻きの表現

上の図は、点列を渦巻状に並べた場合のベジェ曲線の描画結果です。x, y ともに振動が激しく、それぞれで打ち消しあった結果、中央付近に固まった状態になっています。ベジェ曲線の場合、三点で制御する「二次ベジェ曲線 (Quadratic Bézier curves)」か、四点で制御する「三次ベジェ曲線 (Cubic Bézier curves)」を使い、スプライン曲線として描画するのが一般的です。ベジェ曲線では、端点において接線となることが保証されています。そのため、連続した二つの点列を結んだ直線上の任意の点を端点として曲線を描画すると、それぞれの曲線は連続となります。従って、与えられた点列を適当に分割して、隣り合った点列の端点の間の線分上にある点を新たな共通の端点として描画すれば、滑らかな曲線を描くことが可能です。

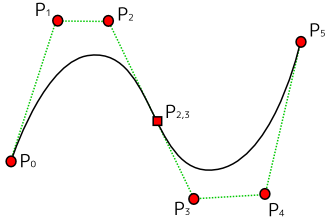ベジェ曲線を利用したスプライン曲線
図 3-3. ベジェ曲線によるスプライン曲線描画

上に示した図は、P0 から P5 までの 6 個の点列から、三次ベジェ曲線を利用してスプライン曲線を描画する例です。三次ベジェ曲線の描画には 4 つの点が必要になるので、P0 から P2 までの 3 点と、線分 P2 - P3 上の任意の点 P2,3 を使って前半部分を描画し、次に P2,3 と P3 から P5 までの合計 4 つの点から同様のやり方でスプライン曲線を描画しています。二つの曲線はどちらも、P2,3 において直線 P2 - P3 に接した状態になるので、曲線は不連続にはなりません。点列が多くなっても、同じ操作を繰り返せば曲線を伸ばしていくことが可能です。

ベジェ曲線によるスプライン曲線の描画サンプル・プログラムを以下に示します。

/*
  DrawSplineBezierCurve : ベジェ曲線によるスプライン曲線描画

  DrawingArea_IF& draw : 描画オブジェクト
  GPixelOp& pset : 描画用関数
  const vector< Coord<double> >& p : 描画する曲線上の点の座標
  unsigned int n : 次数
  double rate : 再帰的に内点を描画するときの内点の位置(比率)

  戻り値 : 計算結果
*/
void DrawSplineBezierCurve( DrawingArea_IF& draw, GPixelOp& pset,
                            const vector< Coord<double> >& p, unsigned int n, double rate )
{
  // n が 1 以下の場合は描画しない
  if ( n < 2 ) return;

  BezierCurve bezier( n + 1 ); // n 次ベジェ曲線(点列数は n + 1)
  Coord<double> edgeP = p.front(); // スプラインの端点

  // 中間点の開始反復子
  vector< Coord<double> >::const_iterator middleP = p.begin() + 1;
  // 次のスプライン開始の反復子
  vector< Coord<double> >::const_iterator nextP =
    ( p.size() > n ) ? p.begin() + n : p.end();

  for (;;) {
    // nextP が末尾を超えている場合は点列の数は n より小さい
    if ( nextP == p.end() ) {
      vector< Coord<double> > tail( middleP, nextP );
      tail.insert( tail.begin(), edgeP );
      BezierCurve bezier( tail );
      DrawParametricCurve( draw, pset, bezier, pair<double,double>( 0, 1 ), rate );
      break;
    }

    // 点列のセット
    bezier.set( 0, edgeP );
    bezier.set( 1, middleP, nextP );

    // 最終点は、第 n - 1 点と第 n 点の中点とする。
    // 但し、第 n 点が点列の末尾なら第 n 点をそのまま使用する
    edgeP = ( nextP + 1 == p.end() ) ?
      *nextP :
      Coord<double>( ( ( nextP - 1 )->x + nextP->x ) / 2,
                     ( ( nextP - 1 )->y + nextP->y ) / 2 );
    bezier.set( n, edgeP );

    DrawParametricCurve( draw, pset, bezier, pair<double,double>( 0, 1 ), rate );

    // 反復子の更新
    middleP = nextP;
    nextP = ( p.end() - ( n - 1 ) <= nextP ) ? p.end() : nextP + n - 1;
  }
}

一回の描画で利用する点列の数は、引数 n で指定することができます。但し、n は次数を表すので、実際に利用される点列の数は一つ多い n + 1 となります。従って、n = 2 のときは二次ベジェ曲線を利用し、n = 3 のときは三次ベジェ曲線を利用します。点列は三つの変数で制御され、スプラインの端点を表す edgeP と、中間にある点列の開始を表す middleP、最後に、次のスプライン曲線の利用開始位置(今のスプライン曲線の末尾より次の点)を表す nextP をそれぞれ定義しています。edgeP だけ座標そのものを保持し、残りの二つは反復子の形であることに注意して下さい。
edgeP は最初、点列の一番目の座標で初期化されます。この変数は、ベジェ曲線描画用オブジェクト bezier が保持する点列の最初の点としてセットされた後に、今度は曲線の末尾の座標として更新され、再び bezier にセットされます。これはそのまま、次のループ処理の時に開始点として再利用されます。なお、更新された edgeP は、nextP とその手前の点の中点になります。
端点以外の点については、middleP を使ってセットを行い、n 次ベジェ曲線を描画します。描画が完了したら、middleP と nextP を更新します。middleP は nextP を代入することで更新ができます。middleP を開始位置で更新しているように見えますが、開始位置は edgeP が保持しており、実際の点列には存在しないことに注意して下さい。nextP は、今の位置から n - 1 個分進んだ位置になります。点列の末尾を過ぎてしまった場合は、末尾の次の位置 p.end() を代入します。

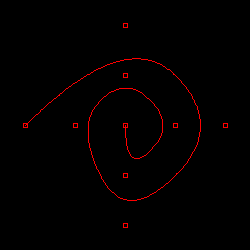
下図は、二次・三次ベジェ曲線を利用したスプライン曲線描画処理の結果です。形はいびつながらも、一応渦巻きの形に曲線が描画できています。

図 3-4. 二次・三次ベジェ曲線を利用したスプライン曲線描画
二次ベジェ曲線三次ベジェ曲線
QuadraticCubic

*3-1) 詳細は「(1) 組み合わせ・順列」の「二項定理(Binomial Theorem)」を参照して下さい。以下のように、直接証明することもできます。

C( N, N - k )=N! / ( N - k )!・[ N - ( N - k ) ]!
=N! / ( N - k )!・k!
=C( N, k )

4) ド・カステリョのアルゴリズム (De Casteljau's Algorithm)

バーンスタイン基底関数には、次のような漸化式が成り立つのでした。

bk,N(t) = t・bk-1,N-1(t) + ( 1 - t )・bk,N-1(t)

点列 Pk を係数とするバーンスタイン多項式 P(t) は、この漸化式を使って次のように変形することができます。

P(t) = Σk{0→N}( Pk・bk,N(t) ) = Σk{0→N}( Pk[ t・bk-1,N-1(t) + ( 1 - t )・bk,N-1(t) ] )

N = 1 の場合、

P(t)=Σk{0→1}( Pk・bk,1(t) )
=Σk{0→1}( Pk[ t・bk-1,0(t) + ( 1 - t )・bk,0(t) ] )
=P0( 1 - t )・b0,0(t) + P1t・b0,0(t)
=P0( 1 - t ) + P1t

となるので、P(t) は線分 P0 - P1 を t : 1 - t の比率で分けたときの内点(重心)に相当します。さらに N = 2 の場合、

P(t)=Σk{0→2}( Pk・bk,2(t) )
=Σk{0→2}( Pk[ t・bk-1,1(t) + ( 1 - t )・bk,1(t) ] )
=P0( 1 - t )・b0,1(t) + P1[ t・b0,1(t) + ( 1 - t )・b1,1(t) ] + P2t・b1,1(t)
=P0( 1 - t )・b0,1(t) + P1[ t・b0,1(t) + ( 1 - t )・b1,1(t) ] + P2t・b1,1(t)
=[ P0( 1 - t ) + P1t ]b0,1(t) + [ P1( 1 - t ) + P2t ]b1,1(t)
=[ P0( 1 - t ) + P1t ]( 1 - t ) + [ P1( 1 - t ) + P2t ]t

より、P(t) は 線分 P0 - P1 と P1 - P2 の t : 1 - t の内点をさらに t : 1 - t の比率で分けた内点になります。N = 3 の場合も、同様の操作によって P(t) が求められることが予想され、実際、

{ [ P0( 1 - t ) + P1t ]( 1 - t ) + [ P1( 1 - t ) + P2t ]t }( 1 - t ) + { [ P1( 1 - t ) + P2t ]( 1 - t ) + [ P2( 1 - t ) + P3t ]t }t
=P0( 1 - t )3 + P1[ 2t( 1 - t )2 + t( 1 - t )2 ] + P2[ t2( 1 - t ) + 2t2( 1 - t ) ] + P3・t3
=P0( 1 - t )3 + P1・3t( 1 - t )2 + P2・3t2( 1 - t ) + P3・t3
=P0・b0,3(t) + P1・b1,3(t) + P2・b2,3(t) + P3・b3,3(t)
=Σk{0→3}( Pk・bk,3(t) )

と求めることができます。これは、

( 1 - t )Σk{0→N-1}( Pk・bk,N-1(t) ) + tΣk{0→N-1}( Pk+1・bk,N-1(t) ) = Σk{0→N}( Pk・bk,N(t) )

が成り立つことを意味し、

( 1 - t )Σk{0→N-1}( Pk・bk,N-1(t) ) + tΣk{0→N-1}( Pk+1・bk,N-1(t) )
=( 1 - t )P0・b0,N-1(t) + Σk{1→N-1}( Pk[ ( 1 - t )bk,N-1(t) + tbk-1,N-1(t) ] ) + tPN・bN-1,N-1(t)
=Σk{0→N}( Pk[ ( 1 - t )bk,N-1(t) + tbk-1,N-1(t) ] )
=Σk{0→N}( Pk・bk,N(t) )

より証明することができます。この性質を利用した、ベジェ曲線描画のアルゴリズムを「ド・カステリョのアルゴリズム (De Casteljau's Algorithm)」といいます。上記の内容から、次のように処理を行うことでベジェ曲線を描画することができます。

  1. 点列 { Pk } ( k = 0, 1, ... N ) の隣り合う点 Pk, Pk+1 からなる線分に対し、t : 1 - t の比率の内点を求め、これを Pk(1) とする。
  2. 求めた点列 { Pk(2) } ( k = 0, 1, ... N - 1 ) の隣り合う点 Pk(2), Pk+1(2) からなる線分に対し、t : 1 - t の比率の内点を求め、これを Pk(2) とする。
  3. この操作を、点列が P0(N) 一つとなるまで繰り返し、この点をプロットする。
  4. 以上の操作を、t を 0 から 1 まで変化させながら繰り返す。
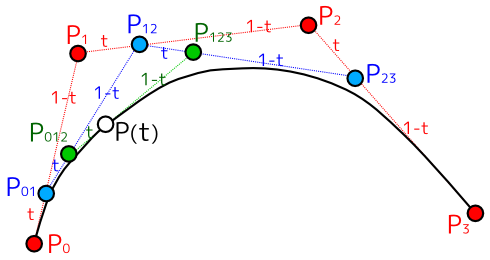ド・カステリョのアルゴリズム
図 4-1. ド・カステリョのアルゴリズム

上の図は、ド・カステリョのアルゴリズムを図で表したものです。P0 から P3 までの 4 つの点列を結んだ線分 3 本 (赤い点線) に対し、t : 1 - t の比率で内点を求めた結果が P01, P12, P23 の 3 点で、それらを結んだ 2 本の線分 (青い点線) に対し、さらに t : 1 - t の比率で内点を求めた結果が P012, P123 の 2 点です。最後に線分 P012 - P123 (緑の点線) に対して t : 1 - t の比率で求めた内点がベジェ曲線の上の点を表します。これを、t を 0 から 1 まで変化させながら繰り返すと、目的の曲線の軌跡が得られます。点列の数が多くなっても、処理の内容は全く同じです。

ド・カステリョのアルゴリズムを使ったベジェ曲線描画のサンプル・プログラムを以下に示します。

/*************************************************************
  DeCasteljau : De Casteljau のアルゴリズムを使ったベジェ曲線
*************************************************************/
class DeCasteljau : public BezierCurveBase
{
  vector<double> buff_;

  virtual double calc( const vector<double>& p, double t );

 public:

  DeCasteljau( unsigned int n )
    : BezierCurveBase( n ), buff_( ( size() == 0 ) ? 0 : size() - 1 ) {}
  DeCasteljau( vector< Coord<double> >::const_iterator it0,
               vector< Coord<double> >::const_iterator it1 )
    : BezierCurveBase( it0, it1 ), buff_( ( size() == 0 ) ? 0 : size() - 1 ) {}
  DeCasteljau( const vector< Coord<double> >& p )
    : BezierCurveBase( p ), buff_( ( size() == 0 ) ? 0 : size() - 1 ) {}
};

/*
  DeCasteljau::calc : De Casteljau のアルゴリズムを使って曲線の X/Y 座標を求める

  const vector<double>& p : 点列の座標成分(多項式の係数)
  double t : 関数に代入する値

  戻り値 : 計算結果
*/
double DeCasteljau::calc( const vector<double>& p, double t )
{
  if ( size() <= 1 ) return( NAN );

  // 点列から最初の内点を求めて buff_ に格納する
  for ( unsigned int s = 1 ; s < p.size() ; ++s )
    buff_[s - 1] = t * p[s - 1] + ( 1 - t ) * p[s];

  // 再帰的に内点を計算
  for ( unsigned int e = buff_.size() ; e > 1 ; --e )
    for ( unsigned int s = 1 ; s < e ; ++s )
      buff_[s - 1] = t * buff_[s - 1] + ( 1 - t ) * buff_[s];

  return( buff_[0] );
}

曲線の座標計算以外は、先ほど示した BezierCurve クラスの処理ルーチンがそのまま利用できるので、BezierCurveBase からの派生クラスにしてメンバ関数 calc だけ切り替えをしています。わざわざ BezierCurveBase クラスを用意してそこから派生するようにしたのはそのためです。DeCasteljau クラスでは、バーンスタイン基底関数は利用する必要がないので、func_ の代わりに内点を求めるためのバッファ配列 buff_ をメンバ変数として用意しています。内点の数は、ループ処理の中で一つずつ少なくなり、最後の一点となったところでループを抜けます。こうして残った要素が求めたい座標となります。

ベジェ曲線スプライン(二次)スプライン(三次)
DeCasteljau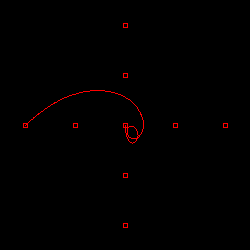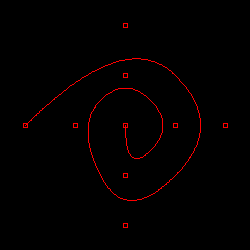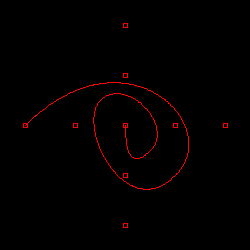渦巻状の点列に対するベジェ曲線(DeCasteljau)Quadratic(DeCasteljau)Cubic(DeCasteljau)
BezierCurve渦巻状の点列に対するベジェ曲線(BezierCurve)Quadratic(BezierCurve)Cubic(BezierCurve)

上の図は、BezierCurve クラスの描画テストと同じ条件の点列を使って、DeCasteljau クラスでベジェ曲線 (通常のベジェ曲線と二次・三次スプライン曲線) を描画した結果です。比較対象として、下側に BezierCurve クラスの描画結果を表示しています。これを見る限り、両者に大きな違いはありません。

このアルゴリズムを考案したのは、先に紹介したシトロエン社のド・カステリョです (そのため、このアルゴリズムには彼の名前が付けられています)。曲線にはベジェの名前が使われ、有用なアルゴリズムにはド・カステリョの名前が利用されていることになります。ベジェは 1999 年になくなっているのに対し、ベジェに先立ってベジェ曲線を発見したド・カステリョは今でもご健在のようです。2012 年には「Pierre Bézier Award」を受賞しました。この賞は 2007 年から始まっているのに最初の受賞者が彼というわけではなかったようです。しかし、過去の努力がようやく報われたと考えることもできるでしょうか。少なくとも、このアルゴリズムのおかげで、我々は曲線を簡単に表現することができるわけなので、感謝して利用していきたいですね。

補足1) ワイエルシュトラスの近似定理

閉区間 [ a, b ] 上の任意の連続関数 f(t) に対し、任意の ε ( > 0 ) について || f(t) - p(t) ||∞ < ε を満たす多項式 p(t) が必ず存在します。この定理を「ワイエルシュトラスの近似定理 (Weierstrass Approximation Theorem)」といいます。||f(t)||∞ は「一様ノルム (Uniform Norm)」と呼ばれ、|f(t)| の最大値を意味します。よって、任意の f(t) に対して一様収束するような多項式 p(t) が存在するということになります。

ワイエルシュトラスの近似定理の証明に利用された関数は具体的に演算できるようなものではなかったため、さらに具体的な式を使った証明法として使われたのがバーンスタイン多項式です。バーンスタイン基底関数 bNk を基底としたときの f( k / N ) を係数とした線形結合 BNf(t) は

BNf(t) = Σk{0→N}( f( k / N )・bNk )

と表されます。この式は、f(t) を多項式の形に変換する操作です。このような、関数から別の関数に写す操作のことを「作用素 (Operator)」といいます。微分 df / dt や積分 ∫f dt、フーリエ変換などは作用素の一例です。関数 f への作用素 T による変換を Tf で表した時、p, q を任意の定数、f, g を任意の関数として

T( pf + qg ) = pTf + qTg

が成り立つ場合、この作用素を「線形作用素 (Linear Operator)」といいます。微分・積分演算子やフーリエ変換は線形作用素になります。また、任意の変数に対して f ≥ 0 である関数に対して常に Tf ≥ 0 が成り立つならば、その作用素は「正値作用素 (Positive Operator)」といいます。微分・積分演算子やフーリエ変換は正値作用素ではありません。

バーンスタイン基底関数を使った作用素を BN とします。この作用素は

BN( pf + qg )=Σk{0→N}( [ pf(k/N) + qg(k/N) ]bNk )
=pΣk{0→N}( f(k/N)・bNk ) + qΣk{0→N}( g(k/N)・bNk )
=pBNf + qBNg

より線形作用素であり、bNk > 0 より正値作用素でもあります。両者の性質を満たす線形作用素の列 {TN} が、閉区間 [ 0, 1 ] 上で pi(t) = ti ( i = 0, 1, 2 ) に対して

|| TNpi - pi ||∞ → 0 ( N → ∞ )

を満たすとき、任意の関数 f(t) も閉区間 [ 0, 1 ] 上で

|| TNf - f ||∞ → 0 ( N → ∞ )

が成り立ちます。この定理を「コロフキンの近似定理 (Korovkin's Approximation Theory)」といいます。上式は大雑把に言えば、N を大きくすると TN を使って変換しても元の状態とほとんど変わらないことを意味します。つまり、f(t) = 1, t, t2 の三つの関数に対して、N → ∞ の極限において変換後の形が変わらないことを確認すれば、どの関数に対しても同様に成り立つことが示されます。

BN の場合、f(t) = C (定数) ならば、

BNf(t) = CΣk{0→N}( bNk ) = C

より完全に一致します。また、f(t) = pt + q (一次式) ならば、

BNf(t)=Σk{0→N}( ( pk / N + q )・bNk )
=pΣk{0→N}( ( k / N )・[ N! / k!・( N - k )! ]tk( 1 - t )N-k ) + q
=pΣk{0→N}( { ( N - 1 )! / ( k - 1 )!・[ ( N - 1 ) - ( k - 1 ) ]! }tk( 1 - t )N-k ) + q
=ptΣk{0→N}( C( N - 1, k - 1 )tk-1( 1 - t )(N-1)-(k-1) ) + q
=ptΣk{0→N}( bN-1k-1 ) + q = pt + q

となって、やはり完全に一致します。t2 の場合は本章の中で示しているので、コロフキンの近似定理から、N を限りなく大きくすれば任意の関数に対して BNf(t) が f(t) に一様収束することになります。

ワイエルシュトラスの近似定理は、どのような連続関数も任意の有限な範囲を指定すれば多項式で表せることを示しています。実際、任意の関数 f(t) は、N 次のテイラー級数を利用して

f(t) = f(a) + f(1)(a)( t - a ) + f(2)(a)( t - a )2 / 2 + ... + f(N)(a)( t - a )N / N! + RN+1

と多項式の形に表すことができます。但し、f(k)(x) は k 階の導関数で、RN+1 は N + 1 次以降の成分(剰余項)を表します。f(t) 上の点を N 個サンプリングして多項式に近似した時、その点を ( ti, f(ti) ) ( i = 0, 1, ... N ) とすれば、これらの点における剰余項はゼロのはずなので

RN+1 = α( t - t0 )( t - t1 ) ... ( t - tn ) = αΠi{0→N}( t - tn )

と表されます。N + 1 次の項の係数は f(N+1)(a) / ( N + 1 )! であり、α = f(N+1)(a) / ( N + 1 )! より、

RN+1 = [ f(N+1)(a) / ( N + 1 )! ]Πi{0→N}( t - tN )

となって、これが f(t) とその近似多項式の差になります。N を大きくすれば RN+1 の次数も大きくなり、それがゼロに収束すれば f(t) と多項式は限りなく近づいてゆくはずです。しかし、サンプリングする点を等間隔にしたとき、N が大きくなるに従って RN+1 が発散してしまうために、特に区間の端の付近で振動する場合があります。この現象を「ルンゲの現象(Runge's phenomenon)」といいます。サンプリングする点を増やして多項式の次数を多くするほど、実際の関数に近い結果が得られると思えるのですが、実際には次数を増やすほどこの現象が顕著に現れるようになります。前回示したパラメトリック曲線において、理想的な曲線との差異は区間の端 (曲線の両端の方) に特に大きく発生していましたが、これはルンゲの現象によるものです。理想的な曲線になるように t の値を決めるというのは非常に難しい話ですが、よく知られた方法として「チェビシェフ・ノード(Chebyshev Nodes)」を利用するというものがあります。チェビシェフ・ノードは、区間 -1 ≤ t ≤ 1 に対して

ti = cos( ( 2i - 1 )π / 2N ) ( i = 1, 2, ... N )

で与えられます。また、任意の区間 a ≤ t ≤ b に対しては

ti = ( a + b ) / 2 + [ ( b - a ) / 2 ]cos( ( 2i - 1 )π / 2N ) ( i = 1, 2, ... N )

となるので、a = 0, b = 1 ならば

ti = [ 1 + cos( ( 2i - 1 )π / 2N ) ] / 2 ( i = 1, 2, ... N )

で求められます。また、バーンスタイン多項式は N を大きくするほど元の関数に近づくことが保証されています。これは通常の多項式を使った近似と比べると大きな利点になります。

<参考文献>
1. IDAV - Institute for Data Analysis and Visualization - 「BERNSTEIN POLYNOMIALS」
バーンスタイン多項式の性質などについて非常に分かりやすくまとめてあります。
2.「Chapter 5 - Properties of Blending Functions」
ブレンディング関数の性質をまとめた資料です。
3. University of California - 「Rida T. Farouki」 - 「The Bernstein polynomial basis : a centennial retrospective」
ワイエルシュトラスの近似定理とバーンスタイン多項式の関係についてまとめてあります。
4. 信州大学 工学部 情報工学科 基礎研究室 様 - 「Let's Learn」 - 「コンピュータグラフィックス」
「第 4章 ベジェ(Bezier)曲線」の内容を参考にさせていただきました。
5. (株) O2(オーツー) 様 - 「メディアライブラリ」 - 「技術記事」
「CADデータ流通」の中にある「3次元図形処理技術解説 第6回　Bezier曲線(1)」と「3次元図形処理技術解説 第7回　Bezier曲線(2)」を参考にさせていただきました。
6. The Pierre Bézier Award - 「Paul de Faget de Casteljau - The 2012 Pierre Bézier Award Recipient」
7. Wikipedia
毎度お世話になっています。
[Go Back]前に戻る [Back to HOME]タイトルに戻る
inserted by FC2 system