 |
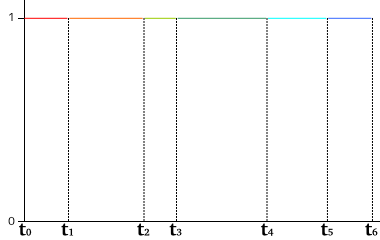
| 図 1-1. Nj0 のグラフ (階段関数) |
ベジェ曲線は、バーンスタイン基底関数をブレンディング関数として使ったパラメトリック曲線であることを前回紹介しました。ブレンディング関数は他にも様々な形式を考えることができますが、今回はその中の一つとして「B-スプライン基底関数(B-Spline Basis Function)」をブレンディング関数とした「B-スプライン曲線(B-Spline Curve)」を紹介します。
「B-スプライン基底関数 (B-Spline Basis Function)」は、「De Boor-Coxの漸化式」と呼ばれる以下の漸化式で表される関数です。
| Nj,p(t) | = | [ ( t - tj ) / ( tj+p - tj ) ]・Nj,p-1(t) + [ ( tj+p+1 - t ) / ( tj+p+1 - tj+1 ) ]・Nj+1,p-1(t) |
| = | [ ( t - tj ) / ( tj+p - tj ) ]・Njp-1 + [ ( tj+p+1 - t ) / ( tj+p+1 - tj+1 ) ]・Nj+1p-1 |
但し、二番目の式において、Nj,p(t) = Njp と表しています。tj は「ノット (Knot)」と呼ばれる数列で、ここでは要素数を M + 1 とします。すなわち、0 を開始番号とすれば、{ tj } = ( t0, t1, ... tM ) となります。但し、i < j ならば ti ≤ tj である必要があります。また、p はこの基底関数の次数を表します。この式のなかで、ノット列の添字の最大は j + p + 1 なので、M ≥ j + p + 1 が成り立ち、基底関数は N0,p(t) から NM-p-1,p(t) までの M - p 個になります。
p = 0 のときは、上に示した漸化式は使えません。この時は、次のように定義されます。
| Nj,0(t) | = | 1 | ( tj ≤ t ≤ tj+1 ) |
| = | 0 | ( それ以外 ) |
Nj,0(t) による線形結合はいわゆる「階段関数 (Step Function)」と呼ばれる不連続な関数です。
M は p より大きければどんな値でも取りえます。また、p は M に依存することなく決めることができます。p = 1 の場合、漸化式から
| Nj,1(t) | = | [ ( t - tj ) / ( tj+1 - tj ) ]・Nj0 + [ ( tj+2 - t ) / ( tj+2 - tj+1 ) ]・Nj+10 | |
| = | ( t - tj ) / ( tj+1 - tj ) | ( tj ≤ t ≤ tj+1 ) | |
| = | ( tj+2 - t ) / ( tj+2 - tj+1 ) | ( tj+1 ≤ t ≤ tj+2 ) | |
| = | 0 | ( それ以外 ) | |
となるので、Nj,1(t) は t = tj のとき 0 となり、線形に増加しながら t = tj+1 で 1 に、その後今度は線形に減少して t = tj+2 で再び 0 になります。よって Nj,1(t) のグラフは、底辺が tj から tj+2 で、高さが 1 の三角形になります。
p = 2 になると、式がかなり複雑になってきます。そこで、tj+m = tm と表して j は書かないようにして、さらに
と表すと、
| Nj,2(t) | = | [ ( t - t0 ) / ( t2 - t0 ) ]・Nj1 + [ ( t3 - t ) / ( t3 - t1 ) ]・Nj+11 | |
| = | u0,2・Nj1 + u3,1・Nj+11 | ||
| = | u0,2・u0,1 | ( t0 ≤ t ≤ t1 ) | |
| = | u0,2・u2,1 + u3,1・u1,2 | ( t1 ≤ t ≤ t2 ) | |
| = | u3,1・u3,2 | ( t2 ≤ t ≤ t3 ) | |
| = | 0 | ( それ以外 ) | |
と三つの区分に分かれた二次式で表現されます。t = tm のとき um,n = 0、t = tn のとき um,n = 1 になることに注意すると、t = t0, t3 のとき Nj,2(t) = 0 であり、tm - tn = Dm,n で表すと、t = t1 のときは
になります。Nj,2( t1 ) の計算には、t0 ≤ t ≤ t1, t1 ≤ t ≤ t2 のどちらの定義域の式を使っても結果が同じであることに注意して下さい。同様に、t = t2 のときは
になります。定義域 tm ≤ t ≤ tm+1 での Nj,2( t ) を Nj,2[m]( t ) で表すと、Nj,2[0]( t ), Nj,2[2]( t ) はそれぞれ
Nj,2[0]( t ) = ( t - t0 )2 / D2,0D1,0
Nj,2[2]( t ) = ( t - t3 )2 / D1,3D2,3
なので、t = t0, t3 で極値を持つことがわかります。従って (二次項の係数は正なので)、t0 ≤ t ≤ t1 では短調増加、t2 ≤ t ≤ t3 では単調減少であり、もし Nj,2( t ) が連続なら t1 ≤ t ≤ t2 では極値を持たなければなりません。実際、この定義域での極値を求めると、
より、
| d( um,n・ur,s ) / dt | = | u'm,n・ur,s + um,n・u'r,s |
| = | [ ( t - tr ) / Dn,mDs,r ] + [ ( t - tm ) / Dn,mDs,r ] | |
| = | [ 2t - ( tm + tr ) ] / Dn,mDs,r |
なので、
| N'j,2[1]( t ) | = | d( u0,2・u2,1 ) / dt + d( u3,1・u1,2 ) / dt |
| = | [ 2t - ( t0 + t2 ) ] / D2,0D1,2 + [ 2t - ( t3 + t1 ) ] / D1,3D2,1 | |
| = | { D3,1[ -2t + ( t0 + t2 ) ] - D2,0[ 2t - ( t3 + t1 ) ] } / D2,0D2,1D3,1 | |
| = | { [ -2D3,1t + ( t0 + t2 )( t3 - t1 ) ] - [ 2D2,0t - ( t3 + t1 )( t2 - t0 ) ] } | |
| / D2,0D2,1D3,1 | ||
| = | [ -2( D2,0 + D3,1 )t + ( t0 + t2 )( t3 - t1 ) + ( t3 + t1 )( t2 - t0 ) ] | |
| / D2,0D2,1D3,1 | ||
| = | -2[ ( D2,0 + D3,1 )t - ( t2t3 - t0t1 ) ] / D2,0D2,1D3,1 | |
と計算できて、左辺がゼロの時は
になります。この値と t1 の差は
| ( t2t3 - t0t1 ) / ( D2,0 + D3,1 ) - t1 | |
| = | [ ( t2t3 - t0t1 ) - ( D2,0 + D3,1 )t1 ] / ( D2,0 + D3,1 ) |
| = | ( t2t3 - t0t1 - t1t2 + t0t1 - t3t1 + t12 ) / ( D2,0 + D3,1 ) |
| = | [ t3( t2 - t1 ) - t1( t2 - t1 ) ] / ( D2,0 + D3,1 ) |
| = | D3,1D2,1 / ( D2,0 + D3,1 ) ≥ 0 |
であり、t2 との差は
| ( t2t3 - t0t1 ) / ( D2,0 + D3,1 ) - t2 | |
| = | [ ( t2t3 - t0t1 ) - ( D2,0 + D3,1 )t2 ] / ( D2,0 + D3,1 ) |
| = | ( t2t3 - t0t1 - t22 + t0t2 - t2t3 + t1t2 ) / ( D2,0 + D3,1 ) |
| = | [ t0( t2 - t1 ) - t2( t2 - t1 ) ] / ( D2,0 + D3,1 ) |
| = | -D2,0D2,1 / ( D2,0 + D3,1 ) ≤ 0 |
なので、確かに極値は必ず t1 ≤ t ≤ t2 の範囲内に存在します。また、
と表せることを利用して、この導関数に t = t1, t2 をそれぞれ代入すると、
| N'j,2[1]( t1 ) | = | ( D1,0 + D1,2 ) / D2,0D1,2 + D1,3 / D1,3D2,1 |
| = | ( -D1,0 + D2,1 ) / D2,0D2,1 + 1 / D2,1 | |
| = | ( -D1,0 + D2,1 + D2,0 ) / D2,0D2,1 | |
| = | 2D2,1 / D2,0D2,1 | |
| = | 2 / D2,0 | |
| N'j,2[1]( t2 ) | = | D2,0 / D2,0D1,2 + ( D2,3 + D2,1 ) / D1,3D2,1 |
| = | -1 / D2,1 + ( D3,2 - D2,1 ) / D3,1D2,1 | |
| = | ( -D3,1 + D3,2 - D2,1 ) / D3,1D2,1 | |
| = | -2D2,1 / D3,1D2,1 | |
| = | -2 / D3,1 |
となり、Nj,2[0](t), Nj,2[2](t) の導関数が
N'j,2[0]( t ) = 2( t - t0 ) / D2,0D1,0
N'j,2[2]( t ) = 2( t - t3 ) / D1,3D2,3
であることから、各式に t = t1, t2 をそれぞれ代入すると、N'j,2[0]( t1 ) = N'j,2[1]( t1 ), N'j,2[1]( t2 ) = N'j,2[2]( t2 ) であることが容易にわかります。従って、Nj,2(t) の導関数は t = t1, t2 にて連続であることになります。しかし、二階導関数は各区分において定数となり、
N(2)j,2[0](t) = 2 / D2,0D1,0
N(2)j,2[1](t) = -2( D2,0 + D3,1 ) / D2,0D2,1D3,1
N(2)j,2[2](t) = 2 / D1,3D2,3
なので、連続にはなりません。
p = 3 の場合、
| Nj,3( t ) | = | u0,3N02 + u4,1N12 | |
| = | u0,3( u0,2N01 + u3,1N11 ) | ||
| + u4,1( u1,3N11 + u4,2N21 ) | |||
| = | u0,3[ u0,2( u0,1N00 + u2,1N10 ) + u3,1( u1,2N10 + u3,2N20 ) ] | ||
| + u4,1[ u1,3( u1,2N10 + u3,2N20 ) + u4,2( u2,3N20 + u4,3N30 ) ] | |||
| = | u0,3u0,2u0,1N00 + [ u0,3( u0,2u2,1 + u3,1u1,2 ) + u4,1u1,3u1,2 ]N10 | ||
| + [ u0,3u3,1u3,2 + u4,1( u1,3u3,2 + u4,2u2,3 ) ]N20 + u4,1u4,2u4,3N30 | |||
| = | u0,3u0,2u0,1 | ( t0 ≤ t ≤ t1 ) | |
| = | u0,3( u0,2u2,1 + u3,1u1,2 ) + u4,1u1,3u1,2 | ( t1 ≤ t ≤ t2 ) | |
| = | u0,3u3,1u3,2 + u4,1( u1,3u3,2 + u4,2u2,3 ) | ( t2 ≤ t ≤ t3 ) | |
| = | u4,1u4,2u4,3 | ( t3 ≤ t ≤ t4 ) | |
となります。ここでも、t = tm のとき um,n = 0、t = tn のとき um,n = 1 になることを利用すれば、
Nj,3( t0 ) = Nj,3( t4 ) = 0
Nj,3( t1 ) = u0,3u0,2
Nj,3( t2 ) = u0,3u3,1 + u4,1u1,3
Nj,3( t3 ) = u4,1u4,2
であり、しかも各区分の境界で連続であることが容易にわかります。また、
Nj,3[0]( t ) = ( t - t0 )3 / D3,0D2,0D1,0
Nj,3[3]( t ) = ( t - t4 )3 / D1,4D2,4D3,4
となるので、それぞれの式は三重根 t0, t4 を持ち、この点は変曲点になります。Nj,3[0]( t ) は三次項の係数が正なのに対し、Nj,3[3]( t ) は負であることから、Nj,3[0]( t ) は t ≥ t0 で短調増加、Nj,3[3]( t ) は t ≤ t4 で短調減少です。さらに、um,n・ur,s・uv,w の導関数が
| d( um,n・ur,s・uv,w ) / dt | = | u'm,n・ur,s・uv,w + um,n・u'r,s・uv,w + um,n・ur,s・u'v,w |
| = | [ ( t - tr )( t - tv ) + ( t - tv )( t - tm ) + ( t - tm )( t - tr ) ] | |
| / ( tn - tm )( ts - tr )( tw - tv ) | ||
| = | ur,suv,w / Dn,m + uv,wum,n / Ds,r + um,nur,s / Dw,v | |
であることを利用すると、N'j,3[1]( t ) は
| N'j,3[1]( t ) | = | d( u0,3u0,2u2,1 ) / dt + d( u0,3u3,1u1,2 ) / dt + d( u4,1u1,3u1,2 ) / dt |
| = | u0,2u2,1 / D3,0 + u0,3u2,1 / D2,0 + u0,3u0,2 / D1,2 | |
| + u3,1u1,2 / D3,0 + u0,3u1,2 / D1,3 + u0,3u3,1 / D2,1 | ||
| + u1,3u1,2 / D1,4 + u4,1u1,2 / D3,1 + u4,1u1,3 / D2,1 | ||
となるので、再び um,n( tm ) = 0, um,n( tn ) = 1 を利用して N'j,3[1]( t1 ), N'j,3[1]( t2 ) を計算すると
| N'j,3[1]( t1 ) | = | u0,2( t1 ) / D3,0 + u0,3( t1 ) / D2,0 + u0,3( t1 )u0,2( t1 ) / D1,2 |
| + u0,3( t1 ) / D2,1 | ||
| = | D1,0 / D2,0D3,0 + D1,0 / D3,0D2,0 + D1,02 / D3,0D2,0D1,2 | |
| + D1,0 / D3,0D2,1 | ||
| = | ( 2D1,0D2,1 - D1,02 + D1,0D2,0 ) / D2,0D2,1D3,0 | |
| = | D1,0[ 2( t2 - t1 ) - ( t1 - t0 ) + ( t2 - t0 ) ] / D2,0D2,1D3,0 | |
| = | 3D1,0D2,1 / D2,0D2,1D3,0 | |
| = | 3D1,0 / D2,0D3,0 | |
| N'j,3[1]( t2 ) | = | u0,3( t2 ) / D1,2 + u3,1( t2 ) / D3,0 + u0,3( t2 ) / D1,3 |
| + u0,3( t2 )u3,1( t2 ) / D2,1 + u1,3( t2 ) / D1,4 + u4,1( t2 ) / D3,1 | ||
| + u4,1( t2 )u1,3( t2 ) / D2,1 | ||
| = | D2,0 / D3,0D1,2 + D2,3 / D1,3D3,0 + D2,0 / D3,0D1,3 | |
| + D2,0D2,3 / D3,0D1,3D2,1 + D2,1 / D3,1D1,4 + D2,4 / D1,4D3,1 | ||
| + D2,4D2,1 / D1,4D3,1D2,1 | ||
| = | -D2,0 / D2,1D3,0 + D3,2 / D3,0D3,1 - D2,0 / D3,0D3,1 | |
| + D2,0D3,2 / D2,1D3,0D3,1 - D2,1 / D3,1D4,1 + 2D4,2 / D3,1D4,1 | ||
| = | D2,0( D3,2 - D3,1 ) / D2,1D3,0D3,1 + ( D3,2 - D2,0 ) / D3,0D3,1 | |
| + ( 2D4,2 - D2,1 ) / D3,1D4,1 | ||
| = | -D2,0D2,1 / D2,1D3,0D3,1 + ( D3,2 - D2,0 ) / D3,0D3,1 | |
| + ( 2D4,2 - D2,1 ) / D3,1D4,1 | ||
| = | [ D4,1( D3,2 - 2D2,0 ) + D3,0( 2D4,2 - D2,1 ) ] / D3,0D3,1D4,1 | |
となります。同様に、N'j,3[2]( t ) が
| N'j,3[2]( t ) | = | d( u0,3u3,1u3,2 ) / dt + d( u4,1u1,3u3,2 ) / dt + d( u4,1u4,2u2,3 ) / dt |
| = | u3,1u3,2 / D3,0 + u0,3u3,2 / D1,3 + u0,3u3,1 / D2,3 | |
| + u1,3u3,2 / D1,4 + u4,1u3,2 / D3,1 + u4,1u1,3 / D2,3 | ||
| + u4,2u2,3 / D1,4 + u4,1u2,3 / D2,4 + u4,1u4,2 / D3,2 | ||
であることを利用して N'j,3[2]( t2 ), N'j,3[2]( t3 ) を計算すると、
| N'j,3[2]( t2 ) | = | u3,1( t2 ) / D3,0 + u0,3( t2 ) / D1,3 + u0,3( t2 )u3,1( t2 ) / D2,3 |
| + u1,3( t2 ) / D1,4 + u4,1( t2 ) / D3,1 + u4,1( t2 )u1,3( t2 ) / D2,3 | ||
| + u4,1( t2 ) / D3,2 | ||
| = | D2,3 / D1,3D3,0 + D2,0 / D3,0D1,3 + D2,0D2,3 / D3,0D1,3D2,3 | |
| + D2,1 / D3,1D1,4 + D2,4 / D1,4D3,1 + D2,4D2,1 / D1,4D3,1D2,3 | ||
| + D2,4 / D1,4D3,2 | ||
| = | D3,2 / D3,0D3,1 - D2,0 / D3,0D3,1 - D2,0 / D3,0D3,1 | |
| - D2,1 / D3,1D4,1 + D4,2 / D3,1D4,1 - D2,1D4,2 / D3,1D3,2D4,1 | ||
| + D4,2 / D3,2D4,1 | ||
| = | ( D3,2 - 2D2,0 ) / D3,0D3,1 + ( D4,2 - D2,1 ) / D3,1D4,1 | |
| + D4,2( D3,1 - D2,1 ) / D3,1D3,2D4,1 | ||
| = | ( D3,2 - 2D2,0 ) / D3,0D3,1 + ( D4,2 - D2,1 ) / D3,1D4,1 | |
| + D4,2D3,2 / D3,1D3,2D4,1 | ||
| = | [ D4,1( D3,2 - 2D2,0 ) + D3,0( 2D4,2 - D2,1 ) ] / D3,0D3,1D4,1 | |
| N'j,3[2]( t3 ) | = | u4,1( t3 ) / D2,3 + u4,2( t3 ) / D1,4 + u4,1( t3 ) / D2,4 |
| + u4,1( t3 )u4,2( t3 ) / D3,2 | ||
| = | D3,4 / D1,4D2,3 + D3,4 / D2,4D1,4 + D3,4 / 1,4D2,4 | |
| + D3,42 / D1,4D2,4D3,2 | ||
| = | ( -D4,2D4,3 - 2D3,2D4,3 + D4,32 ) / D3,2D4,1D4,2 | |
| = | D4,3[ -( t4 - t2 ) - 2( t3 - t2 ) + ( t4 - t3 ) ] / D3,2D4,1D4,2 | |
| = | -3D4,3D3,2 / D3,2D4,1D4,2 | |
| = | -3D4,3 / D4,1D4,2 | |
という結果が得られ、N'j,3[1]( t2 ) = N'j,3[2]( t2 ) であることが証明できます。また、
| N'j,3[0]( t1 ) | = | 3( t1 - t0 )2 / ( t3 - t0 )( t2 - t0 )( t1 - t0 ) |
| = | 3D1,0 / D3,0D2,0 | |
| N'j,3[3]( t3 ) | = | 3( t3 - t4 )2 / ( t1 - t4 )( t2 - t4 )( t3 - t4 ) |
| = | -3D4,3 / D4,1D4,2 |
なので、p = 2 の場合と同様に、導関数も t = t1, t2, t3 において連続であることになります。
さらに二階導関数を求めてみましょう。N(2)j,3[0]( t ), N(2)j,3[3]( t ) は、
| N(2)j,3[0]( t ) | = | 6( t - t0 ) / ( t3 - t0 )( t2 - t0 )( t1 - t0 ) |
| = | 6( t - t0 ) / D3,0D2,0D1,0 | |
| N(2)j,3[3]( t ) | = | 6( t - t4 ) / ( t1 - t4 )( t2 - t4 )( t3 - t4 ) |
| = | -6( t - t4 ) / D4,1D4,2D4,3 |
なので、
N(2)j,3[0]( t1 ) = 6 / D3,0D2,0
N(2)j,3[3]( t3 ) = 6 / D4,1D4,2
です。N(2)j,3[1]( t ), N(2)j,3[2]( t ) は、um,n・ur,s・uv,w の二階導関数が
| d2( um,n・ur,s・uv,w ) / dt2 | = | ( ur,suv,w )' / Dn,m + ( uv,wum,n )' / Ds,r + ( um,nur,s )' / Dw,v |
| = | uv,w / Dn,mDs,r + ur,s / Dn,mDw,v + um,n / Ds,rDw,v | |
| + uv,w / Ds,rDn,m + ur,s / Dw,vDn,m + um,n / Dw,vDs,r | ||
| = | 2( um,n / Ds,rDw,v + ur,s / Dw,vDn,m + uv,w / Dn,mDs,r ) | |
であることを利用して
| N(2)j,3[1]( t ) | = | d2( u0,3u0,2u2,1 ) / dt2 + d2( u0,3u3,1u1,2 ) / dt2 + d2( u4,1u1,3u1,2 ) / dt2 |
| = | 2( u0,3 / D2,0D1,2 + u0,2 / D3,0D1,2 + u2,1 / D3,0D2,0 ) | |
| + 2( u0,3 / D1,3D2,1 + u3,1 / D3,0D2,1 + u1,2 / D3,0D1,3 ) | ||
| + 2( u4,1 / D3,1D2,1 + u1,3 / D1,4D2,1 + u1,2 / D1,4D3,1 ) | ||
| N(2)j,3[2]( t ) | = | d2( u0,3u3,1u3,2 ) / dt2 + d2( u4,1u1,3u3,2 ) / dt2 + d2( u4,1u4,2u2,3 ) / dt2 |
| = | 2( u0,3 / D1,3D2,3 + u3,1 / D3,0D2,3 + u3,2 / D3,0D1,3 ) | |
| + 2( u4,1 / D3,1D2,3 + u1,3 / D1,4D2,3 + u3,2 / D1,4D3,1 ) | ||
| + 2( u4,1 / D2,4D3,2 + u4,2 / D1,4D3,2 + u2,3 / D1,4D2,4 ) | ||
となるので、
| N(2)j,3[1]( t1 ) | = | 2[ u0,3( t1 ) / D2,0D1,2 + u0,2( t1 ) / D3,0D1,2 + 1 / D3,0D2,0 ] |
| + 2[ u0,3( t1 ) / D1,3D2,1 + 1 / D3,0D2,1 ] | ||
| + 2 / D3,1u2,1 | ||
| = | 2( D1,0 / D3,0D2,0D1,2 + D1,0 / D2,0D3,0D1,2 + 1 / D3,0D2,0 ) | |
| + 2( D1,0 / D3,0D1,3D2,1 + 1 / D3,0D2,1 + 1 / D3,1u2,1 ) | ||
| = | 2( -2D1,0 / D2,0D2,1D3,0 + 1 / D2,0D3,0 ) | |
| + 2[ ( D3,0 - D1,0 ) / D2,1D3,0D3,1 + 1 / u2,1D3,0 ] | ||
| = | -4D1,0 / D2,0D2,1D3,0 + 2 / D2,0D3,0 + 4 / D2,1D3,0 | |
| = | 4( D2,0 - D1,0 ) / D2,0D2,1D3,0 + 2 / D2,0D3,0 | |
| = | 4 / D2,0D3,0 + 2 / D2,0D3,0 | |
| = | 6 / D2,0D3,0 | |
| N(2)j,3[1]( t2 ) | = | 2[ u0,3( t2 ) / D2,0D1,2 + 1 / D3,0D1,2 ] |
| + 2[ u0,3( t2 ) / D1,3D2,1 + u3,1( t2 ) / D3,0D2,1 + 1 / D3,0D1,3 ] | ||
| + 2[ u4,1( t2 ) / D3,1D2,1 + u1,3( t2 ) / D1,4D2,1 + 1 / D1,4D3,1 ] | ||
| = | 2( D2,0 / D3,0D2,0D1,2 + 1 / D3,0D1,2 ) | |
| + 2( D2,0 / D3,0D1,3D2,1 + D2,3 / D1,3D3,0D2,1 + 1 / D3,0D1,3 ) | ||
| + 2( D2,4 / D1,4D3,1D2,1 + D2,1 / D3,1D1,4D2,1 + 1 / D1,4D3,1 ) | ||
| = | 2( -2 / D2,1D3,0 | |
| - D2,0 / D2,1D3,0D3,1 + D3,2 / D2,1D3,0D3,1 - 1 / D3,0D3,1 | ||
| + D4,2 / D2,1D3,1D4,1 - 2 / D3,1D4,1 ) | ||
| = | 2[ -3 / D2,1D3,0 | |
| - D2,0 / D2,1D3,0D3,1 + D3,2 / D2,1D3,0D3,1 + ( D3,1 - D2,1 ) / D2,1D3,0D3,1 | ||
| + ( D4,2 + D2,1 ) / D2,1D3,1D4,1 - 3 / D3,1D4,1 ] | ||
| = | 2[ -3 / D2,1D3,0 | |
| - D2,0 / D2,1D3,0D3,1 + 2D3,2 / D2,1D3,0D3,1 | ||
| + 1 / D2,1D3,1 - 3 / D3,1D4,1 ] | ||
| = | 2[ -3 / D2,1D3,0 | |
| + ( D3,0 - D2,0 ) / D2,1D3,0D3,1 + 2D3,2 / D2,1D3,0D3,1 | ||
| - 3 / D3,1D4,1 ] | ||
| = | 6( D3,2 / D2,1D3,0D3,1 - 1 / D2,1D3,0 - 1 / D3,1D4,1 ) | |
| = | 6[ ( D3,2 - D3,1 ) / D2,1D3,0D3,1 - 1 / D3,1D4,1 ] | |
| = | -6( 1 / D3,0D3,1 + 1 / D3,1D4,1 ) | |
| N(2)j,3[2]( t2 ) | = | 2[ u0,3( t2 ) / D1,3D2,3 + u3,1( t2 ) / D3,0D2,3 + 1 / D3,0D1,3 ] |
| + 2[ u4,1( t2 ) / D3,1D2,3 + u1,3( t2 ) / D1,4D2,3 + 1 / D1,4D3,1 ] | ||
| + 2[ u4,1( t2 ) / D2,4D3,2 + 1 / D1,4D3,2 ] | ||
| = | 2( D2,0 / D3,0D1,3D2,3 + D2,3 / D1,3D3,0D2,3 + 1 / D3,0D1,3 ) | |
| + 2( D2,4 / D1,4D3,1D2,3 + D2,1 / D3,1D1,4D2,3 + 1 / D1,4D3,1 ) | ||
| + 2( D2,4 / D1,4D2,4D3,2 + 1 / D1,4D3,2 ) | ||
| = | 2( D2,0 / D3,0D3,1D3,2 - 2 / D3,0D3,1 | |
| - D4,2 / D3,1D3,2D4,1 + D2,1 / D3,1D3,2D4,1 - 1 / D3,1D4,1 | ||
| - 2 / D3,2D4,1 ) | ||
| = | 2[ ( D2,0 + D3,2 ) / D3,0D3,1D3,2 - 3 / D3,0D3,1 | |
| - D4,2 / D3,1D3,2D4,1 + D2,1 / D3,1D3,2D4,1 + ( D3,1 - D3,2 ) / D3,1D3,2D4,1 | ||
| - 3 / D3,2D4,1 ] | ||
| = | 2( 1 / D3,1D3,2 - 3 / D3,0D3,1 | |
| - D4,2 / D3,1D3,2D4,1 + 2D2,1 / D3,1D3,2D4,1 | ||
| - 3 / D3,2D4,1 ) | ||
| = | 2[ ( D4,1 - D4,2 ) / D3,1D3,2D4,1 - 3 / D3,0D3,1 | |
| + 2D2,1 / D3,1D3,2D4,1 | ||
| - 3 / D3,2D4,1 ] | ||
| = | 6( D2,1 / D3,1D3,2D4,1 - 1 / D3,0D3,1 - 1 / D3,2D4,1 ) | |
| = | 6[ ( D2,1 - D3,1 ) / D3,1D3,2D4,1 - 1 / D3,0D3,1 ] | |
| = | -6[ 1 / D3,1D4,1 + 1 / D3,0D3,1 ] | |
| N(2)j,3[2]( t3 ) | = | 2 / D1,3D2,3 |
| + 2[ u4,1( t3 ) / D3,1D2,3 + 1 / D1,4D2,3 ] | ||
| + 2[ u4,1( t3 ) / D2,4D3,2 + u4,2( t3 ) / D1,4D3,2 + 1 / D1,4D2,4 ] | ||
| = | 2( 1 / D1,3D2,3 + D3,4 / D1,4D3,1D2,3 + 1 / D1,4D2,3 ) | |
| + 2( D3,4 / D1,4D2,4D3,2 + D3,4 / D2,4D1,4D3,2 + 1 / D1,4D2,4 ) | ||
| = | 2[ ( D4,1 - D4,3 ) / D3,1D3,2D4,1 + 1 / D3,2D4,1 ] | |
| + 2( -2D4,3 / D3,2D4,1D4,2 + 1 / D4,1D4,2 ) | ||
| = | 4 / D3,2D4,1 - 4D4,3 / D3,2D4,1D4,2 + 2 / D4,1D4,2 | |
| = | 4( D4,2 - D4,3 ) / D3,2D4,1D4,2 + 2 / D4,1D4,2 | |
| = | 6 / D4,1D4,2 | |
と求めることができて、t = t1, t2, t3 では二階導関数も連続であることを示すことができます。三階導関数は定数で、
N(3)j,3[0]( t ) = 6 / D3,0D2,0D1,0
N(3)j,3[1]( t ) = 6 / D3,0D2,0D1,2 + 6 / D3,0D1,3D2,1 + 6 / D1,4D3,1D2,1
N(3)j,3[2]( t ) = 6 / D3,0D1,3D2,3 + 6 / D1,4D3,1D2,3 + 6 / D1,4D2,4D3,2
N(3)j,3[3]( t ) = -6 / D4,1D4,2D4,3
なので、これは連続にはなりません。
かなり苦労して p = 3 までの関数の様子を確認しました。この結果を見ると、以下のことが推察できます。
Nj,p( t ) の漸化式は次のようなものでした。
Nj,p( t ) は、Nj,p-1( t ) と Nj+1,p-1( t ) の和によって計算されます。Nj,0( t ) は tj ≤ t ≤ tj+1 の範囲のみにゼロ以外の正値 1 を持った階段関数であり、Nj,p( t ) は最終的に Nj,0( t ) で表すことができるので、ノットによって多項式が区分けされるのは明らかです。また、p = 1 において、t ≤ tj, tj+2 ≤ t の領域では Nj,1( t ) = 0 でした。つまり、tj から tj+2 以外の領域において Nj,1( t ) が値を持たないことを意味します。Nj,2( t ) が、Nj,1( t ) と Nj+1,1( t ) の和で表されるということは、前者が tj から tj+2、後者が tj+1 から tj+3 までの領域のみ値を持っていることから、tj から tj+3 までの領域のみ値を持つということになります。これを繰り返し考えれば、Nj,p( t ) が tj から tj+p+1 までの領域のみ値を持つということが示されます。
t = tj のとき、漸化式の右辺第一項は明らかにゼロです。また第二項も、Nj+1,p-1( tj ) = 0 が成り立てばゼロになります。同様に、t = tj+p+1 のとき、漸化式の右辺第二項はゼロになり、第一項は、Nj,p-1( tj+p+1 ) = 0 が成り立てばゼロになります。Nj+1,p-1( t ) は tj+1 から t(j+1)+(p-1)+1 までの領域以外はゼロであり、Nj,p-1( t ) は tj から tj+(p-1)+1 までの領域以外はゼロなので、Nj+1,p-1( tj ) = Nj,p-1( tj+p+1 ) = 0 であり、Nj,p( tj ) = Nj,p( tj+p+1 ) = 0 であることが証明できます。
p = 1 のとき、任意の t に対して Nj,1( t ) ≥ 0 になります。p > 2 の任意の p に対して Nj,p-1( t ) ≥ 0 が成り立つと仮定したとき、漸化式において右辺第一項にある ( t - tj ) / ( tj+p - tj ) は t ≥ tj においてゼロ以上であり、第二項にある ( tj+p+1 - t ) / ( tj+p+1 - tj+1 ) は t ≤ tj+p+1 においてゼロ以上なので、tj ≤ t ≤ tj+p+1 の範囲で Nj,p( t ) ≥ 0 が成り立ちます。tj ≤ t ≤ tj+p+1 以外の範囲では Nj,p-1( t ) も Nj+1,p-1( t ) もともにゼロですから、全ての領域において Nj,p( t ) ≥ 0 が成り立ちます。従って、帰納法により任意の p に対して Nj,p( t ) はゼロ以上の値をとることになります。
Nj,p-1( t ) と Nj+1,p-1( t ) が連続であると仮定した時、[ ( t - tj ) / ( tj+p - tj ) ]・Nj,p-1( t ) と [ ( tj+p+1 - t ) / ( tj+p+1 - tj+1 ) ]・Nj+1,p-1( t ) はやはり連続であり、その和である Nj,p( t ) も連続です。Nj,1( t ) が連続なので、これも帰納法から p ≥ 1 の任意の p に対して Nj,p( t ) は連続であることが示されます。Nj,p( t ) が連続であるのは、正値をとる範囲 tj ≤ t ≤ tj+p+1 のみではないことに注意して下さい。Nj,p( tj ) = Nj,p( tj+p+1 ) = 0 が必ず成り立つことから、全領域に対して Nj,p( t ) は連続です。
さらに Nj,p( t ) の p - 1 階までの導関数が連続であることを証明するためには、一階導関数に対する以下の漸化式が成り立つことを示す必要があります。
N'jp+1 は、積の導関数の公式を利用して
| N'jp+1 | = | ( [ ( t - tj ) / ( tj+p+1 - tj ) ]・Njp )' + ( [ ( tj+p+2 - t ) / ( tj+p+2 - tj+1 ) ]・Nj+1p )' |
| = | [ 1 / ( tj+p+1 - tj ) ]・Njp + [ ( t - tj ) / ( tj+p+1 - tj ) ]・N'jp | |
| + [ -1 / ( tj+p+2 - tj+1 ) ]・Nj+1p + [ ( tj+p+2 - t ) / ( tj+p+2 - tj+1 ) ]・N'j+1p | ||
と展開することができますが、先ほどの漸化式が成り立つと仮定したとき、
| [ 1 / ( tj+p+1 - tj ) ]・Njp | = | [ 1 / ( tj+p+1 - tj ) ]{ [ ( t - tj ) / ( tj+p - tj ) ]・Njp-1 | |
| + [ ( tj+p+1 - t ) / ( tj+p+1 - tj+1 ) ]・Nj+1p-1 } | --- (1) | ||
| [ ( t - tj ) / ( tj+p+1 - tj ) ]・N'jp | = | [ ( t - tj ) / ( tj+p+1 - tj ) ]{ [ p / ( tj+p - tj ) ]・Njp-1 | |
| - [ p / ( tj+p+1 - tj+1 ) ]・Nj+1p-1 } | --- (2) | ||
| [ -1 / ( tj+p+2 - tj+1 ) ]・Nj+1p | = | [ -1 / ( tj+p+2 - tj+1 ) ]{ [ ( t - tj+1 ) / ( tj+p+1 - tj+1 ) ]・Nj+1p-1 | |
| + [ ( tj+p+2 - t ) / ( tj+p+2 - tj+2 ) ]・Nj+2p-1 } | --- (3) | ||
| [ ( tj+p+2 - t ) / ( tj+p+2 - tj+1 ) ]・N'j+1p | = | [ ( tj+p+2 - t ) / ( tj+p+2 - tj+1 ) ]{ [ p / ( tj+p+1 - tj+1 ) ]・Nj+1p-1 | |
| - [ p / ( tj+p+2 - tj+2 ) ]・Nj+2p-1 } | --- (4) | ||
とさらに展開することができます。項の数が増えたので再び tj+m を tm で表し、(1), (2) の和に対する Njp-1 と Nj+1p-1 の係数をそれぞれ K1, K2 としてその値を求めると
| K1 | = | [ 1 / ( tp+1 - t0 ) ][ ( t - t0 ) / ( tp - t0 ) ] + [ ( t - t0 ) / ( tp+1 - t0 ) ][ p / ( tp - t0 ) ] |
| = | ( p + 1 )( t - t0 ) / ( tp - t0 )( tp+1 - t0 ) | |
| K2 | = | [ 1 / ( tp+1 - t0 ) ][ ( tp+1 - t ) / ( tp+1 - t1 ) ] - [ ( t - t0 ) / ( tp+1 - t0 ) ][ p / ( tp+1 - t1 ) ] |
| = | [ ( tp+1 - t ) - p( t - t0 ) ] / ( tp+1 - t0 )( tp+1 - t1 ) | |
| = | [ ( tp+1 + pt0 ) - ( p + 1 )t ) ] / ( tp+1 - t0 )( tp+1 - t1 ) |
(3), (4) の和に対する Nj+1p-1 と Nj+2p-1 の係数をそれぞれ K3, K4 とすると
| K3 | = | [ -1 / ( tp+2 - t1 ) ][ ( t - t1 ) / ( tp+1 - t1 ) ] + [ ( tp+2 - t ) / ( tp+2 - t1 ) ][ p / ( tp+1 - t1 ) ] |
| = | [ -( t - t1 ) + p( tp+2 - t ) ] / ( tp+1 - t1 )( tp+2 - t1 ) | |
| = | [ ( t1 + ptp+2 ) - ( p + 1 )t ] / ( tp+1 - t1 )( tp+2 - t1 ) | |
| K4 | = | [ -1 / ( tp+2 - t1 ) ][ ( tp+2 - t ) / ( tp+2 - t2 ) ] - [ ( tp+2 - t ) / ( tp+2 - t1 ) ][ p / ( tp+2 - t2 ) ] |
| = | -( p + 1 )( tp+2 - t ) / ( tp+2 - t1 )( tp+2 - t2 ) |
になり、K2 + K3 は
| K2 + K3 | = | [ ( tp+1 + pt0 ) - ( p + 1 )t ] / ( tp+1 - t0 )( tp+1 - t1 ) |
| + [ ( t1 + ptp+2 ) - ( p + 1 )t ] / ( tp+1 - t1 )( tp+2 - t1 ) | ||
| = | { ( tp+2 - t1 )[ ( tp+1 + pt0 ) - ( p + 1 )t ] + ( tp+1 - t0 )[ ( t1 + ptp+2 ) - ( p + 1 )t ] } | |
| / ( tp+1 - t0 )( tp+1 - t1 )( tp+2 - t1 ) | ||
| = | ( p + 1 )[ ( tp+1tp+2 - t0t1 ) - ( tp+2 - t1 )t - ( tp+1 - t0 )t ] | |
| / ( tp+1 - t0 )( tp+1 - t1 )( tp+2 - t1 ) | ||
| = | ( p + 1 )[ ( tp+2 - t1 )tp+1 + ( tp+1 - t0 )t1 - ( tp+2 - t1 )t - ( tp+1 - t0 )t ] | |
| / ( tp+1 - t0 )( tp+1 - t1 )( tp+2 - t1 ) | ||
| = | ( p + 1 )[ ( tp+2 - t1 )( tp+1 - t ) + ( tp+1 - t0 )( t1 - t ) ] | |
| / ( tp+1 - t0 )( tp+1 - t1 )( tp+2 - t1 ) | ||
| = | ( p + 1 )( tp+1 - t ) / ( tp+1 - t0 )( tp+1 - t1 ) | |
| - ( p + 1 )( t - t1 ) / ( tp+1 - t1 )( tp+2 - t1 ) | ||
となることから、N'jp+1 は最終的に
| N'jp+1 | = | K1・Njp-1 + ( K2 + K3 )・Nj+1p-1 + K4・Nj+2p-1 |
| = | [ ( p + 1 )( t - t0 ) / ( tp - t0 )( tp+1 - t0 ) ]・Njp-1 | |
| + [ ( p + 1 )( tp+1 - t ) / ( tp+1 - t0 )( tp+1 - t1 ) - ( p + 1 )( t - t1 ) / ( tp+1 - t1 )( tp+2 - t1 ) ]・Nj+1p-1 | ||
| - [ ( p + 1 )( tp+2 - t ) / ( tp+2 - t1 )( tp+2 - t2 ) ]・Nj+2p-1 | ||
| = | [ ( p + 1 ) / ( tp+1 - t0 ) ]{ [ ( t - t0 ) / ( tp - t0 ) ]・Njp-1 + [ ( tp+1 - t ) / ( tp+1 - t1 ) ]・Nj+1p-1 } | |
| - [ ( p + 1 ) / ( tp+2 - t1 ) ]{ [ ( t - t1 ) / ( tp+1 - t1 ) ]・Nj+1p-1 + [ ( tp+2 - t ) / ( tp+2 - t2 ) ]・Nj+2p-1 } | ||
| = | [ ( p + 1 ) / ( tp+1 - t0 ) ]・Njp - [ ( p + 1 ) / ( tp+2 - t1 ) ]・Nj+1p | |
となり、p で漸化式が成り立てば、p + 1 でも同じ式が成り立つことになります。p = 1 のとき、導関数 N'j,1( t ) は、
N'j,1[0]( t ) = 1 / ( t1 - t0 )
N'j,1[1]( t ) = -1 / ( t2 - t1 ) より
N'j,1( t ) = [ 1 / ( t1 - t0 ) ]・Nj0 - [ 1 / ( t2 - t1 ) ]・Nj+10
なので漸化式が成り立ち、帰納法により、ゼロより大きな任意の p に対しても成り立つことになります。
導関数に対する漸化式から、N'j,p( t ) は Nj,p-1( t ) と Nj+1,p-1( t ) の線形結合で表されることがわかります。p > 1 ならば、Nj,p-1( t ) と Nj+1,p-1( t ) は連続です。また、Nj,p-1( t ) は [ tj, tj+p ] のみ値を持ち、Nj,p-1( tj ) = Nj,p-1( tj+p ) = 0 が成り立ちます。同様に、Nj+1,p-1( t ) は [ tj+1, tj+p+1 ] のみ値を持ち、Nj+1,p-1( tj+1 ) = Nj+1,p-1( tj+p+1 ) = 0 なので、それらの線形結合である N'j,p( t ) は連続で、[ tj, tj+p+1 ] のみ値を持ち、N'j,p( tj ) = N'j,p( tj+p+1 ) = 0 が成り立ちます。
二階導関数は N'j,p-1( t ) と N'j+1,p-1( t ) の線形結合で表されることになるので、上記と同様に考えれば、二階導関数 N(2)j,p( t ) は連続であり、[ tj, tj+p+1 ] のみ値を持ち、N(2)j,p( tj ) = N(2)j,p( tj+p+1 ) = 0 であることがわかります。これを繰り返すと、0 ≤ k ≤ p - 1 の範囲において k 階導関数は連続であり、[ tj, tj+p+1 ] のみ値を持ち、N(k)j,p( tj ) = N(k)j,p( tj+p+1 ) = 0 であることが示されます。しかし、p 階導関数では成り立たなくなります。例えば p = 1 のとき、上式をみれば明らかなように N'j,1( t ) は不連続です。N(2)j,2( t ) は N'j,1( t ) と N'j+1,1( t ) の線形結合ですから、これも連続になるとは限りません。
Nj,p( t ) は「基底関数」という名が付けられていることから推測できるように、基底として利用することができます。Nj,p( t ) による線形結合を
としたとき、PM,p( t ) = 0 が任意の t で成り立つためには全ての係数 aj がゼロになる必要があることが示されれば Nj,p( t ) は基底関数になります。p = 0 のとき、
より、任意の t に対して PM,p( t ) がゼロになるためには明らかに全ての係数 aj がゼロでなければなりません。Nj,p-1( t ) が基底関数であると仮定したとき、
より
| PM,p( t ) | = | Σj{0→M-p-1}( ajNj,p( t ) ) |
| = | Σj{0→M-p-1}( aj{ [ ( t - tj ) / ( tj+p - tj ) ]・Njp-1 + [ ( tj+p+1 - t ) / ( tj+p+1 - tj+1 ) ]・Nj+1p-1 } ) | |
| = | a0[ ( t - t0 ) / ( tp - t0 ) ]・N0p-1 | |
| + Σj{1→M-p-1}( [ aj-1( tj+p - t ) / ( tj+p - tj ) + aj( t - tj ) / ( tj+p - tj ) ]・Njp-1 ) | ||
| + aM-p-1[ ( tM - t ) / ( tM - tM-p ) ]・NM-(p-1)-1p-1 | ||
| = | [ a0( t - t0 ) / ( tp - t0 ) ]・N0p-1 | |
| + Σj{1→M-p-1}( { [ aj-1( tj+p - t ) + aj( t - tj ) ] / ( tj+p - tj ) }・Njp-1 ) | ||
| + [ aM-p-1( tM - t ) / ( tM - tM-p ) ]・NM-(p-1)-1p-1 | ||
と表されるので、
a0( t - t0 ) = 0
aj-1( tj+p - t ) + aj( t - tj ) = 0 ( j = 1, 2, ... M - p - 1 )
aM-p-1( tM - t ) = 0
が任意の t に対して成り立たなければなりません。最初の式によって、a0 = 0 である必要があることは明らかです。j = 1 の場合、第二式に a0 = 0 を代入すると a1( t - t1 ) = 0 が任意の t に対して成り立つ必要があることになって、a1 = 0 でなければなりません。これを繰り返すと、任意の j に対して aj = 0 である必要があることになり、Nj,p( t ) も基底関数になります。よって、帰納法によって、任意の p に対して Nj,p( t ) は基底関数です。
ところで、aj が全て 1 だったとき、1 ≤ j ≤ M - p - 1 における Njp-1 の係数は
となるので、
となります。N0,p-1( t ) が値を持つのは t0 ≤ t ≤ tp の範囲であり、NM-(p-1)-1,p-1( t ) が値を持つのは tM-p ≤ t ≤ tM の範囲なので、tp ≤ t ≤ tM-p の範囲においては N0p-1 と NM-(p-1)-1,p-1( t ) の項は無視することができて
となります。実際に、p = 1 の場合を求めてみると、
| PM,1( t ) | = | Σj{0→M-2}( Nj,1( t ) ) |
| = | Σj{0→M-2}( [ ( t - tj ) / ( tj+1 - tj ) ]・Nj0 + [ ( tj+2 - t ) / ( tj+2 - tj+1 ) ]・Nj+10 ) | |
| = | [ ( t - t0 ) / ( t1 - t0 ) ]・N00 + Σj{1→M-2}( Nj0 ) + [ ( tM - t ) / ( tM - tM-1 ) ]・NM-10 |
となりますが、Nj0 は tj ≤ t ≤ tj+1 のみ 1 で残りの範囲はゼロなので、
| PM,1( t ) | = | ( t - t0 ) / ( t1 - t0 ) | ( t0 ≤ t ≤ t1 ) |
| = | 1 | ( t1 ≤ t ≤ tM-1 ) | |
| = | ( tM - t ) / ( tM - tM-1 ) | ( tM-1 ≤ t ≤ tM ) |
という結果が得られます。これは、t1 ≤ t ≤ tM-1 において Σj{0→M-2}( Nj1 ) = 1 であることを意味し、p = 2 に対して同じ処理を行うと t2 ≤ t ≤ tM-2 の範囲で PM,2( t ) = Σj{1→M-3}( Nj1 ) となるので、N01 が t0 ≤ t ≤ t2、NM-21 が tM-2 ≤ t ≤ tM の範囲でしか値を持たないことから
になります。これを繰り返し適用することによって、任意の p に対して
という結果を得ることができます。
B-スプライン基底関数を求めるためのサンプル・プログラムを以下に示します。
/* CalcBSplineBasisFunc : B-スプライン基底関数の計算 const vector<double>& knot : ノット列 unsigned int j : ノット列の開始番号 unsigned int p : 次数 double t : 計算対象の独立変数 ノット列は昇順である必要があるが、そのチェックは行わない 戻り値 : 計算結果 */ double CalcBSplineBasisFunc( const vector<double>& knot, unsigned int j, unsigned int p, double t ) { if ( knot.size() == 0 ) return( NAN ); // ノット列のデータ長が充分でない場合は nan を返す unsigned int m = knot.size() - 1; if ( m < j + p + 1 ) return( NAN ); // 正値をとる範囲外ならゼロを返す if ( ( t < knot[j] ) || ( t > knot[j + p + 1] ) ) return( 0 ); // p = 0 かつ knot[j] <= t <= knot[j + p + 1] なら 1 を返す if ( p == 0 ) return( 1 ); // p = 1 の場合、三角の頂点の値は特別扱い if ( p == 1 && t == knot[j + 1] ) return( 1 ); // 漸化式の計算 double d1 = ( knot[j + p] == knot[j] ) ? 0 : ( t - knot[j] ) * CalcBSplineBasisFunc( knot, j, p - 1, t ) / ( knot[j + p] - knot[j] ); double d2 = ( knot[j + p + 1] == knot[j + 1] ) ? 0 : ( knot[j + p + 1] - t ) * CalcBSplineBasisFunc( knot, j + 1, p - 1, t ) / ( knot[j + p + 1] - knot[j + 1] ); return( d1 + d2 ); }
内容は非常にシンプルで、「deBoor-Coxの漸化式」を使って次数の低い式から順に再帰的に計算をしているだけです。p = 0 なら階段関数になるので、値のある領域内なら 1 を返します。また、p の値に関係なく、t が値を持つ領域を外れている場合は即座にゼロを返しています。
なお、Nj,0( tj+1 ) = Nj+1,0( tj+1 ) = 1 にすると、漸化式による Nj,1( tj+1 ) の計算結果は
となってしまい、本来の値 1 とは異なる結果となります。それを防ぐため、Nj,1( tj+1 ) の計算は特別扱いして常に 1 を返すようにしています。
漸化式を計算するときの注意点として、tj = tj+p となるようなノットが含まれた場合、漸化式の項の中でゼロ除算が発生します。このときは、tj ≤ tj+1 ≤ ... ≤ tj+p-1 ≤ tj+p が成り立たなければならないことから tj = tj+1 = ... = tj+p-1 = tj+p であることを意味します。tj = tj+p のとき、次数が p の B-スプライン基底関数でゼロ除算が発生するのは
Nj-1,p( t ) = [ ( t - tj-1 ) / ( tj+p-1 - tj-1 ) ]・Nj-1p-1 + [ ( tj+p - t ) / ( tj+p - tj ) ]・Njp-1
Nj,p( t ) = [ ( t - tj ) / ( tj+p - tj ) ]・Njp-1 + [ ( tj+p+1 - t ) / ( tj+p+1 - tj+1 ) ]・Nj+1p-1
のときで、Nj-1,p( t ) のときは第二項、Nj,p( t ) のときは第一項がゼロ除算を含みます。それらは Njp-1 を含みますが、その定義域は tj ≤ t ≤ tj+p であり、存在しないものとみなしても問題はないことになります。よって、ゼロ除算が発生する項は無視する(ゼロとする)対処が必要です。
B-スプライン基底関数をブレンディング関数とした曲線を「B-スプライン曲線 (B-Spline Curve)」といいます。M 個の点列 { Pj } ( j = 0, 1, ... M - 1 ) に対し、B-スプライン曲線 S(t) は以下の式で表されます。
NM-1,p( t ) は、tM-1 ≤ t ≤ t(M-1)+p+1 のみの領域で正値をもつので、ブレンディング関数の数は M なのに対し、必要なノット列は t0 から tM+p までの M + p + 1 個になることに注意して下さい。また、t0 ≤ t ≤ t1 においては S( t ) の和の成分は N0,p( t ) のみであり、N0,p( t0 ) = 0 であることから、S( t0 ) = 0 となります。また、同様の考え方によって S( tM+p ) = 0 です。したがって、t0 ≤ t ≤ tM+p の範囲で曲線を描画した場合は、必ず原点でつながった閉曲線の形になります。
後ほど説明をしますが、ベジェ曲線のブレンディング関数であるバーンスタイン基底関数は B-スプライン基底関数の特殊形です。従って、ベジェ曲線の持つ特性の多くは B-スプライン曲線にもあります。
| 曲線の特性 | ベジェ曲線 | B-スプライン曲線 |
|---|---|---|
| アフィン不変性 | ○ | ○ |
| 凸閉包性 | ○ | ○ |
| 対称性 | ○ | × |
| 変動減少特性 | ○ | ○ |
| 線形独立 | ○ | ○ |
| 端点通過 | ○ | × |
| 端点で接線になる | ○ | × |
| 局所制御 | × | ○ |
B-スプライン基底関数が基底となることは前節ですでに証明しています。また、tp ≤ t ≤ tM の範囲においては Σj{0→M-p-1}( Nj,p( t ) ) = 1 であり、Nj,p( t ) がゼロ以上の値であることもわかっているので、tp ≤ t ≤ tM の範囲で描画すればアフィン不変性と凸閉包性が成り立ちます。
対称性に対しては、
が成り立てば
| S( t ) | = | Σj{0→M-1}( Pj・Nj,p( t ) ) |
| = | Σj{0→M-1}( Pj・NM-1-j,p( t0 + tM+p - t ) ) | |
| = | Σj{0→M-1}( PM-1-j・Nj,p( t0 + tM+p - t ) ) |
となるので、点列を PM-1 から P0 へ、t を tM+p から t0 へと逆側にたどっても曲線は同じになります。しかし、ベジェ曲線については対称性が常に成り立つのに対し、B-スプライン曲線の場合は常に成り立つとは限りません。例えば p = 0 のとき、NM-1-j,0( t0 + tM - t ) は t0 + tM - t が tM-1-j から tM-j の間にあるときだけ 1 になるので、
より
で 1 になります。Nj,0( t ) が tj から tj+1 の間で 1 となることから、
tj = t0 + tM - tM-j より tj + tM-j = t0 + tM
tj+1 = t0 + tM - tM-1-j より tj+1 + tM-1-j = t0 + tM
でなければならず、ノット列を両端から中央方向へ順番に抽出して求めた和が全て等しくなる必要があります。例えば、ノット列を中央で二つに分けた時、前半と後半でそれぞれ同値となったり、ノット列が自然数列などの等差数列になればこの条件を満たします。
t = tp のとき S( tp ) = P0 となるためには、N0,p( tp ) = 1、Nj,p( tp ) = 0 ( j > 0 ) である必要があります。しかし、これは明らかに、常には成り立ちません。同様に、S( tM ) = PM-1 も常には成り立たないので、B-スプライン曲線は一般には端点を通過しません。しかし、p = 1 のときは常に Nj,1( tj+1 ) = 1 であり、N0,1( t1 ) = NM-1,1( tM ) = 1 なので、必ず端点を通過するのみでなく、全ての点を通過することも保証されます。すなわち、p = 1 の場合の B-スプライン曲線は各点を結んだ折れ線になります。
以上の結果だけでは、ベジェ曲線に比べて特性としては劣っているようにみえますが、ベジェ曲線にはない優れた特性として「局所制御」があります。ベジェ曲線の場合、点列の一つを移動すると曲線全体にその影響が及びます。ベジェ曲線では基底関数が全定義域にわたって値を持ち、係数の変化が全定義域に及ぶためにそうなるのですが、B-スプライン基底関数の定義域は次数 p で決まるので、ある点 Pk が変化した時に影響を受ける基底関数は tk を定義域に含むもの、すなわち Nk-p-1p から Nkp までとなります。しかし、Nk-p-1p と Nkp は tk が定義域の端にあたり、そこでの値はゼロなので、曲線の軌跡には影響を与えません。結局、影響のある基底関数は Nk-pp から Nk-1p までの p 個となります。また、S( t ) が変化する定義域は tk-p ≤ t ≤ tk+p となります。
ベジェ曲線では新たな点を追加した上でいくつかの区分に分けてスプライン曲線として描画をすることで局所制御できるように対応していましたが、B-スプライン曲線の場合は p を制御することによって局所性を持たせながら曲線を描画することができます。ベジェ曲線の場合、端点で接線となるため、スプライン曲線として描画するときに分割する二点(一つのスプライン曲線の終点と、次のスプライン曲線の始点のこと)を結んだ線分上に新たな点を追加してそれを各スプライン曲線の終点・始点とすれば、二つのスプライン曲線は滑らかに接続されます。これは、それぞれの端点における接線の方向が等しくなることから成り立つのですが、さらに高階の導関数については必ずしも成り立ちません。実際、ベジェ曲線のブレンディング関数であるバーンスタイン基底関数の導関数は
| dbk,N(t) / dt | = | N・C( N - 1, k - 1 )・tk-1( 1 - t )N-k - N・C( N - 1, k )・tk( 1 - t )N-k-1 | ( 0 < k < N ) |
| = | -N( 1 - t )N-1 | ( k = 0 ) | |
| = | NtN-1 | ( k = N ) |
なので、二階導関数は
| d2bk,N(t) / dt2 | = | N( N - 1 )・C( N - 2, k - 2 )・tk-2( 1 - t )N-k - N( N - 1 )・C( N - 2, k - 1 )・tk-1( 1 - t )N-k-1 | |
| - N( N - 1 )・C( N - 2, k - 1 )・tk-1( 1 - t )N-k-1 + N( N - 1 )・C( N - 2, k )・tk( 1 - t )N-k-2 | |||
| = | N( N - 1 )[ C( N - 2, k - 2 )・tk-2( 1 - t )N-k - 2C( N - 2, k - 1 )・tk-1( 1 - t )N-k-1 | ||
| + C( N - 2, k )・tk( 1 - t )N-k-2 ] | ( 1 < k < N - 1 ) | ||
| = | -N( N - 1 )・( 1 - t )N-2 - N( N - 1 )・( 1 - t )N-2 + N( N - 1 )( N - 2 )・t( 1 - t )N-3 | ||
| = | -2N( N - 1 )・( 1 - t )N-2 + N( N - 1 )( N - 2 )・t( 1 - t )N-3 | ( k = 1 ) | |
| = | N( N - 1 )( N - 2 )・tN-3( 1 - t ) - N( N - 1 )・tN-2 - N( N - 1 )・tN-2 | ||
| = | N( N - 1 )( N - 2 )・tN-3( 1 - t ) - 2N( N - 1 )・tN-2 | ( k = N - 1 ) | |
| = | N( N - 1 )( 1 - t )N-2 | ( k = 0 ) | |
| = | N( N - 1 )tN-2 | ( k = N ) | |
となって、t = 0 のとき
| d2bk,N(0) / dt2 | = | 0 | ( 2 < k ≤ N ) |
| = | N( N - 1 ) | ( k = 0, 2 ) | |
| = | -2N( N - 1 ) | ( k = 1 ) |
t = 1 のとき
| d2bk,N(1) / dt2 | = | 0 | ( 0 ≤ k < N - 2 ) |
| = | N( N - 1 ) | ( k = N - 2, N ) | |
| = | -2N( N - 1 ) | ( k = N - 1 ) |
なので、ベジェ曲線の t = 0, 1 での二階導関数の値は
| d2P(0) / dt2 | = | Σk{0→N}( Pk・d2bk,N(0) / dt2 ) |
| = | N( N - 1 )( P0 - 2P1 + P2 ) | |
| = | N( N - 1 )( P1,0 + P1,2 ) | |
| d2P(1) / dt2 | = | Σk{0→N}( Pk・d2bk,N(1) / dt2 ) |
| = | N( N - 1 )( PN-2 - 2PN-1 + PN ) | |
| = | N( N - 1 )( PN-1,N-2 + PN-1,N ) |
となります。但し、Pm,n は、点 Pm から点 Pn までを結んだベクトルを表します。点 Pn と 点 Pn+1 を結んだ線分上に新たな点 Pm を用意し、Pm を終点及び始点としてスプライン曲線の形でベジェ曲線を描画する場合、二つのベジェ曲線は Pm で滑らかにつながるのでした。しかし、Pm における両曲線の二階導関数の値は N( N - 1 )( Pn,n-1 + Pn,m ) と N( N - 1 )( Pn+1,m + Pn+1,n+2 ) なので、Pn,n-1 + Pn,m = Pn+1,m + Pn+1,n+2 が成り立たない限り一致しません。
曲線において、k 階導関数の値が連続である場合は「Ck-連続 (Ck-Continuity)」といいます。曲線が全てつながっていれば C0-連続であり、接線の向きと大きさが連続であれば C1-連続となります。上述のようにベジェ曲線をスプライン曲線として描画した場合、曲線は滑らかになりますが、スプライン曲線どうしがつながった点 Pm での接線ベクトルは N( Pm - Pn ) と N( Pn+1 - Pm ) なので、Pm - Pn = Pn+1 - Pm が成り立たなければ、方向が等しいだけで連続にはならず、C1-連続にはなりません。このように、k 階導関数ベクトルの方向だけが等しく、大きさは異なるような場合は「Gk-連続 (Gk-Continuity)」といいます。従って、ベジェ曲線によるスプライン曲線は G1-連続ということになります。ベジェ曲線では二階導関数ベクトルが向きも大きさも一致するとは限らないことから、C2-連続でも G2-連続でもありません。Ck-連続や Gk-連続は曲線の滑らかさを表す指標となり、大きな k に対して成り立つほど滑らかさの度合いは高くなります (ベジェ曲線のブレンディング関数であるバーンスタイン基底関数は高階導関数が存在するので、点列全てを使ってベジェ曲線を描画した場合は充分滑らかな曲線が得られます。上記の説明は、あくまでも点列をいくつかのグループに分割してスプライン曲線の形でベジェ曲線を描画した場合であることに注意して下さい)。
B-スプライン基底関数 Nj,p( t ) は、任意の t に対し、0 ≤ k ≤ p - 1 の整数 k について k 階導関数まで連続でした。従って、Nj,p( t ) の線形結合である S( t ) も k 階導関数まで連続であることになり、B-スプライン曲線は Cp-1-連続なので、ベジェ曲線を使ったスプライン曲線よりも滑らかな曲線を描画することができます。
B-スプライン曲線は、ノットの配列の仕方によって三つのタイプに分類されます。
ノット列の間隔が等しければ、漸化式の一部は定数化することができます。例えば、tj = j ( j = 0, 1, ... M ) である場合、
| Nj,p( t ) | = | [ ( t - tj ) / ( tj+p - tj ) ]・Njp-1 + [ ( tj+p+1 - t ) / ( tj+p+1 - tj+1 ) ]・Nj+1p-1 |
| = | { ( t - j ) / [ ( j + p ) - j ] }・Njp-1 + { [ ( j + p + 1 ) - t ] / [ ( j + p + 1 ) - ( j + 1 ) ] }・Nj+1p-1 | |
| = | { ( t - j )・Njp-1 + [ ( p + 1 ) - ( t - j ) ]・Nj+1p-1 } / p |
となります。p = 0 のときは幅が一定の矩形になり、形状は全て等しくなります。p = 1 ならば
| Nj,1( t ) | = | ( t - j )・Nj0 + [ 2 - ( t - j ) ]・Nj+10 | |
| = | t - j | ( j ≤ t ≤ j + 1 ) | |
| = | 2 - ( t - j ) | ( j + 1 ≤ t ≤ j + 2 ) | |
であり、全ての j に対して底辺が 2 で高さ 1 の三角形となります。一様のときは、任意の p に対し、B-スプライン基底関数は定義域が異なるだけで全て同じ形状になります。従って、N0,p( t ) さえ求めてしまえば、形状をシフトするだけで任意の j に対する基底関数が得られます。
開一様は、ノット列の両端の値が p + 1 だけ等しい場合を指します。開一様なノット列の最初の値を a とした時、t0 = t1 = ... = tp = a なので、N0,p( t ) は
| N0,p( t ) | = | [ ( t - t0 ) / ( tp - t0 ) ]・N0p-1 + [ ( tp+1 - t ) / ( tp+1 - t1 ) ]・N1p-1 |
| = | [ ( tp+1 - t ) / ( tp+1 - a ) ]・N1p-1 | |
| = | [ ( tp+1 - t ) / ( tp+1 - a ) ]・[ ( tp+1 - t ) / ( tp+1 - a ) ]・N2p-2 | |
| : | ||
| = | [ ( tp+1 - t ) / ( tp+1 - a ) ]p・Np0 |
となり、Np0 の定義域が [ tp, tp+1 ] = [ a, tp+1 ] なので N0,p( tp ) = N0,p( a ) = 1 になります。同様に、ノット列の最後の値を b とした時の NM-1,p( t ) は、tM = tM+1 = ... = tM+p = b より
| NM-1,p( t ) | = | [ ( t - tM-1 ) / ( tM+p-1 - tM-1 ) ]・NM-1p-1 + [ ( tM+p - t ) / ( tM+p - tM ) ]・NMp-1 |
| = | [ ( t - tM-1 ) / ( b - tM-1 ) ]・NM-1p-1 | |
| = | [ ( t - tM-1 ) / ( b - tM-1 ) ]・[ ( t - tM-1 ) / ( b - tM-1 ) ]・NM-1p-2 | |
| : | ||
| = | [ ( t - tM-1 ) / ( b - tM-1 ) ]p・NM-10 |
となり、NM-10 の定義域が [ tM-1, tM ] = [ tM-1, b ] なので NM-1,p( tM ) = NM-1,p( b ) = 1 になります。この結果は、開一様である場合は端点を通過するということを表します。ここで、ノット列の数を 2p + 2 とし、前半の p + 1 個を 0、残り後半を 1 としたとき、p = 0 ならばノット列は { 0, 1 } であり
| N0,0( t ) | = | 1 | ( 0 ≤ t ≤ 1 ) |
| = | 0 | ( それ以外 ) |
となります。p = 1 ならば、ノット列は { 0, 0, 1, 1 } で
| N0,1( t ) | = | [ ( t - t0 ) / ( t1 - t0 ) ]・N00 + [ ( t2 - t ) / ( t2 - t1 ) ]・N10 |
| = | 1 - t | |
| N1,1( t ) | = | [ ( t - t1 ) / ( t2 - t1 ) ]・N10 + [ ( t3 - t ) / ( t3 - t2 ) ]・N20 |
| = | t |
であり、任意の p に対しては t0 = t1 = ... = tp = 0、tp+1 = tp+2 = ... = t2p+1 = 1 なので
| Nj,p( t ) | = | [ ( t - tj ) / ( tj+p - tj ) ]・Njp-1 + [ ( tj+p+1 - t ) / ( tj+p+1 - tj+1 ) ]・Nj+1p-1 |
| = | t・Njp-1 + ( 1 - t )・Nj+1p-1 |
という結果が得られます。バーンスタイン基底関数の漸化式は
なので、Nj,p( t ) と bj+1,p( t ) は 1 ≤ j ≤ p - 1 の間で右辺が一致します。左辺は添字が一つ分シフトしているので、下図 2-3 を見ると N0,p( t ) と等しくなるバーンスタイン基底関数は bp,p( t ) となるようにみえますが、実際には
| N0,p( t ) | = | [ ( t - t0 ) / ( tp - t0 ) ]・N0p-1 + [ ( tp+1 - t ) / ( tp+1 - t1 ) ]・N1p-1 |
| = | ( 1 - t )・N1p-1 | |
| = | ( 1 - t )・{ [ ( t - t1 ) / ( tp-1 - t1 ) ]・N1p-2 + [ ( tp+1 - t ) / ( tp+1 - t2 ) ]・N2p-2 } | |
| = | ( 1 - t )2・N2p-2 | |
| : | ||
| = | ( 1 - t )p | |
| = | b0,p( t ) |
より、N0,p( t ) と b0,p( t ) が一致します。同様に、N10 から Np+10 までの式で再帰的に得られる N1,p( t ) と ( 実際には存在しませんが ) b10 から bp+10 までの式で再帰的に得られる bp+1,p( t ) が一致し、bp+1,p( t ) は b1,p( t ) を意味します。さらに、Np0 から N2p0 までの式で再帰的に得られる Np,p( t ) と bp0 から b2p0 までの式で再帰的に得られる b2p,p( t ) が一致し、b2p,p( t ) は bp,p( t ) を意味します。よって、この場合の Nj,p( t ) はバーンスタイン基底関数そのものであり、描画される曲線もベジェ曲線そのものとなります。
下のグラフは、ノット列を { 0, 0, 0, 1, 1, 1 } としたときの二次の B-スプライン基底関数を表しています。
これは、二次のバーンスタイン基底関数
b0,2(t) = ( 1 - t )2
b1,2(t) = 2t( 1 - t )
b2,2(t) = t2
と同一であることがこのグラフからもわかります。
非一様なノット列を利用すると、表現できる曲線の形状は増えます。例えば、二次の B-スプライン関数に対し、ノット列の途中に、値が等しいノットを次数と等しい二個だけ挿入すると、その開始番号を j としたとき、tj = tj+1 なので、tm - tn = Dm,n と表すと
| N'j-1,2[0]( t ) | = | 2( t - tj-1 ) / Dj+1,j-1Dj,j-1 |
| = | 2( t - tj-1 ) / Dj,j-12 | |
| = | 2( t - tj-1 ) / ( tj - tj-1 )2 | |
| N'j-1,2[2]( t ) | = | 2( t - tj+2 ) / Dj,j+2Dj+1,j+2 |
| = | 2( t - tj+2 ) / Dj,j+22 | |
| = | 2( t - tj+2 ) / ( tj - tj+2 )2 |
となり、N'j-1,2[1]( t ) は定義できません。このとき、導関数は tj で不連続で、正値 1 / ( tj - tj-1 ) から負値 1 / ( tj - tj+2 ) に変わります。一般に、次数 p の B-スプライン曲線に対してノット列の途中に p 個の同数を挿入すると「尖点(Cusp)」として表現することができるので、急激に折れ曲がり尖った部分を作りたい時に有効です。
上に示したグラフの左側は、ノット列を { 0, 0.2, 0.5, 1.5, 2.2, 3.0 } としたときの二次の B-スプライン関数です、右側は、中央の値を少し変えて { 0, 1.0, 1.5, 1.5, 2.2, 3.0 } としたもので、j = 1 のときのグラフは最大値をとるところで線が折れ曲がった状態になっています。この性質を利用すると、曲線に尖点を持たせることができるわけです。
B-スプライン曲線の軌跡を計算するためのサンプル・プログラムを以下に示します。
/********************************************************** BSplineCurveBase : B-スプライン曲線描画用基底クラス **********************************************************/ class BSplineCurveBase : public ParametricEquation { unsigned int p_; // 次数 vector<double> x_; // 点列の x 座標 vector<double> y_; // 点列の y 座標 protected: vector<double> knot_; // ノット列(protected) private: // calc : 曲線の X/Y 座標値を計算する(純粋仮想関数) virtual double calc( const vector<double>& p, double t ) = 0; // set : メンバ変数の初期化 void set( vector<double>::const_iterator knot0, vector<double>::const_iterator knot1, vector< Coord<double> >::const_iterator p0, vector< Coord<double> >::const_iterator p1, unsigned int p ); public: /* BSplineCurveBase コンストラクタ */ /* 配列の範囲を指定 vector<double>::const_iterator knot0, knot1 : ノット列の範囲 vector< Coord<double> >::const_iterator p0, p1 : 点列の範囲 (knot1,p1 は末尾の次を表すため含まれない) unsigned int p : 次数 */ BSplineCurveBase( vector<double>::const_iterator knot0, vector<double>::const_iterator knot1, vector< Coord<double> >::const_iterator p0, vector< Coord<double> >::const_iterator p1, unsigned int p ) { set( knot0, knot1, p0, p1, p ); } /* 配列全体を指定 const vector<double>& knot : ノット列 const vector< Coord<double> >& pnt : 点列 unsigned int p : 次数 */ BSplineCurveBase( const vector<double>& knot, const vector< Coord<double> >& pnt, unsigned int p ) { set( knot.begin(), knot.end(), pnt.begin(), pnt.end(), p ); } // 点列のサイズを返す unsigned int size() const { return( x_.size() ); } // 次数を返す unsigned int order() const { return( p_ ); } // x, y の値を求める virtual double x( double t ) { return( calc( x_, t ) ); } virtual double y( double t ) { return( calc( y_, t ) ); } // 仮想デストラクタ virtual ~BSplineCurveBase() {} }; /* BSplineCurveBase::set : メンバ変数の初期化 vector<double>::const_iterator knot0, knot1 : ノット列の範囲 vector< Coord<double> >::const_iterator p0, p1 : 点列の範囲 (knot1,p1 は末尾の次を表すため含まれない) unsigned int p : 次数 */ void BSplineCurveBase::set( vector<double>::const_iterator knot0, vector<double>::const_iterator knot1, vector< Coord<double> >::const_iterator p0, vector< Coord<double> >::const_iterator p1, unsigned int p ) { p_ = p; // 点列の大きさ unsigned int pntSize = std::distance( p0, p1 ); // ノット列の大きさ unsigned int knotSize = std::distance( knot0, knot1 ); // ノット列の初期化 // 用意したノット列の要素が pntSize + p_ + 1 より少なければ、末尾側は最後の要素で補う // 逆に多ければ末尾側の要素は無視する if ( knotSize < pntSize + p_ + 1 ) { knot_.assign( knot0, knot1 ); for ( unsigned int i = knotSize ; i < pntSize + p_ + 1 ; ++i ) knot_.push_back( knot_.back() ); } else { knot_.assign( knot0, knot0 + pntSize + p_ + 1 ); } // 点列を X/Y に分解して初期化 while ( p0 != p1 ) { x_.push_back( p0->x ); y_.push_back( p0->y ); ++p0; } } /********************************************************** BSplineCurve : B-スプライン曲線描画用クラス B-スプライン基底関数をそのまま利用 **********************************************************/ class BSplineCurve : public BSplineCurveBase { // calc : 曲線の X/Y 座標値を計算する virtual double calc( const vector<double>& p, double t ); public: /* BSplineCurve コンストラクタ BSplineCurveBase をそのまま利用 */ BSplineCurve( vector<double>::const_iterator knot0, vector<double>::const_iterator knot1, vector< Coord<double> >::const_iterator p0, vector< Coord<double> >::const_iterator p1, unsigned int p ) : BSplineCurveBase( knot0, knot1, p0, p1, p ) {} BSplineCurve( const vector<double>& knot, const vector< Coord<double> >& pnt, unsigned int p ) : BSplineCurveBase( knot, pnt, p ) {} }; /* BSplineCurve::calc : 曲線の X/Y 座標値を計算する const vector<double>& pnt : 点列の X/Y 座標 double t : 計算対象の独立変数 返り値 : 計算結果 */ double BSplineCurve::calc( const vector<double>& pnt, double t ) { double ans = 0; // 計算結果 unsigned int p = order(); // 次数 for ( unsigned int j = 0 ; j < size() ; ++j ) { double d = pnt[j] * CalcBSplineBasisFunc( knot_, j, p, t ); if ( ! isnan( d ) ) ans += d; } return( ans ); }
ベジェ曲線描画のサンプル・プログラムの場合と同様に、B-スプライン曲線描画でも基底クラス BSplineCurveBase を用意し、純粋仮想関数 calc によって曲線の軌跡の計算方法が切り替えられるようにしています。メンバ変数は、次数 p_ と点列の X, Y 座標 x_, y_、ノット列 knot_ の 4 つあり、最後の knot_ は限定公開メンバです。
BSplineCurveBase のメンバ関数 set はメンバ変数を初期化するためのもので、コンストラクタから呼び出して利用します。点列のサイズ pntSize に対し、ノット列は pntSize + p_ + 1 以上のサイズである必要があるので、不足している場合はノット列の末尾の要素を使って補います。逆に多すぎる場合は末尾側の要素は無視して、ノット列のサイズがちょうど pntSize + p_ + 1 に等しくなるように調節しています。
BSplineCurve は、B-スプライン基底関数の計算処理関数 CalcBSplineBasisFunc を利用して曲線の軌跡を求めるためのクラスで、BSplineCurveBase からの派生クラスになっています。仮想関数の calc は、CalcBSplineBasisFunc を利用してB-スプライン基底関数の値を求め、点列の x, y 座標を係数として多項式を求めています。
次数 p、点列の数 M の B-スプライン曲線の軌跡は通常 tp ≤ t ≤ tM の範囲のみを描画します。それ以外の範囲を含めた場合、アフィン不変性と凸閉包性が成り立たなくなり、特に全てのノット列を含めた定義域で描画すると、曲線は必ず原点を含む閉曲線となってしまいます。このクラスは ( CalcBSplineBasisFunc 自身も ) 描画する範囲は限定していないため、t としてどのような値を渡しても何らかの値を返します。特に M < p となった場合、アフィン不変性と凸閉包性が成り立つ曲線は描画できなくなります。
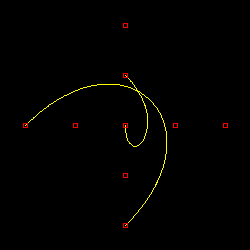
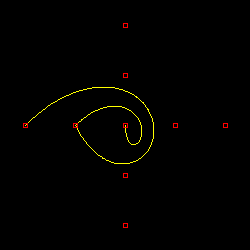
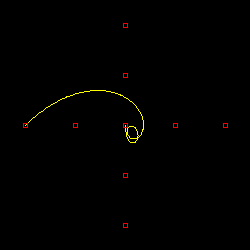
渦巻状に並べた九つの点列に対し、一様ノット列を使って曲線を描画した結果を以下に示します。ノット列は 0 から始まり、次数 p に対して p + 9 までの、p + 10 個の要素からなる自然数列になります。また、描画する範囲は、最後の曲線を除いて、アフィン不変性と凸閉包性が成り立つ tp ≤ t ≤ t9 までとしています。
p = 1 の場合は各点を結んだ線分になり、端点だけではなく全ての点列が直線上に含まれますが、p > 1 の場合、曲線は端点を通りません。最後の描画結果は、p = 3 の場合に対してノット列の全領域 t0 ≤ t ≤ t12 で軌跡を求めたもので、左上原点で曲線の両端がつながった形になります。
同じ点列を開一様ノット列で描画した結果は以下のようになります。p + 10 個のノット列に対し、前半と後半の p + 1 個の要素はそれぞれ 0 と 2 で、中間の値を 1 としています ( 実際のノット列の値は各図形の下側に示してあります )。
| p = 3 | p = 4 | p = 8 | ベジェ曲線 |
|---|---|---|---|
 |
 |
 |
 |
| 0 0 0 0 1 1 1 1 1 2 2 2 2 | 0 0 0 0 0 1 1 1 1 2 2 2 2 2 | 0 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2 2 2 |
p = 3 の場合、曲線は途中で途切れた形になります。j = 4 のとき、N43 はゼロ以外の値を持つ範囲が全くなく無視することができるので、B-スプライン基底関数は j = 0, 1, 2, 3 と j = 5, 6, 7, 8 が左右対称となるような形状になり、しかも t = 1 のところで完全に分断された形になります。
上図のグラフから明らかに、t = 1 のところでは N3,3( 1 ) = N5,3( 1 ) = 1 であり、S( 1 ) は P3・N33 か P5・N53、つまり P3 と P5 そのものと等しくなり、ここで曲線は切断された形になります。p = 4 のときは切断はされていませんが、同じ値が次数と等しい 4 つ分だけ並んでいるために尖点が発生しています。p = 8 ではノット列に 9 個の 0 と 2 を並べており、このときはベジェ曲線と同じ形状になっています。
下図は、ノット列をランダムに作成して非一様二次 B-スプライン曲線として描画した例です。
B-スプライン基底関数の漸化式
を使い、バーンスタイン基底関数に対する「ド・カステリョのアルゴリズム」導出のときと同様に、点列 Pj を係数とする B-スプライン多項式 S(t) を変形すると以下のようになります。
| S(t) | = | Σj{0→M-1}( Pj・Nj,p( t ) ) |
| = | Σj{0→M-1}( Pj{ [ ( t - tj ) / ( tj+p - tj ) ]・Njp-1 + [ ( tj+p+1 - t ) / ( tj+p+1 - tj+1 ) ]・Nj+1p-1 } ) | |
| = | Σj{0→M-1}( Pj( uj,j+p・Njp-1 + uj+p+1,j+1・Nj+1p-1 ) ) |
定義域を [ tp, tp+1 ] に限定すると、S(t) の値に影響する B-スプライン基底関数は N0p から Npp までのみになります。そこで、この定義域に限定すると、p = 1 の場合は
| S(t) | = | Σj{0→1}( Pj・Nj1 ) | |
| = | P0( u0,1・N00 + u2,1・N10 ) + P1( u1,2・N10 + u3,2・N20 ) | ||
| = | P0・u2,1 + P1・u1,2 | ( t1 ≤ t ≤ t2 ) | |
| = | [ P0・( t2 - t ) + P1・( t - t1 ) ] / ( t2 - t1 ) | ( t1 ≤ t ≤ t2 ) |
となるので、S(t) は線分 P0 - P1 を t - t1 : t2 - t の比率で分けたときの内点(重心)に相当します。さらに p = 2 の場合、
| S(t) | = | Σj{0→2}( Pj・Nj2 ) | |
| = | Σj{0→2}( Pj・( uj,j+2・Nj1 + uj+3,j+1・Nj+11 ) ) | ||
| = | Σj{0→2}( Pj・[ uj,j+2・( uj,j+1・Nj0 + uj+2,j+1・Nj+10 ) ] | ||
| + [ uj+3,j+1・( uj+1,j+2・Nj+10 + uj+3,j+2・Nj+20 ) ] ) | |||
| = | P0・u3,1u3,2 + P1・( u1,3u3,2 + u4,2u2,3 ) + P2・u2,4u2,3 | ( t2 ≤ t ≤ t3 ) | |
| = | u3,2( P0・u3,1 + P1・u1,3 ) + u2,3( P1・u4,2 + P2・u2,4 ) | ( t2 ≤ t ≤ t3 ) | |
より、S(t) は 線分 P0 - P1 の t - t1 : t3 - t の内点と P1 - P2 の t - t2 : t4 - t の内点を結んだ線分をさらに t - t2 : t3 - t の比率で分けた内点になります。p = 3 の場合、
| S(t) | = | Σj{0→3}( Pj・Nj3 ) | |
| = | Σj{0→3}( Pj・( uj,j+3・Nj2 + uj+4,j+1・Nj+12 ) ) | ||
| = | Σj{0→3}( Pj・[ uj,j+3( uj,j+2・Nj1 + uj+3,j+1・Nj+11 ) | ||
| + uj+4,j+1( uj+1,j+3・Nj+11 + uj+4,j+2・Nj+21 ) ] ) | |||
| = | Σj{0→3}( Pj・{ uj,j+3[ uj,j+2( uj,j+1・Nj0 + uj+2,j+1・Nj+10 ) + uj+3,j+1( uj+1,j+2・Nj+10 + uj+3,j+2・Nj+20 ) ] | ||
| + uj+4,j+1[ uj+1,j+3( uj+1,j+2・Nj+10 + uj+3,j+2・Nj+20 ) + uj+4,j+2( uj+2,j+3・Nj+20 + uj+4,j+3・Nj+30 ) ] } ) | |||
| = | P0u4,1u4,2u4,3 + P1[ u1,4u4,2u4,3 + u5,2( u2,4u4,3 + u5,3u3,4 ) ] | ||
| + P2[ u2,5( u2,4u4,3 + u5,3u3,4 ) + u6,3u3,5u3,4 ] + P3u3,6u3,5u3,4 | ( t3 ≤ t ≤ t4 ) | ||
| = | u4,2u4,3( P0u4,1 + P1u1,4 ) + u2,4u4,3( P1u5,2 + P2u2,5 ) | ||
| + u5,3u3,4( P1u5,2 + P2u2,5 ) + u3,5u3,4( P2u6,3 + P3u3,6 ) | ( t3 ≤ t ≤ t4 ) | ||
| = | u4,3[ u4,2( P0u4,1 + P1u1,4 ) + u2,4( P1u5,2 + P2u2,5 ) ] | ||
| + u3,4[ u5,3( P1u5,2 + P2u2,5 ) + u3,5( P2u6,3 + P3u3,6 ) ] | ( t3 ≤ t ≤ t4 ) | ||
となるので、S(t) は 線分 P0 - P1 の t - t1 : t4 - t の内点と P1 - P2 の t - t2 : t5 - t の内点を結んだ線分を t - t2 : t4 - t の比率で分けた内点、P1 - P2 の t - t2 : t5 - t の内点と P2 - P3 の t - t3 : t6 - t の内点を結んだ線分を t - t3 : t5 - t の比率で分けた内点を結び、その線分を t - t3 : t4 - t の比率で分けた内点に相当します。この結果から、任意の p に対する S(t) を [ tp, tp+1 ] の範囲について求めるためには、まず Pj-1 と Pj ( j = 1, ... p ) を結んだ線分を t - tj : tj+p - t の比率で分けた p 個の内点 Pj-1(1) を求め、次に Pj-1(1) と Pj(1) ( j = 1, ... p - 1 ) を結んだ線分を t - tj+1 : tj+p - t の比率で分けた p - 1 個の内点 Pj-1(2) を求める、という具合に、1 個の内点 P0(p) になるまで繰り返し求めればよいことがわかります。[ tp+1, tp+2 ] の定義域に対しては点列を一つずらして P1 から Pp+1 までを使えばよく、最後の [ tM-1, tM ] に対しては PM-p-1 から PM-1 までを使って求めます。このようにして曲線の軌跡を求めるアルゴリズムを「De Boor-Cox のアルゴリズム (De Boor-Cox Algorithm)」といいます。ノット列を p + 1 個のゼロと p + 1 個の 1 にした場合は、1 ≤ j ≤ p に対して t - tj : tj+p - t = t : 1 - t が成り立ち、これは「ド・カステリョのアルゴリズム (De Casteljau's Algorithm)」と同じ操作になります。すなわち、「ド・カステリョのアルゴリズム」は「De Boor-Cox のアルゴリズム」の特殊形であると考えることができます。
「De Boor-Cox のアルゴリズム」を使って B-スプライン曲線の軌跡を計算するサンプル・プログラムを以下に示します。
/****************************************************************** DeBoorCox : De Boor-Cox のアルゴリズムを使った B-スプライン曲線 ******************************************************************/ class DeBoorCox : public BSplineCurveBase { vector<double> buff_; // 内点の計算結果を保持するバッファ // calc : 曲線の X/Y 座標値を計算する virtual double calc( const vector<double>& p, double t ); public: /* DeBoorCox コンストラクタ BSplineCurveBase をそのまま利用 */ DeBoorCox( vector<double>::const_iterator knot0, vector<double>::const_iterator knot1, vector< Coord<double> >::const_iterator p0, vector< Coord<double> >::const_iterator p1, unsigned int p ) : BSplineCurveBase( knot0, knot1, p0, p1, p ), buff_( p ) {} DeBoorCox( const vector<double>& knot, const vector< Coord<double> >& pnt, unsigned int p ) : BSplineCurveBase( knot, pnt, p ), buff_( p ) {} }; /* DeBoorCox::calc : 曲線の X/Y 座標値を計算する const vector<double>& pnt : 点列の X/Y 座標 double t : 計算対象の独立変数 返り値 : 計算結果 */ double DeBoorCox::calc( const vector<double>& pnt, double t ) { if ( size() <= 1 ) return( NAN ); unsigned int p = order(); // 次数 // t を含むノット列の領域 [ knot_[s-1], knot_[s] ] の添字 s を求める unsigned int s = 0; for ( ; s < knot_.size() ; ++s ) if ( t < knot_[s] ) break; if ( s <= p || s > size() ) return( NAN ); s -= p; // p = 0 のときは点列の座標値そのものを返す if ( p == 0 ) return( pnt[s - 1] ); // 点列から最初の内点を求めて buff_ に格納する vector<double>::iterator it = buff_.begin(); for ( unsigned int j = s ; j < p + s ; ++j ) *it++ = ( ( knot_[j + p] - t ) * pnt[j - 1] + ( t - knot_[j] ) * pnt[j] ) / ( knot_[j + p] - knot_[j] ); // 再帰的に内点を計算 for ( unsigned int e = p ; e > 1 ; --e ) { unsigned int inc = p - e + 1; // 前側のノットの添字に対する増分 it = buff_.begin(); for ( unsigned int j = s ; j < s + e - 1 ; ++j ) { *it = ( ( knot_[j + p] - t ) * *it + ( t - knot_[j + inc] ) * *( it + 1 ) ) / ( knot_[j + p] - knot_[j + inc] ); ++it; } } return( buff_[0] ); }
曲線の軌跡を求める前に、ノット列の中で t を含む領域の添字を求める処理を行います。得られた添字 s は、領域の終端を表すことに注意して下さい。また、このとき t が tp から tM ( M は点列のサイズ ) の範囲内にあるかをチェックし、そうでなければ nan を返しています。BSplineCurve クラスの場合とは異なり、「De Boor-Cox のアルゴリズム」では tp ≤ t ≤ tM 以外の領域の計算はできないため、計算処理前に必ずチェックをする必要があります。チェック後は p を減算し、点列の添字に合わせた値に切り替えます。
p = 0 のとき、計算式の分母はゼロになってしまうため、点列の座標をそのまま返します。そうでなければ、先ほど示したアルゴリズムに従って再帰的に内点の計算を繰り返し、内点が一つになったところでその値を返します。
一様・開一様・非一様のそれぞれに対し、三次の B-スプライン曲線を、BSplineCurve と DeBoorCox それぞれのクラスを使って描画した結果を以下に示します。ノット列は図の下側に示してあります。どちらの描画方法を使っても、全ての場合において曲線は一致します。
| 一様 | 開一様 | 非一様 | |
|---|---|---|---|
| BSplineCurve |  |
 |
 |
| DeBoorCox |  |
 |
 |
| ノット列 | 0 1 2 3 4 5 6 7 8 9 10 11 12 | 0 0 0 0 1 1 1 1 1 2 2 2 2 | 0 0.5 1.5 3.0 4.5 6 6 6 6.25 6.5 7.5 10 15 |
B-スプライン曲線においては、ノット列をコントロールすることによって、曲線を任意の箇所で折れ曲がった状態にするなど、曲線を自由に描くことができることを前節で説明しました。ノット列は、一つ一つの B-スプライン基底関数の幅や形状を変化させることができます。
ここで、各基底関数に対する重み値 wj を定義してスプライン曲線を表現してみます。
wj = 0 ならば、wj・Pj・Nj,p( t ) の項は存在しないことになり、Pj は曲線の形状に影響を与えないことになります。逆に、wj の値が大きくなるほど Pj の影響力は大きくなります。
さて、このままだと Σj{0→M-1}( wj・Nj,p( t ) ) ≠ 1 なので、アフィン不変性が成り立たなくなります。そこで、全体を Σj{0→M-1}( wj・Nj,p( t ) ) で割ることで正規化します。よって、スプライン曲線は
となります。これを「非一様有理 B-スプライン ( Non-Uniform Rational B-Spline ; NURBS )」といいます。
B-スプライン曲線の描画ができるのなら、NURBS の実装は非常に簡単です。早速サンプル・プログラムを示したいと思います。
/************************************** NurbsCurve : NURBS 曲線描画用クラス **************************************/ class NurbsCurve : public BSplineCurveBase { std::vector< double > w_; // 重み値 // calc : 曲線の X/Y 座標値を計算する virtual double calc( const std::vector< double >& p, double t ); // setWeight : 重み値の取り込み void setWeight( std::vector< double >::const_iterator w0, std::vector< double >::const_iterator w1 ); public: /* NurbsCurve コンストラクタ */ /// 配列の範囲を指定して構築 /// /// knot0,knot1 : ノット列の範囲 (knot1 は末尾の次を表すため含まれない) /// p0,p1 : 点列の範囲 (p1 は末尾の次を表すため含まれない) /// w0,w1 : 重み値の範囲 (w1 は末尾の次を表すため含まれない) /// p : 次数 NurbsCurve( std::vector< double >::const_iterator knot0, std::vector< double >::const_iterator knot1, std::vector< Coord< double > >::const_iterator p0, std::vector< Coord< double > >::const_iterator p1, std::vector< double >::const_iterator w0, std::vector< double >::const_iterator w1, size_t p ) : BSplineCurveBase( knot0, knot1, p0, p1, p ) { setWeight( w0, w1 ); } /// 配列全体を指定して構築 /// /// knot : ノット列 /// pnt : 点列 /// w : 重み値の列 /// p : 次数 NurbsCurve( const std::vector< double >& knot, const std::vector< Coord< double > >& pnt, const std::vector< double >& w, size_t p ) : BSplineCurveBase( knot, pnt, p ) { setWeight( w.begin(), w.end() ); } }; /* NurbsCurve::setWeight : 重み値の取り込み w0,w1 : 重み値の範囲 (w1 は末尾の次を表すため含まれない) */ void NurbsCurve::setWeight( vector< double >::const_iterator w0, vector< double >::const_iterator w1 ) { w_.assign( size(), 1 ); // 重み値のデフォルトは 1 とする size_t sz = std::distance( w0, w1 ); if ( sz <= size() ) std::copy( w0, w1, w_.begin() ); // データは範囲内 else std::copy( w0, w0 + size(), w_.begin() ); // データ数が超過している場合、末尾は捨てる } /* NurbsCurve::calc : 曲線の X/Y 座標値を計算する pnt : 点列の X/Y 座標 t : 計算対象の独立変数 返り値 : 計算結果 */ double NurbsCurve::calc( const vector< double >& pnt, double t ) { size_t p = order(); // 次数 vector< double > bs( size() ); // B-Spline 基底関数の計算結果(重み値を積算) double wSum = 0; // bs の合計 for ( size_t j = 0 ; j < size() ; ++j ) { bs[j] = w_[j] * GCurve::CalcBSplineBasisFunc( knot_, j, p, t ); wSum += bs[j]; } double ans = 0; // 計算結果 for ( size_t j = 0 ; j < size() ; ++j ) { double d = pnt[j] * bs[j] / wSum; if ( ! isnan( d ) ) ans += d; } return( ans ); }
NURBS 曲線を描画するためのクラス NurbsCurve も、BSplineCurveBase からの派生になっています。BSplineCurve などとの違いは、構築時に重み値を受け取る箇所と、座標値の計算式のみです。重み値はメンバ変数 w_ に格納しますが、デフォルトは 1 として、引数の範囲が点列の数より小さければ末尾側をデフォルトのままとし、大きければ引数の配列の末尾側を無視するような処理になっています。
NURBS を利用することで、例えば円を簡単に描画することができます。円の方程式は
なので、0 ≤ θ ≤ π / 2 の範囲のみを考えると
より
となります。一方、点列を P0 = ( 1, 0 ), P1 = ( 1, 1 ), P2 = ( 0, 1 ) の 3 点とした時、二次のバーンスタイン基底関数を利用して NURBS を表現すると
| Sx( t ) | = | [ w0・b0,2( t ) + w1・b1,2( t ) ] / Σj{0→2}( wj・bj,2( t ) ) |
| = | [ w0( 1 - t )2 + 2w1t( 1 - t ) ] / [ w0( 1 - t )2 + 2w1t( 1 - t ) + w2t2 ] | |
| = | [ w0 - 2( w0 - w1 )t + ( w0 - 2w1 )t2 ] / [ w0 - 2( w0 - w1 )t + ( w0 - 2w1 + w2 )t2 ] | |
| Sy( t ) | = | [ w1・b1,2( t ) + w2・b2,2( t ) ] / Σj{0→2}( wj・bj,2( t ) ) |
| = | [ 2w1t( 1 - t ) + w2t2 ] / [ w0( 1 - t )2 + 2w1t( 1 - t ) + w2t2 ] | |
| = | [ 2w1t - ( 2w1 - w2 )t2 ] / [ w0 - 2( w0 - w1 )t + ( w0 - 2w1 + w2 )t2 ] |
となり、w0 = w1 = 1, w2 = 2 とすれば円の方程式と一致することがわかります。
円全体を描画する場合はもう少し複雑で、ノット列を { 0, 0, 0, 1/4, 1/4, 1/2, 1/2, 3/4, 3/4, 1, 1, 1 } とし、重み値を { 1, 1/√2, 1, 1/√2, 1, 1/√2, 1, 1/√2, 1 }、点列を ( 0, 1 ), ( 1, 1 ), ( 1, 0 ), ( 1, -1 ), ( 0, -1 ), ( -1, -1 ), ( -1, 0 ), ( -1, 1 ), ( 0, 1 ) とすることで描画できます。下図は、この条件で B-スプラインと NURBS の両方を使って曲線を描画した結果を示しています。
NURBS で描画した側は、四隅にある各点に対してより離れた位置に曲線が移動している様子が確認できます。この点に対する重み値が 1 より小さいため、点の位置による影響が小さくなっていることがこの結果からもわかります。重みを大きくすれば影響が大きくなるので、曲線は四角形に近い形となるでしょう。
今回は、B-スプライン曲線の描画方法を中心に紹介しました。ベジェ曲線は B-スプライン曲線の中に含まれることから、さらに多様な形状も表現することが可能となり、ベジェ曲線を使ったスプライン曲線と比べても、より滑らかな曲線を描画することが可能となります。
少し、宣伝です。
趣味で小説を書いています。以前から、書いてみたいという思いがあり、アマチュアの小説を扱うサイトを見つけたことから実際に始めてみました。
最初は、小説を書ければ満足で、アクセス数が少なくてもいいかなと思っていましたが、やはりせっかく書いたからには読んでもらいたいし、感想をいただきたいという欲も出てきました。
もし、よろしければ、読んでもらえると嬉しいですし、今後の励みにもなります。
小説は、以下のリンク先から読むことができます。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |