 |
対称行列の固有値を求めるためのアルゴリズムを前回紹介しました。この章では、固有値分解がどのような用途に利用されているのかを、基本的な手法であるカルーネン・レーベ展開の内容を軸として紹介したいと思います。
二次の項のみからなる多項式を「二次形式 ( Quadratic Form )」と言います。二次式とは異なり、一次の項や定数項は含まないことに注意してください。n 個の変数 xi ( i = 1, 2, ... n ) を持つ二次形式は、次のように表せます。
| f | = | a11x12 + a22x22 + ... + annxn2 + 2a12x1x2 + 2a13x1x3 + ... + 2an,n-1xnxn-1 |
| = | Σi,j{1→n}( aijxixj ) ( 但し、aij = aji ) |
さらに、対称行列 A を使うと、上式は次の簡単な式に表すことができます ( 実際に内積を計算すると、上式が得られることを確認することができます )。
| | | x1 | | | | | a11, | a12, | ... | a1n | || | x1 | | | |||
| | | x2 | | | | | a12, | a22, | ... | a2n | || | x2 | | | |||
| | | : | | | | | : | : | ... | : | || | : | | | |||
| f = ( x, Ax ) | = ( | | | xn | | | , | | | a1n, | a2n, | ... | ann | || | xn | | ) |
このときの対称行列 A を、二次形式 f の「係数行列 ( Coefficient Matrix )」と言います。
Aの固有値を対角成分とする対角行列を D、固有ベクトルからなる直交行列を Q としたとき、固有値分解の式より、
が成り立ちます (*1-1)。ここで、x' = QTx とすると、Q は直交行列なので Qx' = x になり、上式は次のようになります。
AQx' = QDx' より
QTAQx' = Dx'
よって、二次形式 (x, Ax) は次のように変形することができます。
| ( x, Ax ) | = | ( Qx', AQx' ) |
| = | ( x', QTAQx' ) ... ( Ax, y ) = ( x, ATy )より (*1-1) | |
| = | ( x', Dx' ) |
上式より、x' = ( x'1, x'2 ... )、対称行列 A の固有値を λ1, λ2 ... とすると、
が成り立ちます。これを、二次形式の標準形と呼びます。
実際に、次の二次形式を使ってその固有値と固有ベクトルを求め、標準形に変形してみたいと思います。
これを対称行列を使って表すと次のようになります。
| | | x | | | | | 6, | 2 | || | x | | | |||
| f = ( x, Ax ) | = ( | | | y | | | , | | | 2, | 3 | || | y | | ) |
係数行列の固有値は 2 と 7、それぞれの固有ベクトルは ( 1 / √5, -2 / √5 ), ( 2 / √5, 1 / √5 )と求めることができるので、係数行列を次のように対角化することができます。
| QTAQ = | | | 1/√5, | -2/√5 | | | | 6, | 2 | | | | 1/√5, | 2/√5 | | = | | | 2, | 0 | | |
| | | 2/√5, | 1/√5 | | | | 2, | 3 | | | | -2/√5, | 1/√5 | | | | | 0, | 7 | | |
ここで、( x', y' ) を次のように定義します。
| | | x' | | | = | | | 1/√5, | -2/√5 | | | | x | | | = | | | (1/√5)x - (2/√5)y | | |
| | | y' | | | | | 2/√5, | 1/√5 | | | | y | | | | | (2/√5)x + (1/√5)y | | |
( x, y ) を ( x', y' ) で表すと次のようになります。
| | | x | | | = | | | 1/√5, | 2/√5 | | | | x' | | | = | | | (1/√5)x' + (2/√5)y' | | |
| | | y | | | | | -2/√5, | 1/√5 | | | | y' | | | | | (-2/√5)x' + (1/√5)y' | | |
この時、二次形式は次のように変形することができます。
| | | x | | | | | 6, | 2 | || | x | | | |||
| f | = ( | | | y | | | , | | | 2, | 3 | || | y | | ) |
| | | 1/√5, | 2/√5 | || | x' | | | | | 6, | 2 | || | 1/√5, | 2/√5 | || | x' | | | |||
| = ( | | | -2/√5, | 1/√5 | || | y' | | | , | | | 2, | 3 | || | -2/√5, | 1/√5 | || | y' | | ) | |
| | | x' | | | | | 1/√5, | -2/√5 | || | 6, | 2 | || | 1/√5, | 2/√5 | || | x' | | | |||
| = ( | | | y' | | | , | | | 2/√5, | 1/√5 | || | 2, | 3 | || | -2/√5, | 1/√5 | || | y' | | ) | |
| | | x' | | | | | 2, | 0 | || | x' | | | |||
| = ( | | | y' | | | , | | | 0, | 7 | || | y' | | ) | |
| = | 2x'2 + 7y'2 | ||||||||||
よって、二次形式 f の標準形は f = 2x'2 + 7y'2 となることがわかります。
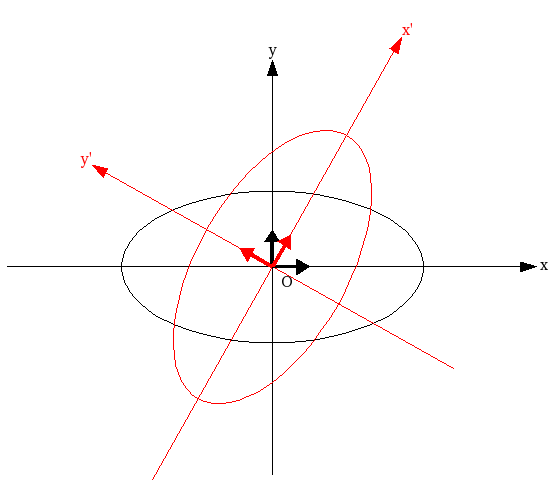
f = (定数) のとき、この方程式は楕円を表しています。x から x' へは直交行列による変換なので、回転と鏡映を組み合わせた変換のみが行なわれ、形は変化しません (*1-1)。つまり、二次形式 6x2 + 4xy + 3y2 = (定数) と 2x'2 + 7y'2 = (定数) は軸の方向が変わっただけで形に変化がないことになります。QT によって、x 軸上の単位ベクトル ( 1, 0 ) は ( 1 / √5, 2 / √5 ) に、y 軸上の単位ベクトル ( 0, 1 ) は ( -2 / √5, 1 / √5 ) にそれぞれ変換されます。変換された結果もノルムは 1 であり、二つのベクトルは直交するので、座標軸自体が原点を中心に回転した形をイメージすることができると思います。6x2 + 4xy + 3y2 = (定数) は、この回転した座標軸において 2x'2 + 7y'2 = (定数) の形に書けます。この時の、固有ベクトルに沿った軸を「主軸」といい、主軸を座標軸に取った座標系で表すことを「主軸変換」と言います。
上記の例では、二次形式の標準形が楕円となりました。しかし、常に楕円の形になるわけではなく、固有値の一つがゼロであれば f = kx2 の形になるので、f = (定数) のとき二本の直線を表すことになり、さらに固有値どうしが異符号であれば、f = k1x2 - k2y2 ( 但し k1 > 0, k2 > 0 ) なので、f = (定数) のとき双曲線になります。
このことから分かるように、f = λ1x2 + λ2y2 の値を z 軸に取って、三次元空間上の曲面で f の変化を表現したとき、その形は固有値の符号によって異なります。二つの固有値が同符号のとき、その形は f = 0 平面に接するお椀型の曲面となり、xy平面に平行な面での切り口は楕円になるので「楕円型」といいます。固有値がどちらも正ならば、「お椀」は f 軸の正の向きに広がり、負であれば逆に負の向きに広がります。固有値の一つがゼロならば、xy 平面に垂直な面での切り口が、f = 0 平面に接する放物線となるので「放物型」と呼ばれます。これも「楕円形」と同様に、ゼロではない固有値の符号により、放物線の向きは変化します。固有値が互いに異符号の場合が最もイメージしにくいのですが、f > 0 の範囲の平面での切り口は双曲線になり、それが f = 0 平面での切り口は二本の直線 y = ±Kx となって、f < 0 の範囲では、切り口が、f > 0 の場合に対して向きが直交しているような双曲線になります。これを「双曲型」といいます。以下に、それぞれの形のサンプル図を示します。平面上の曲線は、xy 平面上での切り口を表しています。
対称行列に対し、固有値が全て正である場合を「正値対称行列」、ゼロまたは正である場合を「半正値対称行列」といいます。正値対称行列であれば、
同様に、半正値対称行列であれば ( x, Ax ) ≥ 0 を満たすことになります。
x を単位ベクトルとしたとき、( x, Ax ) の最大値は何になるでしょうか。固有値を降順に λ1 ≥ λ2 ≥ ... ≥ λn となるように並べたとき、
| Σi{1→n}( λix'i2 ) | ≤ | Σi{1→n}( λ1x'i2 ) |
| = | λ1Σi{1→n}( x'i2 ) = λ1 |
となり、( x, Ax ) の最大値は λ1 になります。この時の単位ベクトルを x'1 とすると、x'1 = ( 1, 0, ... , 0 )T になり、固有値 λi に対する A の固有ベクトルを ui としたとき、Q = ( u1, u2, ... un ) なので、
| Qx'1 | = | ( u1, u2, ... un ) | | | 1 | | = u1 |
| | | 0 | | | |||
| | | : | | | |||
| | | 0 | | | |||
つまり、λ1 に対する固有ベクトルになります。このことから、( x, Ax ) を最大にする単位ベクトルは最大固有値に対する固有ベクトルであり、その最大値は最大固有値に等しくなることが分かります。次に、u1 に直交する単位ベクトルの中で ( x, Ax ) を最大にするものを考えます。標準形に表したとき、求めるベクトルが x'2 = ( x'21, x'22, ... x'2n ) に変換されたとすると、それは x'1 と直交することになるので、
が成り立ちます。従って、
これが最大になるのは、x'2 = ( 0, 1, 0, ... 0 ) のときで、その最大値は λ2 になります。また、Qx'2 = u2 より、その時の単位ベクトルは u2 になります。同様に考えると、x が u1, u2, ... ui-1 に直交する単位ベクトルであるとき、( x, Ax ) が最大になるためには x = ui である必要があり、そのときの最大値は i 番目の固有値 λi になります。
( x, Ax ) = (一定) となる二次形式の曲面に対し、原点からの距離が最も近い方向は、( x, Ax ) の値の増加が他の方向よりも大きくなります。ちょうど、地図の等高線において、線の密度が高い場所の勾配が大きいのと同じように考えることができます。この方向は、距離 1 だけ原点から進んだときの ( x, Ax ) の値が他の方向へ進んだときよりも大きくなります。これに垂直な方向に限定しても、その中から、原点からの距離が最も近い方向を選ぶことができます。上記の説明は、そのような方向が、係数行列 A の固有ベクトルであることを示しています。
二次元上の二次形式を思い浮かべると、もう少し理解しやすいと思います。平面上の二次形式 f = λ1x2 + λ2y2 ( 但し 0 < λ1 < λ2 とする ) が点 ( 0, 1 ) と交わる場合、f = λ2 になります。これは、原点から uy = ( 0, 1 ) 方向に距離 1 だけ進んだとき、ちょうど f = λ2 になることを意味しています。しかし、同じ距離だけ、ux = ( 1, 0 ) 方向へ進んだとき、まだ f = λ2 の曲面には到達していないので、このとき f < λ2です。つまり、同じ距離だけ進んでも、uy 方向に進んだ方が、ux 方向よりも f の値を大きくすることができます。
λ1x2 + λ2y2 = (定数) の半径は、1 / √λ1 と 1 / √λ2 になります。λ1 < λ2 ならば、1 / √λ1 > 1 / √λ2 であり、楕円の長径は x 軸方向、短径は y 軸方向になります。
*1-1) 「固有値問題 (1) 対称行列の固有値」の「直交行列 ( Orthogonal Matrix )」参照
ある集団 ( 例えば学校の 1 クラスなど ) のデータ ( 身長や体重、テストの点数など ) の中には、「正規分布 ( Normal Distribution )」と呼ばれる以下の式のような確率分布に従うものがあることが知られています。
但し、exp( x ) はネイピア数 e の x 乗、μ は分布の平均値、σ2 は分布の分散を表します。これを一般に N( μ, σ2 ) と表し、特に N( 0, 1 ) を「標準正規分布 ( Standard Normal Distribution )」といいます。
ある二つのデータ ( 例えば、身長と体重など ) を ( xi, yi ) として、これらが直線 y = ax + b に近似できたとしたとき、実際の測定データでは直線に完全に一致することはなく、ある程度の誤差が発生します。この誤差を
で表します。誤差 εi が平均値 0、分散 σ2 の正規分布に従うとしたとき、その確率密度は
になるので、各データが独立であるとき、誤差が { ε1, ε2, ... εN } のようになる同時確率は
| Πi{1→N}( f(εi) ) | = | Πi{1→N}( [ 1 / (2π)1/2σ ] exp( -εi2 / 2σ2 ) ) |
| = | [ 1 / (2π)1/2σ ]N exp( -Σi{1→N}( εi2 ) / 2σ2 ) |
よって、この確率が最大になるのは、Σi{1→N}( εi2 ) が最小であるときになります。すなわち、
を最小にするような a, b の値を求めれば、最も発生する可能性の高い誤差の分布になるように直線を決めることができます。この手法を「最小二乗法(Least Squares)」といいます。
理論的には以上のような説明になりますが、それぞれのデータと直線との差の二乗に対して和を求めたとき、その和を最小にすれば、最もよい近似になることは直感的にも納得できると思います。
誤差 εi に定数を掛けても最小値となるときの a, b に変化はないので、次の関数 J(a,b) の最小値を求めることを考えます。定数の 1 / 2 は、後の計算を見やすくするためのものなので、特別な意味はありません。
関数 J(a,b) は、二変数 a, b を持ちます。これが最大・最小値を取る点では各変数に対する偏微分がゼロになるので、∂J/∂a = 0, ∂J/∂b = 0 を解けば a, b を求めることができます。
| ∂J/∂a | = | Σi{1→N}( [ yi - ( axi + b ) ]( -xi ) ) |
| = | aΣi{1→N}( xi2 ) + bΣi{1→N}( xi ) - Σi{1→N}( xiyi ) = 0 |
| ∂J/∂b | = | Σi{1→N}( [ yi - ( axi + b ) ]( -1 ) ) |
| = | aΣi{1→N}( xi ) + bΣi{1→N}( 1 ) - Σi{1→N}( yi ) = 0 |
よって、
| | | Σi{1→N}( xi2 ), | Σi{1→N}( xi ) | || | a | | | = | | | Σi{1→N}( xiyi ) | | |
| | | Σi{1→N}( xi ), | Σi{1→N}( 1 ) | || | b | | | | | Σi{1→N}( yi ) | | |
これを解いて a, b を決定します。この方程式を「正規方程式」といいます。
とすれば、正規方程式は
となるので、
と計算して求めることができます。
最小二乗法による直線への近似を行なうためのサンプル・プログラムを以下に示します。
/* LinearLeastSquares : 最小二乗法により直線を求める data : データ列 a, b : 直線の傾きと切片 */ template< class T > void LinearLeastSquares( const vector< pair< T, T > >& data, T* a, T* b ) { T xSum = 0; // xの和 T ySum = 0; // yの和 T x2Sum = 0; // xの二乗の和 T xySum = 0; // xyの和 T n = data.size(); // データ数 for ( unsigned int i = 0 ; i < n ; ++i ) { T x = data[i].first; T y = data[i].second; xSum += x; ySum += y; x2Sum += x * x; xySum += x * y; } *a = ( n * xySum - xSum * ySum ) / ( n * x2Sum - xSum * xSum ); *b = ( x2Sum * ySum - xSum * xySum ) / ( n * x2Sum - xSum * xSum ); }
データ列用に、STL で標準装備されている pair 型を要素とする、可変長配列の vector を利用しています。pair 型からは、first と second の二つのメンバ変数を利用することができるので、それぞれを x, y としています。
最小二乗法の考え方は、直線だけでなく多項式に利用することもできます。二次式に近似するのであれば、求める方程式を y = ax2 + bx + c として、a, b, c それぞれで偏微分することで三つの式が得られるので、正規方程式は三変数の連立方程式となります。同様に、n 次の多項式に近似する場合、n 変数の連立方程式を解くことで近似式を得ることができます ( 補足 1 )。
ここで、ある m 次元ベクトル a = ( a1, a2, ... am )T に対して、N 個の m 次元ベクトル ui = ( ui1, ui2, ... uim )T の線形結合を使って次のように近似することを考えます。
a ≅ Σk{1→N}( ckuk )
各成分について、ai ≅ Σk{1→N}( ckuki )これも最小二乗法によって、下式の値 J を最小にする係数 ciを求めることができます。
直線の場合と同様に、∂J/∂c1 = 0, ∂J/∂c2 = 0, ... ∂J/∂cN = 0 を解きます。
| ∂J/∂cj | = | Σi{1→m}( { ai - Σk{1→N}( ckuki ) }{ -uji } ) |
| = | Σi{1→m}( -aiuji + Σk{1→N}( ckujiuki ) ) = 0 |
ここで、
Σi{1→m}( aiuji ) = ( a, uj )
Σi{1→m}( ujiuki ) = ( uj, uk )となることから、
よって、正規方程式は
| | | ||u1||2, | ( u1, u2 ), | ... | ( u1, uN ) | || | c1 | | | = | | | ( a, u1 ) | | |
| | | ( u2, u1 ), | ||u2||2, | ... | ( u2, uN ) | || | c2 | | | | | ( a, u2 ) | | | |
| | | : | : | ... | : | || | : | | | | | : | | | |
| | | ( uN, u1 ), | ( uN, u2 ), | ... | ||uN||2 | || | cN | | | | | ( a, uN ) | | |
これを解くためには、N 個の変数を持った連立方程式を解く必要があります。しかし、もし各 uj が正規直交基底であれば、( ui, uj ) は i = j のとき 1、i ≠ j のとき 0 になるので、正規方程式は簡単に解くことができるようになり、
になります。
求めた係数 ck を、近似式 a ≅ Σk{1→N}( ckuk ) に代入すると、
右辺にある a の近似成分を a' としたとき、a と近似成分 a' の差は a - a' = a - Σk{1→N}( ( a, uk )uk ) になります。ここで、a - a' と ui ( i = 1, 2, ... N ) との内積を計算すると、
| ( a - a', ui ) | = | ( a - Σk{1→N}( ( a, uk )uk ), ui ) | |
| = | ( a, ui ) - ( Σk{1→N}( ( a, uk )uk ), ui ) | ||
| = | ( a, ui ) - ( ( a, ui )ui, ui ) | ( k ≠ i ならば ( ( a, uk )uk, ui ) = 0 なので ) | |
| = | ( a, ui ) - ( a, ui )||ui||2 | ||
| = | ( a, ui ) - ( a, ui ) = 0 |
従って、a - a' と ui は互いに直交することになります。
a' は ui を基底とする線形結合で表されています。a を最もよく近似するようにするには、それぞれの基底 ui からなる線形結合の集合 ( これを、{ ui } の張る「部分空間 ( Subspace )」といいます ) に対して a から垂線を下ろし、その足を a' とすればいいと解釈することができます。このとき、a' を { ui } の張る部分空間への「直交射影 ( Orthogonal Projection )」といいます。
N = m であれば、任意の a に対して a' は一致します。一般に、計量ベクトル空間において、任意の元が m 個の(正規)直交基底による最小二乗法の近似と一致するとき、その計量ベクトル空間は m 次元計量ベクトル空間であるといいます。その場合、上の図において、任意の元が { ui } の張る部分空間上に存在することになります。
N 個の m 次元ベクトルを { fi } = f1, f2, ... fN とし、その平均を
とします。この時、各ベクトル fi から g0 を引いた
は、各ベクトルの平均からの差を表し、{ xi } の和は原点になります。
{ xi } を、下式のような、正規直交規定による線形結合の形に表すことを考えます。
最小二乗法より、最もよく近似されている場合の係数は次のように表されます。
今、gj はまだ未知のベクトルです。gj と { xi } との差の二乗の和を J としたとき、J は次のような式で表すことができます。
この式を変形すると、
| Σi{1→N}( || xi - cijgj ||2 ) | = | Σi{1→N}( ||xi||2 - 2cij( xi, gj ) + cij2||gj||2 ) |
| = | Σi{1→N}( ||xi||2 - 2( xi, gj )2 + ( xi, gj )2 ) | |
| = | Σi{1→N}( ||xi||2 - ( xi, gj )2 ) |
ここで、gj は正規直交基底なので、||gj|| = 1 であることを用いています。
上式より、J の大きさは Σi{1→N}( ( xi, gj )2 ) によって変わります。これを展開すると、
| Σi{1→N}( ( xi, gj )2 ) | = | Σi{1→N}( ( gj, xi )( xi, gj ) ) |
| = | Σi{1→N}( gjTxixiTgj ) | |
| = | gjT{ Σi{1→N}( xixiT ) }gj | |
| = | gjTAgj = ( gj, Agj ) |
但し、A = Σi{1→N}( xixiT ) としています。xi = ( xi1, xi2, ... xin )T とすると、Aの r 行 c 列の成分 arc は
また、c 行 r 列の成分 acr は
よって、arc = acr となり、A は対称行列です。さらに、上記の結果から ( gj, Agj ) = Σi{1→N}( ( gj, xi )2 ) なので、( gj, Agj ) ≥ 0 が成り立ち、A は半正値対称行列であることになります。従って、( gj, Agj ) は二次形式であり、固有値からなる対角行列を D、固有ベクトルからなる直交行列を Q とすれば、固有値分解の式から A = QDQT なので、
QTgj = g'j とすれば、
但し、A の固有値をλ1, λ2, ... λm、また g'j = ( g'j1, g'j2, ... g'jm ) としています。
二次形式のところで説明したように、( gj, Agj ) が最大となるときの固有ベクトルは、A の最大固有値に対する固有ベクトルになります。この固有ベクトルを g1 としたとき、J の値が最小となるのは g1 のときで、従って { xi } を最もよく近似しているベクトルは g1 になります。二番目に大きい固有値に対する固有ベクトルを g2 とすれば、これが次に { xi } をよく近似しているベクトルとなり、以下、固有値の大きさの順に近似性は小さくなってゆきます。
このように、各ベクトルの平均との差に対する和を使って対称行列を求め、その固有ベクトルを正規直交基底として線形結合の形に表す展開方法を「カルーネン・レーベ展開 ( Karhunen-Loeve Expansion ; KLT )」と言います。この手法は「Kari Karhunen」と「Michel Loeve」の二名の数学者によって考案されました。
KLT を行なうためには、A = Σi{1→N}( xixiT ) を計算してその固有値と固有ベクトルを求める必要があります。対称行列に対し、固有値と固有ベクトルを求めるプログラムは前回紹介しましたので、あとは A を計算する処理を追加すれば、KLT を実現することができます。
KLT を使って、あるデータ列を正規直交基底による線形結合の形に表せたとき、高次の項に対する係数 ( つまり A の固有値 ) が低次のそれに対して無視できるほど小さければ、データを低次の項だけで表しても誤差を小さく抑えることができます。自然画像はこのような性質を持っているため、KLT は、パターン認識やデータ圧縮などの技術に応用されています。この手法を「固有空間法」といいます。また、多変量のデータに対して KLT を使い、互いに相関のない因子に変換した上で解析を行なう統計手法を「主成分分析」といいます。このように、KLT は様々な場面で利用されている重要な手法です。
まずは、カルーネン・レーベ展開が統計解析の中でどのように利用されているかを紹介します。
{ xi } は各点の平均値との差を表しているとします。従って、{ xi } の和は原点になります。原点 O を通る、部分空間上の任意の単位ベクトル e に沿う直線に、点 xi から垂線を下ろし、直線との交点を H としたとき、線分 OH の長さを ti とすると、ベクトル OH = tie と表すことができます。垂線は xi - tie であり、これが e と直交することから、
左辺を展開すると
となり、( e, xi ) = ti、つまり、xi と e の内積が、線分 OH の長さに等しくなります。
ti の和は、( e, xi ) の和と等しいことになるので、
になります。{ xi } の和が原点なので、e に沿う直線に射影したベクトルの長さの和もゼロになるわけです。よって、ti の平均値もゼロです。そこで、ti の分散を考えると、
| (1/N)Σi{1→N}( ( 0 - ti )2 ) | = | (1/N)Σi{1→N}( ( e, xi )2 ) |
| = | (1/N)Σi{1→N}( ( e, xi )( xi, e ) ) | |
| = | (1/N)Σi{1→N}( eTxixiTe ) | |
| = | eT{ (1/N)Σi{1→N}( xixiT ) }e | |
| = | eTVe = ( e, Ve ) |
但し、V = ( 1 / N )Σi{1→N}( xixiT ) としています。これは、カルーネン・レーベ展開で求めた対称行列 A をデータ数 N で割ったものと等しくなります。この行列 V を「共分散行列 ( Covariance Matrix )」といいます。V は A を正のスカラーで割っただけなので半正値対称行列であり、二次形式の標準形に表すことができます。最大固有値は分散の最大値を表し、その方向は最大固有値に対する固有ベクトルになります。
V の r 行 c 列の成分 arc は
であり、データ列を fi = ( fi1, fi2, ... fim )T、その平均を g0 = ( g1, g2, ... gm )T とすれば、
| xi | = | ( xi1, xi2, ... xim )T |
| = | fi - g0 = ( fi1 - g1, fi2 - g2, ... fim - gm )T |
になるので、arc は
と表すことができます。r = c のとき、上式は Σi{1→N}( ( fir - gr )2 ) / N となり、これはデータ列 fi の r 番目の成分に対する標本分散を意味します。r ≠ c のときは、r 番目と c 番目の成分を含んでおり、fir > gr のとき fic > gc、または fir < gr のとき fic < gc となるデータが多い場合、arc は正の値、逆に fir > gr のとき fic < gc、または fir < gr のとき fic > gc となるデータが多い場合、arc は負の値になります。そのような傾向がない場合、二つのデータに依存性はなく、arc はほとんどゼロになります。よって、arc は二つのデータ間の依存度を表すパラメータとなり、これを「(標本)共分散 ( Covariance )」といいます。
x'r = ( f1r - gr, f2r - gr, ... fNr - gr )
x'c = ( f1c - gc, f2c - gc, ... fNc - gc )
としたとき、コーシー = シュワルツの不等式から
を満たします。不等式の中辺を R として、ベクトルの成分で表すと、
分母と分子それぞれを N で割ると、
分子は r 番目と c 番目の成分に対する共分散なので、これを γrc とし、分母は r 番目と c 番目それぞれの成分に対する標準偏差 ( 分散の平方根 ) なので、これをそれぞれ σr, σc とすると、R は次のように表すことができます。
このパラメータ R を「相関係数 ( Correlation Coefficient )」といいます。コーシー = シュワルツの不等式より、相関係数は -1 から 1 までの値を取り、二つのデータが独立であれば R = 0 になり、二つのデータは無相関であるといいます。また、R > 0 なら正の相関、R < 0 なら負の相関があるといいます。
実際のデータを使って、共分散行列を求めてみます。下表は、ある 30 名のグループの身長と体重を表したものです。
| No. | 身長(cm) | 体重(kg) | No. | 身長(cm) | 体重(kg) | No. | 身長(cm) | 体重(kg) |
|---|---|---|---|---|---|---|---|---|
| 1 | 173.72 | 87.52 | 11 | 167.66 | 59.03 | 21 | 154.53 | 71.64 |
| 2 | 159.58 | 61.12 | 12 | 171.70 | 76.65 | 22 | 178.77 | 92.68 |
| 3 | 177.76 | 91.64 | 13 | 173.72 | 90.54 | 23 | 158.57 | 55.32 |
| 4 | 176.75 | 78.10 | 14 | 175.74 | 55.59 | 24 | 151.50 | 59.68 |
| 5 | 180.79 | 78.44 | 15 | 166.65 | 52.77 | 25 | 153.52 | 61.28 |
| 6 | 178.77 | 89.48 | 16 | 168.67 | 65.43 | 26 | 160.59 | 77.37 |
| 7 | 159.58 | 78.94 | 17 | 174.73 | 88.54 | 27 | 176.75 | 62.48 |
| 8 | 161.60 | 80.96 | 18 | 162.61 | 50.24 | 28 | 167.66 | 61.84 |
| 9 | 173.72 | 90.54 | 19 | 177.76 | 69.52 | 29 | 173.72 | 63.38 |
| 10 | 152.51 | 65.13 | 20 | 153.52 | 63.63 | 30 | 165.64 | 49.39 |
身長と体重の平均値は 167.63(cm) と 70.96(kg) なので、平均値との差を求めると下表のようになります。
| No. | 身長(cm) | 体重(kg) | No. | 身長(cm) | 体重(kg) | No. | 身長(cm) | 体重(kg) |
|---|---|---|---|---|---|---|---|---|
| 1 | 6.09 | 16.56 | 11 | 0.03 | -11.93 | 21 | -13.10 | 0.68 |
| 2 | -8.05 | -9.84 | 12 | 4.07 | 5.69 | 22 | 11.14 | 21.72 |
| 3 | 10.13 | 20.67 | 13 | 6.09 | 19.57 | 23 | -9.06 | -15.64 |
| 4 | 9.12 | 7.14 | 14 | 8.11 | -15.37 | 24 | -16.13 | -11.29 |
| 5 | 13.16 | 7.48 | 15 | -0.98 | -18.19 | 25 | -14.11 | -9.68 |
| 6 | 11.14 | 18.52 | 16 | 1.04 | -5.53 | 26 | -7.04 | 6.41 |
| 7 | -8.05 | 7.98 | 17 | 7.10 | 17.58 | 27 | 9.12 | -8.48 |
| 8 | -6.03 | 9.99 | 18 | -5.02 | -20.72 | 28 | 0.03 | -9.12 |
| 9 | 6.09 | 19.57 | 19 | 10.13 | -1.44 | 29 | 6.09 | -7.59 |
| 10 | -15.12 | -5.84 | 20 | -14.11 | -7.33 | 30 | -1.99 | -21.58 |
この差の二乗を平均したものが分散になり、それぞれ 82.05(cm2), 181.21(kg2) になります。身長と体重を掛けた積は、次のようになります。
| No. | 身長 x 体重(cm・kg) | No. | 身長 x 体重(cm・kg) | No. | 身長 x 体重(cm・kg) |
|---|---|---|---|---|---|
| 1 | 100.89 | 11 | -0.40 | 21 | -8.87 |
| 2 | 79.21 | 12 | 23.17 | 22 | 242.03 |
| 3 | 209.51 | 13 | 119.28 | 23 | 141.67 |
| 4 | 65.14 | 14 | -124.70 | 24 | 182.00 |
| 5 | 98.50 | 15 | 17.76 | 25 | 136.60 |
| 6 | 206.41 | 16 | -5.77 | 26 | -45.07 |
| 7 | -64.23 | 17 | 124.86 | 27 | -77.37 |
| 8 | -60.23 | 18 | 103.95 | 28 | -0.31 |
| 9 | 119.28 | 19 | -14.64 | 29 | -46.23 |
| 10 | 88.21 | 20 | 103.35 | 30 | 42.86 |
これらの平均値が共分散となり、その値は 58.56(cm・kg) になります。以上から、共分散行列は次のようになります。
| V = | | | 82.05, | 58.56 | | |
| | | 58.56, | 181.21 | | |
また、相関係数は
になります。
身長と体重の平均差について相関図を描画すると、それぞれの平均は原点になるためデータは原点を中心に分布します。
共分散行列 V が対角行列になるように主軸変換を行なうと、共分散は全てゼロになります。新しい座標系が表す成分は、元の成分の線形結合によって表され、その成分によってそれぞれのデータは互いに無相関な状態になります。また、V の固有値は新たな成分の分散を表し、成分全体の中の寄与の程度を示すことになります。新たな座標系によって表される成分のことを「主成分 ( Principal Component )」といい、主成分を使ってデータを分析する手法を「主成分分析 ( Principal Component Analysis ; PCA )」といいます。
上記例において、V の固有値は λ1 = 208.36 と λ2 = 54.90 で、対応する固有ベクトルはそれぞれ
になります。上に示した相関図には、これらが示す主軸が赤線で描画されています。u1 方向が最も分散が大きく、その値は λ1 になります。また、それに直交する方向の分散は λ2 になります。
身長・体重のデータを fi = ( hi, wi ) ( i = 1, 2, ... 30 ) とします。その平均値は g0 = ( 167.63, 70.96 ) になることは先に示した通りです。
身長・体重の平均差は xi = fi - g0 = ( hi - 167.63, wi - 70.96 ) と表すことができます。Q = ( u1, u2 ) としたとき、x'i = ( x'i1, x'i2 ) = QTxi を計算すると、
x'i1 と x'i2 に対する共分散はゼロであり、互いに無相関な成分になります。x'i1 は身長と体重の両方の大きさの程度を表し、x'i2 は逆に身長と体重の差を表しているので、それぞれをその人の「体力」「肥満度」などと解釈することができます。それぞれのメンバに対して、身長と体重ではなく体力と肥満度の形でデータを提示する方が、全体の中での自分の体の状態を把握しやすくなるでしょう。
もちろん、これはデータを元にした「仮説」なので、科学的に実証されているわけではありませんが、より多くのサンプルデータを使って同じような結果が得られれば、仮説に対する信頼性はより高くなります。
| No. | 体力 | 肥満度 | No. | 体力 | 肥満度 | No. | 体力 | 肥満度 |
|---|---|---|---|---|---|---|---|---|
| 1 | 17.58 | 1.44 | 11 | -10.81 | -5.05 | 21 | -4.89 | 12.17 |
| 2 | -12.31 | 3.16 | 12 | 6.87 | -1.30 | 22 | 24.39 | -0.97 |
| 3 | 23.02 | -0.50 | 13 | 20.32 | 2.70 | 23 | -18.00 | 1.64 |
| 4 | 10.31 | -5.27 | 14 | -10.53 | -13.83 | 24 | -17.02 | 9.88 |
| 5 | 12.32 | -8.79 | 15 | -16.92 | -6.77 | 25 | -14.72 | 8.72 |
| 6 | 21.49 | -2.32 | 16 | -4.58 | -3.27 | 26 | 2.85 | 9.08 |
| 7 | 3.86 | 10.66 | 17 | 18.93 | 0.95 | 27 | -3.86 | -11.84 |
| 8 | 6.53 | 9.67 | 18 | -20.91 | -4.16 | 28 | -8.26 | -3.87 |
| 9 | 20.32 | 2.70 | 19 | 2.95 | -9.80 | 29 | -4.32 | -8.72 |
| 10 | -11.65 | 11.26 | 20 | -12.58 | 9.72 | 30 | -20.41 | -7.27 |
互いに独立で無相関な m 個のデータ列 f = ( f1, f2, ... fm ) があったとします。それぞれのデータが正規分布に従うとき、その確率分布は次のように表すことができます。
但し、μi は fi の平均値、σi2 は fi の分散を表しています。ここで xi = fi - μi として平均値がゼロになるようにすると、上式は次のようになります。
個々のデータは独立なので、m 個のデータが { f1, f2, ... fm } となる同時確率分布は各データの確率分布の積で求められ、
ここで、ネイピア数 e の指数は Σi{1→m}( xi2 / 2σi2 ) となっており、これは二次形式の標準形を表しています。分母にある分散 σi2 は固有値を表し、その値はゼロ以上になるので、分布は楕円体を示すことになります。上式を固有値を使って表すと、
さらに固有値からなる対角行列を D とすると、x = ( x1, x2, ... xm ) としたとき、
となるので、
主成分分析は、共分散行列を固有値分解することによって、データを互いに無相関な状態にして分析する手法でした。上式は、共分散行列に対して固有値が逆数になっているという違いはあるものの、固有値分解によって対角化されたような状態にあたり、元に戻すことによって、次のように表すことができます。
V-1 は D-1 を相似変換したものであり、行列式の値は等しいままで、|D-1| = |V-1| です。上式は主軸変換によって座標系を回転・鏡映しただけなので、分布の形状は変わりませんが、それぞれのデータは無相関であるとは限らなくなります。なお、ここでは、V-1 を固有値分解すると D-1 になることを暗黙のうちに使っていますが、これは後ほど証明します。
最小二乗法のところで紹介した正規分布は一次元正規分布と呼ばれ、一つの確率変数に対する確率分布を表していました。上式は、これを m 次元に拡張したときの正規分布を表しています。
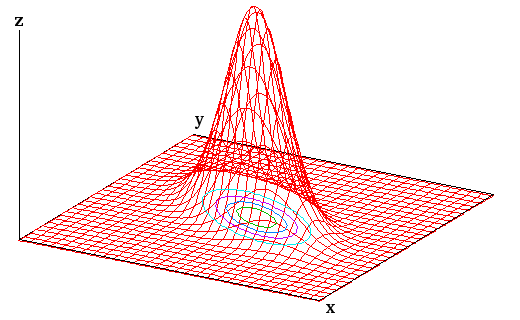 |
上の図は、二次元正規分布を表しています。この正規分布が以下の式で表されるとします。
この分布が定数値 z = K を取るとき、上式を変形することで以下の式が得られます。
これは楕円の方程式を表しており、分布を xy 平面で切ったときの切り口の形にあたります。この方程式は ( x, V-1x ) を主軸変換した結果なので、( x, V-1x ) = (定数) は ( x, y ) の分布を表す式であることになります。また、主軸に沿うように、xy 平面に垂直な平面で切ると、その切り口は、原点を通る z軸について左右対称な釣り鐘状になります ( この形状をベルカーブといいます )。これは、一次元正規分布の形そのものになります。
xi の分布を二次形式で近似したものを f = ( x, V-1x ) とすると、V-1 の最大固有値に対する固有ベクトルの方向は、f = (一定) となる曲面が原点から最も近い方向になるのでした。つまりそれはデータの分布において分散が最小になる方向であり、V の最小固有値に対する固有ベクトルがそれにあたります。以下、V の二番目に小さい固有値に対する固有ベクトルは、V-1 において二番目に大きい固有値に対する固有ベクトルになり、最後に、曲面が原点から最も遠い方向は、分散が最大になる方向なので、V の最大固有値に対する固有ベクトルが V-1 の最小固有値に対する固有ベクトルとなります。m 次元正規分布での説明で示したように、V とその逆行列は固有ベクトルは変化せず、その固有値は逆数の関係になります。
逆行列の固有ベクトルが元の行列と一致し、その固有値が逆数の関係になることは、次のように示すことができます。
に対して両辺に V-1 を左側から掛けると、
なので、固有ベクトルは等しく、固有値は逆数になります。
また、( x, V-1x ) が楕円体になるならば、V-1 は正値対称行列である必要があります。これは次のように証明できます。
両辺の転置をとると
V は対称行列なので VT = V。従って、
よって、(V-1)T は V の逆行列であり、
よって、V-1 は対称行列になります。固有値は V の逆数なので、V の固有値にゼロが含まれていなければ、V-1 の固有値は全て正数であり、V-1 は正値対称行列であることになります。
もし、V の固有値にゼロが含まれていたら、行列式は固有値の積に等しいことから |V| = 0 になり、逆行列 V-1 は存在しないことになります。固有値がゼロということはその固有ベクトル方向の分散がゼロということなので、例えば二次元平面上では、そのような分布は一本の直線になります。そのような分布を表すような楕円の方程式は存在しません。
/* CovarianceMatrix : 共分散行列を求める 引数として渡されるデータ列は、ある列に同種のデータが並ぶ ( 行が一つの標本の独立変数である ) とする。 data : データ列 cov : 求めた共分散行列を保持する対称行列へのポインタ */ template< class T, class U > void CovarianceMatrix( const Matrix< T >& data, SymmetricMatrix< U >* cov ) { assert( &data != 0 && cov != 0 ); // 行列に対する各型 typedef typename Matrix< T >::size_type size_type; typedef typename Matrix< T >::const_iterator const_iterator; size_type m = data.cols(); // データ種の数 cov->resize( m ); if ( m == 0 ) return; // 共分散行列の要素を計算する for ( size_type c1 = 0 ; c1 < m ; ++c1 ) { const_iterator col1 = data.column( c1 ); ( *cov )[c1][c1] = SampleVariance< U >( col1, col1.end() ); for ( size_type c2 = c1 + 1 ; c2 < m ; ++c2 ) { const_iterator col2 = data.column( c2 ); ( *cov )[c1][c2] = Covariance< U >( col1, col1.end(), col2, col2.end() ); } } } /** PrincipalComponentAnalysis : 主成分分析用関数オブジェクト データ列 X の共分散行列 V を求め、固有値分解 ( スペクトル分解 ) V = QD(Qt)を行う。 D は固有値からなる対角行列で、Q は固有ベクトルからなる直交行列、Qt はその転置行列を表す。 各標本の独立変数ベクトルを xi としたとき、(Qt)xi は主成分を表し、D の固有値はその分散となる。 **/ class PrincipalComponentAnalysis { // 固有値をキーに固有ベクトルへのインデックスを保持する型 typedef std::multimap< double, SquareMatrix< double >::size_type, std::greater< double > > EigenValue; SymmetricMatrix< double > cov_; // 標本共分散行列 size_t sampleSize_; // 標本数 EigenValue ev_; // 固有値と固有ベクトルへのインデックス SquareMatrix< double > q_; // QR分解後の直交行列(固有ベクトル) double evTotal_; // 固有値の総和 std::vector< SquareMatrix< double >::const_iterator > idx_; // 固有値を大きい順に並べた時の固有ベクトルの位置 public: // 対象データ data を指定して構築 template< class T > PrincipalComponentAnalysis( const Matrix< T >& data ) : sampleSize_( data.rows() ) { CovarianceMatrix( data, &cov_ ); } // operator() : 主成分分析を行う // // e : 対角化を行うときに、非対角成分をゼロと判断するためのしきい値 // maxCnt : 対角化を行うときの反復処理最大回数 void operator()( double e, unsigned int maxCnt ); // contribution : i 番目のデータ種の寄与率を返す // // 寄与率は、対象のデータ種の固有値に対して固有値の総和との比率から求められる。 // 範囲外を指定した場合ゼロが、固有値の総和がゼロの場合 NAN がそれぞれ返される。 double contribution( size_t i ) const; // eigenvalue : i 番目の主成分の分散(固有値)を返す // // 主成分の分散は、固有値分解後の固有値そのものである。番号は、固有値の大きいものから // 順番に付けられる。 // 範囲外を指定した場合、例外 ExceptionInvalidLength< size_t > を投げる。 double eigenvalue( size_t i ) const; // eigenvector : i 番目の主成分の固有ベクトルを返す // // 番号は、固有値の大きいものから順番に付けられる。 // 範囲外を指定した場合、例外 ExceptionInvalidLength< size_t > を投げる。 std::vector< double > eigenvector( size_t i ) const; // size : 主成分の数を返す size_t size() const { return( ev_.size() ); } // sampleSize : 標本数を返す size_t sampleSize() const { return( sampleSize_ ); } }; /* PrincipalComponentAnalysis::operator() : 主成分分析を行う e : 対角化を行うときに、非対角成分をゼロと判断するためのしきい値 maxCnt : 対角化を行うときの反復処理最大回数 */ void PrincipalComponentAnalysis::operator()( double e, unsigned int maxCnt ) { SquareMatrix< double > r; // 上三角行列(対角成分が固有値になる) // 対象行列の対角化 EigenLib::Householder_DoubleShiftQR< double >( cov_, &r, &q_, e, maxCnt ); evTotal_ = 0; // 固有値の総計 for ( SquareMatrix< double >::size_type i = 0 ; i < r.size() ; ++i ) { // 固有ベクトルの位置を値として登録しておく ev_.insert( std::pair< double, SquareMatrix< double >::size_type >( r[i][i], i ) ); evTotal_ += r[i][i]; } } /* PrincipalComponentAnalysis::contribution : i 番目のデータ種の寄与率を返す */ double PrincipalComponentAnalysis::contribution( size_t i ) const { if ( i >= ev_.size() ) return( 0 ); // 範囲外指定ならゼロ if ( evTotal_ == 0 ) return( NAN ); // 総和がゼロなら NAN // 対象のデータ種を指す反復子 EigenValue::const_iterator cit = ev_.begin(); std::advance( cit, i ); return( cit->first / evTotal_ ); } /* PrincipalComponentAnalysis::eigenvalue : i 番目のデータ種の固有値を返す */ double PrincipalComponentAnalysis::eigenvalue( size_t i ) const { if ( i >= ev_.size() ) throw ExceptionInvalidLength< size_t >( "PrincipalComponentAnalysis::eigenvalue : Specified index is too large.", i ); // 対象のデータ種を指す反復子 EigenValue::const_iterator cit = ev_.begin(); std::advance( cit, i ); return( cit->first ); } /* PrincipalComponentAnalysis::eigenvector : i 番目のデータ種の固有ベクトルを返す */ vector< double > PrincipalComponentAnalysis::eigenvector( size_t i ) const { if ( i >= ev_.size() ) throw ExceptionInvalidLength< size_t >( "PrincipalComponentAnalysis::eigenvector : Specified index is too large.", i ); // 対象のデータ種を指す反復子 EigenValue::const_iterator cit = ev_.begin(); std::advance( cit, i ); // ベクトルをコピー SquareMatrix< double >::const_iterator col = q_.column( cit->second ); vector< double > ans( col, col.end() ); return( ans ); }
主成分分析を実行するためのクラスは PrincipalComponentAnalysis で、コンストラクタにおいて、データ列として double型を要素とする行列 Matrix インスタンスを渡しています ( Matrix クラスの実装は省略しています )。列の要素が m 次元空間上の一点を表し ( つまりこの中に身長や体重といった個々のデータが入っていて )、行方向に複数個連なっていると考えればプログラムの中が読みやすくなると思います。CovarianceMatrix が共分散行列を求めるための関数で、個々の点に対する二つの列 col1 ( c1 番目の列 ) と col2 ( c2 番目の列 ) の平均差の積和をデータ数で除算して共分散を求める処理を繰り返し、c1 行 c2 列 ( かつ c2 行 c1 列 ) の要素とします。共分散の計算は Covariance が、対角成分の、c1 = c2 となる箇所の計算は ( 標本分散を求めることになるので ) SampleVariance を利用するようになっていますが、どちらも内容は単純なので実装は省略しています。引数として列の開始と末尾の次の位置を渡す仕様であり、開始位置は Matrix クラスのメンバ関数 column で反復子として取得し、その末尾の次の位置は反復子のメンバ関数 end で取得します。vector などのコンテナ・クラスのように、開始と末尾の次の位置の両方についてコンテナ・クラスのメンバ関数で取得する仕様ではないことに注意してください。また、共分散行列は対称行列となるので、結果を受け取るための引数 cov は対称行列を表す SymmetricMatrix 型となっています。そのため、プログラム内では行列の右上側半分しか値を代入していません。
メンバ関数 operator()は「ウィルキンソンの移動法」を利用して固有値分解しています。固有値分解により求めた対角行列に並ぶ固有値が値の大きさの順で常に並んでいるとは限らないので、結果を大きさの順で得られるようにするため、STL(Standard Template Library) で用意されているコンテナ・クラス multimap を利用しています。このクラスはキーの重複を許容した連想配列で、登録時に自動的に並べ替えがされるので先頭要素からデータを取得すればソート済の結果が得られるようになります。map クラスも同様の処理ができますが、こちらはキーの重複が許されず、キーが一致した場合は上書きされてしまいます。なお、multimap はテンプレート・クラスであり、テンプレート引数の一番目はキーの型、二番目はキーにリンクした要素の型、最後の引数はソート時の大小比較用叙述関数 ( Predicate Functions ) になります。
叙述関数とは、bool 値を戻り値とする関数オブジェクト ( または関数 ) です。STL では、叙述関数とコンテナ・クラス、汎用アルゴリズムを組み合わせて様々な処理 ( 探索やソートなど ) を行なうためのライブラリ群が用意されています。greater の場合、
greater< double > cmp; cmp( d1, d2 );
で d1と d2の大きさを比較して、d1 の方が大きければ ture、そうでなければ false を返します。multimap は greater を使ってキーの大小を比較し、大きい方が先頭側になるように要素を並べます。STLには、例えば比較対象の片側を固定値にして、引数が二つの関数を、引数が一つの関数として利用できるようにするための「バインダ ( Binder )」や、メンバ関数または一般の関数を引数として利用する場合に利用できる「アダプタ ( Adapter )」、叙述関数に対して逆の値を返すようにするための「ネゲータ ( Negater )」といった機能も用意されています。これらは、うまく利用すると非常に便利な反面、何をしているかが直感的にわかりづらくなるといった問題を抱える場合もあります。
以下に、主成分分析の結果を示すためのサンプル・プログラムと、例で示した身長と体重のデータを主成分分析した結果を示します。
void PCA_Test( const Matrix< double >& vx ) { cout << "***** Principal Component Analysis start *****" << endl << endl; PrincipalComponentAnalysis pca( vx ); pca( 1e-6, 1000 ); cout << "#data set = " << pca.sampleSize() << endl; // 標本数 cout << "#data = " << pca.size() << endl << endl; // 主成分の数 // 標本共分散行列 cout << "***** Covariance Matrix *****" << endl; SymmetricMatrix< double > cov; CovarianceMatrix( vx, &cov ); cout << cov << endl << endl; // 固有値(主成分の分散) cout << "***** Variance *****" << endl; cout << pca.eigenvalue( 0 ); for ( size_t j = 1 ; j < pca.size() ; ++j ) cout << ", " << pca.eigenvalue( j ); cout << endl << endl; // 固有ベクトル(主成分)とその寄与率 cout << "***** Principal Component *****" << endl; double contSum = 0; for ( size_t j = 0 ; j < pca.size() ; ++j ) { cout << "x'" << j << " = "; std::vector< double > q = pca.eigenvector( j ); cout << "(" << q[0] << ")x0"; for ( size_t i = 1 ; i < q.size() ; ++i ) cout << " + (" << q[i] << ")x" << i; contSum += pca.contribution( j ); cout << "\t: contribution = " << pca.contribution( j ) << " [" << contSum << "]" << endl; } cout << endl << "***** Principal Component Analysis end *****" << endl; }
***** Principal Component Analysis start ***** #data set = 30 #data = 2 ***** Covariance Matrix ***** | 82.0489, 58.5572 | | 58.5572, 181.21 | ***** Variance ***** 208.357, 54.9015 ***** Principal Component ***** x'0 = (-0.420603)x0 + (-0.907245)x1 : contribution = 0.791454 [0.791454] x'1 = (-0.907245)x0 + (0.420603)x1 : contribution = 0.208546 [1] ***** Principal Component Analysis end *****
主成分の右側にあるパラメータ contribution は「寄与率 ( Contribution )」、さらに[]で囲まれた数値は「累積寄与率」を示しています。寄与率は、その主成分が全体の中でどの程度「寄与しているか」を示す尺度になり、固有値を、その合計で割った比率を示しています。寄与率の低い主成分は、分散が小さいためデータ間の差が小さいことになり、無視できると判断されます。寄与率の大きい、または累積寄与率がある範囲内にある主成分だけを見ることで、分析対象とする主成分を少なくすることができるわけです。
最小二乗法や、それを元に考えられたカルーネン・レーベ変換、主成分分析は、データの確率分布が正規分布に従っていることを前提にしています。しかし、どんなデータでも必ず正規分布に従うかというと、必ずしもそうとは限りません。主成分分析で示した身長と体重の例でも、例えば極端に体の小さいグループと、極端に体の大きいグループの二つからデータを採取して、それらが混在した状態で分析しようとした場合、そのデータの分布は、二つの山のような形になることが想像できます。それぞれのグループのデータが正規分布に近いと仮定しても、混在したデータはもはや正規分布とは呼べず、正しい分析結果を得ることはできなくなります。主成分分析を行う場合、扱うデータがどのような分布を示しているかを前もって調べておくことが大切です。
最小二乗法によって得られた近似直線を「回帰直線 ( Regression Line )」といいます。グラフ描画用ソフトなどで、よくデータに対する近似直線や近似曲線を表示する機能があるのをご存知の方も多いと思いますが、通常は、近似式を求める場合に最小二乗法が利用されています。
最小二乗法を使って、一般の多項式による近似をしてみたいと思います。求める n 次の多項式を
とし、近似したいデータを ( xi, yi ) ( i = 1, 2, ... N ) とすると、次の値 J を最小にする係数 ck を求めればよいことになります。
∂J/∂cj = 0 を解くと、
| ∂J/∂cj | = | Σi{1→N}( { yi - Σk{0→n}( ckxin-k ) }( -xin-j ) ) |
| = | Σi{1→N}( Σk{0→n}( ckxi2n-j-k ) -yixin-j ) = 0 |
より
よって、正規方程式は
| | | Σi{1→N}( xi2n ), | Σi{1→N}( xi2n-1 ), | ... | Σi{1→N}( xin ) | || | c0 | | = | | | Σi{1→N}( yixin ) | | |
| | | Σi{1→N}( xi2n-1 ), | Σi{1→N}( xi2n-2 ), | ... | Σi{1→N}( xin-1 ) | || | c1 | | | | | Σi{1→N}( yixin-1 ) | | |
| | | : | : | ... | : | || | : | | | | | : | | |
| | | Σi{1→N}( xin ), | Σi{1→N}( xin-1 ), | ... | Σi{1→N}( xi0 ) | || | cn | | | | | Σi{1→N}( yixi0 ) | | |
これは、n + 1 個の未知数を持つ連立方程式になります。n が数十個程度であれば、直接法を使ったとしても処理にそれほど時間はかからないので、コンピュータを利用すれば近似多項式を求めることはそれほど難しくありません。また、左辺の行列は対称行列になるので、固有値分解を行なうことによって逆行列を求め、係数を得るようなことも可能です。
内積が定義されたベクトル空間は「計量ベクトル空間 ( Metric Vector Space )」というのでした ( *n1-1 )。計量ベクトル空間内の元 a を、n 個の元 ui の線形結合で近似するときの正規方程式は、ベクトルの場合と同じ形になって、次のように表すことができます。
| | | ||u1||2, | ( u1, u2 ), | ... | ( u1, un ) | || | c1 | | | = | | | ( a, u1 ) | | |
| | | ( u2, u1 ), | ||u2||2, | ... | ( u2, un ) | || | c2 | | | | | ( a, u2 ) | | | |
| | | : | : | ... | : | || | : | | | | | : | | | |
| | | ( un, u1 ), | ( un, u2 ), | ... | ||un||2 | || | cn | | | | | ( a, un ) | | |
これを、第 r 行の正規方程式だけに限定して、次のように書き表すことにします。
書き方は同じですが、内積やノルムの定義はベクトルのそれとは限らなくなることに注意して下さい。例えば、区間 [a,b] 上の連続関数 f(x), g(x) に対して、
と定義した場合、φ(x) を fi(x) の線形結合で近似するときに係数を求めるための正規方程式は
になります。先に示した多項式による近似の場合、a = ( y1, y2, ... yN ), xr = ( x1n-r, x2n-r, ... xNn-r ) として、a を xr の線形結合で近似することを意味していたことになります。この時の内積は、
( xi, xj ) = Σi{1→N}( xi2n-i-j )
( a, xr ) = Σi{1→N}( yixin-r )
になります。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |