
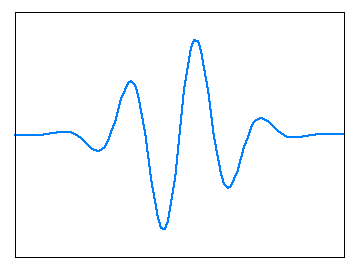
ヒトをはじめとする哺乳類において、目から入った情報を解析してモノや空間を認識するために脳の中の「視覚野 ( Visual Cortex ) 」と呼ばれる領域が使われていることが知られています。目から入ってきた信号は、最初に大脳の中の「一次視覚野 ( V1 ) 」に到達し、その中の「受容野 ( Receptive Field ) 」が反応することによって処理され、さらに高次の視覚野に伝達されていきます。「デイヴィッド・ハンター・ヒューベル ( David Hunter Hubel ) 」と「トルステン・ニルズ・ウィーセル ( Torsten Nils Wiesel ) 」は 1959 年に、ネコを使って視覚野のニューロンの電気信号を調べる実験の中で、個々の細胞が特定の傾きを持った線分に対して反応することを発見し、この業績によって 1981 年にノーベル生理学・医学賞を受賞しました。さらに「Judson P. Jones」と「Larry A. Palmer」によって、ネコの視覚野にある単純型細胞の形が二次元の「ガボール・フィルタ ( Gabor Filter ) 」によって表せることが示され、このフィルタは虹彩認識や指紋認識などの生体認証に必要なパターン認識技術にも利用されるようになりました。今回は、このガボール・フィルタの紹介をしたいと思います。
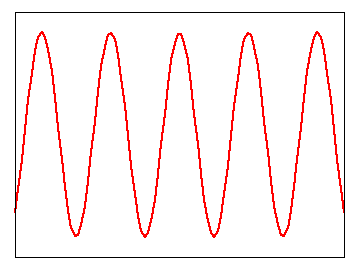
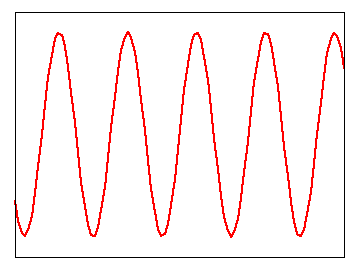
ガボール・フィルタは、「正弦波」と「ガウス関数」の積として定義されます。
g(t) = K・w(t)・exp( iφ )・s(t)
但し w(t) = exp( -t2 / 2σ2 ), s(t) = exp( iω0t )
上式において、w(t) がガウス関数、s(t) が正弦波を表します。s(t) は指数関数の形をしていますが、以下のように「オイラーの公式 ( Euler's formula ) 」を使って三角関数の形に表すことができます。
i は虚数単位を表しており、i2 = -1 となります。つまり、ガボール・フィルタは複素関数であることになります。
ω0 は周波数を表し、値が大きくなるほど正弦波の周期は小さくなります。また、
より、φ は波を原点からずらす ( 位相オフセットの ) 役割を持っています。
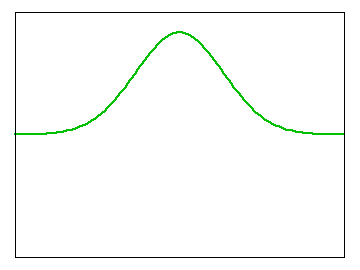
ガウス関数の形を持つ確率密度関数としては、以下の式で表される正規分布が有名です。
但し、μ は確率分布の平均値、σ2 は確率分布の分散を表します。この確率分布は、平均値 μ を軸として左右対称な釣鐘の形を取ります。
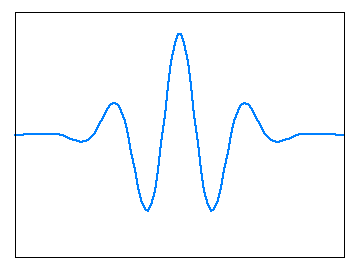
実部、または虚部だけを抽出すれば、正規分布のような釣鐘型を正弦波と合成したものが ガボール・フィルタとなり、ちょうど下図に示したような形となります。
 |
+ |  |
= |  |
 |
+ |  |
= |  |
ガボール・フィルタをフーリエ変換に掛けた結果は次のようになります ( 補足 1 )。
| G(ω) | = | sqrt( 2π )σK exp( iφ ) exp( (-1/2)[ σ( ω - ω0 ) ]2 ) |
| = | sqrt( 2π )σK exp( iφ ) w( σ2( ω - ω0 ) ) |
一般に、フーリエ変換の結果は複素数なので、各周波数毎のエネルギーを表すためにその絶対値がよく利用されます。これを「パワースペクトル ( Power Spectrum ) 」といいます。ガボール・フィルタのパワースペクトルは
| || G(ω) ||2 | = | || sqrt( 2π )σK exp(iφ) w( σ2( ω - ω0 ) ) ||2 |
| = | [ sqrt( 2π )σK w( σ2( ω - ω0 ) ) ]2 || cosφ + isinφ ||2 | |
| = | [ sqrt( 2π )σK w( σ2( ω - ω0 ) ) ]2 ( cos2φ + sin2φ ) | |
| = | [ sqrt( 2π )σK w( σ2( ω - ω0 ) ) ]2 |
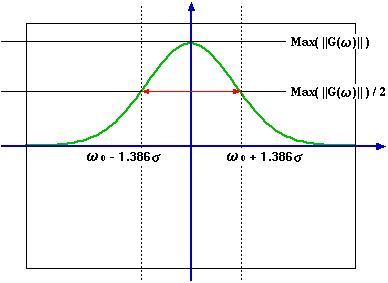
となるので、w( σ2( ω - ω0 ) ) が ω = ω0 のとき最大となることから、ガボール・フィルタは ω = ω0 を中心とする釣鐘型のエネルギー分布を持ち、ω0 付近の周波数領域だけを増幅する「帯域フィルタ ( Band-pass Filter, BPF ) 」として利用することができます(「サンプル補間」の中の「5) 補間関数と畳み込み積分」に詳しい説明があります)。
|| G(ω) || のピーク値 ( = sqrt( 2π )σK ) の半分の値を取る時の周波数を ωh とすると、
|| G(ωh) || = sqrt( 2π )σK w( σ2( ωh - ω0 ) ) = sqrt( 2π )σK / 2 より
exp( (-1/2)[ σ( ωh - ω0 ) ]2 ) = 0.5
ωh = ω0 ± sqrt( -2・ln( 0.5 ) ) / σ ≅ ω0 ± 1.386 / σ
従って、ω0 を中心に正負両側へ約 1.386 / σ だけ進んだところでピークの半分となることが分かります。この二倍の値 2.773 / σ は、ピークから半分の大きさまでの帯域幅 ( Half-magnitude Bandwidth ) を表すことになります。ここで、
とおくと、
で、帯域幅はほぼ a に等しくなります。このとき、ガウス関数は
と表すことができます。
 |
ガボール・フィルタを二次元に拡張します。
g( x, y ) = K wr( x, y ) s( x, y )
wr( x, y ) は一次元ガボール・フィルタにおけるガウス関数にあたり、s( x, y ) は正弦波に該当します。
wr( x, y ) は次の式のように表されます。
但し、( x', y' ) は以下の式で定義され、原点 ( 0, 0 ) を中心に ( x, y ) を時計回りに θ だけ回転した結果が ( x', y' ) になります。
x' = xcosθ + ysinθ
y' = -xsinθ + ycosθ
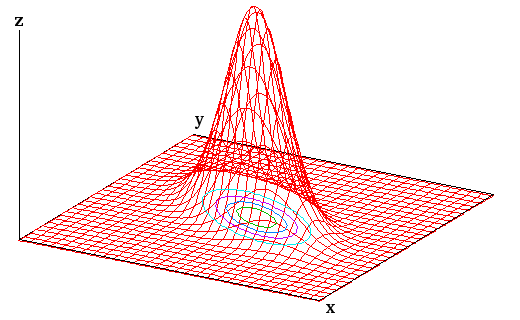
[ x'2 + ( γy' )2 ] / 2σ2 は楕円形を表し、これは xy 平面に平行な面で切ったときの切り口を表しています ( 下図参照 )。wr( x, y ) は ( x, y ) = ( 0, 0 ) において最大となり、その周辺に向かうに従って単調に減少します。また、x' 軸や y' 軸に平行で、xy 平面に垂直な平面で切った時の切り口は、ガウス関数による釣鐘状の曲線になります。
 |
s( x, y ) は次の式のように表されます。
| s( x, y ) | = | exp( i( ω0x' + φ ) ) |
| = | exp( i( ω0( xcosθ + ysinθ ) + φ ) ) |
実部および虚部のみを抽出した式は次のようになります。
Re( s( x, y ) ) = cos( ω0x' + φ )
Im( s( x, y ) ) = sin( ω0x' + φ )
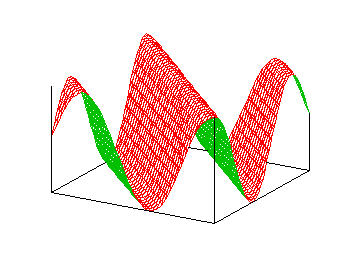
x' は θ だけ時計回りに傾いた軸を表しているため、s( x, y ) はその軸に沿って波が進んだ形を取ることになります ( 下図参照 )。
 |
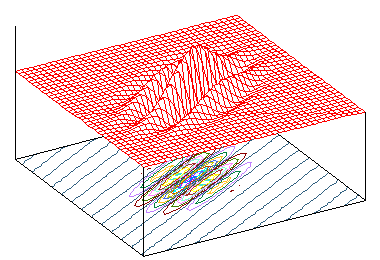
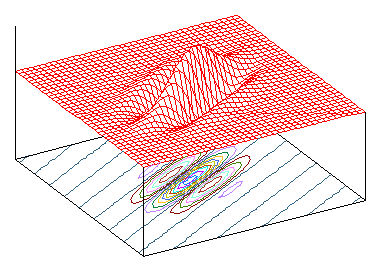
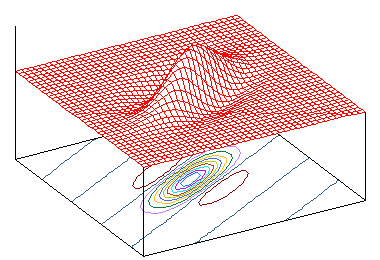
この二つの波を重ね合わせると、下図のような形になります ( 実部のみ )。下図において、x' 軸に平行で xy 平面に垂直な平面で切ったときの断面は、ちょうど一次元ガボール・フィルタの形になります。
| ω0 = 3π | ω0 = 2π | ω0 = π |
|---|---|---|
 |
 |
 |
画像の各ピクセルに対して、ガボール・フィルタの原点 ( ピークとなる位置 ) と重なるようにして合成したとき、フィルタの山や谷に重なる部分の値だけが増幅されます。周辺全体の値に変化がなければ、山と谷のそれぞれで増幅された値どうしが打ち消しあって全体の和はゼロに近くなる反面、山や谷の部分のみに値が集中することで全体の和の絶対値は大きくなります。画像のエッジ部分が波と重なることで、そのような状況が発生することから、ガボール・フィルタはエッジ抽出に利用できることが直感的に理解できると思います。
正弦波の周波数 ω0 を大きくすれば、波の周期が細かくなって、ガウス関数によって周辺が減衰する間にピークが何回も発生します。逆に小さくすれば、波のピークはほとんど発生しなくなります ( ω0 = 0 ならば正弦波が定数 ( 直流成分 ) になり、ガウス関数そのものになります )。正弦波の周波数によって画像と合成したときの値も変化し、変化の激しい ( 高周波成分の高い ) 画像は周波数の高いフィルタによって増幅され、逆に変化の緩やかな ( 低周波成分の大きな ) 画像は周波数の低いフィルタで増幅されます。
ガウス関数の広がりは σ で制御することができ、σ が大きくなるほど周囲に分散するようになります。分布が小さければ、周囲のピクセルの値の影響は小さくなり、逆に広い分布を持っていれば、より広範囲のピクセルの値による影響を受けるようになります。γ は楕円形の扁平率を制御することができるので、波の進行方向やそれに垂直な方向に広がるピクセルの影響だけをカットするようなことが可能です。
二次元ガボール・フィルタのフーリエ変換は以下のような式になります ( 補足2 )。
| G( u, v ) | = | ( 2πKσ2 / γ ) exp( iφ ) exp( -σ2{ ( u' - ω0 )2 + ( v' / γ )2 } / 2 ) |
| = | ( 2πKσ2 / γ ) exp( iφ ) wr( σ2( u' - ω0 ), σ2v' / γ ) |
但し、u, v はそれぞれが周波数を表し、
u' = ucosθ + vsinθ
v' = -usinθ + vcosθ
となります。また、パワースペクトルは
| || G( u, v ) ||2 | = | || ( 2πKσ2 / γ ) exp( iφ ) exp( -σ2{ ( u' - ω0 )2 + ( v' / γ )2 } / 2 ) ||2 |
| = | { ( 2πKσ2 / γ ) wr( σ2( u' - ω0 ), σ2v' / γ ) }2 |
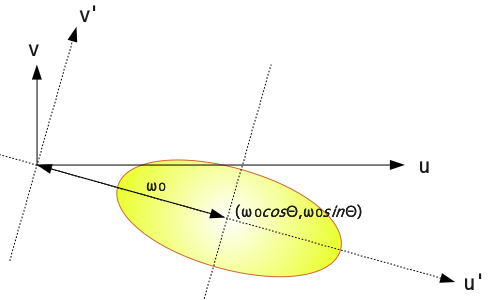
wr( σ2( u' - ω0 ), σ2v' / γ ) は、その中心 ( u' , v' ) = ( ω0, 0 ) ( すなわち ( u, v ) = ( ω0cosθ, ω0sinθ ) ) をピークとする釣鐘状の形を取るので、二次元ガボール・フィルタは一次元の場合と同様に、特定の周波数領域だけを増幅して他はカットする帯域フィルタとして作用することになります。
 |
ガボール・フィルタを生成するためのクラスを以下に示します。
/* GaborFilter : Gabor Filter Kernel ガボール・フィルタは、以下の「正弦波」と「ガウス関数」の積で表される G( λ,θ,φ,σ,γ ; x,y ) = N( γ,σ ; X,Y )H( λ,φ ; X ) ガウス関数 : N( γ,σ; X,Y ) = exp( -( X^2 + (γX )^2 ) / 2σ^2 ) 正弦波 : H( λ,φ; X ) = cos( 2πX / λ + φ ) X = xcosθ + ysinθ Y = -xsinθ + ycosθ 帯域幅 b = log2( ( σπ / λ + K ) / ( σπ / λ - K ) ) 但し K = ( ln2 / 2 )^(1/2) */ class GaborFilter { double lambda_; // cosine関数の波長 λ double theta_; // フィルタの方向 θ double offset_; // cosine関数の位相オフセット φ double ratio_; // ガウス関数のアスペクト比 γ double bandWidth_; // 帯域幅 b double sigma_; // 標準偏差 σ int wSize_; // 窓サイズ std::vector< double > gaborKernel_; // 窓関数の値 // 窓関数の作成 void createKernel(); public: /* デフォルト値 */ static const double DEFAULT_LAMBDA = 8; /// デフォルトの波長 static const double DEFAULT_RATIO = 1; /// デフォルトのアスペクト比 static const double DEFAULT_BANDWIDTH = 1; /// デフォルトの帯域幅 static const int DEFAULT_WINSIZE = 8; /// デフォルトの窓サイズ // 正弦波とガウス関数の各パラメータを指定して構築 GaborFilter( double lambda, double theta, double offset, double ratio = DEFAULT_RATIO, double bandWidth = DEFAULT_BANDWIDTH, int wSize = DEFAULT_WINSIZE ); // 座標 c のガボール・フィルタの値を返す double operator[]( const Coord< int >& c ) const { int i = ( c.y + wSize_ ) * ( wSize_ * 2 + 1 ) + c.x + wSize_; return( ( i < 0 || static_cast< std::vector< double >::size_type >( i ) >= gaborKernel_.size() ) ? 0 : gaborKernel_[i] ); } // 窓サイズを返す int wSize() const { return( wSize_ ); } // パラメータどうしの大小比較 bool operator<( const GaborFilter& dest ) const; }; /* GaborFilter コンストラクタ lambda : 調和関数の波長 λ theta : 波の方向 θ offset : 位相のオフセット φ ratio : アスペクト比 γ bandWidth : 帯域幅 wSize : 窓のサイズ */ GaborFilter::GaborFilter( double lambda, double theta, double offset, double ratio, double bandWidth, int wSize ) : lambda_( ErrLib::PNum( lambda ) ), theta_( theta ), offset_( offset ), ratio_( ErrLib::PNum( ratio ) ), bandWidth_( ErrLib::PNum( bandWidth ) ), wSize_( ErrLib::PNum( wSize ) ) { sigma_ = std::sqrt( std::log( 2.0 ) / 2.0 ) * ( std::pow( 2.0, bandWidth_ ) + 1 ) * lambda_ / ( ( std::pow( 2.0, bandWidth_ ) - 1 ) * MathLib::Pi< double >() ); createKernel(); } /* GaborFilter::createKernel : GaborFilterカーネルの作成 */ void GaborFilter::createKernel() { size_t matSize = wSize_ * 2 + 1; // カーネルの行列数 gaborKernel_.clear(); gaborKernel_.resize( matSize * matSize ); for ( int y = -wSize_ ; y <= wSize_ ; ++y ) { for ( int x = -wSize_ ; x <= wSize_ ; ++x ) { // 座標の回転 double rx = std::cos( theta_ ) * x + std::sin( theta_ ) * y; double ry = -std::sin( theta_ ) * x + std::cos( theta_ ) * y; // ガウス関数の値 double gauss = std::exp( ( -std::pow( rx, 2 ) - std::pow( ratio_ * ry, 2 ) ) / ( 2 * std::pow( sigma_, 2 ) ) ); // 正弦波の値 double cosine = std::cos( 2 * MathLib::Pi< double >() * rx / lambda_ + offset_ ); gaborKernel_[( y + wSize_ ) * matSize + x + wSize_] = gauss * cosine; } } } /* GaborFilter::operator< : パラメータどうしの大小比較 map / set 等のキーとして利用するために必要となる dest : 比較対象 戻り値 : dest より小さいと判断されたら true を返す */ bool GaborFilter::operator<( const GaborFilter& dest ) const { if ( lambda_ != dest.lambda_ ) return( lambda_ < dest.lambda_ ); if ( theta_ != dest.theta_ ) return( theta_ < dest.theta_ ); if ( offset_ != dest.offset_ ) return( offset_ < dest.offset_ ); if ( ratio_ != dest.ratio_ ) return( ratio_ < dest.ratio_ ); if ( bandWidth_ != dest.bandWidth_ ) return( bandWidth_ < dest.bandWidth_ ); return( false ); }
コンストラクタに各パラメータを指定することで、ガボール・フィルタの各点での値を計算して可変長配列 gaborKernel_ に格納します。ガウス関数は無限遠まで広がっていますが、原点からある程度離れれば値がほとんどゼロと見なせるため、計算する範囲を有限にしても大きな誤差にはなりません。計算する範囲は、引数 wSize で指定します。
サンプル・プログラムの中でガボール・フィルタとして定義されている式は以下のようになります。
上式は、正弦波の実部のみを抽出したものです。λ は正弦波の波長を表し、ω0 = 2π / λ の関係になります。ピクセル数から波長を決められるように考えると、周波数をパラメータとするよりも分かりやすくなります。
σ は波長 λ から次式によって計算します。
σ = ( K / π )・λ・( 2b + 1 ) / ( 2b - 1 )
但し K = sqrt( ln 2 / 2 )ここで b は帯域幅 ( Bandwidth ) を表します。これを b について解くと
になります。2b は、ピークの半分になるときの周波数について、最大値と最小値の比率を計算した時の値を表しています ( 補足 3 )。
なお、GaborFilter オブジェクトは値の大小比較ができるようにメンバ関数 operator< を持っています。これは、後で定義するガボール・フィルタのグループを作成するときに利用します。
以前「補間関数と畳み込み積分」でも紹介したように、二つの信号を畳み込み積分した結果をフーリエ変換したものと、それぞれをフーリエ変換した結果の積は等しくなります (「畳み込み積分定理 ( Convolution Theorem )」)。式で表すと次のようになります。
∫{-∞→∞} f(t) * g(t) exp( -iωt ) dt = F(ω)G(ω)
但し、f(t) * g(t) = ∫{-∞→∞} f(s)g(t - s) ds ( 畳み込み積分 )
上式において、F(ω) と G(ω) はそれぞれ f(t) と g(t) のフーリエ変換を表しています。ガボール・フィルタは、そのフーリエ変換の結果から、周波数 ω0 の付近だけを増幅してその他はカットする帯域フィルタとして作用し、その作用は、入力された信号をガボール・フィルタと畳み込み積分することによって実現できます。入力信号として画像データを利用する場合、信号は離散データとなって、
ここで、hx と hy は積分を行う範囲を示しています。実際には無限長に対して ( といっても画像データ自体が有限長であるため全データに対して ) 積分を行う必要がありますが、ガボール・フィルタはピークから離れた位置の値がゼロに近くなるため、処理速度を考慮して途中までの計算で打ち切ることになります。Imn は画像データを表し、G( x - m, y - n ) がガボール・フィルタの ( x - m, y - n ) における値になります。
特定の周波数成分だけを増幅するために ω0 を利用するだけではなく、ガボール・フィルタでは他にも画像データが持つ波形の傾きを θ を使って制御することができます。ある傾きを持ったエッジ部分に対してガボール・フィルタを作用させると、傾きをエッジに垂直な方向にした時に積分値が最大となります。従って、エッジの傾きとその周波数成分 ( エッジの鋭さ ) を同時に検出することがガボール・フィルタによって可能になります。
一次視覚野(V1)にある、単純型細胞と呼ばれる種類の神経細胞には、様々な角度や周期に対して反応するための形を持った細胞受容野が折り重なるように存在していることが知られています。また、これはちょうど、種々のパラメータを持ったガボール・フィルタによる処理を行っていることと同等であることが示されており、ガボール・フィルタが画像認識技術などに利用されるのはこのためです。
ガボール・フィルタを使った畳み込み積分を行うためのサンプル・プログラムを以下に示します。
// ガボール・フィルタ群を定義する型 typedef std::set< GaborFilter > GaborFilterGroup; /* 単項関数で値を処理してから加算するための関数オブジェクト 渡された数を処理してから加算して返す。 ループ処理により和の計算を行うことを想定した関数オブジェクトであり、例えば typedef double ( *Func )( double, double ); std::accumulate( s, e, 0.0, OpBind( std::bind2nd( std::ptr_fun( static_cast< Func >( std::pow ) ), 2.0 ) ) ); とすれば、[ s, e ) に対し二乗和を計算することができる。 テンプレート引数の Res は戻り値の型、Op は加算前の処理を行なう関数を表す。 */ template< class Op > class AddBinder { Op op_; // 加算前に処理を行なうための関数 public: /* 処理用の単項関数 op を指定して構築 */ AddBinder( Op op ) : op_( op ) {} /* 値 value を処理してから init に加算する テンプレート引数の Res は戻り値及び初期値の型、T は単項関数で処理する値の型をそれぞれ表す。 */ template< class Res, class T > Res operator()( Res init, T value ) { return( init + op_( value ) ); } }; /* 処理用単項関数 op から AddBinder 関数オブジェクトを生成する */ template< class Op > AddBinder< Op > OpBind( Op op ) { return( AddBinder< Op >( op ) ); } /************************************************************* 畳み込み結果を重ね合わせる(Superposition)方式 複数のガボール・フィルタの処理結果を合成するときに利用する *************************************************************/ namespace GSuperposition { /* L1ノルム(絶対値の和)による重ね合わせ [s,e) 対象のデータ列 */ template< class In > typename std::iterator_traits< In >::value_type L1Norm( In s, In e ) { typedef typename std::iterator_traits< In >::value_type value_type; // 要素の型 typedef double (*Func)( double ); // abs 関数の型 return ( std::accumulate( s, e, OpBind( std::ptr_fun( static_cast< Func >( std::abs ) ) ), value_type() ) ); } /* L2ノルム(二乗和の平方根)による重ね合わせ [s,e) 対象のデータ列 */ template< class In > typename std::iterator_traits< In >::value_type L2Norm( In s, In e ) { typedef typename std::iterator_traits< In >::value_type value_type; // 要素の型 return( std::sqrt( std::inner_product( s, e, s, value_type() ) ) ); } /* L∞ノルム(最大値)による重ね合わせ [s,e) 対象のデータ列 */ template< class In > typename std::iterator_traits< In >::value_type LinfNorm( In s, In e ) { typedef typename std::iterator_traits< In >::value_type value_type; // 要素の型 value_type max = value_type(); // 絶対値の最大値(ゼロで初期化) for ( ; s != e ; ++s ) max = std::max( max, std::abs( *s ) ); return( max ); } } /********************************************************** ガボール・フィルタを使った畳込み積分による顕著性データ **********************************************************/ class ImageSaliency_Gabor { // Superposition関数の型定義 typedef double (*Superposition)( std::vector< double >::const_iterator, std::vector< double >::const_iterator ); Matrix< double > lumi_; // 輝度データ const GaborFilterGroup& filters_; // ガボール・フィルタの配列 Superposition normFunc_; // 重ねあわせ関数へのポインタ public: /* 顕著性データを求める対象画像 draw を指定して構築 filters : ガボール・フィルタの配列 normFunc : 重ねあわせ関数へのポインタ */ ImageSaliency_Gabor( const DrawingArea_IF& draw, const GaborFilterGroup& filters, Superposition normFunc ) : filters_( filters ), normFunc_( normFunc ) { CreateByLuminance( draw, &lumi_ ); } // c の位置の顕著性データを求める double operator()( Coord< int > c ) const; }; /* ImageSaliency_Gabor::operator() : c の位置の顕著性データを求める */ double ImageSaliency_Gabor::operator()( Coord< int > c ) const { vector< double > isSum( filters_.size(), 0 ); // 各フィルタによる畳み込み積分の結果 // 畳み込み積分 size_t i = 0; for ( GaborFilterGroup::const_iterator it = filters_.begin() ; it != filters_.end() ; ++it ) { int wSize = it->wSize(); // 窓サイズ for ( int y = c.y - wSize ; y <= c.y + wSize ; ++y ) { Coord< int > gc( 0, std::min( std::max( y, 0 ), static_cast< int >( lumi_.rows() ) - 1 ) ); // 読み取り位置 for ( int x = c.x - wSize ; x <= c.x + wSize ; ++x ) { gc.x = std::min( std::max( x, 0 ), static_cast< int >( lumi_.cols() ) - 1 ); isSum[i] += lumi_[gc.y][gc.x] * (*it)[Coord< int >( c.x - x, c.y - y )]; } } ++i; } // ノルムの計算 return( (*normFunc_)( isSum.begin(), isSum.end() ) ); } /* CreateByGabor : ガボール・フィルタを使った顕著性データへの変換 draw : 対象の画像 saliency : 変換した顕著性データを登録する変数へのポインタ filters : ガボール・フィルタ normFunc : 重ねあわせ関数 */ template< class NormFunc > void CreateByGabor( const DrawingArea_IF& draw, Matrix< double >* saliency, const GaborFilterGroup& filters, NormFunc normFunc ) { ImageSaliency_Gabor isGabor( draw, filters, normFunc ); Create( saliency, draw.size(), isGabor ); } /* CreateByGabor_L1Norm : ガボール・フィルタを使った顕著性データへの変換 ( 各フィルタの合成に L1-Norm を使用 ) draw : 対象の画像 saliency : 変換した顕著性データを登録する変数へのポインタ filters : ガボール・フィルタ */ void CreateByGabor_L1Norm( const DrawingArea_IF& draw, Matrix< double >* saliency, const GaborFilterGroup& filters ) { CreateByGabor( draw, saliency, filters, GSuperposition::L1Norm< vector< double >::const_iterator > ); } /* CreateByGabor_L2Norm : ガボール・フィルタを使った顕著性データへの変換 ( 各フィルタの合成に L2-Norm を使用 ) draw : 対象の画像 saliency : 変換した顕著性データを登録する変数へのポインタ filters : ガボール・フィルタ */ void CreateByGabor_L2Norm( const DrawingArea_IF& draw, Matrix< double >* saliency, const GaborFilterGroup& filters ) { CreateByGabor( draw, saliency, filters, GSuperposition::L2Norm< vector< double >::const_iterator > ); } /* CreateByGabor_LinfNorm : ガボール・フィルタを使った顕著性データへの変換 ( 各フィルタの合成に Linf-Norm を使用 ) draw : 対象の画像 saliency : 変換した顕著性データを登録する変数へのポインタ filters : ガボール・フィルタ */ void CreateByGabor_LinfNorm( const DrawingArea_IF& draw, Matrix< double >* saliency, const GaborFilterGroup& filters ) { CreateByGabor( draw, saliency, filters, GSuperposition::LinfNorm< vector< double >::const_iterator > ); }
ガボール・フィルタを使った顕著性の計算は複数のフィルタの出力結果を合成することによって行います。そのため、任意のパラメータを持ったガボール・フィルタを追加・変更・削除するための型を用意します。これには STL ( Standard Template Library ) にあるコンテナ・クラス set をそのまま利用しています。set はキーだけを持った連想配列で、大小比較が可能な型であれば何でも保持することができます。GaborFilter に対して operator< 関数を実装して大小比較ができるようにしたのはこのためです。
畳み込み積分によって顕著性を求めるためのクラスが ImageSaliency_Gabor で、その中のメンバ関数 operator() で畳み込み積分を行っています。各フィルタを使って積分した結果を求め、最後にそのノルムを計算した結果を顕著性としています。ノルムの計算は切り替えができるようにしてあり、その計算法として、名前空間 GSuperposition にある三つの関数 ( L1Norm, L2Norm, LinfNorm) が用意されています。L1Norm は各結果の絶対値の和を返し ( L1-Norm )、L2Norm は各結果の二乗値の和の平方根を返し ( L2-Norm )、LinfNorm は各結果の絶対値の中から最大となる値を返します ( Maximum Norm )。
コンストラクタの中で呼び出している関数 CreateByLuminance は輝度を使った顕著性を求めるためのもので前章にてサンプル・プログラムを紹介しています。CreateByLuminance と同様な形で、CreateByLuminance を使って画像データから顕著性を求めるヘルパ関数が CreateByGabor で、各ノルム計算用に CreateByGabor_L1Norm, CreateByGabor_L2Norm, CreateByGabor_LinfNorm も用意してあります。
サンプル・プログラムを利用して顕著性を求めた結果を以下に示します。テストに利用した画像は "Lenna"(下図) です(実際には 512 x 512 のサイズです)。
 |
まずは、軸の傾きを 0 度, 45 度, 90 度, 135 度に変化させながら畳み込み積分を行った結果です ( 実際のテスト結果を縦横半分の 256 x 256 に縮小してあります )。
その他のパラメータは、波長 λ = 8、アスペクト比 γ = 1、位相のオフセット φ = 0、帯域幅 b = 1、畳み込み積分を行う窓サイズ -8 〜 8 としてあります。また、下側にある合成結果に対して、ノルムは L1Norm を使って求めています。
| θ = 0 | θ = 45 | θ = 90 | θ = 135 |
|---|---|---|---|
 |
 |
 |
 |
| 合成結果 | |||
 |
"θ = 0" では縦方向のエッジ、"θ = 90" では横方向のエッジに対して反応していることが分かります。このように、エッジがフィルタの波形の方向と垂直になるときに最も顕著性が高くなります。これらを合成すると画像の輪郭が浮かび上がる様子が、下側の画像から理解できると思います。
下図は、波長 ( 周波数 ) を変化させた時の様子を示した結果です。どの結果も、軸の傾きを 0 度, 45 度, 90 度, 135 度に変化させた顕著性を L1Norm を使って合成してあります。
| λ = 2 | λ = 4 | λ = 8 | λ = 16 |
|---|---|---|---|
 |
 |
 |
 |
エッジの立ち上がりが鋭いほど、波長の小さい ( 高周波成分を増幅する ) フィルタに対して反応する傾向が見られます。λ = 16 の場合は、窓サイズがフィルタの大きさに対して小さすぎるため、正しく処理ができていません。窓サイズを 16 とした場合、次のように正しい結果が得られます。
 |
フィルタの大きさは、波長と帯域幅によって決まります。帯域幅をデフォルトの b = 1 としたとき、波長が 8 のときはガウス関数の標準偏差が σ = 4.49 となるのに対し、波長が 16 のときは σ = 8.99 となるため、それだけフィルタが横に広がります。ある程度ピークから離れればフィルタの値はほとんどゼロになり、窓サイズとしては σ の二倍程度取れば大きな誤差はなくなります。
位相オフセットを 0 度と -90 度 ( = 270 度 ) とした時の処理結果は次のようになります。
| φ = 0 | φ = -90 |
|---|---|
 |
 |
位相オフセットを -90 度としたとき、ガボール・フィルタは次のような式で表されます。
| G(x,y) | = | exp( -[ x'2 + (γy')2 ] / 2σ2 ) cos( 2πx'/λ - π / 2 ) |
| = | exp( -[ x'2 + (γy')2 ] / 2σ2 ) sin( 2πx'/λ ) |
これはちょうどガボール・フィルタの虚部と一致し、x' 軸に沿った、x'y' 平面に垂直な平面での切り口を見ると、下図のように、原点に対して対称な奇関数になります。位相オフセットが 0 度や 180 度の場合は y' 軸に対称な偶関数となるため Symmetric Gabor Function と呼ばれるのに対し、位相オフセットが ±90 度の場合は Antisymmetric Gabor Function と呼ばれます。
 |
細胞受容野による画像認識をシミュレートする場合、Symmetric Gabor Function と Antisymmetric Gabor Function の両方を使って処理を行い、二つのデータのノルムを値として用いるのが一般的のようです。このようなフィルタは Gabor Energy Filter と呼ばれています。
下に示した画像は、軸の傾きを 0 度, 45 度, 90 度, 135 度、位相オフセットを 0 度, -90 度に変化させた計 8 パターンのフィルタに対して L2Norm を使って合成した結果です。位相オフセットを Symmetric Gabor Function 一種類だけにしていたときはエッジに対して二本の線分が出力されるのに対し、Antisymmetric Gabor Function を加えることで一本の線分として強調されることが、この結果から分かります。
 |
ガボール・フィルタを使った顕著性データを使って、前章で紹介したシーム・カービング処理を行ってみます。サンプル画像も、前回と同じもの ( 下図 ) を使います。
| Splash | Sailboat on lake |
|---|---|
 |
 |
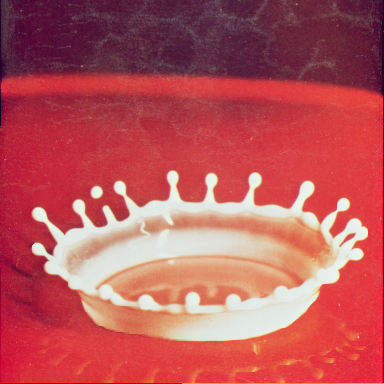
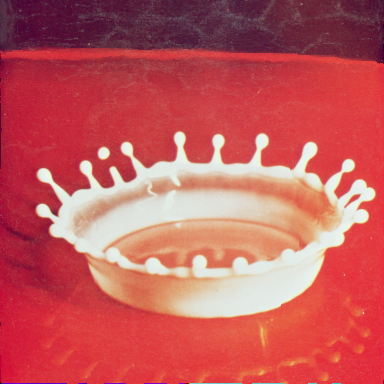
下図が処理した結果で、左側が前章でテストした輝度による顕著性、右側が今回のガボール・フィルタによる顕著性を使った時の画像です。ガボール・フィルタによる処理では、波長 λ = 8、アスペクト比 γ = 1、帯域幅 b = 1、畳み込み積分を行う窓サイズは -8 〜 8 として、軸の傾きを 0 度, 45 度, 90 度, 135 度、位相オフセットを 0 度, -90 度に変化させた計 8 パターンのフィルタに対して L2Norm を使って合成した結果を利用しています。なお、輝度、ガボール・フィルタのどちらも、エネルギー算出には L1 ノルムを使い、探索パスは八連結としています。
| Splash | ||
|---|---|---|
| 輝度 | ガボール・フィルタ | 顕著性(シーム・カービング後) |
 |
 |
 |
| Sailboat on lake | ||
| 輝度 | ガボール・フィルタ | 顕著性(シーム・カービング後) |
 |
 |
 |
"Splash" の方は、王冠の形が崩れることなく、周囲がトリミングされたような状態で処理されており、輝度を使った場合と比較してもかなり良好な結果が得られました。"Sailboat on lake" の方は、中央の部分が削除されているという傾向に変化はなく、ヨットの形状は輝度を使った方が保たれています。しかし、これは偶然である可能性が高く、輝度を使った方は、ヨットを含む湖のところが縦方向に削除されたので、ヨットの部分は縦横両方向に均等に削除されたのに対し、ガボール・フィルタを使った場合は遠くにある森の部分が縦方向に削除されているため、結果としてヨットの形状が横方向のみに縮んでしまったのではないかと考えられます。
今回は、ガボール・フィルタが物体の輪郭を抽出する処理に利用できることを紹介しました。抽出した輪郭をうまく利用すれば、画像パターンの認識などへ応用することもできますし、今回の例のように顕著性を求めるために使うなど、様々な場面で利用することができます。
ガボール・フィルタのフーリエ変換は以下のように計算することができます。
| G(ω) | = | ∫{-∞→∞} g(t)exp( -iωt )dt | |
| = | K・exp(iφ)∫{-∞→∞} exp( -t2 / 2σ2 ) exp( iω0t ) exp( -iωt ) dt | ||
| = | K・exp(iφ)∫{-∞→∞} exp( -t2 / 2σ2 - i( ω - ω0 )t ) dt | ||
| = | K・exp(iφ)∫{-∞→∞} exp( - [ t + iσ2( ω - ω0 ) ]2 / 2σ2 - (1/2)[ σ( ω - ω0 ) ]2 ) dt | ||
| = | K・exp(iφ)・exp( -(1/2)[ σ( ω - ω0 ) ]2 )∫{-∞→∞} exp( - [ t + iσ2( ω - ω0 ) ]2 / 2σ2 ) dt | ||
z = t + iσ2( ω - ω0 ) とすると、dz = dt で、t → ±∞ のとき z → ±∞ + iσ2( ω - ω0 ) なので、これを ±∞ + iv として
exp( - z2 / 2σ2 ) は複素関数なので、実関数と同じように積分することができません。この関数を f(z) として、- z2 / 2σ2 は複素数なのでこれを x + iy としたとき、オイラーの定理を使って
u( x, y ) = ex cos y , v( x, y ) = ex sin y としたとき、f(z) = u( x, y ) + i v( x, y ) になります。u( x, y ) と v( x, y ) を x, y で微分した結果をそれぞれ ux, uy, vx, vy としたとき、
ux = ex cos y ; uy = - ex sin y
vx = ex sin y ; vy = ex cos y
となるので、
ux = vy ; uy = - vx
が、任意の x, y について成り立ちます。上式は「コーシー・リーマンの関係式 ( Cauchy-Riemann Differential Equations )」と呼ばれ、この関係式を満たすとき、f(z) は z = x + iy で微分可能となります。複素平面上のある領域 D で f(z) が微分可能ならば、f(z) は D で「正則な関数 ( Holomorphic Function )」であり、複素平面上の任意の点 ( これを |z| < ∞ と表します ) で正則な関数を「整関数 ( Entire Function )」といいます。以上のことから、f(z) = ex + iy は整関数であることになります。
複素平面上の曲線 C が z = z(t) ( t は実数 ) で表されているとき、C の両端が α = z0 = z(t0)、β = zn = z(tn) となるように適当な点 zk = z(tk) ( k = 0, 1, ... n ) で区切ります。閉区間 [ tk-1, tk ] 上の任意の実数 τk を使って ζk = z(τk) を決めて、C 上の関数 f(z) に対して次のような和を考えます。
各点の距離の最大値 MAX| tk - tk-1 | がゼロに収束するように分割を細かくしたとき、分割方法や ζk の選び方に依存せずに和が一定の複素数に収束するならば f(z) は C 上で複素積分可能であるといい、その値を I としたとき、
で表します。C が実軸上の線分 [ α, β ] ならば、z(t) = t ( α ≤ t ≤ β ) で表されることになって、
になります。実関数のときは、x 軸上の閉区間を適当な点で分割して上記と同様な和を考え、その和の極限がある値に収束すれば、その値を積分値として定義していました。ちょうど、xy 平面上の関数を適当な幅で切って、それぞれを長方形の形と見なして和を計算し、その幅がゼロに収束したときの値を求めることになります。複素関数の場合も同様な方法で積分を定義しています。
実関数において、置換積分というものがあります。ある区間 I で連続な関数を f(x) とし、さらに x = φ(t) が区間 J で微分可能で、φ(J) が区間 I に含まれるとき、区間 J 内の任意の点 α, β がそれぞれ φ によって a, b にうつるなら、f(x) = f(φ(t)) の積分について以下の式が成り立ちます ( この章の中でも何度か利用しています )。
複素積分においても同様な式が成り立ちます。すなわち、閉区間 [α , β] における曲線 C : z = z(t) について、
曲線 C が閉じているとき、すなわち端点がなく、上の例において α = β であるような曲線であるとき、f(z) が正則であれば、次の定理が成り立ちます。
これを「コーシーの積分定理 ( Cauchy's Integral Theorem )」といいます。実関数の場合と同様に、dF(z) / dz = f(z) となる関数 F(z) を f(z) の原始関数 (Primitive Function) といいます。曲線 C の両端の点を α、β としたとき、やはり実関数と同様に
が成り立ちます。閉曲線は端点がつながった状態なので F(β) = F(α) と考えることができて、コーシーの積分定理が成り立つことが何となく実感できると思います。また、閉曲線が連続でなくてもこの定理は成り立ちます。
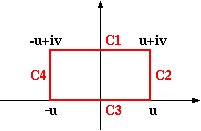
本題に戻って、∫{-∞ + iv → ∞ + iv} exp( - z2 / 2σ2 ) dz の積分について考えます。下図のような、C1 [ -u + iv , u + iv ] , C2 [ u + iv , u ] , C3 [ u , -u ] , C4 [ -u , -u + iv ] から成る閉曲線 C において、コーシーの積分定理から
が成り立ちます。
 |
閉曲線 C に沿って積分を行うと、
C2の積分値については、z = u + ivt としたとき次の式が成り立ちます。
| ∫C2 exp( - z2 / 2σ2 ) dz | = | ∫{0→1} exp( - ( u + ivt )2 / 2σ2 )・iv dt |
| = | iv∫{0→1} exp( ( v2t2 - u2 ) / 2σ2 )・exp( -iuvt / σ2 ) dt | |
| = | iv∫{0→1} exp( ( v2t2 - u2 ) / 2σ2 )・( cos ( uvt / σ2 ) - isin ( uvt / σ2 ) ) dt | |
| = | v∫{0→1} exp( ( v2t2 - u2 ) / 2σ2 )・sin ( uvt / σ2 ) ) dt + iv∫{0→1} exp( ( v2t2 - u2 ) / 2σ2 )・cos ( uvt / σ2 ) dt |
上式のノルムを求めると、
| || ∫C2 exp( - z2 / 2σ2 ) dz ||2 | = | v2∫{0→1} exp( ( v2t2 - u2 ) / σ2 )・sin2 ( uvt / σ2 ) ) dt + v2∫{0→1} exp( ( v2t2 - u2 ) / σ2 )・cos2 ( uvt / σ2 ) dt |
| ≦ | 2v2∫{0→1} exp( ( v2t2 - u2 ) / σ2 ) dt |
exp( ( v2t2 - u2 ) / σ2 ) は単調増加であり、閉区間 [0,1] において t = 1 のとき最大値を取るため、
u → ∞ において、不等式の右辺はゼロに収束するため、C2の積分値もゼロへ収束します。C4についても同様なので、C の積分は u → ∞ において次のようになります。
| ∫C exp( - z2 / 2σ2 ) dz | = | ∫C1 exp( - z2 / 2σ2 ) dz + ∫C3 exp( - z2 / 2σ2 ) dz |
| = | ∫{-∞ + iv → ∞ + iv} exp( - z2 / 2σ2 ) dz + ∫{∞ → -∞} exp( - t2 / 2σ2 ) dt | |
| = | ∫{-∞ + iv → ∞ + iv} exp( - z2 / 2σ2 ) dz - ∫{-∞ → ∞} exp( - t2 / 2σ2 ) dt |
コーシーの積分定理から左辺がゼロになるため、次の式が成り立つことになります。
結論として、虚部を取り除いて積分しても結果は同じであるということになります。これで、実関数での積分によって計算が可能な状態になりましたが、∫{-∞ → ∞} exp( - t2 / 2σ2 ) dt を計算するのも結構大変です。これについては重積分を利用した巧妙な方法が知られていますが、まずは重積分における変数変換の公式を知っておく必要があります。
多変数関数 f(x) = f( x1, x2, ... xn ) において、xk = φk(u) = φk( u1, u2, ... un ) ( k = 1,2, ... n ) と変数変換されるとき、φ(u) = ( φ1(u), φ2(u), ... φn(u) ) として
ここで、J(u) は「ヤコビ行列 ( Jacobian Matrix )」と呼ばれる次のように定義された行列です。また、その行列式 det( J(u) ) は「ヤコビアン ( Jacobian Determinant ; 通常は Jacobian )」と呼ばれています。
| J(u) | = | | | dx1/du1 | , | dx1/du2 | , ... , | dx1/dun | | |
| | | dx2/du1 | , | dx2/du2 | , ... , | dx2/dun | | | ||
| | | : | , | : | , ... , | : | | | ||
| | | dxn/du1 | , | dxn/du2 | , ... , | dxn/dun | | | ||
二変数関数の場合、次のような形に表すことができます。
直交座標 ( x, y ) を、x = rcosθ, y = rsinθ によって極座標 ( r, θ ) に変換すると、そのヤコビアンは
| det( J ) | = | dx/dr・dy/dθ - dx/dθ・dy/dr |
| = | cosθ・rcosθ - ( -rsinθ )・sinθ | |
| = | rcos2θ + rsin2θ = r |
になります。
I = ∫{-∞ → ∞} exp( - x2 / 2σ2 ) dx としたとき、I2 を次のように求めることができます。
| I2 | = | ∫{-∞ → ∞} exp( - x2 / 2σ2 ) dx ∫{-∞ → ∞} exp( - y2 / 2σ2 ) dy |
| = | ∫{-∞ → ∞}∫{-∞ → ∞} exp( - ( x2 + y2 ) / 2σ2 ) dxdy |
直交座標を極座標に変換すると、-∞ ≤ x ≤ ∞ , -∞ ≤ y ≤ ∞ は 0 ≤ r ≤ ∞ , 0 ≤ θ ≤ 2π にうつされて、
| I2 | = | ∫{0 → 2π}∫{0 → ∞} exp( -r2 / 2σ2 )・r drdθ |
| = | ∫{0 → 2π} dθ ∫{0 → ∞} r・exp( -r2 / 2σ2 ) dr | |
| = | [r]{0 → 2π} [ σ2 exp( -r2 / 2σ2 ) ]{0 → ∞} | |
| = | 2πσ2 |
I > 0 なので、I = sqrt( 2π )σ になります。従って、
これで、ガボール・フィルタのフーリエ変換式を求めることができたことになります。ちなみに、これまでの求め方はそのままガウス関数のフーリエ変換式を求める手段として使うことができます。ガウス関数のフーリエ変換はやはりガウス関数になり、ガウス関数の幅 ( パラメータ σ の値 ) が大きいとそのフーリエ変換の幅は狭くなり、逆に幅が小さいときはそのフーリエ変換の幅は広くなります。量子力学では、光や電波は粒子としても波動としても振舞うということを習います。また、それらが存在する位置は確率波として定義されています。ガウス関数のフーリエ変換に関する特徴は、素粒子の位置を正確に求めようとするほど波としての性質に対する測定誤差が大きくなり、またその逆も成り立つことを意味します。これを「不確定性原理」といいます。
一次元の場合と同様にガボール・フィルタ g( x, y ) をフーリエ変換によって G( u, v ) の形に変換してみましょう。
| G(u,v) | = | ∫{-∞→∞}∫{-∞→∞} g(x,y)exp( -i( ux + vy ) )dxdy |
| = | K・exp(iφ)∫{-∞→∞}∫{-∞→∞} exp( -( x'2 + ( γy' )2 ) / 2σ2 ) exp( iω0x' ) exp( -i( ux + vy ) ) dxdy | |
| = | K・exp(iφ)∫{-∞→∞}∫{-∞→∞} exp( -( x'2 + ( γy' )2 ) / 2σ2 ) exp( -i( ux - ω0x' + vy ) ) dxdy |
但し、( x', y' ) は以下の式で定義されます。
x' = xcosθ + ysinθ
y' = -xsinθ + ycosθ
上式を ( x, y ) について解くと、
x = x’cosθ - y'sinθ
y = x'sinθ + y'cosθ
( x, y ) を ( x', y' ) に変数変換すると、ヤコビアンは
| det( J ) | = | dx/dx'・dy/dy' - dx/dy'・dy/dx' |
| = | cosθ・cosθ - ( -sinθ )・sinθ = 1 |
また、
| ux + vy | = | u( x’cosθ - y'sinθ ) + v( x'sinθ + y'cosθ ) |
| = | ( ucosθ + vsinθ )x' - ( usinθ - vcosθ )y' |
よって、( u', v' ) = ( ucosθ + vsinθ, usinθ - vcosθ ) としたとき、
| G( u, v ) | = | K・exp(iφ)∫{-∞→∞}∫{-∞→∞} exp( -( x'2 + ( γy' )2 ) / 2σ2 ) exp( -i( ( u' - ω0 )x' + v'y' ) ) dx'dy' |
| = | K・exp(iφ)∫{-∞→∞}∫{-∞→∞} exp( -x'2 / 2σ2 ) exp( -( γy' )2 / 2σ2 ) exp( -i( u' - ω0 )x' ) exp( -iv'y' ) dx'dy' | |
| = | K・exp(iφ)∫{-∞→∞} ( ∫{-∞→∞} exp( -( γy' )2 / 2σ2 ) exp( -iv'y' ) dy' ) exp( -x'2 / 2σ2 ) exp( -i( u' - ω0 )x' ) dx' |
y' に対する積分 Iy' を計算すると、
| Iy' | = | ∫{-∞→∞} exp( -( γy' )2 / 2σ2 ) exp( -iv'y' ) dy' |
| = | ∫{-∞→∞} exp( -( γy' )2 / 2σ2 - iv'y' ) dy' | |
| = | ∫{-∞→∞} exp( -( γy' + iσ2v' / γ )2 / 2σ2 - (σv'/γ)2 / 2 ) dy' | |
| = | exp( -(σv'/γ)2 / 2 )∫{-∞→∞} exp( -( γy' + iσ2v' / γ )2 / 2σ2 ) dy' |
z = γy' + iσ2v' / γ とすると dz = γdy' で、y' → ±∞ のとき z → ±∞ + iσ2v' なので、これを ±∞ + iW として上式は
∫{-∞ + iW → ∞ + iW} exp( -z2 / 2σ2 ) dz = sqrt( 2π )σ より、
x' に対する積分 Ix' も同様のやり方で、
| Ix' | = | ∫{-∞→∞} exp( -x'2 / 2σ2 ) exp( -i( u' - ω0 )x' ) dx' |
| = | ∫{-∞→∞} exp( -x'2 / 2σ2 - i( u' - ω0 )x' ) dx' | |
| = | ∫{-∞→∞} exp( - ( x' + iσ2( u' - ω0 ) )2 / 2σ2 - {σ( u' - ω0 )}2 / 2 ) dx' | |
| = | exp( -{σ( u' - ω0 )}2 / 2 )∫{-∞→∞} exp( - ( x' + iσ2( u' - ω0 ) )2 / 2σ2 ) dx' | |
| = | sqrt( 2π )σ exp( -[ σ( u' - ω0 ) ]2 / 2 ) |
よって、フーリエ変換式は
| G(u,v) | = | K・exp(iφ) ( sqrt( 2π )σ/γ ) exp( -(σv'/γ)2 / 2 ) ( sqrt( 2π )σ ) exp( -[ σ( u' - ω0 ) ]2 / 2 ) |
| = | (2πKσ2/γ) exp(iφ) exp( -σ2[ ( u' - ω0 )2 + (v'/γ)2 ] / 2 ) |
となります。
二次元ガボール・フィルタのフーリエ変換式から、エネルギーが最大となるのは ( u', v' ) = ( ω0, 0 ) のときで
最大値のちょうど半分の値となるときの ( u', v' ) を ( u'h, v'h ) としたとき、上式から
両辺の対数を取って
よって、上式を変形すると
上式は u'v' 軸を主軸とする楕円体を表しています。u'h の絶対値が最大となるのは v'h = 0 の時で、この時 u'h の値は
上記のように求めた周波数の大きい方を ωmax、小さい方を ωmin とします。また、K = sqrt( ln2 / 2 ) としたとき、比率 ωmax / ωmin は
| ωmax / ωmin | = | ( ω0 + 2K / σ ) / ( ω0 - 2K / σ ) |
| = | ( σω0 + 2K ) / ( σω0 - 2K ) |
b = log2( ωmax / ωmin ) として、
| b | = | log2( ( σω0 + 2K ) / ( σω0 - 2K ) ) |
| = | log2( ( πσ + Kλ0 ) / ( πσ - Kλ0 ) ) |
但し、上式において λ0 は周波数 ω0 での波長を表し、ω0 = 2π / λ0 の関係式を満たします。この値 b が帯域幅と呼ばれるパラメータになり、比率 ωmax / ωmin が二倍になると、b は 1 増加します。このような周波数の倍率の表記法をオクターブ ( Octave ) といいます。音楽の世界では基準音として 440Hz が利用され、これは "ラ" の音を表します。周波数を二倍の 880Hz にすれば、これは 1 オクターブ高い "ラ" の音になるわけです。b の値が大きくなると、ピークの半分になるときの周波数の比率も大きくなります。上式において K は定数なので、σω0 の値は小さくなることになります。b の値によって決まるのは σ なので、結果として σ の値が小さくなることになり、フィルタの幅は狭くなります。σについて解くと、次のような式になります。
| σ | = | (2K/ω0)・( 2b + 1 ) / ( 2b - 1 ) |
| = | (Kλ0/π)・( 2b + 1 ) / ( 2b - 1 ) |
b がゼロに収束すると、σ は発散してしまいます。b = 1 のとき、右辺は 6K/ω0 ( = 3.53 / ω0 ) になり、値が大きくなるに従い 2K/ω0 ( = 1.18 / ω0 ) に近づきます。
少し、宣伝です。
趣味で小説を書いています。以前から、書いてみたいという思いがあり、アマチュアの小説を扱うサイトを見つけたことから実際に始めてみました。
最初は、小説を書ければ満足で、アクセス数が少なくてもいいかなと思っていましたが、やはりせっかく書いたからには読んでもらいたいし、感想をいただきたいという欲も出てきました。
もし、よろしければ、読んでもらえると嬉しいですし、今後の励みにもなります。
小説は、以下のリンク先から読むことができます。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |