前章において、網膜神経節細胞によって光の強度の差 ( コントラスト ) やエッジを抽出する仕組みについて紹介しました。人はモノを見るとき、画像からエッジを抽出する処理をいつも自然に行っています。これをシミュレートすることは画像処理の上で非常に重要です。例えば、画像の中にあるオブジェクトを自動認識したり抽出するためには、オブジェクトとそれ以外の部分の境界となるエッジの抽出処理は必須となります。エッジ抽出のためのフィルタとして以前ガボール・フィルタを紹介しましたが、エッジ抽出にはそれ以外にも多くの手法が存在します。今回は、エッジ抽出の方法について紹介したいと思います。
エッジ抽出の最も素朴な考え方は、隣り合った画素の色の強度の差を使ってエッジかどうかを判定するというものです。エッジ部分では、色の強度が急激に変化しているはずなので、その差は大きくなっています。差分を計算することで、エッジ部分が抽出できると考えることができます。
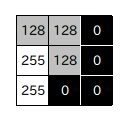
ここで問題となるのが、隣り合った画素をどのように定義するかです。一般に、エッジに対して垂直な方向に差分を計算するのが最適となりますが、事前にそれを判定することはできないので、いくつかの方向に差分計算をした上で最適値を判断することになります。次のような画像を例に実際に計算してみましょう。
 |
上図において、一つの格子が画素を表しています。また、各画素の中の数値は色の強度を示しています。この小さな範囲を見る限りは、水平方向に大きな傾きがあり、垂直なエッジが存在していると想定することができます。但し、これが画像の一部だけを表示しているのであれば、もしかしたら斜めのエッジが存在しているのかもしれません。いずれにしても、情報としてはこれだけしかないので、いずれか判断することはできません。
中央のグレーの画素に着目して、その左隣の画素との差を計算すると 128 - 255 = -127 となります。それに対して上隣の画素との差は 128 - 128 = 0 であり、水平方向の差の方が大きいので、この結果を見ると垂直方向のエッジが存在すると判断することができます。また、差分は負値であることから、強度は下がる方向に向かっていると考えることができます。
前述のやり方は隣り合った画素どうしでの計算でしたが、中央の画素に対してその両隣を使って差分を計算する方法も考えることができます。上の例では、中央の画素に対して左右の画素の差分は 0 - 255 = -255 であり、上下の画素の差分は 0 - 128 = -128 です。ここでも水平方向の差分がより大きな値となっていますが、今度は上下方向にもある程度の差分が得られました。ここで得られた差分は、前述のものに比べて少し緩やかなエッジを抽出したことになります。逆に最初の例では、より急激な差異を有したエッジを見つけることになるので、注目している画素からどの程度離れた画素を使うかによって、エッジの勾配の調整を行うことが可能であることをこの結果は示しています。
差異を計算する画素の距離によって、本来エッジであるべき部分が抽出されなかったり、逆にノイズなどの無関係な部分をエッジと判断してしまう場合があります。例えば下図のように、中央に一本の垂直なエッジがある場合を考えます。
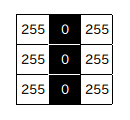 |
中央の画素に対してその両端を使って水平方向に差分を計算した場合、255 - 255 = 0 となってエッジとして認識されなくなります。想定しているエッジの勾配より実際のエッジが急なときにこのような問題が発生します。また、次の例のように中央のピクセルだけが異なる値を持つ場合、
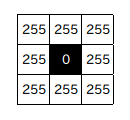 |
隣り合った画素でエッジを抽出すると中央部分は水平・垂直方向ともにエッジとして判別されますが、本来これはノイズとして扱うべきものになります。このように、ノイズに対して過敏に反応してしまうようなときもあり、どのようなパターンに対しても完璧にエッジを抽出するようなアルゴリズムを用意するのは簡単ではないことがわかります。
エッジ抽出用のフィルタはよく行列 ( ニ次元配列 ) 形式で表されます。元のデータも二次元配列なので、重ね合わせたときに一致したものどうしを掛け合わせて和を取るような計算を行います。ちょうどベクトルの内積に似た計算方法です。例えば、隣り合った画素の差分によるエッジ抽出の場合、以下のような行列になります。赤字は基準となる位置 ( 変換対象 ) を示しています。| ■ | 水平方向 | |||
| | | -1 | 1 | | | |
| ■ | 垂直方向 | |||
| | | -1 | | | ||
| | | 1 | | | ||
中央の画素に対してその両端を使って差分計算した場合は以下のような行列になります。
| ■ | 水平方向 | ||||
| | | -1 | 0 | 1 | | | |
| ■ | 垂直方向 | ||||
| | | -1 | | | |||
| | | 0 | | | |||
| | | 1 | | | |||
エッジの値として水平・垂直の二成分が抽出されるため、それぞれ個別に扱うことも可能ですが、たいていは両方の強度を併せた値を利用します。例えば、水平成分のエッジを fx、垂直成分のエッジを fy としたとき、
f = ( fx2 + fy2 )1/2
f = | fx | + | fy |
などが一般的です。前者は L2 ノルム、後者は L1 ノルムとして知られています。また、比率 fy / fx の逆正接関数 tan-1 はエッジ方向として利用されます。
上に示したエッジ抽出処理のサンプル・プログラムを以下に示します。
/* H_Move : x 座標 x0 の水平方向に dx ( 正数で右側 ) 進んだ x 座標を返す szX : 描画領域の x サイズ */ inline int H_Move( int x0, int dx, int szX ) { x0 += dx; if ( dx < 0 ) { if ( x0 < 0 ) x0 = -x0; if ( x0 >= szX ) x0 = 0; } else { if ( x0 >= szX ) x0 = ( szX - 1 ) * 2 - x0; if ( x0 < 0 ) x0 = 0; } return( x0 ); } /* V_Move : y 座標 y0 の垂直方向に dy ( 正数で下側 ) 進んだ y 座標を返す szY : 描画領域の y サイズ */ inline int V_Move( int y0, int dy, int szY ) { y0 += dy; if( dy < 0 ) { if ( y0 < 0 ) y0 = -y0; if ( y0 >= szY ) y0 = 0; } else { if ( y0 >= szY ) y0 = ( szY - 1 ) * 2 - y0; if ( y0 < 0 ) y0 = 0; } return( y0 ); } /* Edge_Diff_H : 水平方向の後退差分エッジ抽出 data : 差分抽出対象データ(行列)への参照 c : 差分抽出対象座標 戻り値 : 計算した差分データ */ template< class T > T Edge_Diff_H( const Matrix< T >& data, Coord< int > c ) { CheckCoord( c, data ); // | -1 1 | return( data[c.y][c.x] - data[c.y][H_Move( c.x, -1, data.cols() )] ); } /* Edge_Diff_V : 垂直方向の後退差分エッジ抽出 data : 差分抽出対象データ(行列)への参照 c : 差分抽出対象座標 戻り値 : 計算した差分データ */ template< class T > T Edge_Diff_V( const Matrix< T >& data, Coord< int > c ) { CheckCoord( c, data ); // | -1 | // | 1 | return( data[c.y][c.x] - data[V_Move( c.y, -1, data.rows() )][c.x] ); } /* Edge_Diff_HV : 水平・垂直方向の後退差分エッジ抽出 data : 差分抽出対象データ(行列)への参照 c : 差分抽出対象座標 戻り値 : 計算した差分データ */ template< class T > T Edge_Diff_HV( const Matrix< T >& data, Coord< int > c ) { return( std::sqrt( std::pow< T >( Edge_Diff_H( data, c ), 2 ) + std::pow< T >( Edge_Diff_V( data, c ), 2 ) ) ); } /* Edge_Diff_H2 : 水平方向の中央差分エッジ抽出 data : 差分抽出対象データ(行列)への参照 c : 差分抽出対象座標 戻り値 : 計算した差分データ */ template< class T > T Edge_Diff_H2( const Matrix< T >& data, Coord< int > c ) { CheckCoord( c, data ); // | -1 0 1 | return( data[c.y][H_Move( c.x, 1, data.cols() )] - data[c.y][H_Move( c.x, -1, data.cols() )] ); } /* Edge_Diff_V2 : 垂直方向の中央差分エッジ抽出 data : 差分抽出対象データ(行列)への参照 c : 差分抽出対象座標 戻り値 : 計算した差分データ */ template< class T > T Edge_Diff_V2( const Matrix< T >& data, Coord< int > c ) { CheckCoord( c, data ); // | -1 | // | 0 | // | 1 | return( data[V_Move( c.y, 1, data.rows() )][c.x] - data[V_Move( c.y, -1, data.rows() )][c.x] ); } /* Edge_Diff_HV2 : 水平・垂直方向の中央差分エッジ抽出 data : 差分抽出対象データ(行列)への参照 c : 差分抽出対象座標 戻り値 : 計算した差分データ */ template< class T > T Edge_Diff_HV2( const Matrix< T >& data, Coord< int > c ) { return( std::sqrt( std::pow< T >( Edge_Diff_H2( data, c ), 2 ) + std::pow< T >( Edge_Diff_V2( data, c ), 2 ) ) ); }
エッジ抽出関数はどの場合も行列 data のある位置 c の要素に対してその周囲の値を併せて計算した値を返す形になっています。引数の型は行列 Matrix への参照とその位置 Coord< int > で、data[c.y][c.x] で行列 data の位置 c における値を取得・代入できることを想定していますが、その実装は省略しています。また、data.cols() で行列の列数を、data.rows() で行数をそれぞれ取得することができます。
H_Move, V_Move は指定した座標からそれぞれ水平方向・垂直方向に指定数分だけ移動した座標を返す関数で、行列のサイズをチェックして範囲外なら範囲内になるように座標を調整します。調整の仕方はいろいろありますが、ここでは境界を鏡面として反対方向へ進めることで内部の座標を取得するようにしています。例えば H_Move の場合、左側 ( 移動量が負数の場合は左側に進みます ) にはみ出した場合は折り返して右側に進めるようにします。但し、画像サイズが小さな場合はまたはみ出すことになるので、その場合の調整がまた必要になります。進む数は任意なので、例えば H_Move では左に |dx| 進んで負数になった場合、符号を逆転します。しかし、サイズ szX が求めた値以下ならばまたはみ出すことになるので、かなり乱暴なやり方ですが強制的に値を 0 とします。
Edge_Diff_H は水平方向の、Edge_Diff_V は垂直方向の差分からエッジを計算する関数で、一つ前の要素との差分を計算しています ( 後退差分 )。関数内部の先頭にある CheckCoord は座標 c が行列の範囲内にあるかをチェックする関数で、ここでは実装はしていません。範囲外だった場合の処理方法はいろいろと考えられ、例えば例外を投げたり、エラーコードを返す ( 但し、サンプルプログラムではエラーコードをチェックするようにはなっていないので、例外を使うことを想定しています ) やり方があります。チェック後は、各要素の値を抽出して差分計算を行うだけです。一つ前の要素の座標を取得するために、H_Move と V_Move を使用しています。Edge_Diff_HV は、Edge_Diff_H と Edge_Diff_V の差分計算結果から L2 ノルムを計算して水平・垂直方向の差分を一つにまとめた値を返す関数です。
Edge_Diff_H2 は水平方向の、Edge_Diff_V2 は垂直方向の差分からエッジを計算する関数で前述のものとほぼ同様ですが、対象座標の前後の要素との差分を計算しているところが異なります ( 中央差分 )。Edge_Diff_HV2 はやはり、Edge_Diff_H2 と Edge_Diff_V2 の差分計算結果から L2 ノルムを計算して水平・垂直方向の差分を一つにまとめた値を返す関数です。
サンプル・プログラムを使ってエッジ処理を行った結果を以下に示します。テストに使った画像は "Leena"(下図) です ( 実際には 512 x 512 のサイズです )。
 |
計算は RGB 成分ではなく輝度に対して行っています。RGB 成分から輝度 Y への変換式は以下のようになります。
変換式から、輝度 Y の値は 0 から 255 の範囲を取ります。二つの値の差分を計算した場合、その値は -255 から 255 の値をとり得ます。そのため、テスト結果画像は、値が 0 から 255 の間に入るよう正規化を行い、それを RGB 各成分に代入しています ( グレースケール画像 )。正規化処理は以下のような計算式になります。
上式において、minY, maxY はそれぞれ画像中の Y の最小値・最大値を表します。この計算式によって、正規化した値は 0 から 255 の範囲をとるようになります。中央値 127.5 ではエッジは存在せず、255 (白) に近いほど急激に増加する方向の、0 (黒) に近いほど急激に減少する方向のエッジであることを示します。
| Edge_Diff_H | Edge_Diff_V | Edge_Diff_HV |
|---|---|---|
 |
 |
 |
| Edge_Diff_H2 | Edge_Diff_V2 | Edge_Diff_HV2 |
 |
 |
 |
Edge_Diff_H/V と Edge_Diff_H2/V2 の結果は、明るさが増加するエッジは白く、逆に減少するエッジは黒く、予想通りのものとなっています。増加・減少方向は、Edge_Diff_H/H2 の場合は左から右へ、Edge_Diff_V/V2 の場合は上から下へとなることに注意して下さい。隣どうしで差分計算 ( 後退差分 ) する Edge_Diff_H/V に対して、対象位置の前後どうしで差分計算 ( 中央差分 ) する Edge_Diff_H2/V2 の方が若干強めにエッジ抽出されているのは、自然画が低周波領域を強く持つ傾向にあることが原因でしょう。
Edge_Diff_HV/HV2 は、水平・垂直方向のエッジ抽出結果について L2 ノルムを計算した値を表しているのでした。そのためエッジのない個所は 0 に近くなり、増加・減少に関係なくエッジ部分は 255 に近い値になります。つまり、エッジの強度だけが得られ、その方向は情報としては消失してしまいます。
水平・垂直方向ではなく斜め方向に差分を計算する方法も考えられます。次のように斜め方向に差分計算して L2 ノルムを利用する手法は「ロバート・クロス ( Roberts Cross )」と呼ばれます。
| ■ | 左下方向 | |||
| | | 0 | 1 | | | |
| | | -1 | 0 | | | |
| ■ | 右下方向 | |||
| | | 1 | 0 | | | |
| | | 0 | -1 | | | |
ロバート・クロスのサンプル・プログラムを以下に示します。
/* Edge_Diff_LD : 左下方向の後退差分エッジ抽出 data : 差分抽出対象データ(行列)への参照 c: 差分抽出対象座標 戻り値 : 計算した差分データ */ template< class T > T Edge_Diff_LD( const Matrix< T >& data, Coord< int > c ) { CheckCoord( c, data ); // | 0 1 | // | -1 0 | return( data[c.y][H_Move( c.x, 1, data.cols() )] - data[V_Move( c.y, 1, data.rows() )][c.x] ); } /* Edge_Diff_RD : 右下方向の前進差分エッジ抽出 data : 差分抽出対象データ(行列)への参照 c: 差分抽出対象座標 戻り値 : 計算した差分データ */ template< class T > T Edge_Diff_RD( const Matrix< T >& data, Coord< int > c ) { CheckCoord( c, data ); // | 1 0 | // | 0 -1 | return( data[c.y][c.x] - data[V_Move( c.y, 1, data.rows() )][H_Move( c.x, 1, data.cols() )] ); } /* Edge_Robert : 斜め方向の前進差分エッジ抽出(Robert Cross) data : 差分抽出対象データ(行列)への参照 c : 差分抽出対象座標 戻り値 : 計算した差分データ */ template< class T > T Edge_Robert( const Matrix< T >& data, Coord< int > c ) { return( std::sqrt( std::pow< T >( Edge_Diff_LD( data, c ), 2 ) + std::pow< T >( Edge_Diff_RD( data, c ), 2 ) ) ); }
計算に使うデータは、現在注目している箇所とその右・下・右下です。先の水平・垂直方向のエッジ抽出の例では左・上側のデータも利用していました。処理は通常、左上端から右方向または下方向へ、端まで到達したらその下の行または右側の列へ移って右下端に到達するまで行います。よって、先の例において処理結果を元データに上書きするようにすると上書きしたデータを利用して処理することになり結果が正しくなりません。しかし、今回の例では、処理結果を元データに上書きする形でも問題はありません。
| Edge_Diff_LD | Edge_Diff_RD | Edge_Robert |
|---|---|---|
 |
 |
 |
上図は、斜め方向に差分を計算した場合のエッジ抽出結果です。Edge_Robert は、Edge_Diff_HV と Edge_Diff_HV2 のちょうど中間程度の強さでエッジ抽出されています。これは、斜め方向のためデータ間の距離が Edge_Diff_HV と Edge_Diff_HV2 の中間程度となっていることから予想できる結果です。
隣どうしのピクセルで差分計算した場合、ノイズをエッジと誤判定しやすいという話を少し前にしましたが、これを防ぐには画像のノイズをあらかじめ減らしておいてからエッジ抽出すればよいことになります。そこでノイズを減らすための平滑化(平均化)処理とエッジ抽出処理をひとまとめにして行う手法が存在し、それらを「プレウィット・フィルタ ( Prewitt Filter )」「ソーベル・フィルタ ( Sobel Filter )」といいます。
| ■ | 水平方向の | プレウィット・フィルタ ( Prewitt Filter ) | ||||
| | | -1 | 0 | 1 | | | ||
| | | -1 | 0 | 1 | | | ||
| | | -1 | 0 | 1 | | | ||
| ■ | 垂直方向の | プレウィット・フィルタ ( Prewitt Filter ) | ||||
| | | -1 | -1 | -1 | | | ||
| | | 0 | 0 | 0 | | | ||
| | | 1 | 1 | 1 | | | ||
| ■ | 水平方向の | ソーベル・フィルタ ( Sobel Filter ) | ||||
| | | -1 | 0 | 1 | | | ||
| | | -2 | 0 | 2 | | | ||
| | | -1 | 0 | 1 | | | ||
| ■ | 垂直方向の | ソーベル・フィルタ ( Sobel Filter ) | ||||
| | | -1 | -2 | -1 | | | ||
| | | 0 | 0 | 0 | | | ||
| | | 1 | 2 | 1 | | | ||
例えば、プレウィット・フィルタの水平方向の処理は、水平方向が中心差分によるエッジ抽出で垂直方向は平滑化(平均化)処理となっています。ソーベル・フィルタの場合、中心をより強調できるように係数が調整されています。
プレウィット・フィルタとソーベル・フィルタのサンプル・プログラムを以下に示します。
/* Edge_Prewitt_H : 水平方向の Prewitt フィルタ data : エッジ抽出対象データ(行列)への参照 c : エッジ抽出対象座標 戻り値 : 計算した結果 */ template< class T > T Edge_Prewitt_H( const Matrix< T >& data, Coord< int > c ) { CheckCoord( c, data ); // | -1 0 1 | // | -1 0 1 | // | -1 0 1 | return( data[V_Move( c.y, -1, data.rows() )][H_Move( c.x, 1, data.cols() )] + data[c.y][H_Move( c.x, 1, data.cols() )] + data[V_Move( c.y, 1, data.rows() )][H_Move( c.x, 1, data.cols() )] - data[V_Move( c.y, -1, data.rows() )][H_Move( c.x, -1, data.cols() )] - data[c.y][H_Move( c.x, -1, data.cols() )] - data[V_Move( c.y, 1, data.rows() )][H_Move( c.x, -1, data.cols() )] ); } /* Edge_Prewitt_V : 垂直方向の Prewitt フィルタ data : エッジ抽出対象データ(行列)への参照 c : エッジ抽出対象座標 戻り値 : 計算した結果 */ template< class T > T Edge_Prewitt_V( const Matrix< T >& data, Coord< int > c ) { CheckCoord( c, data ); // | -1 -1 -1 | // | 0 0 0 | // | 1 1 1 | return( data[V_Move( c.y, 1, data.rows() )][H_Move( c.x, -1, data.cols() )] + data[V_Move( c.y, 1, data.rows() )][c.x] + data[V_Move( c.y, 1, data.rows() )][H_Move( c.x, 1, data.cols() )] - data[V_Move( c.y, -1, data.rows() )][H_Move( c.x, -1, data.cols() )] - data[V_Move( c.y, -1, data.rows() )][c.x] - data[V_Move( c.y, -1, data.rows() )][H_Move( c.x, 1, data.cols() )] ); } /* Edge_Prewitt : 水平・垂直方向の Prewitt フィルタ data : エッジ抽出対象データ(行列)への参照 c : エッジ抽出対象座標 戻り値 : 計算した結果 */ template< class T > T Edge_Prewitt( const Matrix< T >& data, Coord< int > c ) { return( std::sqrt( std::pow< T >( Edge_Prewitt_H( data, c ), 2 ) + std::pow< T >( Edge_Prewitt_V( data, c ), 2 ) ) ); } /* Edge_Sobel_H : 水平方向の Sobel フィルタ data : エッジ抽出対象データ(行列)への参照 c : エッジ抽出対象座標 戻り値 : 計算した結果 */ template< class T > T Edge_Sobel_H( const Matrix< T >& data, Coord< int > c ) { CheckCoord( c, data ); // | -1 0 1 | // | -2 0 2 | // | -1 0 1 | return( data[V_Move( c.y, -1, data.rows() )][H_Move( c.x, 1, data.cols() )] + data[c.y][H_Move( c.x, 1, data.cols() )] * 2 + data[V_Move( c.y, 1, data.rows() )][H_Move( c.x, 1, data.cols() )] - data[V_Move( c.y, -1, data.rows() )][H_Move( c.x, -1, data.cols() )] - data[c.y][H_Move( c.x, -1, data.cols() )] * 2 - data[V_Move( c.y, 1, data.rows() )][H_Move( c.x, -1, data.cols() )] ); } /* Edge_Sobel_V : 垂直方向の Sobel フィルタ data : エッジ抽出対象データ(行列)への参照 c : エッジ抽出対象座標 戻り値 : 計算した結果 */ template< class T > T Edge_Sobel_V( const Matrix< T >& data, Coord< int > c ) { CheckCoord( c, data ); // | -1 -2 -1 | // | 0 0 0 | // | 1 2 1 | return( data[V_Move( c.y, 1, data.rows() )][H_Move( c.x, -1, data.cols() )] + data[V_Move( c.y, 1, data.rows() )][c.x] * 2 + data[V_Move( c.y, 1, data.rows() )][H_Move( c.x, 1, data.cols() )] - data[V_Move( c.y, -1, data.rows() )][H_Move( c.x, -1, data.cols() )] - data[V_Move( c.y, -1, data.rows() )][c.x] * 2 - data[V_Move( c.y, -1, data.rows() )][H_Move( c.x, 1, data.cols() )] ); } /* Edge_Sobel : 水平・垂直方向の Sobel フィルタ data : エッジ抽出対象データ(行列)への参照 c : エッジ抽出対象座標 戻り値 : 計算した結果 */ template< class T > T Edge_Sobel( const Matrix< T >& data, Coord< int > c ) { return( std::sqrt( std::pow< T >( Edge_Sobel_H( data, c ), 2 ) + std::pow< T >( Edge_Sobel_V( data, c ), 2 ) ) ); }
プレウィット・フィルタとソーベル・フィルタのサンプル・プログラムを使ってエッジ抽出をした結果を以下に示します。
| Edge_Prewitt_H | Edge_Prewitt_V | Edge_Prewitt |
|---|---|---|
 |
 |
 |
| Edge_Sobel_H | Edge_Sobel_V | Edge_Sobel |
 |
 |
 |
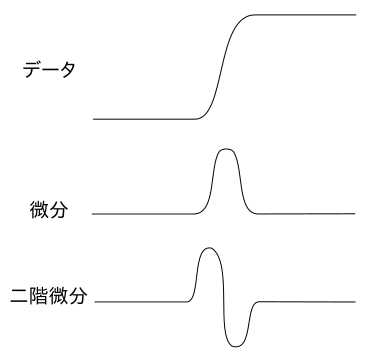
今までは差分からエッジを抽出するやり方を検討してきましたが、これは画像が離散データだからであって、もし連続データを使ってエッジを検出したい場合は微分することになります。例えば以下のようなデータの場合、その微分は山が一つ形成されます。このような山や谷をエッジとして検出するわけです。
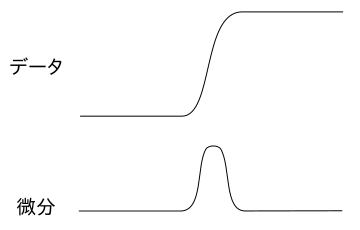 |
これをもう一度微分すると、最初に山が形成され、その後に谷が続くので、その間にはゼロ点が存在することになります。このゼロ点を検出することによってエッジを抽出することもできます。
 |
二階微分を離散データで表現すると次のように計算できます。まず、一階微分を後退差分で表します。
f'(x) = f(x) - f(x-1)
f'(x+1) = f(x+1) - f(x)
この差分からもう一度差分を計算します。
| f''(x) | = | f'(x+1) - f'(x) |
| = | [ f(x+1) - f(x) ] - [ f(x) - f(x-1) ] | |
| = | f(x+1) - 2f(x) + f(x-1) |
これを二階微分に対する差分として扱うことができます。画像は x, y 方向があるので、それぞれを加算して
| ∇2 | = | ∂2f / ∂x2 + ∂2f / ∂y2 |
| = | [ f(x+1,y) - 2f(x,y) + f(x-1,y) ] + [ f(x,y+1) - 2f(x,y) + f(x,y-1) ] | |
| = | f(x+1,y) + f(x,y+1) - 4f(x,y) + f(x-1,y) + f(x,y-1) |
行列で表すと
| 0 1 0 | | 1 -4 1 | | 0 1 0 |
をエッジ抽出用フィルタとして用います。∇2 は「ラプラス演算子 ( Laplace operator ; Laplacian )」と呼ばれる演算子なので、このフィルタは「ラプラシアン・フィルタ ( Laplacian Filter )」と呼ばれます。
さらに斜め方向も加算したフィルタもよく用いられます。これは以下のような計算式になります。
f(x+1,y+1) + f(x,y+1) + f(x-1,y+1) + f(x+1,y) - 8f(x,y) + f(x-1,y) + f(x+1,y-1) + f(x,y-1) + f(x-1,y-1)
| 1 1 1 | | 1 -8 1 | | 1 1 1 |
ラプラシアン・フィルタのサンプル・プログラムを以下に示します。
/* Edge_Laplacian_4 : 4 近傍の Laplacian フィルタ data : エッジ抽出対象データ(行列)への参照 c : エッジ抽出対象座標 戻り値 : 計算した結果 */ template< class T > T Edge_Laplacian_4( const Matrix< T >& data, Coord< int > c ) { CheckCoord( c, data ); // | 0 1 0 | // | 1 -4 1 | // | 0 1 0 | return( data[V_Move( c.y, -1, data.rows() )][c.x] + data[c.y][H_Move( c.x, 1, data.cols() )] + data[V_Move( c.y, 1, data.rows() )][c.x] + data[c.y][H_Move( c.x, -1, data.cols() )] - data[c.y][c.x] * 4 ); } /* Edge_Laplacian_8 : 8 近傍の Laplacian フィルタ data : エッジ抽出対象データ(行列)への参照 c : エッジ抽出対象座標 戻り値 : 計算した結果 */ template< class T > T Edge_Laplacian_8( const Matrix< T >& data, Coord< int > c ) { CheckCoord( c, data ); // | 1 1 1 | // | 1 -8 1 | // | 1 1 1 | return( data[V_Move( c.y, -1, data.rows() )][c.x] + data[V_Move( c.y, -1, data.rows() )][H_Move( c.x, 1, data.cols() )] + data[c.y][H_Move( c.x, 1, data.cols() )] + data[V_Move( c.y, 1, data.rows() )][H_Move( c.x, 1, data.cols() )] + data[V_Move( c.y, 1, data.rows() )][c.x] + data[V_Move( c.y, 1, data.rows() )][H_Move( c.x, -1, data.cols() )] + data[c.y][H_Move( c.x, -1, data.cols() )] + data[V_Move( c.y, -1, data.rows() )][H_Move( c.x, -1, data.cols() )] - data[c.y][c.x] * 8 ); }
ラプラシアン・フィルタを使ってエッジ抽出を行った結果を以下に示します。
| Edge_Laplacian_4 | Edge_Laplacian_8 |
|---|---|
 |
 |
今までのフィルタに比べるとエッジ部分が弱く、しかもノイズをエッジと誤判定している箇所が多いなどいくつかの課題があります。
ラプラシアン・フィルタも後退差分によるフィルタ同様にノイズをエッジと誤判定しやすい問題を持っています。そこで、ガウシアン・フィルタで平滑化処理をした上でラプラシアン・フィルタを行うことでノイズによる誤判定を少なくすることができます。このような処理は「LoG フィルタ ( Laplacian of Gaussian Filter )」と呼ばれます。ガウシアン・フィルタは以下のガウス関数による畳み込み積分です。
g( x, y ; σ ) = ( 1 / 2πσ2 ) exp( - ( x2 + y2 ) / 2σ2 )
( f * g )( x, y ; σ) = ∫∫ f( t, u )g( x - t, y - u ; σ ) dtdu
これにラプラス演算子を適用すると、以下のように式を変形することができます。
| ∇2 ( I * g )( x, y ; σ ) | = | ∇2∫∫ I( t, u )g( x - t, y - u ; σ ) dtdu |
| = | ∫∫ I( t, u )∇2g( x - t, y - u ; σ )dtdu |
| ∇2g( x - t, y - u ; σ ) | = | ( d / dx )-( 1 / 2πσ2 )( x / σ2 )exp( -( x2 + y2 ) / 2σ2 ) + ( d / dy )-( 1 / 2πσ2 )( y / σ2 )exp( -( x2 + y2 ) / 2σ2 ) |
| = | ( 1 / 2πσ2 )[ ( x / σ2 )2 - 1 / σ2 ]exp( -( x2 + y2 ) / 2σ2 ) + ( 1 / 2πσ2 )[ ( y / σ2 )2 - 1 / σ2 ]exp( -( x2 + y2 ) / 2σ2 ) | |
| = | ( 1 / 2πσ2 )[ ( x / σ2 )2 + ( y / σ2 )2 - 2 / σ2 ]exp( -( x2 + y2 ) / 2σ2 ) | |
| = | ( 1 / 2πσ6 )( x2 + y2 - 2σ2 )exp( -( x2 + y2 ) / 2σ2 ) |
より
で計算することができます。ガウシアン・フィルタを掛けてからラプラシアン・フィルタを行うのではなく、ラプラス演算子を適用したガウシアン・フィルタで畳み込み積分を行うということになります。
LoG フィルタを使ったエッジ抽出のサンプル・プログラムを以下に示します。
/** LoG ( Laplacian of Gaussian ) フィルタ **/ template< class T > class LoG { Matrix< T > filter_; // フィルタ本体 int s3_; // 3σ (フィルタサイズ) public: // パラメータ σ を指定して構築 LoG( double sigma ); // @brief 行列 data の位置 c に LoG フィルタを適用する T operator()( const Matrix< T >& data, Coord< int > c ); }; /* LoG< T > コンストラクタ : パラメータσを指定して構築 */ template< class T > LoG< T >::LoG( double sigma ) { assert( sigma > 0 ); s3_ = round( sigma * 3 ); filter_.assign( s3_ * 2 + 1, s3_ * 2 + 1 ); for ( int y = -s3_ ; y <= s3_ ; ++y ) { for ( int x = -s3_ ; x <= s3_ ; ++x ) { double norm = pow( x, 2 ) + pow( y, 2 ); double s2_2 = 2 * pow( sigma, 2 ); filter_[y + s3_][x + s3_] = ( norm - s2_2 ) * exp( -norm / s2_2 ) / ( 2 * M_PI * pow( sigma, 6 ) ); } } } /* LoG< T >::operator() : 行列 data の位置 c に対して LoG フィルタを適用する */ template< class T > T LoG< T >::operator()( const Matrix< T >& data, Coord< int > c ) { T ans = 0; for ( int y = -s3_ ; y <= s3_ ; ++y ) for ( int x = -s3_ ; x <= s3_ ; ++x ) ans += data[V_Move( c.y, y, data.rows() )][H_Move( c.x, x, data.cols() )] * filter_[s3_ - y][s3_ - x]; return( ans ); }
LoG フィルタは無限遠の範囲について畳み込み積分が必要になります。しかし、実際の処理ではそれは不可能なので、フィルタの値がゼロに近くなったところで計算を打ち切ることになります。ここでは、-3σ から 3σ までの範囲で計算を行います。また、フィルタの値はあらかじめ行列 k_ に保持しておき、フィルタを適用するときに再計算する必要がないようにしています。
LoG フィルタを使ってエッジ抽出を行った結果を以下に示します。
| σ = 1 | σ = 3 | σ = 5 |
|---|---|---|
 |
 |
 |
σ の値を大きくするに従ってエッジそのものがぼやけていくのは、ガウシアン・フィルタによって画像にぼかしが入るからです。ラプラシアン・フィルタに比べるとエッジがはっきりとしていることから、ガウシアン・フィルタによる効果が大きいことを示しています。
ガウス関数の σ を変数とみなして微分すると次のようになります。
| ∂g / ∂σ | = | ( ∂ / ∂σ )( 1 / 2πσ2 ) exp( - ( x2 + y2 ) / 2σ2 ) |
| = | [ ( 1 / 2πσ2 )( x2 + y2 ) / σ3 - 1 / σ3 ) ] exp( - ( x2 + y2 ) / 2σ2 ) | |
| = | [ ( x2 + y2 ) / 2πσ5 - 1 / πσ3 ) ] exp( - ( x2 + y2 ) / 2σ2 ) | |
| = | ( 1 / 2πσ5 )( x2 + y2 - 2σ2 ) exp( - ( x2 + y2 ) / 2σ2 ) | |
| = | σ∇2g |
kσ と σ が非常に近ければ
と近似できるので、
が成り立ちます。エッジの抽出だけを目的とした場合、LoG フィルタの代わりに、σ, kσ によるガウシアン・フィルタの結果の差分を利用することができることをこの結果は示しています。これを「DoG ( Difference of Gaussian ) フィルタ」といいます。
LoG フィルタの欠点は、σ の値が大きくなるとフィルタのサイズも大きくなり極端に処理速度が遅くなる点です。これは DoG フィルタにも当てはまりますが、DoG フィルタの場合は水平・垂直方向それぞれに処理を分解することで LoG フィルタよりも性能の劣化を防ぐことができます。一般に、フィルタ φ( x, y ) が
のように x, y の関数の積に分解できるとき、その畳み込み積分は
| ( f * φ )( x, y ) | = | ∫∫ f( t, u )φ( x - t, y - u ) dtdu |
| = | ∫∫ f( t, u )τ( x - t )μ( y - u ) dtdu | |
| = | ∫ [ ∫ f( t, u )τ( x - t ) dt ] μ( y - u ) du | |
| = | ( f * τ * μ )( x, y ) |
となるので、先に水平方向のみに畳み込み積分を行い、その結果に垂直方向への畳み込み積分を行っても同じ結果を得ることができます。二次元フィルタをそのまま適用した場合、フィルタのサイズを n として、画像サイズが X, Y ならば、演算回数は n2XY となるのに対し、一次元フィルタに分解した場合は 2nXY となるので、フィルタのサイズが大きくなるほどその効果は大幅に向上します。
LoG フィルタの場合、明らかに x, y の関数の積に分解することはできません。DoG フィルタの場合は、
より
| f( x, y ) * [ g( x, y ; kσ ) - g( x, y ; σ ) ] / ( k - 1 )σ2 | |
| = | f( x, y ) * [ g( x ; kσ )g( y ; kσ ) - g( x ; σ )g( y ; σ ) ] / ( k - 1 )σ2 |
| = | [ f( x, y ) * g( x ; kσ ) * g( y ; kσ ) - f( x, y ) * g( x ; σ ) * g( y ; σ ) ] / ( k - 1 )σ2 |
となるので、画像に対して kσ, σ それぞれのパラメータでガウシアン・フィルタを掛けて、各座標ごとに差分を計算すれば目的の値を得ることができます。
DoG フィルタを使ったエッジ抽出のサンプル・プログラムを以下に示します。
/* CreateGaussianFilter : ガウシアン・フィルタの構築 sigma : ガウシアン・フィルタの標準偏差 filter : 構築するフィルタへのポインタ */ template< class T > void CreateGaussianFilter( T sigma, std::vector< T >* filter ) { assert( sigma > 0 ); assert( filter != 0 ); // フィルタのサイズ(片側のサイズとする) int sz = filter->size(); if ( sz < 1 ) return; sz = ( sz - 1 ) / 2; for ( int i = -sz ; i <= sz ; ++i ) { T norm = std::pow( i, T( 2 ) ); T s2_2 = 2 * std::pow( sigma, T( 2 ) ); (*filter)[i + sz] = exp( -norm / s2_2 ) / ( sqrt( M_PI * s2_2 ) ); } } /* GaussianFilter : ガウシアン・フィルタの適用 data : 適用対象のデータ filter : ガウシアン・フィルタ c : フィルタ適用対象位置 isHorizontal : 水平方向への適用か 戻り値 : 適用結果 */ template< class T > T GaussianFilter( const Matrix< T >& data, const std::vector< T >& filter, Coord< int > c, bool isHorizontal ) { T ans = 0; int sz = filter.size(); if ( sz < 1 ) return( T() ); sz = ( sz - 1 ) / 2; for ( int i = -sz ; i <= sz ; ++i ) { if ( isHorizontal ) { ans += data[c.y][H_Move( c.x, i, data.cols() )] * filter[sz - i]; } else { ans += data[V_Move( c.y, i, data.rows() )][c.x] * filter[sz - i]; } } return( ans ); } /* DoGFilter : DoG フィルタを適用する data : 適用対象のデータへのポインタ sigma1,sigma2 : ガウシアン・フィルタの標準偏差 */ template< class T > void DoGFilter( Matrix< T >* data, T sigma1, T sigma2 ) { assert( 0 < sigma1 && sigma1 < sigma2 ); assert( data != 0 ); T sDelta = pow( sigma2, 2 ) - pow( sigma1, 2 ); // フィルタ 1, 2 でのσの差 int s3 = round( sigma2 * 3 ); // 3σ(フィルタ 2 を基準とする) std::vector< T > filter1( s3 * 2 + 1 ); // フィルタ 1 std::vector< T > filter2( s3 * 2 + 1 ); // フィルタ 2 CreateGaussianFilter( sigma1, &filter1 ); CreateGaussianFilter( sigma2, &filter2 ); // 水平方向のガウシアン・フィルタ結果を保持するバッファ Matrix< T > buffer1( data->rows(), data->cols() ); Matrix< T > buffer2( data->rows(), data->cols() ); Coord< int > c; for ( c.y = 0 ; c.y < static_cast< int >( data->rows() ) ; ++( c.y ) ) { for ( c.x = 0 ; c.x < static_cast< int >( data->cols() ) ; ++( c.x ) ) { buffer1[c.y][c.x] = GaussianFilter( *data, filter1, c, true ); buffer2[c.y][c.x] = GaussianFilter( *data, filter2, c, true ); } } for ( c.y = 0 ; c.y < static_cast< int >( data->rows() ) ; ++( c.y ) ) { for ( c.x = 0 ; c.x < static_cast< int >( data->cols() ) ; ++( c.x ) ) { (*data)[c.y][c.x] = ( GaussianFilter( buffer2, filter2, c, false ) - GaussianFilter( buffer1, filter1, c, false ) ) / sDelta; } } }
CreateGaussianFilter はガウシアン・フィルタを構築するための関数です。フィルタのサイズはあらかじめ定義しておく必要があることに注意が必要です。GaussianFilter はガウシアン・フィルタを使って畳み込み積分をするための関数です。引数 isHorizontal で水平・垂直のいずれの方向へ適用するかを示し、この値が true なら水平方向へ適用します。最後の DoGFilter が DoG フィルタを行うための関数ですが、前述の計算式で二つの標準偏差を kσ, σ と表していたのに対してここでは sigma1, sigma2 の別々の標準偏差で渡すようにしています。処理の流れとしては、まず水平方向に sigma1, sigma2 それぞれのパラメータでガウシアン・フィルタを行いバッファに保持しておいて、それを垂直方向に処理しながら差分を計算します。
サンプル・プログラムを使った処理結果を以下に示します。
| σ = 1, 1.1 | σ = 3, 3.1 | σ = 5, 5.1 | |
|---|---|---|---|
| DoG |  |
 |
 |
| σ = 1 | σ = 3 | σ = 5 | |
| LoG |  |
 |
 |
表の上側が DoG フィルタでの処理結果、下側は同じ条件下での LoG フィルタでの処理結果です。両者は見分けができないほど似通っています。
Canny 法は「ジョン・キャニー ( John F.Canny )」が 1986 年に発表して以来、現在のところ最も性能の良いエッジ抽出法として知られています。主な処理の流れは次のようになります。
1, 2 については問題ないと思います。3 は、ガウシアン・フィルタやソーベル・フィルタによって太くなったエッジ部分を細線化するために行います。ソーベル・フィルタによってエッジ強度とエッジ方向が計算できるので、エッジ方向を量子化して以下の 4 パターンに振り分けた上で、その方向について極大となっている点以外はゼロとしてしまいます。
4 は二段階のしきい値判定を行います。しきい値のうち大きい側を Th, 小さい側を Tl としたとき、Th より大きな値を持つエッジはそのまま残し、Tl より小さな値を持つエッジはゼロにします。Tl と Th の間にある場合、最近傍にエッジが存在すればそのまま残し、そうでなければゼロクリアします。
Canny 法を使ったエッジ抽出のサンプル・プログラムを以下に示します。
/* Canny_ExtractMax : エッジの極大値を抽出する ( Canny 法 ) src : 適用対象のデータ dest : 抽出結果を保持する行列への参照 */ template< class T > void Canny_ExtractMax( const Matrix< T >& src, Matrix< T >* dest ) { dest->assign( src.rows(), src.cols() ); Matrix< T > ei( src.rows(), src.cols() ); // エッジ強度 Matrix< T > eo( src.rows(), src.cols() ); // エッジ方向 // エッジ強度・方向の計算 Coord< int > c; for ( c.y = 0 ; c.y < static_cast< int >( src.rows() ) ; ++( c.y ) ) { for ( c.x = 0 ; c.x < static_cast< int >( src.cols() ) ; ++( c.x ) ) { T eh = Edge_Sobel_H( src, c ); T ev = Edge_Sobel_V( src, c ); ei[c.y][c.x] = std::sqrt( eh * eh + ev * ev ); eo[c.y][c.x] = ( eh == 0 ) ? std::numeric_limits< T >::max() : ev / eh; } } // 極大値であるか判定する for ( c.y = 0 ; c.y < static_cast< int >( src.rows() ) ; ++( c.y ) ) { for ( c.x = 0 ; c.x < static_cast< int >( src.cols() ) ; ++( c.x ) ) { T ei1, ei2; // -π/8 〜 π/8 ; 7π/8 〜 9π/8 if ( -0.4142 <= eo[c.y][c.x] || eo[c.y][c.x] < 0.4142 ) { ei1 = ei[c.y][H_Move( c.x, -1, src.cols() )]; ei2 = ei[c.y][H_Move( c.x, 1, src.cols() )]; // π/8 〜 3π/8 ; 9π/8 〜 11π/8 } else if ( 0.4142 <= eo[c.y][c.x] || eo[c.y][c.x] < 2.4142 ) { ei1 = ei[V_Move( c.y, -1, src.rows() )][H_Move( c.x, 1, src.cols() )]; ei2 = ei[V_Move( c.y, 1, src.rows() )][H_Move( c.x, -1, src.cols() )]; // 3π/8 〜 5π/8 ; 11π/8 〜 13π/8 } else if ( 2.4142 <= eo[c.y][c.x] || eo[c.y][c.x] < -2.4142 ) { ei1 = ei[V_Move( c.y, -1, src.rows() )][c.x]; ei2 = ei[V_Move( c.y, 1, src.rows() )][c.x]; // 5π/8 〜 7π/8 ; 13π/8 〜 15π/8 } else { ei1 = ei[V_Move( c.y, -1, src.rows() )][H_Move( c.x, -1, src.cols() )]; ei2 = ei[V_Move( c.y, 1, src.rows() )][H_Move( c.x, 1, src.cols() )]; } if ( ei[c.y][c.x] > ei1 && ei[c.y][c.x] > ei2 ) (*dest)[c.y][c.x] = ei[c.y][c.x]; else (*dest)[c.y][c.x] = 0; } } } /* Canny_HasNeighborEdge : エッジが連続しているかを判定する ( Canny 法 ) dest : 判定対象のデータ(上側のth以上の値を持つエッジは抽出済のもの) c : 判定位置 tl : 下側のしきい値 */ template< class T > bool Canny_HasNeighborEdge( const Matrix< T >& dest, Coord< int > c, T tl ) { if ( dest[c.y][H_Move( c.x, -1, dest.cols() )] >= tl ) return( true ); // 左 if ( dest[V_Move( c.y, -1, dest.rows() )][H_Move( c.x, -1, dest.cols() )] >= tl ) return( true ); // 左上 if ( dest[V_Move( c.y, -1, dest.rows() )][c.x] >= tl ) return( true ); // 上 if ( dest[V_Move( c.y, -1, dest.rows() )][H_Move( c.x, 1, dest.cols() )] >= tl ) return( true ); // 右上 if ( dest[c.y][H_Move( c.x, 1, dest.cols() )] >= tl ) return( true ); // 右 if ( dest[V_Move( c.y, 1, dest.rows() )][H_Move( c.x, 1, dest.cols() )] >= tl ) return( true ); // 右下 if ( dest[V_Move( c.y, 1, dest.rows() )][c.x] >= tl ) return( true ); // 下 if ( dest[V_Move( c.y, 1, dest.rows() )][H_Move( c.x, -1, dest.cols() )] >= tl ) return( true ); // 左下 return( false ); } /* Canny_Threshold : エッジのしきい値判定を行う ( Canny 法 ) src : 判定対象のデータ dest : 判定結果を保持する行列へのポインタ th : 上側のしきい値 tl : 下側のしきい値 */ template< class T > void Canny_Threshold( const Matrix< T >& src, Matrix< T >* dest, T th, T tl ) { dest->assign( src.rows(), src.cols() ); Coord< int > c; // th 以上はエッジとみなす for ( c.y = 0 ; c.y < static_cast< int >( src.rows() ) ; ++( c.y ) ) for ( c.x = 0 ; c.x < static_cast< int >( src.cols() ) ; ++( c.x ) ) if ( src[c.y][c.x] >= th ) (*dest)[c.y][c.x] = src[c.y][c.x]; else (*dest)[c.y][c.x] = 0; // tl 以上 th より小さい場合は近傍にエッジがある場合のみエッジとみなす for ( c.y = 0 ; c.y < static_cast< int >( src.rows() ) ; ++( c.y ) ) { for ( c.x = 0 ; c.x < static_cast< int >( src.cols() ) ; ++( c.x ) ) { if ( src[c.y][c.x] < tl ) continue; if ( Canny_HasNeighborEdge( *dest, c, tl ) ) (*dest)[c.y][c.x] = src[c.y][c.x]; } } } /* Canny_Main : Canny 法 src : 判定対象のデータ dest : 判定結果を保持する行列へのポインタ th : 上側のしきい値 tl : 下側のしきい値 */ template< class T > void Canny_Main( const Matrix< T >& src, Matrix< T >* dest, T sigma, T th, T tl ) { // ガウシアン・フィルタ std::vector< T > filter( round( sigma * 3 ) ); CreateGaussianFilter( sigma, &filter ); Coord< int > c; Matrix< T > gaussDataH( src.rows(), src.cols() ); Matrix< T > gaussDataV( src.rows(), src.cols() ); for ( c.y = 0 ; c.y < static_cast< int >( src.rows() ) ; ++( c.y ) ) { for ( c.x = 0 ; c.x < static_cast< int >( src.cols() ) ; ++( c.x ) ) { gaussDataH[c.y][c.x] = GaussianFilter( src, filter, c, true ); } } for ( c.y = 0 ; c.y < static_cast< int >( src.rows() ) ; ++( c.y ) ) { for ( c.x = 0 ; c.x < static_cast< int >( src.cols() ) ; ++( c.x ) ) { gaussDataV[c.y][c.x] = GaussianFilter( gaussDataH, filter, c, false ); } } // 極大値の抽出 Matrix< T > peakData; Canny_ExtractMax( gaussDataV, &peakData ); // しきい値判定 Canny_Threshold( peakData, dest, th, tl ); }
最後の Canny_Main がメイン・ルーチンになります。最初にガウシアン・フィルタを行い、Canny_ExtractMax, Canny_Threshold の順に関数を呼び出して処理を進めます。
Canny_ExtractMax ではまずエッジ強度と方向の計算を行います。この計算にはソーベル・フィルタ ( Edge_Sobel_H/V ) を使って水平・垂直方向のエッジ強度をそれぞれ eh, ev として求め、L2 ノルム ( eh2 + ev2 )1/2 をエッジ強度 ei、比率 ev / eh をエッジ方向 eo とします。
この二つの値を使い、次に極大値判定を行います。eo の値からエッジ方向を 4 つの場合に分け、その方向に見て ei が極大値となっているときのみ値を残し、それ以外はゼロとします。例えば、-0.4142 ≤ eo < 0.4142 の場合、その逆正接 tan-1 を計算すればエッジ方向 θ は -π / 8 ≤ θ < π / 8 ; 7π / 8 ≤ θ < 9π / 8 の範囲にあるので水平方向に見て極大値かどうか判定を行います。左右の値に対してより大きな値であれば極大値であるとみなし、そうでなければゼロにします。
Canny_Threshold では二つのしきい値 th と tl を使います。但し、th > tl とします。まず、th 以上の値を持つエッジは無条件でエッジとみなします。次に、tl 以上 th より小さい値のエッジは、Canny_HasNeighborEdge を使って近傍にエッジがあるかを判定し、あればエッジとみなします。Canny_HasNeighborEdge では水平・垂直方向に斜め方向を加えた 8 近傍についてエッジであるかどうかをチェックしています。th 以上の値はすでにエッジとして判定済みになっていることに注意して下さい。
Canny 法をいくつかのパラメータを使って適用した結果を以下に示します。
| Th = 64 ; Tl = 16 | Th = 32 ; Tl = 8 | Th = 4 ; Tl = 1 | |
|---|---|---|---|
| σ = 1 |  |
 |
 |
| σ = 3 |  |
 |
 |
| σ = 5 |  |
 |
 |
σ の値を大きくすれば画像はだんだんぼやけてしまうので、エッジは検出されなくなります。また、しきい値を調整することで、不要な部分を消して主要な輪郭線だけを浮かび上がらせることも可能です。σ で大まかに必要な線を取得して、しきい値によって微調整するという使い方になるのかと思いますが、しきい値の調整は試行錯誤が必要となりそうです。
最初に述べたように、エッジ抽出は単独で用いられるだけでなく画像の自動認識などでも頻繁に利用される重要なアルゴリズムなので、その種類も多岐にわたります。今回は、単純な差分によるエッジ抽出から始めてより複雑なフィルタなども紹介しました。複雑といっても難解な部分は少なく、自分なりのアレンジもしやすい領域なのではないかと思います。特に Canny 法ではガウシアン・フィルタやソーベル・フィルタを他のものに置き換えることでまた違った効果が得られるかもしれません。
少し、宣伝です。
趣味で小説を書いています。以前から、書いてみたいという思いがあり、アマチュアの小説を扱うサイトを見つけたことから実際に始めてみました。
最初は、小説を書ければ満足で、アクセス数が少なくてもいいかなと思っていましたが、やはりせっかく書いたからには読んでもらいたいし、感想をいただきたいという欲も出てきました。
もし、よろしければ、読んでもらえると嬉しいですし、今後の励みにもなります。
小説は、以下のリンク先から読むことができます。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |