数値演算法
(2) 多倍長整数の演算
前回、コンピュータ上での数値計算処理方法について紹介しました。二進数を使った計算を考えた場合、全ての計算を論理演算から構築することが可能です。今回はこの考え方を応用して、多倍長整数の演算について紹介したいと思います。
1) 多倍長整数の表現
「位取り記数法」を使って、任意の数を基数として数を表現することができることを前回説明しました。通常利用されている「10 進法」で 25 という数が記述されているとき、これを 16 進法で表すと 19、二進法で表すと 11001 になります。
基数として利用できる数に制限はないので、もっと大きな数を基数に使うこともできます。例えば 10 進法で表された 12345678 という数を 1000 進法で表せば (12)(345)(678) と記述することができます。ここで ( ) 内の数は "一桁の数" を表していることになりますが、1000 個もの記号を用意するわけにもいかないので、中身は 10 進法で表現してあります。
32 ビット CPU は、32 ビットのデータに対して一度に演算処理を行うことができます。整数演算の場合、232 = 4294967296 より小さな値を扱うことができることになります。よって、このデータ 1 個を一桁と見なした場合、その配列は 232 進法で表した数値と考えることができます。
以下に、多倍長整数をクラス定義したサンプル・プログラムの一部を示します。なお、このクラスでは正の数だけを扱うことにしているため、符号は考慮していません。
namespace BigNum
{
typedef unsigned short int Digit;
typedef unsigned long int UnsignedBuff;
typedef long int SignedBuff;
class Unsigned
{
std::vector< Digit > number_;
bool nan_;
static const size_t DIGIT_BIT;
static const Digit DIGIT_MAX;
void resize( size_t sz ) { number_.resize( sz, Digit() ); }
void push_upper( Digit i = 0 ) { number_.push_back( i ); }
void push_lower( Digit i = 0 ) { ushift(); number_[0] = i; }
void ushift( size_t cnt = 1 );
void lshift( size_t cnt = 1 );
void negZero();
:
public:
Unsigned( long int i = 0 );
void clear() { number_.clear(); push_upper(); nan_ = false; }
bool isNaN() const { return( nan_ ); }
bool operator!() const { return( nan_ ); }
Unsigned& operator>>=( UnsignedBuff num );
Unsigned& operator<<=( UnsignedBuff num );
bool operator==( const Unsigned& num ) const;
bool operator<( const Unsigned& num ) const;
bool operator>( const Unsigned& num ) const;
bool operator!=( const Unsigned& num ) const;
bool operator<=( const Unsigned& num ) const;
bool operator>=( const Unsigned& num ) const;
size_t size() const { return( number_.size() ); }
:
};
template< class T >
void Unsigned::init( T t )
{
assert( sizeof( Digit ) * 2 <= sizeof( UnsignedBuff ) );
nan_ = false;
if ( t < 0 ) {
nan_ = true;
return;
} else if ( t > DIGIT_MAX ) {
UnsignedBuff buff = t;
do {
push_upper( buff & DIGIT_MAX );
buff >>= DIGIT_BIT;
} while ( buff > DIGIT_MAX );
if ( buff > 0 ) push_upper( buff );
} else {
push_upper( t );
}
}
Unsigned::Unsigned( long int i )
{ init< long int >( i ); }
}
数列の表現に、STL ( Standard Template Library ) にある可変長配列の vector を利用しています。配列の要素 ( 一つの桁 ) の型は unsigned short int としているため、一桁は通常 16 ビットになります ( CPU や言語仕様によって大きさは変わります )。通常 32 ビットの型である unsigned long int ではなく unsigned short int を利用したのは演算時の桁上がりを考慮するためです。一桁どうしの演算の結果が unsigned long int 型の大きさを越えなければ、桁あふれを気にしなくてもよくなるので実装が簡単になります。
なお、型のサイズに関する約束事として「short int 型と int 型は最低でも 16 ビット」、「long int 型は最低でも 32 ビット」、「short int 型のサイズ ≤ int 型のサイズ ≤ long int 型のサイズ」であることが厳密に定義されているため、逆に言えば「short int 型と long int 型のサイズが等しい」ことも想定されます。そのような環境はほとんどないのですが、UnsignedBuff 型のサイズは Digit 型の二倍以上であることを前提として実装しているので、念のためコンストラクタの中で assert を使い、条件に合わない場合はプログラムが停止するようにしてあります。
数列には下位側の桁から順に並べる方式を取ります。よって 0 番めが一桁目の数を表し、末尾が最上位となります。演算は通常、下位側の桁から行われ、桁の追加・削除は最上位側の方が発生頻度が高いため、下位側から並べた方が処理を効率良く行えます。しかし、除算処理では逆に上位側から処理を行い、下位側への桁の追加が発生します。除算処理は他の演算に比べて複雑になるため、全体的に見ればどちらも一長一短がありそうです。
メンバ変数 nan_ は、数として成り立っているかどうかを判定するフラグとして利用します。例えば、0 で除算した結果は存在しない ( 0 / 0 ならば不定になる ) ため値としては無効になり、このときは nan_ を true とします。一度無効になったら、有効な値を再度代入しない限り、それを使った演算結果は常に無効となるようにします。なお、isNaN と否定演算子 ( operator! ) はどちらも、対象が無効値だった場合に真を返す関数です。
コンストラクタは、long int型の整数値データから構築するバージョンだけを用意しています。よって、最初に構築できる値は 216 進二桁までに限定されてしまいます。最終的には文字列から取得するバージョンが必要になりますが、演算処理が必要になるため、ここではまだ用意できません。
メンバ関数の negZero は、最上位にあるデータが 0 だった場合にそれを除去するために使用します。減算や除算をしたときに、最上位の桁が 0 になる場合があり、その後の処理に影響を及ぼす可能性があるため、これを使って除去するようにします。
四則演算の処理で必要になるシフト演算や比較演算、桁単位のシフト処理用メンバ関数 ( lshift, ushift ) が定義されていますが、実際のコーディング内容はここでは省略してあります。また、negZero も実装については記述してありません。lshift と ushift はそれぞれ、vector の先頭の要素を削除するか追加するだけの処理であり、negZero も末尾のデータをチェックして、0 ならば削除するだけの簡単な処理なので、どのような実装になるかについては容易に想像できると思います。
2) 加算・減算処理
まずは簡単な演算処理として、加算と減算を実装します。最下位桁から順に、同じ桁の数どうしを加算・減算するだけなので、桁上がりや桁借りに気を付ければ簡単に実装できます。
namespace BigNum
{
bool Unsigned::isNaN( const Unsigned& num )
{
if ( isNaN() ) return( true );
if ( ! num ) {
nan_ = true;
return( true );
}
return( false );
}
void Unsigned::partialAdd( const Unsigned& num, size_t start )
{
if ( isNaN( num ) ) return;
if ( num == 0 ) return;
if ( start + num.size() > size() ) resize( start + num.size() );
size_t cnt = size();
UnsignedBuff carry = 0;
for ( size_t i = start ; i < cnt ; i++ ) {
if ( carry == 0 && i >= start + num.size() ) break;
carry += number_[i];
if ( i < start + num.size() ) carry += num.number_[i - start];
number_[i] = carry & DIGIT_MAX;
carry >>= DIGIT_BIT;
}
if ( carry > 0 )
push_upper( carry );
}
Unsigned& Unsigned::operator+=( const Unsigned& num )
{
partialAdd( num, 0 );
return( *this );
}
Unsigned& Unsigned::operator-=( const Unsigned& num )
{
if ( isNaN( num ) ) return( *this );
if ( this == &num ) {
clear();
return( *this );
}
if ( *this < num ) {
nan_ = true;
return( *this );
}
size_t cnt = size();
SignedBuff carry = 0;
for ( size_t i = 0 ; i < cnt ; i++ ) {
if ( i >= num.size() && carry == 0 ) break;
SignedBuff n = number_[i] - carry;
if ( i < num.size() ) n -= num.number_[i];
if ( n < 0 ) {
n += DIGIT_MAX + 1;
carry = 1;
} else {
carry = 0;
}
number_[i] = n;
}
negZero();
return( *this );
}
}
加算・減算のどちらも 16 ビットどうしの演算を 32 ビット変数を使って行い、桁あふれを防いでいます。加算処理では、一桁どうしの演算結果から下位 16 ビットだけを抽出し、上位 16 ビット分は繰り上がり分として一つ上の桁でいっしょに加算します。なお、指定した位置 ( 桁 ) から加算を行う処理があとで必要となるため partialAdd というメンバ関数を用意し、加算処理はこれを利用しています。
減算処理の場合、ある桁の処理において被減数が減数より小さい場合は結果が負数になるため、上位の桁から借りる処理が必要になります。また、被減数そのものが減数よりも小さいときは演算結果が負数になりますが、このクラスでは正の数のみを扱っているため、被減数 < 減数の時に結果をどう返すのかを検討する必要があります。考えられる処理方法としては
- 絶対値を返す
- 0 を返す
- 無効値を返す
といったものが挙げられます。今回はその中から「無効値を返す」を選択することにしました。絶対値を返すようにすると、符号付き多倍長整数の演算処理を構築するときなどに便利な場面があるので、そちらを採用するという手もあります。
気を付けなければならないこととして、演算対象となる二数が同じ参照元であった場合の処理があります。通常の場合、参照元が等しければ片側を別の変数にコピーしておかないと、同じ箇所を変更することになって、結果がおかしくなる危険性があります。幸い、加算・減算処理では処理後に数列へ代入しているため、そのような問題は発生しません。さらに減算処理では、参照元が同じ場合は同じ数どうしで処理することになるので、0 に初期化してすぐに処理を終了しています。
3) 乗算処理
乗算処理では、前回紹介した二進数での処理と同様に、筆算のやり方をそのまま実装することで実現させることができます。216 ( = 65536 ) 進数の二数 [ ( 10000 )( 20000 )( 30000 ) ]65536 と [ ( 30000 )( 20000 )( 10000 ) ]65536 を筆算で計算した場合、以下のようになります。
(10000)(20000)(30000) X (10000) = (1525)(57600)(0)(0) + (3051)(49664)(0) + (4577)(41728)
= (1525)(60651)(54241)(41728)
(10000)(20000)(30000) X (20000) = (3051)(49664)(0)(0) + (6103)(33792)(0) + (9155)(17920)
= (3051)(55767)(42947)(17920)
(10000)(20000)(30000) X (30000) = (4577)(41728)(0)(0) + (9155)(17920)(0) + (13732)(59648)
= (4577)(50883)(31652)(59648)
(10000)(20000)(30000)
X) (30000)(20000)(10000)
-------------------------
(1525)(60651)(54241)(41728)
(3051)(55767)(42947)(17920)
(4577)(50883)(31652)(59648)
------------------------------------------
(4577)(53935)(23410)(32175)(06625)(41728)
上の例に示したように、乗数の各桁で m 桁 x 1 桁の乗算を行い、桁を合わせながら各結果を加算することにより、結果を得ることができます。そのため、m 桁 x 1 桁の乗算処理を最初に実装します。
namespace BigNum
{
void Unsigned::mulOneDigit( Digit mulnum )
{
if ( mulnum == 0 ) {
clear();
return;
}
UnsignedBuff carry = 0;
for ( size_t i = 0 ; i < size() ; i++ ) {
carry += static_cast< UnsignedBuff >( number_[i] ) * mulnum;
number_[i] = carry & DIGIT_MAX;
carry >>= DIGIT_BIT;
}
if ( carry > 0 ) push_upper( carry );
}
}
処理の流れは加算処理にかなり近く、下位の桁から順に乗算処理をして、繰り上がり分を一つ上の桁に加算する処理を繰り返しています。乗数が 0 の場合、結果は 0 の数列になってしまうため、最初にチェックを行っています。
m 桁 x 1 桁の乗算ができれば、m 桁 x n 桁の乗算は簡単に実装できます。
namespace BigNum
{
Unsigned& Unsigned::operator*=( const Unsigned& num )
{
if ( isNaN( num ) ) return( *this );
Unsigned u( *this );
const Unsigned* v = ( this == &num ) ? new Unsigned( num ) : #
try {
clear();
for ( UnsignedBuff i = v->size() ; i > 0 ; i-- ) {
Unsigned ans( u );
ans.mulOneDigit( v->number_[i - 1] );
partialAdd( ans, i - 1 );
}
}
catch(...) {
if ( this == &num ) delete v;
throw;
}
if ( this == &num ) delete v;
return( *this );
}
}
被乗数は変数 u にコピーしてから 0 で初期化し、乗数と被乗数の参照先が等しい場合は乗数を変数 v にコピーしています ( 等しくなければ参照先だけをコピーします )。あとは v の下位側から一桁ずつ取り出しては乗算処理を行い、桁を合わせてから加算する処理を繰り返します。例外処理が加わったため複雑に見えますが、実際の処理は try 文の中だけなので、処理自体は非常にシンプルです。
なお、処理の中で partialAdd を呼び出して、処理を始める位置を変えて ( 桁を合わせて ) 加算処理するようにしています。前節の加算処理で partialAdd を実装していたのはこのためです。
4) 除算処理
四則演算の中で実装が一番難しいのが除算の処理です。除算処理も、乗算と同様に筆算法をそのまま実装するような形になります。しかし、手計算で筆算を行う場合を考えると分かるように試行錯誤を行う場面があるため、その部分を機械的に行うための工夫が必要になります。例として、37810 を 345 で割る処理を筆算を使って行ってみたいと思います。
____109_
345 ) 37810
345
------
331
0
-----
3310
3105
-----
205
筆算処理の流れを見れば分かるように、除数と同じもしくは一つだけ大きい桁分だけ被除数の上位側から抽出して除算を繰り返しているので、除数の桁数を N とすると、( N + 1 ) 桁 / N 桁、または N 桁 / N 桁 の除算処理についてまずは考える必要があります。
最初の除算で、378 と 345 の商を 1 としています。手計算で処理をする場合、除数にいくらかの値を掛けて被除数と比較し、被除数より大きくならない最大の数を求めるという作業を頭の中で計算しているため、この処理を機械的に行う場合は以下のような流れになります。
- 仮の商 q を 1 で初期化する
- q と除数 v を乗算処理する
- 乗算結果 m を被除数の上位桁 u と比較して、m > u になれば q - 1 が求める商になる。そうでなければ q に 1 を加算して 2 を繰り返す
この場合、例えば 99 / 10 を計算すると、10 回の乗算処理を行う必要があり効率がいいとは言えません。そこで、この回数を減らすための工夫が必要になります。
通常、大きな数どうしを手計算で除算するときは、上位の数桁を見て仮の商を決め、実際に計算して判断することを繰り返します。このやり方を真似て、上位数桁を使った除算処理から仮の商を求めることにします。一度に除算する大きさを 32 ビットとして、今回は上位二桁を取り出して除算した結果を仮の商と決めることにします。
b 進数 N + 1 桁の数 u = [ UNUN-1 ... U0 ]b を b 進数 N 桁の数 v = [ VN-1VN-2 ... V0 ]b で割ったときの商が q、余りが r であったとき、u = qv + r ( 但し r < v ) になります。ここで、u から上位二桁を抽出した数 u0 = [ UNUN-1 ]b を、v から上位一桁を抽出した数 v0 = [ VN-1 ]b で割った仮の商を q0 とすると、q 及び q0 の取りうる値に対して以下の不等式が成り立ちます。
( UNb + UN-1 )bN-1 / v ≤ q < ( ( UNb + UN-1 )bN-1 + bN-1 ) / v --- (1)
( UNb + UN-1 )bN-1 / v ≤ q0 ≤ u / VN-1bN-1 --- (2)
ここで (1) 式は、( UNb + UN-1 )bN-1 ≤ u < ( UNb + ( UN-1 + 1 ) )bN-1 であることを、(2) 式は q0 = ( UNb + UN-1 )bN-1 / VN-1bN-1 であり、この式において (分子) ≤ u、(分母) ≤ v になることを利用しています。
(1),(2) 式を使うと、q0 と q の差 q0 - q が取りうる値に対して以下の不等式を導くことができます。
| q0 - q | > | [ ( UNb + UN-1 )bN-1 / v ] - { [ ( UNb + UN-1 )bN-1 + bN-1 ] / v } |
| = | -bN-1 / v ≥ -1 |
| q0 - q | ≤ | ( u / VN-1bN-1 ) - [ ( UNb + UN-1 )bN-1 / v ] |
| ≤ | ( u / VN-1bN-1 ) - ( u / v - 1 ) |
| = | ( uv - uVN-1bN-1 ) / vVN-1bN-1 + 1 |
| = | ( u / v )[ ( v - VN-1bN-1 ) / VN-1bN-1 ] + 1 |
| < | ( u / v )( bN-1 / VN-1bN-1 ) + 1 |
| = | ( u / v )( 1 / VN-1 ) + 1 |
よって、u / v < b が成り立つとき、上式は以下のようになります。
-1 < q0 - q < b / VN-1 + 1
q0 - q は必ず整数になるので、上式から、仮の商は実際の商以上の数に必ずなることが保証されます。また、VN-1 ≥ b / 2 ならば上式の最右辺は 3 以下となり、q0 - q は 2 以下になることが保証されます。
「u / v < b が成り立つ場合」とは、筆算で除算を行うときに最初の処理を除いた場合全てを指します。前の除算処理で求めた余りは必ず v より小さくなり、下位の桁を追加した数を新たな u として b で割ったとしても、必ず b より小さくなります ( さもないと商が二桁となってしまいます )。例外は最初の処理の時だけで、このときだけは商が b 以上になる可能性があります。商が b 以上になるのは、u ≥ vb となる時です。その場合は N 桁 / N 桁で処理するか、最上位を 0 と見なして普通に処理するかのいずれかで対応する必要があります。
上記内容を普通の数値で確認してみたいと思います。例として 53611928 / 7199354 を使って q と q0 の取りうる値の範囲を計算すると、
53000000 / 7199354 < q < ( 53000000 + 1000000 ) / 7199354 --- (1)'
53000000 / 7199354 < q0 ( = 53000000 / 7000000 ) < 53611928 / 7000000 --- (2)'
よって、
| q0 - q | > | 53000000 / 7199354 - ( 53000000 + 1000000 ) / 7199354 |
| = | -1000000 / 7199354 > -1 |
| q0 - q | < | ( 53611928 / 7000000 ) - ( 53000000 / 7199354 ) |
| < | ( 53611928 / 7000000 ) - ( 53611928 / 7199354 - 1 ) |
| = | ( 53611928 x 7199354 - 53611928 x 7000000 ) / 7199354 x 7000000 + 1 |
| = | ( 53611928 / 7199354 )[ ( 7199354 - 7000000 ) / 7000000 ] + 1 |
| < | 10 x ( 1000000 / 7000000 ) + 1 |
| = | 10 x ( 1 / 7 ) + 1 |
つまり、0 ≤ q0 - q ≤ 2 となります。ちなみに q0 の値は 7 であり実際の商と一致しているため、今回は差がなかったことになります。これが例えば 45000000 / 5999999 を求める場合になると、q0 の値は 9 であり、実際の商 q の値が 7 となるため差は 2 となります。また、v の最上位桁が 5 より小さくなって 18000000 / 2999999 を計算するような場合、q0 の値の 9 に対して q の値が 6 になり、差は 3 になります。
以下に、N + 1 桁と N 桁での除算処理用サンプル・プログラムを示します。
namespace BigNum
{
Digit Unsigned::divNDigit( const Unsigned& v )
{
if ( this == &v ) {
clear();
return( 1 );
}
UnsignedBuff digit = v.size();
UnsignedBuff q = number_[digit-1];
if ( size() > digit ) q += static_cast< UnsignedBuff >( number_[digit] ) << DIGIT_BIT;
q /= v.number_[digit-1];
if ( q > DIGIT_MAX ) q = DIGIT_MAX;
Unsigned qv( v );
qv.mulOneDigit( q );
while ( operator<( qv ) ) {
--q;
operator+=( v );
}
operator-=( qv );
return( q );
}
}
divNDigit では、被除数の桁数は除数と同じか一つだけ大きいものとしています。そのため仮の商を求めるときに被除数と除数の桁数を比較して、被除数の上位桁から取るべき桁数を決定しています。仮の商が決まったら除数との積を求めて被除数と比較します。積の値が被除数より大きければ、仮の商が大きすぎることになるため補正を行い、被除数よりも小さくなったところで処理が完了します。
N + 1 桁と N 桁での除算ができるようになれば、それを利用して任意の桁の数に対して除算ができるようになります。
namespace BigNum
{
void Unsigned::copy( const Unsigned& num, size_t s, size_t e )
{
if ( this == &num ) return;
number_.clear();
if ( e - s + 1 > number_.capacity() )
number_.reserve( e - s + 1 );
while ( s <= e ) {
if ( s >= num.size() ) break;
push_upper( num.number_[s++] );
}
if ( size() == 0 ) push_upper();
negZero();
}
bool Unsigned::div( Unsigned v, Unsigned* r )
{
const Digit half = 1 << ( DIGIT_BIT - 1 );
if ( this == r ) return( false );
if ( isNaN( v ) ) return( false );
if ( v == 0 ) {
nan_ = true;
return( false );
}
if ( operator<( v ) ) {
*r = *this;
clear();
return( true );
}
vector< Digit > ans;
Digit msMem = v.number_[v.size() - 1];
UnsignedBuff shiftNum = 0;
while ( msMem < half ) {
msMem <<= 1;
shiftNum++;
}
v <<= shiftNum;
operator<<=( shiftNum );
size_t s = size() - v.size();
r->copy( *this, s, s + v.size() - 1 );
if ( *r < v )
r->push_lower( number_[--s] );
while ( *r >= v ) {
ans.push_back( r->divNDigit( v ) );
while ( s > 0 ) {
r->push_lower( number_[--s] );
if ( *r >= v ) break;
ans.push_back( 0 );
}
}
number_.clear();
for ( size_t i = ans.size() ; i > 0 ; --i )
push_upper( ans[i-1] );
*r >>= shiftNum;
return( true );
}
Unsigned& Unsigned::operator/=( const Unsigned& num )
{
Unsigned r;
div( num, &r );
return( *this );
}
Unsigned& Unsigned::operator%=( const Unsigned& num )
{
Unsigned u( *this );
u.div( num, this );
return( *this );
}
}
v の最上位桁が基数の半分以上になるためには、最上位ビットが 1 となるように v に対して上位側にシフト演算を行う必要があります。u についても同じ量だけシフト演算をしておいた場合、商は変化しませんが、余りについては後で補正しておく必要があります。
divNDigit を使って処理した後、下位の桁を取り出すところでは、被除数と除数の大きさをチェックして被除数の方がまだ小さければ再び下位から桁を取り出し、結果に 0 を追加しています。筆算処理をしていると、余りに下位の桁を追加しても、まだ除数より小さすぎて除算ができないという経験をされたことがあると思います。この場合、結果に 0 を書いてさらに下位の桁から数を取り出して計算するので、その処理をそのままコーディングしています。
5) その他の計算処理
主要な演算処理ができたところで、それらを利用した演算処理を実装してみます。まずは、べき乗のサンプル・プログラムです。
namespace BigNum
{
bool Unsigned::lBitShift()
{
bool ans = ( number_[0] & 1 ) > 0;
operator>>=( 1 );
return( ans );
}
Unsigned& Unsigned::pow( Unsigned exp )
{
if ( isNaN( exp ) ) return( *this );
if ( *this == 0 ) {
if ( exp == 0 ) nan_ = true;
return( *this );
}
Unsigned curVal( *this );
if ( ! exp.lBitShift() ) {
clear();
number_[0] = 1;
}
while ( exp != 0 ) {
curVal *= curVal;
if ( exp.lBitShift() )
operator*=( curVal );
}
return( *this );
}
}
べき乗の処理では、以前紹介した繰り返し自乗法が利用されています。例えば 2131 を計算する場合、131 = 128 + 2 + 1 = 27 + 21 + 20 なので、2131 = 2128・22・21 と分解することができ、
| 21 | | = | 2 |
| 22 | = | (21)2 | = | 22 | = | 4 |
| 24 | = | (22)2 | = | 42 | = | 16 |
| 28 | = | (24)2 | = | 162 | = | 256 |
| 216 | = | (28)2 | = | 2562 | = | 65536 |
| 232 | = | (216)2 | = | 655362 | = | 4294967296 |
| 264 | = | (232)2 | = | 42949672962 | = | 18446744073709551616 |
| 2128 | = | (264)2 | = | 184467440737095516162 | = | 340282366920938463463374607431768211456 |
から、
2131 = 340282366920938463463374607431768211456 x 4 x 2 = 2722258935367507707706996859454145691648
と求めることができます。サンプル・プログラムの中では、変数 curVal 内に繰り返し自乗法で求めた底のべき乗を保持して、指数の下位側からビットを取得しながら、ビットが立っていれば結果に curVal を乗算しています。
次は階乗計算のサンプル・プログラムです。
void Fact( BigNum::UnsignedBuff n, BigNum::Unsigned* ans )
{
*ans = 1;
for ( BigNum::UnsignedBuff u = 2 ; u <= n ; ++u )
*ans *= u;
}
階乗は、ある数 n に対して 1 から n まで順に乗算した値を指し、n! と表します。計 n 回の乗算処理が必要になるため、n が大きくなると桁数と処理時間は飛躍的に増大します。
そこでまずは少しでも乗算回数を少なくしてみます。ある値 k の両側にある数はそれぞれ k - 1 と k + 1 なので、この二数を乗算した結果は k2 - 1 になります。さらにその隣の二数を乗算すると、( k - 2 )( k + 2 ) = k2 - 4 となり、これらの値は k2 から求めることが可能です。k2 から減算する数は、1 を初期値として 4, 9, 16 ... と増加していきます。減算する数の増分は 2 ずつ増加していくため、この増分は前回の値から計算することが可能です。よって、数列の中央値を取得してその二乗を計算し、左右に並んだ数どうしの積を中央値の二乗から計算するようにすれば、乗算処理を半分にすることができます。
例) 10! = 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10
中央値 =6
5 x 7 = ( 6 - 1 ) x ( 6 + 1 ) = 36 - 1 = 35
4 x 8 = ( 6 - 2 ) x ( 6 + 2 ) = 36 - 4 = 32
3 x 9 = ( 6 - 3 ) x ( 6 + 3 ) = 36 - 9 = 27
2 x 10 = ( 6 - 4 ) x ( 6 + 4 ) = 36 - 16 = 20
10! = 6 x 35 x 32 x 27 x 20
上記内容をコーディングしたサンプル・プログラムを以下に示します。
void Fact2( BigNum::UnsignedBuff n, BigNum::Unsigned* ans )
{
BigNum::UnsignedBuff factNum[] = {
1, 1, 2, 6, 24, 120, 720, 5040, 40320,
362880, 3628800, 39916800, 479001600,
};
if ( n < sizeof( factNum ) / sizeof( factNum[0] ) ) {
*ans = factNum[n];
return;
}
BigNum::Unsigned x( n );
x >>= 1; x += 1;
BigNum::Unsigned cnt( x );
cnt -= ( ( n & 1 ) != 0 ) ? 1 : 2;
*ans = x;
x *= x;
BigNum::Unsigned subNum( 1 );
while ( cnt > 0 ) {
x -= subNum;
*ans *= x;
subNum += 2;
cnt -= 1;
}
}
中央値は、数列の個数が奇数の時のみ一つに決めることができるため、数列の個数が奇数のときと偶数のときで処理を場合分けする必要があります。しかし、1 は結果に影響しないので、1 を含めるかどうかで個数の調節を行うことが可能で、上記サンプル・プログラムでもそのように処理しています。
また、小さな値に対してはテーブル化を行い、結果をテーブルから取得して返すようにしています。
初期バージョンに比べると処理がかなり複雑になった分、効果があればいいのですが、実際には処理速度が逆に遅くなります。乗算ルーチンの呼出回数は確かに減少したものの、計算する数の桁数に変化はないため、乗算処理そのものは減少せず、この方法はあまり意味がありません。そのため、別の手段を検討してみます。
数列を偶数と奇数に分解してみます。偶数の列に着目し、要素を全て 2 で割ると、元の数列よりサイズが半分となった新たな数列が作られます。この操作を繰り返すと、数列を奇数の列だけに分解することができます。
| 例) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 奇数 ... | | 3 | | 5 | | 7 | | 9 | |
| 偶数 ... | 2 | | 4 | | 6 | | 8 | | 10 |
↓
| 25 x | ( | 2 | 3 | 4 | 5 | ) |
| 奇数 ... | | | 3 | | 5 | |
| 偶数 ... | | 2 | | 4 | | |
↓
↓
10! = ( 3 x 5 x 7 x 9 ) x ( 3 x 5 ) x 2
8
2 のべき乗はシフト演算を利用することができ、奇数部分の乗算も重複する部分に関しては計算を省くことができるため、さらに演算処理の回数を減らすことができます。
以下に、サンプル・プログラムを示します。
void OddFact( BigNum::UnsignedBuff min, BigNum::UnsignedBuff max, BigNum::Unsigned* num )
{
BigNum::Unsigned n( ( max - min ) / 2 + min );
BigNum::Unsigned cnt( n );
cnt -= min; cnt >>= 1;
BigNum::Unsigned subNum;
if ( ( n & 1 ) == 1 ) {
*num *= n;
n *= n;
subNum = 4;
} else {
n *= n;
n -= 1;
*num *= n;
subNum = 8;
}
while ( cnt > 0 ) {
n -= subNum;
*num *= n;
subNum += 8;
cnt -= 1;
}
}
void Fact3( BigNum::UnsignedBuff n, BigNum::Unsigned* ans )
{
std::vector< BigNum::UnsignedBuff > odd;
BigNum::UnsignedBuff k = 0;
while ( n >= 10 ) {
odd.push_back( ( ( n & 1 ) != 0 ) ? n : n - 1 );
n /= 2;
k += n;
}
*ans = 1;
for ( BigNum::Unsigned i( 2 ) ; i <= n ; i++ )
*ans *= i;
BigNum::Unsigned oddNum( 1 );
BigNum::UnsignedBuff min( 3 );
for ( size_t i = odd.size() ; i > 0 ; i-- ) {
OddFact( min, odd[i - 1], &oddNum );
*ans *= oddNum;
min = odd[i - 1] + 2;
}
*ans <<= k;
}
OddFactは、奇数列に対する階乗計算 ( これを奇数の二重階乗といい、n!! で表します ) を行うためのルーチンで、前に示した Fact2 と処理の内容はほぼ同じです。但し、数列の個数が偶数と奇数の場合で処理を分けているため、若干複雑な構造になっています。Fact3 では奇数列の二重階乗を計算した後、2 のべき乗の指数分だけシフト演算を行います。
最後に、文字列からの変換を行うプログラムを紹介します。
namespace BigNum
{
const size_t Unsigned::DIGIT_LEN10 = std::numeric_limits< Digit >::digits10;
const Digit Unsigned::DIGIT_MAX10 = std::pow( static_cast< Digit >( 10 ), static_cast< Digit >( DIGIT_LEN10 ) );
UnsignedBuff StoI( const string& str, size_t s, size_t e )
{
UnsignedBuff ans = 0;
while ( s < e ) {
ans *= 10;
ans += str[s++] - '0';
}
return( ans );
}
Unsigned::Unsigned( const string& s )
: nan_( false )
{
assert( sizeof( Digit ) * 2 <= sizeof( UnsignedBuff ) );
push_upper( 0 );
if ( s.size() == 0 ) return;
for ( size_t i = 0 ; i < s.length() ; i++ ) {
if ( s[i] < '0' || s[i] > '9' ) {
nan_ = true;
return;
}
}
size_t l = s.length() % DIGIT_LEN10;
if ( l > 0 )
operator+=( StoI( s, 0, l ) );
size_t cnt = s.length() / DIGIT_LEN10;
for ( size_t i = 0 ; i < cnt ; i++ ) {
operator*=( DIGIT_MAX10 );
operator+=( StoI( s, i * DIGIT_LEN10 + l, ( i + 1 ) * DIGIT_LEN10 + l ) );
}
}
}
文字列から数値に変換するために、一桁で表すことのできる 10 進法での最大桁数 ( 例えば 16 ビット整数型なら 0 から 65535 までの値を扱うことができるので 5 桁 ) 分だけ上位側から文字列を読み込み、それを数値変換して ( このとき、変換した数値は一桁を表す型の範囲内になります ) 加算してから、今度は一桁で表すことのできる 1E+xx 形式の最大値 ( 例えば 16 ビット整数型なら 1E+04 = 10000 ) を掛けあわせていきます。これで、大きな数も文字列で表すことで変換が可能となります。
6) 性能評価
作成した各演算ルーチンの処理速度を計測した結果を示しておきます。どのグラフも Y 軸は演算にかかった時間 ( 秒 ) を表します。計測は Windows7 上の VirtualBox でゲスト OS を Xubuntu 16.04 LTS として行っています。CPU は Intel Core i7-2600 3.40GHz で、ゲスト OS 上ではコア数を 1 としています。
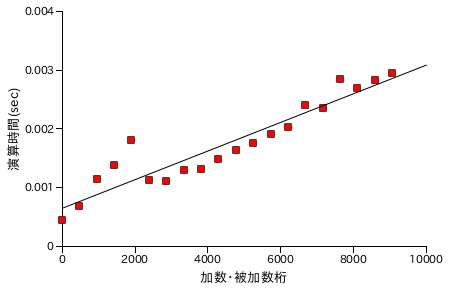
図表 6-1. 加算処理時間の計測結果
| 被加数の桁数 | 加数の桁数 | 結果桁数 | 演算時間(sec) |
|---|
| 5 | 5 | 6 | 0.000438 |
| 483 | 483 | 483 | 0.000686 |
| 960 | 960 | 960 | 0.001145 |
| 1439 | 1437 | 1439 | 0.001376 |
| 1916 | 1915 | 1916 | 0.001796 |
| 2393 | 2393 | 2393 | 0.001120 |
| 2870 | 2869 | 2870 | 0.001104 |
| 3349 | 3347 | 3349 | 0.001300 |
| 3826 | 3823 | 3826 | 0.001316 |
| 4301 | 4300 | 4301 | 0.001475 |
| 4781 | 4780 | 4781 | 0.001629 |
| 5259 | 5258 | 5259 | 0.001752 |
| 5737 | 5736 | 5737 | 0.001909 |
| 6213 | 6211 | 6213 | 0.002026 |
| 6691 | 6690 | 6691 | 0.002399 |
| 7170 | 7166 | 7170 | 0.002354 |
| 7645 | 7645 | 7645 | 0.002836 |
| 8125 | 8124 | 8125 | 0.002694 |
| 8604 | 8599 | 8604 | 0.002817 |
| 9080 | 9075 | 9080 | 0.002948 |
|
|
上の図表は、加算の演算時間を X 軸を処理する数の桁数としてプロットしたものです。各プロットは同じ数値について 1000 回の演算を行った合計時間を表しています。また、どの場合もほぼ同じ桁の数どうしを演算処理させています。加算は桁数に比例して処理時間が線形で増加しています。
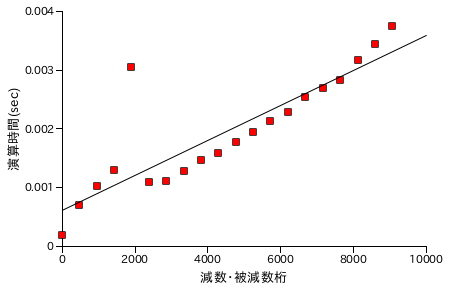
図表 6-2. 減算処理時間の計測結果
| 被減数の桁数 | 減数の桁数 | 結果桁数 | 演算時間(sec) |
|---|
| 5 | 5 | 4 | 0.000195 |
| 483 | 483 | 483 | 0.000704 |
| 960 | 960 | 960 | 0.001026 |
| 1438 | 1438 | 1438 | 0.001299 |
| 1916 | 1915 | 1915 | 0.003039 |
| 2393 | 2392 | 2393 | 0.001093 |
| 2870 | 2870 | 2868 | 0.001106 |
| 3351 | 3350 | 3351 | 0.001278 |
| 3828 | 3826 | 3828 | 0.001470 |
| 4302 | 4300 | 4302 | 0.001589 |
| 4780 | 4778 | 4780 | 0.001768 |
| 5259 | 5258 | 5258 | 0.001943 |
| 5735 | 5734 | 5735 | 0.002124 |
| 6214 | 6213 | 6214 | 0.002283 |
| 6690 | 6689 | 6690 | 0.002538 |
| 7167 | 7166 | 7167 | 0.002680 |
| 7646 | 7645 | 7646 | 0.002819 |
| 8126 | 8124 | 8126 | 0.003168 |
| 8600 | 8598 | 8600 | 0.003437 |
| 9079 | 9078 | 9079 | 0.003748 |
|
|
減算処理の演算時間も、加算処理と同様の条件で計測・プロットしています。こちらもほぼ線形で増加する結果となりました。加算も減算も処理の内容はほとんど変わらないのにも関わらず、減算処理の方が若干時間が長くなっています。
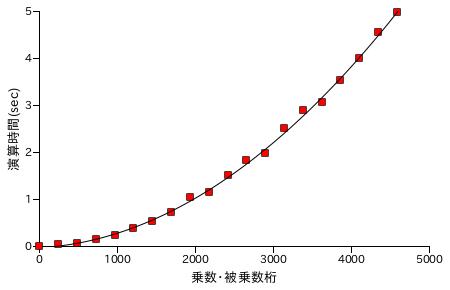
図表 6-3. 乗算処理時間の計測結果
| 被乗数の桁数 | 乗数の桁数 | 結果桁数 | 演算時間(sec) |
|---|
| 5 | 5 | 10 | 0.000698 |
| 247 | 246 | 492 | 0.03126 |
| 487 | 487 | 973 | 0.061997 |
| 729 | 728 | 1457 | 0.143154 |
| 969 | 969 | 1938 | 0.240540 |
| 1211 | 1210 | 2420 | 0.374879 |
| 1452 | 1452 | 2904 | 0.521545 |
| 1693 | 1692 | 3384 | 0.731898 |
| 1935 | 1933 | 3867 | 1.03327 |
| 2176 | 2174 | 4350 | 1.15794 |
| 2417 | 2416 | 4833 | 1.50425 |
| 2657 | 2656 | 5313 | 1.82364 |
| 2898 | 2898 | 5795 | 1.98289 |
| 3141 | 3137 | 6278 | 2.50876 |
| 3381 | 3381 | 6761 | 2.88496 |
| 3622 | 3621 | 7242 | 3.06465 |
| 3863 | 3862 | 7724 | 3.52556 |
| 4105 | 4104 | 8208 | 3.99606 |
| 4347 | 4346 | 8692 | 4.54119 |
| 4587 | 4585 | 9171 | 4.98249 |
|
|
乗算処理は桁数の 2 乗に比例しています。これは、N 桁 x 1 桁の処理を N 回繰り返しているためです。そのため、桁数の増加に伴い処理時間が急激に長くなっています。
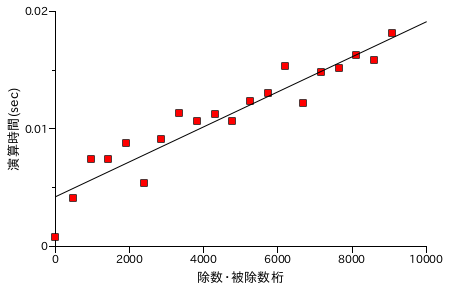
図表 6-4. 除算処理時間の計測結果 ( N 桁 / N 桁 )
| 被除数の桁数 | 除数の桁数 | 結果桁数 | 演算時間(sec) |
|---|
| 5 | 5 | 1 | 0.0008 |
| 483 | 483 | 1 | 0.004108 |
| 960 | 960 | 1 | 0.007439 |
| 1438 | 1437 | 1 | 0.007374 |
| 1916 | 1915 | 1 | 0.008738 |
| 2394 | 2393 | 1 | 0.005365 |
| 2871 | 2870 | 1 | 0.009079 |
| 3349 | 3346 | 4 | 0.011350 |
| 3826 | 3823 | 3 | 0.010661 |
| 4303 | 4302 | 1 | 0.011269 |
| 4783 | 4780 | 3 | 0.010663 |
| 5258 | 5257 | 1 | 0.012370 |
| 5735 | 5733 | 3 | 0.012983 |
| 6212 | 6211 | 2 | 0.015343 |
| 6692 | 6692 | 1 | 0.012201 |
| 7171 | 7170 | 2 | 0.014833 |
| 7647 | 7646 | 1 | 0.015115 |
| 8123 | 8122 | 1 | 0.016221 |
| 8600 | 8600 | 1 | 0.015785 |
| 9078 | 9077 | 1 | 0.018118 |
|
|
除算処理の場合、同じ桁どうしの演算では処理速度が桁数にほぼ比例するという結果になりました。ちなみに、被除数が除数より必ず大きくなるようにしてあるので、毎回必ず除算処理をしています。
図表 6-5. 除算処理時間の計測結果 ( 2N 桁 / N 桁 )
| 被除数の桁数 | 除数の桁数 | 結果桁数 | 演算時間(sec) |
|---|
| 5 | 5 | 1 | 0.000752 |
| 487 | 246 | 242 | 0.053846 |
| 970 | 487 | 483 | 0.105859 |
| 1452 | 729 | 724 | 0.168998 |
| 1932 | 970 | 963 | 0.333003 |
| 2418 | 1212 | 1207 | 0.465389 |
| 2899 | 1451 | 1448 | 0.892077 |
| 3382 | 1692 | 1690 | 0.972009 |
| 3864 | 1935 | 1930 | 1.32701 |
| 4343 | 2175 | 2169 | 1.41098 |
| 4831 | 2417 | 2414 | 1.80753 |
| 5307 | 2659 | 2648 | 2.49937 |
| 5794 | 2899 | 2895 | 3.67194 |
| 6275 | 3137 | 3138 | 3.81666 |
| 6757 | 3385 | 3373 | 3.78345 |
| 7240 | 3622 | 3618 | 5.45258 |
| 7720 | 3862 | 3859 | 5.78252 |
| 8203 | 4105 | 4099 | 4.76274 |
| 8682 | 4346 | 4336 | 6.68483 |
| 9167 | 4587 | 4581 | 5.91951 |
|
|
被除数の桁数を 2 倍にすると( X 軸は除数の桁数を示しています )、処理速度は桁数の 2 乗に比例するようになります。除算処理の場合、桁数だけではなく被除数と除数の間の桁数の差にも処理時間に影響を及ぼすことが分かります。
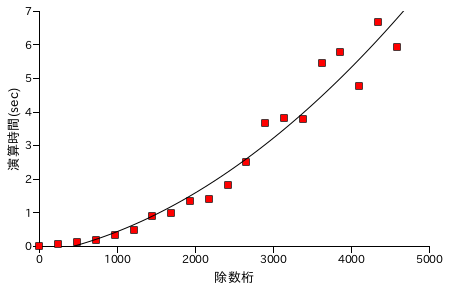
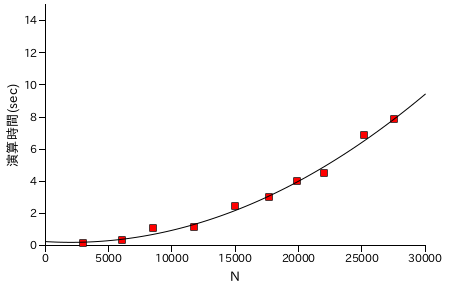
最後に階乗処理の処理時間を示します。プロットあたりの演算回数は 10 回とし、その合計時間が示されています。また、X 軸は桁数ではなく実際の数値です。最大でも 5 桁までの数値を使った処理ですが、結果は 10 万桁を越えます。
図表 6-6. 階乗 N! の計算時間の計測結果 ( 通常版 )
| N | N! の桁数 | 演算時間(sec) |
|---|
| 2991 | 9100 | 0.115487 |
| 6102 | 20452 | 0.299572 |
| 8543 | 29880 | 1.07194 |
| 11772 | 42812 | 1.08967 |
| 15058 | 56372 | 2.40826 |
| 17674 | 67395 | 2.99126 |
| 19878 | 76813 | 3.98860 |
| 22021 | 86073 | 4.50721 |
| 25185 | 99908 | 6.83351 |
| 27573 | 110466 | 7.85610 |
|
|
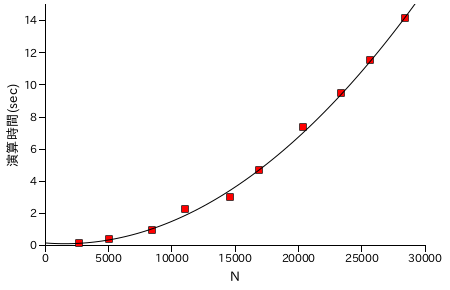
図表 6-7. 階乗 N! の計算時間の計測結果 ( 乗算処理を半分に )
| N | N! の桁数 | 演算時間(sec) |
|---|
| 2728 | 8191 | 0.142807 |
| 5078 | 16615 | 0.351828 |
| 8466 | 29578 | 0.959851 |
| 11064 | 39940 | 2.23642 |
| 14633 | 54599 | 2.98669 |
| 16955 | 64347 | 4.68748 |
| 20394 | 79034 | 7.34229 |
| 23422 | 92176 | 9.45060 |
| 25660 | 102001 | 11.5376 |
| 28426 | 114259 | 14.1327 |
|
|
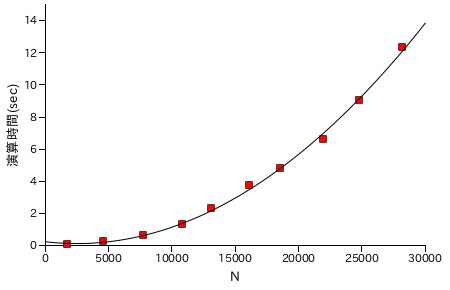
図表 6-8. 階乗 N! の計算時間の計測結果 ( 奇数の階乗計算のみ )
| N | N! の桁数 | 演算時間(sec) |
|---|
| 1769 | 4979 | 0.061755 |
| 4615 | 14909 | 0.231405 |
| 7757 | 26806 | 0.626648 |
| 10866 | 39140 | 1.28969 |
| 13148 | 48448 | 2.32581 |
| 16091 | 60703 | 3.74446 |
| 18579 | 71248 | 4.79235 |
| 21990 | 85938 | 6.60046 |
| 24799 | 98211 | 9.06189 |
| 28239 | 113427 | 12.3563 |
|
|
結果としては、普通に計算したバージョンが最も処理時間が短くなりました。乗算処理の回数を減らしても、内部の各桁の処理回数は減少しないことが主な理由ですが、奇数のみを計算する場合は 2 のべき乗分をビットシフトで行うので処理時間がもっと短くなってもよさそうな気もします。いずれにしても、さらに能力を上げるためには乗算処理そのものを改良する必要があるでしょう。
性能評価の結果、乗算処理が特に重いことが分かります。次回は、乗算処理の高速化を中心に話を進めたいと思います。
<参考文献>
- Oh!X 1992年10月号 X68000マシン後プログラミング 「大きな数の話」
- Sophere 様 - 多倍長演算について
- Wikipedia

![[Go Back]](../images/back1.png) 前に戻る
前に戻る![[Back to HOME]](../images/home1.png) タイトルに戻る
タイトルに戻る