今まで、整数を演算するための処理方法を扱ってきました。しかし、数値計算を行うときに扱う数は整数だけに限らず、小数や分数など多岐に渡ります。今回は、演算できる数の範囲を広げ、有理数や無理数による演算方法を紹介したいと思います。
まずは、数の種類について簡単な表にまとめます。[]内は、その数に対する略語になります。
| 自然数(正の整数)[N] | 整数[Z] | 有理数[Q] | 実数[R] | 複素数[C] |
| 0 | ||||
| 負の整数 | ||||
| 有限小数 | 分数 | |||
| 循環小数 | ||||
| 代数的無理数 | 無理数 | |||
| 超越数 | ||||
| 虚数 | ||||
数の分類方法は、他にも様々なものがあります。例えば自然数一つにしても、素数と合成数、偶数と奇数などに分類できます。
素数の概念は複素数にも存在し、それは「ガウス素数(Gaussian Primes)」と呼ばれます。実数部と虚数部のいずれも整数となる複素数を「ガウス整数(Gaussian Integer)」といい、その中で、ガウス整数における単数 ( 1, -1, i, -i ) 及び単数と自分自身の積 ( ガウス整数 α に対し、α, -α, iα, -iα ) のみで割り切れる ( 除算結果がガウス整数となる ) ものをガウス素数といいます。5 という数値は自然数としては素数になりますが、ガウス整数としては 5 = ( 2 + i )( 2 - i ) なのでガウス素数ではありません。
0 を自然数に含めるか含めないかは分野ごとに様々らしく、集合論や論理学などでは 0 を含めることが多い一方、数論の分野では含めない場合が多いようです。表の中では自然数を「正の整数」として 0 は除外しています。
有理数 ( Rational Number ) は、二つの整数 a, b を使って、その比 a / b ( つまり分数 ) で表される数を意味します ( 但し、分母の b は 0 以外の整数でなければなりません )。比 ( Ratio ) を持つ数という意味で英語では Rational Number といいますが、なぜか日本語では「有理数」と訳されています。
一方の無理数 ( Irrational Number ) は、整数の比で表されない数のことを指します。無理数の存在は、古代ギリシャの有名な数学者である「ピタゴラス ( Pythagoras )」の時代にすでに発見されていたようです。しかし、ピタゴラスはその存在を否定し、√2 が整数の比で表せないことを発見した「ヒッパソス ( Hippasus )」という弟子に対して、溺死による死刑を言い渡したという言い伝えもあります。その後、「ユークリッド ( Euclid )」は「背理法」を使って、√2 が無理数であることを証明しました。
有理数と無理数を合わせて「実数 ( Real Number )」といいます。任意の実数は数直線上の点で表すことができ、その位置関係によって大小関係を決めることができます。それに対し、複素数は実数部と虚数部を持つため数直線では表すことができず、「複素平面 ( Complex Plane )」または「ガウス平面 ( Gaussian Plane )」と呼ばれる平面上の点で表します。横軸が実数の大きさを表す実軸、縦軸が虚数の大きさを表す虚軸となり、複素数 z = a + bi は点 ( a, b ) で示されます。また、原点から点 ( a, b ) までの距離 ( a2 + b2 )1/2 を z の絶対値といいます。
有理数を小数で表現したとき、「有限小数」と「循環小数」の二種類に分類することができます。「有限小数」とは、有限桁の数字で表現できる小数のことを指し、例として 1 / 4 = 0.25 などがあります。「循環小数」は、同じ数字の並びが無限に続く小数のことを指し、例えば 1 / 7 = 0.14285714285714... などがそれに該当します ( 142857 が続いていることがわかると思います )。ある分数が有限小数になるか循環小数になるかは、数値を表記するときに利用している基数に依存します。例えば 1 / 7 は、基数として 7 を使った場合 0.1 と表すことができるため有限小数となります。逆に 10 進表記の 0.1 は分数では 1 / 10 となり、これを 2 進数で表すと 1 / 1010 となるため、小数で表記すると 0.00011001100... で循環小数になります。
循環小数は、繰り返す部分の先頭と末尾に "." を付けて表現します。
. .
1/7 = 0.14285714285714... = 0.142857
. .
1/14 = 0.0714285714285... = 0.0714285
以下に、有理数をクラス定義したサンプルコード(一部)を示します。
namespace BigNum { /* CalcGCD : ユークリッドの互除法を使った最大公約数の計算 x, y : 最大公約数を求める二数 */ template< class T > T CalcGCD( T x, T y ) { if ( x < y ) std::swap( x, y ); if ( y == 0 ) return( x ); do { T r = x % y; x = y; y = r; } while ( y != 0 ); return( x ); } /* Reduce : 約分(最大公約数で二数を割る) x, y : 対象の二数へのポインタ */ template< class T > void Reduce( T* x, T* y ) { T gcd = CalcGCD( *x, *y ); if ( gcd > 1 ) { *x /= gcd; *y /= gcd; } } /** BugNum::Rational : 多倍長有理数 多倍長整数を分子・分母とする有理数の型 **/ class Rational { bool isPos_; // 符号は正か ? Unsigned a_; // 分子 Unsigned b_; // 分母 public: // コンストラクタ Rational( const Unsigned& a = 0, const Unsigned& b = 1, bool isPos = true ); // 小数表記で文字列を返す std::string circulator() const; // 無効値判定 bool isNaN() const { return( b_ == 0 ); } }; /* Rational コンストラクタ(分子・分母指定) a : 分子 b : 分母 isPos : 符号は正か */ Rational::Rational( const Unsigned& a, const Unsigned& b, bool isPos ) { if ( a.isNaN() || b.isNaN() ) { b_ = 0; } else { a_ = a; b_ = b; isPos_ = isPos; } Reduce( &a_, &b_ ); } /* Rational::circulator : 小数表記に変換した文字列を返す 循環小数の場合、循環節を[]で示す */ string Rational::circulator() const { if ( isNaN() ) return( "NaN" ); Unsigned num( a_ ); std::stringstream ss; ss << ( ( isPos_ ) ? "+" : "-" ); // 商と余りを求める Unsigned r; num.div( b_, &r ); // 整数部まで出力 ss << num; if ( r != 0 ) ss << "."; // 小数部の計算 std::map< Unsigned, std::vector< Unsigned >::size_type > flag; // 余りと位置を記録するmap std::vector< Unsigned > numVec; // 小数部の数値を記録するvector std::vector< Unsigned >::size_type i = 0; while ( r != 0 ) { if ( flag.find( r ) != flag.end() ) break; flag[r] = i++; num = r * 10; num.div( b_, &r ); numVec.push_back( num ); } // 小数部の出力 for ( i = 0 ; i < numVec.size() ; ++i ) { if ( r != 0 && i == ( flag.find( r ) )->second ) ss << "["; ss << numVec[i]; } if ( r != 0 ) ss << "]"; return( ss.str() ); } }
circulator は分数を小数に変換するメンバ関数で、循環小数の場合は循環節を"[]"で区切って表現します。分子を分母で割って商 ( これが整数部の値となります ) と余りを求め、余りに 10 を掛けては分母で割る操作を、余りがゼロになるか、同じ値の余りが再度出現するまで繰り返します。同じ値の余りが出現した場合、その先は、前に同値の余りが出現した位置からの数列が繰り返されることになります。余りの値は分母より小さいので、処理を繰り返せば必ず同じ値が出現します。これが、有理数が有限小数か循環小数になる理由になります。
下表は、1 / 7 に対して上記操作を行った結果を示したものです。一行目は整数部分を求めた結果です。黄色く塗られたセルの部分 ( 余りが 3 となる箇所 ) が循環節の開始部分であり、同じ値が繰り返される様子がよくわかると思います。
| 被除数 | 商 | 余り |
|---|---|---|
| - | 0. | 1 |
| 10 | 1 | 3 |
| 30 | 4 | 2 |
| 20 | 2 | 6 |
| 60 | 8 | 4 |
| 40 | 5 | 5 |
| 50 | 7 | 1 |
| 10 | 1 | 3 |
| 30 | 4 | 2 |
| 20 | 2 | 6 |
| 60 | 8 | 4 |
| 40 | 5 | 5 |
| : | : | : |
逆に、循環小数を分数に変換することもできます。次の循環小数で試してみましょう。
. .
x = 0.1492
循環節の部分を一つだけ左側へ移動するように 10 のべき乗倍 ( この例では 1000 倍 ) します。
. .
1000x = 149.2492
ここから x の値を引きます。
. .
1000x = 149.2492
. .
-) x = 0.1492
---------------------
999x = 149.1
循環節の部分はちょうど打ち消しあう形になるので、右辺は有限小数となります。あとは x の係数で除算をすれば、求めようとしていた分数を得ることができます。
x = 149.1 / 999 = 1491 / 9990 = 497 / 3330
小数から分数への変換用サンプル・プログラムを以下に示します。
namespace BigNum { /* LTrim : 左側の空白をスキップした位置を返す str : 対象の文字列 s : チェック開始位置 戻り値 : 空白をスキップした最初の文字の位置(全て空白なら文字列長と等しい) */ string::size_type LTrim( const string& str, string::size_type s ) { while ( s < str.length() ) { if ( ! isspace( str[s] ) ) break; ++s; } return( s ); } /* RTrim : 右側の空白をスキップした位置を返す str : 対象の文字列 e : チェック開始位置(チェック対象の末尾の次の位置) 戻り値 : 空白をスキップした末尾の次の文字の位置(全て空白ならゼロと等しい) */ string::size_type RTrim( const string& str, string::size_type e ) { if ( e > str.length() ) e = str.length(); while ( e > 0 ) { if ( ! isspace( str[e - 1] ) ) break; --e; } return( e ); } /* Str2Num : 文字列→整数値変換 str : 文字列 e : 読み込み開始位置・終了位置 + 1 num : 変換結果(絶対値)へのポインタ isPos : 変換結果(符号)へのポインタ (+/-)[0-9] 形式で、空白文字はチェックしない isPos が NULL ポインタの場合は 符号は取得しない 戻り値 : 文字列が数値変換できなかった場合は false を返す */ bool Str2Num( const string& str, string::size_type s, string::size_type e, Unsigned* num, bool* isPos ) { if ( s >= e ) return( false ); // 符号のチェック if ( isPos != 0 ) { if ( str[s] == '-' || str[s] == '+' ) { if ( str[s] == '-' ) *isPos = false; ++s; if ( s >= e ) return( false ); } else { *isPos = true; } } *num = Unsigned( str.substr( s, e - s ) ); return( ! num->isNaN() ); } /* Rational::toDecimal : 小数表記の文字列から有理数を構築 const string& s : 文字列 */ void Rational::toDecimal( const string& s ) { b_ = 0; // NaN にしておく string::size_type sp = LTrim( s, 0 ); // 開始位置 string::size_type ep = RTrim( s, s.length() ); // 末尾の次の位置 string::size_type dp = s.find( '.' ); // 小数点 string::size_type rdp; // 循環節の開始位置 // 整数表記の場合 if ( dp == string::npos || dp + 1 == ep ) { if ( dp == string::npos ) dp = ep; if ( ! Str2Num( s, sp, dp, &a_, &isPos_ ) ) return; b_ = 1; return; } // 有限小数を取得 if ( ! Str2Num( s, sp, dp, &a_, &isPos_ ) ) return; for ( rdp = dp + 1 ; rdp < ep ; ++rdp ) { if ( s[rdp] == '[' ) break; if ( ! isdigit( s[rdp] ) ) return; } if ( rdp > dp + 1 ) { Unsigned fdA; // 有限小数部 if ( ! Str2Num( s, dp + 1, rdp, &fdA, 0 ) ) return; b_ = 10; b_.pow( rdp - dp - 1 ); a_ = a_ * b_ + fdA; } // 循環節を取得 if ( rdp < ep ) { Unsigned rdA; // 循環小数部 if ( s[ep - 1] != ']' ) return; if ( ! Str2Num( s, rdp + 1, ep - 1, &rdA, 0 ) ) return; if ( b_ == 0 ) b_ = 1; Unsigned rdB( 10 ); rdB = ( rdB.pow( ep - rdp - 2 ) - 1 ) * b_; Rational rd( rdA, rdB, true ); if ( isPos_ ) operator+=( rd ); else operator-=( rd ); } Reduce( &a_, &b_ ); } }
小数表記の文字列から有理数へ変換するためのメンバ関数は toDecimal です。ここでも循環節は "[]" で区切って表現します。最初に小数部が存在するかをチェックし、小数部があれば次に循環節が存在するかをチェックして、有限小数部と循環節のそれぞれで有理数へ変換します。有限小数部は、小数点を無視して整数値で表した数を 10 の「小数部の桁数」乗で割れば求めることができます。また循環節は、小数第一位に初めてゼロ以外の数値があるように桁を調整した上で、10 の「循環節にある数値の個数」乗から 1 を引いた値で割ることで得られます ( 何故このやり方で得られるのかについては、循環節の部分だけに対して循環小数から分数への変換操作を試せば理解できると思います )。最後に二つの有理数の和を計算すれば結果が得られます。
以下に、上記アルゴリズムで小数を有理数変換した例を示します。
. .
x = 0.1492
有限小数部 0.1 = 1 / 10
. . . .
循環節 0.0492 = 0.492 x 1 / 10
= ( 492 / 999 ) x ( 1 / 10 )
= 492 / 9990
x = 1 / 10 + 492 / 9990
= ( 999 + 492 ) / 9990
= 1491 / 9990
= 497 / 3330
このアルゴリズムから、全ての循環小数は必ず有理数へ変換できることが分かります。
ところで、
.
1 / 3 = 0.3
の両辺に 3 を掛けると
.
1 = 0.9
という結果になります。実際、
.
x = 0.9
.
-) 10x = 9.9
-------------
9x = 9
x = 1
と計算できるため、0.9999... = 1 という結論になります。
初項が a、公比が r の「等比数列 ( Geometric Progression )」 arn の第 n 項までの和を S としたとき、
| S | = | a + | ar + ar2 + ar3 + ... + arn |
| rS | = | ar + ar2 + ar3 + ... + arn + arn+1 | |
| (1 - r)S | = | a - | arn+1 |
なので、S = a( 1 - rn+1 ) / ( 1 - r ) になります。これを「等比級数 ( Geometric Series )」といいます。| r | < 1 のとき、n→∞ に対して S は収束し、「無限級数 ( Infinite Geometric Series )」 a / ( 1 - r ) になります。0.999... = 9 / 10 + ( 9 / 10 )・( 1 / 10 ) + ( 9 / 10 )・( 1 / 102 ) + ... なので、これは初項 9 / 10、公比 1 / 10 の無限級数とみなすことができ、その値は
なので、やはりここでも 0.9999... = 1 は正しいことになります。
9 が無限に続く場合、0.9999... は 1 に「無限に」近づくことになります。ここでもし両者が異なるとした場合、その間にすき間が生じることになり、「実数の連続性」に反してしまうことになります。
最後に、四則演算子と比較演算子のサンプル・プログラムを示しておきます。
namespace BigNum { /* 比較演算子の多重定義 num : 比較対象の有理数 大小比較は以下のように行う a/b < num.a/num.b → a*num.b < num.a*b a/b > num.a/num.b → a*num.b > num.a*b 少なくとも一方が無効値なら常に false を返す */ bool Rational::operator==( const Rational& num ) const { if ( isNaN() || num.isNaN() ) return( false ); return( a_ == num.a_ && b_ == num.b_ && isPos_ == num.isPos_ ); } bool Rational::operator!=( const Rational& num ) const { if ( isNaN() || num.isNaN() ) return( false ); return( ! operator==( num ) ); } bool Rational::operator<( const Rational& num ) const { if ( isNaN() || num.isNaN() ) return( false ); if ( isPos_ && ( ! num.isPos_ ) ) return( false ); if ( ( ! isPos_ ) && num.isPos_ ) return( true ); return( ( isPos_ ) ? a_ * num.b_ < num.a_ * b_ : a_ * num.b_ > num.a_ * b_ ); } bool Rational::operator>( const Rational& num ) const { if ( isNaN() || num.isNaN() ) return( false ); if ( isPos_ && ( ! num.isPos_ ) ) return( true ); if ( ( ! isPos_ ) && num.isPos_ ) return( false ); return( ( isPos_ ) ? a_ * num.b_ > num.a_ * b_ : a_ * num.b_ < num.a_ * b_ ); } bool Rational::operator<=( const Rational& num ) const { if ( isNaN() || num.isNaN() ) return( false ); return( ! operator>( num ) ); } bool Rational::operator>=( const Rational& num ) const { if ( isNaN() || num.isNaN() ) return( false ); return( ! operator<( num ) ); } /* Rational::calcNumerator : 分子の加算・減算処理 ( operator+=,-=用 ) num : 演算対象の有理数 cmpSign : 二数の符号比較結果 ( += の場合異なる場合が true,-= の場合同じ場合が true ) */ void Rational::calcNumerator( const Rational& num, bool cmpSign ) { Unsigned gcd = CalcGCD( b_, num.b_ ); a_ *= num.b_ / gcd; Unsigned numA = num.a_ * b_ / gcd; if ( cmpSign ) { // 減算処理 if ( a_ < numA ) { a_ = numA - a_; isPos_ = ! isPos_; } else { a_ -= numA; } } else { // 加算処理 a_ += numA; } b_ *= num.b_ / gcd; Reduce( &a_, &b_ ); } /* operator+=(-=)(*=)(/=) : 四則演算子の多重定義 const Rational& num : 演算対象の有理数 */ Rational& Rational::operator+=( const Rational& num ) { if ( this == &num ) { a_ *= 2; Reduce( &a_, &b_ ); return( *this ); } calcNumerator( num, isPos_ != num.isPos_ ); return( *this ); } Rational& Rational::operator-=( const Rational& num ) { if ( this == &num ) { a_ = 0; return( *this ); } calcNumerator( num, isPos_ == num.isPos_ ); return( *this ); } Rational& Rational::operator*=( const Rational& num ) { a_ *= num.a_; b_ *= num.b_; isPos_ = ( isPos_ == num.isPos_ ); Reduce( &a_, &b_ ); return( *this ); } Rational& Rational::operator/=( const Rational& num ) { if ( this == &num ) { a_ = b_ = 1; return( *this ); } if ( isNaN() || num.isNaN() ) { b_ = 0; return( *this ); } a_ *= num.b_; b_ *= num.a_; isPos_ = ( isPos_ == num.isPos_ ); Reduce( &a_, &b_ ); return( *this ); } }
有理数どうしの大小比較を行うのは簡単で、"a/b" と "c/d" を比較する代わりに "ad" と "bc" を比較します。また、加減算は手計算の場合と同様に通分して計算することで実現できます。
無理数を小数で表すと、小数部に繰り返しのない無限小数となるため、完全な形で小数表記をすることは不可能です。しかし「連分数 ( Continued Fraction )」を利用することによって、規則性を持たせることが可能になります。
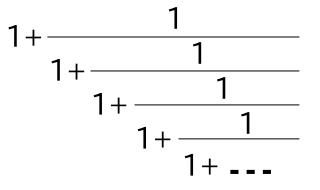
連分数は、分母の中にさらに分数が含まれるような分数の表記法を指します。例えば、
 |
は「黄金比 ( Golden Ratio )」 φ ( = ( √5 + 1 ) / 2 ) の連分数表現になります。この書き方は縦方向に場所を取るため、次のような書き方をする場合もあります ( 符号 "+" の位置に注意してください )。
 |
さらに、ここでは次のように "[]" を使って、分母側に式があることを強調して表記するようにします。
また、分子が全て 1 である連分数は「正則連分数 ( Regular Continued Fraction )」と呼ばれ、分子の値を省略して次のように記述することができます。";" で整数部分と分数部分が区切られていることに注意してください。
まずは連分数を使って平方根を表現してみます。未知数 a ( > 0 ) に対し、a を越えない最大の整数 ( ガウスの記号を用いると ⌊a⌋ ) を C としたとき、a - C を連分数で次のように表記することができます。
a - C = ( a - C )( a + C ) / ( a + C )
= ( a - C )( a + C ) / [ 2C + ( a - C ) ]
= ( a - C )( a + C ) / [ 2C + ( a - C )( a + C ) / ( a + C ) ]
= ( a - C )( a + C ) / [ 2C + ( a - C )( a + C ) / 2C + ( a - C ) ]
= ( a - C )( a + C ) / [ 2C + ( a - C )( a + C ) / [ 2C + ( a - C )( a + C ) / ( a + C ) ] ]
= ... = ( a - C )( a + C ) / [ 2C + ( a - C )( a + C ) / [ 2C + ( a - C )( a + C ) / [ 2C + ...
( a - C )( a + C ) = a2 - C2 より、a が平方根 √x だったとき、上式は次のようになります。
例えば √2 は連分数で次のように表記できます。
連分数の周期性を利用した平方根の計算用サンプル・プログラムを以下に示します。
/* CF_sqrt : 連分数を用いて平方根を求める x : 対象の数 (符号なし整数型 UI を想定) 戻り値 : x の平方根 ( 浮動小数点型 Res を想定) */ template< class Res, class UI > Res CF_sqrt( UI x ) { // C = [x]を求める UI c; for ( c = 1 ; c * c <= x ; ++c ); --c; if ( x == c * c ) return( c ); // ちょうど割り切れた Res r( x - c * c ); // [x]とC^2の誤差 Res c2( 2 * c ); // 2C Res num( r / c2 ); // [x] - C^2 / 2C // 有効桁数の限界まで計算を繰り返す for (;;) { Res d( r / ( num + c2 ) ); if ( std::abs( d - num ) < std::numeric_limits< Res >::epsilon() ) break; num = d; } num += c; return( num ); }
連分数は、ユークリッドの互助法を利用して構築することができます。例えば有理数 31 / 11 に対してユークリッドの互助法を使うと
31 = 2 * 11 + 9 11 = 1 * 9 + 2 9 = 4 * 2 + 1 2 = 2 * 1 + 0
となるため、
31 / 11 = ( 2 * 11 + 9 ) / 11
= 2 + 1 / [ 11 / 9 ]
= 2 + 1 / [ ( 1 * 9 + 2 ) / 9 ]
= 2 + 1 / [ 1 + 1 / [ 9 / 2 ] ]
= 2 + 1 / [ 1 + 1 / [ ( 4 * 2 + 1 ) / 2 ] ]
= 2 + 1 / [ 1 + 1 / [ 4 + 1 / 2 ] ]
と連分数に変換することができます。これと同じことをネイピア数 e と 1 に対して試してみると、次のようになります。
e = 2 * 1 + ( e - 2 ) [ 2.7182818285 = 2 * 1 + 0.7182818285 ]
1 = 1 * ( e - 2 ) + ( 3 - e ) [ 1 = 1 * 0.7182818285 + 0.2817181715 ]
e - 2 = 2 * ( 3 - e ) + ( 3e - 8 ) [ 0.7182818285 = 2 * 0.2817181715 + 0.1548454854 ]
3 - e = 1 * ( 3e - 8 ) + ( 11 - 4e ) [ 0.2817181715 = 1 * 0.1548454854 + 0.1268726862 ]
3e - 8 = 1 * ( 11 - 4e ) + ( 7e - 19 ) [ 0.1548454854 = 1 * 0.1268726862 + 0.0279727992 ]
11 - 4e = 4 * ( 7e - 19 ) + ( 87 - 32e ) [ 0.1268726862 = 4 * 0.0279727992 + 0.0149814893 ]
7e - 19 = 1 * ( 87 - 32e ) + ( 39e - 106 ) [ 0.0279727992 = 1 * 0.0149814893 + 0.0129913099 ]
87 - 32e = 1 * ( 39e - 106 ) + ( 193 - 71e ) [ 0.0149814893 = 1 * 0.0129913099 + 0.0019901794 ]
39e - 106 = 6 * ( 193 - 71e ) + ( 465e - 1264 ) [ 0.0129913099 = 6 * 0.0019901794 + 0.0010502335 ]
:
この結果から、ネイピア数の連分数が以下の形になることが予想でき、実際にそうなります。
e = 2 + 1 / [ 1 + 1 / [ 2 + 1 / [ 1 + 1 / [ 1 + 1 / [ 4 + 1 / [ 1 + 1 / [ 1 + 1 / [ 6 ... = [ 2 ; 1, 2, 1, 1, 4, 1, 1, 6, 1, ..., 1, 2n, 1, ,,, ]
円周率 π で同様の操作を行ってみます。
π = 3 * 1 + ( π - 3 ) [ 3.1415926536 = 3 * 1 + 0.1415926536 ]
1 = 7 * ( π - 3 ) + ( 22 - 7π ) [ 1 = 7 * 0.1415926536 + 0.0088514249 ]
π - 3 = 15 * ( 22 - 7π ) + ( 106π - 333 ) [ 0.1415926536 = 15 * 0.0088514249 + 0.0088212805 ]
22 - 7π = 1 * ( 106π - 333 ) + ( 355 - 113π ) [ 0.0088514249 = 1 * 0.0088212805 + 0.0000301444 ]
106π - 333 = 292 * ( 355 - 113π ) + ( 33102π - 103993 ) [ 0.0088212805 = 292 * 0.0000301444 + 0.0000191293 ]
355 - 113π = 1 * ( 33102π - 103993 ) + ( 104348 - 33215π ) [ 0.0000301444 = 1 * 0.0000191293 + 0.0000110150 ]
33102π - 103993 = 1 * ( 104348 - 33215π ) + ( 66317π - 208341 ) [ 0.0000191293 = 1 * 0.0000110150 + 0.0000081143 ]
104348 - 33215π = 1 * ( 66317π - 208341 ) + ( 312689 - 99532π ) [ 0.0000110150 = 1 * 0.0000081143 + 0.0000029007 ]
:
残念ながら、こちらは規則性がありません。しかし規則性のある連分数として、次のようなものがあります。
黄金比・ネイピア数・円周率を連分数を使って計算するためのサンプル・プログラムを以下に示します。
/* CF_goldnum : 連分数を用いて黄金比 φ を求める init : 演算精度 (演算回数 符号なし整数型 UI を想定) 戻り値 : 黄金比 (浮動小数点型 Res を想定) */ template< class Res > Res CF_goldnum() { Res ans( 1 ); for ( ; ; ) { Res buff( 1 / ( ans + 1 ) ); if ( std::abs( buff - ans ) <= std::numeric_limits< Res >::epsilon() ) break; ans = buff; } ans += 1; return( ans ); } /* CF_napier : 連分数を用いてネイピア数 e を求める init : 演算精度(init*2を初期値として連分数を計算 符号なし整数型 UI を想定) 戻り値 : ネイピア数 (浮動小数点型 Res を想定) */ template< class Res, class UI > Res CF_napier( UI init ) { Res ans = Res(); for ( init *= 2 ; init >= 2 ; init -= 2 ) { ans = 1 / ( ans + 1 ); ans = 1 / ( ans + init ); ans = 1 / ( ans + 1 ); } ans += 2; return( ans ); } /* CF_pi : 連分数を用いて円周率 π を求める init : 演算精度(initを初期値として連分数を計算 符号なし整数型 UI を想定) 戻り値 : ネイピア数 (浮動小数点型 Res を想定) */ template< class Res, class UI > Res CF_pi( UI init ) { Res ans( 2 * init + 1 ); for ( UI i = init ; i > 0 ; --i ) ans = ( 2 * i - 1 ) + ( i * i ) / ans; ans = 4 / ans; return( ans ); }
計算は、連分数に対して右側から ( 分母側に連なるより深いところから ) 行う必要があるので、ネイピア数と円周率は初期値を渡してそこから左側へ順番に計算をしていくようになっています。初期値を大きくするほど精度が上がることになります。
連分数を利用することによって、いくらでも無理数に近い有理数を得ることができます。しかし、この操作は無限に続くため、完全に等しい有理数を求めることは不可能です。
最後に、インドの天才数学者「ラマヌジャン ( Srinivasa Aiyangar Ramanujan )」による、黄金数 φ・ネイピア数 e・円周率 π を含んだ不思議な連分数を紹介します。
連分数の例として最初に示した黄金比は、最も美しいとされる比率を表し、パルテノン神殿や凱旋門・ミロのビーナス像など、建築物や芸術作品などでも利用されています。黄金比の定義は、線分を二つに分割したときに、長い線分と短い線分の比が、線分全体と長い線分との比と等しくなる時の比になります。長い線分の長さを φ、短い線分の長さを 1 としたとき、
φ : 1 = φ + 1 : φ より
φ = ( φ + 1 ) / φ
になります。この式を変形すると
φ2 = φ + 1 より
φ2 - φ - 1 = 0
になり、この二次方程式を解くと、φ = ( 1 ± √5 ) / 2 となります。φ > 0 を満たす必要があるので、黄金比の値は
になります。
「フィボナッチ数列 ( Fibonacci Numbers )」の隣り合う項の比は黄金比に収束します。フィボナッチ数列は、イタリアの数学者「レオナルド・フィボナッチ ( Leonardo Fibonacci )」によって考案された次の問題で登場する数列です。
第一の月に、ウサギの赤ん坊のつがいから始まる。
一年後にはウサギは何組になるか ?
一ヶ月後、それらは大人になる。
次の月、大人のウサギは赤ん坊を一つがい産む。
以後一ヶ月ごとに、大人のつがいはいずれも一つがいの赤ん坊を産み、赤ん坊のつがいは大人になる。
第一の月から順番に数を数えると、次のようになります。
| 月 | 赤ん坊のつがい | 大人のつがい | 合計 |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 2 | 0 | 1 | 1 |
| 3 | 1 | 1 | 2 |
| 4 | 1 | 2 | 3 |
| 5 | 2 | 3 | 5 |
| 6 | 3 | 5 | 8 |
| 7 | 5 | 8 | 13 |
| 8 | 8 | 13 | 21 |
| 9 | 13 | 21 | 34 |
| 10 | 21 | 34 | 55 |
| 11 | 34 | 55 | 89 |
| 12 | 55 | 89 | 144 |
| 1 年後 | 89 | 144 | 233 |
毎月、大人のつがいの数だけ赤ん坊のつがいが産まれ、先月の赤ん坊のつがいの数だけ大人のつがいが増えるので、今月のつがいの合計は
で計算することができます。先月の大人のつがいの数 = 先々月のつがいの合計 なので、上式は
と書き換えることができ、第 n 月のつがいの合計を Fn としたとき、
で求めることができることになります。これがフィボナッチ数列の漸化式になります。
フィボナッチ数列を計算し、隣り合う項の比 Fn / Fn-1 を求めるためのサンプル・プログラムを以下に示します。
/* Fibonacci : フィボナッチ数列と隣り合う項の比 Fn/Fn-1 を求める テンプレート引数 D は比の型を表す。 cnt : 求める項の数 (符号なし整数型 UI を想定) */ template< class D, class UI > void Fibonacci( UI cnt ) { UI f0( 1 ); UI f1( 1 ); std::cout << "F1 = " << f0 << std::endl; std::cout << "F2 = " << f1 << " : F2/F1 = " << D( f1 ) / D( f0 ) << std::endl; for ( UI i( 2 ) ; i < cnt ; ++i ) { UI f2( f0 + f1 ); std::cout << "F" << i + 1 << " = " << f2 << " : F" << i + 1 << "/" << "F" << i << " = " << D( f2 ) / D( f1 ) << std::endl; f0 = f1; f1 = f2; } }
このプログラムを使って、フィボナッチ数列と隣り合う項の比を計算した結果を以下に示します。
| n | Fn | Fn/Fn-1 |
|---|---|---|
| 1 | 1 | - |
| 2 | 1 | 1.00000 |
| 3 | 2 | 2.00000 |
| 4 | 3 | 1.50000 |
| 5 | 5 | 1.66667 |
| 6 | 8 | 1.60000 |
| 7 | 13 | 1.62500 |
| 8 | 21 | 1.61538 |
| 9 | 34 | 1.61905 |
| 10 | 55 | 1.61765 |
| 11 | 89 | 1.61818 |
| 12 | 144 | 1.61798 |
| 13 | 233 | 1.61806 |
| 14 | 377 | 1.61803 |
| 15 | 610 | 1.61804 |
| 16 | 987 | 1.61803 |
| 17 | 1597 | 1.61803 |
| 18 | 2584 | 1.61803 |
| 19 | 4181 | 1.61803 |
| 20 | 6765 | 1.61803 |
| 21 | 10946 | 1.61803 |
| 22 | 17711 | 1.61803 |
| 23 | 28657 | 1.61803 |
| 24 | 46368 | 1.61803 |
| 25 | 75025 | 1.61803 |
| 26 | 121393 | 1.61803 |
| 27 | 196418 | 1.61803 |
| 28 | 317811 | 1.61803 |
| 29 | 514229 | 1.61803 |
| 30 | 832040 | 1.61803 |
黄金比 φ = ( 1 + √5 ) / 2 ≅ ( 1 + 2.23607 ) / 2 = 1.61803 であり、隣り合う項の比は確かに黄金比に収束するようです。
とりあえず、Fn / Fn-1 ≅ α を満たす未知の定数 α が存在するものと仮定すると、
同様に、Fn-1 ≅ α Fn-2 が成り立つので
これらを、フィボナッチ数列の漸化式 Fn = Fn-1 + Fn-2 に代入すると
Fn-2 で両辺を割ると、未知数 α は二次方程式
の解となり、これはまさしく黄金比 φ を解くための方程式そのものです。解 α は二つ存在し、その解は ( 1 ± √5 ) / 2 になります。どちらの解も、上記二次方程式の解になることから、上式の両辺に αn-2 を掛けて少し変形させた以下の式
を満たします。これはフィボナッチ数列の漸化式とよく似た構成を持っています。ここで、
として、
とおいたとき ( 但し、c1, c2 は任意の定数 )、
| Hn-1 + Hn-2 | = | ( c1α1n-1 + c2α2n-1 ) + ( c1α1n-2 + c2α2n-2 ) |
| = | c1( α1n-1 + α1n-2 ) + c2( α2n-1 α2n-2 ) | |
| = | c1α1n + c2α2n | |
| = | Hn |
になるので、フィボナッチ数列の漸化式を満たします。一番目と二番目のフィボナッチ数はともに 1 なので、
を満たす c1, c2 の値を計算すると、c1 = 1 / √5、c2 = -1 / √5 となり、以上をまとめると、フィボナッチ数列の第 n 項は「ビネの公式 ( Binet's formula )」と呼ばれる次の式で得ることができます。
( 1 - √5 ) / 2 の分子を整数化するため、分子と分母に 1 + √5 を掛けると、
となるので、ビネの公式は黄金数 φ を使って次のようにも表すことができます。
φ > 1 より ( 1 / φ ) < 1 なので、( -φ )-nは n が大きい場合に無視できるほど小さくなります。よって、n 番めのフィボナッチ数は近似的に
で計算することができます。隣り合う項の比が黄金数に収束する理由もこのことから理解できると思います。
ところで、黄金比の連分数表現は、二次方程式 x2 - x - 1 = 0 の解であることを利用して得ることができます。この方程式を、次のように変形します。
x2 = x + 1 より
x = 1 + 1/x
この式の右辺にある x は、やはりこの式の右辺に置き換えることが可能です。
置き換えをしても x が消えるわけではないため、これだけで x の値を求められるわけではありません。しかし、この操作は何回でも続けることが可能です。
このようにして、黄金比の連分数表現を得ることができます。
「2)有理数の表現方法」にて、初項 a、公比 r の等比級数の和の公式
を紹介しました。さらに、|r| < 1 のとき、n→∞ に対して S は収束し、
になります。公比 r を変数 x とみなしたとき、この級数は、定義域 |x| < 1 における関数として定義することができ、特に初項が 1 の時は
と変形することができます。不思議なことに、定義域 |x| < 1 においては、関数 1 / ( 1 - x ) が無限級数の形に変換できることになります。それでは、他の任意の関数でも級数の形に変換できるのでしょうか ?
ここで、微分可能な任意の関数 f(x) を級数の形に変換することができるかを検討してみます。まず、関数 f(x) が、以下のように第 n 項までの級数の形に書けると仮定します。
上式より、f(x) の高階導関数 f(k)(x) を、n + 1 階まで求めてみます。
| f(0)(x) | = | a0 + a1x + a2x2 + a3x3 + a4x4 + ... + anxn |
| f(1)(x) | = | a1 + 2a2x + 3a3x2 + 4a4x3 + ... + nanxn-1 |
| f(2)(x) | = | 2a2 + 3・2a3x + 4・3a4x2 + ... + n(n-1)anxn-2 |
| f(3)(x) | = | 3・2a3 + 4・3・2a4x + ... + n(n-1)(n-2)anxn-3 |
| : | ||
| f(k)(x) | = | k・k-1・...・2ak + k+1・k・...・2ak+1x + ... + n(n-1)(n-2)...(n-k+1)anxn-k |
| : | ||
| f(n)(x) | = | n(n-1)(n-2)...3・2an = n!an |
| f(n+1)(x) | = | 0 |
f(x) は n 次式なので、n + 1 階以上の導関数は全て 0 になります。こうして得られた各階の導関数に x = 0 を代入すると、
| f(0)(0) | = | a0 |
| f(1)(0) | = | a1 |
| f(2)(0) | = | 2a2 |
| f(3)(0) | = | 3・2a3 = 3!a3 |
| : | ||
| f(k)(0) | = | k・k-1・...・2ak = k!ak |
| : | ||
| f(n)(0) | = | n(n-1)(n-2)...3・2an = n!an |
これを、係数 ak について解くと、
よって、関数 f(x) を級数の形に変換した式は次のようになります。
この式を「n 次のテイラー多項式」といいます。x = a で展開した場合、x 座標を平行移動させることにより、
で求めることができます。
与えられた関数 f(x) を n 次のテイラー多項式に変換してもまだ n + 1 次以上の「余り」があるとき、この「余り」の項を「剰余項 ( Remainder )」といい、Rn+1 と表します。よって、テイラー多項式は、次のように書き表すことができます。
また剰余項は、次の式で与えられます。
Rn+1 = ( 1 / n! )∫{0→x}( x - t )nf(n+1)(t) dt
Rn+1 = ( f(n+1)(c) / ( n + 1 )! )xn+1 ( 但し 0 < c < x )下側の式は特に「ラグランジュ型の剰余項」と名付けられています ( 補足 1 )。
この剰余項が限りなく 0 に近づくとき、すなわち
ならば、与えられた関数は無限級数
f(x) = Σk{0→∞}( ( 1 / k! )f(k)(0)xk ) = f(0)(0) + f(1)(0)x + ( 1 / 2! )f(2)(0)x2 + ...
f(x) = Σk{0→∞}( ( 1 / k! )f(k)(a)( x - a )k ) = f(0)(a) + f(1)(a)( x - a ) + ( 1 / 2! )f(2)(a)( x - a )2 + ...に展開することができます。この級数を「テイラー級数 ( Taylor Series )」といい、特に上側の ( a = 0 の ) 級数は「マクローリン級数 ( Maclaurin Series )」とも呼ばれます。変数のべき乗を項とする級数を「べき級数 ( Power Series )」といい、任意の関数をこのようにべき級数に展開することを「テイラー展開 ( Taylor Expansion )」といいます。
ここで、指数関数 f(x) = ex をテイラー展開してみます。まずは、f(x) = ex を n 次のテイラー多項式で書き表してみます。
f(k)(x) = ex ( つまり、何回微分しても関数の形は同じ ) なので、f(k)(0) = e0 = 1 であり、
| ex | = | Σk{0→n}( ( 1 / k! )xk ) + Rn+1 |
| = | 1 + x + ( 1 / 2! )x2 + ... + ( 1 / n! )xn + Rn+1 |
になります。ラグランジュ型の剰余項を用いて Rn+1 の評価をすると、
になります。任意の定数 D に対し、lim{n→∞}( Dn / n! ) = 0 が成り立つので ( 補足 2 )、上式の極限は 0 となり、最終的には次の式が成り立つことになります。
x = 1 を代入すると、ネイピア数 e は次の計算で求めることができます。
この式を使ったネイピア数の計算プログラムを以下に示します。
/* TS_napier : テイラー展開を用いてネイピア数 eを求める 戻り値 : ネイピア数 */ template< class Res > Res TS_napier() { Res fact( 1 ); Res d( 2 ); // n=1まで計算 for ( Res i = 2 ; fact >= numeric_limits< Res >::epsilon() ; i += 1 ) { fact /= i; d += fact; } return( d ); }
三角関数も、テイラー級数に変換することが可能です ( sin x を微分すると cos x になり、cos x を微分すると -sin x になることから導くことができます )。
ここで、正接関数 tan x に対してその逆関数を定義します。
三角関数の逆関数を逆三角関数といい、その中で tan x の逆関数は逆正接関数といいます。tan-1 x はべき級数に展開することができ、
と変形することが可能です。tan( π / 4 ) = 1 であることから tan-1 1 = π / 4 なので、上式に x = 1 を代入することによって
という関係式が得られます。これは「グレゴリーの公式」あるいは「ライプニッツの公式」と呼ばれています。
「グレゴリー ( James Gregory )」は 1671 年に、「ライプニッツ ( Gottfried Wilhelm Leibniz )」は 1674 年にこの公式を発見しています。しかし、それより 300 年近く前に、インドの数学者・天文学者の「マーヴェダ ( Madhava of Sangamagrama )」によってこの公式はすでに発見されていました。
グレゴリーの公式は残念ながら収束が遅いため、あまり実用的ではありません。実用的なもの、またそうでないものも含め、円周率を求める公式は他にも次のようなものがあります ( 補足 3 )。
「マチン ( John Machin ) の公式」は、グレゴリーの公式と同じように逆正接関数を利用したものです。tan α = 1 / 5, tan β = 1 / 239 となる α, β に対し、tan ( 4α - β ) = 1 となることを利用して得ることができます。同様な式は大量に存在します。
「ゼータ関数 ( Zeta Function )」は、ζ(s) = Σk{1→∞}( 1 / ks ) で表される関数で、最初に "ζ" で表したのが「リーマン ( Georg Friedrich Bernhard Riemann )」であることから「リーマン・ゼータ関数 ( Riemann Zeta Function )」とも呼ばれます。リーマンは、ゼータ関数を s ≠ 1 である複素数全体へ拡張した場合、
ことを予想しました。これが有名な「リーマン予想(Riemann Hypothesis)」です。
「ウォリス積 ( Wallis Product )」は正弦関数の乗積展開
に Z = 1 / 2 を代入することで得られます。
今まで挙げた式を使って円周率を計算するためのサンプル・プログラムを以下に示します。
/* Gregory_pi : グレゴリーの公式を用いて円周率πを求める cnt : 演算回数(精度) 戻り値 : 円周率 */ template< class Res, class UI > Res Gregory_pi( UI cnt ) { Res d = 1; // n=1まで計算 for ( UI i = 1 ; i < cnt ; ++i ) d += ( ( i % 2 != 0 ) ? -1 : 1 ) / Res( i * 2 + 1 ); return( d * 4 ); } /* Machin_pi : マチンの公式を用いて円周率πを求める cnt : 演算回数(精度) 戻り値 : 円周率 */ template< class Res, class UI > Res Machin_pi( UI cnt ) { const Res d1( 1.0 / 5.0 ); const Res d2( 1.0 / 239.0 ); Res d( d1 * Res( 4 ) - d2 ); // n=1まで計算 for ( UI i = 1 ; i < cnt ; ++i ) { d += std::pow( d1, Res( i * 2 + 1 ) ) * Res( 4 ) * ( ( i % 2 != 0 ) ? -1 : 1 ) / Res( i * 2 + 1 ); d -= pow( d2, Res( i * 2 + 1 ) ) * ( ( i % 2 != 0 ) ? -1 : 1 ) / Res( i * 2 + 1 ); } return( d * Res( 4 ) ); } /* Zeta_pi : ゼータ関数を用いて円周率πを求める cnt : 演算回数(精度) 戻り値 : 円周率 */ template< class Res, class UI > Res Zeta_pi( UI cnt ) { Res d = 0; for ( UI i = 1 ; i < cnt ; ++i ) d += 1 / std::pow( Res( i ), Res( 2 ) ); return( std::pow( d * 6, 0.5 ) ); } /* Wallis_pi : ウォリス積を用いて円周率πを求める cnt : 演算回数(精度) 戻り値 : 円周率 */ template< class Res, class UI > Res Wallis_pi( UI cnt ) { Res d = 1; for ( UI i = 1 ; i < cnt ; ++i ) { d *= std::pow( Res( i * 2 ), Res( 2 ) ); d /= i * 2 + 1; d /= i * 2 - 1; } return( d * 2 ); }
連分数を含め、それぞれの計算式で円周率を計算したとき、演算回数に対する実際の値との差のグラフは次のようになります。
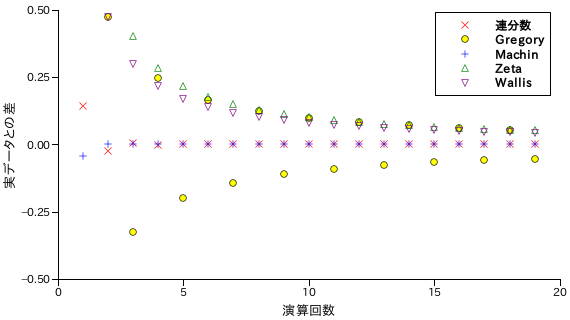 |
下表は、計算結果と実値との差を示したものです。long double 型を使って計算していますが、精度は小数点以下 15 桁までとなります。そのため、マチンの公式を使った場合は誤差が途中でゼロとなっています。
| 演算回数 | 計算結果 | 実データとの差 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 連分数 | グレゴリー | マチン | ゼータ | ウォリス | 連分数 | グレゴリー | マチン | ゼータ | ウォリス | |
| 1 | 3.00000 | 4.00000 | 3.18326 | 0.00000 | 2.00000 | 1.4159E-01 | -8.5841E-01 | -4.1671E-02 | 3.1416E00 | 1.1416E00 |
| 2 | 3.16667 | 2.66667 | 3.14060 | 2.44949 | 2.66667 | -2.5074E-02 | 4.7493E-01 | 9.9562E-04 | 6.9210E-01 | 4.7493E-01 |
| 3 | 3.13725 | 3.46667 | 3.14162 | 2.73861 | 2.84444 | 4.3378E-03 | -3.2507E-01 | -2.8376E-05 | 4.0298E-01 | 2.9715E-01 |
| 4 | 3.14234 | 2.89524 | 3.14159 | 2.85774 | 2.92571 | -7.4969E-04 | 2.4635E-01 | 8.8141E-07 | 2.8385E-01 | 2.1588E-01 |
| 5 | 3.14146 | 3.33968 | 3.14159 | 2.92261 | 2.97215 | 1.2924E-04 | -1.9809E-01 | -2.8815E-08 | 2.1898E-01 | 1.6944E-01 |
| 6 | 3.14161 | 2.97605 | 3.14159 | 2.96339 | 3.00218 | -2.2253E-05 | 1.6555E-01 | 9.7448E-10 | 1.7820E-01 | 1.3942E-01 |
| 7 | 3.14159 | 3.28374 | 3.14159 | 2.99138 | 3.02317 | 3.8285E-06 | -1.4215E-01 | -3.3762E-11 | 1.5022E-01 | 1.1842E-01 |
| 8 | 3.14159 | 3.01707 | 3.14159 | 3.01177 | 3.03867 | -6.5829E-07 | 1.2452E-01 | 1.191E-12 | 1.2982E-01 | 1.0292E-01 |
| 9 | 3.14159 | 3.25237 | 3.14159 | 3.02730 | 3.05059 | 1.1314E-07 | -1.1077E-01 | -4.3E-14 | 1.1429E-01 | 9.1003E-02 |
| 10 | 3.14159 | 3.04184 | 3.14159 | 3.03951 | 3.06003 | -1.9441E-08 | 9.9753E-02 | 1E-15 | 1.0209E-01 | 8.1558E-02 |
| 11 | 3.14159 | 3.23232 | 3.14159 | 3.04936 | 3.06770 | 3.3395E-09 | -9.0723E-02 | 0 | 9.2231E-02 | 7.3889E-02 |
| 12 | 3.14159 | 3.05840 | 3.14159 | 3.05748 | 3.07406 | -5.7357E-10 | 8.3190E-02 | 0 | 8.4111E-02 | 6.7537E-02 |
| 13 | 3.14159 | 3.21840 | 3.14159 | 3.06429 | 3.07940 | 9.8498E-11 | -7.6810E-02 | 0 | 7.7305E-02 | 6.2191E-02 |
| 14 | 3.14159 | 3.07025 | 3.14159 | 3.07008 | 3.08396 | -1.6913E-11 | 7.1338E-02 | 0 | 7.1517E-02 | 5.7629E-02 |
| 15 | 3.14159 | 3.20819 | 3.14159 | 3.07506 | 3.08790 | 2.904E-12 | -6.6593E-02 | 0 | 6.6536E-02 | 5.3691E-02 |
| 16 | 3.14159 | 3.07915 | 3.14159 | 3.07939 | 3.09134 | -4.99E-13 | 6.2439E-02 | 0 | 6.2203E-02 | 5.0256E-02 |
| 17 | 3.14159 | 3.20037 | 3.14159 | 3.08319 | 3.09436 | 8.6E-14 | -5.8773E-02 | 0 | 5.8400E-02 | 4.7234E-02 |
| 18 | 3.14159 | 3.08608 | 3.14159 | 3.08656 | 3.09704 | -1.5E-14 | 5.5513E-02 | 0 | 5.5035E-02 | 4.4555E-02 |
| 19 | 3.14159 | 3.19419 | 3.14159 | 3.08956 | 3.09943 | 3E-15 | -5.2595E-02 | 0 | 5.2036E-02 | 4.2163E-02 |
マチンの公式と連分数を利用した算出法は他と比較して収束が非常に早く、実用的であることが分かります。グラフでは差が分からないですが、表の値から見てマチンの公式の方が連分数より収束は早いです。式の特徴から、グレゴリーの式は π をはさんで上下に移動しながら収束しています。これは連分数やマチンの公式でも同様です。
次のような二次関数 f(x) を定義します。
f(x) の零点 ( x 軸との交点 ) における x の値を求めると、
x2 - C = 0 より
x = ±√Cなので、x は C の平方根になります。f(x) を微分すると、
になり、f(x) 上の点 ( x0, f(x0) ) を通る接線の方程式は、
| y | = | f(1)(x0)( x - x0 ) + f(x0) |
| = | 2x0x - ( x02 + C ) |
と計算することができます。この接線の零点における x の値を x1 としたとき、
2x0x1 - ( x02 + C ) = 0 より
x1 = ( x02 + C ) / 2x0 = (1/2)( x0 + C / x0 )になります。x0 を x0 > √C となるように決めたとき、x1 は x0 よりも √C に近い値になります。また、上記処理は何回も繰り返すことができ、繰り返す度に求められた値は √C に近づいていきます。この繰り返しは、次の漸化式で表すことができます。
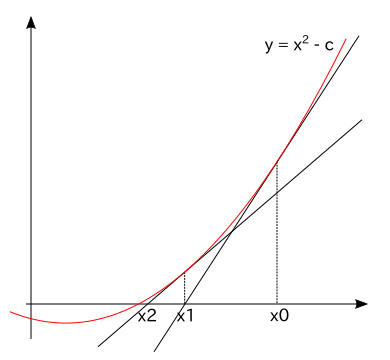 |
この反復処理方法を「ニュートン - ラフソン法 ( Newton-Raphson method )」といいます。この方法は、平方根を求めること以外にも利用することができます。一般に、微分可能な関数 f(x) において、点 ( xn, f(xn) ) を通る接線の方程式は、
なので、零点における x の値を xn+1 としたとき、
f(1)(xn)( xn+1 - xn ) + f(xn) = 0 より
xn+1 = xn - f(xn) / f(1)(xn)になり、これが任意の関数 f(x) のための漸化式になります。f(x) = x3 - C のとき、
になるため、これが立方根を計算するための漸化式となります。
ニュートン - ラフソン法を使った、任意のべき乗根の計算プログラムを以下に示します。
/* Newton_PowerRoot : ニュートン - ラフソン法を用いてべき乗根を求める c : べき乗根を求める数値 n : べき数 戻り値 : べき乗根 */ template< class Res, class UI > Res Newton_PowerRoot( UI c, UI n ) { Res x( c ); for ( ; ; ) { Res fx( std::pow( x, n ) - c ); // f(x)の値 Res dfx( std::pow( x, n - 1 ) * n ); // df(x)/dxの値 if ( std::abs( fx / dfx ) <= numeric_limits< double >::epsilon() ) break; x = x - fx / dfx; } return( x ); }
無理数を有理数で近似するプログラムをいくつか紹介しましたが、それらの中で利用している変数は通常、int 型を代表とする整数型や、double 型を代表とする浮動小数点数型であり有効桁数に限界があるため、求めることのできる精度も限られます。しかし、有理数クラスを利用するように変更することで、高精度の近似値を求めることも可能になります。
ちなみに、円周率計算の世界記録では 10 兆桁を越えているそうです。しかし、ネイピア数計算の世界記録というのはあまり聞かないですね。円周率に比べるとマイナーだからなのでしょうか。
関数 f(t) が任意階数の導関数を持っていると仮定します。一階導関数 f(1)(t)を 0 から x まで積分したとき、
となるので、これを f(x) について解くと
となって、この場合の剰余項は
となります。このとき、関数 f(x) は f(0) で近似され、その剰余が R1 で表されていると見ることができます。次に R1 から有効な項を抽出します。まずは f1(t) = ( x - t )f(1)(t)を t で微分して、
とし、これを f(1)(t) について解いて
という結果を得ます。これを R1 に代入すると、f(x) は
| f(x) | = | f(0) + ∫{0→x}( ( x - t )f(2)(t) - f1(1)(t) )dt |
| = | f(0) + ∫{0→x} ( x - t )f(2)(t) dt - ∫{0→x} f1(1)(t) dt | |
| = | f(0) + ∫{0→x} ( x - t )f(2)(t) dt - [ ( x - t )f(1)(t) ]{0→x} | |
| = | f(0) + f(1)(0)x + ∫{0→x} ( x - t )f(2)(t) dt |
となって、このときの剰余項は
となります。同様の処理を繰り返し、R2 から有効な項を抽出するため、今度は f2(t) = ( x - t )2f(2)(t) を t で微分して、
f2(1)(t) = -2( x - t ) f(2)(t) + ( x - t )2 f(3)(t) より
( x - t ) f(2)(t) = (1/2)( x - t )2 f(3)(t) - (1/2)f2(1)(t)を R2 に代入すると、f(x) は
| f(x) | = | f(0) + f(1)(0)x + ∫{0→x}( (1/2)( x - t )2 f(3)(t) - (1/2)f2(1)(t) )dt |
| = | f(0) + f(1)(0)x + (1/2)∫{0→x} ( x - t )2 f(3)(t) dt - (1/2)∫{0→x} f2(1)(t) dt | |
| = | f(0) + f(1)(0)x + (1/2)∫{0→x} ( x - t )2 f(3)(t) dt - (1/2)[ ( x - t )2f(2)(t) ]{0→x} | |
| = | f(0) + f(1)(0)x + (1/2)f(2)(0)x2 + (1/2)∫{0→x} ( x - t )2 f(3)(t) dt |
よって、このときの剰余項は
この処理を繰り返すことによって、f(t) を任意の次数の多項式で表現することができます。また、n 次の多項式で表現した場合、剰余項は
であることが、この操作からわかります。
最大値・最小値の定理より、閉区間 [ 0, x ] において f(n+1)(t) には最大値と最小値が存在します。t = α において最小値を、t = β において最大値を取るとき、閉区間 [ 0, x ] では
が成り立ちます。閉区間内では 0 ≤ t ≤ x なので ( x - t ) ≥ 0 であり、( x - t )n は 0 以上となることから、
であり、全体を n! で割り、0 から x まで積分することにより
(1/n!)∫{0→x} ( x - t )n f(n+1)(α) dt ≤ (1/n!)∫{0→x} ( x - t )n f(n+1)(t) dt ≤ (1/n!)∫{0→x} ( x - t )n f(n+1)(β) dt より
(1/n!)∫{0→x} ( x - t )n f(n+1)(α) dt ≤ Rn+1 ≤ (1/n!)∫{0→x} ( x - t )n f(n+1)(β) dt
という結果が得られます。左辺の式は、次のように変形できます。
| (1/n!)∫{0→x} ( x - t )n f(n+1)(α) dt | = | (1/n!)f(n+1)(α) ∫{0→x} ( x - t )n dt |
| = | (1/n!)f(n+1)(α) [ ( -1 / ( n + 1 ) )( x - t )n+1 ]{0→x} | |
| = | (1/n!)f(n+1)(α) xn+1/ ( n + 1 ) | |
| = | ( f(n+1)(α) / ( n + 1 )! )xn+1 |
右辺も同様に変形することができるため、不等式は次のようになります。
ここで、g(t) = ( f(n+1)(t) / ( n + 1 )! )xn+1 とすると、閉区間 [ 0, x ] において f(n+1)(α) ≤ f(n+1)(t) ≤ f(n+1)(β) であることから、g(α) ≤ g(t) ≤ g(β) が成り立ちます。中間値の定理から、g(c) = Rn+1 を満たす定数 c が区間内に少なくとも一つ存在することから、
これで、ラグランジュ型の剰余項が証明されたことになります。
数列 an において、n がある番号より大きい場合に | an+1 / an | < 1 が常に成り立つとすると、
を満たす 0 < r < 1 の正数が存在します。上式は、項の番号をいくら大きくしても成り立つので、
| -ran | < | an+1 | < | ran |
| -ran+1 | < | an+2 | < | ran+1 |
| : | ||||
| -ran+k-1 | < | an+k | < | ran+k-1 |
となり、上の式から順に、rk-1, rk-2, ... と掛けていくと、
| -rkan | < | rk-1an+1 | < | rkan |
| -rk-1an+1 | < | rk-2an+2 | < | rk-1an+1 |
| : | ||||
| -ran+k-1 | < | an+k | < | ran+k-1 |
となって、これは一つの不等式
にまとめることができるので、結局
になります。k を限りなく大きくした時、上式は
になり、| r | < 1 より右辺の極限値は 0 になるので lim{k→∞}( | an+k | ) = 0 となることから、
が成り立ちます。以上をまとめると
lim{n→∞}( |an+1/an| ) < 1 ならば、
lim{n→∞}( an ) = 0という結果が得られます。an = Dn / n! ( 但し、D は任意の定数 ) としたとき、
| an+1 / an | = | ( Dn+1 / ( n + 1 )! ) / ( Dn / n! ) |
| = | D / ( n + 1 ) |
なので、n を限りなく大きくした時、上式は
よって、
が成り立ちます。
◎ マチンの公式
tan α = 1 / 5、tan β = 1 / 239 としたとき、tan-1( 1 / 5 ) = α、tan-1( 1 / 239 ) = β。
tan 2α = 2tan α / ( 1 - tan2 α ) = ( 2 / 5 ) / ( 1 - 1 / 25 ) = 5 / 12
tan 4α = 2tan 2α / ( 1 - tan2 2α ) = ( 5 / 6 ) / ( 1 - 25 / 144 ) = 120 / 119
( 正接関数に対する倍角の公式 tan 2θ = 2tan θ / ( 1 - tan2 θ ) を利用 )なので、
| tan ( 4α - β ) | = | ( tan 4α - tan β ) / ( 1 + tan 4α tan β ) |
| = | ( 120 / 119 - 1 / 239 ) / ( 1 + 120 / 119・1 / 239 ) = 1 |
( 加法定理より tan (α - β) = ( tan α - tan β ) / ( 1 + tan αtan β ) )
tan ( π / 4 ) = 1 より 4α - β = π / 4 となり、
を求めることができます。
◎ ゼータ関数
sin x のテイラー展開
によって、sin x は多項式の形に変形することができます。次に、展開された形ではなく、因数分解された形で表現することを考えてみます。
sin x は、x = nπ ( 但し n = 0, ±1, ±2, ... ) のときに 0 になるので、
と表すことができます。
lim{x→0}( sin x / x ) = 1 より ( いくつかの証明法がありますが、テイラー展開の右辺を見れば明らかに成り立つことがわかると思います )、上式の右辺を x で割ったとき、x→0 の極限は同じく 1 にならなければならないため C = 1 となり、
| sin x | = | x( 1 + x / π )( 1 - x / π )( 1 + x / 2π )( 1 - x / 2π )...( 1 + x / nπ )( 1 - x / nπ )... |
| = | x( 1 - x2 / π2 )( 1 - x2 / (2π)2 )...( 1 - x2 / (nπ)2 )... |
と表せます。この式を順番に展開してみましょう。
| sin x | = | x( 1 - x2 / π2 )( 1 - x2 / (2π)2 )( 1 - x2 / (3π)2 )( 1 - x2 / (4π)2 ) ... ( 1 - x2 / (nπ)2 ) ... |
| = | x[ 1 - ( 1 + 1 / 22 )( x / π )2 + ( 1 / 22 )( x / π )4 ]( 1 - x2 / (3π)2 )( 1 - x2 / (4π)2 ) ... ( 1 - x2 / (nπ)2 ) ... | |
| = | x[ 1 - ( 1 + 1 / 22 + 1 / 32 )( x / π )2 + ( 1 / (1・2)2 + 1 / (1・3)2 + 1 / (2・3)2 )( x / π )4 - | |
| ( 1 / (1・2・3)2 )( x / π )6 ]( 1 - x2 / (4π)2 ) ... ( 1 - x2 / (nπ)2 ) ... | ||
| = | x[ 1 - ( 1 + 1 / 22 + 1 / 32 + 1 / 42 )( x / π )2 + | |
| ( 1 / (1・2)2 + 1 / (1・3)2 + 1 / (1・4)2 + 1 / (2・3)2 + 1 / (2・4)2 + 1 / (3・4)2 )( x / π )4 - | ||
| ( 1 / (1・2・3)2 + 1 / (1・2・4)2 + 1 / (1・3・4)2 + 1 / (2・3・4)2 )( x / π )6 + | ||
| ( 1 / (1・2・3・4)2 )( x / π )8 ]...( 1 - x2 / (nπ)2 )... | ||
この結果から、3 次項の係数について、展開した結果とテイラー展開の式を比較したとき、次の等式が成り立ちます。
左辺の括弧内は ζ(2) そのものなので、ζ(2) / π2 = 1 / 6 になり、ζ(2) = π2 / 6 が成り立つことになります。また、他の項の係数からも、以下の関係式を導くことができます。
ゼータ関数の値を初めて求めたのは「オイラー ( Leonhard Euler )」で、1735 年に ζ(2) を求めることに成功しました。ζ(1) はいわゆる調和級数と呼ばれ、これは発散するということが「ニコル・オレーム ( Nicole Oresme )」によって 14 世紀に証明されていました。しかし、この事実は忘れ去られ、17 世紀になって、複数の人物によって別の方法で証明されています。
調和級数が発散することを証明した数学者の中にベルヌーイ兄弟がいます。証明法を発表した本の中で、ベルヌーイは ζ(2) の正確な値 (「閉じた形」と言います。これに対して近似値は「開いた形」になります ) を求める問題を発表しました。これは、ベルヌーイ兄弟が数学教授を務めた大学のある町の名にちなんで「バーゼル問題」と呼ばれました。オイラーがこの問題を解いたのは、発表されてから 46 年後のことであり、そのときオイラーは 20 代後半でした。
オレームが示した、調和級数が発散する証明は、非常にわかりやすいものです。
| ζ(1) | = | 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + ... |
| = | 1 + 1/2 + ( 1/3 + 1/4 ) + ( 1/5 + 1/6 + 1/7 + 1/8 ) + ... | |
| > | 1 + 1/2 + 1/2 + 1/2 + ... → ∞ |
1/3 + 1/4 は 1/2 より大きく、1/5 + 1/6 + 1/7 + 1/8 も、1/9 + 1/10 + 1/11 + 1/12 + 1/13 + 1/14 + 1/15 + 1/16 もやはり 1/2 より大きくなります。前に取った項の数の 2 倍を取って和を計算すれば、それは常に 1/2 より大きくなるため、それを無限に繰り返せばその総和は発散することになります。
sin x の乗積展開は、すでに「ゼータ関数」のところで示しました。
両辺を x で割って、x = πZ を代入すると、
となり、逆数を取ると、
| πZ / sin πZ | = | ( 1 / ( 1 - Z2 ) )( 1 / ( 1 - Z2 / 22 ) )...( 1 / ( 1 - Z2 / n2 ) )... |
| = | ( 1 / ( 1 - Z2 ) )( 22 / ( 22 - Z2 ) )...( n2 / ( n2 - Z2 ) )... | |
| = | Π{1→∞}( n2 / ( n2 - Z2 ) ) |
を求めることができます。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |