「パターン認識 ( Pattern Recognition )」は、割と昔から研究されてきた分野でした。例えば、手描きの文字を判別したり声を言葉に変換するなどの処理が挙げられます。初期の頃は認識率が悪く実用にはほど遠いものでしたが、今では非常に性能がよくなって、顔を識別する技術においては双子の区別も可能になり、人間の識別能力を超えているのではないかと思わせるようなものも登場しています。
今回は、パターン認識技術の中から「凝集型クラスタリング ( Agglomerative Clustering )」を中心に紹介したいと思います。
入力されたパターンは通常、そのままで利用されることはありません。例えば手書きの文字をスキャナなどで入力した場合、ノイズや濃淡の違いなどによって認識率が落ちてしまう場合があります。そのため、最初にノイズの除去や正規化処理などの「前処理 ( Preprocessing )」が行われます。その後、入力されたパターンの持つ識別に必要な特徴を抽出する「特徴抽出 ( Feature Extraction )」処理に移ります。実はこの処理が最も重要な部分で、この処理によって識別性能が大きく変わります。しかし、この分野は体系化された手法があるわけではなく、各々が独自のノウハウを持っています。また、データの形式やどのような識別をしたいかによっても特徴は変化するので、結局は経験と勘が必要な分野となります。
特徴抽出が終わったら「識別 ( Classification )」を行い、入力パターンが何なのかを認識することになります。この識別に使われるデータを「特徴ベクトル ( Feature Vector )」といいます。特徴抽出によって特徴ベクトルはそのパターンの特徴を表すデータとなっているはずなので、類似したパターンの特徴ベクトルは互いに近いところにあるはずです。そのような一つの塊は「クラスタ ( Cluster )」と呼ばれます。例えば、各文字に対応する特徴ベクトルがすでに得られていれば、どのベクトルに最も近いかによって文字を識別することができます。そのようなベクトルは「プロトタイプ ( Prototype )」と呼ばれます。あらかじめプロトタイプを決めておくために、模範となる手書き文字を使って各文字の特徴ベクトルを得るやり方が「学習 ( Learning )」であり、使用されたパターンは「学習パターン ( Learning Pattern )」と呼ばれます。
手書き文字の認識などの場合、通常はお手本となる学習パターンをあらかじめ決めて分類することになりますが、単純に似たものどうしを同じグループとして分類したい場合もあります。このような手法は「クラスタリング ( Clustering )」と呼ばれます。一度クラスタが形成されれば、新たなパターンがどのクラスタに属するかによって識別することができるので、クラスタリングも学習の一つであると言えます。但し、学習パターンが決まっている場合とは異なり、どのようなクラスタが形成されるかは前もって知ることができません。同じ 'A' という文字が二つのクラスタに分割されるかもしれないし、 'V' と 'Y' が一つのクラスタに集まってしまうかもしれません。
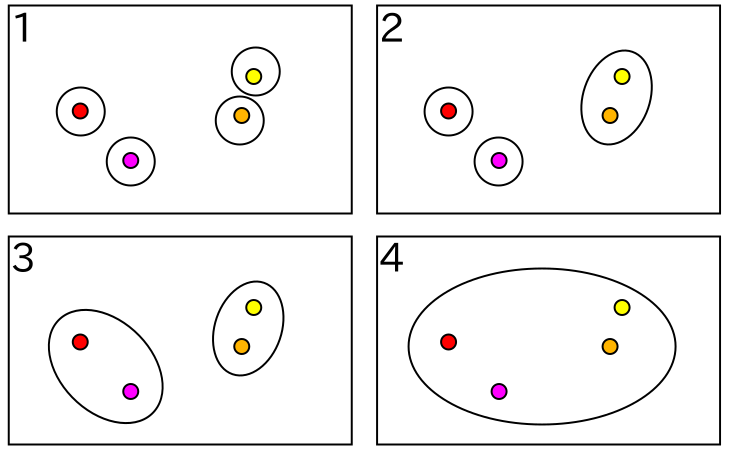
最も素朴なクラスタリングの考え方は、最も近いものどうしを順番にまとめていくというやり方です。このような手法を「凝集型クラスタリング ( Agglomerative Clustering )」といいます。初期状態は各特徴ベクトルが別々の異なるクラスタに属しているものとして、この中から最も近いクラスタどうしをつなげて少しずつ大きなクラスタを形成していきます。以下に、その例を示します。
 |
この一連の処理の流れは「樹形図 ( Dendrogram )」と呼ばれる図で表すことができます。上記の例の場合、樹形図は次のようになります。
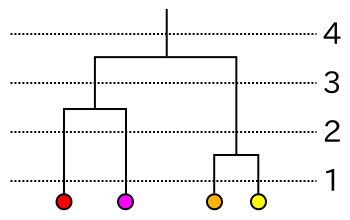 |
樹形図においてクラスタは下から上に向かって二つの線が交差したところで結合され、最も上の位置では一つのクラスタとなっています。水平にひいた点線と樹形図が交差した場所の数はクラスタの数を表していて、例えば "3" では二つのクラスタが存在し、その内容は先に示した図 2-1.の番号 "3" に一致します。
1 回の結合でクラスタの数は一つずつ減少します。N 個の特徴ベクトルがあった場合、N - 1 回で全ての特徴ベクトルは一つのクラスタにまとめられます。クラスタとして新規に形成されたときの処理回数と、別のクラスタとして一つにまとめられたときの処理回数を保持しておけば、任意の処理回数におけるクラスタの内容を得ることもできます。これについてはサンプル・プログラムを示した後で紹介したいと思います。
特徴ベクトルどうしがどの程度近いのかを判断する方法は様々です。ベクトルどうしの距離を利用するのなら、「ユークリッド・ノルム ( Euclidean Norm )」が一般的です。
ここで xm, xn は特徴ベクトルで xm = ( xm1, xm2, ... ) です。ノルムとしては他に次のようなものがあります。
マンハッタン・ノルム ( Manhattan Norm )
無限大ノルム ( Infinity Norm )
p-ノルム ( p-norm )
p-ノルムにおいて、p = 1 のときはマンハッタン・ノルム、p = 2 のときはユークリッド・ノルムを意味するのでそれぞれ L1 ノルム、L2 ノルムとも呼ばれます。また、Δxi = | xmi - xni | の最大値を ΔxM としたとき、
| || xm - xn ||p | = | [ Σi( Δxip ) ]1/p |
| = | ΔxM[ Σi( ( Δxi / ΔxM )p ) ]1/p | |
| → | ΔxM・10 = ΔxM (p→∞) |
となることから、無限大ノルムは L∞ノルムともいいます。
その他に、距離とは異なる概念ですが類似度というものも存在します。よく利用されるのは「コサイン類似度 ( Cosine Similarity )」です。
式から明らかなように、これは二つのベクトル xm, xn のなす角 θ の余弦 cos θ を表します。従って、値の範囲は -1 から 1 までとなります。この場合、値が大きいほどより近いことを意味するので、ノルムと同じように扱うためには値の変換が必要です。例えば
とすれば 0 から 1 までの範囲をとることになりますが、大小関係だけが必要なときは 1 / 2 を掛ける処理はなくても問題はありません。コサイン類似度は文書の中での単語の発生有無をベクトル化して比較するような場合によく利用されます。発生有無が単純に 0 か 1 だけで表現されているなら、コサイン類似度は常に正値となりますが、例えばポジティブな単語とネガティブな単語をそれぞれ 1, -1 で表現したベクトルでは負値の場合に正反対な意味を持つと考えることができます。
ノルム・類似度を算出するためのサンプル・プログラムを以下に示します。
// 二つの値 t1, t2 の差の絶対値を返す template< class T > T L1Norm( T t1, T t2 ) { return( std::abs( t1 - t2 ) ); } // 二つの値 t1, t2 の差の二乗を返す template< class T > T L2Norm( T t1, T t2 ) { return( ( t1 - t2 ) * ( t1 - t2 ) ); } /** L1 ノルム計算用関数オブジェクト **/ struct L1Distance { /* 配列どうしの L1 ノルムを求める 配列 2 の末尾についてはチェックしていないことに注意。 s1,e1 : 配列 1 の範囲 ( e1 は含まれない ) s2 : 配列 2 の開始位置 */ template< class In1, class In2 > typename std::iterator_traits< In1 >::value_type operator()( In1 s1, In1 e1, In2 s2 ) { typedef typename std::iterator_traits< In1 >::value_type value_type; return( std::inner_product( s1, e1, s2, value_type(), std::plus< value_type >(), std::ptr_fun( L1Norm< value_type > ) ) ); } }; /** L2 ノルム計算用関数オブジェクト **/ struct L2Distance { /* 配列どうしの L2 ノルムを求める 配列 2 の末尾についてはチェックしていないことに注意。 s1,e1 : 配列 1 の範囲 ( e1 は含まれない ) s2 : 配列 2 の開始位置 */ template< class In1, class In2 > typename std::iterator_traits< In1 >::value_type operator()( In1 s1, In1 e1, In2 s2 ) { typedef typename std::iterator_traits< In1 >::value_type value_type; return( std::sqrt( std::inner_product( s1, e1, s2, value_type(), std::plus< value_type >(), std::ptr_fun( L2Norm< value_type > ) ) ) ); } }; /** L∞ノルム計算用関数オブジェクト **/ struct LinfDistance { /* 配列どうしの L∞ノルムを求める 配列 2 の末尾についてはチェックしていないことに注意。 s1,e1 : 配列 1 の範囲 ( e1 は含まれない ) s2 : 配列 2 の開始位置 */ template< class In1, class In2 > typename std::iterator_traits< In1 >::value_type operator()( In1 s1, In1 e1, In2 s2 ) { typedef typename std::iterator_traits< In1 >::value_type value_type; return( std::inner_product( s1, e1, s2, value_type(), std::ptr_fun( std::max< value_type > ), std::ptr_fun( L1Norm< value_type > ) ) ); } }; /** コサイン類似度計算用関数オブジェクト **/ struct CosineSimilarity { /* 配列どうしのコサイン類似度を求める 距離として扱えるように、求めた値を 1 から減算して返す。そのため値の範囲は 0 から 2 までとなる。 配列 2 の末尾についてはチェックしていないことに注意。 s1,e1 : 配列 1 の範囲 ( e1 は含まれない ) s2 : 配列 2 の開始位置 */ template< class In1, class In2 > typename std::iterator_traits< In1 >::value_type operator()( In1 s1, In1 e1, In2 s2 ) { typedef typename std::iterator_traits< In1 >::value_type value_type; value_type innerProduct = std::inner_product( s1, e1, s2, value_type() ); value_type norm1 = std::sqrt( std::inner_product( s1, e1, s1, value_type() ) ); In2 e2 = s2; std::advance( e2, std::distance( s1, e1 ) ); value_type norm2 = std::sqrt( std::inner_product( s2, e2, s2, value_type() ) ); return( 1.0 - innerProduct / ( norm1 * norm2 ) ); } };
inner_product は STL ( Standard Template Library ) で提供されている内積計算用の関数ですが、最後の引数で二つの配列の要素どうしの計算式、その前の引数で計算結果どうしを積算する式を指定することができます ( デフォルトはそれぞれ乗算と和の計算になります )。L1Distance は差の絶対値の和を計算し、L2Distance は差の二乗和の平方根を計算しています。LinfDistance は差の絶対値から最大値を取得し、CosineSimilarity は通常の内積をノルムで割る処理を行っています。どの場合も inner_product が利用されていることからわかるように、この関数は非常に応用範囲が広くて便利です。
クラスタ化が進むと、クラスタと特徴ベクトル、またはクラスタどうしでノルムや類似度を比較する必要が生じます。この場合もいくつかの比較方法があります。
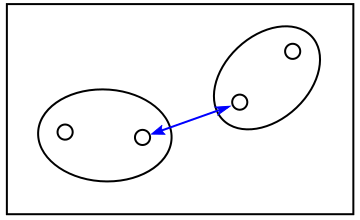
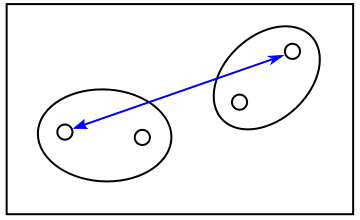
「単連結法 ( Single Linkage Method )」は二つのクラスタの中で最も近い特徴ベクトルのノルムをクラスタのノルムとして採用する方法で、「最短距離法 ( Nearest Neighbor Method )」ともいいます。逆に「完全連結法 ( Complete Linkage Method )」では最も遠い特徴ベクトルどうしのノルムをクラスタのノルムとするので「最長距離法 ( Farthest Neighbor Method )」とも呼ばれます。前者はクラスタが長く伸びて細長くなりやすく、後者はそのようなクラスタは生成しにくく球状のクラスタになりやすいという性質があります。各クラスタの特徴ベクトルの重心 ( 平均 ) を求め、重心どうしのノルムを採用する方法を「重心法 ( Centroid Method )」といい、単連結法と完全連結法の中間の性質を持ちます。
| 単連結法 | 完全連結法 | 重心法 |
|---|---|---|
 |
 |
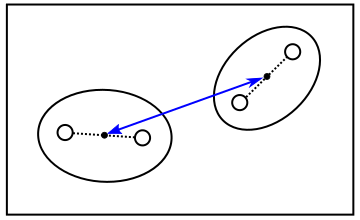 |
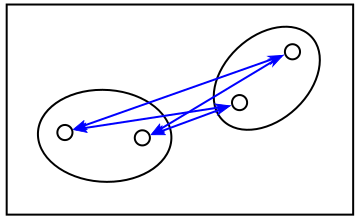
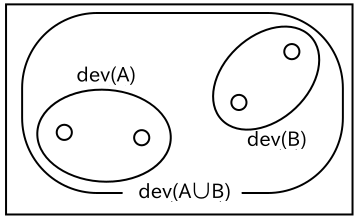
「群平均法 ( Group Average Method または Unweighted Pair-Group Using Arithmetic Averages ; UPGMA )」ではクラスタ間の各特徴ベクトルの全ての組み合わせについてノルムを求め、その平均を採用します。また「ウォード法 ( Ward's Method )」は、二つのクラスタを結合した場合の偏差の和 ( 通常は偏差の二乗和 ) と、それぞれのクラスタの偏差の和との差を採用する方法です。
| 群平均法 | ウォード法 |
|---|---|
 |
 |
その他に、簡略化した方法として「重み付き平均法 ( Weighted Average Method または Weighted Pair-Group Using Arithmetic Averages ; WPGMA )」や「メディアン法 ( Median Method または Unweighted Pair-Group Using Centroids ; WPGMC )」というものもありますが、コンピュータの発達に従いこれらは使われなくなってきたようです。
これらの比較方法を実現するため、クラスタは以下のような構造体で表すことにします。
/** クラスタのノード **/ struct Node { size_t parent; // 親ノード std::vector< double > sum; // データの合計 unsigned int count; // データ数 std::vector< size_t > nodes; // クラスタに含まれるノード size_t right; // 右の子ノード size_t left; // 左の子ノード unsigned int minLevel; // クラスタ化されたときのレベル unsigned int maxLevel; // 他のクラスタに結合されたときのレベル double norm; // クラスタ間のノルム /* インデックスの最大値を返す この値は NULL ノードの番号として利用する */ static size_t max_size() { return( std::numeric_limits< size_t >::max() ); } // 左右の子ノード r, l を指定して構築 Node( size_t r, size_t l ) : parent( max_size() ), count( 0 ), right( r ), left( l ), minLevel( 0 ), maxLevel( 0 ), norm( 0 ) {} }; /* InitNode : cluster を data で初期化する */ void InitNode( const vector< vector< double > >& data, vector< Node >* cluster ) { typedef vector< vector< double > >::const_iterator const_iterator; cluster->clear(); for ( const_iterator cit = data.begin() ; cit != data.end() ; ++cit ) { cluster->push_back( Node( Node::max_size(), Node::max_size() ) ); ( cluster->back() ).sum = *cit; ( cluster->back() ).count = 1; ( cluster->back() ).nodes.push_back( cluster->size() - 1 ); } } /* AddNode : cluster に、right を右、left を左の子ノードとした新たなノードを追加する count はクラスタ化した回数、norm は子ノードのクラスタのノルムをそれぞれを表す */ void AddNode( vector< Node >* cluster, size_t right, size_t left, unsigned int count, double norm ) { assert( right < cluster->size() && left < cluster->size() ); assert( (*cluster)[right].sum.size() == (*cluster)[left].sum.size() ); // 親ノードを登録 (*cluster)[right].parent = cluster->size(); (*cluster)[left].parent = cluster->size(); // 結合時のレベルを登録 (*cluster)[right].maxLevel = count; (*cluster)[left].maxLevel = count; // ノードを追加 cluster->push_back( Node( right, left ) ); // 子ノードのデータ合計と個数を算出 for ( size_t i = 0 ; i < (*cluster)[right].sum.size() ; ++i ) ( cluster->back() ).sum.push_back( (*cluster)[right].sum[i] + (*cluster)[left].sum[i] ); ( cluster->back() ).count = (*cluster)[right].count + (*cluster)[left].count; // 子ノードのクラスタを一つにまとめて登録 ( cluster->back() ).nodes.insert( ( cluster->back() ).nodes.end(), (*cluster)[right].nodes.begin(), (*cluster)[right].nodes.end() ); ( cluster->back() ).nodes.insert( ( cluster->back() ).nodes.end(), (*cluster)[left].nodes.begin(), (*cluster)[left].nodes.end() ); // 新たなノードのレベルを登録 ( cluster->back() ).minLevel = count; // 子ノードのクラスタのノルムを登録 ( cluster->back() ).norm = norm; }
構造体 Node にあるメンバ変数の中で、parent は親ノードの、left と right はそれぞれ左右の子ノードを表し、これらの変数で樹形図を表現することができます。sum はノードにつながっている全ての葉(末端のノード)のデータの合計、count はその数、さらに nodes はその全ての番号を保持します。また、minLevel と maxLevel はそれぞれクラスタが形成されたときの処理回数と、他のクラスタに結合されたときの処理回数を保持し、これによって、ある処理後のクラスタの形成される状態を知ることができます。最後の norm はノード間のノルムを保持します。
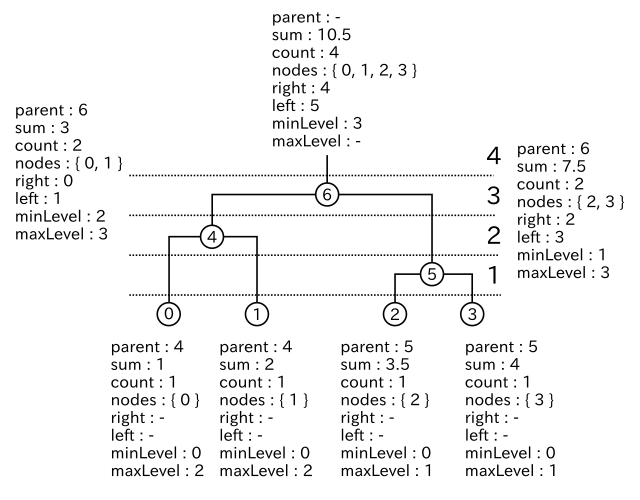 |
上図は、クラスタ形成時に Node に書き込まれる変数の値を示した例です。例えば 5 番目のノードは、2, 3 番目のノードが結合したクラスタを表すため、子ノードは 2, 3 であり、そのデータの和は 3.5 + 4 = 7.5、ノード数は 2 となります。また、1 回目の処理で形成されたクラスタなので minLevel は 1 であり、3 回目の処理で 6 番目のノードにクラスタの一部として取り込まれているので maxLevel は 3 となります。
6 番目のノードに含まれるノードは 4, 5 ではなく 0, 1, 2, 3 となっていることに注意して下さい。nodes はクラスタではなく特徴ベクトルの番号 ( すなわち葉のノードの番号 ) を保持します。
関数 InitNode はクラスタ列の初期化を行うために使います。最初は全て一つの特徴ベクトルを持ったクラスタとして初期化を行います。上の例において、0 から 3 までのノードを作成するのに相当します。また、AddNode は二つのクラスタをつないで一つのクラスタとして新たな Node を追加する処理を行う関数です。
Node に以上の情報をインプットしておくことで、先に説明したクラスタどうしのノルム比較方法に対応した処理を行うことができるようになります。まずは完全連結法のサンプル・プログラムを示します。
/** 最小ノルムを持つクラスタを取得する関数オブジェクト **/ class SimilarityMeasureMethod { /* クラスタ間のノルムを計算する cluster : 対象のクラスタがある配列 i1,i2 : 対象のクラスタへの反復子 */ virtual double getSimilarity ( const std::vector< Node >& cluster, std::vector< Node >::const_iterator i1, std::vector< Node >::const_iterator i2 ) = 0; protected: // デストラクタ(限定公開) ~SimilarityMeasureMethod() {} public: /* 最小ノルムを持つクラスタのペアを取得する cluster : クラスタ列 result : 抽出したクラスタの反復子を取得するための変数 */ double operator() ( const std::vector< Node >& cluster, std::pair< std::vector< Node >::const_iterator, std::vector< Node >::const_iterator >* result ) { typedef std::vector< Node >::const_iterator const_iterator; double minNorm = std::numeric_limits< double >::max(); // 現在の最小ノルム(最大値に初期化) for ( const_iterator i1 = cluster.begin() ; i1 != cluster.end() ; ++i1 ) { if ( i1->parent != Node::max_size() ) continue; // 親が NULL でないなら途中のノードなので無視 for ( const_iterator i2 = i1 + 1 ; i2 != cluster.end() ; ++i2 ) { if ( i2->parent != Node::max_size() ) continue; // 親が NULL でないなら途中のノードなので無視 // 各クラスタ間の最小ノルムを取得する double d = getSimilarity( cluster, i1, i2 ); if ( minNorm > d ) { minNorm = d; result->first = i1; result->second = i2; } } } return( minNorm ); } }; /** 完全連結法によるクラスタ選択関数オブジェクト 二つのクラスタの中で最も遠いノードどうしの距離を採用し、その距離が最も近いクラスタを抽出する テンプレートの NormOp はノルム計算用関数オブジェクトの型を表す **/ template< class NormOp > class CompleteLinkMethod : public SimilarityMeasureMethod { /* 指定した二つのクラスタに含まれるノードの中の最大ノルムを求める cluster : クラスタ列 i1,i2 : 対象のクラスタへの反復子 */ virtual double getSimilarity ( const std::vector< Node >& cluster, std::vector< Node >::const_iterator i1, std::vector< Node >::const_iterator i2 ) { typedef std::vector< size_t >::const_iterator const_iterator; double maxNorm = std::numeric_limits< double >::min(); // 現在の最大ノルム(最小値に初期化) for ( const_iterator s1 = ( i1->nodes ).begin() ; s1 != ( i1->nodes ).end() ; ++s1 ) { for ( const_iterator s2 = ( i2->nodes ).begin() ; s2 != ( i2->nodes ).end() ; ++s2 ) { double d = NormOp()( cluster[*s1].sum.begin(), cluster[*s1].sum.end(), cluster[*s2].sum.begin() ); maxNorm = std::max( d, maxNorm ); } } return( maxNorm ); } }; /* 凝集型クラスタリング テンプレートの NormOp はノルム計算用関数オブジェクトの型を、 Method はクラスタ選択用関数オブジェクトの型をそれぞれ表す。 data : クラスタリング対象のデータ列 cluster : 生成したクラスタ列 method : クラスタ選択用関数オブジェクト */ template< class NormOp, template< class NormOp > class Method > void AgglomerativeClustering( const std::vector< std::vector< double > >& data, std::vector< Node >* cluster, Method< NormOp > method ) { std::pair< std::vector< Node >::const_iterator, std::vector< Node >::const_iterator > result; InitNode( data, cluster ); unsigned int count = 0; // 結合処理回数 double norm; // クラスタ間のノルム while ( ( norm = method( *cluster, &result ) ) != std::numeric_limits< double >::max() ) { std::vector< Node >::const_iterator begin = cluster->begin(); AddNode( cluster, std::distance( begin, result.first ), std::distance( begin, result.second ), ++count, norm ); } }
SimilarityMeasureMethod は、全てのノルム比較方法に共通して利用できる、最小ノルムを持ったクラスタのペアを返すための関数オブジェクトです。全てのクラスタ対の組み合わせについてノルムを求め、その中から最小のノルムを持ったペアへの反復子を返します。ノルムの計算はメンバ関数 getSimilarity が行い、これは純粋仮想関数となっているので、個々の比較方法に対して後で実装することができます。クラスタ対の組み合わせを選択するとき、parent を持つノードは無視していることに注意して下さい。また、比較対象のクラスタ対がなくなったら false を返します。
CompleteLinkMethod は完全連結法のノルム計算関数オブジェクトで、SimilarityMeasureMethod からの派生クラスになります。実装の内容は非常に単純で、それぞれのクラスタ内にある特徴ベクトルどうしのノルムを計算してその中で最大のものを返します。特徴ベクトルを取得するときに、Node 内にあるメンバ変数 nodes を利用しています。なお、ノルム計算方法はテンプレート引数 NormOp で指定することができます。
最後の関数 AgglomerativeClustering がクラスタリングを行うための関数で、InitNode でクラスタを初期化した後、比較するクラスタ対がなくなるまで method を使って最小ノルムを持つクラスタ対を取得し、それらを AddNode で結合します。テンプレート引数が少しややこしくなっていますが、最初の引数 NormOp はノルム計算用関数の型、二番目の引数 Method はクラスタ間のノルム比較方法を表す関数の型で、今回の場合は CompleteLinkMethod を指します。CompleteLinkMethod はテンプレート引数 NormOp を持つので、テンプレート引数にもテンプレートが指定された形になっています。
次に、単連結法のサンプル・プログラムを示します。
/** 単連結法によるクラスタ選択関数オブジェクト 二つのクラスタの中で最も近いノードどうしの距離を採用し、その距離が最も近いクラスタを抽出する テンプレートの NormOp はノルム計算用関数オブジェクトの型を表す **/ template< class NormOp > class SingleLinkMethod { typedef std::pair< size_t, size_t > NodePair; typedef std::multimap< double, NodePair > Distance; Distance distance_; // ノード間の距離をキー、ノード番号のペアを値とした multimap Distance::const_iterator current_; // distance_ の次の取得位置 // cluster からノード番号 i のノードの親をたどってその番号を返す size_t getParent( const std::vector< Node >& cluster, size_t i ) { while ( cluster[i].parent != Node::max_size() ) i = cluster[i].parent; return( i ); } // cluster の i1, i2 番のノードが同じクラスタに属していたら true を返す bool isSame( const std::vector< Node >& cluster, size_t* i1, size_t* i2 ) { *i1 = getParent( cluster, *i1 ); *i2 = getParent( cluster, *i2 ); return( *i1 == *i2 ); } public: // データ列 data を指定して構築 SingleLinkMethod( const std::vector< std::vector< double > >& data ) { typedef std::vector< std::vector< double > >::size_type size_type; NormOp op; for ( size_type i1 = 0 ; i1 < data.size() ; ++i1 ) { for ( size_type i2 = i1 + 1 ; i2 < data.size() ; ++i2 ) { double d = op( data[i1].begin(), data[i1].end(), data[i2].begin() ); distance_.insert( std::pair< double, NodePair >( d, NodePair( i1, i2 ) ) ); } } current_ = distance_.begin(); } /* 単連結法によるクラスタ選択 cluster : クラスタ列 result : 抽出したクラスタの反復子を取得するための変数 */ double operator() ( const std::vector< Node >& cluster, std::pair< std::vector< Node >::const_iterator, std::vector< Node >::const_iterator >* result ) { // 現時点で最小のノルムを持つデータの番号を取得 if ( current_ == distance_.end() ) return( std::numeric_limits< double >::max() ); size_t i1 = ( current_->second ).first; size_t i2 = ( current_->second ).second; // 親のクラスタ番号をたどり、異なるクラスタならループを抜ける while ( isSame( cluster, &i1, &i2 ) ) { ++current_; if ( current_ == distance_.end() ) return( std::numeric_limits< double >::max() ); i1 = ( current_->second ).first; i2 = ( current_->second ).second; } // 親のクラスタ番号を登録 result->first = cluster.begin() + i1; result->second = cluster.begin() + i2; return( ( current_++ )->first ); } };
単連結法の場合、クラスタ内の最も近い特徴ベクトルのノルムを選択するので、最も近い特徴ベクトルの中で同じクラスタに含まれないものを選択することと同じ意味になります。従って、特徴ベクトルどうしのノルムをあらかじめ昇順に並べておいて、小さいものから順に、異なるクラスタならばそれを選択することで処理時間を短縮させることができます。クラス SingleLinkMethod の中のメンバ変数 distance_ がそのノルムとデータ番号の対を保持するためのコンテナで、STL ( Standard Template Library ) で提供されているコンテナ・クラスの multimap を利用しています。multimap を使うことで、要素はあらかじめノルムの順番に並んだ状態で保持されるので、先頭から順番に取得すれば目的を達成することができます。なお、メンバ関数の isSame は二つの特徴ベクトルが同じクラスタに属しているかをチェックするためのもので、親のノードをたどってその根の番号を調べることで同じクラスタに属していないかを判定します。
最後に、重心法・群平均法・ウォード法のサンプル・プログラムを紹介します。これらは SimilarityMeasureMethod からの派生クラスとなっています。
/** 重心法によるクラスタ選択関数オブジェクト クラスタの重心(データ平均)を採用し、その距離が最も近いクラスタを抽出する テンプレートの NormOp はノルム計算用関数オブジェクトの型を表す **/ template< class NormOp > class CentroidMethod : public SimilarityMeasureMethod { /* 重心ベクトルどうしの距離を求める cluster : クラスタ列 i1,i2 : 対象のクラスタへの反復子 */ double getSimilarity ( const std::vector< Node >& cluster, std::vector< Node >::const_iterator i1, std::vector< Node >::const_iterator i2 ) { std::vector< double > mean1( ( i1->sum ).size() ); // クラスタ 1 の重心 std::vector< double > mean2( ( i2->sum ).size() ); // クラスタ 2 の重心 std::transform( ( i1->sum ).begin(), ( i1->sum ).end(), mean1.begin(), std::bind2nd( std::divides< double >(), i1->count ) ); std::transform( ( i2->sum ).begin(), ( i2->sum ).end(), mean2.begin(), std::bind2nd( std::divides< double >(), i2->count ) ); return( NormOp()( mean1.begin(), mean1.end(), mean2.begin() ) ); } }; /** 群平均法によるクラスタ選択関数オブジェクト 各データのノルムの平均を採用し、その距離が最も近いクラスタを抽出する テンプレートの NormOp はノルム計算用関数オブジェクトの型を表す **/ template< class NormOp > class GroupAverageMethod : public SimilarityMeasureMethod { /* 指定した二つのクラスタに含まれるノードの中のノルムの平均を求める cluster : クラスタ列 i1,i2 : 対象のクラスタへの反復子 */ virtual double getSimilarity ( const std::vector< Node >& cluster, std::vector< Node >::const_iterator i1, std::vector< Node >::const_iterator i2 ) { typedef std::vector< size_t >::const_iterator const_iterator; double sumNorm = 0; // ノルムの和 for ( const_iterator s1 = ( i1->nodes ).begin() ; s1 != ( i1->nodes ).end() ; ++s1 ) { for ( const_iterator s2 = ( i2->nodes ).begin() ; s2 != ( i2->nodes ).end() ; ++s2 ) { sumNorm += NormOp()( cluster[*s1].sum.begin(), cluster[*s1].sum.end(), cluster[*s2].sum.begin() ); } } return( sumNorm / ( i1->count * i2->count ) ); } }; /** ウォード法によるクラスタ選択関数オブジェクト 二つのクラスタをまとめたときの偏差の和と各クラスタの偏差の和の差を採用し、その値が最も近いクラスタを抽出する テンプレートの NormOp はノルム計算用関数オブジェクトの型を表す **/ template< class NormOp > class WardMethod : public SimilarityMeasureMethod { /* 偏差の和を求める cluster : クラスタ列 i : 対象のクラスタへの反復子 mean : クラスタ平均 init : 偏差の和の初期値 */ double getDev( const std::vector< Node >& cluster, std::vector< Node >::const_iterator i, const std::vector< double >& mean, double init ) { for ( std::vector< size_t >::const_iterator it = ( i->nodes ).begin() ; it != ( i->nodes ).end() ; ++it ) init += NormOp()( cluster[*it].sum.begin(), cluster[*it].sum.end(), mean.begin() ); return( init ); } /* 指定した二つのクラスタに含まれるノードの中のノルムの平均を求める cluster : クラスタ列 i1,i2 : 対象のクラスタへの反復子 */ virtual double getSimilarity ( const std::vector< Node >& cluster, std::vector< Node >::const_iterator i1, std::vector< Node >::const_iterator i2 ) { std::vector< double > mean1( ( i1->sum ).size() ); // クラスタ 1 の重心 std::vector< double > mean2( ( i2->sum ).size() ); // クラスタ 2 の重心 std::transform( ( i1->sum ).begin(), ( i1->sum ).end(), mean1.begin(), std::bind2nd( std::divides< double >(), i1->count ) ); std::transform( ( i2->sum ).begin(), ( i2->sum ).end(), mean2.begin(), std::bind2nd( std::divides< double >(), i2->count ) ); std::vector< double > meanAll( ( i1->sum ).size() ); // 二つのクラスタの重心 std::transform( ( i1->sum ).begin(), ( i1->sum ).end(), ( i2->sum ).begin(), meanAll.begin(), std::plus< double >() ); std::transform( meanAll.begin(), meanAll.end(), meanAll.begin(), std::bind2nd( std::divides< double >(), i1->count + i2->count ) ); double dev1 = getDev( cluster, i1, mean1, 0 ); // クラスタ 1 の偏差の和 double dev2 = getDev( cluster, i2, mean2, 0 ); // クラスタ 2 の偏差の和 double devAll = getDev( cluster, i1, meanAll, 0 ); // 二つのクラスタの偏差の和 devAll = getDev( cluster, i2, meanAll, devAll ); return( devAll - dev1 - dev2 ); } };
重心法において、重心は、Nodes のメンバ変数である特徴ベクトルの和 sum を同じくメンバ変数の特徴ベクトル数 count で割ることで求めることができます。但し、sum はベクトルであるため、個々の要素に対して除算を行う必要があります。二つのクラスタに対して重心を求めるベクトルを mean1, mean2 として、sum の先頭から末尾まで順に count で割る操作を、STL の関数 transform, bind2nd, divides を使って実現しています。transform は、第一引数から第二引数までの範囲の値を第四引数で処理して第三引数の位置から順に代入する操作を行います。今回は定数 count で割る処理を行えばいいので divides を利用すればよいのですが、divides は二つの引数を指定して処理する二項関数です。そのため、バインダの bind2nd を使って第二引数である除数に count を指定することで定数での除算をしています。
群平均法の場合、各特徴ベクトルどうしの距離を求めてその和を計算し、最後に二つのクラスタの特徴ベクトル数の積で除算します。二つのクラスタの特徴ベクトル数をそれぞれ N1, N2 としたとき、片側のクラスタのある特徴ベクトルと組み合わせられるもう一方のクラスタの特徴ベクトルは N2 個あるので、全ての組み合わせは N1・N2 で計算することができます。
ウォード法では、重心法で使った方法で二つのクラスタの重心を求める他に、結合したクラスタの重心も transform を利用して求めています。結合したクラスタの重心は、それぞれの Node にある特徴ベクトル合計値 sum を足しあわせてから特徴ベクトル数の合計で除算すれば求められます。この加算処理では transform のもう一つの多重定義、第一引数と第二引数が一つめのデータの範囲、第三引数が二つめのデータの先頭、第四引数が結果を返す配列の先頭、最後の引数が二つのデータを操作する二項関数を使います。あとは、それぞれの重心を使って偏差の和を求めノルムを計算します。
一次元データの簡単な例を使ってクラスタリングを行ったときの樹形図を以下に示します。ノルムとしてデータの差の絶対値を採用します。
| 完全連結法の場合 | 完全連結法以外の場合 |
|---|---|
 |
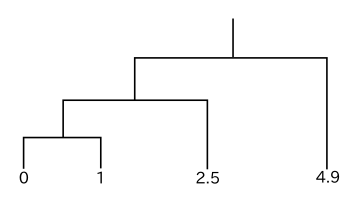 |
どの方法においても、最初にクラスタとして結合されるのは明らかに 0 と 1 のデータです。単連結法の場合、クラスタ { 0, 1 } とデータ 2.5, 4.9 とのノルムはそれぞれ 1.5, 3.9 であり、2.5 と 4.9 の間のノルムは 2.4 なので、先に { 0, 1 } と 2.5 が結合し、最後に { 0, 1, 2.5 } と 4.9 が結合して処理が完了します。しかし完全連結法では、クラスタ { 0, 1 } とデータ 2.5, 4.9 とのノルムはそれぞれ 2.5, 4.9 であり、2.5 と 4.9 の間のノルム 2.4 の方が小さくなるので、先に 2.5 と 4.9 が結合し、最後に { 0, 1 } と { 2.5, 4.9 } が結合します。
重心法の場合、クラスタ { 0, 1 } の重心は 0.5 なので、{ 0, 1 } とデータ 2.5, 4.9 とのノルムはそれぞれ 2, 4.4 です。従って、{ 0, 1 } と 2.5 の間のノルムが最も小さく、結果として単連結法と同じ樹形図が得られます。群平均法でも、{ 0, 1 } とデータ 2.5, 4.9 とのノルムはそれぞれ 2, 4.4 であり、やはり単連結法と同じ結果になります。
最後のウォード法は、{ 0, 1 } の偏差の和 Dev( { 0, 1 } ) が
であり、{ 0, 1, 2.5 } の場合は
なので、
です。{ 2.5, 4.9 } の偏差の和は
となることから { 0, 1, 2.5 } の方が先に生成され、単連結法と同じ結果が得られます。
別の例での樹形図を以下に示します。
| 単連結法以外の場合 | 単連結法の場合 |
|---|---|
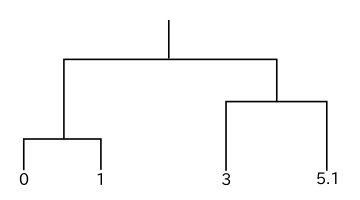 |
 |
この場合も最初にクラスタとして結合されるのは 0 と 1 のデータです。単連結法の場合、クラスタ { 0, 1 } とデータ 3, 5.1 とのノルムはそれぞれ 2, 4.1 であり、3 と 5.1 の間のノルムは 2.1 なので、先に { 0, 1 } と 3 が結合し、最後に { 0, 1, 3 } と 5.1 が結合して処理が完了します。しかし完全連結法では、クラスタ { 0, 1 } とデータ 3, 5.1 とのノルムはそれぞれ 3, 5.1 であり、3 と 5.1 の間のノルム 2.1 の方が小さくなるので、先に 3 と 5.1 が結合し、最後に { 0, 1 } と { 3, 5.1 } が結合します。ここまでの結果は、先程の例と全く同じ流れとなっています。
重心法の場合、クラスタ { 0, 1 } の重心は 0.5 なので、{ 0, 1 } とデータ 3, 5.1 とのノルムはそれぞれ 2.5, 4.6 です。従って、3 と 5.1 の間のノルム 2.1 が最も小さく、先ほどとは逆に完全連結法と同じ樹形図が得られます。群平均法でも { 0, 1 } とデータ 3, 5.1 とのノルムはそれぞれ 2.5, 4.6 であり、やはり完全連結法を同じ結果になります。
ウォード法は、{ 0, 1 } の偏差の和 Dev( { 0, 1 } ) = 1 に対して { 0, 1, 3 } の場合は
なので、
です。{ 3, 5.1 } の偏差の和は
となることから { 3, 5.1 } の方が先に生成され、完全連結法と同じ結果が得られます。単連結法が細長いクラスタを生成しやすく、逆に完全連結法がそれを嫌う性質があること、重心法・群平均法・ウォード法が中間の性質を持つことがこの例からわかります。
以下に、データ数に対するクラスタリングの処理時間を示します。各データ数・処理方法ごとに 5 回ずつ計測し、その平均を示しています。
| データ数 | ||||||
|---|---|---|---|---|---|---|
| 10 | 50 | 100 | 500 | 1000 | 2000 | |
| 完全連結法 | 2.18E-05 | 8.91E-04 | 6.77E-03 | 0.434 | 3.27 | 28.08 |
| 単連結法 | 2.86E-05 | 6.21E-04 | 3.11E-03 | 0.106 | 0.475 | 2.21 |
| 重心法 | 3.68E-05 | 3.57E-03 | 3.02E-02 | 1.51 | 11.90 | - |
| 群平均法 | 1.80E-05 | 1.05E-03 | 1.02E-02 | 0.490 | 3.78 | 32.80 |
| ウォード法 | 5.66E-05 | 9.80E-03 | 4.67E-02 | 2.74 | 21.86 | - |
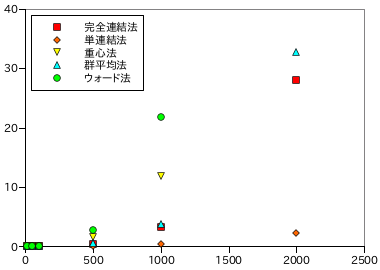 |
データ数 N に対し、単連結法ではほぼ N2、その他の方法では約 N3 近くまで増大する場合もあります。クラスタリングは処理時間がかなり長くなるアルゴリズムに属し、クラスタどうしのノルムが定数時間で計算できたとしても、p 個のクラスタに対するノルム比較回数は pC2 = p( p + 1 ) / 2 回であり、一回の結合処理によってクラスタは一つずつしか減少しないので、データが N 個あれば結合処理は N 回繰り返されることになります。従って、今のアルゴリズムの場合では N3 のオーダーで処理量は増加していくことになります。
ノルム比較回数を減らす方法はあり、単連結法のようにあらかじめノルムを昇順に並べ替えておけば先頭の要素を取得するだけで最小ノルムを得ることができます。しかし、このためには計算したノルムを配列にしてソートする処理を毎回行う必要があります。そこで、ノルムの更新方法を変更する方法を次節で検討したいと思います。
前節で紹介したクラスタ間のノルム計算方法は全て、クラスタどうしを結合した時に新たなノルムを更新する式が存在します。二つのクラスタを結合した後、あるクラスタとの距離がどのように更新されるかをそれぞれについて確認します。まず、二つのクラスタを C1, C2、その特徴ベクトル数をそれぞれ N1, N2 とします。ある他のクラスタ C の特徴ベクトル数を N とし、C1, C2 とのノルムをそれぞれ d1, d2 とします。また、C1 と C2 の間のノルムを d12 とします。
 |
単連結法の場合、C1, C2 に含まれる特徴ベクトルの中から最短のノルムを採用すればいいのですが、前回の更新で d1, d2 はすでに個々のクラスタの中で最短のノルムが選ばれているはずなので、そのうちより短い方を採用すればいいはずです。逆に完全連結法ではより長い方を採用します。このとき、次のような式で表すことができます。
単連結法 : ( d1 + d2 - | d1 - d2 | ) / 2
完全連結法 : ( d1 + d2 + | d1 - d2 | ) / 2
d1 > d2 のとき、単連結法では d1 の項が互いに打ち消し合い d2 となり、完全連結法では逆に d2 の項が互いに打ち消し合い d1 となるので、目的の値が得られます。
群平均法では、各特徴ベクトル間のノルムの平均が利用されているので、特徴ベクトル i, j 間のノルムを Dij で表すと d1, d2 は以下の式で求められています。
d1 = Σi{1→N}( Σj{1→N1}( Dij ) ) / ( N * N1 )
d2 = Σi{1→N}( Σj{1→N2}( Dij ) ) / ( N * N2 )
従って、求めるノルムを d とすると、
| d | = | Σi{1→N}( Σj{1→N1+N2}( Dij ) ) / [ N * ( N1 + N2 ) ] |
| = | Σi{1→N}( Σj{1→N1}( Dij ) + Σj{1→N2}( Dij ) ) / [ N * ( N1 + N2 ) ] | |
| = | [ ( N * N1 )d1 + ( N * N2 )d2 ] / [ N * ( N1 + N2 ) ] | |
| = | ( N1d1 + N2d2 ) / ( N1 + N2 ) |
となります。
重心法の場合、C1, C2, C の間のノルムは以下の式で求められています。
d1 = D( S1 / N1, S / N )
d2 = D( S2 / N2, S / N )
d12 = D( S1 / N1, S2 / N2 )
ここで S1, S2, S はそれぞれ C1, C2, C の特徴ベクトルの和、D( X, Y ) は二つの特徴ベクトル間のノルムを求める関数を表します。クラスタを結合した後に求めたいノルムは以下の式で表されます。
残念ながら、重心法の場合は任意のノルム演算に対する一意な更新式は得られません。そこで、L2 ノルムの場合だけに限定して考えると、上記の式は以下のようになります。
d1 = Σi{1→p}( ( S1i / N1 - Si / N )2 )
d2 = Σi{1→p}( ( S2i / N2 - Si / N )2 )
d12 = Σi{1→p}( ( S1i / N1 - Si2 / N2 )2 )
ここで S1i, S2i, Si はそれぞれ S1, S2, S の要素です。d の値は
| d | = | Σi{1→p}( [ ( S1i + S2i ) / ( N1 + N2 ) - Si / N ]2 ) |
| = | Σi{1→p}( [ N( S1i + S2i ) - ( N1 + N2 )Si ]2 ) / [ N( N1 + N2 ) ]2 | |
| = | Σi{1→p}( [ ( NS1i - N1Si ) + ( NS2i - N2Si ) ]2 ) / [ N( N1 + N2 ) ]2 | |
| = | Σi{1→p}( ( NS1i - N1Si )2 + 2( NS1i - N1Si )( NS2i - N2Si ) + ( NS2i - N2Si )2 ) / [ N( N1 + N2 ) ]2 | |
| = | [ N2N12d1 + 2Σi{1→p}( ( NS1i - N1Si )( NS2i - N2Si ) ) + N2N22d2 ] / [ N( N1 + N2 ) ]2 |
と表せて、
| Σi{1→p}( ( NS1i - N1Si )( NS2i - N2Si ) ) | |
| = | Σi{1→p}( N2S1iS2i - NN2S1iSi - NN1S2iSi + N1N2Si2 ) |
| = | Σi{1→p}( -( N2N1N2 / 2 )( S1i / N1 - S2i / N2 )2 + ( N2N2 / 2N1 )S1i2 + ( N2N1 / 2N2 )S2i2 |
| - NN2S1iSi - NN1S2iSi + N1N2Si2 ) | |
| = | Σi{1→p}( -( N2N1N2 / 2 )( S1i / N1 - S2i / N2 )2 + ( N2N1N2 / 2 )( S1i / N1 - Si / N )2 + ( N2N1N2 / 2 )( S2i / N2 - Si / N )2 ) |
| = | ( N2N1N2 / 2 )( d1 - d12 + d2 ) |
より
| d | = | [ N2N12d1 + N2N1N2( d1 - d12 + d2 ) + N2N22d2 ] / [ N( N1 + N2 ) ]2 |
| = | [ N1( N1 + N2 )d1 - N1N2d12 + N2( N1 + N2 )d2 ] / ( N1 + N2 )2 |
で求めることができます。
ウォード法も、扱えるのは L2 ノルムのみです。クラスタ C1, C2, C の各要素をそれぞれ x1, x2, x、重心をそれぞれ m1, m2, m、C1 と C を結合したときの重心を M1、C2 と C を結合したときの重心を M2、C1 と C2 を結合したときの重心を M12 としたとき、各クラスタ間のノルムは以下の式で求められています。
| d1 | = | Σ( ( x1 - M1 )2 ) + Σ( ( x - M1 )2 ) - Σ( ( x1 - m1 )2 ) - Σ( ( x - m )2 ) |
| = | Σ( x12 ) + Σ( x2 ) - [ Σ( x1 ) + Σ( x ) ]2 / ( N1 + N ) - Σ( x12 ) + [ Σ( x1 ) ]2 / N1 - Σ( x2 ) + [ Σ( x ) ]2 / N | |
| ≡ | -( S1 + S )2 / ( N1 + N ) + S12 / N1 + S2 / N | |
| = | [ -N1N( S12 + 2S1S + S2 ) + N( N1 + N )S12 + N1( N1 + N )S2 ] / N1N( N1 + N ) | |
| = | ( -2N1NS1S + N2S12 + N12S2 ) / N1N( N1 + N ) | |
| = | ( NS1 - N1S )2 / N1N( N1 + N ) | |
| d2 | ≡ | ( NS2 - N2S )2 / N2N( N2 + N ) |
| d12 | ≡ | ( N1S2 - N2S1 )2 / N1N2( N1 + N2 ) |
わかりやすいように、和の添字は省略して記述しています。また、途中で二乗和 ( 分散 ) に対する公式
を利用しています。全クラスタの重心を M で表すと、更新後のノルム d は、
| d | = | Σ( ( x1 - M )2 ) + Σ( ( x2 - M )2 ) + Σ( ( x - M )2 ) - Σ( ( x1 - M12 )2 ) - Σ( ( x2 - M12 )2 ) - Σ( ( x - m )2 ) |
| ≡ | -( S1 + S2 + S )2 / ( N1 + N2 + N ) + ( S1 + S2 )2 ) / ( N1 + N2 ) + S2 / N | |
| = | [ -N( N1 + N2 )( S1 + S2 + S )2 + N( N1 + N2 + N )( S1 + S2 )2 + ( N1 + N2 )( N1 + N2 + N )S2 ] | |
| / N( N1 + N2 )( N1 + N2 + N ) | ||
となります。分子のところだけ計算すると
| (分子) | = | -N( N1 + N2 )[ ( S1 + S2 )2 + 2S( S1 + S2 ) + S2 ] + N( N1 + N2 + N )( S1 + S2 )2 + ( N1 + N2 )( N1 + N2 + N )S2 |
| = | N2( S1 + S2 )2 - 2N( N1 + N2 )S( S1 + S2 ) + ( N1 + N2 )2S2 | |
| = | [ ( N1 + N2 ) / N1 ]( NS1 - N1S )2 + [ ( N1 + N2 ) / N2 ]( NS2 - N2S )2 - ( N2N2 / N1 )S12 - ( N2N1 / N2 )S22 + 2N2S1S2 | |
| = | [ ( N1 + N2 ) / N1 ]( NS1 - N1S )2 + [ ( N1 + N2 ) / N2 ]( NS2 - N2S )2 - ( N2 / N1N2 )( N2S1 - N1S2 )2 | |
| = | N( N1 + N2 )( N1 + N )d1 + N( N1 + N2 )( N2 + N )d2 - N2( N1 + N2 )d12 |
と計算できます。二行目から三行目への変形は、2N( N1 + N2 )S( S1 + S2 ) が消えるように二乗項を作ることで自然に現れます。この結果から、
となります。
重み付き平均法やメディアン法も含め、係数だけが異なるだけで全て共通の更新式としてまとめることができます。この更新式は「Lance-Williams の更新式 ( Lance-Williams Updating Formula )」と呼ばれます。更新式の係数をまとめると以下のようになります。
| α1 | α2 | β | γ | |
|---|---|---|---|---|
| 単連結法 | 1 / 2 | 1 / 2 | 0 | -1 / 2 |
| 完全連結法 | 1 / 2 | 1 / 2 | 0 | 1 / 2 |
| 群平均法 | N1 / ( N1 + N2 ) | N2 / ( N1 + N2 ) | 0 | 0 |
| 重心法 | N1 / ( N1 + N2 ) | N2 / ( N1 + N2 ) | -N1N2 / ( N1 + N2 )2 | 0 |
| ウォード法 | ( N1 + N ) / ( N1 + N2 + N ) | ( N2 + N ) / ( N1 + N2 + N ) | -N / ( N1 + N2 + N ) | 0 |
| 重み付き平均法 | 1 / 2 | 1 / 2 | 0 | 0 |
| メディアン法 | 1 / 2 | 1 / 2 | -1 / 4 | 0 |
ノルムの初期化には、特徴ベクトル数 N に対して 1 から N までの和 N( N + 1 ) / 2 回の計算が必要になるので処理時間は N2 に比例します。しかし、更新は結合されたクラスタとのノルムだけに対して行えばいいので、一つのノルム計算時間が特徴ベクトル数に依存しないなら N に比例する処理時間で行うことができます。クラスタは 1 回の結合処理で一つずつ減少するので、計算時間は全体で N2 に比例することになります。
Lance-Williams の更新式を利用したクラスタリング処理を行うためのサンプル・プログラムを以下に示します。まずは、すべての処理方法に対する基底クラスを示します。
/** クラスタのノード **/ struct Node { size_t parent; // 親ノード unsigned int count; // データ数 size_t right; // 右の子ノード size_t left; // 左の子ノード unsigned int minLevel; // クラスタ化されたときのレベル unsigned int maxLevel; // 他のクラスタに結合されたときのレベル double norm; // クラスタ間のノルム /* インデックスの最大値を返す この値は NULL ノードの番号として利用する */ static size_t max_size() { return( std::numeric_limits< size_t >::max() ); } // 左右の子ノード r,l を指定して構築 Node( size_t r, size_t l ) : parent( max_size() ), count( 0 ), right( r ), left( l ), minLevel( 0 ), maxLevel( 0 ), norm( 0 ) {} }; /* AddNode : cluster に、right を右、left を左の子ノードとした新たなノードを追加する count はクラスタ化した回数、norm は子ノードのクラスタのノルムをそれぞれを表す */ void AddNode( vector< Node >* cluster, size_t right, size_t left, unsigned int count, double norm ) { assert( right < cluster->size() && left < cluster->size() ); // 親ノードを登録 (*cluster)[right].parent = cluster->size(); (*cluster)[left].parent = cluster->size(); // 結合時のレベルを登録 (*cluster)[right].maxLevel = count; (*cluster)[left].maxLevel = count; // ノードを追加 cluster->push_back( Node( right, left ) ); // 子ノードのデータ個数を算出 ( cluster->back() ).count = (*cluster)[right].count + (*cluster)[left].count; // 新たなノードのレベルを登録 ( cluster->back() ).minLevel = count; // 子ノードのクラスタのノルムを登録 ( cluster->back() ).norm = norm; } /** 順序対 **/ class OrderedPair { // クラスタに対する添字の型 typedef std::vector< Node >::size_type size_type; size_type first_; // 第一要素 size_type second_; // 第二要素 public: /* 二つの要素 s1, s2 を指定して構築 要素のうち小さい側を first、大きい側を second とする */ OrderedPair( size_type s1, size_type s2 ) : first_( std::min( s1, s2 ) ), second_( std::max( s1, s2 ) ) {} // 要素のうち小さい側を返す size_type first() const { return( first_ ); } // 要素のうち大きい側を返す size_type second() const { return( second_ ); } /* dest より小さい場合は true を返す first, second の順で大小比較をする */ bool operator<( const OrderedPair& dest ) const { if ( first_ != dest.first_ ) return( first_ < dest.first_ ); else return( second_ < dest.second_ ); } }; /** @brief クラスタ間の距離 **/ struct ClusterDistance { double distance; // クラスタ間距離 OrderedPair index; // 対象のクラスタ番号 // 距離 d と対象のクラスタ i を指定して構築 ClusterDistance( double d, OrderedPair i ) : distance( d ), index( i ) {} /* dest より大きい場合は true を返す 降順で並べるために大小記号が逆転していることに注意 */ bool operator<( const ClusterDistance& dest ) const { return( distance > dest.distance ); } }; /** Lance-Williams更新式を利用したクラスタリング **/ class LanceWilliams { // クラスタに対する添字の型 typedef std::vector< Node >::size_type size_type; std::map< OrderedPair, double > distance_; // 各クラスタ間のノルム std::priority_queue< ClusterDistance > sorted_; // 降順ソート済みのクラスタ間距離 /* ノルムの更新結果を返す n : 対象クラスタのノード数 n1,n2 : 結合する二つのクラスタの各ノード数 d1,d2 : 結合する二つのクラスタと対象クラスタの間のノルム d12 : 結合する二つのクラスタ間のノルム */ virtual double getDistance( double n, double n1, double n2, double d1, double d2, double d12 ) = 0; /* init : data から cluster を初期化する テンプレートの NormOp はノルム計算用関数オブジェクトの型を表す */ template< class NormOp > void init( const std::vector< std::vector< double > >& data, std::vector< Node >* cluster ); /* update : i1, i2 番目のクラスタを結合したときの各ノルムを更新する */ void update( const std::vector< Node >& cluster, size_type i1, size_type i2 ); /* getMinNorm : cluster から最小ノルムを持つペアを result に取得する これ以上取得するペアがない場合は std::numeric_limits< double >::max() を返す */ double getMinNorm( const std::vector< Node >& cluster, std::pair< size_type, size_type >* result ); public: // 仮想デストラクタ(何もしない) virtual ~LanceWilliams() {} /* クラスタリングを行う テンプレートの NormOp はノルム計算用関数オブジェクトの型を表す data : 対象のデータ cluster : クラスタリングを行った結果(樹形図)を返す配列へのポインタ */ template< class NormOp > void clustering( const std::vector< std::vector< double > >& data, std::vector< Node >* cluster ); }; /* LanceWilliams::init : data から cluster を初期化する テンプレートの NormOp はノルム計算用関数オブジェクトの型を表す */ template< class NormOp > void LanceWilliams::init( const std::vector< std::vector< double > >& data, std::vector< Node >* cluster ) { size_type nodeSize = data.size(); cluster->clear(); distance_.clear(); while ( ! sorted_.empty() ) sorted_.pop(); for ( size_type i = 0 ; i < nodeSize ; ++i ) { // 各クラスタは一つのデータで初期化する cluster->push_back( Node( Node::max_size(), Node::max_size() ) ); ( cluster->back() ).count = 1; // 各データ間のノルムを算出 for ( size_type j = i + 1 ; j < nodeSize ; ++j ) { double d = NormOp()( data[i].begin(), data[i].end(), data[j].begin() ); distance_.insert( std::pair< OrderedPair, double >( OrderedPair( i, j ), d ) ); sorted_.push( ClusterDistance( d, OrderedPair( i, j ) ) ); } } } /* LanceWilliams::update : cluster の i1, i2 番目のクラスタを結合したときの各ノルムを更新する */ void LanceWilliams::update( const std::vector< Node >& cluster, size_type i1, size_type i2 ) { size_type nodeSize = cluster.size(); for ( size_type i = 0 ; i < nodeSize ; ++i ) { // 結合するクラスタは無視 if ( i == i1 || i == i2 ) continue; std::map< OrderedPair, double >::iterator it1 = distance_.find( OrderedPair( i, i1 ) ); std::map< OrderedPair, double >::iterator it2 = distance_.find( OrderedPair( i, i2 ) ); // 要素が存在しない場合は無視 if ( it1 == distance_.end() || it2 == distance_.end() ) continue; double d = getDistance( cluster[i].count, cluster[i1].count, cluster[i2].count, it1->second, it2->second, distance_[OrderedPair( i1, i2 )] ); distance_.insert( std::pair< OrderedPair, double >( OrderedPair( i, nodeSize ), d ) ); sorted_.push( ClusterDistance( d, OrderedPair( i, nodeSize ) ) ); distance_.erase( it1 ); distance_.erase( distance_.find( OrderedPair( i, i2 ) ) ); } } /* LanceWilliams::getMinNorm : cluster から最小ノルムを持つペアを result に取得する これ以上取得するペアがない場合は std::numeric_limits< double >::max() を返す */ double LanceWilliams::getMinNorm( const std::vector< Node >& cluster, std::pair< size_type, size_type >* result ) { double norm; do { if ( sorted_.empty() ) return( std::numeric_limits< double >::max() ); ClusterDistance cd( sorted_.top() ); result->first = cd.index.first(); result->second = cd.index.second(); sorted_.pop(); norm = cd.distance; } while ( cluster[result->first].parent != Node::max_size() || cluster[result->second].parent != Node::max_size() ); return( norm ); } /* LanceWilliams::clustering : data のクラスタリングを行い結果を cluster に返す テンプレートの NormOp はノルム計算用関数オブジェクトの型を表す */ template< class NormOp > void LanceWilliams::clustering( const std::vector< std::vector< double > >& data, std::vector< Node >* cluster ) { std::pair< size_type, size_type > result; init< NormOp >( data, cluster ); unsigned int count = 0; // 結合処理回数 double norm; // クラスタ間のノルム while ( ( norm = getMinNorm( *cluster, &result ) ) != std::numeric_limits< double >::max() ) { update( *cluster, result.first, result.second ); AddNode( cluster, result.first, result.second, ++count, norm ); } }
クラス LanceWilliams は内部でクラス OrederedPair と構造体 ClusterDistance を利用しています。OrederedPair はクラスタ番号のペアを表す型で、大小比較ができるようにメンバ関数 operator< が定義されています。二つのクラスタ番号を指定して構築しますが、番号のうち小さい方が必ず第一要素 first になるように内部で並べ替えをしています。これにより、例えば ( 1, 3 ) と ( 3, 1 ) が同じものとして扱われることになります。ClusterDistance はクラスタ番号のペアにその間のノルムをメンバ変数として追加した構造体で、大小関係はノルムの大きさで決められるようにしてあります。
LanceWilliams のメンバ変数は、各クラスタ間の距離を保持する distance_ と sorted_ の二つです。distance_ と sorted_ は保持している内容は全く同じで、異なるのは並べ方のみです。distnace_ は OrderedPair をキー、クラスタ間のノルムを値とする map 型であり、クラスタ番号のペアを指定することでノルムの値を取得することができるのに対して、sorted_ は ClusterDistance を要素の型とする priority_queue で、クラスタ間のノルムによってあらかじめ並べ替えが行われ、最も小さなノルムを持つクラスタのペアが取得できるようになっています。priority_queue は「優先度付きキュー ( Priority Queue )」と呼ばれ、キュー内では要素があらかじめ並べ替えられた状態で保持され、要素の取得に対して常に最も大きな値を持つデータが返される仕組みになっています。ClusterDistance の operator< は、ノルムが小さいほど "大きい" と判定されることに注意して下さい。このため、キューから返される要素は常に最小のノルムを持つことになります。
メンバ関数 init はクラスタを初期化するために利用します。個々の特徴ベクトルを一つのクラスタとして構築するのは前節で紹介したサンプル・プログラムの InitNode 関数と同じですが、同時に各クラスタ ( つまりデータ ) 間のノルムを計算して distance_, sorted_ それぞれに登録するところが新たに追加されています。update はノルム更新のための関数で、この中で Lance-Williams の更新式が利用されます。この中で行われている処理の内容を例を使って以下に示します。使用するノルム計算方法は「完全連結法」とします。
(0) <---3---> (1) <-1-> (2) <--2--> (3) <----4----> (4)
() 内の数値が特徴ベクトルに付けられた番号で、その間の数値がノルムを表します。この一次元データに対して各クラスタ間のノルムを計算すると次のような結果になります。
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 0 | 3 | 4 | 6 | 10 |
| 1 | 1 | 3 | 7 | |
| 2 | 2 | 6 | ||
| 3 | 4 |
最も小さなノルムを持つクラスタのペアは { 1, 2 } になるので、これを新たなクラスタ 5 とします。ノルムの更新が必要になるのは { 0, 1 }, { 0, 2 } と { 3, 1 }, { 3, 2 } と { 4, 1 }, { 4, 2 } で、それぞれ大きいノルムの方を採用するので { 0, 5 } = 4, { 3, 5 } = 3, { 4, 5 } = 7 となります。1, 2 を要素として持つクラスタのペアは除外されることになります。
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 0 | 3 | 4 | 6 | 10 | 4 |
| 1 | 1 | 3 | 7 | ||
| 2 | 2 | 6 | |||
| 3 | 4 | 3 | |||
| 4 | 7 |
次の最小ノルムは { 3, 5 } が持っているので、これを次のクラスタ 6 とします。ノルムの更新が必要になるのは { 0, 3 }, { 0, 5 } と { 4, 3 }, { 4, 5 } で、それぞれ { 0, 6 } = 6, { 4, 6 } = 7 になります。また、3, 5 を要素として持つクラスタのペアは除外されます。
| 3 | 4 | 5 | 6 | |
|---|---|---|---|---|
| 0 | 6 | 10 | 4 | 6 |
| 3 | 4 | 3 | ||
| 4 | 7 | 7 |
最後に最小ノルムを持つペア { 0, 6 } が選択され、これを次のクラスタ 7 としてノルムの更新を行います。{ 4, 0 }, { 4, 6 } から大きいノルムの方を選択して { 4, 7 } = 10 とし、0, 6 を要素として持つクラスタのペアを削除します。こうして最後に { 4, 7 } = 10 だけが残り、この二つが結合されて処理が完了します。
更新したノルムの取得には getDistance を使っていますが、これは純粋仮想関数で、ノルム計算方法ごとに実装を行います。getMinNorm は、最小ノルムを持つクラスタのペアを取得するための関数です。処理は非常に単純で、キュー sorted_ から末端にある要素を取得し、それがまだ結合されていないクラスタであるかをチェックして、もしそうでなければ次の末端要素を取得するといった動作を繰り返すだけです。最後に、getMinNorm、update、AddNode を順に呼び出す形でメイン・ルーチン clustering が実装されています。
個々のノルム計算方法に対する派生クラスは以下のようになります。
/* 単連結法用 Lance-Williams 更新式 二つのクラスタの中で最も近いノードどうしの距離を採用し、その距離が最も近いクラスタを抽出する */ inline double SingleLinkageMethod( double d1, double d2 ) { return( 0.5 * d1 + 0.5 * d2 - 0.5 * std::abs( d1 - d2 ) ); } /* 完全連結法用 Lance-Williams 更新式 二つのクラスタの中で最も遠いノードどうしの距離を採用し、その距離が最も近いクラスタを抽出する */ inline double CompleteLinkageMethod( double d1, double d2 ) { return( 0.5 * d1 + 0.5 * d2 + 0.5 * std::abs( d1 - d2 ) ); } /* 重心法用 Lance-Williams 更新式 二つのクラスタの重心を採用し、その距離が最も近いクラスタを抽出する */ inline double CentroidMethod( double n1, double n2, double d1, double d2, double d12 ) { double n12 = n1 + n2; return( ( n1 / n12 ) * d1 + ( n2 / n12 ) * d2 - ( n1 * n2 / std::pow( n12, 2.0 ) ) * d12 ); } /* 群平均法用 Lance-Williams 更新式 二つのクラスタの加重平均を採用し、その距離が最も近いクラスタを抽出する */ inline double GroupAverageMethod( double n1, double n2, double d1, double d2 ) { double n12 = n1 + n2; return( ( n1 / n12 ) * d1 + ( n2 / n12 ) * d2 ); } /* ウォード法用 Lance-Williams 更新式 結合前後での分散差を採用し、その差が最も小さいクラスタを抽出する */ inline double WardMethod( double n, double n1, double n2, double d1, double d2, double d12 ) { double n12 = n1 + n2; return( ( ( n + n1 ) / ( n + n12 ) ) * d1 + ( ( n + n2 ) / ( n + n12 ) ) * d2 - ( n / ( n + n12 ) ) * d12 ); } /** 単連結法によるクラスタ選択関数オブジェクト 二つのクラスタの中で最も近いノードどうしの距離を採用し、その距離が最も近いクラスタを抽出する **/ class LW_SingleLinkageMethod : public LanceWilliams { virtual double getDistance( double n, double n1, double n2, double d1, double d2, double d12 ) { return( SingleLinkageMethod( d1, d2 ) ); } }; /** 完全連結法によるクラスタ選択関数オブジェクト 二つのクラスタの中で最も遠いノードどうしの距離を採用し、その距離が最も近いクラスタを抽出する **/ class LW_CompleteLinkageMethod : public LanceWilliams { virtual double getDistance( double n, double n1, double n2, double d1, double d2, double d12 ) { return( CompleteLinkageMethod( d1, d2 ) ); } }; /** 重心法によるクラスタ選択関数オブジェクト 二つのクラスタの重心を採用し、その距離が最も近いクラスタを抽出する **/ class LW_CentroidMethod : public LanceWilliams { virtual double getDistance( double n, double n1, double n2, double d1, double d2, double d12 ) { return( CentroidMethod( n1, n2, d1, d2, d12 ) ); } }; /** 群平均法によるクラスタ選択関数オブジェクト 二つのクラスタの加重平均を採用し、その距離が最も近いクラスタを抽出する **/ class LW_GroupAverageMethod : public LanceWilliams { virtual double getDistance( double n, double n1, double n2, double d1, double d2, double d12 ) { return( GroupAverageMethod( n1, n2, d1, d2 ) ); } }; /** ウォード法によるクラスタ選択関数オブジェクト 結合前後での分散差を採用し、その差が最も小さいクラスタを抽出する **/ class LW_WardMethod : public LanceWilliams { virtual double getDistance( double n, double n1, double n2, double d1, double d2, double d12 ) { return( WardMethod( n, n1, n2, d1, d2, d12 ) ); } };
実装の内容は前に説明したとおりですが、重心法とウォード法は L2 ノルムのみに対応した計算式になっていることには注意が必要です。初期化に対しては任意のノルムが利用できるので、初期化に L2 ノルムを指定した場合は正しい結果になりません。
以下に、データ数に対するクラスタリングの処理時間を示します。前節と同様、各データ数・処理方法ごとに 5 回ずつ計測し、その平均を示しています。
| データ数 | ||||||
|---|---|---|---|---|---|---|
| 10 | 50 | 100 | 500 | 1000 | 2000 | |
| 完全連結法 | 6.38E-05 | 2.15E-03 | 1.33E-02 | 0.236 | 1.18 | 6.42 |
| 単連結法 | 7.20E-05 | 2.76E-03 | 1.54E-02 | 0.230 | 1.17 | 6.36 |
| 重心法 | 7.16E-05 | 1.31E-03 | 1.15E-02 | 0.237 | 1.13 | 6.24 |
| 群平均法 | 3.14E-05 | 2.37E-03 | 1.75E-02 | 0.236 | 1.16 | 6.34 |
| ウォード法 | 6.96E-05 | 2.74E-03 | 1.08E-02 | 0.231 | 1.17 | 6.30 |
 |
どのノルム計算方法についても性能に変化はありません。増加比率はデータ数 N に対して N2 を上回っていますが、前節の方式に比較すれば、単連結法を除いて小さくなっています。特に重心法とウォード法に対する効果は非常に大きく、ようやく実用的になったとも言えます。
ノルムの更新時間は一つのクラスタあたり定数時間で行えるので、前に述べた通り更新にかかる時間は N2 に比例します。しかし、優先度付きキューへの要素の追加は一般的に log2N 必要となるので ( 例えば「二部探索 ( Binary Search )」など )、一回のノルム更新に対しては Nlog2N、全体として N2log2N に比例する処理量になります。
クラスタリングは、最もノルムの小さい ( つまり最もよく似た ) クラスタまたは特徴ベクトルどうしの結合を繰り返す処理です。従って、結合する二つのクラスタの間のノルムは、結合した後のクラスタと他のクラスタの間のノルムよりたいていは小さいはずです。しかし、ノルム更新方法によってはこれが成り立たない場合があります。このような状態を「反転 ( Reversal, Inversion )」といいます。反転が発生した場合、樹形図の枝の高さをノルムで表現している場合は枝が「交差 ( Crossover )」した形で表現されます。反転が発生しないことが保証されている場合、すなわち結合する二つのクラスタの間のノルムが結合した後のクラスタと他のクラスタの間のノルム以下になる場合を「単調性 ( Monotonicity )」といいます。
 |
各ノルム更新方法が単調であるかどうかを確認するには、Lance-Williams の更新式で更新された距離 d が結合前のクラスタ間の距離 d12 より必ず大きくなることを示せばよく、単連結法と完全連結法は結合前のクラスタとの各距離 d1, d2 のいずれかに更新され、d1 ≥ d12, d2 ≥ d12 であることから d ≥ d12 が明らかに成り立ちます。群平均法の場合、
| d | = | [ N1 / ( N1 + N2 ) ]d1 + [ N2 / ( N1 + N2 ) ]d2 |
| ≥ | [ N1 / ( N1 + N2 ) ]d12 + [ N2 / ( N1 + N2 ) ]d12 | |
| = | [ N1 / ( N1 + N2 ) + N2 / ( N1 + N2 ) ]d12 = d12 |
であり、ウォード法は
| d | = | [ ( N1 + N ) / ( N1 + N2 + N ) ]d1 + [ ( N2 + N ) / ( N1 + N2 + N ) ]d2 - [ N / ( N1 + N2 + N ) ]d12 |
| ≥ | [ ( N1 + N ) / ( N1 + N2 + N ) ]d12 + [ ( N2 + N ) / ( N1 + N2 + N ) ]d12 - [ N / ( N1 + N2 + N ) ]d12 | |
| = | { [ ( N1 + N ) + ( N2 + N ) - N ] / ( N1 + N2 + N ) }d12 = d12 |
なのでどちらも単調ですが、重心法については成り立ちません。例えば、三つのクラスタが二等辺三角形を形成し、底辺が d12 であるとしたとき ( つまり、底辺を形成するクラスタどうしが結合するとき )、d1 = d2 ≥ d12 であり、
がピタゴラスの定理から成り立つので、
| d2 - d122 | = | ( d12 - d122 / 4 ) - d122 |
| = | d12 - 5d122 / 4 |
となって、d ≥ d12 であるためには d1 ≥ √5d12 / 2 となる必要があります。しかし、これは常には成り立ちません。
もう一つの性質として「可約性 ( Reducibility )」があります。今、二つのクラスタ i, j が最小のノルム D( i, j ) を持ち次の処理で結合するとき、i, j 以外の任意のクラスタ k について
を満たす ρ が存在します。結合後のクラスタを { i, j } としたとき、
が全ての k について成り立つ性質が可約性です。簡単に言えば、結合後のクラスタのノルムが結合前のもののいずれかより小さくならないことを意味します。Lance-Williams の更新式において、d12 ( ≤ ρ ) ≤ d1 ≤ d2 としたとき d - d1 ≥ 0 ならば可約性が成り立つことになります。単連結法の場合 d = d1、完全連結法の場合 d = d2 なので明らかに成り立ちます。群連結法の場合は
| d - d1 | = | [ N1 / ( N1 + N2 ) - 1 ]d1 + [ N2 / ( N1 + N2 ) ]d2 |
| = | [ N2 / ( N1 + N2 ) ]( d2 - d1 ) ≥ 0 |
であり、ウォード法の場合は
| d - d1 | = | [ ( N1 + N ) / ( N1 + N2 + N ) - 1 ]d1 + [ ( N2 + N ) / ( N1 + N2 + N ) ]d2 - [ N / ( N1 + N2 + N ) ]d12 |
| = | [ ( N2 + N ) / ( N1 + N2 + N ) ]d2 - [ N2 / ( N1 + N2 + N ) ]d1 - [ N / ( N1 + N2 + N ) ]d12 | |
| ≥ | [ ( N2 + N ) / ( N1 + N2 + N ) ]d1 - [ N2 / ( N1 + N2 + N ) ]d1 - [ N / ( N1 + N2 + N ) ]d12 | |
| = | [ N / ( N1 + N2 + N ) ]( d1 - d12 ) ≥ 0 |
なのでどちらも成り立ちますが、重心法はこの性質も常には成り立ちません。単調性での例を使うと、
| d2 - d12 | = | ( d12 - d122 / 4 ) - d12 |
| = | -d122 / 4 < 0 |
なので常に成り立たないことになります。
凝集型クラスタリングは、全体の中から最もノルムの小さいクラスタどうしを順に結合していくという "貪欲な ( Greedy )" アルゴリズムです。全体から選択する代わりに、ある一つのクラスタに着目して最もノルムの小さいクラスタを選び、その操作を順番に繰り返すことで一種の鎖を形成する処理を考えてみます。
最もノルムの小さなクラスタを順番に選択していくので、ノルムの大きさはだんだんと小さくなっていくはずです。やがて、より小さなノルムを持った新たなクラスタは見つからなくなり、相互につながったクラスタのペアが形成され、そのペアはクラスタの鎖の中で最小のノルムとなります。このような鎖状の構造は「最近傍グラフ ( Nearest Neighbor Graph )」と呼ばれ、クラスタ間を一方向に進む「有向グラフ ( Directed Graph または Digraph )」として扱われます。そして、最小のノルムを持つクラスタ間だけ相互に進むことができます。以下、そのようなクラスタのペアを「相互最近傍 ( Reciprocal Nearest Neighbors )」の略で RNNs とします。
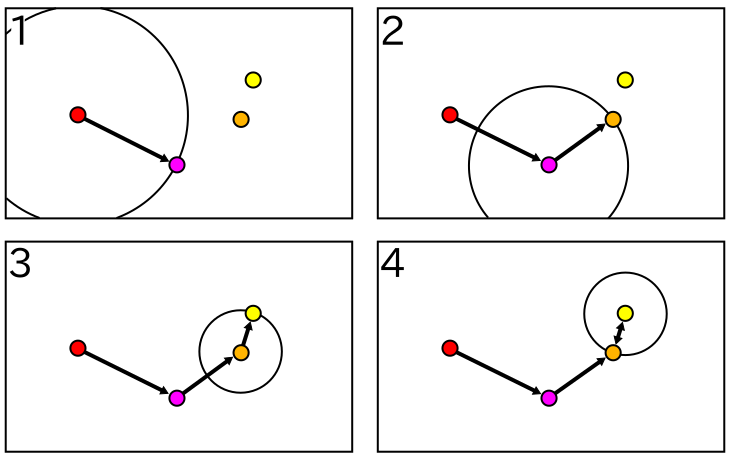 |
全てのクラスタは必ず他のいずれかのクラスタと最近傍グラフを形成します。グラフの数は単一とは限らないので、RNNs も複数形成されます。形成された全てのペアを新たなクラスタとし、最近傍グラフを再び作成する処理を繰り返すことで、最終的には全てのデータをクラスタリングすることができます。この場合、データ数 N に対し、最近傍グラフの形成に N2 に比例する処理時間が必要になります。RNNs の総数は N - 1 個になるので反復処理により N3 のオーダーの処理時間になり、このままではパフォーマンスとしてはよくありません。しかし可約性を満たすならば、RNNs から形成されるクラスタが他のクラスタより近づくことはないので、グラフの構造が変化することはありません。よって、最初に最近傍グラフを作成した後は、クラスタとして結合された RNNs とその前のクラスタだけを再作成すれば充分です。そのクラスタの数がグラフ一つあたり定数個であるならば、全体の処理時間は N2 に比例することになります。
残念ながら、最近傍グラフにおいて、RNNs の前にあるクラスタの数に制限はありません。極端な例として、ρ < 1 のノルムを持つ RNNs に対して N 個のクラスタが ρ = 1 のノルムでつながり、個々の N 個のクラスタ間は ρi > 1 ( i = 1, 2, ... N ) のノルムを持つような場合が考えられます。N に制限はないので、最悪のパフォーマンスとしては N3 に比例することになる可能性もあります。
一度に全ての最近傍グラフを生成する限りは上記の問題は回避することができないので、分岐のない一本のグラフとしてあるクラスタからスタートして RNNs まで生成し、一つずつクラスタに置き換える方法を考えます。クラスタに置き換えたら一つ前のクラスタからグラフの生成を再開します。但し、RNNs がグラフの最後の二点であった場合、再び新たなクラスタからグラフの生成を行います。この場合は処理の順番が選択されたクラスタに依存しますが、可約性が満たされる限りは結合されるクラスタは処理順番に影響しないので、樹形図としては一意で正しいことが保証されます。この方法なら、再作成されるクラスタの数は定数個 ( RNNs から成るクラスタとその前のクラスタの 2 個 ) なので、N2 に比例した時間で処理できます。
最近傍グラフを利用したクラスタリングのサンプル・プログラムを以下に示します。
/** NN-Graph を利用したクラスタリング **/ class NNGraph { // クラスタに対する添字の型 typedef std::vector< Node >::size_type size_type; std::unordered_map< OrderedPair, double, Hash_OrderedPair, Eq_OrderedPair > distance_; // 各クラスタ間のノルム std::vector< size_type > nngraph_; // 最近傍グラフ /* ノルムの更新結果を返す n : 対象クラスタのノード数 n1,n2 : 結合する二つのクラスタの各ノード数 d1,d2 : 結合する二つのクラスタと対象クラスタの間のノルム */ virtual double getDistance( double n, double n1, double n2, double d1, double d2, double d12 ) = 0; /* init : data から cluster を初期化する テンプレートの NormOp はノルム計算用関数オブジェクトの型を表す */ template< class NormOp > void init( const std::vector< std::vector< double > >& data, std::vector< Node >* cluster ); /* createNNGraph : i1, i2 番目のクラスタを結合したときの各ノルムを更新する */ void createNNGraph( const std::vector< Node >& cluster ); /* update : i1, i2 番目のクラスタを結合したときの各ノルムを更新する */ void update( const std::vector< Node >& cluster, size_type i1, size_type i2 ); /* getMinNorm : cluster から最小ノルムを持つペアを result に取得する これ以上取得するペアがない場合は std::numeric_limits< double >::max() を返す */ double getMinNorm( const std::vector< Node >& cluster, std::pair< size_type, size_type >* result ); public: // 仮想デストラクタ(何もしない) virtual ~NNGraph() {} /* クラスタリングを行う テンプレートの NormOp はノルム計算用関数オブジェクトの型を表す data : 対象のデータ cluster : クラスタリングを行った結果(樹形図)を返す配列へのポインタ */ template< class NormOp > void clustering( const std::vector< std::vector< double > >& data, std::vector< Node >* cluster ); }; /* NNGraph::init : data から cluster を初期化する テンプレートの NormOp はノルム計算用関数オブジェクトの型を表す */ template< class NormOp > void NNGraph::init( const std::vector< std::vector< double > >& data, std::vector< Node >* cluster ) { size_type nodeSize = data.size(); cluster->clear(); distance_.clear(); for ( size_type i = 0 ; i < nodeSize ; ++i ) { // 各クラスタは一つのデータで初期化する cluster->push_back( Node( Node::max_size(), Node::max_size() ) ); ( cluster->back() ).count = 1; // 各データ間のノルムを算出 for ( size_type j = i + 1 ; j < nodeSize ; ++j ) { double d = NormOp()( data[i].begin(), data[i].end(), data[j].begin() ); distance_.insert( std::pair< OrderedPair, double >( OrderedPair( i, j ), d ) ); } } nngraph_.clear(); createNNGraph( *cluster ); } /* NNGraph::createNNGraph : 最近傍グラフの生成 */ void NNGraph::createNNGraph( const std::vector< Node >& cluster ) { // 一つ前の辺のノルム(辺がない場合は最大値とする) double preNorm = ( nngraph_.size() < 2 ) ? std::numeric_limits< double >::max() : distance_[OrderedPair( nngraph_[nngraph_.size() - 1], nngraph_[nngraph_.size() - 2] )]; // 最近傍グラフが空なら新たなノードを追加する if ( nngraph_.empty() ) { for ( size_type i = 0 ; i < cluster.size() ; ++i ) { if ( cluster[i].parent == Node::max_size() ) { nngraph_.push_back( i ); break; } } } for ( ; ; ) { double minNorm = preNorm; // 追加する辺に対する最小のノルム size_type nextNode = Node::max_size(); // 追加するノード for ( size_type i = 0 ; i < cluster.size() ; ++i ) { if ( i == nngraph_.back() ) continue; // 末尾と等しければスキップ if ( cluster[i].parent != Node::max_size() ) continue; // すでに結合されたクラスタはスキップ // 最小のノルムを持つノードを取得する double norm = distance_[OrderedPair( i, nngraph_.back() )]; if ( norm < minNorm ) { minNorm = norm; nextNode = i; } } if ( nextNode == Node::max_size() ) break; // 追加するノードがなければ終了 preNorm = minNorm; nngraph_.push_back( nextNode ); } } /* NNGraph::update : cluster の i1, i2 番目のクラスタを結合したときの各ノルムを更新する */ void NNGraph::update( const std::vector< Node >& cluster, size_type i1, size_type i2 ) { typedef std::unordered_map< OrderedPair, double, Hash_OrderedPair, Eq_OrderedPair > UMap; size_type nodeSize = cluster.size(); for ( size_type i = 0 ; i < nodeSize ; ++i ) { // 結合するクラスタは無視 if ( i == i1 || i == i2 ) continue; UMap::iterator it1 = distance_.find( OrderedPair( i, i1 ) ); UMap::iterator it2 = distance_.find( OrderedPair( i, i2 ) ); // 要素が存在しない場合は無視 if ( it1 == distance_.end() || it2 == distance_.end() ) continue; double d = getDistance( cluster[i].count, cluster[i1].count, cluster[i2].count, it1->second, it2->second, distance_[OrderedPair( i1, i2 )] ); distance_.insert( std::pair< OrderedPair, double >( OrderedPair( i, nodeSize ), d ) ); } } /* NNGraph::getMinNorm : cluster から最小ノルムを持つペアを result に取得する これ以上取得するペアがない場合は std::numeric_limits< double >::max() を返す */ double NNGraph::getMinNorm( const std::vector< Node >& cluster, std::pair< size_type, size_type >* result ) { if ( nngraph_.size() < 2 ) return( std::numeric_limits< double >::max() ); result->first = nngraph_.back(); nngraph_.pop_back(); result->second = nngraph_.back(); nngraph_.pop_back(); return( distance_[OrderedPair( result->first, result->second )] ); } /* NNGraph::clustering : data のクラスタリングを行い結果を cluster に返す テンプレートの NormOp はノルム計算用関数オブジェクトの型を表す */ template< class NormOp > void NNGraph::clustering( const std::vector< std::vector< double > >& data, std::vector< Node >* cluster ) { std::pair< size_type, size_type > result; init< NormOp >( data, cluster ); unsigned int count = 0; // 結合処理回数 double norm; // クラスタ間のノルム while ( ( norm = getMinNorm( *cluster, &result ) ) != std::numeric_limits< double >::max() ) { update( *cluster, result.first, result.second ); AddNode( cluster, result.first, result.second, ++count, norm ); createNNGraph( *cluster ); } } /** 単連結法によるクラスタ選択関数オブジェクト 二つのクラスタの中で最も近いノードどうしの距離を採用し、その距離が最も近いクラスタを抽出する **/ class NNG_SingleLinkageMethod : public NNGraph { virtual double getDistance( double n, double n1, double n2, double d1, double d2, double d12 ) { return( SingleLinkageMethod( d1, d2 ) ); } }; /** 完全連結法によるクラスタ選択関数オブジェクト 二つのクラスタの中で最も遠いノードどうしの距離を採用し、その距離が最も近いクラスタを抽出する **/ class NNG_CompleteLinkageMethod : public NNGraph { virtual double getDistance( double n, double n1, double n2, double d1, double d2, double d12 ) { return( CompleteLinkageMethod( d1, d2 ) ); } }; /** 重心法によるクラスタ選択関数オブジェクト 二つのクラスタの重心を採用し、その距離が最も近いクラスタを抽出する **/ class NNG_CentroidMethod : public NNGraph { virtual double getDistance( double n, double n1, double n2, double d1, double d2, double d12 ) { return( CentroidMethod( n1, n2, d1, d2, d12 ) ); } }; /** 群平均法によるクラスタ選択関数オブジェクト 二つのクラスタの加重平均を採用し、その距離が最も近いクラスタを抽出する **/ class NNG_GroupAverageMethod : public NNGraph { virtual double getDistance( double n, double n1, double n2, double d1, double d2, double d12 ) { return( GroupAverageMethod( n1, n2, d1, d2 ) ); } }; /** ウォード法によるクラスタ選択関数オブジェクト 結合前後での分散差を採用し、その差が最も小さいクラスタを抽出する **/ class NNG_WardMethod : public NNGraph { virtual double getDistance( double n, double n1, double n2, double d1, double d2, double d12 ) { return( WardMethod( n, n1, n2, d1, d2, d12 ) ); } };
Lance-Williams のサンプル・プログラムと大きな差はありませんが、違いはメンバ関数 createNNGraph の追加と getMinNorm の実装内容、そしてメンバ変数 distance_ のデータ構造の変更の三つです。
メンバ変数 nngraph_ は最近傍グラフを表す配列で、その要素はクラスタ番号です。この生成を行うのがメンバ関数 createNNGraph で、nngraph_ が空なら新たなクラスタを追加した上で、最近傍のクラスタを、その長さがだんだんと小さくなるようにつないでいきます。そのようなクラスタがなくなった時点で、最後の二つのクラスタが RNNs となります。ここで一点、注意するべきこととして、長さが等しかった場合はつないではいけません ( つまり、長さが前の辺以下となるようにつなぐのはダメということです )。これを許してしまうと、例えば平面上で正三角形の形にクラスタが配置されている場合、環状のグラフが構成されてしまう可能性があります。メンバ関数 getMinNorm の実装内容は非常に単純で、最近傍グラフ nngraph_ の末尾の二点を取得して新たなクラスタとして返すだけです。
Lance-Williams のサンプル・プログラムでは、二つのクラスタ間の距離は、クラスタ番号のペアをキーとした map でノルムを管理していました。map はおそらく探索木のデータ構造を持っているので、キーから値を探索するにはデータ数 N に対して N log2 N の処理量となります。このままでは処理量は N2 log2 N に比例したままとなってしまうので、ここでは unordered_map を利用してノルムを管理します。unordered_map はハッシュ法を利用しているので、探索はほぼ定数時間となります。
以下に、データ数に対するクラスタリングの処理時間を示します。前節と同様、各データ数・処理方法ごとに 5 回ずつ計測し、その平均を示しています。
| データ数 | ||||||
|---|---|---|---|---|---|---|
| 10 | 50 | 100 | 500 | 1000 | 2000 | |
| 完全連結法 | 5.28E-05 | 1.53E-03 | 6.24E-03 | 0.162 | 0.67 | 2.64 |
| 単連結法 | 5.10E-05 | 1.59E-03 | 3.67E-03 | 0.165 | 0.66 | 2.63 |
| 重心法 | 5.80E-05 | 1.58E-03 | 1.18E-02 | 0.165 | 0.68 | 2.65 |
| 群平均法 | 5.52E-05 | 1.62E-03 | 6.31E-03 | 0.164 | 0.68 | 2.64 |
| ウォード法 | 5.86E-05 | 7.29E-04 | 6.46E-03 | 0.168 | 0.69 | 2.70 |
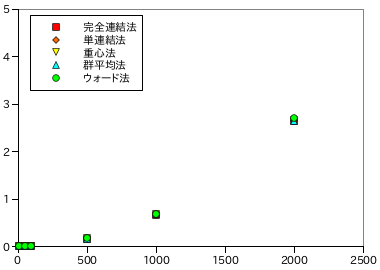 |
処理時間が短くなっただけでなく、その増加量もデータ数の二乗に比例する程度まで改善しています。
凝集型クラスタリングは処理の途中で任意の数のクラスタとして扱うことができるなど便利な部分がある反面、処理速度がデータ数の二乗は必要となるため時間のかかるアルゴリズムの部類に入ります。次回は、別の手法でのクラスタリングを紹介したいと思います。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |