今回、紹介する検索アルゴリズムは「二分探索 ( Binary Search )」と「二分探索木 ( Binary Search Tree )」です。
前回紹介した線形検索は、N 個のデータ列に対して平均 N / 2 回の比較操作が必要となるため、処理速度は N に比例することになります。これに対して「二分探索 (Binary Search)」では、N 個のデータ列に対して最悪でも log2N 回の比較回数で済むので、線形検索に対してかなりの性能向上が期待できます。
ただし、二分探索を行うためにはデータ列がソートされている必要があり、線形検索に比べて前処理のための時間が必要となります。また、一回の処理にかかる時間も線形検索より長くなるため、データ数が少ない場合は二分探索の方が逆に遅くなる場合もあります。
二分探索では、まずデータ列の中央にある要素 ( 以下、これを M0 と表します ) と検索対象データ ( 以下、これを X と 表します ) を比較し、一致しなければ、X と M0 の大小関係より X が M0 の位置より手前にあるか、それとも後ろにあるかを判断します。データ列が昇順でソートされている場合、
に X が存在するはずなので、データ列を中央 ( M0 のある位置 ) で分割して、X が存在する可能性のある区間に対して新たな中央の要素 M1 と X を比較します。この操作を、Mk ( k 回目の操作での中央の要素 ) と X が一致するか、これ以上データ列が分割ができなくなるまで繰り返します。分割できなくなった場合は目的の要素が見つからなかったことを意味します。
データ列の要素数が偶数の場合、ちょうど半分ずつにデータ列が分割されることになります。このときの中央の要素 Mk は、前半の列の末尾か、後半の列の先頭のいずれでも問題はありません。逆に、要素数が奇数の場合は中央に位置する要素が一つ決まります。いずれの場合も、探索対象の X が Mk と一致しない場合、その要素は次に対象となるデータ列から除外することができます。
正数 1 から 10 までのデータ列から、二分探索で 7 の値を検索した場合の流れを以下に示します。この例において、データ列の要素数が偶数の場合、前半の列の末尾を中央の値として採用しています。
| 表 1-1. 二分探索の流れ | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||
上記の例では、データ列の要素が一つになるまで処理が終わらなかったという最悪の場合を想定していますが、要素数 10 個に対して 4 回の比較で処理が完了しています。これが要素数 100 個になったとき、最悪でも 7 回の比較で検索処理が終了するので、要素が多くなるほど線形検索より処理時間が短くなっていきます。
線形検索では一つの要素に対する比較処理は一致したどうかの 1 回だけで済みますが、二分探索ではその他にも大小の比較を行う分、比較の処理時間は大きくなります。ソートするための前処理にかかる時間も考慮すると、要素数が数十個程度であればかえって線形検索を使用した方が速いと考えられます。もちろん、データの順番を変更することができない場合 ( 例えば文字列の中から特定の文字を探索する場合など ) はこの方法は利用できません。
また、データの重複がある場合、線形検索は最初に見つかった先頭側 ( 末尾側から検索した場合はもちろん末尾側 ) に近い要素にヒットしますが、二分探索の場合はヒットする位置は不定になります。常に先頭や末尾により近い要素の位置を返すような場合は、要素が見つかったらそこから先頭・末尾側へたどる処理を行う必要があります。
以下に、二分探索のサンプルを示します。
/* BinarySearch : 二分探索 For first, last : 前方反復子(探索開始と末尾の次) const T& val : 探索対象の値 Cmp cmp : 比較用関数オブジェクト(叙述関数) 戻り値 : val が見つかった ... true ; 見つからなかった ... false */ template<class For, class T, class Cmp> bool BinarySearch( For first, For last, const T& val, Cmp cmp ) { // first と last の差を求める typename std::iterator_traits<For>::difference_type diff = std::distance( first, last ); if ( diff == 0 ) return( false ); // 中央の位置を求める For middle = first; std::advance( middle, diff / 2 ); if ( cmp( val, *middle ) ) { return( BinarySearch( first, middle, val, cmp ) ); } else if ( cmp( *middle, val ) ) { ++middle; return( BinarySearch( middle, last, val, cmp ) ); } else { return( true ); } }
BinarySearch は、反復子 first から last の一つ手前までの中から val と一致する要素を探索し、その要素が見つかったら true を返します。前回示した LinearSearch などの関数とは異なり、一致した位置を返すわけではないことに注意して下さい。これは、STL (Standard Template Library) と仕様を合わせたためです。
first と last の間の要素数は、STL にある専用の関数 std::distance を使って求めています。また、要素数を半分にして先頭からその数分だけ先に進めるときも、やはり専用の std::advance 関数を利用しています。
この関数は再帰的に処理するようになっていて、中央の要素 *middle と比較対象の値 val の大小関係から、val < *middle なら first から middle、val > *middle なら middle + 1 から last を新たな範囲として再度 BinarySearch を呼び出します。再帰処理が完了する条件は二つあって、val = *middle ならば、目的の要素が見つかったので true を返し、first と last が等しくなれば、それ以上要素は存在しないので false を返します。
LinearSearch のように、要素が見つかったらその位置を返す関数の方が利用価値は高いと考えられます。実際、STL にもそのような関数が存在します。線形探索とは異なり、二分探索の場合は、一致した要素が見つかったとしても、それが配列の中で最初に一致する要素であるとは限りません。しかし、少しの変更でそのような関数にすることができます。以下に、そのサンプル・プログラムを示します。
/* BinarySearch_Lower : 二分探索(先頭に近い位置を返す) For first, last : 前方反復子(探索開始と末尾の次) const T& val : 探索対象の値 Cmp cmp : 比較用関数オブジェクト(叙述関数) 戻り値 : 見つかった要素列の先頭位置 一致する要素がない場合、val より大きな要素の先頭 */ template<class For, class T, class Cmp > For BinarySearch_Lower( For first, For last, const T& val, Cmp cmp ) { // first と last の差を求める typename std::iterator_traits<For>::difference_type diff = std::distance( first, last ); if ( diff == 0 ) return( first ); // 中央の位置を求める For middle = first; std::advance( middle, diff / 2 ); if ( cmp( *middle, val ) ) { ++middle; return( BinarySearch_Lower( middle, last, val, cmp ) ); } else { return( BinarySearch_Lower( first, middle, val, cmp ) ); } } /* BinarySearch_Upper : 二分探索(末尾に近い位置を返す) For first, last : 前方反復子(探索開始と末尾の次) const T& val : 探索対象の値 Cmp cmp : 比較用関数オブジェクト(叙述関数) 戻り値 : 見つかった要素列の末尾の次の位置 一致する要素がない場合、val より大きな要素の先頭 */ template<class For, class T, class Cmp > For BinarySearch_Upper( For first, For last, const T& val, Cmp cmp ) { // first と last の差を求める typename std::iterator_traits<For>::difference_type diff = std::distance( first, last ); if ( diff == 0 ) return( first ); // 中央の位置を求める For middle = first; std::advance( middle, diff / 2 ); if ( cmp( val, *middle ) ) { return( BinarySearch_Upper( first, middle, val, cmp ) ); } else { ++middle; return( BinarySearch_Upper( middle, last, val, cmp ) ); } }
BinarySearch と異なる点は、後半の要素比較の部分です。BinarySearch_Lower の場合は *middle < val ならば middle + 1 と last の間を、*middle ≥ val ならば first と middle の間をそれぞれ再帰的に処理しています。よって、要素が一致しても処理は終了せず、配列の前半部分を再度探索することになります。*middle = val になっても、まだ等しい要素が前半部分に存在する可能性があるので、これ以上要素がないという状態になるまで探索を続けるわけです。BinarySearch_Upper の場合はちょうど逆の方法で処理を行なっています。この結果、BinarySearch_Lower は等しい要素の先頭の位置を、BinarySearch_Upper は等しい要素列の末尾の次の位置を返します。また副作用として、等しい要素が見つからなかった場合は val より大きな要素の先頭の位置が返されます。これは、ソートされた状態を維持するように要素を挿入したい場合に非常に便利です。
数列 1 1 2 2 2 4 5 5 6 7 に対し、BinarySearch_Lower で 5 の値を検索した場合、以下のような処理の流れになります。なお、[] 内は添字を表しています。
| 表 1-2. BinarySearch_Lower の処理の流れ | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||
同じ条件で BinarySearch_Upper を使うと、以下のようになります。
| 表 1-3. BinarySearch_Upper の処理の流れ | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||
BinarySearch_Upper では、末尾の次の添字が返されることに注意して下さい。数列内にない要素 3 を BinarySearch_Lower で探索すると、
| 表 1-4. 要素が存在しない場合の処理の流れ | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||
となります。これは、BinarySearch_Upper でも同様の処理の流れになります。
二分探索の処理時間を計測した結果を以下に示します。条件は線形探索と同様とし、対象の要素は整数値、要素の取りうる最大値 DATA_MAX は 32 ビットで表現できる最大値 ( 0xFFFFFFFF ) と 1000 の二つとしています。また、テストは各条件で 10 回行い、その平均処理時間を示してあります。計測対象の関数は、サンプル・プログラム BinarySearch, BinarySearch_Lower, BinarySearch_Upper の他に、STL にある binary_search, lower_bound, upper_bound も加えてあります。STL の関数の詳細については後述します。
グラフにおいて、横軸の要素数は対数目盛になっていることに注意して下さい。二分探索では、探索にかかる時間は要素数に依存していないようにみえます。要素数が最大値の 1000 万のとき、比較回数は最大でも 20 回程度です。50 回以上になるには一京程度の要素数になる必要があります。従って、処理時間は要素数に対して横ばい状態に見えるわけです。最大比較回数が少ないため、目的の要素があってもなくても処理時間には影響しません。線形探索の時のように、要素が見つからなかった場合の最悪のケースは考慮しなくてもよいことになります。
なお、今回は STL の可変長配列 vector クラスを使って計測を行なっています。vector クラスは配列のメモリ上の配置が添字順通りでかつ連続であることが保証されているので、例えば a[2] は正確に a の先頭から 3 番目にあたるアドレス上にあり、途中でアドレスが別の位置にジャンプしたりすることはありません。従って、サンプル・プログラムで利用していた std::distance や std::advance は単純に二つの要素間のアドレスの差を求めたり、アドレスに指定した要素分の合計サイズを加算すれば処理できます。しかし、例えば list のような線形リストを用いた場合は開始位置から末尾まで順にたどる必要があるので、処理時間は線形に増加することになり、効率は落ちることになります。
このように、アルゴリズムがシンプルで処理速度も速いので、何もかもが線形探索より優れているように見えますが、二分探索の最大の弱点は要素をソートする必要があるということです。要素の順番が重要になる場合は二分探索は利用できませんし、ソートに必要な時間を加味すれば決して線形探索より処理時間が速いとは言い切れません。どちらも必須の探索手法ですし、場合に応じて使い分けてゆく必要があります。
STL には、二分探索用に以下の関数が用意されています。
| 関数名 | 関数宣言 | 用途 |
|---|---|---|
| binary_search | template<class For, class T> bool binary_search( For first, For last, const T& val ) |
val で指定した値を first から last の手前まで二分探索し、値が存在するかどうかを示す bool を返す |
| template<class For, class T, class Cmp> bool binary_search( For first, For last, const T& val, Cmp cmp ) |
叙述関数 cmp を使って val を first から last の手前まで二分探索し、値が存在するかどうかを示す bool を返す | |
| lower_bound | template<class For, class T> For lower_bound( For first, For last, const T& val ) |
val で指定した値を first から last の手前まで二分探索し、最初に見つかった要素の反復子を返す |
| template<class For, class T, class Cmp> For lower_bound( For first, For last, const T& val, Cmp cmp ) |
叙述関数 cmp を使って val を first から last の手前まで二分探索し、最初に見つかった要素の反復子を返す | |
| upper_bound | template<class For, class T> For upper_bound( For first, For last, const T& val ) |
val で指定した値を first から last の手前まで二分探索し、最後に見つかった要素の次の反復子を返す |
| template<class For, class T, class Cmp> For upper_bound( For first, For last, const T& val, Cmp cmp ) |
叙述関数 cmp を使って val を first から last の手前まで二分探索し、最後に見つかった要素の次の反復子を返す | |
| equal_range | template<class For, class T> pair<For,For> equal_range( For first, For last, const T& val ) |
val で指定した値を first から last の手前まで二分探索し、最初と末尾の次の反復子のペアを返す |
| template<class For, class T, class Cmp> pair<For,For> equal_range( For first, For last, const T& val, Cmp cmp ) |
叙述関数 cmp を使って val を first から last の手前まで二分探索し、最初と末尾の次の反復子のペアを返す |
equal_range 以外は、先ほど示したサンプル・プログラムと同じ動作になります。equal_range は一度にまとめて処理させようとすると結構面倒ですが、BinarySearch_Lower と BinarySearch_Upper を個別に呼び出すようにすれば簡単に実装できます。また、BinarySearch_Lower を呼び出して先頭を得たら、そこから一致する部分をたどる方法もあります。重複がほとんど発生しないのであれば、後者の方が処理は速いでしょう。
最後に、二分探索を使った応用例を示したいと思います。平方根を求める方法としては、「ニュートン-ラフソン法」や「連分数」を利用したものなどがありますが、二分探索を使っても計算することが可能です。以下に、二分探索を利用して平方根を求めるためのサンプル・プログラムを示します。
double SquareRoot( double d, double threshold ) { if ( d < 0 ) return( NAN ); double sqrt = d / 2; // 平方根(求める解) for ( double gap = sqrt / 2 ; gap >= threshold ; gap /= 2 ) { if ( d > sqrt * sqrt ) sqrt += gap; else if ( d < sqrt * sqrt ) sqrt -= gap; else break; std::cout << "sqrt = " << sqrt << " ; gap = " << gap << std::endl; } return( sqrt ); }
関数 SquareRoot は、与えられた浮動小数点数 d の平方根を返す関数です。d の 1 / 2 を sqrt の初期値とし、そのさらに 1 / 2 を増減分 gap として
という操作を、gap < threshold になるまで繰り返します。このとき、gap の値は一回のループ毎に 1 / 2 にしていきます。
f(x) = x2 - d は x ≥ 0 において単調に増加します。f(x) から任意に点列を抽出したとき、x の値に対して昇順にソートすれば、f(x) の値も昇順に並ぶことになります。よって、二分探索において配列から目的の値を探索する操作と同等の手法によって f(x) = x2 - d = 0 のときの x の値を求めれば、それが d の平方根になります。f(x) > 0 ならば、x > d を意味するので x - gap によって x を減少させ、逆に f(x) < 0 なら x < d なので x + gap によって x を増加させます。先ほど示した、平方根計算のサンプル・プログラムでは sqrt * sqrt と d を直接比較していますが、これを f(x) と 0 との比較に置き換えても処理の内容は変わりません。このような手法を「二分法 (Bisection Method)」といい、数値解析法の一つとして利用されています。
f(x) は どのような式でもよく、例えば f(x) = x3 - d なら d の累乗根を、さらに一般化して f(x) = xn - d なら d の n 乗根を求めることができます。一般的には、f(x) = 0 の解を求めるための手法であり、「ニュートン-ラフソン法」と比較すると収束は遅い反面、解の存在する範囲さえ指定することができれば、どんな関数に対しても確実に任意の精度の解を得ることができます。
二分法のサンプル・プログラムを以下に示します。
/* BisectionMethod : 二分法による f(x) = 0 の解の計算 double (*f)( double ) : 関数 f(x) std::pair<double,double> x : 解の存在する範囲 double xThreshold : x の収束範囲 double fThreshold : f(x) と 0 との誤差範囲 戻り値 : f(x) = 0 の解 */ double BisectionMethod( double (*f)( double ), std::pair<double,double>& x, double xThreshold, double fThreshold ) { if ( x.first > x.second ) std::swap( x.first, x.second ); // 定義域の小さい側における f(x) の符号 bool sign = (*f)( x.first ) >= 0; // 両端で符号が等しければ NAN を返す if ( sign == ( (*f)( x.second ) >= 0 ) ) return( NAN ); // 収束・誤差範囲が不正なら NAN を返す if ( xThreshold <= 0 && fThreshold <= 0 ) return( NAN ); double gap = x.second - x.first; // 定義域の大きさ(補正値に使用) double m = ( x.first + x.second ) / 2; // 中央値 double fm = (*f)( m ); // 中央値における f(x) の値 while ( gap >= xThreshold && fabs( fm ) >= fThreshold ) { gap /= 2; std::cout << "gap = " << gap << " ; "; if ( sign == ( fm >= 0 ) ) // 小さい側と符号が等しい(解は大きい側) x.first += gap; else // 大きい側と符号が等しい(解は小さい側) x.second -= gap; m = ( x.first + x.second ) / 2; fm = (*f)( m ); std::cout << "m = " << m << " ; "; std::cout << "f(m) = " << fm << std::endl; } return( ( x.first + x.second ) / 2 ); }
引数としては、double 型の引数一つと、同じく double型の戻り値を持つ関数ポインタ f、定義域を表す pair<double,double> 型の変数 x、定義域の収束する範囲のしきい値 xThreshold と、求めた解に対する f(x) の値とゼロとの誤差のしきい値 fThreshold の四つを渡します。関数 f は、一変数を引数として渡した時に何らかの値を返すものであればどんなものでも渡すことができますが、正しい解を得るためには指定した定義域 [ a, b ] に対して f(a)・f(b) ≤ 0 の条件を満たす必要があります。
解が中央値 m の前側にあるか、後ろ側にあるかは f(x) の符号のみで判断しているので、f(x) が短調増加・短調減少でなくても正しい解は得られます。しかし、サンプル・プログラムの中では、定義域の両端における符号が逆転しているかをチェックしているだけなので、定義域内で x 軸と交差していたとしても両端の符号が一致すれば NAN を返しますし、複数の解が存在した場合は求めたい解にならない可能性があります。
前述の通り、中央値 m の前後のどちらに解が存在するかは f(x) の符号を比較することで判断しています。最初に、定義域の下限値における f(x) の符号を求め、それを変数 sign に格納します。中央値 m における f(x) の符号が sign と等しければ、解は中央より大きい値になることを意味するので後半部分を新たな定義域とし、sign と等しくなければ、解は中央より小さい値になることを意味するので前半部分を新たな定義域とします。このように、定義域を徐々に狭めながら処理を繰り返し、定義域が xThreshold より小さくなるか、f(x) の絶対値が fThreshold より小さくなった段階でループを抜けます。なお、定義域を表す x は収束後の定義域をそのまま保持する形になるので、呼び出し後に精度を確認することができるようになっています。
SquareRoot と BisectionMethod は計算過程を出力するようにしてあるので、このの二つを使い、5 の平方根を求めた時の出力結果を以下に示しておきます。なお、BisectionMethod で 5 の平方根を求めるため、x2 - 5 の値を求めるための関数 square5 を以下のように実装して呼び出しています。また、しきい値は全て 1E-6 に統一し、BisectionMethod の定義域は [ 2, 3 ] としてあります。
double square5( double d )
{
return( pow( d, 2 ) - 5 );
}
sqrt = 1.25 ; gap = 1.25 sqrt = 1.875 ; gap = 0.625 sqrt = 2.1875 ; gap = 0.3125 sqrt = 2.34375 ; gap = 0.15625 sqrt = 2.265625 ; gap = 0.078125 sqrt = 2.2265625 ; gap = 0.0390625 sqrt = 2.24609375 ; gap = 0.01953125 sqrt = 2.236328125 ; gap = 0.009765625 sqrt = 2.2314453125 ; gap = 0.0048828125 sqrt = 2.23388671875 ; gap = 0.00244140625 sqrt = 2.235107421875 ; gap = 0.001220703125 sqrt = 2.2357177734375 ; gap = 0.0006103515625 sqrt = 2.23602294921875 ; gap = 0.00030517578125 sqrt = 2.23617553710938 ; gap = 0.000152587890625 sqrt = 2.23609924316406 ; gap = 7.62939453125e-05 sqrt = 2.23606109619141 ; gap = 3.814697265625e-05 sqrt = 2.23608016967773 ; gap = 1.9073486328125e-05 sqrt = 2.23607063293457 ; gap = 9.5367431640625e-06 sqrt = 2.23606586456299 ; gap = 4.76837158203125e-06 sqrt = 2.23606824874878 ; gap = 2.38418579101562e-06 sqrt = 2.23606705665588 ; gap = 1.19209289550781e-06
gap = 0.5 ; m = 2.25 ; f(m) = 0.0625 gap = 0.25 ; m = 2.125 ; f(m) = -0.484375 gap = 0.125 ; m = 2.1875 ; f(m) = -0.21484375 gap = 0.0625 ; m = 2.21875 ; f(m) = -0.0771484375 gap = 0.03125 ; m = 2.234375 ; f(m) = -0.007568359375 gap = 0.015625 ; m = 2.2421875 ; f(m) = 0.02740478515625 gap = 0.0078125 ; m = 2.23828125 ; f(m) = 0.0099029541015625 gap = 0.00390625 ; m = 2.236328125 ; f(m) = 0.00116348266601562 gap = 0.001953125 ; m = 2.2353515625 ; f(m) = -0.00320339202880859 gap = 0.0009765625 ; m = 2.23583984375 ; f(m) = -0.00102019309997559 gap = 0.00048828125 ; m = 2.236083984375 ; f(m) = 7.15851783752441e-05 gap = 0.000244140625 ; m = 2.2359619140625 ; f(m) = -0.000474318861961365 gap = 0.0001220703125 ; m = 2.23602294921875 ; f(m) = -0.000201370567083359 gap = 6.103515625e-05 ; m = 2.23605346679688 ; f(m) = -6.48936256766319e-05 gap = 3.0517578125e-05 ; m = 2.23606872558594 ; f(m) = 3.34554351866245e-06 gap = 1.52587890625e-05 ; m = 2.23606109619141 ; f(m) = -3.07740992866457e-05 gap = 7.62939453125e-06 ; m = 2.23606491088867 ; f(m) = -1.37142924359068e-05 gap = 3.814697265625e-06 ; m = 2.2360668182373 ; f(m) = -5.18437809660099e-06 gap = 1.9073486328125e-06 ; m = 2.23606777191162 ; f(m) = -9.19418198463973e-07
√5 = 2.236067977... なので、1E-6 の桁までは一致した結果が得られています。
二分探索は、配列がソートされていることが前提条件となることを除けば、データ探索の用途にはかなり有用なアルゴリズムでした。配列に要素を格納するときの順番が必要でない場合は、最初からソートされた状態で配列を形成することができれば常に二分探索によって高速な探索処理を実現することができます。ここでは二分探索と同等なデータ探索が可能となるデータ構造の「二分探索木 (Binary Search Tree)」を紹介します。
二分探索木は、ソート・ルーチンの「ヒープ・ソート」の章で紹介した「二分木 (Binary Tree)」と同じ構成を持ちます。各要素は「節点 (Node)」と呼ばれる位置にあり、各節点は最大二つの「子 (Child Node)」を左右に持ちます。このとき、子に対する上側の節点が「親 (Parent Node)」となり、親を持たない最も上側の節点を「根 (Root Node)」、逆に子を持たない最下層の節点を「葉 (Leaf Node)」といいます。二分探索木の形にするには、任意の節点を A としたとき、左側の子から始まる部分木には A に入ったデータより小さなデータ、逆に右側の子から始まる部分木には A に入ったデータより大きなデータが位置するように木を構成する必要があります。
二分探索木からのデータ検索は次の手順で行えます。
| 1) | 節の位置を示す変数 N を、根の位置 R で初期化する |
| 2) | 検索対象のデータ X を、N に置いたデータ Y と比較する |
| 3) |
|
| 4) | 葉に突き当たった時点で対象データがなく探索不成功 |
探索が不成功 (対象データが存在しない) の場合にどのような処理にするかは利用目的によって異なりますが、通常は二分木の中に新たな要素として追加します。また、見つかった場合の処理内容も同様で、例えば見つかった回数を数えたり、他のデータを登録するなどの用途が考えられます。
まずは、二分探索木のデータ構成の定義と、データを探索する処理のサンプル・プログラムを示します。
/* BinarySearchTree : 二分探索木クラス */ template<class K, class T, class Cmp = std::less<K> > class BinarySearchTree { /* Node_ : 節を表す構造体(内部クラス) */ struct Node_ { K key_; // キー T value_; // 値 Node_* left_; // 左側の子へのポインタ Node_* right_; // 右側の子へのポインタ // コンストラクタ Node_() : key_( K() ), value_( T() ), left_( 0 ), right_( 0 ) {} }; public: // size_type型 typedef typename vector<Node_>::size_type size_type; private: vector<Node_> nodes_; // 節を保持する配列 Cmp cmp_; // 要素を比較する関数 size_type sz_; // 登録した要素数 /* add : キー・値の追加 const K& key : キー const T& value : 登録する値 戻り値 : 登録した節へのポインタ(失敗した場合はNULL) */ Node_* add( const K& key, const T& value ); public: /* コンストラクタ size_t sz : 登録可能な要素の最大数 const Cmp& cmp : 比較用関数 */ BinarySearchTree( size_t sz, const Cmp& cmp = Cmp() ) : nodes_( sz ), cmp_( cmp ), sz_( 0 ) {} /* get : 値の取得 const K& key : キー T& value : 取得した値を保持する変数 戻り値 : 取得に成功 ... true ; キーが見つからなかった ... false */ bool get( const K& key, T& value ) const; /* put : 値の登録 const K& key : キー const T& value : 登録する値 戻り値 : 登録に成功 ... true ; これ以上登録できない ... false */ bool put( const K& key, const T& value ); // 登録された要素の数 size_type size() { return( sz_ ); } // 登録可能な要素の最大数 size_type capacity() { return( nodes_.size() ); } }; /* BinarySearchTree<K,T,Cmp>::add : キー・値の追加 const K& key : キー const T& value : 登録する値 戻り値 : 登録した節へのポインタ(失敗した場合はNULL) */ template<class K, class T, class Cmp> typename BinarySearchTree<K,T,Cmp>::Node_* BinarySearchTree<K,T,Cmp>::add( const K& key, const T& value ) { // すでに満杯なら NULL を返す if ( sz_ >= nodes_.size() ) return( 0 ); nodes_[sz_].key_ = key; nodes_[sz_].value_ = value; ++sz_; return( &nodes_[sz_ - 1] ); } /* BinarySearchTree<K,T,Cmp>::get : 値の取得 const K& key : キー T& value : 取得した値を保持する変数 戻り値 : 取得に成功 ... true ; キーが見つからなかった ... false */ template<class K, class T, class Cmp> bool BinarySearchTree<K,T,Cmp>::get( const K& key, T& value ) const { if ( sz_ == 0 ) return( false ); // 現在の節(根のポインタで初期化) const Node_* node = &nodes_[0]; while ( node != 0 ) { if ( cmp_( key, node->key_ ) ) { node = node->left_; } else if ( cmp_( node->key_, key ) ) { node = node->right_; } else { value = node->value_; return( true ); } } return( false ); } /* BinarySearchTree<K,T,Cmp>::put : 値の登録 const K& key : キー const T& value : 登録する値 戻り値 : 登録に成功 ... true ; これ以上登録できない ... false */ template<class K, class T, class Cmp> bool BinarySearchTree<K,T,Cmp>::put( const K& key, const T& value ) { // 要素が一つもなければ無条件で登録 if ( sz_ == 0 ) return( add( key, value ) != 0 ); // 現在の節(根のポインタで初期化) Node_* node = &nodes_[0]; for ( ; ; ) { if ( cmp_( key, node->key_ ) ) { if ( node->left_ == 0 ) { // 左側の子に追加 node->left_ = add( key, value ); return( node->left_ != 0 ); } else { node = node->left_; } } else if ( cmp_( node->key_, key ) ) { if ( node->right_ == 0 ) { // 右側の子に追加 node->right_ = add( key, value ); return( node->right_ != 0 ); } else { node = node->right_; } } else { // キーが一致する要素が見つかった node->value_ = value; return( true ); } } return( false ); }
BinarySearchTree は二分探索木を構築するためのクラスで、テンプレート引数として K, T, Cmp の三つを持っています。K は要素をソートするときに使われるキーの型を表し、T は実際の値に対するデータの型を表します。従って、要素は実際の値ではなくキーを使ってソートされることになります。当然、キーと値は同じものが利用できる場合も多々ありますが、その場合はキーと値の両方に同じ値をセットするか、キーだけを利用して値は無視することになります。また、通常はキー(値)のみを要素としたクラスを別途用意することになるでしょう。
Cmp はキーを比較するための関数オブジェクトなので、デフォルトを STL (Standard Template Library) にある less<K> としています。文字列に対して大文字と小文字を区別しない比較など、特別な要素比較が必要な場合は他の比較関数に切り替えることで対応が可能です。
BinarySearchTree クラスは、内部クラスとして Node_ を持ちます。これは各節を表す構造体であり、キー key_ と値 value_、二つの子へのポインタ left_, right_ を変数として定義しています。二分探索木は、この Node_ 型の要素を持つ可変長配列 vector を使って構築されています。このクラス変数は nodes_ で、コンストラクタであらかじめ指定されたサイズに初期化しておきます。このサイズは後で変更することはできません。リサイズした時、配列はメモリ上に再配置される可能性があり、要素にある子へのポインタが無効になる場合があるためです。リサイズを許可する場合は、再配置の場合を想定してポインタを更新する処理が必要になります。なお、メンバ変数 sz_ は登録した要素数を表し、その値はメンバ関数 size を使って取得することができます。また、確保した領域の大きさは capacity を使って確認することができます。
値の検索は get、登録は put をそれぞれ使います。get は、引数として渡したキー key を各節にあるキーと比較して、引数側が小さければ left_、大きければ right_ 側へたどる操作を繰り返します。一致した節が見つかったらその値を value にセットして true を返し、見つからなかったら (節へのポインタが NULL になったら) false を返します。put も基本的な処理の流れは変わりませんが、子のポインタが NULL になったら新たな節を追加する処理が追加され、一致した節が見つかったら新たな値に置き換えるようになっている部分が異なります。
二分探索木を使い、要素の登録と検索の処理時間を計測した結果を以下に示します。今回も、対象の要素は整数値、要素の取りうる最大値 DATA_MAX は 32 ビットで表現できる最大値 ( 0xFFFFFFFF ) と 1000 の二つとしています。put に対するテストでは、あらかじめ用意した datasize 分のデータ列を順番に BinarySearchTree へ登録する処理を 10 回行い、一回の登録に要する平均時間を示しています。また、get ではランダムな数を探索する処理を 1000 回行い、その時間の平均を示しています。どちらの時間も単位は μsec になります。
比較材料として、STL のコンテナクラス map を使い、登録関数 (operator[]) と探索関数 (find) による全く同じ条件での計測結果を併せて示してあります。map も内部では二分探索木を利用していると思われます。
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
グラフの横軸は今回も対数目盛にしてあります。登録時は、DATA_MAX = 0xFFFFFFFF の場合、要素数が多くなると処理時間が長くなる傾向が見られますが、DATA_MAX = 1000 の場合は逆に処理時間は短くなっています。重複する要素が多ければ値の更新のみで完了する処理が増えるので、一回あたりの処理が短くなるのは納得できる結果です。探索に対しては、DATA_MAX = 0xFFFFFFFF ではやはり要素数が多くなると処理時間が長くなっています(サンプル・プログラムの場合のみ)。DATA_MAX = 1000 のときは時間の変化はないように見えます。最大要素数を増やしても登録される要素は千個程度にしかならないので、これは当然の結果です。
map クラスと比較すると、傾向は非常によく似ています。map よりも性能がよいのは、サンプル・プログラムが必要最低限の機能しか実装していないからでしょう。map では最大要素数の指定はなく、登録できる数に制限はないので、必要に応じて内部でデータの再配置などを実施しているはずです。なお、map クラスの場合、探索処理は DATA_MAX に関係なく処理時間に変化がないように見えます。
二分探索木のパフォーマンスは登録するデータの配列の傾向に大きく影響を受けます。下図は、データ列をソートした状態で二分探索木に登録・探索した時の処理時間を示したものです。
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
サンプル・プログラムでは、DATA_MAX = 0xFFFFFFFF の場合に要素数と比例して処理時間が長くなる傾向が見られます。これは、線形探索と同様の傾向です。二分探索木は、各節にあるデータとの大小関係を見て左右の子のいずれかに値をセットします。ソート済みのデータ列では常に左右いずれかの子だけをたどることになり、結果として線形リストと同等の状態になります。ソート済みのデータ列を利用してしまうような場合は容易に想定できるので、それに対処するための手段が必要となります。
検索アルゴリズムでは、データを比較する回数が処理速度を左右します。二分探索木の場合、探索回数は木の高さ以下になりますが、木の高さは節の個数 (すなわちデータ数) だけではなくて、木の形にも左右されます。
N 個の節からなる二分探索木の高さは、節が左右均等に配分されている場合 log2N 程度になります。しかし、木が完全に退化して線形リストと同じ形になった場合は N と等しくなります。データの挿入を同時に行っている場合は木がどのような形に成長するか予測することができないため、最悪 N 回の比較を行う必要が生じる可能性もあるわけです。前節で最後に示したように、ソート済みのデータを追加した場合は二分探索木が線形リストと同じ状態になり、処理時間はデータ数に比例した状態になりました。
木の左右のバランスがとれた状態のことを平衡な (Balanced) 状態といいます。特に、すべての節において、左右の部分木に含まれる節の個数の差が 0 か 1 である状態を「完全平衡 (Perfectly Balanced)」といいます。
完全平衡木は、同じ個数の節を持つ木の中で最も高さが低いので、二分検索木を常に完全平衡状態に保つことができれば比較回数を最小に抑えることができます。しかし、二分検索木に節を追加してから完全平衡に戻す処理はかなり複雑らしく、探索処理が多少早くなったくらいでは元をとることができないようです。
そこで、木の高さを最小にすることはあきらめて、"すべての節において、左右の部分木の高さの差が 1 以下"という、条件をやや緩めた平衡性の定義が存在します。この平衡木は、提案者であるロシアの二人の数学者「Georgy Maximovich Adelson-Velsky」と「Evgenii Mikhailovich Landis」の名をとって「AVL木 (AVL Tree)」と呼ばれています。AVL 木の高さは、完全平衡木よりせいぜい 50% 程度しか高くならないことが証明されています。
ある節を挿入したときに平衡が崩れる可能性があるのは、挿入した節の「祖先 (Ancestor ; ある節から根までさかのぼるときに通った節)」に限られるので、平衡を保ちながら節を挿入する処理フローは次のようになります。
最も重要なのが三番目の処理ですが、再平衡化のためにどのように節を回転させればよいかは、どのようなときに平衡性が崩れるかを考えてみれば自ずと明らかになります。根に節がひとつぶら下がった最も単純な二分探索木を考えてみた場合、この木に節を追加することで左右の節の高さが 1 より大きくなるパターンは、以下の 4 つになります (ここで根の節を A、その子の節を B、新たに追加する節を C としておきます)。
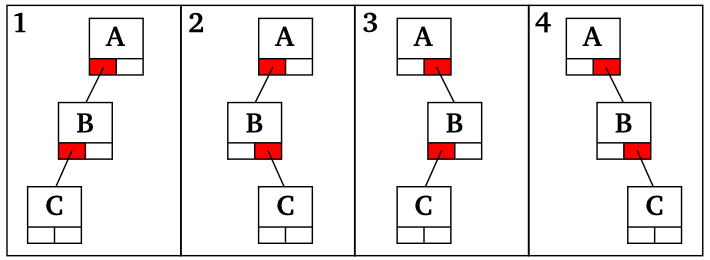 |
| 図 3-1. 節の追加により平衡性が崩れるパターン |
上に示した三つの節を持つ部分木において、節の高さの差が 1 になるようにするには、それぞれ次のように節を回転させればよいことになります。
 |
| 図 3-2. 平衡性が回復した状態 |
ここでは二つの節のみを持つ部分木に新たな節を挿入した場合を考えましたが、節 A, B, C にも部分木がぶら下がっていて、かつ A と C の部分木における高さの差が 1 である場合、節 C の部分木に新たな節が挿入されて高さの差が 1 より大きくなる場合と、それを再平衡化したときのパターンも上に示した 4 つのみとなります。すなわち
文章にしただけでは少々わかりづらいので、下の図を参考にしてください。
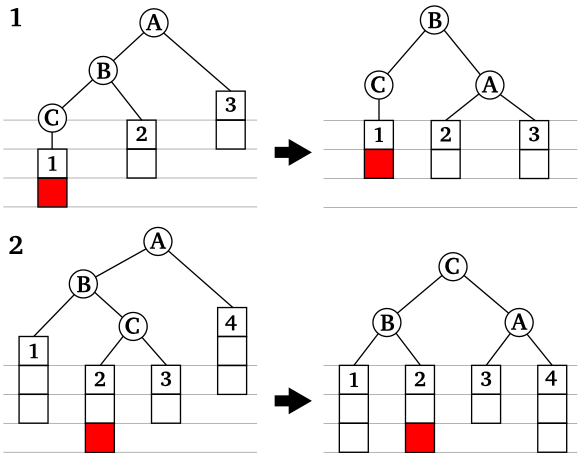 |
| 図 3-3. 平衡性が崩れる場合とその回復の例 |
上の図では、1 と 2 の二つのパターンしか示していませんが、3, 4 はそれぞれ 1, 2 のパターンを左右反転させたものになります。
A, B, C を回転させて再平衡化した後に、下にぶら下がっていた部分木が別の節へつなぎ直されている場合がありますが、再リンク後もそれぞれの節における大小関係が崩れていないことに注意してください。たとえば、パターン 1 では B の右部分木 ( 図中の部分木 2 ) は A の左部分木に再リンクされていますが、部分木 2 の全要素は A の要素と比べて小さいと判断された節しかないので ( 部分木 2 の全要素 ) < ( A の要素 ) が成立しています。
文献 2 に記載された内容に従い、上記再平衡化はそれぞれ
と呼ぶことにします。この呼び方は一般的なものではないようですが、内容を非常によく表している名前だと思います。LL や LR は子の節が左(Left) と右(Right) のどちらにぶら下がっているかを示していて、例えば LL ならば、B は A の左側、C も A の左側にリンクされていることを表しています。また、一重・二重回転とは、回転操作が一回で完了できる場合と二回必要な場合の二通りあることを意味しています。というのも、LR 二重回転なら、根から遠い側から順に RR 一重回転と LL 一重回転を行う処理と同等ですし、RL 二重回転ならその逆で LL 一重回転と RR 一重回転の組み合わせで処理することができます。
| RR 一重回転 |
|---|
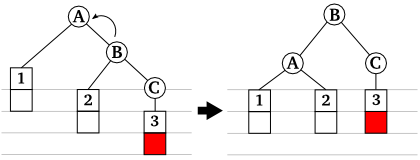 |
| LL 一重回転 |
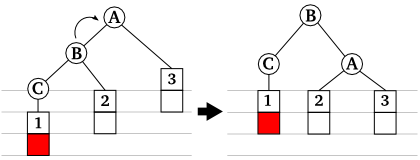 |
| LR 二重回転 |
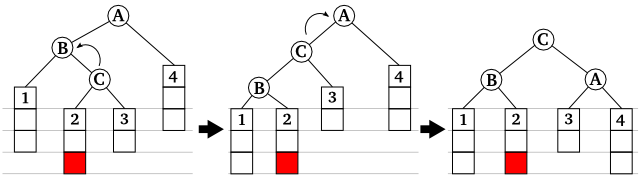 |
上図は、RR / LL 一重回転と LR 二重回転の処理の流れを表しています。RR 一重回転では、B を親の A と入れ替えて、B の左側に A がぶら下がるようにしています。また、元々 B の左側にあった部分木 2 は、A の右側にぶら下げます。LL 一重回転は、右と左が入れ替わっただけで、処理の流れには変化はありません。
LR 二重回転では、最初に B, C の節と部分木 3 の根を使って RR 一重回転を行い、次に A, C, B を使って LL 一重回転を行います。前述の通り、一重回転を二回行なっているので、二重回転という名が付けられています。RL 二重回転も右と左が入れ替わるだけで処理は LR 二重回転と同等です。
AVL 木を使ったデータ探索処理のサンプル・プログラムを以下に示します。
/* AVLTree : AVL平衡木クラス */ template<class K, class T, class Cmp = std::less<K> > class AVLTree { /* Node_ : 節を表す構造体(内部クラス) */ struct Node_ { K key_; // キー T value_; // 値 int balance_; // 節の平衡度 Node_* left_; // 左側の子へのポインタ Node_* right_; // 右側の子へのポインタ // コンストラクタ Node_() : key_( K() ), value_( T() ), balance_( 0 ), left_( 0 ), right_( 0 ) {} }; /* LRFlg_ : 節のバランスを表す構造体(内部クラス) */ struct LRFlg_ { Node_* node_; // 対象の節へのポインタ int flag_; // 左右どちらの節が重くなったか // 右側なら +1、左側なら -1、等しいなら 0 // コンストラクタ LRFlg_( Node_* node = 0, int flag = 0 ) : node_( node ), flag_( flag ) {} }; public: // size_type型 typedef typename vector<Node_>::size_type size_type; private: vector<Node_> nodes_; // 節を保持する配列 Node_* root_; // 根の反復子 Cmp cmp_; // 要素を比較する関数 size_type sz_; // 登録した要素数 // LRFlg の size_type 型 typedef typename vector<LRFlg_>::size_type LRFlg_st; /* add : キー・値の追加 const K& key : キー const T& value : 登録する値 戻り値 : 登録した節へのポインタ(失敗した場合はNULL) */ Node_* add( const K& key, const T& value ); /* avlCheck : AVL平衡のチェック const vector<LRFlg_>& lfFlg : 各節のバランスを表す配列 */ void avlCheck( const vector<LRFlg_>& lfFlg ); /* linkUpperNode : 上位の節のリンクを修正する const vector<LRFlg_>& lrFlg : 各節のバランスを表す配列 LRFlg_st ai, bi 節 A, B に対する添字 */ void linkUpperNode( const vector<LRFlg_>& lrFlg, LRFlg_st ai, LRFlg_st bi ); /* l/rRotate : Left/Right回転 const vector<LRFlg_>& lrFlg : 各節のバランスを表す配列 LRFlg_st ai, bi 節 A, B に対する添字 */ void lRotate( const vector<LRFlg_>& lrFlg, LRFlg_st ai, LRFlg_st bi ); void rRotate( const vector<LRFlg_>& lrFlg, LRFlg_st ai, LRFlg_st bi ); /* ll/rrSingleRotate : LL/RR一重回転 const vector<LRFlg_>& lrFlg : 各節のバランスを表す配列 LRFlg_st ai, bi 節 A, B に対する添字 */ void llSingleRotate( const vector<LRFlg_>& lrFlg, LRFlg_st ai, LRFlg_st bi ); void rrSingleRotate( const vector<LRFlg_>& lrFlg, LRFlg_st ai, LRFlg_st bi ); /* lr/rlDoubleRotate : LR/RL二重回転 const vector<LRFlg_>& lfFlg : 各節のバランスを表す配列 LRFlg_st i : 節 A の位置を示す添字 */ void lrDoubleRotate( const vector<LRFlg_>& lrFlg, LRFlg_st i ); void rlDoubleRotate( const vector<LRFlg_>& lrFlg, LRFlg_st i ); public: /* コンストラクタ size_t sz : 登録可能な要素の最大数 const Cmp& cmp : 比較用関数 */ AVLTree( size_t sz, const Cmp& cmp = Cmp() ) : nodes_( sz ), root_( 0 ), cmp_( cmp ), sz_( 0 ) {} /* get : 値の取得 const K& key : キー T& value : 取得した値を保持する変数 戻り値 : 取得に成功 ... true ; キーが見つからなかった ... false */ bool get( const K& key, T& value ) const; /* put : 値の登録 const K& key : キー const T& value : 登録する値 戻り値 : 登録に成功 ... true ; これ以上登録できない ... false */ bool put( const K& key, const T& value ); // 登録された要素の数 size_type size() { return( sz_ ); } // 登録可能な要素の最大数 size_type capacity() { return( nodes_.size() ); } }; /* AVLTree<K,T,Cmp>::add : キー・値の追加 const K& key : キー const T& value : 登録する値 戻り値 : 登録した節へのポインタ(失敗した場合はNULL) */ template<class K, class T, class Cmp> typename AVLTree<K,T,Cmp>::Node_* AVLTree<K,T,Cmp>::add( const K& key, const T& value ) { // すでに満杯なら NULL を返す if ( sz_ >= capacity() ) return( 0 ); nodes_[sz_].key_ = key; nodes_[sz_].value_ = value; if ( sz_ == 0 ) root_ = &nodes_[0]; // 初登録なら root_ を初期化 ++sz_; return( &nodes_[sz_ - 1] ); } /* AVLTree<K,T,Cmp>::get : 値の取得 const K& key : キー T& value : 取得した値を保持する変数 戻り値 : 取得に成功 ... true ; キーが見つからなかった ... false */ template<class K, class T, class Cmp> bool AVLTree<K,T,Cmp>::get( const K& key, T& value ) const { // 現在の節(根のポインタで初期化) const Node_* node = root_; while ( node != 0 ) { if ( cmp_( key, node->key_ ) ) { node = node->left_; } else if ( cmp_( node->key_, key ) ) { node = node->right_; } else { value = node->value_; return( true ); } } return( false ); } /* AVLTree<K,T,Cmp>::put : 値の登録 const K& key : キー const T& value : 登録する値 戻り値 : 登録に成功 ... true ; これ以上登録できない ... false */ template<class K, class T, class Cmp> bool AVLTree<K,T,Cmp>::put( const K& key, const T& value ) { vector<LRFlg_> lrFlg; // 各節のバランスを登録する配列 // 要素が一つもなければ無条件で登録 if ( sz_ == 0 ) return( add( key, value ) != 0 ); // 現在の節(根のポインタで初期化) Node_* node = root_; for ( ; ; ) { // データは左側へ if ( cmp_( key, node->key_ ) ) { lrFlg.push_back( LRFlg_( node, -1 ) ); // 左部分木が重くなった if ( node->left_ == 0 ) { // 左側の子に追加 node->left_ = add( key, value ); if ( node->left_ != 0 ) { lrFlg.push_back( LRFlg_( node->left_ ) ); avlCheck( lrFlg ); } return( node->left_ != 0 ); } else { node = node->left_; } // データは右側へ } else if ( cmp_( node->key_, key ) ) { lrFlg.push_back( LRFlg_( node, 1 ) ); // 右部分木が重くなった if ( node->right_ == 0 ) { // 右側の子に追加 node->right_ = add( key, value ); if ( node->right_ != 0 ) { lrFlg.push_back( LRFlg_( node->right_ ) ); avlCheck( lrFlg ); } return( node->right_ != 0 ); } else { node = node->right_; } } else { // キーが一致する要素が見つかった node->value_ = value; return( true ); } } return( false ); } /* AVLTree<K,T,Cmp>::avlCheck : AVL平衡のチェック const vector<LRFlg_>& lrFlg : 各節のバランスを表す配列 */ template<class K, class T, class Cmp> void AVLTree<K,T,Cmp>::avlCheck( const vector<LRFlg_>& lrFlg ) { unsigned int i = lrFlg.size(); if ( i < 2 ) return; for ( --i ; i > 0 ; --i ) { ( lrFlg[i - 1].node_ )->balance_ += lrFlg[i - 1].flag_; // 平衡度の更新 // 平衡度は 0 ... 平衡性は改善されたのでループを抜ける if ( ( lrFlg[i - 1].node_ )->balance_ == 0 ) break; // 平衡度は 1 を超えた ... 再平衡化が必要 if ( ( lrFlg[i - 1].node_ )->balance_ > 1 ) { if ( ( lrFlg[i].node_ )->balance_ > 0 ) rrSingleRotate( lrFlg, i - 1, i ); // 次の節の平衡度は正 ... RR一重回転 else rlDoubleRotate( lrFlg, i - 1 ); // 次の節の平衡度は負 ... RL二重回転 // 次の節の平衡度はゼロにはならない。ゼロならば前の処理でループを抜けている break; // 平衡度は -1 を超えた ... 再平衡化が必要 } else if ( ( lrFlg[i - 1].node_ )->balance_ < -1 ) { if ( ( lrFlg[i].node_ )->balance_ > 0 ) lrDoubleRotate( lrFlg, i - 1 ); // 次の節の平衡度は正 ... LR二重回転 else llSingleRotate( lrFlg, i - 1, i ); // 次の節の平衡度は負 ... LL一重回転 // 次の節の平衡度はゼロにはならない。ゼロならば前の処理でループを抜けている break; } } } /* AVLTree<K,T,Cmp>::linkUpperNode : 上位の節のリンクを修正する const vector<LRFlg_>& lrFlg : 各節のバランスを表す配列 LRFlg_st ai, bi 節 A, B に対する添字 */ template<class K, class T, class Cmp> void AVLTree<K,T,Cmp>::linkUpperNode( const vector<LRFlg_>& lrFlg, LRFlg_st ai, LRFlg_st bi ) { Node_* b = lrFlg[bi].node_; // 節 B へのポインタ // 節 A が lrFlg の最初の要素なら A は根なので、B へ切り替える if ( ai == 0 ) { root_ = b; } else { const LRFlg_& p = lrFlg[ai - 1]; // 節 A の親 // 親からたどった側へ B をリンクさせる if ( p.flag_ > 0 ) ( p.node_ )->right_ = b; else ( p.node_ )->left_ = b; } } /* AVLTree<K,T,Cmp>::lRotate : Left回転 const vector<LRFlg_>& lrFlg : 各節のバランスを表す配列 LRFlg_st ai, bi 節 A, B に対する添字 */ template<class K, class T, class Cmp> void AVLTree<K,T,Cmp>::lRotate( const vector<LRFlg_>& lrFlg, LRFlg_st ai, LRFlg_st bi ) { Node_* a = lrFlg[ai].node_; // 節 A のポインタ Node_* b = lrFlg[bi].node_; // 節 B のポインタ // 節 B の右の子へのポインタを一時退避 Node_* buff = b->right_; b->right_ = a; // B->right = A a->left_ = buff; // A->left = B->right // 一レベル上位のリンクポインタを更新 linkUpperNode( lrFlg, ai, bi ); } /* AVLTree<K,T,Cmp>::rRotate : Right回転 const vector<LRFlg_>& lrFlg : 各節のバランスを表す配列 LRFlg_st ai, bi 節 A, B に対する添字 */ template<class K, class T, class Cmp> void AVLTree<K,T,Cmp>::rRotate( const vector<LRFlg_>& lrFlg, LRFlg_st ai, LRFlg_st bi ) { Node_* a = lrFlg[ai].node_; // 節 A のポインタ Node_* b = lrFlg[bi].node_; // 節 B のポインタ // 節 B の左の子へのポインタを一時退避 Node_* buff = b->left_; b->left_ = a; // B->left = A a->right_ = buff; // A->right = B->left // 一レベル上位のリンクポインタを更新 linkUpperNode( lrFlg, ai, bi ); } /* AVLTree<K,T,Cmp>::llSingleRotate : LL一重回転 const vector<LRFlg_>& lrFlg : 各節のバランスを表す配列 LRFlg_st ai, bi 節 A, B に対する添字 */ template<class K, class T, class Cmp> void AVLTree<K,T,Cmp>::llSingleRotate( const vector<LRFlg_>& lrFlg, LRFlg_st ai, LRFlg_st bi ) { lRotate( lrFlg, ai, bi ); // 節 A, B をLeft回転 // 平衡度のリセット ( lrFlg[ai].node_ )->balance_ = 0; ( lrFlg[bi].node_ )->balance_ = 0; } /* AVLTree<K,T,Cmp>::rrSingleRotate : RR一重回転 const vector<LRFlg_>& lrFlg : 各節のバランスを表す配列 LRFlg_st ai, bi 節 A, B に対する添字 */ template<class K, class T, class Cmp> void AVLTree<K,T,Cmp>::rrSingleRotate( const vector<LRFlg_>& lrFlg, LRFlg_st ai, LRFlg_st bi ) { rRotate( lrFlg, ai, bi ); // 節 A, B をRight回転 // 平衡度のリセット ( lrFlg[ai].node_ )->balance_ = 0; ( lrFlg[bi].node_ )->balance_ = 0; } /* lrDoubleRotate : LR二重回転 const vector<LRFlg_>& lfFlg : 各節のバランスを表す配列 LRFlg_st i : 節 A の位置を示す添字 */ template<class K, class T, class Cmp> void AVLTree<K,T,Cmp>::lrDoubleRotate( const vector<LRFlg_>& lrFlg, LRFlg_st i ) { rRotate( lrFlg, i + 1, i + 2 ); // B, C を Right回転 lRotate( lrFlg, i, i + 2 ); // A, C を Left回転 // 平衡度のリセット if ( ( lrFlg[i + 2].node_ )->balance_ > 0 ) { // 節 C は右が重い ( lrFlg[i].node_ )->balance_ = 0; // 節 A は偏りなし ( lrFlg[i + 1].node_ )->balance_ = -1; // 節 B は左に偏る } else if ( ( lrFlg[i + 2].node_ )->balance_ < 0 ) { // 節 C は左が重い ( lrFlg[i].node_ )->balance_ = 1; // 節 A は右に偏る ( lrFlg[i + 1].node_ )->balance_ = 0; // 節 B は偏りなし } else { // 節 C は偏りなし ( lrFlg[i].node_ )->balance_ = 0; // 節 A は偏りなし ( lrFlg[i + 1].node_ )->balance_ = 0; // 節 B は偏りなし } ( lrFlg[i + 2].node_ )->balance_ = 0; } /* rlDoubleRotate : RL二重回転 const vector<LRFlg_>& lfFlg : 各節のバランスを表す配列 LRFlg_st i : 節 A の位置を示す添字 */ template<class K, class T, class Cmp> void AVLTree<K,T,Cmp>::rlDoubleRotate( const vector<LRFlg_>& lrFlg, LRFlg_st i ) { lRotate( lrFlg, i + 1, i + 2 ); // B, C を Left回転 rRotate( lrFlg, i, i + 2 ); // A, C を Right回転 // 平衡度のリセット if ( ( lrFlg[i + 2].node_ )->balance_ > 0 ) { // 節 C は右が重い ( lrFlg[i].node_ )->balance_ = -1; // 節 A は左に偏る ( lrFlg[i + 1].node_ )->balance_ = 0; // 節 B は偏りなし } else if ( ( lrFlg[i + 2].node_ )->balance_ < 0 ) { // 節 C は左が重い ( lrFlg[i].node_ )->balance_ = 0; // 節 A は偏りなし ( lrFlg[i + 1].node_ )->balance_ = 1; // 節 B は右に偏る } else { // 節 C は偏りなし ( lrFlg[i].node_ )->balance_ = 0; // 節 A は偏りなし ( lrFlg[i + 1].node_ )->balance_ = 0; // 節 B は偏りなし } ( lrFlg[i + 2].node_ )->balance_ = 0; }
AVL 木のクラス AVLTree は、前の節で示した BinarySearchTree クラスを元に作成しています。内部クラスの Node_ に対しては、新たなメンバ変数 balance_ を追加して、各節の平衡度 ( 左右の部分木の高さの差 ) はこの変数に格納します。balance_ は、右側が重い場合に正値、左側が重い場合に負値をとり、等しい場合はゼロとします。
Node_ とは別の新たな内部クラスとして、新しい節を追加することによって左右どちらの節が重くなったのかを保持するための LRFlg_ クラスを定義します。このクラスは、対象の節へのポインタ node_ と重くなった側の節を表す flag_ をメンバ変数として持ちます。flag_ は、右側が重くなった場合 +1、左側が重くなった場合 -1 を代入し、正負で判断ができるようにします。bool 型を使ってもよいのですが、あとで balance_ を更新するときにこの値を利用するため整数型を利用しています。
メンバ変数は、根の節を保持するための root_ を新規に追加しています。BinarySearchTree クラスは配列の先頭が常に根の節になりますが、AVLTree は平衡性を保つための回転によって根の節が変化するため、その場所を保持しておく必要があります。
メンバ関数の中での大きな変更点は put 関数で、対象のキーと値を登録すべき節への道筋を LRFlg_ 型の配列 lrFlg に根から順番に登録し、各節において左右のどちらの子へたどったのかを記録しておきます。キーが一致する節が見つかった場合は節は追加されていないので平衡性のチェックは不要ですが、キーが一致する節が見つからず、新たに節を追加した場合は平衡性が崩れた可能性があるため、ここでメンバ関数 avlCheck に lrFlg を引き渡してチェック処理を行います。
メンバ関数 avlCheck は追加された節の親から根の方向へたどりながら平衡度 balance_ を更新し、その絶対値が 1 を超えたら再平衡化を行います。その振り分け方は以下のようになります。
再平衡化が必要となる
再平衡化が必要となる
平衡度が +1, -1 の場合は、今注目している節については許容範囲であるものの、この影響で上位の節の平衡性が崩れている可能性があるためチェックを続けなければなりません。また、一度平衡性を回復させたら、その上位側の節については平衡度の変化はないので、それ以上チェックを行う必要はなくループを抜けることができます。
平衡性を改善するために節を回転する処理では、節のポインタのつなぎ替えと平衡度 balance_ のリセットが必要になります。節の回転処理は lRotate と rRotate が行いますが、回転後に一つ上位の節とのリンクポインタも更新する必要があり、その処理を関数 linkUpperNode で行っています。特に、回転させた節の中に根が含まれていた場合は根の節が入れ替わるため、節が根であったかどうかを調べる必要があることも注意しなければなりません。平衡度 balance_ のリセットは、平衡性改善のための各処理 ll(rr)SingleRotate, lr(rl)DoubleRotate で行っています。一重回転ならば、入れ替えた節の平衡度はゼロにリセットされるので、balance_ にゼロを代入するだけで済みます。しかし、二重回転の場合、新たに親となった節 (節 C) の平衡度はゼロとなるのに対し、節 A, B は節 C が元々持っていた平衡度によって値が変化するため、少し処理がややこしくなっています。例えば、LR 二重回転において節 C の元々の平衡度が正 (すなわち 1 ) だった場合、節 C は右側の部分木の方が高さが一つだけ高かったことになり、節 A の左側には節 C の右部分木がつながることにより平衡性がリセットされるのに対し、節 B の右側には節 C の左部分木がつながることにより左側の方が 1 だけ高くなり、平衡度は -1 となります。
AVL 木を使い、要素の登録と検索の処理時間を計測した結果を以下に示します。BinarySearchTree と同様に、対象の要素は整数値、要素の取りうる最大値 DATA_MAX は 32 ビットで表現できる最大値 ( 0xFFFFFFFF ) と 1000 の二つとしています。put に対するテストでは、あらかじめ用意した datasize 分のデータ列を順番に AVLTree へ登録する処理を 10 回行い、一回の登録に要する平均時間を示しています。また、get ではランダムな数を探索する処理を 1000 回行い、その時間の平均を示しています。どちらの時間も単位は μsec になります。また、比較材料としては前節で示した BinarySearchTree による同じ条件での計測結果を示しています。
まずは乱数列を AVL 木に登録した場合の結果を示します。
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
登録時は、BinarySearchTree と比べると処理時間が長くなっているのに対し、検索時間は両者にほとんど差がありません。節の回転処理は登録時のみに発生するので、これは納得できる結果です。
次に、ソート済みの数列を AVL 木に登録した場合の結果を示します。ここでの比較材料は、STL のコンテナクラス map の登録関数 (operator[]) と探索関数 (find) です。
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
BinarySearchTree では処理時間が線形に変化していたのに対し、AVLTree では変化がほとんど見られません。節の回転により平衡性が保たれ、処理回数が抑えられていることがこの結果からわかります。完全にランダムなデータを登録することが保証されない限りは平衡性を保つ処理は必須になります。多少のオーバーヘッドが許容できるのであれば、BinarySearchTree よりは AVLTree を利用した方が処理時間は安定します。map クラスも平衡性を保つための処理を行なっていることはほぼ間違いなさそうです。但し、今回紹介した AVL 木と同じ構成であるかは不明です。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |