ソート・ルーチン

(3) ヒープ・ソート

この章では「ヒープ・ソート(Heap Sort)」と呼ばれるソート処理を紹介したいと思います。「ヒープ・ソート」は「選択ソート」の一種で、データの初期並びにはほとんど影響されず、安定した性能を発揮するのが特徴です。

1) ヒープ構造

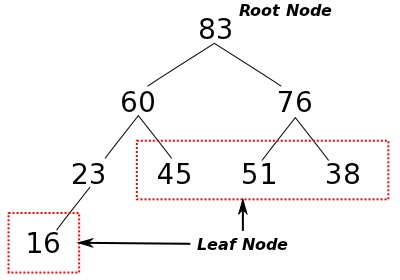
「ヒープ・ソート(Heap Sort)」の名前は、「ヒープ(Heap)」と呼ばれる「二分木 (Binary Tree; 二進木ともいう)」を使うところから付けられています。二分木は下図のような形をしていて、各要素は「節点(Node)」と呼ばれる位置にあり、各節点は最大二つの「子(Child Node)」を下側に持ちます。このとき、子に対してつながった上側の節点を「親(Parent Node)」といいます。また、親を持たない、すなわち二分木の最も上側にある節点は「根(Root Node)」になり、子を持たない最下層の節点は「葉(Leaf Node)」になります。ヒープは、二分木に対して「親の値と子の値の順序関係が全て同一である」という制約条件を満たす必要があります。つまりヒープは、全ての節点に対して、親の値が子の値よりも大きいか等しい(または小さいか等しい)ことになります。よって、ヒープの根には最も大きい(または小さい)値が入ります。

図 1.1 ヒープの例

根からある節点までを結ぶ「経路(Path)」は、その方向が必ず親から子への一方通行であるならば必ず一通りに決まります。この経路の長さ(経路の数)のことをその節点の「深さ(Depth)」といい、深さの等しい節点全体は「レベル(Level)」が等しいといいます。また、ある節点から子の方向に葉までたどったときの経路の長さの中で最大のものをその節点の「高さ(Height)」といいます。
根は深さゼロの節点であり、ただ一つのみになります。その子は深さが 1 で、最大で二つ持つことができます。もっと一般に、深さ d の節点は最大で 2^d 個存在することになり、このとき全ての葉は等しいレベル d の上にあります。そして、葉ではない節点の数は、

なので、葉の数の方が一つ多くなります(補足1)。葉が一つ少なくなれば、両方の数は等しくなりますが、一つしか子を持たない節点が二つ以上存在しないという制約条件を付ければ、さらに葉を一つ少なくすると、子を持たない節点が一つ上のレベルに新たに発生することになり、葉の数は変わらずそれ以外の節点の数が一つ減ることになります。このことから、先ほど述べた制約条件のもとでは、葉の数は全節点数の半分より少なくなることはありません。

ヒープは二分木の一種なので、そのデータ構造も二分木で表現することになります。二分木は、各節点の値とその左右の子の節点の参照先を備えた再帰的な構造体で表現するのが一般的です。例えば int 型の数値データを要素とする二分木の場合、

struct node {
  int key;     // 節点の値
  node* left;  // 左の子の参照先
  node* right; // 右の子の参照先
};

のような構造体で一つの節点を表し、left で左側の子、right で右側の子を参照する形とします。しかし、二分木は配列で擬似的に表現することが可能であり、木の根に配列の先頭要素を、根の左側の子に第二要素、右側の子に第三要素、というように、配列の各要素を上→下、左→右の順序で対応づけていくと(下図参照)、ある節点が配列 a[i] に対応しているとき、左側の子は a[( i + 1 ) * 2 - 1]、右側の子は a[( i + 1 ) * 2] にそれぞれ対応するという規則性を持つようになります。

図 1.2 配列とヒープの対応

あるデータ列をヒープの形に再構成するために、次のような処理を行います。

前にも述べたように、一つの葉を持つ節点が高々一つしかない場合、葉の部分は全体の半分か、それより一つ多い数になります。配列の後半部分が葉の要素であると仮定し、最も下側のレベルから順番に要素を追加して順序関係を正しくすれば、最終的にはヒープの形にすることができます。以下に、ヒープを構成する処理の例を示します。

図 1.3 ヒープ構成の例

a) 初期状態	b) 23をヒープに収める
45 51 76 23|38 83 16 60	45 51 76|23 38 83 16 60
c) 23を正しい位置までふるい落とす	d) 76をヒープに収め、ふるい落とす
45 51 76|60 38 83 16 23	45 51|83 60 38 76 16 23
e) 51をヒープに収め、ふるい落とす	f) 45をヒープに収め、ふるい落として完了
45|60 83 51 38 76 16 23	|83 60 76 51 38 45 16 23

葉ではない末尾の節点から根の方向へ順番に親子の要素の大小関係を確認し、親の方が小さければ要素を入れ替える処理を繰り返すので、全ての節点において、親の要素は子の要素よりも必ず小さくなります。従って、根の要素は必ず最大値になります。

ヒープを構成する処理のサンプル・プログラムを以下に示します。

/*
  SwapHeapNode : ヒープが正しい順番に構成されるよう要素を入れ替える

  Ran first : ヒープ領域の根を示すランダム・アクセス反復子
  Ran::difference_type p : 開始する節点の添字(親の節点)
  Ran::difference_type cnt : ヒープの大きさ
  Less less : 要素比較用関数オブジェクト(boolを返す二項叙述関数)
*/
template<class Ran, class Less> void SwapHeapNode( Ran first, typename Ran::difference_type p, typename Ran::difference_type cnt, Less less )
{
  typename Ran::difference_type c = ( p + 1 ) * 2 - 1; // 左側の子の節点

  while ( c < cnt ) {
    // 右側に子があれば大きい方を選択する
    if ( c + 1 < cnt )
      if ( less( first[c], first[c + 1] ) ) ++c;

    if ( less( first[c], first[p] ) ) break;
    swap( first + c, first + p );

    // 入れ替えた子の節点を新たな親として繰り返す
    p = c;
    c = ( p + 1 ) * 2 - 1;
  }
}

/*
  MakeHeap : ヒープを構成する

  Ran first, last : ランダム・アクセス反復子(ヒープ領域の先頭、終了の次の反復子)
  Less less : 要素比較用関数オブジェクト(boolを返す二項叙述関数)
*/
template<class Ran, class Less> void MakeHeap( Ran first, Ran last, Less less )
{
  // 反復子の位置の差
  typedef typename Ran::difference_type difference_type;

  difference_type cnt = last - first;       // データ数
  if ( cnt < 2 ) return;
  difference_type i = ( last - first ) / 2; // 葉の要素の直前の位置
  do {
    --i;
    SwapHeapNode( first, i, cnt, less );
  } while ( i > 0 );
}

SwapHeapNode は、ある節点 p の要素をふるい落とすための関数で、次に紹介するヒープ・ソートの処理でも利用します。要素の交換が行われたら、交換した子の節点を新たな親の節点として、その下側にある節点と比較・交換処理を繰り返します。この関数は、子の節点を引数 p に代入して再帰的に処理させることも可能で、その方が実装もシンプルになりますが、ここではループ処理の形で実現しています。MakeHeap がヒープを構成するメイン・ルーチンで、配列の中央位置から先頭方向(ヒープの上側)をたどりながら、SwapHeapNode を使って各節点の要素をふるい落とす処理を行います。

2) ヒープ・ソート

次は、構築したヒープを使ってデータ列をソートするわけですが、これはヒープを作成したときの処理の流れを少し変更するだけで実現できます。

以下に、ヒープ・ソートの例を示します。

図 2.1 ヒープ・ソートの例

a) 初期状態	b) 根の83を末尾の23と交換する
83 60 76 51 38 45 16 23	23 60 76 51 38 45 16|83
c) 新たな根となった23をふるい落とす	d) 根の76を末尾の16と交換し、16をふるい落とす
76 60 45 51 38 23 16|83	60 51 45 16 38 23|76 83
e) 根の60を末尾の23と交換し、23をふるい落とす	f) 根の51を末尾の23と交換し、23をふるい落とす
51 38 45 16 23|60 76 83	45 38 23 16|51 60 76 83
g) 根の45を末尾の16と交換し、16をふるい落とす	h) 根の38を末尾の23と交換し、23をふるい落とす
38 16 23|45 51 60 76 83	23 16|38 45 51 60 76 83
i) 根の23を末尾の16と交換してソート完了
16 23 38 45 51 60 76 83

ヒープ・ソートのコーディング例を以下に示します。

/*
  HeapSort : ヒープ・ソートによるソート・ルーチン

  Ran first, last : ランダム・アクセス反復子(ヒープ領域の先頭、終了の次の反復子)
  Less less : 要素比較用関数オブジェクト(boolを返す二項叙述関数)
*/
template<class Ran, class Less> void HeapSort( Ran first, Ran last, Less less )
{
  // 反復子の位置の差
  typedef typename Ran::difference_type difference_type;

  MakeHeap( first, last, less );

  difference_type cnt = last - first; // データ数
  while ( cnt > 1 ) {
    --cnt;
    swap( first, first + cnt );
    SwapHeapNode( first, 0, cnt, less );
  }
}

根の要素をふるい落とす処理は、ヒープ構成処理の実装時に SwapHeapNode としてすでに用意してありましたので、ヒープ・ソート処理では、ヒープ構成のための MakeHeap を呼び出し、ヒープの末尾と根の要素を交換してから根の要素を SwapHeapNode でふるい落とす処理を、ヒープの要素がなくなるまで繰り返すだけで実現することができます。

3) 動作テスト

ヒープ・ソートを使ってデータ列をソートさせたときにかかる時間を計測した結果、以下のようになりました。テスト回数は 20 回で、その平均値を示しています。

グラフ 3-1. データ数に対する処理時間の推移グラフ

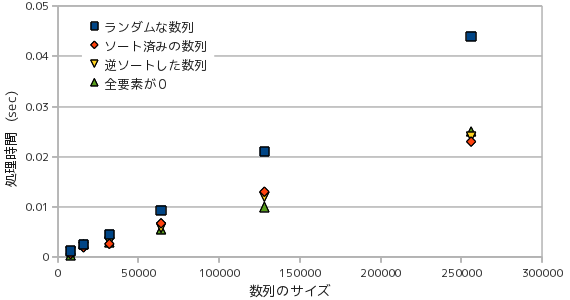グラフを見ると、どの種類のデータ列についても、処理時間はデータ数にほぼ比例する形となっています。深さ d の節点の数は 2^d なので、高さ d の節点の総数は Σ_i{0→d}( 2ⁱ ) = 2^d+1 - 1 であり、ヒープの高さは 2 を底とするデータ数の対数に比例することになります。ヒープ・ソートにおいて、未ソートの列から根となる最大値を抽出するときに発生する交換処理はヒープの高さ以下なので、2 を底とするデータ数の対数にほぼ等しいことになり、それをデータ数分だけ繰り返すことから、ヒープ・ソートの処理時間は、データ数 N に対して N log N にほぼ比例します。これは、N が小さければ N にほぼ比例するとみなすことができることを意味します。乱数列に対するデータ数 N と処理時間 f(N) の関係を、回帰曲線 f(N) = aN log₂ N ( a : 定数 ) でフィッティングした結果のグラフを以下に示します。このとき、a の値は 9.6 x 10^-9 となりました。

グラフ 3-2. データ数に対する処理時間の回帰曲線 ( データ列 : Random )

乱数列と比較すると、ソート済み、逆ソート、ゼロ要素のデータ列は処理時間が短くなっているものの、やはりデータ数にほぼ比例して処理時間が長くなっています。ヒープ・ソートは「選択ソート」の一種と考えられるため、その特徴もそのまま継承しています。よって、「交換ソート」や「挿入ソート」で見られた、ソート済みデータ列での圧倒的な処理時間の速さはここでは見られません。

ヒープ・ソートは、前回紹介したシェル・ソートやコム・ソートよりもさらに処理時間が速いという結果が得られました。次回は、これよりもさらに速いソート法である「クイック・ソート」を紹介します。

補足1) 等比級数の和

数列 A_n が次のような式で表されるとき、A_n を「等比数列(Geometric Progression)」といいます。

ここで、a は「初項(Scale Factor)」、r は「公比(Common Ratio)」と呼ばれます。a は数列の最初の要素を表し、ある要素はその前の要素に r を掛けたものになります。よって、具体的に書けば

となります。この数列の第 n 項までの和を S_n で表したとき、S_n を「等比級数(Geometric Series)」といいます。S_n には次のような公式があります。

レベル n の節点の数は 2ⁿ でした。しかし、レベルは根のゼロから始まるので、1 から開始するようにすれば、節点の数は 2^n-1 となります。これは、初項 1、公比 2 の等比数列なので、深さ d までの節点の総数は

になります。

1. 「X68000マシン語プログラミング <入門編>」 村田敏幸 著 (ソフトバンク)
2. Wikipedia

前に戻る

タイトルに戻る