今まで紹介した推定や検定は、一標本の分布に対する手法が主体となっていました。二標本の分布が同じものであるかを判別する検定法も一部ありましたが、これらはそれぞれの分布の標本間に何の関連性もないことが前提となっています。この章では、二つのデータにある関連性の調べ方や、関連性のあるデータを解析するための手法について紹介したいと思います。
「相関係数(Correlation Coefficient)」や「回帰曲線(Regression Curve)」の定義については、「(4) 多変数の確率分布」の中で前に紹介していますが、もう少し具体的なデータを使ってもう一度その内容を確認しておきたいと思います。
| 都道府県 | 人口(H.20) (千人) | 交通事故発生件数 (H.19) | 都道府県 | 人口(H.20) (千人) | 交通事故発生件数 (H.19) | 都道府県 | 人口(H.20) (千人) | 交通事故発生件数 (H.19) |
|---|---|---|---|---|---|---|---|---|
| 北海道 | 5,535 | 23,582 | 石川 | 1,168 | 7,438 | 岡山 | 1,948 | 19,265 |
| 青森 | 1,392 | 6,856 | 福井 | 812 | 4,658 | 広島 | 2,869 | 19,819 |
| 岩手 | 1,352 | 5,369 | 山梨 | 871 | 6,992 | 山口 | 1,463 | 8,939 |
| 宮城 | 2,340 | 12,803 | 長野 | 2,171 | 12,471 | 徳島 | 794 | 6,251 |
| 秋田 | 1,108 | 4,365 | 岐阜 | 2,100 | 13,080 | 香川 | 1,003 | 12,243 |
| 山形 | 1,188 | 8,411 | 静岡 | 3,800 | 38,682 | 愛媛 | 1,444 | 10,262 |
| 福島 | 2,052 | 12,744 | 愛知 | 7,403 | 55,604 | 高知 | 773 | 4,563 |
| 茨城 | 2,964 | 20,415 | 三重 | 1,875 | 12,790 | 福岡 | 5,054 | 45,703 |
| 栃木 | 2,011 | 13,693 | 滋賀 | 1,402 | 9,626 | 佐賀 | 856 | 8,906 |
| 群馬 | 2,012 | 21,649 | 京都 | 2,629 | 17,094 | 長崎 | 1,440 | 7,938 |
| 埼玉 | 7,113 | 44,820 | 大阪 | 8,806 | 59,060 | 熊本 | 1,821 | 12,091 |
| 千葉 | 6,122 | 31,161 | 兵庫 | 5,586 | 38,551 | 大分 | 1,200 | 7,327 |
| 東京 | 12,838 | 68,603 | 奈良 | 1,404 | 7,522 | 宮崎 | 1,136 | 9,820 |
| 神奈川 | 8,917 | 50,450 | 和歌山 | 1,012 | 7,785 | 鹿児島 | 1,717 | 11,526 |
| 新潟 | 2,391 | 12,791 | 鳥取 | 595 | 2,539 | 沖縄 | 1,376 | 6,525 |
| 富山 | 1,101 | 6,996 | 島根 | 725 | 2,676 |
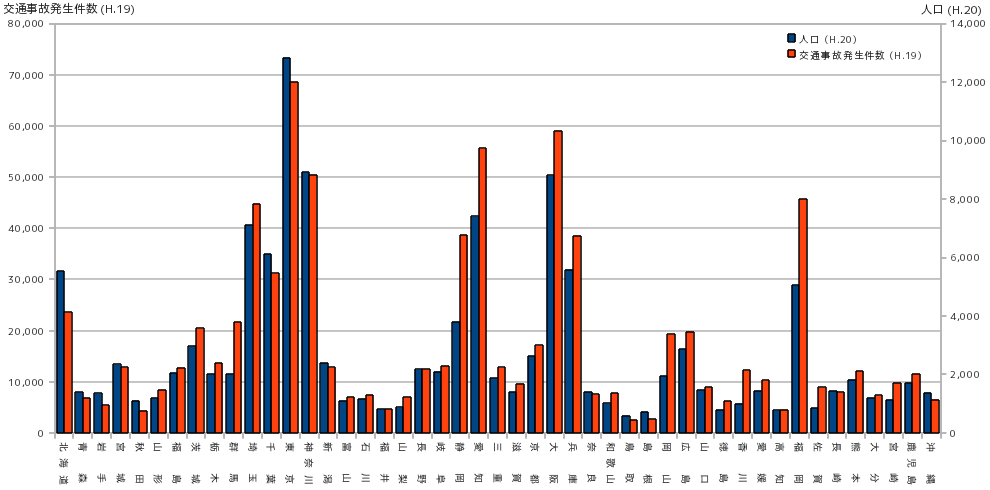
上に示した表は、統計局ホームページから取得した、人口(千人単位)と年間の交通事故発生件数を各都道府県別に表したものです。集計時の年代に差がありますが、同じ年代のデータが揃わなかったため近い年代のものを使っています。下図は、それぞれの分布をヒストグラムで表したものです。
ある程度予想できる結論にはなりますが、人口の多い都道府県ほど交通事故の発生件数は多くなる傾向がヒストグラムからもはっきりとわかります。発生件数だけを見ると東京が突出しているように見えますが、「人が多いほど事故が多い」と考えれば当然の結論になるわけです。そこで、交通事故の発生件数を人口(千人単位)で割った比率を求めて分布を調べると、下図のような結果になります。
発生件数を千人単位の人口で割ったということは、千人あたりで換算した発生件数と考えることもできるので、10 を超えている群馬・静岡・香川・佐賀などは百人あたり年間一回程度は事故に遭っていることになります。
次に、横軸を人口、縦軸を交通事故発生件数としてグラフに点をプロットしてみます。
人口が多くなるほど交通事故の発生件数が多くなる様子が、このグラフからはっきりと認識できます。このようなグラフは「散布図(Scatter Plot ; Scattergraph)」と呼ばれ、二変数間の関係を確認するときに便利です。複数の変数に対する関連性のことを「相関(Correlation)」といい、散布図を見ると、交通事故発生件数は人口に対して直線状に増加する傾向が見られるので、このような場合は「正の相関がある」ことになります。逆に、横軸方向に増加するに従って縦軸が減少するような場合、「負の相関がある」ことになり、そのどちらとも判別できないようなときは「相関がない」と判断されます。
人口の少ない地域は過疎化のため高齢者の占める割合が多いことが予想されます。そこで、65 歳以上の人口が全人口に対して占める割合を都道府県別に計算すると、次のような結果になります。
予想通り、人口が少ないほど高齢者の占める割合は増加する傾向にあるようです。このような場合は「負の相関がある」ということになります。
相関図を見れば、二変数間の関連性を読み取ることが可能になります。関連性があると判断できたとき、それがどの程度の強さなのかを定量的に測るための指標として「相関係数(Correlation Coefficient)」があります。多変数の確率密度関数から求められる理論上の相関係数は「母相関係数(Population Correlation Coefficient)」で「相関係数(Correlation Coefficient)」の章で、また、実際のデータから求められる相関係数は「標本相関係数(Sample Correlation Coefficient)」で「主成分分析(Principal Component Analysis ; PCA)」の章でそれぞれ紹介しています。
母相関係数を ρ、標本相関係数を r で表すと、それぞれの式は以下のようになります。
| ρ | = | σxy / σxσy |
| = | E[( x - μx )( y - μy )] / { E[( x - μx )2] }1/2{ E[( y - μy )2] }1/2 | |
| = | ∫x∈R∫y∈R( x - μx )( y - μy ) p( x, y ) dxdy / { ∫x∈R( x - μx )2 px(x) dx }1/2{ ∫y∈R( y - μy )2 py(y) dy }1/2 | |
| r | = | sxy / sxsy |
| = | Σi{1→N}( ( xi - mx )( yi - my ) ) / { Σi{1→N}( ( xi - mx )2 ) }1/2{ Σi{1→N}( ( yi - my )2 ) }1/2 |
σxy は「母共分散(Population Covariance)」 E[( x - μx )( y - μy )] = ∫x∈R∫y∈R( x - μx )( y - μy ) p( x, y ) dxdy を表します。ここで p( x, y ) は x, y を確率変数とする二変数の確率密度関数、μx と μy はそれぞれ x, y の母平均であり、σxy は ( x - μx )( y - μy ) に対する p( x, y ) の期待値を意味します。これに対し、sxy は「標本共分散(Sample Covariance)」であり、確率密度確率 p( x, y ) に従う標本 ( xi, yi ) ( i = 1, 2, ... N ) を使った ( xi - mx )( yi - my ) の和で求められます。ここで、mx と my はそれぞれ xi, yi から得られる標本平均を表しています。
σx, σy は p( x, y ) に対する x, y の母標準偏差であり、sx, sy は標本標準偏差を表します。ちなみに sxy は N で、sx, sy は √N で和を割っているため、分母と分子で N が消されることで r は上記に示した最後の式のようになります。
二つの変数の関連性を定量的に調べるための他の方法として、曲線への当てはめがあります。一般的には、曲線を M 個の関数 fi(x) ( i = 1, 2, ... M ) による線形結合
で表すことができると仮定して、まずは N 個のデータ ( xj, yj ) ( j = 1, 2, ... N ) の xj を上記関数に代入し、y を求めます。求めた y は、実測値である yj とは完全に一致することはなく、ある程度のズレがあるはずです。そこで、求めた y と実測値 yj の差の二乗を各データに対して求め、その和を求めた上で、和が最小となるような係数 a0, a1, a2, ... aM を求めます。この手法を「最小二乗法(Least Squares)」といいます。
直線へ当てはめる場合は y = ax + b として計算すればよいので、求める和を J とすると、
で求めることができます。2 で割っているのは計算時に生じる係数を打ち消すためで、結果には影響しません。J が最小となるときの係数 a, b は、∂J / ∂a = 0、∂J / ∂b = 0 を解くことで得ることができて、
| ∂J / ∂a | = | Σj{1→N}( - xj{ yj - ( axj + b ) } ) |
| = | aΣj{1→N}( xj2 ) + bΣj{1→N}( xj ) - Σj{1→N}( xjyj ) = 0 | |
| ∂J / ∂b | = | Σj{1→N}( - { yj - ( axj + b ) } ) |
| = | aΣj{1→N}( xj ) + bΣj{1→N}( 1 ) - Σj{1→N}( yj ) = 0 |
となります。これは連立一次方程式の形であり、
| | | Σj{1→N}( xj2 ), | Σj{1→N}( xj ) | || | a | | | = | | | Σj{1→N}( xjyj ) | | |
| | | Σj{1→N}( xj ), | Σj{1→N}( 1 ) | || | b | | | | | Σj{1→N}( yj ) | | |
と表されます。これを「正規方程式」といいます。上側に Σj{1→N}( 1 ) = N、下側に Σj{1→N}( xj ) を掛けて辺々引くと
となって、a を求めることができますが、上式の中の a に対する係数は ( データの二乗和 x N ) と ( 和の二乗 ) の差となっていて、データ x の標本平均を mx としたとき
| Σj{1→N}( ( xj - mx )2 ) | = | Σj{1→N}( xj2 - 2mxxj + mx2 ) |
| = | Σj{1→N}( xj2 ) - 2mxΣj{1→N}( xj ) + Nmx2 ) | |
| = | Σj{1→N}( xj2 ) - { Σj{1→N}( xj ) }2 / N |
となることから分かるように、この値は標本分散 vx = Σj{1→N}( ( xj - mx )2 ) に N を掛けた N・vx と等しくなります。右辺はデータ y の標本平均を my として
| Σj{1→N}( ( xj - mx )( yj - my ) ) | = | Σj{1→N}( xjyj - myxj - mxyj + mxmy ) |
| = | Σj{1→N}( xjyj - myxj - mxyj + mxmy ) | |
| = | Σj{1→N}( xjyj ) - myΣj{1→N}( xj ) - mxΣj{1→N}( yj ) + Nmxmy ) | |
| = | Σj{1→N}( xjyj ) - Σj{1→N}( xj )Σj{1→N}( yj ) / N |
より、標本共分散 sxy = Σj{1→N}( ( xj - mx )( yj - my ) ) に N を掛けた N・sxy に等しくなるので、係数 a の値は
と非常にシンプルな式となります。また、この値を二式のうちのどちらかに代入すれば、b の値は
と求められます。よって、直線の方程式は
になります。x = ay + b とした場合も同様の計算によって、
という結果が得られます。どちらの直線も点 ( mx, my ) を通りますが、その傾きは異なります。前者の式は、x に対して y がどのように変化しているかを表し、逆に後者の式は、y に対して x がどのように変化しているかを表しています。そのため、y = ax + b としたときの x は「独立変数(Independent Variable)」または「説明変数(Explanatory Variable)」と呼ばれ、y は「従属変数(Dependent Variable)」または「目的変数(Objective Variable)」と呼ばれます。英語では一般的に "Independent Variable", "Dependent Variable" という名が用いられ、説明変数や目的変数の呼び名はあまり使われないようです。「独立変数」という名前で表されるように、x はそれぞれ独立したデータで、y は各 x に従う値であると考えるとこの名前の意味が理解できるのではないかと思います。
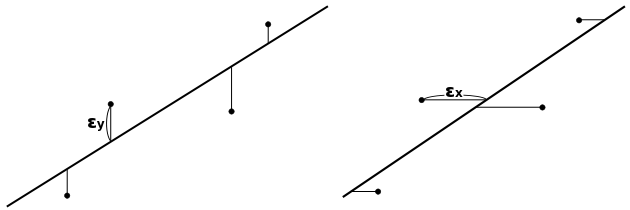
誤差が全く無く、全てのデータが直線上にある状態ならば、y = a( x - mx ) + my に対して x = (1/a)( y - my ) + mx となって、どちらの直線も一致します。これが一致しないのは誤差の見方によるもので、y = a( x - mx ) + my では各データを表す点から y 軸に沿って、当てはめた直線に伸ばした線分の距離が全体的に最も小さくなるようにしているのに対し、x = a( y - my ) + mx の場合は x 軸に沿った線分の距離を最小にする式を求めているという違いから生じます。
前節で紹介した「人口」と「交通事故発生件数」の相関では、人口が多いから交通事故も多くなると考えることができます。よって、人口が独立変数で、交通事故発生件数が従属変数であると考えるのが自然です。人口に比例して交通事故も多くなると考えたとき、誤差によってある程度のズレは発生するものの、それは直線で近似することができます。その式は、人口を x、交通事故発生件数を y としたとき、y = ( sxy / vx )( x - mx ) + my で求められることになります。実際に求めてみると、
より y = 5.95x + 1.56 x 103 になります。
「回帰曲線(Regression Curve)」の定義は、次のような式で表されるのでした。
| μy(x) | = | ∫{-∞→∞} y・p(y|x) dy |
| = | ∫{-∞→∞} y・p( x, y ) / px( x ) dy |
p(y|x) = p( x, y ) / px( x ) は、二変数の確率密度関数 p( x, y ) における y の x に関する条件付確率密度であり、x をある値に固定したときの y の確率密度関数を表しています。よって、μy(x) は、それぞれの x について y の平均値を求めてそれをプロットしたときの曲線を表すことになります。
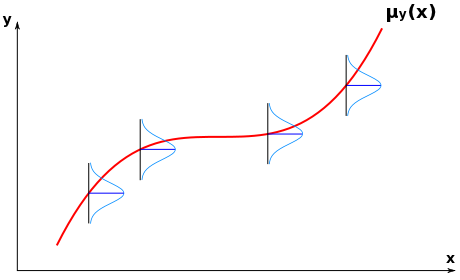
最小二乗法は、回帰曲線を推定するための一つの手法と考えることができます。各 x について y はある確率密度分布に従って分布していると仮定して、点全体の分布が確率的に最も高くなるような曲線を回帰曲線と推定するわけです。このとき、後て述べるように「最尤法(Maximum Likelihood Estimation ; MLE)」が利用されています。
二変数の確率密度関数 p( x, y ) において、回帰曲線 y = μy(x) が M 個の関数 fi(x) ( i = 1, 2, ... M ) による線形結合
で表されると仮定します(ここで、f0(x) = 1 とします)。N 個の測定値 ( xj, yj ) ( j = 1, 2, ... N ) は、真の値 μy(xj) に対してランダムな誤差 εj が加わって yj になると考えれば
と表すことができます。誤差 εj が平均 0、分散 σ2 の正規分布 N( 0, σ2 ) に従い、しかも分散は x によらず常に一定であると仮定すると、尤度 L( ε1, ε2, ... εN ; a0, a1, a2, ... aM ) = L( ε, a ) は
| L( ε, a ) | = | Πj{1→N}( exp( -εj2 / 2σ2 ) / ( 2πσ2 )1/2 ) |
| = | exp( -Σj{1→N}( εj2 ) / 2σ2 ) / ( 2πσ2 )N/2 |
となり、対数を取って
になります。尤度を最大にするためには、上式の右辺が最大になればよく、変数となる係数 ai を持つ項は -Σj{1→N}( εj ) / 2σ2 なので、
が最小になるような ai を求めればよいことになります。これは、最小二乗法そのものであり、求められた係数 ai は最尤推定量であるということになります。
直線への当てはめを行うとき、y ( または x ) だけの誤差ではなく、両方の誤差が混在していると考えると、真の値を ( μxj, μyj ) としたとき、各データ ( xj, yj ) は
と表すことができます。ここで、( εxj, εyj ) は各データに対する x, y 方向の誤差成分を表します。この誤差成分が平均 0、分散 σ2 の正規分布 N( 0, σ2 ) に従い、しかも分散は x, y によらず常に一定であると仮定すると、尤度 L( εx1, εx2, ... εxN ; εy1, εy2, ... εyN ) = L( εx, εy ) は
| L( εx, εy ) | = | Πj{1→N}( { exp( -εxj2 / 2σ2 ) / ( 2πσ2 )1/2 }{ exp( -εyj2 / 2σ2 ) / ( 2πσ2 )1/2 } ) |
| = | exp( -Σj{1→N}( εxj2 + εyj2 ) / 2σ2 ) / ( 2πσ2 )N |
であり、対数を取って
となるので、
が最小になるような εxj, εyj を求めればよいことになります。
を J の式に代入すれば、
となるので、真の値 ( μxj, μyj ) が直線 ax + by + c = 0 上にあるとして、右辺が最小になるような ( μxj, μyj ) を、aμxj + bμyj + c = 0 という制約条件下で求めると(補足1)、
より a / b = α, c / b = β として J の式に代入すれば
| J | = | Σj{1→N}( ( xj - μxj )2 + ( yj + αμxj + β )2 ) / 2 |
| = | Σj{1→N}( xj2 - 2xjμxj + μxj2 + yj2 + α2μxj2 + β2 + 2αyjμxj + 2αβμxj + 2βyj ) / 2 | |
| = | Σj{1→N}( ( α2 + 1 )μxj2 - 2( xj - αyj - αβ )μxj + ( xj2 + yj2 + 2βyj + β2 ) ) / 2 |
これを μxj で偏微分すると
なので、左辺がゼロになる時
| μxj | = | ( xj - αyj - αβ ) / ( α2 + 1 ) |
| = | ( xj - (a/b)yj - ac / b2 ) / ( (a/b)2 + 1 ) | |
| = | ( b2xj - abyj - ac ) / ( a2 + b2 ) |
になります。μyj に対しても同様の手法で求めると
となって、これを J の式に戻すと
| J | = | Σj{1→N}( { xj - ( b2xj - abyj - ac ) / ( a2 + b2 ) }2 + { yj - ( a2yj - abxj - bc ) / ( b2 + a2 ) }2 ) / 2 |
| = | Σj{1→N}( { ( a2xj + abyj + ac ) / ( a2 + b2 ) }2 + { ( b2yj + abxj + bc ) / ( b2 + a2 ) }2 ) / 2 |
ここで、ax + by + c = 0 の両辺に任意のゼロでない数を掛けても直線は変化しないことから、a2 + b2 = 1 と正規化すれば、
| J | = | Σj{1→N}( ( a2xj + abyj + ac )2 + ( b2yj + abxj + bc )2 ) / 2 |
| = | Σj{1→N}( a2( axj + byj + c )2 + b2( axj + byj + c )2 ) / 2 | |
| = | Σj{1→N}( ( a2 + b2 )( axj + byj + c )2 ) / 2 | |
| = | Σj{1→N}( ( axj + byj + c )2 ) / 2 |
となります。これを c で偏微分すると
なので、∂J / ∂c = 0 のとき
と求められます。ここで、mx, my はそれぞれ xj, yj から得られる標本平均を表しています。これをもう一度 J の式に代入すれば
| J | = | Σj{1→N}( { a( xj - mx ) + b( yj - my ) }2 ) / 2 |
| = | Σj{1→N}( ( xj - mx )2a2 + 2( xj - mx )( yj - my )ab + ( yj - my )2b2 ) / 2 |
と変形できますが、二次形式
は、対象行列
| V | = | | | p, | q | | |
| | | q, | r | | | ||
とベクトル n = ( a, b )T を使って
と表すことができるのを利用すれば、
| V | = | | | Σj{1→N}( ( xj - mx )2 ), | Σj{1→N}( ( xj - mx )( yj - my ) ) | | |
| | | Σj{1→N}( ( xj - mx )( yj - my ) ), | Σj{1→N}( ( yj - my )2 ) | | | ||
としたとき J = ( n, Vn ) / 2 であり、a2 + b2 = 1 より ||n|| = 1 すなわち n は単位ベクトルということになります。
J = Σj{1→N}( ( xj - μxj )2 + ( yj - μyj )2 ) / 2 という式は、( xj, yj ) から ( μxj, μyj ) までの距離の二乗の和を表しています。( μxj, μyj ) が直線 ax + by + c = 0 上にある場合、J が最小になるためには 線分 ( xj, yj ) - ( μxj, μyj ) が直線 ax + by + c = 0 に垂直である必要があります。このとき、a2 + b2 = 1 と正規化すれば J = Σj{1→N}( ( axj + byj + c )2 ) / 2 という式で表されることになりますが、これは直線 ax + by + c = 0 の式に ( x, y ) = ( xj, yj ) を代入した値の二乗和を意味します。さらに J が最小になるように c を定めると、直線は ( xj, yj ) の標本平均 ( mx, my ) を通ることになり、この時 J = Σj{1→N}( { a( xj - mx ) + b( yj - my ) }2 ) / 2 になります。
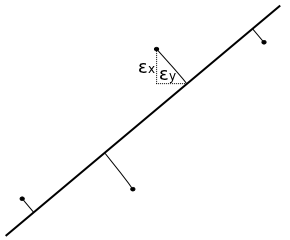
上に示したように、この式は二次形式であり、( n, Vn ) / 2 の形で表すことができます。
vx = Σj{1→N}( ( xj - mx )2 ) / N
vy = Σj{1→N}( ( yj - my )2 ) / N
sxy = Σj{1→N}( ( xj - mx )( yj - my ) ) / N
とすれば V は
| V | = | | | N・vx, | N・sxy | | |
| | | N・sxy, | N・vy | | | ||
で表されます。J を N で割っても最小値に対する n に変化はないので、V の要素を N で割っても問題はありません。すると、V は「(標本)共分散行列 ( (Sample) Covariance Matrix )」 そのものになります。よって、共分散 E[( x - μx )( y - μy )] を要素とする「(母)共分散行列」を抽出した標本から推定するとき、誤差が正規分布 N( 0, σ2 ) に従うと仮定すれば、最尤推定量として標本共分散行列の V を利用することができて、共分散の最尤推定量は sxy になることが以上のことから証明されたことになります。
「人口」と「交通事故発生件数」において、vx = 6.81 x 106, vy = 2.63 x 108, sxy = 4.05 x 107 より V は
| V | = | | | 6.81 x 106, | 4.05 x 107 | | |
| | | 4.05 x 107, | 2.63 x 108 | | | ||
になります。V の固有値 λ は | λE - V | = ( λ - vx )( λ - vy ) - sxy2 の解であり、
で求められ、その解は 2.70 x 108, 5.74 x 105 になります。λ = 2.70 x 108 のときの固有ベクトルは、連立方程式
( 6.81 x 106 )a + ( 4.05 x 107 )b = ( 2.70 x 108 )a
( 4.05 x 107 )a + ( 2.63 x 108 )b = ( 2.70 x 108 )b
を解くことで求められ、両式とも b = 6.49a という式に変形できるので、a2 + b2 = 1 という制約から ( a, b ) = ( 0.152, 0.988 ) という結果が得られます。λ = 5.74 x 105 の場合も同様の方法によって、( a, b ) = ( -0.988, 0.152 ) と求めることができます。この二つの固有ベクトルは互いに直交し、最大固有値である λ = 2.70 x 108 に対する単位ベクトル ( a, b ) = ( 0.152, 0.988 ) は、二次形式 f = ( n, Vn ) で表される楕円体の長軸方向を、最小固有値である λ = 5.74 x 105 に対する単位ベクトル ( a, b ) = ( -0.988, 0.152 ) は楕円体の短径をそれぞれ表すことになります。よって、直線 ax + by + c = 0 は、点 ( mx, my ) = ( 2.72 x 103, 1.71 x 104 ) を通り、( -0.988, 0.152 ) 方向を向いた直線であり、
と表されます。
y ( または x ) だけの誤差を考えるか、それとも x, y 両方の誤差を考えるかによって、二通りのモデルが考えられました。前者は、x を入力データとみなして、その出力結果 y に誤差があるとして、その誤差を最小にするときの直線を、後者は x, y 両方とも測定データであり、それぞれに誤差があるとしてそれを最小にするときの直線をそれぞれ求めていることになります。どちらを採用するかは、データをどのように解釈するかに依存することになり、どちらが正しいモデルなのかということは言えません。前例において、人口に対して交通事故発生件数が一意に決まるという前提で考えて、測定の誤差(例えば記録されない事故の存在など)によってバラツキが発生すると考えれば前者の方法が、人口にも交通事故発生件数にも同等のバラツキがあって、そのバラツキを最小限にするような近似直線を求めたい場合には後者の方法が利用されることになります。
相関係数には別の見方をすることもできます。N 個からなる x の値によるベクトルを x, 同じく y の値によるベクトルを y としたとき、共分散 sxy はこの二つのベクトルの内積 ( x - μx, y - μy ) を N で割ったもので表されます。また、分散 vx = ( x - μx, x - μx ) / N = || x - μx ||2 / N, vx = || y - μy ||2 / N なので、標本相関係数 r は
となります。「コーシー = シュワルツの不等式(Cauchy-Schwarz Inequality)」より、r は -1 から 1 までの値をとります。x - μx / || x - μx || は x - μx をその大きさで割ったことになるので、単位ベクトルとなり、y - μy についても同様に考えられるので、この単位ベクトルをそれぞれ ex, ey とすれば、r = ( ex, ey ) と表されます。この二つの単位ベクトルがなす角度を θ としたとき、
なので、r とは x と y のなす角度を表すことになります。
N 次元ベクトル空間上にあるベクトル x, y に対し、それらが同じ方向か全く逆の方向を向いているとき、|r| は 1 になります。また、直交していれば r = 0 になります。同じ方向か全く逆の方向を向いているということは、任意の定数 a, b (但し a ≠ 0) を使って y = ax + b と表されることになるので、xy 平面上にプロットすれば直線上に並ぶことになります。また、例えば
で表されるとき、( Kcosα, Ksinα ) と ( Kcos(-α), Ksin(-α) ) どうしが互いに打ち消し合って、r = 0 になります。K の値をいろいろと変化させれば、平均を原点に、周囲に散らばったような分布を作ることができるので、そのような場合は r がゼロに近い値になります。
ところで、上記の r = 0 になる例では、x2 + y2 = K2 という関係式が成り立ちます。つまり、x と y の間には、線形ではないものの相関があるということになります。この例から分かるように、x と y が互いに独立な場合、
なので相関係数は必ずゼロになりますが、相関係数がゼロでも x と y が互いに独立であるとは限りません。他の例として、y = Kx に従うデータと y = -Kx に従うデータが混在していたような場合、標本を元に相関係数を計算するとほぼゼロに近い値が得られますが、実際には相関のある二つのデータが混在しているものと見なすことができます。よって、相関係数だけで判断するのではなく、相関図で分布の確認をするということも必要であるということになります。
x の確率密度関数が一様分布 p-1,1(x) に、また、y の確率密度関数が同じく一様分布 p-2,2(y) に従うと仮定します。ここで、一様分布 pa,b(x) は
| pa,b(x) | = | 1 / ( b - a ) | ( a ≤ x ≤ b ) |
| = | 0 | ( x < a または x > b ) |
で表されます。x は -1 ≤ x ≤ 1 の区間、y は -2 ≤ y ≤ 2 の区間で等しい確率で分布することになるわけです。x と y が独立であれば、ある x に対して y は -2 ≤ y ≤ 2 の区間で等しい確率で発生します。よって、x と y をプロットしていくと、矩形 ( -1, -2 ) - ( 1, 2 ) 内に等しい確率で分布することになります。このとき、標本相関係数はゼロに近い値になります。しかし、y が x に対して一意に決まるとき、y は -2 ≤ y ≤ 2 の中のある定数を常に示すことになります。測定誤差などによってある程度揺らぐことがあったとしても、それは定数の付近に密集するので、分布は矩形ではなく、ある帯状の形になるでしょう。その形状が直線に近ければ、標本相関係数は 1 に近くなります。
その他に、相関係数の絶対値は x, y が一次変換されても変化しないという特徴もあります。すなわち、
と変換したとき、x, y, u, v の母平均をそれぞれ μx, μy, μu, μv、分散をそれぞれ vx, vy, vu, vv、x,y の共分散を γxy、u,v の共分散を γxy とすれば、
μu = E[u] = E[ax + b] = aμx + b
μv = E[v] = E[cy + d] = cμy + d
| vu | = | E[( u - μu )2] |
| = | E[{ ( ax + b ) - ( aμx + b ) }2] | |
| = | a2E[( x - μx )2] = a2vx | |
| vv | = | c2vy |
| γuv | = | E[( u - μu )( v - μv )] |
| = | acE[( x - μx )( y - μy )] = acγxy |
という関係式が得られます。よって、x,y の相関係数を ρxy、u,v の相関係数を ρuv としたとき、
となります。
二変数間の相関は、常に線形関係で表されるわけではありません。相関図での例で示した、65 歳以上の人口が全人口に対して占める割合の人口との相関は負の相関がありますが、その関係は直線では示されないように見えます。回帰曲線を使う場合、一次式ではなく二次以上の多項式を利用したり、もっと一般的な関数の和で表すようなことも考えられますが、x, y のいずれかを変数変換することによって、線形関係で表すことができる場合があります。このときよく利用されるのが、対数やべき乗への変換です。
上のグラフはどちらも、65 歳以上の人口が全人口に対して占める割合の人口との相関を示したものですが、右側は x 軸(人口)を底を 10 とする対数に変換しています。両者を比較すると、右側の対数で変換した結果のほうが、線形に近似されている様子が分かります。両者の相関係数は、左側が -0.611、右側が -0.668 となって、対数に変換したほうが相関は強くなります。
標本共分散を計算するためのサンプル・プログラムを以下に示します。
/* sampleCovariance : 標本共分散を求める const vector<T> &x, &y : データ データの個数が一致しない場合はゼロを返す データの個数がゼロならゼロを返す 戻り値 : 標本共分散 */ template<class T> T sampleCovariance( const vector<T>& x, const vector<T>& y ) { unsigned int n = x.size(); if ( n != y.size() ) return( 0 ); if ( n == 0 ) return( 0 ); // 標本平均の算出 T mx = sampleAverage( x ); T my = sampleAverage( y ); // ( x - mx )( y - my ) を求める vector<T> xy( n ); for ( unsigned int i = 0 ; i < n ; ++i ) xy[i] = ( x[i] - mx ) * ( y[i] - my ); return( sampleAverage( xy ) ); } template double sampleCovariance( const vector<double>& x, const vector<double>& y ); template long double sampleCovariance( const vector<long double>& x, const vector<long double>& y );
共分散を求めることができれば、x, y の標本標準偏差で割れば相関係数を、また x, y の分散と標本平均を使って、回帰直線の傾きと切片を求めることができます。
今まで、相関係数として定義していた式
ρ = σxy / σxσy
r = sxy / sxsy
は、「ピアソンの積率相関係数(Pearson Product-moment Correlation Coefficient)」と呼ばれ、測定などによる誤差が正規分布に従うことを前提にしています。また、二変数間の関係は線形であるという条件も必要です。これらの前提条件が成り立たない場合でも二つのデータの相関を表すことができるパラメータとして「順位相関係数(Rank Correlation Coefficient)」というものがあります。
順位相関係数の考え方は単純で、量的データの代わりに順序尺度としての順位を用いて相関係数を計算するというものです。二つのデータ ( x, y ) において、x, y それぞれについて大小関係から順位を付け、得られた順位から相関係数を計算します。人口と交通事故発生件数のデータを例に順位相関係数を計算すると、
| 都道府県 | 人口(H.20) (千人) | 交通事故発生件数 (H.19) | 人口 [Rank] | 交通事故発生件数 [Rank] | 都道府県 | 人口(H.20) (千人) | 交通事故発生件数 (H.19) | 人口 [Rank] | 交通事故発生件数 [Rank] |
|---|---|---|---|---|---|---|---|---|---|
| 北海道 | 5,535 | 23,582 | 40 | 38 | 滋賀 | 1,402 | 9,626 | 19 | 20 |
| 青森 | 1,392 | 6,856 | 18 | 9 | 京都 | 2,629 | 17,094 | 35 | 33 |
| 岩手 | 1,352 | 5,369 | 16 | 6 | 大阪 | 8,806 | 59,060 | 45 | 46 |
| 宮城 | 2,340 | 12,803 | 33 | 30 | 兵庫 | 5,586 | 38,551 | 41 | 40 |
| 秋田 | 1,108 | 4,365 | 11 | 3 | 奈良 | 1,404 | 7,522 | 20 | 14 |
| 山形 | 1,188 | 8,411 | 14 | 17 | 和歌山 | 1,012 | 7,785 | 9 | 15 |
| 福島 | 2,052 | 12,744 | 30 | 27 | 鳥取 | 595 | 2,539 | 1 | 1 |
| 茨城 | 2,964 | 20,415 | 37 | 36 | 島根 | 725 | 2,676 | 2 | 2 |
| 栃木 | 2,011 | 13,693 | 28 | 32 | 岡山 | 1,948 | 19,265 | 27 | 34 |
| 群馬 | 2,012 | 21,649 | 29 | 37 | 広島 | 2,869 | 19,819 | 36 | 35 |
| 埼玉 | 7,113 | 44,820 | 43 | 42 | 山口 | 1,463 | 8,939 | 23 | 19 |
| 千葉 | 6,122 | 31,161 | 42 | 39 | 徳島 | 794 | 6,251 | 4 | 7 |
| 東京 | 12,838 | 68,603 | 47 | 47 | 香川 | 1,003 | 12,243 | 8 | 25 |
| 神奈川 | 8,917 | 50,450 | 46 | 44 | 愛媛 | 1,444 | 10,262 | 22 | 22 |
| 新潟 | 2,391 | 12,791 | 34 | 29 | 高知 | 773 | 4,563 | 3 | 4 |
| 富山 | 1,101 | 6,996 | 10 | 11 | 福岡 | 5,054 | 45,703 | 39 | 43 |
| 石川 | 1,168 | 7,438 | 13 | 13 | 佐賀 | 856 | 8,906 | 6 | 18 |
| 福井 | 812 | 4,658 | 5 | 5 | 長崎 | 1,440 | 7,938 | 21 | 16 |
| 山梨 | 871 | 6,992 | 7 | 10 | 熊本 | 1,821 | 12,091 | 25 | 24 |
| 長野 | 2,171 | 12,471 | 32 | 26 | 大分 | 1,200 | 7,327 | 15 | 12 |
| 岐阜 | 2,100 | 13,080 | 31 | 31 | 宮崎 | 1,136 | 9,820 | 12 | 21 |
| 静岡 | 3,800 | 38,682 | 38 | 41 | 鹿児島 | 1,717 | 11,526 | 24 | 23 |
| 愛知 | 7,403 | 55,604 | 44 | 45 | 沖縄 | 1,376 | 6,525 | 17 | 8 |
| 三重 | 1,875 | 12,790 | 26 | 28 |
より、人口と交通事故発生件数の平均 mr(x), mr(y)、分散 vr(x), vr(y)、共分散 sr(x,y) を求めると、
mr(x) = mr(y) = 24
vr(x) = vr(y) = 184
sr(x,y) = 1.71 x 102
となるので、順位相関係数は 171 / 184 = 0.927 になります。実際のデータから求められた分散 vx, vy と共分散 sxy はそれぞれ 6.81 x 106, 2.63 x 108, 4.05 x 107 なので、相関係数は 0.956 となり、ほぼ同じ値が得られることになります。この順位相関係数は「スピアマンの順位相関係数(Spearman's Rank Correlation Coefficient)」と呼ばれ、イギリスの心理学者「チャールズ・エドワード・スピアマン(Charles Edward Spearman)」によって提唱されました。彼は「因子分析」の先駆者としても知られています。この値は通常、ρ を使って表されます。
データ数が N の場合、順位は 1 から N までとなるので、その平均は mr = Σi{1→N}( i ) / N = ( N + 1 ) / 2 で求められます。また、自然数の二乗和は ( 2N3 + 3N2 + N ) / 6 (求め方については「数値積分法 -1-」の「ベルヌーイ数」参照) となるので、分散は vr = ( 2N3 + 3N2 + N ) / 6N - { ( N + 1 ) / 2 }2 = ( N2 - 1 ) / 12 になります。共分散は、各データの順位を ( rxi, ryi ) とすれば
| sr(x,y) | = | Σi{1→N}( ( rxi - mr )( ryi - mr ) ) / N |
| = | Σi{1→N}( rxiryi - mr( rxi + ryi ) + mr2 ) / N | |
| = | Σi{1→N}( rxiryi - mr2 ) / N | |
| = | Σi{1→N}( rxiryi ) / N - ( N + 1 )2 / 4 |
となります。途中で Σi{1→N}( rxi ) = Σi{1→N}( ryi ) = N・mr であることを利用しています。ところで、
| Σi{1→N}( ( rxi - ryi )2 ) / N | = | Σi{1→N}( rxi2 - 2rxiryi + ryi2 ) / N |
| = | ( 2N2 + 3N + 1 ) / 3 - 2Σi{1→N}( rxiryi ) / N |
より ( rxi - ryi )2 = di2 とすれば Σi{1→N}( rxiryi ) / N = ( 2N2 + 3N + 1 ) / 6 - Σi{1→N}( di2 ) / 2N になります。よって、
| sr(x,y) | = | ( 2N2 + 3N + 1 ) / 6 - Σi{1→N}( di2 ) / 2N - ( N + 1 )2 / 4 |
| = | ( N2 - 1 ) / 12 - Σi{1→N}( di2 ) / 2N |
なので、順位相関係数の式は
になります。Σi{1→N}( di2 ) は ( x, y ) のペアに対する順位差の二乗和を意味するので、この値を利用することで比較的簡単な計算で求めることができることになります。データそのものの代わりに順位を使って計算しているだけで、相関係数の式としてはピアソンの積率相関係数と変わらないので、必ず -1 ≤ ρ ≤ 1 の範囲の値を示すなど同様の特徴を持っています。
順位を決めるとき、等しいデータがある場合は平均順位を計算します。i 番目から j 番目の順位のデータが全て等しい場合 ( j > i )、i から j までの和をそのデータ数で割れば平均順位が求められ、i から j までの和は Σk{i→j}( k ) = { j( j + 1 ) - i( i - 1 ) } / 2、データ数は j - i + 1 になるので、平均順位は
| Σk{i→j}( k ) / ( j - i + 1 ) | = | { j( j + 1 ) - i( i - 1 ) } / 2( j - i + 1 ) |
| = | ( j - i + 1 )( j + i ) / 2( j - i + 1 ) | |
| = | ( j + i ) / 2 |
を計算することで求めることができます。例えば、3 番目から 5 番目が等しいデータである場合は
になります。i 番目と j 番目のちょうど中央にあたる場所が平均順位となると考えれば分かりやすいと思います。
順位相関係数の中でよく利用される他の種類として「ケンドールの順位相関係数(Kendall Tau Rank Correlation Coefficient)」というものがあります。"Tau"という言葉が含まれていることから想像できるように、一般的には τ で表されます。この場合も、各データについて順位を求めるところまではスピアマンの順位相関係数と同じです。すると、各データのペア ( xi, yi ) ( i = 1, 2, ... N ) に対してその順位 ( rxi, ryi ) が得られます。次に、この順位を各データのペアの全組み合わせに対して rxi, ryi 両方に対して比較します。比較するデータ列の順位を ( rxi, ryi ), ( rxj, ryj ) としたとき、rxi > rxj かつ ryi > ryj または rxi < rxj かつ ryi < ryj であれば P に、rxi > rxj かつ ryi < ryj または rxi < rxj かつ ryi > ryj であれば Q に 1 を加え、rxi = rxj または ryi = ryj である場合は無視します( P, Q のどちらにも加算しません)。簡単に言えば、順位の大小関係が x, y のどちらも一致していれば P を、逆転していれば Q をそれぞれ加算することになります。x を昇順に並べたとき、y が昇順に並んでいれば、P の値が最大、Q の値が最小(ゼロ)となります。逆に、y が降順に並んだ場合、Q の値が最大、P の値が最小になります。よって、P と Q の差の絶対値は、( x, y ) に相関があるような場合に大きくなる傾向にあります。
具体的な例を示します。国語と数学の試験で各生徒が以下のような順位になったとき、二教科のあいだで相関があるかを調べたいとします。
| 生徒 | 順位 | |
|---|---|---|
| 国語 | 数学 | |
| A | 4 | 1 |
| B | 2 | 3 |
| C | 1 | 2 |
| D | 5 | 4 |
| E | 3 | 5 |
A から E までの生徒それぞれの組み合わせについて、国語と数学の順位の大小関係が同じであれば P、逆であれば Q とします。例えば、A, B 両者を比較したとき、国語は B の方が順位が高く、数学は A の方が順位が高いので逆の関係となっています。よって、このときは Q で示されます。
| 生徒 | 順位 | 生徒 | ||||
|---|---|---|---|---|---|---|
| 国語 | 数学 | B | C | D | E | |
| A | 4 | 1 | Q | Q | P | Q |
| B | 2 | 3 | - | P | P | P |
| C | 1 | 2 | - | - | P | P |
| D | 5 | 4 | - | - | - | Q |
| E | 3 | 5 | - | - | - | - |
P, Q の数を数えるとそれぞれ 6, 4 になります。従って、P - Q = 6 - 4 = 2 と求めることができます。
N 個のデータから 2 個のデータを選ぶ組み合わせは NC2 = N( N - 1 ) / 2 になります。同順位がなければ P + Q = NC2 であり、0 ≤ P ≤ NC2, 0 ≤ Q ≤ NC2 なので、P - Q / NC2 は -1 から 1 の間の値をとります。そこで、
とすれば、τ は -1 と 1 の間の値をとり、相関係数として扱うことができるようになります。これがケンドールの順位相関係数になります。上の例では τ = ( 2 x 2 ) / ( 5 * 4 ) = 0.2 と求められます。
x の順位は配列のインデックスを表しているとすれば、y の順位が逆転している場合、配列の要素の大小関係が逆転している(ソートされていない)ことを意味するので、Q はその個数を表すことになります。2Q / N( N - 1 ) はその比率を表し、この値がゼロなら全ての要素はソートされていることを、1 なら要素は逆順にソートされていることを意味します。この値のことを "Kendall Tau Distance" または "Bubble-sort Distance" といいます。後者の名前は、この値がソートをするときの交換回数を表すために付けられたようです。
順位相関係数を求めるためのサンプル・プログラムを以下に示します。
/* getRank : データ列から順位を求める const vector<T>& data : データ列 vector<double>& rank : 順位を登録する配列 */ template<class T> void getRank( const vector<T>& data, vector<double>& rank ) { // データ型の宣言 typedef typename std::pair<T,unsigned int> pair; typedef typename std::multimap<T,unsigned int> mmap; typedef typename mmap::const_iterator mmap_cit; typedef typename mmap::iterator mmap_it; typedef typename mmap::difference_type mmap_diff; unsigned int sz = data.size(); // データ列のサイズ rank.resize( sz ); if ( sz == 0 ) return; /* データのソート multimapへの登録によってキー順にソートされる */ mmap orderedData; for ( unsigned int i = 0 ; i < sz ; ++i ) orderedData.insert( pair( data[i], i ) ); // 順位への変換 mmap_cit cit = orderedData.begin(); unsigned int r = 0; // 現在の順位 while ( cit != orderedData.end() ) { mmap_cit ub = orderedData.upper_bound( cit->first ); // キーが等しい範囲の末尾 mmap_diff diff = std::distance( cit, ub ); // キーが等しい要素の個数 // 平均順位の計算 double rankAvg = ( diff == 1 ) ? r : ( (double)( r * 2 ) + (double)( diff - 1 ) ) / 2.0; // 平均順位を対象位置に登録 while ( cit != ub ) { rank[cit->second] = rankAvg; ++cit; } r += diff; } } template void getRank( const vector<int>& data, vector<double>& rank ); template void getRank( const vector<unsigned int>& data, vector<double>& rank ); template void getRank( const vector<double>& data, vector<double>& rank ); /* spearmanRankCorrCoef : スピアマンの順位相関係数を求める const vector<T> &x, &y : データ列 戻り値 : スピアマンの順位相関係数 */ double spearmanRankCorrCoef( const vector<double>& x, const vector<double>& y ) { // x, y の順位を登録する配列 vector<double> rank_x; vector<double> rank_y; unsigned int n = x.size(); // データ列のサイズ if ( n != y.size() ) { cout << "The size of data ( x, y ) must be the same size." << endl; return( NAN ); } if ( n < 2 ) { cout << "The size of data must be greater than one." << endl; return( NAN ); } // 順位の計算 getRank( x, rank_x ); getRank( y, rank_y ); // 順位差の二乗を求める vector<double> d( n ); for ( unsigned int i = 0 ; i < n ; ++i ) d[i] = pow( rank_x[i] - rank_y[i], 2 ); double d_sum = sum( d ); // 順位差の二乗和 double denom = (double)n * ( pow( n, 2 ) - 1.0 ); // 分母( N( N*N - 1 ) ) return( ( denom - 6.0 * d_sum ) / denom ); } /* kendallRankCorrCoef : ケンドールの順位相関係数を求める const vector<T> &x, &y : データ列 戻り値 : ケンドールの順位相関係数 */ double kendallRankCorrCoef( const vector<double>& x, const vector<double>& y ) { // x, y の順位を登録する配列 vector<double> rank_x; vector<double> rank_y; unsigned int n = x.size(); // データ列のサイズ if ( n != y.size() ) { cout << "The size of data ( x, y ) must be the same size." << endl; return( NAN ); } if ( n < 2 ) { cout << "The size of data must be greater than one." << endl; return( NAN ); } // 順位の計算 getRank( x, rank_x ); getRank( y, rank_y ); int p = 0; // 順位の大小関係が x と y で同じ数 int q = 0; // 順位の大小関係が x と y で異なる数 for ( unsigned int i = 0 ; i < n - 1 ; ++i ) { for ( unsigned int j = i + 1 ; j < n ; ++j ) { if ( rank_x[i] == rank_x[j] || rank_y[i] == rank_y[j] ) continue; if ( ( rank_x[i] > rank_x[j] && rank_y[i] > rank_y[j] ) || ( rank_x[i] < rank_x[j] && rank_y[i] < rank_y[j] ) ) { ++p; } else { ++q; } } } return( (double)( p - q ) * 2.0 / (double)( n * ( n - 1 ) ) ); }
getRank はデータ列からその順位を求めて返す関数です。データ列を引数 data として渡せば、同じく引数として渡された配列 rank に各要素に対する順位を格納して返すようになっています。例えば、data = { 0.5, 0.1, 0.3, 0.4, 0.2 } ならば、rank = { 4, 0, 2, 3, 1 } として返されます。データのソートには STL(Standard Template Library)で提供されている連想配列 multimap を利用しています。キーが一意になる map に対し、multimap は重複を許す連想配列です。実データをキー、配列 data のインデックスを値としてメンバ関数 insert を使って挿入すると、その要素はキーの持つ大小関係によって自動的にソートされていきます。よって、全てのデータを登録した段階でソートは完了した状態になり、反復子(iterator)を使って先頭から順に配列のインデックスを取り出して、その位置に順位を書き込むことで求める順位の配列が得られます。
重複した値がある場合、平均順位を計算して rank に格納します。そのため、現在の反復子にあるキーに等しい範囲の末尾をメンバ関数 upper_bound で、キーの等しい要素の数をメンバ関数 distance でそれぞれ求め、重複要素があれば平均順位を計算して各位置に格納しています。
spearmanRankCorrCoef は「スピアマンの順位相関係数」を求めるための関数です。getRank を使ってデータ列 x, y それぞれの順位を求めたら、順位差の二乗和を求めてから計算式に従い値を求めるだけの単純な処理です。kendallRankCorrCoef は「ケンドールの順位相関係数」を求める関数で、こちらも最初にデータ列の順位を計算し、順位の大小関係をチェックしながら変数 p, q にその数を計算した上で、計算式に従い順位相関係数を求めます。
条件 x + y = 1 の元で、関数 f( x, y ) = 2x2 + 3y2 を最小にするときの ( x, y ) と、その最小値を求めるというような場合、通常は y = 1 - x を f( x, y ) に代入して y を消去して極値を求めるという方法を利用しますが、変数の消去を使わずにこのような問題を解く手法として「ラグランジュの未定乗数法」があります。
f( x, y ) = 2x2 + 3y2 は、( x, y ) = ( 0, 0 ) でゼロになり、xy 平面に接した状態になります。また、その形状は楕円型で、ちょうどお椀のように見え、xy 平面に平行な面で切ったときの切り口は楕円の形になります。xy 平面上に直線 x + y = 1 を描画して、その線上に、xy 平面に垂直な平面を描画したとき、その面で切られた楕円型の切り口は放物線となるので、その極小値となるところが最小値となります。ちょうど、楕円形の粘土模型があって、直線 x + y = 1 上にあるひもを上に持ち上げると、粘土が切れたときの切り口が放物線となる様子を思い浮かべると分かりやすいと思います。すると、そのひもが粘土に接したときの点が、求める ( x, y ) とその最小値になります。もし、ひもが粘土に接しておらず、交差した(粘土にひもが食い込んだような)状態になっているとすれば、その点から切り口をたどると値が大きく、または小さく変化するので、その点は最小値とならないからです。
楕円型 f( x, y ) が直線 x + y = 1 と接している点を含むように、xy 平面に平行な面で切ったとき、楕円 f( x, y ) = c (定数) に直線 x + y = 1 が接した形状を見ることができます。この時、f( x, y ) = c の接点での法線ベクトルと直線 x + y = 1 の法線ベクトルは平行になるので、f( x, y ) = c の法線ベクトルを ∇f、直線 x + y = 1 の法線ベクトルを ∇g としたとき、ある定数 λ があって
と表すことができます。f( x, y ) = c と x + y = 1 の接点における、f( x, y ) = c の接線の傾きを求めるため、f( x, y ) = c を x で微分すると、
より dy / dx = -2x / 3y となるので、接線に垂直なベクトルは ( 2x, 3y ) となって、
∇f = ( 2x, 3y )
∇g = ( 1, 1 )
より、
となります。 x + y = 1 に ( x, y ) = ( λ / 2, λ / 3 ) を代入して λ = 6 / 5 となり、これより
という解が得られ、最小値は 2 x ( 3 / 5 )2 + 3 x ( 2 / 5 )2 = 6 / 5 になります。
一般的に、制約条件 g( x1, x2, ... xN ) = g(x) = 0 もとでの N 変数関数 f( x1, x2, ... xN ) = f(x) の極値を求める問題を考えた場合、g(x) = 0 は N 次元空間上の曲面を表し、f(x) が極値をとる点において、その点を含む曲面 f((x) = c (定数) が g(x) = 0 と接しています。よって、接点における両者の法線ベクトルは平行になり、f((x) = c の法線ベクトルを ∇f、g(x) = 0 の法線ベクトルを ∇g としたとき、ある定数 λ があって
と表すことができます。このときの定数 λ を「ラグランジュ乗数(Lagrange Multiplier)」といいます。
∇f, ∇g は、偏微分係数 ∂f / ∂xi, ∂g / ∂xi ( i = 1, 2, ... N ) を使って次のように表すことができます。
∇f = ( ∂f / x1, ∂f / x2, ... ∂f / xN )
∇g = ( ∂g / x1, ∂g / x2, ... ∂g / xN )
よって、各成分 xi に対して
が成り立つ xi と λ を求めればよいことになりますが、未知数が N + 1 個なのに対し、式は N 個で一つ足りないので、もうひとつ制約条件
を方程式に加える必要があります。そこで、
として、N + 1 個の方程式を
と定義すると、F( x, λ ) を xi で偏微分すれば
なので、左辺がゼロということは ∂f / ∂xi = λ∂g / ∂xi を意味し、これが i = 1, 2, ... N で成り立つので ∇f = λ∇g であることを意味します。また、λ で偏微分すれば
となり、左辺がゼロならば制約条件 g(x) = 0 を意味するので、N + 1 個の連立方程式を解くことで解が得られることになります。
直線への当てはめの中で
が最小になるような ( μxj, μyj ) を制約条件
の下で求めるような場合、ラグランジュの未定乗数法を利用することができます。まず、
| F( μxj, μyj, λj ) | = | J - λj( aμxj + bμyj + c ) |
| = | Σj{1→N}( ( xj - μxj )2 + ( yj - μyj )2 ) / 2 - λj( aμxj + bμyj + c ) |
として、三つの連立方程式 ∂F / ∂μxj = 0, ∂F / ∂μyj = 0, ∂F / ∂λj = 0 を求めると、
∂F / ∂μxj = - ( xj - μxj ) - λja = 0
∂F / ∂μyj = - ( yj - μyj ) - λjb = 0
∂F / ∂λj = - ( aμxj + bμyj + c ) = 0
上側の二式から μxj = λja + xj, μyj = λjb + yj を三式目に代入して
より
a2 + b2 = 1 と正規化すれば λj = -( axj + byj + c ) なので、
| μxj | = | -a( axj + byj + c ) + xj |
| = | ( 1 - a2 )xj - abyj - ac | |
| = | b2xj - abyj - ac | |
| μyj | = | -b( axj + byj + c ) + yj |
| = | -abxj + ( 1 - b2 )yj - bc | |
| = | a2yj - abxj - bc |
となって、変数を消去して求めた場合と同様の結果が得られます。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |