確率・統計

(13) 回帰分析法

前回、二標本の解析法として回帰係数の推定法を紹介しました。この理論は、そのまま多変量の解析に応用することが可能で、二変量での推定はその特別な場合と考えることができます。今回は、重回帰分析法に関する話題を中心に紹介したいと思います。

(注) 数式などの記法について (ドキュメントの中で使用している数式の表現方法に関する注意点です)

1) 線形重回帰モデル(Linear Multiple Regression Model)

今までは、一つの要因(独立変数 x)に対して従属変数 y が変化し、それが線形関係であるとしてモデルを構築してきましたが、実際には複数の要因が関係していることの方が多いことは容易に推測できます。例えば、交通事故発生件数に対する独立変数としては、人口だけでなく道路の整備状況や交通量、さらには数値化の難しいようなパラメータ(その土地特有の性格や風土など)も考えることができます。そこで、これらの独立変数が全て従属変数に線形的に影響していると考えて、次のようなモデルを考えます。

y = a0 + a1x1 + a2x2 + ... + apxp

xj ( j = 1, 2, ... p ) はそれぞれが異なる独立変数を表します。各独立変数の線形式によって目的変数が得られると考えるわけです。各独立変数と従属変数の標本が N 個あったとき、各独立変数の標本を xj,i、従属変数の標本を yi ( i = 1, 2, ... N ) として、上に示したモデルを元に、

yi = a0 + a1x1,i + a2x2,i + ... + apxp,i + εi ( i = 1, 2, ... N )

と表します。ここで、εi は独立変数だけでは説明のできない(測定などの)誤差成分を表し、誤差成分どうしは互いに独立であるとします。この式を「線形重回帰モデル(Linear Multiple Regression Model)」といいます。p = 1 であれば、この式は(単)回帰係数を求めたときのモデルと同一です。最小二乗法の考え方から、誤差成分 εi の平方和 Σi{1→N}( εi2 ) を最小とするような係数 a^j を求めると、それが aj の最尤推定量となるのでした。平方和の 1/2 を J で表すと

J = Σi{1→N}( εi2 ) / 2 = Σi{1→N}( { yi - ( a0 + a1x1,i + a2x2,i + ... + apxp,i ) }2 ) / 2

となるので、J を aj で微分すると

∂J / ∂a0 = - Σi{1→N}( { yi - ( a0 + a1x1,i + a2x2,i + ... + apxp,i ) } )

∂J / ∂aj = - Σi{1→N}( xj,i{ yi - ( a0 + a1x1,i + a2x2,i + ... + apxp,i ) } )

となり、J が最小となるのは ∂J / ∂aj = 0 ( i = 0, 1, 2, ... p ) のときなので、上式を整理して

N・a0 + Σi{1→N}( x1,i )a1 + Σi{1→N}( x2,i )a2 + ... + Σi{1→N}( xp,i )ap = Σi{1→N}( yi )

Σi{1→N}( xj,i )a0 + Σi{1→N}( xj,ix1,i )a1 + Σi{1→N}( xj,ix2,i )a2 + ... + Σi{1→N}( xj,ixp,i )ap = Σi{1→N}( xj,iyi )

よって、正規方程式は、

|N,Σi{1→N}( x1,i ),Σi{1→N}( x2,i ),...Σi{1→N}( xp,i )||a0|=|Σi{1→N}( yi )|
|Σi{1→N}( x1,i ),Σi{1→N}( x1,i2 ),Σi{1→N}( x1,ix2,i ),...Σi{1→N}( x1,ixp,i )||a1||Σi{1→N}( x1,iyi )|
|Σi{1→N}( x2,i ),Σi{1→N}( x2,ix1,i ),Σi{1→N}( x2,i2 ),...Σi{1→N}( x2,ixp,i )||a2||Σi{1→N}( x2,iyi )|
|:::...:||:||:|
|Σi{1→N}( xp,i ),Σi{1→N}( xp,ix1,i ),Σi{1→N}( xp,ix2,i ),...Σi{1→N}( xp,i2 )||ap||Σi{1→N}( xp,iyi )|

となり、これを解くと aj の最尤推定量 a^j が求められます。ところで、求めた推定量を正規方程式の第一式に代入すると(以下、推定量 a^j は aj で表します)

N・a0 + Σi{1→N}( x1,i )a1 + Σi{1→N}( x2,i )a2 + ... + Σi{1→N}( xp,i )ap = Σi{1→N}( yi )

となるので、両辺を N で割ると

a0 + Σj{1→p}( mxjaj ) = my

となります。但し、

mxj = Σi{1→N}( xj,i ) / N

my = Σi{1→N}( yi ) / N

とします。つまり、mxj と my は xj,i、yi の標本平均を表すことになります。この結果から、

a0 = my - Σj{1→p}( mxjaj )

となるので、正規方程式の中の a0 を左辺に置き換えると、j = 0 のときは

N{ my - Σk{1→p}( mxkak ) } + Σk{1→p}( Σi{1→N}( xk,i )ak ) = Σi{1→N}( yi )

より

Σk{1→p}( Σi{1→N}( xk,i - mxk )ak ) = Σi{1→N}( yi - my ) --- (1)

また、j > 0 のときは

NΣi{1→N}( xj,i ){ my - Σk{1→p}( mxkak ) } + Σk{1→p}( Σi{1→N}( xj,ixk,i )ak ) = Σi{1→N}( xj,iyi )

より

Σk{1→p}( Σi{1→N}( xj,i( xk,i - mxk ) )ak ) = Σi{1→N}( xj,i( yi - my ) ) --- (2)

となります。(1) に mxj を掛けると

Σk{1→p}( Σi{1→N}( mxj( xk,i - mxk ) )ak ) = Σi{1→N}( mxj( yi - my ) ) --- (1')

になるので、(2) - (1') を求めると

Σk{1→p}( Σi{1→N}( ( xj,i - mxj )( xk,i - mxk ) )ak ) = Σi{1→N}( ( xj,i - mxj )( yi - my ) ) --- (3)

ここで、

sjk = Σi{1→N}( ( xj,i - mxj )( xk,i - mxk ) ) / N

syj = Σi{1→N}( ( xj,i - mxj )( yi - my ) ) / N

とすれば sjk は xj,i と xk,i、syj は xj,i と yi との標本共分散を表し、(3) 式は

Σk{1→p}( sjkak ) = syj

で表され、j = 1, 2, ... p に対して p 個の連立方程式に変形されたことになるので、これを解いても最尤推定量 a^j を求めることができます。連立方程式を行列で表すと

|s11,s12,s13,...s1p||a1|=|sy1|
|s21,s22,s23,...s2p||a2||sy2|
|:::...:||:||:|
|sp1,sp2,sp3,...spp||ap||syp|

となり、左辺の係数行列は共分散行列そのものです。従って、共分散行列を V、a = ( a1, a2, ... ap )T、sy = ( sy1, sy2, ... syp )T とすれば、上式は

Va = sy

と表されます。また、このとき a^0 は

a^0 = my - Σj{1→p}( mxja^j )

から求められます。各独立成分どうし、あるいはそれらと従属成分の間の標本共分散を求めれば、それらを係数とする p 個の連立方程式が得られ、それを解くことによって回帰係数の最尤推定量を求めることができます。p = 1 のときは、式の数は一つのみとなって、二変量での回帰係数を求める場合と一致することもこの結果から分かります。

a^j の解は、V-1 の j 行 k 列の要素を sjk で表せば

a^j=Σk{1→p}( sjksyk )
=Σk{1→p}( sjk( Σi{1→N}( ( xk,i - mxk )( yi - my ) ) / N ) )
=Σk{1→p}( sjk( { Σi{1→N}( ( xk,i - mxk )yi ) - myΣi{1→N}( xk,i - mxk ) } / N ) )
=Σk{1→p}( sjk( Σi{1→N}( ( xk,i - mxk )yi ) ) ) / N
=Σi{1→N}( Σk{1→p}( sjk( xk,i - mxk )yi ) ) / N

で求められます。ここで、Σi{1→N}( xk,i - mxk ) = 0 になることを利用していることに注意してください。「回帰係数の推定」の場合と同様に、εi だけが確率分布に従うと考えると、その確率密度が平均 0、分散 σ2 の正規分布 N( 0, σ2 ) であるとすれば、yi も正規分布に従うことになり、その期待値 E[yi] と分散 V[yi] は

E[yi] = E[a0 + Σl{1→p}( alxl,i ) + εi] = a0 + Σl{1→p}( alxl,i )

V[yi] = E[{ a0 + Σl{1→p}( alxl,i ) + εi - E[yi] }2] = E[εi2] = σ2

となるので、a^j の期待値 E[a^j] は

E[a^j]=E[Σi{1→N}( Σk{1→p}( sjk( xk,i - mxk )yi ) ) / N]
=Σi{1→N}( Σk{1→p}( sjk( xk,i - mxk )E[yi] ) ) / N
=Σk{1→p}( sjkΣi{1→N}( ( xk,i - mxk ){ a0 + Σl{1→p}( alxl,i ) } ) ) / N

Ak = Σi{1→N}( ( xk,i - mxk ){ a0 + Σl{1→p}( alxl,i ) } ) として Ak を計算すると

Ak=Σi{1→N}( ( xk,i - mxk ){ a0 + Σl{1→p}( alxl,i ) } )
=a0Σi{1→N}( xk,i - mxk ) + Σl{1→p}( alΣi{1→N}( ( xk,i - mxk )xl,i ) )
=Σl{1→p}( al{ Σi{1→N}( ( xk,i - mxk )xl,i ) - Σi{1→N}( ( xk,i - mxk )mxl ) } )
=Σl{1→p}( alΣi{1→N}( ( xk,i - mxk )( xl,i - mxl ) ) )
=NΣl{1→p}( alskl )

ここでも、Σi{1→N}( xk,i - mxk ) = 0 になることを利用しています。特に、Σi{1→N}( ( xk,i - mxk )mxl ) = 0 なので、この項を追加しても値に変化はなく、共分散の形で表すことができるようになります。

この値を元の式に戻せば

E[a^j] = Σk{1→p}( sjkΣl{1→p}( alskl ) )

となります。Σl{1→p}( alskl ) は Va の第 k 行を表し、上式は ( sj1, sj2, ... sjp ) と Va の第 k 行ベクトルとの内積を表しているので、行列で表すと、

E[a^j] = ( sj1, sj2, ... sjp )|s11,s12,s13,...s1p||a1|
|s21,s22,s23,...s2p||a2|
|:::...:||:|
|sp1,sp2,sp3,...spp||ap|

となり、( sj1, sj2, ... sjp ) は V-1 の第 j 行であることから、V との積は第 j 番目の要素のみ 1 で残りはゼロのベクトルになります。従って、

E[a^j] = aj

が解として得られます。E[a^0] は

E[a^0]=E[my - Σj{1→p}( mxja^j )]
=E[my] - Σj{1→p}( mxjE[a^j] )
=E[my] - Σj{1→p}( mxjaj )

となり、E[my] は

E[my]=E[Σi{1→N}( yi ) / N]
=Σi{1→N}( E[a0 + Σj{1→p}( ajxj,i ) + εi] ) / N
=Σi{1→N}( a0 + Σj{1→p}( ajxj,i ) ) / N
=a0 + Σi{1→N}( Σj{1→p}( ajxj,i ) ) / N
=a0 + Σj{1→p}( ajΣi{1→N}( xj,i ) / N )
=a0 + Σj{1→p}( ajmxj )

なので、

E[a^0] = a0

となって、a^j の不偏推定量は ( j = 0 のときも含めて全て ) aj になることが分かります。a^j の分散 V[a^j] は、独立成分 xj,i と誤差成分 εi が互いに独立であることから yi も互いに独立であることになるので、

V[a^j]=V[Σi{1→N}( Σk{1→p}( sjk( xk,i - mxk )yi ) ) / N]
=Σi{1→N}( { Σk{1→p}( sjk( xk,i - mxk ) ) }2V[yi] ) / N
=Σi{1→N}( { Σk{1→p}( sjk( xk,i - mxk ) ) }2 )σ2 / N
=Σi{1→N}( Σk{1→p}( Σl{1→p}( sjksjl( xk,i - mxk )( xl,i - mxl ) ) ) )σ2 / N
=Σk{1→p}( Σl{1→p}( sjksjlΣi{1→N}( ( xk,i - mxk )( xl,i - mxl ) ) ) )σ2 / N
=Σk{1→p}( Σl{1→p}( sjksjlskl ) )σ2 / N
=Σk{1→p}( sjkΣl{1→p}( sjlskl ) )σ2 / N

と計算できます。Σl{1→p}( sjlskl ) は V-1 の第 j 行 ( sj1, sj2, ... sjp ) と V の第 k 列 ( sk1, sk2, ... skp )T との内積を意味します(実際には V の第 k 行ベクトルの要素を意味しますが、V は対称行列で skl = slk が成り立つので第 k 列ベクトルと見なすことができます)。V-1V = E なので、積の値は j = k のとき 1 で、j ≠ k のときゼロになります。よって、j = k のときだけ値が残ることになって、

V[a^j] = sjjσ2 / N

が求める結果になります。a^j と a^k の共分散 E[( a^j - aj )( a^k - ak )] = E[a^ja^k] - ajak は

E[a^ja^k]=E[{ Σr{1→N}( Σt{1→p}( sjt( xt,r - mxt )yr ) ) / N }
 ・{ Σs{1→N}( Σu{1→p}( sku( xu,s - mxu )ys ) ) / N }]
=E[Σt{1→p}( sjtΣu{1→p}( skuΣr{1→N}( Σs{1→N}( ( xt,r - mxt )( xu,s - mxu )yrys ) ) ) ) / N2]
=Σt{1→p}( sjtΣu{1→p}( skuΣr{1→N}( Σs{1→N}( ( xt,r - mxt )( xu,s - mxu )E[yrys] ) ) ) ) / N2

より、E[yrys] は

E[yrys]=E[{ a0 + Σl{1→p}( alxl,r ) + εr }{ a0 + Σl{1→p}( alxl,s ) + εs }]
=E[{ a0 + Σl{1→p}( alxl,r ) }{ a0 + Σl{1→p}( alxl,s ) }
 + { a0 + Σl{1→p}( alxl,s ) }εr + { a0 + Σl{1→p}( alxl,r ) }εs + εrεs]
={ a0 + Σl{1→p}( alxl,r ) }{ a0 + Σl{1→p}( alxl,s ) } ( r ≠ s )
={ a0 + Σl{1→p}( alxl,r ) }2 + σ2 ( r = s )

となるので、

Σr{1→N}( Σs{1→N}( ( xt,r - mxt )( xu,s - mxu )E[yrys] ) ) / N2
=Σr{1→N}( Σs{1→N}( ( xt,r - mxt )( xu,s - mxu ){ a0 + Σl{1→p}( alxl,r ) }{ a0 + Σl{1→p}( alxl,s ) } ) ) / N2
 + σ2Σr{1→N}( ( xt,r - mxt )( xu,r - mxu ) ) / N2
=Σr{1→N}( ( xt,r - mxt ){ a0 + Σl{1→p}( alxl,r ) }Σs{1→N}( ( xu,s - mxu ){ a0 + Σl{1→p}( alxl,s ) } ) ) / N2
 + σ2stu / N
=Σr{1→N}( ( xt,r - mxt ){ a0 + Σl{1→p}( alxl,r ) }{ Σl{1→p}( alsul ) } ) / N + σ2stu / N
=Σl{1→p}( alstl )Σl{1→p}( alsul ) + σ2stu / N

よって、

E[a^ja^k]=Σt{1→p}( sjtΣu{1→p}( sku{ Σl{1→p}( alstl )Σl{1→p}( alsul ) + σ2stu / N } ) )
=Σt{1→p}( sjtΣl{1→p}( alstl ) )Σu{1→p}( skuΣl{1→p}( alsul ) )
  + σ2Σt{1→p}( sjtΣu{1→p}( skustu ) ) / N
=Σt{1→p}( Σl{1→p}( sjtstlal ) )Σu{1→p}( Σl{1→p}( skusulal ) )
  + σ2Σt{1→p}( sjtδtk ) / N
=ajak + sjkσ2 / N

となって、a^j と a^k の共分散は sjkσ2 / N になります。Σt{1→p}( Σl{1→p}( sjtstlal ) ) = aj, Σu{1→p}( Σl{1→p}( skusulal ) ) = ak が成り立つのは、E[a^j] を求める時と同じ理由で、これらの式が V-1 の第 j 行, 第 k 行と Va との内積を表しているからです。また、Σt{1→p}( sjtΣu{1→p}( skustu ) ) の計算も V[a^j] の計算で一度登場しています。Σu{1→p}( skustu ) は V-1 の第 k 行と V の第 t 列ベクトルの内積なので、k = t のときのみ 1 で残りは全てゼロになります。よって、計算結果を「クロネッカーのデルタ」δtk で表しています。

V[a^0] は

V[a^0]=E[{ my - Σj{1→p}( a^jmxj ) - a0 }2]
=E[{ Σi{1→N}( a0 + Σj{1→p}( ajxj,i ) + εi ) / N - Σj{1→p}( a^jmxj ) - a0 }2]
=E[{ Σj{1→p}( ajΣi{1→N}( xj,i ) / N ) + Σi{1→N}( εi ) / N - Σj{1→p}( a^jmxj ) }2]
=E[{ Σj{1→p}( ( aj - a^j )mxj ) + Σi{1→N}( εi ) / N }2]

と表すことができます。Σi{1→N}( εi ) の二乗は εi2 の項だけが残り、その値は Nσ2 になるので、上式を展開すると

V[a^0] = E[{ Σj{1→p}( ( aj - a^j )mxj ) }2] + 2E[Σj{1→p}( ( aj - a^j )mxj )Σi{1→N}( εi )] / N + σ2 / N

となり、第一項は

E[{ Σj{1→p}( ( aj - a^j )mxj ) }2]=E[Σj{1→p}( Σk{1→p}( mxjmxk( aj - a^j )( aj - a^k ) ) )]
=Σj{1→p}( Σk{1→p}( mxjmxkE[( aj - a^j )( aj - a^k )] ) )
=Σj{1→p}( Σk{1→p}( mxjmxksjkσ2 / N ) )

第二項は

2E[Σj{1→p}( ( aj - a^j )mxj )Σi{1→N}( εi )] / N=2E[Σi{1→N}( Σj{1→p}( ( aj - a^j )mxjεi ) )] / N
=2Σi{1→N}( Σj{1→p}( ajmxjE[εi] - mxjE[a^jεi] ) ) / N
=-2Σj{1→p}( mxjΣi{1→N}( E[a^jεi] ) ) / N

となって、

Σi{1→N}( E[a^jεi] )=Σi{1→N}( E[Σl{1→N}( Σk{1→p}( sjk( xk,l - mxk )εiyl ) ) / N] )
=Σi{1→N}( Σl{1→N}( Σk{1→p}( sjk( xk,l - mxk )E[εiyl] ) ) ) / N
=Σi{1→N}( Σk{1→p}( sjk( xk,i - mxk )E[εiyi] ) ) / N
=Σi{1→N}( Σk{1→p}( sjk( xk,i - mxk ) ) )σ2 / N
=Σk{1→p}( sjkΣi{1→N}( xk,i - mxk ) ) )σ2 / N

より、Σi{1→N}( xk,i - mxk ) = 0 なのでこの項は無視することができます。よって、

V[a^0] = { 1 / N + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) / N }σ2

が求める解になります。最後に、a^0 と a^j ( j > 0 ) の共分散 E[( a^0 - a0 )( a^j - aj )] を計算すると、

E[( a^0 - a0 )( a^j - aj )]=E[a^0a^j] - a0aj
=E[{ my - Σk{1→p}( mxka^k ) }a^j] - a0aj
=E[mya^j] - Σk{1→p}( mxkE[a^ka^j] ) - a0aj

と表すことができます。第一項の E[mya^j] は

E[mya^j]=E[Σi{1→N}( a^jyi ) / N]
=E[Σi{1→N}( a^j{ a0 + Σk{1→p}( akxk,i ) + εi } ) / N]
=E[Σi{1→N}( a^j{ a0 + Σk{1→p}( akxk,i ) } + a^jεi ) / N]
=Σi{1→N}( { a0 + Σk{1→p}( akxk,i ) }E[a^j] ) / N + Σi{1→N}( E[a^jεi] ) / N
=Σi{1→N}( { a0 + Σk{1→p}( akxk,i ) }aj ) / N
={ Na0 + Σk{1→p}( akΣi{1→N}( xk,i ) ) }aj / N
=a0aj + Σk{1→p}( ajakmxk )

と求められます。ここで、先ほど求めた結果 Σi{1→N}( E[a^jεi] ) = 0 を利用していることに注意してください。第二項は

Σk{1→p}( mxkE[a^ka^j] )=Σk{1→p}( mxk( ajak + sjkσ2 / N ) )
=Σk{1→p}( mxkajak ) + Σk{1→p}( mxksjkσ2 / N )

なので、

E[( a^0 - a0 )( a^j - aj )]=a0aj + Σk{1→p}( ajakmxk ) - { Σk{1→p}( mxkajak ) + Σk{1→p}( mxksjkσ2 / N ) } - a0aj
=-Σk{1→p}( mxksjkσ2 / N )

という結果が得られます。

以上の結果をまとめると、

E[a^j] = aj ; E[a^0] = a0

V[a^j] = sjjσ2 / N

E[( a^j - aj )( a^k - ak )] = sjkσ2 / N

V[a^0] = { 1 / N + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) / N }σ2

E[( a^0 - a0 )( a^j - aj )] = -Σk{1→p}( mxksjkσ2 / N )

であり、特に p = 1 のときは s11 = vx としたとき s11 = 1 / vx なので、a1 = a, a^1 = a^, a0 = b, a^0 = b^, mx1 = mx で表せば

E[a^] = a ; E[b^] = b

V[a^] = σ2 / Nvx

V[b^] = ( 1 / N + mx2 / Nvx )σ2

E[( b^ - b )( a^ - a )] = -mxσ2 / Nvx

と求められ、前回得られたニ標本での回帰係数に対する期待値や分散と一致します。

a^j は yi の線形結合で表されることから、yi が正規分布に従うならば a^j も正規分布に従うのでした。また、a^0 は my と a^j の線形結合なので、やはり正規分布に従います。よって、それぞれの期待値と分散から、a^j は N( aj, sjjσ2 / N )、a^0 は N( a^0, { 1 / N + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) / N }σ2 ) に従うとして推定や検定を行うことができます。しかし、式中の σ2 は未知の値なので、このままでは計算ができません。そこで、二変量の場合と同じように yi と ( a^0 + Σj{1→p}( a^jxj,i ) ) の差の平方和 (つまり aj の推定量 a^j を使って求めた y の値と実測値としての y の差の平方和) に対してその期待値を求めると、

E[Σi{1→N}( [ yi - { a^0 + Σj{1→p}( a^jxj,i ) } ]2 )]
=E[Σi{1→N}( [ { a0 + Σj{1→p}( ajxj,i ) + εi } - { a^0 + Σj{1→p}( a^jxj,i ) } ]2 )]
=E[Σi{1→N}( { ( a0 - a^0 ) + Σj{1→p}( ( aj - a^j )xj,i ) + εi }2 )]
=E[Σi{1→N}( ( a0 - a^0 )2 + Σj{1→p}( Σk{1→p}( ( aj - a^j )( ak - a^k )xj,ixk,i ) ) + εi2
 + 2( a0 - a^0 )Σj{1→p}( ( aj - a^j )xj,i ) + 2εi( a0 - a^0 ) + 2εiΣj{1→p}( ( aj - a^j )xj,i ) )]
=Σi{1→N}( E[( a0 - a^0 )2] + Σj{1→p}( Σk{1→p}( E[( aj - a^j )( ak - a^k )]xj,ixk,i ) ) + E[εi2]
 + 2Σj{1→p}( E[( a0 - a^0 )( aj - a^j )]xj,i ) + 2E[εi( a0 - a^0 )] + 2Σj{1→p}( E[εi( aj - a^j )]xj,i ) )
=Σi{1→N}( { 1 / N + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) / N }σ2 + Σj{1→p}( Σk{1→p}( sjkxj,ixk,i / N ) )σ2 + σ2
 - 2Σj{1→p}( Σk{1→p}( mxksjk )xj,i / N )σ2 - 2E[εia^0] - 2Σj{1→p}( E[εia^j]xj,i ) )

Σi{1→N}( E[εia^j] ) = 0 であることはすでに証明できているので、これを利用して Σi{1→N}( E[εia^0] ) を求めると

Σi{1→N}( E[εia^0] )=Σi{1→N}( E[εi{ my - Σj{1→p}( a^jmxj ) }] )
=Σi{1→N}( E[εimy] ) - Σj{1→p}( mxjΣi{1→N}( E[εia^j] ) )
=Σi{1→N}( E[εiΣl{1→N}( yl )] ) / N
=Σi{1→N}( Σl{1→N}( E[εiεl] ) ) / N = σ2

また、

Σi{1→N}( E[a^jεi]xj,i )=Σi{1→N}( E[Σl{1→N}( Σk{1→p}( sjk( xk,l - mxk )εiylxj,i ) ) / N] )
=Σi{1→N}( Σl{1→N}( Σk{1→p}( sjkxj,i( xk,l - mxk )E[εiyl] ) ) ) / N
=Σi{1→N}( Σk{1→p}( sjkxj,i( xk,i - mxk )E[εiyi] ) ) / N
=Σi{1→N}( Σk{1→p}( sjkxj,i( xk,i - mxk ) ) )σ2 / N
=Σk{1→p}( sjkΣi{1→N}( xk,ixj,i - mxkxj,i ) )σ2 / N
=Σk{1→p}( sjkΣi{1→N}( xk,ixj,i / N ) - mxjmxksjk )σ2

よって、

E[Σi{1→N}( [ yi - { a^0 + Σj{1→p}( a^jxj,i ) } ]2 )]
={ 1 + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) }σ2 + Σj{1→p}( Σk{1→p}( sjkΣi{1→N}( xj,ixk,i / N ) ) )σ2 + Nσ2
 - 2Σj{1→p}( Σk{1→p}( mxksjk )Σi{1→N}( xj,i / N ) )σ2 - 2σ2
 - 2Σj{1→p}( Σk{1→p}( sjkΣi{1→N}( xk,ixj,i / N ) - mxjmxksjk ) )σ2
=Nσ2 - σ2 + Σj{1→p}( Σk{1→p}( mxjmxksjk ) )σ2 + Σj{1→p}( Σk{1→p}( sjkΣi{1→N}( xj,ixk,i / N ) ) )σ2
 - 2Σj{1→p}( Σk{1→p}( mxjmxksjk ) )σ2
 - 2Σj{1→p}( Σk{1→p}( sjkΣi{1→N}( xk,ixj,i / N ) ) )σ2 + 2Σj{1→p}( Σk{1→p}( mxjmxksjk ) )σ2
=Nσ2 - σ2 + Σj{1→p}( Σk{1→p}( mxjmxksjk ) )σ2 - Σj{1→p}( Σk{1→p}( sjkΣi{1→N}( xj,ixk,i / N ) ) )σ2
=Nσ2 - σ2 + Σj{1→p}( Σk{1→p}( sjk( mxjmxk - Σi{1→N}( xj,ixk,i / N ) ) ) )σ2

mxjmxk - Σi{1→N}( xj,ixk,i / N ) は xj,i と xk,i の共分散 sjk に -1 を掛けたものを表しています。一応証明しておくと、

mxjmxk - Σi{1→N}( xj,ixk,i / N )=Σi{1→N}( ( mxk - xk,i )xj,i / N )
=Σi{1→N}( ( mxk - xk,i )xj,i / N ) - mxjΣi{1→N}( mxk - xk,i ) / N
=-Σi{1→N}( ( mxk - xk,i )( mxj - xj,i ) / N ) = -sjk

唐突に出現した mxjΣi{1→N}( mxk - xk,i ) / N の項は、Σi{1→N}( mxk - xk,i ) = 0 より追加しても結果には影響しません。以上から、

E[Σi{1→N}( [ yi - { a^0 + Σj{1→p}( a^jxj,i ) } ]2 )]
=Nσ2 - σ2 - Σj{1→p}( Σk{1→p}( sjksjk ) )σ2
=Nσ2 - σ2 - Σj{1→p}( 1 )σ2
=( N - p - 1 )σ2

Σk{1→p}( sjksjk ) は V-1V の j 行 j 列めの要素を表すので 1 になり、上記のような結果になります。

この結果から、vε = Σi{1→N}( [ yi - { a^0 + Σj{1→p}( a^jxj,i ) } ]2 ) / ( N - p - 1 ) としたとき、vε は σ2 の不偏推定量になります。特に、p = 1 のときは前回求めた二変量の場合の結果とも一致します。そこで二変量の場合と同様に

zj = ( a^j - aj ) / ( sjjσ2 / N )1/2

z0 = ( a^0 - a0 ) / [ { 1 / N + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) / N }σ2 ]1/2

が標準正規分布に従い、

tj = ( a^j - aj ) / ( sjjσ2 / N )1/2( √vε / σ ) = ( a^j - aj ) / ( sjjvε / N )1/2

t0=( a^0 - a0 ) / [ { 1 / N + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) / N }σ2 ]1/2( √vε / σ )
=( a^0 - a0 ) / [ { 1 / N + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) / N }vε ]1/2

が自由度 N - p - 1 の t-分布に従うことを利用して推定・検定を行うことができます(補足1)。

sjk は共分散行列 V の逆行列の要素です。従って、tj や t0 を求めるためには逆行列を求める必要があります。二次、三次の正方行列であれば公式があり、それより高次の場合は余因子行列を利用した解法がよく紹介されます。しかし、余因子行列を利用する解法は非常に処理が重く、通常は連立方程式を解くアルゴリズムを利用して逆行列を求めます。具体的な処理方法は「数値演算法」の「(7) 連立方程式を解く -1-」にある「3) 連立方程式による逆行列の計算」をご覧ください。

線形重回帰モデルでの回帰係数を推定するためのサンプル・プログラムを以下に示します。

/*
  MultipleRegressionCoefficient : 重回帰係数
*/
class MultipleRegressionCoefficient
{
  vector<double> _est_a; // 回帰係数 ai の推定量 ( i = 1, 2, ... )
  double _est_a0;        // 回帰係数 a0 の推定量
  unsigned int _cnt;     // 標本数
  vector<double> _mx;    // x[i] の平均
  vector<double> _var_x; // x[i] の分散
  double _se;            // 誤差項の平方和
  double _sy;            // y の平均差の平方和
  LinearEquationSystem<double> _s_inv; // 共分散行列の逆行列

  bool _isValid;     // 正しく計算できたか？

  // 回帰直線の区間推定
  bool regCoef_iEst( const ContDist& dist, double var, double b,
                     vector< pair<double,double> >& interval_a,
                     double threshold = DEFAULT_THRESHOLD ) const;

public:

  /*
    コンストラクタ
  */
  MultipleRegressionCoefficient( const vector< vector<double> >& x, const vector<double>& y )
    : _s_inv( LinearEquationSystem<double>( 0 ) )
    { init( x, y ); }

  // 初期化処理
  void init( const vector< vector<double> >& x, const vector<double>& y );

  // 利用可能な状態か？
  bool isValid() const { return( _isValid ); }
  bool operator!() const { return( ! isValid() ); }

  // 独立変数の数
  unsigned int size() const { return( _est_a.size() ); }

  // 回帰係数の推定値を返す
  double a( unsigned int i ) const
  { return(
           ( i == 0 ) ? _est_a0 :
           ( ( i <= size() ) ? _est_a[i - 1] : NAN )
           );
  }

  // 共分散行列の逆行列の要素を返す
  double s_inv( unsigned int r, unsigned int c ) const
  { return( ( isValid() ) ? _s_inv[r][c] : NAN ); }

  // 誤差項の分散の不偏推定量を返す
  double ve() const { return( ( isValid() ) ? _se / (double)( _cnt - size() - 1 ) : NAN ); }

  // 従属変数の推定値を返す
  double y( const vector<double>& x ) const;
  double y( const vector< vector<double> >& vec_x, unsigned int i ) const;

  // 重回帰式を出力する
  void printEquation() const;

  /*
    区間推定
  */

  /*
    regCoef_iEst : 回帰直線の区間推定(誤差項の分散が既知の時)

    double var : 誤差項の分散
    double b : 信頼度
    pair<double,double> &interval_a, &interval_b : 求める信頼区間
    double threshold : binSearchでtを求める時のしきい値

    戻り値 : True ... 成功 , False ... 利用不可, 信頼度が不正
  */
  bool regCoef_iEst( double var, double b, vector< pair<double,double> >& interval_a,
                     double threshold = DEFAULT_THRESHOLD ) const
  { return( regCoef_iEst( NormalDistribution( 0, 1 ), var, b, interval_a, threshold ) ); }

  // 回帰係数の区間推定(誤差項の分散が未知の場合)
  bool regCoef_iEst( double b, vector< pair<double,double> >& interval_a,
                     double threshold = DEFAULT_THRESHOLD ) const;

  // 回帰の有意性検定
  int regCoef_Test( double a, double threshold = DEFAULT_THRESHOLD ) const;
};

/*
  MultipleRegressionCoefficient::init 初期化処理

  const vector< vector<double> >&x : 独立変数
  const vector<double>&y : 従属変数
*/
void MultipleRegressionCoefficient::init( const vector< vector<double> >& x, const vector<double>& y )
{
  unsigned int p = x.size(); // 独立変数ベクトルのサイズ
  _isValid = false;
  _est_a0 = _se = _sy = NAN;

  if ( p < 1 ) {
    cerr << "The size of independent variable x must be greater than zero." << endl;
    return;
  }

  _cnt = x[0].size();
  if ( y.size() != _cnt ) {
    cerr << "The size of data ( x, y ) must be the same size." << endl;
    return;
  }
  if ( _cnt <= p + 1 ) {
    cerr << "The size of data must be greater than the size of independent variable." << endl;
    return;
  }
  for ( unsigned int i = 1 ; i < p ; ++i ) {
    if ( x[i].size() != _cnt ) {
      cerr << "The size of data x[" << i << "] seems to not be the same as x[0]." << endl;
      return;
    }
  }

  // x, y の平均
  _mx.resize( p );
  for ( unsigned int i = 0 ; i < p ; ++i )
    _mx[i] = sampleAverage( x[i] );
  double my = sampleAverage( y );

  // 共分散行列の作成
  LinearEquationSystem<double> s( p );
  for ( unsigned int r = 0 ; r < p ; ++r ) {
    s[r][r] = sampleVariance( x[r] );
    s.ans( r ) = sampleCovariance( x[r], y );
    for ( unsigned int c = r + 1 ; c < p ; ++c )
      s[r][c] = s[c][r] = sampleCovariance( x[r], x[c] );
  }

  // 共分散行列の逆行列の計算
  if ( ! Inverse( s, _s_inv ) ) {
    cerr << "Failed to determine an inverse of covariance matrix." << endl;
    return;
  }

  // 回帰係数の推定値
  _est_a.resize( p );
  if ( ! GaussianElimination( s ) ) {
    cerr << "Failed to determine an estimator of regression coefficient." << endl;
    return;
  }
  for ( unsigned int i = 0 ; i < p ; ++i )
    _est_a[i] = s.ans( i );
  _est_a0 = my;
  for ( unsigned int i = 0 ; i < p ; ++i )
    _est_a0 -= _mx[i] * _est_a[i];

  // 誤差項の平方和
  vector<double> est_y( _cnt, _est_a0 ); // y の予測値
  vector<double> dy( _cnt );             // y の実測値と予測値の差の平方
  for ( unsigned int i = 0 ; i < _cnt ; ++i ) {
    for ( unsigned int j = 0 ; j < p ; ++j ) {
      est_y[i] += _est_a[j] * x[j][i];
    }
    dy[i] = pow( y[i] - est_y[i], 2 );
  }
  _se = sum( dy );

  // y の平均差の平方和
  Deviation<double> dev( my );
  _sy = sum( y, dev );

  _isValid = true;
}

/*
  MultipleRegressionCoefficient::y : 従属変数の推定値を返す

  const vector<double>& x : 独立変数

  戻り値 : 従属変数の推定値(エラー時は NAN)
*/
double MultipleRegressionCoefficient::y( const vector<double>& x ) const
{
  if ( ! isValid() ) {
    cerr << "It seems to fail to initialize." << endl;
    return( NAN );
  }
  if ( x.size() != size() ) {
    cerr << "The size of x must be same as the size of independent variables." << endl;
    return( NAN );
  }

  double est_y = 0;
  for ( unsigned int i = 0 ; i < size() ; ++i )
    est_y += _est_a[i] * x[i];

  return( est_y + _est_a0 );
}

/*
  MultipleRegressionCoefficient::y : 従属変数の推定値を返す

  const vector< vector<double> >& vec_x : 独立変数の配列
  unsigned int i : 対象となる vec_x 内の要素番号

  戻り値 : 従属変数の推定値(エラー時は NAN)
*/
double MultipleRegressionCoefficient::y( const vector< vector<double> >& vec_x, unsigned int i ) const
{
  vector<double> x( vec_x.size() );
  for ( unsigned int j = 0 ; j < x.size() ; ++j ) {
    if ( i >= vec_x[j].size() ) {
      cerr << i << " is bigger than the size of vec_x[" << j << "]." << endl;
      return( NAN );
    }
    x[j] = vec_x[j][i];
  }

  return( y( x ) );
}

/*
  MultipleRegressionCoefficient::printEquation : 重回帰式を出力する
*/
void MultipleRegressionCoefficient::printEquation() const
{
  if ( ! isValid() ) {
    cerr << "It seems to fail to initialize." << endl;
    return;
  }

  cout << "y = " << a( 0 );
  for ( unsigned int i = 1 ; i <= size() ; ++i )
    cout << " + " << a( i ) << "x" << i;
  cout << endl;
}

/*
  MultipleRegressionCoefficient::regCoef_iEst : 回帰直線の区間推定

  const ContDist& dist : 確率密度関数(左右対称を前提)
  double var : 誤差項の分散
  double b : 信頼度
  vector< pair<double,double> >& interval_a : 回帰係数 ai の信頼区間
  double threshold : binSearchでtを求める時のしきい値

  戻り値 : True ... 成功 , False ... 利用不可, 信頼度が不正
*/
bool MultipleRegressionCoefficient::regCoef_iEst( const ContDist& dist, double var, double b,
                                                  vector< pair<double,double> >& interval_a,
                                                  double threshold ) const
{
  if ( ! isValid() ) {
    cerr << "It seems to fail to initialize." << endl;
    return( false );
  }
  if ( b < 0 || b > 1 ) {
    cerr << "Confidence value b must have the range [0,1]." << endl;
    return( false );
  }

  double t = binSearch( dist, b / 2.0, threshold ); // 確率分布の片側信頼区間

  interval_a.resize( size() + 1 );
  for ( unsigned int i = 1 ; i <= size() ; ++i ) {
    double diff_a = t * sqrt( _s_inv[i - 1][i - 1] * var / (double)_cnt );
    interval_a[i].first = a( i ) - diff_a;
    interval_a[i].second = a( i ) + diff_a;
  }

  double sum = 0;
  for ( unsigned int j = 0 ; j < size() ; ++j )
    for ( unsigned int i = 0 ; i < size() ; ++i )
      sum += _mx[j] * _mx[i] * _s_inv[j][i];
  double diff_a0 = t * sqrt( var * ( sum + 1 ) / (double)_cnt );

  interval_a[0].first = _est_a0 - diff_a0;
  interval_a[0].second = _est_a0 + diff_a0;

  return( true );
}

/*
  MultipleRegressionCoefficient::regCoef_iEst : 回帰直線の区間推定(誤差項の分散が未知の時)

  double b : 信頼度
  vector< pair<double,double> >& interval_a : 回帰係数 ai の信頼区間
  double threshold : binSearchでtを求める時のしきい値

  戻り値 : True ... 成功 , False ... 利用不可, 信頼度が不正, データ数が 2 以下
*/
bool MultipleRegressionCoefficient::regCoef_iEst( double b, vector< pair<double,double> >& interval_a,
                                                  double threshold ) const
{
  // データ数は 3 以上必要
  if ( _cnt <= size() + 1 ) {
    cerr << "The size of data must be greater than ( independent variable size + 1 )." << endl;
    return( false );
  }

  return( regCoef_iEst( TDistribution( _cnt - size() - 1 ), ve(),
                        b, interval_a, threshold )
          );
}

MultipleRegressionCoefficient は線形重回帰モデルの回帰係数に対する推定量を保持するクラスです。その内容は前回示した単回帰での場合とほとんど同じで、回帰係数の個数が可変となるので配列の形で保持するようにしたのが単回帰の場合との大きな違いとなります。
回帰係数の推定量は連立方程式を解くことによって求めています。サンプル・プログラムでは、連立方程式を表すクラスとして LinearEquationSystem クラスを利用し、「ガウスの消去法(Gaussian Elimination)」を利用した関数 GaussianElimination を使って解を求めています。

回帰係数の推定量を求めたら、誤差項の平方和 _se と y の平均差の平方和 _sy を求めます。これらは、後で紹介する「重相関係数」の計算に利用されます。また、誤差項の不偏推定量は _se を N - p - 1 で割ることで求められ、メンバ関数 ve() にて値を得ることができます。

2) 重相関係数(Multiple Correlation Coefficient)

単回帰の場合と同様に、回帰係数の推定量を線形重回帰モデルに適用することで未測定の独立変数から従属変数の予測値を得ることができます。すなわち、ある独立変数 xj ( j = 1, 2, ... p ) に対して

y^ = a^0 + Σj{1→p}( a^jxj )

として得られた y^ が従属変数の予測値となります。この式は、推定量を求めるために利用した観測値に対しても適用できるので、独立変数 xj,i ( i = 1, 2, ... N ) に対して

y^i = a^0 + Σj{1→p}( a^jxj,i )

は従属変数の予測値であり、従属変数の観測値 yi との差

εi = yi - y^i

は予測値に対する測定誤差と見ることができます。予測値 y^i の標本平均を m^y = Σi{1→N}( y^i ) / N、標本分散を v^y = Σi{1→N}( ( y^i - m^y )2 ) / N、観測値 yi の標本平均を my = Σi{1→N}( yi ) / N、標本分散を vy = Σi{1→N}( ( yi - my )2 ) / N、また観測値 yi と予測値 y^i の共分散を syy^ = Σi{1→N}( ( yi - my )( y^i - m^y ) ) / N としたとき、yi と y^i の標本相関係数 ryy^ は

ryy^ = syy^ / ( vy・v^y )1/2 = Σi{1→N}( ( yi - my )( y^i - m^y ) ) / { Σi{1→N}( ( yi - my )2 ) }1/2{ Σi{1→N}( ( y^i - m^y )2 ) }1/2

となります。ryy^ は「重相関係数(Multiple Correlation Coefficient)」と呼ばれ、観測値がその平均より大きい(小さい)傾向にある場合に、予測値もまた平均より大きければ(小さければ)、その値は 1 に近づくことになります。

ところで、正規方程式の第一式は

N・a^0 + Σi{1→N}( x1,i )a^1 + Σi{1→N}( x2,i )a^2 + ... + Σi{1→N}( xp,i )a^p = Σi{1→N}( yi )

であり、左辺の和の部分をまとめて表現して N で割ると

Σi{1→N}( a^0 + a^1x1,i + a^2x2,i + ... + a^pxp,i ) / N = Σi{1→N}( yi ) / N = my

になります。ところが、

Σi{1→N}( yi ) / N = Σi{1→N}( a^0 + a^1x1,i + a^2x2,i + ... + a^pxp,i + εi ) / N

でもあるので(つまり、回帰係数の最尤推定量を代入して得られる予測値 y^i に誤差項 εi を加えたものが観測値 yi になることを意味しています)、最尤推定量 a^j は、測定誤差の和 Σi{1→N}( εi ) がゼロになるような回帰係数を表していることにもなります。よって、my と m^y の間には my = m^y の関係が成り立ち、syy^ の値は

syy^=Σi{1→N}( ( yi - my )( y^i - m^y ) ) / N
=Σi{1→N}( ( yi - m^y )( y^i - m^y ) ) / N
=Σi{1→N}( { ( yi - y^i ) + ( y^i - m^y ) }( y^i - m^y ) ) / N
=Σi{1→N}( ( yi - y^i )( y^i - m^y ) + ( y^i - m^y )2 ) / N
=Σi{1→N}( εi( y^i - m^y ) ) / N + Σi{1→N}( ( y^i - m^y )2 ) / N

となります。上式の第一項は

Σi{1→N}( εi( y^i - m^y ) ) / N=Σi{1→N}( εiy^i ) / N - m^yΣi{1→N}( εi ) / N
=Σi{1→N}( εi{ a^0 + Σj{1→p}( a^jxj,i ) } ) / N
={ a^0Σi{1→N}( εi ) + Σj{1→p}( a^jΣi{1→N}( εixj,i ) ) } / N

となりますが、正規方程式の第 j + 1 式を見ると

Σi{1→N}( xj,i )a0 + Σi{1→N}( xj,ix1,i )a1 + Σi{1→N}( xj,ix2,i )a2 + ... + Σi{1→N}( xj,ixp,i )ap = Σi{1→N}( xj,iyi )

であり、左辺の和の部分をまとめて表現して N で割ると

Σi{1→N}( xj,i( a0 + a1x1,i + a2x2,i + ... + apxp,i ) ) = Σi{1→N}( xj,i( a0 + a1x1,i + a2x2,i + ... + apxp,i + εi ) )

なので、Σi{1→N}( xj,iεi ) = 0 が成り立つことにもなります(つまり、最尤推定量は j = 1, 2, ... p に対して Σi{1→N}( xj,iεi ) = 0 が成り立つような回帰係数を表していることにもなります)。よって、

Σi{1→N}( εi( y^i - m^y ) ) / N = 0

となって、

syy^ = Σi{1→N}( ( y^i - m^y )2 ) / N = v^y ≥ 0

が成り立ちます。また、vy は

vy=Σi{1→N}( ( yi - my )2 ) / N
=Σi{1→N}( { ( yi - y^i ) + ( y^i - m^y ) }2 ) / N
=Σi{1→N}( εi2 + 2εi( y^i - m^y ) + ( y^i - m^y )2 ) / N
=Σi{1→N}( εi2 ) / N + v^y

上式を変形して

Σi{1→N}( εi2 ) / N=vy - v^y
=vy( 1 - v^yv^y / vyv^y )
=vy( 1 - syy^2 / vyv^y )
=vy( 1 - ryy^2 )

左辺はゼロ以上の値になるため、1 - ryy^2 ≥ 0 が成り立ち、-1 ≤ ryy^ ≤ 1 になります(これは、ryy^ が標本相関係数であることからも明らかです)。以上から、

0 ≤ ryy^ ≤ 1

が成り立つことになります。

回帰係数の最尤推定量は

a^j = Σk{1→p}( sjksyk )

で表されるので、共分散 syy^ は

syy^=Σi{1→N}( ( yi - my )( y^i - m^y ) ) / N
=Σi{1→N}( ( yi - my )[ { a0 + Σj{1→p}( a^jxj,i ) } - { a0 + Σj{1→p}( a^jmxj ) } ] ) / N
=Σi{1→N}( ( yi - my ){ Σj{1→p}( a^j( xj,i - mxj ) ) } ) / N
=Σj{1→p}( a^jΣi{1→N}( ( yi - my )( xj,i - mxj ) ) ) / N
=Σj{1→p}( a^jsyj )
=Σk{1→p}( Σj{1→p}( syjsjksyk ) )

と表されます。sy = ( sy1, sy2, ... syp )T, sk = ( s1k, s2k, ... spk )T としたとき、Σj{1→p}( syjsjk ) = ( sy, sk ) であり、この内積を syk で表すと、上式は ( sy1, sy2, ... syp ) と sy との内積を意味します。( sy1, sy2, ... syp ) は

( sy1, sy2, ... syp )
=( sy1, sy2, ... syp )|s11,s12,...s1p|
|s21,s22,...s2p|
|::...:|
|sp1,sp2,...spp|
=syTV-1 = V-1sy

と表すことができます(最後で積の順番を反転できるのは、V-1 が対称行列だからです)。よって、

syy^ = ( sy, V-1sy )

がなりたち、v^y = syy^ だったので、

ryy^=syy^ / ( vyv^y )1/2
=( v^y / vy )1/2
={ ( sy, V-1sy ) / vy }1/2

と表すこともできます。

vy=Σi{1→N}( εi2 ) / N + v^y
=Σi{1→N}( εi2 ) / N + ( sy, V-1sy )

より、誤差項の二乗和がゼロならば重相関係数は 1 になり、誤差項が大きくなるほどゼロに近づくことになります。つまり、重相関係数を見ることで、求めた重回帰式に対して分布がどの程度密集しているかを定量的に知ることができます。また、syj を変数と考えると ( sy, V-1sy ) は二次形式であり、V-1 の固有値は正値なのでこの式は楕円体を表します。よって、v^y = syy^ は sy を楕円体の形に近似した式を表し、その誤差成分を加えることで vy が得られると見ることもできます(「固有値問題 (2) カルーネン・レーベ展開」参照)。

重相関係数 ryy^ は、次のような式で表すこともできます。

ryy^ =( Σi{1→N}( ( y^i - m^y )2 ) / Σi{1→N}( ( yi - my )2 ) )1/2

上式の分子は予測値に対する分散、分母は観測値に対する分散を表しています。この二つの値には次の関係式が成り立つのでした。

vy = v^y + Σi{1→N}( εi2 ) / N より

Σi{1→N}( ( yi - my )2 ) = Σi{1→N}( ( y^i - m^y )2 ) + Σi{1→N}( ( yi - y^i )2 )

この式は、観測値の分散が、回帰分析によって説明可能な予測値の分散と、説明のできない残差部分に二つに分けられることを意味しています。そして、重相関係数の式と比較すると、残差部分が大きくなるほど重相関係数の値は小さくなるのでした。そこで、重相関係数の二乗を R2 として

R2 = v^y / vy

を「決定係数(Coefficient Of Determination)」または「寄与率(Contribution Ratio)」といい、回帰分析によって説明できる部分の比率を表す指標として利用されます。

Σi{1→N}( { ( yi - y^i ) / σ }2 ) = ( N - p - 1 )vε / σ2 は自由度 N - p - 1 の χ2-分布 TN-p-1(y) に従います(補足1)。また、Σi{1→N}( { ( yi - my ) / σ }2 ) = Ns2 / σ2 は自由度 N - 1 の χ2-分布 TN-1(y) に従います(「(6) 標本分布」の「カイ二乗分布に対する性質」参照)。残る Σi{1→N}( { ( y^i - m^y ) / σ }2 ) は自由度 p の χ2-分布 Tp(y) に従い(補足2)、aj = 0 ( j = 1, 2, ... p ) を満たすとき、すなわち y の値が xj,i に依存しない場合は ( N - p - 1 )vε / σ2 とは互いに独立になります( y の値が xj,i に依存してしまうと、どちらにも xj,i を含んでいることから互いに独立とはなり得なくなります)。左辺は TN-1(y) に従うことから、標準正規分布に従う N - 1 個の確率変数の二乗和を表すとも言えます。右辺は、それぞれが標準正規分布に従う N - p - 1 個、p 個の確率変数の二乗和を表すことから、N - 1 個の確率変数が N - p - 1 個と p 個の二つに分解されたと考えると覚えやすいと思います。

観測値の平方和 Sy = Σi{1→N}( ( yi - my )2 )

予測値の平方和 S^y = Σi{1→N}( ( y^i - m^y )2 )

残差の平方和 Sε = Σi{1→N}( ( yi - y^i )2 )

と表すと、「補足2」の内容から、予測値の不偏分散 v^y = S^y / p であり、残差の不偏分散 vε = Sε / ( N - p - 1 ) になります。F-分布は、それぞれ自由度 M, N の χ2-分布に従う互いに独立な確率変数 t, u に対して

f = ( t / M ) / ( u / N )

としたとき f が示す分布を意味するので(「(6) 標本分布」の「F-分布」参照)、

F0 = v^y / vε = ( S^y / p ) / { Sε / ( N - p - 1 ) }

は自由度 ( p, N - p - 1 ) の F-分布に従うことになります。これが成り立つ前提条件は、aj = 0 ( j = 1, 2, ... p ) すなわち y の値が xj,i に依存しないことになるので、この条件を帰無仮説として推定や検定を行うことができます。この仮説が棄却されれば、y の値は xj,i に依存する、すなわち y の値を予測するのに有効であると言えることになります。上記の各値は、以下に示すような分散分析表でよく表されます。

変動要因平方和自由度不偏分散分散比
予測値(回帰による)S^y = Σi{1→N}( ( y^i - m^y )2 )pv^y = S^y / pF0 = v^y / vε
残差(回帰との)Sε = Σi{1→N}( ( yi - y^i )2 )N - p - 1vε = Sε / ( N - p - 1 )
観測値(全体)Sy = Σi{1→N}( ( yi - my )2 )N - 1  

重相関係数を求め、回帰の有意性を検定するためのサンプル・プログラムを以下に示します。

// 重相関係数を返す
double MultipleRegressionCoefficient::mcc() const
{
  return( ( isValid() ) ? sqrt( ( _sy - _se ) / _sy ) : NAN );
}

/*
  MultipleRegressionCoefficient::regCoef_Test : 回帰の有意性検定

  double a : 危険率
  double threshold : binSearchでtを求める時のしきい値

  戻り値 :  1 ... 有意性あり(帰無仮説は棄却) , 0 ... 有意性なし(帰無仮説は保留)
           -1 ... 利用不可
*/
int MultipleRegressionCoefficient::regCoef_Test( double a, double threshold ) const
{
  cout << "***** Test for Regression Coefficient (ANOVA) *****" << endl << endl;

  if ( ! isValid() ) {
    cerr << "It seems to fail to initialize." << endl;
    return( -1 );
  }

  double vr = ( _sy - _se ) / (double)size(); // 予測値の不偏分散
  double f0 = vr / ve(); // F0値

  FDistribution fDist( size(), _cnt - size() - 1 );

  cout << "<ANOVA Table>" << endl;
  cout << "\tSS\tDOF\tUnbiased Var." << endl;
  cout << "EXP.\t" << _sy - _se << "\t" << size() << "\t" << vr << "\t\tF0 = " << f0 << endl;
  cout << "ERR.\t" << _se << "\t" << _cnt - size() - 1 << "\t" << ve() << endl;
  cout << "MEAS.\t" << _sy << "\t" << _cnt - 1 << endl << endl;

  cout << "p-value = " << 1.0 - fDist.p( 0, f0 ) << endl;

  double f = binSearch( fDist, 1.0 - a, threshold ); // 危険率 a での上側確率
  cout << "f(P<=" << a << ") = " << f << endl << endl;

  if ( f0 >= f ) {
    cout << "It seems to be significant (Null hypothesis is rejected)." << endl;
    return( 1 );
  } else {
    cout << "It seems not to be significant (Null hypothesis is accepted)." << endl;
    return( 0 );
  }
}

mcc は重相関係数を求めるためのメンバ関数です。重相関係数は、予測値の分散と観測値の分散の比の平方根を計算することで求められますが、ここでは ( 予測値の分散 ) = ( 観測値の分散 ) - ( 誤差項の分散 ) であることを利用して観測値の分散と誤差項の分散から求めています。

regCoef_Test は、求めた回帰の有意性を検定するための関数です。予測値(EXP.)、残差(ERR.)、観測値(MEAS.)それぞれの平方和を求め、さらに予測値と残差の不偏分散から f0 を得ています。これを自由度 ( size(), _cnt - size() - 1 ) の F-分布 ( size() は独立変数の数、_cnt は標本数をそれぞれ表します ) における危険率 a での F 値 f と比較して、f0 ≥ f ならば帰無仮説は棄却されて有意性があると判断し、そうでなければ仮説を保留して有意性なしと判断します。

重回帰分析を使った解析の一例を挙げておきます。以下は、あるクラスでの二教科のテストの点数と、全教科を総合評価するための総合テストの得点を表にまとめたものです。

総合テスト教科A教科B総合テスト教科A教科B
709037778466
525241878969
788049605140
707736878778
788438716856
668625606037
849839597634
789630495728
645281668432
765680698640

総合テストの得点を y、教科 A, B の得点をそれぞれ x1, x2 として、重回帰モデル

y = a0 + a1x1 + a2x2

への当てはめを考えると、各変数の平均、分散、共分散は

mx1 = 75.65 , mx2 = 46.80 , my = 70.05

vx1 = 231.73 , vx2 = 313.16 , vy = 111.35

sy1 = 110.17 , sy2 = 85.41 , s12 = -53.57

となるので、回帰係数を求める連立方程式は

|231.73,-53.57||a1|=|110.17|
|-53.57,313.16||a2||85.41|

となって、これを解くと a^1 = 0.56, a^2 = 0.37 になります。a^0 は

a^0 = my - mx1a^1 - mx2a^2 = 70.05 - 75.65・0.56 - 46.80・0.37 = 10.39

となるので、重回帰式として

y = 10.39 + 0.56x1 + 0.37x2

という結果が得られます。この式を使って y の予測値を求めると次のような結果になります。

観測値(y)予測値(y^)誤差項(ε)観測値(y)予測値(y^)誤差項(ε)
7074.48-4.487781.81-4.81
5254.65-2.658785.721.28
7873.304.706053.726.28
7066.833.178787.91-0.91
7871.496.517169.151.85
6667.82-1.826057.662.34
8479.704.305965.53-6.53
7875.272.734952.66-3.66
6469.40-5.406669.28-3.28
7671.274.736973.35-4.35

観測値、予測値、誤差項の分散はそれぞれ 110.35, 93.25, 17.10 となり、重相関係数は

ryy^ = ( 93.25 / 110.35 )1/2 = 0.92

また、決定係数は

R2 = ryy^2 = 0.85

になります。分散分析表を求めると

変動要因平方和自由度不偏分散分散比
予測値(回帰による)S^y = 1865.002v^y = 932.50F0 = 46.36
残差(回帰との)Sε = 341.9517vε = 20.11
観測値(全体)Sy = 2206.9519  

自由度 ( 2, 17 ) の F-分布における上側確率 1% での F 値は 6.11 なので、F0 はそれよりもかなり大きく、回帰は有意性ありと判断することができます。サンプル・プログラムを利用して検定した結果を以下に示します。

***** Test for Regression Coefficient (ANOVA) *****

<ANOVA Table>
        SS      DOF     Unbiased Var.
EXP.    1865    2       932.498         F0 = 46.3586
ERR.    341.953 17      20.1149
MEAS.   2206.95 19

p-value = 1.30763e-07
f(P<=0.01) = 6.11211

It seems to be significant (Null hypothesis is rejected).

重相関係数の値は 1 にかなり近く、予測値と観測値の誤差はかなり小さい、すなわち回帰式が y 値をよく表しているということが言えます。係数をみるとどちらも正値であり、二教科のテストの点数が高いほど総合テストでも高得点になる傾向があることが統計的に示されたことになります(ちなみにこれは実在のデータではなく、ある程度回帰式に当てはまるように適当に作ったデータです)。

3) 偏相関係数(Partial Correlation Coefficient)

ある独立変数 x, y と従属変数 z の、次式のような重回帰モデルを考えます。

z = a + bx + cy

x と y の間に相関がなければ、x の変化に対して y は影響しないので、x が Δx だけ変化したときの z の変化量 Δz は

Δz = bΔx

になります。しかし、x と y の間に次のような関係式

y = p + qx

が成り立つとすれば、x が Δx だけ変化したとき y は qΔx 変化することになるので、

Δz = ( b + cq )Δx

となって、x だけの単回帰モデルを考えた場合は真の回帰係数(さらには真の相関係数)と異なる結果が得られることになります。

二変数の回帰モデルは、三次元空間上の平面で表すことができます。独立変数のいずれかを固定して、もう一方だけを変化させたときの直線は、単回帰モデルとして考えた場合の回帰直線を表します。しかし、固定したつもりの独立変数がもう片方の変数に影響されて変化してしまうと、得られる直線は真の回帰直線とはズレてしまい、実際には相関があるにもかかわらず相関がないように見えたり、逆に実際よりも強い相関が見えるような現象が発生します。このように、ある変数 z が他の二つの変数 x, y と相関を持つとき、z の影響を受けて得られる x, y の相関を「見かけの相関(Spurious Correlation)」といいます。

見かけの相関

y を固定したとき、z は重回帰式で表される平面上にある傾き b の直線で表されます。しかし、x の増減によって y が変化すれば、直線は平面上を回転することになるので、傾きは変化してしまいます。よって、得られる相関係数も変化するわけです。この現象は、独立変数の数が増えるほど複雑になっていきます。

そこで、次のような重回帰モデルを考えます。

y = a0 + Σj{1→p;j≠k}( ajxj )

xk = b0 + Σj{1→p;j≠k}( bjxj )

これはちょうど、xk と y を他の p - 1 個の独立変数から予測する式を表しています。標本 ( xj,i, yi ) ( i = 1, 2, ... N ) を使い、最小二乗法によって各回帰係数の推定量 a^j, b^j を求めると、予測値からの誤差は

ui = yi - { a^0 + Σj{1→p;j≠k}( a^jxj,i ) }

vi = xk,i - { b^0 + Σj{1→p;j≠k}( b^jxj,i ) }

になります。すると、ui と vi は他の p - 1 個の独立変数から受ける影響を除外した y と xk を表します。ui と vi は測定値と予測値の誤差なので、その平均はゼロです。従って、

ryk・1,2,...,k-1,k+1,...p = Σi{1→N}( uivi ) / { Σi{1→N}( ui2 )Σi{1→N}( vi2 ) }1/2

とすれば、ryk・1,2,...,k-1,k+1,...p は y と xk だけの(他の独立変数の影響を受けない)相関係数になります。これを「偏相関係数(Partial Correlation Coefficient)」といいます。

二変数であれば、k = 1 の偏相関係数を求める場合、y と x2 及び x1 と x2 の単回帰式は

y = a0 + a2x2

x1 = b0 + b2x2

と表され、予測値からの誤差は

ui = yi - ( a^0 + a^2x2,i ) = yi - ( sy2 / s22 )( x2,i - mx2 ) - my

vi = x1,i - ( b^0 + b^2x2,i ) = x1,i - ( s12 / s22 )( x2,i - mx2 ) - mx1

となるので、

Σi{1→N}( uivi ) / N=Σi{1→N}( { ( yi - my ) - ( sy2 / s22 )( x2,i - mx2 ) }
 { ( x1,i - mx1 ) - ( s12 / s22 )( x2,i - mx2 ) } ) / N
=Σi{1→N}( ( yi - my )( x1,i - mx1 ) - ( s12 / s22 )( x2,i - mx2 )( yi - my )
 - ( sy2 / s22 )( x2,i - mx2 )( x1,i - mx1 ) + ( sy2 / s22 )( s12 / s22 )( x2,i - mx2 )2 ) / N
=sy1 - s12sy2 / s22 - s12sy2 / s22 + s12sy2 / s22
=sy1 - s12sy2 / s22
=√syy√s11{ sy1 / √syy√s11 - ( s12 / √s11√s22 )( sy2 / √syy√s22 ) }
=√syy√s11( ry1 - r12・ry2 )
Σi{1→N}( ui2 ) / N=Σi{1→N}( { ( yi - my ) - ( sy2 / s22 )( x2,i - mx2 ) }2 ) / N
=Σi{1→N}( ( yi - my )2 - 2( sy2 / s22 )( yi - my )( x2,i - mx2 )
 + ( sy2 / s22 )2( x2,i - mx2 )2 ) / N
=syy - 2sy22 / s22 + sy22 / s22
=syy - sy22 / s22
=syy( 1 - sy22 / syys22 )
=syy( 1 - ry22 )
Σi{1→N}( vi2 ) / N=Σi{1→N}( { ( x1,i - mx1 ) - ( s12 / s22 )( x2,i - mx2 ) }2 ) / N
=Σi{1→N}( ( x1,i - mx1 )2 - 2( s12 / s22 )( x1,i - mx1 )( x2,i - mx2 )
 + ( s12 / s22 )2( x2,i - mx2 )2 ) / N
=s11 - 2s122 / s22 + s122 / s22
=s11 - s122 / s22
=s11( 1 - s122 / s11s22 )
=s11( 1 - r122 )

よって、

ry1・2=√syy√s11( ry1 - r12・ry2 ) / { syy( 1 - ry22 )s11( 1 - r122 ) }1/2
=( ry1 - r12・ry2 ) / ( 1 - ry22 )1/2( 1 - r122 )1/2

という式が得られ、x1 と y, x2 と y, x1 と x2 のそれぞれの相関係数から偏相関係数を計算することができます。

任意の変量に拡張した場合、

ui=yi - { a^0 + Σj{1→p;j≠k}( a^jxj,i ) }
=yi - [ { my - Σj{1→p;j≠k}( mxja^j ) } + Σj{1→p;j≠k}( a^jxj,i ) ]
=( yi - my ) - Σj{1→p;j≠k}( a^j( xj,i - mxj ) )
=( yi - my ) - Σj{1→p;j≠k}( ( xj,i - mxj )Σl{1→p;l≠k}( sjlsyl ) )

Σl{1→p;l≠k}( sjlsyl ) は共分散行列の逆行列の j 行目と ベクトル ( sy1, sy2, ... syp )T との内積を表しています。但し、共分散行列には k 番目の要素 xk は含まれず、p - 1 行 p - 1 列の行列になり、ベクトルにも syk は含まれません。よって、これらを V-k-1, sy,-k と表すことにします。この和を j = 1 から p まで求め、それぞれに ( xj,i - mxj ) を掛けることになるので、これは V-k-1sy,-k とベクトル ( x1,i - mx1, x2,i - mx2, ... xp,i - mxp )T (もちろん、要素 xk,i - mxk は含まれません) の内積になります。このベクトルを xi,-k - mx,-k と表せば

ui=( yi - my ) - ( xi,-k - mx,-k, V-k-1sy,-k )
=( yi - my ) - ( xi,-k - mx,-k )TV-k-1sy,-k

という式が得られます。但し、最後の等式は V-k-1 が対称行列なので成り立ちます。同様に、

vi=( xk,i - mxk ) - ( xi,-k - mx,-k, V-k-1sk,-k )
=( xk,i - mxk ) - ( xi,-k - mx,-k )TV-k-1sk,-k

但し、sk,-k = ( sk1, sk2, ... skp )T で、skk を要素として含まない p - 1 変数のベクトルを表します。

この結果から、

Σi{1→N}( uivi ) / N=Σi{1→N}( { ( yi - my ) - ( xi,-k - mx,-k, V-k-1sy,-k ) }
 { ( xk,i - mxk ) - ( xi,-k - mx,-k, V-k-1sk,-k ) } ) / N
=Σi{1→N}( ( yi - my )( xk,i - mxk )
 - ( xi,-k - mx,-k, V-k-1sk,-k )( yi - my ) - ( xi,-k - mx,-k, V-k-1sy,-k )( xk,i - mxk )
 + ( xi,-k - mx,-k, V-k-1sy,-k )( xi,-k - mx,-k, V-k-1sk,-k ) ) / N

となり、

Σi{1→N}( ( yi - my )( xk,i - mxk ) ) / N = syk
 
Σi{1→N}( ( xi,-k - mx,-k, V-k-1sk,-k )( yi - my ) ) / N
=( Σi{1→N}( ( yi - my )( xi,-k - mx,-k ) ) / N, V-k-1sk,-k )
=( sy,-k, V-k-1sk,-k )
 
Σi{1→N}( ( xi,-k - mx,-k, V-k-1sy,-k )( xk,i - mxk ) ) / N
=( Σi{1→N}( ( xk,i - mxk )( xi,-k - mx,-k ) ) / N, V-k-1sy,-k )
=( sk,-k, V-k-1sy,-k )
=( sy,-k, V-k-1sk,-k )
 
Σi{1→N}( ( xi,-k - mx,-k, V-k-1sy,-k )( xi,-k - mx,-k, V-k-1sk,-k ) ) / N
=Σi{1→N}( ( V-k-1( xi,-k - mx,-k ), sy,-k )( xi,-k - mx,-k, V-k-1sk,-k ) ) / N
=Σi{1→N}( ( sy,-k, V-k-1( xi,-k - mx,-k ) )( xi,-k - mx,-k, V-k-1sk,-k ) ) / N
=Σi{1→N}( sy,-kTV-k-1( xi,-k - mx,-k )( xi,-k - mx,-k )TV-k-1sk,-k ) / N
=sy,-kTV-k-1V-kV-k-1sk,-k
=sy,-kTV-k-1sk,-k
=( sy,-k, V-k-1sk,-k )

より

Σi{1→N}( uivi ) / N = syk - ( sy,-k, V-k-1sk,-k )

と計算できます。また、

Σi{1→N}( ui2 ) / N=Σi{1→N}( { ( yi - my ) - ( xi,-k - mx,-k, V-k-1sy,-k ) }2 ) / N
=Σi{1→N}( ( yi - my )2 - 2( yi - my )( xi,-k - mx,-k, V-k-1sy,-k )
 + ( xi,-k - mx,-k, V-k-1sy,-k )2 ) / N

より、

Σi{1→N}( ( yi - my )2 ) / N = syy
 
Σi{1→N}( ( yi - my )( xi,-k - mx,-k, V-k-1sy,-k ) ) / N
=( Σi{1→N}( ( yi - my )( xi,-k - mx,-k ) ) / N, V-k-1sy,-k )
=( sy,-k, V-k-1sy,-k )
 
Σi{1→N}( ( xi,-k - mx,-k, V-k-1sy,-k )2 ) / N
=Σi{1→N}( ( V-k-1( xi,-k - mx,-k ), sy,-k )( xi,-k - mx,-k, V-k-1sy,-k ) ) / N
=Σi{1→N}( ( sy,-k, V-k-1( xi,-k - mx,-k ) )( xi,-k - mx,-k, V-k-1sy,-k ) ) / N
=Σi{1→N}( sy,-kTV-k-1( xi,-k - mx,-k )( xi,-k - mx,-k )TV-k-1sy,-k ) / N
=sy,-kTV-k-1V-kV-k-1sy,-k
=sy,-kTV-k-1sy,-k
=( sy,-k, V-k-1sy,-k )

となるので、

Σi{1→N}( ui2 ) / N = syy - ( sy,-k, V-k-1sy,-k )

同様に、

Σi{1→N}( vi2 ) / N = skk - ( sk,-k, V-k-1sk,-k )

なので、偏相関係数 ryk・1,2,...,k-1,k+1,...p は、

ryk・1,2,...,k-1,k+1,...p = { syk - ( sy,-k, V-k-1sk,-k ) } / { syy - ( sy,-k, V-k-1sy,-k ) }1/2{ skk - ( sk,-k, V-k-1sk,-k ) }1/2

という式で計算することもできます。二変数で k = 1 のときは、sy,-k = sy2, sk,-k = s12, V-k-1sk,-k = s12 / s22, V-k-1sy,-k = sy2 / s22 なので

ry1・2 = ( sy1 - sy2s12 / s22 ) / ( syy - sy22 / s22 )1/2( s11 - s122 / s22 )1/2 = ( ry1 - ry2r12 ) / ( 1 - ry22 )1/2( 1 - r122 )1/2

となって、先ほど求めた二変数の場合の結果と一致します。

偏相関係数を求めるためのサンプル・プログラムを以下に示します。

/*
  partialCorrCoef, partialCorrCoef2 : 偏相関係数を求める

  const vector< vector<double> >& x : 独立変数
  const vector<double>& y : 従属変数
  unsigned int k : 偏相関係数を求める対象の独立変数

  戻り値 : 偏相関係数
*/
double partialCorrCoef( const vector< vector<double> >& x, const vector<double>& y, unsigned int k )
{
  if ( k >= x.size() ) {
    cerr << "k is bigger than the size of x." << endl;
    return( NAN );
  }

  const vector<double>& xk = x[k]; // k 番目の標本
  // k 番目の独立変数を除いた標本を作成
  vector< vector<double> > xl;
  for ( unsigned int i = 0 ; i < x.size() ; ++i ) {
    if ( i == k ) continue;
    const vector<double>& xi = x[i]; // i 番目の標本
    xl.push_back( xi );
  }

  MultipleRegressionCoefficient mrc_y( xl, y );   //  y と xl の重回帰モデル
  MultipleRegressionCoefficient mrc_xk( xl, xk ); // xk と xl の重回帰モデル

  if ( ( ! mrc_y ) || ( ! mrc_xk ) ) return( NAN );

  unsigned int sz = y.size(); // 標本数
  double syk = 0; // xk と y の標本共分散
  double vk = 0;  // xk の分散
  double vy = 0;  // y の分散
  for ( unsigned int i = 0 ; i < sz ; ++i ) {
    double ek = xk[i] - mrc_xk.y( xl, i );
    double ey = y[i] - mrc_y.y( xl, i );
    syk += ek * ey;
    vk += ek * ek;
    vy += ey * ey;
  }

  return( syk / sqrt( vk * vy ) );
}

double partialCorrCoef2( const vector< vector<double> >& x, const vector<double>& y, unsigned int k )
{
  if ( k >= x.size() ) {
    cerr << "k is bigger than the size of x." << endl;
    return( NAN );
  }

  const vector<double>& xk = x[k]; // k 番目の標本
  // k 番目の独立変数を除いた標本を作成
  vector< vector<double> > xl;
  for ( unsigned int i = 0 ; i < x.size() ; ++i ) {
    if ( i == k ) continue;
    const vector<double>& xi = x[i]; // i 番目の標本
    xl.push_back( xi );
  }

  MultipleRegressionCoefficient mrc( xl, y );   //  y と xl の重回帰モデル
  if ( ! mrc ) return( NAN );

  unsigned int p = xl.size();
  double skk = sampleVariance( xk ); // xk の分散
  double syy = sampleVariance( y );  // y の分散
  double syk = sampleCovariance( xk, y ); // xk と y の標本共分散

  vector<double> vec_sk( p ); // ski ( i = 0,1,...,p-1 ) のベクトル
  vector<double> vec_sy( p ); // syi ( i = 0,1,...,p-1 ) のベクトル
  for ( unsigned int i = 0 ; i < p ; ++i ) {
    vec_sk[i] = sampleCovariance( xl[i], xk );
    vec_sy[i] = sampleCovariance( xl[i], y );
  }

  vector<double> vec_Vsk( p, 0 ); // 共分散行列の逆行列と vec_sk の積
  vector<double> vec_Vsy( p, 0 ); // 共分散行列の逆行列と vec_sy の積
  for ( unsigned int r = 0 ; r < p ; ++r ) {
    for ( unsigned int c = 0 ; c < p ; ++c ) {
      vec_Vsk[r] += mrc.s_inv( r, c ) * vec_sk[c];
      vec_Vsy[r] += mrc.s_inv( r, c ) * vec_sy[c];
    }
  }

  double syVsk = 0, skVsk = 0, syVsy = 0; // 各内積の値
  for ( unsigned int i = 0 ; i < p ; ++i ) {
    syVsk += vec_sy[i] * vec_Vsk[i];
    skVsk += vec_sk[i] * vec_Vsk[i];
    syVsy += vec_sy[i] * vec_Vsy[i];
  }

  return( ( syk - syVsk ) / sqrt( ( syy - syVsy ) * ( skk - skVsk ) ) );
}

偏相関係数を求める関数として二種類用意しています。最初の関数は、k 番目の独立変数を取り除いた上で、取り除いた k 番目の変数と y それぞれに対して重回帰モデルを適用し、予測値との誤差を使って偏相関係数を求めています。そして、その次の関数は、同じく k 番目の独立変数を取り除くところまでは同じですが、重回帰モデルは y のみに適用し、共分散行列の逆行列を利用して求める方法を利用しています。

重相関係数の章で示した例において、教科 A, B それぞれと総合テストとの相関係数はそれぞれ 0.69, 0.46 になります。また、教科 A, B の点数に対する相関係数は -0.20 でほんの少しだけ負の相関があると考えられます。ここで、教科 A, B それぞれと総合テストとの偏相関係数を求めると、その値は 0.90, 0.84 となって、相関係数よりも値が大きくなります。教科 A, B の点数どうしでの相関は非常に弱いものでしたが、それでもかなりの違いが生じることになります。

関連性がないのに相関があるように見える例として次のようなものがあります(ここでの「関連性」とは、x が要因となって y の値が決まる、といった意味になります)。下図のグラフは、身長に対する 50m 走のタイムを散布図で示したものです。

身長に対する 50m 走タイムの散布図

このグラフを見ると、明らかに身長が 50m 走のタイムに影響を与えているように見えます。しかし、常識的に考えれば背の高い人ほど足が早いとは言えません。これは、年齢と身長、年齢と 50m 走のタイムのそれぞれに正の相関があることから、背の高さと 50m 走のタイムの間に相関があるように見えているために発生したものです。

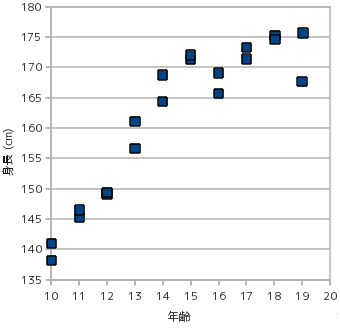
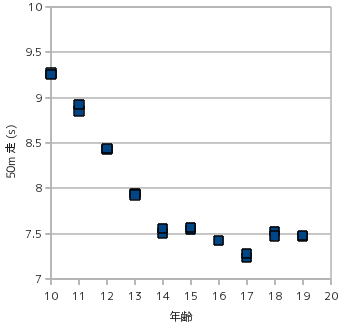
年齢に対する身長の散布図 年齢に対する 50m 走タイムの散布図

上の図は、年齢に対する、身長及び 50m 走タイムの散布図を示したものです。年齢に従って身長が高くなり、また 50m 走のタイムは短くなっていきます。年齢層を見ればこれは納得のできる結果であり、この結果に影響を受けて身長と 50m 走のタイムに関連性があるように見えたと考えられます。これは簡単な例ですが、実際には関連性がないにもかかわらず、相関が強く現れる例は他にも様々なパターンが考えられ、このように簡単には見つけられないものもあるので注意が必要です(ちなみにこのデータは、日本全国の平均を元に適当に作成した架空のデータです)。

この例において偏相関係数を計算すると、身長に対しては -0.80、年齢に対しては -0.018 と、年齢に対する相関がないような結果になってしまいます。身長と 50m 走のタイムに対する相関係数の方が年齢との相関係数よりも高いことが原因ですが、データの取り方によっては意図していない結果が得られてしまう例の一つです。この重回帰式は、身長を x1、年齢を x2、50m 走のタイムを y としたとき

y = 16.26 - 0.051x1 - 0.0029x2

となって、x2 の変化に対して y がほとんど影響を受けない結果になっていることが分かります。

今回は、重回帰分析モデルを主なテーマとしてその利用法を紹介しました。ある従属変数に関連する独立変数は通常多岐に渡り、しかも互いに複雑に関連していることが多いので、どんな場合でも重回帰モデルに適用すれば正しい結果が得られるというわけではなく、変数として何を採用するのか、ということも非常に重要になります(むしろこちらの方が大事で、かつ難しい作業だと思います)。現在はコンピュータを利用して、大量のパラメータを使って手軽に結果が得られるようになっていますが、その結果が本当に信頼性の高いものか、意味のあるものなのかはコンピュータは判断してくれないので、最終的には人間が判断する必要があります。大量のデータに埋もれてしまって本当の意味するところを見失ってしまうことがないようにすることが大事だと思います。以上、自分に対する戒めの意味も込めて、まとめとしたいと思います。

補足1) 重回帰係数と t-分布

独立変数がひとつだった場合、

ta = ( a^ - a ) / ( σ2 / Nvx )1/2( √vε / σ ) = ( a^ - a ) / ( vε / Nvx )1/2

tb = ( b^ - b ) / { ( 1 / N + mx2 / Nvx )σ2 }1/2( √vε / σ ) = ( b^ - b ) / { ( 1 / N + mx2 / Nvx )vε }1/2

が自由度 N - 2 の t-分布に従うことは前章で示しました(「回帰係数と t-分布」参照)。同様の方法で、

tj = ( a^j - aj ) / ( sjjσ2 / N )1/2( √vε / σ ) = ( a^j - aj ) / ( sjjvε / N )1/2

t0=( a^0 - a0 ) / [ { 1 / N + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) / N }σ2 ]1/2( √vε / σ )
=( a^0 - a0 ) / [ { 1 / N + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) / N }vε ]1/2

が自由度 N - p - 1 の t-分布に従うことが証明できます。まず、( N - p - 1 )vε / σ2 が自由度 N - p - 1 の χ2-分布 TN-p-1(y) に従うことを証明します。

( N - p - 1 )vε / σ2 = Σi{1→N}( [ { yi - ( a^0 + Σj{1→p}( a^jxj,i ) ) } / σ ]2 )

と表され、zi = { yi - ( a^0 + Σj{1→p}( a^jxj,i ) ) } / σ とすると、zi は平均

E[zi]=E[{ yi - ( a^0 + Σj{1→p}( a^jxj,i ) ) } / σ]
=E[ { ( a0 + Σj{1→p}( ajxj,i ) + εi ) - ( a^0 + Σj{1→p}( a^jxj,i ) ) } / σ]
={ ( a0 + Σj{1→p}( ajxj,i ) + E[εi] ) - ( a0 + Σj{1→p}( ajxj,i ) ) } / σ = 0

であり、分散は

V[zi]=V[{ yi - ( a^0 + Σj{1→p}( a^jxj,i ) ) } / σ]
=E[{ ( a0 - a^0 ) + Σj{1→p}( ( aj - a^j )xj ) + εi }2] / σ2
={ 1 / N + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) / N } + Σj{1→p}( Σk{1→p}( sjkxj,ixk,i / N ) ) + 1
 - 2Σj{1→p}( Σk{1→p}( mxksjk )xj,i / N ) - 2E[εia^0] / σ2 - 2Σj{1→p}( E[εia^j]xj,i ) / σ2

と計算できます。分散を求める式は、vε が σ2 の不偏推定量であることを証明したときの内容から拝借しています。E[εia^j] = Σk{1→p}( sjk( xk,i - mxk ) )σ2 / N であることもすでに証明されているので、これを利用して E[εia^0] を求めると

E[εia^0]=E[εi{ my - Σj{1→p}( a^jmxj ) }]
=E[εi{ Σl{1→N}( ( a0 + Σj{1→p}( ajxj,l ) + εl ) - Σj{1→p}( a^jxj,l ) ) }] / N
=Σl{1→N}( E[εiεl] ) / N - E[εiΣl{1→N}( Σj{1→p}( a^jxj,l / N ) )]
=σ2 / N - Σl{1→N}( Σj{1→p}( E[εia^j]xj,l / N ) )
=σ2 / N - Σj{1→p}( { Σk{1→p}( sjk( xk,i - mxk ) )σ2 / N }Σl{1→N}( xj,l / N ) )
={ 1 / N - Σj{1→p}( Σk{1→p}( sjk( xk,i - mxk ) )mxj / N ) }σ2

となります。

MMS = Σj{1→p}( Σk{1→p}( mxjmxksjk ) )

SXX(i,j) = Σk{1→p}( Σl{1→p}( sklxk,ixl,j ) )

MSX(i) = Σj{1→p}( Σk{1→p}( mxksjkxj,i ) )

と表すと、

V[zi]=( 1 / N + MMS / N ) + SXX(i,i) / N + 1
 - 2MSX(i) / N - 2{ 1 / N - ( MSX(i) - MMS ) / N } - 2( SXX(i,i) - MSX(i) ) / N
=1 - 1 / N - MMS / N - SXX(i,i) / N + 2MSX(i) / N
=1 - 1 / N - Σj{1→p}( Σk{1→p}( sjk( xj,ixk,i - 2mxjxk,i + mxjmxk ) / N ) )

という結果が得られます。zi と zj ( i ≠ j ) の共分散は

E[zizj]=E[{ yi - ( a^0 + Σk{1→p}( a^kxk,i ) ) }{ yj - ( a^0 + Σl{1→p}( a^lxl,j ) ) } / σ2]
=E[{ ( a0 - a^0 ) + Σk{1→p}( ( ak - a^k )xk,i ) + εi }{ ( a0 - a^0 ) + Σl{1→p}( ( al - a^l )xl,j ) + εj } / σ2]
=E[{ ( a0 - a^0 )2 + ( a0 - a^0 )Σk{1→p}( ( ak - a^k )xk,i ) + ( a0 - a^0 )Σl{1→p}( ( al - a^l )xl,j )
 + ( a0 - a^0 )( εi + εj ) + Σk{1→p}( ( ak - a^k )xk,i )Σl{1→p}( ( al - a^l )xl,j )
 + εiΣl{1→p}( ( al - a^l )xl,j ) + εjΣk{1→p}( ( ak - a^k )xk,i ) + εiεj } / σ2]
={ E[( a0 - a^0 )2] + Σk{1→p}( E[( a0 - a^0 )( ak - a^k )]xk,i ) + Σl{1→p}( E[( a0 - a^0 )( al - a^l )]xl,j )
 - E[a^0( εi + εj )] + Σk{1→p}( Σl{1→p}( E[( ak - a^k )( al - a^l )]xk,ixl,j ) )
 - Σl{1→p}( E[εia^l]xl,j )] - Σk{1→p}( E[εja^k]xk,i ) } / σ2]

になります。

E[( a^k - ak )( a^l - al )] = sklσ2 / N

E[( a^0 - a0 )( a^k - ak )] = -Σr{1→p}( mxrskrσ2 / N )

E[εia^l] = Σr{1→p}( slr( xr,i - mxr ) )σ2 / N

E[εia^0] = { 1 / N - Σk{1→p}( Σl{1→p}( skl( xl,i - mxl ) )mxk / N ) }σ2

E[( a0 - a^0 )2] = V[a^0] = { 1 / N + Σk{1→p}( Σl{1→p}( mxkmxlskl ) ) / N }σ2

を代入すると、

E[zizj]={ 1 / N + Σk{1→p}( Σl{1→p}( mxkmxlskl ) ) / N } - Σk{1→p}( Σr{1→p}( mxrskr / N )xk,i )
 - Σl{1→p}( Σr{1→p}( mxrslr / N )xl,j ) - { 1 / N - Σk{1→p}( Σl{1→p}( skl( xl,i - mxl ) )mxk / N ) }
 - { 1 / N - Σk{1→p}( Σl{1→p}( skl( xl,j - mxl ) )mxk / N ) } + Σk{1→p}( Σl{1→p}( sklxk,ixl,j / N ) )
 - Σl{1→p}( Σr{1→p}( slr( xr,i - mxr ) )xl,j / N ) - Σk{1→p}( Σr{1→p}( skr( xr,j - mxr ) )xk,i / N )
=-1 / N + MMS / N - MSX(i) / N - MSX(j) / N + ( MSX(i) - MMS ) / N + ( MSX(j) - MMS ) / N
 + SXX(i,j) / N - ( SXX(j,i) - MSX(j) ) / N - ( SXX(i,j) - MSX(i) ) / N
=-1 / N - MMS / N + MSX(i) / N + MSX(j) / N - SXX(i,j) / N
=-1 / N - Σk{1→p}( Σl{1→p}( sklxk,ixl,j - mxlsklxk,i - mxlsklxk,j + mxkmxlskl ) ) / N
=-1 / N - Σk{1→p}( Σl{1→p}( skl( xk,i - mxk )( xl,j - mxl ) ) ) / N

skl = slk なので、SXX(j,i) = SXX(i,j) が成り立つことに注意してください。xj = ( x1,j, x2,j, ... xp,j )T, mx = ( mx1, mx2, ... mxp )T としたとき、Σl{1→p}( skl( xl,j - mxl ) ) は xj - mx と ( sk1, sk2, ... skp ) との内積であり、( sk1, sk2, ... skp ) は V-1 の第 k 行を表しています。V-1 は対称行列なので、( sk1, sk2, ... skp )T は V-1 の第 k 列でもあり、

( xj - mx )TV-1

は xj - mx と ( sk1, sk2, ... skp ) の内積からなるベクトルを表します。先ほど示した和の部分は、このベクトルと xi - mx の内積を意味するので、

E[zizj] = -1 / N - ( xj - mx )TV-1( xi - mx ) / N

と表すことができます。そこで、r 行 c 列めの要素 arc を

arc = -( xr - mx )TV-1( xc - mx ) / N + δrc - 1 / N

とする行列 A を定義します。但し、δrc は「クロネッカーのデルタ」で r ≠ c のとき 0、r = c のとき 1 になります。すると、z = ( z1, z2, ... zN ) は平均ベクトルが 0 で共分散行列が A である多変量正規分布に従うことになります。これを以下 N( 0, A ) で表します。A は共分散行列であり、arc = acr となることも明らかなので対称行列になります。

A2 の r 行 c 列の要素を a2rc と表し、この値を求めると、

a2rc=Σi{1→N}( { -( xr - mx )TV-1( xi - mx ) / N + δri - 1 / N }{ -( xi - mx )TV-1( xc - mx ) / N + δic - 1 / N } )
=Σi{1→N}( ( xr - mx )TV-1( xi - mx )( xi - mx )TV-1( xc - mx ) / N2
 + ( xr - mx )TV-1( xi - mx ) / N2 + ( xi - mx )TV-1( xc - mx ) / N2 + 1 / N2
 - δri{ ( xi - mx )TV-1( xc - mx ) / N + 1 / N } - δic{ ( xr - mx )TV-1( xi - mx ) / N + 1 / N } + δriδic )

( xi - mx )( xi - mx )T は p 行 p 列の行列であり、その r 行 c 列の要素は ( xr,i - mxr )( xc,i - mxc ) なので、Σi{1→N}( ( xi - mx )( xi - mx )T ) / N = V になります。従って、

Σi{1→N}( ( xr - mx )TV-1( xi - mx )( xi - mx )TV-1( xc - mx ) ) / N2
=( xr - mx )TV-1VV-1( xc - mx ) / N
=( xr - mx )TV-1( xc - mx ) / N

また、Σi{1→N}( xi - mx ) = 0 すなわちゼロベクトルなので、2, 3 項めはゼロになり無視できます。よって、

a2rc=( xr - mx )TV-1( xc - mx ) / N + 1 / N
 - { ( xr - mx )TV-1( xc - mx ) / N + 1 / N } - { ( xr - mx )TV-1( xc - mx ) / N + 1 / N } + δrc
=-( xr - mx )TV-1( xc - mx ) / N + δrc - 1 / N = arc

となって、A2 = A、つまり A は「べき等行列(Idempotent Matrix)」ということになります。A は対称行列なので、Aの固有ベクトルからなる直交行列を Q、固有値を対角成分とする行列を D としたとき、

A = QDQT

と表すことができます(「固有値分解 - (2) カルーネン・レーベ展開」の「1) 対称行列と二次形式」参照)。A2 は

A2 = QDQTQDQT = QD2QT

と求められるので(ここで QTQ = E(単位行列) であることを利用しています)、A2 = A から D2 = D であることになり、各対角成分 dii ( i = 1, 2, ... N ) に対して dii2 = dii となるので、対角成分すなわち固有値は 0 か 1 のどちらかであることになります。z' = QTz とすれば、

( z, Az ) = ( z, QDQTz ) = ( QTz, DQTz ) = ( z', Dz' )

と求められるので(ここで、( x, Ax ) = ( ATx, x ) であることを利用しています)、D の対角成分が 1 の個数を r としたとき、z' 内の互いに独立な r 個の要素が標準正規分布に従うことが分かります。また、直交変換によって残り N - r 個の変数は消失します。これは、Az を N 個の線形方程式と見たときに r 個だけが独立で、残り N - r 個は線形従属であることを表しています。直交変換を行ってもノルムは変化しないので、||z|| = ||z'|| が成り立ちます。従って、||z||2 は標準正規分布に従う r 個の独立な確率変数の二乗和であり、この値は自由度 r の χ2-分布に従います(「(6) 標本分布」の「1) カイ二乗分布(Chi-square Distribution)」参照)。

r は行列 A の「階数(rank)」であり、行列の列ベクトル(または行ベクトル)の中で線形独立なものの個数を表します。べき等行列の階数は対角成分の和に等しい (「(12) 二標本の解析 -2-」の「補足2) べき等行列の階数」参照) ことから、A の対角成分の和を求めると

Σi{1→N}( aii )=Σi{1→N}( -Σk{1→p}( Σl{1→p}( skl( xk,i - mxk )( xl,i - mxl ) ) ) / N + δii - 1 / N )
=-Σk{1→p}( Σl{1→p}( sklΣi{1→N}( ( xk,i - mxk )( xl,i - mxl ) ) / N ) ) + N - 1
=-Σk{1→p}( Σl{1→p}( sklskl ) ) + N - 1
=-p + N - 1 = N - p - 1

よって、階数は常に N - p - 1 になり、||z||2 すなわち ( N - p - 1 )vε / σ2 は自由度 N - p - 1 の χ2-分布に従うことが証明されました。

次に、( a^j - aj ) / ( sjjσ2 / N )1/2, ( a^0 - a0 ) / [ { 1 / N + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) / N }σ2 ]1/2 と ( N - p - 1 )vε / σ2 = Σi{1→N}( [ { yi - ( a^0 + Σk{1→p}( a^kxk,i ) ) } / σ ]2 ) が互いに独立であることを証明します。

まず、xj = ( a^j - aj ) / ( sjjσ2 / N )1/2 と zi = { yi - ( a^0 + Σk{1→p}( a^kxk,i ) ) } / σ に対して、E[xjzi] を求めてみます。xj, zi はどちらも平均ゼロの正規分布に従う確率変数です。

E[xjzi]=E[{ ( a^j - aj ) / ( sjjσ2 / N )1/2 }[ { yi - ( a^0 + Σk{1→p}( a^kxk,i ) ) } / σ ]]
=E[( a^j - aj ){ yi - ( a^0 + Σk{1→p}( a^kxk,i ) ) }] / { σ2( sjj / N )1/2 }
=E[( a^j - aj ){ ( a0 - a^0 ) + Σk{1→p}( ( ak - a^k )xk,i ) + εi }] / { σ2( sjj / N )1/2 }
={ -E[( a^j - aj )( a^0 - a0 )] - Σk{1→p}( E[( a^j - aj )( a^k - ak )]xk,i )
 + E[( a^j - aj )εi] } / { σ2( sjj / N )1/2 }
={ Σk{1→p}( mxksjkσ2 / N ) - Σk{1→p}( sjkσ2xk,i / N )
 + Σk{1→p}( sjk( xk,i - mxk ) )σ2 / N } / { σ2( sjj / N )1/2 }
={ Σk{1→p}( mxksjk ) - Σk{1→p}( sjkxk,i )
 + Σk{1→p}( sjkxk,i - mxksjk ) } / { σ2( Nsjj )1/2 }
=0 = E[xj]E[zi]

となるので、(xj と zi が正規分布に従うことから) xj と zi は互いに独立です。確率変数 x, y が互いに独立であるとは同時分布 p( x, y ) が p(x) と p(y) の積で表されることだったので、p(zi) に対して ui = zi2 と変数変換をしても独立性は保たれます。さらに y = Σi{1→N}( ui ) と変数変換しても、全ての i に対して xj と ui は互いに独立なので、やはり xj , yの独立性は保たれます。

今度は、x0 = ( a^0 - a0 ) / [ { 1 / N + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) / N }σ2 ]1/2 と zi = { yi - ( a^0 + Σj{1→p}( a^jxj,i ) ) } / σ に対して、E[x0zi] を求めてみます。x0, zi はやはり平均ゼロの正規分布に従う確率変数です。式を見やすくするために、x0 = ( a^0 - a0 ) / ( Aσ2 / N )1/2 で表します( A = 1 + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) になります )。

E[x0zi]=E[{ ( a^0 - a0 ) / ( Aσ2 / N )1/2 }[ { yi - ( a^0 + Σj{1→p}( a^jxj,i ) ) } / σ ]]
=E[( a^0 - a0 ){ yi - ( a^0 + Σj{1→p}( a^jxj,i ) ) }] / { σ2( A / N )1/2 }
=E[( a^0 - a0 ){ ( a0 - a^0 ) + Σj{1→p}( ( aj - a^j )xj,i ) + εi }] / { σ2( A / N )1/2 }
={ -E[( a^0 - a0 )2] - Σj{1→p}( E[( a^0 - a0 )( a^j - aj )]xj,i )
 + E[( a^0 - a0 )εi] } / { σ2( A / N )1/2 }
=[ -{ 1 / N + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) / N }σ2 + Σj{1→p}( Σk{1→p}( mxksjkσ2 / N )xj,i )
 + { 1 / N - Σj{1→p}( Σk{1→p}( sjk( xk,i - mxk ) )mxj / N ) }σ2 ] / { σ2( A / N )1/2 }
={ -1 - Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) + Σj{1→p}( Σk{1→p}( mxksjkxj,i ) )
 + 1 - Σj{1→p}( Σk{1→p}( mxjsjkxk,i ) + Σj{1→p}( Σk{1→p}( mxjmxksjk ) ) } / ( AN )1/2
=0 = E[xj]E[zi]

よって、同様な考えによって x0 と y は互いに独立であることが示され、これで tj, t0 が自由度 N - p - 1 の t-分布に従うことが証明されました。

補足2) 予測値の標本分散

zi = ( y^i - m^y ) / σ を次のように変形します。

zi=[ { a^0 + Σj{1→p}( a^jxj,i ) } - { a^0 - Σj{1→p}( a^jmxj ) } ] / σ
=Σj{1→p}( a^j( xj,i - mxj ) ) / σ

zi は a^j の一次式なので、a^j が正規分布に従うことから zi も正規分布に従うことになり、また

E[zi] = Σj{1→p}( aj( xj,i - mxj ) ) / σ

になります。zr と zc の共分散 E[( zr - E[zr] )( zc - E[zc] )] は

E[( zr - E[zr] )( zc - E[zc] )]=E[Σj{1→p}( ( a^j - aj )( xj,r - mxj ) )Σl{1→p}( ( a^l - al )( xl,c - mxl ) ) / σ2]
=Σj{1→p}( Σl{1→p}( E[( a^j - aj )( a^l - al )]( xj,r - mxj )( xl,c - mxl ) ) ) / σ2
=Σj{1→p}( Σl{1→p}( ( sjlσ2 / N )( xj,r - mxj )( xl,c - mxl ) ) ) / σ2
=Σj{1→p}( Σl{1→p}( sjl( xj,r - mxj )( xl,c - mxl ) ) ) / N
=( xr - mx )TV-1( xc - mx ) / N

になることから(最後の変形は「補足1) 重回帰係数と t-分布」を参照してください)、zi は zr と zc の共分散を r 行 c 列とする N x N 共分散行列 A を持つ p 変量の正規分布になります。A2 の r 行 c 列成分 a2rc は

a2rc=Σi{1→N}( ( xr - mx )TV-1( xi - mx )( xi - mx )TV-1( xc - mx ) ) / N2
=( xr - mx )TV-1VV-1( xc - mx ) / N
=( xr - mx )TV-1( xc - mx ) / N = E[zrzc]

となるので、A は「べき等行列(Idempotent Matrix)」です。よって、ここでも固有値すなわち分散は 0 か 1 のいずれかになり、べき等行列の階数が対角成分の和に等しい(「(12) 二標本の解析 -2-」の「補足2) べき等行列の階数」参照) ことから、A の対角成分の和を求めると

Σi{1→N}( E[zi2] )=Σi{1→N}( Σj{1→p}( Σl{1→p}( sjl( xj,i - mxj )( xl,i - mxl ) ) ) ) / N
=Σj{1→p}( Σl{1→p}( sjlΣi{1→N}( ( xj,i - mxj )( xl,i - mxl ) / N ) ) )
=Σj{1→p}( Σl{1→p}( sjlsjl ) ) = p

となります。従って、Σi( zi2 ) = Σi( { ( y^i - m^y ) / σ }2 ) は自由度 p の χ2-分布に従うことが証明できたことになります。

<参考文献>
1. 「多変量統計解析法」 田中豊 / 脇本和晶 共著 (現代数学社)
2. KogoLab 早稲田大学 人間科学学術院・向後千春研究室 - アイスクリーム屋さんで学ぶ 楽しい統計学 - 5. 偏相関
3. 日本女子大学心理学科 岡本安晴のホームページ - 統計入門 - 偏相関係数と擬似相関
4. Wikipedia

◆◇◆更新履歴◆◇◆

  1. サンプル・プログラムに修正を行いました。エラーチェックなどがメインで、処理の内容はほとんど変わっていません (2012-05-20)
[Go Back]前に戻る [Back to HOME]タイトルに戻る
inserted by FC2 system