![[Go Back]](../images/back1.png) 前に戻る
前に戻る![[Back to HOME]](../images/home1.png) タイトルに戻る
タイトルに戻るトランプのカードは、ジョーカーを除くと全部で 52 枚あります。その中から 5 枚のカードを抽出したときの組み合わせを利用してポーカーというゲームが成り立っています。その中から特定の役となる組み合わせがいくつあるかを調べると、その役がどの程度発生しにくいのかを把握することができます。ここでは、組み合わせをはじめとする「場合の数」をどのように計算すればよいかを中心に紹介します。
● 総和(Σ)の記法について
n Σ k (1からnまでの自然数の和) k=1
しかし、HTML形式のドキュメントで表現しようとすると非常に見づらくなるため、ここでは以下のように表現するようにします。
Σk{1→n}( k )● 積分(∫)の記法について
b b ∫ f(x) dx = [ F(x) ] a a
は、次のように記述します。
∫{a→b} f(x) dx = [ F(x) ]{a→b}あらかじめ、御了承ください。
1 〜 3 の番号が付いた三枚のカードがあるとします。これを適当に並べ替えて三桁の数字を作るとき、その数はいくつ作ることができるでしょうか。
最初の(百の位の)カードを 1 に固定すると、次の二つの数字を作ることができます。
1 2 3 1 3 2
最初のカードを 2、3 と入れ替えてもそれぞれ二つの数字を作ることができるので、合計で 6 種類の数字を作ることができることになります。全てを列挙すると次のようになります。
123 132 213 231 312 321
1 〜 4 の番号が付いた四枚のカードに増やしたとき、最初のカードをどれか一枚に固定すれば、残りは三枚のカードによる並べ方になり、それは 6 通りであることが分かっているので、6 x 4 = 24 通りであることが分かります。全てを列挙すると次のようになります。
1234 1243 1324 1342 1423 1432 2134 2143 2314 2341 2413 2431 3124 3142 3214 3241 3412 3421 4123 4132 4213 4231 4312 4321
以下、枚数を増やす毎に、前の結果に枚数を掛けた値を求めていけば、並べ方を求めていくことができます。n 枚のカードの並べ方が Pn 通りだったとき、漸化式は
であり、P1 = 1 なので、一般項は
と非常にシンプルな式になります。この式を使って 52 枚のトランプのカードを全て並べるときの並べ方を計算すると、次のような巨大な値となります。
全てを並べるのではなく、一部だけを使った場合はどうなるでしょうか。例えば、五枚のカードから三枚を抜き取って並べた場合の数を数えてみると、最初に選択できるカードは 1 から 5 までの 5 通りあって、次はまだ選ばれていない 4 枚から、最後は残りの 3 枚から選ぶことができるので、5 x 4 x 3 = 60 通りになります。このように、n 枚のカードから、r 枚のカードを抽出して並べる場合の数は、n から順番に一つずつ数を減らしながら r 回乗算をすれば求めることができます。これは、n! を ( n - r )! で徐算することと同じなので、場合の数を nPr としたとき、この値は次のような式で表すことができます。
| nPr | = | n・( n - 1 )・...・( n - r + 2 )・( n - r + 1 ) |
| = | n! / ( n - r )! |
0 〜 9 までの 10 枚のカードを使ってできる 3 桁の数字(百の位がゼロでも可とします)を作るとき、その種類は
になります。
n 個の中から r 個の要素を抽出して並べる場合の数を「順列(Permutation)」といい、上述のように nPr で表されます。
上記操作において、同じカードを重複して選ぶことはできませんでした。これを許すようにすると、毎回 n 枚の中から選択することができるようになるので、場合の数は nr になります。これを「重複順列」といい、nΠr で表します。
アルファベット 26 文字を使って 5 文字の単語を作るとき、その種類は 265 = 11881376 個になります。
式を比較しても、また制限が少なくなることからも明らかなように nΠr ≧ nPr になります。等号は r = 1 のときに成り立ちます。
次に、m 個の要素 ak ( k = 1,2, ... m ) の中から、それぞれの要素をちょうど nk 個ずつ、合計 N = Σk{1→m}( nk ) 個抽出するときの並べ方を考えてみます。簡単な例として、A, B 二つのアルファベットを二つずつ並べて 4 文字の単語を作るときの並べ方を調べてみましょう。それぞれ二つの A, B に番号を付けて A1, A2, B1, B2 とすることで、4 つのアルファベットが全て異なるものとしたとき、その並べ方は 4! = 24 通りになります。それらを実際に並べてみます。
[A1 A2 B1 B2] [A2 A1 B1 B2] [A1 A2 B2 B1] [A2 A1 B2 B1] → AABB [A1 B1 A2 B2] [A2 B1 A1 B2] [A1 B2 A2 B1] [A2 B2 A1 B1] → ABAB [A1 B1 B2 A2] [A2 B1 B2 A1] [A1 B2 B1 A2] [A2 B2 B1 A1] → ABBA [B1 A1 A2 B2] [B1 A2 A1 B2] [B2 A1 A2 B1] [B2 A2 A1 B1] → BAAB [B1 A1 B2 A2] [B1 A2 B2 A1] [B2 A1 B1 A2] [B2 A2 B1 A1] → BABA [B1 B2 A1 A2] [B1 B2 A2 A1] [B2 B1 A1 A2] [B2 B1 A2 A1] → BBAA
同じ行にある並べ方は実際には全て同じものであり、右側にはその並べ方が示されています。同じ行の内容を見てみると、A1 と A2、B1 と B2 がそれぞれ入れ替わったために、その組み合わせ分だけ重複が発生していることが分かります。従って、それぞれ異なるものとして求めた順列を、各要素が重複した数(つまり同じ要素を異なるものと見なしたときの並べ方の数)の積で徐算すれば、求める答えが得られることになります。上記の場合、4! / ( 2! x 2! ) = 6 通りと求めることができます。以上をまとめると、一般には次の式で計算することができます。
n! / Πk{1→m}( nk! ) = n! / n1!n2!...nm!
但し、Σk{1→m}( nk ) = n
今まで紹介した順列を計算するためのサンプル・プログラムを以下に示します(重複順列は単純なので除きます)。
/* perm : 順列の計算 T n : 要素数 T r : 要素から選択する数 戻り値 : 順列の値 */ template<class T> T perm( T n, T r ) { if ( n < r ) return( 0 ); // n < r なら nPr = 0 if ( r < 0 ) return( 0 ); // nP-r = 0 if ( r == 0 ) return( 1 ); // nP0 = 1 T ans = n; // 計算結果 // n( n - 1 )...( n - r + 1 ) を求める for ( T t = n - r + 1 ; t < n ; ++t ) ans *= t; return( ans ); } /* repPerm : m 個の要素からそれぞれ k1 〜 km 個ずつ合計 n 個並べる場合の数を求める vector<unsigned int> k : 各要素で選択する数( k1 〜 km ) 戻り値 : 求めた場合の数 */ template<class T> T repPerm( vector<unsigned int> k ) { if ( k.size() == 0 ) return( 0 ); // 要素数がゼロなら結果もゼロ if ( k.size() == 1 ) return( 1 ); // 要素数が 1 なら場合の数は 1 unsigned int n = 0; // 並べる合計の数 map<unsigned int, T> mapFact; // 0! 〜 n! の階乗リスト for ( unsigned int i = 0 ; i < k.size() ; ++i ) { n += k[i]; if ( mapFact.find( k[i] ) == mapFact.end() ) mapFact[k[i]] = 0; } // 階乗の計算 T fact = 1; // 最後に n! が得られる if ( mapFact.find( 0 ) != mapFact.end() ) mapFact[0] = fact; for ( unsigned int i = 1 ; i <= n ; ++i ) { fact *= i; if ( mapFact.find( i ) != mapFact.end() ) mapFact[i] = fact; } // 各要素数の階乗で徐算 for ( unsigned int i = 0 ; i < k.size() ; ++i ) fact /= mapFact[k[i]]; return( fact ); }
処理は非常に単純で、公式にしたがって計算を行っているだけです。repPerm は、m 個の要素からそれぞれ k1 〜 km 個ずつ合計 n 個並べる場合の数を求めるためのプログラムで、n までの階乗を計算しながらそれを配列などに登録しておいて、分母にある階乗計算を省略しています。但し、全ての階乗を登録する必要はなく、各要素の数にあたる分だけあれば十分なので、ki( 1 ≦ k ≦ m ) の値をチェックして必要なものをあらかじめチェックしておくようにします。ここでは、階乗を保持するためのコンテナクラスとして Standard Template Library(STL) にある連想配列の map を利用しています。
計算に使う値やその結果は、型を変えることができるようにテンプレートを使っています。これで、任意の型の変数を使った処理ができるようになります。
// 多倍長整数 UBigNum n_ubn = 5; UBigNum r_ubn = 3; UBigNum ans_ubn = perm( n_ubn, r_ubn ); cout << "P(" << n_ubn << "," << r_ubn << ") = " << ans_ubn << endl; // 整数型 unsigned int n_uint = 5; unsigned int r_uint = 3; unsigned int ans_uint = perm( n_uint, r_uint ); cout << "P(" << n_uint << "," << r_uint << ") = " << ans_uint << endl; // 浮動小数点数型 double n_dbl = 5; double r_dbl = 3; double ans_dbl = perm( n_dbl, r_dbl ); cout << "P(" << n_dbl << "," << r_dbl << ") = " << ans_dbl << endl; vector<unsigned int> k; k.push_back( 3UL ); k.push_back( 2UL ); k.push_back( 2UL ); ans_ubn = repPerm<UBigNum>( k ); // 多倍長整数 ans_uint = repPerm<unsigned int>( k ); // 整数型 ans_dbl = repPerm<double>( k ); // 浮動小数点数型 cout << "P( 7 ; 3, 2, 2 ) = " << ans_ubn << endl; cout << "P( 7 ; 3, 2, 2 ) = " << ans_uint << endl; cout << "P( 7 ; 3, 2, 2 ) = " << ans_dbl << endl;
テンプレートについては以前、「円を描く (3)サンプル・プログラム」の中でも簡単に説明しています。要素の型に関係なく何らかの処理をしたりコンテナクラスを作成するようなときに威力を発揮する反面、使いこなすのが難しく敬遠されることもあるようです。例えば、テンプレートを使ったとき、型を指定して利用されない限りはその型専用の関数・クラスは作成されないので、テンプレートを使ったソースとは別の場所で利用しようとするとコンパイラがエラーを返します(昔、このエラーの原因が分からずに苦労した経験があります)。
他の場所でも利用ができるようにするには、テンプレートを使った関数やクラスは実装を含め全てヘッダファイルに記述してしまうか、またはテンプレートを明示的にインスタンス化するかのどちらかになります。明示的なインスタンス化は次のように行います。
template UBigNum perm( UBigNum n, UBigNum r ); template unsigned int repPerm( vector<unsigned int> k );
クラスの場合は次のように記述します。
template<class T> class SomeClass { : }; template class SomeClass<unsigned int>;
個人的には、単純で短い関数やクラスであればヘッダファイルに記述して必要に応じて生成されるようにしておき、ある程度大きなものは型を明示するようにして使い分けています。
順列は、選択した要素の並び順を考慮していましたが、並び順は区別せずに選択した要素だけで場合の数を数えてみます。n 枚のカードから r 枚のカードを抽出して並べたときの場合の数は nPr でした。選択した r 枚のカードについて、並び順だけが異なり要素は同じものがどれだけあるかを考えてみると、r 枚のカードを並べる場合の数は r! なのでそれは r! 通りになるはずです。よって、順列 nPr を求めた後で、それを r! で徐算すればよいことになります。
例えば、0 〜 3 までの四枚のカードから任意の三枚を選び、それを大きい数から順に並べる操作を考えてみます。この時、選んだ順番に関係なく、選択したカードで数が決まってしまいます。例えば、四枚のカードから 0, 1, 2 の三枚のカードが選ばれたとき、その並べ方は 3! = 6 通りありますが、それらは全て 210 という数字になります。よって、順列 4P3 = 24 を 6 で徐算した 4 通りの数が得られることになります。実際の組み合わせは簡単に求めることができて 210, 310, 320, 321 となります。
並べ方を考慮せず、ある集合からいくつかの要素を取り出す場合の数を「組み合わせ(Combination)」といい、n 個の要素から r 個を抽出する組み合わせを nCr で表します。組み合わせは、上記の内容から
| nCr | = | nPr / r! |
| = | n! / r! ( n - r )! |
で求めることができます。この式の計算結果が必ず整数になることは、上記考察から理解できると思います(補足1)。
カードを一枚増やして 0 〜 4 までとして、この中から任意の三枚を選択する操作を行うとします。4 を除いた四枚のカードから三枚を選択する場合の数はすでに 4C3 = 4 であることが分かっています。残りの組み合わせには、必ず 4 が含まれていることになり、それは 4 を除いた四枚のカードから二枚を選択してそれに 4 を追加することで得られるので 4C2 = 6 になります。よって、これらを合計した数 10 が求める組み合わせの数になります。実際の組み合わせは 210, 310, 320, 321, 410, 420, 430, 421, 431, 432 で、4 を含む組み合わせが 6 通り、それ以外が 4 通りとなっています。以上のことから、組み合わせに関して次の公式が成り立つことが分かります。
次に、トランプのスペードとハートの札から J, Q, K をそれぞれ三枚ずつ、合計六枚取り出して、この中から三枚抜き取ったときの組み合わせを考えます。スペードのカードは SJ, SQ, SK を、ハートのカードは HJ, HQ, HK をそれぞれ J, Q, K のカードとしたとき、実際の組み合わせは次のように 6C3 = 20 通りになります。
{ SJ SQ SK }
{ SJ SQ HJ } { SJ SQ HQ } { SJ SQ HK }
{ SJ SK HJ } { SJ SK HQ } { SJ SK HK }
{ SQ SK HJ } { SQ SK HQ } { SQ SK HK }
{ HJ HQ SJ } { HJ HQ SQ } { HJ HQ SK }
{ HJ HK SJ } { HJ HK SQ } { HJ HK SK }
{ HQ HK SJ } { HQ HK SQ } { HQ HK SK }
{ HJ HQ HK }
{ SJ SQ SK } はスペードのみで、ハートからひとつも選ばれていない組み合わせです。その下側の 9 個の組み合わせはスペードが二枚とハートが一枚、さらにその下の 9 個はスペードが一枚とハートが一枚、最後にハートのみの組み合わせとなっています。スペードを二枚選ぶときの組み合わせは 3 通りあります。残りの一枚のカードとしてハートから選べるのは 3 通りあります。従って、スペード二枚とハート一枚からなる組み合わせは 3 x 3 = 9 通りとなっています。これはスペード一枚とハート二枚からなる組み合わせでも同様です。このことから、m + n 個の中から r 個を選ぶ組み合わせは、m 個の中から k 個、n 個の中から r - k 個選ぶときの組み合わせを求めてその積を計算し、それを全ての k ( 0 ≦ k ≦ r ) について加算した結果と等しくなることが分かります。式に表すと次のようになります。
重複順列の場合と同じように、組み合わせについても重複を許すような操作について検討してみます。これは、一度選択した要素を元に戻す、いわゆる復元抜き取りを行う場合の数になります。今回も簡単な例として、1, 2, 3 の三枚のカードから復元抜き取りによって 5 回カードを選ぶ場合を考えます。選んだカードの数字は小さい順に左側から並べるとして、その結果を以下に示します。
11111 11112 11122 11222 12222 22222 11113 11123 11223 12223 22223 11133 11233 12233 22233 11333 12333 22333 13333 23333 33333
要素が異なる箇所に仕切りを付けてみます。仕切りは必ず二箇所、1 と 2 の間、2 と 3 の間に付けるものとします。従って、要素がない箇所は仕切りの間が空の状態になります。
[11111||] [1111|2|] [111|22|] [11|222|] [1|2222|] [|22222|] [1111||3] [111|2|3] [11|22|3] [1|222|3] [|2222|3] [111||33] [11|2|33] [1|22|33] [|222|33] [11||333] [1|2|333] [|22|333] [1||3333] [|2|3333] [||33333]
さらに、1, 2, 3 各要素を全て '.' で表すと、次のようになります。
[.....||] [....|.|] [...|..|] [..|...|] [.|....|] [|.....|] [....||.] [...|.|.] [..|..|.] [.|...|.] [|....|.] [...||..] [..|.|..] [.|..|..] [|...|..] [..||...] [.|.|...] [|..|...] [.||....] [|.|....] [||.....]
これは、5 つの '.' と 2 つの '|' の並べ方を意味しています。仕切りで要素を 3 つに仕切り、左側から順に、仕切り内は全て同じになるように要素を並べると、目的のものが得られることになります。よって、順列のところで説明した、各要素の個数を固定した並べ方の数を求める式がそのまま利用できて、7! / ( 5! x 2! ) = 21 通りと計算できます。この結果は、先ほど数えた結果の数とも一致します。一般的に、n 個の要素から復元抜き取りで r 個の要素を選択するときの組み合わせの数は nHr で表し、その値は下式で求められます。
ところで、上式の右辺は n+r-1Cr とも等しいので、次の式が成り立ちます。
これは次のように考えることができます。
先ほどの例で、5 つ並んだ数字の左から順に 0 から 4 まで加えていくと、次のようになります。
11111 → 12345 11112 → 12346 11122 → 12356 11222 → 12456 12222 → 13456 22222 → 23456 11113 → 12347 11123 → 12357 11223 → 12457 12223 → 13457 22223 → 23457 11133 → 12367 11233 → 12467 12233 → 13467 22233 → 23467 11333 → 12567 12333 → 13567 22333 → 23567 13333 → 14567 23333 → 24567 33333 → 34567
右側の結果にはもはや重複した要素はなく、それぞれの結果は 1 から 7 までの値から 5 つを抽出して小さい順に並べたものを表すことになります。左側の場合の数は nHr で、右側の場合の数は n+r-1Cr、それぞれの組み合わせの結果は、上の表のように一対一に対応させることができます。
/* comb : 組み合わせの計算 T n : 要素数 T r : 要素から選択する数 戻り値 : 組み合わせの値 */ template<class T> T comb( T n, T r ) { if ( n < r ) return( 0 ); // n < r なら C( n, r ) = 0 if ( r < 0 ) return( 0 ); // C( n, -r ) = 0 if ( r > n - r ) r = n - r; // C( n, n - r ) = C( n, r ) if ( r == 0 ) return( 1 ); // C( n, 0 ) = 1 if ( r == 1 ) return( n ); // C( n, 1 ) = n T ans = n; // 計算結果 // n( n - 1 )...( n - r + 1 ) を求める for ( T t = n - r + 1 ; t < n ; ++t ) ans *= t; // 階乗 r! を求める T fact = r; for ( --r ; r > 1 ; --r ) fact *= r; ans /= fact; return( ans ); }
順列の計算結果を r! で徐算するだけなので、順列計算用の perm とほとんど大差はありません。次の二項定理で詳細は示しますが、nCn-r = nCr が成り立つので、計算量を少なくするため r > n - r なら r を n - r に置き換えています。
二項式 x + y のべき乗 ( x + y )n を展開したとき、各項の係数がどうなるかを調べてみます。まず、n = 2 のときは
| ( x + y )2 | = | ( x + y )( x + y ) |
| = | x2 + xy + yx + y2 | |
| = | x2 + 2xy + y2 |
n = 3 のときを計算すると
| ( x + y )3 | = | ( x + y )2( x + y ) |
| = | ( x2 + 2xy + y2 )( x + y ) | |
| = | x3 + 2xyx + y2x + x2y + 2xy2 + y3 | |
| = | x3 + 3x2y + 3xy2 + y3 |
以下、べき乗の計算を続けていくと、次のような式が得られます。
| n | 展開式 |
|---|---|
| 1 | x + y |
| 2 | x2 + 2xy + y2 |
| 3 | x3 + 3x2y + 3xy2 + y3 |
| 4 | x4 + 4x3y + 6x2y2 + 4xy3 + y4 |
| 5 | x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + y5 |
| 6 | x6 + 6x5y + 15x4y2 + 20x3y3 + 15x2y4 + 6xy5 + y6 |
| 7 | x7 + 7x6y + 21x5y2 + 35x4y3 + 35x3y4 + 21x2y5 + 7xy6 + y7 |
| : |
各式の中から係数だけを取り出してみると、以下の表のようになります。
| n | 係数 |
|---|---|
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| 7 | 1 7 21 35 35 21 7 1 |
| : |
但し、n = 0 は x + y ≠ 0 のとき ( x + y )0 = 1 になることから係数を 1 としています。上下の係数の値を比較すると、上側の隣り合った係数の和が下側の係数となっていることが分かります。但し、両端については必ず 1 になる(もしくは上側の両端にゼロがあると見なす)とします。実際にこれが全ての指数 n について成り立つかについては、帰納法を使って証明することができます(補足2)。上の表にある、係数だけを抽出して三角形の形に配置したものは「パスカルの三角形(Pascal's Triangle)」と呼ばれています。
( x + y )n の展開式に対し、xn-k ( 0 ≦ k ≦ n ) 項の係数を an(k) としたとき、上記結果から an(0) = an(n) = 1、an(k) = an-1(k-1) + an-1(k) ( 1 ≦ k ≦ n - 1 ) が成り立ちます。この漸化式は、組み合わせの式 nCr でも成り立つことを前章で紹介しました。従って、nC0 = 1 と約束すれば(実際、何も選択しないときの結果は空集合一つのみとなります)、各係数は組み合わせの値と等しいということになります。このように、二項式 x + y の展開式が組み合わせの公式を使って表せることを「二項定理(Binomial Theorem)」といい、その係数を「二項係数(Binomial Coefficient)」といいます。
| ( x + y )n | = | Σk{0→n}( nCk xn-k yk ) |
| = | nC0 xn + nC1 xn-1 y + nC2 xn-2 y2 + ... + nCn-1 x yn-1 + nCn yn |
組み合わせの式は nCr で表していましたが、二項係数としては、下に示したように、n と r を縦に並べて括弧で囲むのが通例です。nCr のような表現はあまり用いられないようなのですが、HTML上では下記表現が難しいので、以下、n と r を横に並べた上で、組み合わせ(Combination)の頭文字を付けて C( n, r ) と表現することにします。ちなみに、nCr が使われない理由として、重要なパラメータである n と r があまり目立たないということもあるようです。
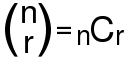
パスカルの三角形を見ると明らかなように、係数は左右対称となっています。従って、次の公式が成り立ちます。
n 個の要素から r 個を選択するという操作は、n 個の要素から n - r 個を除外する操作と同じことになることからも上記の式の意味が理解できると思います。
ここまでは組み合わせの数という意味で二項係数を考えてきましたが、ここで n を実数にまで拡張して次のような定義を行います。
C( a, r ) = a( a - 1 )( a - 2 ) ... ( a - r + 1 ) / r! ( r > 0 )
C( a, 0 ) = 1
C( a, r ) = 0 ( r < 0 )
この時、以下の命題が成り立ちます。
( 1 + x )a = 1 + C( a, 1 )x + C( a, 2 )x2 + ... + C( a, r )xr + ...
これを「一般の二項定理(Generalized Binomial Theorem)」といいます(補足3)。
初項 a、公比 x の等比数列 axr の 0 から r までの総和(等比級数)を Sr とすると、
Sr = ax0 + ax1 + ax2 + ... + axr-1 + axr
xSr = ax1 + ax2 + ax3 + ... + axr + axr+1
より
よって
|x| < 1 ならば、r → ∞ のとき Sr は収束して、
になります。初項 1、公比を -t ( |t| < 1 ) としたとき、
なので、一般の二項定理と係数を比較することで
となります。これは、二項係数の定義から
| C( -1, r ) | = | ( -1 )( -1 - 1 )( -1 - 2 )...( -1 - r + 1 ) / r! |
| = | ( -1 )( -2 )( -3 )...( -r ) / 1・2・3・...・r | |
| = | ( -1 / 1 )( -2 / 2 )( -3 / 3 )...( -r / r ) | |
| = | (-1)r |
と計算することによっても導くことができます。先ほどの初項 1、公比 -t の等比級数において、両辺を微分すると
-1 + 2t - 3t2 + ... + (-1)rrtr-1 + ... = - ( 1 + t )-2 より
1 - 2t + 3t2 - ... + (-1)r+1rtr-1 + ... = ( 1 + t )-2
よって、
これも、二項係数の定義から同様の結果を得ることができます。さらに、( n - 1 ) 階導関数は
- ( n - 1 )! + n!t - { ( n + 1 )! / 2 }t2 + ... + (-1)r-n{ r! / ( r - n + 1 )! }tr-n+1 + ... + (-1)r-1{ ( r + n - 1 )! / r! }tr + ... = - ( n - 1 )!( 1 + t )-n より
1 - nt + { n( n + 1 ) / 2 }t2 + ... + (-1)r-n+1{ r! / ( r - n + 1 )!( n - 1 )! }tr-n+1 + ... + (-1)r{ ( r + n - 1 )! / r!( n - 1 )! }tr + ... = ( 1 + t )-n
よって、
となります。二項係数の定義から
| C( -n, r ) | = | ( -n )( -n - 1 )( -n - 2 )...( -n - r + 1 ) / r! |
| = | (-1)r( n + r - 1 )...( n + 2 )( n + 1 )n / r! | |
| = | (-1)r{ ( n + r - 1 )! / r!( n - 1 )! } |
になるため、ここでも結果は一致します。
であることから、a > 0 のときに負の二項係数について次の等式が成り立ちます。
また、組み合わせの考え方から求めた以下の等式は、一般の二項定理でも成り立ちます。
C( a + 1, r ) = C( a, r - 1 ) + C( a, r )
Σk{0→r}( C( a, k )・C( b, r - k ) ) = C( a + b, r )
これらの等式は、組み合わせの考えから求めたときは具体例を使って証明をしましたが、二項展開式の等式を使って係数を比較することで簡単に証明することができます。
( 1 + x )a+1 = ( 1 + x )( 1 + x )a = x( 1 + x )a + ( 1 + x )a より
Σr{0→∞}( C( a + 1, r )xr ) = Σr{0→∞}( C( a, r )xr+1 ) + Σr{0→∞}( C( a, r )xr )
xr 項の係数は左辺が C( a + 1, r )、右辺が C( a, r - 1 ) + C( a, r ) になり、それらは等しいので C( a + 1, r ) = C( a, r - 1 ) + C( a, r ) が成り立つ。
( 1 + x )a+b = ( 1 + x )a( 1 + x )b より
Σr{0→∞}( C( a + b, r )xr ) = { Σr{0→∞}( C( a, r )xr ) }{ Σr{0→∞}( C( b, r )xr ) }
右辺の xr 項の係数は、C( a, r )xr1 と C( b, r )xr2 において r = r1 + r2 となる項の係数の和に等しいので
C( a + b, r ) = Σr1,r2{ r1 + r2 = r }( C( a, r1 )C( b, r2 ) ) = Σk{0→r}( C( a, k )C( b, r - k ) )
よって、Σk{0→r}( C( a, k )C( b, r - k ) ) = C( a + b, r ) が成り立つ。
「 - 5 個の中から 3 個選ぶ組み合わせ」とか「π 個の中から 2 個選ぶ組み合わせ」などと考えると訳が分からなくなりますが、組み合わせの概念から離れて二項展開式の導関数の係数から考えると、一般の二項定理が成り立つことは理解できます。この定理を見つけたのは、物理学者としても、また数学者としても数多くの業績を残したアイザック・ニュートン(Isaac Newton)で、そのため一般の二項定理は英語で Newton's Generalized Binomial Theorem と呼ばれているようです。ニュートンは、パスカルの三角形を見てその行間に何があるのかを考えた末に一般の二項定理を発見したそうです。凡人にはとても思いつかない考えかたではないでしょうか。
二項係数を求めるサンプル・プログラムを以下に示します。
/* binCoef : 二項係数 C( a, r ) の計算 D a : C( a, r ) の パラメータ a (実数値) I r : C( a, r ) の パラメータ r (整数値) 戻り値 : 組み合わせの値 */ template<class D, class I> D binCoef( D a, I r ) { if ( r < 0 ) return( 0 ); // C( a, -r ) = 0 if ( r == 0 ) return( 1 ); // C( a, 0 ) = 1 if ( r == 1 ) return( a ); // C( a, 1 ) = a D ans = a; // 計算結果 // a( a - 1 )...( a - r + 1 ) を求める for ( D d = a - ( r - 1 ) ; d < a ; ++d ) ans *= d; // 階乗 r! を求める I fact = r; for ( --r ; r > 1 ; --r ) fact *= r; ans /= fact; return( ans ); }
処理の内容は組み合わせの計算プログラム comb とほとんど同じで、要素数を表す n が実数値 a に変化しただけです。そのため、テンプレートで定義する型は二種類 ( D と I ) になり、前者が実数型、後者が整数型となります。また、C( a, a - r ) = C( a, r ) は一般には成り立たないので、r を n - r に置き換える処理は省かれています。
二項定理では、二項式のべき乗の展開式を二項係数で表す公式について検討しました。これを一般の多項式のべき乗に拡張するとどうなるでしょうか。
簡単な例として、三項式 x + y + z のべき乗を計算してみます。
| ( x + y + z )1 | = | x + y + z |
| ( x + y + z )2 | = | ( x + y + z )( x + y + z ) |
| = | xx + xy + xz + yx + yy + yz + zx + zy + zz | |
| = | x2 + 2xy + 2zx + y2 + 2yz + z2 | |
| ( x + y + z )3 | = | ( xx + xy + xz + yx + yy + yz + zx + zy + zz )( x + y + z ) |
| = | xxx + xyx + xzx + yxx + yyx + yzx + zxx + zyx + zzx + | |
| xxy + xyy + xzy + yxy + yyy + yzy + zxy + zyy + zzy + | ||
| xxz + xyz + xzz + yxz + yyz + yzz + zxz + zyz + zzz | ||
| = | x3 + y3 + z3 + 3x2y + 3zx2 + 3xy2 + 3z2x + 3y2z + 3yz2 + 6xyz | |
| ( x + y + z )4 | = | ( xxx + xyx + xzx + yxx + yyx + yzx + zxx + zyx + zzx + |
| xxy + xyy + xzy + yxy + yyy + yzy + zxy + zyy + zzy + | ||
| xxz + xyz + xzz + yxz + yyz + yzz + zxz + zyz + zzz )( x + y + z ) | ||
| = | xxxx + xyxx + xzxx + yxxx + yyxx + yzxx + zxxx + zyxx + zzxx + | |
| xxyx + xyyx + xzyx + yxyx + yyyx + yzyx + zxyx + zyyx + zzyx + | ||
| xxzx + xyzx + xzzx + yxzx + yyzx + yzzx + zxzx + zyzx + zzzx + | ||
| xxxy + xyxy + xzxy + yxxy + yyxy + yzxy + zxxy + zyxy + zzxy + | ||
| xxyy + xyyy + xzyy + yxyy + yyyy + yzyy + zxyy + zyyy + zzyy + | ||
| xxzy + xyzy + xzzy + yxzy + yyzy + yzzy + zxzy + zyzy + zzzy + | ||
| xxxz + xyxz + xzxz + yxxz + yyxz + yzxz + zxxz + zyxz + zzxz + | ||
| xxyz + xyyz + xzyz + yxyz + yyyz + yzyz + zxyz + zyyz + zzyz + | ||
| xxzz + xyzz + xzzz + yxzz + yyzz + yzzz + zxzz + zyzz + zzzz | ||
| = | x4 + y4 + z4 + 4x3y + 4xy3 + 4y3z + 4yz3 + 4z3x + 4zx3 + 6x2y2 + 6z2x2 + 6y2z2 + 12x2yz + 12xy2z + 12xyz2 |
展開式の各項の次数は、べき乗の数と必ず一致します。従って、展開式の項数は必ず、x, y, z の三項を指数 n 個分重複を許して選ぶときの重複組み合わせの数 3Hn = ( n + 2 )! / 2n! だけあることになります。また、上に示したように、指数を使わず変数の交換も行わないで各項を並べた場合、その数は重複順列の数 3Πn = 3n となります。展開式の項のひとつを xrxyryzrz ( rx + ry + rz = n )としたとき、これは x を rx 個、 y を ry 個、 z を rz 個それぞれ並べたもの全ての和となるので、これは順列のところで求めたように、n! / rx!・ry!・rz! で求めることができ、これが xrxyryzrz の係数となります。例えば ( x + y + z )4 の展開式にある x3y 項は、xxxy, xxyx, xyxx, yxxx の和から計算されているので、係数は 4 になります。
以上のことから、k 項式の n 乗 ( x1 + x2 + ... + xk )n において、x1r1x2r2...xkrk ( r1 + r2 + ... + rk = n ) の係数は n! / r1!・r2!・...・rk! であることが分かります。この係数を「多項係数(Multinomial Coefficients)」といい、多項係数を求めるこの公式を「多項定理(Multinomial Theorem)」といいます。各項の係数の和は重複順列の数を表すことになるので、必ず kn になります。
多項定理にて項数を二つにしたときは二項定理と等しくなります。二項係数がなぜ組み合わせの式と等しくなるのかは、多項定理に対する以上の考察からも理解できると思います。
f(t) = e-at を 0 から ∞ まで積分します。
左辺を a について微分すると
右辺は -a-2 なので、
a について微分を続けると、次のようになります。
ここで、a = 1 とすると、
となって、階乗を積分に置き換えた形ができます。左辺の n を正の実数 x に置き換えて、
とすると、x が整数値ならば積分の結果は ( x - 1 )! となります。このとき、
| Γ(x + 1) | = | ∫{0→∞} tx e-t dt |
| = | [ tx ( -e-t ) ]{0→∞} - ∫{0→∞} x tx-1 ( -e-t ) dt |
lim{t→∞}( tx e-t ) = 0 なので(補足4)
| Γ(x + 1) | = | - ∫{0→∞} x tx-1 ( -e-t ) dt |
| = | x∫{0→∞} tx-1 e-t dt | |
| = | x Γ(x) |
よって、Γ(x + 1) = xΓ(x) = x( x - 1 )Γ(x - 1) = ... が成り立ち、これは階乗を実数に拡張したことになります。この関数を「ガンマ関数(Gamma Function)」といいます。ガンマ関数を使うと、一般の二項定理は次のように表すことができます。
C( a, r ) = Γ( a + 1 ) / Γ( r + 1 )Γ( a - r + 1 )
ガンマ関数は、整数値以外の任意の正の実数に対しても収束します(補足5)。よって、0 < x < 1 の範囲に対しても計算を行うことができます。Γ(1/2) の値は
より、u2 = t と変数変換すると 2udu = dt だから
| Γ(1/2) | = | ∫{0→∞} (1/u) exp( -t2 ) 2udu |
| = | 2∫{0→∞} exp( -t2 ) du |
∫{0→∞} exp( -t2 ) du = √π / 2 だから (「ガボール・フィルタのフーリエ変換」の後半部分に、積分の計算方法が紹介されています)
が得られます。
次に、二つのガンマ関数の積を計算してみます。それぞれを
Γ(x) = ∫{0→∞} ux-1 e-u du
Γ(y) = ∫{0→∞} vy-1 e-v dv
とすると、
| Γ(x)Γ(y) | = | ∫{0→∞} ux-1 e-u du ∫{0→∞} vy-1 e-v dv |
| = | ∫{0→∞}∫{0→∞} ux-1 vy-1 e-u-v dudv |
まずは u = x2、v = y2 で変数変換すると、du = 2xdx、dv = 2ydy より
| Γ(x)Γ(y) | = | ∫{0→∞}∫{0→∞} x2x-2 y2y-2 exp( -x2-y2 ) 2x・2y dxdy |
| = | 4∫{0→∞}∫{0→∞} x2x-1 y2y-1 exp( -x2-y2 ) dxdy |
さらに x = rcosθ、y = rsinθ と極座標に変換すると、dxdy = r drdθ で、x, y > 0 より 0 < θ < π / 2 なので (「ガボール・フィルタのフーリエ変換」の後半部分に、多変数関数の重積分における変数変換方法が記載されており、極座標変換の例もその中に示してあります)、
| Γ(x)Γ(y) | = | 4∫{0→π/2}∫{0→∞} ( rcosθ )2x-1 ( rsinθ )2y-1 exp( -r2 ) r drdθ |
| = | 4∫{0→∞} r2x+2y-1 exp( -r2 ) dr ∫{0→π/2} cos2x-1θ sin2y-1θ dθ |
ここで、
| 2∫{0→∞} r2x+2y-1 exp( -r2 ) dr | = | ∫{0→∞} sx+y-1 e-s ds [s = r2 で変数変換] |
| = | Γ( x + y ) |
となるため、
β( x, y ) = 2∫{0→π/2} cos2x-1θ sin2y-1θ dθ とすれば、
という関係式が得られます。こうして得られた関数 β( x, y ) を「ベータ関数(Beta Function)」といいます。
ベータ関数において、t = cos2θ としたとき、dt = -2sinθcosθ dθ で、θ = 0 のとき t = 1、θ = π/2 のとき t = 0、さらに sin2θ = 1 - cos2θ = 1 - t となるので
| β( x, y ) | = | 2∫{0→π/2} cos2x-1θ sin2y-1θ dθ |
| = | -∫{0→π/2} ( cos2θ )x-1 ( 1 - cos2θ )y-1 -2sinθcosθ dθ | |
| = | -∫{1→0} tx-1 ( 1 - t )y-1 dt | |
| = | ∫{0→1} tx-1 ( 1 - t )y-1 dt |
と表すことができます。すっきりとした形で覚えやすいので、書籍などを見るとこちらの方をよく見かけます。上式において、u = 1 - t とすれば du = -dt で、t = 0 のとき u = 1、t = 1 のとき u = 0 なので
| β( x, y ) | = | -∫{1→0} ( 1 - u )x-1 uy-1 du |
| = | ∫{0→1} uy-1 ( 1 - u )x-1 du | |
| = | β( y, x ) |
となります。
ガンマ関数も、ベータ関数と同様にいくつかの異なる定義式があります。まず、ガンマ関数において u = e-t ( t = -logeu ) とすれば、du = -e-t dt となり、t = 0 のとき u = 1、t → ∞ のとき u → 0 なので、
また、t = u2 とすれば dt = 2u du で、t = 0 のとき u = 0、t → ∞ のとき u → ∞ なので、
無限乗積での定義式は次のようになります。このとき、定義域は負の整数( 0, -1, -2, ... ) を除く全実数になります。
ガンマ関数もベータ関数もともに、大数学者の「レオンハルト・オイラー(Leonhard Euler)」が、階乗を整数だけでなく実数にも一般化することを目的に研究をしたのが最初であると言われています。今まで紹介した式は基本的に、オイラーが、友人の「クリスティアン・ゴールドバッハ(Christian Goldbach)」に宛てた書簡の中で示したもので、その重要性から他の様々な数学者によってその後も研究が進められ、統計学においてもガンマ関数とベータ関数が利用されています。なお、積分式については、ベータ関数が「第一種オイラー積分」、ガンマ関数が「第二種オイラー積分」とも呼ばれます。
この他に、カール・ワイエルシュトラス(Karl Weierstrass)が示した、「ワイエルシュトラスの乗積表示(Weierstrass Formula)」という別の定義式があります。
| nx | = | ex ln(n) = exp( x( ln(n) - 1 - 1/2 - ... - 1/n ) + x( 1 + 1/2 + ... + 1/n ) ) |
| = | exp( x( ln(n) - 1 - 1/2 - ... - 1/n ) ) exp( x + x/2 + ... + x/n ) |
但し、ln(n) = logen
より、これを無限乗積での定義式に代入すると
| Γ( x ) | = | lim{n→∞}( exp( x( ln(n) - 1 - 1/2 - ... - 1/n ) )・exp( x + x/2 + ... + x/n )・n! / Πk{0→n}( x + k ) ) |
| = | lim{n→∞}( exp( x( ln(n) - 1 - 1/2 - ... - 1/n ) )・ex・2ex/2・ ... ・nex/n / x( x + 1 )( x + 2 )...( x + n ) ) | |
| = | lim{n→∞}( exp( x( ln(n) - 1 - 1/2 - ... - 1/n ) )・( 1 / x )・{ ex / ( x + 1 ) }・{ 2ex/2 / ( x + 2 ) }・ ... ・{ nex/n / ( x + n ) } ) | |
| = | lim{n→∞}( exp( x( ln(n) - 1 - 1/2 - ... - 1/n ) )・( 1 / x )・{ ex / ( 1 + x ) }・{ ex/2 / ( 1 + x/2 ) }・ ... ・{ ex/n / ( 1 + x/n ) } ) | |
| = | lim{n→∞}( exp( x( ln(n) - 1 - 1/2 - ... - 1/n ) )・( 1 / x )・Πk{1→n}( ekx / ( 1 + x/k ) ) ) |
よって、両辺の逆数は、
| 1 / Γ( x ) | = | lim{n→∞}( exp( x( 1 + 1/2 + ... + 1/n - ln(n) ) )・x・Πk{1→n}( ( 1 + x/k ) e-kx ) |
| = | x・lim{n→∞}( exp( x( 1 + 1/2 + ... + 1/n - ln(n) ) ) ) lim{n→∞}( Πk{1→n}( ( 1 + x/k ) e-kx ) ) | |
| = | x・eγx Πk{1→∞}( ( 1 + x/k ) e-kx ) |
但し、γ = lim{n→∞}( exp( Σk{1→n}( 1 / k ) - ln(n) ) ) = 0.5772...
γ は「オイラーの定数(Euler’s Constant)」と呼ばれる定数になります。これは、調和級数 Σk{1→n}( 1 / k ) と対数関数 ln(n) の差を表しており、極限においてはこの差が収束することもオイラーが証明しました。このことは、調和級数の増え方は極限において対数関数と等しくなることを示しています。
以上をまとめると、次のようになります。
| Γ(x) | = | ∫{0→∞} tx-1 e-t dt |
| = | ∫{0→1} ( -loget )x-1 dt | |
| = | 2∫{0→∞} t2x-1 exp( -t2 ) dt |
Γ( x ) = lim{n→∞}( nxn! / Πk{0→n}( x + k ) ) [無限乗積]
Γ( x ) = x・eγx Πk{1→∞}( ( 1 + x/k ) e-kx ) [ワイエルシュトラスの乗積表示]
| β( x, y ) | = | ∫{0→1} tx-1 ( 1 - t )y-1 dt |
| = | 2∫{0→π/2} cos2x-1θ sin2y-1θ dθ |
ある個数の要素から決められた分だけ抽出するときの順列や組み合わせは今まで紹介した公式を使えば簡単に求めることができます。しかし、組み合わせを考えるときの条件はたいてい、もう少し複雑であることが多いため、その解き方も様々なパターンがあります。ここで、いくつかの例を紹介したいと思います。
三大トランプゲームの一つとされる「ポーカー」は、五枚のカードの組み合わせ(ハンド)の強さを競うゲームです。ハンドには下表のようなものがあり、上にあるものほど強いハンドになります。
| ハンド | 組み合わせの内容 | ハンドの例 |
|---|---|---|
| ロイヤル・ストレート・フラッシュ(Royal Flush) | 全て同じスートで、10, J, Q, K, A の組み合わせ | S[10] S[J] S[Q] S[K] S[A] |
| ストレート・フラッシュ(Straight Flush) | 全て同じスートで、五枚のカードが連番となったもの | S[3] S[4] S[5] S[6] S[7] |
| フォー・カード(Four of a Kind) | 同じランクのカードが四枚そろったもの | S[A] D[A] C[A] H[A] C[4] |
| フル・ハウス(Full House) | 二枚と三枚の、それぞれ同じランクのカードがそろったもの | S[3] H[3] S[6] D[6] H[6] |
| フラッシュ(Flush) | 全て同じスートのカード | H[4] H[5] H[9] H[J] H[K] |
| ストレート(Straight) | 五枚のカードが連番となったもの | H[5] C[6] S[7] D[8] C[9] |
| スリー・カード(Three of a Kind) | 同じランクのカードが三枚そろったもの | S[A] D[A] C[A] C[10] S[K] |
| ツー・ペア(Two Pair) | 二枚の同じランクのカードが二つそろったもの | S[7] C[7] D[9] H[9] S[J] |
| ワン・ペア(One Pair) | 二枚の同じランクのカードが一つそろったもの | D[J] H[J] S[2] D[8] H[10] |
| ノー・ペア(High Card) | 上記のどのハンドにも当てはまらないもの | D[A] H[5] C[7] H[J] S[K] |
ランクとはカードの番号を表し、1 から 13 までの連番になります。その中でも 1 は Ace、11 は Jack、12 は Queen、13 は King という特別な呼び方があります。スートはシンボルのことで、スペード(Spades), ダイヤ(Diamonds), クラブ(Clubs), ハート(Hearts) の四種類あります。それぞれのスートに 13 種類のランクがあるので、トランプの総数は 4 x 13 = 52 枚ということになります。なお、これは世界標準タイプと呼ばれるもので、国によって様々な種類のものもあるようです。表にあるハンドの例では、一文字目がスートを表し(S=Spades, D=Diamonds, C=Clubs, H=Hearts)、[]内の番号がランクを示しています(但し、A=Ace, J=Jack, Q=Queen, K=King)。
ハンドに対する注意点として、ストレートなどの連番の組み合わせにおいては Ace は 2 にも King にもつなげることができるというルールがあります。しかし、Ace は必ず端にあることが条件となるので、例えば Q, K, A, 2, 3 のような組み合わせはストレートとはなりません。ちなみに、ロイヤル・ストレート・フラッシュはストレート・フラッシュの中で最も強いハンドであることを意味しているので、ハンドとしてはストレート・フラッシュの一種という扱いになるようです。
52枚の中から 5 枚のカードを選ぶときの組み合わせは
通りになります。次に、各ハンドが何通りの組み合わせを持っているかを調べてみます。
まず、一番簡単な「ロイヤル・ストレート・フラッシュ」から確認してみます。それぞれのスートに対して、10, J, Q, K, A となるのは一通りしかありません。よって、この組み合わせは 4 通りしかないことになります。「ストレート・フラッシュ」は、A, 2, 3, 4, 5 から 10, J, Q, K, A までの 10 通りの組み合わせが各スートごとにあるので、全部で 40 通りの組み合わせがあります。但し、「ロイヤル・ストレート・フラッシュ」を特別視すれば、4 通りを除いた 36 通りとなります。
「フォー・カード」は、A から K までの 13 通りの組み合わせで 4 枚のカードを並べることができ、残り一枚はどれでもいいので、4 枚を除いた残り 48 枚の中から一枚を選ぶ場合の数だけ組み合わせが存在します。よって、13 x 48 = 624 通りとなります。このとき、他のハンドと重複するような組み合わせは存在しないことに注意して下さい。例えば、4 枚の同じランクのカードは全てスートが異なるので「フラッシュ」にはなり得ません。
「フル・ハウス」では、同じランクのカードを 3 枚選ぶ組み合わせをまず考えます。例えば、A を 3 枚選ぶ場合を考えると、C( 4, 3 ) = 4 通りの組み合わせがあって、それぞれのランクで同様の場合の数があるので、全体としては 4 x 13 = 52 通りあることになります。次に、別のランクのカードから同一ランクのペアを一つ選ぶことになるので、それは 12 x C( 4, 2 ) = 72 通りとなり、それぞれを組み合わせることで 52 x 72 = 3744 通り存在することになります。
これは、次のように考えることもできます。3 枚と 2 枚の同一ランクのカードを選ぶ場合の数は、A から K までの中から二つを選んで並べる順列と等しくなるので、それは 13P2 = 156 通りあります。その中の一つ、例えば A を 2 枚、2 を 3 枚並べる方法は、C( 4, 2 ) * C( 4, 3 ) = 24 通りとなるので、それぞれを掛け合わせて 156 x 24 = 3744 通りとなります。ここでも、他のハンドとの重複は発生しません。
「フラッシュ」は同じスートを並べる場合の数を求めればいいので、例えば Spades に対して考えれば 13 枚の中から 5 枚を選ぶ組み合わせの数になり、C( 13, 5 ) = 1287 通りになります。それが各スートごとにあるので、4 x 1287 = 5148 通りと求められますが、この中には「ストレート・フラッシュ」が含まれるので、その組み合わせ 40 通りを除いた数 5108 通りが「フラッシュ」の組み合わせの数となります。なお、同じスートが並んだ場合は同一ランクのカードは存在しないので、同一ランクの組み合わせによるハンドとは重複することはありません。
「ストレート」は、連番となる組み合わせから「ストレート・フラッシュ」の組み合わせの数 40 を引いたものになります。例えば、10, J, Q, K, A となる組み合わせを考えると、それぞれのランクに対して 4 枚のカードから一枚選ぶ場合の数だけ組み合わせがあるので、C( 4, 1 )5 = 1024 通りになり、これが A, 2, 3, 4, 5 から 10, J, Q, K, A までの 10 パターンあるので、答えは 1024 x 10 - 40 = 10200 通りになります。
「スリー・カード」では、まず A のスリー・カードだけを考えると、4 枚の中から 3 枚を選ぶ組み合わせが C( 4, 3 ) = 4 通りだけあって、あとの 2 枚は、残ったカードの中から A を除く 48 枚のうち 2 枚を選ぶ場合の数 C( 48, 2 ) = 1128 通りだけ組み合わせがあるので、4 x 1128 = 4512 通りと計算できます。これが各ランクに対してあるので 13 x 4512 = 58656 通りとなります。しかし、この中には「フル・ハウス」も含まれているので、その組み合わせを引いた数 58656 - 3744 = 54912 通りが求める値となります。
「ツー・ペア」は、2 枚のペアを異なるランクで二つ作る場合の数 C( 13, 2 ) = 78 通りに対し、各ペアでの組み合わせの数 C( 4, 2 ) x C( 4, 2 ) = 36 通りがあり、残り 1 枚はペアとして使われたランクを除く 44 枚の中から選べばよいので、全てを掛け合わせて 78 x 36 x 44 = 123552 通りと計算できます。
「ワン・ペア」の組み合わせを計算するのが一番複雑なのですが、まず一つのランクから 2 枚のペアを一つ作る場合の数 C( 4, 2 ) = 6 通りがそれぞれのランクに対してあるので 6 x 13 = 78 通りのペアの作り方があります。残り 3 枚はペアとして使われたランクを除く 48 枚の中から選べばよいので、C( 48, 3 ) = 17296 通りになりますが、この中には 2 枚もしくは 3 枚の重複したランクのカードが存在するため「ツー・ペア」や「フル・ハウス」が混在し、それらを除外する必要があります。しかし、例えば最初に A のペアを作り、3 枚の中に 2 のカードが 2 枚含まれている場合と、最初に 2 のペアを作り、3 枚の中に A のカードが 2 枚含まれている場合では重複が発生しているため、単純に「ツー・ペア」や「フル・ハウス」の場合の数を減算するだけでは正しい値が得られません。3 枚のカードは全て異なるランクを持つ必要があるので、そのような場合の数を考えると、それは 12 種類のランクから異なるランクを 3 つ選ぶときの組み合わせになります。ランクだけに注目すると、その組み合わせは C( 12, 3 ) = 220 通りで、それぞれのランクの組み合わせに対してスートを並べる方法は重複順列の式により 43 = 64 通りなので、それらを掛け合わせると 220 x 64 = 14080 通りとなります。ペアを作る組み合わせが 78 通りだったので、「ワン・ペア」の組み合わせは 78 x 14080 = 1098240 通りとなります。
最後の「ノー・ペア」は、まず全てのランクが異なる並べ方が C( 13, 5 ) * 45 = 1317888 通りで、この中から「全てのスートが同じとなる組み合わせ」と「ストレート」を除くと 1317888 - 5148 - 10200 = 1302540 になります。もちろん、これは全ての組み合わせからハンドの組み合わせ総数を減算しても求めることができます。
こうして計算してみると明らかなように、組み合わせや順列の計算式を利用してはいるものの、組み合わせ方を注意深く吟味しながら場合の数を求める処理が必要になります。さらにジョーカーをワイルドカードとして使えば組み合わせは複雑になり、組み合わせを調べる作業はさらに困難になります。こういった問題を解決するための手法を研究する数学の分野は「組合せ数学(Combinatorics)」と呼ばれています。
コンピュータのなかった時代は、組み合わせを考えながら手計算で数え上げる作業が必要なことから、スマートな方法で問題を解決する手法は非常に重要だったわけですが、扱う要素の数がそれほど大きくなければ、コンピュータを利用して実際に組み合わせを「数え上げる」ことも十分に実用的なやり方になります。実際に組み合わせを出力するためのサンプル・プログラムを以下に示します。
/* createCombination : 各組み合わせに対して処理を行う const vector<T>& src : 全要素 unsigned int sIdx : src からの読み込み開始位置 vector<T>& dest : 組み合わせ結果 unsigned int dIdx : dest への書き込み開始位置 void(*func)( vector<T>& ) : 組み合わせが完成した時に実行する関数 */ template<class T> void createCombination( const vector<T>& src, unsigned int sIdx, vector<T>& dest, unsigned int dIdx, void(*func)( vector<T>& ) ) { if ( src.size() == 0 || dest.size() == 0 ) return; if ( dIdx >= dest.size() ) { if ( func != 0 ) (*func)( dest ); return; } for ( unsigned int i = sIdx ; i < src.size() ; ++i ) { dest[dIdx] = src[i]; createCombination( src, i + 1, dest, dIdx + 1, func ); } } /* print : 組み合わせの内容を出力する vector<T>& data : 対象の組み合わせ */ template<class T> void print( vector<T>& data ) { if ( data.size() == 0 ) return; for ( unsigned int i = 0 ; i < data.size() - 1 ; ++i ) cout << data[i] << " "; cout << data[data.size() - 1] << endl; }
組み合わせを作成してそれに対して処理をする関数は createCombination になります。処理を開始するときは、次のように記述します(以下の例では、組み合わせの内容を print 関数で出力する処理を行うことができます)。
最初に、dest の最初の要素に src の最初の要素を代入し、再帰的に createCombination を呼び出します。次は dest の二番目の要素に src の二番目の要素を代入してまた createCombination を呼び出すという処理を、dest の全ての要素が埋まるまで続け、全要素が決まったところで func で指定した関数を呼び出します。処理が完了して呼び出し先から戻ったら、dest の同じ場所に src の次の要素が代入され、さらに処理が続きます。このように、末尾側から要素を変化させながら処理を繰り返す操作をループ処理と再起呼び出しで実現しています。
ハンドの組み合わせ数を数えるためのサンプル・プログラムは次のようになります。
/* スートの種類 */ enum SUIT { SPADE = 0, DIAMOND = 1, CLUB = 2, HEART = 3, }; /* ランク(A,J,Q,K) */ enum RANK { ACE = 1, JACK = 11, QUEEN = 12, KING = 13, }; /* ハンドの種類 */ enum HAND { ROYAL_FLUSH, STRAIGHT_FLUSH, FOUR_OF_A_KIND, FULL_HOUSE, FLUSH, STRAIGHT, THREE_OF_A_KIND, TWO_PAIR, ONE_PAIR, HIGH_CARD, HAND_MAX, // ハンドの総数 }; /* トランプカード */ struct Card { unsigned char suit; // 絵柄(Spade/Diamond/Club/Heart) unsigned char rank; // 番号(A,2-10,J,Q,K) // ストリーム出力 friend std::ostream& operator<<( std::ostream& os, const Card& card ) { return( os << card.suit << "[" << card.rank << "]" ); } }; unsigned int HandCount[HAND_MAX]; // 各ハンドの組み合わせ総数 /* checkHand : カードの組み合わせからハンドを決める vector<Card>& hand : 対象のハンド */ void checkHand( vector<Card>& hand ) { vector<char> rank( hand.size() ); // ハンドが持つランク for ( unsigned int i = 0 ; i < rank.size() ; ++i ) rank[i] = hand[i].rank; sort( rank.begin(), rank.end() ); // スートが全て一致した場合 if ( ( hand[0].suit == hand[1].suit ) && ( hand[1].suit == hand[2].suit ) && ( hand[2].suit == hand[3].suit ) && ( hand[3].suit == hand[4].suit ) ) { // Royal Flush のチェック if ( rank[0] == ACE && rank[1] == 10 && rank[2] == JACK && rank[3] == QUEEN && rank[4] == KING ) ++( HandCount[ROYAL_FLUSH] ); // Straight Flush のチェック else if ( ( rank[4] - rank[3] == 1 ) && ( rank[3] - rank[2] == 1 ) && ( rank[2] - rank[1] == 1 ) && ( rank[1] - rank[0] == 1 ) ) ++( HandCount[STRAIGHT_FLUSH] ); // そうでなければ全て Flush else ++( HandCount[FLUSH] ); } else { // A,10,J,Q,K は Straight if ( ( rank[0] == ACE && rank[1] == 10 && rank[2] == JACK && rank[3] == QUEEN && rank[4] == KING ) ) ++( HandCount[STRAIGHT] ); // 連続した数値であれば Straight else if ( ( rank[4] - rank[3] == 1 ) && ( rank[3] - rank[2] == 1 ) && ( rank[2] - rank[1] == 1 ) && ( rank[1] - rank[0] == 1 ) ) ++( HandCount[STRAIGHT] ); // 中央の三枚がそろった場合 else if ( ( rank[1] == rank[2] ) && ( rank[2] == rank[3] ) ) { // 両端のいずれかも同じ数なら Four of a Kind if ( rank[0] == rank[1] || rank[3] == rank[4] ) ++( HandCount[FOUR_OF_A_KIND] ); // そうでなければ Three of a Kind else ++( HandCount[THREE_OF_A_KIND] ); } // 左端の三枚がそろった場合 else if ( ( rank[0] == rank[1] ) && ( rank[1] == rank[2] ) ) { // 右端の二枚がそろえば Full House if ( rank[3] == rank[4] ) ++( HandCount[FULL_HOUSE] ); // そうでなければ Three of a Kind else ++( HandCount[THREE_OF_A_KIND] ); } // 右端の三枚がそろった場合 else if ( ( rank[2] == rank[3] ) && ( rank[3] == rank[4] ) ) { // 左端の二枚がそろえば Full House if ( rank[0] == rank[1] ) ++( HandCount[FULL_HOUSE] ); // そうでなければ Three of a Kind else ++( HandCount[THREE_OF_A_KIND] ); } // 左端の二枚がそろった場合 else if ( rank[0] == rank[1] ) { // 他に二枚そろっていたら Two Pair if ( rank[2] == rank[3] || rank[3] == rank[4] ) ++( HandCount[TWO_PAIR] ); // そうでなければ One Pair else ++( HandCount[ONE_PAIR] ); } // 左から二枚目と三枚目がそろった場合 else if ( rank[1] == rank[2] ) { // 四枚目と五枚目がそろったら Two Pair if ( rank[3] == rank[4] ) ++( HandCount[TWO_PAIR] ); // そうでなければ One Pair else ++( HandCount[ONE_PAIR] ); } // 他に二枚そろっているときは One Pair else if ( rank[2] == rank[3] || rank[3] == rank[4] ) ++( HandCount[ONE_PAIR] ); else ++( HandCount[HIGH_CARD] ); // High Card (該当なし) } } /* PokerHands : ハンドの組み合わせを数える */ void PokerHands() { vector<Card> deck( KING * 4 ); // カードの山 vector<Card> hand( 5 ); // ハンド // deck の作成 for ( unsigned char c = ACE ; c <= KING ; ++c ) { deck[( c - 1 ) * 4].suit = SPADE; deck[( c - 1 ) * 4].rank = c; deck[( c - 1 ) * 4 + 1].suit = DIAMOND; deck[( c - 1 ) * 4 + 1].rank = c; deck[( c - 1 ) * 4 + 2].suit = CLUB; deck[( c - 1 ) * 4 + 2].rank = c; deck[( c - 1 ) * 4 + 3].suit = HEART; deck[( c - 1 ) * 4 + 3].rank = c; } // ハンドの総数を初期化 for ( unsigned int i = 0 ; i < sizeof( HandCount ) / sizeof( HandCount[0] ) ; ++i ) HandCount[i] = 0; createCombination( deck, 0, hand, 0, checkHand ); }
checkHand は非常に長いプログラムですが、処理している内容は各カードのランクとスートを見てハンドの判定を行っているだけです。最初に全スートが等しいかをチェックして、ここで場合分けを行っています。スートが全て等しければ、その組み合わせには同じランクのカードは重複していないことになるので、同一ランクを含むハンドは考慮しなくていいことになるためです。また、判定前にランクをソートしておきます。これによって、連番や同一ランクの比較が簡単にできるようになります。処理結果は HandCount に格納されるので、その内容を見ることで各ハンドの組み合わせ数を確認することができます。
組み合わせを数えるためのメイン・ルーチンが PokerHands になります。ここでは最初に 52枚のカードの山 (deck) を作成してから、createCombination を呼び出してカードの組み合わせを作成しては checkHand を呼び出す処理を再起的に繰り返しています。
B) 酔歩(Random Walk)
居酒屋から自宅までを酔っ払いが徒歩で帰るとします。道は二本あって、どちらの道にも途中に公園があるので、酔っ払いは必ず公園のベンチで休憩をします。すると、帰る方向が分からなくなり、進む方向がランダムに変わるとします。つまり、公園から居酒屋に戻ってしまう場合もあることになります。公園から自宅の方向へ進むことができれば、他に障害はないので、どちらの道から進んでも無事に自宅まで到着するとしたとき、酔っ払いが辿る道筋はどれだけあるでしょうか。
居酒屋を B、公園を P1, P2、自宅を H で表したとき、最短のコースは B → P1 → H または B → P2 → H になります。しかし、後戻りが起こるような場合、例えば、B → P1 → B → P2 → H や B → P1 → B → P1 → B → P1 → H などの組み合わせもあります。最悪、B → P1 → B を繰り返した挙句、そのままベンチで寝てしまうような場合もあるでしょう。理論的には、永久に戻ることができない道筋もあるので組み合わせも無限に考えられます。
進む回数を 5 回に限定して、全ての組み合わせを調べてみます。

組み合わせを調べる場合によく「樹形図(Tree Diagram)」が用いられます。組み合わせを習うのは中学生の頃からだと思いますが、その時すでに樹形図は登場していたと記憶しています。樹形図を使うことで、その組み合わせの特徴がよく見えるようになります。上の図を見ても、偶数回めは必ず自宅か居酒屋に到達し、奇数回目が公園にいることがまず理解できます(これは少し考えれば気付くことですが)。最大五回進むことで、自宅に戻ることができるのは 6 通り、戻れないパターンは 8 通りあることが分かります。
奇数回目の、公園にいるときの組み合わせは前より二倍に増えていますが、偶数回目は半数が自宅に到着するのでその後に続く道筋の数に変化はありません。従って、2N - 1 回(奇数回)進んだときにまだ公園にいる場合の道筋は 2N 通りあり、それまでに自宅に到着する場合は 2 + 4 + 8 + ... + 2N-1 = 2N - 2 通りになります。また、2N 回(偶数回)進んだときは全部で 2N+1 の道筋が残っていて、その中の半数が自宅になります。よって、まだ到着していない場合が 2N通りで、それまでに自宅に到着した場合は、奇数回での数に新たに 2N通りを加えればいいので ( 2N - 2 ) + 2N = 2N+1 - 2 通りになります。
下に示したように、十字路が追加されたもう少し複雑な道筋で同様なことを考えてみます。今回も、居酒屋から自宅へ帰る道は二本あり、どちらも途中に三叉路が二箇所あって(下図中の C1 〜 C4 )、一方は家へ向かい、もう一方は全て中央で交わっています( 下図中の C5 )。酔っ払いは、例によって分岐点で方向が分からなくなり、ランダムに進むものとします。道筋としては、例えば B → C1 → C2 → H や B → C4 → C5 → C3 → H などがありますが、距離に関しては考慮していないので、前者より後者の方が距離が短い可能性もあります。ここでは距離は考慮せず、通過点の組み合わせをもう一度検討してみましょう。
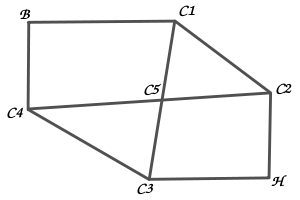
自宅に戻るまでに少なくとも二つの通過点を通る必要があるので、三回移動した場合の道筋を以下に示します。
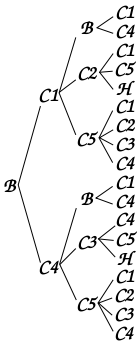
三回の移動だけで 18 通りの道筋が得られ、自宅に戻れたのはその中の 2 通りのみです。その後も続けると、考えられる道筋の数は急激に増えていきます。N 回移動したときの現在位置が通過点 P ( = { B, H, C1〜C5 } ) である道筋の個数を CNT( P, N ) として、それぞれの漸化式を調べてみます。例えば、B は C1 と C4 から移動することができるので、
CNT( B, 0 ) = 1
CNT( B, N ) = CNT( C1, N - 1 ) + CNT( C4, N - 1 )
になります。他の通過点も同様に考えて、
| CNT( B, N ) | = | CNT( C1, N - 1 ) | + | CNT( C4, N - 1 ) | ||||||||
| CNT( C1, N ) | = | CNT( B, N - 1 ) | + | CNT( C2, N - 1 ) | + | CNT( C5, N - 1 ) | ||||||
| CNT( C2, N ) | = | CNT( C1, N - 1 ) | + | CNT( C5, N - 1 ) | ||||||||
| CNT( C3, N ) | = | CNT( C4, N - 1 ) | + | CNT( C5, N - 1 ) | ||||||||
| CNT( C4, N ) | = | CNT( B, N - 1 ) | + | CNT( C3, N - 1 ) | + | CNT( C5, N - 1 ) | ||||||
| CNT( C5, N ) | = | CNT( C1, N - 1 ) | + | CNT( C2, N - 1 ) | + | CNT( C3, N - 1 ) | + | CNT( C4, N - 1 ) | ||||
| CNT( H, N ) | = | CNT( C2, N - 1 ) | + | CNT( C3, N - 1 ) |
よって、各通過点は次のように増加します。下表から、6 回の移動で道筋の組み合わせは 398 通りになり、その中で自宅に到達できる組み合わせは 36 通りのみであることが分かります。
| N | B | C1 | C2 | C3 | C4 | C5 | H | 合計 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 2 |
| 2 | 2 | 0 | 1 | 1 | 0 | 2 | 0 | 6 |
| 3 | 0 | 5 | 2 | 2 | 5 | 2 | 2 | 18 |
| 4 | 10 | 4 | 7 | 7 | 4 | 14 | 4 | 50 |
| 5 | 8 | 31 | 18 | 18 | 31 | 22 | 14 | 142 |
| 6 | 62 | 48 | 53 | 53 | 48 | 98 | 36 | 398 |
酔歩の場合も、ある程度の回数までは、実際の組み合わせをコンピュータで出力することが可能です。道筋を表現するデータ構造としては、「有向グラフ(Directed Graph ; Digraph)」を利用することができます。「グラフ(Graph)」とは「頂点(Vertex)」と「辺(Edge)」からなる集合のことで、例えば上図のような道筋において、{ B, H, C1〜C5 } が頂点、各頂点を結ぶ道が辺と考えることができます。有向グラフは辺が一方通行となるようなグラフのことで、自宅にあたる H から C2, C3 へ戻ることはないので、H - C2 間と H - C3 間のみ一方通行であることになります。先ほどの道筋を有向グラフで表すと、次のようになります。
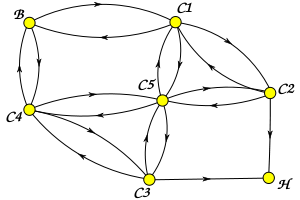
有向グラフを表現するクラスのサンプル・プログラムを以下に示します。
/* 有向グラフ */ class DiGraph { public: typedef unsigned char VertexType; // 頂点の要素の型 private: typedef pair<VertexType, VertexType> EdgeType; // 辺の型 typedef multimap<VertexType, VertexType> EdgeMapType; // 辺集合の型 typedef EdgeMapType::iterator ItEdge; // EdgeMapTypeの反復子 typedef EdgeMapType::const_iterator CitEdge; // EdgeMapTypeの定数反復子 VertexType _vertexCount; // 頂点の数 EdgeMapType _edge; // 辺集合 public: // コンストラクタ DiGraph() : _vertexCount( 0 ) {} // 頂点の追加 void addVertex( VertexType vCnt = 1 ); // 辺の追加 bool addEdge( VertexType v1, VertexType v2, bool isDirected = false ); // 指定した頂点とつながっている頂点の集合を取得する bool nextVertex( VertexType curVertex, vector<VertexType>& vertex ) const; }; /* DiGraph::addVertex : 頂点の追加 VertexType vCnt : 追加する頂点の数 */ void DiGraph::addVertex( VertexType vCnt ) { if ( _vertexCount > UCHAR_MAX - vCnt ) _vertexCount = UCHAR_MAX; else _vertexCount += vCnt; } /* DiGraph::addEdge : 辺の追加 isDirected = false ならば、"始点→終点" だけでなく "終点→始点" も追加する VertexType v1 : 始点 VertexType v2 : 終点 bool isDirected : 有向か */ bool DiGraph::addEdge( VertexType v1, VertexType v2, bool isDirected ) { if ( v1 >= _vertexCount || v2 >= _vertexCount ) return( false ); _edge.insert( EdgeType( v1, v2 ) ); if ( ! isDirected ) _edge.insert( EdgeType( v2, v1 ) ); return( true ); } /* DiGraph::nextVertex : 指定した頂点とつながっている頂点の集合を取得する VertexType curVertex : 指定した頂点 vector<VertexType>& vertex : curVertexとつながった頂点の集合 */ bool DiGraph::nextVertex( VertexType curVertex, vector<VertexType>& vertex ) const { vertex.clear(); if ( curVertex >= _vertexCount ) return( false ); pair<CitEdge, CitEdge> range = _edge.equal_range( curVertex ); for ( CitEdge p = range.first ; p != range.second ; ++p ) vertex.push_back( p->second ); return( vertex.size() != 0 ); }
サンプル版のクラスはかなり簡略化されたもので、通常であれば各頂点に何らかの要素を代入することができますが、ここでは各頂点に連番が付けられているだけです。連番は unsigned char 型なので通常は 0 から 255 番までとなり、従って頂点の最大数は 256 になります。辺集合 _edge には Standard Template Library(STL) にある連想配列のひとつ multimap を利用しています。もう一つの連想配列 map ではキーの重複を認めていないのに対し、multimap はキーが重複しても追加することが可能です。_edge には、辺の始点の番号をキー、終点の番号を値として登録していますが、始点に対する辺の数は複数になるため、multimap を使う必要があるわけです。
頂点は番号で管理すればよいので、頂点自身を要素として持つ必要はなく、頂点の数だけを _vertexCount に保持しています。頂点を追加するときは addVertex を使い、ここでは追加する頂点の個数を _vertexCount に加算するだけの処理を行っています。addEdge が辺を追加するためのメンバ関数です。始点と終点の番号の他に、有向を考慮するかを isDirected で指定することができるようにして、これが true の場合は、始点をキー、終点を値としたペアだけを _edge に登録し、false ならば 終点をキー、始点を値とした辺もいっしょに登録しておきます。ある頂点からどの頂点へ移動することができるかは、メンバ関数 nextVertex で取得することが可能で、ここで multimap 特有の機能である範囲検索を行っています。
pair<CitEdge, CitEdge> range = _edge.equal_range( curVertex );
for ( CitEdge p = range.first ; p != range.second ; ++p ) {
:
}
equal_range は、指定したキーの範囲を検索して返す multimap 専用のメンバ関数です(一応 map でも利用できるようになっていますが利用する意味はあまりありません)。返り値は反復子のペアで返され、一番目の要素が範囲の最初の位置を、二番目は要素の最後の要素の次の位置をそれぞれ保持しています。よって、この二つの反復子を使ったループ処理で、同じキーを持った要素に対する処理ができるようになります。なお、map と multimap は要素がキーでソートされているので、最初と最後が決まればその中の要素は全て同じキーであることが保証されます。
今回の例では自宅を表す頂点だけが有向となるので、それ以外は始点と終点を入れ替えた辺も登録する必要があります。しかし、これは addEdge の引数を利用することで一度に行うことができます。向きだけの違いで二重に登録するのは無駄なような気もしますが、例えば二頂点間の辺が、有向であるかどうかを別として実際に二本に分かれている場合や、二本に分かれていてその中の一本だけ一方通行になるなど、複雑なグラフに対応するときは二重に登録した方が実装もシンプルになります。
次に、道筋の組み合わせを保持しておくデータを用意します。データの型として、以前にも紹介した「トライ木(Trie Tree)」を利用します。
/* トライ木の節点 */ template<class T> struct TrieNode { T element; // 要素 unsigned int brosIdx; // 兄弟の節点の位置 unsigned int childIdx; // 子の節点の位置 unsigned int level; // 節点の高さ // コンストラクタ TrieNode( T t, unsigned int l ) : element( t ), brosIdx( 0 ), childIdx( 0 ), level( l ) {} }; /* addChild : ある頂点から移動可能な頂点をトライ木に追加する const DiGraph& graph : 道筋を持った有向グラフ vector< TrieNode<DiGraph::VertexType> >& trie : トライ木 unsigned int curIdx : 対象の頂点を持った節点 unsigned int maxLevel : 移動回数の最大値 */ void addChild( const DiGraph& graph, vector< TrieNode<DiGraph::VertexType> >& trie, unsigned int curIdx, unsigned int maxLevel ) { if ( trie[curIdx].level >= maxLevel ) return; // 移動可能な節点を取得する vector<DiGraph::VertexType> nextVertex; graph.nextVertex( trie[curIdx].element, nextVertex ); unsigned int brosIdx = 0; // 兄弟の節点の位置 for ( unsigned int i = 0 ; i < nextVertex.size() ; ++i ) { trie.push_back( TrieNode<DiGraph::VertexType>( nextVertex[i], trie[curIdx].level + 1 ) ); if ( i == 0 ) { trie[curIdx].childIdx = trie.size() - 1; // 最初の節点を子とする } else { trie[brosIdx].brosIdx = trie.size() - 1; // 他は兄弟の接点としてつなげる } brosIdx = trie.size() - 1; addChild( graph, trie, brosIdx, maxLevel ); } }
トライ木の節点 TrieNode には、下位レベルにある子の節点だけでなく、同レベルにある兄弟の節点へのリンクも保持します。図で表すと次のようになり、下側にある節点が子(下位レベル)、右側に並ぶ節点が兄弟(同レベル)を表しています。
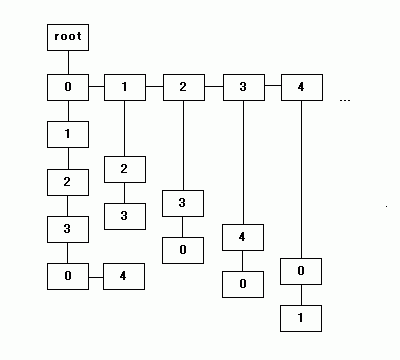
トライ木は、TrieNode を要素とする vector を利用しています。関数 addChild は、指定された頂点から移動可能な有向グラフの頂点を取得して、トライ木の新たな接点として追加する処理を行います。ここでは、新たな接点のうち最初のものを子としておいて、あとは前に追加した接点に兄弟としてつなげるようにしています。この処理が、節点にある level が移動回数の最大値 maxLevel 以上になるまで行われます。
節点どうしのリンクにはポインタやリファレンスではなく添字(インデックス)を使っています。これは、vector に対して要素を追加すると要素の再配置などが発生する場合があるので、再配置などが発生しても正しくリンクされるようにするためです。vector が持つメンバ関数 reserve を使うと、追加やリサイズによって拡張される領域をあらかじめ確保しておくことができます。これを利用すると、ポインタやリファレンスでの管理も可能になりますが、最大となるサイズをあらかじめ決めておく必要があります。
有向グラフにて指定回数だけ移動したときの組み合わせを表示して、到達した場所を計算するサンプル・プログラムを以下に示します。
/* printTrie : トライ木の内容を出力する vector< TrieNode<DiGraph::VertexType> >& trie : トライ木 unsigned int curIdx : 出力開始位置 */ void printTrie( vector< TrieNode<DiGraph::VertexType> >& trie, unsigned int curIdx ) { printf( "-%d", trie[curIdx].element ); if ( trie[curIdx].childIdx > 0 ) printTrie( trie, trie[curIdx].childIdx ); else printf( "\n" ); if ( trie[curIdx].brosIdx > 0 ) { for ( unsigned int i = 0 ; i < trie[curIdx].level ; ++i ) printf( " " ); printTrie( trie, trie[curIdx].brosIdx ); } } /* graphTest : 道筋の組み合わせを求める DiGraph& graph : 道筋(有向フラグ) unsigned int maxLevel : 移動回数の最大値 */ void graphTest( DiGraph& graph, unsigned int maxLevel ) { vector< TrieNode<DiGraph::VertexType> > trie; trie.push_back( TrieNode<DiGraph::VertexType>( 0, 0 ) ); addChild( graph, trie, 0, maxLevel ); printTrie( trie, 0 ); unsigned int count[] = { 0, 0, 0, 0, 0, 0, 0, }; unsigned int totalCount = 0; for ( unsigned int i = 0 ; i < trie.size() ; ++i ) if ( trie[i].level == maxLevel ) count[trie[i].element] += 1; for ( unsigned int i = 0 ; i < sizeof( count ) / sizeof( count[0] ) ; ++i ) { cout << i << " = " << count[i] << endl; totalCount += count[i]; } cout << "Total = " << totalCount << endl; }
先ほどの例について求める場合、次のように処理させます。
DiGraph graph; graph.addVertex( 7 ); /* 0 ... B 1〜5 ... C1〜C5 6 ... H */ graph.addEdge( 0, 1 ); graph.addEdge( 0, 4 ); graph.addEdge( 1, 2 ); graph.addEdge( 1, 5 ); graph.addEdge( 4, 3 ); graph.addEdge( 4, 5 ); graph.addEdge( 2, 5 ); graph.addEdge( 2, 6, true ); // C2 → H (一方通行) graph.addEdge( 3, 5 ); graph.addEdge( 3, 6, true ); // C3 → H (一方通行) graphTest( graph, 3 );
今回は、組み合わせや順列の話題を中心に紹介してみました。実際にはもっと奥深い話題もあるようですが、それについては次の機会にしたいと思います(自分自身、まだ消化しきれていない部分も多々あるので)。
「組み合わせ」の考えかたから nCr = n! / r!( n - r )! が整数となることは明らかですが、純粋にこれが整数であることを証明することは意外と難しい作業になります。
まずは、簡単な証明方法として、組み合わせに関する公式 n+1Cr = nCr-1 + nCr を利用します。n = 1 のとき、
なので、0 ≦ r ≦ 1 となる全ての r に対して 1Cr が整数になります。1 から n までの全ての nCr ( 0 ≦ r ≦ n )が整数になるとしたとき、
n+1C0 = 1
n+1Cr = nCr-1 + nCr ( 1 ≦ r ≦ n )
n+1Cn+1 = 1
なので n+1Cr ( 0 ≦ r ≦ n + 1 ) も整数となります。よって、帰納法により nCr が整数となることが証明されました。
n! / r!( n - r )! が整数であることを直接証明するには次のようにします。
整数 k の素因数分解が p1q1p2q2...prqr であったとします。このとき、qs ( 1 ≦ s ≦ r ) は psqs が k を割り切る最大の整数となります。素数 p に対するこの値を IDXpk と表すと、IDXpk! は 1 から k までの中で p で割り切れる数について IDXpm ( 1 ≦ m ≦ k ) を求め、その和を計算することで得られますが、これは、1 から k までの中で IDXpm = q となる整数の個数を求め、その個数に q を乗算したものの和と同じ意味になります。すなわち
| IDXpk! | = | Σm{1→k}( IDXpm ) |
| = | Σq{1→∞}( { IDXpm = q ( 1 ≦ m ≦ k ) となる整数の個数 } x q ) |
IDX28! を例にとると、
| IDX21 | = | 0 | , | IDX25 | = | 0 |
| IDX22 | = | 1 | , | IDX26 | = | 1 |
| IDX23 | = | 0 | , | IDX27 | = | 0 |
| IDX24 | = | 2 | , | IDX28 | = | 3 |
なのでその和は 7 となりますが、IDX2m = 1 となる個数が二個、IDX2m = 2, 3 となる個数がそれぞれ一個なので、1 x 2 + 2 x 1 + 3 x 1 = 7 と計算しても求めることができます。また、実際 8! = 40320 = 27・32・5・7 であり IDX28! = 7 になります。先ほどの和の計算で ∞ までの和としていますが、q の値は有限となるので実際には途中で計算は完了します。ところで、上記の例において 1 から 8 までの 2 の倍数の個数は 4 つになり、この中には 4 と 8 の倍数も含まれています。さらに、4 の倍数の個数は二つで、この中には 8 の倍数が含まれています。このように、各べき数の倍数を数えていくと、あるべき乗 pq までの倍数を数えた時に、pq に対する倍数はちょうど q 回(つまり q - 1 回余分に)数えたことになり、よって倍数の個数を数えることでも同じ値を得ることができてしまいます。k! より小さい pq の倍数の個数は、ガウス記号 [X] ( X を超えない最大の整数) を使って [ k! / pq ] で計算できるので、結局 IDXpk! は
で計算することができます。IDXpk ≧ IDXpl ならば、l は k を割り切ることができるので、n! と r!( n - r )! に対し、任意の素数 p について IDXpn! ≧ IDXpr! + IDXp( n - r )! を示すことができれば r!( n - r )! が n! を割り切ることが示されます。ここで、次の不等式が成り立つことを利用します。
| [ x + y ] | = | [ [x] + ( x - [x] ) + [y] + ( y - [y] ) ] |
| = | [x] + [y] + [ ( x - [x] ) + ( y - [y] ) ] | |
| ≧ | [x] + [y] |
よって、
[ ( x + y ) / pq ] ≧ [ x / pq ] + [ y / pq ] より
IDXp( k + l )! ≧ IDXpk! + IDXpl!
従って、k = r, l = n - r と置き換えると k + l = r + ( n - r ) = n となり、IDXpn! ≧ IDXpr! + IDXp( n - r )! が示されました。
指数 n のときの展開式を、y が k 次となる項の係数を an(k) で表し fn( x, y ) = Σk{0→n}( an(k)・xn-kyk ) として、これに x + y を掛けることにより ( x + y )n+1 の展開式 fn+1( x, y ) を求めると、
| fn+1( x, y ) | = | Σk{0→n}( an(k)・xn-kyk ) ・ ( x + y ) |
| = | Σk{0→n}( an(k)・xn-k+1yk ) + Σk{0→n}( an(k)・xn-kyk+1 ) | |
| = | { an(0)・xn+1 + Σk{1→n}( an(k)・xn-k+1yk ) } + { Σk{0→n-1}( an(k)・xn-kyk+1 ) + an(n)・yn+1 } | |
| = | an(0)・xn+1 + Σk{1→n}( an(k)・xn-k+1yk ) + Σk{1→n}( an(k-1)・xn-k+1yk ) + an(n)・yn+1 | |
| = | an(0)・xn+1 + Σk{1→n}( ( an(k-1) + an(k) )xn-k+1yk ) + an(n)・yn+1 |
n = 1 のとき、a1(0) = a1(1) = 1 なので、全ての指数 n について an(0) = an(1) = 1 となります。それ以外は上記結果より an+1(k) = an(k-1) + an(k) (1 ≦ k ≦ n) が成り立ち、二項定理が証明されました。
f(x) = ( 1 + x )a ( |x| < 1 )とすると、f(x) の n 階導関数は
なので、f(x) のマクローリン展開(数値演算法 (5) 有理数と無理数の演算 の 5) テイラー展開を参照) を行うと
| f(x) | = | f(0)(0) + f(1)(0)・x + (1/2!)f(2)(0)・x2 + ... + (1/n!)f(n)(0)・xn + Rn+1 |
| = | 1 + ax + { a( a - 1 ) / 2! }x2 + ... + { a( a - 1 )( a - 2 )...( a - n + 1 ) / n! }xn + Rn+1 | |
| = | C( a, 0 ) + C( a, 1 )x + C( a, 2 )x2 + ... + C( a, n )xn + Rn+1 | |
| = | Σk{0→n}( C( a, k )xk ) + Rn+1 |
但し、Rn+1 は剰余項で、下式で表されます。
| Rn+1 | = | (1/n!)∫{0→x}( x - t )nf(n+1)(t) dt |
| = | (1/n!)∫{0→x}( x - t )na( a - 1 )( a - 2 )...( a - n )( 1 + t )a-n-1 dt | |
| = | ( a - n )・C( a, n )∫{0→x}( x - t )n( 1 + t )a-n-1 dt |
lim{n→∞}( Rn+1 ) = 0 が成り立てば、f(x) のマクローリン展開は無限級数の形に表すことができるので、一般の二項定理が証明されたことになります。
0 < t < x < 1 のとき、0 < ( x - t ) / ( 1 + t ) < x / ( 1 + t ) < x、また 0 > t > x > -1 ならば 0 > ( x - t ) / ( 1 + t ) > x / ( 1 + t ) > x、よってどちらの場合も | ( x - t ) / ( 1 + t ) | < |x| が成立します。従って、
| ∫{0→x} | ( x - t )n( 1 + t )a-n-1 | dt | = | ∫{0→x} { | ( x - t ) / ( 1 + t ) | }n ( 1 + t )a-1 dt |
| ≦ | ∫{0→x} | x |n ( 1 + t )a-1 dt | |
| = | | x |n∫{0→x}( 1 + t )a-1 dt |
従って、
但し、K = ∫{0→x}( 1 + t )a-1 dt としています。| ( a - n )・C( a, n ) | の部分に着目して、
| | ( a - n )・C( a, n ) | | = | | a( a - 1 )( a - 2 ) ... ( a - n + 1 )( a - n ) | / n! |
| = | | a | | a - 1 | | ( a - 2 ) / 2 | ... | { a - ( n - 1 ) } / ( n - 1 ) | | ( a - n ) / n | | |
| = | | a | | a - 1 | | a / 2 - 1 | ... | a / ( n - 1 ) - 1 | | a / n - 1 | | |
| = | | a | | 1 - a | | 1 - a / 2 | ... | 1 - a / ( n - 1 ) | | 1 - a / n | | |
| ≦ | | a | ( 1 + | a | )( 1 + | a | / 2 ) ... ( 1 + | a | / ( n - 1 ) )( 1 + | a | / n ) |
( 1 + | a | / k ) は k の値が大きくなるほど小さくなります。ここで、|x| < r < 1 となるような実数 r をとり、それに対して m を充分大きくとって ( 1 + | a | / m ) < 1 / r となるようにすると、
| | a | ( 1 + | a | )( 1 + | a | / 2 ) ... ( 1 + | a | / ( n - 1 ) )( 1 + | a | / n ) | ≦ | | a | ( 1 + | a | )( 1 + | a | / 2 ) ... ( 1 + | a | / m )( 1 / r )n - m |
| = | | a | ( 1 + | a | )( 1 + | a | / 2 ) ... ( 1 + | a | / m ) rm ( 1 / r )n | |
| = | Am ( 1 / r )n |
但し、Am = | a | ( 1 + | a | )( 1 + | a | / 2 ) ... ( 1 + | a | / m ) rm としています。よって、
| | Rn+1 | | ≦ | K・Am・| x |n ( 1 / r )n |
| = | K・Am・( | x | / r )n |
|x| < r なので右辺は n → ∞ のときゼロに収束し、lim{n→∞}( Rn+1 ) = 0 が成り立つことが証明されました。
f(t) = et / tx としたとき、f(t) → ∞ ( t → +∞ ) を示すことができれば tx / et = 1 / f(t) → 0 ( t → +∞ ) であることになります。与式の両辺の対数をとると
ln(t) → ∞ ( t → +∞ ) なので、t / ln(t) → ∞ ( t → +∞ ) ならば f(t) → ∞ ( t → +∞ ) になります。
et の マクローリン展開は
なので、et / t を多項式で表すと
(1/2)t → ∞ ( t → +∞ ) で、それより高次の項も正の値を取るので、et / t → ∞ ( t → +∞ ) になります。u = et とすれば、t → +∞ のとき u → +∞ なので、
よって、t / ln(t) → ∞ ( t → +∞ ) となり、f(t) → ∞ ( t → +∞ ) を示すことができました。従って、
になります。
lim{t→α}( f(t) ) = lim{t→α}( g(t) ) = 0 のとき、lim{t→α}( f(t) / g(t) ) を 0 / 0 の形の「不定形の極限(Limit of Indeterminate Forms)」といいます。lim{t→α}( |f(t)| ) = lim{t→α}( |g(t)| ) = ∞ ならば、∞ / ∞ の形の不定形の極限になります。この不定形の極限については、以下に示す「ロピタルの定理(L'Hopital's Rule)」と呼ばれる強力な定理があります。
高次導関数が存在する限り、lim{t→α}( f(n)(t) / g(n)(t) ) が存在すれば lim{t→α}( f(t) / g(t) ) の値が得られることになります。これを使うと、f(t) = tx、g(t) = et としたとき、n > x において f(n)(t) = 0、g(n)(t) = et なので、t → ∞ のとき極限値はゼロになることが簡単に示されます。
ガンマ関数は半開区間 [ 0, ∞ ) 上での積分であり、さらに x < 1 において、tx-1 e-t → ∞ ( t → +0 ) なので、
と極限の形で考える必要があります。このような積分は「広義積分」と呼ばれ、上記を通常の書き方 ∫{0→∞} tx-1 e-t dt と定義しているので、見た目は通常の(閉区間での有界関数の)積分と変わりません。このようなときは、
と、0 < t ≦ 1 と 1 < t ≦ ∞ のそれぞれの区間に分けて収束性を調べます。まず、0 < t ≦ 1 の範囲では
となるので、
t ≧ 1 の範囲では、et のマクローリン展開から
より
x - n - 1 < 0 になるように充分大きな n を選ぶことで、上式の最右辺は Ct-m ( C > 0, m > 1 ) の形に表すことができるので、
よって、ガンマ関数が収束することが証明されました。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |