
今回は、ある事象が発生した日付や時刻のデータを扱う場合を考えます。医学・薬学の分野では、投薬や施術による生存時間の差異を調べることはよく行われます。また、工学において、装置などが故障するまでの時間は非常に重要なデータとなります。このようなデータは一般的に「生存時間 (Survival Time)」と呼ばれます。この章では、生存時間を解析するための一般的な手法について紹介します。
確率変数 T は生存時間を表すとし、その確率密度関数を f(t) とします。t は当然非負値となります。この時、多くても生存時間が t を超えない ( つまり時間 t より前に死亡する ) 確率 P( T < t ) は、累積確率分布関数により
で表されます。逆に、時間 t 以上生存する確率を S(t) とすると、これは
となります。この S(t) を「生存関数 ( Survivor Function )」といいます。
時間 t ≤ T < t + δt の間に死亡する確率 P( t ≤ T < t + δt ) は
ですが、t まで生存していたときの条件付き確率 P( t ≤ T < t + δt | T ≥ t ) は
| P( t ≤ T < t + δt | T ≥ t ) | = | P( t ≤ T < t + δt ∩ T ≥ t ) / P( T ≥ t ) |
| = | P( t ≤ T < t + δt ) / S(t) | |
| = | [ F( t + δt ) - F(t) ] / S(t) |
となります。T = t から t + δt の間の F(T) の増加量は
であり、δt → 0 での極限値
は確率密度関数 f(t) そのものなので、
| h(t) | ≡ | lim{δt→0}( P( t ≤ T < t + δt | T ≥ t ) / δt ) |
| = | lim{δt→0}( { [ F( t + δt ) - F(t) ] / δt }・[ 1 / S(t) ] ) | |
| = | f(t) / S(t) |
という関係式が得られます。この関数 h(t) を「ハザード関数 (Hazard Function)」といいます。S(t) = 1 - F(t) より
なので ( ln は自然対数 )、
となり、
| H(t) | ≡ | ∫{0→t} h(T) dT |
| = | -ln S(t) |
または
と表せます。この H(t) は「累積ハザード関数 (Cumulative Hazard Function)」または「積分ハザード関数 (Integrated Hazard Function)」と呼ばれています。
確率密度関数 f(t) をあらかじめ特定のものに仮定して解析を行うパラメトリックなモデルを利用する場合、最も単純な確率密度関数は「指数分布」です。
「指数分布 (Exponential Distribution)」は「確率・統計 (3) 離散確率分布」の中の「2) ポアソン分布(Poisson Distribution)」でポアソン分布より導かれる連続確率分布として紹介しています。その平均と分散はそれぞれ 1 / θ、1 / θ2 となります。生存関数 S(t) は
であり、ハザード関数 h(t) は
累積ハザード関数 H(t) は
となります。ハザード関数が定数 θ となるということは、死亡率の増加量が時間に依存しない定数であることを意味します。例えば、装置の故障率は経年劣化によって時間が経過するごとに増大することが見込まれ、そのような場合は指数分布はモデルとして適さないことになります。
指数分布の中央値は、
| F(t) | ≡ | ∫{0→t} f(T) dT |
| = | 1 - e-θt = 1 / 2 |
より
となります。ln 2 ≅ 0.693 なので、平均が 1 / θ であることと比較すると、中央値はその 7 割程度となっています。指数分布は値の大きい側に裾を引いたような歪んだ形状をしているので、平均値は裾の部分の影響を受けてピークよりも上側にシフトします。そのため、一般的には平均値よりも中央値の方が代表値としては望ましいとされます。この中央値は「中央生存時間 (Median Survival Time)」と呼ばれます。指数分布に限らず、生存時間解析で利用される確率分布は一般的に上側に裾を引くものが多いため、平均値よりも中央値が利用される傾向があります。
もう一つの代表的な確率密度関数として「ワイブル分布 (Weibull Distribution)」があります。この確率分布は「確率・統計 (20) 順序ロジスティック回帰」の中の「補足 1) 極値分布」でも紹介されているように「極値分布 (Generalized Extreme Value Distribution)」の一種です。累積確率密度は
であり、確率密度関数は
| f( x ; μ, θ, λ ) | = | dF / dx |
| = | exp( -[ -( x - μ ) / θ ]λ )・{ -λ[ -( x - μ ) / θ ]λ-1 }・( -1 / θ ) | |
| = | { λ[ -( x - μ ) ]λ-1 / θλ }exp( -[ -( x - μ ) / θ ]λ ) |
と表すことができます。ここで t = -( x - μ ) とすると、x ≤ μ より t ≥ 0 であり、| dt / dx | = 1 なので
と表すことができます。この式がワイブル分布として一般的に用いられる形です。また、φ = θ-λ として
とも表せます。λ は「形状パラメータ (Shape Parameter)」、θ は「尺度パラメータ (Scale Parameter)」と呼ばれます。λ = 1 ならば、ワイブル分布は指数分布と一致しますが、φ = 1 / θ よりハザード関数は θ の逆数となります。
累積確率密度を再計算すると
| F( t ; φ, λ ) | = | ∫{0→t} λφTλ-1exp( -φTλ ) dT |
| = | [ exp( -φTλ ) ]{t→0} | |
| = | 1 - exp( -φtλ ) |
となるので、生存関数 S( t ; φ, λ ) は
ハザード関数 h( t ; φ, λ ) は
累積ハザード関数 H( t ; φ, λ ) は
という結果になります。
期待値 E[t] は
| E[t] | = | ∫{0→∞} t・λφtλ-1exp( -φtλ ) dt |
| = | ∫{0→∞} λφtλexp( -φtλ ) dt |
より u = φtλ とすると、du = λφtλ-1dt、t → 0 のとき u → 0、t → ∞ のとき u → ∞ なので、
| E[t] | = | ∫{0→∞} t・exp( -φtλ )・λφtλ-1dt |
| = | ∫{0→∞} ( u / φ )1/λe-u du | |
| = | φ-1/λΓ( 1 + 1 / λ ) | |
| = | θΓ( 1 + 1 / λ ) |
となります。但し、Γ(x) = ∫{0→∞} tx-1e-t dt は「ガンマ関数」です。t2 の期待値 E[t2] も同様な求め方により
| E[t2] | = | ∫{0→∞} t2・exp( -φtλ )・λφtλ-1dt |
| = | ∫{0→∞} ( u / φ )2/λe-u du | |
| = | φ-2/λΓ( 1 + 2 / λ ) | |
| = | θ2Γ( 1 + 2 / λ ) |
となるので、分散 V[t] は
| V[t] | = | E[t2] - E[t]2 |
| = | φ-2/λ[ Γ( 1 + 2 / λ ) - Γ( 1 + 1 / λ )2 ] | |
| = | θ2[ Γ( 1 + 2 / λ ) - Γ( 1 + 1 / λ )2 ] |
という結果が得られます。「中央生存時間」は
のときなので、
となります。
生存時間を実際に計測する場合、正確な生存時間が得られないような場合が多く発生します。例えば、ある装置やその部品が故障するまでの時間を調べる時、装置や部品が稼働を開始した日時がわからなければ正確な時間はわかりません。また、ある疾患に対して死亡するまでの時間を調べる場合は、その調査が完了するまで生存し続けたときには生存時間は得られないことになります。このような場合、データは打ち切られた ( Censored ) といいます。装置・部品の稼働時間の例では開始以前の状態がわからないので「左側打ち切り (Left Censored)」、疾患に対する生存時間の例は終了後の状態がわからないので「右側打ち切り (Right Censored)」と呼ばれます。生存時間の解析では、この打ち切りデータについても考慮する必要があります。
標本数 n のデータについて、i 番目の標本の生存時間を ti、打ち切り指標を δi とします。但し、δi は非打ち切りの場合を 1、そうでない(打ち切りの)場合は 0 とします。このとき、標本 i が非打ち切りデータであるなら、その尤度は確率密度関数と等しく f( ti ) となります。一方、打ち切りデータでは生存時間が少なくとも ti であることだけがわかっているので、その確率は
になります。従って、全尤度 L は
であり、対数尤度関数 l は
| l | = | Σi{1→n}( δiln( f( ti ) ) + ( 1 - δi )ln( S( ti ) ) ) |
| = | Σi{1→n}( δiln( f( ti ) / S( ti ) ) + ln( S( ti ) ) ) | |
| = | Σi{1→n}( δiln( h( ti ) ) + ln( S( ti ) ) ) |
になります。
確率密度関数 f(t) として指数分布を適用した場合、対数尤度関数 l( θ ; t ) は
| l( θ ; t ) | = | Σi{1→n}( δiln θ + ln( e-θti ) ) |
| = | ln θΣi{1→n}( δi ) - θΣi{1→n}( ti ) |
となります。非打ち切りデータの個数が r ( ≤ n ) ならば Σi{1→n}( δi ) = r なので、上式は
であり、これは指数分布を適用した最小モデルを表しています。最小モデルのスコア統計量 U は対数尤度関数 l の導関数 dl / dθ と等しく、U = 0 となるときの θ が最尤推定量となることから、
U = dl / dθ = r / θ - Σi{1→n}( ti ) = 0 より
1 / θ = Σi{1→n}( ti ) / r
という結果が得られます。打ち切りデータがない場合は r = n なので右辺は生存時間の標本平均そのものです (*2-1)。
飽和モデルに対しては
| l( θ ; t ) | = | Σi{1→k}( Σj{1→ni}( δijln θi + ln( e-θitij ) ) ) |
| = | Σi{1→k}( ln θiΣj{1→ni}( δij ) - θiΣj{1→ni}( tij ) ) |
が対数尤度の式になります。ここで j は独立変数の等しいデータの中の番号を表し、そのようなデータが ni 個存在することを意味します。したがって、i は独立変数が相異なるデータの番号を表し、その個数は k 個になります。θi で偏微分すると
となるので、∂l / ∂θi = 0 のとき
となります。但し、全てが打ち切りデータだったときは Σj{1→ni}( δij ) = 0 なので、θi = 0 としてその項は無視するものとします。
ワイブル分布なら、対数尤度関数 l( θ, λ ; t ) は
| l( θ, λ ; t ) | = | Σi{1→n}( δiln( λθ-λtiλ-1 ) + ln( exp( -θ-λtiλ ) ) ) |
| = | Σi{1→n}( δi[ ln λ - λln θ + ( λ - 1 )ln ti ] ) - θ-λΣi{1→n}( tiλ ) |
となるので、
| ∂l / ∂θ | = | Σi{1→n}( -δiλ / θ ) + λθ-λ-1Σi{1→n}( tiλ ) |
| ∂l / ∂λ | = | Σi{1→n}( δi[ 1 / λ - ln θ + ln ti ] ) - Σi{1→n}( ( ti / θ )λln ( ti / θ ) ) |
の二式がゼロになるときの θ, λ が最尤推定量となります。∂l / ∂θ = 0 のとき、θ ≠ 0、λ ≠ 0 ならば、θ / λ を掛けることで
より
となります。但し r は非打ち切りデータの個数です。これを ∂l / ∂λ = 0 に代入すると
| r( 1 / λ - ln θ ) + Σi{1→n}( δiln ti ) - rΣi{1→n}( tiλln ( ti / θ ) ) / Σi{1→n}( tiλ ) | |
| = | r( 1 / λ - ln θ ) + Σi{1→n}( δiln ti ) - rΣi{1→n}( tiλln ti ) / Σi{1→n}( tiλ ) + rln θ |
| = | r / λ + Σi{1→n}( δiln ti ) - rΣi{1→n}( tiλln ti ) / Σi{1→n}( tiλ ) = 0 |
となって、θ を打ち消すことができます。この式を使って λ を求め、θ-λ = r / Σi{1→n}( tiλ ) に代入することで θ が得られますが、λ を求めるためには「勾配法 ( Gradient Method )」などを使う必要があります。
飽和モデルの場合、対数尤度関数 l( θ, λ ; t ) は
| l( θ, λ ; t ) | = | Σi{1→k}( Σj{1→ni}( δijln( λθi-λtijλ-1 ) + ln( exp( -θi-λtijλ ) ) ) ) |
| = | Σi{1→k}( Σj{1→ni}( δij[ ln λ - λln θi + ( λ - 1 )ln tij ] - θi-λtijλ ) ) |
となるので、
より λ ≠ 0、θi ≠ 0 なら ∂l / ∂θi = 0 のとき
となります。∂l / ∂λ は
となりますが、ln θi を含む項に着目すると
| Σi{1→k}( Σj{1→ni}( -δijln θi + θi-λtijλln θi ) ) | |
| = | Σi{1→k}( -ln θi[ Σj{1→ni}( δij ) - θi-λΣj{1→ni}( tijλ ) ] ) |
| = | Σi{1→k}( -ln θi{ Σj{1→ni}( δij ) - [ Σj{1→ni}( δij ) / Σj{1→ni}( tijλ ) ]Σj{1→ni}( tijλ ) } ) = 0 |
となって打ち消すことができるので、
| Σi{1→k}( Σj{1→ni}( δij( 1 / λ + ln tij ) - [ Σj{1→ni}( δij ) / Σj{1→ni}( tijλ ) ]tijλln tij ) ) | |
| = | Σi{1→k}( Σj{1→ni}( δij( 1 / λ + ln tij ) ) - Σj{1→ni}( δij )Σj{1→ni}( tijλln tij ) / Σj{1→ni}( tijλ ) ) |
| = | Σi{1→k}( Σj{1→ni}( δij[ 1 / λ + ln tij - Σj{1→ni}( tijλln tij ) / Σj{1→ni}( tijλ ) ] ) ) |
を解くことによって λ を求め、それを元に各 θi を得ることができます。
打ち切りが全くないデータに対しては、「スコア法 (Method of Scoring)」をそのまま適用すれば任意のモデル式を使って係数の推定を行うことができます。しかし、打ち切りデータがある場合は確率密度関数 f(t) の代わりに生存関数 S(t) を適用しなければならないため、従来のスコア法をそのまま適用することはできません。スコア法では、連結関数を使って
のように期待値を変数とする関数が独立変数の線形式で表されるとしていました。指数分布の平均は μi = 1 / θi なので、対数尤度関数は
であり、
( ∂ / ∂αj )( 1 / μi ) = ( ∂ / ∂μi )μi-1( ∂μi / ∂ξi )( ∂ξi / ∂αj ) = -xij / μi2g'(μi)
( ∂ / ∂αj )ln( 1 / μi ) = μi( ∂ / ∂αj )( 1 / μi ) = -xij / μig'(μi)
より
| uj ≡ ∂l / ∂αj | = | Σi{1→n}( δi[ ∂ln( 1 / μi ) / ∂αj ] - ti( ∂ / ∂αj )( 1 / μi ) ) |
| = | Σi{1→n}( -δixij / μig'(μi) + xijti / μi2g'(μi) ) | |
| = | Σi{1→n}( ( ti - δiμi )xij / μi2g'(μi) ) |
となります。指数関数の場合、分散は 1 / θi2 = μi2 なので、もし打ち切りがなく δi = 1 ならば、この式は一般化線形モデルで得られる式と一致します。
スコア法では ∂uj / ∂αk = ∂2l / ∂αj∂αk が必要となるのでこれを求めてみると、
| ∂uj / ∂αk | = | Σi{1→n}( ( ∂ / ∂αk )[ ( ti - δiμi )xij / μi2g'(μi) ] ) |
| = | Σi{1→n}( ( ∂ / ∂μi )[ ( ti / μi2 - δi / μi ) / g'(μi) ]xij( ∂μi / ∂αk ) ) | |
| = | Σi{1→n}( { [ ( -2ti / μi3 + δi / μi2 )g'(μi) - ( ti / μi2 - δi / μi )g(2)(μi) ] / g'(μi)2 }[ xijxik / g'(μi) ] ) | |
| = | Σi{1→n}( [ ( -2ti / μi2 + δi / μi )g'(μi) - ( ti / μi - δi )g(2)(μi) ]xijxik / μig'(μi)3 ) |
となります。スコア法では ∂uj / ∂αk ≈ E[∂uj / ∂αk] が成り立つと仮定することで g(2)(θi) の項などを消していましたが、打ち切りがある場合はこの仮定が成り立たなくなってしまうので、∂uj / ∂αk を k 行 j 列成分とする行列を
で表した時 ( ここで X はデザイン行列で行ベクトルが各標本の独立変数ベクトルを表し、W は対角行列とします )、W の i 番目の対角成分 wi は
となって連結関数に対しては二階導関数が必要になります。しかし、g(μi) = ln(μi) ならば g'(μi) = 1 / μi、g(2)(μi) = -1 / μi2 なので、
| wi | = | [ ( -2ti / μi2 + δi / μi ) / μi + ( ti / μi - δi ) / μi2 ] / ( μi / μi3 ) |
| = | ( -2ti / μi3 + δi / μi2 + ti / μi3 - δi / μi2 )μi2 | |
| = | -ti / μi |
となり打ち切りの有無に依存しない値になります。
ワイブル分布は
| f( t ; φ, λ ) | = | λφtλ-1exp( -φtλ ) |
| = | exp( -φtλ + ln λφtλ-1 ) | |
| = | exp( -φtλ + ( λ - 1 )ln t + ln λ + ln φ ) |
と表すことができるので、λ を局外パラメータとすれば 1-母数指数型分布族と考えることができます (*2-2)。しかし、T(t) = tλ となることから正準形ではなく、λ の値を決める必要もあるのでこれも変数として扱う必要があります。ワイブル分布の場合、
とします。このとき、
∂φi / ∂αj = xij / g'(φi)
∂ln φi / ∂αj = xij / φig'(φi)
∂φi / ∂λ = -θi-λln θi = -φiln θi
∂ln φi / ∂λ = -ln θi
より
| uj | = | ( ∂ / ∂αj )Σi{1→n}( δi[ ln λ + ln φi + ( λ - 1 )ln ti ] - φitiλ ) |
| = | Σi{1→n}( ( δi / φi - tiλ )xij / g'(φi) ) |
| uλ ≡ ∂l / ∂λ | = | ( ∂ / ∂λ )Σi{1→n}( δi[ ln λ + ln φi + ( λ - 1 )ln ti ] - φitiλ ) |
| = | Σi{1→n}( δi( 1 / λ - ln θi + ln ti ) + φitiλln θi - φitiλln ti ) | |
| = | Σi{1→n}( δi[ 1 / λ + ln( ti / θi ) ] - φitiλln( ti / θi ) ) |
となります。また、
| ( ∂ / ∂αk )( δi / φi ) | = | ( ∂ / ∂φi )( δi / φi )( ∂φi / ∂αk ) |
| = | ( -δi / φi2 )[ xik / g'(φi) ] |
| ( ∂ / ∂αk )g'(φi) | = | ( ∂ / ∂φi )g'(φi)( ∂φi / ∂αk ) |
| = | g(2)(φi)[ xik / g'(φi) ] |
| ( ∂ / ∂λ )g'(φi) | = | ( ∂ / ∂φi )g'(φi)( ∂φi / ∂λ ) |
| = | -φig(2)(φi)ln θi |
より ∂uj / αk は
| ∂uj / ∂αk | = | ( ∂ / ∂αk )Σi{1→n}( ( δi / φi - tiλ )xij / g'(φi) ) |
| = | Σi{1→n}( { [ -δig'(φi) / φi2 - ( δi / φi - tiλ )g(2)(φi) ]xij / g'(φi)2 }[ xik / g'(φi) ] ) | |
| = | Σi{1→n}( [ -δig'(φi) / φi2 - ( δi / φi - tiλ )g(2)(φi) ]xijxik / g'(φi)3 ) |
∂uj / ∂λ は
| ∂uj / ∂λ | = | ( ∂ / ∂λ )Σi{1→n}( ( δi / φi - tiλ )xij / g'(φi) ) |
| = | Σi{1→n}( { [ ( -δi / φi2 )( -φiln θi ) - tiλln ti ]g'(φi) - ( δi / φi - tiλ )( ∂g'(φi) / ∂λ ) }xij / g'(φi)2 ) | |
| = | Σi{1→n}( { [ ( δiln θi / φi ) - tiλln ti ]g'(φi) + ( δi / φi - tiλ )φig(2)(φi)ln θi }xij / g'(φi)2 ) | |
| = | Σi{1→n}( { δi[ g'(φi) / φi + g(2)(φi) ]ln θi - tiλ[ g'(φi)ln ti + φig(2)(φi)ln θi ] }xij / g'(φi)2 ) |
さらに ∂uλ / ∂λ は
| ∂uλ / ∂λ | = | ( ∂ / ∂λ )Σi{1→n}( δi[ 1 / λ + ln( ti / θi ) ] - φitiλln( ti / θi ) ) |
| = | Σi{1→n}( -δi / λ2 - [ ( -φiln θi )tiλ + φitiλln ti ]ln( ti / θi ) | |
| = | Σi{1→n}( -δi / λ2 - φitiλln( ti / θi )2 ) |
となります。ここで g(φi) = ln φi とすれば
uj = Σi{1→n}( ( δi - φitiλ )xij )
| ∂uj / ∂αk | = | Σi{1→n}( [ -δi / φi3 + ( δi / φi - tiλ ) / φi2 ]xijxikφi3 ) |
| = | Σi{1→n}( -φitiλxijxik ) |
| ∂uj / ∂λ | = | Σi{1→n}( { δi[ 1 / φi2 - 1 / φi2 ]ln θi - tiλ[ ln ti / φi - ln θi / φi ] }xijφi2 ) |
| = | Σi{1→n}( -φitiλxijln( ti / θi ) ) |
となって、かなり単純な式に変形することができます。
生存時間解析を行うため、指数分布とワイブル分布を用いた一般化線形モデルの最尤推定を行うためのサンプル・プログラムを以下に示します。かなり長いリストになるので、いくつかに分けて説明していきます。
/* 生存時間構造体 */ struct SurvivalTime { double time; // 生存時間 bool censored; // 打ち切りの有無 // 生存時間t と打ち切りの有無 c を指定して構築 SurvivalTime( double t, bool c = false ) : time( t ), censored( c ) { assert( t >= 0 ); } // 値の比較(Less)用関数オブジェクト // // 自分の方が生存時間が短ければ true を返す // // s : 比較対象の生存時間 bool operator<( const SurvivalTime& s ) const { return( time < s.time ); } };
生存時間には打ち切りの有無があるため、これらのパラメータをまとめた構造体 SurvivalTime を用意します。後ほど、値の比較を行う必要があるため、比較用のメンバ関数 operator< を持つようにしています。値の比較には生存時間 time をそのまま使います。なお、time は非負である必要があるので、構築時に assert を使ってチェックをしています。
/* PrintVector : 可変長配列 vec の要素表示 */ void PrintVector( const string& header, const vector< double >& vec ) { cout << header << "( "; vector< double >::size_type sz = vec.size(); for ( vector< double >::size_type i = 1 ; i < sz ; ++i ) cout << vec[i - 1] << ", "; cout << vec[sz - 1] << " )" << endl; } void PrintVector( const string& header, const vector< SurvivalTime >& vec ) { cout << header << "( "; vector< double >::size_type sz = vec.size(); for ( vector< double >::size_type i = 1 ; i < sz ; ++i ) { cout << vec[i - 1].time; if ( vec[i - 1].censored ) cout << '*'; cout << ", "; } cout << vec[sz - 1].time; if ( vec[sz - 1].censored ) cout << '*'; cout << " )" << endl; } /* PrintMatrix : 二次元可変長配列(行列) mat の要素表示 */ void PrintMatrix( const string& header, const vector< vector< double > >& mat ) { vector< vector< double > >::size_type sz = mat.size(); if ( sz == 0 ) return; PrintVector( header, mat[0] ); string tab( header.length(), ' ' ); for ( vector< vector< double > >::size_type i = 1 ; i < mat.size() ; ++i ) PrintVector( tab, mat[i] ); } /* 生存時間解析 */ class SurvivalAnalysis { public: typedef size_t size_type; // サイズの型 // 独立変数 x と従属変数(生存時間) t を指定して構築 SurvivalAnalysis( const vector< vector< double > >& x, const vector< SurvivalTime >& t ); // スコア法を使った係数の推定 // // a : 求める係数を保持する配列へのポインタ // var_a : 係数の分散を保持する配列へのポインタ // verbose : 冗長モード(ON/OFF) // maxCount : 反復処理の最大回数 // threshold : 収束条件(全係数の前回との差がが threshold 以下なら処理終了) bool scoringMethod ( vector< double >* a, vector< double >* var_a, bool verbose, unsigned int maxCount = 100, double threshold = 1E-3 ); // 仮想デストラクタ(何もしない) ~SurvivalAnalysis() {} protected: const vector< vector< double > >& x_; // 独立変数ベクトルへの参照 const vector< SurvivalTime >& t_; // 従属変数(生存時間)への参照 // 独立変数ベクトルの個数を返す size_type varSize() const { return( x_.size() ); } // スコア法での初期化を行う // // a : 初期化対象の係数ベクトルへのポインタ // les : 連立方程式へのポインタ virtual void init( vector< double >* a, LinearEquationSystem< double >* les ); private: // 係数を求めるための連立方程式を構築する // // a : 現在までに求めた係数ベクトル // les : 連立方程式へのポインタ virtual void createLES( const vector< double >& a, LinearEquationSystem< double >* les ) const = 0; // 係数の数を返す virtual size_type coefSize() const = 0; }; /* SurvivalAnalysis コンストラクタ : 独立変数ベクトル x と従属変数(生存時間) t を指定して構築 */ SurvivalAnalysis::SurvivalAnalysis( const vector< vector< double > >& x, const vector< SurvivalTime >& t ) : x_( x ), t_( t ) { assert( &x_ != 0 && &t_ != 0 ); size_type rows = x_.size(); // 独立変数ベクトルの数 if ( rows == 0 ) throw std::domain_error( "SurvivalAnalysis : x size is zero." ); // 従属変数の数と一致するか if ( t_.size() != rows ) throw std::domain_error( "SurvivalAnalysis : size x and y not matched." ); size_type cols = x_[0].size(); // 独立変数ベクトルのサイズ for ( size_type i = 1 ; i < rows ; ++i ) { if ( x_[i].size() != cols ) throw std::domain_error( "SurvivalAnalysis : vector size of x must be equal each other." ); } } /* SurvivalAnalysis::init : スコア法での初期化を行う ここでは係数の初期化(ゼロクリア)と連立方程式用インスタンスのリサイズを行う。 */ void SurvivalAnalysis::init( vector< double >* a, LinearEquationSystem< double >* les ) { a->assign( coefSize(), 0 ); // 係数の初期化 les->resize( coefSize() ); // 連立方程式のリサイズ } /* SurvivalAnalysis::scoringMethod : スコア法による係数の推定 a : 求めた係数を保持する配列へのポインタ var_a : 係数の分散を保持する配列へのポインタ verbose : 冗長モード(ON/OFF) maxCount : 反復処理の最大回数 threshold : 収束条件(全係数が threshold 以下なら処理終了) */ bool SurvivalAnalysis::scoringMethod ( vector< double >* a, vector< double >* var_a, bool verbose, unsigned int maxCount, double threshold ) { assert( a != 0 ); if ( threshold <= 0 ) throw std::domain_error( "SurvivalAnalysis::scoringMethod : threshold must be positive." ); LinearEquationSystem< double > s; // 連立方程式計算用インスタンス init( a, &s ); cout << "*** Survival Analysis ***" << endl << endl; cout << "N = " << varSize() << "; p = " << coefSize() << endl << endl; if ( verbose ) { PrintMatrix( "x = ", x_ ); cout << endl; PrintVector( "t = ", t_ ); cout << endl; } /* 係数の計算 */ bool isMatched; // 収束したか unsigned int cnt; // 計算回数 for ( cnt = 0 ; cnt < maxCount ; ++cnt ) { createLES( *a, &s ); // 連立方程式の構築 if ( verbose ) { cout << "----- cnt = " << cnt + 1 << " -----" << endl << endl; cout << "Equation System :" << endl; s.print( cout ); cout << endl; } // 連立方程式の計算 if ( ! GaussianElimination( s ) ) throw std::runtime_error( "SurvivalAnalysis::scoringMethod : Failed to calculate coefficients." ); // 各係数が収束しているかを確認する isMatched = true; for ( size_type j = 0 ; j < coefSize() ; ++j ) { if ( fabs( (*a)[j] - s.ans( j ) ) >= threshold ) isMatched = false; (*a)[j] = s.ans( j ); } if ( verbose ) { PrintVector( "a = ", *a ); cout << endl; } if ( isMatched ) break; } if ( cnt >= maxCount ) return( false ); /* 係数の分散を計算 */ if ( var_a != 0 ) { LinearEquationSystem< double > inv; createLES( *a, &s ); // 連立方程式の構築 Inverse( s, inv ); var_a->resize( inv.size() ); for ( size_type i = 0 ; i < inv.size() ; ++i ) (*var_a)[i] = -inv[i][i]; } return( true ); }
生存時間解析を行うためのクラスを次に用意します。このクラスでは、スコア法の処理を行うことがメインとなりますが、スコア法で用いる連立方程式の構築は派生先のクラスに任せます。そのため、連立方程式構築用のメンバ関数 createLES は純粋仮想関数として実装は行なっていません。また、推定するパラメータのサイズは通常は独立変数ベクトルのサイズと等しくなりますが、ワイブル分布を用いるときは λ もパラメータとして扱う必要があるため一つ多くなります。このため、係数の数を返すメンバ関数 coefSize も派生側で実装するように純粋仮想関数としてあります。
コンストラクタでは、独立変数ベクトル x と従属変数 (生存時間) t を引数として渡します。どちらも参照を渡し、それをそのままメンバ変数として取り込んでいます。また、線形式として成り立っているかをチェックして、成り立たない場合は例外クラス domain_error を投げます。このクラスは STL(Standard Template Library) に標準で用意されている例外クラスです。
スコア法による係数の推定は scoringMethod で行います。処理の内容は「確率・統計 (18) 一般化線形モデル (Generalized Linear Model)」で示したスコア法のサンプル・プログラムとほぼ同じですが、先述の通り連立方程式の構築は派生クラス側に任せるようにしてあります。
/* MultCoefVec : 連立方程式 les の係数行列と解ベクトル a の積を求めて xa に返す */ void MultCoefVec( const LinearEquationSystem< double >& les, const vector< double >& a, vector< double >* xa ) { for ( size_t i = 0 ; i < les.size() ; ++i ) { (*xa)[i] = 0; for ( size_t j = 0 ; j < les.size() ; ++j ) (*xa)[i] += les[i][j] * a[j]; } } /* GetParam : 独立変数ベクトル x と係数ベクトル a から exp( ( x, a ) ) を求めて param に返す */ void GetParam( const vector< vector< double > >& x, const vector< double >& a, vector< double >* param ) { for ( size_t i = 0 ; i < x.size() ; ++i ) { double d = 0; for ( size_t j = 0 ; j < x[i].size() ; ++j ) d += x[i][j] * a[j]; (*param)[i] = exp( d ); } } /* 指数分布を用いた生存時間解析 */ class SurvivalAnalysis_Exponential : public SurvivalAnalysis { public: // 独立変数 x と従属変数(生存時間) t を指定して構築 SurvivalAnalysis_Exponential( const vector< vector< double > >& x, const vector< SurvivalTime >& t ) : SurvivalAnalysis( x, t ) {} private: // 係数行列の計算 void calcCoef( const vector< double >& mu, LinearEquationSystem< double >* les ) const; // 対数尤度の係数による偏微分値を求める void calcUj( const vector< double >& mu, vector< double >* uj ) const ; // 連立方程式の右辺を求める void calcRSide( const vector< double >& a, const vector< double >& mu, LinearEquationSystem< double >* les ) const; // 係数を求めるための連立方程式を構築する virtual void createLES( const vector< double >& a, LinearEquationSystem< double >* les ) const; // 係数の数を返す virtual size_type coefSize() const { return( ( varSize() == 0 ) ? 0 : x_[0].size() ); } }; /* SurvivalAnalysis_Exponential::calcCoef : 連立方程式 les の係数行列を計算する coef_j,k = Σ -t[i] * x[i][j] * x[i][k] / μ[i] */ void SurvivalAnalysis_Exponential::calcCoef( const vector< double >& mu, LinearEquationSystem< double >* les ) const { for ( size_type k = 0 ; k < coefSize() ; ++k ) { for ( size_type j = k ; j < coefSize() ; ++j ) { (*les)[k][j] = 0; for ( size_type i = 0 ; i < varSize() ; ++i ) (*les)[k][j] += -t_[i].time * x_[i][j] * x_[i][k] / mu[i]; (*les)[j][k] = (*les)[k][j]; } } } /* SurvivalAnalysis_Exponential::calcUj : u_j = ∂l / ∂a[j] を計算する u_j = Σ ( t[i] - δ[i] * μ[i] ) * x[i][j] / μ[i] */ void SurvivalAnalysis_Exponential::calcUj( const vector< double >& mu, vector< double >* uj ) const { for ( size_type j = 0 ; j < coefSize() ; ++j ) { (*uj)[j] = 0; for ( size_type i = 0 ; i < varSize() ; ++i ) (*uj)[j] += ( t_[i].time - ( ( t_[i].censored ) ? 0 : mu[i] ) ) * x_[i][j] / mu[i]; } } /* SurvivalAnalysis_Exponential::calcRSide : 連立方程式 les の右辺を計算する */ void SurvivalAnalysis_Exponential::calcRSide ( const vector< double >& a, const vector< double >& mu, LinearEquationSystem< double >* les ) const { // u_j の計算 vector< double > uj( coefSize() ); calcUj( mu, &uj ); // 独立変数ベクトルと係数の積 xa を求める vector< double > xa( coefSize() ); MultCoefVec( *les, a, &xa ); // (右辺) = xa - u_j for ( size_type i = 0 ; i < coefSize() ; ++i ) les->ans( i ) = xa[i] - uj[i]; } /* SurvivalAnalysis_Exponential::createLES : スコア法の連立方程式を作成する */ void SurvivalAnalysis_Exponential::createLES ( const vector< double >& a, LinearEquationSystem< double >* les ) const { vector< double > mu( varSize() ); // μ[i] GetParam( x_, a, &mu ); calcCoef( mu, les ); calcRSide( a, mu, les ); } /* ワイブル分布を用いた生存時間解析 */ class SurvivalAnalysis_Weibull : public SurvivalAnalysis { public: // 独立変数 x と従属変数(生存時間) t を指定して構築 SurvivalAnalysis_Weibull( const vector< vector< double > >& x, const vector< SurvivalTime >& t ) : SurvivalAnalysis( x, t ) {} private: // 係数行列の計算 void calcCoef( const vector< double >& d1, const vector< double >& d2, double lambda, LinearEquationSystem< double >* les ) const; // 対数尤度の係数による偏微分値を求める void calcUj( const vector< double >& d1, const vector< double >& d2, double lambda, vector< double >* uj ) const; // 連立方程式の右辺を求める void calcRSide( const vector< double >& a, const vector< double >& d1, const vector< double >& d2, double lambda, LinearEquationSystem< double >* les ) const; // スコア法での初期化を行う virtual void init( vector< double >* a, LinearEquationSystem< double >* les ); // 係数を求めるための連立方程式を構築する virtual void createLES( const vector< double >& a, LinearEquationSystem< double >* les ) const; // 係数の数を返す virtual size_type coefSize() const { return( ( varSize() == 0 ) ? 1 : x_[0].size() + 1 ); } }; /* SurvivalAnalysis_Weibull::init : スコア法での初期化を行う λ成分の初期値がゼロの場合処理に失敗するため 1 を代入する */ void SurvivalAnalysis_Weibull::init( vector< double >* a, LinearEquationSystem< double >* les ) { SurvivalAnalysis::init( a, les ); a->back() = 1; } /* SurvivalAnalysis_Weibull::calcCoef : 係数行列を計算する coef_j,k = Σ -φ[i] * t[i]^λ * x[i][j] * x[i][k] coef_j,λ = Σ -φ[i] * t[i]^λ * x[i][j] * ln( t[i] / θ[i] ) coef_λ,λ = Σ -δ[i] / λ^2 - φ[i] * t[i]^λ * ln( t[i] / θ[i] )^2 pht = φ[i] * t[i]^λ ; lnt = ln( t[i] / θ[i] ) */ void SurvivalAnalysis_Weibull::calcCoef ( const vector< double >& pht, const vector< double >& lnt, double lambda, LinearEquationSystem< double >* les ) const { // 線形式の係数どうし ( a[j] と a[k] ) に対する成分 coef_j,k = ∂u_j / ∂a[k] を求める for ( size_type k = 0 ; k < coefSize() - 1 ; ++k ) { for ( size_type j = k ; j < coefSize() - 1 ; ++j ) { (*les)[k][j] = 0; for ( size_type i = 0 ; i < varSize() ; ++i ) (*les)[k][j] += -pht[i] * x_[i][j] * x_[i][k]; (*les)[j][k] = (*les)[k][j]; } } // 線形式の係数 a[j] と λ に対する成分 coef_j,λ = ∂u_j / ∂λ を求める for ( size_type j = 0 ; j < coefSize() - 1 ; ++j ) { (*les)[coefSize() - 1][j] = 0; for ( size_type i = 0 ; i < varSize() ; ++i ) (*les)[coefSize() - 1][j] += -pht[i] * x_[i][j] * lnt[i]; (*les)[j][coefSize() - 1] = (*les)[coefSize() - 1][j]; } // λ に対する成分 coef_λ,λ = ∂u_λ / ∂λ を求める (*les)[coefSize() - 1][coefSize() - 1] = 0; for ( size_type i = 0 ; i < varSize() ; ++i ) (*les)[coefSize() - 1][coefSize() - 1] += ( ( t_[i].censored ) ? 0 : -1 / pow( lambda, 2 ) ) - pht[i] * pow( lnt[i], 2 ); } /* SurvivalAnalysis_Weibull::calcUj : u[j] = ∂l / ∂a[j] を計算する u_j = Σ ( δ[i] - φ[i] * t[i]^λ ) * x[i][j] u_λ = Σ δ[i] * [ 1 / λ + ln( t[i] ) ] - φ[i] * t[i]^λ * ln( t[i] / θ[i] ) pht = φ[i] * t[i]^λ ; lnt = ln( t[i] / θ[i] ) */ void SurvivalAnalysis_Weibull::calcUj ( const vector< double >& pht, const vector< double >& lnt, double lambda, vector< double >* uj ) const { for ( size_type j = 0 ; j < coefSize() - 1 ; ++j ) { (*uj)[j] = 0; for ( size_type i = 0 ; i < varSize() ; ++i ) (*uj)[j] += ( ( ( t_[i].censored ) ? 0 : 1 ) - pht[i] ) * x_[i][j]; } (*uj)[coefSize() - 1] = 0; for ( size_type i = 0 ; i < varSize() ; ++i ) (*uj)[coefSize() - 1] += ( ( t_[i].censored ) ? 0 : 1 / lambda + lnt[i] ) - pht[i] * lnt[i]; } /* SurvivalAnalysis_Weibull::calcRSide : 連立方程式の右辺を計算する pht = φ[i] * t[i]^λ ; lnt = ln( t[i] / θ[i] ) */ void SurvivalAnalysis_Weibull::calcRSide ( const vector< double >& a, const vector< double >& pht, const vector< double >& lnt, double lambda, LinearEquationSystem< double >* les ) const { // u_j の計算 vector< double > uj( coefSize() ); calcUj( pht, lnt, lambda, &uj ); // 独立変数ベクトルと係数の積 xa を求める vector< double > xa( coefSize() ); MultCoefVec( *les, a, &xa ); // (右辺) = xa - u_j for ( size_type i = 0 ; i < coefSize() ; ++i ) les->ans( i ) = xa[i] - uj[i]; } /* SurvivalAnalysis_Weibull::createLES : スコア法の連立方程式を作成する */ void SurvivalAnalysis_Weibull::createLES ( const vector< double >& a, LinearEquationSystem< double >* les ) const { vector< double > phi( varSize() ); // φ[i] GetParam( x_, a, &phi ); vector< double > pht( varSize() ); // φ[i] * t[i]^λ vector< double > lnt( varSize() ); // ln( t[i] / θ[i] ) for ( size_type i = 0 ; i < varSize() ; ++i ) { pht[i] = phi[i] * pow( t_[i].time, a.back() ); lnt[i] = log( t_[i].time / pow( phi[i], -1 / a.back() ) ); } calcCoef( pht, lnt, a.back(), les ); calcRSide( a, pht, lnt, a.back(), les ); }
最後に、指数分布・ワイブル分布それぞれを使った生存時間解析用のクラスを作成します。これらはクラス SurvivalAnalysis から派生し、連立方程式の構築などを具体的に実装したものになります。
SurvivalAnalysis_Exponential クラスは確率分布に指数分布を用いています。メインとなるのは連立方程式を構築する createLES で、最初に関数 GetParam を使って μi の計算を行います。一般化線形モデルにおけるスコア法は連結関数を任意に選択することができたのに対し、ここでは対数関数に固定しています。従って、GetParam は各独立変数ベクトルと前に求めた係数との内積を計算し、その値を指数として exp 関数を呼び出すだけで実装できます。これを任意の連結関数に対応させると、連結関数に対する二階導関数を新たに定義する必要がありますが、生存時間解析では後述するように連結関数として対数関数を用いる場合が圧倒的に多いため、ここではそれ以外の連結関数は考えないことにします。
μi の計算が終わったら、それを使って連立方程式の係数行列を求めます。この処理にはメンバ関数 calcCoef が利用されています。計算処理の内容は先述の通りです。また、右辺の計算には calcRSide 関数を使います。この関数では、uj = ∂l / ∂ak を calcUj 関数で求め、さらに独立変数ベクトルと前に求めた係数との内積を関数 MultCoefVec で計算してその差を求めます。これはスコア法の漸化式の右辺を求める処理に相当するものです。
ワイブル分布を用いる場合は SurvivalAnalysis_Weibull クラスを使いますが、ワイブル分布では λ も値を求める必要があるため、パラメータ数は独立変数ベクトルのサイズよりも一つだけ大きくなります。そのため、メンバ関数 coefSize では係数の数として x_[0].size() + 1 を返すようになっています。また、係数の初期値はメンバ関数 init で行いますが、λ の初期値をゼロにすると正しい計算ができなくなるため値を 1 にする処理を追加してあります。なお、スコア法の反復処理回数を少なくするためには初期値をできるだけ真値に近くすると有効ですが、ここでは係数の初期値は単純にゼロにしています。
連立方程式の構築処理の流れは指数分布の場合とほとんど変わりませんが、λ を係数用配列の最後の要素とし、通常の係数と λ を区別して計算するために処理が少し複雑になっています。
*2-1) 生存時間に対してある確率分布を仮定する、いわゆるパラメトリックなモデルを利用した生存時間解析は、一般化線形モデルの一つにあたります。スコア統計量などの用語については「確率・統計 (18) 一般化線形モデル (Generalized Linear Model)」にて紹介しています。
*2-2) 指数型分布族については「確率・統計 (18) 一般化線形モデル (Generalized Linear Model)」の「2) 指数型分布族 (Exponential Family of Distributions)」に詳しく紹介してあります。もちろん、指数分布は指数型分布族に該当します。
指数分布の場合、期待値 E[t] = 1 / θ であり、E[t] = xTα とすることで連結関数を恒等関数とする一般化線形モデルが適用できます。しかし、E[t] > 0, θ > 0 なので、通常は
というモデル式を使うことが多いようです。これは、前の節で連結関数を g(μ) = ln μ としたことに相当します (実際には μ = 1 / θ なので符号が逆転することになります)。ハザード関数 h(t) = θ なので、x = ( 1, x1, x2, ... xp )T、α = ( α0, α1, α2, ... αp )T としたとき
| h( t ; α ) | = | exp( xTα ) |
| = | Πj{0→p}( exp( xjαj ) ) | |
| ≡ | h0Πj{1→p}( exp( xjαj ) ) |
のような乗法形式になります。但し、h0 = exp( α0 ) とします。xj が、ある試行の成功・失敗を表す「二値確率変数 (Binary Random Variable)」であるとすれば、全ての試行が失敗した場合 ( 1 ≤ j ≤ p において xj = 0 のとき ) のハザード関数は h0 と等しくなるので、この値は「基準ハザード (Baseline Hazard)」と呼ばれます。また、j 番目以外の変数は全て同じ値をとるとき、xj = δ ( δ = { 0, 1 } ) の場合のハザード関数を hj=δ( t ; α ) とすると、その比率 hj=1( t ; α ) / hj=0( t ; α ) は
となり、これを、試行に「成功」した場合の「失敗」のときに対する「ハザード比 (Hazard Ratio)」または「相対ハザード (Relative Hazard)」といいます。ハザード比が高いということは、対象の独立変数が死亡率に対して高い影響を及ぼしていることを意味します。
ワイブル分布も前節に示したように φ を以下のようにモデル化します。但し、x と α は指数分布で定義した内容と同一とします。
このとき、ハザード関数 h( t ; φ, λ ) は
| h( t ; α, λ ) | = | λtλ-1exp( xTα ) |
| = | α0λtλ-1exp( Σj{1→p}( xjαj ) ) |
となり、基準ハザードは
なので、指数関数の場合とは異なり t を変数とする関数となります。
指数分布・ワイブル分布のいずれの場合も、ハザード関数は基準ハザードに独立変数が比例定数の形で作用しています。このようなモデルは「(コックス)比例ハザードモデル ( ( Cox ) Proportional Hazards Model)」と呼ばれます。比例ハザードモデルの一般形は
で表され (*3-1)、x = 0 ならば h( t ; α ) = h0( t ) すなわち基準ハザードと等しくなります。指数分布ならば基準ハザードは定数であり、ワイブル分布の場合は λ - 1 次式で表されるのでした。
比例ハザードモデルにおける累積ハザード関数は
| H( t ; α ) | = | ∫{0→t} h( τ ; α ) dτ |
| = | ∫{0→t} h0( τ )exp( xTα ) dτ | |
| = | H0( t )exp( xTα ) |
となります。但し、H0( t ) は基準ハザードに対する累積ハザード関数を表します。この両辺の対数をとると
となるので、独立変数のうち j 番目の値 ( xj ) のみが 0 または 1 と異なり、他の変数は全て同じ値である二つの群に対し、xj = 0 である群の累積ハザード関数を Hj=0( t )、xj = 1 である群の累積ハザード関数を Hj=1( t ) としたとき、
ln Hj=1( t ; α ) - ln Hj=0( t ; α ) = αj
または ln Hj=1( t ; α ) = ln Hj=0( t ; α ) + αj
より二群の累積ハザード関数の対数の差 ( つまり、ハザード比の対数 ) は任意の t に対して定数であることになります。ワイブル分布の累積ハザード関数は
なので、その対数は
となって、ln H( t ; φ, λ ) は ln t に比例することになります ( 特に傾きが 1 なら λ = 1 ということになるので指数分布を意味することになります )。このことから、実際の値を使って累積ハザード関数を表現することができれば、指数分布やワイブル分布をモデルとして適用できるかどうかを調べることが可能となります。
実際の値を用いて累積ハザード関数を評価するための指標として「カプラン・マイヤー推定値 ( Kaplan-Meier Estimate )」がよく用いられます。この推定値は「積極限推定値 ( Product Limit Estimate )」とも呼ばれます。
生存関数 S( t ) の推定値 S~( t ) は
で求められます。但し、n( T ≥ t ) は生存時間が t 以上の標本数であり、N は総標本数を表しています。標本を生存時間の短い順に { t1, t2, ... tN } と並べ、時間 tk での死亡数を dk、tk の直前まで生存していた数を nk としたとき、時間 tk まで生存していた標本の中で tk 以降も生存する確率 pk は
となります。時間 tk ごとの事象が互いに独立であると仮定した時、tk ≤ t < tk+1 にてそれまでの事象が同時に発生する確率は pj ( 1 ≤ j ≤ k ) の積で求められ、
がカプラン・マイヤー推定値になります。tk ≤ t < tk+1 にて定数となるので、カプラン・マイヤー推定値は単調減少な階段関数であり、グラフは右下方向に進む階段状の形をとります。また、確率の積であることから明らかに値域は 0 と 1 の間となります。
打ち切りがない場合、nj+1 = nj - dj となるので、カプラン・マイヤー推定値はある項の分母 nj+1 が直前の項の分子 nj - dj と打ち消し合って、
と単純な形になります。しかし、打ち切りデータは死亡数 dk としてはカウントしない ( 但し、nk+1 からは除外する必要があります ) ため、その分だけ推定値は大きくなります。
累積ハザード関数は S( t ) の対数から求められるので ( H( t ) = -ln S( t ) )、さらにその対数である ln( -ln S~( t ) ) を縦軸とし、ln t を横軸にプロットしたとき、それが直線になれば、確率密度関数としてワイブル分布や指数分布が適用できると判断することができます。
カプラン・マイヤー推定値を求めるためのサンプル・プログラムを以下に示します。
/* カプラン・マイヤー推定値 ( Kaplan-Meier Estimate ) 算出用クラス */ class KMEstimate : public map< SurvivalTime, double > { public: // 反復子の型 using map< SurvivalTime, double >::iterator; // 定数反復子の型 using map< SurvivalTime, double >::const_iterator; // キーの型 using map< SurvivalTime, double >::key_type; // 値の型 using map< SurvivalTime, double >::mapped_type; // 要素の型 using map< SurvivalTime, double >::value_type; // 生存時間の配列 [ s, e ) を指定して構築 template< class In > KMEstimate( In s, In e ); }; /* KMEstimate コンストラクタ : 生存時間の配列 [ s, e ) を指定して構築 */ template< class In > KMEstimate::KMEstimate( In s, In e ) { // 配列の長さ(要素数) unsigned int n = std::distance( s, e ); // 生存時間ごとの要素数をカウントするためのバッファ // 値は pair 型であり、first が死亡数、second が打ち切りを含めた死亡数を表す typedef map< SurvivalTime, pair< unsigned int, unsigned int > > Buffer; Buffer buff; // 要素数のカウント for ( ; s != e ; ++s ) { typename Buffer::iterator it = buff.find( *s ); if ( it == buff.end() ) { pair< unsigned int, unsigned int > death( ( s->censored ) ? 0 : 1, 1 ); buff.insert( typename Buffer::value_type( *s, death ) ); } else { if ( ! s->censored ) ( it->second ).first += 1; ( it->second ).second += 1; } } // カウンタからカプラン・マイヤー推定値を算出 double d = 1.0; for ( typename Buffer::iterator it = buff.begin() ; it != buff.end() ; ++it ) { // ( 直前の生存数 - 死亡数 ) / 直前の生存数 を算出 if ( ( it->second ).first > 0 ) { d *= static_cast< double >( n - ( it->second ).first ) / n; (*this)[it->first] = d; } // 要素数からは打ち切りも含めて減算する n -= ( it->second ).second; } }
カプラン・マイヤー推定値を算出・保持するクラス KMEstimate は STL(Standard Template Library) にあるコンテナ・クラス map からの派生クラスとしています。このクラスは、キーとその値を保持する連想配列として機能するので、キーを生存時間として、その値にカプラン・マイヤー推定値を保持します。配列の先頭と末尾の次の位置を渡せば、自動的に推定値を算出するようにしてあります。
算出に先立って、生存時間ごとの要素数をカウントします。要素数としては、打ち切りを含めない純粋な死亡数と、打ち切りも含めた数の二つを同時にカウントします。このとき、バッファとしてキーを生存時間とした map を利用します。map はキーによって自動的に要素が並べ替えられるため、最後に推定値を計算する時に並べ替えを行う処理が不要になります。しかし、キーは大小関係が比較できることが必須となるため、生存時間として利用するクラス SurvivalTime のために比較関数を用意する必要があります。前に示した SurvivalTime クラスにて大小比較用の関数 operator< が用意されていたのはこのためです。
要素数のカウントが完了したら、あとは生存時間の短いものから順番に推定値を計算します。推定値は、( [直前の生存数] - [死亡数] ) / [直前の生存数] を算出して前回の結果に掛け合わせることで求められます。計算後、今度は打ち切りも含めた死亡数を直前の生存数から減算すれば、次に計算するときの「直前の生存数」が得られます。
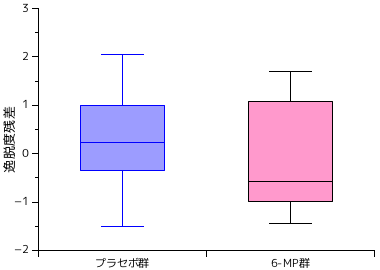
参考文献にあったデータを使ってカプラン・マイヤー推定値を計算してみます。このデータは、寛解 (病状が回復) した急性白血病患者を対象に、6-mercaptopurine (6-MP) を使って治療した群とプラセボ (何もしない) 群に分けて再発までの期間 (週単位) を調査した結果です。
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| プラセボ群 | 1 | 1 | 2 | 2 | 3 | 4 | 4 | 5 | 5 | 8 | 8 | 8 | 8 | 11 | 11 | 12 | 12 | 15 | 17 | 22 | 23 |
| 6-MP 群 | 6 | 6 | 6 | 6* | 7 | 9* | 10 | 10* | 11* | 13 | 16 | 17* | 19* | 20* | 22 | 23 | 25* | 32* | 32* | 34* | 35* |
データに "*" の付いたものは打ち切りデータであることを示しています。プラセボ群については打ち切りはないのに対し、6-MP 群では 12 個と半数以上が打ち切りとなっています。両者について、カプラン・マイヤー推定値を算出した結果が以下のようになります。
| プラセボ群 | 6-MP 群 | ||||||
|---|---|---|---|---|---|---|---|
| 生存時間 t | 対数生存時間 ln t | 推定値 S~(t) | 対数累積ハザード ln H(t) | 生存時間 t | 対数生存時間 ln t | 推定値 S~(t) | 対数累積ハザード ln H(t) |
| t < 1 | ln t < 0.000 | 1.00 | - | t < 6 | ln t < 1.79 | 1.00 | - |
| 1 ≤ t < 2 | 0.000 ≤ ln t < 0.693 | 0.905 | -2.30 | 6 ≤ t < 7 | 1.79 ≤ ln t < 1.95 | 0.857 | -1.87 |
| 2 ≤ t < 3 | 0.693 ≤ ln t < 1.10 | 0.810 | -1.55 | 7 ≤ t < 10 | 1.95 ≤ ln t < 2.30 | 0.807 | -1.54 |
| 3 ≤ t < 4 | 1.10 ≤ ln t < 1.39 | 0.762 | -1.30 | 10 ≤ t < 13 | 2.30 ≤ ln t < 2.56 | 0.753 | -1.26 |
| 4 ≤ t < 5 | 1.39 ≤ ln t < 1.61 | 0.667 | -0.903 | 13 ≤ t < 16 | 2.56 ≤ ln t < 2.77 | 0.690 | -0.992 |
| 5 ≤ t < 8 | 1.61 ≤ ln t < 2.08 | 0.571 | -0.581 | 16 ≤ t < 22 | 2.77 ≤ ln t < 3.09 | 0.627 | -0.763 |
| 8 ≤ t < 11 | 2.08 ≤ ln t < 2.40 | 0.381 | -0.036 | 22 ≤ t < 23 | 3.09 ≤ ln t < 3.14 | 0.538 | -0.478 |
| 11 ≤ t < 12 | 2.40 ≤ ln t < 2.48 | 0.286 | 0.225 | 23 ≤ t | 3.14 ≤ ln t | 0.448 | -0.220 |
| 12 ≤ t < 15 | 2.48 ≤ ln t < 2.71 | 0.190 | 0.506 | ||||
| 15 ≤ t < 17 | 2.71 ≤ ln t < 2.83 | 0.143 | 0.666 | ||||
| 17 ≤ t < 22 | 2.83 ≤ ln t < 3.09 | 0.0952 | 0.855 | ||||
| 22 ≤ t < 23 | 3.09 ≤ ln t < 3.14 | 0.0476 | 1.11 | ||||
| 23 ≤ t | 3.14 ≤ t | 0.000 | - | ||||
生存時間としては、通常の値 (週単位) の他にその対数も示してあります。また、対数累積ハザード ln H(t) は ln( -ln S~(t) ) で計算することができます。
 |
| 図 3-1. 生存時間に対するカプラン・マイヤー推定値 |
上図は、生存時間に対するカプラン・マイヤー推定値の推移をプラセボ群と 6-MP 群のそれぞれに対して示したグラフです。この結果から、明らかに 6-MP 群側の方が生存時間が長くなる傾向にあることがわかります。
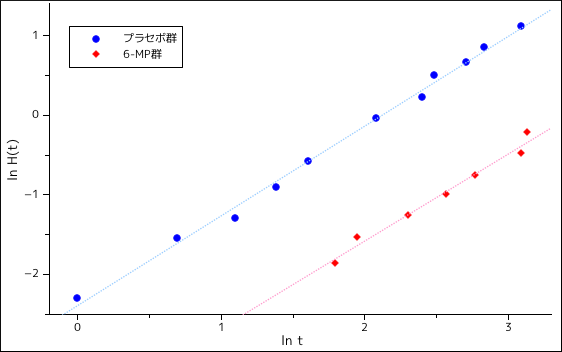 |
| 図 3-2. 対数生存時間と対数累積ハザードの相関図 |
次のグラフは、対数生存時間と対数累積ハザードの相関を示したグラフです。二群ともほぼ直線となっていることから、ワイブル分布をモデルとして利用することが可能であると仮定することができます。特に傾きが 1 に近いことから指数分布を利用することもできそうです。また、両者の傾きはほぼ等しいことから、プラセボ群の対数累積ハザード関数を H0( t ) とした時、6-MP 群の対数累積ハザード関数 H1( t ) は H0( t ) にある定数 K を加え、H1( t ) = H0( t ) + K と表すことができると考えることができます。これは、比例ハザードモデルを仮定することが可能であることを意味します。
このデータを使い、サンプル・プログラムを使って指数分布とワイブル分布それぞれについて処理した結果を以下に示します。独立変数ベクトルとしては、プラセボ群を ( 1, 0 )T、6-MP 群を ( 1, 1 )T としたので、プラセボ群が基準ハザードに相当することになります。
指数分布 μ = exp( 2.16 + 1.53x )
ワイブル分布 φ = exp( -3.07 - 1.73x ) ; λ = 1.37
| 指数分布 | ワイブル分布 | |||
|---|---|---|---|---|
| 推定値 | 標準誤差 | 推定値 | 標準誤差 | |
| 切片 α0 | 2.16 | 0.218 | -3.07 | 0.227 |
| 傾き α1 | 1.53 | 0.398 | -1.73 | 0.424 |
| 形状パラメータ λ | - | - | 1.37 | 0.201 |
指数分布とワイブル分布で切片と傾きの符号が逆転しています。これは線形モデルを当てはめたパラメータの差異によるもので、指数分布の場合、ワイブル分布に対して λ = 1, φ = 1 / θ と変形した分布に相当するために生じたものです。ワイブル分布では
φ = θ-λ = exp( xTα ) より
ln θ = -xTα / λ
となるので、指数分布に合わせて θ に対する係数として表すには -λ で割ればよく、その時の値は切片が 2.25、傾きが 1.27 となり、指数分布の値と比較的近くなります (補足 1)。
プラセボ群に対する 6-MP 群のハザード比は、指数分布の場合 e-1.53 = 0.217、ワイブル分布では e-1.73 = 0.177 となります。6-MP の使用により生存確率は 4 〜 5 倍程度改善できたことをこの結果は示しています。
指数分布・ワイブル分布それぞれの対数尤度を計算すると次のようになります。対数尤度は、打ち切りがない場合 ln h(t) + ln S(t) であるのに対し、打ち切りありの場合は ln S(t) となることに注意して下さい。
| 群 | No. | 生存時間 t | 打ち切り 有=0/無=1 | 指数分布 | ワイブル分布 | ||||
|---|---|---|---|---|---|---|---|---|---|
| ln h(t) | ln S(t) | 対数尤度 | ln h(t) | ln S(t) | 対数尤度 | ||||
| プラセボ群 | 1 | 1 | 1 | -2.16 | -0.115 | -2.27 | -2.76 | -0.0464 | -2.81 |
| 2 | 1 | 1 | -2.16 | -0.115 | -2.27 | -2.76 | -0.0464 | -2.81 | |
| 3 | 2 | 1 | -2.16 | -0.231 | -2.39 | -2.51 | -0.120 | -2.63 | |
| 4 | 2 | 1 | -2.16 | -0.231 | -2.39 | -2.51 | -0.120 | -2.63 | |
| 5 | 3 | 1 | -2.16 | -0.346 | -2.51 | -2.36 | -0.208 | -2.57 | |
| 6 | 4 | 1 | -2.16 | -0.462 | -2.62 | -2.25 | -0.308 | -2.56 | |
| 7 | 4 | 1 | -2.16 | -0.462 | -2.62 | -2.25 | -0.308 | -2.56 | |
| 8 | 5 | 1 | -2.16 | -0.577 | -2.74 | -2.17 | -0.418 | -2.59 | |
| 9 | 5 | 1 | -2.16 | -0.577 | -2.74 | -2.17 | -0.418 | -2.59 | |
| 10 | 8 | 1 | -2.16 | -0.923 | -3.08 | -2.00 | -0.794 | -2.79 | |
| 11 | 8 | 1 | -2.16 | -0.923 | -3.08 | -2.00 | -0.794 | -2.79 | |
| 12 | 8 | 1 | -2.16 | -0.923 | -3.08 | -2.00 | -0.794 | -2.79 | |
| 13 | 8 | 1 | -2.16 | -0.923 | -3.08 | -2.00 | -0.794 | -2.79 | |
| 14 | 11 | 1 | -2.16 | -1.27 | -3.43 | -1.88 | -1.23 | -3.11 | |
| 15 | 11 | 1 | -2.16 | -1.27 | -3.43 | -1.88 | -1.23 | -3.11 | |
| 16 | 12 | 1 | -2.16 | -1.38 | -3.54 | -1.85 | -1.38 | -3.23 | |
| 17 | 12 | 1 | -2.16 | -1.38 | -3.54 | -1.85 | -1.38 | -3.23 | |
| 18 | 15 | 1 | -2.16 | -1.73 | -3.89 | -1.77 | -1.87 | -3.64 | |
| 19 | 17 | 1 | -2.16 | -1.96 | -4.12 | -1.72 | -2.22 | -3.95 | |
| 20 | 22 | 1 | -2.16 | -2.54 | -4.70 | -1.63 | -3.16 | -4.79 | |
| 21 | 23 | 1 | -2.16 | -2.65 | -4.81 | -1.61 | -3.36 | -4.97 | |
| 6-MP群 | 1 | 6 | 1 | -3.69 | -0.150 | -3.84 | -3.83 | -0.0949 | -3.93 |
| 2 | 6 | 1 | -3.69 | -0.150 | -3.84 | -3.83 | -0.0949 | -3.93 | |
| 3 | 6 | 1 | -3.69 | -0.150 | -3.84 | -3.83 | -0.0949 | -3.93 | |
| 4 | 6 | 0 | -3.69 | -0.150 | -0.150 | -3.83 | -0.0949 | -0.0949 | |
| 5 | 7 | 1 | -3.69 | -0.175 | -3.86 | -3.78 | -0.117 | -3.90 | |
| 6 | 9 | 0 | -3.69 | -0.226 | -0.226 | -3.69 | -0.165 | -0.165 | |
| 7 | 10 | 1 | -3.69 | -0.251 | -3.94 | -3.65 | -0.191 | -3.84 | |
| 8 | 10 | 0 | -3.69 | -0.251 | -0.251 | -3.65 | -0.191 | -0.191 | |
| 9 | 11 | 0 | -3.69 | -0.276 | -0.276 | -3.61 | -0.217 | -0.217 | |
| 10 | 13 | 1 | -3.69 | -0.326 | -4.01 | -3.55 | -0.273 | -3.82 | |
| 11 | 16 | 1 | -3.69 | -0.401 | -4.09 | -3.48 | -0.362 | -3.84 | |
| 12 | 17 | 0 | -3.69 | -0.426 | -0.426 | -3.45 | -0.394 | -0.394 | |
| 13 | 19 | 0 | -3.69 | -0.476 | -0.476 | -3.41 | -0.458 | -0.458 | |
| 14 | 20 | 0 | -3.69 | -0.501 | -0.501 | -3.39 | -0.492 | -0.492 | |
| 15 | 22 | 1 | -3.69 | -0.552 | -4.24 | -3.36 | -0.560 | -3.92 | |
| 16 | 23 | 1 | -3.69 | -0.577 | -4.26 | -3.34 | -0.595 | -3.94 | |
| 17 | 25 | 0 | -3.69 | -0.627 | -0.627 | -3.31 | -0.667 | -0.667 | |
| 18 | 32 | 0 | -3.69 | -0.802 | -0.802 | -3.22 | -0.934 | -0.934 | |
| 19 | 32 | 0 | -3.69 | -0.802 | -0.802 | -3.22 | -0.934 | -0.934 | |
| 20 | 34 | 0 | -3.69 | -0.852 | -0.852 | -3.20 | -1.01 | -1.01 | |
| 21 | 35 | 0 | -3.69 | -0.877 | -0.877 | -3.19 | -1.06 | -1.06 | |
| 計 | -108.52 | 計 | -106.58 | ||||||
この結果から、対数尤度統計量 D = 2[ -106.58 - ( -108.52 ) ] = 3.89 であり、パラメータ数は、ワイブル分布が 3 なのに対して指数分布は 2 なので、D は自由度 3 - 2 = 1 の χ2-分布に従い、その p 値を計算すると 0.0486 となります。よって、多少の差異はあるものの、ワイブル分布の方が極端に当てはめ方がよいというわけではなさそうです。下図は、生存時間と生存関数の関係を、実測値と当てはめ値の両方についてプロットした結果で、階段上の点線と点で表現された方が実測値、実線で表された方が当てはめた曲線になります。グラフで見ても、指数分布とワイブル分布で大きな差は見られません。
| 指数分布 | ワイブル分布 |
|---|---|
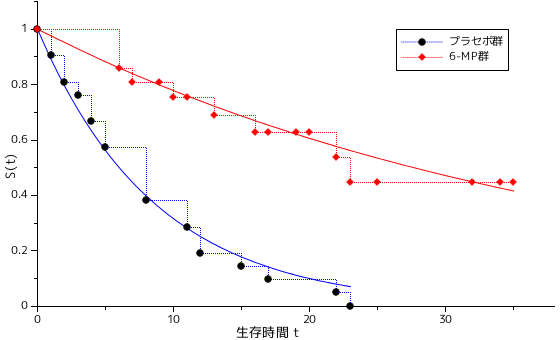 |
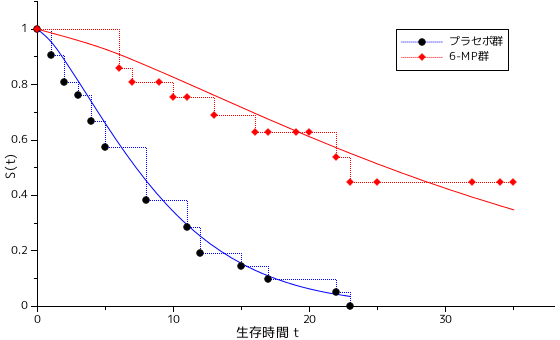 |
| 図 3-3. 対数生存時間と対数累積ハザードの相関図 | |
*3-1) 一般化した比例ハザードモデルは
となり、r( x ) = exp( xTα ) としたものを「コックス比例ハザードモデル」というようです。しかし、ほとんどの場合はコックス比例ハザードモデルが利用されるので、これを単に比例ハザードモデルと呼ぶことが多いらしく、参考文献でもそのような記述となっていました。ここでは、"コックス" の文字は省略して記述しています。
生存時間解析における対数尤度関数 l は
と表されるのでした。ここで、h(t) はハザード関数、S(t) は生存関数です。指数分布の場合は h(t) = θ より時間に依存せず一定であることになり、ワイブル分布は h(t) = λφtλ-1 より時間とともに増加すると仮定されます。ハザード関数 h(t) は、t まで生存していた時に t ≤ T < t + δt の間に死亡する条件付き確率の極限を意味していました。つまり、指数分布によるモデルなら死亡率が常に一定であり、ワイブル分布は時間に依存して増加することになります。比例ハザードモデルは、この死亡率が独立変数によって比例するというモデルでした。
l の式は、この死亡率 ( ハザード関数 h(t) ) に生存関数が作用した形になっています。すなわち、打ち切りがないデータに対しては
| li | = | ln( h( ti ) ) + ln( S( ti ) ) |
| = | ln( h0( ti )exp( xTα ) ) + ln( S( ti ) ) |
より、ln( S( ti ) ) はモデルに対する残差であると見ることができます。この値は、S(t) が確率値であることから必ず負数となるため、
を残差とします。これを「コックス・スネル残差 (Cox-Snell Residuals)」といいます。但し、S(t) はスコア法にて求めた係数から計算した推定生存関数とします。また、打ち切りデータに対しては残差を大きく見積もるため、正値の定数 Δ を加算します。すなわち、コックス・スネル残差 rCi は
と定義されます。Δ として 1 または ln 2 が一般的に利用されるようです。
S(t) は確率値なので定義域は [ 0, 1 ] です。S(t) が「一様分布 (Uniform Distribution)」P0,1(t) に従うと仮定すると、x = -ln t と変数変換した時 dx = -dt / t = -e-xdt で、t→0 のとき x→∞、t→1 のとき x→0 なので、確率密度関数は e-x、すなわち θ = 1 の指数分布に従います。このことからコックス・スネル残差は、モデルの当てはめがよければ指数分布 e-x に従い、その平均と分散はどちらも 1 に近い値となります。また、式から明らかにコックス・スネル残差は正値しかとらず、指数分布に従うことから正の方向に歪んだ分布となります。
その他の残差としては「マルチンゲール残差 (Martingale Residuals)」が挙げられます。この残差は以下の式で定義されます。
ri が指数分布 e-x に従うなら、非打ち切りデータのみの場合 rMi の平均はゼロになりますが、分布としてはコックス・スネル残差とは逆に負の方向に歪んだ分布となります。
残差を、ゼロを中心とした対称な分布になるよう調整したものに「逸脱度残差 (Deviance Residuals)」があります。これは以下の式で定義されます。
但し、sign( x ) は x の符号を表し、x が正値なら 1、負値なら -1 になります。
前節のデータから残差を計算した結果を以下に示します。コックス・スネル残差 rCi は (1) と (2) の二種類がありますが、それぞれ Δ = 1, Δ = ln 2 として計算した結果を表しています。
| 群 | No. | 生存時間 t | 打ち切り 有=0/無=1 | 指数分布 | ワイブル分布 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ri | rCi(1) | rCi(2) | rMi | rDi | ri | rCi(1) | rCi(2) | rMi | rDi | ||||
| プラセボ群 | 1 | 1 | 1 | 0.115 | 0.115 | 0.115 | 0.885 | 1.60 | 0.0464 | 0.0464 | 0.0464 | 0.954 | 2.06 |
| 2 | 1 | 1 | 0.115 | 0.115 | 0.115 | 0.885 | 1.60 | 0.0464 | 0.0464 | 0.0464 | 0.954 | 2.06 | |
| 3 | 2 | 1 | 0.231 | 0.231 | 0.231 | 0.769 | 1.18 | 0.120 | 0.120 | 0.120 | 0.880 | 1.58 | |
| 4 | 2 | 1 | 0.231 | 0.231 | 0.231 | 0.769 | 1.18 | 0.120 | 0.120 | 0.120 | 0.880 | 1.58 | |
| 5 | 3 | 1 | 0.346 | 0.346 | 0.346 | 0.654 | 0.902 | 0.208 | 0.208 | 0.208 | 0.792 | 1.25 | |
| 6 | 4 | 1 | 0.462 | 0.462 | 0.462 | 0.538 | 0.685 | 0.308 | 0.308 | 0.308 | 0.692 | 0.985 | |
| 7 | 4 | 1 | 0.462 | 0.462 | 0.462 | 0.538 | 0.685 | 0.308 | 0.308 | 0.308 | 0.692 | 0.985 | |
| 8 | 5 | 1 | 0.577 | 0.577 | 0.577 | 0.423 | 0.504 | 0.418 | 0.418 | 0.418 | 0.582 | 0.762 | |
| 9 | 5 | 1 | 0.577 | 0.577 | 0.577 | 0.423 | 0.504 | 0.418 | 0.418 | 0.418 | 0.582 | 0.762 | |
| 10 | 8 | 1 | 0.923 | 0.923 | 0.923 | 0.0769 | 0.0790 | 0.794 | 0.794 | 0.794 | 0.206 | 0.222 | |
| 11 | 8 | 1 | 0.923 | 0.923 | 0.923 | 0.0769 | 0.0790 | 0.794 | 0.794 | 0.794 | 0.206 | 0.222 | |
| 12 | 8 | 1 | 0.923 | 0.923 | 0.923 | 0.0769 | 0.0790 | 0.794 | 0.794 | 0.794 | 0.206 | 0.222 | |
| 13 | 8 | 1 | 0.923 | 0.923 | 0.923 | 0.0769 | 0.0790 | 0.794 | 0.794 | 0.794 | 0.206 | 0.222 | |
| 14 | 11 | 1 | 1.27 | 1.27 | 1.27 | -0.269 | -0.248 | 1.23 | 1.23 | 1.23 | -0.227 | -0.211 | |
| 15 | 11 | 1 | 1.27 | 1.27 | 1.27 | -0.269 | -0.248 | 1.23 | 1.23 | 1.23 | -0.227 | -0.211 | |
| 16 | 12 | 1 | 1.38 | 1.38 | 1.38 | -0.385 | -0.344 | 1.38 | 1.38 | 1.38 | -0.381 | -0.341 | |
| 17 | 12 | 1 | 1.38 | 1.38 | 1.38 | -0.385 | -0.344 | 1.38 | 1.38 | 1.38 | -0.381 | -0.341 | |
| 18 | 15 | 1 | 1.73 | 1.73 | 1.73 | -0.731 | -0.604 | 1.87 | 1.87 | 1.87 | -0.874 | -0.701 | |
| 19 | 17 | 1 | 1.96 | 1.96 | 1.96 | -0.962 | -0.759 | 2.22 | 2.22 | 2.22 | -1.22 | -0.921 | |
| 20 | 22 | 1 | 2.54 | 2.54 | 2.54 | -1.54 | -1.10 | 3.16 | 3.16 | 3.16 | -2.16 | -1.42 | |
| 21 | 23 | 1 | 2.65 | 2.65 | 2.65 | -1.65 | -1.16 | 3.36 | 3.36 | 3.36 | -2.36 | -1.51 | |
| 平均 | 1.00 | 1.00 | 0.000 | 0.207 | 平均 | 1.00 | 1.00 | 0.000 | 0.345 | ||||
| Median | 0.923 | 0.923 | 0.0769 | 0.0790 | Median | 0.794 | 0.794 | 0.206 | 0.222 | ||||
| 不偏分散 | 0.557 | 0.557 | 0.557 | 0.657 | 不偏分散 | 0.934 | 0.934 | 0.934 | 1.09 | ||||
| 6-MP群 | 1 | 6 | 1 | 0.150 | 0.150 | 0.150 | 0.850 | 1.45 | 0.0949 | 0.0949 | 0.0949 | 0.905 | 1.70 |
| 2 | 6 | 1 | 0.150 | 0.150 | 0.150 | 0.850 | 1.45 | 0.0949 | 0.0949 | 0.0949 | 0.905 | 1.70 | |
| 3 | 6 | 1 | 0.150 | 0.150 | 0.150 | 0.850 | 1.45 | 0.0949 | 0.0949 | 0.0949 | 0.905 | 1.70 | |
| 4 | 6 | 0 | 0.150 | 1.15 | 0.844 | -0.150 | -0.548 | 0.0949 | 1.09 | 0.788 | -0.095 | -0.436 | |
| 5 | 7 | 1 | 0.175 | 0.175 | 0.175 | 0.825 | 1.35 | 0.117 | 0.117 | 0.117 | 0.883 | 1.59 | |
| 6 | 9 | 0 | 0.226 | 1.23 | 0.919 | -0.226 | -0.672 | 0.165 | 1.17 | 0.858 | -0.165 | -0.575 | |
| 7 | 10 | 1 | 0.251 | 0.251 | 0.251 | 0.749 | 1.13 | 0.191 | 0.191 | 0.191 | 0.809 | 1.30 | |
| 8 | 10 | 0 | 0.251 | 1.25 | 0.944 | -0.251 | -0.708 | 0.191 | 1.19 | 0.884 | -0.191 | -0.618 | |
| 9 | 11 | 0 | 0.276 | 1.28 | 0.969 | -0.276 | -0.743 | 0.217 | 1.22 | 0.910 | -0.217 | -0.659 | |
| 10 | 13 | 1 | 0.326 | 0.326 | 0.326 | 0.674 | 0.946 | 0.273 | 0.273 | 0.273 | 0.727 | 1.07 | |
| 11 | 16 | 1 | 0.401 | 0.401 | 0.401 | 0.599 | 0.793 | 0.362 | 0.362 | 0.362 | 0.638 | 0.869 | |
| 12 | 17 | 0 | 0.426 | 1.43 | 1.12 | -0.426 | -0.923 | 0.394 | 1.39 | 1.09 | -0.394 | -0.887 | |
| 13 | 19 | 0 | 0.476 | 1.48 | 1.17 | -0.476 | -0.976 | 0.458 | 1.46 | 1.15 | -0.458 | -0.957 | |
| 14 | 20 | 0 | 0.501 | 1.50 | 1.19 | -0.501 | -1.00 | 0.492 | 1.49 | 1.18 | -0.492 | -0.992 | |
| 15 | 22 | 1 | 0.552 | 0.552 | 0.552 | 0.448 | 0.541 | 0.560 | 0.560 | 0.560 | 0.440 | 0.529 | |
| 16 | 23 | 1 | 0.577 | 0.577 | 0.577 | 0.423 | 0.504 | 0.595 | 0.595 | 0.595 | 0.405 | 0.478 | |
| 17 | 25 | 0 | 0.627 | 1.63 | 1.32 | -0.627 | -1.12 | 0.667 | 1.67 | 1.36 | -0.667 | -1.15 | |
| 18 | 32 | 0 | 0.802 | 1.80 | 1.50 | -0.802 | -1.27 | 0.934 | 1.93 | 1.63 | -0.934 | -1.37 | |
| 19 | 32 | 0 | 0.802 | 1.80 | 1.50 | -0.802 | -1.27 | 0.934 | 1.93 | 1.63 | -0.934 | -1.37 | |
| 20 | 34 | 0 | 0.852 | 1.85 | 1.55 | -0.852 | -1.31 | 1.01 | 2.01 | 1.71 | -1.01 | -1.42 | |
| 21 | 35 | 0 | 0.877 | 1.88 | 1.57 | -0.877 | -1.32 | 1.06 | 2.06 | 1.75 | -1.06 | -1.45 | |
| 平均 | 1.00 | 0.825 | 0.000 | -0.107 | 平均 | 1.00 | 0.825 | 0.000 | -0.0451 | ||||
| Median | 1.23 | 0.919 | -0.226 | -0.672 | Median | 1.17 | 0.858 | -0.165 | -0.575 | ||||
| 不偏分散 | 0.432 | 0.264 | 0.432 | 1.19 | 不偏分散 | 0.512 | 0.333 | 0.512 | 1.43 | ||||
下図は、コックス・スネル残差 (Δ = 1) と逸脱度残差の箱ひげ図をプラセボ群と 6-MP 群それぞれで比較した結果で、上側が指数分布、下側がワイブル分布をモデルにした場合のグラフです。マルチンゲール残差は、式からも明らかなようにコックス・スネル残差の分布を逆にした形状となるだけなのでグラフは省略しています。
| 指数分布 | |
|---|---|
| コックス・スネル残差 | 逸脱度残差 |
 |
 |
| ワイブル分布 | |
| コックス・スネル残差 | 逸脱度残差 |
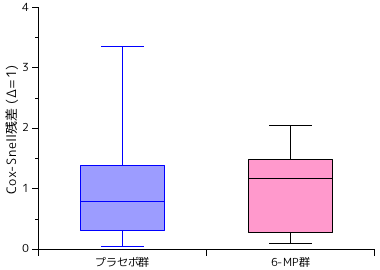 |
 |
| 図 4-1. 各モデルの残差の分布 | |
コックス・スネル残差が正値の方向に歪んだ分布となっているのに対し、逸脱度残差はゼロを中心とした対称に近い分布形状となっていることがこの結果から読み取れます。
生存時間解析については一冊の分厚い書籍が出版されているほど内容が豊富で奥が深い分野です。今回は、その中の一部分だけを紹介しただけの形となります。もし、詳細について興味のある方は、一度書籍を調べて見ることをお勧めします。
ワイブル分布に対する最大対数尤度の計算においては、
としていましたが、θ に対して
とするやり方も考えることができます。この場合、uλ の値は変化しませんが、uj は
∂φi / ∂αj = ( ∂ / ∂θi )θi-λ( ∂θi / ∂αj ) = -λθi-λ-1xij / g'(θi)
∂ln φi / ∂αj = -λθi-λ-1xij / φig'(θi) = -λxij / θig'(θi)
より
| uj | = | ( ∂ / ∂αj )Σi{1→n}( δi[ ln λ + ln φi + ( λ - 1 )ln ti ] - φitiλ ) |
| = | Σi{1→n}( λ( -δi / θi + θi-λ-1tiλ )xij / g'(θi) ) | |
| = | Σi{1→n}( λ( -δi + θi-λtiλ )xij / θig'(θi) ) | |
| = | Σi{1→n}( λ( -δi + φitiλ )xij / θig'(θi) ) |
となり、
( ∂ / ∂αk )( δi / θi ) = ( -δi / θi2 )[ xik / g'(θi) ]
( ∂ / ∂αk )θi-λ-1 = -( λ + 1 )θi-λ-2[ xik / g'(θi) ]
( ∂ / ∂αk )g'(θi) = g(2)(θi)[ xik / g'(θi) ]
より ∂uj / αk は
| ∂uj / ∂αk | = | ( ∂ / ∂αk )Σi{1→n}( λ( -δi / θi + θi-λ-1tiλ )xij / g'(θi) ) |
| = | Σi{1→n}( λ{ [ δi / θi2 - ( λ + 1 )θi-λ-2tiλ ]g'(θi) - ( -δi / θi + θi-λ-1tiλ )g(2)(θi) }[ xij / g'(θi)2 ][ xik / g'(θi) ] ) | |
| = | Σi{1→n}( λ{ [ δi - ( λ + 1 )θi-λtiλ ]g'(θi) + ( δi - θi-λtiλ )θig(2)(θi) }xijxik / θi2g'(θi)3 ) | |
| = | Σi{1→n}( λ{ [ δi - ( λ + 1 )φitiλ ]g'(θi) + ( δi - φitiλ )θig(2)(θi) }xijxik / θi2g'(θi)3 ) |
∂uj / ∂λ は
| ∂uj / ∂λ | = | ( ∂ / ∂λ )Σi{1→n}( λ( -δi / θi + θi-λ-1tiλ )xij / g'(θi) ) |
| = | Σi{1→n}( [ ( -δi / θi + θi-λ-1tiλ ) + λ( -θi-λ-1tiλln θi + θi-λ-1tiλln ti ) ]xij / g'(θi) ) | |
| = | Σi{1→n}( { ( -δi + θi-λtiλ ) + λ[ θi-λtiλln( ti / θi ) ] }xij / θig'(θi) ) | |
| = | Σi{1→n}( { -δi + φitiλ[ λln( ti / θi ) + 1 ] }xij / θig'(θi) ) |
となります。ここで g(θi) = ln θi とすれば
uj = Σi{1→n}( λ( -δi + φitiλ )xij )
| ∂uj / ∂αk | = | Σi{1→n}( λ{ [ δi - ( λ + 1 )φitiλ ] / θi - ( δi - φitiλ ) / θi }xijxikθi ) |
| = | Σi{1→n}( λ[ -( λ + 1 )φitiλ + φitiλ ]xijxik ) | |
| = | Σi{1→n}( -λ2φitiλxijxik ) |
∂uj / ∂λ = Σi{1→n}( { -δi + φitiλ[ λln( ti / θi ) + 1 ] }xij )
という結果が得られます。この式を用いて係数を求めた場合、以下のような結果が得られました。
θ = exp( 2.25 + 1.27x ) ; λ = 1.37
| θ モデル | φ モデル | |||
|---|---|---|---|---|
| 推定値 | 標準誤差 | 推定値 | 標準誤差 | |
| 切片 α0 | 2.25 | 0.166 | -3.07 | 0.227 |
| 傾き α1 | 1.27 | 0.311 | -1.73 | 0.424 |
| 形状パラメータ λ | 1.37 | 0.201 | 1.37 | 0.201 |
表の右側は φ = ln xTα としたときの ( 本章で求めた ) 係数です。どちらのモデルでも λ の推定結果は等しく、φ = θ-λ より、φ モデルでの切片と傾きを -λ で割れば θ モデルの値と等しくなります。
計算式の複雑さはどちらも同程度であり、指数分布と比較するには θ モデルの方がよさそうなのですが、参考文献では φ を用いていたことと、θ モデルでは初期値の問題でスコア法による反復処理が収束しなかったため ( 上記計算は、初期値を近い値に固定しておいて処理させました )、φ モデルの方を本章では採用しています。初期値の設定は、係数をゼロ、λ を 1 に固定しているため、実際には近似値を計算して代入するような前処理が必要です。サンプル・プログラムではこのあたりを手抜きしているため、このような問題が発生しています。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |