最小二乗法を原理とする重回帰モデルは、標本数が推定したい係数 ( 独立変数の種類 ) に対して十分に大きいことを前提としています。しかし、場合によっては十分な標本が得られなかったり、波形データなど、変数の種類が非常に多い場合があり、しかも独立変数どうしで相関があるような場合、通常の重回帰モデルでは処理ができなかったり、処理できたとしても正しい結果が得られないような場合があります。これは、独立変数の種類を少なくして相関を減らすことで回避することができるため、今回はそのための手法である「主成分回帰 ( Principal Component Regression ; PCR )」と「部分最小二乗法 ( Partial Least Squares ; PLS )」を紹介したいと思います。
以前、連立方程式の解法についていくつかのアルゴリズムを紹介しました。この中で、連立方程式を解くことができない場合として、解を求めることができない「不能」と解が定まらない「不定」について説明をしました。まずは、この内容をもう一度整理しておきます。
連立方程式が少なくとも一つ解を持つ場合を「無矛盾 ( Consistent )」といいます。"普通に" 解が得られる場合の他に、解が「不定」の場合も無矛盾となります。解を一つも持たなければ「矛盾 (Inconsistent)」といいます。よって「不能」ということは「矛盾している」ということになります。例として、
は解を持たないため「矛盾」となります。また、
は、( x, y ) = ( 1, 2 ), ( 3, 1 ) など無数にあるため「不定」になりますが「無矛盾」です。
は唯一の解 ( x, y ) = ( 2, 3 ) を持つのでこれも「無矛盾」となります。
連立方程式が「無矛盾」となるのはどのような場合でしょうか。矛盾な方程式の例を以下のように書きなおしてみます。
| x | | | 3 | | | + | y | | | 2 | | | = | | | 6 | | |
| | | 6 | | | | | 4 | | | | | 8 | | | ||||
この式が成り立つためには、ベクトル ( 6, 8 )T が ( 3, 6 )T と ( 2, 4 )T の線形結合で表すことが可能でなければなりません。それが可能な時、x, y は線形和の係数を意味します。しかし、この例では x, y をどのようにしても両辺を等しくすることができません。一般的に、係数行列 A の連立方程式 Ax = b が無矛盾であるためには、b が A の列ベクトルの線形結合で表せることが必要十分条件となります。
また連立方程式が「無矛盾」なとき、解が一意に決まるためには、A の列ベクトルが全て線形独立でなければなりません (*1-1)。このとき、A は逆行列 A-1 を持ち、連立方程式 Ax = b の解は
によって求められます。
式の数に対して未知数の数が多ければ、未知数の決め方は複数考えることができるので必ず「不定」になります。逆に未知数の数が少ない時、通常は「不能」となりますが、式に適当な数を乗除することで同じ式になるものが混在していれば、解が一意に決まったり、逆に「不定」となる場合もあります。
係数行列 A が逆行列を持たず解が一意に決まらなかったり、矛盾しているために解が得られないような場合も「意味のある解」を得たい場合があります。「最小二乗法 ( Least Squares )」はその代表的な例であり、左辺の式によって得られる値と右辺の解との差を全ての式について二乗して和を計算した時、その値が最小になるような未知数を解とするのが最小二乗法の考え方でした。また、不定であれば解は無数にあるので、その中から「代表」となるような解を決める方法が考えられます。
逆行列を持つ行列は「正則行列 (Regular Matrix)」と呼ばれます。正則ではない正方行列である「特異行列 (Singular Matrix)」や、もっと一般に正方ではない行列に対しても逆行列の概念を導入するため、m 行 n 列の行列 A に対して次のような定義の n 行 m 列の行列 A- を考えます。
もし A が正則行列なら、逆行列 A-1 は上式を満たすので、A- は逆行列の一般化と考えることができます。これを「一般逆行列 (Generalized Inverse )」または「擬似逆行列 (Pseudo Inverse)」といいます。連立方程式 Ax = b の両辺に AA- を左側から掛けると
となり、左辺は Ax と等しいので、A-b は連立方程式の解と考えることができます。
全ての行列は必ず一般逆行列を持ちます。また、無矛盾な連立方程式で解が無数に存在する場合があることからも明らかなように、一般逆行列は一つだけとは限りません (補足 1)。例えば、
| | | 2, | 4 | | |
| | | 1, | 2 | | |
の一般逆行列を
| | | a, | c | | |
| | | b, | d | | |
としたとき、2a + 4b + c + 2d = 1 を満たす任意の ( a, b, c, d ) を持つ行列は全て対象になるので、例えば
| | | 0, | 1 | | | | | 1, | -1 | | | |
| | | 0, | 0 | | | , | | | 1, | -2 | | |
などが一般逆行列となります。
先述の通り、正則行列を除いて一般逆行列は無尽蔵に作成することができますが、この中でも有用なものが存在します。まず、
を満たす ( すなわち A-A が対称行列となる ) 一般逆行列 A- を A の「最小ノルム形一般逆行列 (Minimum Norm Generalized Inverse)」といいます。これも一般逆行列の一つなので、
が成り立ちますが、この式から得られる解 x = A-b のノルム ||x|| が最小となるという特徴を持つためこの名が付けられています (補足 2)。先ほど示した、解が不定な連立方程式
は、x = 5 - 2y が成り立つので、x2 + y2 は
| x2 + y2 | = | ( 5 - 2y )2 + y2 |
| = | 5( y - 2 )2 + 5 |
より ( x, y ) = ( 1, 2 ) のとき最小値をとります。
| A- = | | | a, | c | | |
| | | b, | d | | |
としたとき、
| | | a, | c | || | 10 | | | = | | | 1 | | |
| | | b, | d | || | 5 | | | | | 2 | | |
より
を満たす ( a, b, c, d ) であれば何でもよく、例えば
| A- = | | | 0, | 1/5 | | |
| | | 1/10, | 1/5 | | |
は上式を満たし、
| A-A = | | | 0, | 1/5 | || | 2, | 4 | | | = | | | 1/5, | 2/5 | | |
| | | 1/10, | 1/5 | || | 1, | 2 | | | | | 2/5 | 4/5 | | |
なので確かに A-A は対称行列となっています。
A の一般逆行列 A- が
を満たす ( すなわち AA- が対称行列となる ) とき、A- を A の「最小二乗形一般逆行列 (Least Squares Generalized Inverse)」といいます。最小二乗法の正規方程式 XTXa = XTy の解を Gy としたとき、
より ( y が任意であれば ) XTXG = XT が成り立ちます (補足 3)。両辺に右側から X を掛けて
より XGX = X が成り立つので (補足 3) G は X の一般逆行列であり、XTXG = XT の両辺を転置した
の両辺に右側から G を掛けて
となります。任意の行列とその転置行列の積は対称行列なので、XG は対称行列となり、G は最小二乗形一般逆行列であることになります。
「最小ノルム形一般逆行列」と「最小二乗形一般逆行列」の条件を満たし、さらに
の条件を満たす一般逆行列を「ムーア-ペンローズ形逆行列 ( Moore-Penrose Inverse )」といい A+ で表します。一般逆行列が複数あり得るのに対してムーア-ペンローズ形は一意に決まり (補足 4)、A = LR とし、LTART = (LTL)(RRT) が逆行列を持つとき、
とすれば、
AA+A = LRRT(RRT)-1(LTL)-1LTLR = LR = A
A+AA+ = RT(RRT)-1(LTL)-1LTLRRT(RRT)-1(LTL)-1LT = RT(RRT)-1(LTL)-1LT = A+
となるので、反射形の一般逆行列となります。また、
より
であり、LTL は対称行列でその逆行列も対称であることから [ (LTL)-1 ]T = (LTL)-1 なので、
が成り立ちます。さらに
なので同様に
となり、A+ は「最小ノルム形一般逆行列」「最小二乗形一般逆行列」の条件も満たすことになります。
最小二乗法によって得られる線形重回帰モデルの正規方程式は以下の式となるのでした。
もし、XTX が逆行列を持つならば、(XTX)-1XTy が求める最小二乗解となり、(XTX)-1XT は
より X の一般逆行列であり、
より反射形であり、
より最小二乗形であり、
より最小ノルム形なので、ムーア-ペンローズ形逆行列の条件を満たします。しかし、XTX が逆行列を持たなければ、正規方程式の解は一意にはならず、XTX の一般逆行列を G としたとき、正規方程式の両辺に左側から XTXG を掛けて
XTXGXTXa = XTXGXTy より
XTXa = XTXGXTy
なので、GXTy がその解の一つとなります。このとき、G が XTX の一般逆行列であることから
が成り立ち、XT(XGXTX) = XTX とすることで
が成り立つことがわかるので (補足 3) GXT は X の一般逆行列となります。
G は複数存在しますが、その中で XTX の最小ノルム形一般逆行列 H を選択したとします。このとき、
が成り立つので HXT は X の最小ノルム形一般逆行列であり、
より
が成り立つので (補足 3)、
より両辺に右側から HXT を掛けると
(HXT)TXTX(HXT) = X(HXT) より
(XHXT)T(XHXT) = XHXT
となり、XHXT は対称行列であることから HXT は X の最小二乗形一般逆行列です。最後に
なので HXT は反射形であり、HXT はムーア-ペンローズ形逆行列であることになります。
線形重回帰モデルでは、各独立変数ベクトルを行とした行列 X ( これを「デザイン行列 (Design Matrix)」といいます ) は通常 "縦長" の形となります。つまり、独立変数の種類 ( 例えば身長や体重などの連続値や性別などのカテゴリなど ) と比較してサンプルの数 ( 例えば被験者数など ) が十分に多いことが一般的であり、この場合は XTX の行列数が独立変数の種類と等しく、たいていは逆行列を持つので最小二乗解も一意に決まります。しかし、サンプル数が極端に少なかったり、独立変数の要素数が非常に多い場合はこの前提が成り立ちません。その場合、解は一意に決めることができませんが、一つの決め方として XTX の最小ノルム形一般逆行列 H を選択して HXTy を解とすれば、HXT はムーア-ペンローズ形逆行列なので一意に解が決まり、その解は最小二乗解であると同時に最小ノルム解にもなります。特に、H が XTX のムーア-ペンローズ形逆行列であったとき、L = XT, R = X とすれば、
と表されるので、
という結果が得られます。これは XXT が逆行列を持つ場合に相当し、比較的簡単に解を得ることができることを意味します。
最後に、対称行列の「固有値分解 (Eigendecomposition)」や「特異値分解 (Singular Value Decomposition)」とムーア-ペンローズ形逆行列の関係について紹介します (*1-2)。まず、二つの直交行列 P, Q に挟まれた任意の行列 PAQT のムーア-ペンローズ形逆行列を考えます。このとき、
とすると、
PAQTQA+PTPAQT = PAA+AQT = PAQT (一般逆行列)
QA+PTPAQTQA+PT = QA+AA+PT = QA+PT (反射形)
(PAQTQA+PT)T = P(AA+)TPT = PAA+PT = PAQTQA+PT (最小二乗形)
(QA+PTPAQT)T = Q(A+A)TQT = QA+AQT = QA+PTPAQT (最小ノルム形)
となり、四つの条件を全て満たしていることがわかります。特に、A が ( 対角成分にゼロを含むことも許容した ) 対角行列 D であったとき、D の i 行 i 列目の要素を λi として、D+ の対角成分 λ+i を
| λ+i | = | 1 / λi | ( λi ≠ 0 ) |
| = | 0 | ( λi = 0 ) |
とすれば ( D と D+ の積は対角行列なので、対角成分のみを計算して )、
DD+D = { δ, δ, ... δ }D = { λ1, λ2, ... } = D (一般逆行列)
D+DD+ = { δ, δ, ... δ }D+ = { λ+1, λ+2, ... } = D+ (反射形)
であり ( 但し δ は λi ≠ 0 のとき 1、λi = 0 のとき 0 を表すとします )、DD+, D+D は明らかに対称行列なのでムーア-ペンローズ形逆行列となります。
任意の非特異な対称行列 A は、固有値からなる対角行列 D と固有ベクトルを列とする直交行列 Q を使って以下の式で表すことができます。
これを「固有値分解 (Eigendecomposition)」というのでした。さらに、A が任意の行列になっても、AAT と ATA のゼロでない固有値が全て等しく なることから、ゼロでない固有値を対角成分とした対角行列を D、AAT の固有ベクトルを列ベクトルとする行列を U、ATA の固有ベクトルを列ベクトルとする行列を V としたとき、
| A = U | | | D, | 0 | |VT |
| | | 0, | 0 | | |
で表されます。A が m 行 n 列の行列ならば、U はサイズ m、V はサイズ n の正方行列となります。これを「特異値分解 (Singular Value Decomposition)」というのでした。従って、今までの議論から
| A+ = V | | | D+, | 0 | |UT |
| | | 0, | 0 | | |
という結果が得られ、任意の行列は特異値分解の結果から簡単にムーア-ペンローズ形逆行列が得られることを意味しています。
*1-1) あるベクトル群が線形独立なとき、任意のベクトル ( 但しベクトル群に対して線形従属でなければなりません ) はそのベクトル群を使って一意の線形結合で表すことができます。詳細は「数値演算法 (8) 連立方程式を解く -2-」の「5) 固有値と固有ベクトル」で紹介しています。
*1-2) 「固有値 (Eigenvalue)」と「固有ベクトル (Eigenvector)」及びそれらを使った「行列の対角化」については「数値演算法 (8) 連立方程式を解く -2-」の中の「5) 固有値と固有ベクトル」で紹介しています。また、対称行列の「固有値分解 (Eigendecomposition)」は「固有値問題 (1) 対称行列の固有値」の中の「3) 直交行列 (Orthogonal Matrix)」で、「特異値分解 (Singular Value Decomposition)」は「固有値問題 (3) 画像の固有空間」の中の「3) 特異値分解 (Singular Value Decomposition)」でそれぞれ説明しています。
線形重回帰モデルでは通常、標本数が回帰係数よりも多いので XTX は逆行列を持ち、最小二乗解として (XTX)-1XTy が得られます。この時、前節で説明した連立方程式の解の状態は「不能」です。ところが、標本の内容によっては逆に回帰係数の方が標本数より多いような場合もあり、この時に得られる解は最小ノルム解になるので本来得ようとしていたデータとはたいていかけ離れたものになります。また、各独立変数間で高い相関があったりするような場合を「多重共線性 (Multicollinearity)」といい、XTX の逆行列を計算しようとしても ( 係数の数よりランクが小さくなって ) 失敗したり、計算できたとしても実際とはかけ離れた結果になることもあります。
「計量化学 (Chemometrics)」と呼ばれる、実験データをコンピュータを利用して解析する化学の一分野では、大量の測定値を使って解析をする反面、その標本数は少なく、測定値間の相関が複雑に絡まって誤った解釈をしてしまう場合が多々あります。このようなときに利用できる手法の一つに「主成分回帰 ( Principal Component Regression ; PCR )」があります。
名前の通り、独立変数から共分散行列を求め、その固有値分解から主成分を抽出する「主成分分析 ( Principal Component Analysis ; PCA )」を利用した回帰分析で、独立変数の各要素間が無相関になるよう「主軸変換」され、その固有値は変換後の主軸で新たに表現される値 ( これを主成分と言います ) の分散値を意味します。固有値の大きな主軸のみを利用することで精度の高い近似値が得られるので次元を少なくすることも可能になり、先に述べたような多重共線性の問題を回避することができるようになります。
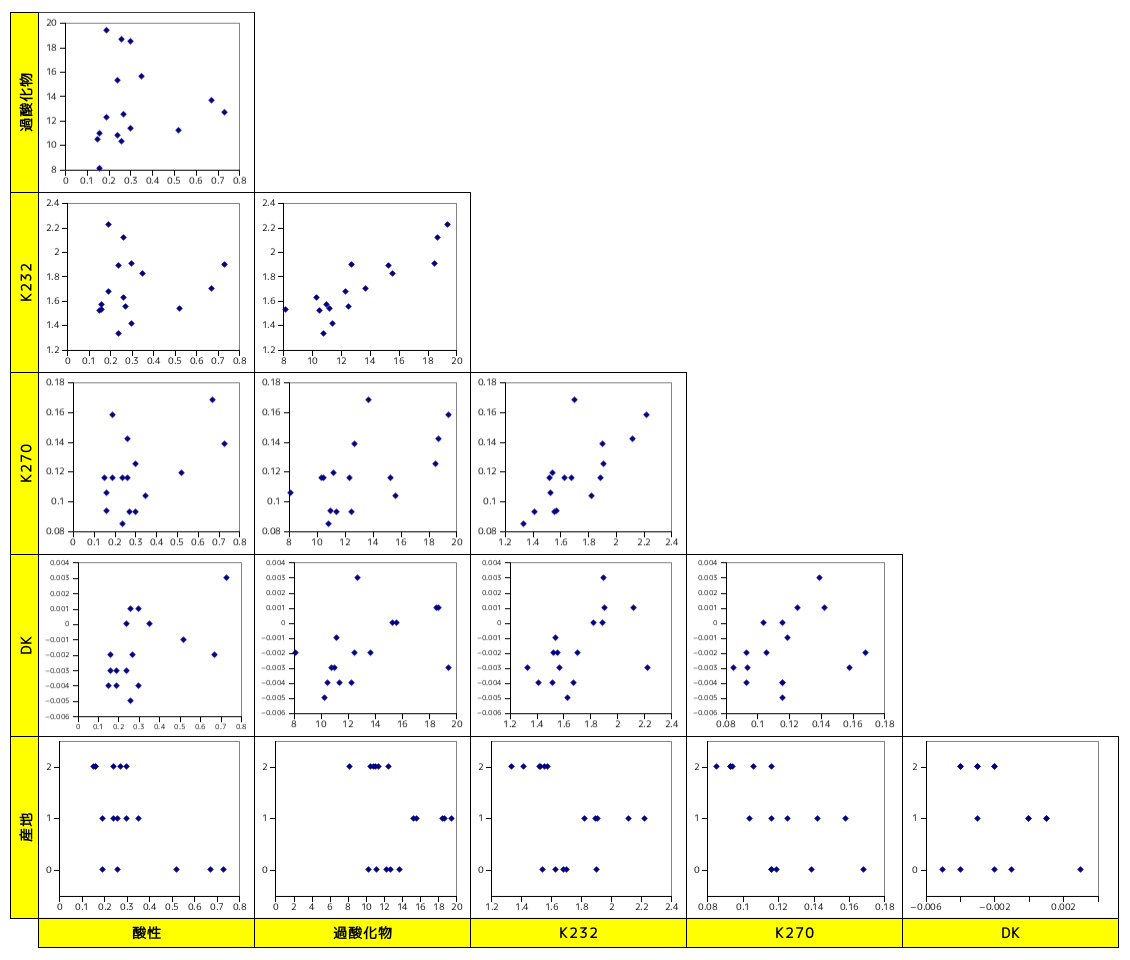
実際のデータで主成分回帰を試してみます。下記データは、統計計算用ツール R のパッケージ "pls" に付属しているサンプル・データの一つで、5 種類の物理化学的品質パラメータと官能検査から得られた 6 種類の特性値を 16 種類のオリーブオイルから得た結果です。最初の G1 〜 G5 がギリシャ産、次の I1 〜 I5 がイタリア産、最後の S1 〜 S6 がスペイン産です。
| オリーブオイル | 物理化学的品質パラメータ | 官能特性値 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 酸性 | 過酸化物 | K232 | K270 | DK | 黄色味 | 緑色味 | 茶色味 | 光沢 | 透明度 | 甘み | |
| G1 | 0.73 | 12.7 | 1.900 | 0.139 | 0.003 | 21.4 | 73.4 | 10.1 | 79.7 | 75.2 | 50.3 |
| G2 | 0.19 | 12.3 | 1.678 | 0.116 | -0.004 | 23.4 | 66.3 | 9.8 | 77.8 | 68.7 | 51.7 |
| G3 | 0.26 | 10.3 | 1.629 | 0.116 | -0.005 | 32.7 | 53.5 | 8.7 | 82.3 | 83.2 | 45.4 |
| G4 | 0.67 | 13.7 | 1.701 | 0.168 | -0.002 | 30.2 | 58.3 | 12.2 | 81.1 | 77.1 | 47.8 |
| G5 | 0.52 | 11.2 | 1.539 | 0.119 | -0.001 | 51.8 | 32.5 | 8.0 | 72.4 | 65.3 | 46.5 |
| I1 | 0.26 | 18.7 | 2.117 | 0.142 | 0.001 | 40.7 | 42.9 | 20.1 | 67.7 | 63.5 | 52.2 |
| I2 | 0.24 | 15.3 | 1.891 | 0.116 | 0 | 53.8 | 30.4 | 11.5 | 77.8 | 77.3 | 45.2 |
| I3 | 0.30 | 18.5 | 1.908 | 0.125 | 0.001 | 26.4 | 66.5 | 14.2 | 78.7 | 74.6 | 51.8 |
| I4 | 0.35 | 15.6 | 1.824 | 0.104 | 0 | 65.7 | 12.1 | 10.3 | 81.6 | 79.6 | 48.3 |
| I5 | 0.19 | 19.4 | 2.222 | 0.158 | -0.003 | 45.0 | 31.9 | 28.4 | 75.7 | 72.9 | 52.8 |
| S1 | 0.15 | 10.5 | 1.522 | 0.116 | -0.004 | 70.9 | 12.2 | 10.8 | 87.7 | 88.1 | 44.5 |
| S2 | 0.16 | 8.14 | 1.527 | 0.106 | -0.002 | 73.5 | 9.7 | 8.3 | 89.9 | 89.7 | 42.3 |
| S3 | 0.27 | 12.5 | 1.555 | 0.093 | -0.002 | 68.1 | 12.0 | 10.8 | 78.4 | 75.1 | 46.4 |
| S4 | 0.16 | 11.0 | 1.573 | 0.094 | -0.003 | 67.6 | 13.9 | 11.9 | 84.6 | 83.8 | 48.5 |
| S5 | 0.24 | 10.8 | 1.331 | 0.085 | -0.003 | 71.4 | 10.6 | 10.8 | 88.1 | 88.5 | 46.7 |
| S6 | 0.30 | 11.4 | 1.415 | 0.093 | -0.004 | 71.4 | 10.0 | 11.4 | 89.5 | 88.5 | 47.2 |
まずは、このデータに対して重回帰分析を行なってみます。独立変数は、5 つの物理化学的品質パラメータに産地 ( ギリシャ産 = 0, イタリア産 = 1, スペイン産 = 2 ) を追加して、「黄色味」から「甘み」まで個々に従属変数として処理します。処理結果を ANOVA 表で以下に示します。
| 従属変数 | 変動要因 | 平方和 | 自由度 | 不偏分散 | 分散比 ( F 値 ) | p 値 |
|---|---|---|---|---|---|---|
| 黄色味 | 予測値(回帰による) | 4551.7 | 6 | 758.6 | 6.05 | 0.0087 |
| 残差(回帰との) | 1127.9 | 9 | 125.3 | |||
| 観測値(全体) | 5679.6 | 15 | ||||
| 緑色味 | 予測値(回帰による) | 6194.9 | 6 | 1032.5 | 4.47 | 0.023 |
| 残差(回帰との) | 2079.7 | 9 | 231.1 | |||
| 観測値(全体) | 8274.6 | 15 | ||||
| 茶色味 | 予測値(回帰による) | 354.5 | 6 | 59.1 | 13.29 | 0.00051 |
| 残差(回帰との) | 40.0 | 9 | 4.45 | |||
| 観測値(全体) | 394.6 | 15 | ||||
| 光沢 | 予測値(回帰による) | 386.4 | 6 | 64.4 | 3.08 | 0.063 |
| 残差(回帰との) | 187.9 | 9 | 20.9 | |||
| 観測値(全体) | 574.4 | 15 | ||||
| 透明度 | 予測値(回帰による) | 680.5 | 6 | 113.4 | 2.88 | 0.075 |
| 残差(回帰との) | 354.7 | 9 | 39.4 | |||
| 観測値(全体) | 1035.2 | 15 | ||||
| 甘み | 予測値(回帰による) | 89.9 | 6 | 15.0 | 2.64 | 0.092 |
| 残差(回帰との) | 51.1 | 9 | 5.67 | |||
| 観測値(全体) | 141.0 | 15 |
p 値 < 0.01 は「黄色味」と「茶色味」だけで、全体として当てはめはあまりよくなさそうです。重相関係数と決定係数は次のようになります。
| 従属変数 | 重相関係数 | 決定係数 | 自由度調整済み決定係数 |
|---|---|---|---|
| 黄色味 | 0.895 | 0.801 | 0.669 |
| 緑色味 | 0.865 | 0.749 | 0.581 |
| 茶色味 | 0.948 | 0.899 | 0.831 |
| 光沢 | 0.820 | 0.673 | 0.455 |
| 透明度 | 0.811 | 0.657 | 0.429 |
| 甘み | 0.799 | 0.638 | 0.396 |
「自由度調整済み決定係数 (Adjusted R2)」とは、通常の決定係数が独立変数の種類を多くとるほど 1 に近づくので (「過剰適合 (Overfitting)」にも関係する現象で、要するに統計的な ( コントロールできない ) 誤差分がゼロに近づくためにそのようになります )、調整のために以下のような計算をした値です。
p = 0 のときは R~2 = R2 となり、p → n - 1 で R~2 → -∞ となります。調整の結果、茶色味以外はかなり低い値となっています。
 |
上図は、独立変数間の相関を表したグラフです。いくつかの変数について、互いに相関関係にあるものが見つかります。このことから、多重共線性によって回帰モデルが正しく生成されなかったことが考えられます。そこで、独立変数を主成分分析により主成分へ変換してみます。
| 固有値 | 寄与率 | 固有ベクトル |
|---|---|---|
| 10.6 | 0.938 | ( 0.00295189, 0.996187, 0.0650423, 0.00397745, 0.000325868, -0.0579344 ) |
| 0.665 | 0.0590 | ( 0.134083, -0.0616059, 0.0571816, 0.0144666, 0.000420742, -0.987293 ) |
| 0.0184 | 1.64E-03 | ( -0.932987, -0.0257005, 0.342861, -0.0125361, -0.00688786, -0.105433 ) |
| 0.0103 | 9.13E-04 | ( 0.331543, -0.0561684, 0.932844, 0.0768262, 0.00855904, 0.103689 ) |
| 0.000159 | 1.41E-05 | ( 0.0385293, -0.000922421, 0.0681348, -0.994623, 0.0675893, -0.00530878 ) |
| 1.10E-06 | 9.74E-08 | ( -0.0119536, 6.75257e-05, -0.0102973, 0.066631, 0.997653, -0.000822524 ) |
ほとんど第一主成分で近似ができることがこの結果からわかります。第一主成分の大部分は「過酸化物」で構成され、次の第二主成分は「産地」がほとんどを占めます。データをこの二つの主成分の固有ベクトルで変換し、再度重回帰モデルで検証してみます。
| 従属変数 | 変動要因 | 平方和 | 自由度 | 不偏分散 | 分散比 ( F 値 ) | p 値 |
|---|---|---|---|---|---|---|
| 黄色味 | 予測値(回帰による) | 4448.0 | 2 | 2224.0 | 23.48 | 4.84E-05 |
| 残差(回帰との) | 1231.6 | 13 | 94.7 | |||
| 観測値(全体) | 5679.6 | 15 | ||||
| 緑色味 | 予測値(回帰による) | 5909.9 | 2 | 2955.0 | 16.2 | 2.91E-04 |
| 残差(回帰との) | 2364.7 | 13 | 181.9 | |||
| 観測値(全体) | 8274.6 | 15 | ||||
| 茶色味 | 予測値(回帰による) | 257.0 | 2 | 128.5 | 12.1 | 1.06E-03 |
| 残差(回帰との) | 137.6 | 13 | 10.6 | |||
| 観測値(全体) | 394.6 | 15 | ||||
| 光沢 | 予測値(回帰による) | 359.9 | 2 | 179.9 | 10.9 | 1.66E-03 |
| 残差(回帰との) | 214.5 | 13 | 16.5 | |||
| 観測値(全体) | 574.4 | 15 | ||||
| 透明度 | 予測値(回帰による) | 631.4 | 2 | 315.7 | 10.2 | 2.20E-03 |
| 残差(回帰との) | 403.8 | 13 | 31.1 | |||
| 観測値(全体) | 1035.2 | 15 | ||||
| 甘み | 予測値(回帰による) | 86.8 | 2 | 43.4 | 10.4 | 1.99E-03 |
| 残差(回帰との) | 54.2 | 13 | 4.17 | |||
| 観測値(全体) | 141.0 | 15 |
重相関係数と決定係数は次のようになります。
| 従属変数 | 重相関係数 | 決定係数 | 自由度調整済み決定係数 |
|---|---|---|---|
| 黄色味 | 0.885 | 0.783 | 0.750 |
| 緑色味 | 0.845 | 0.714 | 0.670 |
| 茶色味 | 0.807 | 0.651 | 0.598 |
| 光沢 | 0.792 | 0.627 | 0.569 |
| 透明度 | 0.781 | 0.610 | 0.550 |
| 甘み | 0.785 | 0.616 | 0.557 |
独立変数の要素が減った分、F 値や p 値は改善されています。自由度調整済み決定係数も多少よくなっていますが、大幅に改善されたかというとそういうわけでもありません。
わざわざ主成分分析を使って独立変数の直交化を行ったわけですが、結果としては、「過酸化物」と「産地」の二つだけを選んで重回帰分析を行ったのと変わりはありません。他の独立変数が従属変数に関与しているかどうかは、結局わからないわけです。このように、主成分回帰は独立変数間の相関だけを考慮するため従属変数との相関は無視して変換され、結果として、従属変数と相関の強い状態で本当に独立変数が変換されたかはわかりません。最悪、全く無相関な主成分が選択され、正しい結果が得られない可能性もあります。
主成分回帰では、従属変数が主成分の決定になにも関与していないのが問題となるのでした。寄与率が大きな主成分を見つけても、それが従属変数と強い相関を持っているとは限りません。そこで、独立変数ベクトル X の転置と、従属変数からなる行列 Y ( 今までの重回帰モデルと違い、従属変数はベクトルではなく行列として扱います。もちろん、その特別な場合としてベクトルでも適用は可能です。なお、重回帰モデルでも従属変数を行列に拡張することは簡単にできます ) の積 XTY についての特異値分解をまずは行います。但し、前もって、X と Y の列ベクトルが、平均ゼロ、標準偏差 1 となるように正規化しておきます。
X は N 行 p 列 ( すなわち p 個の独立変数の要素を持った N 個の標本からなる行列 )、Y は N 行 q 列 とし、Ur は p 行 r 列、Dr はサイズ r の対角行列 ( 対角成分は全てゼロでないとします )、Vr は q 行 r 列 とします。このとき、r は XTY の階数 ( Rank ) を意味します。
Dr の対角成分は XTY の固有値です。i 番目の固有値を λi として λ1 ≥ λ2 ≥ ... λr の順に並べられてあるとします。また、対応する固有ベクトル ( Ur, Vr の列ベクトル ) をそれぞれ ui, vi とします。このとき、uiTXTYvi = λi が最大になるのは i = 1 のときであり、
より Xu1 は X の各独立変数ベクトルを主軸 u1 で直交変換したもの、Yv1 は同じく Y の各従属変数ベクトルを主軸 v1 で直交変換したものです。これにより、両者の変換後の値 ( 主成分分析における主成分 ) の内積、すなわち分散値が最大になるように変換されたことになります。そこで、主成分を
t1 = Xu1 / ||Xu1||
w1 = Yv1 / ||Yv1||
として、t1 と w1 の間に回帰式
を仮定し、b1 を推定します。t1Tt1 = 1 なので、
であり、w1 はこの b1 を使って
と近似できることになります。この操作はちょうど、X, Y それぞれの主成分どうしで回帰係数を推定したことに相当します。次に、
p1 = XTt1
q1 = YTw1
を求め、
X = X - t1p1T
Y = Y - w1q1T
として、再度特異値分解のところから反復処理します。その結果、X, Y がどちらも 0 に十分近い状態になったとすれば、最初の処理の X, Y を X0, Y0 とし、以下、処理を重ねるごとに添字を一つずつ更新すると、
X0 = X1 + t1p1T = X2 + t2p2T + t1p1T = ... ≅ Σi( tipiT ) = TPT
Y0 ≅ Σi( wiqiT ) = WQT
となります。ここで T, P, W, Q はそれぞれ ti, pi, wi, qi を列ベクトルとする行列になります。このとき、bi を i 番目の対角成分とする対角行列 B を使って W ≅ TB と表すことができるので、この値を W~ とすれば
と定義することができて、X = TPT より XT = PTT なので、
という結果が得られます。T は「潜在ベクトル (Latent Vector)」と呼ばれていますが、その実体は主軸変換された独立変数の成分 ( 一般に「スコア行列 ( Score Matrix )」と呼ばれます ) です。Y は T と BQT の積で近似され、T は主成分なので、前述の通り Y~ = TBQT は主成分を使った回帰モデルであると考えることができます。また、XTY は、PTT と TBQT の二つの積に分解され、その分解の中で T が生成された形になっています。
より、両辺を転置して
となるので、両辺に左側から PT を掛けて
という形になりますが、これは P を係数行列とし、TT を未知数、XT を右辺の値とした最小二乗法の正規方程式と同じ形となっています。但し、未知数と右辺の値はベクトルではなく行列です。これは、複数の連立方程式が係数行列は共通で横に並んだ様子を思い浮かべれば理解しやすいかと思います。この解を T~ = GXT としたとき ( 最小二乗法なので T は推定値 T~ です )、G は最小二乗形一般逆行列となるのでした。よって、これを Y の式に代入すると
と表現できて、X と Y の間の回帰モデルとすることができます。特に、P の行が標本数なのに対して列数は抽出した主成分の数であり、通常は主成分の数が少なくなるようにするのが目的となるので、PTP は逆行列を持つと考えてたいていは問題ありません。したがって、
とすれば、
| PGP = P( PTP )-1PTP = P | ( P の一般逆行列 ) |
| GPG = ( PTP )-1PTP( PTP )-1PT = ( PTP )-1PT = G | ( 反射形 ) |
| ( PG )T = [ P( PTP )-1PT ]T = P( PTP )-1PT = PG | ( 最小二乗形 ) |
| ( GP )T = [ ( PTP )-1PTP ]T = E | ( 最小ノルム形 ) |
であり、G は P のムーア-ペンローズ形逆行列になります。
特異値分解は、係数を一つ計算する度に行われるので、毎回全ての特異値を導き出すのは効率的に問題があります。そのため、PLS 回帰では「べき乗法 (Power Iteration)」に似た方法が一般的に採用されています。このアルゴリズムは「Nonlinear Iterative Partial Least Squares ( NIPALS )」と呼ばれています。
べき乗法は、固有値の中で絶対値が最大のものを求める手法です。ある正方行列 A の固有値を λi とします。ここで、固有値は絶対値の大きい順に並べ替えられているとします ( よって λ1 が絶対値最大の固有値となります )。各固有値に対応する固有ベクトルを ui としたとき、
となります。ui は基底であり、任意のベクトル x はその線形結合
で表されるので、
より c1 ≠ 0 ならば
となり、λi / λ1 < 1 ( i > 1 ) より Anx は c1λ1nu1 へ収束していきます。x の初期値を x0 として、
とすると、
であり、n が十分大きければ c1λ1n-1u1 へ収束します。但し、|| Ax || は A の要素によって変化していくので、計算の度にノルムで割って正規化する必要があります。
|| x(n) ||2 ≅ || c1λ1nu1 ||2 = c12λ12n
( x(n-1), x(n) ) ≅ ( c1λ1n-1u1, c1λ1nu1 ) = c12λ12n-1
より
で最初の固有値を求めることができます。
べき情報を使った固有値・固有ベクトル算出用のプログラムを以下に示します。
/* Normalize : 配列 [ s, e ) に対して正規化を行う 中心化は行わず、ノルムで割るのみである。 */ template< class In > void Normalize( In s, In e ) { typedef typename std::iterator_traits< In >::value_type value_type; // ノルムの計算 value_type norm = 0; for ( In i = s ; i != e ; ++i ) norm += std::pow( *i, 2.0 ); norm = std::sqrt( norm ); if ( norm != 0 ) for ( ; s != e ; ++s ) *s /= norm; } /* PowerIter : べき乗法による一番目の固有値・固有ベクトルの抽出 Test 型の引数 test は前回の解からの収束を判定するための関数オブジェクトで、初期化するための init、判定対象の値を収集 するための operator()、収束判定を行うための isConvergent をメンバ関数として持つことを前提とする。 固有ベクトル x は初期値としても利用されるため、要素数が行列のサイズと等しいことを前提としている。 また、処理終了時には第一固有値(絶対値最大の固有値)に対する固有ベクトルが返されるが、このときユークリッド・ノルムの値は 1 に正規化されている。 a : 対象の行列への参照 x : 第一固有ベクトルへのポインタ(渡される要素は初期値として利用される) test : 収束判定用関数オブジェクト maxCnt : 反復処理の最大回数 戻り値 : 第一固有値 */ template< class T, template< class T > class MATRIX, class Test > T PowerIter( const MATRIX< T >& a, std::vector< T >* x, Test test, unsigned int maxCnt ) { // 更新後の固有ベクトルを x で初期化して正規化 std::vector< T > newX( *x ); if ( ! Normalize( newX.begin(), newX.end() ) ) return( std::numeric_limits< T >::quiet_NaN() ); unsigned int cnt = 0; // 処理回数 for ( ; cnt < maxCnt ; ++cnt ) { *x = newX; // 新たな x を Ax で更新 MatrixLib::mult( a, x->begin(), x->end(), newX.begin(), newX.end() ); if ( ! MathLib::Normalize( newX.begin(), newX.end() ) ) return( std::numeric_limits< T >::quiet_NaN() ); // 収束判定 test.init(); for ( typename std::vector< T >::size_type i = 0 ; i < x->size() ; ++i ) test( (*x)[i], newX[i] ); if ( test.isConvergent() ) break; } if ( cnt >= maxCnt ) throw ExceptionExcessLimit( maxCnt ); MatrixLib::mult( a, x->begin(), x->end(), newX.begin(), newX.end() ); return( std::inner_product( newX.begin(), newX.end(), newX.begin(), T() ) / std::inner_product( x->begin(), x->end(), newX.begin(), T() ) ); }
テンプレート引数の MATRIX は行列の型を表し、この型を持つ引数は a です。MATRIX 自体もテンプレート・クラスであり、テンプレート引数として T を持つので、"template< class T > class MATRIX" というように、テンプレート引数の中でさらにテンプレートを使っています。MatrixLib::mult は行列とベクトルの積を計算するための関数で、第一引数に行列、第二・第三引数はベクトルの開始と末尾の次の位置をそれぞれ表します。また、最後の二つの引数は計算結果を返すベクトルの先頭と末尾の次の位置になります。具体的な実装はここでは示していませんが、行列の各行に対してベクトルとの内積を計算するだけの簡単な処理で実現できます ( ベクトルどうしの内積の計算には、STL ( Standard Template Library ) にある inner_product 関数が利用できます。この関数は、べき乗法の実装の中でも使用しています )。
収束したかどうかは、ベクトルの各要素が変化しないことで判定するのが通常ですが、この判定はいくつかの方法が考えられるので、これも具体的な実装は示さず抽象化しています。テンプレート引数 Test がその判定用関数オブジェクトの型を表し、三番めの引数 test がその型を持ちます。test オブジェクトは init 関数で初期化を行い、operator() で前の値と現在の値を引数として各要素をチェック ( 例えば差分の最大値で判定するなら各要素の差分の大きさを比較して最大値を取得 ) し、isConvergent で ( 例えばあるしきい値以下になっているかなどによって ) 収束判定を行います。収束しない場合を想定して、チェック回数は maxCnt までとし、それを超えた場合は例外を投げる仕様となっています。
処理の内容は前に説明した通りであり、ベクトル x に行列 a を掛けて正規化することを収束するまで繰り返し、最後に固有値を求めて戻り値として返します。また、固有ベクトルは引数 x にて返されます。
べき乗法を応用して、以下のような処理を考えます。なお、式の中で "∝" は左辺のベクトルをノルムが 1 になるよう正規化することを意味します。
最初、u は適当な値で初期化しておきます。この処理を t が収束するまで繰り返し、収束したら b = tTw で回帰係数を推定し、p = XTt, q = YTw を求めて X = X - tpT, Y = Y - wqT としてから再度反復処理を繰り返します。
この反復処理によって、左辺の各々のベクトルは以下のような式で表すことができます。
従って、ある定数 λ について XTYYTXu = λu が成り立つことから u は XTYYTX の固有ベクトルであり、同様に v は YTXXTY の固有ベクトルです。これらはちょうど、先に示した特異値分解の Ur と Vr に相当し、t と w もそれぞれ明らかに先述のベクトル t, w と同種のものです。
NIPALS を使って PLS 回帰を行うためのサンプル・プログラムを以下に示します。
/** PLS 回帰 ( NIPALS アルゴリズム ) **/ class PLS_Regression_NIPALS { Matrix< double > x_; // 独立変数 X Matrix< double > y_; // 従属変数 Y std::vector< double > b_; // 主成分 t, w での回帰係数 Matrix< double > pT_; // p = Xt・t を列ベクトルとする行列の転置 Matrix< double > qT_; // Q = Yt・w を列ベクトルとする行列の転置 // 反復処理により u, t, v, w を求める関数 void iterProc( Matrix< double >* x, Matrix< double >* y, size_t latentVecIdx, double e, unsigned int maxCnt ); public: /// 独立変数 X と従属変数 Y を指定して構築 /// /// x : 独立変数 X /// y : 従属変数 Y template< class T, class U > PLS_Regression_NIPALS( const Matrix< T >& x, const Matrix< U >& y ); /// PLS回帰を行い、回帰係数を a に返す /// /// a : 回帰係数を得るための行列へのポインタ /// latentVecs : 回帰係数(計算する潜在ベクトル)の個数 /// e : 反復処理でベクトルが収束したかを判定するためのしきい値 /// maxCnt : 反復処理の最大処理回数(反復処理は各回帰係数の算出で繰り返されるため、それぞれの処理での最大回数を意味する) void operator()( Matrix< double >* a, size_t latentVecs, double e, unsigned int maxCnt ); }; /* Centralize : データ [ s, e ) を中心化・正規化する テンプレート引数の In はコンテナの iterator の型であることが前提となる。 標準偏差がゼロである場合は正規化できないため何も処理せず false を返す。 */ template< class In > bool Centralize( In s, In e ) { typedef typename std::iterator_traits< In >::value_type value_type; value_type sz = std::distance( s, e ); if ( sz <= 0 ) return( false ); value_type mu = std::accumulate( s, e, value_type() ) / sz; // 平均値 value_type sigma = 0; // 標準偏差 for ( In i = s ; i != e ; ++i ) sigma += std::pow( *i - mu, 2.0 ); sigma = std::sqrt( sigma ); if ( sigma == 0 ) return( false ); for ( ; s != e ; ++s ) *s = ( *s - mu ) / sigma; return( true ); } /* PLS_Regression_NIPALS コンストラクタ : 独立変数 X と従属変数 y を指定して構築 */ template< class T, class U > PLS_Regression_NIPALS::PLS_Regression_NIPALS( const Matrix< T >& x, const Matrix< U >& y ) { assert( &x != 0 && &y != 0 ); if ( x.rows() != y.rows() ) throw ExceptionNotEqualLength< typename Matrix< T >::size_type >( x.rows(), y.rows() ); if ( x.rows() == 0 ) throw ExceptionNotPositiveLength< typename Matrix< T >::size_type >( x.rows() ); x_.assign( x.begin(), x.end(), x.rows(), true ); y_.assign( y.begin(), y.end(), y.rows(), true ); for ( Matrix< double >::size_type c = 0 ; c < x_.cols() ; ++c ) { Matrix< double >::iterator col = x_.column( c ); Centralize( col, col.end() ); } for ( Matrix< double >::size_type c = 0 ; c < y_.cols() ; ++c ) { Matrix< double >::iterator col = y_.column( c ); Centralize( col, col.end() ); } } /* MultMatByVec : 行列 m と ベクトル [ is, ie ) の積を計算し、[ os, oe ) に返す 結果は必ず Normalize される。 */ template< class In, class Out > void MultMatByVec( const Matrix< double >& m, In is, In ie, Out os, Out oe ) { MatrixLib::mult( m, is, ie, os, oe ); Normalize( os, oe ); } /* MultMatByVec : 行列 m の転置と ベクトル [ is, ie ) の積を計算し、[ os, oe ) に返す needToNorm が true なら結果は Normalize される。 */ template< class In, class Out > void MultTransByVec( const Matrix< double >& m, In is, In ie, Out os, Out oe, bool needToNorm ) { Out o = os; for ( Matrix< double >::size_type c = 0 ; c < m.cols() ; ++c ) { Matrix< double >::const_iterator col = m.column( c ); *o++ = std::inner_product( is, ie, col, double() ); } if ( needToNorm ) Normalize( os, oe ); } /* SubMat : 列ベクトル [ rs, re ) と行ベクトル [ cs, ce ) の積を計算し(結果は行列になる)、m から減算する */ template< class Row, class Column > void SubMat( Row rs, Row re, Column cs, Column ce, Matrix< double >* m ) { Matrix< double >::iterator i = m->begin(); for ( ; cs != ce ; ++cs ) for ( Row r = rs ; r != re ; ++r ) *i++ -= *r * *cs; } /* MultMatByTrans : src とその転置行列の積を計算し、dest に返す */ void MultMatByTrans( const Matrix< double >& src, SymmetricMatrix< double >* dest ) { for ( Matrix< double >::size_type r = 0 ; r < src.rows() ; ++r ) { for ( Matrix< double >::size_type c = r ; c < src.rows() ; ++c ) { Matrix< double >::const_iterator row = src.row( r ); Matrix< double >::const_iterator column = src.row( c ); (*dest)[r][c] = std::inner_product( row, row.end(), column, double() ); } } } /* PLS_Regression_NIPALS::operator() : PLS 回帰メインルーチン */ void PLS_Regression_NIPALS::operator()( Matrix< double >* a, size_t latentVecs, double e, unsigned int maxCnt ) { assert( a != 0 ); // 潜在ベクトルの個数は X のサイズより小さいことを前提とする if ( latentVecs > x_.cols() ) throw ExceptionTooGreatNumber< size_t >( latentVecs, x_.cols() ); if ( latentVecs > x_.rows() ) throw ExceptionTooGreatNumber< size_t >( latentVecs, x_.rows() ); pT_.assign( latentVecs, x_.cols() ); qT_.assign( latentVecs, y_.cols() ); // x_, y_ は更新されるためコピーして使う Matrix< double > x( x_ ); Matrix< double > y( y_ ); for ( size_t cnt = 0 ; cnt < latentVecs ; ++cnt ) iterProc( &x, &y, cnt, e, maxCnt ); SymmetricMatrix< double > pTp( pT_.rows() ); // Pt・P MultMatByTrans( pT_, &pTp ); SquareMatrix< double > pTpM; // ( Pt・P )^-1 InverseMatrix( pTp, &pTpM ); Matrix< double > gT; // Gt ( G = ( Pt・P )^-1・Pt ) MatrixLib::mult( pTpM, pT_, &gT ); gT.transpose(); for ( vector< double >::size_type c = 0 ; c < gT.cols() ; ++c ) for ( vector< double >::size_type r = 0 ; r < gT.rows() ; ++r ) gT[r][c] *= b_[c]; MatrixLib::mult( gT, qT_, a ); // A = Gt・Qt } /* PLS_Regression_NIPALS::iterProc : 反復処理により u, t, v, w を求める関数 t = X・u v = Yt・t w = Y・v u = Xt・w を繰り返す */ void PLS_Regression_NIPALS::iterProc( Matrix< double >* x, Matrix< double >* y, size_t latentVecIdx, double e, unsigned int maxCnt ) { typedef vector< double > Vec; Vec u( x->cols(), 1.0 / std::sqrt( static_cast< double >( x->cols() ) ) ); // u ベクトル vector< Vec > t( 2, Vec( x->rows() ) ); // t ベクトル(収束判定のため前の値を保持できるよう二つ分確保) Vec v( y->cols() ); // v ベクトル Vec w( y->rows() ); // w ベクトル Vec::size_type tIdx = 0; // t ベクトルの現在の計算対象インデックス (0/1) unsigned int cnt; // 反復処理回数 for ( cnt = 0 ; cnt < maxCnt ; ++cnt ) { Vec& ct = t[tIdx]; // t ベクトルの現在の計算対象 MultMatByVec( *x, u.begin(), u.end(), ct.begin(), ct.end() ); // t = X・u MultTransByVec( *y, ct.begin(), ct.end(), v.begin(), v.end(), true ); // v = Yt・t MultMatByVec( *y, v.begin(), v.end(), w.begin(), w.end() ); // w = Y・v MultTransByVec( *x, w.begin(), w.end(), u.begin(), u.end(), true ); // u = Xt・w // 収束チェック ConvergenceTest_ByMax< double > test( e ); for ( Vec::size_type i = 0 ; i < t[tIdx ^ 1].size() ; ++i ) test( t[tIdx ^ 1][i], ct[i] ); if ( test.isConvergent() ) break; tIdx ^= 1; // t ベクトルの現在の計算対象を反転 } if ( cnt >= maxCnt ) throw ExceptionExcessLimit( maxCnt ); Vec& ct = t[tIdx]; // t ベクトルの現在の計算対象 // 回帰係数の登録 b_.push_back( std::inner_product( ct.begin(), ct.end(), w.begin(), double() ) ); // w は回帰係数を元に予測値にする for ( Vec::size_type i = 0 ; i < w.size() ; ++i ) w[i] = b_.back() * ct[i]; Matrix< double >::iterator pTRow = pT_.row( latentVecIdx ); MultTransByVec( *x, ct.begin(), ct.end(), pTRow, pTRow.end(), false ); // p = Xt・t Matrix< double >::iterator qTRow = qT_.row( latentVecIdx ); MultTransByVec( *y, w.begin(), w.end(), qTRow, qTRow.end(), false ); // q = Yt・w SubMat( ct.begin(), ct.end(), pTRow, pTRow.end(), x ); // X = X - t・pt SubMat( w.begin(), w.end(), qTRow, qTRow.end(), y ); // Y = Y - w・qt }
コンストラクタでは、受け取った独立変数と従属変数を中心化・正規化してコピーするだけの処理を行っています。実際の処理は operator() を呼び出して行いますが、このとき回帰係数を得るための行列へのポインタと回帰係数の個数、反復処理で使用するしきい値と最大処理回数をそれぞれ渡します。回帰係数の個数は明示する必要があることに注意してください。また、その個数は独立変数の行列数よりも小さいことを前提とします。反復処理を行う iterProc が主要な処理を行うところになります。4 つのベクトル t, v, w, u を収束するまで反復処理し、t と w の内積から回帰係数を求めます。最後に行列 x, y からそれぞれ tpT と wqT を減算し ( この処理があるので行列 x, y はコピーして使います )、処理を完了します。必要な係数をすべて求めたら、G = ( PTP )-1PT を計算し、QT との積から X に対応した回帰係数を計算します。
べき乗法のサンプル・プログラムではテンプレート引数としていた Matrix クラスはここでも行列を提供するために利用し、内部で行・列方向の反復子が使えるようになっています。begin, end 関数は通常の配列と同じような扱いをした反復子で、行方向に要素をたどって行末に達したら次の列の先頭行に移るような進み方をします。また、row は指定した行番号の行の反復子を、column は指定した列番号の列の反復子をそれぞれ返します。反復子の末尾は、反復子自身が end 関数を持っているため、通常のコンテナ・クラスのようにコンテナの end 関数を呼び出すのではないことに注意してください。なお、正方行列用に SquareMatrix、対称行列用に SymmetricMatrix もそれぞれ用意されています。べき乗法で登場した MatrixLib::mult は多重定義 ( オーバーロード ) されていて、二つの行列の積を計算するための関数も登場します。また、transpose は対象の行列を転置するメンバ関数です。
InverseMatrix は逆行列を計算するための関数で、第一引数の行列の逆行列を第二引数の行列にコピーします。具体的な実装方法は、「数値演算法 (7) 連立方程式を解く -1-」にて紹介しています。ConvergenceTest_ByMax は収束を判定するための関数オブジェクトで、前の値との差分と値自身との比率を求め、その最大値がしきい値以内なら処理が完了するようになっています。これは、べき乗法で登場したテンプレートによる抽象クラス Test の具体的な実装の一つになります。最後に、いくつかの例外用クラスが定義されていますが、これもその名前や判定内容からどんなものか判別できると思います。
サンプル・プログラムを使って主成分回帰のときに使ったデータを処理してみたところ、回帰係数は下表のような結果になりました。但し、潜在ベクトルは 6 個分 ( すなわち全て ) 算出しています。
| 黄色味 | 緑色味 | 茶色味 | 光沢 | 透明度 | 甘み | |
|---|---|---|---|---|---|---|
| 酸性 | -0.058 | 0.056 | -0.042 | 0.062 | 0.037 | 0.009 |
| 過酸化物 | -0.081 | 0.049 | 0.291 | -0.237 | -0.215 | 0.321 |
| K232 | -0.054 | 0.010 | 0.312 | -0.118 | -0.061 | 0.185 |
| K270 | -0.125 | 0.126 | 0.206 | -0.039 | -0.039 | 0.019 |
| DK | -0.111 | 0.141 | -0.134 | -0.147 | -0.156 | 0.008 |
| 産地 | 0.370 | -0.378 | 0.251 | 0.260 | 0.306 | -0.095 |
上表において、係数が 0.2 以上のところを色付けしてあります。主成分回帰のときと同様に、どの従属変数も過酸化物と産地の影響が大きいことがこの結果からわかります。
| 黄色味 | 緑色味 | 茶色味 | 光沢 | 透明度 | 甘み | |
|---|---|---|---|---|---|---|
| G1 | -1.003 | 1.047 | -0.336 | -0.595 | -0.693 | 0.271 |
| G2 | -0.277 | 0.271 | -0.297 | -0.137 | -0.184 | -0.011 |
| G3 | -0.189 | 0.197 | -0.495 | 0.127 | 0.049 | -0.246 |
| G4 | -0.865 | 0.866 | 0.082 | -0.301 | -0.410 | 0.221 |
| G5 | -0.501 | 0.569 | -0.817 | -0.079 | -0.224 | -0.196 |
| I1 | -0.507 | 0.421 | 1.056 | -0.864 | -0.740 | 0.887 |
| I2 | -0.173 | 0.146 | 0.292 | -0.400 | -0.344 | 0.351 |
| I3 | -0.377 | 0.329 | 0.605 | -0.704 | -0.636 | 0.695 |
| I4 | -0.138 | 0.118 | 0.097 | -0.330 | -0.303 | 0.325 |
| I5 | -0.406 | 0.240 | 1.663 | -0.746 | -0.567 | 1.033 |
| S1 | 0.711 | -0.689 | -0.043 | 0.686 | 0.709 | -0.542 |
| S2 | 0.718 | -0.646 | -0.464 | 0.740 | 0.739 | -0.772 |
| S3 | 0.636 | -0.614 | -0.180 | 0.469 | 0.488 | -0.325 |
| S4 | 0.752 | -0.732 | -0.193 | 0.597 | 0.630 | -0.467 |
| S5 | 0.833 | -0.768 | -0.625 | 0.773 | 0.737 | -0.677 |
| S6 | 0.787 | -0.757 | -0.344 | 0.765 | 0.748 | -0.546 |
| 分散 | 0.377 | 0.352 | 0.391 | 0.333 | 0.313 | 0.297 |
上表は、独立変数 X と BPLS の積から従属変数 Y の予測値を計算した結果です。スペイン産は黄色味が強く、光沢や透明度も高いこと、イタリア産は甘みが強いことなど、産地ごとの特性がはっきりとこの結果からわかるようになります。
| 黄色味 | 緑色味 | 茶色味 | 光沢 | 透明度 | 甘み | |
|---|---|---|---|---|---|---|
| G1 | -0.561 | 0.707 | -0.114 | 0.410 | 0.321 | 0.513 |
| G2 | -1.181 | 1.171 | -0.213 | -0.366 | -0.996 | 1.266 |
| G3 | -0.776 | 0.682 | -0.236 | 0.121 | 0.573 | -0.621 |
| G4 | -0.232 | 0.224 | -0.108 | 0.349 | 0.274 | -0.280 |
| G5 | 0.550 | -0.614 | -0.056 | -1.325 | -1.379 | -0.301 |
| I1 | -0.033 | -0.009 | 0.508 | -1.325 | -1.087 | 0.536 |
| I2 | 0.328 | -0.283 | -0.459 | -0.103 | 0.233 | -1.286 |
| I3 | -0.922 | 1.122 | -0.229 | 0.352 | 0.189 | 0.594 |
| I4 | 0.925 | -1.060 | -0.506 | 0.461 | 0.478 | -0.215 |
| I5 | 0.094 | -0.311 | 1.573 | -0.107 | -0.091 | 0.593 |
| S1 | 0.352 | -0.248 | -0.266 | 0.464 | 0.523 | -0.629 |
| S2 | 0.483 | -0.401 | -0.347 | 0.777 | 0.691 | -1.140 |
| S3 | 0.278 | -0.332 | -0.128 | -0.872 | -0.873 | -0.206 |
| S4 | 0.135 | -0.131 | 0.107 | 0.035 | 0.067 | 0.644 |
| S5 | 0.256 | -0.240 | 0.317 | 0.443 | 0.544 | 0.247 |
| S6 | 0.302 | -0.277 | 0.156 | 0.685 | 0.533 | 0.285 |
| 分散 | 0.319 | 0.363 | 0.233 | 0.410 | 0.438 | 0.463 |
残渣 ( 実測値 - 予測値 ) をみると、予測値と同程度のバラツキ ( 分散値 ) を持っていることがわかります。PLS 回帰は、残渣をできるだけ小さくする最小二乗法の考え方とは異なるため、分散比で判断することはあまり意味がないようです。実際、実測値は正規化されていたので分散値は 1 であり、通常の回帰分析での決定係数は予測値の分散と等しくなります。しかし、予測値と残渣の分散値の和は 1 にはならず、すべてそれより小さくなっています。
下表は、潜在ベクトルを 2 個までとして、回帰係数 BPLS と、従属変数の予測値及び残渣を求めた結果です。
| 黄色味 | 緑色味 | 茶色味 | 光沢 | 透明度 | 甘み | |
|---|---|---|---|---|---|---|
| 酸性 | -0.192 | 0.209 | -0.190 | -0.048 | -0.088 | -0.029 |
| 過酸化物 | -0.057 | 0.031 | 0.293 | -0.167 | -0.129 | 0.206 |
| K232 | -0.093 | 0.069 | 0.260 | -0.177 | -0.146 | 0.202 |
| K270 | -0.156 | 0.147 | 0.089 | -0.145 | -0.143 | 0.126 |
| DK | -0.120 | 0.115 | 0.056 | -0.106 | -0.107 | 0.089 |
| 産地 | 0.196 | -0.204 | 0.107 | 0.086 | 0.115 | -0.023 |
| 黄色味 | 緑色味 | 茶色味 | 光沢 | 透明度 | 甘み | |
|---|---|---|---|---|---|---|
| G1 | -1.192 | 1.209 | -0.240 | -0.704 | -0.823 | 0.394 |
| G2 | 0.054 | -0.037 | -0.188 | 0.119 | 0.096 | -0.140 |
| G3 | 0.085 | -0.037 | -0.525 | 0.287 | 0.218 | -0.361 |
| G4 | -0.984 | 1.009 | -0.315 | -0.530 | -0.646 | 0.254 |
| G5 | -0.432 | 0.494 | -0.714 | 0.019 | -0.114 | -0.243 |
| I1 | -0.525 | 0.420 | 1.148 | -0.858 | -0.732 | 0.944 |
| I2 | -0.123 | 0.079 | 0.492 | -0.299 | -0.237 | 0.358 |
| I3 | -0.371 | 0.298 | 0.794 | -0.598 | -0.512 | 0.656 |
| I4 | -0.145 | 0.120 | 0.277 | -0.220 | -0.191 | 0.236 |
| I5 | -0.386 | 0.262 | 1.362 | -0.857 | -0.690 | 1.012 |
| S1 | 0.664 | -0.642 | -0.216 | 0.545 | 0.562 | -0.434 |
| S2 | 0.649 | -0.609 | -0.422 | 0.625 | 0.611 | -0.554 |
| S3 | 0.526 | -0.508 | -0.170 | 0.431 | 0.444 | -0.343 |
| S4 | 0.718 | -0.698 | -0.186 | 0.568 | 0.593 | -0.441 |
| S5 | 0.786 | -0.730 | -0.590 | 0.791 | 0.763 | -0.719 |
| S6 | 0.677 | -0.628 | -0.506 | 0.680 | 0.657 | -0.618 |
| 分散 | 0.370 | 0.346 | 0.375 | 0.320 | 0.299 | 0.292 |
| 黄色味 | 緑色味 | 茶色味 | 光沢 | 透明度 | 甘み | |
|---|---|---|---|---|---|---|
| G1 | -0.373 | 0.545 | -0.209 | 0.518 | 0.451 | 0.389 |
| G2 | -1.512 | 1.478 | -0.322 | -0.621 | -1.276 | 1.395 |
| G3 | -1.050 | 0.916 | -0.206 | -0.039 | 0.404 | -0.506 |
| G4 | -0.113 | 0.081 | 0.288 | 0.578 | 0.510 | -0.313 |
| G5 | 0.481 | -0.539 | -0.158 | -1.423 | -1.489 | -0.254 |
| I1 | -0.015 | -0.007 | 0.416 | -1.330 | -1.095 | 0.479 |
| I2 | 0.279 | -0.216 | -0.659 | -0.204 | 0.126 | -1.293 |
| I3 | -0.928 | 1.153 | -0.417 | 0.246 | 0.065 | 0.633 |
| I4 | 0.932 | -1.061 | -0.686 | 0.351 | 0.365 | -0.127 |
| I5 | 0.074 | -0.332 | 1.874 | 0.003 | 0.032 | 0.614 |
| S1 | 0.399 | -0.295 | -0.093 | 0.605 | 0.670 | -0.737 |
| S2 | 0.552 | -0.438 | -0.390 | 0.892 | 0.819 | -1.358 |
| S3 | 0.388 | -0.438 | -0.138 | -0.834 | -0.829 | -0.187 |
| S4 | 0.170 | -0.164 | 0.099 | 0.064 | 0.104 | 0.617 |
| S5 | 0.303 | -0.278 | 0.282 | 0.425 | 0.518 | 0.290 |
| S6 | 0.413 | -0.405 | 0.319 | 0.770 | 0.625 | 0.357 |
| 分散 | 0.406 | 0.436 | 0.340 | 0.478 | 0.519 | 0.514 |
潜在ベクトルを減らしても、予測値を見ると産地ごとの特性ははっきりと読み取ることができます。
| 産地 | 潜在ベクトル数 | 黄色味 | 緑色味 | 茶色味 | 光沢 | 透明度 | 甘み |
|---|---|---|---|---|---|---|---|
| Greece | 1 | -0.264 | 0.246 | 0.183 | -0.259 | -0.252 | 0.232 |
| 2 | -0.494 | 0.527 | -0.396 | -0.162 | -0.254 | -0.019 | |
| 4 | -0.567 | 0.590 | -0.371 | -0.198 | -0.294 | 0.012 | |
| 6 | -0.567 | 0.590 | -0.373 | -0.197 | -0.292 | 0.008 | |
| Italy | 1 | -0.497 | 0.464 | 0.344 | -0.488 | -0.474 | 0.437 |
| 2 | -0.310 | 0.236 | 0.815 | -0.566 | -0.472 | 0.641 | |
| 4 | -0.320 | 0.251 | 0.741 | -0.606 | -0.514 | 0.651 | |
| 6 | -0.320 | 0.251 | 0.742 | -0.609 | -0.518 | 0.658 | |
| Spain | 1 | 0.634 | -0.592 | -0.439 | 0.622 | 0.605 | -0.558 |
| 2 | 0.670 | -0.636 | -0.348 | 0.607 | 0.605 | -0.518 | |
| 4 | 0.739 | -0.701 | -0.308 | 0.670 | 0.674 | -0.553 | |
| 6 | 0.740 | -0.701 | -0.308 | 0.672 | 0.675 | -0.555 |
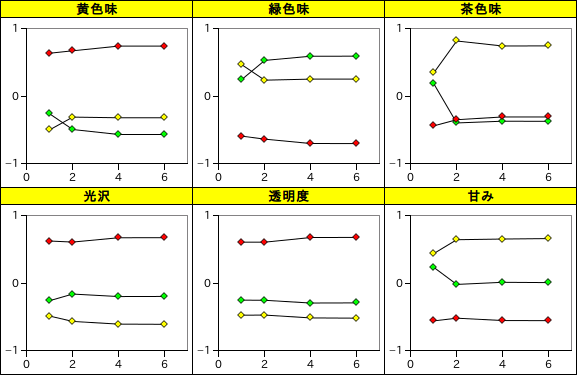 |
潜在ベクトル数に対する産地ごとの予測値平均を見ると、二つほどあれば十分であることがこの結果から読み取れます。
NIPALS の場合、主成分 ti と wi の間に回帰式 wi = biti が成り立つと仮定して、
pi = Xti
qi = Ywi
を求めていましたが、wi は使わずに
pi = XTti
qi = YTti
を求め、
X = X - tipiT
Y = Y - tiqiT
として反復処理をする方法もあります。Y は X ではなくスコア行列の T による線形回帰で表せたとしたとき、その係数を B とすれば
となります ( Y^ は Y の推定値を意味します )。両辺に左側から TT を掛けて
なので、T の列数が行数より少ない ( すなわち、独立変数の要素数より少ない主成分で X が表せる ) とすれば、TTT は非特異で逆行列が存在すると仮定して、
と B を表すことができます。また、X = TPT より
なので、
より
となります。ここで、
とすれば、
T = XR
BPLS = RQT
が成り立ちます。この場合、XTY は
となって、NIPALS と比較して係数行列 B が取り除かれたような形で表されます。この手法は「SIMPLS」と呼ばれています。
SIMPLS を使った PLS 回帰処理用のサンプル・プログラムを以下に示します。
/** PLS 回帰 ( SIMPLS アルゴリズム ) **/ class PLS_Regression_SIMPLS { Matrix< double > x_; // 独立変数 X Matrix< double > y_; // 従属変数 Y Matrix< double > u_; // S = Xt・Y の左特異ベクトルを列ベクトルとする行列 Matrix< double > pT_; // p = X・t を列ベクトルとする行列の転置 Matrix< double > qT_; // Q = Y・t を列ベクトルとする行列の転置 // u, t, v, w を求める関数 void calcVector( Matrix< double >* x, Matrix< double >* y, size_t latentVecIdx, double e, unsigned int maxCnt ); public: /// 独立変数 X と従属変数 Y を指定して構築 /// /// x : 独立変数 X /// y : 従属変数 Y template< class T, class U > PLS_Regression_SIMPLS( const Matrix< T >& x, const Matrix< U >& y ); /// PLS回帰を行い、回帰係数を a に返す /// /// a : 回帰係数を得るための配列へのポインタ /// latentVecs : 回帰係数(計算する潜在ベクトル)の個数 /// e : 反復処理でベクトルが収束したかを判定するためのしきい値 /// maxCnt : 反復処理の最大処理回数(反復処理は各回帰係数の算出で繰り返されるため、それぞれの処理での最大回数を意味する) void operator()( Matrix< double >* a, size_t latentVecs, double e, unsigned int maxCnt ); }; /* MultTransByMat : mat1 の転置行列と mat2 の積を計算し、dest に返す */ void MultTransByMat( const Matrix< double >& mat1, const Matrix< double >& mat2, Matrix< double >* dest ) { for ( Matrix< double >::size_type r = 0 ; r < mat1.cols() ; ++r ) { Matrix< double >::const_iterator row = mat1.column( r ); for ( Matrix< double >::size_type c = 0 ; c < mat2.cols() ; ++c ) { Matrix< double >::const_iterator column = mat2.column( c ); (*dest)[r][c] = std::inner_product( row, row.end(), column, double() ); } } } /* PLS_Regression_SIMPLS::operator() : PLS 回帰メインルーチン */ void PLS_Regression_SIMPLS::operator()( Matrix< double >* a, size_t latentVecs, double e, unsigned int maxCnt ) { assert( a != 0 ); // 潜在ベクトルの個数は X のサイズより小さいことを前提とする if ( latentVecs > x_.cols() ) throw ExceptionTooGreatNumber< size_t >( latentVecs, x_.cols() ); if ( latentVecs > x_.rows() ) throw ExceptionTooGreatNumber< size_t >( latentVecs, x_.rows() ); u_.assign( x_.cols(), latentVecs ); pT_.assign( latentVecs, x_.cols() ); qT_.assign( latentVecs, y_.cols() ); // x_, y_ は更新されるためコピーして使う Matrix< double > x( x_ ); Matrix< double > y( y_ ); for ( size_t cnt = 0 ; cnt < latentVecs ; ++cnt ) calcVector( &x, &y, cnt, e, maxCnt ); // Pt・U SquareMatrix< double > pTu( pT_.rows(), u_.cols() ); MatrixLib::mult( pT_, u_, &pTu ); // ( Pt・U )^-1 SquareMatrix< double > pTuM; MathLib::InverseMatrix( pTu, &pTuM ); // U・( Pt・U )^-1 Matrix< double > upTuM; MatrixLib::mult( u_, pTuM, &upTuM ); // A = U・( Pt・U )^-1・Qt MatrixLib::mult( upTuM, qT_, a ); } /* PLS_Regression_SIMPLS::calcVector : u, t, p, q を求める関数 u は Xt・Y の第一左特異ベクトル t = X・u / ||X・u|| p = X・t q = Y・t */ void PLS_Regression_SIMPLS::calcVector( Matrix< double >* x, Matrix< double >* y, size_t latentVecIdx, double e, unsigned int maxCnt ) { typedef vector< double > Vec; // S = Xt・Y Matrix< double > s( x->cols(), y->cols() ); MultTransByMat( *x, *y, &s ); // S・St = ( Xt・Y )・( Xt・Y )t SymmetricMatrix< double > ssT( s.rows() ); MultMatByTrans( s, &ssT ); // S = Xt・Y の第一左特異ベクトル ( S・St の第一固有ベクトル ) を u に求める Vec u( x->cols(), 1.0 / std::sqrt( static_cast< double >( x->cols() ) ) ); ConvergenceTest_ByMax< double > test( e ); EigenLib::PowerIter( ssT, &u, test, maxCnt ); for ( typename Vec::size_type i = 0 ; i < u.size() ; ++i ) u_[i][latentVecIdx] = u[i]; // t = Xu Vec t( x->rows() ); MultMatByVec( *x, u.begin(), u.end(), t.begin(), t.end() ); // p = Xt・t Matrix< double >::iterator row = pT_.row( latentVecIdx ); MultTransByVec( *x, t.begin(), t.end(), row, row.end(), false ); SubMat( t.begin(), t.end(), row, row.end(), x ); // X = X - t・pt // q = Yt・t row = qT_.row( latentVecIdx ); MultTransByVec( *y, t.begin(), t.end(), row, row.end(), false ); SubMat( t.begin(), t.end(), row, row.end(), y ); // Y = Y - t・qt }
基本的な構成は NIPALS の場合とよく似ています。各ベクトルを求める関数は calcVector で、これを潜在ベクトルの数分だけ処理することで行列 U, T, P, Q が得られます。これらの行列を使い、BPLS を引数 a に求めて処理が完了します。calcVector の中で特異ベクトルを求める処理が必要になりますが、これは前に紹介したべき乗法のサンプル・プログラムをそのまま利用しています。求めたいのは特異値分解
の左特異ベクトルからなる行列 U なので、
より XTY(XTY)T の固有ベクトルを求めれば目的を達成することができます。
なお、コンストラクタの内容は NIPALS と全く同じなので実装は省略しています。
SIMPLSを使って NIPALS と同じデータを処理した結果を以下に示します。潜在ベクトルは 6 個分 ( すなわち全て ) 算出しています。
| 黄色味 | 緑色味 | 茶色味 | 光沢 | 透明度 | 甘み | |
|---|---|---|---|---|---|---|
| 酸性 | 0.243 | -0.332 | 0.248 | 0.346 | 0.372 | 0.229 |
| 過酸化物 | -0.180 | 0.140 | 0.393 | -0.503 | -0.560 | 0.765 |
| K232 | 0.198 | -0.386 | 0.747 | 0.147 | 0.385 | 0.252 |
| K270 | -0.274 | 0.366 | 0.199 | -0.034 | -0.093 | -0.274 |
| DK | -0.187 | 0.349 | -0.560 | -0.330 | -0.380 | -0.261 |
| 産地 | 0.824 | -0.837 | 0.551 | 0.615 | 0.727 | -0.193 |
上表において、係数が 0.5 以上のところを色付けしてあります。NIPALS と比較して係数の絶対値は大きくなる傾向にありますが、ここでも過酸化物と産地の影響が大きいという結果が得られました。
| 黄色味 | 緑色味 | 茶色味 | 光沢 | 透明度 | 甘み | |
|---|---|---|---|---|---|---|
| G1 | -0.935 | 1.033 | -0.624 | -0.498 | -0.540 | 0.058 |
| G2 | -0.984 | 0.921 | -0.531 | -0.561 | -0.679 | 0.124 |
| G3 | -0.727 | 0.616 | -0.565 | 0.014 | -0.084 | -0.186 |
| G4 | -1.154 | 1.167 | 0.338 | -0.177 | -0.401 | 0.261 |
| G5 | -0.863 | 0.989 | -1.368 | -0.270 | -0.532 | -0.236 |
| I1 | -0.625 | 0.570 | 1.306 | -1.204 | -1.035 | 1.044 |
| I2 | -0.254 | 0.247 | 0.198 | -0.663 | -0.571 | 0.408 |
| I3 | -0.526 | 0.547 | 0.545 | -1.194 | -1.179 | 1.035 |
| I4 | -0.026 | -0.037 | 0.082 | -0.509 | -0.443 | 0.700 |
| I5 | -0.522 | 0.177 | 2.789 | -0.804 | -0.503 | 1.516 |
| S1 | 0.924 | -0.853 | 0.043 | 1.031 | 1.053 | -0.985 |
| S2 | 1.020 | -0.819 | -0.817 | 1.131 | 1.181 | -1.645 |
| S3 | 1.112 | -1.095 | -0.155 | 0.712 | 0.763 | -0.283 |
| S4 | 1.128 | -1.121 | -0.172 | 0.885 | 0.984 | -0.658 |
| S5 | 1.161 | -1.041 | -0.909 | 0.944 | 0.841 | -0.744 |
| S6 | 1.273 | -1.300 | -0.161 | 1.164 | 1.146 | -0.408 |
| 分散 | 0.801 | 0.749 | 0.899 | 0.673 | 0.657 | 0.638 |
| 黄色味 | 緑色味 | 茶色味 | 光沢 | 透明度 | 甘み | |
|---|---|---|---|---|---|---|
| G1 | -0.629 | 0.721 | 0.174 | 0.313 | 0.167 | 0.726 |
| G2 | -0.474 | 0.520 | 0.021 | 0.059 | -0.501 | 1.131 |
| G3 | -0.238 | 0.263 | -0.166 | 0.235 | 0.707 | -0.681 |
| G4 | 0.056 | -0.077 | -0.364 | 0.225 | 0.265 | -0.320 |
| G5 | 0.912 | -1.033 | 0.495 | -1.134 | -1.071 | -0.261 |
| I1 | 0.085 | -0.157 | 0.258 | -0.984 | -0.792 | 0.379 |
| I2 | 0.409 | -0.384 | -0.366 | 0.160 | 0.460 | -1.343 |
| I3 | -0.773 | 0.903 | -0.169 | 0.841 | 0.732 | 0.254 |
| I4 | 0.813 | -0.904 | -0.491 | 0.641 | 0.618 | -0.590 |
| I5 | 0.211 | -0.248 | 0.447 | -0.049 | -0.155 | 0.109 |
| S1 | 0.139 | -0.085 | -0.351 | 0.119 | 0.178 | -0.186 |
| S2 | 0.181 | -0.228 | 0.005 | 0.386 | 0.249 | -0.267 |
| S3 | -0.197 | 0.149 | -0.154 | -1.115 | -1.148 | -0.248 |
| S4 | -0.240 | 0.259 | 0.086 | -0.253 | -0.287 | 0.834 |
| S5 | -0.072 | 0.034 | 0.601 | 0.273 | 0.440 | 0.314 |
| S6 | -0.184 | 0.266 | -0.026 | 0.286 | 0.136 | 0.147 |
| 分散 | 0.199 | 0.251 | 0.101 | 0.327 | 0.343 | 0.362 |
従属変数 Y の予測値と、実測値との残渣を計算した結果です。ここでも NIPALS と同様の結果が得られました。
| 産地 | 潜在ベクトル数 | 黄色味 | 緑色味 | 茶色味 | 光沢 | 透明度 | 甘み |
|---|---|---|---|---|---|---|---|
| Greece | 1 | -0.351 | 0.328 | 0.244 | -0.345 | -0.335 | 0.309 |
| 2 | -0.724 | 0.776 | -0.611 | -0.224 | -0.363 | -0.047 | |
| 4 | -0.933 | 0.944 | -0.546 | -0.303 | -0.456 | 0.022 | |
| 6 | -0.933 | 0.945 | -0.550 | -0.298 | -0.447 | 0.004 | |
| Italy | 1 | -0.674 | 0.629 | 0.467 | -0.661 | -0.643 | 0.593 |
| 2 | -0.382 | 0.278 | 1.137 | -0.756 | -0.621 | 0.872 | |
| 4 | -0.388 | 0.298 | 0.981 | -0.865 | -0.729 | 0.914 | |
| 6 | -0.391 | 0.301 | 0.984 | -0.875 | -0.746 | 0.941 | |
| Spain | 1 | 0.854 | -0.797 | -0.592 | 0.838 | 0.815 | -0.752 |
| 2 | 0.922 | -0.879 | -0.438 | 0.817 | 0.820 | -0.688 | |
| 4 | 1.101 | -1.035 | -0.363 | 0.973 | 0.988 | -0.780 | |
| 6 | 1.103 | -1.038 | -0.362 | 0.978 | 0.995 | -0.787 |
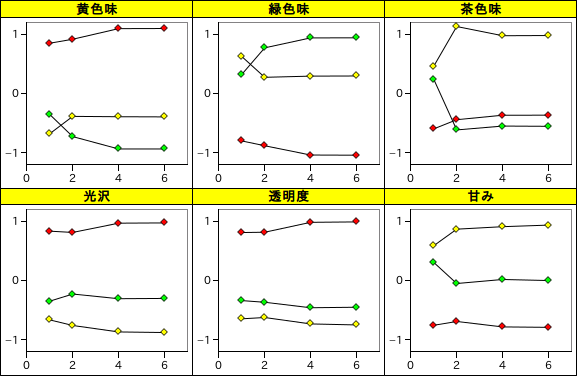 |
潜在ベクトル数に対する産地ごとの予測値平均も NIPALS とほぼ同等の結果であり、潜在ベクトルが二つほどあれば識別には十分な精度が得られる結果となりました。今回は、潜在ベクトルの数を変化させて最適値を調べてみましたが、本来であれば処理前に前もって決めておく必要があります。この方法としては、例えば標本を K 個に分割してそのうちの一つを検証用、残り全てを係数の計算用に利用する操作を、検証用の標本を K 個全てに対して切り替えて行う手法があります。これは一般に「交差検証 ( Cross-Validation )」として知られる手法です。
NIPALS や SIMPLS に対して今回紹介したものとは異なる式を採用したバージョンがあり、さらに「カーネル法」を採用したものなど全く別のアルゴリズムなども多く存在します。X や Y を近似するやり方が複数あるだけでなく正規化を行う位置も様々なので、各アルゴリズムにおいて結果を直接比較することを困難とする要因となっています。比較的新しい手法であり、書籍としては参考になるものがなく論文などで情報を入手するしかないので、まだうまくまとめられていない部分もありますが、理解できた部分が増えてきたら都度更新をしていきたいと思います。
任意の m 行 n 列行列 A の階数(ランク)が r であるとき、A = LR となるような m 行 r 列の行列 L と r 行 n 列の行列 R が必ず存在します。m 行 m 列の単位行列 Em のランクは m なので、
を満たす m 行の行列 L と m 列の行列 R が存在し、L は R の「左逆行列 (Left Inverse)」、R は L の「右逆行列 (Right Inverse)」といいます。これらについては「確率・統計 (12) 二標本の解析 -2-」の「補足 2) べき等行列の階数」にて証明法を紹介していますので、そちらをご覧ください。
m 行 n 列の行列 A のランクが r で、m 行 r 列の行列 B と r 行 n 列の行列 C を使って A = BC と表されるとき、B の左逆行列が L で C の右逆行列が R ならば、
なので、RL は A の一般逆行列となります。これは、任意の行列に対して一般逆行列が存在することを意味します。
G が A の一般逆行列のとき、Z を任意の ( 但し行列数が G と等しい ) 行列として
とすると、
| AG*A | = | A( G + Z - GAZAG )A |
| = | AGA + AZA - AGAZAGA | |
| = | A + AZA - AZA = A |
となります。また、S, T を (しかるべき行列数の) 任意の行列として
とすると、
| AG*A | = | A[ G + ( E - GA )T - S( E - AG ) ]A |
| = | AGA + A( E - GA )TA - AS( E - AG )A | |
| = | AGA + AETA - AGATA - ASEA + ASAGA | |
| = | A + ATA - ATA - ASA + ASA = A |
となります。このことから、一般逆行列が一つ決まれば、それからいくらでも異なる一般逆行列を作ることができます。但し、G が通常の逆行列であれば、どちらの式も G* = G なので異なる逆行列を作ることはできません。
を満たす一般逆行列に対し、連立方程式 Ax = b の解 A-b が最小のノルムを持つことを証明するにはいくつかの段階を踏む必要があります。
まず、Ax = 0 の形の連立方程式を「同次線形系 (Homogeneous Linear System)」といいます。x* がその解のとき、Ax* = 0 なので
と表すことができます。ここで任意のベクトル y を使って
としたとき、
なので、任意のベクトル y について ( E - A-A )y は Ax = 0 になり、全ての解はこの形で表せることになります。
次に、右辺を b ≠ 0 として Ax = b の形の連立方程式「非同次線形系 (Nonhomogeneous Linear System)」について、解の一つを x* とし、右辺を 0 にした Ax = 0 の解の一つを z* とすると、
なので x* + z* は Ax = b の解になります。特に、A の任意の一般逆行列 A- に対し、A-b は解の一つであり、( E - A-A )y は Ax = 0 の解の一つなので、
は Ax = b の解の一つになり、全ての解がこの形で表せることになります。このノルムの二乗を計算すると、
より ( A-b, ( E - A-A )y ) を計算すると
| ( A-b, ( E - A-A )y ) | = | ( A-b )T( E - A-A )y |
| = | ( A-Ax )T( E - A-A )y | |
| = | xT( A-A )T( E - A-A )y |
となります。ここで (A-A)T = A-A が成り立つとすると
| ( A-b, ( E - A-A )y ) | = | xTA-A( E - A-A )y |
| = | xT( A-A - A-AA-A )y | |
| = | xT( A-A - A-A )y = 0 |
なので、
となり、|| ( E - A-A )y || = 0 となるような y を選べばノルムが最小となります。
一般に、行列 A と二つのベクトル x, y の間で Ax = Ay のとき x = y が成り立つとは限りません。例として、
| A = | | | 1, | 1 | | |
| | | 1, | 1 | | |
に対して x ≠ y ですが、Ax = Ay = 0 になります。Ax = Ay のとき x = y が成り立つためには、A が逆行列を持つ必要があります。これは、連立方程式の解が一意になるか、不定になるかについての議論と同じ内容です。ベクトルについて成り立たないので、行列 B, C について AB = AC のときも B = C が成り立つとは限りません。
特定の条件下では、上記の関係が成り立つ場合があります。もし、
が成り立てば、必ず AB = AC が成り立ちます。これを証明するために、行列の「トレース (Trace)」を利用します。トレースとは対角成分の和であり、正方行列に対してのみ定義されます。正方行列 A のトレースを tr( A ) で表します。
AAT のトレース tr( AAT ) は、A の i 番目の列ベクトルを ai としたとき
となり、tr( AAT ) = 0 ならば ai = 0 なので A = 0 です。AAT = 0 のとき、そのトレースはゼロになるので、AAT = 0 ならば A = 0 ということになります。
ATAB = ATAC が成り立つとき、
| ( AB - AC )T( AB - AC ) | = | ( BTAT - CTAT )( AB - AC ) |
| = | BTATAB - BTATAC - CTATAB + CTATAC | |
| = | ( BT - CT )ATAB - ( BT - CT )ATAC | |
| = | ( BT - CT )( ATAB - ATAC ) = 0 |
なので、AB - AC = 0、すなわち AB = AC が成り立つことになります。
また、「ATAB = ATAC ならば AB = AC」両辺の転置をとって
なので、AT → A、BT → B、CT → C と置き直せば
も成り立つことになります。
なお、任意のベクトル yに対して Ay = By が成り立てば A = B となることの証明については、任意のベクトル yに対して成り立つなら i 番目のみが 1 で他はすべてゼロであるベクトルでも成り立ち、そのとき Ay と By はそれぞれ i 番目の列ベクトルと等しくなることから証明できます。
かなり技巧的なやり方ですが、参考文献では以下のように証明されています。
A+ に対して異なるムーア-ペンローズ形逆行列 G があると仮定します。このとき、ムーア-ペンローズ形逆行列の性質を利用すると
| A+ | = | A+AA+ = A+(AA+)T = A+(A+)TAT = A+(A+)T(AGA)T = A+(A+)TATGTAT |
| = | A+(AA+)T(AG)T = A+AA+AG = A+AG | |
| = | A+A(GAG) = (A+A)T(GA)TG = AT(A+)TATGTG = (AA+A)TGTG | |
| = | ATGTG = (GA)TG = GAG = G |
よって G = A+ すなわち A+ は一意であることが証明されました。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |