
前回は「確率空間」の定義という抽象的な話題を中心に紹介しましたが、ここからはもう少し具体的な確率分布を紹介したいと思います。まずは、二項分布を代表とする「離散確率分布」を中心に取り上げます。
前回、ベルヌーイ列について説明をしました。もう一度おさらいしておくと、
一回の独立な試行で事象 A が起こった場合を 1、起こらなかった場合を 0 で表したとき、長さ N のベルヌーイ列は
で表す。
になります。事象 A がどのように発生したのか、1 と 0 からなる N 個の数列 ( x1, x2, ... xN ) をどのように見るのかによって、確率分布の見方も変わります。あるときは、偶数回めでは事象 A が全く起こらなかった確率を求めたいこともあるかも知れないし、最初と最後だけは事象 A が必ず起こる確率を求めたい場合も時にはあるかも知れません。しかし、たいていの場合、事象 A が発生した回数に注目することになると思います。例えば、ある製品を加工する装置では稀に処理に失敗する場合があって、その確率は今までの経験によってある程度判明しているとしたとき、N 個の製品の中に不良品がどの程度発生するかを調べるため、失敗する回数に対する確率を求めるといった利用方法が考えられます。
事象 A が起こる確率を p ( 0 < p < 1 ) とすると、起こらない確率は q = 1 - p ( 0 < q < 1 ) になります。N 回の試行の中で、事象 A が r 回起こるような標本点の確率を
と定義します。各試行は独立であるとしたので、事象 A が発生する箇所に関係なく、回数が同じであれば確率も同じであると仮定しているわけです。ここで、N 回の試行の中で事象 A が r 回発生する場合の数を考えると、それは、1 から N までの数字から r 個の数字を抽出する組み合わせと等しくなるので NCr となり( r 個の数字は、ベルヌーイ列において 1 となる位置を表すと考えれば理解しやすいと思います)、N 回の試行の中で確率 p を持つ事象 A が r 回発生する事象全体の確率を BN,p(r) で表すと
と求めることができます。これを「二項分布(Binomial Distribution)」といいます。Ω = { 1, 2, ... N }、β は Ω のべき集合とすれば、全事象の確率は
| Σr{0→N}( BN,p(r) ) | = | Σr{0→N}( NCrprqN-r ) |
| = | ( p + q )N (二項定理より) | |
| = | 1 |
であり、定義から正値を取ることも加法性が成り立つことも明らかなので、確率空間として成り立っていることが分かります。ちなみに、NCrprqN-r は二項定理での展開式の各項を表しているので、この名が付けられたようです。
前章で紹介した積率母関数 g(θ) = E[eθx] を利用して、二項分布 BN,p(r) の平均 μ と分散 σ2 を求めてみます。
| g(θ) | = | Σr{0→N}( eθrNCrprqN-r ) |
| = | Σr{0→N}( NCr( peθ )rqN-r ) | |
| = | ( peθ + q )N |
より、g'(θ) を計算すると、
となるので、
また、
なので、
| E[r2] = g(2)(0) | = | Np( p + q )N-1 + N( N - 1 )p2( p + q )N-2 |
| = | Np + N( N - 1 )p2 |
よって、
| σ2 = E[r2] - μ2 | = | Np + N( N - 1 )p2 - ( Np )2 |
| = | Np - Np2 | |
| = | Np( 1 - p ) = Npq |
となります。平均が Np であるということは、N 回あたり r 回は事象 A が発生する ( つまり確率が r / N ) としたとき、N 回の試行では平均が N x ( r / N ) = r になるということを表しているので、言わば当然の結果が得られたということになります。分散は Npq で、pq = p - p2 = -( p - 1 / 2 )2 + 1 / 4 なので p = 1 / 2 で最大となります。これは、どちらになるかわからない状態ではバラツキが大きくなり、p が非常に小さいかまたは非常に大きい時(起こること・起こらないことがほぼ確実であるような場合)は逆にバラツキが非常に小さくなることを示しています。これらのことは、二項分布が実際の経験に基づく結果と非常に合致したモデルであることを示しています。
以上をまとめると、
二項分布 BN,p(r) = NCrprqN-r
平均 : μ = Np、分散 : σ2 = Npq
となります。
二項分布用のサンプル・プログラムを以下に示します。
/* BinomialDistribution : 二項分布 B(n,p) = nCk p^k q^(n-k) p : ある事象 A が一回の試行で起こる確率 q : ある事象 A が一回の試行で起こらない確率( = 1 - p ) n : 独立試行の回数 */ class BinomialDistribution : public DiscDist { double _p; // 一回の試行で起こる確率 unsigned int _n; // 独立試行の回数 public: /* BinomialDistribution コンストラクタ p : ある事象 A が一回の試行で起こる確率 n : 独立試行の回数 */ BinomialDistribution( double p, unsigned int n ) : _p( p ), _n( n ) {} double average() const // 平均値 { return( ( _p < 0 || _p > 1 ) ? NAN : (double)_n * _p ); } double variance() const // 分散 { return( ( _p < 0 || _p > 1 ) ? NAN : (double)_n * _p * ( 1.0 - _p ) ); } // 確率変数 r に対する確率密度を返す double operator[]( int r ) const; }; /* BinomialDistribution::operator[] : 確率変数 r に対する確率密度を返す int r : 確率変数 戻り値 : 確率密度 */ double BinomialDistribution::operator[]( int r ) const { // _p < 0 または _p > 1 のときは無効値を返す if ( _p < 0 || _p > 1 ) return( NAN ); // r < 0 または r > _n なら戻り値は 0 if ( r < 0 ) return( 0 ); if ( (unsigned int)r > _n ) return( 0 ); // _p = 0 なら常に r = 0 しか発生しない if ( _p == 0 ) return( ( r == 0 ) ? 1 : 0 ); // _p = 1 なら常に r = _n しか発生しない if ( _p == 1 ) return( ( (unsigned int)r == _n ) ? 1 : 0 ); // n = 0 かつ r = 0 なら comb の戻り値は 1 double c = comb( (double)_n, (double)r ); return( c * pow( _p, r ) * pow( 1.0 - _p, _n - r ) ); } /* binomialDistribution : 二項分布を求める B(n,p) = Σ nCr p^r q^(n-r) p : ある事象 Aが一回の試行で起こる確率 q : ある事象 Aが一回の試行で起こらない確率( = 1 - p ) n : 独立試行の回数 double p : 一回の試行でAが起こる確率 unsigned int n : 独立試行の回数 vector<double>& ans : 求める確率分布 戻り値 : 途中で計算ができなくなった場合はfalseを返す */ bool binomialDistribution( double p, unsigned int n, vector<double>& ans ) { double c = 1.0; // 組み合わせ nCr (初期値 = nC0 = 1) double q = 1.0 - p; // 余事象の確率 ans.clear(); // 要素をいったん削除 // p < 0 または p > 1 の場合は処理を行わない if ( p < 0 || p > 1 ) return( false ); ans.assign( n + 1, 0 ); // 要素は 0 で初期化 // n = 0 なら r = 0 のとき 1 // p = 0 なら r = 0 のとき 1 で残りは 0 if ( p == 0 || n == 0 ) { ans[0] = 1; return( true ); } // q = 0 なら r = n のとき 1 で残りは 0 if ( q == 0 ) { ans[n] = 1; return( true ); } for ( unsigned int r = 0 ; r < n ; ++r ) { ans[r] = c * pow( p, r ) * pow( q, n - r ); c *= n - r; c /= r + 1; if ( isinf( c ) || isnan( c ) ) return( false ); } ans[n] = pow( p, n ); // r = n のとき nCr = 1とならないので個別に計算 return( true ); }
BinomialDistribution は前回紹介した離散分布用の基底クラス DiscDist から派生しています。確率密度を求める operator[] において利用されている comb は組み合わせ nCr を計算するための関数で、以前、組み合わせの説明の中で紹介したサンプル・プログラムをそのまま利用しています。
事象に対する確率 p は 0 ≤ p ≤ 1 を満たす必要があることから、範囲外にある値がを渡された場合、平均値と分散の値は無効値(NAN)としています。operator[] では、想定外の値に対して場合分けを行い、p が 0 ≤ p ≤ 1 の範囲にない場合は無条件で無効値を返しています。また p = 0 だった場合、事象が起こることは皆無なので、r = 0 の時だけ確率は 1 で、その他は 0 になります。逆に、p = 1 ならば事象は必ず起こるので、r = _n の時だけ確率は 1 で、その他は 0 です。p = 0 や q = 0 の場合は、二項分布の式において p0 や q0 が 00 と不定値になるので、あらかじめチェックしているわけです。
その他の想定外な値として、事象が発生した回数を示す r が負数または試行回数 _n を超えている場合が考えられます。この場合、comb の戻り値は 0 となり、計算結果も 0 となって正しい結果が得られるので場合分けは不要になります。しかし、r と _n が等しいかをチェックする箇所では符号付きと符合なしの整数を比較することになるため、r < 0 の場合を除外する目的であらかじめ処理を行うようにしてあります。また、試行回数 _n = 0 の場合も考えられ、このときは r = 0 のみ計算処理が行われます(その他は r > _n となるので 0 を返します)。この時の計算結果は 1 となり正しい結果が得られるので、この条件だけ場合分けは行っていません。
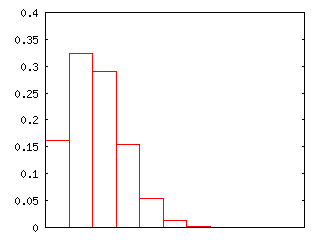
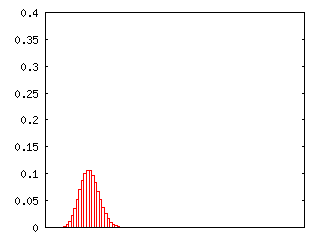
クラスとは別に、全ての確率密度を一度に計算する専用の関数 binomialDistribution を用意してあります。これを利用して計算した結果を元に作成したグラフを以下に示します。サイコロを投げる試行を繰り返した時ある一つの目が出る回数を、10/100/1000 回の試行に対して表しています。
| 10回の試行 | 100回の試行 | 1000回の試行 |
|---|---|---|
 |
 |
 |
試行回数が増加するに従い、各事象が発生する確率は小さくなっていきます。平均が Np、分散が Npq となることから、試行回数を増やすほど、平均が大きくなると同時に分散も大きくなり、試行回数 N が充分大きい場合は、ゼロ回発生するときも N 回発生するときも、それ以外の場合でも確率はほとんどゼロになってしまいます。つまり、どうなるかは判別できない状態になり、分布を考える意味がなくなってしまいます。
しかし、確率変数を発生回数 r からその比率 r / N へ変換すると、平均は p、分散は pq / N となり、今度は試行回数を増やすほどバラツキが小さくなっていきます。つまり、極限においては発生回数は全体の中の p に収束していくことになるのですが、これは例えば、サイコロを数回投げただけではそれぞれの目が出る比率は 1 / 6 とはならないのに対し、その試行を何回も繰り返していくと、だんだんと 1 / 6 に近づいていくことを表しています。この法則を「大数の法則(Law of Large Numbers)」といいますが、これについては別途紹介したいと思います。
二項分布において、平均 Np = λ (正の定数) として式を変形します。
| BN,p(r) | = | NCrprqN-r |
| = | { N! / r! ( N - r )! }( λ / N )r( 1 - λ / N )N-r | |
| = | { N( N - 1 ) ... ( N - r + 1 ) / r!・Nr }・λr( 1 - λ / N )N( 1 - λ / N )-r | |
| = | [ ( N / N ){ ( N - 1 ) / N } ... { ( N - r + 1 ) / N } ]・( λr / r! )( 1 - λ / N )(-N/λ)(-λ)( 1 - λ / N )-r |
ここで、
は全て、N → ∞ において 1 に収束します。また、ネイピア数の定義から
なので、( 1 - λ / N )(-N/λ)(-λ) は e-λ に収束することになって、
となります。この確率分布を「ポアソン分布(Poisson Distribution)」といいます。二項分布での平均 Np を定数 λ として N を限りなく大きくしたということは、延々と続く試行の中で平均して λ 回発生する事象に対する確率分布を表していると考えることができます。例えば、一週間で発生する事故の件数や、ある製品の加工で一日あたりに不良品が発生する回数などを考える場合によく利用されます。
二項分布を利用しているものの、本当に確率分布として成り立っているかを確認してみます。まず、Pλ(r) = λre-λ / r! としたとき、λ > 0 なので、任意の正の整数 r に対して Pλ(r) > 0 が成り立ちます。全事象の確率の和は
となりますが、Σr{0→∞}( λr / r! ) は eλ のマクローリン展開式なので、P(Ω) = 1 となって、確率分布としての条件を満たしています。この確率分布の平均は、
| 平均 μ | = | Σr{0→∞}( rPλ(r) ) |
| = | Σr{0→∞}( re-λλr / r! ) | |
| = | λe-λΣr{1→∞}( λr-1 / ( r - 1 )! ) | |
| = | λe-λeλ = λ |
また、
| E[r2] | = | Σr{0→∞}( r2Pλ(r) ) |
| = | Σr{0→∞}( r2e-λλr / r! ) | |
| = | λΣr{1→∞}( re-λλr-1 / ( r - 1 )! ) | |
| = | λΣr{1→∞}( ( r - 1 )e-λλr-1 / ( r - 1 )! + e-λλr-1 / ( r - 1 )! ) | |
| = | λ( λ + 1 ) |
よって、
となって、平均も分散も同じ λ となります。λ は二項分布における Np になるので、平均が λ になることは容易に予想できます。また、二項分布での分散は Npq = Np( 1 - p ) で、Np = λ かつ N → ∞ ならば p → 0 であり 1 - p → 1 なので、これも λ となることは納得できると思います。
ポアソン分布についてまとめると
ポアソン分布 Pλ(r) = λre-λ / r!
平均 : μ = λ、分散 : σ2 = λ
のようになります。
ポアソン分布のサンプル・プログラムを以下に示します。
/* PoissonDistribution : ポアソン分布 Pλ(r) = λ^r・e^-λ / r! */ class PoissonDistribution : public DiscDist { double _lambda; // 定数 λ // 階乗の計算 static double fact( int n ); public: /* PoissonDistribution コンストラクタ lambda : 定数 λ */ PoissonDistribution( double lambda ) : _lambda( lambda ) {} double average() const // 平均値 { return( ( _lambda < 0 ) ? NAN : _lambda ); } double variance() const // 分散 { return( ( _lambda < 0 ) ? NAN : _lambda ); } // 確率変数 r に対する確率密度を返す double operator[]( int r ) const; }; /* PoissonDistribution::fact 階乗 n! の計算 戻り値 : 計算結果 */ double PoissonDistribution::fact( double n ) { if ( n <= 1 ) return( 1 ); return( n * fact( n - 1 ) ); } /* PoissonDistribution::operator[] : 確率変数 r に対する確率密度を返す 戻り値 : 確率密度 */ double PoissonDistribution::operator[]( int r ) const { if ( _lambda < 0 ) return( NAN ); if ( r < 0 ) return( 0 ); // λ = 0 なら事象の確率 p = 0 を意味する if ( _lambda == 0 ) return( ( r == 0 ) ? 1 : 0 ); return( exp( -_lambda ) * pow( _lambda, r ) / fact( r ) ); }
λ = 1, 4, 10 及び λ = 1, 0.5, 0.1 でのポアソン分布を以下に示します。
| λ = 1, 4, 10 | λ = 1, 0.5, 0.1 |
|---|---|
 |
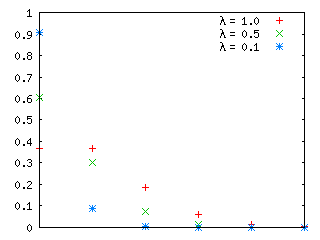 |
ポアソン分布は、二項分布において試行回数を多くしたときの近似式と考えることもできます。以下は、サンプル・プログラムを使って二項分布とポアソン分布の確率密度を計算して比較した表です。試行回数に対して一回は事象が起こるような確率として、試行回数を 10/100/1000/10000 回と変化させたときの二項分布 BN,1/N(r) と、平均 1 回は事象が発生するときのポアソン分布 P1(r) を求めています。
| r | B10,0.1(r) | B100,0.01(r) | B1000,0.001(r) | B10000,0.0001(r) | P1(r) |
|---|---|---|---|---|---|
| 0 | 0.348678 | 0.366032 | 0.367695 | 0.367861 | 0.367879 |
| 1 | 0.387420 | 0.369730 | 0.368063 | 0.367898 | 0.367879 |
| 2 | 0.193710 | 0.184865 | 0.184032 | 0.183949 | 0.183940 |
| 3 | 0.0573956 | 0.0609992 | 0.0612825 | 0.0613102 | 0.0613132 |
| 4 | 0.0111603 | 0.0149417 | 0.0152900 | 0.0153245 | 0.0153283 |
| 5 | 0.00148803 | 0.00289779 | 0.00304881 | 0.00306398 | 0.00306566 |
| 6 | 0.000137781 | 0.000463451 | 0.000506100 | 0.000510458 | 0.000510944 |
| 7 | 8.74800e-06 | 6.28635e-05 | 7.19381e-05 | 7.28862e-05 | 7.29920e-05 |
| 8 | 3.64500e-07 | 7.38169e-06 | 8.93826e-06 | 9.10530e-06 | 9.12399e-06 |
| 9 | 9.00000e-09 | 7.62195e-07 | 9.86181e-07 | 1.01099e-06 | 1.01378e-06 |
試行回数を増やすに従って、二項分布とポアソン分布との差が小さくなることが上の表から分かります。試行回数が充分大きければ、二項分布の代わりにポアソン分布を使ってもそれほど精度上の問題はないので、手計算で確率密度を求めるような場合は有効な手段になりますが、現在ではコンピュータを利用して求めることができるので、二項分布の代わりとして利用することはあまり価値がないと思います。
ポアソン分布は、ある事象が起こる頻度の平均だけが既知であるような場合に有効となります。例えば、日本国内で一日に車が利用される回数や、一台あたりが一日に事故を起こす確率などを簡単に得ることはできませんが、一日に発生する事故の回数は比較的調査しやすいので、二項分布ではなくポアソン分布が有効になります。
ある街において、一週間あたり平均二件の交通事故が発生していたとしたとき、これがポアソン分布に従うとすれば、一週間で r 件の交通事故が発生する確率は
になります。事故が一件も発生しない確率は、
で、同様に r = 5 まで計算すると
| r | P2( r ) |
|---|---|
| 0 | 0.1353 |
| 1 | 0.2707 |
| 2 | 0.2707 |
| 3 | 0.1804 |
| 4 | 0.09022 |
| 5 | 0.03609 |
また、r ≥ 6 となる確率は上表の和を 1 から減算した値になるので、0.0166 と確率的には低いことになります。
ポアソン分布において、λ は単位時間あたりの事象の平均発生回数を表しています。ここで、時間 t の間に発生した事象の回数に対する確率がポアソン分布に従うとすれば、
と表すことができます。これは、時間 t の間に事象が r 回発生した確率を表しているので、r を固定して t を変数とすることによって、どの程度の時間で事象が発生するのかを調べることができるようになります。特に、時間 t の間に事象が発生しなかった確率は
となるので、事象が発生しない確率は t = 0 のとき 1 で、t が大きくなるにつれその確率密度は減少していきます。t を確率変数として考えて、上式を確率分布としたとき、全事象に対する確率は [ 0, ∞ ) における積分値となるので
| ∫Ω Pλ( t ) dt | = | ∫{0→∞} e-λt dt |
| = | [ ( -1 / λ )e-λt ]{0→∞} = 1 / λ |
このままでは全事象の確率が 1 にならないので、λ を式に掛けて
これは「指数分布(Exponential Distribution)」と呼ばれる連続確率分布の一つで、例えばモノが故障するまでの時間を推定する場合などに利用できます。年に平均一回故障する装置が t 年で故障する確率が指数分布 P1(t) = e-t に従うとすれば、一年以内に故障する確率は
| ∫{0→1} P1(t) dt | = | ∫{0→1} e-t dt |
| = | [ -e-t ]{0→1} | |
| = | 1 - e-1 = 0.632 |
なのに対し、10 年間で故障する確率は
となって、非常に高い確率になります。指数分布の累積分布関数 F(x) は
| F(x) | = | ∫{0→x} Pλ(t) dt |
| = | ∫{0→x} λe-λt dt | |
| = | [ -e-λt ]{0→x} | |
| = | 1 - 1 / eλx |
なので、λ が大きいほど、ある定数値 x に対する 1 / eλx の値は小さく、F(x) は急激に大きくなります。λ が故障頻度を表しているとすれば、指数分布を使って経過時間における故障の頻度を表すことができるわけです。
指数分布の積率母関数は、θ < λ のとき
| g(θ) | = | ∫{0→∞} eθtλe-λt dt |
| = | ∫{0→∞} λe( θ - λ )t dt | |
| = | [ { λ / ( θ - λ ) }e( θ - λ )t ]{0→∞} | |
| = | λ / ( λ - θ ) |
なので、
g'(θ) = λ / ( λ - θ )2 より
μ = g'(0) = 1 / λ
また、
g(2)(θ) = 2λ / ( λ - θ )3 より
σ2 = g(2)(0) - μ2 = 2 / λ2 - 1 / λ2 = 1 / λ2
になります。
指数分布についてまとめておきます。
指数分布 Pλ(t) = λe-λt
平均 : μ = 1 / λ、分散 : σ2 = 1 / λ2
指数分布のサンプル・プログラムを以下に示します。
/* ExponentialDistribution : 指数分布 P(t) = λe^(-λt) */ class ExponentialDistribution : public ContDist { double _lambda; // 定数 λ public: /* ExponentialDistribution コンストラクタ lambda : 定数 λ */ ExponentialDistribution( double lambda ) : _lambda( lambda ) {} double average() const // 平均値 { return( ( _lambda > 0 ) ? 1.0 / _lambda : NAN ); } double variance() const // 分散 { return( ( _lambda > 0 ) ? 1.0 / pow( _lambda, 2 ) : NAN ); } // 確率変数 t における確率密度を返す double operator[]( double t ) const; // 区間 (-∞,a] における確率を返す double lower_p( double a ) const; }; /* ExponentialDistribution::operator[] : 確率変数 t に対する確率密度を返す 戻り値 : 確率密度 */ double ExponentialDistribution::operator[]( double t ) const { if ( _lambda <= 0 ) return( NAN ); if ( t < 0 ) return( 0 ); return( _lambda * exp( -_lambda * t ) ); } /* ExponentialDistribution::lower_p : 区間 (-∞,a] における確率を返す double a : 区間の上限 戻り値 : 確率 */ double ExponentialDistribution::lower_p( double a ) const { if ( _lambda <= 0 ) return( NAN ); if ( a <= 0 ) return( 0 ); // 区間が負の領域なら 0 を返す return( 1.0 - exp( -_lambda * a ) ); }
λ = 2, λ = 1, λ = 0.5 での指数分布を以下に示します。
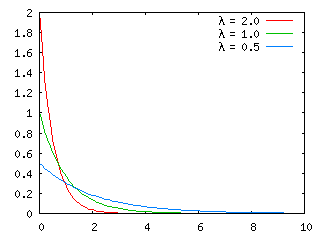
N 回のベルヌーイ試行において、ある事象が k 回起こる確率は二項分布を使って表すことができました。ここで、ある事象が k 回発生するまでに、その事象が起こらなかった回数を確率変数としたときの分布を検討してみます。
そのような回数を r としたとき、試行回数は r + k と表すことができ、その各標本点に対する確率を二項分布の場合と同様に pkqr と表すことができます。r + k 回中 r 回事象が発生しなかった場合の組み合わせは r+kCr となりますが、その中の最後は必ず事象が起こったことになるので組み合わせとしては r + k - 1 回の試行で r 回事象が発生しなかったときの組み合わせを考えればよくて、それは r+k-1Cr になります。従って、この場合の確率分布を NBk,p(r) とすれば、
になります。これを「負の二項分布(Negative Binomial Distribution)」といいます。この場合、事象の起こった回数を k 回と固定した時に、r 回事象が起こらなかったときの確率を表していると考えることができます。ここで、n = r + k とすれば、この分布のパラメータは n と k にすることができて、NBk,p(n) として
と表すことができます。これは、事象が k 回起こるために必要な試行回数が n 回である場合の確率と考えることができます。
二項分布は、全事象の和が二項定理の展開式となっていましたが、負の二項分布では、負の二項係数に関する以下の等式
を使って全事象の和を計算することができます。
| Σr{0→∞}( NBk,p(r) ) | = | Σr{0→∞}( C( r + k - 1, r ) pkqr ) |
| = | pkΣr{0→∞}( C( -k, r ) ( -q )r ) |
ここで、一般の二項定理が
なので、
| pkΣr{0→∞}( C( -k, r ) ( -q )r ) | = | pk( 1 - q )-k |
| = | pkp-k = 1 |
になります。
積率母関数は
| g(θ) | = | Σr{0→∞}( eθrNBk,p(r) ) |
| = | Σr{0→∞}( eθr C( r + k - 1, r ) pkqr ) | |
| = | pkΣr{0→∞}( C( -k, r ) ( -qeθ )r ) | |
| = | pk( 1 - qeθ )-k |
なので、
g'(θ) = kpkqeθ( 1 - qeθ )-k-1 より
μ = g'(0) = kpkq( 1 - q )-k-1 = k( 1 - p ) / p
また、分散は
g(2)(θ) = kpkq{ eθ( 1 - eθq )-k-1 + ( k + 1 )qe2θ( 1 - eθq )-k-2 } より
| σ2 = g(2)(0) - μ2 | = | kpkq{ ( 1 - q )-k-1 + ( k + 1 )q( 1 - q )-k-2 } - { kq / p }2 |
| = | kpkq{ p-k-1 + ( k + 1 )qp-k-2 } - { kq / p }2 | |
| = | kq / p + k( k + 1 )( q / p )2 - k2( q / p )2 | |
| = | k{ ( 1 - p ) / p }{ 1 + ( 1 - p ) / p } | |
| = | k( 1 - p ) / p2 |
になります。
よく利用されるパターンとしては、初めて事象が起こるまでに何回の試行が必要であるかを推定するようなものが考えられます。この場合、式は非常に単純になって、
になります。上式は、事象が初めて発生するまでに試行を r 回繰り返した場合の確率を表しており、特別に「幾何分布(Geometric Distribution)」という名が付けられています。負の二項分布の特別な形であり確率分布として成り立つのは当然ですが、全事象の和が等比級数(幾何級数) Σr{1→∞}( pqr-1 ) の形になっていることが名前の由来となっています。
幾何分布の積率母関数は
| g(θ) | = | Σr{1→∞}( eθrGp(r) ) |
| = | Σr{1→∞}( eθrpqr-1 ) | |
| = | Σr{1→∞}( peθ( qeθ )r-1 ) |
ここで、qeθ < 1 ならば Sn = Σr{1→n}( peθ( qeθ )r-1 ) としたとき
| Sn | = | peθ | + | peθ( qeθ ) | + ... + | peθ( qeθ )n-1 | |||
| - ) | qeθSn | = | peθ( qeθ ) | + ... + | peθ( qeθ )n-1 | + | peθ( qeθ )n | ||
| ( 1 - qeθ )Sn | = | peθ | - | peθ( qeθ )n | |||||
より
よって、
これを θ で微分して
| g'(θ) | = | peθ / ( 1 - qeθ ) + pqe2θ / ( 1 - qeθ )2 |
| = | { peθ( 1 - qeθ ) + pqe2θ } / ( 1 - qeθ )2 | |
| = | peθ / ( 1 - qeθ )2 |
よって、
また、
| g(2)(θ) | = | peθ / ( 1 - qeθ )2 + 2pqe2θ / ( 1 - qeθ )3 |
| = | { peθ( 1 - qeθ ) + 2pqe2θ } / ( 1 - qeθ )3 | |
| = | ( peθ + pqe2θ ) / ( 1 - qeθ )3 |
よって、
| 分散 σ2 | = | g(2)(0) - μ2 |
| = | ( p + pq ) / ( 1 - q )3 - 1 / p2 | |
| = | p( 1 + q ) / p3 - 1 / p2 | |
| = | ( 1 - p ) / p2 |
負の二項分布において k = 1 とした場合、分散は両者が一致しますが平均は異なっています。これは、負の二項分布においては確率変数が事象の発生しなかった回数を表しているのに対し、幾何分布では試行を行った回数を表しているという違いによるものです。実際、事象の発生しなかった回数を r とすれば、
なので、積率母関数は
| g(θ) | = | Σr{0→∞}( eθrpqr ) |
| = | Σr{0→∞}( p( qeθ )r ) | |
| = | p / ( 1 - qeθ ) |
これを θ で微分すると
よって、平均は
となって、負の二項分布と一致します。逆に、負の二項分布において確率変数を試行回数 n にした場合は、
| g(θ) | = | Σn{k→∞}( eθnNBk,p(n) ) |
| = | Σn{k→∞}( eθnn-1Ck-1 pkqn-k ) |
r = n - k とすれば、
| g(θ) | = | Σr{0→∞}( eθ( r + k )r+k-1Ck-1 pkqr ) |
| = | Σr{0→∞}( eθ( r + k )r+k-1Cr pkqr ) | |
| = | ( peθ )kΣr{0→∞}( C( -k, r )( -qeθ )r ) | |
| = | ( peθ )k( 1 - qeθ )-k | |
| = | { peθ / ( 1 - qeθ ) }k |
θ で微分して
| g'(θ) | = | k{ peθ / ( 1 - qeθ ) }k-1{ peθ / ( 1 - qeθ )2 } |
| = | k{ ( peθ )k / ( 1 - qeθ )k+1 } |
よって、平均は
となって、幾何分布の場合と一致することになります。事象の起こらなかった(失敗した)回数と試行回数のどちらを確率変数とするか、場合によって使い分けることになります。試行回数は事象の起こった回数と起こらなかった回数との和になる ( n = r + k ) ので、
であり、NBk,p(n) の確率密度のグラフは、NBk,p(r) のグラフを k だけ右側に平行移動するだけで、その分布の形状は変化しません。よって、平均値は異なるものの、分散はどちらも等しくなるわけです。
以上の結果をまとめると、
負の二項分布(1) NBk,p(r) = r+k-1Cr pkqr
平均 : μ = k( 1 - p ) / p、分散 : σ2 = k( 1 - p ) / p2
負の二項分布(2) NBk,p(n) = n-1Ck-1 pkqn-k
平均 : μ = k / p、分散 : σ2 = k( 1 - p ) / p2
幾何分布 Gp(r) = NB1,p(r) = pqr-1 ( r ≥ 1 )
平均 : μ = 1 / p、分散 : σ2 = ( 1 - p ) / p2
となります。
負の二項分布のサンプル・プログラムを以下に示します。
/* NegativeBinomialDistribution : 負の二項分布 NB(k,p,r) = r+k-1Cr p^k q^r p : ある事象 A が一回の試行で起こる確率 q : ある事象 A が一回の試行で起こらない確率( = 1 - p ) k : 事象 A の発生回数 r : 事象 A の発生しなかった回数 事象 A が k 回発生するまでに、r 回は発生しなかったときの確率 */ class NegativeBinomialDistribution : public DiscDist { double _p; // 一回の試行で起こる確率 unsigned int _k; // 事象の発生回数 public: /* NegativeBinomialDistribution コンストラクタ p : ある事象 A が一回の試行で起こる確率 k : 事象の発生回数 */ NegativeBinomialDistribution( double p, unsigned int k = 1 ) : _p( p ), _k( k ) {} double average() const // 平均値 { return( ( _p > 0 && _p <= 1 && _k > 0 ) ? (double)_k * ( 1 - _p ) / _p : NAN ); } double variance() const // 分散 { return( ( _p > 0 && _p <= 1 && _k > 0 ) ? (double)_k * ( 1 - _p ) / ( _p * _p ) : NAN ); } // 確率変数 r に対する確率密度を返す double operator[]( int r ) const; }; /* NegativeBinomialDistribution::operator[] : 確率変数 r に対する確率密度を返す 戻り値 : 確率密度 */ double NegativeBinomialDistribution::operator[]( int r ) const { // _p < 0 または _p > 1 のときは無効値を返す if ( _p < 0 || _p > 1 ) return( NAN ); // 事象の発生回数がゼロの場合は計算できない if ( _k == 0 ) return( NAN ); // 確率変数がゼロより小さければ確率は常にゼロ if ( r < 0 ) return( 0 ); // 事象の起こらない確率がゼロなら r = 0 のとき 1 でそれ以外は 0 if ( _p == 1 ) return( ( r == 0 ) ? 1 : 0 ); double c = comb( (double)( r + _k - 1 ), (double)r ); return( c * pow( _p, _k ) * pow( 1 - _p, r ) ); } /* NegativeBinomialDistribution_N : 負の二項分布(2) NB(k,p,n) = n-1Ck-1 p^k q^n-k p : ある事象 A が一回の試行で起こる確率 q : ある事象 A が一回の試行で起こらない確率( = 1 - p ) k : 事象 A の発生回数 n : 試行回数 事象 A が k 回発生するまでに、n 回の試行が必要だったときの確率 */ class NegativeBinomialDistribution_N : public DiscDist { double _p; // 一回の試行で起こる確率 unsigned int _k; // 事象の発生回数 public: /* NegativeBinomialDistribution_N コンストラクタ p : ある事象 A が一回の試行で起こる確率 k : 事象の発生回数 */ NegativeBinomialDistribution_N( double p, unsigned int k = 1 ) : _p( p ), _k( k ) {} double average() const // 平均値 { return( ( _p > 0 && _p <= 1 && _k > 0 ) ? (double)_k / _p : NAN ); } double variance() const // 分散 { return( ( _p > 0 && _p <= 1 && _k > 0 ) ? (double)_k * ( 1 - _p ) / ( _p * _p ) : NAN ); } // 確率変数 n に対する確率密度を返す double operator[]( int n ) const; }; /* NegativeBinomialDistribution_N::operator[] : 確率変数 n に対する確率密度を返す 戻り値 : 確率密度 */ double NegativeBinomialDistribution_N::operator[]( int n ) const { // _p < 0 または _p > 1 のときは無効値を返す if ( _p < 0 || _p > 1 ) return( NAN ); // 事象の発生回数がゼロの場合は計算できない if ( _k == 0 ) return( NAN ); // 試行回数がゼロ以下か _k に満たない場合は確率ゼロ if ( n <= 0 ) return( 0 ); if ( (unsigned int)n < _k ) return( 0 ); // 事象の起こらない確率がゼロなら n = _k のとき 1 でそれ以外は 0 if ( _p == 1 ) return( ( (unsigned int)n == _k ) ? 1 : 0 ); double c = comb( (double)( n - 1 ), (double)( _k - 1 ) ); return( c * pow( _p, _k ) * pow( 1 - _p, n - _k ) ); } /* negativeBinomialDistribution : 負の二項分布を求める NB(k,p,r) = r+k-1Cr p^k q^r p : ある事象 A が一回の試行で起こる確率 q : ある事象 A が一回の試行で起こらない確率( = 1 - p ) k : 事象 A の発生回数 r : 事象 A の発生しなかった回数 事象 A が k 回発生するまでに、r 回は発生しなかったときの確率 double p : 一回の試行でAが起こる確率 unsigned int k : 事象 A の発生回数 vector<long double>& ans : 求める確率分布 unsigned int cnt : 計算する回数 戻り値 : 途中で計算ができなくなった場合はfalseを返す */ bool negativeBinomialDistribution( double p, unsigned int k, vector<double>& ans, unsigned int cnt ) { double c = 1.0; // 組み合わせ nCr (初期値 = nC0 = 1) double q = 1.0 - p; // 余事象の確率 ans.clear(); // 要素をいったん削除 // p < 0 または p > 1 の場合は処理を行わない if ( p < 0 || p > 1 ) return( false ); // 事象の発生回数がゼロの場合は計算できない if ( k == 0 ) return( false ); // 計算回数がゼロなら何もしない if ( cnt == 0 ) return( true ); ans.assign( cnt, 0 ); // 要素は 0 で初期化 // p = 0 なら常に確率密度はゼロ if ( p == 0 ) return( true ); // p = 1 なら r = 0 のときだけ 1 if ( p == 1 ) { ans[0] = 1; return( true ); } double pk = pow( p, k ); // 定数 p^k for ( unsigned int r = 0 ; r < cnt ; ++r ) { ans[r] = c * pk * pow( q, r ); c *= (double)( k + r ); c /= (double)( r + 1 ); if ( isinf( c ) || isnan( c ) ) return( false ); } return( true ); } /* negativeBinomialDistribution_N : 負の二項分布を求める NB(k,p,n) = n-1Ck-1 p^k q^n-k p : ある事象 A が一回の試行で起こる確率 q : ある事象 A が一回の試行で起こらない確率( = 1 - p ) k : 事象 A の発生回数 n : 試行回数 事象 A が k 回発生するまでに、n 回の試行が必要なときの確率 double p : 一回の試行でAが起こる確率 unsigned int k : 事象 A の発生回数 vector<long double>& ans : 求める確率分布 unsigned int cnt : 計算する回数 戻り値 : 途中で計算ができなくなった場合はfalseを返す */ bool negativeBinomialDistribution_N( double p, unsigned int k, vector<double>& ans, unsigned int cnt ) { double c = 1.0; double q = 1.0 - p; ans.clear(); // p < 0 または p > 1 の場合は処理を行わない if ( p < 0 || p > 1 ) return( false ); // 事象の発生回数がゼロの場合は計算できない if ( k == 0 ) return( false ); // 計算回数がゼロなら何もしない if ( cnt == 0 ) return( true ); ans.assign( cnt, 0 ); // 要素は 0 で初期化 // p = 0 なら常に確率密度はゼロ if ( p == 0 ) return( true ); // p = 1 なら n = k のときだけ 1 if ( p == 1 ) { if ( k < cnt ) ans[k] = 1; return( true ); } double pk = pow( p, k ); // 定数 p^k for ( unsigned int n = k ; n < cnt ; ++n ) { ans[n] = c * pk * pow( q, n - k ); c *= (double)n; c /= (double)( n - k + 1 ); if ( isinf( c ) || isnan( c ) ) return( false ); } return( true ); }
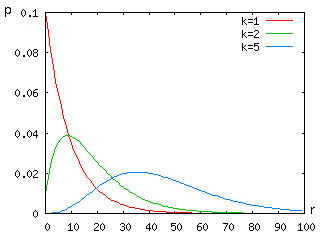
下図のグラフは、0.1, 0.5, 0.9 の確率で起こる事象が k 回成功するまでに失敗する回数 r を横軸としたときの確率分布を表したものです。
| p = 0.1 | p = 0.5 | p = 0.9 |
|---|---|---|
 |
 |
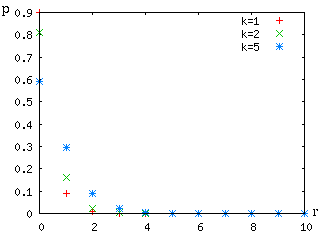 |
一回の成功に対しては、全ての p において、失敗の回数がゼロのときが最も確率が高く、失敗の回数が多くなるほと単調に確率が減少するような分布となっています。ちょうど r + 1 回目に成功する確率は r が大きくなるに従って小さくなっていきますが、r + 1 回目以内に成功する確率はそれまでの和となるので、
になり、逆に r + 1 回より多く失敗する確率は qr+1 になります。
負の二項分布は、確率の創始者の一人である「ブレーズ・パスカル(Blaise Pascal)」の名前を取って、「パスカル分布(Pascal Distribution)」とも呼ばれています。
負の二項分布において、kq = λ (正の定数) として式を変形するとどうなるかを見てみます。
| NBk,p(r) = r+k-1Cr pkqr | = | { ( r + k - 1 )( r + k - 2 )...( r + k - r ) / r! } ( λ / k )r ( 1 - λ / k )k |
| = | [ { ( r + k - 1 ) / k }{ ( r + k - 2 ) / k } ... { ( r + k - r ) / k } ] ( λr / r! ) ( 1 - λ / k )(-k/λ)(-λ) |
( r + k - 1 ) / k, ( r + k - 2 ) / k, ... ( r + k - r ) / k は、k → ∞ において 1 に収束し、( 1 - λ / k )(-k/λ) は同じく k → ∞ において e に収束するので、
となって、ポアソン分布に近づいていきます。二項分布では、試行回数を大きくするとポアソン分布に近づいていきましたが、負の二項分布では事象が発生する回数を大きくするとポアソン分布に近づくことになります。このとき q は非常に小さくなるので、「ほとんど失敗することはないが長い試行の中で稀に失敗する」ような状況でポアソン分布による近似を利用することができます。
以下は、二項分布の場合と同様に、負の二項分布とポアソン分布の確率密度を計算して比較した表です。試行回数に対して一回は事象が起こらないような確率として、試行回数を 10/100/1000/10000 回と変化させたときの負の二項分布 NBN,1-1/N(r) と、平均 1 回は事象が発生するときのポアソン分布 P1(r) を求めています。ポアソン分布では「事象が平均 1 回発生する」ときの分布としていることに注意して下さい。
| r | NB10,0.9(r) | NB100,0.99(r) | NB1000,0.999(r) | NB10000,0.9999(r) | P1(r) |
|---|---|---|---|---|---|
| 0 | 0.348678 | 0.366032 | 0.367695 | 0.367861 | 0.367879 |
| 1 | 0.348678 | 0.366032 | 0.367695 | 0.367861 | 0.367879 |
| 2 | 0.191773 | 0.184846 | 0.184032 | 0.183949 | 0.183940 |
| 3 | 0.0767093 | 0.0628478 | 0.0614665 | 0.0613286 | 0.0613132 |
| 4 | 0.0249305 | 0.0161833 | 0.0154127 | 0.0153367 | 0.0153283 |
| 5 | 0.00698054 | 0.00336613 | 0.00309488 | 0.00306858 | 0.00306566 |
| 6 | 0.00174514 | 0.000589072 | 0.000518392 | 0.000511685 | 0.000510944 |
| 7 | 3.98888e-04 | 8.92023e-05 | 7.45003e-05 | 7.31417e-05 | 7.2992e-05 |
| 8 | 8.47637e-05 | 1.19308e-05 | 9.37773e-06 | 9.14911e-06 | 9.12399e-06 |
| 9 | 1.69527e-05 | 1.43170e-06 | 1.05031e-06 | 1.01738e-06 | 1.01378e-06 |
箱の中に、赤い球が a 個、白い球が b 個入っていて、その中から任意に k 個の球を取り出すとき、赤い球が r 個、白い球が k - r 個になる確率を考えます。
赤い球が 3 個、白い球が 2 個あって、その中から紅白それぞれ 1 個ずつ球を取り出す場合を例に検討してみると、全体は 5 個の球があって、そこから 2 個の球を取り出す組み合わせは 5C2 = 10 通りあります。赤を一つだけ取り出す場合の数は 3C1 = 3 通り、白の場合は 2C1 = 2 通りとなって、それぞれの場合を組み合わせる場合の数は両者を掛け合わせた数となるので、紅白一つずつ選ぶ場合の数は 6 通りになります。従って、確率は 6 / 10 = 3 / 5 と求めることができます。これを元に考えれば、
が求める確率となります。確率変数 r は 0 ≤ r ≤ k の範囲の整数値となって、全事象の和は
なので、上式の値は 1 になり、確率分布として成り立っていることになります。
平均は
| μ | = | Σr{0→k}( r aCr bCk-r / a+bCk ) |
| = | Σr{0→k}( r aCr bCk-r ) / a+bCk |
となるので、和の部分 S = Σr{0→k}( r aCr bCk-r ) だけを計算すると、
| S | = | Σr{0→k}( { ra! / r! ( a - r )! }{ b! / ( k - r )! { b - ( k - r ) }! ) |
| = | Σr{1→k}( [ a( a - 1 )! / ( r - 1 )! { ( a - 1 ) - ( r - 1 ) }! ][ b! / { ( k - 1 ) - ( r - 1 ) }! { b - ( ( k - 1 ) - ( r - 1 ) ) }! ] ) | |
| = | Σr{1→k}( a a-1Cr-1 bC(k-1)-(r-1) ) | |
| = | a a+b-1Ck-1 |
よって、
| μ | = | a a+b-1Ck-1 / a+bCk |
| = | { a( a + b - 1 )! / ( k - 1 )! ( a + b - k )! }{ k! ( a + b - k )! / ( a + b )! } | |
| = | ak / ( a + b ) |
分散は、まず r2 の期待値を計算すると、
| E[r2] | = | Σr{0→k}( r2 aCr bCk-r / a+bCk ) |
| = | Σr{1→k}( ra a-1Cr-1 bC(k-1)-(r-1) ) / a+bCk |
となって、和の部分 S1 = Σr{1→k}( ra a-1Cr-1 bC(k-1)-(r-1) ) だけを計算すると
| S1 | = | Σr{1→k}( ( r - 1 )a a-1Cr-1 bC(k-1)-(r-1) + a a-1Cr-1 bC(k-1)-(r-1) ) |
| = | Σr{1→k}( ( r - 1 )a a-1Cr-1 bC(k-1)-(r-1) ) + a a+b-1Ck-1 |
さらに、和の部分 S2 = Σr{1→k}( ( r - 1 )a a-1Cr-1 bC(k-1)-(r-1) ) は S を計算したときと同様のやり方で
となるので、
| E[r2] | = | { a( a - 1 ) a+b-2Ck-2 + a a+b-1Ck-1 } / a+bCk |
| = | [ { a( a - 1 )( a + b - 2 )! / ( k - 2 )! ( a + b - k )! } + { a( a + b - 1 )! / ( k - 1 )! ( a + b - k )! } ]{ k! ( a + b - k )! / ( a + b )! } | |
| = | { ak( a - 1 )( k - 1 ) / ( a + b )( a + b - 1 ) } + { ak / ( a + b ) } | |
| = | { ak / ( a + b ) }{ ( a - 1 )( k - 1 ) / ( a + b - 1 ) + 1 } | |
| = | { ak / ( a + b ) }[ { ( ak - a - k + 1 ) + ( a + b - 1 ) } / ( a + b - 1 ) ] | |
| = | { ak / ( a + b ) }{ ( ak + b - k ) / ( a + b - 1 ) } |
よって、
| σ2 | = | E[r2] - μ2 |
| = | { ak / ( a + b ) }{ ( ak + b - k ) / ( a + b - 1 ) } - { ak / ( a + b ) }2 | |
| = | { ak / ( a + b ) }{ ( ak + b - k ) / ( a + b - 1 ) - ak / ( a + b ) } | |
| = | { ak / ( a + b ) }[ { ( a + b )( ak + b - k ) - ak( a + b - 1 ) } / ( a + b )( a + b - 1 ) ] | |
| = | { ak / ( a + b ) }{ b( a + b - k ) / ( a + b )( a + b - 1 ) } | |
| = | abk( a + b - k ) / ( a + b )2( a + b - 1 ) |
と求めることができます。
超幾何分布についてまとめておきます。
超幾何分布 Pa,b,k(r) = aCr bCk-r / a+bCk
平均 : μ = ak / ( a + b )、分散 : σ2 = abk( a + b - k ) / ( a + b )2( a + b - 1 )
超幾何分布のサンプル・プログラムを以下に示します。
/* HypergeometricDistribution : 超幾何分布 Pa,b,k(r) = aCr bCk-r / a+bCk a,b : 二種類の要素の個数 k : 要素から選択する個数 r : 片側の要素が選択される個数 */ class HypergeometricDistribution : public DiscDist { unsigned int _a; // 要素 A の個数 unsigned int _b; // 要素 B の個数 unsigned int _k; // 要素から選択する個数 public: // コンストラクタ HypergeometricDistribution( unsigned int a, unsigned int b, unsigned int k ) : _a( a ), _b( b ), _k( k ) {} double average() const; // 平均値 double variance() const; // 分散 // 確率変数 r に対する確率密度を返す double operator[]( int r ) const; }; /* HypergeometricDistribution::average : 平均値を返す 戻り値 : 平均値 */ double HypergeometricDistribution::average() const { if ( _k > _a + _b ) return( NAN ); if ( _a + _b == 0 ) return( NAN ); return( ( (double)_a * (double)_k ) / ( (double)_a + (double)_b ) ); } /* HypergeometricDistribution::variance : 分散を返す 戻り値 : 分散 */ double HypergeometricDistribution::variance() const { if ( _k > _a + _b ) return( NAN ); if ( _a + _b <= 1 ) return( NAN ); return( ( (double)_a * (double)_b * (double)_k * (double)( _a + _b - _k ) ) / ( (double)( _a + _b ) * (double)( _a + _b ) * (double)( _a + _b - 1 ) ) ); } /* HypergeometricDistribution::operator[] : 確率変数 r に対する確率密度を返す 戻り値 : 確率密度 */ double HypergeometricDistribution::operator[]( int r ) const { if ( _k > _a + _b ) return( NAN ); if ( r < 0 ) return( 0 ); if ( (unsigned int)r > _k ) return( 0 ); if ( (unsigned int)r > _a + _b ) return( 0 ); double c1 = comb( (double)_a, (double)r ); double c2 = comb( (double)_b, (double)( _k - r ) ); double c3 = comb( (double)( _a + _b ), (double)_k ); return( c1 * c2 / c3 ); }
下のグラフは、1000 個ある二種類の要素 A, B が A:B = 1:9, 2:8, 5:5, 9:1 の比率であった場合、その中から 100 個の要素を抽出したときの A の要素数に対する確率を図示したものです。

下表は、比率を 1:9 から 9:1 まで 10 段階に変化させた時の平均値と分散を計算した結果です。
| 比率 | 平均値 | 分散 |
|---|---|---|
| 1:9 | 10 | 8.10811 |
| 2:8 | 20 | 14.4144 |
| 3:7 | 30 | 18.9189 |
| 4:6 | 40 | 21.6216 |
| 5:5 | 50 | 22.5225 |
| 6:4 | 60 | 21.6216 |
| 7:3 | 70 | 18.9189 |
| 8:2 | 80 | 14.4144 |
| 9:1 | 90 | 8.10811 |
平均が、比率に応じて変化していく様子や、比率の偏りが大きくなるほど分散は小さくなっていく傾向を見ることができますが、これも経験上納得のいく結果になっていると思います。
今まで説明した確率分布を実際に利用する例をいくつか紹介したいと思います。
品物を一つ購入したときにそれが故障しているという事象が発生する確率が 1 / 10 で、その試行を 5 回繰り返すとき、故障する事象が r 回発生する事象が二項分布に従うとすれば、
と表すことができて、B5, 1/10(0) = ( 9 / 10 )5 = 0.59049 と計算できます。平均は 5 x ( 1 / 10 ) = 0.5 なので、一個くらいは故障品がある可能性があるものの、故障品が一個以下の確率は B5, 1/10(0) + B5, 1/10(1) = 0.59049 + 5 x ( 1 / 10 ) x ( 9 / 10 )4 = 0.91854 なので二個以上になる可能性は低く、予備として一つ余分に買っておけば大丈夫であると判断できそうです。
10 個中一つの故障品があることから 5 個購入すれば平均 0.5 個の故障品があることになるので、これをポアソン分布 P0.5(r) = ( 0.5 )re-0.5 / r! に置き換えてみると、
P0.5(0) = e-0.5 = 0.60653
P0.5(1) = 0.5 x e-0.5 = 0.30327
となって、ある程度近い値が得られます。
別の考え方として、試行を繰り返したときに初めて故障する事象が発生するまでの回数を確率変数とする方法もあります。これは、幾何分布
を使って表すことができるので、r が 1 から 5 までの値を取るときの確率を求めて
| G1/10(1) = ( 1 / 10 )( 9 / 10 )0 | = | 0.10000 |
| G1/10(2) = ( 1 / 10 )( 9 / 10 )1 | = | 0.09000 |
| G1/10(3) = ( 1 / 10 )( 9 / 10 )2 | = | 0.08100 |
| G1/10(4) = ( 1 / 10 )( 9 / 10 )3 | = | 0.07290 |
| G1/10(5) = ( 1 / 10 )( 9 / 10 )4 | = | 0.06561 |
| 計 ) | 0.40951 |
となり、r > 5 である確率は 1 - 0.40951 = 0.59049 と計算できて、二項分布の場合と等しくなります。
初めて事象が起こるまでに何回の試行が必要であるかを推定する場合、幾何分布がよく用いられます。うるう年を無視すれば、ある人の誕生日が自分と同じである確率は 1 / 365 と考えることができるので、r 回目に初めて事象が起こる確率は
で計算することができます。10 人目までに初めて見つかる確率は、
となって極めて低い確率になります。これを 365 回繰り返せば一人くらいは当たりそうな気もしますが、その時の確率は 0.633 です。
似たような問題に、n 人中同じ誕生日であるグループが一つでもある確率を求めるというものがあります。n > 365 であれば確率は当然 1 になるので、n ≤ 365 での確率分布を考えることになります。これに似た問題が後の方で紹介されています。
100 個中当たりは一つなので、当たる確率は一回の試行で 1 / 100 であると考えることができます。当たりが 3 個得られるために必要な試行回数が n 回である確率は負の二項分布を使って次のように求めることができます。
一箱分 ( 100 個 ) 以内で 3 個の当たりが得られる確率を求めればいいので、少なくとも 3 個は買わなければならないことから、
を計算すれば解が求められ、これを計算すると 0.0794 になります。
ところで、この例題は「100 個あたり 1 個の当たりがある時に、100 個あたり r 個の当たりが得られる確率」と考えることもできます。この場合、すでに 3 個の当たりが出ても 100 個になるまでは買い続けるという意味になって、微妙に考え方の差があるものの、近い値は得られると予想することができます。この確率は、ポアソン分布を使って求めることができて、当たりが 0 個から 2 個までであったという事象の余事象の確率を計算すればいいので、
より、
となって、負の二項分布の場合と近い値が得られます。100 個中 1 個という条件を 100000 個中 1 個に置き換えた場合、100000 個以内でオマケがもらえる確率は
となって、ポアソン分布における値とほとんど変わらないことが分かります。
n 個の玉があって、その中の k 個が当たりだったとします。出てきた玉をもとに戻す場合、当たりが出る確率は常に k / n になります。初めて当たりが出るまでの回数に対する確率を考えればいいので、幾何分布を利用すると
が求める解として得られます。出てきた玉をもとに戻さない場合において r 回目に当たりが出る確率を Pk,n( r ) とします。Pk,n( 1 ) = k / n は明らかです。n - 1 個の中から k 個の当たりが出る確率を考えれば k / ( n - 1 ) になりますが、すでに 1 回目の試行でハズレを出しているので、その確率 1 - k / n の中の k / ( n - 1 ) 分と考えて、
を 2 回目の試行で当たりが出る確率とします。3 回目で当たる確率は、同様な考え方で
| Pk,n( 3 ) | = | { 1 - Pk,n( 1 ) - Pk,n( 2 ) } x k / ( n - 2 ) |
| = | k( n - k )( n - k - 1 ) / n( n - 1 )( n - 2 ) | |
| = | k( n - k )!( n - 3 )! / n!( n - k - 2 )! |
となります。
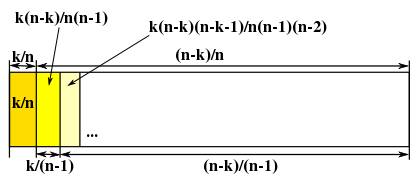
そこで、
であると仮定すると、
| Pk,n( r + 1 ) | = | { 1 - Σi{1→r}( Pk,n( i ) ) } x k / ( n - r ) |
| = | { 1 - k / n - k( n - k ) / n( n - 1 ) - k( n - k )( n - k - 1 ) / n( n - 1 )( n - 2 ) - ... | |
| - k( n - k )( n - k - 1 )...( n - k - r + 2 ) / n( n - 1 )( n - 2 )...( n - r + 1 ) } x k / ( n - r ) |
となって、差を計算する部分を先頭の項から順番に求めていくと、
1 - k / n = ( n - k ) / n
( n - k ) / n - k( n - k ) / n( n - 1 )
= { ( n - k )( n - 1 ) - k( n - k ) } / n( n - 1 )
= ( n - k )( n - k - 1 ) / n( n - 1 )
( n - k )( n - k - 1 ) / n( n - 1 ) - k( n - k )( n - k - 1 ) / n( n - 1 )( n - 2 )
= { ( n - k )( n - k - 1 )( n - 2 ) - k( n - k )( n - k - 1 ) } / n( n -1 )( n - 2 )
= ( n - k )( n - k - 1 )( n - k - 2 ) / n( n - 1 )( n - 2 )
:
( n - k )( n - k - 1 )...( n - k - r + 2 ) / n( n - 1 )( n - 2 )...( n - r + 2 )
- k( n - k )( n - k - 1 )...( n - k - r + 2 ) / n( n - 1 )( n - 2 )...( n - r + 2 )( n - r + 1 )
= { ( n - k )( n - k - 1 )...( n - k - r + 2 )( n - r + 1 ) - k( n - k )( n - k - 1 )...( n - k - r + 2 ) }
/ n( n - 1 )( n - 2 )...( n - r + 2 )( n - r + 1 )
= ( n - k )( n - k - 1 )...( n - k - r + 2 )( n - k - r + 1 ) / n( n - 1 )( n - 2 )...( n - r + 2 )( n - r + 1 )
となるので、
| Pk,n( r + 1 ) | = | k( n - k )( n - k - 1 )...( n - k - r + 2 )( n - k - r + 1 ) / n( n - 1 )( n - 2 )...( n - r + 2 )( n - r + 1 )( n - r ) |
| = | k( n - k )!{ n - ( r + 1 ) }! / n!( n - k - ( r + 1 ) + 1 )! |
と計算できて、r + 1 の場合でも式が成り立ちます。
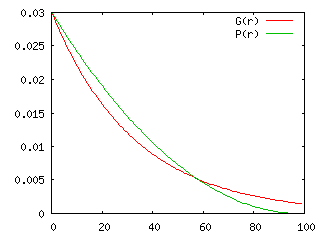
100 個の玉の中に当たりが 3 個含まれているとして、両者の確率分布とその累積を求めた結果を以下に示します。確率分布は「ちょうど r 回目で当たりが出る確率」を、その累積は「 r 回目までに当たりが出る確率」をそれぞれ表しています。
| 確率分布 | 累積分布 |
|---|---|
 |
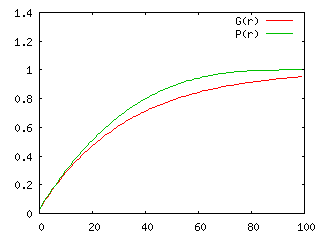 |
グラフの中の "G(r)" が玉をもとに戻す場合、"P(r)" が玉をもとに戻さない場合での分布を示しています。r の小さい時は、P(r) の方が高く、回数が多くなるに従いある時点で大小関係が逆転して G(r) の方が確率が大きくなります。これは、玉をもとに戻さない方が、回数の少ないうちに当たりの出る確率が高いことを示しています。累積分布を見ても、P(r) の方がより少ない回数で当たりが出やすいことを表しています。
玉をもとに戻さなければ、ハズレの数は減少していくので、その分だけ、もとに戻す場合よりも当たりが出やすくなっていきます。よって、この例題は当然の結果を述べているに過ぎないともいえます。これは、数式を使ってそれを裏付けたものになります。
マス目に 1 から 25 までの番号を付けて、i 番目の碁石 ( 1 ≤ i ≤ 10 ) に対するマス目の番号を gi = j ( 1 ≤ j ≤ 25 ) と表したとき、10 個の碁石それぞれが 25 個のマス目のいずれかに落ちたときの事象 A は
になります。このような場合の数は、1 から 25 までのカードを重複を許して 10 枚並べる場合の数と等しく、それは重複順列 25Π10 = 2510 通りあります。その中で、重複なしで入れる場合は順列 25P10 = 25! / 15! 通りになるので、求める確率は
と計算することができます。
これは、次のように考えることもできます。箱に碁石を落としたときに、25 個あるマス目のいずれかに落ちる確率が同等であるとすれば、その確率は 1 / 25 になります。碁石を順番に落として同じマス目に 2 個以上入るのは 2 回目からであり、その時 2 個の碁石が同じマス目に入る確率を P(2) とすれば、25 個のマス目の中に 1 個の碁石がすでにある状態で、そのマス目の中に 2 個目の碁石が落ちる確率を考えればいいので
になります。その余事象は 2 個の碁石がそれぞれ異なるマス目に入っている確率で、1 - P(2) = 24 / 25 になります。その中で、3 個目の碁石を落とした時に、2 個の碁石が入ったマス目ができる確率は、25 個のマス目の中に 2 個の碁石がすでにある状態で 3 個目の碁石が落ちる確率を考えればいいので 2 / 25 であり、
と求めることができます。これを繰り返すと、
となるので、同じマス目に入らない場合の確率は
と計算することができます。先に紹介した抽選器によるくじ引きの例と似たような考えかたですが、くじ引きの例では分母の数が一つずつ減っていたのに対し、この例では分子の数が一つずつ増えています。
実際に P(r) を計算した結果は次のようになります。
| r | P(r) | P(r) の累積 | r | P(r) | P(r) の累積 |
|---|---|---|---|---|---|
| 1 | 0.00000E+00 | 0.00000E+00 | 14 | 1.13004E-02 | 9.89569E-01 |
| 2 | 4.00000E-02 | 4.00000E-02 | 15 | 5.84141E-03 | 9.95410E-01 |
| 3 | 7.68000E-02 | 1.16800E-01 | 16 | 2.75381E-03 | 9.98164E-01 |
| 4 | 1.05984E-01 | 2.22784E-01 | 17 | 1.17496E-03 | 9.99339E-01 |
| 5 | 1.24355E-01 | 3.47139E-01 | 18 | 4.49422E-04 | 9.99789E-01 |
| 6 | 1.30572E-01 | 4.77711E-01 | 19 | 1.52275E-04 | 9.99941E-01 |
| 7 | 1.25349E-01 | 6.03060E-01 | 20 | 4.50056E-05 | 9.99986E-01 |
| 8 | 1.11143E-01 | 7.14203E-01 | 21 | 1.13698E-05 | 9.99997E-01 |
| 9 | 9.14549E-02 | 8.05658E-01 | 22 | 2.38767E-06 | 1.00000E+00 |
| 10 | 6.99630E-02 | 8.75621E-01 | 23 | 4.00218E-07 | 1.00000E+00 |
| 11 | 4.97515E-02 | 9.25373E-01 | 24 | 5.02092E-08 | 1.00000E+00 |
| 12 | 3.28360E-02 | 9.58209E-01 | 25 | 4.19138E-09 | 1.00000E+00 |
| 13 | 2.00598E-02 | 9.78269E-01 | 26 | 1.74641E-10 | 1.00000E+00 |
26 個の碁石を投げれば必ず重複が発生することから、確率変数は 1 から 26 までの値を取り、Σr{1→26}( P(r) ) = 1 となります (有効桁数の関係で途中から累積が 1 になっているように見えますが、実際には r = 26 でちょうど 1 になります)。11 個目の投下で、重複する確率の累積は 0.9 を超えているので、10 個以上の碁石を落として重複しない確率は非常に少ないということになります。全てのマス目に均等に落ちる確率などほとんどないに等しく、もはや奇跡に近い現象です。
マス目を 365 個として、この中に n 個の碁石を落とす試行を考えれば、ちょうど誕生日が同じグループが一つでもある確率に置き換えることができます。n = 10 として、重複が発生しない確率を求めてみると、
なので、グループが一つでも発生する確率は 0.117 になります。確率が 50% を超えるのは n = 23 のときで、確率は 0.507 です。90% を超えるのは n = 41 の時なので、40 人程度のグループがあれば、その中に誕生日が同じ人が混ざっている確率は非常に高いことになります。自分と同じ誕生日が見つけられる確率は、40 人に聞いたとしても 0.104 なので、その差は非常に大きいことが分かります。
これは「誕生日問題(Birthday Problem)」と呼ばれる非常に有名な問題で、直感とは異なる結果が得られる例の一つです。会社の組織や学校のクラスが 40 人前後だった時に、その中に誕生日が同じグループがあるかと聞かれたら「ありえない」と考えそうですが、実際にはその確率は高いことを意味しているわけです。この問題は自分自身も経験していて、小学生の頃に自分と同じ誕生日だった子がクラス内にいてビックリしたことがあります。その時は「自分と誕生日が同じ」だったので、その確率は非常に低いわけですが、クラス全体から見れば、人数が 40 人程度だったこともあり特に珍しい話ではなかったわけです。
くじ引きのために先頭で並んでいた人が初めてくじを引くと仮定すれば、当たりが 30 枚、ハズレが 70 枚入っていて、その中から任意に 5 枚を取り出すときの確率を考えればいいので、超幾何分布を利用して
を計算して求めてみると、
| r | P30,70,5(r) |
|---|---|
| 0 | 0.160757 |
| 1 | 0.365357 |
| 2 | 0.316280 |
| 3 | 0.130233 |
| 4 | 0.025480 |
| 5 | 0.001893 |
と求めることができます。これを、当たりの確率が 0.3 として 5 回の試行で r 回当たる確率を二項分布 B5,0.3(r) を使って求めると、
| r | B5,0.3(r) |
|---|---|
| 0 | 0.16807 |
| 1 | 0.36015 |
| 2 | 0.30870 |
| 3 | 0.13230 |
| 4 | 0.02835 |
| 5 | 0.00243 |
となって、かなり近い値が得られます。
こうして見てみると、今回紹介した確率分布はそれぞれ密接に関係していることが分かります。その中で基本となるのが二項分布で、他の分布はそこから派生したものであると考えることもできます。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |