


前回は、標本を抽出して、ヒストグラムや要約統計量によって分布の性質を調べる方法について紹介をしました。これらは「記述統計学(Descriptive Statistics)」または「古典統計学(Classical Statistics)」と呼ばれる「古典的な」統計学です。もちろん、ヒストグラムを調べたり平均値や分散を求めることはデータを解析するための重要な手法の一つであり、今でもこれらは利用されています。
しかし、今までにも述べたように、全ての標本を元にその分布を調べるのは、特に母集団が巨大になると実質不可能な場合が多々あります。それは、調査に非常にお金がかかったり、時間がかかり過ぎたりすることが原因として挙げられます。そのような場合は、母集団から一部の標本を抽出してデータを解析するわけですが、それが母集団の分布状態を正しく反映していなければ、調査をしても無意味になってしまいます。そこで、一部の標本を元に調べた結果が本当に有用であるかを調べることを目的に「推計統計学(Inferential Statistics)」が誕生することになります。この章では、推計統計学の考え方から始めて、その中の手法の一つである「推定(Estimation)」について紹介したいと思います。
例えば、紙に書かれた 10 個のデータがあって、その平均を求めたいとします。しかし、コンピュータはおろか、電卓もそろばんもなく、しかも暗算は苦手でできればしたくないので、かなり手抜きをして 10 個のデータから 2 個だけ抽出して平均を求めたとします。この時の平均値は、母集団である 10 個のデータに対する平均値として利用できるでしょうか。
平均 μ、分散 σ2 の母集団から N 個のデータを抽出した時、その標本平均の分布は平均 μ、分散 σ2 / N となることは今までにも何度か登場しました。10 個のデータの平均が μ、分散が σ2 であれば、そこから 2 個のデータで平均を取る操作を繰り返すと得られる平均値は 10C2 = 45 個となって、その平均は μ、分散は σ2 / 2 になると予想できます(実際には母集団の要素数が有限個なので分散は σ2 / 2 にはならないのですが、これについては後述します)。よって、要素を一個だけ抽出するよりもバラツキは半分に抑えられ、分布を要約する量としてはランダムに一つ選ぶよりも適していることになります。しかし、平均を求めるために抽出する標本の数を多くすればさらにバラツキは小さくなり、10 個全てを使って平均値を計算すれば分散はゼロになるので、平均値として扱う値としては最も適したものになります。
上で述べたことは当たり前のことで、実際のデータに対して適当な値を一つ選んでそれを代表値として使うようなことは行わず、できるだけ多くのデータ(可能なら全データ)で平均値を計算して代表値として利用しようとするのが普通の考え方です。標本平均の分布は、それを数学を使って表したものに過ぎないわけです。
問題は、母集団が大きすぎて全てのデータを扱うことができない場合、一部のデータだけで全体の様子をどのように推定すればよいかということになります。記述統計学では、抽出した標本の状態を調べることが目的であるのに対し、その標本が全体の中の一部であるとして、その状態から全体の様子を観察するわけです。ちょうど、窓から見える景色から全体を考えるようなイメージで考えると分かりやすいかもしれません。窓から見える風景が海だけであったとしても、その外側に崖があったり、実は巨大な湖だったということもあるので、窓はできるだけ大きい方がいいのですが、それに限界があるのなら、見えている部分だけで全体を推測するしか手はないわけです。どのような推測・推定をすれば母集団を正しく見ることができるのかを調査する目的の学問を「推計統計学(Inferential Statistics)」といいます。推計統計学には大きく分けて、次の二つの手法があります。
推定とは、標本から求めた要約統計量から母集団の統計量を推測するための手法です。標本から得られた情報がどれだけ母集団の様子を反映しているかを確率的に調べることが主な目的になります。それに対して検定は、ある仮説に対して母集団の状態が一致するかどうかを確率的に判定するための手法で、仮説が正しいかどうかを検証することが主な目的になります。例えば、ある学校の身体検査で得られた体重の分布に対して、日本全国にある学校で測定された体重の分布を推定するという考え方と、日本全国での分布が分かっているとして、その学校の分布はそれと一致するかどうかを検定するという考え方の二種類に分けることができます。
この章ではまず、推定について紹介します。推定は大きく、以下の二つの種類に細分されます。
まず、母集団は非常に大きく、全ての要素から要約統計量を求めることは不可能であるとします。もちろん、非常に大きいといっても有限ではあるので、理論的には求めることができるのですが、それを実現することが不可能な状態を考えます。このような母集団は、有限な大きさではありますが非常に大きいので通常は無限母集団として扱います。
母集団は、ある確率分布に従うと考えることができます。それは具体的なもの(例えば正規分布など)と考えられるものもあれば、そうでない場合もあります。その中からいくつかの標本を抽出し、母集団の確率分布が持つパラメータ(平均や分散など)に対する精度の高い「推定量(Estimator)」を求める手法のことを「点推定(Point Estimation)」といいます。
母集団から抽出した標本を x = ( x1, x2, ... xN ) とします。母集団の確率分布に対するパラメータ θ に対して、x を使った関数を使って推定量 θ^ を求めるとしたとき("^"はハットといって、推定量を表すためによく用いられます。通常はパラメータの上側に書くのですが、HTML では簡単に表現できないので右側に書いて表します)、その関数を δ(x) とすると、
と表すことができます。ここで、「良い推定量」を定義するため、二つの推定量 θ^1, θ^2 の優劣を決める基準を考えます。もし、任意の x について常に | θ^1 - θ | < | θ^2 - θ | が成り立つのであれば、θ^1 の方が θ^2 よりも良い推定量であると考えることができます。しかし、θ は未知数であり、通常はこのような比較はできません。そこで、θ^1, θ^2 が確率変数 x から得られた別の確率変数であることを利用して、θ^1, θ^ 2 に対する平均 E[θ^1], E[θ^2] を使って | θ^1 - E[θ^1] | と | θ^2 - E[θ^2] | の大小を比較することにします。さらに、任意の x について大小関係を比較する代わりに | θ^1 - E[θ^1] |, | θ^2 - E[θ^2] | の平均の大小関係を調べるようにします。よって、
ならば θ^1 の方が良いと判断するわけです。しかし、絶対値は数学的に扱いづらいので、差の二乗を利用して
とします。結局これは θ^1, θ^2 の分散を表しており、θ^ の分散が小さいほど良い推定量であると判断していることになります。これを「有効性(Efficiency)」といい、分散が小さいほどより有効であることになります。その中で最も分散の小さな推定量が見つかれば、それは「最良推定量(Best Estimator)」または「最小分散推定量(Minimum-variance Estimator)」などと呼ばれます。
有効性だけを基準に最良な推定量を求めることは難しいので、通常は「不偏性(Unbiasedness)」を持った推定量に限定してその中から最良のものを見つけます。そのような不偏性を持った推定量を「不偏推定量(Unbiased Estimator)」といい、その中で分散が最小な推定量は「最小分散不偏推定量((Uniformly) Minimum-variance Unbiased Estimator ; UMVUE or MVUE)」といいます。不偏推定量については以前にも紹介したことがありますが、ある要約統計量 θ に対する推定量 θ^ の平均 E[θ^] が θ と等しくなること、すなわち
を満たす推定量のことを指します。例えば、不偏分散 u2 = Σi{1→N}( ( xi - m )2 ) / ( N - 1 ) は分散に対する不偏推定量になります。
有効性と不偏性の他に、推定量の優劣を判断する基準として「一致性(Consistency)」があります。標本の数を大きくするほど推定量が母集団の要約値に近づくとき、その推定量は「一致推定量(Consistent Estimator)」といいます。式で表すと
が任意の正数 ε について成り立つことになります。これは、標本数が大きくなるにつれて分散がゼロに収束すると考えることもできるので、「大数の法則(Law of Large Numbers)」での式と同じ意味を持つことになります。この式を満たすとき、θ^ は θ に「確率収束する(Converge in Probability)」といいます。
以上の三つの性質は、的に矢を射つ操作をイメージすると分かりやすいと思います。「不偏性」とは、矢を何回も射つとその分布が的の中央(これが θ を表します)を中心に広がることを意味します。「有効性」は、そのバラツキ方が小さいこと、「一致性」は、操作を繰り返していくほど同じ位置に当たる確率が増えていくことを表します。推定量の目的は θ をよく近似する代わりの値を求めることなので、不偏性は最も重要な性質になります。不偏性を持っているとき、バラツキが小さければ、推定量を一回求めた時にそれが真の値からズレている程度は小さいと考えられますし、一致性によって、標本数を多くするほど推定量が真の値に近づいていくことになります。
一致性に近い性質として「漸近的正規性(Asymptotic Normality)」があります。これは、推定量の分布が正規分布に近似できる性質を意味します。標本平均が正規分布に従う性質である「中心極限定理(Central Limit Theorem)」は漸近的正規性の代表例です。
たくさんある不偏推定量の中から最小の分散を持つものを調べるのは大変な上に、それが最小の分散であるかどうかを判断することはできないのですが、「クラーメル-ラオの不等式(Cramér-Rao Bound)」を利用すると最小分散不偏推定量であるかを判断することができます。
クラーメル-ラオの不等式(Cramér-Rao Bound)
確率分布 p( x, θ ) に従う任意の標本 x = ( x1, x2, ... xN ) から不偏推定量 θ^ = δ(x) が得られるとき、関数 p, δ がある条件(これを正則条件という)を満たせば以下の不等式が成り立つ。
V[θ^] ≥ 1 / N・E[ ( ∂log p( x, θ ) / ∂θ )2 ]
正則条件を満たす確率密度関数としてはほとんどのものが当てはまりますが、一様分布は正則条件を満たしません。また、推定量の関数 δ にもある条件を満たす必要がありますが、これも弱い条件なのでほとんどの関数が条件を満たすと考えられます。この不等式の右辺と分散が等しい不偏推定量が見つかれば、それは最小の分散を持つ推定量になります(補足1)。
例として、平均 μ の推定量である標本平均 m を用いた場合を考えます。標本平均は、どのような分布(但し、平均 μ と分散 σ2 が存在することが条件です)に対しても正規分布 N( μ σ2 / N ) に従うことから漸近的正規性を満たしています。また、標本の数を多くするほど分散はゼロに近づくので一致推定量でもあります。さらに標本平均の平均は μ であり、不偏推定量であることが成り立ちます。
標本平均の標本数を多くするほど、分散は小さくなります。つまり、標本数が多い方が有効性が高く、従ってより良い推定量であるといえます。では、標本平均は最小分散不偏推定量になるかという問題になりますが、ここで対象となる確率分布を正規分布 N( μ, σ2 ) に限定してクラーメル-ラオの不等式を用いると、
p( x, μ ) = { 1 / (2π)1/2σ }exp( -( x - μ )2 / 2σ2 ) より
log p( x, μ ) = -log( (2π)1/2σ ) - ( x - μ )2 / 2σ2
∂ log p( x, μ ) / ∂u = ( x - μ ) / σ2
| E[( ∂ log p( x, μ ) / ∂u )2] | = | E[( x - μ )2 / σ4] |
| = | σ2 / σ4 = 1 / σ2 |
となるので、
が得られます。N 個の標本に対する標本平均の分散が σ2 / N になることから、正規分布の標本平均は最小分散不偏推定量になることが分かります。指数分布や二項分布、ポアソン分布に対しても同様に成り立ちます。
分散の不偏推定量である不偏分散 u2 = Σi{1→N}( ( xi - m )2 ) / ( N - 1 ) に対し、u は標準偏差の不偏推定量にはなりません。一般に、θ^ が不偏推定量であるとき、f(θ^) が不偏推定量であることが成り立つとは限りません。正規母集団の標準偏差に対する不偏推定量は、次のように求めることができます。
カイ二乗分布に関する性質から、
正規分布 N( μ, σ2 ) から N 個の標本 x1, x2, ... xN を抽出したとき
y = Σi{1→N}( ( xi - m )2 ) / σ2 = Ns2 / σ2 は自由度 N - 1 の χ2-分布に従う
ことが成り立ちます。z = √y としたとき、dz = dy / 2√y ( dy = 2z・dz ) となって、自由度 N - 1 の χ2-分布は
なので、z に変数変換した確率密度関数は p(z)dz = TN-1(y)dy より
| p(z) | = | { 2z / 2(N-1)/2Γ( ( N - 1 ) / 2 ) } zN-3 exp( -z2 / 2 ) |
| = | { 2 / 2(N-1)/2Γ( ( N - 1 ) / 2 ) } zN-2 exp( -z2 / 2 ) ( z > 0 ) |
z の期待値 E[z] は
| E[z] | = | { 2 / 2(N-1)/2Γ( ( N - 1 ) / 2 ) } ∫{0→∞} z・zN-2 exp( -z2 / 2 ) dz |
| = | { 2 / 2(N-1)/2Γ( ( N - 1 ) / 2 ) } ∫{0→∞} zN-1 exp( -z2 / 2 ) dz |
となって、積分値 I = ∫{0→∞} zN-2 exp( -z2 / 2 ) dz において t = z2 / 2 としたとき dt = z・dz ( dz = (2t)-1/2dt ) で積分範囲は変わらないので
| I | = | ∫{0→∞} ( 2t )(N-1)/2 e-t (2t)-1/2dt |
| = | 2(N-2)/2・∫{0→∞} tN/2-1 e-t dt | |
| = | 2(N-2)/2・Γ( N / 2 ) |
よって、
| E[z] | = | { 2 / 2(N-1)/2Γ( ( N - 1 ) / 2 ) }・2(N-2)/2・Γ( N / 2 ) |
| = | √2Γ( N / 2 ) / Γ( ( N - 1 ) / 2 ) |
ここで、z = { Σi{1→N}( ( xi - m )2 ) / σ2 }1/2 = √N・s / σ であることから
よって、
すなわち、正規母集団の標準偏差に対する不偏推定量としては
という非常に複雑な値が得られます。これは、aN = ( N / 2 )1/2{ Γ( ( N - 1 ) / 2 ) / Γ( N / 2 ) } としたとき、標本標準偏差に aN を掛けたものを表します。ガンマ関数にスターリングの公式を適用すると、N が充分に大きければ
| aN | = | ( N / 2 )1/2{ Γ( ( N - 1 ) / 2 ) / Γ( N / 2 ) } |
| ≅ | ( N / 2 )1/2[ { 2π( N - 3 ) / 2 }1/2{ ( N - 3 ) / 2e }(N-3)/2 / { 2π( N - 2 ) / 2 }1/2{ ( N - 2 ) / 2e }(N-2)/2 ] | |
| = | ( N / 2 )1/2[ { ( N - 3 ) / 2 }(N-2)/2 e-(N-3)/2 / { ( N - 2 ) / 2 }(N-1)/2 e-(N-2)/2 ] | |
| = | ( N / 2 )1/2[ ( N / 2 )-(N-1)/2{ 1 - 1 / ( N / 2 ) }-(N/2)(1-1/N) e1/2 / ( N / 2 )-(N-2)/2{ 1 - 1 / ( N / 3 ) }-(N/3)(3/2-3/N) ] | |
| ≅ | ( N / 2 )1/2{ e1-1/N e1/2 / ( N / 2 )1/2 e3/2-3/N } | |
| = | exp( 1 - 1 / N + 1 / 2 - 3 / 2 + 3 / N ) | |
| = | exp( 2 / N ) ≅ 1 |
になるので、N が充分に大きければ標本標準偏差をそのまま不偏推定量として用いても大きな誤差はないということになります。そもそも、標本分散にしても N が大きければ期待値は母集団の分散に近似できます。従って、N が大きい場合は分散の平方根をそのまま標準偏差の不偏推定量として扱うことが多いようです。
今までは、非常に大きな母集団の推定量を調べてきました。母集団は非常に大きいので無限母集団として扱ってきたのですが、これが有限の母集団になった場合の推定量は無限母集団のときと同じになるのかを検証したいと思います。
まず、母集団の要素数を M とします。その要素を ai ( i = 1, 2, ... M ) としたとき、母集団の平均 μ を
と定義します。また、母集団の分散 σ2 は
とします。この母集団から N 個の標本 xj ( j = 1, 2, ... N ) を抽出した時、その標本平均 m と標本分散 s2 がどのようになるかを求めてみます。まず、xj がとり得る値は a1 から aM までのいずれかで、どの要素も等しい確率で抽出されるとすれば、xj の確率分布は
なので、xj の期待値 E[xj] は
になります。標本平均 m は
なので、その期待値は
で、標本平均 m は平均 μ の不偏推定量になっています。また、xj の分散 E[( xj - μ )2] は、
となって、やはり母集団の分散と等しくなります。
そこで、標本平均 m の分散 V[m] = E[( m - μ )2] を計算すると、
| V[m] | = | E[( m - μ )2] |
| = | E[{ ( Σj{1→N}( xj ) - Nμ ) / N }2] | |
| = | E[{ Σj{1→N}( xj - μ ) }2] / N2 | |
| = | E[Σj{1→N}( ( xj - μ )2 ) + Σj,k{1→N;j≠k}( ( xj - μ )( xk - μ ) )] / N2 | |
| = | σ2 / N + Σj,k{1→N;j≠k}( E[( xj - μ )( xk - μ )] ) / N2 |
xj - μ = yj とすれば、{ Σj{1→N}( xj - μ ) }2 = ( y1 + y2 + ... + yN )2 なので、これを展開すると、y12 + y22 + ... + yN2 = Σj{1→N}( yj2 ) と、Σj,k{1→N;j≠k}( yjyk ) すなわち異なる要素どうしの積の和の二つに分解できて、上のような結果が得られます。
M 個の母集団から二つの標本を抽出する時の順列は MP2 = M( M - 1 ) 通りあって、それらは全て等しい確率であるとすれば、aj, ak ( j, k = 1, 2, ... M ; j ≠ k ) の順番で標本を抽出する確率 P( j ∩ k ) は 1 / M( M - 1 ) になります。しかし、j が抽出された事象に限定した時に k が抽出される条件付確率 P(k|j) は
で、P(j) = 1 / M なので、P(k|j) = 1 / ( M - 1 ) になります。この結果は、要素を一つ抽出した後は M - 1 個しか要素が残らないことからも容易に導くことができます。ここで、「P(j) と P(k) が独立である」とは j が抽出された事象が、その後 k を抽出する事象に影響しない、すなわち P(k|j) = P(k) が成り立つことを意味します。しかし、P(k) = 1 / M であり、P(k|j) ≠ P(k) なので、P(j) と P(k) は独立ではありません。従って、E[( xj - μ )( xk - μ )] = E[xj - μ]E[xk - μ] = 0 とはならず、無限母集団の場合とは標本平均の分散が異なることになります。E[( xj - μ )( xk - μ )] を計算すると、
| E[( xj - μ )( xk - μ )] | = | Σj,k{1→M;j≠k}( ( aj - μ )( ak - μ ) / M( M - 1 ) ) |
| = | Σj{1→M}( ( aj - μ ){ Σk{1→M}( ak - μ ) - ( aj - μ ) } ) / M( M - 1 ) | |
| = | { Σj{1→M}( aj - μ )Σk{1→M}( ak - μ ) - Σj{1→M}( ( aj - μ )2 ) } / M( M - 1 ) | |
| = | -Σj{1→M}( ( aj - μ )2 ) / M( M - 1 ) = -σ2 / ( M - 1 ) |
Σj{1→M}( aj ) = Mμ なので、Σj{1→M}( aj - μ ) = 0 になって、上記結果が得られます。よって、標本平均の分散 V[m] は
| V[m] | = | σ2 / N - Σj,k{1→N;j≠k}( σ2 / ( M - 1 ) ) / N2 |
| = | σ2 / N - N( N - 1 )σ2 / N2( M - 1 ) | |
| = | { ( M - 1 )σ2 - ( N - 1 )σ2 } / N( M - 1 ) | |
| = | { ( M - N ) / ( M - 1 ) }{ σ2 / N } |
M→∞ ならば ( M - N ) / ( M - 1 ) → 1 なので、V[m] → σ2 / N となって、無限母集団における標本平均の分散と等しくなります。
標本分散 s2 = Σj{1→N}( ( xj - m )2 ) / N は、
| s2 | = | Σj{1→N}( ( xj - m )2 ) / N |
| = | Σj{1→N}( xj2 - 2m・xj + m2 ) / N | |
| = | Σj{1→N}( ( xj - μ )2 + 2μ・xj - μ2 - 2m・xj + m2 ) / N | |
| = | Σj{1→N}( ( xj - μ )2 ) / N + 2( μ - m )Σj{1→N}( xj ) / N - μ2 + m2 | |
| = | Σj{1→N}( ( xj - μ )2 ) / N - { μ2 - 2m( μ - m ) - m2 } | |
| = | Σj{1→N}( ( xj - μ )2 ) / N - ( μ2 - 2μm + m2 ) | |
| = | Σj{1→N}( ( xj - μ )2 ) / N - ( m - μ )2 |
と求めることができます。よって、s2 の期待値 E[s2] は
| E[s2] | = | E[Σj{1→N}( ( xj - μ )2 ) / N - ( m - μ )2] |
| = | E[Σj{1→N}( ( xj - μ )2 ) / N] - E[( m - μ )2] | |
| = | Σj{1→N}( E[( xj - μ )2] ) / N - V[m] | |
| = | σ2 - { ( M - N ) / ( M - 1 ) }{ σ2 / N } | |
| = | { N( M - 1 )σ2 - ( M - N )σ2 } / N( M - 1 ) | |
| = | M( N - 1 )σ2 / N( M - 1 ) |
となるので、
| E[s2 / { M( N - 1 ) / N( M - 1 ) }] | = | E[Σj{1→N}( ( xj - m )2 ) / { M( N - 1 ) / ( M - 1 ) }] |
| = | σ2 |
より、Σj{1→N}( ( xj - m )2 ) / { M( N - 1 ) / ( M - 1 ) } = s2 / { M( N - 1 ) / N( M - 1 ) } は σ2 の不偏推定量となります。ここで、M→∞ とすれば、この値は Σj{1→N}( ( xj - m )2 ) / ( N - 1 ) に収束するので、無限母集団の場合と同じ結果が得られます。また、母集団の分散を
で定義すれば、
E[( xj - μ )2] = Σi{1→M}( ( ai - μ )2 / M ) = ( M - 1 )σ2 / M
E[( xj - μ )( xk - μ )] = -Σj{1→M}( ( aj - μ )2 ) / M( M - 1 ) = -σ2 / M
| V[m] | = | E[Σj{1→N}( ( xj - μ )2 ) + Σj,k{1→N;j≠k}( ( xj - μ )( xk - μ ) )] / N2 |
| = | ( M - 1 )σ2 / NM - ( N - 1 )σ2 / NM | |
| = | ( M - N )σ2 / NM |
より
| E[s2] | = | Σj{1→N}( E[( xj - μ )2] ) / N - V[m] |
| = | ( M - 1 )σ2 / M - ( M - N )σ2 / NM | |
| = | { N( M - 1 ) - ( M - N ) }σ2 / NM | |
| = | ( N - 1 )σ2 / N |
よって、E[Ns2 / ( N - 1 )] = σ2 となって、無限母集団の場合と等しくなります。このことから、母集団の分散として
を利用する場合もあります。
推定量に対する標準偏差のことを「標準誤差(Standard Error ; SE)」といいます。特に、標本平均の標準偏差のことを指すのが通常ですが、"Standard Error of the Mean"の略語で SEM と表記されることもあるようです。今までの説明の中で、V[θ^] や V[m] として表していたパラメータは標準誤差の二乗を表しています。(標本)標準偏差は文字通り標本の標準偏差であり、標準誤差とは異なるので混同しないようにしましょう。標準偏差は各標本と標本平均の誤差から求めるのに対し、標準誤差は推定量(例えば標本平均など)を何度も求めた時に得られる誤差が対象となります。
「良い推定量」を見つけるための条件として「有効性」「不偏性」「一致性」があることを紹介しました。期待値が母集団の値と一致する要約統計量を求め(不偏推定量)、その中から最も分散の小さいもの(有効推定量)を見つけ出すことで「良い推定量」を得ることができるわけですが、ここで不偏性を得るためには母集団の値が必要になります。しかし、母集団がどのようなパラメータを持っているのかもわからない場合、不偏推定量であるかを知ることはできません。有効推定量であるかを求めることはできても、果たしてそれが母集団の要約統計量を表しているかどうかは知ることができないわけです。今までに紹介した標本平均や標本分散での例では、母集団の要約統計量との関係式から不偏推定量となるパラメータを見つけ出し、それが有効推定量であるかを調べることで推定量として最適であるかを判断してきました。ここでは、それとは異なる方法で推定量を求めてみたいと思います。
例として、二項分布における一回の試行の確率が未知である場合を考えます。例えば、いびつなコインやサイコロを使った試行で、表が出る確率が 1/2 と表せなかったり、一の目が出る確率が 1/6 とはいえないような場合を想定します。二項分布の確率密度関数は
で表されます。通常、一回の試行において事象が発生する確率 p は固定なのですが、この値を変数として扱い、実際に試行を何回か繰り返して事象が発生した回数を数えてみます。N 回の試行で事象が r 回発生したとすれば、これらの値は定数として扱えることになります。よって、上式を次のように表します。
変わったのは左辺だけで、右辺は同じ式のままです。左辺は、N と r が定数で p が変数であることを明示しています。今、この関数が最大値をなるような(つまり全体として最も確率が高くなるような) p の値を求めることを考えた時、NCr ( > 0 ) は定数になるので、これを無視してしまえば、
に対する最大値を求めればいいことになります。これは、各試行が独立だと仮定した時の同時分布の式と等しくなります。すなわち、事象が発生した回数が r 回でその確率が p、発生しなかった回数が N - r 回でその確率が 1 - p なので、その積が LN,r(p) であることになります。LN,r(p) の定義域は 0 ≤ p ≤ 1 で、LN,r(0) = LN,r(1) = 0 であり、また LN,r(p) ≥ 0 なので、常にゼロであるのでなければ必ず極大値を持ち、それが最大値になります。そこで、L(p) を p で微分してみると、
| dL / dp | = | rpr-1( 1 - p )N-r - ( N - r )pr( 1 - p )N-r-1 |
| = | pr-1( 1 - p )N-r-1{ r( 1 - p ) - ( N - r )p } | |
| = | pr-1( 1 - p )N-r-1( r - Np ) |
より p = 0, 1, r / N のときに極値をとり、p = 0, 1 のときは L(p) = 0 で極小値になることから、p = r / N のときに極大値(=最大値)となることがわかります。この結果は直感的にも当然のように思えます。N 回の試行で r 回成功したならば、一回の試行で成功する確率は r / N とするのは自然な考え方です。
離散確率分布 p( x, θ ) に従う確率変数を N 回抽出した時、各試行が独立ならば、x = ( x1, x2, ... xN ) となるときの同時確率分布 p( x, θ ) は
になります。ここで、x を定数、θ を変数と考え、上記関数が最も最大となる時の θ を求めると、それは同時確率が最も高い、つまり最も発生しやすいときの θ であると考えることができます。この考え方を連続分布の場合にも拡大して、
が最大値となるような θ が存在した時、その推定量を「最尤推定量(Maximum likelihood estimator ; MLE)」といい、最尤推定量を求めるこの方法を「最尤法(Maximum Likelihood Estimation ; MLE)」といいます。L(θ) は「尤度(関数)( Likelihood (Function) )」と呼ばれ、確率密度とは異なるものとして扱われます。実際、連続分布においては確率変数がちょうど x となるときの確率は常にゼロです。しかし、離散分布ならば同時確率と尤度は等しくなります。
L(θ) は確率の積で表されるので、非常に小さな値となる可能性があります。対数関数は単調増加なので、対数を取っても最大値となるときの θ に変化はなく、log L(θ) が微分可能であれば、d log L(θ) / dθ = 0 の根を最尤推定量とするのが一般的です。この方程式を「尤度方程式(Likelihood Equation)」といいます。変数が複数あれば、方程式は偏微分の形で表され、
になります。
連続分布での例として、正規分布 N( μ, σ2 ) における μ と σ2 ( = v ) の最尤推定量を求めると、
p( x, μ, v ) = { 1 / (2πv)1/2 } exp( -( x - μ )2 / 2v ) より
L( μ, v ) = { 1 / (2πv)N/2 } exp( -Σi{1→N}( ( xi - μ )2 ) / 2v )
となるので、対数を取って
よって、尤度方程式は
∂ log L / ∂μ = Σi{1→N}( xi - μ ) / v = 0
∂ log L / ∂v = - N / 2v + Σi{1→N}( xi - μ )2 / 2v2 = 0
第一式より、v ≠ 0 ならば Σi{1→N}( xi - μ ) = 0 なので、Σi{1→N}( xi ) = Nμ となって、μ の最尤推定量は Σi{1→N}( xi ) / N = m、すなわち標本平均になります。第二式は、やはり v ≠ 0 として 2v を両辺に掛けて式を変形すると
μ の最尤推定量( = 方程式の解 )は m だったので、v = σ2 の最尤推定量は Σi{1→N}( xi - m )2 / N = s2 すなわち標本分散になります。
最尤法を利用した有名な手法に「最小二乗法(Least Squares)」があります。最も簡単な例として、入力データ x に対する出力結果 y が一次式 y = ax + b の関係式で表されるとした時、x と y の値から最適な a, b を求めるとき、y と ax + b との誤差 ε = y - ( ax + b ) が正規分布 N( 0, σ2 ) に従うとして、尤度の最も高いときの a, b を求めることを考えると、入力データ x = ( x1, x2, ... xN ) に対する出力結果 y = ( y1, y2, ... yN ) との誤差を εi = yi - ( axi + b ) としたとき、尤度は
となり、対数を取って
| log L( a, b ) | = | N・log( 1 / (2π)1/2σ ) - Σi{1→N}( εi2 ) / 2σ2 |
| = | N・log( 1 / (2π)1/2σ ) - Σi{1→N}( { yi - ( axi + b ) }2 ) / 2σ2 |
よって尤度方程式は
∂ log L / ∂a = Σi{1→N}( xi{ yi - ( axi + b ) } ) / σ2 = 0
∂ log L / ∂b = Σi{1→N}( { yi - ( axi + b ) } ) / σ2 = 0
これを変形すると、
aΣi{1→N}( xi2 ) + bΣi{1→N}( xi ) = Σi{1→N}( xiyi )
aΣi{1→N}( xi ) + Nb = Σi{1→N}( yi )
となって、a, b を未知数とする連立方程式になります。
点推定では推定量として最もふさわしい値を決定する手法でした。しかし、実際に真の値と一致することはほとんど期待できず、ある程度のズレはあると考えられます。そのズレの程度も含めて推定を行う手法が「区間推定(Interval Estimation)」になります。ここで、未知のパラメータ θ を持った母集団の確率分布 pθ(x) に対して抽出した標本 x = ( x1, x2, ... xN ) から θ を推定したときの推定量を θ^( x ) とします。このとき、θ^ も確率変数なので別の確率分布 P(θ^) に従うと考えることができます。よって、P( θ^ ∈ Θ ) = β ( 0 < β < 1 ) となるような集合 Θ に対して θ ∈ Θ であると推定します。ここで β を推定の「信頼度(Confidence Value)」、1 - β を「危険率(Critical Value)」といいます。
Θ は通常ひとつの区間となり、その区間は「信頼区間(Confidence Intervals)」と呼ばれます。区間で表される場合は、次のように表すことができます。
P( θ^ - εL < θ < θ^ + εH ) = β
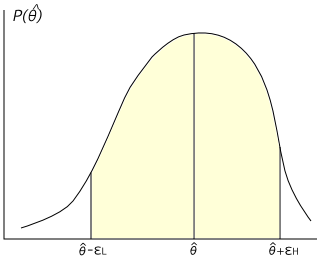
εL や εH の値は小さい方が精度が高いことを意味しており、β はできるだけ大きい方が信頼性が高いことになります。しかし、100% の信頼度で推定を行えば、Θ は全事象を意味するので、区間で表せば ( -∞, ∞ ) になるのが一般的で、推定をする意味がなくなります。β を大きくすれば信頼区間は広がるので、推定の結果も焦点が定まらない様なボヤけた状態になって、あまり役に立つ結論は得られなくなります。一般的には、信頼度を 0.95 や 0.99 に設定して信頼区間を求めることがよく行われますが、この値が絶対というわけではなく、例えば五分五分と考えた上で(つまり β = 0.5 )推定を行うことも場合によってはあり得ます。
信頼度を定数 β と決めたら、母集団から抽出した標本 x と推定したいパラメータ θ を変数とする関数 Θx(θ) を決め、t = Θx(θ) を確率変数とする確率密度関数 P(t) について
となるような区間 ( a, b ) を求めます。区間 ( a, b ) が決まれば、Θx(θa) = a, Θx(θb) = b を満たす θa, θb を求めることで、信頼区間 ( θa, θb ) または ( θb, θa ) を得ることができます。ここで、θa と θb の大小関係は Θx(θ) によって変化します。
ところで、上記方法で信頼区間を求めるといっても、その区間は Q(t) の積分値が β になればよいので決め方は無数にあります。しかし、β を固定したとき、信頼区間は小さい方が精度が高いことになるので、| θa - θb | ができるだけ小さくなるような区間を選ぶことになります。場合によっては最適な区間を求めることが困難な場合もあり得ます。
要約統計量に対する区間推定では、要約統計量を含んだ関数に対する確率密度関数を利用することになります。今まで、正規分布や χ2-分布、F-分布、t-分布などの性質を紹介してきましたが、あの複雑なパラメータに関する性質は、区間推定や、今後紹介する検定などでの利用を目的の一つとしたものです。これらの説明については「(6)標本分布」に細かく紹介しています。
t-分布に対しては以下の性質がありました。
ここで、m は標本平均、μ は推定したい母集団の平均、N は標本の個数で、u は不偏分散の平方根を表します。
としたとき、t に対する確率密度関数が自由度 N - 1 の t-分布に従うので
として P(ta) が信頼度 β となるような ta を求めれば、
-ta < ( m - μ )√N / u < ta より
m - u・ta / √N < μ < m + u・ta / √N
が信頼区間となります。ゼロを中心に左右対称に区間を決めているのは、t-分布が t = 0 を最大確率密度とする左右対称の分布であるからです。
この方法は、母集団の分散 σ2 が未知の場合でも利用することができるという利点がありますが、分散が既知の場合は、正規母集団 N( μ, σ2 ) における N 個の標本からなる標本平均が N( μ, σ2 / N ) に従うことを利用して、
が標準正規分布 N( 0, 1 ) に従うことから
として P(za) が信頼度 β となるような za を求めれば、
-za < ( m - μ )√N / σ < za より
m - σ・za / √N < μ < m + σ・za / √N
信頼区間において変化したのは不偏分散が母分散となったところで、あとは対象となる確率密度関数が t-分布から正規分布になっているだけです。
正規分布以外の一般の分布に従う標本に対しては、上記方法を利用することはできませんが、標本の数が大きくなったときは、中心極限定理より、一般の分布に対してもその標本平均が正規分布に従うので、分散に標本分散 s2 = Σi{1→N}( ( xi - m )2 / N ) を利用すれば、
が標準正規分布にほぼ従うことになって、
-za < ( m - μ )√N / s < za より
m - s・za / √N < μ < m + s・za / √N
が信頼区間となります。
平均値の区間推定を行うためのサンプル・プログラムを以下に示します。
/* binSearch : 確率が b になる区間 [0,t] に対して t を求める(二部探索) const ContDist& dist : 確率密度関数 double b : 確率 double threshold : しきい値(pを求める精度) 戻り値 : t */ double binSearch( const ContDist& dist, double b, double threshold ) { const double delta = 1.0; // 範囲を探索するときの単位 double t = delta; // t は delta で初期化 double gap = delta / 2.0; // t を調整するための差分 // delta 刻みで範囲を探索 for ( ; b > dist.p( 0, t ) ; t += 1.0 ); // t - delta から t の間で二部探索 t -= gap; gap /= 2.0; while ( gap >= threshold ) { double p = dist.p( 0, t ); if ( fabs( p - b ) < std::numeric_limits<double>::epsilon() ) break; t = ( p > b ) ? t - gap : t + gap; gap /= 2.0; } return( t ); } /* avg_iEst : 平均値の区間推定 const ContDist& dist : 確率密度関数 double mean : 標本平均 double sigma : 標準偏差 unsigned int n : 標本数 double b : 信頼度 pair<double,double>& interval : 信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... データ数が 1 以下 */ void avg_iEst( const ContDist& dist, double mean, double sigma, unsigned int n, double b, pair<double,double>& interval, double threshold ) { double ta = binSearch( dist, b / 2.0, threshold ); double d = sigma * ta / sqrt( n ); interval.first = mean - d; interval.second = mean + d; } /* avg_iEst : 平均値の区間推定(t-分布による推定) const vector<double>& data : データ列 double b : 信頼度 pair<double,double>& interval : 信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... データ数が 1 以下 */ bool avg_iEst( const vector<double>& data, double b, pair<double,double>& interval, double threshold ) { unsigned int n = data.size(); if ( n <= 1 ) return( false ); if ( b < 0 || b > 1 ) return( false ); double mean = sampleAverage( data ); // 標本平均 double u = sqrt( sampleVariance( data, true ) ); // 不偏分散の平方根 TDistribution tDist( n - 1 ); avg_iEst( tDist, mean, u, n, b, interval, threshold ); return( true ); } /* avg_iEst : 平均値の区間推定(正規分布による推定) const vector<double>& data : データ列 double b : 信頼度 double sigma : 母集団の標準偏差 pair<double,double>& interval : 信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... データ数がゼロ */ bool avg_iEst( const vector<double>& data, double b, double sigma, pair<double,double>& interval, double threshold ) { unsigned int n = data.size(); if ( n == 0 ) return( false ); if ( b < 0 || b > 1 ) return( false ); double mean = sampleAverage( data ); // 標本平均 NormalDistribution nDist( 0, 1 ); avg_iEst( nDist, mean, sigma, n, b, interval, threshold ); return( true ); }
確率密度関数 p(x) に対する累積分布関数 F(t) = ∫{-∞→t} p(x) dx の値がちょうど b になるような区間 ( -∞, t ) が信頼区間を表すので、本来なら各確率密度関数用の累積分布関数に対して逆関数 F-1(t) を求めるルーチンを用意する必要がありますが、ここでは二部探索(Binary Search)を利用して F(t) の値が b にできるだけ近くなるような t を求める方法を利用しています。これなら、どのような確率密度関数に対しても利用することができます。
二部探索を使って信頼区間を求める関数は binSearch です。累積密度関数の値は、[ 0, t ] の範囲で求めるようにしていますが、これは確率密度関数が 0 を中心に左右対称であったり(正規分布や t-分布など)、x ≥ 0 の範囲のみに分布がある(χ2-分布やF-分布など)ものだけを考えれば今回は十分であるためです。最初に、delta(今回は 1.0 として定義)刻みで値のある範囲を探索し、その範囲内で二部探索を使って近似値を求めます。値の精度は threshold を使って調整をすることができます。
平均値の区間推定には t-分布を利用したものと正規分布を利用したものがあり、後者は標準偏差の値が既知の場合に利用できるのでした。サンプル・プログラムでも両方の推定用関数が用意されています。これらは標本平均や不偏分散を求める必要があるので、前回紹介した要約統計量算出用の関数 sampleAverage と sampleVariance を利用しています。
具体的な例を以下に示しておきます。
ある機械で加工した製品の重さを測定したところ、次のような結果になった。
このとき、重さの平均値を信頼度 99% で区間推定しなさい。
まず、上記データの標本平均 m と不偏分散 u2 を求めると、
標本平均 m = 5.04
不偏分散 u2 = 0.100
になります。重さの分布は正規分布に従うと仮定すれば、t = ( m - μ )√N / u は自由度 9 の t-分布に従うので、確率が 0.5% になる区間 [ t0, ∞ ) を求めると、t0 = 3.25 となって、
-3.25 ≤ ( 5.04 - μ )√10 / √0.100 ≤ 3.25 より
5.04 - 3.25 x 0.316 / 3.16 ≤ μ ≤ 5.04 + 3.25 x 0.316 / 3.16
これを計算すると、信頼区間は [ 4.72, 5.37 ] になります。信頼度を 95% にすれば、t0 = 2.26 になるので、
-2.26 ≤ ( 5.04 - μ )√10 / √0.100 ≤ 2.26 より
5.04 - 2.26 x 0.316 / 3.16 ≤ μ ≤ 5.04 + 2.26 x 0.316 / 3.16
を計算して信頼区間は [ 4.81, 5.27 ] になります。信頼度を上げれば信頼区間は広がって、結果はぼやけてしまう様子がこの結果からわかります。また、抽出する標本の数を増やせば t-分布の自由度が大きくなり、同じ信頼度でも信頼区間は狭くなるので、精度を上げるためには標本数を増やせばよいことになります。ところで、z = ( m - μ )√N / s が標準正規分布にほぼ従うことを利用すると、標本分散 s2 = 0.0904 で、確率が 0.5% になる区間 [ z0, ∞ ) に対して z0 = 2.58 になるので、
-2.58 ≤ ( 5.04 - μ )√10 / √0.0904 ≤ 2.58 より
5.04 - 2.58 x 0.301 / 3.16 ≤ μ ≤ 5.04 + 2.58 x 0.316 / 3.16
を計算すれば、信頼度 99% のときの信頼区間は [ 4.79, 5.29 ] になります。t-分布を利用した場合と比較すると信頼区間が若干狭くなっています。
正規母集団の分散の区間推定には、χ2-分布に対する以下の性質が利用できます。
正規分布 N( μ, σ2 ) から N 個の標本 x1, x2, ... xN を抽出したとき
y = Σi{1→N}( ( xi - m )2 ) / σ2 = Ns2 / σ2 は自由度 N - 1 の χ2-分布に従う
ここで v = σ2 とすれば
が χ2-分布に従うことから
| P( χa2, χb2 ) | = | ∫{χa2→χb2} TN-1(χ2) dχ2 |
| = | { γ( ( N - 1 ) / 2, χb2 / 2 ) - γ( ( N - 1 ) / 2, χa2 / 2 ) } / Γ( ( N - 1 ) / 2 ) |
ここで、Γ( α ) = ∫{0→∞} tα-1 e-t dt は「ガンマ関数 (Gamma Function)」を、γ( α, x ) = ∫{0→x} tα-1 e-t dt は「(第一種)不完全ガンマ関数 ( (Lower) Incomplete Gamma Function )」をそれぞれ表します。χ2-分布の累積分布関数については「(6) 標本分布」の章の「1) カイ二乗分布」の中で記載されていますので、詳しくはそちらをご覧ください。
上式において、P( χa2, χb2 ) が定数 β のとき Θx-1(χb2) - Θx-1(χa2) が最短となるような区間を求めればそれが信頼区間として最適な値となるのですが、一般的には、危険率 α = 1 - β を求めた上で、
∫{0→χa2} TN-1(χ2) dχ2 = γ( ( N - 1 ) / 2, χa2 / 2 ) / Γ( ( N - 1 ) / 2 ) = α / 2
∫{χb2→∞} TN-1(χ2) dχ2 = 1 - γ( ( N - 1 ) / 2, χb2 / 2 ) / Γ( ( N - 1 ) / 2 ) = α / 2
となるような χa2, χb2 を求めてそれを元に信頼区間を計算します。
より、
が求める信頼区間になります。ここで、母集団の平均 μ が既知であれば、
正規分布 N( μ, σ2 ) から N 個の標本 x1, x2, ... xN を抽出したとき
y = Σi{1→N}( ( xi - μ )2 ) / σ2 は自由度 N の χ2-分布に従う
を利用して同様の方法で
を信頼区間とすることができます。ここで、χa2 と χb2 は自由度 N の χ2-分布を使って求めることに注意してください。
分散の区間推定を行うためのサンプル・プログラムを以下に示します。
/* var_iEst : 分散の区間推定 const vector<double>& data : データ列 double b : 信頼度 pair<double,double>& interval : 信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... データ数がゼロ */ bool var_iEst( const vector<double>& data, double b, pair<double,double>& interval, double threshold ) { unsigned int n = data.size(); if ( n <= 1 ) return( false ); if ( b < 0 || b > 1 ) return( false ); double aHalf = ( 1.0 - b ) / 2.0; // a/2 = ( 1 - b ) / 2 double var = sampleVariance( data ); // 標本分散 ChiSquareDistribution chiDist( n - 1 ); interval.first = var * (double)n / binSearch( chiDist, 1.0 - aHalf, threshold ); interval.second = var * (double)n / binSearch( chiDist, aHalf, threshold ); return( true ); } /* var_iEst : 分散の区間推定 const vector<double>& data : データ列 double b : 信頼度 double mean : 母集団の平均 pair<double,double>& interval : 信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... データ数がゼロ */ bool var_iEst( const vector<double>& data, double b, double mean, pair<double,double>& interval, double threshold ) { unsigned int n = data.size(); if ( n <= 1 ) return( false ); if ( b < 0 || b > 1 ) return( false ); double aHalf = ( 1.0 - b ) / 2.0; // a/2 = ( 1 - b ) / 2 Deviation<double> dev( mean ); double sqSum = sum( data, dev ); // 平均との差の平方 ChiSquareDistribution chiDist( n ); interval.first = sqSum / binSearch( chiDist, 1.0 - aHalf, threshold ); interval.second = sqSum / binSearch( chiDist, aHalf, threshold ); return( true ); }
分散の区間推定も、平均値が未知の場合と既知の場合の二種類を用意しています。平均値が既知の場合は平均との差の平方による和を求める必要があり、そのために関数オブジェクト Deviation と和を求める関数 sum を利用しています。Deviation はメンバ関数 operator() を持ち、そのインスタンスを生成するときにパラメータ(サンプル・プログラムでは変数 mean)を渡しておけば、そのインスタンスを dev としたときに dev( x ) で渡したパラメータと x の差の平方を返すことができます。関数 sum はそれを利用して、配列 data と平均との差の平方和を返します。これらの定義は要約統計量のサンプル・プログラムで確認することができます。
独立に繰り返した試行の結果から、一回の試行において事象 A が起こる確率 p に対して区間推定を行う場合、一回の試行は以下に示す「ベルヌーイ分布(Bernoulli Distribution)」に従うと考えることができます。
P(A) = p
P(A~) = 1 - p = q
ベルヌーイ分布に従う独立した試行を N 回繰り返した時の標本点は「ベルヌーイ列(Bernoulli Sequence)」といい、次のように表されるのでした。
ベルヌーイ列に対して r = Σi{1→N}( ai ) としたとき、r は 0 から N までの値をとり、r に対する確率分布が二項分布 BN,p(r) = NCrprqN-r になります。今、N 回の試行で r 回事象が発生したとすれば、二項分布の式に対して p を変数と考えれば
となるので、危険率 α に対して
Σi{r→N}( BN( i, pa ) ) = α / 2
Σi{0→r}( BN( i, pb ) ) = α / 2
から信頼区間 ( pa, pb ) を求めます。第一の式は、事象が発生する回数が r から N までの場合の累積が α / 2 と等しくなるような pa を求める式で、pa が小さいほど累積は小さくなります。よって、それより小さくなれば事象の発生回数が r 回以上になる確率が α / 2 より小さくなってしまうような最小値が pa であることを意味しています。今は r を使って p を推定しているので、試行の結果、p の値に対してあまりにも r が大きくなっていたとしても、その確率が α / 2 より小さくならない限度が pa になるわけです。また、第二の式は、事象が発生する回数が 0 から r までの場合の累積が α / 2 と等しくなるような pb を求める式で、今度は pb が大きいほど( 1 - pb が小さくなるので)累積は小さくなります。よって、pb がそれより大きくなれば事象の発生回数が r 回以下になる確率が α / 2 より小さくなってしまうような最大値が pb であることを意味しています。こちらは、試行の結果、p の値に対してあまりにも r が小さくなっていたとしても、その確率が α / 2 より小さくならない限度が pb ということになります。p がその間にあれば、事象の発生回数が r 回より少なくなる確率も多くなる確率もともに α / 2 以上になるので、r の値が実際の p の値に対して極端に大きすぎたり小さすぎることのない範囲を表すことになります。
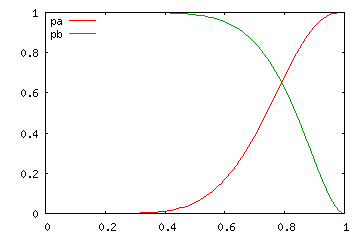
| N = 10 | ||
|---|---|---|
| r = 2 | r = 5 | r = 8 |
 |  |  |
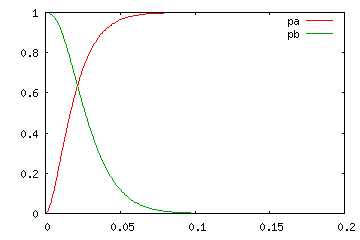
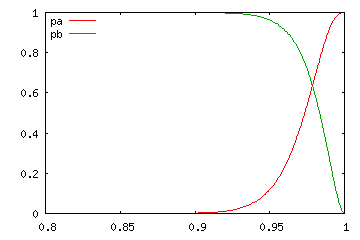
| N = 100 | ||
| r = 2 | r = 50 | r = 98 |
 |  |  |
上のグラフは、一回の試行で事象が発生する確率 p の変化に対し、N 回の試行で r 回以上事象が発生する確率 pa と、r 回以下発生する確率 pa を表したもので、横軸は確率 p、縦軸は pa, pb です。p が大きくなるに従って、pa はだんだんと大きく、逆に pb は小さくなる様子がグラフから読み取れます。pa, pb のどちらも α / 2 より大きくなる範囲が求める信頼区間になります。試行回数が多くなるほど信頼区間となる範囲が狭くなる様子が上記結果からわかります。
ここで、先ほどの式をどのように解けばよいのかが問題になるわけですが、これには F-分布と二項分布に対する次の関係式が利用できます。
Σi{r+1→N}( BN,p( i ) ) = ∫{0→np/mq} Gm,n( x ) dx
Σi{0→r}( BN,p( i ) ) = ∫{np/mq→∞} Gm,n( x ) dx
但し、m = 2( r + 1 )、n = 2( N - r )
上式において、Gm,n( x ) は F-分布の確率密度関数 Gm,n( x ) = mm/2 nn/2 xm/2-1 / Β( m / 2, n / 2 ) ( mx + n )(m+n)/2 を表します。右辺が α / 2 になるような p の値を求め、上式の p を pa、下式の p を pb として信頼区間を得ることができます。
N が非常に大きい時、二項分布が正規分布に近似できることは「ド・モアブル = ラプラスの定理(De Moivre-Laplace Theorem)」と呼ばれています。式に表すと
であり、t = ( r - μ ) / σ とすれば、
となって、標準正規分布に従います。よって、信頼度 β に対して ∫{-ta→ta} BN,p( t ) dt = β を満たす ta を求めると、
が求める信頼区間となるので、BN,p( r ) の平均 μ が Np、分散 σ2 が Np( 1 - p ) となることから、
上式は、次の不等式を解くことと同じことになります。
これを変形していくと、
r2 - 2Nrp + N2p2 < Nta2p( 1 - p )
( N2 + Nta2 )p2 - ( 2Nr + Nta2 )p + r2 < 0
これを解くと
[ ( 2Nr + Nta2 ) - { ( 2Nr + Nta2 )2 - 4( N2 + Nta2 )r2 }1/2 ] / 2( N2 + Nta2 ) < p
p < [ ( 2Nr + Nta2 ) + { ( 2Nr + Nta2 )2 - 4( N2 + Nta2 )r2 }1/2 ] / 2( N2 + Nta2 )
二つの式は、符号が違うのみなので、上側の式だけを解いていきます。左辺を変形すると
| [ ( 2Nr + Nta2 ) - { ( 2Nr + Nta2 )2 - 4( N2 + Nta2 )r2 }1/2 ] / 2( N2 + Nta2 ) | |
| = | { ( 2Nr + Nta2 ) - ( 4N2r2 + 4N2rta2 + N2ta4 - 4N2r2 - 4Nr2ta2 )1/2 } / 2( N2 + Nta2 ) |
| = | { ( r / N + ta2 / 2N ) - ta( r / N2 - r2 / N3 + ta2 / 4N2 )1/2 } / ( 1 + ta2 / N ) |
| = | [ ( r / N + ta2 / 2N ) - ta{ r( N - r ) / N3 + ta2 / 4N2 }1/2 ] / ( 1 + ta2 / N ) |
1 / N 程度の大きさの量は、N が非常に大きい場合は無視できるので除外すると(但し、r / N は r が N に依存するので残して)、左辺は
になります。よって、信頼区間は
と求めることができます。
F-分布を利用した最初の推定法は、標本の数が小さい場合に利用する方法なので「小標本区間推定」と呼ばれるのに対し、後者の近似法は標本の数が大きい場合に適用できるので「大標本区間推定」といいます。
百分率の区間推定を行うためのサンプル・プログラムを以下に示します。
/* percent_SS_iEst : 百分率の区間推定(小標本) unsigned int cnt : 試行回数 N unsigned int r : 試行が成功した回数 double b : 信頼度 pair<double,double>& interval : 信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... データ数がゼロ */ bool percent_SS_iEst( unsigned int cnt, unsigned int r, double b, pair<double,double>& interval, double threshold ) { if ( cnt < r ) return( false ); if ( b < 0 || b > 1 ) return( false ); double aHalf = ( 1.0 - b ) / 2.0; // a/2 = ( 1 - b ) / 2 // 百分率の下限 ta を求める unsigned int m = 2 * r; // 自由度 m = 2r unsigned int n = 2 * ( cnt - r + 1 ); // 自由度 n = 2( N - r + 1 ) FDistribution fDist_a( m, n ); double ta = binSearch( fDist_a, aHalf, threshold ); interval.first = (double)m * ta / ( (double)m * ta + (double)n ); // 百分率の上限 tb を求める m = 2 * ( r + 1 ); // 自由度 m = 2( r + 1 ) n = 2 * ( cnt - r ); // 自由度 n = 2( N - r ) FDistribution fDist_b( m, n ); double tb = binSearch( fDist_b, 1.0 - aHalf, threshold ); interval.second = (double)m * tb / ( (double)m * tb + (double)n ); return( true ); } /* percent_LS_iEst : 百分率の区間推定(大標本) unsigned int cnt : 試行回数 unsigned int r : 試行が成功した回数 double b : 信頼度 pair<double,double>& interval : 信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... データ数がゼロ */ bool percent_LS_iEst( unsigned int cnt, unsigned int r, double b, pair<double,double>& interval, double threshold ) { if ( cnt < r ) return( false ); if ( b < 0 || b > 1 ) return( false ); NormalDistribution nDist( 0, 1 ); double ta = binSearch( nDist, b / 2.0, threshold ); interval.first = (double)r / (double)cnt - ta * sqrt( (double)r * (double)( cnt - r ) / pow( cnt, 3 ) ); interval.second = (double)r / (double)cnt + ta * sqrt( (double)r * (double)( cnt - r ) / pow( cnt, 3 ) ); return( true ); }
百分率の区間推定では、コイントスやサイコロの例などがよく取り上げられます。
10 回中 9 回は表だったということは、表がかなり出やすいコインだとも考えられますが、単なる偶然である可能性もあります(普通なら裏も表も五分五分と考えられます)。
まず、表になる確率が p のとき、N 回中 r 回表が出る確率を二項分布から求めると、
になるので、信頼率 90% で推定するのであれば、9 〜 10 回表が出る確率が 5%以上、0 〜 9 回表が出る確率が 5%以上になる場合を考えればよくて
Σi{9→10}( BN,p(i) ) ≥ 0.05
Σi{0→9}( BN,p(i) ) ≥ 0.05
となる p の区間を求めればよいことになります。F-分布と二項分布に対する関係式から、
Σi{r+1→N}( BN,p( i ) ) = ∫{0→np/mq} Gm,n( x ) dx
Σi{0→r}( BN,p( i ) ) = ∫{np/mq→∞} Gm,n( x ) dx
但し、m = 2( r + 1 )、n = 2( N - r )
なので、上式に N = 10, r = 8 を代入すれば、m = 18, n = 4 となって
下式に N = 10, r = 9 を代入すれば、m = 20, n = 2 となって
と表すことができます。∫{0→0.34} G18,4( x ) dx = 0.05, ∫{19.45→∞} G20,2( x ) dx = 0.05 なので、
となって、これを解くと
4p / 18q = 4p / 18( 1 - p ) ≥ 0.34 より p ≥ 0.60
2p / 20q = 2p / 20( 1 - p ) ≤ 19.45 より p ≤ 0.99
よって、0.60 ≤ p ≤ 0.99 となります。
標準正規分布を利用すると、∫{-ta→ta} ( 1 / 2π )1/2 exp( -t2 / 2 ) dt = 0.90 を持たす ta は 1.64 となるので、
に N = 10, r = 9, ta = 1.64 を代入して
0.9 - 1.64{ 9 / 1000 }1/2 ≤ p ≤ 0.9 + 1.64{ 9 / 1000 }1/2 より
0.74 ≤ p ≤ 1.0
と求めることができます。
比率が変化しなくても試行回数が変化すれば区間推定が変化することは容易に想像することができます。100 回中 90 回表が出るのならば、推定される確率の区間は狭くなるでしょう。実際、この場合は
∫{0→22p/180q} G180,22( x ) dx ≥ 0.05
∫{20p/182q→∞} G182,20( x ) dx ≥ 0.05
をとくことになって、信頼率 90% での推定区間は [0.84, 0.94] になります。これは、試行回数が多くなるほど推定値の信頼性は上がるということを意味します。
今回は、推定を中心に紹介してきました。繰り返しになりますが、母集団全体の分布を調査するために一部の標本から類推を行うのが推定の目的になります。よって、今まで説明した方法を正しく使ったとしても、元の標本の抽出方法が誤っていれば正しい結果は得られません。数学的に非常に高度な手法を利用しているので、これさえ利用すればどんなデータでも正しく推定できると考えるのは誤りで、データの内容が最も重要であることは理解しておく必要があります。
次回は、推計統計学のもう一つの手法である「検定」について紹介したいと思います。
ある母集団の確率変数 x とパラメータ θ からなる確率分布を p( x, θ ) として、θ の不偏推定量の一つを
とします。ここで、x = ( x1, x2, ... xN ) はそれぞれ独立した確率変数であるとします。θ^ は不偏推定量なので、その期待値 E[θ^] に対して
が成り立ちます。E[θ^] は下式のように表すことができます。
| E[θ^] | = | ∫{-∞→∞}...∫{-∞→∞} δ( x1, x2, ... xN ) p( x1, θ ) p( x2, θ ) ... p( xN, θ ) dx1dx2...dxN |
| = | ∫...∫ δ( x ) f( x, θ ) dx |
下側の式は、積分範囲を省略し、Π{1→N}( p( xi, θ ) ) = f( x, θ ) として略記しています。
E[θ^] = θ の両辺を θ で微分すると
となるので、微分と積分が交換できるならば
となります。ここで、
を利用すると、
が成り立ちます。
また、f( x, θ ) は独立した N 個の確率変数に対する同時確率分布を表しており、この全積分 ∫...∫ f( x, θ ) dx は 1 になります。よって、先ほどと同様に θ で両辺を微分すると
| ( d / dθ ) ∫...∫ f( x, θ ) dx | = | ∫...∫ ∂f( x, θ ) / ∂θ dx |
| = | ∫...∫ { ∂ log f( x, θ ) / ∂θ } f( x, θ ) dx = 0 |
になります。両辺に θ を掛けて、
よって、(1)式と(2)式を辺々引くと、
となります。ここで、積分に対する「コーシー = シュワルツの不等式」より
が成り立つので、f( x, θ ) ≥ 0 より
a(x) = { δ( x ) - θ } { f( x, θ ) }1/2
b(x) = { ∂ log f( x, θ ) / ∂θ } { f( x, θ ) }1/2
として「コーシー = シュワルツの不等式」を適用すれば
| ∫...∫ { δ( x ) - θ }2 f( x, θ ) dx ∫...∫ { ∂ log f( x, θ ) / ∂θ }2 f( x, θ ) dx | |
| ≥ | [ ∫...∫ { δ( x ) - θ } { ∂ log f( x, θ ) / ∂θ } f( x, θ ) dx ]2 = 1 |
よって、
となります。ところで、θ^ の分散 V[θ^] は
| V[θ^] | = | E[ ( θ^ - E[θ^] )2 ] |
| = | ∫...∫ ( θ^ - E[θ^] )2 f( x, θ ) dx | |
| = | ∫...∫ { δ( x ) - θ }2 f( x, θ ) dx |
であり、先ほど求めた不等式の左辺になります。よって、
が成り立ちます。右辺にある積分の部分は、さらに以下のように計算を進めることができます。
| ∫...∫ { ∂ log f( x, θ ) / ∂θ }2 f( x, θ ) dx | |
| = | ∫...∫ { ∂ log Πi{1→N}( p( xi, θ ) ) / ∂θ }2 Πk{1→N}( p( xk, θ ) ) dx |
| = | ∫...∫ { Σi{1→N}( ∂ log p( xi, θ ) / ∂θ ) }2 Πk{1→N}( p( xk, θ ) ) dx |
ここで、
| ∫...∫ { ∂ log p( xi, θ ) / ∂θ } { ∂ log p( xj, θ ) / ∂θ } Πk{1→N}( p( xk, θ ) ) dx | |
| = | ∫...∫ { ∂ log p( xi, θ ) / ∂θ }p( xi, θ ) { ∂ log p( xj, θ ) / ∂θ }p( xj, θ ) Πk{1→N;k≠i,j}( p( xk, θ ) ) dx |
| = | ∫∫ { ∂p( xi, θ ) / ∂θ } { ∂p( xj, θ ) / ∂θ } dxidxj |
| = | ∫ { ∂p( xi, θ ) / ∂θ } dxi ∫ { ∂p( xj, θ ) / ∂θ } dxj = 0 |
となります。但し、
となることと、
より θ で微分すれば
となることを利用しています。つまり、{ Σi{1→N}( ∂ log p( xi, θ ) / ∂θ ) }2 が p( xi, θ )・p( xj, θ ) 項に展開されたとき、i ≠ j になる項はすべてゼロになり、i = j になる項だけが残ります。よって、
| ∫...∫ { ∂ log f( x, θ ) / ∂θ }2 f( x, θ ) dx | |
| = | ∫...∫ Σi{1→N}( { ∂ log p( xi, θ ) / ∂θ }2 p( xi, θ ) ) dx |
| = | N ∫ { ∂ log p( x, θ ) / ∂θ }2 p( x, θ ) dx |
| = | N・E[ { ∂ log p( x, θ ) / ∂θ }2 ] |
これで、クラーメル-ラオの不等式
が得られました。クラーメル-ラオの不等式が成り立つために確率密度関数 p( x, θ ) が満たすための条件は、f( x, θ ) = Πi{1→N}( p( xi, θ ) ) に対して
( d / dθ ) ∫...∫ f( x, θ ) dx = ∫...∫ ∂f( x, θ ) / ∂θ dx = 0
( d / dθ ) ∫...∫ δ( x ) f( x, θ ) dx = ∫...∫ δ( x ) { ∂f( x, θ ) / ∂θ } dx = 1
が成り立つ必要があることが上記証明の内容からわかります。正規分布 Nσ( xi, μ ) = { 1 / (2π)1/2σ }exp( -( xi - μ )2 / 2σ2 ) を μ で微分すると、
| ∂Nσ( xi, μ ) / ∂μ | = | { 1 / (2π)1/2σ }{ ( xi - μ ) / σ2 }exp( -( xi - μ )2 / 2σ2 ) |
| = | { ( xi - μ ) / σ2 }Nσ( xi, μ ) |
となるので、xi について積分を行えば E[ ( xi - μ ) / σ2 ] = 0 となります。また、δ( x ) = Σi{1→N}( xi ) / N = m の場合、δ( xi ) = xi / N とすれば
となるので、上式において xi に対する積分だけを抽出すると、
| ∫ { xi( xi - μ ) / Nσ2 } Nσ( xi, μ ) dxi | = | E[ xi2 / Nσ2 ] - E[ μxi / Nσ2 ] |
| = | { V[xi] + ( E[xi] )2 } / Nσ2 - E[ μxi / Nσ2 ] | |
| = | ( σ2 + μ2 ) / Nσ2 - μ2 / Nσ2 = 1 / N |
で、xi 以外の部分の積分は 1 なので
よって、
となります。これらのことから、正規分布に対して標本平均 m を不偏推定量とした場合はクラーメル-ラオの不等式が適用できることになります。一般に、f( x, θ ) とそれを θ で微分した ∂f( x, θ ) / ∂θ が有界な区間で連続であれば、θ に対する有界な区間を [ θ1, θ2 ] としたときに ∫x1...∫xN f( x, θ ) dx は [ θ1, θ2 ] 上で微分可能で
が成り立ちます。但し、上記の積分は x = ( x1, x2 ... xN ) の各成分に対して有界な区間 xi = [ xi1, xi2 ] での積分値を表しています。広義積分になると、∫x1...∫xN f( x, θ ) dx が任意の θ で収束し、かつ ∫x1...∫xN ∂f( x, θ ) / ∂θ dx が任意の θ で一様収束する(簡単に言えば、全体が一斉にある関数へ収束すること) という条件が満たされれば必ず成り立ちます(その条件を満たさなくても成り立つ場合もあります)。たいていの確率密度関数や不偏推定量はこの条件を満たすことができるので、あまり気にする必要はないようですが、一様分布だけはこの条件を満たさないことに注意が必要です。
[ 0, θ ] の範囲のみに値を持つ一様分布 f( x, θ ) は以下のように定義することができます。
| f( x, θ ) | = | 1 / θ | ( 0 ≤ x ≤ θ ) |
| = | 0 | ( x < 0 ; θ < x ) |
このとき、確率変数 xi ( i = 1, 2, ... N ) のすべてが 0 ≤ xi ≤ θ を満たしているならば f( x, θ ) = 1 / θN で、一つでも 0 ≤ xi ≤ θ を満たさないものがあれば f( x, θ ) = 0 になります。よって、∂f( x, θ ) / ∂θ は
| ∂f( x, θ ) / ∂θ | = | -N / θN+1 | ( 0 ≤ xi ≤ θ ) |
| = | 0 | ( xi < 0 ; θ < xi ) |
よって、
| ∫...∫ ∂f( x, θ ) / ∂θ dx | = | ( -N / θN+1 ) ∫{0→θ}...∫{0→θ} 1 dx |
| = | ( -N / θN+1 )[ x1 ]{0→θ}...[ xN ]{0→θ} = -N / θ |
となって、クラーメル-ラオの不等式が成り立つための条件を満たさないことになります。
◆◇◆更新履歴◆◇◆
(誤) NormalDistribution nDist( mean, sigma );
(正) NormalDistribution nDist( 0, 1 );
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |