前回は、標本から母集団の分布の様子を推測するための手法として「推定(Estimation)」について紹介しました。推定法としては、分布を表す統計量(平均や分散など)としてできるだけふさわしい値を決めるための「点推定」と、一つに決めることは不可能なので、ある程度のマージンをとって範囲で表す「区間推定」の二種類がありました。
今回は、推計統計学のもう一つの手法である「検定」について紹介します。「推定」は文字通り分布を推定するのが目的なのに対し、「検定」はある仮説に対してそれが正しいかどうかを統計学や確率論の手法を用いて判定することが目的になります。実は「推定」と「検定」は表裏一体の関係にあって、どちらも用いる理論はほぼ同じです。
検定は正しくは「統計学的仮説検定(Statistical Hypothesis Testing)」または「仮説検定」というそうです。文字通り、ある「仮説」に対して「統計学的」に「検定」するということになり、最初に「仮説」を決める必要があります。ここで、非常に簡単な例を挙げてみます。
当たりとハズレのクジが合計三つ入った箱から五人の人にクジを引いてもらいます。但し、引いたクジは元に戻します。
全員がクジを引いた後、当たりとハズレそれぞれを引いた数を調べると、当たりが一人であったのに対してハズレが四人いました。当たりとハズレがそれぞれいくつあったと考えられるでしょうか。
当たりもハズレも少なくとも一つあることは間違いないので、あとは当たりが一つなのか、それとも二つなのかを考えればいいことになります。一回の試行で当たりが出る確率を p とすれば、p は 1/3 か 2/3 のいずれかなので、五回の試行で当たりが一回だけ出る確率は二項分布から
B5,1/3( 1 ) = 5C1( 1 / 3 )1( 2 / 3 )4 = 0.329
B5,2/3( 1 ) = 5C1( 2 / 3 )1( 1 / 3 )4 = 0.0412
になります。仮説として「当たりは一つである」としたとき、上記のような事象が発生する確率は 32.9% であり、別の仮説として「当たりは二つである」とすれば、その確率は 4.12% であると求められたことになります。今回はいずれか一方しか発生しないことが明らかなので、「当たりは一つである」方を採用するのが妥当だと考えられるでしょう。
この例では、実際に試行を行ってから判断していましたが、試行を行う前にあらかじめ判定方法を決めておく場合、五人の人にクジを引いてもらったときに起こり得る事象は
| E0 | : | 当たり 0 回, ハズレ 5 回 |
| E1 | : | 当たり 1 回, ハズレ 4 回 |
| E2 | : | 当たり 2 回, ハズレ 3 回 |
| E3 | : | 当たり 3 回, ハズレ 2 回 |
| E4 | : | 当たり 4 回, ハズレ 1 回 |
| E5 | : | 当たり 5 回, ハズレ 0 回 |
の六通りです。p が 1/3 と 2/3 の場合それぞれについて確率を求めると、
| 事象 | p=1/3 | p=2/3 |
|---|---|---|
| E0 | 0.132 | 0.00412 |
| E1 | 0.329 | 0.0412 |
| E2 | 0.329 | 0.165 |
| E3 | 0.165 | 0.329 |
| E4 | 0.0412 | 0.329 |
| E5 | 0.00412 | 0.132 |
となるので、ここで p = 1/3 の場合を仮説 H0、それに対立する p = 2/3 の場合を仮説 H1 としたとき、
E4 か E5 のいずれかの事象が発生したら H0 を棄却する ( H1 を採用する )
E0 から E3 までのいずれかの事象が発生したら H0 を採用する ( H1 を棄却する )
と考えれば、p = 1/3 の状態で四人以上の人が当たりを引く確率は 0.0453 で 5% より低いので、そんなことは滅多に起こらないことから p = 1/3 であるとは考えられない、よって、四人以上の人が当たりを引いた場合は H0 を棄却して、逆に当たりを引いた人が三人以下ならば H0 が採用できる、と判断することができます。これが基本的な検定の考え方です。
この例では、考えられる可能性は p = 1/3 か p = 2/3 の二つのみでした。しかし、例えばクジが五つ入っているのなら、当たりとハズレは最低一つは入っているとした場合は 4 通りの可能性があるので、仮説も 4 通り考えられます。一般に、考えられる仮説というのは非常に多いので、それぞれに対して発生する確率を求めて検証することは不可能です。そこで、仮説は一つだけに絞って、その発生する確率から判断することになります。上記の例において、H0 を仮説として採用したとき、実際には H0 が正しいのに、それが正しくないとして棄却してしまう確率は、上の結果から 0.0453 になります。それでは、H0 は正しくないのに、それが正しいとして採用してしまう確率はどうなるかを考えると、p = 2/3 なのに、E0 から E3 までのいずれかの事象が発生してしまった場合を考えればいいので、
となって、確率は 50% よりも高くなってしまいます。H0 が正しいのにそれを棄却してしまう誤りのことを「第一種の誤り(Type I Error)」または「偽陽性(False Positive)」、逆に H0 が誤っているのにそれを採用してしまう誤りのことを「第二種の誤り(Type II Error)」または「偽陰性(False Negative)」といい、第一種の誤りが発生する確率を低くするほど第二種の誤りが発生する確率は高くなる傾向があります。例えば、E0 から E2 までのいずれかが発生したら H0 を採用するとすれば、第二種の誤りは p = 2/3 なのに E0 から E2 までのいずれかの事象が発生してしまった場合になるので、その確率は 0.210 と低くなりますが、第一種の誤りは p = 1/3 なのに E3 から E5 までのいずれかの事象が発生した場合で、その確率も 0.210 と高くなってしまいます。一般に、一つの仮説に対する他の仮説(これを「対立仮説(Alternative Hypothesis)」といいます)は非常に多く、第二種の誤りが発生する確率を上記の例のように具体的に求めることは非常に困難です。したがって、第一種の誤りに対する確率を小さく設定して、第二種の誤りはできるだけ小さくできるような手法が理想的な検定となります。
また、事象 E3 が発生した場合、H0 は棄却できないことになりますが、それでも p = 1/3 であるときの発生確率は 0.21 です。一般に、仮説が棄却できないと判定されたとしても、設定している確率は非常に低くしているのが通常なので、仮説が発生する確率は設定値以上になっただけで相変わらず低いままのはずです。すると、棄却できないからといってそれを採用することはできないことになります。設定する仮説は一般に、棄却されるときにだけ意味を持ち、棄却されなかったからといってそれを採用することはできません。よって、「無に帰す」仮説という意味から「帰無化説(Null Hypothesis)」と呼ばれます。上記の例においては、E2 や E3 が発生したときは結論を保留してさらに試行を繰り返すというのが具体的な解決法になります。
ところで、前回紹介した「百分率の区間推定」から考えれば、当たりが一人だった場合 90% の信頼度では 1/3 が唯一の選択肢となるので、その結果から「当たりは一つである」と推測することもできます。つまり、(区間)推定をすることで、仮説検定を行うことは可能であるということになります。推定は、母集団の統計量がどの範囲にありそうなのかを定量的に求める手法であるのに対し、検定はある決められた値や別の母集団の統計量に「一致するかどうか」を調べる定性的な手法です。「白黒はっきりさせる」といった場合には検定は有効ですが、それがどの程度外れているのか、また他の基準値や母集団を使った場合はどうなのかを知りたいときなどは、信頼区間を求めておいて比較する方が効率的です。よって、最終的な結論を述べるところだけ検定の手法を使い、詳細な分析には推定の結果を利用するというように、両方をうまく使い分けていく必要があると思います。通常は、いきなり検定法を使って結論を得ようとしてもたいていは失敗することが多いです。
ここでは、区間推定を利用して得られる検定について説明をします。
一般的な検定では、母集団の未知のパラメータ θ が、何らかの基準値 θ0 と等しい(θ = θ0) ということを帰無仮説として利用します。すると、対立仮説は「基準値 θ0 と等しくない(θ ≠ θ0) 」になります。基準値と等しくなるといってもピッタリ一致するなどということはまずあり得ないので、等しいと考えた場合にそのようになる確率がどの程度であるかをみて、その確率が非常に低ければ帰無仮説を棄却して「等しくない」とするわけです。しかし、ある程度の確率で「あり得る」と判断されれば、結論は保留されます(等しいということも言えないことに注意してください)。前に述べたように、その判断をするときに区間推定で使った手法がそのまま利用できます。
母集団が正規分布に従う場合、平均値の区間推定では t = ( m - μ )√N / u (m:標本平均 ; μ:母集団の平均 ; N:標本数 ; u:不偏分散) が自由度 N - 1 の t-分布に従うことを利用していました。よって、信頼区間に対して基準値となる値 μ0 が範囲外であるときに帰無仮説を棄却することで検定ができます。信頼度 β に対する信頼区間は、自由度 N - 1 の t-分布 fN-1(t) において
となるような t を求めた上で、次の不等式で計算することができます。
また、一般の分布に対しても、標本数が充分大きければ、中心極限定理によって標本平均は正規分布に近似できるので、z = ( m - μ )√N / s (s2:標本分散) が標準正規分布 N0,1(z) に近似的に従うことを利用して
を満たす z を求めた上で、
から検定を行うことができます。検定の場合は、基準値が信頼区間の外側にある場合、帰無仮説を棄却する(つまり対立仮説を採用する)ことになります。その区間はそれぞれ
μ < m - u・t / √N ; m + u・t / √N < μ
μ < m - s・z / √N ; m + s・z / √N < μ
となり、この区間を「棄却域(Region of Rejection ; Critical Region)」といいます(検定の場合、信頼区間は「採択域(Region of Acceptance)」と呼ばれたりします)。
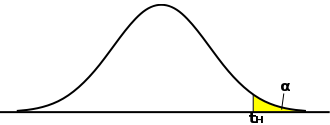
棄却域の定義においては検定独自の考え方が生じる場合があります。推定においては、信頼区間はできるだけ幅が小さくなるように決めるのが望ましいとされていました。t-分布や正規分布の場合、平均を中心として左右に裾が広がった形状をしているため、信頼区間も、標本平均を中心に左右対称な区間で定義すれば幅が最小になることがわかります。しかし、検定の場合は対立仮説として「等しくない(μ ≠ μ0)」の他に、「基準値より小さい(μ < μ0)」と「基準値より大きい(μ > μ0)」という見方ができるので、それに合わせて棄却域を決める必要があります。μ ≠ μ0 ということは、μ が基準値に対して大きくなるのか、それとも小さくなるのかはわからない、または問題にしないということになるので、利用する棄却域(信頼区間)は推定の場合と同じです。しかし、μ > μ0 は基準値より大きくなることを意味するので、区間の最小値に対して μ0 がより小さければ仮説が棄却されます。区間の最小値を tL としたとき、tL は下式で求めることになります。
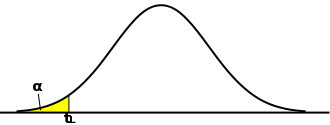
逆に、μ < μ0 は基準値より小さくなることを意味するので、区間の最大値に対して μ0 がより大きければ仮説が棄却されます。区間の最大値を tH としたとき、tH は下式で求められます。
α は危険率を表し、1 - β で求められます。分布が左右対称なことから、両者は同じ結果が得られるので、計算方法は一つにまとめることができます。求める棄却域は、対立仮説が μ > μ0 ならば
μ < μ0 ならば
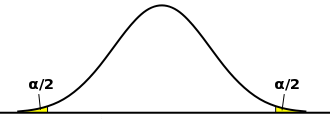
となります。対立仮説が「μ > μ0」である場合、たとえ標本平均が基準値に対して小さすぎたとしても棄却域ではないので結論は保留することになります。「μ < μ0」の場合も同様な考え方になります。「μ ≠ μ0」を対立仮説として、棄却域を両側に設定する検定は「両側検定(Two-Tailed Test ; Two-Sided Test)」、「μ < μ0」または「μ > μ0」を対立仮説として、棄却域を片側に設定する検定は「片側検定(One-Tailed Test ; One-Sided Test)」と呼ばれます。
| 両側検定 ( μ ≠ μ0 ) | 片側検定 ( μ < μ0 ) | 片側検定 ( μ > μ0 ) |
|---|---|---|
 |
 |
 |
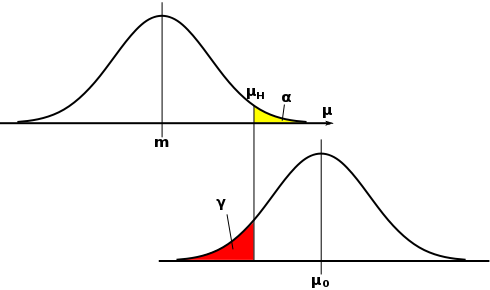
片側検定 μ < μ0 において、α は「第一種の誤り」となる確率を表しています。平均値の推定量が m であるとき、基準値 μ0 が μH = m + u・tH / √N より大きければ仮説を棄却する場合、仮説が正しいにもかかわらず棄却してしまう確率が α であるという意味になります。逆に仮説を保留したとき、μ0 と m はそれほど離れた値ではないということになりますが、実際には二つの値はかなり差があるにもかかわらず誤判定をしてしまう可能性もあります。そのような状態になる確率は、μ0 を中心とした分布において μH より小さくなる範囲で表されます。これが「第二種の誤り」の確率です。以下、この確率を γ で表します(通常は β で表すようですが、信頼度として β を使っているのでここでは γ を用います)。μH を大きくすれば、それだけ α は小さくなりますが、γ は大きくなってしまいます。
下の図は、μ0 が μH より大きな値となっている状態を表しています。m の推定範囲を大きくすれば、μH もより大きな値にシフトするため、μ0 が μH よりも小さくなってしまう可能性もあります。すると 「第二種の誤り」が発生してしまうことになります。逆に m の推定範囲が狭すぎて、本来なら μ0 と μH は近い値であるはずなのに棄却されてしまうときが「第一種の誤り」となるわけです。
t-分布を利用した検定法を総称して「(スチューデントの)t-検定 ( (Student's) t-Test )」といいます。平均値の検定でも t-分布を利用していることから t-検定と呼ばれることが多く、その他にも異なる二つの分布の平均値が等しいかどうかを検定する場合などを指す場合があります。
以下に、平均値の検定を行うサンプル・プログラムを示します。
/* 検定の棄却域 */ enum TEST_CRITICAL_REGION { TEST_GT, // 片側検定( μ > μ0 ) TEST_LT, // 片側検定( μ < μ0 ) TEST_NE, // 両側検定( μ ≠ μ0 ) TEST_SIZE, }; /* avg_Test : 平均値の区間推定 const ContDist& dist : 確率密度関数 double m0 : 基準値 double mean : 標本平均 double sigma : 標準偏差 unsigned int n : 標本数 double a : 危険率 int testType : 検定方法(片側・両側検定) pair<double,double>& interval : 信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 仮説を棄却 , False ... 仮説を保留 または 危険率・検定方法が不正 */ bool avg_Test( const ContDist& dist, double m0, double mean, double sigma, unsigned int n, double a, int testType, pair<double,double>& interval, double threshold ) { if ( a < 0 || a > 1 ) { cout << "Critical value must be greater than zero and less than one." << endl; return( false ); } if ( testType >= TEST_SIZE ) { cout << "Test type is not correct." << endl; return( false ); } if ( testType == TEST_NE ) { avg_iEst( dist, mean, sigma, n, 1.0 - a, interval, threshold ); return( m0 < interval.first || m0 > interval.second ); } else { avg_iEst( dist, mean, sigma, n, fabs( 1.0 - 2.0 * a ), interval, threshold ); if ( testType == TEST_LT ) { if ( a > 0.5 ) interval.second = interval.first; interval.first = NAN; return( m0 > interval.second ); } else { if ( a > 0.5 ) interval.first = interval.second; interval.second = NAN; return( m0 < interval.first ); } } } /* avg_tTest : 平均値の検定(t-分布による検定) const vector<double>& data : データ列 double m0 : 基準値 double a : 危険率 int testType : 検定方法(片側・両側検定) pair<double,double>& interval : 信頼区間 double& t : t値 double& p : p値 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 仮説を棄却 , False ... 仮説を保留 または データ数が 1 以下, 危険率が不正, 検定方法が不正 */ bool avg_tTest( const vector<double>& data, double m0, double a, int testType, pair<double,double>& interval, double& t, double& p, double threshold ) { unsigned int n = data.size(); // データ数 if ( n <= 1 ) { cout << "The data size must be greater than one." << endl; return( false ); } double mean = sampleAverage( data ); // 標本平均 double u = sqrt( sampleVariance( data, true ) ); // 不偏分散の平方根 TDistribution tDist( n - 1 ); // 自由度 n - 1 の t-分布 // t値とp値の計算 if ( &t != 0 ) t = ( mean - m0 ) * sqrt( n ) / u; if ( &p != 0 ) p = 0.5 - tDist.p( 0, fabs( t ) ); return( avg_Test( tDist, m0, mean, u, n, a, testType, interval, threshold ) ); } /* avg_zTest : 平均値の検定(正規分布による検定) const vector<double>& data : データ列 double m0 : 基準値 double a : 危険率 int testType : 検定方法(片側・両側検定) pair<double,double>& interval : 信頼区間 double& z : z値 double& p : p値 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 仮説を棄却 , False ... 仮説を保留 または データ数が 1 以下, 危険率が不正, 検定方法が不正 */ bool avg_zTest( const vector<double>& data, double m0, double a, int testType, pair<double,double>& interval, double& z, double& p, double threshold ) { unsigned int n = data.size(); // データ数 if ( n <= 1 ) { cout << "The data size must be greater than one." << endl; return( false ); } double mean = sampleAverage( data ); // 標本平均 double sigma = sqrt( sampleVariance( data ) ); // 標本分散の平方根(標準偏差) NormalDistribution nDist( 0, 1 ); // 正規分布 // z値とp値の計算 if ( &z != 0 ) z = ( mean - m0 ) * sqrt( n ) / sigma; if ( &p != 0 ) p = 0.5 - nDist.p( 0, fabs( z ) ); return( avg_Test( nDist, m0, mean, sigma, n, a, testType, interval, threshold ) ); }
基準値 m0 を引数として渡した上で、仮説「平均値 μ = m0」が棄却される場合は true を返します。列挙体の TEST_CRITICAL_REGION は検定の棄却域に対する定義を表し、片側検定 (対立仮説を μ > m0 または μ < m0 とする) や両側検定を選択することができます。棄却域の定義によって、棄却域の範囲の計算方法は変化します。
実際の処理は avg_Test が行います。パラメータのチェックを行った後、棄却域の定義によって場合分けをして信頼区間を求め、基準値 m0 がその範囲外にあれば仮説を棄却します。前回紹介した信頼区間算出用のプログラムを流用しているので、平均値の推定の場合は分布の中心から左右対称に区間を求めています。そのため、片側検定の場合は少々強引な計算で片側だけの区間を得た上で基準値との比較を行っています。
ところで、t-分布と F-分布の間には次の関係がありました(「(6) 標本分布」の「3) t-分布(t-Distribution)」参照)。
これは次の定理と同じ意味を持ちます。
よって、F-分布を使って棄却域を求めた上で検定を行うこともできることになります。F-分布はゼロ以上の定義域に対してのみ分布があるため、必ず片側検定となって、次のように f を求めることになります。
こうして求めた f について、
なら帰無仮説を棄却することになります。もちろん、これはそのまま区間推定に利用することもできます。さらに、分散の等しい二つの正規母集団 N( μi, σ2 ) ( i = 1, 2 ) に対して、それぞれ Ni の大きさの標本をランダムに抽出したとき、その標本平均を mi、標本分散を si2 とすれば、F-分布の性質から
となります。棄却域を決めてその境界を f としたとき、
ならば帰無仮説は棄却できることになります。では、何が帰無仮説になるのかというと、上に示した不等式の中での未知数は μ1 と μ2 であり、Δμ = | μ1 - μ2 | の大きさに対して推定や検定を行うことができることを意味します。但し、両分布の分散が一致していることが前提であることに注意してください。この検定の例はこの後紹介する「分散の検定」のところで紹介します。
母集団が正規分布に従うのであれば、分散の区間推定には y = Ns2 / σ2 が自由度 N - 1 の χ2-分布に従うことが利用できたので、これをそのまま検定に使うことができます。分散の基準値として σ02 があって、これよりバラツキが小さいか(あるいは大きいか)を検定したい場合はこの手法を使うことになります。
その他に考えられる検証として、二つの母集団の分散を比較するというものがあります。それぞれの分布の分散が σ12, σ22 だったとして、σ12 = σ22 を帰無仮説とし、対立仮説を σ12 < σ22 または σ12 > σ22 とするわけです。このような場合、F-分布が持つ次の性質を利用することができます。
二つの正規母集団 N( μ1, σ2 ), N( μ2, σ2 ) から、それぞれ大きさ M, N の標本 ( x11, x12, ... x1M ) と ( x21, x22, ... x2N ) をランダムに抽出したとき、
不偏分散の比 u12 / u22 は自由度 ( M - 1, N - 1 ) の F-分布に従う
二つの正規母集団から標本を抽出して、その分布に差があるのかを調べたいとします。ここで、何を持って差があるかを検討するかを決める必要がありますが、ここでは平均と分散を比較するとします。平均が等しいかどうかは、「平均値の検定」の最後に示した、F-分布を使った検定を利用することができます。しかし、分散が等しいことが前提となっているため、先に分散を検定する必要があります。その時、上に示した検定が役に立つわけです。ここで、例題を一つ挙げておきます。
装置にある改良を行った後の製品の歩留まりを調べたところ、改良前と後で次のような結果が得られた。
| 改良前 | 85.3 | 82.6 | 86.4 | 82.1 | 88.9 | 78.4 | 90.3 | 88.8 | 81.4 | 80.6 |
|---|---|---|---|---|---|---|---|---|---|---|
| 改良後 | 79.4 | 81.6 | 87.2 | 84.1 | 86.8 | 91.1 | 90.1 | 90.4 | 82.6 | 83.0 |
改良前後において、歩留まりに差は生じたか。
まず、改良前後での標本平均、標本分散、不偏分散をそれぞれ ( m1, m2 ), ( s12, s22 ), ( u12, u22 ) とします。これらを計算すると、
| 標本平均 mi | 標本分散 si2 | 不偏分散 ui2 | |
|---|---|---|---|
| 改良前(i=1) | 84.5 | 14.7 | 16.3 |
| 改良後(i=2) | 85.6 | 15.0 | 16.7 |
になります。二つの母集団の分散が等しければ f1 = u12 / u22 が自由度 ( 9, 9 ) の F-分布に従うことから、[ 0, fL ] と [ fH, ∞ ) を棄却域とすれば、危険率 5% (片側 2.5%) のとき fL = 0.248、fH = 4.026 となります。従って、
が信頼区間で、二つの母集団の分散が等しいということを帰無仮説とすれば、u12 / u22 = 0.981 より棄却域には入らないため帰無仮説は棄却できず、二つの母集団の分散は等しくないとはいえない(しかし、等しいともいえない)という結論になります。
さて、ここで困ったことになります。検定の結果、帰無仮説は保留されました。しかし、これで対立仮説が成り立たないともいえるわけではありません。結局どちらかは判定できないわけです。しかし、ここで f1 値をみれば 0.981 と 1 に非常に近い値になっています。検定の結果、二つの母集団の分散は等しくないとはいえないとの結果になったことと合わせて、ここでは分散は等しいものと考えて先へ続けるしかありません。もちろん可能であれば、さらに標本数を増やすことで信頼性を上げることができます。
分散が等しいと仮定したので、歩留まり差 μ2 - μ1 = Δμ とすれば
| f2 | = | [ ( 10 + 10 - 2 ){ ( m1 - m2 ) - ( μ1 - μ2 ) }2 ] / [ ( 1 / 10 + 1 / 10 )( 10s12 + 10s22 ) ] |
| = | 9{ ( 84.5 - 85.6 ) + Δμ }2 / ( 14.7 + 15.0 ) | |
| = | 9( Δμ - 1.1 )2 / 29.7 |
は自由度 ( 1, 18 ) の F-分布に従うことになります。| Δμ - 1.1 | が 0 に非常に近い値がどうかは検定する意味はないので(大きい側での信頼区間内に含まれることになるので)、この場合は片側検定を利用することになります。危険率 5% での信頼区間は f2 ≤ 4.41 なので
これを解くと
( Δμ - 1.1 )2 ≤ 14.6 より
-3.82 ≤ Δμ - 1.1 ≤ 3.82
よって、
で、Δμ の信頼区間は -2.7 から 4.9 の間となります。つまり、歩留まりが 5% 上がったと言った場合は危険率 5% でそれを棄却することができますが、4% 上がったといった場合は棄却することはできません。また歩留まりが逆に下がったということも否定はできないことになりますが、3% 以上も下がったという場合は棄却することができます。
歩留まりが 5% 以上も上がったとしたとき、Δμ に 5 を代入して
になるので、F-分布にて f2 ≥ 4.61 での確率を求めると 0.046 になります。この値は「p値(p-value)」と呼ばれ、帰無仮説が正しいとしたときの確率を表します(平均値の検定用サンプル・プログラムでも、p値を計算して返す機能をこっそりと入れてあります)。帰無仮説を「Δμ ≥ 5」としたとき、その p値が 0.046 となるわけです。危険率 5% ではそれを棄却することができますが、危険率が 1% ならこの仮説は棄却されないことになります。
母集団の分散が等しいという帰無仮説の検定と、それが成り立つと仮定したときの母集団の平均が等しいという帰無仮説の検定は、どちらも F-分布を利用しているため「F-検定 (F-Test)」と呼ばれます。また、t が自由度 N の t-分布に従うとき、f = t2 が自由度 ( 1, N ) の F-分布に従うことから、母集団の平均に対しては F-分布の代わりに t-分布を使って上記の推定や検定を行うことも可能なので、そのときは t-検定と呼ばれるようです。あくまでも、利用した確率分布が何かによって名称が決まるので、平均だからとか分散だからというような決め方はありません。その意味では、あまり名前にはこだわる必要はないと思います。
さらに、上記の例では二つの母集団から標本を抽出して検定を行っているため、「二標本の検定(Two Sample Test)」と呼ばれる検定法の一つと考えられます。それに対して「平均値の検定」で紹介したような一つの母集団に対する検定を「一標本の検定(One Sample Test)」といいます。当然、対象の母集団がさらに多くなる場合も考えられ、その場合はさらに別の手法が存在します。
二標本を扱う場合、一標本の形に置き換えて検定を行うことができる場合もあります。例えば、ある改造を行った結果、処理速度が早くなったとか、投薬によって体の機能を表すパラメータが変化したなど、それぞれの母集団の標本が一対一に対応しているようなときは、対応する標本どうしの差や比率を利用することで一標本にすることが可能です。
以下に、二標本の平均値検定を行うサンプル・プログラムを示します。
/* twoSampleAvgTest : 二標本の平均値検定 const vector<double> &data1, &data2 : 二つのデータ列 double a : 危険率 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 仮説を棄却 , False ... 仮説を保留 または データ数が 1 以下, 危険率が不正, 検定方法が不正 */ bool twoSampleAvgTest( const vector<double>& data1, const vector<double>& data2, double a, double threshold ) { cout << "***** Two Sample Average Test *****" << endl; if ( a < 0 || a > 1 ) { cout << "Critical value must be greater than zero and less than one." << endl; return( false ); } // データ数 unsigned int n1 = data1.size(); unsigned int n2 = data2.size(); if ( n1 <= 1 || n2 <= 1 ) { cout << "The data size must be greater than one." << endl; return( false ); } // 標本平均 double m1 = sampleAverage( data1 ); double m2 = sampleAverage( data2 ); // 不偏分散 double u1 = sampleVariance( data1, true ); double u2 = sampleVariance( data2, true ); // 標本分散 double s1 = sampleVariance( data1, false ); double s2 = sampleVariance( data2, false ); cout << "m\ts\tu" << endl; cout << "------- ------- -------" << endl; cout << m1 << "\t" << s1 << "\t" << u1 << endl; cout << m2 << "\t" << s2 << "\t" << u2 << endl << endl; double f = u1 / u2; // 不偏分散比 cout << "u1^2 / u2^2 = " << f << endl << endl; FDistribution fDist1( n1 - 1, n2 - 1 ); double fl = binSearch( fDist1, a / 2.0, threshold ); double fh = binSearch( fDist1, 1.0 - a / 2.0, threshold ); cout << "Confidence interval for u1^2 / u2^2 : [" << fl << "," << fh << "]" << endl; if ( f < fl || fh < f ) { cout << "Null hypothesis ( variance of two samples are the same ) is rejected." << endl; return( false ); } cout << "Null hypothesis ( variance of two samples are the same ) is accepted." << endl << endl; FDistribution fDist2( 1, n1 + n2 - 2 ); fh = binSearch( fDist2, 1.0 - a, threshold ); double d = sqrt( fh * ( 1 / (double)n1 + 1 / (double)n2 ) * ( (double)n1 * s1 + (double)n2 * s2 ) / (double)( n1 + n2 - 2 ) ); double dl = -d - ( m1 - m2 ); double dh = d - ( m1 - m2 ); cout << "Confidence interval for ( m2 - m1 ) : [" << dl << "," << dh << "]" << endl; if ( dl > 0 || dh < 0 ) { cout << "Null hypothesis ( mean of two samples are the same ) is rejected." << endl; return( true ); } cout << "Null hypothesis ( mean of two samples are the same ) is accepted." << endl; return( false ); }
関数 twoSampleAvgTest を呼び出すと、先の「平均値の検定」でのように計算結果を引数に渡して返すような仕組みとは異なり、推定や検定の結果が画面に出力するだけの処理にしてあります。先程の例をこのプログラムで検定すると、次のように出力されます。
***** Two Sample Average Test ***** m s u ------- ------- ------- 84.48 14.7136 16.3484 85.63 14.9981 16.6646 u1^2 / u2^2 = 0.981031 Confidence interval for u1^2 / u2^2 : [0.248384,4.026] Null hypothesis ( variance of two samples are the same ) is accepted. Confidence interval for ( m2 - m1 ) : [-2.66727,4.96727] Null hypothesis ( mean of two samples are the same ) is accepted.
帰無仮説は「二つの母集団の平均が等しい」のみとしてあります。引数として平均差の基準値を渡すようにすれば、平均差が基準値より大きければ仮説を棄却するような形に変更することも簡単にできると思います。出力結果では、平均差の検定前に分散が等しいかを検定して、その仮説が棄却されれば(つまり分散が等しくないと見なされれば)処理を中断しています。よって、二つの検定を行っているわけですが、引数として渡すことのできる危険率は一つにして、どちらも同じ値を利用する形で手抜きしてあります。これも、少し手直しすればそれぞれ別々の危険率を利用することも可能です。
百分率の場合も区間推定がそのまま検定に利用できます。よく見られる事例を以下に示しておきます。
ある装置で加工した製品に対する不良率が 5% であったとする。この装置を改良した後、加工した製品から 100 個の製品を抜き取って調べたところ、不良品は 2 個見つかった。不良率は減少したと考えられるか。
まず、N = 100 個の製品の調査によって r = 2 個の不良品が発生したという事象が二項分布 B100,p( r ) に従うとしたときの p の区間推定を行ないます。これには F-分布 Gm,n( x ) と二項分布 BN,p( r ) に対する次の関係式が利用できるのでした。
Σi{r+1→N}( BN,p( i ) ) = ∫{0→np/m(1-p)} Gm,n( x ) dx
Σi{0→r}( BN,p( i ) ) = ∫{np/m(1-p)→∞} Gm,n( x ) dx
但し、m = 2( r + 1 )、n = 2( N - r )
上式に N = 100, r + 1 = 2 を代入して、m = 4, n = 198 より
下式に N = 100, r = 2 を代入して、m = 6, n = 196 より
となるような p を求めれば信頼区間を得ることができます。但し、α は危険率を表します。α = 5% とすれば、
∫{0→0.121} G4,198( x ) dx = 0.025
∫{2.47→∞} G6,196( x ) dx = 0.025
なので、
0.121 ≤ 99p / 2( 1 - p )
98p / 3( 1 - p ) ≤ 2.47
これを解くと
になります。改良前の不良率が 5% だったので、帰無仮説は p = 0.05 で、危険率 5% ではこれは棄却されず、不良率が下がったとは言えないことになります。
N が非常に大きいければ、二項分布は正規分布に近似できて、信頼区間は次のようになるのでした。
但し、ta は標準正規分布において信頼度を β としたときの信頼区間 [ -ta, ta ] を表す値になります。危険率を 5% としたとき、ta = 1.96 となるので N = 100, r = 2 を代入すれば
これを解いて
p ≥ 0 だから負数になることはないので、0 ≤ p < 0.0474 が求める信頼区間になります。この場合、帰無仮説は棄却され、不良率は下がったとすることができます。利用する手法によって結果が変わってしまったわけですが、これは手法のみならず、棄却率の決め方などにも左右されるし、その前に標本の抽出方法(標本数など)によっても影響を受けます。少なくとも、検定だけではなく区間推定の結果や p 値なども調べた上で結論を出す必要があるということです。p > 0.05 になる確率は、
より
と求められます。不良率が 5% より低い確率は、およそ 90% 近くはあるということになります。
二項分布を利用した百分率の検定は「二項検定(Binomial Test)」と呼ばれます。事象が起こるかどうかはわからない、発生する可能性は五分五分だ、といったような場合は p = 0.5 として検定を行うことになり、このような場合は特に「符号検定(Sign Test)」といいます。例としては、コインを投げたときに表が出る回数が p = 0.5 での二項分布に従うという仮説に対して検定を行い、それが棄却できればそのコインが異常であるとするようなものがあります。
二項検定のサンプル・プログラムを以下に示します。
// 百分率の区間推定関数呼び出し用ポインタ typedef bool (*Percent_iEst)( unsigned int, unsigned int, double, pair<double,double>&, double threshold ); /* binomialTest : 二項検定 unsigned int cnt : 試行回数 unsigned int r : 事象が発生した回数 double p : 事象が発生する確率 double a : 危険率 Percent_iEst func : 百分率の区間推定用関数 double threshold : binSearchで棄却域を求める時のしきい値 戻り値 : True ... 仮説を棄却 , False ... 仮説を保留 または p, a が不正、発生回数が試行回数より大きい */ bool binomialTest( unsigned int cnt, unsigned int r, double p, double a, Percent_iEst func, double threshold ) { cout << "***** Binomal(Sign) Test *****" << endl; if ( p < 0 || p > 1 ) { cout << "Probability must be greater than zero and less than one." << endl; return( false ); } if ( a < 0 || a > 1 ) { cout << "Critical value must be greater than zero and less than one." << endl; return( false ); } if ( cnt < r ) { cout << "Total number of trials must be greater than the number of occurrences." << endl; return( false ); } pair<double,double> interval; // 信頼区間 (*func)( cnt, r, 1.0 - a, interval, threshold ); cout << "Confidence interval for p : [" << interval.first << "," << interval.second << "]" << endl; if ( p < interval.first || interval.second < p ) { cout << "Null hypothesis ( p = " << p << " ) is rejected." << endl; return( true ); } cout << "Null hypothesis ( p = " << p << " ) is accepted." << endl; return( false ); } /* binomial_SS_Test : 二項検定(小標本) unsigned int cnt : 試行回数 unsigned int r : 事象が発生した回数 double p : 事象が発生する確率 double a : 危険率 double threshold : binSearchで棄却域を求める時のしきい値 戻り値 : True ... 仮説を棄却 , False ... 仮説を保留 または p, a が不正、発生回数が試行回数より大きい */ bool binomial_SS_Test( unsigned int cnt, unsigned int r, double p, double a, double threshold ) { return( binomialTest( cnt, r, p, a, &percent_SS_iEst, threshold ) ); } /* binomial_LS_Test : 二項検定(大標本) unsigned int cnt : 試行回数 unsigned int r : 事象が発生した回数 double p : 事象が発生する確率 double a : 危険率 double threshold : binSearchで棄却域を求める時のしきい値 戻り値 : True ... 仮説を棄却 , False ... 仮説を保留 または p, a が不正、発生回数が試行回数より大きい */ bool binomial_LS_Test( unsigned int cnt, unsigned int r, double p, double a, double threshold ) { return( binomialTest( cnt, r, p, a, &percent_LS_iEst, threshold ) ); }
百分率の区間推定には「小標本用」の percent_SS_iEst と「大標本用」である percent_LS_iEst の二種類があったので、検定もそれぞれの推定結果が利用できるように二種類用意しています。どちらも同じ引数と戻り値を持っているので、関数ポインタ Percent_iEst を用意して、ポインタを通して呼び出しができるようにすることで処理自体は共通の関数 binomalTest によって行えるようにしています。小標本用としては binomial_SS_Test、大標本用は binomial_LS_Test が用意されていますが、どちらも、それぞれに合わせた区間推定用関数 ( percent_SS_iEst, percent_LS_iEst ; 「百分率区間推定のサンプル・プログラム」を参照 ) を引数として渡して binomalTest 関数を呼び出しているだけです。
一回の試行 E に対し、k 個の事象 ( E1, E2, ... Ek ) の中の一つだけが必ず起こるとしたとき、それぞれの事象が発生する確率が p1, p2, ... pk ならば、各事象 Ei が ri 回発生した時の確率は「多項分布(Multinomial Distribution)」に従い、以下の式で表されるのでした。
PN,p( r ) = ( N! / r1!・r2!・...・rk! ) p1r1・p2r2・...・pkrk
k = 2 であれば、上式は「二項分布(Binomial Distribution)」と等しくなります。k = 2 なら二変数なので、一変数の二項分布にはならないように思えますが、Σi{1→k}( ri ) = N という条件があるため、多項分布は k - 1 変数の分布になり、k = 2 の場合が一変数の二項分布に等しくなるわけです。
N が非常に大きく、各事象の発生回数 ri も十分に大きい値であると仮定すれば、「スターリングの公式(Stirling's Formula)」
より
| PN,p( r ) | ≅ | { ( 2πN )1/2( N / e )N / Πi{1→k}( ( 2πri )1/2( ri / e )ri ) } Πi{1→k}( piri ) |
| = | { ( 2π )1/2NN+1/2e-N / ( 2π )k/2Πi{1→k}( riri+1/2 )e-Σi{1→k}( ri ) } Πi{1→k}( piri ) | |
| = | { NN+1/2e-N / ( 2π )(k-1)/2e-N } Πi{1→k}( piriri-ri-1/2 ) | |
| = | { NN+1/2 / ( 2π )(k-1)/2Πi{1→k}( √pi ) } Πi{1→k}( ( pi / ri )ri+1/2 ) | |
| = | { N-(k-1)/2 / ( 2π )(k-1)/2Πi{1→k}( √pi ) } Πi{1→k}( ( Npi / ri )ri+1/2 ) |
と変形することができます。ここで、
とすれば、
となるので
| -ln( Πi{1→k}( Npi / ri )ri+1/2 ) | = | ln( Πi{1→k}( 1 + ti / √N・pi )ri+1/2 ) |
| = | Σi{1→k}( ( ri + 1 / 2 )ln( 1 + ti / √N・pi ) ) | |
| = | Σi{1→k}( ( Npi + √N・ti + 1 / 2 )ln( 1 + ti / √N・pi ) ) |
N が十分に大きければ ti / √N・pi はゼロに非常に近いと考えられるので、f(ti) = ln( 1 + ti / √N・pi ) の「マクローリン級数」は、三次以降の項を無視して
と近似することができて、f(0) = 0、f'(0) と f(2)(0) は
f'(ti) = { 1 / ( 1 + ti / √N・pi ) }・( 1 / √N・pi ) より f'(0) = 1 / √N・pi
f(2)(ti) = { -1 / ( 1 + ti / √N・pi )2 }・( 1 / √N・pi )2 より f(2)(0) = 1 / Npi2
と求めることができるので、
これを代入すると
| -ln( Πi{1→k}( Npi / ri )ri+1/2 ) | = | Σi{1→k}( ( Npi + √N・ti + 1 / 2 )( ti / √N・pi - ti2 / 2Npi2 ) ) |
| = | Σi{1→k}( √Nti + ti2 / pi + ti / 2√N・pi - ti2 / 2pi - ti3 / 2√Npi2 - ti2 / 4Npi2 ) | |
| ≅ | Σi{1→k}( √Nti + ti2 / 2pi ) |
ここで、
| Σi{1→k}( ti ) | = | Σi{1→k}( ( ri - Npi ) / √N ) |
| = | Σi{1→k}( ri ) / √N - √NΣi{1→k}( pi ) | |
| = | N / √N - √N = 0 |
なので、
となります。また、tk については
とすることで他の変数を使って表すことができるので、これを代入すると、
となって、k - 1 変数の形に表すことができます。さらに、ri を tj で偏微分すると、i = j ならば
で、i ≠ j なら ∂ri / ∂tj = 0 なので、ヤコビアンは N(k-1)/2 となって、PN,p( t1, t2, ... tk-1 ) = PN,p( r1, r2, ... rk-1 )・N(k-1)/2 より
になります。指数関数の指数部にある f = Σi{1→k-1}( ti2 / pi ) + ( t1 + t2 + ... + tk-1 )2 / pk は「二次形式(Quadratic Form)」の形であり、titj の係数は i = j のとき ( 1 / pi + 1 / pk )、i ≠ j のとき 2 / pk なので、
| A = | | | 1 / p1 + 1 / pk, | 1 / pk, | ... | 1 / pk | | |
| | | 1 / pk, | 1 / p2 + 1 / pk, | ... | 1 / pk | | | |
| | | : | : | ... | : | | | |
| | | 1 / pk, | 1 / pk, | ... | 1 / pk-1 + 1 / pk | | |
のような k - 1 行 k - 1 列の対称行列 A によって f = ( t, At ) の形に表すことができます。但し、t = ( t1, t2, ... tk-1 )T を表しています。そこで、A の固有値からなる対角行列を D、固有ベクトルからなる直交行列を Q とすれば、「固有値分解」によって A = QDQT となって、
となります (このあたりの内容については「直交行列(Orthogonal Matrix)」のところで詳しく示してありますので、そちらをご覧ください)。よって、u = QTt と変換したとき、A の固有値を λi とすれば、
になります。t から u に変換した時のヤコビ行列は QT そのものであり、その行列式は 1 となるので、ヤコビアンも 1 になることに注意してください(詳細については「多変量正規分布」をご覧ください)。また、ti の少なくとも一つがゼロでなければ f > 0 になり、したがって ( t, At ) > 0 です。つまり ( u, Du ) = Σi{1→k-1}( λiui2 ) > 0 が任意の u で成り立ち、A は正値対称行列(つまり固有値はすべて正)となります。
さらに vi = √λiui とすれば ∂ui / ∂vi = 1 / √λi で ヤコビアンは 1 / Πi{1→k-1}( √λi ) となりますが、これは結局 1 / |A| を意味しています。|A| = 1 / Πi{1→k}( pi ) と計算できるので(補足1)、結局、上式は
| PN,p( v ) | = | { 1 / ( 2π )(k-1)/2 } exp( -Σi{1→k-1}( vi2 ) / 2 ) |
| = | Πi{1→k-1}( 1 / ( 2π )1/2 } exp( -vi2 / 2 ) |
となって、vi はそれぞれ独立であり、すべて標準正規分布に従うという結果が得られます。二項分布において、N が十分大きければ正規分布に近似できることを「ド・モアブル = ラプラスの定理(De Moivre-Laplace Theorem)」のいうのでした。多項分布においては、何回かの変数変換を行うことで、独立な正規分布の積に近似することができることが、上記の処理によって証明できたことになります。これはちょうど、「多変量正規分布」にて紹介した処理を逆方向にしたものに等しくなります。vi がすべて標準正規分布に従うとき、その平方和が χ2-分布に従うことは、χ2-分布の定義そのものなので、
という結果が得られます。vi は何を表していたかというと、
| Σi{1→k-1}( vi2 ) | = | Σi{1→k-1}( λiui2 ) |
| = | ( u, Du ) = ( QTt, DQTt ) = ( t, QDQTt ) | |
| = | ( t, At ) = f | |
| = | Σi{1→k-1}( ti2 / pi ) + ( t1 + t2 + ... + tk-1 )2 / pk | |
| = | Σi{1→k}( ti2 / pi ) | |
| = | Σi{1→k}( ( ri - Npi )2 / Npi ) |
となるので、以上をまとめると、
一回の試行 E に対し、k 個の事象 ( E1, E2, ... Ek ) の中の一つだけが必ず起こるとしたとき、それぞれの事象 Ei ( i = 1, 2, ... k ) が発生する確率が pi、発生回数が ri ならば
は自由度 k - 1 の χ2-分布に従う
という結果が得られます。
試行 E に対して事象が複数のグループ ( A1, A2, ... Ak ) と ( B1, B2, ... Bl ) あって、それぞれのグループは互いに独立であったとします。Ai が起こる確率を pi、Bj が起こる確率を qj としたとき、Ai と Bj が同時に起こる確率 P( Ai ∩ Bj ) は
となり、Eij = Ai ∩ Bj とすれば Eij は kl 個あって、その確率が piqj となるので、先程得られた式にこれらを代入すると、
一回の試行 E に対し、k 個の事象 ( A1, A2, ... Ak ) と l 個の事象 ( B1, B2, ... Bl ) の中のそれぞれ一つだけが必ず起こるとする。事象 Ai ( i = 1, 2, ... k ) が発生する確率が pi、事象 Bj ( j = 1, 2, ... l ) が発生する確率が qjで、Ai と Bj がすべて独立ならば、Ai ∩ Bj の発生回数を rij したとき
は自由度 kl - 1 の χ2-分布に従う。但し、
とする。
という結果も得られます。
上記の場合、pi や qj は既知である必要があります。これが未知の場合、代わりに pi = ai / N, qj = bj / N と仮定すれば、Ai だけに着目したとき ( Ai∩B1, Ai∩B2, ... Ai∩Bl ) が発生する確率がそれぞれ aibj / N2 となるので
は自由度 l - 1 の χ2-分布に従うことになります。これが k 個存在するわけですが、χk2 は
| χk2 | = | Σj{1→l}( ( rkj - akbj / N )2 / ( akbj / N ) ) |
| = | Σj{1→l}( [ { bj - Σi{1→k-1}( rij ) } - { N - Σi{1→k-1}( ai ) }・bj / N ] / [ { N - Σi{1→k-1}( ai ) }・bj / N ] ) |
と表せることから線形従属であり、従って自由度は一つ少なくなります。よって、この場合は自由度 l - 1 個の χ2-分布に従う χi2 の k - 1 個の和、つまり ( k - 1 )( l - 1 ) を自由度とする χ2-分布に従うことになります。以上をまとめると、
一回の試行 E に対し、k 個の事象 ( A1, A2, ... Ak ) と l 個の事象 ( B1, B2, ... Bl ) の中のそれぞれ一つだけが必ず起こるとする。Ai と Bj がすべて独立で、Ai ∩ Bj の発生回数を rij したとき、
は自由度 ( k - 1 )( l - 1 ) の χ2-分布に従う。但し、
N = Σi{1→k}( Σj{1→l}( rij ) )
ai = Σj{1→l}( rij )
bj = Σi{1→k}( rij )
とする。
上記変数の関係は以下の表のような形になります。
| A1 | A2 | ... | Ak | 計 | |
|---|---|---|---|---|---|
| B1 | r11 | r21 | ... | rk1 | b1 |
| B2 | r12 | r22 | ... | rk2 | b2 |
| : | : | : | : | : | |
| Bl | r1l | r2l | ... | rkl | bl |
| 計 | a1 | a2 | ... | ak | N |
これらの結果を利用した検定法を「(ピアソンの)χ2-検定( (Pearson's) Chi-square Test)」といい、その中には「適合度の検定」と「独立性の検定」の二種類があります。最初に示した式
において、ri は実測値、Npi は理論値(期待値)を表しているともいえるので、それぞれを Oi, Ei と表して
とも書くことができます。pi がある確率密度関数 p(r) に従っていると仮定すれば、その関数を使って Ei を求めることができます。従って、実測値 Oi との差の二乗を求め、それを Ei で割った値について和を計算した上で、それが χ2-分布に従うとしたときの上側確率 ∫{χ2→∞} Tk-1( x ) dx から推定・検定を行うと、確率密度関数に適合しているかどうかを判断することができます。上側確率が小さいということは、χ2 は非常に大きいということを意味し、それは Oi と Ei の差が非常に大きいということを意味します。よって、仮定した確率密度関数には適合しないということになります。
まずは「適合度の検定」について二つほど例を示したいと思います。
サイコロを 100 回投げて、各目の出現回数を調べたところ、以下のような結果になった。このサイコロは正常であるといえるか。
| サイコロの目 | 1 | 2 | 3 | 4 | 5 | 6 | 計 |
|---|---|---|---|---|---|---|---|
| 出現回数 | 24 | 19 | 14 | 14 | 18 | 11 | 100 |
正常であるとは「どの目も等しい確率で出現するか」を意味するとすれば、各目が出る確率は 1 / 6 で、その期待値は 100 x 1/6 = 50 / 3 になるので、
| サイコロの目 i | 1 | 2 | 3 | 4 | 5 | 6 | 計 |
|---|---|---|---|---|---|---|---|
| 実測値 Oi | 24 | 19 | 14 | 14 | 18 | 11 | 100 |
| 期待値 Ei | 50/3 | 50/3 | 50/3 | 50/3 | 50/3 | 50/3 | 100 |
| ( Oi - Ei )2 / Ei | 3.227 | 0.327 | 0.427 | 0.427 | 0.107 | 1.927 | 6.440 |
各目が出る確率が 1 / 6 であるとしたとき、χ2 = Σ( ( Oi - Ei )2 / Ei ) が自由度 6 - 1 = 5 の χ2-分布に従うので、その値が 6.440 になるときの上側確率を求めると、それは 0.266 になります。危険率 5% での棄却領域は χ2 ≥ 11.07 で、危険率 5% ではこの仮説は棄却できないことになります。およそ 1/4 の確率で「正常ではない」と言えなくもないということになりますが、これだけでは判断はできません。
ある試験の点数が次のような度数分布表に従ったとき、これは正規母集団からの標本と考えることができるか。
| 点数(代表値) | 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 | 計 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 度数 | 1 | 2 | 5 | 12 | 29 | 27 | 11 | 7 | 4 | 2 | 100 |
まず、標本平均と標本分散を求めます。データは代表値に対する度数分布の形でしか表されていないので、代表値と度数の積の和から求めるようにして
標本平均 m = { ( 5 x 1 ) + ( 15 x 2 ) + ( 25 x 5 ) + ( 35 x 12 ) + ( 45 x 29 ) + ( 55 x 27 ) + ( 65 x 11 ) + ( 75 x 7 ) + ( 85 x 4 ) + ( 95 x 2 ) } / 100 = 51.40
二乗の平均 E[x2] = { ( 52 x 1 ) + ( 152 x 2 ) + ( 252 x 5 ) + ( 352 x 12 ) + ( 452 x 29 ) + ( 552 x 27 ) + ( 652 x 11 ) + ( 752 x 7 ) + ( 852 x 4 ) + ( 952 x 2 ) } / 100 = 2915
標本分散 s2 = E[x2] - m2 = 2915 - ( 51.40 )2 = 273 = 16.52
となります。よって、この度数分布が正規分布 N( 51.4, 16.52 ) に従うとしたとき、各分布の確率を求めると、
| 点数(代表値) | 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 |
|---|---|---|---|---|---|---|---|---|---|---|
| 級 | ≤10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90≤ |
| 確率 | 0.0061 | 0.0225 | 0.0688 | 0.1475 | 0.2214 | 0.2327 | 0.1713 | 0.0883 | 0.0319 | 0.0097 |
なので、これに標本数 100 を掛けたものが期待値となって、
| 点数(代表値) | 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 | 計 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 実測値 Oi | 1 | 2 | 5 | 12 | 29 | 27 | 11 | 7 | 4 | 2 | 100 |
| 期待値 Ei | 0.61 | 2.25 | 6.88 | 14.75 | 22.14 | 23.27 | 17.13 | 8.83 | 3.19 | 0.97 | 100 |
| ( Oi - Ei )2 / Ei | 0.25 | 0.03 | 0.51 | 0.51 | 2.13 | 0.60 | 2.19 | 0.38 | 0.21 | 1.09 | 7.90 |
χ2 = Σ( ( Oi - Ei )2 / Ei ) が自由度 10 - 1 = 9 の χ2-分布に従うと考えれば、その値が 7.90 になるときの上側確率を求めると、0.544 と求められます。
ところで、χ2-分布に関するこの性質は、各事象の発生回数が十分に大きいという条件がありました。しかし、点数が極端に小さい(大きい)級についてはこの条件を満たしていないため、この結果が信頼できるのか怪しい部分があります。一般的には、期待値 Ei の値が 5 以上であれば適用は可能であるとされており、それに当てはまらないものは一つにまとめて 5 以上になるようなことが行われます。上の例では、代表値が 5, 15 と、85, 95 の期待値が非常に小さいので、これらを一つにまとめれば自由度は 3 つ減って 6 となります。まとめた部分を「その他」として上表を再計算すると
| 点数(代表値) | 25 | 35 | 45 | 55 | 65 | 75 | その他 | 計 |
|---|---|---|---|---|---|---|---|---|
| 実測値 Oi | 5 | 12 | 29 | 27 | 11 | 7 | 9 | 100 |
| 期待値 Ei | 6.88 | 14.75 | 22.14 | 23.27 | 17.13 | 8.83 | 7.02 | 100 |
| ( Oi - Ei )2 / Ei | 0.51 | 0.51 | 2.13 | 0.60 | 2.19 | 0.38 | 0.56 | 6.88 |
になるので、6.88 になるときの上側確率は 0.332 と求められ、確率が少し小さくなります。しかし、これでも危険率 10% では棄却できない事になります(ちなみに、上のデータはコーシー分布から適当な処理をして作った架空のデータです)。期待値が小さくなるほど、実測値のゆらぎ(誤差)によって ( Oi - Ei )2 / Ei は大きく変動します。すると、それに引きずられる形で χ2 値自体も変動が大きくなり、正しく検定ができなくなる可能性が大きくなるので注意が必要です。
次に「独立性の検定」の例を紹介します。
100 日間の天気予報と実際の天気の日数を集計すると以下のような結果になった。この天気予報は信頼できるか。
| 実際 | 晴 | 曇 | 雨 | 計 |
|---|---|---|---|---|
| 予報 | ||||
| 晴 | 22 | 22 | 1 | 45 |
| 曇 | 11 | 19 | 11 | 41 |
| 雨 | 2 | 8 | 4 | 14 |
| 計 | 35 | 49 | 16 | 100 |
ここでは、
が自由度 ( k - 1 )( l - 1 ) の χ2-分布に従うことを利用します。和を求める各項 χij2 = ( rij - Eij )2 / Eij = ( rij - aibj / N )2 / ( aibj / N ) を計算すると
| 実際 | 晴 | 曇 | 雨 | |||
|---|---|---|---|---|---|---|
| 予報 | E | χ2 | E | χ2 | E | χ2 |
| 晴 | 15.75 | 2.48 | 22.05 | 0.00 | 7.20 | 5.34 |
| 曇 | 14.35 | 0.78 | 20.09 | 0.06 | 6.56 | 3.01 |
| 雨 | 4.90 | 1.72 | 6.86 | 0.19 | 2.24 | 1.38 |
となって、χ2 の和は 14.95 になります。これが自由度 ( 3 - 1 ) x ( 3 - 1 ) = 4 の χ2-分布に従うとしたとき、その上側確率は 0.00480 と非常に小さい値になります。χ2-分布に従うのは、予報と実際の天気が互いに独立であることが前提条件でした。したがって、その可能性は非常に低く、予報と実際の天気は関連性があると結論付けることができます。
実際の予報的中率を計算してみると、晴れと予報したときに実際に晴れになった確率は 22 / 45 = 0.49 で、曇りと雨も同様に計算するとそれぞれ 0.46, 0.29 となるので、当たる確率は半分に満たないことになります。よって、半分しか当たらないのに信頼性があるのかというと疑問が残りますが、少なくとも予報がでたらめではないということは統計的に保証されるといえます。
ところで、上の表では Eij も計算してあります。Eij は 5 以上が望ましいというのが一般的なので、例えば曇と雨の予報を一つにまとめてしまい、自由度 2 の χ2-分布に従うとしてしまうようなことも考えられますが、今回はそのまま計算してあります。5 という値には根拠があるのかどうかも怪しくて、中には 1 以上であればよいというような意見もあるそうなので、極端に期待値が小さくなければ問題ないと考えることもできそうです。それでも気になる場合は、やはり標本数を増やす方を検討したほうがよさそうです。なお、標本数によって実測値も期待値も変化することから明らかなように、比率が分かっているだけでは今までの手法は利用できないことに注意してください。比率が同じでも、標本数が多くなれば χ2 の和は変化します。例えば、全値を単純に 10 倍すると χ2 の和も 10 倍になるので、独立である確率はそれだけ小さくなることになります。
χ2-検定のサンプル・プログラムを以下に示します。
/* getChiSquareValue : カイ二乗値の計算 const vector<unsigned int>& obs : 観測値 const vector<double>& exp : 期待値(を求めるための理論確率) 戻り値 : カイ二乗値(obsとexpのサイズが異なる場合はNANを返す) */ double getChiSquareValue( const vector<unsigned int>& obs, const vector<double>& exp ) { unsigned int cnt = obs.size(); // 級数 if ( cnt != exp.size() ) { cout << "Observed value size and expected value size must be same." << endl; return( NAN ); } // データ数を求める unsigned int n = 0; for ( unsigned int i = 0 ; i < cnt ; ++i ) n += obs[i]; // ( O - E )^2 / E を求める double sum = 0; for ( unsigned int i = 0 ; i < cnt ; ++i ) { if ( exp[i] != 0 ) { double np = (double)n * exp[i]; sum += pow( (double)( obs[i] ) - np, 2 ) / np; } } return( sum ); } /* chiSquareTest_DiscDist : カイ二乗検定による適合度検定(離散確率分布) const DiscDist& dist : 確率密度関数 const map<int,unsigned int>& data : 実測値(各確率変数に対する度数) double a : 危険率 double threshold : binSearchで棄却域を求める時のしきい値 戻り値 : True ... 仮説を棄却 , False ... 仮説を保留 または データ数が 1 以下 */ bool chiSquareTest_DiscDist( const DiscDist& dist, const map<int,unsigned int>& data, double a, double threshold ) { cout << "***** Chi-square test of goodness of fit for discrete distribution *****" << endl; unsigned int n = data.size(); // 級数 if ( n <= 1 ) { cout << "Data size must be more than one." << endl; return( false ); } vector<unsigned int> obs( n ); // 実測値 vector<double> exp( n ); // 期待値を求めるための理論確率 map<int,unsigned int>::const_iterator o = data.begin(); for ( unsigned int i = 0 ; o != data.end() ; ++o, ++i ) { obs[i] = o->second; exp[i] = dist[o->first]; } double chiSquare = getChiSquareValue( obs, exp ); // カイ二乗値の計算 cout << "Chi^2 = " << chiSquare << endl; ChiSquareDistribution chiDist( n - 1 ); double rej = binSearch( chiDist, 1.0 - a, threshold ); // 棄却域の定義域 cout << "Critical Region : >" << rej << endl; double p = 1.0 - chiDist.p( 0, chiSquare ); // p値 cout << "p-value : " << p << endl; if ( chiSquare > rej ) { cout << "Null hypothesis is rejected." << endl; return( true ); } else { cout << "Null hypothesis is accepted." << endl; return( false ); } } /* chiSquareTest_ContDist : カイ二乗検定による適合度検定(連続確率分布) const ContDist& dist : 確率密度関数 const RangeHistogram& hist : 実測値(各確率変数を度数としたヒストグラム) double a : 危険率 double threshold : binSearchで棄却域を求める時のしきい値 戻り値 : True ... 仮説を棄却 , False ... 仮説を保留 または データ数が 1 以下 */ bool chiSquareTest_ContDist( const ContDist& dist, const RangeHistogram& hist, double a, double threshold ) { cout << "***** Chi-square test of goodness of fit for continuous distribution *****" << endl; unsigned int n = hist.size(); // 級数 if ( n <= 1 ) { cout << "Data size must be more than one." << endl; return( false ); } vector<unsigned int> obs( n ); // 実測値 vector<double> exp( n ); // 期待値を求めるための理論確率 double min, max; for ( unsigned int i = 0 ; i < n ; ++i ) { obs[i] = hist[i]; hist.range( i, min, max ); exp[i] = dist.p( min, max ); } double chiSquare = getChiSquareValue( obs, exp ); // カイ二乗値の計算 cout << "Chi^2 = " << chiSquare << endl; ChiSquareDistribution chiDist( n - 1 ); // 棄却域の定義域 double rej = binSearch( chiDist, 1.0 - a, threshold ); cout << "Critical Region : >" << rej << endl; double p = 1.0 - chiDist.p( 0, chiSquare ); // p値 cout << "p-value : " << p << endl; if ( chiSquare > rej ) { cout << "Null hypothesis is rejected." << endl; return( true ); } else { cout << "Null hypothesis is accepted." << endl; return( false ); } } /* chiSquareTest_Independence : カイ二乗検定による独立性検定 const vector< vector<unsigned int> >& data : 実測値(各確率変数に対する度数) double a : 危険率 double threshold : binSearchで棄却域を求める時のしきい値 戻り値 : True ... 仮説を棄却 , False ... 仮説を保留 または データ数が 1 以下 */ bool chiSquareTest_Independence( const vector< vector<unsigned int> >& data, double a, double threshold ) { cout << "***** Chi-square test for independence *****" << endl; unsigned int rowSize = data.size(); // 行数 if ( rowSize == 0 ) { cout << "No data found." << endl; return( false ); } unsigned int colSize = data[0].size(); // 列数 if ( colSize == 0 ) { cout << "No data found." << endl; return( false ); } // 各合計値の計算 vector<unsigned int> rowCnt( rowSize, 0 ); // 一行の合計 vector<unsigned int> colCnt( colSize, 0 ); // 一列の合計 unsigned int total = 0; // 度数の総計 for ( unsigned int r = 0 ; r < rowSize ; ++r ) { const vector<unsigned int>& vec = data[r]; if ( vec.size() != colSize ) { cout << "Every data size must be equal to row size." << endl; return( false ); } for ( unsigned int c = 0 ; c < colSize ; ++c ) { rowCnt[r] += vec[c]; colCnt[c] += vec[c]; } total += rowCnt[r]; } // カイ二乗値の計算 double chiSquare = 0; for ( unsigned int r = 0 ; r < rowSize ; ++r ) { for ( unsigned int c = 0 ; c < colSize ; ++c ) { double e = (double)( rowCnt[r] * colCnt[c] ) / (double)total; if ( e != 0 ) chiSquare += pow( data[r][c] - e, 2 ) / e; } } cout << "chi^2 = " << chiSquare << endl; ChiSquareDistribution chiDist( ( rowSize - 1 ) * ( colSize - 1 ) ); double rej = binSearch( chiDist, 1.0 - a, threshold ); // 棄却域の定義域 cout << "Critical Region : >" << rej << endl; double p = 1.0 - chiDist.p( 0, chiSquare ); // p値 cout << "p-value : " << p << endl; if ( chiSquare > rej ) { cout << "Null hypothesis is rejected." << endl; return( true ); } else { cout << "Null hypothesis is accepted." << endl; return( false ); } }
適合度の検定は離散確率と連続確率の両方に対してそれぞれ専用の関数を用意しています(chiSquareTest_DiscDist, chiSquareTest_ContDist)。どちらも処理の流れは同じですが、データの渡し方が若干異なり、離散確率の場合は、確率変数とその度数をペアとする map クラスの形で実測値を渡しているのに対し、連続確率の場合は以前紹介したヒストグラム用のクラスを使って実測値を渡しています。また、期待値を求めるときの確率も、離散確率は各確率変数に対して求めるのに対して、連続確率では各級数の範囲で確率を求めています。
独立性の検定(chiSquareTest_Independence)ではデータを vector クラスを利用しての二次元配列に似た構造で渡しています。どの関数についても、渡すのはデータそのものではなく各確率変数に対する度数なので、度数の計算をあらかじめ行なっておく必要があることに注意してください。
χ2-検定は、標本数がある程度多いことが前提になります。従って、抽出できる数が制限されるとそのまま適用することはできなくなります。このような場合、近似された χ2-分布ではなく多項分布をそのまま利用した方が精度の高い結果が得られます。特に、二つの事象(例えばコインを投げたときの裏・表など)であれば二項分布に従うことになり、それは「百分率の検定」で紹介した「二項検定」や「符号検定」と同じものになります。また、2 x 2 の対応表であれば、
| A1 | A2 | 計 | |
|---|---|---|---|
| B1 | r11 | r21 | b1 |
| B2 | r12 | r22 | b2 |
| 計 | a1 | a2 | N |
となって、A1 の起こる確率を pa、B1 の起こる確率を pb としたとき、同時確率は
と表されます。しかし、A1 と A2 の事象が発生する回数が a1, a2 になるときの確率は二項分布に従って
B1 と B2 の場合も同様に考えて
となるので、a1, a2, b1, b2 を固定した場合の条件付確率 P(r|a1, a2, b1, b2) は、pa や pb を持つ項がすべて打ち消されて
| P(r|a1, a2, b1, b2) | = | P(r) / ( Pa(r)・Pb(r) ) |
| = | a1!・a2!・b1!・b2! / N!・r11!・r21!・r12!・r22! |
になります。これを利用して、次のような例を検定することができます。
次の日が雨になるかを自動的に予測する装置を開発し、その予測と実績を調べたところ、以下のような結果になった。この装置は信頼できるか。
| 実測 | 雨 | 晴 | 計 |
|---|---|---|---|
| 予測 | |||
| 雨 | 4 | 5 | 9 |
| 晴 | 2 | 1 | 3 |
| 計 | 6 | 6 | 12 |
実際に雨が降ったのは 6 回であり、全体の 2 / 3 は的中したことになりますが、雨と予想したのは 9 回で、半分以上は外れたということでもあり、何とも微妙な結果になっています。ここで、それぞれの合計 ( a1, a2, b1, b2 ) は変わらないとして、4 回以上、雨という予想が当たったとしたときの確率を求めると、i 回的中した場合の確率を Pi としたとき
P4 = 6!・6!・9!・3! / 12!・4!・5!・2!・1!
P5 = 6!・6!・9!・3! / 12!・5!・4!・1!・2!
P6 = 6!・6!・9!・3! / 12!・6!・3!・0!・3!
と計算できるので、その和は
になります。従って、雨という予想が 4 回以上当たるという偏った分布となる事象は 90% 以上の確率で発生しうるという結論になり、この装置は「信頼できない」ということになります。ちなみに、P4 と P5 はどちらも 0.41 という比較的高い確率で発生するので、雨の予想が 4 回当たったとしても"まぐれ"である可能性は十分にあるということになります。
この手法は「フィッシャーの直接確率検定(Fisher's Exact Test)」と呼ばれ、先ほど説明したように標本数が少ない場合に利用されます。
フィッシャーの直接確率検定のサンプル・プログラムを以下に示します。
/* fact : 階乗計算 unsigned int n : n! を求める対象の数 n 戻り値 : 階乗 n! */ double fact( unsigned int n ) { if ( n <= 1 ) return( 1 ); double d = n; for ( unsigned int i = 1 ; i < n ; ++i ) d *= (double)( n - i ); return( d ); } /* fishersExactTest : フィッシャーの直接確率検定(Fisher's Exact Test) const vector< vector<unsigned int> >& data : 実測値(各確率変数に対する度数) double a : 危険率 戻り値 : True ... 仮説を棄却 , False ... 仮説を保留 または データ数が 1 以下 */ bool fishersExactTest( const vector< vector<unsigned int> >& data, double a ) { cout << "***** Fisher's Exact Test *****" << endl; if ( data.size() != 2 ) { cout << "Row size must be 2." << endl; return( false ); } if ( data[0].size() != 2 || data[1].size() != 2 ) { cout << "Data size must be 2." << endl; return( false ); } // 各合計値の計算 unsigned int rowCnt[2] = { data[0][0] + data[0][1], data[1][0] + data[1][1] }; // 一行の合計 unsigned int colCnt[2] = { data[0][0] + data[1][0], data[0][1] + data[1][1] }; // 一列の合計 unsigned int total = rowCnt[0] + rowCnt[1]; // 度数の総計 unsigned int clone[2][2]; // データのコピー for ( unsigned int r = 0 ; r < 2 ; ++r ) for ( unsigned int c = 0 ; c < 2 ; ++c ) clone[r][c] = data[r][c]; // clone[0][0] 以上となる確率の和を求める double pSum = 1 / ( fact( clone[0][0] ) * fact( clone[1][0] ) * fact( clone[0][1] ) * fact( clone[1][1] ) ); while ( clone[1][0] > 0 && clone[0][1] > 0 ) { ++( clone[0][0] ); --( clone[1][0] ); --( clone[0][1] ); ++( clone[1][1] ); pSum += 1 / ( fact( clone[0][0] ) * fact( clone[1][0] ) * fact( clone[0][1] ) * fact( clone[1][1] ) ); } double p = fact( rowCnt[0] ) * fact( rowCnt[1] ) * fact( colCnt[0] ) * fact( colCnt[1] ) * pSum / fact( total ); cout << "p-value = " << p << endl; if ( p < a ) { cout << "Null hypothesis is rejected." << endl; return( true ); } else { cout << "Null hypothesis is accepted." << endl; return( false ); } }
二次元配列 data に対して左上隅( 0, 0 ) にある要素より大きな(つまり度数の偏った)場合の確率を求め、危険率と直接比較を行った上で検定結果を出力します。計算には階乗の値が必要なので、関数 fact を合わせて実装しています。階乗計算は単純に全数を掛けあわせた積を求めているだけなので、あまり大きな数を扱うと急激に処理が遅くなります。
今回は、検定について紹介をしました。多変量解析を除けば、以上の内容で統計解析手法の基本的なところはほぼ説明してきたつもりですが、まだ説明不足な部分もあるので随時追加をしていく予定です。次回からの新しいテーマとしては、多変量解析や、もう少し応用的な話を中心に進めることを考えています。
「対称行列の固有値」の章で、補足として「行列式の定義」について紹介しました。行列数が n である行列の各行に対し、列番号が互いに異なる要素を取り出すとき、各行から選択した列番号からなる数列は 1 から n までの数列の順序を入れ替えたものであり、その選び方は n! 通りあります。これを「順列」と言います。順列は、二つの要素を入れ替えることを繰り返して作成することができるので、この入れ替え回数が偶数の場合を偶順列、奇数の場合を奇順列と区別します。それぞれの順列の番号に従って取り出した要素の積を計算し、偶順列の場合は加算、奇順列の場合は減算をします。こうして得られた結果が行列式になり、式に表すと次のようになります。
但し、行列 A に対し、r 行 c 列目の要素を ar,c とし、σ(i1,i2,...in) は順列 i1,i2,...in が偶順列のとき 1、奇順列のとき -1、それ以外は 0 を表すとします。これを順列符号といいます。各行に対して相異なる列番号の要素を選択した場合と、各列に対して相異なる行番号の要素を選択した場合ではどちらも等しい結果が得られ、順列も全く同一になるので、どちらを基準にしても行列式は等しくなります。また、このことから転置行列の行列式も等しいことがわかります。
さらに、今までにも何度か登場しましたが、三角行列と対角行列の行列式は、対角成分の積と等しくなります。これは、対角成分を選択した場合以外の積が必ずゼロになることから明らかです。また、行または列の中にすべての要素がゼロのものがあれば、行列式はゼロになることもすぐに理解できると思います。
A の行(または列)の一つを k 倍して新たな行列 B を作ったとします。行列式の定義式における和の各項には A に対して k 倍された行または列の要素が必ず存在するので、すべて k 倍された形になります。よって、
が成り立ちます。同様の考え方によって、
であることもわかります。また、A の二つの行(または列)を交換して行列 B を作ったとき、|A| の計算式の中で、交換した行または列の要素によって順列符号が反転したものが |B| の計算式と等しくなることになるので、|B| = -|A| が成り立ちます。もし、二つの行(または列)が等しいと、その二つを交換して得られる行列の行列式は元の行列の行列式の符号を変えたものになります。しかし、行列自体は元の行列と変わらないので、|A| = -|A| であることになり、これが成り立つのは行列式がゼロの場合だけです。従って、同じ行または列があれば、行列式はゼロになります。さらに、ある行(または列)が他の行(または列)のスカラー倍だったとき、対象の行(または列)をスカラーで割れば、行列式もそのスカラーで割った値と等しくなります。しかし、この処理で等しい行(または列)を持った行列となるので、結局この場合も行列式はゼロになります。
最後に、A の行(または列)の一つを
の形に分解したとします。対象の行または列を prc と qrc に置き換えた行列をそれぞれ |P|, |Q| としたとき、行列式 |A| の計算において和の各項には ( prc + qrc ) が存在します。これらを prc と qrc にそれぞれ分解した上で、prc を持つ項と qrc を持つ項に分けると、それぞれは |P| と |Q| を表すことになります。従って、
が成り立ちます。これを利用して、行列 |A| のある行に、別の行の要素のスカラー倍を加えた行列 |B| を考えます。この対象の行は、
の形で表されます。つまり、|A| の r' 行目の要素を K倍して r 行目の要素に加えたことになります。このとき、
と表すことができます。ここで、Arr' は r 行目の要素を r' 行目の要素に変換した行列を示しています。ところが、同じ行が存在することから |Arr'| = 0 が成り立つので、
が成り立つことになります。つまり、他の行をスカラー倍して加えたとしても、行列式に変化はないということになります。これは列の場合も同様に示すことができます。
以上の内容を利用して以下の ( k - 1 ) x ( k - 1 ) 行列の行列式を求めてみます。
| A = | | | 1 / p1 + 1 / pk, | 1 / pk, | 1 / pk, | ... | 1 / pk, | 1 / pk, | 1 / pk | | |
| | | 1 / pk, | 1 / p2 + 1 / pk, | 1 / pk, | ... | 1 / pk, | 1 / pk, | 1 / pk | | | |
| | | 1 / pk, | 1 / pk, | 1 / p3 + 1 / pk, | ... | 1 / pk, | 1 / pk, | 1 / pk | | | |
| | | : | : | : | ... | : | : | : | | | |
| | | 1 / pk, | 1 / pk, | 1 / pk, | ... | 1 / pk-3 + 1 / pk, | 1 / pk, | 1 / pk | | | |
| | | 1 / pk, | 1 / pk, | 1 / pk, | ... | 1 / pk, | 1 / pk-2 + 1 / pk, | 1 / pk | | | |
| | | 1 / pk, | 1 / pk, | 1 / pk, | ... | 1 / pk, | 1 / pk, | 1 / pk-1 + 1 / pk | | |
このままだと見づらいので、1 / pi = ai ( i = 1, 2, ... k ) とすれば、
| A = | | | a1 + ak, | ak, | ak, | ... | ak, | ak, | ak | | |
| | | ak, | a2 + ak, | ak, | ... | ak, | ak, | ak | | | |
| | | ak, | ak, | a3 + ak, | ... | ak, | ak, | ak | | | |
| | | : | : | : | ... | : | : | : | | | |
| | | ak, | ak, | ak, | ... | ak-3 + ak, | ak, | ak | | | |
| | | ak, | ak, | ak, | ... | ak, | ak-2 + ak, | ak | | | |
| | | ak, | ak, | ak, | ... | ak, | ak, | ak-1 + ak | | |
と表されます(ここで、ai ≠ 0 とします)。まず、他の行を加減しても行列式が変化しないことを利用して、一行目から二行目を、二行目から三行目を、という形で順番に引いていくと、次のようになります。
| | | a1, | -a2, | 0, | ... | 0, | 0, | 0 | | |
| | | 0, | a2, | -a3, | ... | 0, | 0, | 0 | | |
| | | 0, | 0, | a3, | ... | 0, | 0, | 0 | | |
| | | : | : | : | ... | : | : | : | | |
| | | 0, | 0, | 0, | ... | ak-3, | -ak-2, | 0 | | |
| | | 0, | 0, | 0, | ... | 0, | ak-2, | -ak-1 | | |
| | | ak, | ak, | ak, | ... | ak, | ak, | ak-1 + ak | | |
一列目でゼロ以外である要素は一番上の行(a1)と一番下の行(ak)の二つのみで、それ以外が選択された場合、各列の要素による積はゼロになります。従って、すべての組み合わせの積を考えるとき、一列目に対してはこの二つを選択したときを考慮すればいいわけです。一番最後(右)の列も同様に、一番下(ak-1 + ak)とそのすぐ上の行(-ak-1)を考えるだけとなります。
まず、一列目から一番上の要素を選択した場合、すべての要素がゼロではない組み合わせとして対角成分を選択したときが考えられます。この時の積は
です。次に、一番最後の列である k - 1 列から、下から二番目の行である k - 2 行目の要素(-ak-1)、代わりにその左側の k - 2 列から、一番下の行である k - 1 行目の要素(ak)を選択した場合、順列符号は -1 となって、各要素の積と掛け合わせると
となります。これはちょうど、ak-2 が除かれた形になっています。k - 1 行の要素が他の列で選択されたことで、k - 1 列は k - 2 行目の要素しか選択肢がない(他を選択すれば積がゼロになる)ことに注意してください。次の選択肢として、k - 3 列において最下行の要素(ak)を選択すると、k - 2 列は k - 3 行目の要素(-ak-2)しか選択肢がないので、積は
になります。ak-2 はマイナスの記号が付いていましたが、置換によって順列符号も変わったので打ち消される形になります。この操作を繰り返していくと、
( 但し、i = 1 のときは i - 1 = 0 となるので a0 はないものとみなします ) が要素の積として得られます。この他には選択肢はなく、行列式は上記すべての項の和から求めることができます。対角成分の積は、
a1・a2・...・ak-2・ak-1
a1・a2・...・ak-2・ak
と分解することができて、これらはちょうど Πj{1→k;j≠i}( aj ) において i = k - 1, k (但し、i = k のときは ak+1 はないものと考える) とした場合と等しいので、結局行列式は
になります。aj = 1 / pj だったので、元に戻した上で通分すれば
となって、Σi{1→k}( pi ) = 1 ならば行列式は 1 / Πi{1→k}( pi ) になります。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |