グラフィック・パターンの扱い

(5) サンプル補間

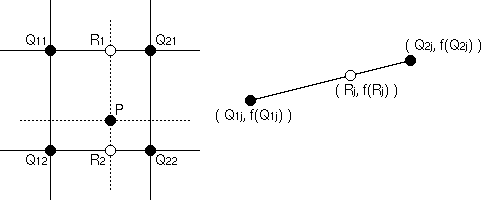
拡大・縮小や回転、自由変形を行う場合、変換先(または変換元)の座標は整数値を取るとは限らないため、今まで紹介してきたプットルーチンでは、実際の座標に対して最も近い位置にあるピクセルを抽出して画面に貼りつける処理を行っていました。この処理方法は「最近傍法(Nearest Neighbour)」と呼ばれています。最近傍法は高速な処理が期待できる反面、場合によってはパターン内の情報がかなり失われてしまうことが容易に想像できます。例えば、あるパターンを縦横半分に縮小した場合、単純計算で 3/4 のピクセルは使われずに捨てられることになります。こうなると、できあがった画像が必ずしも意図した通りの仕上がりになるとは限りません(白黒格子模様のパターンを縦横ちょうど半分に縮小すると、結果は黒か白で塗り潰された四角形になります)。このような現象を、「エイリアシング(Aliasing)」といいます。
エイリアシングの結果、画像の細部が不正確となる他、エッジ部分に「ジャギー(Jaggies)」と呼ばれる階段状のギザギザが出現したり、「モアレ(Moire)」という縞模様が発生することもあります。

ここでは、できるだけ忠実に元の画像を再現するための手法の一つであるサンプル補間処理を、拡大・縮小ルーチンを例にとって考えていきたいと思います。

● 総和(Σ)の記法について

総和は通常、以下のように記述します。 
 n
Σ k (1からnまでの自然数の和)
k=1

しかし、HTML形式のドキュメントで表現しようとすると非常に見づらくなるため、ここでは以下のように表現するようにします。

Σk{1→n}( k )

総積についても同様に、次のように表現します。

Πk{1→n}( k )

● 積分(∫)の記法について

定積分も総和と同様な記述方式を取ります。 
  b                  b
∫ f(x) dx = [ F(x) ]
 a                   a

は、次のように記述します。

∫{a→b} f(x) dx = [ F(x) ]{a→b}

● 行列の記法について

行列は、行と列を()で囲んで表現しますが、このドキュメント内では以下のように表現するようにします。 
| 3, 2, 1 |
| 4, 9, 7 |
| 6, 8, 5 |

各行を'|'で囲ったベクトルで表現する形になります(上の例は 3 x 3の行列を表しています)。
また、行ベクトルは通常どおり(3,2,1)のように表現しますが、列ベクトルは縦長になるため、転置行列の記号Tを使って(3,2,1)Tと表現する場合があります。

あらかじめ、御了承ください。

1) 任意の比率での拡大・縮小処理

パターンを任意の比率で縮小するような場合は、パターン上のピクセルを選んで単純にプロットするのではなく、周りのピクセルの色を合成させてプロットすることで画質を向上させることができます。簡単な例をあげると、あるパターンを縦横半分に縮小するのであれば、パターンの左上から 2 x 2 の範囲のピクセルを取って RGB ごとに平均をとり、再び色コードに合成してプロットすると、ピクセルの損失をある程度防ぐことができます。これにより、先程例として挙げた格子模様の縮小では、結果としてグレーで塗り潰された四角形が描かれることになります。
逆にパターン拡大する場合は多少コーディングに工夫が必要ですが、拡大時に生ずる隙間をパターン隣りどうしのピクセルを使って色合成しながら埋めていくことで対応できます。

上記処理を行なうためのサンプル・プログラムを以下に示します。

/*
  GPattern::redPut : 任意の比率による縮小処理

  GPSet& pset : 描画用関数オブジェクト
  Coord<int> c : 描画開始位置
  const Coord<int>& rate : 比率
  iterator_base& x, y : 描画方向
*/
void GPattern::redPut( GPSet& pset, Coord<int> c, const Coord<int>& rate, iterator_base& x, iterator_base& y )
{
  if ( rate.x <= 0 || rate.y <= 0 ) return;
  unsigned int red, green, blue; // 合成した色コード

  for ( y.set( 0, size.y / rate.y + ( ( size.y % rate.y != 0 ) ? 1 : 0 ) ) ; y.valid() ; y.next() ) {
    if ( c.y >= pset.size().y ) break;
    if ( c.y < 0 ) {
      ++( c.y );
      continue;
    }
    Coord<int> gc( c );
    for ( x.set( 0, size.x / rate.x + ( ( size.x % rate.x != 0 ) ? 1 : 0 ) ) ; x.valid() ; x.next() ) {
      if ( gc.x >= pset.size().x ) break;
      if ( gc.x < 0 ) {
        ++( gc.x );
        continue;
      }

      /* 合成色を計算 */
      red = green = blue = 0;
      unsigned int cnt = 0;
      for ( int py = y.value() * rate.y ; py < ( y.value() + 1 ) * rate.y ; ++py ) {
        if ( py >= size.y ) break;
        for ( int px = x.value() * rate.x ; px < ( x.value() + 1 ) * rate.x ; ++px ) {
          if ( px >= size.x ) break;
          vector<RGB>::const_iterator it = pattern.begin() + size.x * py + px;
          red += it->r();
          green += it->g();
          blue += it->b();
          ++cnt;
        }
      }

      if ( cnt > 0 ) {
        pset.col = RGB( red / cnt, green / cnt, blue / cnt );
        pset( gc );
      }
      ++( gc.x );
    }
    ++( c.y );
  }
}

/*
  GPattern::magPut : 任意の比率による拡大処理

  GPSet& pset : 描画用関数オブジェクト
  Coord<int> c : 描画開始位置
  const Coord<int>& rate : 比率
  iterator_base& x, y : 描画方向
*/
void GPattern::magPut( GPSet& pset, Coord<int> c, const Coord<int>& rate, iterator_base& x, iterator_base& y )
{
  if ( rate.x <= 0 || rate.y <= 0 ) return;

  RGB vertex[2][2]; // 四点の色成分
  RGB rCol, lCol;

  for ( y.set( 0, size.y - 1 ) ; y.valid() ; y.next() ) {
    if ( c.y >= pset.size().y ) break;
    Coord<int> gc( c );
    for ( x.set( 0, size.x - 1 ) ; x.valid() ; x.next() ) {
      if ( gc.x >= pset.size().x ) break;

      /* 4点の色成分を取得する */
      for ( int py = 0 ; py < 2 ; ++py ) {
        if ( y.value() + py >= size.y ) break;
        for ( int px = 0 ; px < 2 ; ++px ) {
          if ( x.value() + px >= size.x ) break;
          vector<RGB>::const_iterator it = pattern.begin() + ( y.value() + py ) * size.x + x.value() + px;
          vertex[px][py] = RGB( it->r(), it->g(), it->b() );
        }
      }

      /* 右端・下端のパターンがない場合は左端・上端と同じ色にする */
      if ( x.value() + 1 >= size.x ) {
        vertex[1][0] = vertex[0][0];
        vertex[1][1] = vertex[0][1];
      }
      if ( y.value() + 1 >= size.y ) {
        vertex[0][1] = vertex[0][0];
        vertex[1][1] = vertex[1][0];
      }

      for ( int gy = 0 ; gy < rate.y ; ++gy ) {
        if ( c.y + gy < 0 ) continue;
        /* 左右の色成分を決定 */
        lCol = RGB( ( (double)( vertex[0][0].r() * ( rate.y - gy ) + vertex[0][1].r() * gy ) ) / (double)rate.y,
                    ( (double)( vertex[0][0].g() * ( rate.y - gy ) + vertex[0][1].g() * gy ) ) / (double)rate.y,
                    ( (double)( vertex[0][0].b() * ( rate.y - gy ) + vertex[0][1].b() * gy ) ) / (double)rate.y );
        rCol = RGB( ( (double)( vertex[1][0].r() * ( rate.y - gy ) + vertex[1][1].r() * gy ) ) / (double)rate.y,
                    ( (double)( vertex[1][0].g() * ( rate.y - gy ) + vertex[1][1].g() * gy ) ) / (double)rate.y,
                    ( (double)( vertex[1][0].b() * ( rate.y - gy ) + vertex[1][1].b() * gy ) ) / (double)rate.y );
        for ( int gx = 0 ; gx < rate.x ; ++gx ) {
          if ( gc.x + gx < 0 ) continue;
          /* 各ピクセルの色成分の計算 */
          pset.col = RGB( ( (double)( lCol.r() * ( rate.x - gx ) + rCol.r() * gx ) ) / (double)rate.x,
                          ( (double)( lCol.g() * ( rate.x - gx ) + rCol.g() * gx ) ) / (double)rate.x,
                          ( (double)( lCol.b() * ( rate.x - gx ) + rCol.b() * gx ) ) / (double)rate.x );
          pset( Coord<int>( gc.x + gx, gc.y + gy ) );
        }
      }
      gc.x += rate.x;
    }
    c.y += rate.y;
  }
}

縮小の方法はいたって簡単で、縮小率分のピクセル数だけ色成分(RGB)毎の和を取って、それを再び色コードに戻してからプロットするだけです。例えば、縦 1/3、横 1/5 に縮小する場合は、5 x 3 のピクセルの色を合成することになります。端数分に対しても正しく処理ができるよう、加算処理したピクセルの数は毎回カウントしてその数で除算するようにしています。
拡大の場合は少し複雑で、隣り合った四点のピクセルを拡大率の大きさのグラデーション・ボックスに引き延ばしてプロットしていくことで処理を行っています。処理の流れは次のようになります。

  1. パターン上の描画位置(LU)と、その右側(RU)・下側(LD)・右下(RD)にあるピクセルの、計四つの色コードを抽出する。
  2. LU と LD、RU と RD を両端とした Y 軸方向のグラデーション・ラインを想定し、X軸方向のライン両端の色成分を計算する。
  3. 計算した両端の色成分を元に、X軸方向のグラデーション・ラインを想定し、各ピクセルを描画する。
  4. 上記 2〜3 の操作を繰り返し、LU, RU, LD, RD を各頂点とするグラデーション・ボックスを描く。

処理の例を以下に示します。

5 x 5に拡大する場合
初期状態
000?????????255
???????????????
???????????????
???????????????
255?????????000
一番上のラインをグラデーション・ラインで描画
000064128192255
???????????????
???????????????
???????????????
255?????????000
次ラインの左右両端の色コードを計算
000064128192255
064?????????192
???????????????
???????????????
255?????????000
グラデーション・ラインの描画
000064128192255
064096128160192
???????????????
???????????????
255?????????000
以下続けていくとこうなる
000064128192255
064096128160192
128128128128128
192160128096064
255192128064000

2) 線形補間法(Bilinear Interpolation)

任意の大きさで拡大・縮小する場合、上記とは別の方法をとる必要があります。
最近傍法では、変換元となる座標値を単純に整数値化して対象のピクセルを決める方法を取っていました。例えば、実際の座標値が (0.5, 0.5)という値を取っていたとしても、Bresenhamのアルゴリズムによってそれは (0, 0)、(1, 0)、(0, 1)、(1, 1) などの整数値で表現され、周囲のピクセルの情報は切り捨てられます。ここで、周囲のピクセルの情報を加味した上で処理することができれば、情報の欠落をある程度防ぐことが期待できます。その方法の一つとして「線形補間法(Bilinear Interpolation)」があります。

線形補間法の考え方は非常に単純です。ピクセルが、座標平面上で整数値を取る点にあるとします。変形後の座標 P( x, y ) が整数値を取らなかったとき、その座標はピクセルの取る点からなる、ある格子の内部に位置します。その格子の四隅の座標を
  • 左上側 Q11 ( x1, y1 )
  • 左下側 Q12 ( x1, y2 )
  • 右上側 Q21 ( x2, y1 )
  • 右下側 Q22 ( x2, y2 )

とし、P を通る Y軸方向の直線と、線分 Q11Q21、Q12Q22との交点をそれぞれ R1、R2 とします。

 線形補間法

Qij ( i,j = 1,2 ) の取る値を f(Qij)としたとき、Rj が取る値 f(Rj) は、線分( Q1j, f(Q1j) ) - ( Q2j, f(Q2j) )上に点 ( Rj, f(Rj) ) があるとみなして、その線分比から次のような式で求めることができます。

| Rj - Q1j | : | Q2j - Rj | = | f(Rj) - f(Q1j) | : | f(Q2j) - f(Rj) |

各点の Y座標は全て等しいので、線分の長さは X成分だけで求められます。x1 ≦ x ≦ x2 より、上式は次のように変形することができます。

x - x1 : x2 - x = f(Rj) - f(Q1j) : f(Q2j) - f(Rj)

f(Rj) は f(Q1j) と f(Q2j) の間にあるため、f(Rj) - f(Q1j) と f(Q2j) - f(Rj) はどちらも正またはどちらも負となり、正負が逆転することはありません。したがって、右辺の絶対値記号も外すことができます。この式を f(Rj) について解くと、

f(Rj) = { ( x2 - x )f(Q1j) + ( x - x1 )f(Q2j) } / ( x2 - x1 )

になります。Rj を用いて同様の計算方法によって、f(P) が次の計算式で求められます。

f(P) = { ( y2 - y )f(R1) + ( y - y1 )f(R2) } / ( y2 - y1 )

二つ合わせると、次のような式になります。

f(P) = { ( x2 - x )( y2 - y )f(Q11) + ( x - x1 )( y2 - y )f(Q21) + ( x2 - x )( y - y1 )f(Q12) + ( x - x1 )( y - y1 )f(Q22) } / ( x2 - x1 )( y2 - y1 )

隣接する四点のピクセルを通る平面上に点が存在すると仮定して、その値を求めることから「線形補間」という名が付けられています。任意の比率で拡大する処理において、四点のピクセルを頂点とするグラデーション・ボックスを描画する処理を紹介しましたが、原理としては全く同じ内容です。

線形補間法を利用して、指定した点の色を求めるためのサンプル・プログラムを以下に示します。

/**************************************************************
 GInterpolation : 補間法
**************************************************************/
class GInterpolation
{
public:
  // operator() : 与えられた座標値を元に色コードを計算して返す
  virtual RGB operator()( const GPattern& pattern, const Coord<double>& p ) const = 0;

  // 仮想デストラクタ
  virtual ~GInterpolation() {}
};

/* 最近傍法(Nearest Neighbour) */
class NNAlgorithm : public GInterpolation
{
public:
  RGB operator()( const GPattern& pattern, const Coord<double>& p ) const
  { return( pattern.point( Coord<int>( roundHalfUp( p.x ), roundHalfUp( p.y ) ) ) ); }
};

/* 線形補間法(Bilinear Interpolation) */
class Bilinear : public GInterpolation
{
public:
  RGB operator()( const GPattern& pattern, const Coord<double>& p ) const;
};

/**************************************************************
 Bilinear : 線形補間法(Bilinear Interpolation)
**************************************************************/

/*
  Bilinear::operator() : 線形補間法(Bilinear Interpolation)による色の補間

  const GPattern& pattern : パターン・オブジェクト
  const Coord<double>& p : 色を求める点の座標
*/
RGB Bilinear::operator()( const GPattern& pattern, const Coord<double>& p ) const
{
  Coord<int> c( p.x, p.y ); // pを含む格子の左上の座標

  // 各格子の色コードを取得
  RGB q11 = pattern.point( c );
  RGB q21 = pattern.point( Coord<int>( c.x + 1, c.y ) );
  RGB q12 = pattern.point( Coord<int>( c.x, c.y + 1 ) );
  RGB q22 = pattern.point( Coord<int>( c.x + 1, c.y + 1 ) );

  // 線形補間処理
  double red = ( ( (double)( c.x + 1 ) - p.x ) * ( (double)( c.y + 1 ) - p.y ) * (double)( q11.r() ) +
                 ( p.x - (double)( c.x ) ) * ( (double)( c.y + 1 ) - p.y ) * (double)( q21.r() ) +
                 ( (double)( c.x + 1 ) - p.x ) * ( p.y - (double)( c.y ) ) * (double)( q12.r() ) +
                 ( p.x - (double)( c.x ) ) * ( p.y - (double)( c.y ) ) * (double)( q22.r() ) );
  double green = ( ( (double)( c.x + 1 ) - p.x ) * ( (double)( c.y + 1 ) - p.y ) * (double)( q11.g() ) +
                   ( p.x - (double)( c.x ) ) * ( (double)( c.y + 1 ) - p.y ) * (double)( q21.g() ) +
                   ( (double)( c.x + 1 ) - p.x ) * ( p.y - (double)( c.y ) ) * (double)( q12.g() ) +
                   ( p.x - (double)( c.x ) ) * ( p.y - (double)( c.y ) ) * (double)( q22.g() ) );
  double blue = ( ( (double)( c.x + 1 ) - p.x ) * ( (double)( c.y + 1 ) - p.y ) * (double)( q11.b() ) +
                  ( p.x - (double)( c.x ) ) * ( (double)( c.y + 1 ) - p.y ) * (double)( q21.b() ) +
                  ( (double)( c.x + 1 ) - p.x ) * ( p.y - (double)( c.y ) ) * (double)( q12.b() ) +
                  ( p.x - (double)( c.x ) ) * ( p.y - (double)( c.y ) ) * (double)( q22.b() ) );

  // 範囲外であった場合に補正
  if ( red < 0 ) red = 0;
  if ( red > UCHAR_MAX ) red = UCHAR_MAX;
  if ( green < 0 ) green = 0;
  if ( green > UCHAR_MAX ) green = UCHAR_MAX;
  if ( blue < 0 ) blue = 0;
  if ( blue > UCHAR_MAX ) blue = UCHAR_MAX;

  return( RGB( (unsigned char)red, (unsigned char)green, (unsigned char)blue ) );
}

/*
  GPattern::point : パターンの色コードを取得する

  指定した座標がパターン外部の場合、もっとも近いピクセルの色コードを取得する

  Coord<int> c : 取得する位置
*/
RGB GPattern::point( Coord<int> c ) const
{
  if ( c.x < 0 ) c.x = 0;
  if ( c.x >= size.x ) c.x = size.x - 1;
  if ( c.y < 0 ) c.y = 0;
  if ( c.y >= size.y ) c.y = size.y - 1;

  return( pattern[c.y * size.x + c.x] );
}

/*
  GPattern::pset : パターンの描画

  指定した座標がパターン外部の場合は処理しない

  const Coord<int>& c : 描画する位置
  const RGB& col : 描画する色コード
*/
void GPattern::pset( const Coord<int>& c, const RGB& col )
{
  if ( c.x >= 0 && c.x < size.x && c.y >= 0 && c.y < size.y )
    pattern[c.y * size.x + c.x] = col;
}

/*
  GPattern::resizePut : パターンの拡大・縮小描画(Bresenhamを使わないバージョン)

  GPSet& pset : 描画用関数オブジェクト
  Coord<int>& s, e : パターンの描画開始・終了位置
  iterator_base& x, y : 描画方向
  const GInterpolation& ipF : 補間処理用関数オブジェクト
*/
void GPattern::resizePut( GPSet& pset, Coord<int>& s, Coord<int>& e, iterator_base& x, iterator_base& y, const GInterpolation& ipF )
{
  if ( size.x == 0 || size.y == 0 ) return;

  // 描画オブジェクトの大きさを取得
  Coord<int> dSize = pset.size();

  // 左上・右下の大小関係が逆の場合は入れ替える
  if ( s.x > e.x ) swap( s.x, e.x );
  if ( s.y > e.y ) swap( s.y, e.y );

  // 描画範囲内か
  if ( s.x >= dSize.x || s.y >= dSize.y ) return;
  if ( e.x < 0 || e.y < 0 ) return;

  // パターンの読み込み位置
  Coord<double> p( 0, 0 );
  // 画像 1ピクセルあたりのパターンのピクセルサイズ
  Coord<double> d;
  d.x = (double)( size.x ) / (double)( e.x - s.x + 1 );
  d.y = (double)( size.y ) / (double)( e.y - s.y + 1 );

  /*
    クリッピング処理
    s.x=e.x, s.y=e.y のときは、これらの処理は必ず行なわれないので、ゼロ除算チェックは不要
  */
  if ( s.x < 0 ) {
    p.x -= s.x * d.x;
    s.x = 0;
  }
  if ( s.y < 0 ) {
    p.y -= s.y * d.y;
    s.y = 0;
  }
  if ( e.x >= dSize.x ) e.x = dSize.x - 1;
  if ( e.y >= dSize.y ) e.y = dSize.y - 1;

  // 描画処理
  for ( y.set( s.y, e.y ) ; y.valid() ; y.next() ) {
    double pxBuff = p.x;
    for ( x.set( s.x, e.x ) ; x.valid() ; x.next() ) {
      pset.col = ipF( *this, p );
      pset( Coord<int>( x.value(), y.value() ) );
      p.x += d.x;
    }
    p.x = pxBuff;
    p.y += d.y;
  }
}

メインルーチンの resizePutは、以前作成した、Bresenhamを利用しない拡大・縮小処理用のルーチンとほとんど変わりません。しかし、補間処理を行う関数を切り替えられるよう、引数として補間処理用関数オブジェクト GInterpolation へのリファレンスを渡しています。また、パターン上の読み取り位置を示す pは double型にしてあります。
補間処理用関数オブジェクトの GInterpolation は、純粋仮想関数として operator() を持っています。よって、このオブジェクトから派生したクラスに具体的な補間方法を記述して利用する形になります。上記サンプルでは、最近傍法の NNAlgorithm と線形補間法の Bilinearが用意されています。最近傍法は前回と同じ処理内容で、線形補間法が今回紹介した手法になります。線形補間法では最初に、対象の点を内部に持つ格子の各頂点の色コードを q11, q21, q12, q22に取り込んでいます。色コードの取り込みには、GPatternクラスに新たに用意したメンバ関数 point を利用しており、格子がパターンからはみ出していた場合(格子上のいくつかの点がパターン外である場合)は、最も近いパターン内のピクセルの色コードを取得するようになっています。色コードが取得できたら、あとは先に説明した計算式を使って補間処理を行なうだけです。

3) 三次スプライン補間法(Bicubic Spline Interpolation)

線形補間法では、格子上の四点を使って線形近似を行いましたが、他に多項式による近似を行う方法もあります。
四点(0,0), (1,0), (0,1), (1,1)からなる格子内の点に対する値が次の多項式の値と等しくなると仮定します。

f(x,y)=a00 + a10x + a20x2 + a30x3
+ a01y + a11xy + a21x2y + a31x3y
+ a02y2 + a12xy2 + a22x2y2 + a32x3y2
+ a03y3 + a13xy3 + a23x2y3 + a33x3y3
=Σi{0→3}Σj{0→3}( aijxiyj )

ここで、aij ( i,j = 0,1,2,3 ) は未知の係数です。まず、上式に格子上の頂点の座標を代入すると、次の式が得られます。

f(0,0)=a00
f(1,0)=a00 + a10 + a20 + a30
f(0,1)=a00 + a01 + a02 + a03
f(1,1)=Σi{0→3}Σj{0→3}( aij )

次に、f(x,y) を x で偏微分します。

fx(x,y)=a10 + 2a20x + 3a30x2
+ a11y + 2a21xy + 3a31x2y
+ a12y2 + 2a22xy2 + 3a32x2y2
+ a13y3 + 2a23xy3 + 3a33x2y3
=Σi{1→3}Σj{0→3}( iaijxi-1yj )

求めた導関数に対しても、格子上の頂点の座標における微分係数と等しくなると仮定したとき、次の式が得られます。

fx(0,0)=a10
fx(1,0)=a10 + 2a20 + 3a30
fx(0,1)=a10 + a11 + a12 + a13
fx(1,1)=Σi{1→3}Σj{0→3}( iaij )

y で偏微分した結果から同様に、

fy(0,0)=a01
fy(1,0)=a01 + a11 + a21 + a31
fy(0,1)=a01 + 2a02 + 3a03
fy(1,1)=Σi{0→3}Σj{1→3}( jaij )

最後に混合微分 fxy(x,y) (つまり、xで偏微分した後 yで偏微分します。yで偏微分してから xで偏微分しても結果は同じです) を求めると、

fxy(x,y)=a11 + 2a21x + 3a31x2
+ 2a12y + 4a22xy + 6a32x2y
+ 3a13y2 + 6a23xy2 + 9a33x2y2
=Σi{1→3}Σj{1→3}( ijaijxi-1yj-1 )

よって、これも格子上の頂点の座標における微分係数と等しくなると仮定して、

fxy(0,0)=a11
fxy(1,0)=a11 + 2a21 + 3a31
fxy(0,1)=a11 + 2a12 + 3a13
fxy(1,1)=Σi{1→3}Σj{1→3}( ijaij )

これで、計 16個の式が得られたので、未知数 aij も 16 個あることから連立方程式によって係数を求めることができます。連立方程式の係数行列を Aとし、未知数からなるベクトルを

α = ( a00, a10, a20, a30, a01, a11, a21, a31, a02, a12, a22, a32, a03, a13, a23, a33 )T

右辺の値からなるベクトルを

x = ( f(0,0), f(1,0), f(0,1), f(1,1), fx(0,0), fx(1,0), fx(0,1), fx(1,1), fy(0,0), fy(1,0), fy(0,1), fy(1,1), fxy(0,0), fxy(1,0), fxy(0,1), fxy(1,1) )T

とすれば、連立方程式は Aα = x で表され、その解は α = A-1x になります。この逆行列 A-1は次のようなものになります。

|1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0|
|0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0|
|-3,3,0,0,-2,-1,0,0,0,0,0,0,0,0,0,0|
|2,-2,0,0,1,1,0,0,0,0,0,0,0,0,0,0|
|0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0|
|0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0|
|0,0,0,0,0,0,0,0,3,-3,0,0,-2,-1,0,0|
|0,0,0,0,0,0,0,0,-2,2,0,0,1,1,0,0|
|-3,0,3,0,0,0,0,0,0,-2,-1,0,0,0,0,0|
|0,0,0,0,-3,0,3,0,0,0,0,0,-2,0,-1,0|
|9,-9,-9,9,6,3,-6,-3,-6,6,3,-3,4,2,2,1|
|-6,6,6,-6,-3,-3,3,3,4,-4,-2,2,-2,-2,-1,-1|
|2,0,-2,0,0,0,0,0,0,1,1,0,0,0,0,0|
|0,0,0,0,2,0,-2,0,0,0,0,0,1,0,1,0|
|-6,6,6,-6,-4,-2,4,2,3,-3,-3,3,-2,-1,-2,-1|
|4,-4,-4,4,2,2,-2,-2,-2,2,2,-2,1,1,1,1|

ここで問題になるのが、各格子上の微分係数をどうやって決めるかということですが、通常は各格子上の値を使って差分を計算し、それを微分係数として利用します。例えば、x方向に ( x0, c0 ), ( x1, c1 ), ( x2, c2 ) ( 但し、xi を x座標値、ci を色コードとする ) とピクセルが並んでいた場合、( x1, c1 )上の x方向の微分係数 fx( x1 )を

fx( x1 ) = ( c2 - c1 ) / 2( x2 - x1 ) + ( c1 - c0 ) / 2( x1 - x0 )

と計算する方法があります。各ピクセルは等間隔に並んでいるので、x i+1 - x i = K(定数) となり、この式はもっとシンプルに

fx( x1 ) = ( c2 - c0 ) / 2K

と表すことができます。この方法で微分係数を求める場合、さらに外側のピクセルが必要になるため、計 16ピクセルを使って処理をすることになります。

三次スプライン補間法を利用して、指定した点の色を求めるためのサンプル・プログラムを以下に示します。

/* 三次スプライン補間法(Bicubic Spline Interpolation) */
class BicubicSpline : public GInterpolation
{
  RGB operator()( const GPattern& pattern, const Coord<double>& p ) const;
};

/**************************************************************
 BicubicSpline : 三次スプライン補間法(Bicubic Spline Interpolation)
**************************************************************/
/*
  BicubicSpline::operator() : 三次スプライン補間法(Bicubic Spline Interpolation)による色の補間

  const GPattern& pattern : パターン・オブジェクト
  const Coord<double>& p : 色を求める点の座標
*/
RGB BicubicSpline::operator()( const GPattern& pattern, const Coord<double>& p ) const
{
  Coord<int> c( p.x, p.y ); // pを含む格子の左上の座標(16点の中の左から二番目、上から二番目)
  Coord<double> un( p.x - (double)( c.x ), p.y - (double)( c.y ) ); // cを原点としたpの座標
  Coord<double> sq( un.x * un.x, un.y * un.y ); // unの二乗
  Coord<double> cb( sq.x * un.x, sq.y * un.y ); // unの三乗
  RGB col[4][4];   // 16点の格子の色コード
  double b[16][3]; // 連立方程式の右辺
  double a[16][3]; // 連立方程式の未知数

  // 係数行列の逆行列
  double coefMat[16][16] = {
    {  1,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0 },
    {  0,  0,  0,  0,  1,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0 },
    { -3,  3,  0,  0, -2, -1,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0 },
    {  2, -2,  0,  0,  1,  1,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0 },
    {  0,  0,  0,  0,  0,  0,  0,  0,  0,  1,  0,  0,  0,  0,  0,  0 },
    {  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  1,  0,  0,  0 },
    {  0,  0,  0,  0,  0,  0,  0,  0,  3, -3,  0,  0, -2, -1,  0,  0 },
    {  0,  0,  0,  0,  0,  0,  0,  0, -2,  2,  0,  0,  1,  1,  0,  0 },
    { -3,  0,  3,  0,  0,  0,  0,  0,  0, -2, -1,  0,  0,  0,  0,  0 },
    {  0,  0,  0,  0, -3,  0,  3,  0,  0,  0,  0,  0, -2,  0, -1,  0 },
    {  9, -9, -9,  9,  6,  3, -6, -3, -6,  6,  3, -3,  4,  2,  2,  1 },
    { -6,  6,  6, -6, -3, -3,  3,  3,  4, -4, -2,  2, -2, -2, -1, -1 },
    {  2,  0, -2,  0,  0,  0,  0,  0,  0,  1,  1,  0,  0,  0,  0,  0 },
    {  0,  0,  0,  0,  2,  0, -2,  0,  0,  0,  0,  0,  1,  0,  1,  0 },
    { -6,  6,  6, -6, -4, -2,  4,  2,  3, -3, -3,  3, -2, -1, -2, -1 },
    {  4, -4, -4,  4,  2,  2, -2, -2, -2,  2,  2, -2,  1,  1,  1,  1 },
  };

  // 色コードの取得
  for ( int y = -1 ; y < 3 ; ++y )
    for ( int x = -1 ; x < 3 ; ++x )
      col[x+1][y+1] = pattern.point( Coord<int>( c.x + x, c.y + y ) );

  // 連立方程式の右辺を計算
  for ( int y = 0 ; y < 2 ; ++y ) {
    for ( int x = 0 ; x < 2 ; ++x ) {
      // 各点の色コード
      b[y*2+x][0] = (double)( col[x+1][y+1].r() );
      b[y*2+x][1] = (double)( col[x+1][y+1].g() );
      b[y*2+x][2] = (double)( col[x+1][y+1].b() );
      // 各点におけるx方向の微分係数
      b[y*2+x+4][0] = ( (double)( col[x+2][y+1].r() ) - (double)( col[x][y+1].r() ) ) / 2;
      b[y*2+x+4][1] = ( (double)( col[x+2][y+1].g() ) - (double)( col[x][y+1].g() ) ) / 2;
      b[y*2+x+4][2] = ( (double)( col[x+2][y+1].b() ) - (double)( col[x][y+1].b() ) ) / 2;
      // 各点におけるy方向の微分係数
      b[y*2+x+8][0] = ( (double)( col[x+1][y+2].r() ) - (double)( col[x+1][y].r() ) ) / 2;
      b[y*2+x+8][1] = ( (double)( col[x+1][y+2].g() ) - (double)( col[x+1][y].g() ) ) / 2;
      b[y*2+x+8][2] = ( (double)( col[x+1][y+2].b() ) - (double)( col[x+1][y].b() ) ) / 2;
      // 各点における混合微分係数
      b[y*2+x+12][0] = ( (double)( col[x+2][y+2].r() ) - (double)( col[x][y].r() ) ) / sqrt( 8 );
      b[y*2+x+12][1] = ( (double)( col[x+2][y+2].g() ) - (double)( col[x][y].g() ) ) / sqrt( 8 );
      b[y*2+x+12][2] = ( (double)( col[x+2][y+2].b() ) - (double)( col[x][y].b() ) ) / sqrt( 8 );
    }
  }

  // 連立方程式を解く(係数行列の逆行列との積)
  for ( int i = 0 ; i < 16 ; ++i ) {
    a[i][0] = a[i][1] = a[i][2] = 0;
    for ( int j = 0 ; j < 16 ; ++j )
      for ( int k = 0 ; k < 3 ; ++k )
        a[i][k] += coefMat[i][j] * b[j][k];
  }

  // 求めた解を三次式の係数として pでの値を計算
  double red = a[0][0] + a[1][0] * un.x + a[2][0] * sq.x + a[3][0] * cb.x +
    a[4][0] * un.y + a[5][0] * un.x * un.y + a[6][0] * sq.x * un.y + a[7][0] * cb.x * un.y +
    a[8][0] * sq.y + a[9][0] * un.x * sq.y + a[10][0] * sq.x * sq.y + a[11][0] * cb.x * sq.y +
    a[12][0] * cb.y + a[13][0] * un.x * cb.y + a[14][0] * sq.x * cb.y + a[15][0] * cb.x * cb.y;
  double green = a[0][1] + a[1][1] * un.x + a[2][1] * sq.x + a[3][1] * cb.x +
    a[4][1] * un.y + a[5][1] * un.x * un.y + a[6][1] * sq.x * un.y + a[7][1] * cb.x * un.y +
    a[8][1] * sq.y + a[9][1] * un.x * sq.y + a[10][1] * sq.x * sq.y + a[11][1] * cb.x * sq.y +
    a[12][1] * cb.y + a[13][1] * un.x * cb.y + a[14][1] * sq.x * cb.y + a[15][1] * cb.x * cb.y;
  double blue = a[0][2] + a[1][2] * un.x + a[2][2] * sq.x + a[3][2] * cb.x +
    a[4][2] * un.y + a[5][2] * un.x * un.y + a[6][2] * sq.x * un.y + a[7][2] * cb.x * un.y +
    a[8][2] * sq.y + a[9][2] * un.x * sq.y + a[10][2] * sq.x * sq.y + a[11][2] * cb.x * sq.y +
    a[12][2] * cb.y + a[13][2] * un.x * cb.y + a[14][2] * sq.x * cb.y + a[15][2] * cb.x * cb.y;

  // 範囲外であった場合に補正
  if ( red < 0 ) red = 0;
  if ( red > UCHAR_MAX ) red = UCHAR_MAX;
  if ( green < 0 ) green = 0;
  if ( green > UCHAR_MAX ) green = UCHAR_MAX;
  if ( blue < 0 ) blue = 0;
  if ( blue > UCHAR_MAX ) blue = UCHAR_MAX;

  return( RGB( (unsigned char)red, (unsigned char)green, (unsigned char)blue ) );
}

線形補間法は、ピクセル間の値を直線で近似しているのに対して、三次スプライン補間法では三次式による近似を行なっており、しかも求めた曲線は各点で連続になるので、より自然な補間が可能だということが直感的に理解できると思います。しかし、難点は処理速度で、非常に時間が掛かります。

「スプライン(Spline)」とは、区分毎に分割された多項式からなる関数のことで、スプラインによって描かれる曲線を「スプライン曲線(Spline Curve)」といいます。簡単な例として、折れ線グラフは、一次式で構成されたスプライン曲線を意味することになります。滑らかな曲線を描くためには、各区分の境界において左右の微分係数が等しくなる必要があります。この条件から求められる多項式を使って補間する方法が三次スプライン補間法であることになります。

4) 三次畳み込み補間法(Bicubic Convolution Interpolation)

線形補間法は、各ピクセル間の値が、隣り合ったピクセルどうしを結んだ線分上にあるものとみなして処理をしていました。三次スプライン補間法ではそれが三次スプライン曲線に変化しています。これらは、各ピクセルの値から連続関数を再現している処理にほかなりません。このような処理を総称して「補間(Interpolation)」といいます。一般的には、次のような性質を持つ関数を利用して補間を行ないます。

φ(t)=1 ( t = 0 )
=0 ( t = ±nh ; n = 1,2,3 ... )

ここで、h は各ピクセルの間隔を表します。このような関数を「補間関数(Interpolation Kernel)」といい、これを用いて

f(t) = Σk{-∞→∞}( fkφ( t - tk ) )

但し、fk は tk = kh におけるピクセルの値

と定義した関数 f(t) は、

k≠i のとき φ( ti - tk ) = φ( ( i - k )h ) = 0

k = i のとき φ( ti - ti ) = φ(0) = 1

なので、f(ti) = fi になります。よって、各ピクセルの点を通る任意の関数を補間関数を使って構築することができることになります。

補間関数 φ(t) として、次のような三次の多項式を考えます。ここで、各ピクセルの間隔 h の値を h = 1 とします。

φ(t)=a3|t|3 + a2|t|2 + a1|t| + a0( 0 < |t| < 1 )
=b3|t|3 + b2|t|2 + b1|t| + b0( 1 < |t| < 2 )
=0( |t| > 2 )

φ(0) = 1、φ(±1) = φ(±2) = 0 より、

φ(0) = a0 = 1

φ(±1) = a3 + a2 + a1 + a0 = 0

φ(±1) = b3 + b2 + b1 + b0 = 0

φ(±2) = 8b3 + 4b2 + 2b1 + b0 = 0

φ(t)が連続であるためには、φ(t)の左側微分係数 φ-'(t) と右側微分係数 φ+'(t) が等しい必要があることから、

φ-'(0) = -a1 = φ+'(0) = a1

φ-'(±1) = 3a3 + 2a2 + a1 = φ+'(±1) = 3b3 + 2b2 + b1

φ-'(±2) = 12b3 + 4b2 + b1 = φ+'(±2) = 0

七つの連立方程式に対して未知数は八つなので、全ての未知数を得ることはできません。そこで、b3 = α として、各未知数をαを使って表すと

( a3, a2, a1, a0 ) = ( α + 2, -α - 3, 0, 1 )

( b3, b2, b1, b0 ) = ( α, -5α, 8α, -4α )

よって、補間関数φ(t)は

φ(t)=( α + 2 )|t|3 - ( α + 3 )|t|2 + 1( 0 < |t| < 1 )
=α|t|3 - 5α|t|2 + 8α|t| - 4α( 1 < |t| < 2 )
=0( |t| > 2 )

φ(t)は -2 ≦ t ≦ 2 の範囲のみ値を持つので、f(t) = Σk{-∞→∞}( fkφ( t - tk ) ) は次のように有限な形で表現することができます。

f(t)=fk-1φ( t - tk-1 ) + fkφ( t - tk ) + fk+1φ( t - tk+1 ) + fk+2φ( t - tk+2 )
=fk-1φ( t - tk + tk - tk-1 ) + fkφ( t - tk + tk - tk ) + fk+1φ( t - tk + tk - tk+1 ) + fk+2φ( t - tk + tk - tk+2 )
=fk-1φ( t - tk + 1 ) + fkφ( t - tk ) + fk+1φ( t - tk - 1 ) + fk+2φ( t - tk - 2 )

ここで、tk は t を超えない最大の整数値を表すことになります。s = t - tk ( 0 ≦ s < 1 ) とすると、

φ(s+1)=α( s + 1 )3 - 5α( s + 1 )2 + 8α( s + 1 ) - 4α
=αs3 - 2αs2 + αs
φ(s)=( α + 2 )s3 - ( α + 3 )s2 + 1
φ(s-1)=-( α + 2 )( s - 1 )3 - ( α + 3 )( s - 1 )2 + 1
=( α + 2 )s3 - ( 2α + 3 )s2 - αs
φ(s-2)=-α( s - 2 )3 - 5α( s - 2 )2 - 8α( s - 2 ) - 4α
=-αs3 + αs2

なので、これらを代入して

f(t) = -{ α( fk+2 - fk-1 ) + ( α + 2 )( fk+1 - fk ) }s3 + { 2α( fk+1 - fk-1 ) + 3( fk+1 - fk ) + α( fk+2 - fk ) }s2 - α( fk+1 - fk-1 )s + fk

ところで、f~(ti) = fiを満たす連続関数 f~(t) が少なくとも三回微分可能であるならば、テイラー多項式 f(x) = Σk{0→n}( (1/k!)f(k)(a)( x - a )k ) によって

fk+1 = f~(tk+1)=f~(tk) + f~(1)(tk)( tk+1 - tk ) + f~(2)(tk)( tk+1 - tk )2 / 2 + R3
=f~(tk) + f~(1)(tk) + f~(2)(tk) / 2 + R3

と表すことができます。ここで、R3 は剰余項を表します。f~(tk+2) と f~(tk-1) も同様に

fk+2 = f~(tk+2) = f~(tk) + 2f~(1)(tk) + 2f~(2)(tk) + R3

fk-1 = f~(tk-1) = f~(tk) - f~(1)(tk) + f~(2)(tk) / 2 + R3

これらを f(t) に代入すると、

f(t) = -( 2α + 1 ){ 2f~(1)( tk ) + f~(2)( tk ) }s3 + { ( 6α + 3 )f~(1)( tk ) + ( 4α + 3 )f~(2)( tk ) / 2 }s2 - 2αf~(1)( tk )s + f~( tk ) + R3

f~(t) を t = tk を中心にテイラー展開した場合は、

f~(t)=f~(tk) + f~(1)(tk)( t - tk ) + f~(2)(tk)( t - tk )2 / 2 + R3
=f~(tk) + f~(1)(tk)s + f~(2)(tk)s2 / 2 + R3

よって、f~(t) と f(t) の差は

f~(t) - f(t)=( 2α + 1 ){ 2f~(1)( tk ) + f~(2)( tk ) }s3 - ( 2α + 1 ){ 3f~(1)( tk ) + f~(2)( tk ) }s2 + ( 2α + 1 )f~(1)(tk)s + R3
=( 2α + 1 )[ { 2f~(1)( tk ) + f~(2)( tk ) }s3 - { 3f~(1)( tk ) + f~(2)( tk ) }s2 + f~(1)(tk)s ] + R3

よって、α = -1/2 のとき、f~(t) と f(t) との差が剰余項 R3 のみになります。f~(t)が三次式なら R3 は定数項であり、ピクセル上では f~(t) = f(t) なので f~(t) と f(t) は完全に一致します。つまり、各ピクセルから三次多項式に補間する場合、α = -1/2 ならば一意に表すことができることになります。α ≠ -1/2 のときは、一次項まで誤差が残る可能性があるので、精度は低くなります。

α = -1/2 のとき、補間関数φ(t)は次のようになります。

φ(t)=(3/2)|t|3 - (5/2)|t|2 + 1( 0 < |t| < 1 )
=-(1/2)|t|3 + (5/2)|t|2 - 4|t| + 2( 1 < |t| < 2 )
=0( |t| > 2 )

三次畳み込み補間法による補間処理を行なうためのサンプル・プログラムを以下に示します。

/* 補間関数 */
class InterpolationKernel
{
public:

  // 補間関数の値を計算する
  virtual void operator()( vector<double>& phai, double t ) const = 0;
  // ゼロ以外の値を持つピクセル幅を返す(実際には半分の値を返す)
  virtual int size() const = 0;
  // 仮想デストラクタ
  virtual ~InterpolationKernel() {}
};

/* 三次畳み込み補間関数 */
class BicubicKernel : public InterpolationKernel
{
  double a;

public:

  BicubicKernel( double _a = -0.5 )
    : a( _a ) {}

  void operator()( vector<double>& phai, double t ) const;
  int size() const { return( 2 ); }
};

/*
  BicubicKernel::operator() : 三次畳み込み補間関数の t ± kh での値を求める

  vector<double>& phai : 求める値
  double t : 変数 t
*/
void BicubicKernel::operator()( vector<double>& phai, double t ) const
{
  if ( phai.size() != (unsigned int)size() * 2 ) return;

  phai[0] = -a * pow( t, 2 ) * ( t - 1 );
  phai[1] = t * ( ( -a - 2 ) * pow( t, 2 ) + ( 2 * a + 3 ) * t - a );
  phai[2] = ( a + 2 ) * pow( t, 3 ) - ( a + 3 ) * pow( t, 2 ) + 1;
  phai[3] = a * t * pow( t - 1, 2 );
}

/* 畳み込みによる補間法 */
class ConvolutionBase : public GInterpolation
{
  const InterpolationKernel& kernel; // 補間関数

  // 畳み込みによる補間法メインルーチン
  RGB convolution( const vector<RGB>& col, double t ) const;

public:

  // コンストラクタ
  ConvolutionBase( const InterpolationKernel& _kernel )
    : kernel( _kernel ) {}

  // 畳み込みによる色の補間
  RGB operator()( const GPattern& pattern, const Coord<double>& p ) const;
};

/*
  ConvolutionBase::operator() : 畳み込みによる色の補間

  const GPattern& pattern : パターン・オブジェクト
  const Coord<double>& p : 色を求める点の座標
*/
RGB ConvolutionBase::operator()( const GPattern& pattern, const Coord<double>& p ) const
{
  if ( &kernel == 0 ) return( RGB( 0 ) );
  int n = kernel.size();
  if ( n <= 0 ) return( RGB( 0 ) );

  Coord<int> c( p.x, p.y ); // pを含む格子の左上の座標
  vector<RGB> col( n * 2 ); // X方向の色コード
  vector<RGB> res( n * 2 ); // Y方向の色コード

  for ( int y = 1 - n ; y <= n ; ++y ) {
    // 色コードの取得
    for ( int x = 1 - n ; x <= n ; ++x )
      col[x+n-1] = pattern.point( Coord<int>( c.x + x, c.y + y ) );
    // X方向の畳み込み積分
    res[y+n-1] = convolution( col, p.x - (double)( c.x ) );
  }

  // Y方向に畳み込み積分を行なって結果を返す
  return( convolution( res, p.y - (double)( c.y ) ) );
}

/*
  ConvolutionBase::convolution : 畳み込みによる補間法メインルーチン

  const vector<RGB>& col : 色コード
  double t : 色コードを求める座標値
*/
RGB ConvolutionBase::convolution( const vector<RGB>& col, double t ) const
{
  unsigned int n = (unsigned int)( col.size() ); // ゼロ以外の値を持つピクセル幅
  vector<double> phai( n ); // 補間関数による計算結果

  // 補間関数による値の計算
  kernel( phai, t );

  // 畳み込み積分を行う
  double ans[] = { 0, 0, 0 };
  for ( unsigned int i = n ; i > 0 ; --i ) {
    ans[0] += ( col[n-i] ).r() * phai[i-1];
    ans[1] += ( col[n-i] ).g() * phai[i-1];
    ans[2] += ( col[n-i] ).b() * phai[i-1];
  }

  // 範囲外であった場合に補正
  for ( int i = 0 ; i < 3 ; ++i ) {
    if ( ans[i] < 0 ) ans[i] = 0;
    if ( ans[i] > UCHAR_MAX ) ans[i] = UCHAR_MAX;
  }

  return( RGB( (unsigned char)ans[0], (unsigned char)ans[1], (unsigned char)ans[2] ) );
}

補間関数を使って各ピクセルにおける値を計算する処理は、別のクラス(BicubicKernel)に持たせています。さらに、BicubicKernel は InterpolationKernelからの派生クラスとし、後々のために補間関数が切り替えられるような作りにしてあります。補間関数の係数にある変数αはコンストラクタにて任意に変更できるようにしてあり、デフォルトで -1/2 としています。BicubicKernelクラスにあるoperator() は、φ(t-1), φ(t), φ(t+1), φ(t+2) の値を求めるための関数です。先に示した式と異なる計算をしているように見えますが、式を変形させているだけで結果は同じになります。
補間処理は、ConvolutionBase クラスの operator()が行ないます。補間関数は一次元関数であるため、最初に x方向の補間処理を各 y座標に対して求め、求めた点を使って y方向の補間処理を行います。サンプル点となる色コードと補間関数の値を掛け合わせる処理は、メンバ関数の convolution で行ないます。ここで「畳み込み積分」という言葉が使われていますが、色コードと補間関数の値を掛け合わせるときの順番がそれぞれで前後逆になっていることに注意してください。「畳み込み積分」については後ほど説明します。

5) 補間関数と畳み込み積分

補間関数 φ(t) を使って、次の式を用いて f(t) を求めたとき、f(t) は各ピクセル tk に対して f(tk) = fk を満たす関数となることを説明しました。これがどのような処理になっているのかをもう少し検討してみます。

f(t) = Σk{-∞→∞}( fkφ( t - tk ) )

但し、fk は tk = kh におけるピクセルの値

ピクセル間の距離 h がゼロに収束するとき、上の式は積分の形になり、以下のような式になります。

f(t) = ∫{-∞→∞} f(s)φ( t - s ) ds

このように定義された式を「畳み込み積分(Convolution)」といい、"f(t) * φ(t)" や "( f * φ )(t)" の形で表されます。

音響や電気回路などで、短い時間の中で発生する信号を「インパルス(Impulse)」といい、ある入出力システムがインパルスに対して出力する信号は「インパルス応答(Impulse response)」と呼ばれています。理想的には、インパルスは時間幅が無限小で高さが無限大の信号であり、これは、「ディラックのデルタ関数(Dirac's Delta Function)」という以下の式を満たす関数 δ(t) になります。

∫{-∞→∞} f(t)δ(t) dt = f(0)

しかし、この式を満たすためには δ(0) が発散する必要があるため、実際にはこのような信号を生成することはできません。

インパルスが入力されたときのインパルス応答が t を変数とする関数 g(t) で表されるとします。また、インパルスの強さによってインパルス応答が線形的に変化するとします。つまり、インパルスの強さが f 倍されればインパルス応答も f 倍されます。

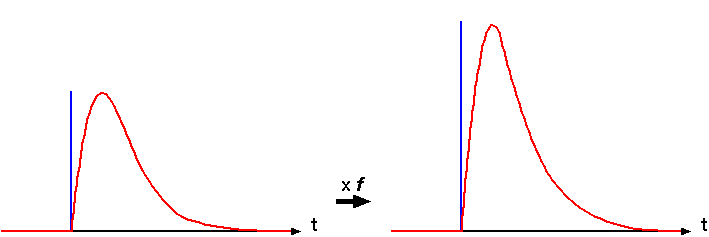
インパルスとインパルス応答

インパルスが発生した時間(位置)を s としたとき、s から 任意の時間(位置) t までは t - s だけ離れているため、s で発生したインパルスの大きさを f(s)とすれば、t でのインパルス応答の大きさは、f(s)g( t - s ) で表されます。よって、各 s で発生したインパルス f(s) に対する t でのインパルス応答を重ね合わせた結果は、次の式によって計算することができます。

∫{-∞→∞} f(s)g(t-s) ds

これは、畳み込み積分の形そのものになります。

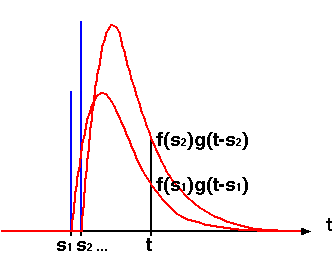
インパルス応答の重ね合わせ

上の図において、sk ( k = 0, 1, 2 ... ) におけるインパルスの大きさが f(sk) ならば、t におけるインパルス応答の大きさは f(sk)g( t - sk ) です。データが連続ではなく離散値であるとき、各インパルスの幅が Δs として、各データが Δs の幅を持つ矩形とすれば、インパルス応答を重ね合わせた結果は

Σk{-∞→∞}( f(sk)g(t-sk)Δs )

になります。ここで Δs をゼロに収束させると、畳み込み積分の式が得られます。コンピュータで実際に処理をする場合は、積分の形で計算することはできないので、和の形で示した式を使って計算を行ないます。

画像のピクセルと補間関数の畳み込み積分によって、離散データを連続データのように扱い、ピクセル間の色コードを求めることが可能であり、そのとき作られる連続データは補間関数の種類によって変化することは容易に予想できます。ここで、補間関数がどのような性質の連続データを作成することができるのかを知るには、畳み込み積分に対する重要な性質を知る必要があります。まずは、その説明をする前に、「フーリエ変換(Fourier Transform)」について簡単に紹介します。

フーリエ変換は、次の式で表されます。

F(ω) = ∫{-∞→∞} f(t)exp(-iωt) dt

但し、exp(x) はネイピア数の x乗を表しています。上式において、t は時間や位置を、ωは周波数(rad/sec)を表します。フーリエ変換を一言で表すと、時間や位置によって変化する関数を、周波数の異なる正弦波の重ね合わせで表したときの周波数成分に変換することになります。画像に対して周波数成分を考えた場合、高周波成分は近隣の画素の強弱を表し、逆に低周波成分は離れた部分との強弱を表します。自然画の場合、一般的に低周波成分の方が大きくなる傾向にあります。
ここで、畳み込み積分の式に対してフーリエ変換を行なうとどうなるでしょうか。

∫f(t) * g(t) exp(-iωt) dt=∫ ( ∫ f(s)g(t-s) ds ) exp(-iωt) dt
=∫ f(s) ( ∫ g(t-s)exp(-iωt) dt ) ds[ 積分の順序を入れ替え ]
=∫ f(s) ( ∫ g(t')exp(-iω(t'+s)) dt' ) ds[ t' = t - s より t = t' + s, dt = dt' ]
=∫ f(s) ( ∫ g(t')exp(-iωt') dt' ) exp(-iωs) ds
=( ∫ f(s)exp(-iωs) ds )( ∫ g(t')exp(-iωt') dt' )
=F(ω)G(ω)

但し、F(ω) と G(ω) はそれぞれ、f(t) と g(t) のフーリエ変換を表しています。これを「畳み込み積分定理(Convolution Theorem)」と呼びます。つまり、二つの信号の畳み込み積分をフーリエ変換した結果は、それぞれの信号をフーリエ変換した結果の積と等しくなるわけです。
G(ω)が次のような式で表されるとします。

G(ω)=1( |ω| ≦ ω0 )
=0( |ω| > ω0 )

任意の F(ω) に対して上記の G(ω) を掛けると、ω0 以上の周波数成分は全てカットされ、低周波成分だけが残ります。これは、元の信号 f(t) と g(t) に対して畳み込み積分を行なった場合も同様の結果になります。補間関数はその内容によって、様々な周波数成分を持っています。よって、補間関数によって畳み込み積分を行なうことは、周波数成分を変化させることと同じ処理をすることになります。この様な操作は、補間関数による「フィルタ」と呼ばれます。低周波成分を増幅し、逆に高周波成分を減衰させるようなフィルタは「低域フィルタ(Low-pass Filter, LPF)」、これとは逆に、高周波成分を増幅し、低周波成分を減衰させるようなフィルタは「高域フィルタ(High-pass Filter, HPF)」といいます。また、特定の周波数領域のみを増幅するようなフィルタは「帯域フィルタ(Band-pass filter, BPF)」になります。

周波数成分から信号に逆変換するには、次の変換式を使います。

f(t) = (1/2π)∫{-∞→∞} F(ω)exp(iωt) dω

上に示した G(ω) を元の信号に戻してみます。

g(t)=(1/2π)∫{-ω0→ω0} exp(iωt) dω
=(1/2π)∫{-ω0→ω0} ( cos(ωt) + isin(ωt) ) dω[ オイラーの公式より exp(iθ) = cosθ + isinθ ]
=(1/π)∫{0→ω0} ( cos(ωt) ) dω[ sinθは奇関数で正負それぞれの領域の値で相殺, cosθは偶関数で正負それぞれの領域の値が等しい ]
=(1/π)[ (1/t)sin(ωt) ]{0→ω0}
=sin(ω0t) / πt

ω0 = π ならば、g(t) = sin(πt) / πt ≡ sinc( t ) になります。よって、信号に対して sinc( t ) を使って畳み込み積分を行なうと、出力された信号はπ(rad/sec)を超える周波数成分を持たない、高周波成分のカットされたものになります。sinc( t ) は理想的な低域フィルタですが、t の有限な範囲に対して値がゼロにはならない(コンパクト・サポートではない)ためある程度の精度を得るためには計算量が多くなってしまいます。そのため、sinc( t ) に形のよく似た関数が代わりに利用され、三次畳み込み補間法で利用する補間関数もその中の一つになります。

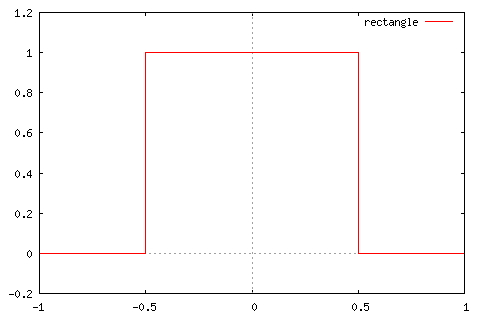
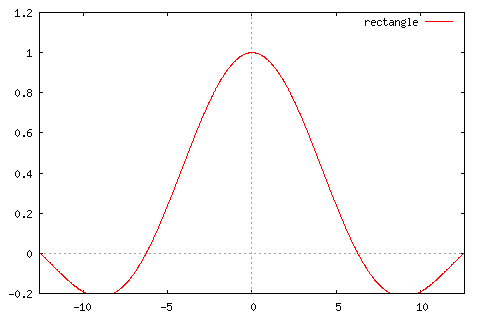
矩形関数 矩形のフーリエ変換

最近傍法(Nearest Neighbour)は、上図の左側に示したような矩形関数を補間関数として畳み込み積分をする処理と同等になります。そのフーリエ変換を行なった結果が右側の図です。

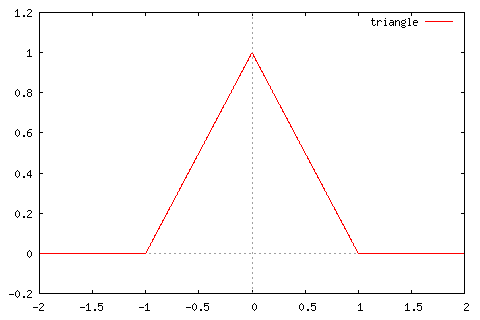
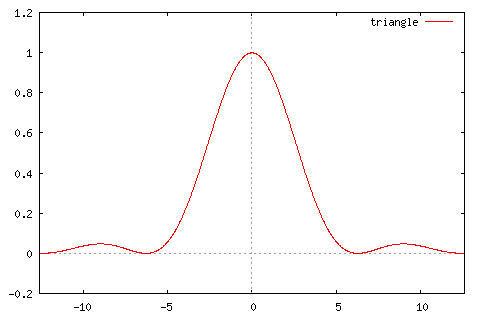
折れ線グラフの補間関数 折れ線グラフ補間関数のフーリエ変換

線形補間法は、三角形の形をした補間関数で畳み込み積分をする処理と同等になります。そのフーリエ変換を行なった結果が右側の図です。

最近傍法は、最も距離の近いピクセルの色を取得するという荒い近似をしているため、変換結果にはジャギーが目立つようになります。逆に、線形補間法は直線近似を行なって色コードを決めているため、変換結果は「ぼやけた」状態になります。矩形関数のフーリエ変換の結果は、高周波領域にもある程度大きな値が残っているため、これが近隣のピクセルに対する振動を生じ、ジャギーを引き起こしていることが感覚的に理解できると思います。また、線形補間法でのフーリエ変換は高周波領域の値がかなりゼロに近いのですが、低周波領域の値の減衰が大きい(ヤマが尖った形である)ために近隣のピクセルに対する濃淡の度合いが小さくなりすぎて、結果としてボヤけた画像が得られることになります。このように、フーリエ変換の形を見ることで、その補間関数の特徴を知ることができます。

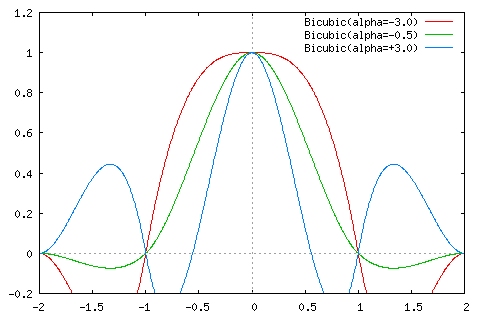
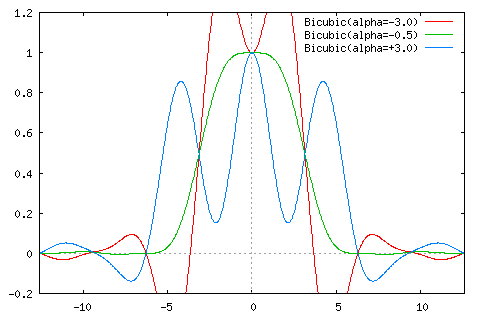
Bicubic補間関数 Bicubic補間関数のフーリエ変換

上図は、三次畳み込み補間関数(左側)とそのフーリエ変換(右側)です。α = -0.5の場合、フーリエ変換の結果が矩形に近いことから、かなり理想的なフィルタとして作用していることがわかります。

Lenna

上記画像は、画像処理テスト用としてよく利用されることで有名な"Lenna"です。このテスト画像(実際には 512 x 512のサイズです)の中央 1/5の部分の画像を切り取って、それを 1/3のサイズに拡大した結果を以下に示します。

拡大処理テスト結果
拡大処理テスト結果
(上側) 左から最近傍法, 線形補間法, 三次スプライン補間法
(下側) 三次畳み込み補間法(左からα = -3.0, -0.5, +3.0)

最近傍法ではジャギーが目立つ反面、線形補間法は画像がボヤけた印象を受けます。三次スプライン補間や三次畳み込み補間(α=-0.5)はジャギーやぼかしは見られず、非常に自然な仕上がりになっています。三次畳み込み補間(α=-3.0)では、フーリエ変換を行なった結果を見ると振幅が非常に大きく、変換した画像はエッジが強調されたような形になっています。α=+3.0 の場合も、同様に振幅が非常に大きい上、低周波成分の減衰が大きいため、ジャギーが目立つ上に全体としてボヤけた画像になっています。

それではここから、いくつかの補間関数を紹介したいと思います。

ランツォシュ補間(Lanczos Interpolation)

ランツォシュ補間関数は次のような式になります。

L(t)=sinc(t)sinc(t/a)( |t| ≦ a )
=0( |t| > a )

サンプル・プログラムを以下に示します。

/* Lanczos補間関数 */
class LanczosKernel : public InterpolationKernel
{
  int n;

public:

  LanczosKernel( int _n = 2 )
    : n( _n ) { if ( n <= 0 ) n = 1; }

  void operator()( vector<double>& phai, double t ) const;
  int size() const { return( n ); }
};

/*
  LanczosKernel::operator() : Lanczos補間関数の t ± kh での値を求める

  vector<double>& phai : 求める値
  double t : 変数 t
*/
void LanczosKernel::operator()( vector<double>& phai, double t ) const
{
  double a = size();
  double x = t - a;
  for ( unsigned int i = 0 ; i < phai.size() ; ++i ) {
    phai[i] = ( x == 0 ) ?
      1 :
      ( a * sin( M_PI * x ) * sin( M_PI * x / a ) / pow( M_PI * x, 2 ) );
    x += 1;
  }
}

パラメータとして、ゼロでない値を持つ範囲を表す変数 n を渡してインスタンス化します。よく利用されるパラメータは n = 2 または 3 で、それぞれ特別に Lanczos2、Lanczos3 とも呼ばれているようです。

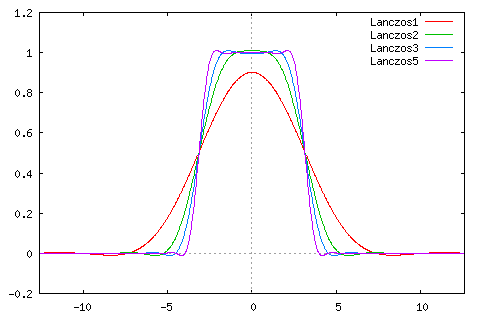
Lanczos補間関数 Lanczos補間関数のフーリエ変換

上図は Lanczos補間関数(左側)とそのフーリエ変換(右側)です。n = 1 を除けば、矩形に近い形であり理想的な補間関数であることがわかります。

Lanczos補間による拡大処理テスト結果
拡大処理テスト結果(Lanczos)
左から Lanczos2, Lanczos3, Lanczos5

拡大処理を行なった結果を見ると、Lanczos2では格子状の模様が発生しています。Lanczos3 や Lanczos5 は非常に良好な仕上がりです。

ミッチェル補間(Mitchell-Netravali Interpolation)

ミッチェル補間関数は次のような式になります。

k(t)=(1/6)( ( 12 - 9B - 6C )|t|3 + ( -18 + 12B + 6C )|t|2 + ( 6 - 2B ) )( |t| < 1 )
=(1/6)( ( -B - 6C )|t|3 + ( 6B + 30C )|t|2 + ( -12B - 48C )|t| + ( 8B + 24C ) )( 1 ≦ |t| < 2 )
=0( |t| ≧ 2 )

サンプル・プログラムを以下に示します。

/* Mitchell-Netravali補間関数 */
class MitchellKernel : public InterpolationKernel
{
  double b;
  double c;

public:

  MitchellKernel( double _b = 1 / 3, double _c = 1 / 3 );

  void operator()( vector<double>& phai, double t ) const;
  int size() const { return( 2 ); }
};

/*
  MitchellKernel コンストラクタ

  double _b : パラメータ B
  double _c : パラメータ C
*/
MitchellKernel::MitchellKernel( double _b, double _c )
  : b( _b ), c( _c )
{
  if ( b < 0 ) b = 0;
  if ( b > 1 ) b = 1;
  if ( c < 0 ) c = 0;
  if ( c > 1 ) c = 1;
}

/*
  MitchellKernel::operator() : Mitchell-Netravali補間関数の t ± kh での値を求める

  vector<double>& phai : 求める値
  double t : 変数 t
*/
void MitchellKernel::operator()( vector<double>& phai, double t ) const
{
  double x = t - 2;
  for ( unsigned int i = 0 ; i < phai.size() ; ++i ) {
    double absX = fabs( x );
    if ( absX < 1 )
      phai[i] = ( ( 12 - 9 * b - 6 * c ) * pow( absX, 3 ) + ( -18 + 12 * b + 6 * c ) * pow( absX, 2 ) + ( 6 - 2 * b ) ) / 6;
    else if ( absX < 2 )
      phai[i] = ( ( -b - 6 * c ) * pow( absX, 3 ) + ( 6 * b + 30 * c ) * pow( absX, 2 ) + ( -12 * b - 48 * c ) * absX + ( 8 * b + 24 * c ) ) / 6;
    else
      phai[i] = 0;
    x += 1;
  }
}

パラメータとして二種類( B, C )存在し、それぞれの値で調節ができるようになっています。B = C = 1/3 とするのが一般的のようです。

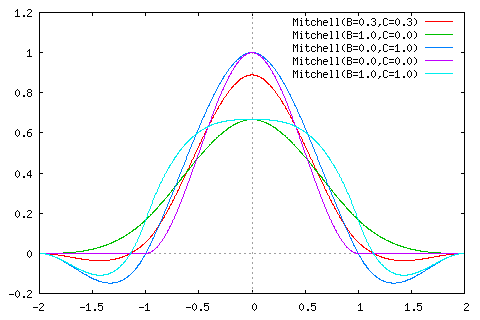
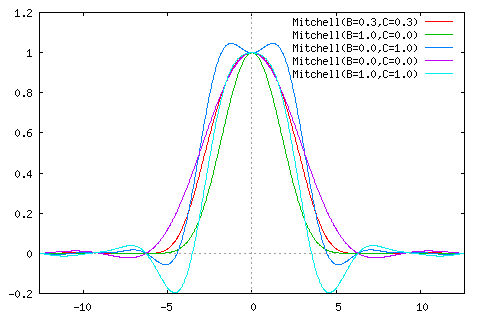
Mitchell-Netravali補間関数 Mitchell-Netravali補間関数のフーリエ変換

ミッチェル補間関数は、二つのパラメータの値によって様々な特徴を持った補間関数を作り出すことができます。理想とするパラメータである B = C = 1/3 の他に、極端な例として B と C を最大または最小値にしたときの波形も併せて載せてあります。

拡大処理テスト結果
拡大処理テスト結果(Mitchell-Netravali)
(上側) 左から ( B, C )=( 1/3, 1/3 ) ( B, C )=( 1, 0 ) ( B, C )=( 0, 1 )
(下側) 左から ( B, C )=( 0, 0 ) ( B, C )=( 1, 1 )

パラメータを極端な値にした場合、( B, C )=( 1, 0 ) では画像がボヤけ、( B, C )=( 1, 1 ) ではジャギーが多少目立つようになります。

6) 多項式補間(Polynomial Interpolation)

( N + 1 ) 個の点が与えられたとき、それらの点を通る N 次式はただ一つに決まります。例えば、三点 ( 1, 0 ), ( 2, 1 ), ( 3, 3 ) を通る二次式を y = ax2 + bx + c としたとき、( x, y ) に三点の値を代入して以下の連立方程式が得られます。

 a +  b + c = 0
4a + 2b + c = 1
9a + 3b + c = 3

この方程式の解は ( a, b, c ) = ( 1/2, -1/2, 0 ) なので、求める二次式は y = 0.5x2 - 0.5x になります。このように、連立方程式を解くことができれば各係数が決まるので、多項式を求めることで補間処理が可能になります。しかし、連立方程式を解く処理は非常に時間がかかるため( 連立方程式を解く -1- と 連立方程式を解く -2- 参照 )、別の手段を使って多項式を求めます。

まず、サンプル点が N + 1 個であるとして、その点を通る多項式を LN( x ) とします。LN( x ) が各点を通ることを保証するため、任意の点 ( xi, yi ) ( i = 0, 1, ... N ) において、

yi = LN( xi )

になる必要があります。ここで、N次式 li( x ) が、xj ( j = 0, 1, ... N ) において、

li( xj )=1 ( i = j )
=0 ( i ≠ j )

を満たすとき、LN( x ) は下式に示すような li( x ) の和で表すことができます。

LN( x ) = Σi{0→N}( yili( x ) )

この式は、yi = LN( xi ) を満たします。ここで、li( x ) を次のように定義します。

li( x )=Πj{0→N,j≠i}( ( x - xj ) / ( xi - xj ) )
=( x - x0 )( x - x1 )...( x - xi-1 )( x - xi+1 )...( x - xN ) / ( xi - x0 )( xi - x1 )...( xi - xi-1 )( xi - xi+1 )...( xi - xN )

x = xj ( j ≠ i ) のとき、li( xj ) = 0、また x = xi のときは総積の各項が 1 になるので、li( x1 ) = 1 になり、条件を満たします。

上記の形で定義された多項式を「ラグランジュの多項式(Lagrange Polynomial)」といいます。多項式を求めることができれば、任意の点における値を計算することができるので、これを利用して補間処理を行なうことが可能になります。

ラグランジュ多項式による補間法のサンプル・プログラムを以下に示します。

/* 多項式による補間 */
class PolynomialInterpolation : public GInterpolation
{
  typedef RGB (*PolynomialFunc)( const vector<RGB>& col, double t );

  int n;
  PolynomialFunc pf;

public:

  PolynomialInterpolation( unsigned int _n, PolynomialFunc _pf )
    : n( _n ), pf( _pf ) { if ( n < 2 ) n = 2; }

  RGB operator()( const GPattern& pattern, const Coord<double>& p ) const;
};

/*
  lagrange() : Lagrange多項式による補間メインルーチン

  const vector<RGB>& col : サンプル点の色コード
  double t : 色を求める位置

  戻り値 : 求めた色コード
*/
RGB lagrange( const vector<RGB>& col, double t )
{
  double ans[3] = { 0, 0, 0 };
  int n = col.size();
  t += ( n - 1 ) / 2;

  for ( int j = 0 ; j < n ; ++j ) {
    double d = 1;
    for ( int i = 0 ; i < n ; ++i ) {
      if ( i == j ) continue;
      d *= ( t - (double)i ) / (double)( j - i );
    }
    ans[0] += ( col[j] ).r() * d;
    ans[1] += ( col[j] ).g() * d;
    ans[2] += ( col[j] ).b() * d;
  }

  // 範囲外であった場合に補正
  for ( int i = 0 ; i < 3 ; ++i ) {
    if ( ans[i] < 0 ) ans[i] = 0;
    if ( ans[i] > UCHAR_MAX ) ans[i] = UCHAR_MAX;
  }

  return( RGB( (unsigned char)ans[0], (unsigned char)ans[1], (unsigned char)ans[2] ) );
}

今度は、多項式を次のように定義します。

N( x )=a0 + Σi{1→N}( aiΠj{0→i-1}( x - xj ) )
=a0 + a1( x - x0 ) + a2( x - x0 )( x - x1 ) + ... + aN( x - x0 )( x - x1 )...( x - xN )

x = x0のとき、N( x0 ) = a0 より、点( x0, y0 ) を通るためには a0 = y0 である必要があります。次に、x = x1 のとき、

N( x1 )=a0 + a1( x1 - x0 )
=y0 + a1( x1 - x0 )

より、点( x1, y1 ) を通るとき、a1 = ( y1 - y0 ) / ( x1 - x0 ) になります。これを 1階差分商といい、[ y0, y1 ] で表します。同様に、x = xi のときを考えると、

N( xi ) = a0 + a1( xi - x0 ) + a2( xi - x0 )( xi - x1 ) + ... + ai( xi - x0 )( xi - x1 )...( xi - xi-1 )

i = 2 のとき、

N( x2 ) = y0 + [ y0, y1 ]( x2 - x0 ) + a2( x2 - x0 )( x2 - x1 ) = y2

となるためには

a2 = ( y2 - y0 - [ y0, y1 ]( x2 - x0 ) ) / ( x2 - x0 )( x2 - x1 )

これを計算すると

(右辺)={ y2 / ( x2 - x0 )( x2 - x1 ) } - { y0 / ( x2 - x0 )( x2 - x1 ) } - { ( y1 - y0 ) / ( x1 - x0 )( x2 - x1 ) }
={ y2( x1 - x0 ) - y0( x1 - x0 ) - y1( x2 - x0 ) + y0( x2 - x0 ) } / ( x1 - x0 )( x2 - x1 )( x2 - x0 )
(分子)=y2( x1 - x0 ) - y1( x2 - x0 ) + y0( x2 - x1 )
=y2( x1 - x0 ) - y1( x1 - x0 ) - y1( x2 - x1 ) + y0( x2 - x1 )
=( y2 - y1 )( x1 - x0 ) - ( y1 - y0 )( x2 - x1 ) より
(右辺)={ ( y2 - y1 ) / ( x2 - x1 )( x2 - x0 ) } - { ( y1 - y0 ) / ( x1 - x0 )( x2 - x0 ) }
={ [ y1, y2 ] - [ y0, y1 ] } / ( x2 - x0 )

{ [ y1, y2 ] - [ y0, y1 ] } / ( x2 - x0 ) を 2階差分商といい、[ y0, y1, y2 ] で表します。この操作を繰り返すと、i番目の係数 ai は i階差分商となり、次の式で表すことができます。

[ y0, y1, ... yi ] = ( [ y1, y2, ... yi ] - [ y0, y1, ... yi-1 ] ) / ( xi - x0 )

このように求めた多項式を「ニュートン多項式(Newton Polynomial)」といいます。ラグランジュ多項式の場合、サンプル点を増やしたときは全ての項を初めから計算し直す必要があるのに対し、ニュートン多項式では以下の漸化式が成り立つので、最後の項だけを計算すればよいという利点があります。

Nk( x ) = Nk-1( x ) + [ y0, y1, ... yk ]Πi{0→k-1}( x - xi )

差分商の計算は、各サンプル点に対して 1階差分商を求め、その値を使って 2階差分商を求め... という操作を繰り返して行ないます。階数が増える度に計算回数は一つずつ減り、サンプル点が N個であれば、最後に N階差分商が一つだけ求められる形になります。その様子は次のような表で表すことができます。

y0
[ y0, y1 ]
y1[ y0, y1, y2 ]
[ y1, y2 ][ y0, y1, y2, y3 ]
y2[ y1, y2, y3 ][ y0, y1, y2, y3, y4 ]
[ y2, y3 ][ y1, y2, y3, y4 ]
y3[ y2, y3, y4 ]
[ y3, y4 ]
y4

ニュートン多項式による補間法のサンプル・プログラムを以下に示します。

/*
  newton() : Newton多項式による補間メインルーチン

  const vector<RGB>& col : サンプル点の色コード
  double t : 色を求める位置

  戻り値 : 求めた色コード
*/
RGB newton( const vector<RGB>& col, double t )
{
  double ans[3] = { ( col[0] ).r(), ( col[0] ).g(), ( col[0] ).b() };
  int n = col.size();
  t += ( n - 1 ) / 2;

  // 差分商の初期化
  vector<double> diffR( n, 0 );
  vector<double> diffG( n, 0 );
  vector<double> diffB( n, 0 );
  for ( int i = 0 ; i < n ; ++i ) {
    diffR[i] = ( col[i] ).r();
    diffG[i] = ( col[i] ).g();
    diffB[i] = ( col[i] ).b();
  }

  double d = t;
  for ( int i = 1 ; i < n ; ++i ) {
    // 差分商の計算
    for ( int j = 0 ; j < n - i ; ++j ) {
      diffR[j] = ( diffR[j+1] - diffR[j] ) / (double)i;
      diffG[j] = ( diffG[j+1] - diffG[j] ) / (double)i;
      diffB[j] = ( diffB[j+1] - diffB[j] ) / (double)i;
    }
    ans[0] += diffR[0] * d;
    ans[1] += diffG[0] * d;
    ans[2] += diffB[0] * d;
    d *= t - (double)i;
  }

  // 範囲外であった場合に補正
  for ( int i = 0 ; i < 3 ; ++i ) {
    if ( ans[i] < 0 ) ans[i] = 0;
    if ( ans[i] > UCHAR_MAX ) ans[i] = UCHAR_MAX;
  }

  return( RGB( (unsigned char)ans[0], (unsigned char)ans[1], (unsigned char)ans[2] ) );
}

多項式補間を行なったときの画像を以下に示します。ラグランジュ多項式、ニュートン多項式それぞれ、サンプル点は五つとしてあります。

拡大処理テスト結果(多項式補間)
左から ラグランジュ多項式, ニュートン多項式

サンプル点の数が増えるほど、演算量は多くなるため処理時間は増えていきます。サンプル点の数を 20 としてテストしたところ、画質に対して特に目立った差は見られないため、サンプル点が多くなっても画質がよくなるわけではなさそうです。

今回は、サンプル補間処理を利用した拡大・縮小処理を紹介しました。この方法は、回転処理や自由変形処理においても利用することが可能です。また、スプライン関数や補間関数、多項式を求める手法については他にも存在するので、これらの言葉をキーワードに検索をしてみると、特殊な用途に応じた処理方法も見つかるかもしれません。

<参考文献>
  1. 「これなら分かる応用数学教室」 金谷健一著 (共立出版)
  2. R. Keys, (1981). "Cubic convolution interpolation for digital image processing".
    IEEE Transactions on Signal Processing, Acoustics, Speech, and Signal Processing 29: 1153. doi:10.1109/TASSP.1981.1163711
  3. アカデミア・ノーツ
    2. 線形システム 2.1 畳み込み積分(Convolution)
  4. Wikipedia

◆◇◆更新履歴◆◇◆

[Go Back]前に戻る [Back to HOME]タイトルに戻る
inserted by FC2 system