
(Bytes)
(Bytes)
(Bytes)
(Bytes)
この章では、現在のデータ圧縮・画像圧縮などで広く用いられている「LZ 法」について説明します。
前章・前々章に説明したハフマン符号化では、個々のデータを出現頻度に応じてハフマン符号に変換して圧縮を試みるというものでした。それに対して「LZ 法」では、あるデータ列に着目して、それが以前に出現したことがあるかをチェックし、すでに出現したことがあるのならば、そのデータ列を示す何らかの符号 ( 当然、データ列より短くなければなりません ) に置き換える処理を行うことにより圧縮を行っています。「LZ 法」にはいくつかの種類があり、その種類によってさらに名称が変わります。しかし、どの場合も先に述べた考え方が基本原理となります。
「LZ 法」は、「Abraham Lempel」と「Jacob Ziv」の共同開発によって 1977 年に誕生しました。Lempel と Ziv は、その翌年にも同じ原理を使った別の手法を発表したため、先に開発された符号化を「LZ77 法」、後者を「LZ78 法」と呼んで区別しています。
「LZ77 法」では、前に出現したデータ列から最も一致した部分列を検索して、その場所を指すことによって圧縮を行います。例えば、
のようなデータ列の場合、6 文字め以降の "0123" は先頭のデータ列 "0123" と一致するため、一致するデータ列の先頭のインデックスと文字数から [1,4]、または「何文字前から」で表わして [5,4] と置換することができます。さらに続く "012340123012340123" は、前者の場合 [1,18]、後者の場合 [9,18] と置換することができます。ここで、[1,9] [1,9] または [9,9] [18,9] とはならないことに注意してください。展開によって新たに追加されたデータ列が一致するならば、展開を開始した位置を超えてさらに展開することができます。
| 012340123 | 012340123012340123 | ||
| +----------------+ | |||
| +----------------+ | |||
| 9文字前から18文字分が一致 | |||
前にあるデータを全てチェックしていたのではデータ量が多くなると処理時間も劇的に長くなるので、LZ77 法では前にあるデータの中から最も近い固定長の部分データを使って比較処理を行っています。この固定長の部分データは「Sliding Window」と呼ばれ、処理が進むごとにシフトしていきます。具体的な処理の流れは以下のようになります。
| Sliding Window | 入力データ列 | 出力データ列 | |
|---|---|---|---|
| 1 | **************** | 012340123012340123012340123 | |
| 2 | ***************0 | 12340123012340123012340123 | 0 |
| 3 | **************01 | 2340123012340123012340123 | 01 |
| 4 | *************012 | 340123012340123012340123 | 012 |
| 5 | ************0123 | 40123012340123012340123 | 0123 |
| 6 | ***********01234 | 0123012340123012340123 | 01234 |
| 7 | *******012340123 | 012340123012340123 | 01234[5,4] |
| 8 | 2340123012340123 | 0123[5,4][9,18] |
上記の例では、6 番目の処理において、データ列先頭から 5 つ前にある "0123" の 4 つが一致しているので [5,4] が出力されています。また、次の 7 番目の処理では、データ列先頭から 9 つ前にある "012340123012340123" の 18 個が一致しているので [9,18] が出力されています。Sliding Window からはみ出しても、比較処理はそのまま続けています。
逆に圧縮したデータを展開する場合、以下のように処理を行います。
| 入力データ列 | 出力データ列 | |
|---|---|---|
| 1 | 01234[5,4][9,18] | |
| 2 | [5,4][9,18] | 01234 |
| 3 | [9,18] | 012340123********* |
| 4 | [9,18] | 012340123012340123 |
| 5 | 012340123012340123012340123 |
3 番目の処理で見られるように、[9,18] の部分では、10 個め以降の 9 つ分のデータ ( "*" で示された部分 ) はまだ出力されていないのですが、9 つ分のデータが出力されたところでこの部分は全て埋められ、コピーすることが可能になります。
Abraham Lempel と Jacob Ziv によって考案された最初の手法では、符号は ( 一致したデータ列の位置, 一致した文字数, 不一致となったデータ ) と構成されていました。この場合、一致したデータ列が見つからなかったときは ( 0, 0, 不一致となったデータ ) と符号化され、位置と長さの情報が冗長になります。先に示した符号化は、「James Storer」と「Thomas Szymanski」の二人によって 1982 年に提唱された「Lempel-Ziv-Storer-Szymanski (LZSS) 法」と呼ばれるアルゴリズムになります。元のアルゴリズムでは、位置・長さ情報の長さを固定長にしておけば順番にデータを読み書きするだけで処理ができるのに対し、LZSS 法の場合は位置・長さ情報とデータそのものを区別するため先頭に判別用のビットを付けるなどの工夫が必要になります。
LZ77 (LZSS) 符号化と復号化処理を行うためのサンプル・プログラムを以下に示します。
/** LZ77 符号の定義 xxxxxxxxxxYYYYYYY | | 位置情報 データ数情報 **/ template<class Code> class LZ77_CodeGenerator { size_t indexBit_; // 位置情報の符号長 size_t countBit_; // 一致したデータ数情報の符号長 // 位置情報とデータ数の符号に対するマスク Code indexMask_; Code countMask_; public: /// 位置情報とデータ数のビット数 indexBit, countBit を指定して構築 LZ77_CodeGenerator( size_t indexBit, size_t countBit ) : indexBit_( indexBit ), countBit_( countBit ) { indexMask_ = ~( ~( static_cast<Code>( 0 ) ) << indexBit_ ); countMask_ = ~( ~( static_cast<Code>( 0 ) ) << countBit_ ); } /// 位置情報 index とデータ数 count の情報を符号化して返す /// /// 位置情報・データ数のいずれも符号長を超えていないことを前提として処理する Code encode( Code index, Code count ) const { return( ( index << countBit_ ) | count ); } /// 符号 code から位置情報 index とデータ数 count を取得する void decode( Code code, Code* index, Code* count ) const { *index = ( code >> countBit_ ) & indexMask_; *count = code & countMask_; } /// 符号長を返す size_t bits() const { return( indexBit_ + countBit_ ); } };
符号化した後のデータは一致するデータ列の位置とその長さを保持します。この位置情報と長さから符号を作成するためのクラスとして LZ77_CodeGenerator を定義します。オブジェクトを構築する時に位置情報・長さのビット数を指定しておき、メンバ関数 encode を使って、上位側に位置情報、下位側に長さを保持した符号を返すようにしています。また decode 関数は逆に、符号から位置情報と長さを取得します。最後の bits 関数は符号のビット数を返します。
符号として扱う変数の型はテンプレート引数として渡し、クラス内ではその型を Code として扱っています。位置情報と長さのビット数の和が Code 型の変数のビット数を超えない限り、Code としてはどのような型も利用できますが、ビット演算子を使っていることから整数型が対象となります。また、符号なし整数型を利用することを前提としています。
/** Sliding Window 上のデータ探索用関数オブジェクト **/ template<class In,class Code> struct SW_Search { /// 現在のデータ列の先頭 dataStart が辞書バッファの中で一致する部分を探し、 /// 位置と長さを index, count に返す /// /// dataEnd はデータ列の末尾の次の反復子、winSize は Sliding Window のサイズ void operator()( In dataStart, In dataEnd, Code winSize, Code maxCountSize, Code* index, Code* count ); }; /** 現在のデータ列の先頭 dataStart が辞書バッファの中で一致する部分を探し、 位置と長さを index, count に返す dataEnd はデータ列の末尾の次の反復子、winSize は Sliding Window のサイズ **/ template<class In,class Code> void SW_Search<In,Code>::operator()( In dataStart, In dataEnd, Code winSize, Code maxCountSize, Code* index, Code* count ) { // 反復子 In の差分に対する型 typedef typename std::iterator_traits<In>::difference_type difference_type; // 位置とデータ数はデフォルト値(ゼロ)で初期化 *index = *count = Code(); // Sliding Window の先頭 In winStart = dataStart; std::advance( winStart, -static_cast<difference_type>( winSize ) ); for ( ; winStart != dataStart ; ++winStart ) { In winP = winStart; // 辞書バッファ内の比較対象データの先頭 // 符号化するデータと一致する部分を探索 for ( In dataP = dataStart ; *winP == *dataP ; ++dataP ) { if ( dataP == dataEnd ) break; ++winP; } // 一致部分のデータ位置と個数を更新 size_t sz = std::distance( winStart, winP ); if ( sz > *count ) { *index = std::distance( winStart, dataStart ); *count = sz; } // 比較対象のデータ数を超えたら処理をやめる if ( *count >= maxCountSize ) { *count = maxCountSize; break; } } } /** 辞書バッファ ( Sliding Window ) winStart_ winStart_ + curIndex_ | | +-------------->+ sliding window +---------------------------------------+ data | | dataStart dataEnd_ **/ template<class In,class Code> class SlidingWindow { // 反復子 In の値に対する型 typedef typename std::iterator_traits<In>::value_type value_type; In dataStart_; // データ列の開始 In dataEnd_; // データ列の末尾の次 In curIndex_; // 符号化するデータの開始(辞書バッファの末尾の次) Code winSize_; // Sliding Window のサイズ Code maxWinSize_; // Sliding Window の最大サイズ Code maxCountSize_; // 比較対象のデータ数最大値 public: /// 対象データ列の開始(s)・末尾の次(e)の反復子を指定して構築 /// /// Sliding Window のサイズはゼロで初期化され、符号化されるに従って maxWinSize まで増大する SlidingWindow( In s, In e, Code maxWinSize, Code maxCountSize ) : dataStart_( s ), dataEnd_( e ), curIndex_( s ), winSize_( 0 ), maxWinSize_( maxWinSize ), maxCountSize_( maxCountSize ) { // データ列が Sliding Window の最大サイズに満たない場合、データ列の大きさを設定する if ( std::distance( s, e ) < maxWinSize_ ) maxWinSize_ = std::distance( s, e ); } /// データ列 container を指定して構築 /// /// Sliding Window のサイズはゼロで初期化され、符号化されるに従って maxWinSize まで増大する template<class Container> SlidingWindow( const Container& container, Code maxWinSize, Code maxCountSize ) : dataStart_( container.begin() ), dataEnd_( container.end() ), curIndex_( container.begin() ), winSize_( 0 ), maxWinSize_( maxWinSize ), maxCountSize_( maxCountSize ) {} /// 現在のデータ列の先頭が辞書バッファの中で一致する部分を探し、位置と長さを返す /// /// search は探索用関数オブジェクトへの参照 template< template<class,class> class SW_Search > void search( SW_Search<In,Code>& search, Code* index, Code* count ) const { search( curIndex_, dataEnd_, winSize_, maxCountSize_, index, count ); } /// 現在の読み込み位置の値を返す value_type value() const { return( *curIndex_ ); } /// 全てのデータ列を読み終えたか bool empty() const { return( curIndex_ == dataEnd_ ); } /// 次に読み込むデータ列の位置を n だけ進める void inc( size_t n ); }; /** 次に読み込むデータ列の位置を n だけ進める **/ template<class In,class Code> void SlidingWindow<In,Code>::inc( size_t n ) { if ( static_cast<size_t>( std::distance( curIndex_, dataEnd_ ) ) < n ) { curIndex_ = dataEnd_; } else { std::advance( curIndex_, n ); } if ( winSize_ < maxWinSize_ ) { winSize_ += n; if ( winSize_ > maxWinSize_ ) winSize_ = maxWinSize_; } }
「Sliding Window」を表すクラスは SlidingWindow で、符号化する対象のデータ列の開始と末尾の次の位置、「Sliding Window」のサイズ、そして符号に含まれる一致データの長さ情報の最大値を渡して構築されます。SlidingWindow の主な役割は、符号化する対象データと「Sliding Window」の現在位置の管理で、一致するデータ列の探索は後述する SW_Search クラスが行います。
メンバ関数 search は、テンプレート引数で渡された関数オブジェクト SW_Search のメンバ関数 operator() を使って処理しているだけで、前述の通り探索は SW_Search に実装されます。次の value 関数は、符号化対象の現在位置 (curIndex_) にあるデータそのものを返します。これは、一致するデータが得られなかった場合にデータそのものを符号列に登録する際に使います。また、empty は全てのデータ列を読み終えたかを判断するための叙述関数、inc は読み込み位置を指定した数だけ進めるための関数です。
SlidingWindow クラスは二つのテンプレート引数 In と Code を持ち、In は符号化対象のデータ列に対する反復子の型、Code は LZ77_CodeGenerator と同様に符号の型を表します。さらに、メンバ関数 search もテンプレート引数 SW_Search を持ち、SW_Search 自身もテンプレート・クラスなので、その宣言は以下のようになっています
template< template<class,class> class SW_Search >
void search( SW_Search<In,Code>& search, Code* index, Code* count ) const
search に対するテンプレート引数 SW_Search の宣言の前にある "template<class,class>" は、SW_Search のテンプレート引数が二つあることを表しています。テンプレート引数そのものは、後の定義部分でコンパイラによって類推が可能なので省略ができます。
SW_Search クラスは SlidingWindow と同じテンプレート引数 In と Code を持ちます。メンバ関数 operator() が最長一致データ列を探索するためのもので、「Sliding Window」の先頭から順に一致するデータ数を求め、その最大値を返すようにしています。線形探索を繰り返し行うことになるので、その処理量は探索対象データ数の二乗のオーダーで増加することになり、あまり効率的なアルゴリズムとは言えません。探索部分を SlidingWindow のメンバ関数にせず独立な関数オブジェクトにしたのは、他のより効率的な探索処理に切り替えできるようにするためです。具体的な手法については後ほど説明します。
/** LZ77法によりデータ列 data を符号化して packed に登録する 符号は LZ77_CodeGenerator により作成され、Code で定義された型で返される。 indexBit は位置情報(現在の位置からの相対距離)のビット数を表し、その他に一致した データ列の長さ (countBit) もまとめて符号列に保持される。 indexBit + countBit が符号のビット数となるように countBit が求められる。 符号列 packed は、処理前に初期化(要素のクリア)がなされる。 データ列 data は符号なし値であることを想定している テンプレート引数の T は data の要素の型 テンプレート引数の SW_SearchType は Sliding Window への探索用関数オブジェクトの型 swSearch は Sliding Window への探索用関数オブジェクト **/ template<class T,class Code,template<class,class> class SW_SearchType> bool LZ77Encode( const std::vector<T>& data, std::vector<Code>* packed, size_t indexBit, SW_SearchType<typename std::vector<T>::const_iterator,Code>& swSearch ) { // 定数宣言 const size_t szCode = sizeof( Code ) / sizeof( char ); // 符号長(バイト数) const size_t bitCode = std::numeric_limits<Code>::digits; // 符号のビット数 const size_t szValue = sizeof( T ) / sizeof( char ); // 値のバイト数 const size_t bitValue = std::numeric_limits<T>::digits; // 値のビット数 if ( &data == 0 || packed == 0 ) return( false ); // indexBit は符号のビット数より小さくなければならない if ( indexBit >= bitCode ) return( false ); size_t countBit = bitCode - indexBit; // 一致したデータ数情報のビット数 Code maxWinSize = pow( 2, indexBit ) - 1; // Sliding Window の最大値 Code maxCountSize = pow( 2, countBit ) - 1; // 一致したデータ数情報の最大値 // 符号ジェネレータ LZ77_CodeGenerator<Code> codeGen( indexBit, countBit ); // Sliding Window SlidingWindow<typename std::vector<T>::const_iterator,Code> sWin( data, maxWinSize, maxCountSize ); Code cacheCode = 0; // 符号のキャッシュ size_t cacheLen = 0; // キャッシュされた符号のビット数 Code index = 0; // 位置情報 Code count = 0; // 一致したデータ長 packed->clear(); // 符号列の初期化 while ( ! sWin.empty() ) { sWin.search( swSearch, &index, &count ); // 符号化 if ( count * szValue > szCode ) { // 先頭ビットに符号を表す 1 を書き込む WriteToArray( static_cast<Code>( 1 ), static_cast<size_t>( 1 ), &cacheCode, &cacheLen, packed ); // 符号の書き込み WriteToArray( codeGen.encode( index, count ), codeGen.bits(), &cacheCode, &cacheLen, packed ); sWin.inc( count ); // データ列をそのまま登録 } else { // 先頭ビットに値を表す 0 を書き込む WriteToArray( static_cast<Code>( 0 ), static_cast<size_t>( 1 ), &cacheCode, &cacheLen, packed ); // 符号の書き込み WriteToArray( sWin.value(), bitValue, &cacheCode, &cacheLen, packed ); sWin.inc( 1 ); } } // 残りビット列の出力 if ( cacheLen > 0 ) packed->push_back( cacheCode << ( bitCode - cacheLen ) ); return( true ); }
LZSS 符号化処理本体の LZ77Encode の、テンプレート引数を含めた宣言もややこしい書き方になっています。
template<class T,class Code,template<class,class> class SW_SearchType>
bool LZ77Encode( const std::vector<T>& data,
std::vector<Code>* packed,
size_t indexBit,
SW_SearchType<typename std::vector<T>::const_iterator,Code>& swSearch )
テンプレート引数の中で、T はデータ列の要素の型、Code は符号データの型、SW_SearchType は SlidingWindow クラスで説明した探索用クラス型を表します。引数の data は符号化対象のデータ列、packed は符号化したデータを保持する配列へのポインタ、indexBit は符号内の位置情報に対するビット数です。最後の swSearch は探索用クラスですが、テンプレート引数の "typename std::vector<T>::const_iterator" が、SlidingWindow や SW_Search で定義された In を意味します。
一致データの長さに対するビット数は引数としては渡されず ( 符号データのビット数 - indexBit ) で計算されるので、符号データの全ビットが利用されることになります。引数として渡すことで、符号長を任意の長さに自由に変えられるようにすることは簡単に対処できます。
一致したデータ列に対し、その長さを符号の長さと比較している個所があります。
if ( count * szValue > szCode ) {
// 符号化して登録
} else {
// データをそのまま登録
}
count * szValue は一致したデータのバイト数、szCode は符号のバイト数で、データのバイト数の方が大きい時だけ符号化を行います。一致する個所がない場合にデータそのものを登録すると前述しましたが、符号化した結果、元のデータより長くなってしまうと符号化する意味がなくなるため、一致個所があっても符号サイズの方が大きければデータをそのまま登録します。符号化する場合は符号の前に 1 を、データをそのまま登録する場合は前に 0 を付け、復号化のときにこのビットを使って処理が振り分けられるようにします。
データをビット単位で配列に書き込む関数は、前章の「圧縮アルゴリズム (4) ハフマン符号化 - 適応型ハフマン圧縮」で紹介した WriteToArray が行います。書き込む内容はいったんバッファ用変数 cacheCode, cacheLen に登録され、バッファが満杯になったら配列に書き込みます。前もってバッファ用変数を用意したり、後始末としてバッファに残ったデータを書き込む処理が必要になるので、クラスとして定義してバッファを内部に持たせた上で、デストラクタでバッファの残りを書かせるようにすれば、呼び出し側をもう少しすっきりした形にすることができそうです。
符号化は count * szValue > szCode が成り立つときだけ行われるので、count > szCode / szValue が成り立ちます。符号の方が元データより小さいサイズならば全てのデータが符号化されるのに対し、符号の方がサイズが大きければ小さな値を持つ count に対しては符号化されない場合があります。例えば、符号サイズが 2 バイト、元のデータが 1 バイトであれば、符号化されるのは count が 3 以上である必要があります。これを利用して、count の最小値がゼロになるように定数を引いておくことで、決められたビット数の中でより大きな長さまで保持できるようにする手法がよく使われます。但し、サンプル・プログラムではその処理は行なっていません。
/** LZ77法により符号列 packed を復号化して data に登録する indexBit は位置情報(現在の位置からの相対距離)のビット数を表し、 データ列の長さ (countBit) は indexBit + countBit が符号のビット数となるように求められる。 テンプレート引数の T は data の要素の型 dataCount は復号化するデータ数 **/ template<class T,class Code> bool LZ77Decode( const std::vector<Code>& packed, std::vector<T>* data, size_t indexBit, typename std::vector<T>::size_type dataCount ) { // 定数宣言 const size_t szCode = sizeof( Code ) / sizeof( char ); // 符号長(バイト数) const size_t bitCode = std::numeric_limits<Code>::digits; // 符号のビット数 const size_t bitValue = std::numeric_limits<T>::digits; // 値のビット数 if ( &packed == 0 || data == 0 ) return( false ); // indexBit は符号のビット数 - 符号長 ( = countBit ) より小さくなければならない if ( indexBit + szCode >= bitCode ) return( false ); size_t countBit = bitCode - indexBit; // 一致したデータ数情報のビット数 Code cacheCode = 0; // 符号のキャッシュ size_t cacheLen = 0; // キャッシュされた符号のビット数 Code code; // 符号情報 Code index = 0; // 位置情報 Code count = 0; // 一致したデータ長 T isCode; // 符号・データ判別フラグ T t; // 符号列からデータを読み込むための変数 // 符号ジェネレータ LZ77_CodeGenerator<Code> codeGen( indexBit, countBit ); // 符号データの現在位置 typename std::vector<Code>::const_iterator cit = packed.begin(); // 復号化したデータ数 typename std::vector<T>::size_type st = 0; while ( st < dataCount ) { // 先頭ビットの取り込み if ( ! ReadFromArray( &cit, packed.end(), &cacheCode, &cacheLen, &isCode, static_cast<size_t>( 1 ) ) ) return( false ); // 符号の場合 if ( isCode != 0 ) { if ( ! ReadFromArray( &cit, packed.end(), &cacheCode, &cacheLen, &code, codeGen.bits() ) ) return( false ); codeGen.decode( code, &index, &count ); typename std::vector<T>::size_type read = data->size() - index; // 前のデータの読み込み開始位置 for ( size_t sz = 0 ; sz < count ; ++sz ) { data->push_back( (*data)[read] ); ++read; } st += count; // データの場合 } else { if ( ! ReadFromArray( &cit, packed.end(), &cacheCode, &cacheLen, &t, bitValue ) ) return( false ); data->push_back( t ); ++st; } } return( true ); }
復号化処理は探索処理や「Sliding Window」の管理等は一切必要がなくなります。符号とデータの判別フラグを 1 ビット読み込み、符号ならばそのビット数分だけ符号列から読み込み、位置と長さの情報に分離してからデータ列の該当部分をコピーします。また、データそのものならばその長さ分だけ符号列から読み込んで、それをデータ列に書き込みます。符号化処理と比較すると非常に単純で高速に処理することができます。符号化に比べて復号処理が非常に速いというのは LZ77 法が持つ特徴の一つになります。なお、データをビット単位で配列から読み込む関数は、前章の「圧縮アルゴリズム (4) ハフマン符号化 - 適応型ハフマン圧縮」で紹介した ReadFromArray が行います。
LZ77 法によって、前章で使ったテスト用の画像を使って処理を行った時の圧縮率を検証した結果を以下に示します。まずは、前章で利用した「風景」画像 10 枚を使った結果です。テスト画像は全て 1024 x 768 のサイズで、1 ピクセルあたり 3 バイトとすれば 2359296 バイトのデータ量です。圧縮率は、符号サイズをこのデータ量で割った比率です。
表の中にある「位置:長さ」は、一致した位置と長さの情報に対するビット数を表しています。符号のサイズは一つを除いて 16 ビットとし、最後のテストだけ 32 ビットで処理しています。「風景」画像の場合、一致した部分の長さに制限をかけて探索範囲を広げた方が圧縮率は高くなる傾向が見られます。しかし、符号を 32 ビットにして制限を緩めても、符号の長さが増えることが逆効果となって圧縮率は悪くなってしまいました。これは、制限を緩めても一致する個所がほとんど得られなかったことを意味します。全体的に、ハフマン符号化よりも圧縮率はよくなっていますが、一部のデータでは符号化すると逆にサイズが増えてしまう場合もあります。
次に、「アニメ」調の画像でテストした結果を示します。
「風景」画像に比べると「アニメ」調の方が圧縮率はよくなっています。また、全体的に見れば探索位置を広げる方が圧縮率はよくなる傾向が見られますが、一部の画像では逆に圧縮率が悪くなる場合もあります。符号長を大きくすることによる効果はほとんど見られません。
最後は、「アニメ」調 GIF 画像です。
前の二つに比べると圧倒的に圧縮率がよくなっています。最も圧縮率がいいのは「位置 : 長さ = 16 : 16 (32bit)」のときで、同じパターンのデータ列がいたるところに、しかも非常に長い部分に対してあることを意味します。
データ列の中の近い位置に同じパターンが多くあるのなら、位置情報は小さめにしておくことができます。逆にパターンが一致する部分の長さが短ければ、長さの情報を小さくすることができます。これとは逆の考え方もできるので、例えば一致する部分は短いが遠くにも一致するパターンが点在しているのなら位置情報を長めにした方が有利になり、一致する部分が長く近隣に同じパターンが集中する傾向にあるなら長さの情報を大きくした方が有利になります。自然画の場合は、一致するパターンが長く連続することはほとんどないので位置情報を長めにした方が有利となり、テスト結果からも実際にその傾向が見られます。アニメ調の画像は逆に、一致するパターンが長めになるので長さ情報が小さいと圧縮率が悪くなります。どのタイプの画像にもそれなりの効率で圧縮できるようにするためには、位置と長さの情報を半々くらいの大きさにしておくのが無難なようです。
前述の通り、一致する部分の探索に対する処理量は探索する幅に依存します。一致する部分の最大の長さを大きくしても、その長さまで比較処理を行うことは稀なので、処理時間に影響するのは位置情報の最大値、すなわち Sliding Window のサイズの方です。サンプル・プログラムの中で紹介した探索法では、位置情報を保持するためのビット数を大きくするほど二乗のオーダーで処理時間が増大するため、あまり効率のいいプログラムとは言えません。これを回避するため、一致するパターンの候補をあらかじめ絞り込むことを検討してみます。
先に述べた通り、符号化は対象となるデータ列の長さが符号のサイズを超えた場合のみ行われます。従って、( 符号サイズ + 1 ) の長さ分だけ一致したデータが同じグループになるように登録しておいて、そのメンバだけを対象に残りの部分を比較するようにすれば、比較処理を大きく削減することができます。グループ化をどのように行うかについてはいろいろな手法が考えられますが、有名なやり方としてハッシュ法や木構造を使った探索法があります。その中のいくつかは企業が特許を取得している場合もありますが、フリーソフトとして公開されているいくつかの圧縮ツールではその特許に抵触しない形で実装されています。また、すでに有効期限が切れている特許も数多くあるようです。
過去に、自由に利用できていた手法に対して企業がライセンスを要求するといったニュースが話題になったことがありました。これは現在でもあまり変わりはなく、特許に抵触していないかを調べるのにかなりの時間を費やすなど、開発以外の部分で余計な時間がかかることもよくあるようです。個人的に、企業がアルゴリズムに対して特許を取得するというのはまさに「百害あって一利なし」だと思います。
STL ( Standard Template Library ) のコンテナ・クラス map を使い、候補を絞り込んだ探索を行う関数オブジェクトのサンプル・プログラムを以下に示します。
/** Sliding Window 上のデータ探索用関数オブジェクト std::map / std::unordered_map を利用して、データ列の先頭が等しい位置を あらかじめコンテナに登録しておく。データ列の一致する部分を探索する時、 このコンテナを使って対象を絞り込む。 **/ template<class In,class Code,class Map> class SW_Search_UseMap { // operator() 関数で前回登録した反復子の次(=今回登録する反復子) // insert 関数で Fragment 型を要素とするコンテナに登録する時、 // curIndex_ から現在位置までをまとめて登録するために使う In curIndex_; Map map_; // 反復子登録用マップ型コンテナ // 反復子 s をコンテナ map_ に追加する typename Map::mapped_type* insert( In s ); public: /// データ列の開始を指定して構築 SW_Search_UseMap( In dataStart ) : curIndex_( dataStart ) {} /// 現在のデータ列の先頭 dataStart が辞書バッファの中で一致する部分を探し、 /// 位置と長さを index, count に返す。 /// /// dataEnd はデータ列の末尾の次の反復子、winSize は辞書バッファのサイズ、 /// maxCountSize はデータ列を比較する長さの最大値。 void operator()( In dataStart, In dataEnd, Code winSize, Code maxCountSize, Code* index, Code* count ); }; /** 反復子 s をコンテナに追加する **/ template<class In,class Code,class Map> typename Map::mapped_type* SW_Search_UseMap<In,Code,Map>::insert( In s ) { typename Map::iterator it = map_.find( s ); if ( it == map_.end() ) { map_[s].push_back( s ); return( 0 ); } else { ( it->second ).push_back( s ); return( &( it->second ) ); } } /** 現在のデータ列の先頭 dataStart が辞書バッファの中で一致する部分を探し、 位置と長さを index, count に返す dataEnd はデータ列の末尾の次の反復子、winSize は辞書バッファのサイズ fragment は Fragment を保持するコンテナで、ここからデータ列が一致する候補を探索する **/ template<class In,class Code,class Map> void SW_Search_UseMap<In,Code,Map>::operator() ( In dataStart, In dataEnd, Code winSize, Code maxCountSize, Code* index, Code* count ) { // 位置とデータ数はデフォルト値(ゼロ)で初期化 *index = *count = Code(); // 未登録分を追加 while ( curIndex_ != dataStart ) { insert( curIndex_ ); ++curIndex_; } // 現在位置をコンテナに追加し、同時に先頭のデータ列が同じ要素のリストを取得 typename Map::mapped_type* inList = insert( dataStart ); if ( inList == 0 ) return; typename Map::mapped_type::const_iterator winList = --( inList->end() ); while ( winList-- != inList->begin() ) { In winStart = *winList; // 辞書バッファ内の比較対象データの先頭 // Sliding Window 外なら処理終了 if ( std::distance( winStart, dataStart ) > winSize ) break; In winP = winStart; // 辞書バッファ内の比較対象データの先頭 In dataP = dataStart; // 符号化対象のデータの先頭 // 符号化するデータと一致する部分を探索 size_t sz = 0; // 一致部分のデータ数 while ( dataP != dataEnd ) { if ( *winP != *dataP || sz == maxCountSize ) break; ++winP; ++dataP; ++sz; } // index と count の更新 if ( sz > *count ) { *index = std::distance( winStart, dataStart ); *count = sz; } // 比較対象の最大データ数に達したら処理をやめる if ( *count == maxCountSize ) { break; } } } /** SW_Search_UseMap を利用して Sliding Window 上のデータを探索する コンテナは std::map を利用 **/ template<class In,class Code> class SW_Search_Map { // 二つの反復子の先頭から符号化可能な最小の長さまで // データの大小を比較する関数オブジェクト struct LessFragment; // 反復子登録用マップ型コンテナ typedef std::map < In, std::vector<In>, LessFragment > container_type; // 探索用オブジェクト (SW_Search_UseMap) SW_Search_UseMap<In,Code,container_type> search_; public: /// データ列の開始を指定して構築 SW_Search_Map( In dataStart ) : search_( dataStart ) {} /// 現在のデータ列の先頭 dataStart が辞書バッファの中で一致する部分を探し、 /// 位置と長さを index, count に返す。 /// /// dataEnd はデータ列の末尾の次の反復子、winSize は辞書バッファのサイズ、 /// maxCountSize はデータ列を比較する長さの最大値。 void operator()( In dataStart, In dataEnd, Code winSize, Code maxCountSize, Code* index, Code* count ) { search_( dataStart, dataEnd, winSize, maxCountSize, index, count ); } }; /** 二つの反復子の先頭から符号化可能な最小の長さまで データの大小を比較する関数オブジェクト **/ template<class In,class Code> struct SW_Search_Map<In,Code>::LessFragment { // データの先頭の大小を比較する bool operator()( In s1, In s2 ) const { // 反復子 In の値に対する型 typedef typename std::iterator_traits<In>::value_type value_type; // 符号化した方が圧縮できるデータ数 const size_t szCmp = sizeof( Code ) / sizeof( value_type ) + 1; for ( size_t st = 0 ; st < szCmp ; ++st ) { if ( *s1 < *s2 ) return( true ); if ( *s1++ > *s2++ ) return( false ); } return( false ); } };
SW_Search_UseMap は、マップ型コンテナを使って候補をグループ化しながら探索を行う機能を実装したクラスです。テンプレート引数の In は符号化対象のデータ列に対する反復子の型、Code は符号の型を表し、最後の Map はグループ化用のコンテナの型として定義されています。Map 型は In 型のキーと配列 ( STL の vector ) 型の値を持つコンテナクラスで、メンバ関数 find 使って引数のキーから値となる対象の配列へのポインタを取得します。値となる配列の要素も In 型で、見つかった順に末尾に追加していきます。
Map 型のコンテナであるメンバ変数 map_ は最初は空の状態で符号化処理が開始されます。符号化処理の中で、一致する部分の探索処理として SW_Search_UseMap のメンバ関数 operator() が呼び出された時、最初に現在のデータ列の位置を map_ へ登録します。このとき、先頭の部分が一致する同じグループが見つかったらそのポインタを返し、ない場合は NULL を返します。NULL が返されたときは他に候補はない (初めて出現したグループ) ということになるので処理を終了し、そうでなければポインタの指す配列の要素から順番に一致する部分の長さを調べ、その最長の位置を戻り値として返します。
現在位置は常に配列の末尾に登録されます。従って、末尾の要素 (これが新規登録された現在位置です) より一つ前の要素から順に前側へたどることで最も近いデータ列から探索を行うことができ、Sliding Window の範囲以上に離れたら処理を終了させることで必要最小限の部分だけ探索することができます。
SW_Search_UseMap を使い、Map 型のコンテナとして map クラスを指定して実際に処理を行うためのクラスが SW_Search_Map で、内部に SW_Search_UseMap 型のオブジェクトを保持してそのメンバ関数を呼び出すだけの処理を行います。キーは In 型の反復子なので、通常の大小判定では正しい結果が得られません。そのため、大小判定を行うための関数オブジェクト LessFragment を作成し、map オブジェクトの構築時にこの関数オブジェクトが使われるようにします。LessFragment の判定用関数 operator() は、符号化した方が小さくなるデータ数分だけ二つの反復子から始まるデータ列を順に比較する処理を行なっています。
コンテナ・クラスを SW_Search_UseMap ではなくわざわざ別クラスで定義するようにしたのは、利用するコンテナを切り替えたいのが目的です。ここでは map を使った例だけを紹介していますが、同様なやり方で ordered_map クラスを使うことも簡単にできます。
線形探索を使った場合 (Linear) と、map 型・unordered_map 型を使って候補を絞り込んだ場合 ( Map, Unordered Map ) で処理時間を計測した結果を以下に示します。利用した画像は圧縮率調査で利用したものと同じです。unordered_map 型はハッシュ値とキーそのものの比較という二段階での探索を行うため、ハッシュ値を計算する関数とキーを比較する関数の二つを定義しておく必要があります。後者の方は、先頭の数個が等しいかを比較するだけなので、map にて定義した LessFragment の判定用関数とほとんど同じ構成になります。前者は、対象のデータ列を先頭から順に必要分だけ読み、各値を 4 ビット上位にシフトしながら排他的論理和 ( XOR ) 演算する処理を繰り返し、最後に STL にあるハッシュ値算出用関数 hash に計算結果を渡してハッシュ値を求めています。
まずは「風景」画像での処理時間です。グラフは各画像の処理時間を積み重ねた棒グラフですが、縦軸の値は時間をミリ秒にした上で底を 10 とした対数に変換しています。従って、目盛りが 10 上がると処理時間は 10 倍になっていることを意味します。
Linear の場合、Sliding Windows の範囲を大きくするに従って時間が大きくなっていく様子を確認することができます。4 ビット ( 長さ 16 倍 ) の増加に対し、だいたい 10 倍ずつ時間が増大しています。それに対して Map, Unordered Map では時間の増大はほとんど見られません。しかし、Sliding Windows の範囲が小さければ、Linear の方が圧倒的に速く処理できることも確認できます。探索範囲が小さければ、処理内容が単純な分 Linear の方が高速になるようです。
「アニメ」調の場合も「風景」画とほぼ同様な結果が得られました。「風景」と比べると全体的に処理時間は短くなる傾向にありますが、Map, Unordered Map による探索で 32 ビット符号を使った場合は非常にバラツキが大きく、合計時間は「風景」の場合よりも増えています。
「アニメ」調 GIF 画像の場合、さらに処理時間は短縮される反面、バラツキも顕著になり、Map や Unordered Map による探索でも 10 秒を超える場合がいくつか見られます。Map や Unordered Map による探索で処理時間が長くなる要因として、先頭の数個だけデータが一致するパターンに偏りがある場合が考えられます。そのようなデータ列が大量に発生した場合、データを一つずつ比較する探索処理は増加することになり、処理時間は Linear の場合に近づいてゆきます。処理が複雑になる分、最悪は単純な線形探索よりも時間がかかることもあり得ます。
LZ77 (LZSS) 符号化に、以前紹介した「ハフマン符号化」を組み合わせることで圧縮率をさらに高める方法があり、これは「デフレート (Deflate)」と呼ばれています。デフレートでは、データそのものと一致した部分の長さをまとめてハフマン符号化し、位置情報については別系統のハフマン木で符号化を行います。ハフマン符号化には「静的ハフマン符号化」が採用されているようですが、あらかじめ値に対して仕様で定義された符号を使う方法もあるようです。また、LZSS 符号化を行わずにそのままハフマン符号化を行うオプションもあります。
「LZ78 法」では、データ列を辞書に登録しておいて、辞書にあるデータはその場所に置き換えることで圧縮を行います。前の例の
において、"012340123" が辞書の先頭 ( = [0] ) にあった場合、一気に
にまで圧縮できることになります。
ここで問題になるのは辞書の作り方です。あらかじめデータ列に存在するものが決まっているならば、例えば住所などの情報を管理する場合に各都道府県や市・町などの情報を辞書に登録しておくように先に辞書を作成することができるのなら、最適化を行うことで ( よく出現する名前はより短い符号に置き換えるなど ) 高い圧縮を実現することが可能になります。しかし画像のように、どのようなデータ列が存在するのか予測できないような場合はこのやり方は採用できません。よって圧縮を行いながら、同時に辞書を作成していく必要があります。
1984 年に「Terry Welch」によって提唱された「Lempel-Ziv-Welch (LZW) 法」では、次のような手順で辞書の作成とデータ圧縮を同時に行っています。
0 から 255 までのデータが、辞書番号と値が一致する形であらかじめ辞書に登録されているとき、データ列 012340123012340123012340123 は以下のように圧縮されます。
| w | K | wK | 新しい辞書番号 ()内は対象のパターン | 出力データ ()内は対象のパターン |
|---|---|---|---|---|
| null | 0 | 0 | ||
| 0 | 1 | 01 | 256 (01) | [0] (0) |
| 1 | 2 | 12 | 257 (12) | [1] (1) |
| 2 | 3 | 23 | 258 (23) | [2] (2) |
| 3 | 4 | 34 | 259 (34) | [3] (3) |
| 4 | 0 | 40 | 260 (40) | [4] (4) |
| 0 | 1 | 01 | ||
| 01 | 2 | 012 | 261 (012) | [256] (01) |
| 2 | 3 | 23 | ||
| 23 | 0 | 230 | 262 (230) | [258] (23) |
| 0 | 1 | 01 | ||
| 01 | 2 | 012 | ||
| 012 | 3 | 0123 | 263 (0123) | [261] (012) |
| 3 | 4 | 34 | ||
| 34 | 0 | 340 | 264 (340) | [259] (34) |
| 0 | 1 | 01 | ||
| 01 | 2 | 012 | ||
| 012 | 3 | 0123 | ||
| 0123 | 0 | 01230 | 265 (01230) | [263] (0123) |
| 0 | 1 | 01 | ||
| 01 | 2 | 012 | ||
| 012 | 3 | 0123 | ||
| 0123 | 4 | 01234 | 266 (01234) | [263] (0123) |
| 4 | 0 | 40 | ||
| 40 | 1 | 401 | 267 (401) | [260] (40) |
| 1 | 2 | 12 | ||
| 12 | 3 | 123 | 268 (123) | [257] (12) |
| 3 | --- | --- | [3] (3) |
LZW 法の利点として、適応型ハフマン圧縮法と同様に辞書を保持しておく必要がないことが挙げられます。辞書は展開時に再度作成することができます。
上の例で圧縮したデータ列を展開する場合、以下のようになります。
| w | K | wK | 新しい辞書番号 ()内は対象のパターン | 出力データ |
|---|---|---|---|---|
| [0] | --- | --- | 0 | |
| [0] | [1] | 01 | 256 (01) | 1 |
| [1] | [2] | 12 | 257 (12) | 2 |
| [2] | [3] | 23 | 258 (23) | 3 |
| [3] | [4] | 34 | 259 (34) | 4 |
| [4] | [256] | 40 | 260 (40) | 01 |
| [256] | [258] | 012 | 261 (012) | 23 |
| [258] | [261] | 230 | 262 (230) | 012 |
| [261] | [259] | 0123 | 263 (0123) | 34 |
| [259] | [263] | 340 | 264 (340) | 0123 |
| [263] | [263] | 01230 | 265 (01230) | 0123 |
| [263] | [260] | 01234 | 266 (01234) | 40 |
| [260] | [257] | 401 | 267 (401) | 12 |
| [257] | [3] | 123 | 268 (123) | 3 |
符号化の様子を見ると明らかなように、新たに追加される辞書は、出力されるデータに K を追加したデータ列になります。K は次に出力されるデータ列の先頭の要素なので、復号化のときは入力した符号が表すデータ列の先頭の要素を直前の符号のデータ列に追加して新たに追加すれば、符号化の時と同じ順序で辞書が作成されます。
ここで、辞書へのデータ登録をどのように行うかによって処理時間やメモリ使用量が大幅に変わります。データ列をそのまま辞書に登録すれば処理が進むに従ってデータ列も長くなるので、メモリの使用量は増加し処理時間も長くなります。また、辞書からの検索時間がなるべく短くなるようなデータ構造にする必要もあります。
辞書検索を高速に行うためのデータ構造に「トライ木 ( Trie )」があります。トライ木は、データの種類分 ( 8 ビットサイズのデータならば 0 - 255 の 256 個分 ) の子を持つことのできる節からなる木構造で、「Digital Tree」「Radix Tree」「Prefix Tree」などとも呼ばれます。
しかし、一つの節に 256 個分の子を登録するためのエリアを確保するとメモリを大量に消費してしまうため、子をリスト構造にして接続することで消費エリアを抑えます。節の部分を構造体で表わすと次のようになります。
template<typename T> struct Node { T value; // 値 size_type bros; // 兄弟の節へのリンク size_type child; // 子の節へのリンク };
bros は同じレベルの節への参照先 (添字)、child は子への参照先を表わします。圧縮処理の前に、各 Node へパターンコードを、bros で接続しながら追加していきます。この時、子へのポインタは NULL 扱いにしておきます。
 |
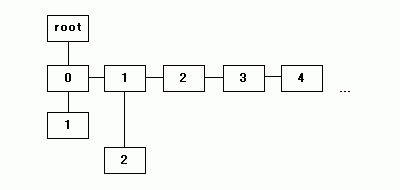
データを読み込みながら child によって子の節をたどっていき、なければ新たに追加していくことで、トライ木は徐々に大きくなっていきますが、子へのリンクをたどるときに、子にあたる節が持っている bros を使ってリンクをたどってデータを検索する部分が通常の二分木とは異なる処理になります。
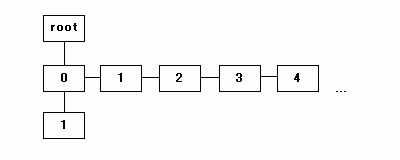 |
 |
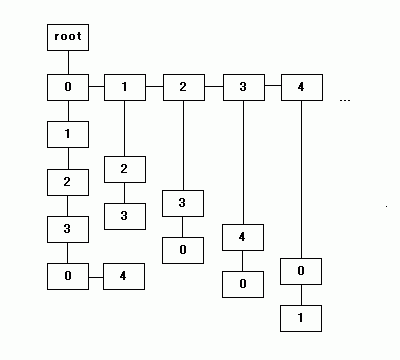 |
上記イメージで、右方向に伸びたリンクが bros での接続、下方向が child での接続を示しています。最後のトライ木では、"0123" と下方向に伸びたリンクの次の子が、"0" と "4" の二つのリスト構造になっています。
前述の通り、トライ木は辞書を効率よく作成・検索することができるデータ構造です。例えば各節に文字を一つずつ登録し、親から子への文字の並びで単語を表すようにした時、"appear" と "apple" はどちらも a-p-p の順で子をたどり、4 文字目の "e" と "l" が兄弟の節に登録されます。また、"applet" という単語は "apple" と同じ子をたどり、5 文字目の "e" の下に子の節 "t" が追加された形で表現されます。
トライ木を表現したクラスのサンプル・プログラムを以下に示します。
/** トライ木 (Trie) クラス **/ template<typename T> class Trie { struct Node; // 節 Node の前方宣言 public: typedef typename std::vector<Node> array_type; // 節の配列の型 typedef typename array_type::size_type size_type; // 配列の添字・大きさの型 private: array_type nodes; // 節の配列 public: /// NULL を表す添字を返す size_type nullNode() { return( nodes.max_size() ); } /// 根の節の添字を返す static size_type rootNode() { return( 0 ); } private: /** 節を表す内部クラス **/ struct Node { T value; // 値 size_type bros; // 兄弟の節へのリンク size_type parent; // 親の節へのリンク size_type child; // 子の節へのリンク unsigned int level; // 根からの距離 // 値・親の節の添字とレベルを指定して構築 Node( T t, size_type p, unsigned int l ) : value( t ), parent( p ), level( l ) {} }; public: /// デフォルト・コンストラクタ /// /// 根の節だけを追加する。根の節の添字は必ずゼロになる。 Trie() { init(); } /// 木の初期化 /// /// 要素を全消去して根の節だけを追加する。 void init() { nodes.clear(); add( nullNode(), 0 ); setChild( rootNode(), nullNode() ); setBros( rootNode(), nullNode() ); } /// 登録されている節の個数を返す size_type size() const { return( nodes.size() ); } /// parent を親として、newVal を値に持つ新たな節を追加する /// /// 戻り値として新しい節の添字を返す size_type add( size_type parent, T newVal ); /// 添字 index の節の子から値が value と一致するものを探し、その添字を返す /// /// 子供の節がない場合は新規に追加を行い nullNode を返す size_type findChild( size_type index, T value ); /// 添字 index の節の兄弟から値が value と一致するものを探し、その添字を返す /// /// 見つからない場合は新規に追加を行い nullNode を返す size_type findBros( size_type index, T value ); /// 添字 index の節の値を返す T operator[]( size_type index ) const { return( nodes.at( index ).value ); } /// 添字 child の節の親を返す size_type parent( size_type child ) const { return( nodes.at( child ).parent ); } /// 添字 index の節のレベルを返す unsigned int level( size_type index ) const { return( nodes.at( index ).level ); } /// 添字 child の節を添字 parent の節の子としてリンクする void setChild( size_type parent, size_type child ) { nodes.at( parent ).child = child; } /// 添字 littleBros の節を添字 bigBros の節の弟としてリンクする void setBros( size_type bigBros, size_type littleBros ) { nodes.at( bigBros ).bros = littleBros; } }; /// parent を親として、newVal を値に持つ新たな節を追加する template<typename T> typename Trie<T>::size_type Trie<T>::add( size_type parent, T newVal ) { nodes.push_back( Node( newVal, parent, ( parent == nullNode() ) ? 0 : nodes.at( parent ).level + 1 ) ); nodes.back().child = nodes.back().bros = nullNode(); return( nodes.size() - 1 ); } /// 添字 index の節の子から値が value と一致するものを探し、その添字を返す /// /// 子供の節がない場合は新規に追加を行い nullNode を返す template<typename T> typename Trie<T>::size_type Trie<T>::findChild( size_type index, T value ) { if ( nodes.at( index ).child == nullNode() ) { setChild( index, add( index, value ) ); return( nullNode() ); } else { return( findBros( nodes.at( index ).child, value ) ); } } /// 添字 index の節の兄弟から値が value と一致するものを探し、その添字を返す /// /// 見つからない場合は新規に追加を行い nullNode を返す template<typename T> typename Trie<T>::size_type Trie<T>::findBros( size_type index, T value ) { for ( ; nodes.at( index ).value != value ; index = nodes.at( index ).bros ) { if ( nodes.at( index ).bros == nullNode() ) { setBros( index, add( nodes.at( index ).parent, value ) ); return( nullNode() ); } } return( index ); }
クラス Trie はテンプレート引数 T を持ち、その引数は節が保持する値の型を表します。内部に節を表す構造体 Node を持っていますが、最初に示した構造体とは少し異なり親へのリンク ( parent ) と階層の深さ ( level ) の二つのメンバ変数が追加されています。
節を登録する配列には STL ( Standard Template Library ) の可変長配列 vector を利用します。根の節は必ず先頭の要素とし、構築時には根の節だけを追加して初期化しておきます。空の節を表す添字は vector が保持可能な最大要素数とし、これは vector のメンバ関数 max_size を使って取得します。
子や兄弟方向へたどりながら指定した値を探索するメンバ関数として findChild, findBros があります。findChild は、子の節がない場合は節を追加し、見つかった場合は findBros を呼び出して兄弟方向へさらに探索を進めます。findBros も兄弟の節の中で目的の値が見つからなければ新たに節を追加します。節 Node に対して外部から直接アクセスすることができないため、子や兄弟とつなげるときは、setChild や setBros を利用します。その他のメンバ関数として、節を追加するための add や、節の値を返す operator[]、親の節の添字を返す parent、節のレベル(階層の深さ)を返す level があります。
トライ木のクラスが完成すれば、LZW 符号化の実現はそれほど難しくはありません。以下にサンプル・プログラムを示します。
/// LZW 符号の型 /// unsigned char 型の Trie クラスの size_type を型とする typedef Trie<unsigned char>::size_type lzw_code_type; /* 辞書を初期化する Trie 型の辞書 trie の根に unsigned char 型の要素を子の節として追加する */ void SetDefaultNode( Trie<unsigned char>* trie ) { trie->init(); // 値ゼロの節を根の最初の子として登録 lzw_code_type bigBros = trie->add( trie->rootNode(), 0 ); trie->setChild( trie->rootNode(), bigBros ); // 兄弟の節の末尾に逐次追加する for ( unsigned int i = 1 ; i <= std::numeric_limits<unsigned char>::max() ; i++ ) { lzw_code_type littleBros = trie->add( trie->rootNode(), i ); trie->setBros( bigBros, littleBros ); bigBros = littleBros; } } /* 添字 index のビット数を数えて返す */ lzw_code_type GetBitSize( lzw_code_type index ) { /// 添字の最大ビット数 lzw_code_type maxBitSize = std::numeric_limits<lzw_code_type>::digits; lzw_code_type res = 0; // 求めるビット数 for ( lzw_code_type i = 1 ; i <= maxBitSize ; ++i ) { if ( ( index & 1 ) != 0 ) res = i; index >>= 1; } return( res ); } /* LZW法により data を符号化して packed に登録する packed は符号化の前に初期化(要素のクリア)を行う */ bool LZWEncode( const std::vector<unsigned char>& data, std::vector<lzw_code_type>* packed ) { // Trie 型の辞書 Trie<unsigned char> dictionary; SetDefaultNode( &dictionary ); // 読み込んだデータを持つ節の添字(符号として登録される値) lzw_code_type dicIdx = dictionary.rootNode(); // 登録した符号の最大値 lzw_code_type maxDicIdx = dicIdx; std::vector<lzw_code_type> buffer; // 符号列を一時的に保持する配列 std::vector<unsigned char>::const_iterator src = data.begin(); // データの読み込み位置 while ( src != data.end() ) { // dicIdx の節に対して、次に読み込んだデータを持つ子の節を探す lzw_code_type childIdx = dictionary.findChild( dicIdx, *src ); // 見つかった場合、dicIdx を子の節の添字に置換して次のデータを読む if ( childIdx != dictionary.nullNode() ) { dicIdx = childIdx; ++src; // 見つからなければ dicIdx 節の添字を符号列に追加して根の節の添字に初期化する } else { // 添字の最小値は根を除いた 1 なので、ゼロになるように 1 を減算しておく --dicIdx; buffer.push_back( dicIdx ); if ( dicIdx > maxDicIdx ) maxDicIdx = dicIdx; // 符号の最大値チェック dicIdx = dictionary.rootNode(); } } // 符号列に登録されていない最後の添字を追加する if ( dicIdx != dictionary.nullNode() ) { // 添字の最小値は根を除いた 1 なので、ゼロになるように 1 を減算しておく --dicIdx; if ( dicIdx > maxDicIdx ) maxDicIdx = dicIdx; buffer.push_back( dicIdx ); } // 実際の符号の最大ビット数に合わせて詰めて登録する size_t bitSize = GetBitSize( maxDicIdx ); // 符号の最大ビット数 lzw_code_type cacheCode = 0; // 符号のキャッシュ size_t cacheLen = 0; // キャッシュされた符号のビット数 packed->clear(); // 符号列の初期化 packed->push_back( bitSize ); // 符号列の先頭に最大ビット数を登録する for ( std::vector<lzw_code_type>::const_iterator cit = buffer.begin() ; cit != buffer.end() ; ++cit ) { WriteToArray( *cit, bitSize, &cacheCode, &cacheLen, packed ); } // 残りビット列の出力 if ( cacheLen > 0 ) packed->push_back( cacheCode << ( std::numeric_limits<lzw_code_type>::digits - cacheLen ) ); return( true ); } /* LZW法により符号列 packed を復号して data に登録する 異なる符号列からまとめて複合できるように、data は初期化(要素のクリア)は行わない。 */ bool LZWDecode( const std::vector<lzw_code_type>& packed, std::vector<unsigned char>* data, std::vector<unsigned char>::size_type dataCount ) { // Trie 型の辞書 Trie<unsigned char> dictionary; SetDefaultNode( &dictionary ); // 直前に読み込んだ符号 lzw_code_type preIndex = dictionary.nullNode(); // 復号データの初期サイズ std::vector<unsigned char>::size_type startCnt = data->size(); // 符号列の読み込み位置 std::vector<lzw_code_type>::const_iterator src = packed.begin(); if ( src == packed.end() ) return( false ); size_t bitSize = *src++; // 符号のビット数は符号列の先頭から取得 lzw_code_type index; // 読み込んだ符号(=節の添字) lzw_code_type cacheCode = 0; // 符号のキャッシュ size_t cacheLen = 0; // キャッシュされた符号のビット数 while ( data->size() - startCnt < dataCount ) { if ( ! ReadFromArray( &src, packed.end(), &cacheCode, &cacheLen, &index, bitSize ) ) return( false ); ++index; // 符号化の時、最小値がゼロになるように 1 減算していたため補正 // 辞書の追加 // 読み込んだ節から先頭の要素を取得して、直前の節を親として追加する if ( preIndex != dictionary.nullNode() ) { lzw_code_type root = ( index >= dictionary.size() ) ? preIndex : index; while ( dictionary.parent( root ) != dictionary.rootNode() ) root = dictionary.parent( root ); dictionary.add( preIndex, dictionary[root] ); } preIndex = index; // 符号の更新 // パレットの展開 unsigned int level = dictionary.level( index ); // 節のレベル(=読み込むデータ数) data->resize( data->size() + level ); // 読み込む数だけリサイズ std::vector<unsigned char>::iterator d = data->end(); while ( dictionary.parent( index ) != dictionary.nullNode() ) { *( --d ) = dictionary[index]; // レベルよりたどった数が多くなることはあり得ない if ( level-- == 0 ) return( false ); index = dictionary.parent( index ); } } return( true ); }
符号は Trie クラスにある size_type 型 ( 節の添字 ) で表されます。これは typedef を使って lzw_code_type と別名で定義します。なお、今までの符号化は値を任意とするため型はテンプレート引数で指定するようにしていましたが、今回は unsigned char 固定としてます。辞書の初期化は SetDefaultNode 関数で行い、根の節に対して 0 を値とする節を子として登録し、1 から 255 までの値を順に兄弟の節として追加します。
符号化は LZWEncode で行います。内容は前節で説明した通りで、値を読み込みながらトライ木を探索し、値が見つからなくなったらその時の添字を符号として登録して探索個所を根の節に戻す操作を繰り返します。なお、符号に変換した後、その最大ビット数を使って不要なビットを削除する処理を最後に行なっています。復号化は LZWDecode が行い、読み込んだ添字の位置の節 ( index ) から親方向にたどって先頭の値を取得し、直前に読み込んだ節 ( preIndex ) にその値を追加します。あとは添字の位置で表現されたデータ列を出力して一回のパスが完了し、これを繰り返すことで元のデータを復元することができます。
辞書を作成するときは、読み込んだ添字の位置の節から親方向にたどって得られる先頭の値を直前の節に追加する処理を行えばいいはずです。しかし、実際の処理は以下のようになっています。
// 辞書の追加 // 読み込んだ節から先頭の要素を取得して、直前の節を親として追加する if ( preIndex != dictionary.nullNode() ) { lzw_code_type root = ( index >= dictionary.size() ) ? preIndex : index; while ( dictionary.parent( root ) != dictionary.rootNode() ) root = dictionary.parent( root ); dictionary.add( preIndex, dictionary[root] ); } preIndex = index; // 符号の更新
具体的には、読み込んだ添字に該当する節が存在しない場合に、直前の節から先頭要素を取得するような仕組みになっています。このような状態は、符号化の時に、直前に追加した辞書が符号として出力された場合に起こり得ます。
| w | K | wK | 新しい辞書番号 ()内は対象のパターン | 出力データ ()内は対象のパターン |
|---|---|---|---|---|
| null | 0 | 0 | ||
| 0 | 1 | 01 | 01 (256) | 0 (0) |
| 1 | 0 | 10 | 10 (257) | 1 (1) |
| 0 | 1 | 01 | ||
| 01 | 0 | 010 | 010 (258) | 256 (01) |
| 0 | 1 | 01 | ||
| 01 | 0 | 010 | ||
| 010 | 1 | 0101 | 0101 (259) | 258 (010) → 直前に追加された辞書番号 |
| 1 | --- | --- | 1 (1) |
| w | K | wK | 新しい辞書番号 ()内は対象のパターン | 出力データ |
|---|---|---|---|---|
| [0] | --- | --- | 0 | |
| [0] | [1] | 01 | 01(256) | 1 |
| [1] | [256] | 10 | 10(257) | 01 |
| [256] | [258] | 01? | 01?(258)→辞書が存在しない | 01? |
| [258] | [1] | 01?1 | 01?1(259) | 1 |
前述の通り、新たに追加される辞書は出力されるデータに K を追加したデータ列になります。例えば上記の例では、辞書番号 258 (010) は出力データ 256 (01) に K の値 "0" が追加されています。従って、符号が直前に追加された辞書であるならば、それは前に出力した辞書に要素を追加した結果の辞書ということになり、直前に展開したときの辞書から先頭要素を取得しても結果は変わらないということになります。
| w | K | wK | 新しい辞書番号 ()内は対象のパターン | 出力データ |
|---|---|---|---|---|
| [0] | --- | --- | 0 | |
| [0] | [1] | 01 | 01 (256) | 1 |
| [1] | [256] | 10 | 10 (257) | 01 |
| [256] | [258]→[256] | 010 | 010 (258) | 010 |
| [258] | [1] | 0101 | 0101 (259) | 1 |
LZ77 符号化の時と同じ条件で LZW 符号化での圧縮率と処理時間を計測した結果を以下に示します。まずは「風景」画像からです。比較用に LZ77 符号化の計測結果 ( 全体的に圧縮率のよい「位置:長さ = 12:4 (16bit)」の条件 ) を併せて示してあります。
| LZW 符号化 | LZ77 符号化 | ||||
|---|---|---|---|---|---|
| 符号サイズ (Bytes) | 圧縮率(%) | 符号化時間 (sec) | 復号化時間 (sec) | 符号サイズ (Bytes) | 圧縮率(%) |
| 1740752 | 73.78 | 1.200 | 0.1301 | 1555894 | 65.95 |
| 1968640 | 83.44 | 1.513 | 0.09012 | 1848430 | 78.35 |
| 1764192 | 74.78 | 1.054 | 0.08227 | 1749036 | 74.13 |
| 2391048 | 101.3 | 2.072 | 0.09990 | 2444150 | 103.6 |
| 2103216 | 89.15 | 1.695 | 0.07875 | 1955186 | 82.87 |
| 2392848 | 101.4 | 1.991 | 0.1003 | 2505376 | 106.2 |
| 1786072 | 75.70 | 1.034 | 0.07821 | 1837206 | 77.87 |
| 2047632 | 86.79 | 1.340 | 0.07865 | 2045092 | 86.68 |
| 2252640 | 95.48 | 1.743 | 0.08951 | 2250662 | 95.40 |
| 1325280 | 56.17 | 0.5633 | 0.05521 | 989242 | 41.93 |
圧縮率は LZ77 符号化と大きな差はありませんでした。若干、LZ77 の方が圧縮率は高いようですが、傾向に違いは見られません。LZ77 符号化も LZW も過去に出現したパターンを使って圧縮するため、大きな差は生じないようです。また、符号化に比べて復号化の方が圧倒的に速いという特徴も一致しています。
次は「アニメ」調画像での結果です。ここでも LZ77 符号化の計測結果は「位置:長さ = 12:4 (16bit)」の条件下でのものを示しています。
| LZW 符号化 | LZ77 符号化 | ||||
|---|---|---|---|---|---|
| 符号サイズ (Bytes) | 圧縮率(%) | 符号化時間 (sec) | 復号化時間 (sec) | 符号サイズ (Bytes) | 圧縮率(%) |
| 1432664 | 60.72 | 1.190 | 0.09156 | 1468350 | 62.24 |
| 1241760 | 52.63 | 0.7458 | 0.07274 | 1265118 | 53.62 |
| 1040984 | 44.12 | 0.5688 | 0.06905 | 1109056 | 47.01 |
| 1392816 | 59.04 | 0.8323 | 0.07324 | 1245790 | 52.80 |
| 482720 | 20.46 | 0.2204 | 0.03632 | 718940 | 30.47 |
| 1728976 | 73.28 | 1.266 | 0.09885 | 1646592 | 69.79 |
| 1603080 | 67.95 | 0.9752 | 0.09116 | 1725116 | 73.12 |
| 1578088 | 66.89 | 1.159 | 0.08115 | 1677518 | 71.10 |
| 888904 | 37.68 | 0.6630 | 0.05607 | 1070506 | 45.37 |
| 1476640 | 62.59 | 0.9412 | 0.08381 | 1349726 | 57.21 |
最後に「アニメ」調 GIF 画像での結果を示します。LZ77 符号化の計測結果は「位置:長さ = 16:16 (32bit)」の条件下でのものになります。
| LZW 符号化 | LZ77 符号化 | ||||
|---|---|---|---|---|---|
| 符号サイズ (Bytes) | 圧縮率(%) | 符号化時間 (sec) | 復号化時間 (sec) | 符号サイズ (Bytes) | 圧縮率(%) |
| 83784 | 3.551 | 0.04604 | 0.02508 | 80528 | 3.413 |
| 249080 | 10.56 | 0.1248 | 0.03278 | 332944 | 14.11 |
| 79504 | 3.370 | 0.03518 | 0.01874 | 79748 | 3.380 |
| 157472 | 6.675 | 0.06761 | 0.02842 | 175612 | 7.443 |
| 85880 | 3.640 | 0.04920 | 0.02624 | 86480 | 3.666 |
| 73624 | 3.121 | 0.04699 | 0.02541 | 79580 | 3.373 |
| 75648 | 3.206 | 0.04114 | 0.02004 | 81584 | 3.458 |
| 118312 | 5.015 | 0.06436 | 0.02984 | 157392 | 6.671 |
| 169840 | 7.199 | 0.06857 | 0.02759 | 206716 | 8.762 |
| 126968 | 5.382 | 0.06501 | 0.02337 | 119708 | 5.074 |
LZW 符号化は UNIX にあったコマンド compress や画像フォーマットの GIF などで利用されていました。しかし特許問題や、より圧縮率の高いデフレート圧縮を使った zip, gzip, PNG フォーマットなどの台頭によって利用頻度は極端に減っているようです。今では特許も期限切れになっていますが、再利用する動きは今のところなさそうです。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |