
この章では、現在最も使用率の高い画像圧縮技術の一つ JPEG ( Joint Photographic Expert Group ) 法について説明したいと思います。
自然画のように、階調数が多くて色コードのパターンもより複雑になってしまうとエントロピーが大きくなり、今まで説明したような符号化圧縮ではサイズを小さくすることが難しくなります。そこで、今までのような可逆的な圧縮 ( 復号した結果が元のデータと完全に一致するような圧縮法 ) をやめて、非可逆圧縮法を利用するアプローチが取られるようになりました。その中で誕生したのが「JPEG 圧縮法」になります。
「JPEG」とは、この画像圧縮法の標準化を「CCIC ( Common Component for Image Communication )」と「ISO IEC/JTC1/SC/WG1」の二つのグループが共同で行うために 1986 年に設立されたグループ名を意味します。この標準化作業は 1994 年に終了し、その内容は三つのパートにわかれていますが、符号化や復号処理などについては「Part 1: ITU-T Rec.T.81 | ISO/IEC 10918-1 : Requirement and Guidlines」として出版されています。
自然画像を非可逆符号化するための方法として、以下の三つに大別することができます。
自然画には近隣画素間に強い相関があり、隣り合う画素間の変化量が小さい傾向があります。この性質を利用して、次に来る画素を予測する手法が予測符号化と呼ばれる手法であり、直交変換によって生じるデータの偏りを利用した手法が直交変換符号化になります。ベクトル量子化は、複数の画素をまとめてカテゴリ分類する手法であり、簡単な例としては、画像をいくつかのブロックに分けて、似たものどうしに同じ番号を付けるようなやり方を指します。「JPEG法」は、この中の直交変換符号化を利用した圧縮法になります。
ある画素 x1 に対し、その右側の画素を x2 として x1 - x2 平面上にプロットしていくと、隣り合う画素の変化量が小さい場合はその点が直線 x2 = x1 上に集中して分布することになります。
そこで、直線 x2 = x1 が x1 軸または x2 軸に重なるように座標変換を行ってみます。例えば、高校時代に習った回転行列を使って、
| |y1| | = | | | cos(π/4), | -sin(π/4) | || | x1 | |= | | | 1/√2, | -1/√2 | || | x1 | | |
| |y2| | | | sin(π/4), | cos(π/4) | || | x2 | | | | | 1/√2, | 1/√2 | || | x2 | | |
により
と座標変換すると、直線 x2 = x1 は直線 y1 = 0 つまり y2 軸に重なることになります。このとき、点の分布もまた y2 軸の周りに集中することになり、二つの画素のペアは偏りを持ったデータ、つまり一つのデータに値が集中してもう一方は 0 に近いデータに変換されたことになります。
ここでは平面上で二画素のペアを用いましたが、これを n 次元空間における n 個の画素に対する座標変換に拡張します。
| y = | | | y1 | | | = | | | a11, | a12, | ... | a1n | || | x1 | | | = Ax |
| | | y2 | | | | | a21, | a22, | ... | a2n | || | x2 | | | |||
| | | : | | | | | : | : | : | || | : | | | ||||
| | | yn | | | | | an1, | an2, | ... | ann | || | xn | | |
x は画像を n 個の画素で区切ったときの「画素系列」、A は「変換行列」になります。また、y は変換後のベクトルを表し、この中の各要素は「変換係数」と呼ばれます。
A の各行(または各列)ベクトルが全て互いに直交しているとき、これらのベクトルは「直交基底 (Orthogonal Basis)」と呼ばれます。特に、各ベクトルのノルムが 1 ならば、「正規直交基底 (Orthonormal Basis)」となります。直交基底を持つ行列は「直交行列 (Orthogonal Matrix)」と呼ばれ、直交行列を用いた変換を「直交変換 (Orthogonal Transformation)」といいます (*1-1)。
座標変換の例で使用した回転行列は、行ベクトルが ( 1/√2, -1/√2 ) と ( 1/√2, 1/√2 ) であり、それぞれ直線 y = -x, y = x と同じ向きになるため互いに直交しています。また、そのノルムはどちらも 1 になるのでこれらは正規直交基底であり、回転行列は直交行列であることになります。
y から x への逆変換には、A の逆行列を使用することになりますが、直交行列では逆行列と転置行列が等しくなるため、逆変換式は
| x | = | A-1y | |||||||
| = | ATy | ||||||||
| = | | | a11, | a21, | ... | an1 | || | y1 | | | |
| | | a12, | a22, | ... | an2 | || | y2 | | | ||
| | | : | : | : | || | : | | | |||
| | | a1n, | a2n, | ... | ann | || | yn | | | ||
になります。先の例では、逆変換式は
| | | x1 | | | = | | | 1/√2, | -1/√2 | |T | | | y1 | | |
| | | x2 | | | | | 1/√2, | 1/√2 | | | | | y2 | | | |
| = | | | 1/√2, | 1/√2 | | | | | y1 | | | |||
| | | -1/√2, | 1/√2 | | | | | y2 | | |
により
となります。
今までの変換は、画像を一次元方向に n 画素ずつブロック化した場合のものですが、画像は二次元平面上で表現されるので、ブロック化する画素も二次元配列 ( 行列 ) の形にすることができます。二次元変換は、以下のような式で行われます。
ここで X は画像を n 行 m 列の画素で区切った行列、Am は m 行 m 列の変換行列を表します。また Y は、変換した n 行 m 列の行列になります。
*1-1) 「直交基底」や「直交行列」の性質については「固有値問題 (1) 対称行列の固有値」の中で詳しく紹介しています。
直交変換符号化の目的は、特定の軸に値が集中するようにすることです。軸の数より少ない係数で近似的に表現することができれば、それだけ情報量を減らすことが可能になります。そのような変換の方式としては、「カルーネン・レーベ変換 (Karhunen-Loeve Transformation ; KLT)」をはじめとして次のようなものがあります。
JPEG 法では「離散コサイン変換 (Discrete Cosine Transform ; DCT)」が使用されています。カルーネン・レーベ変換は、入力された画像から変換行列を毎回求めることになるので最適な変換を行うことができますが、行列を毎回求めなければならない上に計算も煩雑であるため実用化は難しいと言われていました。そこで、変換行列の要素がすでに決まっている他の変換方法が検討され、画像に対してはカルーネン・レーベ変換で求めた変換行列と極めてよく似ていると言われる離散コサイン変換が多用されるようになったようです。
(注) 自己相関係数 ( ≅ 他の画素からの影響の大きさ ) とその画素との距離の関係が負の指数関数で表現できる場合、離散コサイン変換はカルーネン・レーベ変換に近い結果が得られるそうです。自然画の場合はある程度当てはまりそうに思えますが、アニメ調の場合はその関係が当てはまらない ( 離散的になる ) ように感じます。これが、アニメ調の画像には JPEG 法が向かない理由の一つであるように思います。
離散コサイン変換のための変換行列は離散フーリエ変換を利用して求めることができます。離散フーリエ変換は以下のような式です。
| Fk | = | (1/√N)Σm{0→N-1}( fme-i2πkm/N ) |
| = | (1/√N)Σm{0→N-1}( fm[ cos( -2πkm / N ) + i sin( -2πkm / N ) ] ) |
fm は m 番目の画素データ、Fk は変換した k 番目の周波数成分を意味します。下側の式はオイラーの公式
から得られます。
として Fk の各成分 ( F0, F1, ... FN-1 ) の計算式を行列とベクトルで表すと
| | | F0 | | | | | 1, | 1, | 1, | ... | 1 | || | f0 | | | |
| | | F1 | | | | | 1, | ωN-1, | ωN-2, | ... | ωN-(N-1) | || | f1 | | | |
| | | F2 | | | = (1/√N) | | | 1, | ωN-2, | ωN-4, | ... | ωN-2(N-1) | || | f2 | | |
| | | : | | | | | : | : | : | : | || | : | | | ||
| | | FN-1 | | | | | 1, | ωN-(N-1), | ωN-2(N-1), | ... | ωN-(N-1)(N-1) | || | fN-1 | | |
となります。行列は対称行列 ( 対角成分を軸に対称な成分を持ち、転置行列と等しくなるような正方行列 ) であり、しかも直交行列であることが証明できます ( 補足 1 )。よって、離散フーリエ変換は直交変換の一つであることがわかります。逆変換は
| fm | = | (1/√N)Σk{0→N-1}( Fkei2πkm/N ) |
| = | (1/√N)Σk{0→N-1}( Fk[ cos( 2πkm / N ) + i sin( 2πkm / N ) ] ) |
| | | f0 | | | | | 1, | 1, | 1, | ... | 1 | || | F0 | | | |
| | | f1 | | | | | 1, | ωN, | ωN2, | ... | ωNN-1 | || | F1 | | | |
| | | f2 | | | = (1/√N) | | | 1, | ωN2, | ωN4, | ... | ωN2(N-1) | || | F2 | | |
| | | : | | | | | : | : | : | : | || | : | | | ||
| | | fN-1 | | | | | 1, | ωNN-1, | ωN2(N-1), | ... | ωN(N-1)(N-1) | || | FN-1 | | |
であり、これも直交変換です。また、二つの式に登場する行列は明らかに、一方の行列が他方の行列の逆行列になっています。
フーリエ変換は複素数成分を含むため、これを実数だけで表すことを考えます。係数の実部は cos 関数、虚部は sin 関数であり、もし信号 fm が Y 軸について対称ならば、虚部は負の部分と正の部分で打ち消し合って消えます。そこで、左右(前後)対称な 2N 個の信号 { f'0, f'1, ... f2N-1 } についての離散フーリエ変換・逆変換式
F'k = (1/2N)1/2Σm{0→2N-1}( f'me-i2πkm/2N )
f'm = (1/2N)1/2Σk{0→2N-1}( F'kei2πkm/2N )
からスタートして虚部を係数から取り除くことを検討してみます。まず、第一式のフーリエ変換式を変形して
のように前半と後半に分割します。両者に含まれる信号は左右(前後)対称、すなわち f'm = f'2N-m-1 ( 0 ≤ m ≤ N - 1 ) なので、{ f'm } = { f'2N-m-1 } = { fm } とすると、上式は
| F'k | = | (1/2N)1/2[ Σm{0→N-1}( f'me-i2πkm/2N ) + Σm{N-1→0}( f'2N-m-1e-i2πk(2N-m-1)/2N ) ] |
| = | (1/2N)1/2[ Σm{0→N-1}( fme-i2πkm/2N ) + Σm{0→N-1}( fme-i2πk(2N-m-1)/2N ) ] | |
| = | (1/2N)1/2Σm{0→N-1}( fm[ e-i2πkm/2N + e-i2πkei2πk(m+1)/2N ] ) | |
| = | (1/2N)1/2Σm{0→N-1}( fm[ e-iπk(2m+1)/2N+iπk/2N + eiπk(2m+1)/2N+iπk/2N ] ) | |
| = | [ eiπk/2N / ( 2N )1/2 ]Σm{0→N-1}( fm[ e-iπk(2m+1)/2N + eiπk(2m+1)/2N ] ) |
となります。ここで再びオイラーの公式を使って
となるので、上式に適用すれば
となって、
Fk = e-iπk/2NF'k
F0 = F'0 / √2
とすれば
Fk = (2/N)1/2Σm{0→N-1}( fmcos( πk( 2m + 1 ) / 2N ) )
F0 = (1/N)1/2Σm{0→N-1}( fm )
となります。k = 0 の場合だけを特別扱いにした理由は後の方で述べます。第二式のフーリエ逆変換式は
| f'm | = | (1/2N)1/2Σk{0→2N-1}( F'kei2πkm/2N ) |
| = | (1/2N)1/2[ Σk{0→N-1}( F'keiπkm/N ) + Σk{N→2N-1}( F'keiπkm/N ) ] | |
| = | (1/2N)1/2[ Σk{0→N-1}( F'keiπkm/N ) + Σk{N→1}( F'2N-keiπ(2N-k)m/N ) ] | |
| = | (1/2N)1/2[ Σk{0→N-1}( F'keiπkm/N ) + Σk{1→N}( F'2N-kei2πme-iπkm/N ) ] | |
| = | (1/2N)1/2[ Σk{0→N-1}( F'keiπkm/N ) + Σk{1→N}( F'2N-ke-iπkm/N ) ] |
と変形できますが、
| F'2N-k | = | (1/2N)1/2Σm{0→2N-1}( f'me-i2π(2N-k)m/2N ) |
| = | (1/2N)1/2Σm{0→2N-1}( f'me-i2πmei2πkm/2N ) | |
| = | (1/2N)1/2Σm{0→2N-1}( f'mei2πkm/2N ) = ( F'k )~ |
より
であり、
| F'N | = | (1/2N)1/2Σm{0→2N-1}( f'me-i2πNm/2N ) |
| = | (1/2N)1/2Σm{0→2N-1}( f'meiπm ) | |
| = | (1/2N)1/2[ f'0 - f'1 + ... + ( -1 )N-1f'N-1 + ( -1 )Nf'N + ... - f'2N-1 ] | |
| = | (1/2N)1/2[ f'0 - f'1 + ... + ( -1 )N-1f'N-1 + ( -1 )Nf'N-1 + ... - f'0 ] = 0 |
なので
| f'm | = | (1/2N)1/2[ Σk{0→N-1}( F'keiπkm/N ) + Σk{1→N-1}( ( F'k )~e-iπkm/N ) ] |
| = | (1/2N)1/2[ F'0 + Σk{1→N-1}( F'keiπkm/N + ( F'k )~e-iπkm/N ) ] | |
| = | (1/2N)1/2[ √2F0 + Σk{1→N-1}( eiπk/2NFkeiπkm/N + ( eiπk/2NFk )~e-iπkm/N ) ] | |
| = | (1/2N)1/2[ √2F0 + Σk{1→N-1}( Fkeiπk(m+1/2)/N + Fke-iπk(m+1/2)/N ) ] | |
| = | (1/2N)1/2[ √2F0 + 2Σk{1→N-1}( Fkcos( πk( 2m + 1 ) / 2N ) ) ] | |
| = | (2/N)1/2[ F0 / √2 + Σk{1→N-1}( Fkcos( πk( 2m + 1 ) / 2N ) ) ] |
という結果が得られます ( ここで F0 だけ和の成分から外に出すことになるので、先ほど F0 だけを特別扱いにしたわけです )。0 ≤ m ≤ N - 1 では f'm = fm なので、以上をまとめると
F0 = (1/N)1/2Σm{0→N-1}( fm )
Fk = (2/N)1/2Σm{0→N-1}( fmcos( πk( 2m + 1 ) / 2N ) )
fm = (2/N)1/2[ F0 / √2 + Σk{1→N-1}( Fkcos( πk( 2m + 1 ) / 2N ) ) ]
となり、行列の形で表すと
| | | F0 | | | | | 1 / √2, | 1 / √2, | 1 / √2, | ... | 1 / √2 | || | f0 | | | |
| | | F1 | | | | | cos( π / 2N ), | cos( 3π / 2N ), | cos( 5π / 2N ), | ... | cos( ( 2N - 1 )π / 2N ) | || | f1 | | | |
| | | F2 | | | = (2/N)1/2 | | | cos( 2π / 2N ), | cos( 6π / 2N ), | cos( 10π / 2N ), | ... | cos( 2( 2N - 1 )π / 2N ) | || | f2 | | |
| | | : | | | | | : | : | : | : | || | : | | | ||
| | | FN-1 | | | | | cos( ( N - 1 )π / 2N ), | cos( ( N - 1 )3π / 2N ), | cos( ( N - 1 )5π / 2N ), | ... | cos( ( N - 1 )( 2N - 1 )π / 2N ) | || | fN-1 | | |
| | | 1 / √2, | 1 / √2, | 1 / √2, | ... | 1 / √2 | || | f0 | | | ||||
| | | C2N1, | C2N3, | C2N5, | ... | C2N2N-1 | || | f1 | | | ||||
| ≡ (2/N)1/2 | | | C2N2, | C2N6, | C2N10, | ... | C2N2(2N-1) | || | f2 | | | |||
| | | : | : | : | : | || | : | | | |||||
| | | C2NN-1, | C2N(N-1)3, | C2N(N-1)5, | ... | C2N(N-1)(2N-1) | || | fN-1 | | | ||||
| | | f0 | | | | | 1 / √2, | cos( π / 2N ), | cos( 2π / 2N ), | ... | cos( ( N - 1 )π / 2N ) | || | F0 | | | |
| | | f1 | | | | | 1 / √2, | cos( 3π / 2N ), | cos( 6π / 2N ), | ... | cos( ( N - 1 )3π / 2N ) | || | F1 | | | |
| | | f2 | | | = (2/N)1/2 | | | 1 / √2, | cos( 5π / 2N ), | cos( 10π / 2N ), | ... | cos( ( N - 1 )5π / 2N ) | || | F2 | | |
| | | : | | | | | : | : | : | : | || | : | | | ||
| | | fN-1 | | | | | 1 / √2, | cos( ( 2N - 1 )π / 2N ), | cos( 2( 2N - 1 )π / 2N ), | ... | cos( ( N - 1 )( 2N - 1 )π / 2N ) | || | FN-1 | | |
| | | 1 / √2, | C2N1, | C2N2, | ... | C2NN-1 | || | F0 | | | ||||
| | | 1 / √2, | C2N3, | C2N6, | ... | C2N(N-1)3 | || | F1 | | | ||||
| ≡ (2/N)1/2 | | | 1 / √2, | C2N5, | C2N10, | ... | C2N(N-1)5 | || | F2 | | | |||
| | | : | : | : | : | || | : | | | |||||
| | | 1 / √2, | C2N2N-1, | C2N2(2N-1), | ... | C2N(N-1)(2N-1) | || | FN-1 | | | ||||
となります。但し、cos( kπ / N ) ≡ CNk で表しています。また、
| C(k) | = | 1 / √2 | [k = 0] |
| = | 1 | [k > 0] |
とすれば式はひとまとめにすることができて、
Fk = (2/N)1/2Σm{0→N-1}( C(k)・fmcos( πk( 2m + 1 ) / 2N ) )
fm = (2/N)1/2Σk{0→N-1}( C(k)・Fkcos( πk( 2m + 1 ) / 2N ) )
と表すことができます。
変換・逆変換式の行列は互いに転置行列になっています。第一行ベクトルのノルムは
となり、その他のベクトルのノルムは
| ( 2 / N )Σm{0→N-1}( cos2( πk( 2m + 1 ) / 2N ) ) | |
| = | ( 1 / N )Σm{0→N-1}( cos( πk( 2m + 1 ) / N ) + 1 ) |
| = | 1 + ( 1 / N )Σm{0→N-1}( cos( πk( 2m + 1 ) / N ) ) |
から求めることができますが ( 途中で倍角の公式 cos2θ = 2cos2θ - 1 を利用しています )、
| Σm{0→N-1}( cos( πk( 2m + 1 ) / N ) ) | |
| = | Σm{0→N-1}( eiπk(2m+1)/N + e-iπk(2m+1)/N ) / 2 |
| = | [ eiπk/NΣm{0→N-1}( ei2πkm/N ) + e-iπk/NΣm{0→N-1}( e-i2πkm/N ) ] / 2 |
| = | 0 |
となるので ( *2-1 ) ノルムは 1 となります。相異なる k 行目と k' 行目の行ベクトルの内積は
| ( 2 / N )Σm{0→N-1}( cos( πk( 2m + 1 ) / 2N )cos( πk'( 2m + 1 ) / 2N ) ) | |
| = | ( 2 / N )Σm{0→N-1}( cos( π( k + k' )( 2m + 1 ) / 2N ) + cos( π( k - k' )( 2m + 1 ) / 2N ) ) / 2 |
から求めることができます。ここで k ≠ 0 の任意の自然数 k に対して
| f(N-m-1) | ≡ | cos( πk( 2( N - m - 1 ) + 1 ) / 2N ) ) |
| = | cos( πk - πk( 2m + 1 ) / 2N ) | |
| = | cosπk・cos( πk( 2m + 1 ) / 2N ) + sinπk・sin( πk( 2m + 1 ) / 2N ) | |
| = | (-1)kcos( πk( 2m + 1 ) / 2N ) | |
| = | (-1)kf(m) |
が成り立つことから cos( πk( 2m + 1 ) / 2N ) は k が偶数なら縦軸 m = ( N - 1 ) / 2 に対して左右(前後)対称(偶関数)の形に、奇数なら中点 ( m, f(m) ) = ( ( N - 1 ) / 2, 0 ) に対して対称(奇関数)の形になることがわかります。N が奇数の場合、
| f( ( N - 1 ) / 2 ) | ≡ | cos( πk( ( N - 1 ) + 1 ) / 2N ) ) |
| = | cos( πk / 2 ) |
より k が奇数ならゼロになるので、k が奇数なら任意の N について Σm{0→N-1}( f(m) ) は必ずゼロです。k が偶数の時、
| f(N+m) | = | cos( πk( 2( N + m ) + 1 ) / 2N ) ) |
| = | cos( πk + πk( 2m + 1 ) / 2N ) | |
| = | cosπk・cos( πk( 2m + 1 ) / 2N ) - sinπk・sin( πk( 2m + 1 ) / 2N ) | |
| = | (-1)kcos( πk( 2m + 1 ) / 2N ) | |
| = | (-1)kf(m) = f(m) [ k が偶数の時 ] |
より f(m) は間隔 N で周期関数となることがわかります。また、
cos θ = ( eiθ + e-iθ ) / 2
Σm{0→2N-1}( e2iπmk/2N ) = 0 [ k はゼロ以外の整数 ]
を利用すると
| Σm{0→2N-1}( f(m) ) | = | Σm{0→2N-1}( cos( πk( 2m + 1 ) / 2N ) ) |
| = | Σm{0→2N-1}( eiπk(2m+1)/2N + e-iπk(2m+1)/2N ) / 2 | |
| = | Σm{0→2N-1}( e2iπkm/2Neiπk/2N + e-2iπkm/2Ne-iπk/2N ) / 2 | |
| = | [ eiπk/2NΣm{0→2N-1}( e2iπkm/2N ) + e-iπk/2NΣm{0→2N-1}( e-2iπkm/2N ) ] / 2 | |
| = | 0 |
となります。f(m) が間隔 N で周期関数なら Σm{0→N-1}( f(m) ) = Σm{N→2N-1}( f(m) ) が成り立つので、k が偶数の場合も Σm{0→N-1}( f(m) ) = 0 ということになり、k ≠ k' ならば行ベクトルの内積はゼロになります。以上の結果から、離散コサイン変換の係数行列は直交行列であることが証明されたことになります。
二次元の場合、変換式は
| Fv,u | = | (2/N)Σx{0→N-1}( C(u)cos( πu( 2x + 1 ) / 2N )Σy{0→N-1}( fy,xC(v)cos( πv( 2y + 1 ) / 2N ) ) ) |
| = | (2/N)Σx{0→N-1}( Σy{0→N-1}( fy,xC(v)cos( πv( 2y + 1 ) / 2N )C(u)cos( πu( 2x + 1 ) / 2N ) ) ) | |
| = | (2/N)Σx{0→N-1}( Σy{0→N-1}( fy,xC(v)C2Nv(2y+1)C(u)C2Nu(2x+1) ) ) |
逆変換式は
| fy,x | = | (2/N)Σu{0→N-1}( C(u)cos( πu( 2x + 1 ) / 2N )Σv{0→N-1}( Fv,uC(v)cos( πv( 2y + 1 ) / 2N ) ) ) |
| = | (2/N)Σu{0→N-1}( Σv{0→N-1}( Fv,uC(v)cos( πv( 2y + 1 ) / 2N )C(u)cos( πu( 2x + 1 ) / 2N ) ) ) | |
| = | (2/N)Σu{0→N-1}( Σv{0→N-1}( Fv,uC(v)C2Nv(2y+1)C(u)C2Nu(2x+1) ) ) |
になります。行列で表すと
| | | F0,0, | F0,1, | ... | F0,N-1 | | | | | 1 / √2, | 1 / √2, | 1 / √2, | ... | 1 / √2 | || | f0,0, | f0,1, | ... | f0,N-1 | || | 1/√2, | C2N1, | C2N2, | ... | C2NN-1 | | | |
| | | F1,0, | F1,1, | ... | F1,N-1 | | | | | C2N1, | C2N3, | C2N5, | ... | C2N2N-1 | || | f1,0, | f1,1, | ... | f1,N-1 | || | 1/√2, | C2N3, | C2N6, | ... | C2N(N-1)3 | | | |
| | | F2,0, | F2,1, | ... | F2,N-1 | | | = (2/N) | | | C2N2, | C2N6, | C2N10, | ... | C2N2(2N-1) | || | f2,0, | f2,1, | ... | f2,N-1 | || | 1/√2, | C2N5, | C2N10, | ... | C2N(N-1)5 | | |
| | | : | : | : | | | | | : | : | : | : | || | : | : | : | || | : | : | : | : | | | |||||
| | | FN-1,0, | FN-1,1, | ... | FN-1,N-1 | | | | | C2NN-1, | C2N(N-1)3, | C2N(N-1)5, | ... | C2N(N-1)(2N-1) | || | fN-1,0, | fN-1,1, | ... | fN-1,N-1 | || | 1/√2, | C2N2N-1, | C2N2(2N-1), | ... | C2N(N-1)(2N-1) | | | |
| ≡ ATfA | ||||||||||||||||||||||||
| | | f0,0, | f0,1, | ... | f0,N-1 | | | | | 1 / √2, | C2N1, | C2N2, | ... | C2NN-1 | || | F0,0, | F0,1, | ... | F0,N-1 | || | 1 / √2, | 1 / √2, | 1 / √2, | ... | 1 / √2 | | | |
| | | f1,0, | f1,1, | ... | f1,N-1 | | | | | 1 / √2, | C2N3, | C2N6, | ... | C2N(N-1)3 | || | F1,0, | F1,1, | ... | F1,N-1 | || | C2N1, | C2N3, | C2N5, | ... | C2N2N-1 | | | |
| | | f2,0, | f2,1, | ... | f2,N-1 | | | = (2/N) | | | 1 / √2, | C2N5, | C2N10, | ... | C2N(N-1)5 | || | F2,0 | F2,1, | ... | F2,N-1 | || | C2N2, | C2N6, | C2N10, | ... | C2N2(2N-1) | | |
| | | : | : | : | | | | | : | : | : | : | || | : | : | : | || | : | : | : | : | | | |||||
| | | fN-1,0, | fN-1,1, | ... | fN-1,N-1 | | | | | 1 / √2, | C2N2N-1, | C2N2(2N-1), | ... | C2N(N-1)(2N-1) | || | FN-1,0 | FN-1,1, | ... | FN-1,N-1 | || | C2NN-1, | C2N(N-1)3, | C2N(N-1)5, | ... | C2N(N-1)(2N-1) | | | |
| ≡ AFAT | ||||||||||||||||||||||||
となりますが、これはちょうど、前側の係数行列を使って二次元データの各列ベクトルを一次元離散コサイン変換・逆変換して、その結果を後ろ側の係数行列でもう一度一次元離散コサイン変換・逆変換する操作と同等で、最初に示した式の一番目を見ても、一次元の変換を繰り返していることが理解できると思います。
JPEG 圧縮では、通常 8 x 8 画素を 1 ブロックとして離散コサイン変換を行います。このブロックは JPEG 処理の基本単位となり、「MCU ( Minimum Coded Unit )」と呼ばれます。実際に一つの MCU を離散コサイン変換した結果を以下に示します。
変換前 |126, 138, 135, 118, 118, 126, 126, 130| |150, 168, 161, 122, 105, 109, 100, 118| |150, 150, 126, 150, 142, 126, 126, 117| |150, 161, 168, 130, 134, 150, 138, 130| |130, 118, 134, 142, 157, 142, 117, 126| |115, 117, 108, 117, 101, 99, 117, 126| |122, 130, 130, 138, 117, 108, 108, 138| |142, 118, 134, 117, 109, 91, 126, 109| 変換後 |1029, 52, 10, -21, -1, -3, 2, 1| | 39, 21, 0, 6, -22, -17, 4, -7| | -40, 12, 24, -19, -2, 7, -4, 5| | -32, -34, -1, -7, 5, -8, 5, -7| | 22, -14, -10, 16, -12, 4, 12, 18| | 19, -17, 1, -3, -6, -3, -2, -8| | -24, -18, 3, 15, 9, 15, -20, 1| | 9, -16, -30, 14, 29, -2, -5, -5|
変換後の値を見ると、行列の左上側、特に 0 行 0 列成分の値が大きいことがわかります。この成分は x, y どちらの方向に対しても周波数成分がゼロなので「DC (直流)成分」と呼ばれ、その他の成分を「AC (交流)成分」と呼んで区別しています。右側ほど x 成分の、下側ほど y 成分の周波数は高くなり、それに従って係数は小さくなる傾向にあります。このようなデータの偏りを利用して圧縮を行うことが可能となります。
ここから、サンプル・プログラムを示していきます。離散コサイン変換・逆変換を行なうときに座標や行列を利用するため、まずはそれらのクラスを定義します。
/* Coord : 座標定義用構造体 */ template< class T > struct Coord { T x; // x 座標 T y; // y 座標 /* コンストラクタ */ // デフォルト・コンストラクタ // ( x, y ) = ( 0, 0 ) で初期化される Coord() : x( 0 ), y ( 0 ) {} // ( x, y ) 座標を指定して構築 Coord( T x_, T y_ ) : x( x_ ), y ( y_ ) {} // 異なる型の座標から構築 template< class U > Coord( const Coord< U >& c ) : x( c.x ), y( c.y ) {} }; /* Matrix : 行列定義用クラス */ template< class T > class Matrix { // 要素を保持するコンテナの型 typedef typename std::vector< T > array_type; // 行・列のサイズ Coord< typename array_type::size_type > size_; // 行列要素を保持するコンテナ array_type d_; public: // 行列のサイズを表す型 typedef typename array_type::size_type size_type; // 行列の要素の型 typedef T value_type; // デフォルト・コンストラクタ Matrix() {} // コンストラクタ // 行列のサイズを指定して構築 explicit Matrix( Coord< size_type > size, value_type val = value_type() ) : size_( size ), d_( size.x * size.y, val ) {} // 指定したサイズ size と値 val で初期化する void assign( Coord< size_type > size, value_type val = value_type() ) { size_ = size; d_.assign( size.x * size.y, val ); } // 座標 p の要素への参照を返す T& operator[]( Coord< int > p ) { Coord< int > sz( size() ); if ( p.x < 0 || p.y < 0 || p.x >= sz.x || p.y >= sz.y ) throw std::domain_error( "Matrix::operator[] : Invalid coord [p]." ); return( d_[ p.y * xSize() + p.x ] ); } // 座標 p の要素を返す T operator[]( Coord< int > p ) const { Coord< int > sz( size() ); if ( p.x < 0 || p.y < 0 || p.x >= sz.x || p.y >= sz.y ) throw std::domain_error( "Matrix::operator[] : Invalid coord [p]." ); return( d_[ p.y * xSize() + p.x ] ); } // 座標 ( x, y ) の要素への参照を返す T& operator()( int x, int y ) { Coord< int > sz( size() ); if ( x < 0 || y < 0 || x >= sz.x || y >= sz.y ) throw std::domain_error( "Matrix::operator() : Invalid coord [x,y]." ); return( d_[ y * xSize() + x ] ); } // 座標 ( x, y ) の要素を返す T operator()( int x, int y ) const { Coord< int > sz( size() ); if ( x < 0 || y < 0 || x >= sz.x || y >= sz.y ) throw std::domain_error( "Matrix::operator() : Invalid coord [x,y]." ); return( d_[ y * xSize() + x ] ); } // 行列のサイズを返す Coord< size_type > size() const { return( size_ ); } // 列数 ( X 方向のサイズ ) を返す size_type xSize() const { return( size_.x ); } // 行数 ( Y 方向のサイズ ) を返す size_type ySize() const { return( size_.y ); } }; /* SquareMatrix : 正方行列定義用クラス */ template< class T > class SquareMatrix { // 行列の要素を保持するコンテナ ( Matrix クラス ) Matrix< T > mat_; public: // 行列のサイズを表す型 typedef typename Matrix<T>::size_type size_type; // 行列の要素を表す型 typedef T value_type; // コンストラクタ // 行列のサイズを指定して構築 explicit SquareMatrix( size_type size, value_type val = value_type() ) : mat_( Coord< size_type >( size, size ), val ) {} // 座標 p の要素への参照を返す T& operator[]( Coord< int > p ) { return( mat_[p] ); } // 座標 p の要素を返す T operator[]( Coord< int > p ) const { return( mat_[p] ); } // 座標 ( x, y ) の要素への参照を返す T& operator()( int x, int y ) { return( mat_( x, y ) ); } // 座標 ( x, y ) の要素を返す T operator()( int x, int y ) const { return( mat_( x, y ) ); } // 行列のサイズを返す size_type size() const { return( mat_.xSize() ); } };
Coord は二次元座標を表現するために二つのメンバ x, y を持つシンプルな構造体です。座標値の型はテンプレート引数として指定し、サンプル・プログラムの中では int か size_t 型を使います。この二つの型どうしで数値比較する場合、符号付きと符号なしでの比較となるためにコンパイラが警告を出力するので、型を変換することでそれを回避しています。これを実現する目的で、異なる型の座標から構築するためのコンストラクタが用意されています。
Matrix は行列を定義するためのクラスで、その内部では一次元配列 vector に行列の一行目の要素から順に保持しています。要素へのアクセスは operator[] と operator() の二通りで行うことができて、前者は Coord 型を、後者は x, y それぞれの座標値を指定します。Matrix を利用して、正方行列 ( 行と列のサイズが等しい行列 ) 用のクラス SquareMatrix も用意しています。
次に、離散コサイン変換を行うためのサンプル・プログラムを示します。
/* CalcCoeff : 離散コサイン変換(DCT)用の係数を計算して coeff に登録する C[u,x] = cos( πu( 2x + 1 ) / 2N ) 以下のような行列が作成される | 1/√2 cos π/2N ... cos (N-1)π/2N | | 1/√2 cos 3π/2N ... cos (N-1)3π/2N | | : : : | | 1/√2 cos (2N-1)π/2N ... cos (N-1)(2N-1)π/2N | N : 係数行列のサイズ */ void CalcCoeff( SquareMatrix< double >* coeff ) { int mcuSize = coeff->size(); // MCU のサイズ for ( int x = 0 ; x < mcuSize ; ++x ) for ( int u = 0 ; u < mcuSize ; ++u ) (*coeff)( u, x )= cos( ( M_PI * u * ( 2 * x + 1 ) ) / ( 2.0 * mcuSize ) ); } /* GetMCUCount : MCU の X,Y 方向の数を求める gSize は画像サイズ、mcuSize は MCU のサイズ、skip は間引き量をそれぞれ表す */ Coord< int > GetMCUCount( Coord< int > gSize, int mcuSize, Coord< int > skip ) { Coord< int > mcuCount; // 求める値 mcuCount.x = gSize.x / ( mcuSize * skip.x ); if ( gSize.x % ( mcuSize * skip.x ) != 0 ) ++( mcuCount.x ); mcuCount.y = gSize.y / ( mcuSize * skip.y ); if ( gSize.y % ( mcuSize * skip.y ) != 0 ) ++( mcuCount.y ); return( mcuCount ); } /* dct_x : X 成分に対する離散コサイン変換(DCT) yuv は YUVデータの一成分からなる二次元配列を表し、係数行列 coeff を元に DCT 計算をして 結果を f_uy に返す。mcuCoord は対象となる MCU の位置、skip は間引き量をそれぞれ表す。 */ void dct_x( const Matrix< double >& yuv, const SquareMatrix< double >& coeff, SquareMatrix< double >* f_uy, Coord< int > mcuCoord, Coord< int > skip ) { // 画像 ( YUV データ ) のサイズ Coord< int > gSize = yuv.size(); // MCU のサイズ int mcuSize = f_uy->size(); // YUV データ上の対象座標 Coord< int > c_yuv( 0, mcuCoord.y * mcuSize * skip.y ); int y = 0; for ( ; y < mcuSize ; ++y ) { if ( c_yuv.y >= gSize.y ) break; for ( int u = 0 ; u < mcuSize ; u++ ) { double a = 0; // 求める係数 c_yuv.x = mcuCoord.x * mcuSize * skip.x; // y 行について、X 方向の YUV 成分と u 列目の係数ベクトルの内積を求める for ( int x = 0 ; x < mcuSize ; ++x ) { if ( c_yuv.x >= gSize.x ) break; a += yuv[c_yuv] * coeff( u, x ); c_yuv.x += skip.x; } if ( u == 0 ) a /= sqrt( 2 ); (*f_uy)( u, y ) = a; } c_yuv.y += skip.y; } // 残りの行はゼロクリア for ( ; y < mcuSize ; ++y ) for ( int u = 0 ; u < mcuSize ; u++ ) (*f_uy)( u, y ) = 0; } /* dct_y : Y 成分に対する離散コサイン変換(DCT) f_uy は X 方向の成分で計算した結果を表し、係数行列 coeff を元に DCT 計算をして結果を mcu に返す。 */ void dct_y( const SquareMatrix< double >& f_uy, const SquareMatrix< double >& coeff, Coord< int > mcuCoord, Matrix< double >* mcu ) { // MCU のサイズ int mcuSize = f_uy.size(); // mcu への書き込み開始位置 Coord< int > sp( mcuCoord.x * mcuSize, mcuCoord.y * mcuSize ); for ( int v = 0 ; v < mcuSize ; v++ ) { for ( int u = 0 ; u < mcuSize ; u++ ) { double a = 0; // 求める係数 // f_uy の u 列目のベクトルと v 列目の係数ベクトルの内積を求める for ( int y = 0 ; y < mcuSize ; y++ ) a += f_uy( u, y ) * coeff( v, y ); if ( v == 0 ) a /= sqrt( 2 ); (*mcu)( sp.x + u, sp.y + v ) = a * 2 / mcuSize; } } } /* MCU_Encode : 離散コサイン変換(DCT) yuv は YUVデータの一成分からなる二次元配列を表し、DCT 計算をして結果を mcu に返す。 mcuCoord は対象となる MCU の位置を表す。 間引き(サンプリング)処理も含めて行ない、skip は間引き量を表す。 */ void MCU_Encode( const Matrix< double >& yuv, Matrix< double >* mcu, int mcuSize, Coord< int > skip ) { assert( &yuv != 0 ); assert( mcu != 0 ); // 画像 ( YUV データ ) のサイズ Coord< int > gSize = yuv.size(); // X 成分の和を先に計算した結果 SquareMatrix< double > f_uy( mcuSize ); // 係数行列 SquareMatrix< double > coeff( mcuSize ); CalcCoeff( &coeff ); Coord< int > mcuCount = GetMCUCount( gSize, mcuSize, skip ); // MCU の X,Y 方向の数を求める Coord< int > mcuCoord; mcu->assign( Coord< int >( mcuCount.x * mcuSize, mcuCount.y * mcuSize ), 0.0 ); for ( mcuCoord.y = 0 ; mcuCoord.y < mcuCount.y ; ++( mcuCoord.y ) ) { for ( mcuCoord.x = 0 ; mcuCoord.x < mcuCount.x ; ++( mcuCoord.x ) ) { dct_x( yuv, coeff, &f_uy, mcuCoord, skip ); dct_y( f_uy, coeff, mcuCoord, mcu ); } } }
続けて、逆変換のサンプル・プログラムを以下に示します。
/* idct_y : Y 成分に対する離散コサイン逆変換(IDCT) mcu は対象の MCU を指す反復子を表し、係数行列 coeff を元に IDCT 計算をして 結果を f_uy に返す。 */ void idct_y( const Matrix< double >& mcu, Coord< int > mcuCoord, const SquareMatrix< double >& coeff, SquareMatrix< double >* f_uy ) { // MCU のサイズ int mcuSize = f_uy->size(); // mcu からの読み込み開始位置 Coord< int > sp( mcuCoord.x * mcuSize, mcuCoord.y * mcuSize ); for ( int y = 0 ; y < mcuSize ; y++ ) { for ( int u = 0 ; u < mcuSize ; u++ ) { double a = 0; // 求める係数 // u 列目の MCU ベクトルと y 行目の係数ベクトルの内積を求める for ( int v = 0 ; v < mcuSize ; v++ ) { double d = mcu( sp.x + u, sp.y + v ) * coeff( v, y ); if ( v == 0 ) d /= sqrt( 2 ); a += d; } (*f_uy)( u, y ) = a; } } } /* fill_yuv : YUV データの書き込み c を始点として data を yuv 上に書き込む。 間引きがある場合は、間引き数 skip 分だけ同じデータを書き込む。 */ void fill_yuv( double data, Matrix< double >* yuv, Coord< int > c, Coord< int > skip ) { // 画像のサイズ Coord< int > gSize( yuv->size() ); for ( int j = 0 ; j < skip.y ; j++ ) { if ( c.y + j >= gSize.y ) break; for ( int i = 0 ; i < skip.x ; i++ ) { if ( c.x + i >= gSize.x ) break; (*yuv)( c.x + i, c.y + j ) = data; } } } /* idct_x : X 成分に対する離散コサイン逆変換(IDCT) f_uy は X 方向の成分で計算した結果を表し、係数行列 coeff を元に IDCT 計算をして結果を yuv に書き込む。 mcuCoord は対象の MCU の位置を、skip は間引き数をそれぞれ表す。 */ void idct_x( const SquareMatrix< double >& f_uy, const SquareMatrix< double >& coeff, Matrix< double >* yuv, Coord< int > mcuCoord, Coord< int > skip ) { // MCU のサイズ int mcuSize = f_uy.size(); // 画像のサイズ Coord< int > gSize( yuv->size() ); // 画像(YUV成分)に書き込む位置 Coord< int > gc( 0, mcuCoord.y * mcuSize * skip.y ); for ( int y = 0 ; y < mcuSize ; y++ ) { if ( gc.y >= gSize.y ) break; gc.x = mcuCoord.x * mcuSize * skip.x; for ( int x = 0 ; x < mcuSize ; x++ ) { if ( gc.x >= gSize.x ) break; double a = 0; // 求める係数 // f_uy の y 行目のベクトルと x 行目の係数ベクトルの内積を求める for ( int u = 0 ; u < mcuSize ; u++ ) { double d = f_uy( u, y ) * coeff( u, x ); if ( u == 0 ) d /= sqrt( 2 ); a += d; } fill_yuv( a * 2 / mcuSize, yuv, gc, skip ); gc.x += skip.x; } gc.y += skip.y; } } /* MCU_Decode : 離散コサイン逆変換(IDCT) mcu のデータを IDCT 変換し、結果を yuv に書き込む。 mcuSize は MCU のサイズ、skip は間引き量をそれぞれ表す。 */ void MCU_Decode( const Matrix< double >& mcu, Matrix< double >* yuv, int mcuSize, Coord< int > skip ) { assert( &mcu != 0 ); assert( yuv != 0 ); // 画像 ( YUV データ ) のサイズ Coord< int > gSize = yuv->size(); // X 成分の和を先に計算した結果 SquareMatrix< double > f_uy( mcuSize ); // 係数行列 SquareMatrix< double > coeff( mcuSize ); CalcCoeff( &coeff ); Coord< int > mcuCount = GetMCUCount( gSize, mcuSize, skip ); // MCU の X,Y 方向の数を求める Coord< int > mcuCoord; for ( mcuCoord.y = 0 ; mcuCoord.y < mcuCount.y ; ++( mcuCoord.y ) ) { for ( mcuCoord.x = 0 ; mcuCoord.x < mcuCount.x ; ++( mcuCoord.x ) ) { idct_y( mcu, mcuCoord, coeff, &f_uy ); idct_x( f_uy, coeff, yuv, mcuCoord, skip ); } } }
このサンプル・プログラムでは、処理を高速化するためにいくつかの手法を用いています。一つは、変換の中で使われる cos() 計算を先に行っておくことにより毎回の計算を省略することで、この計算は CalcCoeff 関数の中で行っています。また、演算の回数を減らすために、離散コサイン変換 ( DCT )・逆変換式 ( IDCT ) を次のように二つに分解しています。
DCT 変換
F'y,u = C(u)Σx{0→N-1}( fy,xcos( πu( 2x + 1 ) / 2N ) )
Fv,u = (2/N)C(v)Σy{0→N-1}( F'y,ucos( πv( 2y + 1 ) / 2N ) )
IDCT 変換
f'y,u = Σv{0→N-1}( Fv,uC(v)cos( πv( 2y + 1 ) / 2N ) )
fy,x = (2/N)Σu{0→N-1}( f'y,uC(u)cos( πu( 2x + 1 ) / 2N ) )
行列で表した式を使うと、DCT 変換の最初の式は fA を表し、その結果を F' としたとき後半の式は ATF' になります。また IDCT 変換の場合、最初の式が AF で、この結果を f' とすると後半の式は f'AT となります。これにより、一つの MCU に対して変換を行うときに計算する回数は、N = 8 の場合 8 x 8 x 8 x 8 = 4096 回から 8 x 8 x 8 x 2 = 1024 回に減らすことができます。
離散コサイン変換は MCU_Encode で行います。引数として、後述する YUV 成分のいずれかからなる Matrix 型変数の yuv と、変換した MCU を保持する Matrix 型変数の mcu、一つの MCU のサイズ mcuSize、最後にサンプリング ( 間引き ) 量の skip の計 4 つが渡されます。サンプリング ( 間引き ) とは変換対象の画素を間引く処理のことで、例えば skip の値を ( 2, 2 ) とした場合、画素は一つおきに読み込まれ変換されることになるので、変換後の値は画像サイズの約 1 / 4 程度になります。これは、X, Y 方向それぞれに指定が可能で、さらに YUV 各成分に対しても変更することができます。詳細は次の節で説明します。
前処理として、変換対象の画像のサイズを変数 yuv から取得し、係数行列をあらかじめ計算して変数 coeff に保持します。また、MCU のサイズは mcuSize で渡されるので、この値を使って必要な MCU の個数を求め、変数 mcuCount に保持します。なお、MCU は個々に作成するのではなく、一つの行列の中にまとめて保持します。画像の大きさが mcuSize で割り切れない場合、その余り分だけ mcu の方がサイズは大きくなります。またこのとき、端の MCU については画素がない部分が生じることになりますが、これは画素の値がゼロであるとして計算は行わないようにします。
前処理が完了したら、離散コサイン変換処理を行います。この処理は各 MCU ごとに dct_x と dct_y の二つの関数を呼び出して行います。dct_x では画像の X 方向の画素と係数行列の列ベクトルの内積を計算しています。CalcCoeff で求める係数行列は、このドキュメントの中で示される行列 A と同じ内容になる ( 1 / √2 が列方向に並ぶような構成 ) ことに注意すれば処理内容はすぐに理解できると思います。ここで得られた結果を変数 f_uy に保持しておいて、dct_y でもう一度係数行列と掛け合わせるわけですが、今度は f_uy の列ベクトルと係数行列の列ベクトルどうしで内積を求めています。ここでは係数行列が前側、f_uy ( = fA ) が後ろ側になるので、f_uy は列方向の成分で計算する必要があります。また係数行列は転置したもの ( AT ) を使うので、行方向ではなく列方向になることに注意して下さい。
逆変換もほぼ同じような内容になりますが、先に計算するのは Y 方向の成分の方 ( idct_y ) で、その後に X 方向の計算 ( idct_x ) を行なっています。
*2-1) 補足 1 にて、k ≠ 0 ならば Σm{0→N-1}( ei2πkm/N ) = 0 となることが証明してあるので、そちらを参照して下さい。
JPEG 法では離散コサイン変換の他にもう一つ、情報量を小さくするための手法を利用しています。これは人間の目の特性を利用した方法で、そのためにはまず「RGB 表色系」で構成された画像を「YUV 表色系」へ変換する必要があります。
「YUV 表色系」については、以前「ペイント・ルーチン (3) ペイントルーチンの応用」にて取り上げたことがありますが、Y は「輝度」、U は「青み」成分、V は「赤み」成分を表し、RGB と YUV の変換は以下の式で行うことができます。
Y = 0.299R + 0.587G + 0.114B U = -0.1687R - 0.3313G + 0.5B V = 0.5R - 0.4187G - 0.0813B R = Y + 1.402V G = Y - 0.34414U - 0.71414V B = Y + 1.772U
RGB 各成分が 0 から 255 までの値をとるとき、Y は同じ 0 から 255 までの値を取るのに対し、U と V は -127.5 から 127.5 までの範囲になります。JPEG では、これを符号なしの数として表せるように 128 を加算することになっていますが、サンプル・プログラムでは加算せずにそのままとしています。
人間の目は輝度の変化に敏感な反面、色の変化には比較的鈍感であるという性質を持っているため、YUV 成分に変換した後、色成分である U と V 成分についてはデータをある程度間引いてしまっても画質の低下をあまり感じません。逆に輝度成分を間引いてしまうと、すぐに画像の劣化がわかってしまいます。
通常、間引きするパターンは
のいずれかがよく利用されますが、JPEG の規格上は他にもいろいろなパターンがあるようです。上記サンプリング・パターンは、サンプリング用のオプションとしてよく次のように表されます。
サンプリングは、前述した離散コサイン変換のサンプル・プログラムの中で組み込まれており、間引き方法も任意に指定することができます。
RGB と YUV の相互変換のサンプル・プログラムを以下に示します。
/* RGB成分用パレット構造体 */ struct RGB { // 型宣言 typedef unsigned char primary_type; // RGB各成分の型 // 定数宣言 static const primary_type MAX = UCHAR_MAX; // RGB各成分の最大値 // 公開メンバ変数 primary_type r; // 赤成分 primary_type g; // 緑成分 primary_type b; // 青成分 /* 静的メンバ関数 */ // Check_RGBPrimary : 値 p が RGB::primary_type の値の範囲内にあるかを判定し、そうでなければ範囲内に収めて返す template< class T > static RGB::primary_type Check_RGBPrimary( T p ) { if ( p < 0 ) p = 0; if ( p > RGB::MAX ) p = RGB::MAX; return( p ); } /* コンストラクタ */ // RGB コンストラクタ : RGB各成分からの構築 RGB( primary_type red = primary_type(), primary_type green = primary_type(), primary_type blue = primary_type() ) : r( red ), g( green ), b( blue ) {} /* RGB → YUV 成分変換 */ // toY : RGB各成分から Y 成分を求める // // Y 成分を求める計算式は Y = 0.299R + 0.587G + 0.114B double toY() const { return( 0.299 * r + 0.587 * g + 0.114 * b ); } // toU : RGB各成分から U 成分を求める // // U 成分を求める計算式は U = -0.1687R - 0.3313G + 0.5B double toU() const { return( -0.1687 * r - 0.3313 * g + 0.5 * b ); } // toV : RGB各成分から V 成分を求める // // V 成分を求める計算式は V = 0.5R - 0.4187G - 0.0813B double toV() const { return( 0.5 * r - 0.4187 * g - 0.0813 * b ); } }; // toR : YUV(YCbCr) 各成分から R 成分を求める // // R 成分を求める計算式は R = Y + 1.402V RGB::primary_type toR( double y, double u, double v ) { return( RGB::Check_RGBPrimary( y + 1.402 * v + 0.5 ) ); } // toG : YUV(YCbCr) 各成分から G 成分を求める // // G 成分を求める計算式は G = Y - 0.34414U - 0.71414V RGB::primary_type toG( double y, double u, double v ) { return( RGB::Check_RGBPrimary( y - 0.34414 * u - 0.71414 * v + 0.5 ) ); } // toB : YUV(YCbCr) 各成分から B 成分を求める // // B 成分を求める計算式は G = Y + 1.772U RGB::primary_type toB( double y, double u, double v ) { return( RGB::Check_RGBPrimary( y + 1.772 * u + 0.5 ) ); }
RGB 成分から YUV 各成分への変換は RGB クラスのメンバ関数 toY, toU, toV が行うのに対し、YUV 成分から RGB 各成分への変換は toR, toG, toB 各関数を利用します。RGB クラスは画像の色成分の取得や設定で利用するため構造体を用意しているのに対し、YUV 成分はその必要がなかったため、このような構成にしています。他にも、両方とも構造体やクラスで表して、型変換の多重定義やコンストラクタ等で変換する方法が考えられます。なお、圧縮のやり方によっては RGB へ変換した結果が負数になったり最大値を越える場合があるため、RGB 構造体の静的メンバ関数 Check_RGBPrimary で値が範囲内にあるかチェックを行っています。
以下に、サンプル・プログラムで画像を離散コサイン変換した結果を示します。テストに使用した画像は "Lenna" (図 4-1) です ( 実際には 512 x 512 のサイズです )。また、MCU のサイズは 8 としています。
 |
| Y 成分の変換結果 | U 成分の変換結果 | V 成分の変換結果 |
|---|---|---|
 |
 |
 |
YUV 各成分の画像は変換後のデータの大きさを表し、明るいほど値が大きいことを示しています。DC 成分にあたる、各 MCU の左上に値が集中しており、それ以外の成分はあまり変化が見られないことがこの結果からわかります。
変換後のデータをソートしてその値を等間隔に並べると、以下のようなグラフになります。
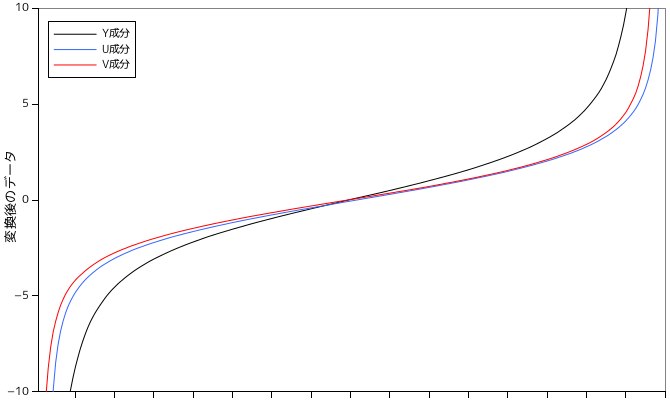 |
極端に絶対値の大きなデータは少なく、ほとんどはゼロ付近に集中している様子がこの結果から読み取れます。
| Y 成分を半分にサンプリング | U 成分を半分にサンプリング |
|---|---|
 |
 |
| V 成分を半分にサンプリング | UV 成分を半分にサンプリング |
 |
 |
上図 4-4 は、YUV 成分のうち一つを半分だけ間引いたときの画像を表しています (画像を半分に縮尺しているため、実際の画像はクリックすることで閲覧できます)。Y 成分を間引いた場合、画像が荒くなるのが顕著にわかるのに対し、U, V 成分を間引いても、元の画像との区別を付けることはできません。これは人間の目が U, V 成分の変化に鈍感なためで、この性質を利用することで画像のサイズを小さくすることができます。右下は U, V 成分の両方を半分に間引いた結果ですが、これでも変化に気づくことはできないと思います。
テスト画像は 512 x 512 の大きさなので、MCU のサイズが 8 x 8 のとき、その数は 512 / 8 x 512 / 8 = 4096 になります。一つの MCU に対しては前にも述べたように 1024 回の演算を行うため、総計算回数は 4096 x 1024 = 4,194,304 回になります。MCU の大きさを倍の 16 x 16 にすると、MCU の個数は 1024、MCU 一つの演算回数は 163 x 2 = 8192 なので、総計算回数は 1024 x 8192 = 8,388,608 回になり、2 倍に増えます。N x N の大きさを持つ MCU を使って gx x gy の大きさの画像を処理すると、総演算回数は
となり、MCU を大きくする程処理時間は増加することになります。
上の表とグラフは、MCU のサイズが変化したときの処理時間を実際に計測した結果を表し、"Encode" は離散コサイン変換を、"Decode" は逆変換をそれぞれ意味しています。計算上では MCU のサイズに比例して計算回数が増加していますが、離散コサイン変換 ( Encode ) の場合は実際の処理時間が直線上には並ばず、指数関数的に増加しているように見えます。この章では紹介していませんが、離散コサイン変換・逆変換は離散フーリエ変換の一種なので、高速フーリエ変換を応用した高速化によって処理時間を改善することができます。
今回は、JPEG 圧縮で利用されている離散コサイン変換をメインに紹介しましたが、今のところデータに偏りが生じただけで、サンプリング処理を除けばまだ圧縮処理を行っていません。次回は、量子化と符号化処理について紹介したいと思います。
離散フーリエ変換に登場する係数行列は直交行列であることが証明できます。フーリエ変換は信号を周波数成分に変換するものと考えることができますが、周波数に対する軸(正規直交基底)に「主軸変換」する操作ともとらえる事が可能です。
このことを証明する前に一点だけ注意すべき点があります。まず、離散フーリエ変換の係数行列の各要素は複素数であるため、内積の定義が実数の場合と異なります。内積は、ノルムがゼロ以上であること(正値性)、ベクトルの前後を交換しても値が等しくなること(対称性)、分配法則が成り立つこと(線形性)を満たす必要があります。そこで複素数成分を持つベクトルの内積に対して正値性を満たすために、各要素の二乗和を求めるのではなく、共役複素数との積を求めるようにします(エルミート内積)。そうすると今度は対称性が成り立たなくなるため、前後を交換した値が共役複素数になるものとします(エルミート対称性)。以下の説明において、内積はすべてこの「エルミート内積」であることに注意して下さい。
各列 ( または行 ) ベクトルにおいて、k 番目と m 番目のベクトルの内積は
| ( 1 + ωN-k・ωNm + ωN-2k・ωN2m + ... + ωN-k(N-1)・ωNm(N-1) ) / N | |
| = | ( 1 + ωNm-k + ωN2(m-k) + ... + ωN(N-1)(m-k) ) / N |
| = | Σj{0→N-1}( ωNj(m-k) ) / N |
で求めることができます。但し、ωN-m の共役複素数 ( ωN-m )~ は
より ωNm になることを利用しています。m = k ならば、和の各項は 1 と等しくなるため内積は 1 になります。m ≠ k のとき、等比級数の公式
より
| Σj{0→N-1}( ωNj(m-k) ) | = | ( 1 - ωNN(m-k) ) / ( 1 - ωN(m-k) ) |
| = | ( 1 - ei2πN(m-k)/N ) / ( 1 - ωN(m-k) ) | |
| = | ( 1 - ei2π(m-k) ) / ( 1 - ωN(m-k) ) | |
| = | 0 |
となります。但し、任意の整数 N に対して
が成り立つことを利用しています。このことから、係数行列は直交行列であることがわかります。
◆◇◆更新履歴◆◇◆
◎ 離散コサイン変換のサンプル・プログラム中 dct_y の内容を少し変更しました (2015-11-09)
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |