前章で、多重解像度解析について Haar のスケーリング・ウェーブレット関数を使って説明しましたが、多重解像度解析に利用できる関数は Haar 以外にも存在します。今回は、多重解像度解析に利用できる関数としての条件を示した上で、その条件を満たす関数の一つである「ドビッシー ( Daubechies ) のウェーブレット関数」と、JPEG2000 の中で利用されているウェーブレット関数の二種類を紹介したいと思います。
また、前にも述べたように、ウェーブレット変換を行ってもデータ量は変化しません。JPEG の場合と同じく、変換後には量子化と符号化を行う必要があります。この章では、量子化の方法についても説明をしたいと思います。
Haar のスケーリング関数を使った多重解像度解析処理では、二つの矩形を平均化して一つの矩形にすることで、解像度を一つ落とす ( レベルを一つあげる ) 処理を行っていました。この時の矩形の高さがスケーリング係数を表すことになります。また、元の二つの矩形は、平均化された矩形との高さの差の絶対値が等しくなり、この値がウェーブレット係数を表していました。
逆に見ると、あるレベルの矩形に誤差成分を加減算することで二つの矩形が生成され、それらの矩形もまたそれぞれ二つの矩形に分割されてゆきます。これは解像度を一つ上げる処理に該当します。このような処理を可能にしているのは、Haar の基本参照波が次のような関係式を満たしているからです。
φ( t ) = φ( 2t ) + φ( 2t - 1 )
ψ( t ) = φ( 2t ) - φ( 2t - 1 )
φ(t) は φ(2t), φ(2t-1) より幅が二倍あります。つまり、幅が二倍になったとき、元の関数を結合して表すことができることを上の式は表しています。このとき、あるレベル j と一つ下のレベル j - 1 のスケーリング・ウェーブレット関数の関係式は次のように書き表せます。
φ0(j)(t) = (1/√2)φ0(j-1)(t) + (1/√2)φ1(j-1)(t)
ψ0(j)(t) = (1/√2)φ0(j-1)(t) - (1/√2)φ1(j-1)(t)
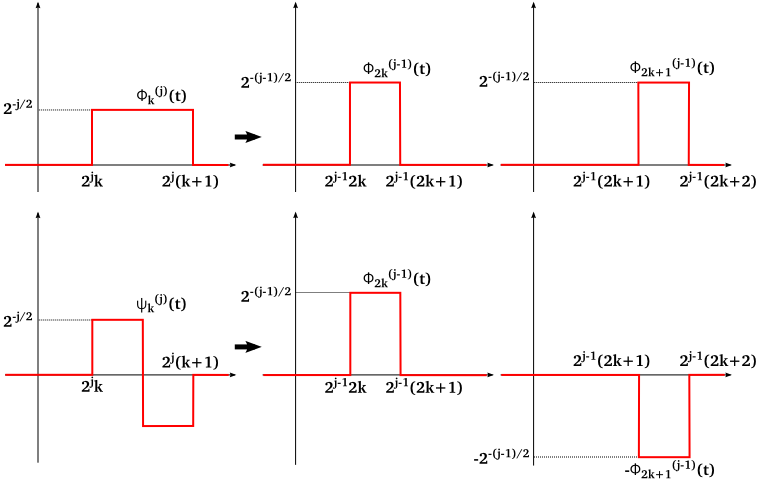
さらに任意の k に対しても下式が成り立ちます。
φk(j)(t) = (1/√2)φ2k(j-1)(t) + (1/√2)φ2k+1(j-1)(t)
ψk(j)(t) = (1/√2)φ2k(j-1)(t) - (1/√2)φ2k+1(j-1)(t)
但し、φk(j)(t) = 2-j/2φ( 2-jt - k ), ψk(j)(t) = 2-j/2ψ( 2-jt - k ) を表します。
このように、あるレベルのスケーリング関数とウェーブレット関数が、それよりもレベルの低いスケーリング関数の線形結合で表現できる関係を「ツースケール関係 ( Two-scale Relation)」と言います。
 |
ツースケール関係は、一般化して下式のように表すことができます。
| φk(j)(t) | = | Σn{0→N-1}( Pnφ2k+n(j-1)(t) ) |
| = | Σn{2k→2k+N-1}( Pn-2kφn(j-1)(t) ) | |
| ψk(j)(t) | = | Σn{0→N-1}( Qnφ2k+n(j-1)(t) ) |
| = | Σn{2k→2k+N-1}( Qn-2kφn(j-1)(t) ) |
または次のようにも表すこともできます。
(1/√2)φ( 2-jt - k ) = Σn{2k→2k+N-1}( Pn-2kφ( 2-j+1t - n ) )
(1/√2)ψ( 2-jt - k ) = Σn{2k→2k+N-1}( Qn-2kφ( 2-j+1t - n ) )
Haar の場合の係数は、先ほど示した式から
P0 = P1 = 1 / √2
Q0 = 1 / √2, Q1 = -1 / √2
となります。
簡単にいえば、ツースケール関係とはスケーリング関数を平行移動した複数の関数を線形結合することで一つ上のレベルの ( スケールが二倍の ) スケーリング・ウェーブレット関数が生成できることを意味します。このとき、線形結合する関数の個数 N は二つと限定する必要はなく任意とすることができます。"ツースケール" が関数の個数ではなくスケールを二倍するという意味であることに注意して下さい。Haar の例は、たまたま結合する関数が二個であるだけです。
内積 ( f, g ) に対し、( f, g ) = 0 となるとき f, g は直交しているといいます (*1-1)。内積は公理を満たしていればベクトル以外にも適用可能で、任意の実数値関数 f(t), g(t) に対して
とすれば、これは内積の公理を満たします。従って関数 φk(j)(t) が
| ( φk(j)(t), φk'(j)(t) ) | = | 1 | [ k = k' ] |
| = | 0 | [ k ≠ k' ] |
の関係を満たすとき、これらの関数は「正規直交基底」となります。積分は和の極限なので、無限長のベクトルによる積和と考えれば直感的に理解できると思います。Haar のスケーリング関数は、あるレベルの関数 φk(j)(t) に対して k ≠ k' の場合、互いに重なる部分がありません。k = k’ ならば
| || φk(j)(t) ||2 | = | ∫{-∞→∞} φk(j)(t)・φk(j)(t) dt |
| = | ∫{2jk→2j(k+1)} 2-j/2・2-j/2 dt | |
| = | [ 2-jt ]{2jk→2j(k+1)} = 1 |
なので正規直交基底となります ( Haar のツースケール関係において係数 1 / √2 を付加したのは、関数を正規直交基底とするためです。しかし、直交さえしていればノルムが 1 でなくても問題はないので係数は省略することも可能です。その場合、ノルムは 2j/2 となります )。ベクトルのなす基底と同じように関数のなす基底を考えれば、あるレベルの Haar のスケーリング関数からなる線形空間があり、レベル 0 での基底の数を N とすれば、レベル j の線形空間の次元は N / 2j となります。同様に、Haar のウェーブレット関数は、あるレベルの関数 ψk(j)(t) に対して k ≠ k' の場合、互いに重なる部分がなく、k = k’ ならば
| || ψk(j)(t) ||2 | = | ∫{-∞→∞} ψk(j)(t)・ψk(j)(t) dt |
| = | ∫{2jk→2j(k+1/2)} 2-j/2・2-j/2 dt + ∫{2j(k+1/2)→2j(k+1)} (-2-j/2)・(-2-j/2) dt | |
| = | [ 2-jt ]{2jk→2j(k+1/2)} + [ 2-jt ]{2j(k+1/2)→2j(k+1)} = 1 |
となるのでやはり正規直交基底となります。
同じレベルのスケーリング関数とウェーブレット関数について調べてみると、k ≠ k' ならやはり重なる部分がなく積分値はゼロとなり、k = k' のときは
| ( φk(j)(t), ψk(j)(t) ) | = | ∫{-∞→∞} φk(j)(t)・ψk(j)(t) dt |
| = | ∫{2jk→2j(k+1/2)} 2-j/2・2-j/2 dt + ∫{2j(k+1/2)→2j(k+1)} 2-j/2・(-2-j/2) dt = 0 |
となるので、常に ( φk(j)(t), ψk'(j)(t) ) = 0 であることになります。基底が直交するので、それぞれの基底の線形結合で表される任意の二つの関数もまた直交し、レベル j のスケーリング関数・ウェーブレット関数からなる線形空間をそれぞれ V(j), W(j) とすれば、
と表すことができます。
ツースケール関係は、あるレベルのスケーリング関数の線形結合によって一つ上のレベルのスケーリング・ウェーブレット関数が表せることを意味するのでした。つまり、あるレベルのスケーリング関数を構成する基底の線形結合によって一つ上のレベルのスケーリング関数を表現することができるので、V(j) の任意の元 (関数) は V(j-1) の元でもあることになります。この時、これらの線形空間は包含関係にあるといい、以下のように表します。
Haar の場合、V(j) と W(j) はどちらも正規直交基底であり、しかも互いに直交していることから全ての基底を合わせた線形空間もまた正規直交基底となります。このような線形空間を「(直交)直和 ( (Orthogonal) Direct Sum )」といい、V(j) ⊕ W(j) で表します。線形空間 V(j-1) の任意の元 φk(j-1)(t) が V(j) ⊕ W(j) の線形結合で表すことができるなら、基底は全て直交で線形独立なので結合の表し方は一意となり (*1-2)、
と表すことができます。これを線形空間 V(j-1) の V(j), W(j) への「(直交)直和分解 ( (Orthogonal) Direct Sum Decomposition)」といいます。
W(j) の任意の元 (関数) は V(j) の任意の元と直交するのでした。包含関係から、j < j' となる V(j') に対して V(j) ⊃ ... ⊃ V(j') ⊃ V(j'-1) であり、V(j'-1) = V(j') ⊕ W(j') ⊃ W(j') なので、異なるレベルに対して W(j) ⊥ W(j') が成り立ち、両者の任意の関数は互いに直交することになります。以上の結果から、直交直和分解
| V(0) | = | W(1) ⊕ V(1) |
| = | W(1) ⊕ W(2) ⊕ V(2) | |
| = | W(1) ⊕ W(2) ⊕ W(3) ⊕ V(3) | |
| : | ||
| = | W(1) ⊕ W(2) ⊕ W(3) ⊕ ... W(n) ⊕ V(n) |
が得られ、最後の V(n) は定数値 (直流成分) となります。Haar のスケーリング・ウェーブレット関数では以下の式が成り立っていました。上式はこれを抽象化して記述したものです。よって、ツースケール関係を満たす直交関数を基底とした場合、常に下式を満たすということになります。このとき、基底が全て直交していれば、その式は一意に決まることに注意して下さい。
| f(0)(t) | = | g(1)(t) + g(2)(t) + ... + g(n)(t) + f(n)(t) |
| = | Σj{1→n}( g(j)(t) ) + f(n)(t) |
離散フーリエ変換は以下のような式で表されるのでした。
Fk = (1/√N)Σl{0→N-1}( fle-i2πkl/N )
fl = (1/√N)Σk{0→N-1}( Fkei2πkl/N )
ei2πkl/N ( 0 ≤ k ≤ N ) は、( ei2πkl/N, ei2πk'l/N ) = (1/N)Σl{0→N-1}( ei2π(k-k')l/N ) を内積としたとき k = k' ならば和は N になるので明らかに 1 であり、k ≠ k' ならば等比数列の和の公式から
となります ( オイラーの公式から ei2π(k-k') = cos 2π(k-k') + isin 2π(k-k') = 1 のため分子はゼロになります )。よって、ei2πkl/N は正規直交基底であり、fl は Fk を係数とした基底の線形結合で表され、係数 Fk は fl と基底の内積となっています。前者は離散フーリエ逆変換、後者は離散フーリエ変換と呼ばれます。
ウェーブレット変換の場合、直交直和分解の式を具体的に表せば
のようになります。ここで M はサンプリングしたデータ数と考えることができます。係数 ωk(j) はフーリエ変換の場合と同様に f(0)(t) と基底との内積で表され、
と表すことができます。このように、フーリエ変換もウェーブレット変換も直交基底による関数の展開という意味では同じですが、決定的な違いは、ウェーブレット変換の方が時間・位置に対する基底を持っているという点です。フーリエ変換の場合は周波数成分を表す基底しか持っていないので、ある時間・位置の状態を調べることができないのに対し、ウェーブレット変換の場合はある時間・位置に対して局所的に状態を調べることができるという利点があります。
V(j), W(j) が正規直交基底ならば、レベル j - 1 のスケーリング関数 φk(j-1)(t) で表された関数 f(j-1) はレベル j のスケーリング関数 φk(j)(t) とウェーブレット関数 ψk(j)(t) の線形結合で一意に表されます。また、その係数は、対象の関数と基底との内積と等しくなります。従って、
| f(j-1)(t) | = | f(j)(t) + g(j)(t) |
| = | Σk{0→M/2j-1}( sk(j)φk(j)(t) + ωk(j)ψk(j)(t) ) |
| sk(j) | = | ∫{0→M} f(t)φk(j)(t) dt |
| ωk(j) | = | ∫{0→M} f(t)ψk(j)(t) dt |
の関係式が得られます。下側の二式にツースケール関係
| φk(j)(t) | = | Σn{2k→2k+N-1}( Pn-2kφn(j-1)(t) ) |
| ψk(j)(t) | = | Σn{2k→2k+N-1}( Qn-2kφn(j-1)(t) ) |
を代入して
| sk(j) | = | ∫{0→M} f(t)Σn{2k→2k+N-1}( Pn-2kφn(j-1)(t) ) dt |
| = | Σn{2k→2k+N-1}( Pn-2k∫{0→M} f(t)φn(j-1)(t) dt ) | |
| = | Σn{2k→2k+N-1}( Pn-2ksn(j-1) ) | |
| ωk(j) | = | Σn{2k→2k+N-1}( Qn-2ksn(j-1) ) |
という関係式が得られます。つまり、数列 { Pn }, { Qn } が既知であれば、スケーリング・ウェーブレット関数がどんなものかわからなくても一つ前のレベルの係数から次のレベルの係数が計算できることを意味します。
また、レベル j での f(j)(t), g(j)(t) の基底による表現式
| f(j)(t) | = | Σk{0→M/2j-1}( sk(j)φk(j)(t) ) |
| g(j)(t) | = | Σk{0→M/2j-1}( ωk(j)ψk(j)(t) ) |
に再びツースケール関係式を代入すると
| f(j)(t) | = | Σk{0→M/2j-1}( sk(j)Σn{2k→2k+N-1}( Pn-2kφn(j-1)(t) ) ) |
| g(j)(t) | = | Σk{0→M/2j-1}( ωk(j)Σn{2k→2k+N-1}( Qn-2kφn(j-1)(t) ) ) |
となり、f(j-1)(t) = f(j)(t) + g(j)(t) より
| Σk{0→M/2j-1-1}( sk(j-1)φk(j-1)(t) ) | = | Σk{0→M/2j-1}( sk(j)Σn{2k→2k+N-1}( Pn-2kφn(j-1)(t) ) ) |
| + Σk{0→M/2j-1}( ωk(j)Σn{2k→2k+N-1}( Qn-2kφn(j-1)(t) ) ) | ||
| = | Σk{0→M/2j-1}( Σn{2k→2k+N-1}( [ Pn-2ksk(j) + Qn-2kωk(j) ]φn(j-1)(t) ) ) | |
となります。左右の辺において、φk(j-1)(t) = φn(j-1)(t) となる項の係数が等しくなればよいので、両辺を実際に分解してみると ( M/2j = L, Pn-2ksk(j) + Qn-2kωk(j) = An-2k,k(j) として )
| (左辺) | = | Σk{0→2L-1}( sk(j-1)φk(j-1)(t) ) |
| = | s0(j-1)φ0(j-1)(t) + s1(j-1)φ1(j-1)(t) + ... + sk(j-1)φk(j-1)(t) + ... + s2L-1(j-1)φ2L-1(j-1)(t) | |
| (右辺) | = | Σk{0→L-1}( Σn{2k→2k+N-1}( An-2k,k(j)φn(j-1)(t) ) ) |
| = | Σk{0→L-1}( A0,k(j)φ2k(j-1)(t) + A1,k(j)φ2k+1(j-1)(t) + ... + AN-1,k(j)φ2k+N-1(j-1)(t) ) | |
| = | A0,0(j)φ0(j-1)(t) + A1,0(j)φ1(j-1)(t) + ... + Ak,0(j)φk(j-1)(t) + ... + AN-1,0(j)φN-1(j-1)(t) | |
| + A0,1(j)φ2(j-1)(t) + A1,1(j)φ3(j-1)(t) + ... + Ak-2,1(j)φk(j-1)(t) + ... + AN-1,1(j)φN+1(j-1)(t) | ||
| + ... | ||
| + A0,L-1(j)φ2(L-1)(j-1)(t) + A1,L-1(j)φ2(L-1)-1(j-1)(t) + ... + Ak-2(L-1),L-1(j)φk(j-1)(t) + ... + AN-1,L-1(j)φ2(L-1)+N-1(j-1)(t) | ||
となって、φk(j-1)(t) の項だけを抽出して
| sk(j-1)φk(j-1)(t) | = | Ak,0(j)φk(j-1)(t) + Ak-2,1(j)φk(j-1)(t) + ... + Ak-2(L-1),L-1(j)φk(j-1)(t) |
| = | Σn{0→L-1}( Ak-2n,n(j) )φk(j-1)(t) | |
| = | Σn{0→M/2j-1}( Pk-2nsn(j) + Qk-2nωn(j) )φk(j-1)(t) |
より
という結果が得られます ( レベル j での基底の数は N / 2j なのに対し、k の値によって項の数は変わるのですが、上記の式に当てはめると含まれない部分は φ(t) の値がゼロになるので問題はありません )。この式は、一つ前のレベルのスケーリング係数を計算することが可能であることを表しています。
Haar の関数を使って上記内容を再計算して検証してみたいと思います。
| sk(j) | = | ∫{0→M} f(t)φk(j)(t) dt |
| ωk(j) | = | ∫{0→M} f(t)ψk(j)(t) dt |
に Haar のツースケール関係
| φk(j)(t) | = | (1/√2)[ φ2k(j-1)(t) + φ2k+1(j-1)(t) ] |
| ψk(j)(t) | = | (1/√2)[ φ2k(j-1)(t) - φ2k+1(j-1)(t) ] |
を代入して
| sk(j) | = | ∫{0→M} f(t)(1/√2)[ φ2k(j-1)(t) + φ2k+1(j-1)(t) ] dt |
| = | (1/√2)[ ∫{0→M} f(t)φ2k(j-1)(t) dt + ∫{0→M} f(t)φ2k+1(j-1)(t) dt ] | |
| = | (1/√2)( s2k(j-1) + s2k+1(j-1) ) | |
| ωk(j) | = | (1/√2)( s2k(j-1) - s2k+1(j-1) ) |
という関係式が得られます。これは、前回のサンプル・プログラムで処理を行った時の式そのものになっています。また、
| f(j)(t) | = | Σk{0→M/2j-1}( sk(j)φk(j)(t) ) |
| g(j)(t) | = | Σk{0→M/2j-1}( ωk(j)ψk(j)(t) ) |
にツースケール関係式を代入して
| f(j)(t) | = | Σk{0→M/2j-1}( sk(j)(1/√2)[ φ2k(j-1)(t) + φ2k+1(j-1)(t) ] ) |
| g(j)(t) | = | Σk{0→M/2j-1}( ωk(j)(1/√2)[ φ2k(j-1)(t) - φ2k+1(j-1)(t) ] ) |
f(j-1)(t) = f(j)(t) + g(j)(t) より
| Σk{0→M/2j-1-1}( sk(j-1)φk(j-1)(t) ) | = | Σk{0→M/2j-1}( sk(j)(1/√2)[ φ2k(j-1)(t) + φ2k+1(j-1)(t) ] ) |
| + Σk{0→M/2j-1}( ωk(j)(1/√2)[ φ2k(j-1)(t) - φ2k+1(j-1)(t) ] ) | ||
| = | Σk{0→M/2j-1}( (1/√2)( sk(j) + ωk(j) )φ2k(j-1)(t) + (1/√2)( sk(j) - ωk(j) )φ2k+1(j-1)(t) ) | |
となります。両辺を分解して ( M/2j = L, (1/√2)( sk(j) + ωk(j) ) = Ak(j), (1/√2)( sk(j) - ωk(j) ) = Bk(j) として )
| (左辺) | = | Σk{0→2L-1}( sk(j-1)φk(j-1)(t) ) |
| = | s0(j-1)φ0(j-1)(t) + s1(j-1)φ1(j-1)(t) + ... + sk(j-1)φk(j-1)(t) + ... + s2L-1(j-1)φ2L-1(j-1)(t) | |
| (右辺) | = | Σk{0→L-1}( Ak(j)φ2k(j-1)(t) + Bk(j)φ2k+1(j-1)(t) ) |
| = | A0(j)φ0(j-1)(t) + B0(j)φ1(j-1)(t) + A1(j)φ2(j-1)(t) + B1(j)φ3(j-1)(t) + ... | |
| + AL-1(j)φ2(L-1)(j-1)(t) + BL-1(j)φ2(L-1)+1(j-1)(t) | ||
となるので、k が偶数なら
であり、奇数なら
になります。前回のサンプル・プログラムで、スケーリング・ウェーブレット各成分の和と差を計算していたことから、これも正しい結果であることがわかると思います。
*1-1) 内積とその公理については「固有値問題 (1) 対称行列の固有値」の中の「補足1) 内積の公理」で紹介されています。
*1-2) 線形独立なベクトルによって、任意のベクトルは一通りの線形結合のみで表されます。これは「数値演算法 (8) 連立方程式を解く -2-」の中の「5) 固有値と固有ベクトル」で証明していますが、直交基底は線形独立なのでやはり任意のベクトルに対する線形結合は一意となります。関数に対しても同様な方法で証明することができます。なお、直交基底が線形独立なのは簡単に証明ができて、仮に線形従属であるとすれば、ある基底の一つが他の基底の線形結合で表せるので、その基底を xj としたとき
と表せます。ところが、両辺に対して xj との内積を計算すると、k ≠ j なら互いに直交していることから右辺はゼロとなり、左辺は正値となるので矛盾します。従って、正規直交基底の線形結合は一意に決まることになります。
ベルギーの物理数学者「イングリッド・ドビッシー ( Ingrid Daubechies )」は、ツースケール関係式を満たし、正規直交基底となるコンパクトサポートな ( ゼロ以外の値を持つ定義域が有限な ) 関数 ( ドビッシーのスケーリング関数とウェーブレット関数 ) を求めました。この関数は、y = f(x) の形で表すことができないのですが、以下のような方法で形状を見ることができます。
ドビッシーのスケーリング関数の中でも単純なものとして、次の関係式を満たすものがあります。
この関数が 0 ≤ t ≤ 3 の範囲でのみ値を持ち、
を満たすとき
| φ(0) | = | [ ( 1+√3)/4 ]φ( 0 ) + [ (3+√3)/4 ]φ( -1 ) + [ (3-√3)/4 ]φ( -2 ) + [ (1-√3)/4 ]φ( -3 ) = [ ( 1+√3)/4 ]φ( 0 ) |
| φ(1) | = | [ ( 1+√3)/4 ]φ( 2 ) + [ (3+√3)/4 ]φ( 1 ) + [ (3-√3)/4 ]φ( 0 ) + [ (1-√3)/4 ]φ( -1 ) = [ ( 1+√3)/4 ]φ( 2 ) + [ ( 3 + √3 ) / 4 ]φ( 1 ) + [ (3-√3)/4 ]φ( 0 ) |
| φ(2) | = | [ ( 1+√3)/4 ]φ( 4 ) + [ (3+√3)/4 ]φ( 3 ) + [ (3-√3)/4 ]φ( 2 ) + [ (1-√3)/4 ]φ( 1 ) = [ ( 3 + √3 ) / 4 ]φ(3) + [ (3-√3)/4 ]φ( 2 ) + [ (1-√3)/4 ]φ( 1 ) |
| φ(3) | = | [ ( 1+√3)/4 ]φ( 6 ) + [ (3+√3)/4 ]φ( 5 ) + [ (3-√3)/4 ]φ( 4 ) + [ (1-√3)/4 ]φ( 3 ) = [ (1-√3)/4 ]φ(3) |
となるので、これらをまとめると
となって、φ(1)とφ(2)は
という結果が得られます。φ(0) から φ(3) までの値があれば、最初に示した関係式を利用してそれらの二等分点を求めることができます。さらにそれを繰り返し行うことによって、この関数の全体像を得ることができます。
| φ(0.5) | = | [ ( 1+√3)/4 ]φ(1) + [ ( 3 + √3 ) / 4 ]φ(0) + [ (3-√3)/4 ]φ(-1) + [ (1-√3)/4 ]φ(-2) = ( 1 + √3 )2 / 8 |
| φ(1.5) | = | [ ( 1+√3)/4 ]φ(3) + [ ( 3 + √3 ) / 4 ]φ(2) + [ (3-√3)/4 ]φ(1) + [ (1-√3)/4 ]φ(0) = 0 |
| φ(2.5) | = | [ ( 1+√3)/4 ]φ(5) + [ ( 3 + √3 ) / 4 ]φ(4) + [ (3-√3)/4 ]φ(3) + [ (1-√3)/4 ]φ(2) = ( 1 - √3 )2 / 8 |
| φ(0.25) | = | [ ( 1+√3)/4 ]φ(0.5) + [ ( 3 + √3 ) / 4 ]φ(-0.5) + [ (3-√3)/4 ]φ(-1.5) + [ (1-√3)/4 ]φ(-2.5) = ( 1 + √3 )3 / 32 |
| φ(0.75) | = | [ ( 1+√3)/4 ]φ(1.5) + [ ( 3 + √3 ) / 4 ]φ(0.5) + [ (3-√3)/4 ]φ(-0.5) + [ (1-√3)/4 ]φ(-1.5) = ( 3 + √3 )( 1 + √3 )2 / 32 |
| : |
以下に、ドビッシーのスケーリング関数とウェーブレット関数を計算するサンプル・プログラムを示します。
// Pn,Qn のリスト double Pn4[] = { +0.683013, +1.183013, +0.316987, -0.183013, }; double Qn4[ sizeof( Pn4 ) / sizeof( Pn4[0] ) ]; // t = 0,1,2,3 での φ(x) の値 double Phi[] = { 0, 1.366026, -0.366026, 0, }; /* Qnの計算 Pn を逆転して奇数の添字は符号を逆転 */ void CalcQn() { size_t size = sizeof( Pn4 ) / sizeof( Pn4[0] ); for ( size_t n = 0 ; n < size ; n++ ) Qn4[n] = pow( -1, n ) * Pn4[size - n - 1]; } /* ψ(t) の初期化 ( t が整数値の値を設定する ) φ(t) の値から計算を行う phi : φ(t) への参照 psi : ψ(t) へのポインタ qn4 : Qn reso : 解像度 */ void InitDaubechiesWavelet( const vector< double >& phi, vector< double >* psi, double* qn4, int reso ) { int size = psi->size(); for ( int i = 0 ; i < size ; i += reso ) { // 整数値の個所をたどる for ( int j = 0 ; j < size / reso ; ++j ) { // 項の数の分だけ線形結合 int idx = i * 2 - reso * j; // 計算に使う φ(t) への添字 if ( idx >= 0 && idx < size ) (*psi)[i] += qn4[j] * phi[idx]; } } } /* 二分点の値を計算してdaubechiesの関数を求める あらかじめ、t が整数値の値は設定されていることを想定している phi : 生成に使う φ(t) への参照 d : 生成した値を格納する配列へのポインタ seq : daubechie の数列 reso : 解像度 */ void Daubechies( const vector< double >& phi, vector< double >* d, double* seq, int reso ) { int size = d->size(); for ( int k = reso / 2 ; k > 0 ; k /= 2 ) { // 初期値を [ 0, 1 ] として二分点を求める for ( int i = k ; i < size ; i += k * 2 ) { // ステップは 2 ステップ分 for ( int j = 0 ; j < size / reso ; ++j ) { // 項の数の分だけ線形結合 int idx = i * 2 - reso * j; // 計算に使う φ(t) への添字 if ( idx >= 0 && idx < size ) (*d)[i] += seq[j] * phi[idx]; } } } } /* メイン・ルーチン */ void DaubechiesMain() { const int RESO = 7; // 解像度 ( 幅 1 に対していくつ刻みで計算するか ; 2 のべき数で表現 ) int reso = pow( 2, RESO ); // 解像度 2^RESO size_t PhiSize = ( sizeof( Pn4 ) / sizeof( Pn4[0] ) ) * reso; // 計算する値のサイズ vector< double > phi( PhiSize, 0 ); // スケーリング成分 φ(t) vector< double > psi( PhiSize, 0 ); // ウェーブレット成分 ψ(t) CalcQn(); // φ(t) で t が整数値の個所を初期化 double* dp = Phi; for ( size_t i = 0 ; i < PhiSize ; i += reso ) phi[i] = *dp++; // ψ(t) で t が整数値の個所を初期化 InitDaubechiesWavelet( phi, &psi, Qn4, reso ); // 二分点の値を埋めていく Daubechies( phi, &phi, Pn4, reso ); Daubechies( phi, &psi, Qn4, reso ); // 結果の出力 cout << "# No. x scaling wavelet" << endl; for ( size_t i = 0 ; i < PhiSize ; i++ ) cout << i << " " << static_cast< double >( i ) / reso << " " << phi[i] << " " << psi[i] << endl; }
φ(0) から φ(3) までの値はあらかじめ計算して配列 Phi に格納してあります。Sn はスケーリング関数に対する漸化式の係数を表し、ウェーブレット関数に対する漸化式の係数 Wn は、以下の式を使って Sn から求めることが可能です (補足 1)。これは関数 CalcWn で行なっています。なお、スケーリング関数の値は自分自身の値を使って二分点を求めるのに対し、ウェーブレット関数の値はスケーリング関数の値を使って計算されることに注意して下さい。
DaubechiesMain がメイン・ルーチンとなり、最初に CalcWn で Wn の初期化を行なっています。φ(0) から φ(3) までの値を設定した後、InitDaubechiesWavelet を使って ψ(0) から ψ(3) までの値を初期化します。あとは、関数 Daubechies を使って二分点の値を次々と計算してすき間を埋めて、最後に結果を出力します。メイン・ルーチン内の定数 RESO は値をいくつ求めるかを示し、2RESO で表される値になります。よって、より細かく計算をしたい場合はこの値を大きくすれば実現できます。
サンプル・プログラムを使って求めたドビッシーのスケーリング関数とウェーブレット関数は次のような姿になります。
| Daubechies's Scaling Function | Daubechies's Wavelet Function |
|---|---|
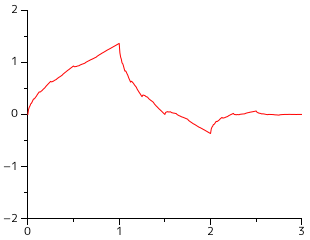 | 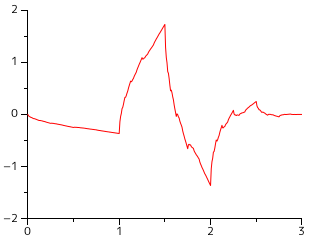 |
この関数が先に示した漸化式を満たしている様子を以下に示します。
| Daubechies's Scaling Function | Daubechies's Wavelet Function |
|---|---|
 | 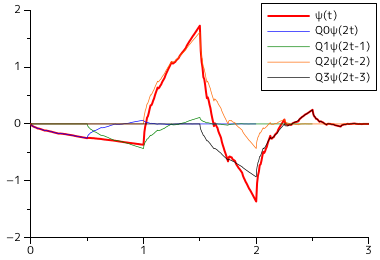 |
図中、赤の太線で示したものが φ(t), ψ(t) で、その他の色で示したものが √2Pnφ( 2t - n )、√2Qnψ( 2t - n ) になります。各関数の和が赤の太線になる様子をこの図から読み取ることができます。
上で示した式は、一般式においてパラメータ N を 2 にした場合のものになります。下表は、N = 1 から N = 4 までのドビッシーの数列 Pn を示したものです。N = 1 は Haar の関数そのもので、N = 2 は先に紹介したスケーリング関数を表す数列になります。
| N | n | Pn |
|---|---|---|
| 1 | 0 | +0.707106781 |
| 1 | +0.707106781 | |
| 2 | 0 | +0.482962913 |
| 1 | +0.836516304 | |
| 2 | +0.224143868 | |
| 3 | -0.129409523 | |
| 3 | 0 | +0.332670553 |
| 1 | +0.806891509 | |
| 2 | +0.459877502 | |
| 3 | -0.135011020 | |
| 4 | -0.085441274 | |
| 5 | +0.035226292 | |
| 4 | 0 | +0.230377813 |
| 1 | +0.714846571 | |
| 2 | +0.630880768 | |
| 3 | -0.027983769 | |
| 4 | -0.187034812 | |
| 5 | +0.030841382 | |
| 6 | +0.032883012 | |
| 7 | -0.010597402 |
N = 2 において、先ほど求めた値と異なっていますが、φk(j)(t) = 2-j/2φ(2-jt - k ) より先ほどの漸化式では √2 だけ掛けられた形になっており、求めた値を √2 で割る必要があります。その処理を行えば表の値と一致します。Haar の場合に漸化式が φ(t) = φ( 2t ) + φ( 2t - 1 ) となるのを考えれば理解しやすいと思います (補足 1)。
画像データをスケーリング係数とウェーブレット係数に分解するときは、前節で示した以下の式を使います。
sk(j) = Σn{2k→2k+N-1}( Pn-2ksn(j-1) )
ωk(j) = Σn{2k→2k+N-1}( Qn-2ksn(j-1) )
sn(j-1) が一つ前のレベルの ( 解像度のより高い ) スケーリング係数で、最初はこれが画像データになります。これと数列 Pn, Qn の積を数列の個数分だけ足す処理を繰り返すだけで計算ができるため、プログラムも非常に単純になります。逆に元に戻すときは
に従って定数項から順に同じような計算を繰り返すだけで実現できます。以下にサンプル・プログラムを示します。
/* WaveletCoef : スケーリング・ウェーブレット係数成分 */ template< class T > struct WaveletCoef { vector< T > s; // スケーリング係数計算結果 vector< T > wv; // ウェーブレット展開係数計算結果(垂直方向成分) vector< T > wh; // ウェーブレット展開係数計算結果(水平方向成分) vector< T > wd; // ウェーブレット展開係数計算結果(対角方向成分) // 配列のサイズを初期化(リサイズ)する void resize( Coord< int > size ) { s.resize( size.x * size.y ); wv.resize( size.x * size.y ); wh.resize( size.x * size.y ); wd.resize( size.x * size.y ); } }; /* DaubechiesCoef : ドビッシーの数列を返すためのクラス */ class DaubechiesCoef { vector< double > coef_; // ドビッシーの数列 public: /* ドビッシーの数列 [ s, e ) をコピーして構築 */ template< class In > DaubechiesCoef( In s, In e ) : coef_( s, e ) {} // 数列のサイズを返す size_t size() const { return( coef_.size() ); } // スケーリング関数に対するツースケール関係の i 番目の係数を返す double scaling( size_t i ) const { return( coef_.at( i ) ); } // ウェーブレット関数に対するツースケール関係の i 番目の係数を返す double wavelet( size_t i ) const { return( coef_.at( size() - i - 1 ) * pow( -1, i ) ); } }; /* Wavelet_Daubechies_1D : 一次元方向の Wavelet 変換 s0 : 入力信号への反復子 ( レベルがひとつ低いスケーリング係数 ) coef : ドビッシーの数列 s1 : スケーリング係数計算結果への反復子 w1 : ウェーブレット係数計算結果への反復子 size : 信号のデータ長 inc : indexの増分(X/Y方向を示す) */ template< class Coef > void Wavelet_Daubechies_1D( vector< double >::const_iterator s0, const Coef& coef, vector< double >::iterator s1, vector< double >::iterator w1, int size, int inc ) { int half = size / 2; // s0[2i+n]と係数の線形和を求める for ( int i = 0 ; i < half ; ++i ) { *s1 = *w1 = 0; for ( size_t n = 0 ; n < coef.size() ; ++n ) { int j = n + 2 * i; // サイズを超えた場合は巡回させる if ( j >= size ) j %= size; *s1 += coef.scaling( n ) * s0[j * inc]; *w1 += coef.wavelet( n ) * s0[j * inc]; } s1 += inc; w1 += inc; } } /* Wavelet_Daubechies_2D : 二次元方向の Wavelet 変換 s0 : 入力信号への参照 ( レベルがひとつ低いスケーリング係数 ) coef : ドビッシーの数列 wc : 係数計算結果へのポインタ size : 画像の大きさ */ template< class Coef > void Wavelet_Daubechies_2D( const vector< double >& s0, const Coef& coef, WaveletCoef< double >* wc, Coord< int > size ) { Coord< int > half( size.x / 2, size.y / 2 ); vector< double > s1x( half.x * size.y ); // 一次元方向のスケーリング係数用バッファ vector< double > w1x( half.x * size.y ); // 一次元方向のウェーブレット係数用バッファ wc->resize( Coord< int >( half.x, half.y ) ); // 水平方向への分解 for ( int i = 0 ; i < size.y ; ++i ) Wavelet_Daubechies_1D( s0.begin() + i * size.x, coef, s1x.begin() + i * half.x, w1x.begin() + i * half.x, size.x, 1 ); for ( int i = 0 ; i < half.x ; ++i ) { // スケーリング成分と垂直方向のウェーブレット成分への分解 Wavelet_Daubechies_1D( s1x.begin() + i, coef, ( wc->s ).begin() + i, ( wc->wv ).begin() + i, size.y, half.x ); // 水平方向のウェーブレット成分と対角方向のウェーブレット成分への分解 Wavelet_Daubechies_1D( w1x.begin() + i, coef, ( wc->wh ).begin() + i, ( wc->wd ).begin() + i, size.y, half.x ); } } /* IWavelet_Daubechies_1D : 一次元方向のWavelet逆変換 s1 : スケーリング係数計算結果への反復子 w1 : ウェーブレット係数計算結果への反復子 coef : ドビッシーの数列 s0 : 逆変換結果への反復子 ( レベルがひとつ低いスケーリング係数 ) size : 信号のデータ長 inc : indexの増分(X/Y方向を示す) */ template< class Coef > void IWavelet_Daubechies_1D( vector< double >::const_iterator s1, vector< double >::const_iterator w1, const Coef& coef, vector< double >::iterator s0, int size, int inc ) { // s1[i-n], w1[i-n] と係数の線形和を求める for ( int i = 0 ; i < size ; i++ ) { *s0 = s0[inc] = 0; for ( size_t n = 0 ; n < coef.size() / 2 ; ++n ) { int j = i - n; // 範囲外の場合は巡回させる if ( j < 0 || j >= size ) j = ( j + size ) % size; s0[inc] += coef.scaling( 2 * n + 1 ) * s1[j * inc] + coef.wavelet( 2 * n + 1 ) * w1[j * inc]; *s0 += coef.scaling( 2 * n ) * s1[j * inc] + coef.wavelet( 2 * n ) * w1[j * inc]; } s0 += 2 * inc; } } /* IWavelet_Daubechies_2D : 二次元方向のWavelet逆変換 wc : 入力信号 coef : ドビッシーの数列 s0 : 逆変換結果へのポインタ ( レベルがひとつ低いスケーリング係数 ) size : データ長 */ template< class Coef > void IWavelet_Daubechies_2D( const WaveletCoef< double >& wc, const Coef& coef, vector< double >* s0, Coord< int > size ) { /* 一次元方向の変換結果格納用バッファ */ Coord< int > half( size.x / 2, size.y / 2 ); vector< double > sx( half.x * size.y ); vector< double > wx( half.x * size.y ); for ( int i = 0 ; i < half.x ; i++ ) { // スケーリング成分と垂直方向のウェーブレット成分の結合→水平方向のスケーリング成分 IWavelet_Daubechies_1D( wc.s.begin() + i, wc.wv.begin() + i, coef, sx.begin() + i, half.y, half.x ); // 水平方向のウェーブレット成分と対角方向のウェーブレット成分の結合→水平方向のウェーブレット成分 IWavelet_Daubechies_1D( wc.wh.begin() + i, wc.wd.begin() + i, coef, wx.begin() + i, half.y, half.x ); } // 水平方向の結合 for ( int i = 0 ; i < size.y ; i++ ) IWavelet_Daubechies_1D( sx.begin() + i * half.x, wx.begin() + i * half.x, coef, s0->begin() + i * size.x, half.x, 1 ); }
形式は前章の Haar ウェーブレットのプログラムと大差ありません。ドビッシーの数列を保持するクラスとして DaubechiesCoef を用意して、この中に数列をコピーすればスケーリング・ウェーブレット両方に対してツースケール関係の係数を渡すことができるようになっています。なお、ウェーブレット側はスケーリング用の係数を逆方向から読み込み、一つおきに -1 を掛けることで得られるため、両方の係数をコピーする必要はありません。
今回は、計算に使う前回のスケーリング・ウェーブレット係数が範囲外にある場合があります。そのため、範囲外ならば巡回するような形にして、添字が負数ならデータ末尾から、逆にサイズをオーバーしたときは先頭から読むようにしてあります。この方法は簡単に実装できるという利点がありますが、画像の端どうしは通常は不連続となるためデータ圧縮の点から見ればいいやり方とは言えません。次の節で、これを改良した方法について紹介します。もう一点の注意事項としては、対象のサイズが水平・垂直方向ともに偶数であることを想定しています。一度処理しただけの場合は、端の 1 ライン分を失うだけで済みますが、スケーリング係数をさらに複数回処理するような場合は結果がおかしくなります。JPEG の場合と同様に、JPEG2000 でも画像をいくつかのユニットに分割してそれぞれで処理を行うため、そのサイズが 2 のべき乗で表されることを想定した作りとなっています。
| N=1 (Haar) | N=2 |
|---|---|
 |  |
| N=3 | N=4 |
 |  |
上図は、N を 1 から 4 まで変化させた時の変換時の画像を示したもので、前章の場合とは異なりスケーリング係数に対して繰り返し計三回の処理を行なっています。一つの画面内に全部で十個の画像があり、最も左上の元画像を縮小したような画像がレベル 3 のスケーリング係数となります。その右側が水平成分、下側が垂直成分、右下が対角成分に対するレベル 3 のウェーブレット係数で、以下、レベルを下げながら同様の並びでレベル 1 までのウェーブレット係数が並びます。四つの画像のうち左上は N = 1 のときで、これは Haar のウェーブレットを利用した場合に該当します。前回同様、スケーリング・ウェーブレット係数は補正を行なっており、レベル j に対してスケーリング係数は (1/2)j、ウェーブレット係数はは 50 x (1/2)j-1 倍 ( つまりレベル 1 のウェーブレット係数は 50 倍 ) としてあります。N が小さい方がエッジがはっきりと現れる様子が確認できます。
コンパクトサポートを持った正規直交化されたウェーブレット関数は、Haar 基底を除いて全て非対称であることが証明されています。前節で示した例も形状は非対称でした。非対称性による影響がどの程度あるのか、はっきりしたことはわかりませんが、人間の視覚が非対称な誤差に対してより敏感であるという性質などの理由から、JPEG2000 では対称なウェーブレットが採用されています。
JPEG2000 で採用されたウェーブレットの一つは「Cohen-Daubechies-Feauveau 5/3 Wavelet ( CDF 5/3 )」で、この中では「リフティング (Lifting)」と呼ばれる手法が利用されています。
まず、データ列の中で奇数番目にあるデータ s02k+1 に対して、その前後にある偶数番目のデータ s02k と s02k+2 の平均との差を計算し、それを s02k+1 から減算してウェーブレット係数として求めた上で、一つ上のレベルのデータ s12k+1 とします。式にすると以下のようになります。
これは、前後のデータを結んだ線上に中央のデータがあればちょうどゼロになるので、データが直線上に並んでいるかを表す指標になります。Haar の場合は水平ならウェーブレット係数がゼロになるのに対し、こちらは傾いていても直線上に並んでいればゼロになります。
偶数番号に対する一つ上のレベルのデータ s12k を先ほど計算した誤差成分 s12k-1, s12k+1 を使って表現するとした時、ある定数 A を使って
と表すことができます。奇数番号のデータに先ほどの式を代入すると
| s12k | = | s02k + A[ s02k-1 - ( s02k-2 + s02k ) / 2 + s02k+1 - ( s02k + s02k+2 ) / 2 ] |
| = | ( 1 - A )s02k + A( s02k-1 + s02k+1 ) - (A/2)( s02k-2 + s02k+2 ) |
と変形できます。ここで、両辺とも全体の合計を計算してみると
| (左辺) | = | Σk( s1[k] ) = Σk( s0[k] ) / 2 |
| = | Σk( s02k + s02k+1 ) / 2 | |
| (右辺) | = | Σk( ( 1 - A )s02k + A( s02k-1 + s02k+1 ) - (A/2)( s02k-2 + s02k+2 ) ) |
| = | Σk( ( 1 - 2A )s02k + 2A・s02k+1 ) |
と表せるので、1 - 2A = 2A = 1 / 2 である必要があり A = 1 / 4 となります ( Σk( s1[k] ) = Σk( s0[k] ) / 2 が成り立つのは、両者の平均が等しいと考えた場合に s1[k] のサイズは半数であるからです )。従って、
が偶数番号のデータに対する計算式、すなわちスケーリング係数の計算式となります。
スケーリング係数の計算式は
となるので、この逆変換は
であり非常に簡単に元に戻すことができます。こうして s02k が得られれば、
をつかって奇数番号に対するデータも簡単に得られます。奇数番号のデータを得る処理部分は「予測 ( Predict )」、偶数番号のデータを得る処理部分は「更新 ( Update )」と呼ばれ、これら二つのステップに分かれて処理が行われるのですが、予測処理で得られる s12k+1 は専用の配列を用意することなく s02k+1 をそのまま置き換えても問題はありません ( むしろ処理しやすくなります )。s12k についてもそのまま置き換えれば、スケーリング係数とウェーブレット係数が交互に並んだ配列に置き換えられることになります。s1, w1 の添字を s0, w0 と同じにしていたのはそのような理由からで、通常は s0 配列がそのまま用いられるからです。このように、処理が単純な上にメモリの使用効率がよいことも JPEG2000 に採用された理由の一つだと思います。
奇数番号のデータに対する逆変換時の計算式は次のようになっています。
| s02k+1 | = | s12k+1 + ( s02k + s02k+2 ) / 2 |
| = | s12k+1 + { [ s12k - (1/4)( s12k-1 + s12k+1 ) ] + [ s12k+2 - (1/4)( s12k+1 + s12k+3 ) ] } / 2 | |
| = | -(1/8)s12k-1 + (1/2)s12k + (3/4)s12k+1 + (1/2)s12k+2 - (1/8)s12k+3 |
偶数番号の s1 がスケーリング係数、奇数番号の s1 がウェーブレット係数なので、Pn にあたる数は P-1 = P1 = 1 / 2、Qn は Q-2 = Q2 = -1 / 8 と Q0 = 3 / 4 です。また、偶数番号のデータに対する逆変換式
から、P0 = 1、Q-1 = Q1 = -1 / 4 となります。従って、この逆変換式に対応する変換式を関数で表すと
φ~( t ) = (1/2)φ~( 2t + 1 ) + φ~( 2t ) + (1/2)φ~( 2t - 1 )
ψ~( t ) = -(1/8)φ~( 2t + 2 ) - (1/4)φ~( 2t + 1 ) + (3/4)φ~( 2t ) - (1/4)φ~( 2t - 1 ) - (1/8)φ~( 2t - 2 )
となり、はじめの変換式とは異なったものになります。はじめの変換式を φ( t ), ψ( t ) としてまとめると次のようになります。
φ( t ) = -(1/8)φ( 2t + 2 ) + (1/4)φ( 2t + 1 ) + (3/4)φ( 2t ) + (1/4)φ( 2t - 1 ) - (1/8)φ( 2t - 2 )
ψ( t ) = -(1/2)φ( 2t + 1 ) + φ( 2t ) - (1/2)φ( 2t - 1 )
φ~( t ) = (1/2)φ~( 2t + 1 ) + φ~( 2t ) + (1/2)φ~( 2t - 1 )
ψ~( t ) = -(1/8)φ~( 2t + 2 ) - (1/4)φ~( 2t + 1 ) + (3/4)φ~( 2t ) - (1/4)φ~( 2t - 1 ) - (1/8)φ~( 2t - 2 )
φ(t) と ψ(t) 及び φ~(t) と ψ~(t) は直交していないのに対し、φ~(t) と ψ(t) 及び φ(t) と ψ~(t) は直交関係にあります。このような関係にある基底の対を「双直交系 ( Biorthogonal System )」といい、双直交系となるウェーブレットは「双直交ウェーブレット ( Biorthogonal Wavelet )」といいます。これはちょうど、スケーリング係数とウェーブレット係数の変換式が交差したような状態となっており、このような構成によって対称となる処理を実現しているわけです。
CDF 5/3 は整数型を利用することを想定しているので、実際の処理では以下のような式を用います。
■ 変換式
s12k+1 = s02k+1 - ⌊ ( s02k + s02k+2 ) / 2 ⌋
s12k = s02k + ⌊ ( s12k-1 + s12k+1 + 2 ) / 4 ⌋
■ 逆変換式
s02k = s12k - ⌊ ( s12k-1 + s12k+1 + 2 ) / 4 ⌋
s02k+1 = s12k+1 + ⌊ ( s02k + s02k+2 ) / 2 ⌋
但し、⌊x⌋ は x を超えない最大の整数を表します。これに対して、浮動小数点数を利用するウェーブレットとして「Cohen-Daubechies-Feauveau 9/7 Wavelet ( CDF 9/7 )」があり、これもリフティングを使って処理を行うことができます。
データ列の中で奇数番目にあるデータ s02k+1 に対して、その前後にある偶数番目のデータ s02k と s02k+2 を使って計算するのは CDF 5/3 と同じですが、単純な平均ではなく重み付き和の形で計算を行います。
偶数番目のデータ s02k に対し、先に求めた結果を使って同様に重み付け和を計算します。
今度は、奇数番目のデータ s12k+1 に対し、s12k のデータを使ってもう一度重み付け和を計算します。
偶数番目のデータ s12k に対しても、s1'2k+1 のデータを使ってもう一度重み付け和を計算して置き換えを行います。
最後に、定数 K を使って、s1'2k+1 は乗算、s1'2k は除算を行います。
s1'2k+1 → K・s1'2k+1
s1'2k → s1'2k / K
以上の式をまとめると次のようになります。
| s1'2k+1 | → | K・s1'2k+1 |
| = | K[ s12k+1 + γ( s12k + s12k+2 ) ] | |
| = | K{ [ s02k+1 + α( s02k + s02k+2 ) ] + γ{ [ s02k + β( s12k-1 + s12k+1 ) ] + [ s02k+2 + β( s12k+1 + s12k+3 ) ] } } | |
| = | K[ βγ・s12k-1 + ( α + γ )s02k + s02k+1 + 2βγ・s12k+1 + ( α + γ )s02k+2 + βγs12k+3 ] | |
| = | K{ βγ[ s02k-1 + α( s02k-2 + s02k ) ] + ( α + γ )s02k + s02k+1 + 2βγ[ s02k+1 + α( s02k + s02k+2 ) ] + ( α + γ )s02k+2 + βγ[ s02k+3 + α( s02k+2 + s02k+4 ) ] } | |
| = | K[ αβγ・s02k-2 + βγ・s02k-1 + ( 3αβγ + α + γ )s02k + ( 1 + 2βγ )s02k+1 + ( 3αβγ + α + γ )s02k+2 + βγ・s02k+3 + αβγ・s02k+4 ] |
| s1'2k | → | s1'2k / K |
| = | [ s12k + δ( s1'2k-1 + s1'2k+1 ) ] / K | |
| = | { [ s02k + β( s12k-1 + s12k+1 ) ] + δ{ [ s12k-1 + γ( s12k-2 + s12k ) ] + [ s12k+1 + γ( s12k + s12k+2 ) ] } } / K | |
| = | [ γδ・s12k-2 + ( β + δ )s12k-1 + s02k + 2γδ・s12k + ( β + δ )s12k+1 + γδ・s12k+2 ] / K | |
| = | { γδ[ s02k-2 + β( s12k-3 + s12k-1 ) ] + ( β + δ )[ s02k-1 + α( s02k-2 + s02k ) ] | |
| + s02k + 2γδ[ s02k + β( s12k-1 + s12k+1 ) ] | ||
| + ( β + δ )[ s02k+1 + α( s02k + s02k+2 ) ] + γδ[ s02k+2 + β( s12k+1 + s12k+3 ) ] } / K | ||
| = | { [ α( β + δ ) + γδ ]s02k-2 + ( β + δ )s02k-1 + [ 2α( β + δ ) + 1 + 2γδ ]s02k + ( β + δ )s02k+1 + [ α( β + δ ) + γδ ]s02k+2 | |
| + βγδ( s12k-3 + 3s12k-1 + 3s12k+1 + s12k+3 ) } / K | ||
| = | { [ α( β + δ ) + γδ ]s02k-2 + ( β + δ )s02k-1 + [ 2α( β + δ ) + 1 + 2γδ ]s02k + ( β + δ )s02k+1 + [ α( β + δ ) + γδ ]s02k+2 | |
| + βγδ{ [ s02k-3 + α( s02k-4 + s02k-2 ) ] + 3[ s02k-1 + α( s02k-2 + s02k ) ] | ||
| + 3[ s02k+1 + α( s02k + s02k+2 ) ] + [ s02k+3 + α( s02k+2 + s02k+4 ) ] } } / K | ||
| = | { αβγδ・s02k-4 + βγδ・s02k-3 + [ 4αβγδ + α( β + δ ) + γδ ]s02k-2 + ( 3βγδ + β + δ )s02k-1 | |
| + [ 6αβγδ + 2α( β + δ ) + 1 + 2γδ ]s02k | ||
| + ( 3βγδ + β + δ )s02k+1 + [ 4αβγδ + α( β + δ ) + γδ ]s02k+2 + βγδ・s02k+3 + αβγδ・s02k+4 } / K | ||
逆変換は全く反対の処理をするだけです。
s1'2k → K・s1'2k
s1'2k+1 → s1'2k+1 / K
s12k = s1'2k - δ( s1'2k-1 + s1'2k+1 )
s12k+1 = s1'2k+1 - γ( s12k + s12k+2 )
s02k = s12k - β( s12k-1 + s12k+1 )
s02k+1 = s12k+1 - α( s02k + s02k+2 )
これもまとめると次のようになります。
| s02k | = | s12k - β( s12k-1 + s12k+1 ) |
| = | [ s1'2k - δ( s1'2k-1 + s1'2k+1 ) ] - β{ [ s1'2k-1 - γ( s12k-2 + s12k ) ] + [ s1'2k+1 - γ( s12k + s12k+2 ) ] } | |
| = | βγ・s12k-2 - ( β + δ )s1'2k-1 + s1'2k + 2βγ・s12k - ( β + δ )s1'2k+1 + βγ・s12k+2 | |
| = | βγ[ s1'2k-2 - δ( s1'2k-3 + s1'2k-1 ) ] - ( β + δ )s1'2k-1 + s1'2k + 2βγ[ s1'2k - δ( s1'2k-1 + s1'2k+1 ) ] - ( β + δ )s1'2k+1 + βγ[ s1'2k+2 - δ( s1'2k+1 + s1'2k+3 ) ] | |
| = | -βγδ・s1'2k-3 + βγ・s1'2k-2 - ( 3βγδ + β + δ )s1'2k-1 + ( 1 + 2βγ )s1'2k - ( 3βγδ + β + δ )s1'2k+1 + βγ・s1'2k+2 - βγδ・s1'2k+3 | |
| → | -βγδ・s1'2k-3 / K + Kβγ・s1'2k-2 - ( 3βγδ + β + δ )s1'2k-1 / K + K( 1 + 2βγ )s1'2k - ( 3βγδ + β + δ )s1'2k+1 / K + Kβγ・s1'2k+2 - βγδ・s1'2k+3 / K |
| s02k+1 | = | s12k+1 - α( s02k + s02k+2 ) |
| = | [ s1'2k+1 - γ( s12k + s12k+2 ) ] - α{ [ s12k - β( s12k-1 + s12k+1 ) ] + [ s12k+2 - β( s12k+1 + s12k+3 ) ] } | |
| = | αβ・s12k-1 - ( α + γ )s12k + s1'2k+1 + 2αβ・s12k+1 - ( α + γ )s12k+2 + αβ・s12k+3 | |
| = | αβ[ s1'2k-1 - γ( s12k-2 + s12k ) ] - ( α + γ )[ s1'2k - δ( s1'2k-1 + s1'2k+1 ) ] | |
| + s1'2k+1 + 2αβ[ s1'2k+1 - γ( s12k + s12k+2 ) ] | ||
| - ( α + γ )[ s1'2k+2 - δ( s1'2k+1 + s1'2k+3 ) ] + αβ[ s1'2k+3 - γ( s12k+2 + s12k+4 ) ] | ||
| = | [ αβ + ( α + γ )δ ]s1'2k-1 - ( α + γ )s1'2k + [ 2( α + γ )δ + 2αβ + 1 ]s1'2k+1 - ( α + γ )s1'2k+2 + [ αβ + ( α + γ )δ ]s1'2k+3 | |
| - αβγ( s12k-2 + 3s12k + 3s12k+2 + s12k+4 ) | ||
| = | [ αβ + ( α + γ )δ ]s1'2k-1 - ( α + γ )s1'2k + [ 2( α + γ )δ + 2αβ + 1 ]s1'2k+1 - ( α + γ )s1'2k+2 + [ αβ + ( α + γ )δ ]s1'2k+3 | |
| - αβγ{ [ s1'2k-2 - δ( s1'2k-3 + s1'2k-1 ) ] + 3[ s1'2k - δ( s1'2k-1 + s1'2k+1 ) ] | ||
| + 3[ s1'2k+2 - δ( s1'2k+1 + s1'2k+3 ) ] + [ s1'2k+4 - δ( s1'2k+3 + s1'2k+5 ) ] } | ||
| = | αβγδ・s1'2k-3 - αβγ・s1'2k-2 + [ 4αβγδ + αβ + ( α + γ )δ ]s1'2k-1 - ( 3αβγ + α + γ )s1'2k | |
| + [ 6αβγδ + 2( α + γ )δ + 2αβ + 1 ]s1'2k+1 | ||
| - ( 3αβγ + α + γ )s1'2k+2 + [ 4αβγδ + αβ + ( α + γ )δ ]s1'2k+3 - αβγs1'2k+4 + αβγδs1'2k+5 | ||
| → | αβγδ・s1'2k-3 / K - Kαβγ・s1'2k-2 + [ 4αβγδ + αβ + ( α + γ )δ ]s1'2k-1 / K - K( 3αβγ + α + γ )s1'2k | |
| + [ 6αβγδ + 2( α + γ )δ + 2αβ + 1 ]s1'2k+1 / K | ||
| - K( 3αβγ + α + γ )s1'2k+2 + [ 4αβγδ + αβ + ( α + γ )δ ]s1'2k+3 / K - Kαβγs1'2k+4 + αβγδs1'2k+5 / K | ||
係数がかなり複雑になるため、スケーリング係数変換式の s0'2k+n に対する係数を P'n、ウェーブレット係数変換式の s0'2k+n+1 に対する係数を Q'n とすると、
s1'2k+1 = Q'-3s02k-2 + Q'-2s02k-1 + Q'-1s02k + Q'0s02k+1 + Q'1s02k+2 + Q'2s02k+3 + Q'3s02k+4
s1'2k = P'-4s02k-4 + P'-3s02k-3 + P'-2s02k-2 + P'-1s02k-1 + P'0s02k + P'1s02k+1 + P'2s02k+2 + P'3s02k+3 + P'4s02k+4
s02k = -P'-3s1'2k-3 + Q'-2s1'2k-2 - P'-1s1'2k-1 + Q'0s1'2k - P'1s1'2k+1 + Q'2s1'2k+2 - P'3s1'2k+3
s02k+1 = P'-4s1'2k-3 - Q'-3s1'2k-2 + P'-2s1'2k-1 - Q'-1s1'2k + P'0s1'2k+1 - Q'1s1'2k+2 + P'2s1'2k+3 - Q'3s1'2k+4 + P'4s1'2k+5
と表すことができます。s02k に対する変換式の係数 { Pn }, { Qn } は
であり、s02k+1 に対する変換式の係数は
となるので、それぞれの変換・逆変換式を関数で表すと ( P'n, Q'n の「'」は省略して )
φ( t ) = P-4φ~( 2t + 4 ) + P-3φ~( 2t + 3 ) + P-2φ~( 2t + 2 ) + P-1φ~( 2t + 1 ) + P0φ~( 2t ) + P1φ~( 2t - 1 ) + P2φ~( 2t - 2 ) + P3φ~( 2t - 3 ) + P4φ~( 2t - 4 )
ψ( t ) = Q-3ψ~( 2t + 3 ) + Q-2ψ~( 2t + 2 ) + Q-1ψ~( 2t + 1 ) + Q0ψ~( 2t ) + Q1ψ~( 2t - 1 ) + Q2ψ~( 2t - 2 ) + Q3ψ~( 2t - 3 )
φ~( t ) = -Q-3φ~( 2t + 3 ) + Q-2φ~( 2t + 2 ) - Q-1φ~( 2t + 1 ) + Q0φ~( 2t ) - Q1φ~( 2t - 1 ) + Q2φ~( 2t - 2 ) - Q3φ~( 2t - 3 )
ψ~( t ) = P-4ψ~( 2t + 4 ) - P-3ψ~( 2t + 3 ) + P-2ψ~( 2t + 2 ) - P-1ψ~( 2t + 1 ) + Q0ψ~( 2t ) - P1ψ~( 2t - 1 ) + P2ψ~( 2t - 2 ) - P3ψ~( 2t - 3 ) + P4ψ~( 2t - 4 )
となり、ここでも双直交系となっていることが確認できます。
実際の係数の値は以下のようになっています。
| n | Pn | Qn |
|---|---|---|
| 0 | 0.6029490182363579 | 1.115087052456994 |
| -1, 1 | 0.2668641184428723 | -0.5912717631142470 |
| -2, 2 | -0.07822326652898785 | -0.05754352622849957 |
| -3, 3 | -0.01686411844287495 | 0.09127176311424948 |
| -4, 4 | 0.02674875741080976 |
また、パラメータ α から K までの値は次のとおりです。
| パラメータ | 値 |
|---|---|
| α | -1.586134342059924 |
| β | -0.052980118572961 |
| γ | 0.882911075530934 |
| δ | 0.443506852043971 |
| K | 1.230174104914001 |
リフティング・アルゴリズムを使った変換・逆変換用のサンプル・プログラムを以下に示します。
/* 9/7 非可逆フィルタ用リフティング・パラメータ */ const double w9_7_alpha = -1.586134342059924; // α const double w9_7_beta = -0.052980118572961; // β const double w9_7_gamma = 0.882911075530934; // γ const double w9_7_delta = 0.443506852043971; // δ const double w9_7_K = 1.230174104914001; // K /* 添字の対称拡張用関数群 テンプレート引数が true ならある添字 i を中心として対称とする[奇数型] ( i - C = i + C ) テンプレート引数が false ならある二つの添字 i, i + 1 の間を中心として対称とする[偶数型] ( i - C = i + C + 1 ) */ /// 先頭側の境界に対する拡張 template< bool > int MirrorL( int i ); template<> int MirrorL< true >( int i ) { return( ( i < 0 ) ? -i : i ); } template<> int MirrorL< false >( int i ) { return( ( i < 0 ) ? -i - 1 : i ); } /// 末尾側の境界に対する拡張 template< bool > int MirrorR( int i, int size ); template<> int MirrorR< true >( int i, int size ) { return( ( i >= size ) ? 2 * size - i - 2 : i ); } template<> int MirrorR< false >( int i, int size ) { return( ( i >= size ) ? 2 * size - i - 1 : i ); } /* 配列の両端に対して添字の対称拡張を行うためのクラス テンプレート引数 L は先頭側の偶奇型、R は末尾側の偶奇型をそれぞれ表す。 */ template< bool L, bool R > class SymIndex { int size_; // 配列のサイズ public: // 配列のサイズを指定して構築 SymIndex( int size ) : size_( size ) {} // 拡張添字に対する実際の位置を返す size_t operator()( int i ) const { while ( i < 0 || i >= size_ ) { i = MirrorL< L >( i ); i = MirrorR< R >( i, size_ ); } return( i ); } }; /* Wavelet_JPEG2K_1D : 一次元方向の JPEG2000 フィルタ変換宣言 s0 : 入力信号への反復子 ( レベルがひとつ低いスケーリング係数 ) s1 : スケーリング係数計算結果(偶数成分)への反復子 w1 : ウェーブレット係数計算結果(奇数成分)への反復子 half : 信号のデータ長の 1/2 inc : indexの増分(X/Y方向を示す) */ template< class T > void Wavelet_JPEG2K_1D( typename vector< T >::const_iterator s0, typename vector< T >::iterator s1, typename vector< T >::iterator w1, int half, int inc ); /* IWavelet_JPEG2K_1D : 一次元方向の JPEG2000 フィルタ逆変換宣言 s1 : スケーリング係数計算結果(偶数成分)への反復子 w1 : ウェーブレット係数計算結果(奇数成分)への反復子 s0 : 逆変換結果への反復子 ( レベルがひとつ低いスケーリング係数 ) half : 信号のデータ長の 1/2 inc : indexの増分(X/Y方向を示す) */ template< class T > void IWavelet_JPEG2K_1D( typename vector< T >::const_iterator s1, typename vector< T >::const_iterator w1, typename vector< T >::iterator s0, int half, int inc ); /* 一次元方向の 5/3 可逆フィルタ変換 ( 整数型 ) */ template<> void Wavelet_JPEG2K_1D< int >( vector< int >::const_iterator s0, vector< int >::iterator s1, vector< int >::iterator w1, int half, int inc ) { SymIndex< true, true > idx0( half * 2 ); // s0 成分用対称拡張添字 SymIndex< false, true > wIdx1( half ); // w1 成分用対称拡張添字 // 奇数成分 w1[i] = Y[2i+1] = s0[2i+1] - ( s0[2i] + s0[2i+2] ) / 2 // for ( int i = 0 ; i < half ; ++i ) w1[i * inc] = s0[idx0( 2 * i + 1 ) * inc] - floor( ( s0[2 * i * inc] + s0[idx0( 2 * i + 2 ) * inc] ) / 2.0 ); // 偶数成分 s1[i] = Y[2i] = s0[2i] + ( Y[2i-1] + Y[2i+1] ) / 2 // = s0[2i] + ( w1[i-1] + w1[i] ) / 2 // for ( int i = 0 ; i < half ; ++i ) s1[i * inc] = s0[2 * i * inc] + floor( ( w1[wIdx1( i - 1 ) * inc] + w1[i * inc] + 2 ) / 4.0 ); } /* 一次元方向の 5/3 非可逆フィルタ変換 ( 浮動小数点型 ) */ template<> void Wavelet_JPEG2K_1D< double >( vector< double >::const_iterator s0, vector< double >::iterator s1, vector< double >::iterator w1, int half, int inc ) { SymIndex< true, true > idx0( half * 2 ); // s0 成分用対称拡張添字 SymIndex< true, false > sIdx1( half ); // s1 成分用対称拡張添字 SymIndex< false, true > wIdx1( half ); // w1 成分用対称拡張添字 // 奇数成分(1) w1[i] = Y[2i+1] = s0[2i+1] + α( s0[2i] + s0[2i+2] ) // for ( int i = 0 ; i < half ; ++i ) w1[i * inc] = s0[( 2 * i + 1 ) * inc] + w9_7_alpha * ( s0[2 * i * inc] + s0[idx0( 2 * i + 2 ) * inc] ); // 偶数成分(1) s1[i] = Y[2i] = s0[2i] + β( Y[2i-1] + Y[2i+1] ) // = s0[2i] + β( w1[i-1] + w1[i] ) for ( int i = 0 ; i < half ; ++i ) s1[i * inc] = s0[2 * i * inc] + w9_7_beta * ( w1[wIdx1( i - 1 ) * inc] + w1[i * inc] ); // 奇数成分(2) w1[i] = Y[2i+1] = Y[2i+1] + γ( Y[2i] + Y[2i+2] ) // = w1[i] + γ( s1[i] + s1[i+1] ) for ( int i = 0 ; i < half ; ++i ) w1[i * inc] += w9_7_gamma * ( s1[i * inc] + s1[sIdx1( i + 1 ) * inc] ); // 偶数成分(2) s1[i] = Y[2i] = Y[2i] + δ( Y[2i-1] + Y[2i+1] ) // = s1[i] + δ( w1[i-1] + w1[i] ) for ( int i = 0 ; i < half ; ++i ) s1[i * inc] += w9_7_delta * ( w1[wIdx1( i - 1 ) * inc] + w1[i * inc] ); // 奇数成分(3) w1[i] *= K for ( int i = 0 ; i < half ; ++i ) w1[i * inc] *= w9_7_K; // 偶数成分(3) s1[i] /= K for ( int i = 0 ; i < half ; ++i ) s1[i * inc] /= w9_7_K; } /* Wavelet_JPEG2K_2D : 二次元方向の JPEG2000 フィルタ変換 s0 : 入力信号への参照 ( レベルがひとつ低いスケーリング係数 ) wc : 係数計算結果へのポインタ size : 画像の大きさ */ template< class T > void Wavelet_JPEG2K_2D( const vector< T >& s0, WaveletCoef< T >* wc, Coord< int > size ) { /* 一次元方向の変換結果格納用バッファ */ Coord< int > half( size.x / 2, size.y / 2 ); // 画像サイズの半分 vector< T > s1x( half.x * size.y ); // 一次元方向のスケーリング係数用バッファ vector< T > w1x( half.x * size.y ); // 一次元方向のウェーブレット係数用バッファ wc->resize( Coord< int >( half.x, half.y ) ); // 水平方向への分解 for ( int i = 0 ; i < size.y ; ++i ) Wavelet_JPEG2K_1D< T >( s0.begin() + i * size.x, s1x.begin() + i * half.x, w1x.begin() + i * half.x, half.x, 1 ); for ( int i = 0 ; i < half.x ; ++i ) { // スケーリング成分と垂直方向のウェーブレット成分への分解 Wavelet_JPEG2K_1D< T >( s1x.begin() + i, ( wc->s ).begin() + i, ( wc->wv ).begin() + i, half.y, half.x ); // 水平方向のウェーブレット成分と対角方向のウェーブレット成分への分解 Wavelet_JPEG2K_1D< T >( w1x.begin() + i, ( wc->wh ).begin() + i, ( wc->wd ).begin() + i, half.y, half.x ); } } /* 一次元方向の 5/3 可逆フィルタ逆変換 ( 整数型 ) */ template<> void IWavelet_JPEG2K_1D< int >( vector< int >::const_iterator s1, vector< int >::const_iterator w1, vector< int >::iterator s0, int half, int inc ) { SymIndex< true, true > idx0( half * 2 ); // s0 成分用対称拡張添字 SymIndex< false, true > wIdx1( half ); // w1 成分用対称拡張添字 // 偶数成分 s0[2i] = Y[2i] - ( Y[2i-1] + Y[2i+1] + 2 ) / 4 // = s1[i] - ( w1[i-1] + w1[i] + 2 ) / 4 for ( int i = 0 ; i < half ; ++i ) s0[2 * i * inc] = s1[i * inc] - floor( ( w1[wIdx1( i - 1 ) * inc] + w1[i * inc] + 2 ) / 4.0 ); // 奇数成分 s0[2i+1] = Y[2i+1] + ( s0[2i] + s0[2i+2] ) / 2 // = w1[i] + ( s0[2i] + s0[2i+2] ) / 2 for ( int i = 0 ; i < half ; ++i ) s0[( 2 * i + 1 ) * inc] = w1[i * inc] + floor( ( s0[2 * i * inc] + s0[idx0( 2 * i + 2 ) * inc] ) / 2.0 ); } /* 一次元方向の 9/7 非可逆フィルタ逆変換 ( 浮動小数点数型 ) */ template<> void IWavelet_JPEG2K_1D< double >( vector< double >::const_iterator s1, vector< double >::const_iterator w1, vector< double >::iterator s0, int half, int inc ) { SymIndex< true, true > idx0( half * 2 ); // s0 成分用対称拡張添字 // 偶数成分(1) s1[i] *= K for ( int i = 0 ; i < half ; ++i ) s0[2 * i * inc] = s1[i * inc] * w9_7_K; // 奇数成分(1) w1[i] /= K for ( int i = 0 ; i < half ; ++i ) s0[( 2 * i + 1 ) * inc] = w1[i * inc] / w9_7_K; // 偶数成分(2) s1[i] = Y[2i] = Y[2i] + δ( Y[2i-1] + Y[2i+1] ) // for ( int i = 0 ; i < half ; ++i ) s0[2 * i * inc] -= w9_7_delta * ( s0[idx0( 2 * i - 1 ) * inc] + s0[idx0( 2 * i + 1 ) * inc] ); // 奇数成分(2) w1[i] = Y[2i+1] = Y[2i+1] + γ( Y[2i] + Y[2i+2] ) // for ( int i = 0 ; i < half ; ++i ) s0[( 2 * i + 1 ) * inc] -= w9_7_gamma * ( s0[2 * i * inc] + s0[idx0( 2 * i + 2 ) * inc] ); // 偶数成分(3) s1[i] = Y[2i] = s0[2i] + β( Y[2i-1] + Y[2i+1] ) // for ( int i = 0 ; i < half ; ++i ) s0[2 * i * inc] -= w9_7_beta * ( s0[idx0( 2 * i - 1 ) * inc] + s0[idx0( 2 * i + 1 ) * inc] ); // 奇数成分(3) w1[i] = Y[2i+1] = s0[2i+1] + α( s0[2i] + s0[2i+2] ) // for ( int i = 0 ; i < half ; ++i ) s0[( 2 * i + 1 ) * inc] -= w9_7_alpha * ( s0[2 * i * inc] + s0[idx0( 2 * i + 2 ) * inc] ); } /* IWavelet_JPEG2K_2D : 二次元方向の JPEG2000 フィルタ逆変換 wc : 入力信号 s0 : 逆変換結果へのポインタ ( レベルがひとつ低いスケーリング係数 ) size : データ長 */ template< class T > void IWavelet_JPEG2K_2D( const WaveletCoef< T >& wc, vector< T >* s0, Coord< int > size ) { /* 一次元方向の逆変換結果格納用バッファ */ Coord< int > half( size.x / 2, size.y / 2 ); // 画像サイズの半分 vector< T > sx( half.x * size.y ); // 一次元方向のスケーリング係数用バッファ vector< T > wx( half.x * size.y ); // 一次元方向のウェーブレット係数用バッファ for ( int i = 0 ; i < half.x ; i++ ) { // スケーリング成分と垂直方向のウェーブレット成分の結合→水平方向のスケーリング成分 IWavelet_JPEG2K_1D< T >( wc.s.begin() + i, wc.wv.begin() + i, sx.begin() + i, half.y, half.x ); // 水平方向のウェーブレット成分と対角方向のウェーブレット成分の結合→水平方向のウェーブレット成分 IWavelet_JPEG2K_1D< T >( wc.wh.begin() + i, wc.wd.begin() + i, wx.begin() + i, half.y, half.x ); } // 水平方向の結合 for ( int i = 0 ; i < size.y ; i++ ) IWavelet_JPEG2K_1D< T >( sx.begin() + i * half.x, wx.begin() + i * half.x, s0->begin() + i * size.x, half.x, 1 ); }
実際の処理を行う際にやっかいな個所が一つあります。基本的な演算はあるデータに対して両端にあるデータを作用させるというものなので、境界にあるデータの扱いを決めておく必要ああります。ドビッシーの数列を使った処理では巡回する方式を利用していましたが、JPEG2000 では境界で不連続が発生するのを抑えるため境界を中心として対称となるような仮想のデータを使います。
| ... | D | E | D | C | B | A | B | C | D | E | D | C | B | A | B | ... |
| 実データ | ||||||||||||||||
この仕様のため、境界にあるデータに対しては添字を変換して処理する必要がある上に、各ステップのデータを計算するために領域外にあたるデータを作成しておく必要も生じ、そのままコーディングするとかなりややこしくなります。幸い、対称的な拡張をすることで境界を中心として各ステップのデータも対称となるため、添字をうまくコントロールできれば比較的シンプルなコーディングにすることができます。
上図は、データ列から 9/7 非可逆フィルタを使ってスケーリング・ウェーブレット係数を求めるための流れを表したもので、最上段に元データが並んでいますが、その中で実データは赤い枠で示された 0 から 5 までのデータのみで、その他は対称拡張表現で表された架空のデータです。二行目以降に並ぶデータは計算結果になりますが、中の数値は実際の処理とは異なり、関係する三つのデータの数値を単純に和にしただけのものです。水色の点線で示されたところが境界を表し、元データだけではなくその計算結果も対称となっていることがこの図から読み取れます。計算結果も対称となるのなら、境界外のデータをバッファに保持する必要はなく、実際の添字を見つけてその値を使って計算するだけで処理が可能になります。
注意点として、元データ・奇数番号のデータ(ウェーブレット係数)・偶数番号のデータ(スケーリング係数)が対称となる境界の見方がそれぞれ異なることが挙げられます。元データの先頭側の境界は番号 0 のデータにあたりますが、ウェーブレット係数の場合は二つのデータの間に境界があります。末尾側に対しても同じように差異があるので、それを考慮してコーディングする必要があります。
サンプル・プログラムの中の SymIndex が対称拡張された添字に対応するためのクラスになりますが、このクラスは二つの bool 型テンプレート引数 L と R を持っています。対称となるときの境界があるデータの位置にあれば true、二つのデータの間にあれば false とし、L が先頭側、R が末尾型をそれぞれ指しているものとします。例えば元データに適用するときは、先頭・末尾のいずれも true とすればよいので SymIndex< true, true > とします。メンバ関数の operator() の中で二つのテンプレート関数 MirrorL と MirrorR を呼び出し、これらも同じ仕様の bool 型テンプレート引数を一つ持っています。この引数によって添字の位置の計算方法を切り替えることができるようになっています。
処理のメインとなる関数は Wavelet_JPEG2K_1D で、これも要素の型をテンプレート引数として宣言し、整数型と浮動小数点型の二つの特別バージョンとして 5/3 可逆フィルタ変換と 9/7 非可逆フィルタ変換を実装しています。対称拡張された添字の変換は SymIndex が自動的に行うので、ここでは計算の流れをそのままコーディングするだけですが、注意点として計算したスケーリング・ウェーブレット係数を保持する専用の配列を別に用意しています。先述の通り、元データの配列の偶奇番号の位置を交互に置き換えることでメモリを節約できるのですが、後処理で分離は必要となるため最初から分離するようにしています。また、SymIndex の宣言はデータのサイズが偶数であることを前提としています。上図 3-1. から見ても明らかなように、スケーリング・ウェーブレット係数に対する末尾側の境界はデータ数によって逆転します。もしデータ数が奇数の場合も対応するのであれば、データ数に応じて bool 値を反転させるだけで ( データ数の最下位ビットをそのまま利用すれば簡単に ) 実現できますが、その場合はテンプレートが利用できないので、通常の引数として渡すなど方式を変更する必要が生じます。
ドビッシーの数列を利用したサンプル・プログラムでも述べましたが、多重解像度解析ではスケーリング係数を再帰的に処理するのが通常です。データ数が奇数となる場合に対応するのであれば、処理ごとにサイズが偶奇のどちらであったかを保持するなど、処理がかなり煩雑になります。例えば処理を三回実施するのであれば、三回目の処理で偶数となればよいので画像サイズを 23 = 8 の倍数に合わせておけば処理がかなり簡略化できます。当然、全ての画像サイズがそのようになってはいないので、例えば YUV 変換をするときにリサイズ (末尾への画素の付加) を行うなどの対応が必要です。
二次元方向の変換は Wavelet_JPEG2K_2D が行いますが、これは整数型・浮動小数点型のどちらも処理が同じなので、テンプレート関数化してまとめてあります。また、逆変換 ( IWavelet_JPEG2K_1D, IWavelet_JPEG2K_2D ) も構成は同じです。
もう一点の注意事項として、5/3 可逆フィルタ変換のために実施する YUV 変換は、YUV 各成分も整数型になるように計算方法が異なっています。サンプル・プログラムには実装されていないので、以下に計算式を示しておきます。
Y = ⌊ ( R + 2G + B ) / 4 ⌋
U = B - G
V = R - G
G = Y - ⌊ ( U + V ) / 4 ⌋
R = V + G
B = U + G
YUV から RGB へ変換するときは、まず G 成分を計算してからその値を利用して R, B 成分を計算します。
5/3 可逆フィルタ変換と 9/7 非可逆フィルタ変換を使ったときの変換結果を、前に示したドビッシー・フィルタとも併せて以下に示します。全てスケーリング係数に対して繰り返し計三回の処理を行なった結果になります。
| 5/3 可逆フィルタ変換 | 9/7 非可逆フィルタ変換 |
|---|---|
 |  |
| Haar フィルタ | ドビッシー・フィルタ(N=2) |
 |  |
| ドビッシー・フィルタ(N=3) | ドビッシー・フィルタ(N=4) |
 |  |
5/3 可逆フィルタ変換の結果だけ他と比べて違和感がありますが、これは全てを整数型で処理しているため YUV 変換式の精度がかなり低いことによるものです。なお、RGB への変換は可逆となっているので、逆変換によってきちんと元の画像に戻ります。
| Y 水平ウェーブレット成分 |
|---|
 |
| Y 垂直ウェーブレット成分 |
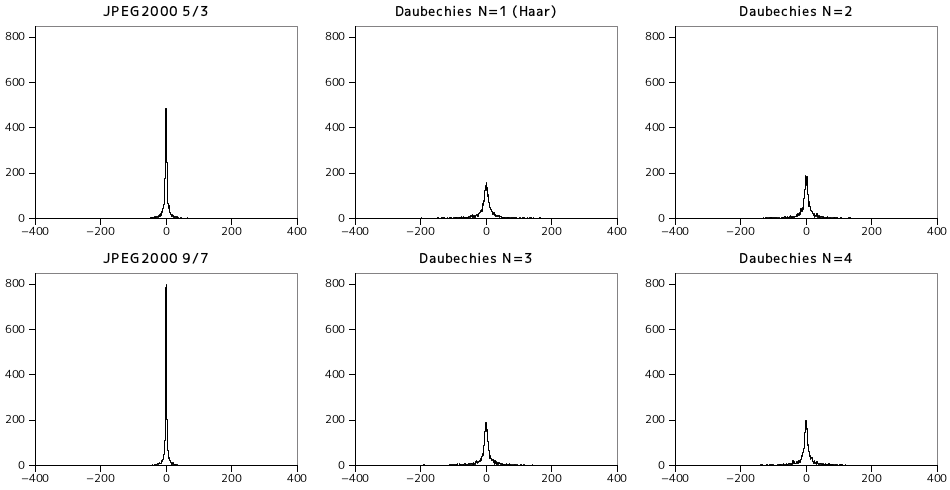 |
| Y 対角ウェーブレット成分 |
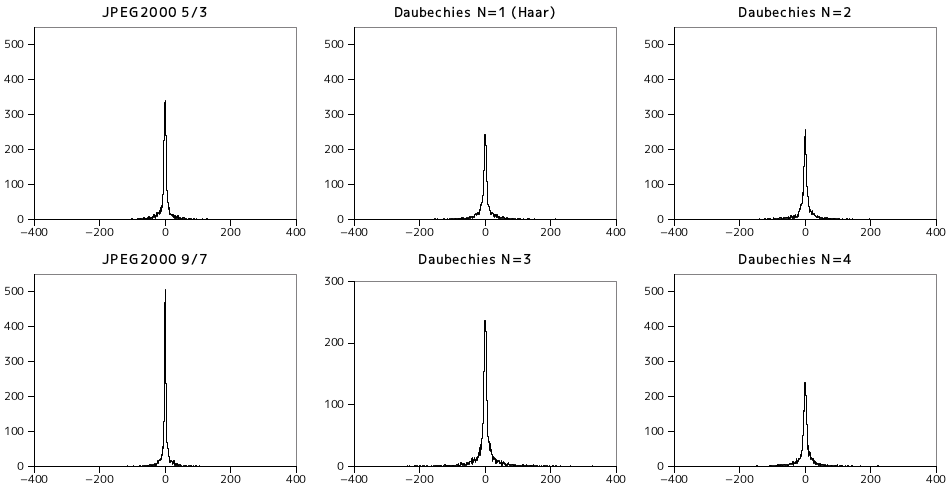 |
上に示したグラフは、Y 成分から変換されたレベル 3 のウェーブレット係数をヒストグラムで表したもので、上から順に水平・垂直・対角成分となっています。左端に JPEG2000 で採用されている 5/3 可逆フィルタ変換と 9/7 非可逆フィルタ変換のヒストグラム、その右側に N = 1 (Haar) から N = 4 までのドビッシーの数列を使った変換のヒストグラムを示しています。結果を見ると、JPEG2000 で採用された変換法は他と比べるとゼロ付近に値が集中しています。このため、特に圧縮用途で考えた場合はこの特性がかなり有利にはたらきます。
JPEG2000 での量子化処理は JPEG の場合同様スカラ量子化を用いていますが、JPEG 法での離散コサイン変換では画素ブロックの左上側に情報が集中するため右下側を中心に間引き処理を行うのに対して、ウェーブレット変換では特定の場所に情報が集中するというような傾向はないことから、特定の場所を中心に間引くような処理はできません。よって、場所ごとに量子化レベルを設定するのではなく各ウェーブレット変換結果 ( 各レベルの水平・垂直・対角ウェーブレット成分と、スケーリング成分 ) を表す「サブバンド ( Sub-band )」によって設定するようになっています。
JPEG2000 の場合も JPEG のときと同じく、定数を使って除算を行うわけですが、この定数は「ステップ・サイズ ( Step Size )」と呼ばれ、サブバンド b に対するステップ・サイズ Δb は以下のような式で求めています。
εb と μb は非負の整数で、それぞれステップ・サイズを表現するための指数・仮数と呼ばれ、0 ≤ εb < 25, 0 ≤ μb < 211 の範囲の値をとります。εb が大きいほど、また μb が小さいほどステップ・サイズは小さくなるので画質は向上しますが圧縮率は低くなります。
Rb は「ダイナミック・レンジ ( Dynamic Range )」と呼ばれる値で、次の式で求められます。
RIは元データのビット精度を表すので、例えば unsigned char 型の値を使っているのなら 8 になります。gainb はウェーブレット変換を行ったことによる値の増分を表したものです。それぞれのサブバンドに対する gainb の値は以下のようになります。
| 成分名 | サブバンド b | gainb |
|---|---|---|
| スケーリング | LL | 1 |
| 水平成分ウェーブレット | HL | 2 |
| 垂直成分ウェーブレット | LH | 2 |
| 対角成分ウェーブレット | HH | 4 |
εb と μb の決め方は二通りあり、それぞれ「明示的な量子化 ( Expounded Quantization )」「暗示的な量子化 ( Derived Quantization )」と呼ばれています。前者はサブバンドはそれぞれに対して値を決める方式で、後者はサブバンド LL に対してのみ定義をする方式です。暗示的な量子化の場合、他のサブバンドの εb, μb は以下の式で求められます。
εb = εLL - NLL + nb
μb = μLL
εLL はサブバンド LL に対して定義した指数で、NLL はウェーブレット変換の総数、nb は対象のサブバンドの変換回数を表します。
こうして求めた Δb を使って、以下のような式で量子化を行います。
ab が 変換処理直後の元データ、qb が量子化後の値になります。また sign( x ) は値 x の符号を、⌊ x ⌋ は値 x 以下の整数の最大値をそれぞれ表します。
これを逆量子化するときの式は
になります。
量子化処理のサンプル・プログラムを以下に示します。
const int STEPSIZE_E_MAXBIT = 5; // ステップサイズ用指数 ( ε ) の最大ビット数 const int STEPSIZE_U_MAXBIT = 11; // ステップサイズ用仮数 ( μ ) の最大ビット数 /* Step Size 保持クラス */ template< class T > class Wavelet_StepSize { T ll_; // スケーリング係数 vector< T > lh_; // 垂直成分のウェーブレット係数 vector< T > hl_; // 水平成分のウェーブレット係数 vector< T > hh_; // 対角成分のウェーブレット係数 public: // レベルの数を指定して構築 Wavelet_StepSize( size_t cnt ) : lh_( cnt ), hl_( cnt ), hh_( cnt ) {} // レベルの数と、スケーリング(LL)成分の ε, μ を指定して構築 // その他の成分についても自動計算を行う Wavelet_StepSize( size_t cnt, unsigned int eLL, unsigned int uLL ); /* 各成分用の Step Size への参照を返す */ T& ll( size_t i ) // スケーリング(LL)成分 { return( ll_ ); } T& lh( size_t i ) // 垂直方向のウェーブレット(LH)成分 { return( lh_.at( i ) ); } T& hl( size_t i ) // 水平方向のウェーブレット(HL)成分 { return( hl_.at( i ) ); } T& hh( size_t i ) // 対角方向のウェーブレット(HH)成分 { return( hh_.at( i ) ); } /* 各成分用の Step Size の値を返す */ T ll( size_t i ) const // スケーリング(LL)成分 { return( ll_ ); } T lh( size_t i ) const // 垂直方向のウェーブレット(LH)成分 { return( lh_.at( i ) ); } T hl( size_t i ) const // 水平方向のウェーブレット(HL)成分 { return( hl_.at( i ) ); } T hh( size_t i ) const // 対角方向のウェーブレット(HH)成分 { return( hh_.at( i ) ); } }; /* Wavelet_StepSize コンストラクタ レベルの数と、スケーリング(LL)成分の ε, μ を指定して構築 その他の成分についても自動計算を行う */ template< class T > Wavelet_StepSize< T >::Wavelet_StepSize( size_t cnt, unsigned int eLL, unsigned int uLL ) : lh_( cnt ), hl_( cnt ), hh_( cnt ) { assert( eLL < pow( 2, STEPSIZE_E_MAXBIT ) && uLL< pow( 2, STEPSIZE_U_MAXBIT ) ); // LL成分の Step Size を求める int rLL = std::numeric_limits< unsigned char >::digits; // 元データのビット精度 ll_ = ( 1 + uLL / pow( 2, STEPSIZE_U_MAXBIT ) ) * pow( 2, rLL - static_cast< int >( eLL ) ); // 各レベルのウェーブレット成分の Step Size を求める for ( size_t i = 0 ; i < cnt ; ++i ) { int eb = eLL - cnt + i + 1; lh_[i] = hl_[i] = ( 1 + uLL / pow( 2, STEPSIZE_U_MAXBIT ) ) * pow( 2, rLL - eb + 1 ); hh_[i] = ( 1 + uLL / pow( 2, STEPSIZE_U_MAXBIT ) ) * pow( 2, rLL - eb + 2 ); } } /* Wavelet_QOp : data の量子化 ( stepSize で割る ) 量子化データ = sign( *data )・⌊ |*data| / stepSize ⌋ */ template< class T > void Wavelet_QOp( vector< T >* data, T stepSize ) { for ( typename vector< T >::iterator i = data->begin() ; i != data->end() ; ++i ) { T t = *i / stepSize; *i = abs( t ); if ( t < 0 ) *i *= -1; } } /* Wavelet_QOp : data の逆量子化 ( stepSize を掛ける ) 量子化データ = sign( *data )・⌊ |*data| / stepSize ⌋ */ template< class T > void Wavelet_DQOp( vector< T >* data, T stepSize ) { for ( typename vector< T >::iterator i = data->begin() ; i != data->end() ; ++i ) *i *= stepSize; } /* Wavelet_Quantization : 量子化/逆量子化計算メインルーチン wc : DWT変換データ stepSize : Step Size op : 処理内容 ( 量子化 / 逆量子化 ) */ template< class T, class Op > void Wavelet_Quantization( vector< WaveletCoef< T > >* wc, const Wavelet_StepSize< T >& stepSize, Op op ) { for ( size_t i = 0 ; i < wc->size() ; ++i ) { op( &( (*wc)[i].wv ), stepSize.lh( i ) ); op( &( (*wc)[i].wh ), stepSize.hl( i ) ); op( &( (*wc)[i].wd ), stepSize.hh( i ) ); } op( &( ( wc->back() ).s ), stepSize.ll( wc->size() - 1 ) ); }
Wavelet_StepSize は、各成分のステップ・サイズを保持するためのクラスで、構築時にスケーリング ( LL ) 成分用の指数・仮数を渡せば自動的に他の成分の値も計算するようになっています。また、変換を行ったレベル数は必須となっています。明示的な量子化が可能なように、全成分に対してアクセスができるようにしてありますが、値の計算は外側で行う必要があります。量子化・逆量子化のどちらも、各データに対して演算を行うだけなので、全データを処理するための関数は Wavelet_Quantization が行い、各データの処理用関数はテンプレート引数で渡すようにしてあります。データの量子化は Wavelet_QOp、逆量子化は Wavelet_DQOp が行うので、例えば double 型のデータで量子化を行いたければ
のように呼び出します。
サンプル・プログラムを使って量子化を行ったときの画像を以下に示します。いずれの場合も 9/7 非可逆フィルタ変換を利用し、スケーリング係数に対して処理は三回行なっています。
| εLL = 4, μLL = 0 | εLL = 6, μLL = 0 |
|---|---|
 |  |
| εLL = 8, μLL = 0 | εLL = 8, μLL = 211-1 |
 |  |
以下の表は、各モードにおける、量子化を行ったときのStep Sizeを示したものです。全て暗示的な量子化によって自動的に計算を行なっています。
| オプション | LL | LH,HL | HH | |||||
|---|---|---|---|---|---|---|---|---|
| εLL | μLL | Level 1 | Level 2 | Level 3 | Level 14 | Level 2 | Level 3 | |
| 4 | 0 | 16 | 128 | 64 | 32 | 256 | 128 | 64 |
| 6 | 0 | 4 | 32 | 16 | 8 | 64 | 32 | 16 |
| 8 | 0 | 1 | 8 | 4 | 2 | 16 | 8 | 4 |
| 4 | 211-1 | 2 | 16 | 8 | 4 | 32 | 16 | 8 |
εLL = 8 であれば元の画像との区別は付かなくなります。画質への影響は指数 ε の方が大きく、仮数 μ を最大にしても多少の劣化が見られる程度となります。今回は圧縮率まで求めてはいませんが、例えば εLL = 4, μLL = 0 においてスケーリング成分は 16 で割られているので、4 ビット分の情報を落としたことになり、半分程度にサイズが縮小されることが期待できます。なお、今回のサンプル・プログラムでは YUV 各成分に対して等しいステップ・サイズで量子化を行っていますが、量子化のときに各成分によってパラメータを変化させると、劣化を抑えながら圧縮率を向上させることも可能になります。例えば、Y 成分に対して UV 成分のステップサイズを大きく ( 荒く ) しても、見た目の劣化はある程度防ぐことができます。
残る JPEG2000 での画像処理は符号化になりますが、JPEG2000 の符号化は EBCOT と呼ばれる算術符号化の一種が利用されているため、次回は算術符号化を取り上げる予定です。実は JPEG2000 においては符号化の後で量子化を行う ( ポスト量子化 ) ことができるため、スカラ量子化はあまり使用しないようです。そのあたりについても取り上げてみたいと思います。
ドビッシーのウェーブレット係数 Qn は、スケーリング係数 Pn を使って以下の式で求められます。
もっと一般に、次の関係が成り立てば、スケーリング関数とウェーブレット関数が常に正規直交系になることが証明できます。
ここで 2K はそれぞれの係数 ( 基底 ) の数を表します。この関係を満たす時、ツースケール関係は次のように表せます。
φ( t ) = Σn{0→2K}( Pnφ( 2t - n ) )
ψ( t ) = Σn{0→2K}( Qnφ( 2t - n ) ) = Σn{0→2K}( ( -1 )n P2K-n-1φ( 2t - n ) )
φ( t ) と ψ( t ) の内積 ( φ( t ), ψ( t ) ) = ∫ φ( t )ψ( t ) dt は
で求められますが、
( 但し、δmn はクロネッカのデルタで m = n のとき 1、m ≠ n のとき 0 ) であれば、
| ( φ( t ), ψ( t ) ) | = | Σn{0→2K}( ( -1 )n Pn P2K-n-1 ) |
| = | P0P2K-1 - P1P2K-2 + ... + P2K-2P1 - P2K-1P0 = 0 |
となります。なお、ドビッシーのスケーリング関数のツースケール関係
から ||φ(t)||2 を求めると、
| ||φ(t)||2 | = | [ (1+√3)/4 ]2 + [ (3+√3)/4 ]2 + [ (3-√3)/4 ]2 + [ (1-√3)/4 ]2 |
| = | ( 1 / 4 + √3 / 8 ) + ( 3 / 4 + 3√3 / 8 ) + ( 3 / 4 - 3√3 / 8 ) + ( 1 / 4 - √3 / 8 ) | |
| = | 2 |
となります。従って、正規直交系にするためには ||φ(t)|| = 1 となるように係数を √2 で割る必要があります。本章の中で、計算には √2 を含めていませんでしたが、表 2-1 に示した係数は √2 で割られた数になっています。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |