
画像の描画や編集に使われる Adobe Illustrator や Adobe Photoshop、フリーウェアの Gimp など、ほぼ全てのお絵かきツールは曲線の描画機能を持っています。直線の描画とは異なり、任意の点に対応する曲線の描き方は複数あります。ここでは、よく知られた手法を紹介する前に、制御しやすい曲線の描画方法を検討するところから始めたいと思います。
2D 平面や 3D 空間上にある任意の点が複数あり、その点を通る(もしくは従う) "滑らかな" 曲線を描画したいとします。"滑らかな" とは、簡単に言えば、折れ線のように急激に折れ曲がったような尖った点 ( 尖点 ; Cusp ) を持たないことを指すと考えることができます。厳密に考えると、曲線の種類によって滑らかさの度合いも異なりますが、それについては各曲線の紹介の中で説明したいと思います。
統計学や信号解析では、サンプリングされたデータを利用した関数への当てはめがよく行われます。統計学でよく利用される回帰分析は、一次関数や対数関数などで近似を行うことで、ある変数を使って予測値を求める操作であり、信号解析の代表であるフーリエ変換(級数)も三角関数の和による近似という意味においては関数への当てはめの一種です。これらは、最小二乗法を使って最も誤差の小さな関数を求める手法なので、対象の点が未知数としての係数の数と等しければ、連立方程式を解くことによって一意の解を得ることができます(連立方程式によっては解が得られなかったり(不能)、定まらない(不定)場合もあります)。簡単な例としては、二つの異なる点 ( x0, y0 ), ( x1, y1 ) を与えられた場合、それらを通る直線は一意に決まり、その式は
| y | = | [ ( y1 - y0 ) / ( x1 - x0 ) ]( x - x0 ) + y0 | ( x0 ≠ x1 ) |
| x | = | x0 | ( x0 = x1 ) |
となります。しかし、二次式 y = ax2 + bx + c は係数が 3 つあるので、一意に式を決めることができません。他の点をもうひとつ追加することによって式を一意にすることができます。さらに、同じ二次式でも x2 + axy + by2 + cx + dy + e = 0 という式では係数が 5 つになり、点も 5 つ必要になります。
関数を多項式に限ると、次数が多くなるほど未知数は増えていき、連立方程式の計算も大変になります。x, y 二変数から成る n 次式に対しては、n 次の項は xn, xn-1y, ... xyn-1, yn の n + 1 個、それより低い次数の項も、その次数が k ならば、k + 1 個の項を持つので、定数項までを含めれば、1 から n + 1 までの和
が項の数になります。しかし上の例で示したように、ある項の係数が 1 になるようにすれば係数の数は一つだけ減らすことができて、未知数の数は ( n + 1 )( n + 2 ) / 2 - 1 = n( n + 3 ) / 2 になります。一次式なら 2 つ、二次式では 5 つで、先ほどの結果と一致します。さらに三次式では 9 つ、四次式になると 14 個と、必要な点の数は増加していきます。
x, y 二変数から成る n 次式 fn( x, y ) は次のように表すことができます。
| fn( x, y ) | = | Σk{0→n}( Σi{0→k}( ak-i,ixk-iyi ) ) |
| = | [ a0,0 ] + [ a1,0x + a0,1y ] + [ a2,0x2 + a1,1xy + a0,2y2 ] + | |
| ... + [ an,0xn + an-1,1xn-1y + ... + a1,n-1xyn-1 + a0,nyn ] | ||
未知数(係数)の数を K = n( n + 3 ) / 2 としたとき、K 個の点があれば、それを上式に代入して K 個の連立方程式を作ることができるので、これを解くことで係数が決まります。
まずは、多項式を表現するためのサンプル・プログラムを以下に示します。
/***************************************************** Coord : 座標定義用構造体 *****************************************************/ template<class T> struct Coord { T x; T y; /* コンストラクタ T x_, y_ : 座標値 */ Coord( T x_ = 0, T y_ = 0 ) : x( x_ ), y ( y_ ) {} }; /***************************************************** BiPolynomial : 二変数の多項式定義用クラス f(x,y) = a[0] + a[1]x + a[2]y + a[3]x^2 + a[4]xy + a[5]y^2 + ... a[n] は係数 x, y は変数を表す *****************************************************/ class BiPolynomial { /* coeff_ : 多項式の係数 定数項から始めて次数の小さい順に、同次ならば x の次数の大きい順に並べる */ vector<double> coeff_; unsigned int order_; // 次数 // ニュートン-ラフソン法での繰り返し回数最大(デフォルト値) static const unsigned int NEWTON_RAPHSON_MAX_COUNT = 10; // ニュートン-ラフソン法でのしきい値(デフォルト値) static const double NEWTON_RAPHSON_THRESHOLD = 1e-1; /*** 内部構造体・クラス群 start ***/ /* LoopFunc : 各項ごとに処理を行うための loopFunc に渡す関数オブジェクトの基底クラス */ struct LoopFunc { /* operator() : 処理用関数(純粋仮想関数) 指定した次数だけを処理し、全体は loopFunc 関数がまとめる const Coord<unsigned int>& k : 対象の次数 double a : 係数 */ virtual void operator()( const Coord<unsigned int>& k, double a ) = 0; }; /* Print : 項を出力するための関数オブジェクト */ struct Print : public LoopFunc { /* operator() : 指定した次数の項を出力する const Coord<unsigned int>& k : 対象の次数 double a : 係数 */ virtual void operator()( const Coord<unsigned int>& k, double a ); }; /* XPartDiff : X 方向の偏微分を行うためのクラス */ class XPartDiff : public LoopFunc { Coord<double> c_; // 偏微分を行う対象の座標 public: double ans; // 解(公開メンバ変数) /* XPartDiff コンストラクタ const Coord<double>& c : 偏微分を行う対象の座標 */ XPartDiff( const Coord<double>& c ) : c_( c ), ans( 0 ) {} /* operator() : 指定した次数の偏微分値を返す const Coord<unsigned int>& k : 対象の次数 double a : 係数 */ virtual void operator()( const Coord<unsigned int>& k, double a ) { if ( k.x > 0 ) ans += a * (double)( k.x ) * pow( c_.x, k.x - 1 ) * pow( c_.y, k.y ); } }; /* YPartDiff : Y 方向の偏微分を行うためのクラス */ class YPartDiff : public LoopFunc { Coord<double> c_; // 偏微分を行う対象の座標 public: double ans; // 解(公開メンバ変数) /* YPartDiff コンストラクタ const Coord<double>& c : 偏微分を行う対象の座標 */ YPartDiff( const Coord<double>& c ) : c_( c ), ans( 0 ) {} /* operator() : 指定した次数の偏微分値を返す const Coord<unsigned int>& k : 対象の次数 double a : 係数 */ virtual void operator()( const Coord<unsigned int>& k, double a ) { if ( k.y > 0 ) ans += a * pow( c_.x, k.x ) * (double)( k.y ) * pow( c_.y, k.y - 1 ); } }; /* FuncValue : 指定した座標の関数値を計算するクラス */ class FuncValue : public LoopFunc { Coord<double> c_; // 計算を行う対象の座標 public: double ans; // 解(公開メンバ変数) /* FuncValue コンストラクタ const Coord<double>& c : 計算を行う対象の座標 */ FuncValue( const Coord<double>& c ) : c_( c ), ans( 0 ) {} /* operator() : 指定した次数の計算結果を返す const Coord<unsigned int>& k : 対象の次数 double a : 係数 */ virtual void operator()( const Coord<unsigned int>& k, double a ) { ans += a * pow( c_.x, k.x ) * pow( c_.y, k.y ); } }; /* LE_Func : 連立方程式クラスに係数をセットするためのクラス ここでは、係数は c_.x^(k.x)・c_.y^(k.y) であり、 求める値が関数 f(x,y) の係数であることに注意 */ class LE_Func : public LoopFunc { Coord<double> c_; // 係数計算を行う対象の座標 LinearEquation<double>& le_; // 連立方程式オブジェクトへの参照 unsigned int index_; // le_ へセットする位置(添字) public: /* LE_Func コンストラクタ const Coord<double>& c : 係数計算を行う対象の座標 LinearEquation<double>& le : 連立方程式オブジェクトへの参照 */ LE_Func( const Coord<double>& c, LinearEquation<double>& le ) : c_( c ), le_( le ), index_( 0 ) {} /* operator() : 係数を計算する const Coord<unsigned int>& k : 対象の次数 double dummy : ダミー変数(未使用) */ virtual void operator()( const Coord<unsigned int>& k, double dummy ) { if ( k.x == 0 && k.y == 0 ) return; // 定数項は 1 に正規化するため除外 if ( index_ < le_.size() ) le_[index_] = pow( c_.x, k.x ) * pow( c_.y, k.y ); ++index_; } }; /*** 内部構造体・クラス群 end ***/ // loopFunc : LoopFunc関数オブジェクトを使って各項の処理をまとめて行う void loopFunc( LoopFunc& f ) const; public: /* コンストラクタ const vector<double>& coeff : 各項の係数 const vector< Coord<double> >& p : 多項式のゼロ点が通る軌跡上の点 */ BiPolynomial( const vector<double>& coeff ); BiPolynomial( const vector< Coord<double> >& p ); // 指定した座標 c 上の f(x,y) の値を返す double operator()( const Coord<double>& c ) const; // 指定した座標 c 上の f(x,y) の X 方向の偏微分値を返す double xPartDiff( const Coord<double>& c ) const; // 指定した座標 c 上の f(x,y) の Y 方向の偏微分値を返す double yPartDiff( const Coord<double>& c ) const; // 指定した座標 c 上から X 方向にたどって、f(x,y) = 0 となる X 座標を返す double xAtZero( Coord<double> c, unsigned int maxCount = NEWTON_RAPHSON_MAX_COUNT, double threshold = NEWTON_RAPHSON_THRESHOLD ) const; // 指定した座標 c 上から Y 方向にたどって、f(x,y) = 0 となる Y 座標を返す double yAtZero( Coord<double> c, unsigned int maxCount = NEWTON_RAPHSON_MAX_COUNT, double threshold = NEWTON_RAPHSON_THRESHOLD ) const; // 多項式の出力 void print() const; }; /* BiPolynomial コンストラクタ const vector<double>& coeff : 各項の係数(定数項を含む) */ BiPolynomial::BiPolynomial( const vector<double>& coeff ) : order_( 0 ) { unsigned int coeffSize = coeff.size(); // 次数を係数(項)の数から求める // 次数 n に対して (n+1)(n+2) / 2 が項の数の最大値なので、 // (n+1)(n+2) / 2 が項の数以上になる n を求める while ( ( ( order_ + 1 ) * ( order_ + 2 ) ) >> 1 < coeffSize ) ++order_; coeff_.assign( coeff.begin(), coeff.end() ); } /* BiPolynomial コンストラクタ const vector< Coord<double> >& p : 多項式のゼロ点が通る軌跡上の点 */ BiPolynomial::BiPolynomial( const vector< Coord<double> >& p ) : order_( 0 ) { // 係数(項)の数は、定数項を含めると未知数より一つ多い unsigned int coeffSize = p.size() + 1; // 次数を係数(項)の数から求める // 次数 n に対して (n+1)(n+2) / 2 が項の数の最大値なので、 // (n+1)(n+2) / 2 が項の数以上になる n を求める while ( ( ( order_ + 1 ) * ( order_ + 2 ) ) >> 1 < coeffSize ) ++order_; // coeff_ を項の数で初期化 coeff_.resize( coeffSize ); coeff_[0] = 1; // 定数項は 1 固定 // 連立方程式の未知数の数は、定数項(連立方程式の右辺)を // -1 固定とするので項の数より一つ少なくする LinearEquationSystem<double> les( coeffSize - 1 ); // p の要素から連立方程式の係数を求め、連立方程式を解く for ( unsigned int i = 0 ; i < coeffSize - 1 ; ++i ) { LE_Func f( p[i], les[i] ); loopFunc( f ); les.ans( i ) = -1; } if ( ! GaussianElimination( les ) ) { std::cerr << "The system has infinitely many, or no solutions" << std::endl; return; } // 求めた未知数は f(x,y) の係数となる。 for ( unsigned int i = 1 ; i < coeffSize ; ++i ) coeff_[i] = les.ans( i - 1 ); } /* BiPolynomial::loopFunc : LoopFunc関数オブジェクトを使って各項の処理をまとめて行う LoopFunc& f : LoopFunc関数オブジェクト */ void BiPolynomial::loopFunc( LoopFunc& f ) const { unsigned int index = 0; // 係数 coeff_ の添字 Coord<unsigned int> a; // x, y の次数 for ( unsigned k = 0 ; k <= order_ ; ++k ) { for ( a.y = 0 ; a.y <= k ; ++( a.y ) ) { if ( index >= coeff_.size() ) break; a.x = k - a.y; f( a, coeff_[index] ); ++index; } } } /* BiPolynomial::xPartDiff : 指定した座標 c 上の f(x,y) の X 方向の偏微分値を返す const Coord<double>& c : 対象の座標値 戻り値 : c における f(x,y) の X 方向の偏微分値 */ double BiPolynomial::xPartDiff( const Coord<double>& c ) const { XPartDiff f( c ); loopFunc( f ); return( f.ans ); } /* BiPolynomial::yPartDiff : 指定した座標 c 上の f(x,y) の Y 方向の偏微分値を返す const Coord<double>& c : 対象の座標値 戻り値 : c における f(x,y) の Y 方向の偏微分値 */ double BiPolynomial::yPartDiff( const Coord<double>& c ) const { YPartDiff f( c ); loopFunc( f ); return( f.ans ); } /* BiPolynomial::xAtZero : 指定した座標 c 上から X 方向にたどって、f(x,y) = 0 となる X 座標を返す Coord<double> c : 対象の座標値 unsigned int maxCount : 最大処理回数 double threshold : 収束判断のしきい値(前回の x 座標との差で判定) 次の場合は NaN を返す ・関数値か偏微分値がNaNの場合 ・関数値がゼロでなく偏微分値がゼロの場合 ・最大演算回数までに収束しなかった場合 戻り値 : f(x,y) = 0 となる X 座標 */ double BiPolynomial::xAtZero( Coord<double> c, unsigned int maxCount, double threshold ) const { for ( unsigned int i = 0 ; i < maxCount ; ++i ) { double f = (*this)( c ); double df = xPartDiff( c ); if ( isnan( f ) || isnan( df ) ) return( NAN ); if ( f == 0 ) return( c.x ); if ( df == 0 ) return( NAN ); double diff = f / df; c.x -= diff; if ( fabs( diff ) < threshold ) return( c.x ); } return( NAN ); } /* BiPolynomial::yAtZero : 指定した座標 c 上から Y 方向にたどって、f(x,y) = 0 となる Y 座標を返す Coord<double> c : 対象の座標値 unsigned int maxCount : 最大処理回数 double threshold : 収束判断のしきい値(前回の x 座標との差で判定) 次の場合は NaN を返す ・関数値か偏微分値がNaNの場合 ・関数値がゼロでなく偏微分値がゼロの場合 ・最大演算回数までに収束しなかった場合 戻り値 : f(x,y) = 0 となる Y 座標 */ double BiPolynomial::yAtZero( Coord<double> c, unsigned int maxCount, double threshold ) const { for ( unsigned int i = 0 ; i < maxCount ; ++i ) { double f = (*this)( c ); double df = yPartDiff( c ); if ( isnan( f ) || isnan( df ) ) return( NAN ); if ( f == 0 ) return( c.y ); if ( df == 0 ) return( NAN ); double diff = f / df; c.y -= diff; if ( fabs( diff ) < threshold ) return( c.y ); } return( NAN ); } /* BiPolynomial::operator() : 指定した座標 c 上の f(x,y) の値を返す const Coord<double>& c : 対象の座標値 戻り値 : c における f(x,y) の値 */ double BiPolynomial::operator()( const Coord<double>& c ) const { FuncValue f( c ); loopFunc( f ); return( f.ans ); } /* BiPolynomial::Print::operator() : 指定した次数の項を出力する const Coord<unsigned int>& k : 対象の次数 double a : 項に対する係数 */ void BiPolynomial::Print::operator()( const Coord<unsigned int>& k, double a ) { if ( k.x != 0 || k.y != 0 ) std::cout << " + "; std::cout << a; if ( k.x > 0 ) std::cout << " * x^" << k.x; if ( k.y > 0 ) std::cout << " * y^" << k.y; } /* BiPolynomial::print : f(x,y) の出力 */ void BiPolynomial::print() const { Print print; loopFunc( print ); std::cout << std::endl; }
BiPolynomial は ( x, y ) 二変数からなる多項式を表現するためのクラスで、先の説明で示したような、定数項から始まって次数の大きい順に係数を並べた配列 coeff_ で多項式を表現しています。次数が等しい項に対しては、x の次数が大きいものが先頭に近くなるように並べているので、例えば 3 次の項に対しては x3, x2y, xy2, y3 の順番で配置されることになります。order_ は多項式の次数を表します。次数は、係数の数から求めることが可能なので、コンストラクタの中で前もって計算して保持しておくようにします。
このクラスでは、各項ごとにループ処理を行うことが多いので、ループ構造を loopFunc 関数で一つにまとめています。個々の要素に対する処理は LoopFunc を基底クラスとする関数オブジェクトで行い、多項式に x, y を代入した時の値と、x, y 方向の偏微分値、多項式の出力に使うクラスなどを内部で定義しています。コンストラクタ以外のメンバ関数としては、f( x, y ) の値を返す関数 operator() と、偏微分値 ∂f / ∂x, ∂f / ∂y を返す xPartDiff, yPartDiff、指定座標から x,y 方向にたどって最初に見つかる f( x, y ) = 0 の時の座標値を返す xAtZero, yAtZero などがあり、これらを使って曲線を描画します。
コンストラクタは、係数をそのまま渡して初期化するものと、曲線を通る点の座標を渡して初期化するものの二種類を用意してあります。前者は係数をメンバ変数にコピーして、その個数から次数を求めるだけです。後者の場合は与えられた点から係数を求める必要があるので、座標値を元に係数を未知数とする連立方程式を作り、「ガウスの消去法 ( Gaussian elimination )」を利用して係数を求めています。このとき、定数項は 1 固定として未知数の数を一つ減らしていることに注意してください。よって、与えられた点の個数に対し、項の数は一つ多くなります。
多項式 f( x, y ) の値は通常は三次元空間上の曲面になります。最もシンプルな多項式は f( x,y ) = ax + by + c の形で、これは平面の方程式を表し、f( x, y ) = 0 上では ( 平面 f = 0 と交差していれば ) 直線を描くことになります。また、f( x,y ) = ax2 + by2 + c なら曲面は楕円型・方物型・双曲型のいずれかで、f( x, y ) = 0 上ではそれぞれ楕円・放物線・双曲線になります。BiPolynomial を利用すれば、任意の多項式に対して f( x, y ) = 0 となる座標値を求めることができるので、その結果を使い、画面を平面 f( x, y ) = 0 に見立てて曲線を描画することができます。
ここで問題となるのが f( x, y ) = 0 を満たす座標値 ( x, y ) を求める方法になります。一変数の関数 y = f( x ) に対し、y = 0 を満たす x を求める方法として以前「ニュートン-ラフソン法 ( Newton-Raphson method )」を紹介しました。今回は二変数の関数を扱うことになるので、そのまま適用することはできませんが、x または y を固定して一変数の関数として扱って、f( x, y ) = 0 を満たす x と y を個別に求めれば同様の処理で座標値が得られます。例えば y = a で固定するということは、xy 平面に垂直で x 軸に平行な平面 y = a で曲面を切った切断面上の曲線を扱うという事になります。x = x0 における、この曲線 fa(x) の接線は
となるので、この接線が平面 y = 0 と交わるときの x の値は
fa'(x0)( x - x0 ) + fa(x0) = 0 より
x = x0 - fa(x0) / fa'(x0)になります。ここで得られた x を新たに使い上記操作を繰り返すと、x は f(x) = 0 の解に近づいていくというのがニュートン-ラフソン法の考え方でした。x を固定して y で微分する場合は平面 x = (定数) の切断面上にある曲線を扱うことになり、同様の手法を使うことができます。x または y を固定して微分するということは x, y で偏微分を行うということになり、そのためのメンバ関数が xPartDiff, yPartDiff です。多項式の微分は
に対して
で求められるので、簡単に処理することができます。
ニュートン-ラフソン法で厄介なのが、収束の判断と初期値の設定です。収束判定としてよく利用されているのは前回求めた x との差分で、i 回目の結果 x(i) に対して、任意の小さな値 ε ( > 0 ) を使って
となったときに処理をやめるという方法です。しかし、x の値がどの程度の大きさかわからない場合は、差分と関数値の比率を使って
とする方法もあります。これなら x の大きさによって精度が変化してしまう問題をある程度防ぐことができるからです ( 差分が 0.1 のとき、x の値が 1000 から 1000.1 の変化のときと、0.1 から 0.2 の変化のときではその程度が全く異なることを考えれば納得できると思います )。また、求めた x を関数に代入して f(x) の値が充分ゼロに近づいたら処理を中断する方法や、x の前後 ( x ± δ ; 但し δ は任意の小さな値 ) で f(x) の符号が逆転しているかをチェックする方法などもあります。但し、f(x) の値がゼロに近いかどうかを判定する場合、f(x) が非常に緩やかな変化しかしないようなときに誤差が大きくなることも考えられます。また、符号の逆転をチェックする手法は、例えば x 軸に接する放物線などのように、重解が存在すると利用できません。
初期値のとり方も厄介な問題で、場合によっては x が収束しないような場合もあります。例えば、x の値が二つ交互に繰り返されるような場合、
x1 = x0 - f(x0) / f'(x0)
x0 = x1 - f(x1) / f'(x1)
より
を満たします。f(x) を三次式 f(x) = ax3 + bx2 + cx + d とすれば、f'(x) = 3ax2 + 2bx + c なので、
となり、x0 = 0, x1 = 1 ならば
を満たす係数の場合、初期値として 0 を使えば収束しなくなります (但し、三次式であることを満たすためには a ≠ 0、また、f(x0) ≠ 0, f(x1) ≠ 0 であるためは a + b + c + d ≠ 0, d ≠ 0 である必要があります)。このような係数はいくらでも存在し、例えば、b = 0, c = -2, d = 2 としたとき、
と求められるので、f(x) = x3 - 2x + 2 がその条件を満たす三次式となります。この式の一階導関数は f'(x) = 3x2 - 2 で、x0 = 0 のとき
x1 = 0 - f(0) / f'(0) = 0 - [ 2 / ( -2 ) ] = 1
x2 = 1 - f(1) / f'(1) = 1 - [ ( 1 - 2 + 2 ) / ( 3 - 2 ) ] = 0 = x0
となって、永久に収束しなくなります。
また、極値付近に解を持つような場合は f'(x) の値は小さくなり、x はなかなか収束しないようになります。特に重解を持つような場合は要注意です。ニュートン-ラフソン法は収束が非常に早いというのが特徴ですが、このように収束しない場合もあるため、処理回数をあらかじめ決めておかないと無限ループに陥る可能性があることに注意が必要です。
BiPolynomial を利用して曲線を描画するためのサンプル・プログラムを以下に示します。
/* RoundHalfUp : 浮動小数点型のデータを小数点以下四捨五入して整数型として返す double d : 対象データ 戻り値 : 四捨五入した整数値 */ int RoundHalfUp( double d ) { if ( d > 0 ) d += 0.5; else d -= 0.5; return( (int)d ); } /* LessCoord<T> : 座標用の比較関数 */ template<class T> struct LessCoord { bool operator()( const Coord<T>& src, const Coord<T>& dest ) { if ( src.y != dest.y ) return( src.y < dest.y ); else return( src.x < dest.x ); } }; /* DrawCurve : 多項式を利用した曲線描画関数 const BiPolynomial& f : 対象の多項式 DrawingArea_IF& draw : 描画オブジェクト GPixelOp& pset : 描画用関数 */ void DrawCurve( const BiPolynomial& f, DrawingArea_IF& draw, GPixelOp& pset ) { Coord<int> sz = draw.size(); // 描画オブジェクトのサイズ LessCoord<int> less; set< Coord<int>, LessCoord<int> > drawCoord( less ); // 求めたゼロ点の座標を保持する set // X 方向にゼロ点を求めながら描画する for ( int y = 0 ; y < sz.y ; ++y ) { for ( int x = -1 ; x <= sz.x ; ++x ) { Coord<double> c( x, y ); if ( ( f( c ) > 0 && f.xPartDiff( c ) > 0 ) || ( f( c ) < 0 && f.xPartDiff( c ) < 0 ) ) continue; double d = f.xAtZero( c ); if ( isnan( d ) ) continue; int ans = RoundHalfUp( d ); if ( ans >= 0 && ans < sz.x ) drawCoord.insert( Coord<int>( ans, y ) ); if ( ans > x ) x = ans; } } // Y 方向にゼロ点を求めながら描画する for ( int x = 0 ; x < sz.x ; ++x ) { for ( int y = -1 ; y <= sz.y ; ++y ) { Coord<double> c( x, y ); if ( ( f( c ) > 0 && f.yPartDiff( c ) > 0 ) || ( f( c ) < 0 && f.yPartDiff( c ) < 0 ) ) continue; double d = f.yAtZero( c ); if ( isnan( d ) ) continue; int ans = RoundHalfUp( d ); if ( ans >= 0 && ans < sz.y ) drawCoord.insert( Coord<int>( x, ans ) ); if ( ans > y ) y = ans; } } // 描画処理 for ( set< Coord<int> >::const_iterator it = drawCoord.begin() ; it != drawCoord.end() ; ++it ) { pset( draw, *it ); } }
処理の内容は非常に単純で、画素上の各座標値を初期値としてニュートン-ラフソン法を使ってゼロ点を求め、その位置をプロットするだけです。しかし、例えば Y を固定して X 方向にゼロ点を求めてプロットした場合、傾きの緩やかな(傾きが 1 より小さな)場所ではプロットした点が飛び飛びの状態になり曲線としてつながった形にならないので、X を固定して Y 方向へもゼロ点を求めることで対応しています。すると同じ位置を二回プロットする場合があり効率が悪いので、得られた座標値をいったん配列に格納して、最後に描画を行うようにしています。
重複は X, Y 方向の二回の処理だけで生じるわけではなく、それぞれの方向で各座標値からゼロ点を求めたときも発生します(むしろ、その時のほうが大量に発生します)。できるだけ無駄な処理をする回数が少なくなるように、得られたゼロ点が処理の進行方向へ進んでいる場合、その位置まで初期値を進めるようにしています。その間の位置を初期値として処理しても、得られるゼロ点は等しいためです。また、関数値もその微分係数も符号が同じならば、ゼロ点は後戻りする方向にあるはずなので、そのような位置に対しても処理をスキップするようにしています。これでようやく、それなりの処理速度で描画できるようになります。
ゼロ点は、Standard Template Library(STL) にあるコンテナクラス set を使って保持します。このコンテナクラスを利用すれば重複した要素は追加されないため、同じ値があるかをプログラム内でチェックする必要はなくなります。しかし、Coord 型は比較演算子 ( <, > ) で比較することができないため、専用の関数オブジェクト LessCoord を用意して、テンプレート引数でこのオブジェクトを指定することで比較ができるようにしてあります。もちろん、比較演算子の多重定義 ( operator<, operator> ) を用意するという手もありますが、座標に対する大小判定はいろいろな考え方があると思うので、汎用の関数としては用意しないという方針でこのようにしました。
描画関数は関数オブジェクト GPixelOp の operator() を利用するようになっています。その引数は、描画対象となるオブジェクト DrawingArea_IF とその位置です。同じ名前のクラスを「グラフィック・パターンの扱い」のサンプル・プログラムでも利用していますが、使い方は多少異なっていて、「グラフィック・パターンの扱い」の中では GPixelOp オブジェクトを生成した時に描画対象 DrawingArea_IF を指定するので固定されるのに対し、今回のサンプル・プログラムでは描画内容だけを GPixelOp が保持して描画対象は後で指定するようになっています。それ以外の内容は同様なので、詳細については「グラフィック・パターンの扱い」の内容をご覧ください。
| 図 1-1. 円弧の描画 ( x - 125 )2 + ( y - 125 )2 = 1002 |
 |
上図は、係数を直接指定して描画した円弧です。パラメータは定数項から順番に 21250 ( = 2 x 1252 - 1002 ), -250, -250, 1, 0, 1 で、この時の多項式は
なので、そのゼロ点の軌跡は 中心 ( 125, 125 )、半径 100 の円弧になります。方程式さえ分かれば、任意の楕円を長軸・短軸の角度を変化させて描画することもできるので、以前紹介した、円や楕円の描画プログラムの代わりに利用することも可能です。もちろん、円や楕円以外でも、多項式であればどんな曲線も描画することが可能です。
精度を多少悪くしても問題がなければ、もっと単純なやり方もあります。ある点とその次の点の間で関数値の符号が逆転していれば、その間にゼロ点が必ず存在するはずです。従って、符号が反転した時にその点をプロットしても曲線は描画することができます。以下に、そのサンプル・プログラムを示します。
/* SimpleDrawCurve : 多項式を利用した曲線描画関数(簡易版) const BiPolynomial& f : 対象の多項式 DrawingArea_IF& draw : 描画オブジェクト GPixelOp& pset : 描画用関数 */ void SimpleDrawCurve( const BiPolynomial& f, DrawingArea_IF& draw, GPixelOp& pset ) { Coord<int> sz = draw.size(); // 描画オブジェクトのサイズ Coord<int> c; // X 方向に、関数値の符号が反転した位置を描画する for ( c.y = 0 ; c.y < sz.y ; ++( c.y ) ) { c.x = 0; double preValue = f( Coord<double>( (double)( c.x ) - 0.5, c.y ) ); while ( c.x < sz.x ) { double curValue = f( Coord<double>( (double)( c.x ) + 0.5, c.y ) ); if ( ( preValue >= 0 && curValue < 0 ) || ( preValue < 0 && curValue >= 0 ) ) pset( draw, c ); preValue = curValue; ++( c.x ); } } // Y 方向に、関数値の符号が反転した位置を描画する for ( c.x = 0 ; c.x < sz.x ; ++( c.x ) ) { c.y = 0; double preValue = f( Coord<double>( c.x, (double)( c.y ) - 0.5 ) ); while ( c.y < sz.y ) { double curValue = f( Coord<double>( c.x, (double)( c.y ) + 0.5 ) ); if ( ( preValue >= 0 && curValue < 0 ) || ( preValue < 0 && curValue >= 0 ) ) pset( draw, c ); preValue = curValue; ++( c.y ); } } }
この方法は、二点間で極値を持つような場合(急激に上または下に凸な状態となっているとき)に検出することができなくなります。しかし、X, Y 方向の両方で検出しているので、曲線が途中で途切れてしまうという現象は回避できます。完全に検出できないのは、X, Y 両方向から見ても二点間に極値があるような場合で、ピクセル内に凸となった部分がある状態がそれにあたります。この時は、そのピクセルを描画することができませんが、描画できたとしても点として表現されるだけなので通常は無視しても問題はないと思います。
| 図 1-2. SimpleDrawCurve を使った円弧の描画 ( x - 125 )2 + ( y - 125 )2 = 1002 |
 |
上図は、簡易版を使って先ほどと同じ円弧を描画した結果です。この結果を見る限りでは、両者の差は全く見られません。
これで、任意の多項式に対して、平面 f( x, y ) = 0 と交差する曲線を描画することができるようになりました。また、平面上の点を指定すれば、その点を通る多項式を計算して描画することもできます。しかし、この処理では期待通りの曲線を描画することができません。通常は、指定された点に対してその順番に、全てがつながった曲線を描画する必要があります。しかし、この方法では順番に描画することはおろか、全てがつながった状態になることも保証できません。
| 図 1-3. 三点 ( 25, 220 ), ( 175, 175 ), ( 225, 20 ) を通る曲線の描画 |
 |
上図は、三点 ( 25, 220 ), ( 175, 175 ), ( 225, 20 ) を指定して曲線を描画した結果です。このとき、多項式は 1 + 0.015x - 6.0x10-3y - 8.4x10-5x2 となるので放物線が描かれます。しかし、実際に描きたいのは黄色で示したような曲線であり、全く異なる結果となります。点を指定してもどのような曲線が描画されるのか予想することができず、その制御も不可能ではこのまま利用することはできません。グラフィック・エディタなどにある曲線描画の機能を実装するには他の手段を検討する必要があります。
関数 y = f(x) は、x を変化させれば y の値を求めることができるので、これをつなぐことでそのグラフを描画することができます。例えば、y = x2 のグラフを描画すれば放物線として表現されます。このような形式の関数を「陽関数(Explicit Function)」といいます。"explicit" には「明確な」という意味がありますが、独立変数である x に対して従属変数である y が明確に(一意に)決められるということからこのような名が付けられています。独立変数はいくつあってもいいので、z = f( x, y ) は独立変数が x, y で従属変数が z である陽関数と考えることができます。しかし、f( x, y ) = 0 は、x が独立変数、y が従属変数と考えればそれらが左辺の一つの式で表されていることになります。このような関数を「陰関数(Implicit Function)」といいます。"implicit" には「間接的な」という意味があります。
陽関数は、陰関数の形に一意に表現することができます。例えば、y = x2 ならば x2 - y = 0 と表せば陰関数になります。しかし、陰関数が常に陽関数に一意に表せるとは限りません。例えば、円の関数 x2 + y2 = r2 は、陽関数に表すと y = ±( r2 - x2 )1/2 となって、一つの式で表せなくなります。これは、ある x の値に対して取りうる y の値が複数存在するためです。陰関数を多項式 Σi( Σj( aijxiyj ) ) = 0 の形だけに限定すれば、x の値に対して y の値の個数は最大で y の次数と等しくなります。y の次数が 1 ならば y の値は一意に決まり、そのときは容易に陽関数で表せることは簡単に示すことができます。二次ならば y に対する二次方程式を解くことで最大二つの解が得られ、四次までなら一般解の解き方があるので機械的に解くことが可能ですが、それより次数が大きくなると一般解を解くことは不可能になります。前に示した方法は、ニュートン-ラフソン法やピクセル間の符号を調べる手法によって解を求める操作を行なっていたことになります。しかし、点を指定した順番で曲線を描画するとなると、もはやこの方法は利用できなくなります。
陰関数である限り解は一つに定まらず、つながった曲線を指定した順に描画することもできません。陽関数の形で表現できれば解は簡単に求められますが、それもできないのなら他の手段を使う必要があります。そこで、今まで一つの式に混在していた x と y を分離することを考えます。それぞれの変数による陽関数を二つ用意するわけですが、例えば y = x2 ならば x(t) = t, y(t) = t2 とすれば t という新たな変数を媒介して y = x2 の関係を満たすように分離することができます。また、x2 + y2 = r2 の場合、x = rcosθ, y = rsinθ ( 0 ≤ θ ≤ 2π ) という別の一般的な表し方があります。このように表現すると、x, y の座標の変化を個別に指定することができるので、指定した順番に x, y 座標が変化するような、t や θ を変数とする陽関数が用意できれば、関数に値を代入するだけで機械的に座標を求めることができるようになります。このような式のことを「パラメトリック方程式 (Parametric Equation)」といい、t や θ のような変数を「媒介変数(Parameter)」といいます。パラメトリック方程式を使えば x, y の関係を意識する必要はなくなり、自由に曲線を描くことができるようになります。また、今まで扱ってきたのは平面上の曲線のみでしたが、これを三次元空間に拡張することも容易になります。
パラメトリック方程式を利用した曲線描画のサンプル・プログラムを以下に示します。
/***************************************************** ParametricEquation : パラメトリック方程式 *****************************************************/ struct ParametricEquation { virtual double x( double t ) = 0; // x の値を求める virtual double y( double t ) = 0; // y の値を求める virtual ~ParametricEquation() {} // 仮想デストラクタ }; /* CalcInnerPoint : パラメトリック曲線の内点を計算する GPixelOp& pset : 描画用関数 DrawingArea_IF& draw : 描画オブジェクト ParametricEquation& f : パラメトリック方程式 const pair<double,double>& range : f の定義域 double rate : 再帰的に内点を描画するときの内点の位置(比率) */ void CalcInnerPoint( double t0, double t1, const Coord<int>& first, const Coord<int>& second, ParametricEquation& f, set< Coord<int>, LessCoord<int> >& drawCoord, double rate ) { // t0 と t1 の差の最小値 const double THRESHOLD = 1E-6; // THRESHOLDより小さければ処理はしない if ( fabs( t0 - t1 ) < THRESHOLD ) return; // 内点に対する t の値 double inner = ( t0 < t1 ) ? ( 1 - rate ) * t0 + rate * t1 : rate * t0 + ( 1 - rate ) * t1; // 内点の座標 Coord<int> c( RoundHalfUp( f.x( inner ) ), RoundHalfUp( f.y( inner ) ) ); drawCoord.insert( c ); // 再帰的に内点を計算 if ( abs( first.x - c.x ) > 1 || abs( first.y - c.y ) > 1 ) CalcInnerPoint( t0, inner, first, c, f, drawCoord, rate ); if ( abs( second.x - c.x ) > 1 || abs( second.y - c.y ) > 1 ) CalcInnerPoint( inner, t1, c, second, f, drawCoord, rate ); } /* DrawPramaetricCurve : パラメトリック曲線描画関数 DrawingArea_IF& draw : 描画オブジェクト GPixelOp& pset : 描画用関数 ParametricEquation& f : パラメトリック方程式 const pair<double,double>& range : f の定義域 double rate : 再帰的に内点を描画するときの内点の位置(比率) */ void DrawParametricCurve( DrawingArea_IF& draw, GPixelOp& pset, ParametricEquation& f, const pair<double,double>& range, double rate ) { // 求めた座標を保持する set LessCoord<int> less; set< Coord<int>, LessCoord<int> > drawCoord( less ); // 両端の点の座標 Coord<int> first( RoundHalfUp( f.x( range.first ) ), RoundHalfUp( f.y( range.first ) ) ); Coord<int> second( RoundHalfUp( f.x( range.second ) ), RoundHalfUp( f.y( range.second ) ) ); // 内点に対する比率の補正 ( 0 < rate < 1 にする ) if ( rate < 0 ) rate -= (int)rate - 1; if ( rate > 1 ) rate -= (int)rate; if ( rate == 0 || rate == 1 ) rate = 0.5; // 両端の点を登録 drawCoord.insert( first ); drawCoord.insert( second ); // 再起処理開始 CalcInnerPoint( range.first, range.second, first, second, f, drawCoord, rate ); // 描画処理 for ( set< Coord<int> >::const_iterator it = drawCoord.begin() ; it != drawCoord.end() ; ++it ) { pset( draw, *it ); } }
パラメトリック方程式を利用して座標を求めて曲線を描画する場合、最も問題になるのが変数 t をどの程度の間隔で変化させればよいかです。t に対する x, y の変化量が大きい場合は t の変化量は小さくする必要があり、逆に変化量が小さい場合は同じピクセルの座標を何回も求めることになり効率が悪くなります。変化量をあらかじめ見積もるためにはパラメトリック方程式の導関数を求める必要があり、しかもその値はたいてい t によって変化します。また、導関数が必ず求められるとは限らないので、いつもこの手を使うというわけにはいきません。サンプル・プログラムでは、t の取りうる範囲内にある内点を決めて、それに対して座標を求める処理を再帰的に繰り返すことで対応しています。初期化と描画を行う関数が DrawParametricCurve で、t の定義域 range から両端の t に対する座標を求めて drawCoord に格納した後、それらのパラメータを CalcInnerPoint に渡します。CalcInnerPoint は、rate を使って t の内点を求め、その座標を drawCoord に登録した上で、もし内点に対する座標が両端にあるそれぞれの点とつながっていなければ、端点と内点を使って再度 CalcInnerPoint を呼び出します。このように次々と内点に対する座標を求めていき、全ての座標がつながった状態になった段階で処理を終了します。最後に、登録した座標を使って描画処理を行います。
内点を求めるときに rate を使っているのは、パラメトリック方程式が周期関数である場合に対処できるようにするためです。例えば、定義域がちょうど 2 周期であった場合、rate = 0.5 ならば両端の点と内点は全て一致してしまいます。具体的には、定義域 0 ≤ θ ≤ 4π における cosθ の値は、rate = 0.5 のとき cos0 = cos2π = cos4π = 1 になります。x, y の両方でそのような状態になってしまった場合は何も描画されないことになるため、内点の位置を少しずらすことでこのような現象を防ぐようにしています。
パラメトリック方程式は ParametricEquation の派生クラスを使って定義します。ParametricEquation は二つの純粋仮想関数 x, y を持ち、それぞれが変数 t に対する x, y の値を返します。例えば、x, y がともに三角関数に従うようなパラメトリック方程式は次のように定義することができます。
/***************************************************** SinCurve : 三角関数を利用したパラメトリック方程式 *****************************************************/ struct SinCurve : public ParametricEquation { Coord<double> scale_; // 倍率 Coord<double> shift_; // 始点のシフト量 Coord<double> cycle_; // 周期 /* コンストラクタ const Coord<double>& scale : 倍率 const Coord<double>& shift : 始点のシフト量 const Coord<double>& cycle : 周期 */ SinCurve( const Coord<double>& scale, const Coord<double>& shift, const Coord<double>& cycle ) : scale_( scale ), shift_( shift ), cycle_( cycle ) {} // x の値を求める virtual double x( double t ) { return( scale_.x * sin( cycle_.x * t ) + shift_.x ); } // y の値を求める virtual double y( double t ) { return( scale_.y * sin( cycle_.y * t ) + shift_.y ); } };
scale_ は、正弦値に対する倍率、shift_ は正弦値のシフト量で、cycle_ は周期を表します。scale_ = 100, shift_ = 125 とし、cycle_ は x に対して 1、y に対して 2 として、0 ≤ t ≤ 2π の定義域で曲線を描画してみると、下図のようになります。cycle_ の値をいろいろと変化させてみると、面白い図形を描くことができます。
| 図 2-1. パラメトリック曲線の描画 |
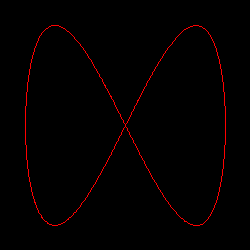 |
次に、与えられた点に対して適切なパラメトリック方程式を求めることを考えてみます。N + 1 個の点 ( xi, yi ) ( i = 0, 1, ... N ) に対しては、N + 1 個の未知数(係数)を持つ関数を使えば、N + 1 個の連立方程式から未知数を求めることで関数の形が決定します。ここでも関数を多項式に限定してしまえば、x, y それぞれに対して N 次の多項式
x(t) = Σi{0→N}( aiti )
y(t) = Σi{0→N}( biti )
を定義して、未知数 ai, bi を求めればパラメトリック方程式が決まります。それぞれの x, y に対して t の値をどのように割り当てるかが問題になりますが、ここでは i 番目の点に対しては t = i / N として ( つまり、t の定義域は 0 から 1 までになります ) 計算してみます。まずは、与えられた点からパラメトリック方程式を求めるためのクラスを定義します。
/***************************************************** Polynomial : 多項式定義用クラス f(x) = a[0] + a[1]t + a[2]t^2 + ... + a[N]t^N a[i] は係数 t は変数を表す *****************************************************/ class Polynomial { vector<double> coeff_; // 多項式の係数(定数項から始めて次数の小さい順に並べる) /* coord : 与えられた点の i 番目の座標を返す const vector< Coord<double> >& p : 点の配列 bool isX : 返す座標値は X 成分か? unsigned int i : 対象の添字 */ double coord( const vector< Coord<double> >& p, bool isX, unsigned int i ) const { return( ( i >= p.size() ) ? 0 : ( isX ) ? p[i].x : p[i].y ); } public: // コンストラクタ Polynomial( const vector< Coord<double> >& p, bool isX ); // 次数を返す unsigned int order() const { return( coeff_.size() - 1 ); } // t に対する計算結果を返す double operator()( double t ) const; }; /* Polynomial コンストラクタ const vector< Coord<double> >& p : 多項式計算対象の座標 bool isX : 計算は X 座標に対してか? */ Polynomial::Polynomial( const vector< Coord<double> >& p, bool isX ) { unsigned int coeffSize = p.size(); // 係数(項)の数 // 点が一つもなければ f(t) = 0 if ( coeffSize == 0 ) { coeff_.push_back( 0 ); return; } // 点が一つしかなければ f(t) = p[0] (定数) if ( coeffSize == 1 ) { coeff_.push_back( coord( p, isX, 0 ) ); return; } // coeff_ を項の数で初期化 coeff_.resize( coeffSize, 0 ); // 定数項は p[0] に等しい coeff_[0] = coord( p, isX, 0 ); /* p の要素から連立方程式の係数を求め、連立方程式を解く 定数項はすでに p[0] であることがわかっているので、未知数は点の数より一つ少ない。 このとき、i 番目の式の右辺は p[i] - p[0] となる(定数項 p[0] を左辺から除外するため) */ LinearEquationSystem<double> les( coeffSize - 1 ); double diff = 1.0 / (double)( coeffSize - 1 ); // t の増分 double t = diff; // t の初期値 for ( unsigned int i = 0 ; i < coeffSize - 1 ; ++i ) { double d = t; // pow( t, j + 1 ) for ( unsigned int j = 0 ; j < coeffSize - 1 ; ++j ) { les[i][j] = d; d *= t; } les.ans( i ) = coord( p, isX, i + 1 ) - coord( p, isX, 0 ); t += diff; // 次の t に更新 } if ( ! GaussianElimination( les ) ) { std::cerr << "The system has infinitely many, or no solutions" << std::endl; return; } // 求めた未知数は f(t) の係数となる。 for ( unsigned int i = 1 ; i < coeffSize ; ++i ) coeff_[i] = les.ans( i - 1 ); } /* Polynomial::operator() : t に対する計算結果を返す double t : 変数 t 戻り値 : 計算結果 */ double Polynomial::operator()( double t ) const { double ans = 0; // 計算結果 double d = 1.0; // pow( t, i ) for ( unsigned int i = 0 ; i < coeff_.size() ; ++i ) { ans += coeff_[i] * d; d *= t; } return( ans ); } /********************************************************** PolyParametricEquation : 多項式によるパラメトリック方程式 **********************************************************/ class PolyParametricEquation : public ParametricEquation { // X,Y それぞれのパラメトリック方程式 Polynomial x_; Polynomial y_; public: /* コンストラクタ const vector< Coord<double> >& p : 曲線を通る点の座標 */ PolyParametricEquation( const vector< Coord<double> >& p ) : x_( p, true ), y_( p, false ) {} // x,y の値を求める virtual double x( double t ) { return( x_( t ) ); } virtual double y( double t ) { return( y_( t ) ); } };
Polynomial が、与えられた点からパラメトリック多項式を求め、任意の変数に対する計算結果を返すためのクラスです。内容は、前に紹介した BiPolynomial とよく似ていますが、こちらは一変数のみを扱えばいいので、その分わかりやすくなっています。コンストラクタには、曲線が通る点を引数として渡します。このとき、対象のパラメトリック方程式が x, y のどちらに対して利用するものかを指定するために bool 型変数 isX も引数として定義しています。この値が true なら、点の x 座標のみを使い、false なら y 座標のみを使って計算します。
変数 t の定義域は 0 から 1 までの固定にしているので、t = 0 を代入したときの式は (定数項) = (最初の座標値) となります。つまり、未知数のうちの一つは簡単に得られるので、未知数の数は点の数よりも一つ少なくて済みます。この時、各式の右辺 (式に対する解の部分) は各座標値から最初の座標値を引いたときの差になることに注意が必要です。なお、ここでは連立方程式を使って係数を求める手法を使っていますが、「グラフィック・パターンの扱い (5) サンプル補間」の「6) 多項式補間 (Polynomial Interpolation)」で紹介した「ラグランジュの多項式 ( Lagrange Polynomial )」や「ニュートン多項式 ( Newton Polynomial )」を使って多項式を求め、t に対する値を計算することももちろん可能で、むしろその方が一般的です。
PolyParametricEquation は、Polynomial を x, y 座標用に二つ持ち、それぞれの値を返すためのクラスで、ParametricEquation から派生しています。このコンストラクタの引数も曲線を通る点の座標値で、x, y それぞれについて Polynomial 用のコンストラクタを使って初期化しているだけの単純なものです。
このクラスを使って、前に多項式のゼロ点を使って描画した時と同じ条件、三点 ( 25, 220 ), ( 175, 175 ), ( 225, 20 ) を通る曲線を描画した結果は下の図のようになります。
| 図 2-2. 三点 ( 25, 220 ), ( 175, 175 ), ( 225, 20 ) を通るパラメトリック方程式を使った曲線の描画 |
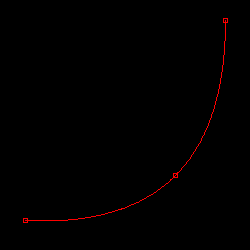 |
今回は、意図した通りの曲線が描画できているようです。点を時計回りに菱形の形になるように並べると、下図のようになりました。
| 図 2-3. 四点 ( 25, 125 ), ( 125, 25 ), ( 225, 125 ), ( 125, 225 ) を通るパラメトリック方程式を使った曲線の描画 |
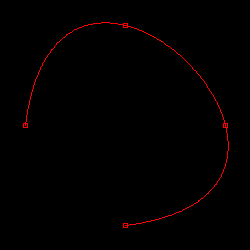 |
この場合もうまく描画できているようなので、さらに内側に曲線が回りこんで渦巻きの状態になるように、内側にも菱形状に点を配置してみます。
| 図 2-4. さらに四点 ( 75, 125 ), ( 125, 75 ), ( 175, 125 ), ( 125, 175 ) を追加したときの曲線の描画 |
 |
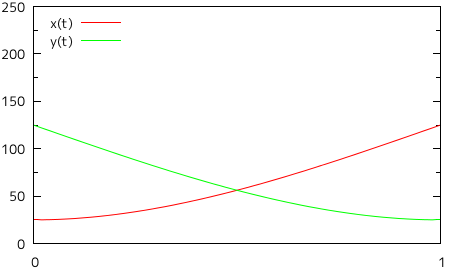
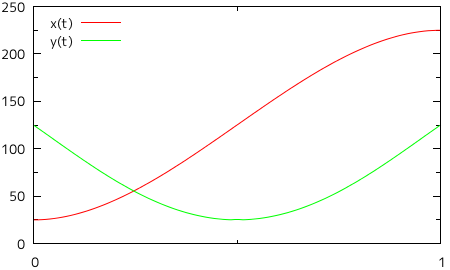
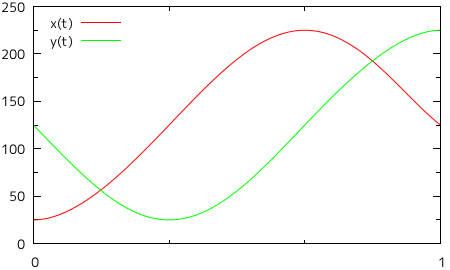
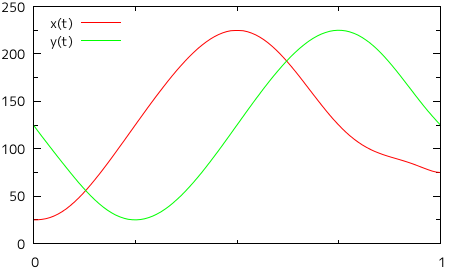
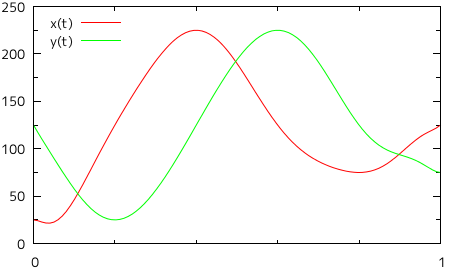
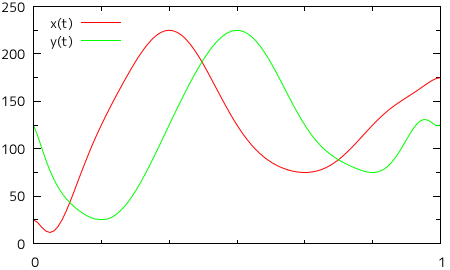
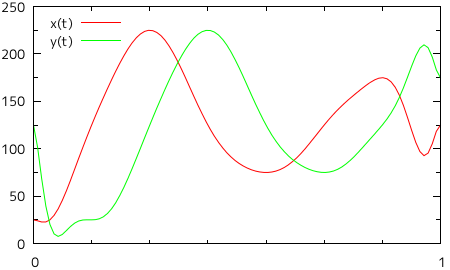
すると、今度は意図した通りの曲線を描画することができませんでした。左側に大きく迂回して曲線が描かれているために画面からはみ出てしまっていたり、ねじれて描画されているような部分もあり、渦巻き状の曲線とはとても呼べる状態ではありません。それぞれのパラメトリック多項式をグラフにしたものを以下に示します。
| 図 2-5. 8 点を通るパラメトリック多項式のグラフ |
 |
グラフの横軸が媒介変数 t を表し、軸上の目盛りがそれぞれの点に対応します。縦軸は X, Y それぞれの大きさを表し、赤線が X 成分、緑の線が Y 成分を示しています。X 成分に対しては、t = 0 から単調増加しながら二目盛り先で極値となり(ここが最も右側にある点になります)、そこから今度は単調減少しながら二目盛り先で二度目の極値となるという具合に、二目盛りごとに極限になりながら合計二つの山と一つの谷が形成されるのが理想的な形で、山と谷は徐々に小さくなっていきます。Y 成分も、最初は単調減少を行い、一目盛りめで極限となる以外は、二目盛りごとに極限になりながら、しかも山と谷が徐々に小さくなる様子は同じです(ちょうど、位相が一目盛り分ずれた形になります)。イメージとしては、下のようなグラフになります。
| 図 2-6. 理想的なパラメトリック方程式 |
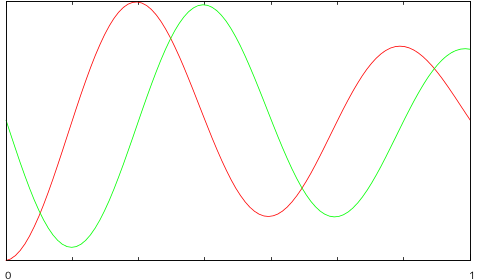 |
指定した n 個の点を通る n - 1 次の多項式は、連立方程式の解さえ存在するのならただ一つに決まりますが、それが必ずしも理想的な曲線に対するパラメトリック方程式になるとは限りません。そこで、二目盛り間隔で極値となるようにしたり、その間は単調増加・減少を繰り返すなど、さらに条件を追加することで制御することを検討します。そのためには、各点における微分係数の値、すなわち曲線の接線の傾きまでを考慮すればいいので、微分係数までを指定して多項式を得るためのコンストラクタを用意してみます。
/* Polynomial コンストラクタ (微分係数まで指定) const vector< Coord<double> >& p : 多項式計算対象の座標 const vector< Coord<double> >& dp : 多項式計算対象の点に対する増分(微分係数) bool isX : 計算は X 座標に対してか? */ Polynomial::Polynomial( const vector< Coord<double> >& p, const vector< Coord<double> >& dp, bool isX ) { unsigned int pSize = min( p.size(), dp.size() ); // 点の数 unsigned int coeffSize = pSize * 2; // 項の数 // 点が一つもなければ f(t) = 0 if ( pSize == 0 ) { coeff_.push_back( 0 ); return; } // 点が一つしかなければ f(t) = p[0] + dp[0]t if ( pSize == 1 ) { coeff_.push_back( coord( p, isX, 0 ) ); coeff_.push_back( coord( dp, isX, 0 ) ); return; } // coeff_ を項の数で初期化 coeff_.resize( coeffSize, 0 ); // 定数項は p[0] に等しい coeff_[0] = coord( p, isX, 0 ); // 一次項は dp[0] に等しい coeff_[1] = coord( dp, isX, 0 ); /* p, dp の要素から連立方程式の係数を求め、連立方程式を解く 定数項と一次項はすでに p[0], dp[0] であることがわかっているので、未知数は項の数より二つ少ない。 */ unsigned int xSize = coeffSize - 2; // 未知数の数 LinearEquationSystem<double> les( xSize ); // 関数に対する方程式 double diff = 1.0 / (double)( pSize - 1 ); // t の増分 double t = diff; // t の初期値 for ( unsigned int i = 0 ; i < xSize / 2 ; ++i ) { double d = pow( t, 2 ); // pow( t, j + 2 ) for ( unsigned int j = 0 ; j < xSize ; ++j ) { les[i][j] = d; d *= t; } les.ans( i ) = coord( p, isX, i + 1 ) - coord( p, isX, 0 ) - coord( dp, isX, 0 ) * t; t += diff; // 次の t に更新 } // 微分係数に対する方程式 t = diff; for ( unsigned int i = 0 ; i < xSize / 2 ; ++i ) { double d = t; // pow( t, j + 1 ) for ( unsigned int j = 0 ; j < xSize ; ++j ) { les[xSize / 2 + i][j] = d * (double)( j + 2 ); d *= t; } les.ans( xSize / 2 + i ) = coord( dp, isX, i + 1 ) - coord( dp, isX, 0 ); t += diff; // 次の t に更新 } if ( ! GaussianElimination( les ) ) { std::cerr << "The system has infinitely many, or no solutions" << std::endl; return; } // 求めた未知数は f(t) の係数となる。 for ( unsigned int i = 2 ; i < coeffSize ; ++i ) coeff_[i] = les.ans( i - 2 ); }
dp が微分係数に対する値の配列になります。点とその微分係数の個数は等しい必要があるので、配列のサイズの小さい方をその数として変数 pSize に代入しています。また、項の数は coeffSize に、未知数の数は xSize で表しています。
点の数が N のとき、多項式の次数は N - 1 であり、項と未知数の数は N となるのでした。今回は微分係数の値も含むため、項と未知数の数は 2N 個とする必要があります。このとき、多項式の次数は 2N - 1 と二倍くらい大きくなります。定数項が最初の点の座標値で決まったように、多項式に対する導関数の定義から一次項の係数は最初の点に対する微分係数の値と等しくなります。よって、項の数 coeffSize は pSize * 2 なのに対し、未知数の数 xSize は pSize * 2 - 2 = coeffSize - 2 と、項の数より二つ減らしています。また、定数項と一次項は式の右辺 (連立方程式の解) へ移項していることにも注意してください。
下の図は、微分係数の値まで定義して描画を行った結果です。2 点から徐々に点の数を増やしていき、最大 8 点までを定義して描画しています。
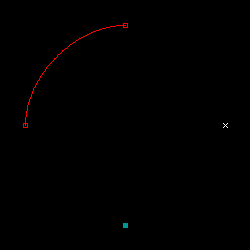 |
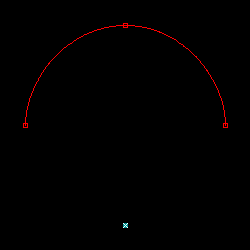 |
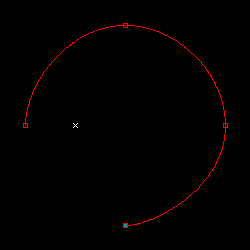 |
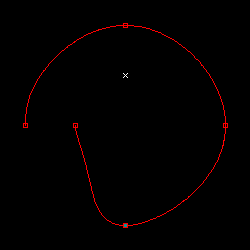 |
 |
 |
 |
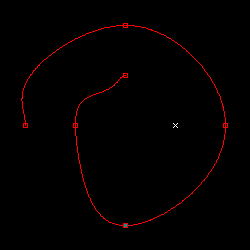
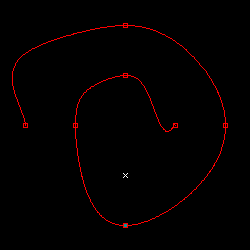
微分係数の値は、対象の点の前後にある点の座標を使って求めています。ある点 p の前後の点の座標をそれぞれ pa, pb とし、点の総数を N とした時、微分係数の値は下式で求められます。
分子の pb - pa は前後の座標の差分で、分母の 2 / ( N - 1 ) は pa, pb に対する媒介変数 t の差になります ( t の定義域は 0 から 1 まで固定で、各点に対して t は等間隔なので、その間隔は 1 / ( N - 1 ) です )。但し、最初と最後の点は片側の点が存在しないため、描画対象ではない架空の点を二点定義しています。D は任意の定数で、微分係数の調整に利用します。今回のテストでは 1.5 としています。
上の図の中の赤い枠で示した位置が指定された各点を表しています。また、青緑色で塗りつぶされた四角は最初の点、×印の箇所は最後の点に対して微分係数を計算するために用意された架空の点です。この結果を見ると、4 点まではきれいに描画できていますが、それを超えたところから、特に両端に近い部分で大きく変形してしまっていることがわかります。各結果に対するパラメトリック方程式は、次のようなグラフになります。
 |
 |
 |
 |
 |
 |
 |
多項式の項の数は、点の数の二倍になるのでした。8 点ならば、項の数は 16 で 15 次の多項式になります。極値は最大で ( 次数 - 1 ) となるので、14 個もの極値が発生する可能性があります。つまり、それだけ多くの波(凹凸)が現れることになり、点と点の間にその波があれば、点から点へ進む方向は異なる向きに線が描かれてしまうことになります。この結果を見る限り、制御ができるのはせいぜい 4 点程度で、それ以上は制御することがかなり困難になります。数十点、数百点のオーダーの点を使って滑らかな曲線を表現したい場合、これは致命的な欠陥になるので、さらにやり方を検討する必要があります。
点を増やすほど、多項式近似によって曲線を表現することは困難になることがわかりました。そこで、一度に多項式近似を行う点の範囲を細かく分割することを検討します。例えば、隣り合う二点ずつを使って多項式 (この場合一次式、すなわち直線の方程式になります) に変換して描画すると、これは各点を直線でつないだ折れ線になります。一度に使う点を三つにすれば、二次式を組み合わせた曲線が得られます。しかし、それぞれの二次式はつなぎ目のところで連続になるとは限らない (というよりも連続になる方が珍しい) ので、滑らかな曲線としては描画されません。そこで、微分係数の値も考慮して曲線を描画するようにします。二点に対しては ( 微分係数も含めて未知数が 4 つなので ) 三次式で表現され、各曲線のつなぎ目は、その点の微分係数の値が等しくなることから連続となります。この方法ならば、曲線は連続になる上に、点の増加に伴う制御困難な状態も回避することができます。このように表現された曲線を「スプライン曲線 (Spline Curve)」といいます。スプラインとは本来、細長い薄板や、回転軸に刻まれた溝・歯の部分をを表し、薄板は変形させて曲線を描くのに用いられていたことからこの名が使われるようになりました ( 曲線を描くのに使われた薄板は Flat Spline と呼ばれていたようです )。また、この言葉が最初に使われたのは 1946 年、数学者 Isaac Jacob Schoenberg の論文の中ということです。
最も単純なのは、二点に対して微分係数の値を指定して曲線を描画する場合です。X 座標に対し、このときのパラメトリック多項式を
とすると、その導関数は
になります。二点の X 座標を x0, x1 とし、その微分係数の X 成分を dx0, dx1 としたとき、t の定義域を 0 から 1 までとすれば、x(0) = x0, x(1) = x1, x'(0) = dx0, x'(1) = dx1 より
となります。この連立方程式を解けば、
となって、各係数を簡単に求めることができます。なお、Y 座標に対しても計算方法は同じです。
このように描画された曲線は「Ferguson/Coons 曲線」と呼ばれています。微分係数の値は、その点における接線方向の向きと大きさを表します。この値を調整すれば、曲線は様々な形にすることが可能です。また、局所的に変形を行うことも比較的簡単にできるので、以前はよく利用されていた手法のようです。
微分係数の値をあらかじめ決めてしまいたい場合、よく使われる計算式は次のようになります。
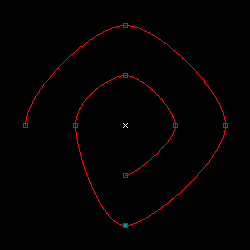
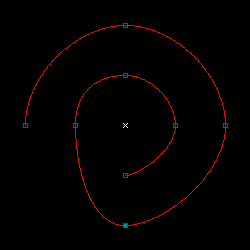
xi-1 は xi の前, xi+1 は xi の後の点の座標値をそれぞれ表しています。この式は、パラメトリック方程式を利用した多項式近似において微分係数の値を計算した時の式とほぼ同じ内容で、対象の前後の点の差分を半分にしているので、計算結果は、前後の点を結んだ線分と平行で大きさが半分のベクトルになります。このように微分係数の値を計算してスプライン曲線を描画する手法は「Catmull-Rom 曲線」と呼ばれます。
Ferguson/Coons 曲線と Catmull-Rom 曲線を利用した曲線描画用のサンプル・プログラムを以下に示します。
/********************************************************** FergusonCoons_Spline : Ferguson/Coons曲線 **********************************************************/ class FergusonCoons_Spline : public ParametricEquation { Coord<double> a[4]; // 係数(高次の項から順に並ぶ) public: /* コンストラクタ const Coord<double>& p0, p1 : 曲線の両端の点の座標 const Coord<double>& dp0, dp1 : p0,p1 での微分係数 */ FergusonCoons_Spline( const Coord<double>& p0, const Coord<double>& p1, const Coord<double>& dp0, const Coord<double>& dp1 ) { a[0].x = 2 * ( p0.x - p1.x ) + ( dp0.x + dp1.x ); a[1].x = -3 * ( p0.x - p1.x ) - ( 2 * dp0.x + dp1.x ); a[2].x = dp0.x; a[3].x = p0.x; a[0].y = 2 * ( p0.y - p1.y ) + ( dp0.y + dp1.y ); a[1].y = -3 * ( p0.y - p1.y ) - ( 2 * dp0.y + dp1.y ); a[2].y = dp0.y; a[3].y = p0.y; } // x,y の値を求める virtual double x( double t ) { return( a[0].x * pow( t, 3 ) + a[1].x * pow( t, 2 ) + a[2].x * pow( t, 1 ) + a[3].x ); } virtual double y( double t ) { return( a[0].y * pow( t, 3 ) + a[1].y * pow( t, 2 ) + a[2].y * pow( t, 1 ) + a[3].y ); } }; /********************************************************** CatmullRom_Spline : Catmull-Rom曲線 **********************************************************/ class CatmullRom_Spline : public FergusonCoons_Spline { /* diff : 微分係数の計算 const Coord<double>& p0, p1 : 計算対象の前後の点の座標 double d : 補正係数 戻り値 : 計算した微分係数 */ static Coord<double> diff( const Coord<double>& p0, const Coord<double>& p1, double d ) { return( Coord<double>( d * ( p1.x - p0.x ) / 2.0, d * ( p1.y - p0.y ) / 2.0 ) ); } public: /* コンストラクタ const Coord<double>& before : p0 の前の点の座標 const Coord<double>& p0, p1 : 曲線の両端の点の座標 const Coord<double>& after : p1 の後の点の座標 const Coord<double>& dp0, dp1 : p0,p1 での微分係数 double d : 補正係数 */ CatmullRom_Spline( const Coord<double>& before, const Coord<double>& p0, const Coord<double>& p1, const Coord<double>& after, double d = 1 ) : FergusonCoons_Spline( p0, p1, diff( before, p1, d ), diff( p0, after, d ) ) {} }; /* FergusonCoons_SplineCurve : Ferguson/Coons曲線の描画 DrawingArea_IF& draw : 描画オブジェクト GPixelOp& pset : 描画用関数 const vector< Coord<double> >& p : 描画する曲線上の点の座標 const vector< Coord<double> >& dp : 各点に対する微分係数 double rate : 再帰的に内点を描画するときの内点の位置(比率) */ void FergusonCoons_SplineCurve( DrawingArea_IF& draw, GPixelOp& pset, const vector< Coord<double> >& p, const vector< Coord<double> >& dp, double rate ) { unsigned int cnt = min( p.size(), dp.size() ); if ( cnt == 0 ) return; for ( unsigned int i = 0 ; i < cnt - 1 ; ++i ) { FergusonCoons_Spline spline( p[i], p[i + 1], dp[i], dp[i + 1] ); DrawParametricCurve( draw, pset, spline, pair<double,double>( 0, 1 ), rate ); } } /* CatmullRom_SplineCurve : Catmull-Rom曲線の描画 p の最初と最後の要素は描画対象の点には含まれない(微分係数の計算のみに使用) DrawingArea_IF& draw : 描画オブジェクト GPixelOp& pset : 描画用関数 const vector< Coord<double> >& p : 描画する曲線上の点の座標 double d : 微分係数計算時の補正係数 double rate : 再帰的に内点を描画するときの内点の位置(比率) */ void CatmullRom_SplineCurve( DrawingArea_IF& draw, GPixelOp& pset, const vector< Coord<double> >& p, double d, double rate ) { unsigned int cnt = p.size(); if ( cnt < 4 ) return; for ( unsigned int i = 0 ; i <= cnt - 4 ; ++i ) { CatmullRom_Spline spline( p[i], p[i + 1], p[i + 2], p[i + 3], d ); DrawParametricCurve( draw, pset, spline, pair<double,double>( 0, 1 ), rate ); } }
二つのクラス FergusonCoons_Spline と CatmullRom_Spline がパラメトリック方程式の値を返すために使われます。インスタンス作成時に多項式の係数を求めておき、t の値を渡すとその結果を渡すような仕組みになっています。CatmullRom_Spline は FergusonCoons_Spline の派生クラスで、インスタンス化の時に微分係数を計算して基底クラスにその結果をそのまま渡すような形にしています。d は求めた微分係数に対する補正係数で、これを使って曲線の形状を制御することができます。
FergusonCoons_SplineCurve と CatmullRom_SplineCurve が曲線を描画するための関数で、点の配列 ( FergusonCoons_SplineCurve はさらに微分係数の配列 ) から二点ずつ取り出しては FergusonCoons_Spline、CatmullRom_Spline を使ってインスタンスを作成し、その区間の曲線を描画する作業を繰り返します。なお、CatmullRom_SplineCurve では、同じ点に対して二回微分係数を計算していることになるので、最初に微分係数を計算しておいてから描画するようにした方が効率的です。
| d = 1 | d = 1.5 |
|---|---|
 |
 |
| d = 2 | d = 4 |
 |
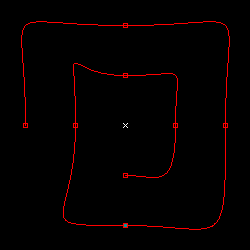 |
上の図は、補正係数 d を変化させながら CatmullRom_SplineCurve を使って曲線を描画した結果です。補正係数をうまく活用すれば、細かく微分係数を指定して FergusonCoons_SplineCurve で描画しなくても、ある程度は曲線の形状を制御することが可能です。もちろん、さらに細かく制御したい場合は各区間で微分係数を調節する必要があります。
今回紹介した曲線描画の手法は、一般的に利用されているものとは異なるものばかりです。実際には B-スプライン曲線やベジェ曲線、NURBS 曲線といった、より洗練された手法が用いられます。しかし、それらの手法は、今回紹介したパラメトリック方程式やスプラインを応用したものになります。次回から、一般的に利用されている手法について紹介をしたいと思いますが、なぜ、それらの手法が利用されるようになったのかを知る手掛かりとして今回の内容が役に立てば幸いです。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |