 |
「数値演算法 (8) 連立方程式を解く -2-」の「5) 固有値と固有ベクトル」にて固有値と固有ベクトルの紹介をしました。空間の一次変換に対し、固有ベクトルは大きさが固有値倍されるだけで、向きを変化させることはありません。この性質は様々な分野で利用され、そのため固有値を解くことが非常に重要なものになります。この章では、様々な分野で広く用いられている対称行列の固有値を求めるためのアルゴリズムを紹介したいと思います。
「数値演算法 (8) 連立方程式を解く -2-」の「5) 固有値と固有ベクトル」で、任意のベクトルは線形結合の形に表すことができることを紹介しました。式で表すと、次のようになります。
上式で、ai は列ベクトル ( a1i, a2i, ... ani )T になります。ここで ai の例として、次のような列ベクトルを定義します。
| e1 | = | ( 1, 0, ... 0, 0 )T |
| e2 | = | ( 0, 1, ... 0, 0 )T |
| : | ||
| en-1 | = | ( 0, 0, ... 1, 0 )T |
| en | = | ( 0, 0, ... 0, 1 )T |
このとき、ベクトル x = ( x1, x2, ... xn )T を ei を使って表すと、
になります。行列を使うと
| x = | | | x1 | | = | | | 1, | 0, | ... | 0, | 0 | || | x1 | | = Ex |
| | | x2 | | | | | 0, | 1, | ... | 0, | 0 | || | x2 | | | |
| | | : | | | | | : | : | ... | : | : | || | : | | | |
| | | xn-1 | | | | | 0, | 0, | ... | 1, | 0 | || | xn-1 | | | |
| | | xn | | | | | 0, | 0, | ... | 0, | 1 | || | xn | | |
と表現することができます ( E は単位行列 )。ここで、ベクトル ei の並び順を逆にしてみます。
| e'1 | = | ( 0, 0, ... 0, 1 )T |
| e'2 | = | ( 0, 0, ... 1, 0 )T |
| : | ||
| e'n-1 | = | ( 0, 1, ... 0, 0 )T |
| e'n | = | ( 1, 0, ... 0, 0 )T |
すると、x は次のように表せることになります。
行列で表すと次のようになります。係数は、ちょうどベクトルの各成分が反転したような形になりました。
| x = | | | x1 | | = | | | 0, | 0, | ... | 0, | 1 | || | xn | | |
| | | x2 | | | | | 0, | 0, | ... | 1, | 0 | || | xn-1 | | | |
| | | : | | | | | : | : | ... | : | : | || | : | | | |
| | | xn-1 | | | | | 0, | 1, | ... | 0, | 0 | || | x2 | | | |
| | | xn | | | | | 1, | 0, | ... | 0, | 0 | || | x1 | | |
n 個の線形独立なベクトルからなる組を選んだとき、任意のベクトルは、選ばれた n 個のベクトルの線形結合で表すことができます。また、線形独立であることから係数は一意に決まります。この時の、n 個の線形独立なベクトルの組を「基底 ( Basis )」と言います。上記の例の中の ei や e'i の組は、線形独立なベクトルからなるため基底になります。
同じベクトルでも基底が異なれば係数は変化します。上記の例では、ちょうど係数が反転したような形をとりました。基底の各成分を二倍すれば係数は半分になるし、逆に基底の値を半分にすれば係数は二倍になります。ei はちょうど、n 次元の空間に存在する座標軸の i 番目における、原点からの長さが 1 の点を表しているものと考えるとイメージしやすくなると思います。ei で表される座標系でベクトルを見たときと e'i の場合とでは見え方が変わりますが、ベクトルそのものに変化はありません。見る側が視点を変えて、同じ対象を観察しているのと同じです。
ある基底を列ベクトルに持つ行列を S として x = Sx' の関係にあるとします。x' は、S で表される基底から見た x の姿を表しています。ベクトル x に対し、行列 A による一次変換を行った結果を y とすると、関係式 Ax = y が得られます。これに x = Sx' を代入すると、
ここで、y は S で表される基底によって y' の形に表されるとします。この時、Sy' = y の関係式が成り立つので、
ASx' = Sy' より
S-1ASx' = y'
つまり、A が x を y に変換するのと同じように、S-1AS は x' を y' に変換します。A を S によって S-1AS の形に変換することを、S による A の「相似変換 ( Similarity Transformation )」と言います。A の固有値を λ、固有ベクトルを x' とした時、
ここで、x' が S によって x に変換されるとすると、Sx' = x より
両辺に左側から S-1 を掛けて
つまり、A と S-1AS は固有値が変わらないことになります。行列 A に対して、A の固有値からなる対角行列 Dと、A の固有ベクトルを列ベクトルとする行列 X の間には以下の関係式が成り立つのでした。これを「行列の対角化」といいます。
これは、A の X による相似変換によって D が得られることを意味しています。つまり、対角行列の対角成分は、その行列の固有値そのものを表していることになります。また、上式が成り立つためには X-1 が存在する必要があるため、固有ベクトルは線形独立でなければなりません。これが成り立つとき、固有ベクトルは基底として利用できることになります。
二つのベクトル u = ( u1, u2, ... un ), v = ( v1, v2, ... vn ) に対して、次のような式を定義します。
(u, v) = Σi{1→n}( uivi )
||u|| = (u, u)1/2 = { Σi{1→n}( ui2 ) }1/2
上式の左辺について、(u, v) を「内積 ( Inner Product )」、||u|| を「ノルム ( Norm )」と言います。また、ノルム ||u|| が 1 になるベクトル u を「単位ベクトル ( Unit Vector )」と言います。内積とノルムは、次の性質を満たします。
1. 任意のベクトル u について ||u||2 = (u, u) ≥ 0 ( u = 0のときのみ等号が成り立つ )
2. 任意のベクトル u, v について ( u, v ) = ( v, u )
3. 任意の実数 c1, c2 と任意のベクトル u1, u2, v について ( c1u1 + c2u2, v ) = c1( u1, v ) + c2( u2, v )
上から順番に「正値性」「対称性」「線形性」と言い、これらはまとめて「内積の公理 ( 補足 1 )」と呼ばれます。
ノルムと内積の間には、次の関係式が成り立ちます。
これを「コーシー = シュワルツの不等式 ( Cauchy-Schwarz Inequality )」と言います。この式から、-1 ≤ ( u, v ) / ||u||・||v|| ≤ 1 になるので、これが cos θ となる角度 θ を定義することができます。すなわち
この時の θ を「二つのベクトルのなす角度」と呼びます。
θ = π / 2 の時 cos θ = 0 なので内積の値は 0 になります。二つのベクトルのなす角度 θ が直角 ( = π / 2 ) となることから、内積が 0 になるとき、二つのベクトルは「直交する」と言います。基底の全てが互いに直交しているとき、この基底は「直交基底 ( Orthogonal Basis )」であり、特に全てのノルムが 1 ならば「正規直交基底 ( Orthonormal Basis )」となります。基底の例として紹介した ei と e'i はどちらも正規直交基底になります。ベクトルを直交基底の線形結合で表すことを「直交展開 ( Orthogonal Expansion )」と言います。
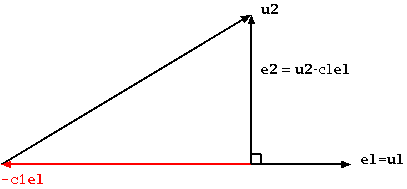
(正規)直交基底は、直交していないベクトルを含む基底を使っていくつでも作り出すことができます。そのような基底 ui から直交基底 ej を作るには、次のような手順を踏みます。
1. e1 = u1 とする。
2. e2 = u2 - c1e1 として、e1 と e2 が直交するように c1 を決める。
| ( e1, e2 ) | = | ( e1, u2 - c1e1 ) |
| = | ( e1, u2 ) - c1( e1, e1 ) | |
| = | ( e1, u2 ) - c1||e1||2 = 0 より |
c1 = ( e1, u2 ) / ||e1||2
よって、e2 = u2 - ( ( e1, u2 ) / ||e1||2 )e1
3. e3 = u3 - c1e1 - c2e2 として、e1, e2 と e3 が直交するように c1, c2 を決める。
| ( e1, e3 ) | = | ( e1, u3 - c1e1 - c2e2 ) |
| = | ( e1, u3 ) - c1( e1, e1 ) - c2( e1, e2 ) | |
| = | ( e1, u3 ) - c1||e1||2 = 0 より |
c1 = ( e1, u3 ) / ||e1||2
| ( e2, e3 ) | = | ( e2, u3 - c1e1 - c2e2 ) |
| = | ( e2, u3 ) - c1( e2, e1 ) - c2( e2, e2 ) | |
| = | ( e2, u3 ) - c2||e2||2 = 0 より |
c2 = ( e2, u3 ) / ||e2||2
よって、e3 = u3 - ( ( e1, u3 ) / ||e1||2 )e1 - ( ( e2, u3 ) / ||e2||2 )e2
4. 以下同様にして、en までの直交基底が得られたとして、en+1 = un+1 - c1e1 - c2e2 - ... - cnen と置いて、e1, e2, ... en と en+1 が直交するように c1, c2, ... cn を決める。
| ( ei, en+1 ) | = | ( ei, un+1 - c1e1 - c2e2 - ... - cnen ) |
| = | ( ei, un+1 ) - c1( ei, e1 ) - c2( ei, e2 ) - ... - cn( ei, en ) | |
| = | ( ei, un+1 ) - ci||ei||2 = 0 より |
ci = ( ei, un+1 ) / ||ei||2 (i = 1, 2, ... n)
よって、en+1 = un+1 - Σi{1→n}( { ( ei, un+1 ) / ||ei||2 }ei )
例として、平面ベクトル u1 = ( 1, 1 ) と u2 = ( 2, 3 ) から上記方法で直交基底を作ります。
1. e1 = ( 1, 1 ) とする。
2. e2 = u2 - c1e1 として、e1と e2 が直交するように c1 を定めると、
| ( e1, e2 ) | = | ( e1, u2 - c1e1 ) |
| = | ( e1, u2 ) - c1( e1, e1 ) | |
| = | ( 1・2 + 1・3 ) - c1( 1・1 + 1・1 ) = 0 より c1 = 5/2 |
よって、e2 = u2 - ( 5/2 )e1 = ( -1/2, 1/2 )
このような直交基底の作成方法を「グラム・シュミットの直交化 ( Gram-Schmidt Orthogonalization )」と言います。得られた基底に対し、それぞれのノルムで割れば、正規直交基底が得られることになります。
e1 に対して e2 が直交するように c1 の値を決めたとき、それぞれのベクトルは次の図のような形になります。
二本の直交ベクトル e1, e2 から成る平面に e3 が直交するように c1 と c2 の値を決めたとき、それぞれのベクトルは次の図のようになります。
次元が大きくなると、図形で正確に表現することはできなくなりますが、すでに作成された直交基底からなる超平面に対して ui から垂線を下ろし、それを新たな直交基底とするのをイメージすると、上記操作の内容が理解できるのではないかと思います。ui が超平面上にある場合、計算によって得られる ei は 0 になります。つまり、線形従属であったことを意味するので、その場合は ui を除外して操作を続けることになります。その結果、線形従属なベクトルが存在する場合は、得られる直交基底は最初のベクトルの数より少なくなります。元のベクトルが基底であった場合は線形独立であることが保証されているので、数は必ず一致することになります。
グラム・シュミットの直交化を行うサンプル・プログラムを以下に示します。
/* GramSchmidt : グラム・シュミットの直交化によって行列 a の列ベクトルを直交基底に変換する 戻り値として行列 a のランクを返す。 e : ノルムがゼロであるかどうかを判定するためのしきい値 */ template< class T > typename SquareMatrix< T >::size_type GramSchmidt( SquareMatrix< T >* a, T e ) { typedef typename SquareMatrix< T >::const_iterator const_iterator; // 行列用定数反復子の型 typedef typename SquareMatrix< T >::size_type size_type; // 行列のサイズの型 assert( a != 0 && e >= 0 ); size_type rank = 0; // ランク size_type sz = a->size(); // 行列のサイズ std::vector< T > norm( sz ); // 列ベクトルのノルム const_iterator col = a->column( 0 ); norm[0] = std::inner_product( col, col.end(), col, T() ); if ( norm[0] != 0 ) ++rank; for ( size_type n = 1 ; n < sz ; ++n ) { const_iterator col1 = a->column( n ); /* 内積の計算 */ std::vector< T > inPro( n ); // 内積 for ( size_type c = 0 ; c < n ; ++c ) { const_iterator col2 = a->column( c ); inPro[c] = std::inner_product( col1, col1.end(), col2, T() ); } /* 係数を計算して直交基底を求める */ for ( size_type c = 0 ; c < n ; ++c ) { if ( norm[c] == 0 ) continue; for ( size_type r = 0 ; r < sz ; ++r ) (*a)[r][n] -= inPro[c] * (*a)[r][c] / norm[c]; } /* ノルムの計算 */ const_iterator col = a->column( n ); norm[n] = std::inner_product( col, col.end(), col, T() ); if ( norm[n] >= e ) ++rank; } return( rank ); }
処理の流れは先述したとおりで、内積とノルムを求めて係数を計算して直交基底を得ます。内積やノルムの計算には、STL ( Standard Template Library ) で提供されている関数 inner_product を利用し、最初の二つの引数で一つめのベクトルの開始と末尾の次の位置を、次の引数で二つめのベクトルの開始位置のみを、最後に初期値を指定して処理を行います。ノルムは各ベクトルに対して一度計算すればよいので、配列に保持しておくようにします。また、計算後に値がゼロかどうかをチェックして、それを元にランクを求めています。
ところで、グラム・シュミットの直交化で示した直交基底の計算式を変形することで、以下の式が得られます。
u1 = e1
u2 = ( ( e1, u2 ) / ||e1||2 )e1 + e2
u3 = ( ( e1, u3 ) / ||e1||2 )e1 + ( ( e2, u3 ) / ||e2||2 )e2 + e3
:
un = Σi{1→n-1}( { ( ei, un ) / ||ei||2 }ei ) + en
この形は、連立方程式をガウスの消去法で解く場合にできる前進消去の結果によく似た形をしています。実際、この式を行列を使って次のように表すことができます。
| ( u1 u2 ... un ) = ( e1 e2 ... en ) | | | 1, | ( e1, u2 ) / ||e1||2, | ( e1, u3 ) / ||e1||2, | ... | ( e1, un ) / ||e1||2 | | |
| | | 0, | 1, | ( e2, u3 ) / ||e2||2, | ... | ( e2, un ) / ||e2||2 | | | |
| | | 0, | 0, | 1, | ... | ( e3, un ) / ||e3||2 | | | |
| | | : | : | : | : | | | ||
| | | 0, | 0, | 0, | ... | 1 | | |
上式は、A = ( u1 u2 ... un )、Q = ( e1 e2 ... en )、上三角行列の部分を R と表して、A = QR の形で表現することができます。Q は直交基底を列ベクトルとする行列であり、特に各基底が単位ベクトル ( つまり正規直交基底 ) ならば、この行列を「直交行列 ( Orthogonal Matrix )」と言います。行列を直交行列と上三角行列に分解する手法を「QR 分解 ( QR decomposition )」と言い、グラム・シュミットの直交化もこの手法の一つということになります。
ちなみに、上三角行列は LU 法において U で表されていましたが、これは Upper Triangular Matrix の略になります。QR 分解ではなぜか、右三角行列 ( Right Triangular Matrix )の略語で R と表されるようです。
直交行列には、いくつかの特別な性質があります。そのことを説明する前に、「転置行列 ( Transposed Matrix )」の紹介をしておきます。
簡単にいうと、転置行列とは、列方向に並んだ要素を行方向に並べ替えた行列のことになります。
| A | = | | | a11, | a12, | ... | a1n | | | AT | = | | | a11, | a21, | ... | an1 | | |
| | | a21, | a22, | ... | a2n | | | | | a12, | a22, | ... | an2 | | | ||||
| | | : | : | ... | : | | | | | : | : | ... | : | | | ||||
| | | an1, | an2, | ... | ann | | | | | a1n, | a2n, | ... | ann | | | ||||
n 行 n 列の任意の正方行列 A と、任意の n 次元ベクトル x = ( x1, x2, ... xn )、y = ( y1, y2, ... yn ) に関して、転置行列を使って次の関係式を導くことができます。
| ( x, ATy ) | = | ( x, ( Σi{1→n}( ai1yi ), Σi{1→n}( ai2yi ), ... Σi{1→n}( ainyi ) ) |
| = | x1( Σi{1→n}( ai1yi ) ) + x2( Σi{1→n}( ai2yi ) ) + ... + xn( Σi{1→n}( ainyi ) ) | |
| = | x1( a11y1 + a21y2 + ... an1yn ) + x2( a12y1 + a22y2 + ... an2yn ) + ... + xn( a1ny1 + a2ny2 + ... annyn ) | |
| = | y1( a11x1 + a12x2 + ... a1nxn ) + y2( a21x1 + a22x2 + ... a2nxn ) + ... + yn( an1x1 + an2x2 + ... annxn ) | |
| = | y1( Σi{1→n}( a1ixi ) ) + y2( Σi{1→n}( a2ixi ) ) + ... + yn( Σi{1→n}( anixi ) ) | |
| = | ( ( Σi{1→n}( a1ixi ), Σi{1→n}( a2ixi ), ... Σi{1→n}( anixi ) ), y ) | |
| = | ( Ax, y ) |
直交行列の転置行列は、行ベクトルが正規直交基底になります。直交行列 Q = ( e1 e2 ... en ) とその転置行列 QT = ( e1T e2T ... enT )T との積を計算すると、
| QTQ | = | | | e1T | | | | | e1 | e2 | ... | en | | = | | | (e1,e1), | (e1,e2), | ... | (e1,en) | | |
| | | e2T | | | | | (e2,e1), | (e2,e2), | ... | (e2,en) | | | ||||||||
| | | : | | | | | : | : | : | | | |||||||||
| | | enT | | | | | (en,e1), | (en,e2), | ... | (en,en) | | | ||||||||
しかし、( ei, ej ) は i ≠ j のとき 0、i = j のとき 1 になるので、右辺の行列は単位行列となります。従って、
つまり、直交行列の転置行列は、同時に逆行列でもあるということになります。任意のベクトルを直交行列で変換した Qx, Qy に対して内積を計算すると、
この結果から、
となるので、直交行列による変換によってベクトルは大きさを変えないということになります。
( Qx, Qy ) = ||Qx|| ||Qy||cos θ'
( x, y ) = ||x|| ||y||cos θ
より、二式の左辺どうしは等しく、||Qx|| = ||x|| かつ ||Qy|| = ||y|| なので、θ' = θ となり、直交行列による変換に対して二つのベクトルの成す角度も変化はしません。つまり、直交行列による変換は「回転」と「鏡映(鏡に写すように反転した変換)」の組み合わせになります。
QTQ = E から、直交行列には逆行列が必ず存在します。行列 A の固有ベクトルが正規直交基底になるとき、固有ベクトルを列ベクトル(行ベクトルでも可)とする行列は直交行列 ( Q ) となり、固有値を対角成分に持つ対角行列 ( D ) との間に次の関係式が成り立ちます。
固有ベクトルが正規直交基底となるような行列 A に対して、二つの異なる固有値を λ1, λ2、対応する固有ベクトルを u1, u2 としたとき、
となるので、第一式の両辺と u2 の内積、u1 と第二式の両辺の内積を取ると、
両辺を差し引くと
ここで、u1 と u2 が直交している場合、右辺は 0 になるので、次の関係式が得られます。
左辺を変形すると、
よって、A = AT であれば、上式が任意の固有ベクトル u1, u2 に対して成り立ち、全ての固有ベクトルは直交することになります。このような行列を「対称行列 ( Symmetric Matrix )」と言います。対称行列は、行と列をひっくり返しても変化しないことになるため、r 行 c 列の要素を arc としたときに arc = acr が成り立つことになります。これはちょうど、対角成分を軸として対称となっていることを意味します。
以上のことから、対称行列の固有ベクトルからなる行列は必ず直交行列になります。対称行列を、固有ベクトルからなる直交行列と、固有値を対角成分に持つ対角行列に分解することを「固有値分解 ( Eigenvalue Decomposition )」と呼び、次の式で表されます。
対称行列のこの性質は様々な技術に応用されているため、固有値を求めるアルゴリズムもたくさん考案されています。以下、対称行列の固有値を求める方法をいくつか紹介していきます。
「ヤコビ法」の名前は、連立方程式の解法にも登場しましたが、こちらは対称行列の固有値を求めるためのアルゴリズムです。簡単な例として、2 行 2 列の対称行列を使って説明します。
| | | p, | q | | | |
| A = | | | q, | r | | |
対称行列 A に対し、任意の直交行列 Q による相似変換を行なった結果は QTAQ となり、固有値は変化しません。そこで、上記の行列に、2 行 2 列の下記回転行列を使って相似変換を行なってみます。
| | | cosθ, | sinθ | | | | | c, | s | | | |
| Q = | | | -sinθ, | cosθ | | = | | | -s, | c | | |
相似変換を行なうと、
| | | c, | -s | || | p, | q | || | c, | s | | | ||
| QTAQ | = | | | s, | c | || | q, | r | || | -s, | c | | |
| | | pc - qs, | qc - rs | || | c, | s | | | ||
| = | | | ps + qc, | qs + rc | || | -s, | c | | | |
| | | pc2 - 2qsc + rs2, | q( c2 - s2 ) + ( p - r )sc | | | ||
| = | | | q( c2 - s2 ) + ( p - r )sc, | rc2 + 2qsc + ps2 | | | |
非対角成分は
になり、
cos2θ = cos2θ - sin2θ
sin2θ = 2sinθcosθ
から、
この値が 0 になるためには、( p - r ) / 2 = α, -q = β として
が成り立つ必要があります。
なので、この式に αsin2θ = βcos2θ を代入すると、
よって、cos2θ ≥ 0 のとき、
但し、α2 + β2 ≠ 0 とします。この値を γ とした時、
| cos2θ | = | cos2θ - sin2θ |
| = | cos2θ - ( 1 - cos2θ ) | |
| = | 2cos2θ - 1 | |
| = | ( 1 - sin2θ ) - sin2θ | |
| = | 1 - 2sin2θ |
より、
ここで、sign(αβ) は αβ の符号を表します。cosθ を正の数としたため、sinθ は αβ の符号によって正負が決まります。このような θ が得られれば、固有値を次のように決めることができます。
ところで、α2 + β2 = 0 のとき、α = β = 0 なので、p = r かつ q = 0 になります。これは、対角成分が等しく、非対角成分が 0 の行列を意味しています。この時、固有値は重解となり、その値は p そのものになります。すでに非対角成分が 0 ならば、わざわざ処理をしなくても固有値はすでに求められているため、このような場合は処理することを考慮する必要はなく、α2 + β2 = 0 の場合は無視できます。
行列数が 2 より大きな対称行列に対しても、同じ手法を使って非対角成分を 0 にすることができます。この時に利用する回転行列は次のようなものです。
| (i) | (j) | ||||||||||
| | | 1, | 0, | ... | 0, | ... | 0, | ... | 0, | 0 | | | |
| | | 0, | 1, | ... | 0, | ... | 0, | ... | 0, | 0 | | | |
| | | : | : | : | : | : | : | | | ||||
| (i) | | | 0, | 0, | ... | cosθ, | ... | sinθ, | ... | 0, | 0 | | |
| | | : | : | : | : | : | : | | | ||||
| (j) | | | 0, | 0, | ... | -sinθ, | ... | cosθ, | ... | 0, | 0 | | |
| | | : | : | : | : | : | : | | | ||||
| | | 0, | 0, | ... | 0, | ... | 0, | ... | 1, | 0 | | | |
| G(i,j,θ) = | | | 0, | 0, | ... | 0, | ... | 0, | ... | 0, | 1 | | |
この行列は直交行列であり、2 行 2 列の場合と同様に、相似変換によって i 行 j 列と j 行 i 列の要素を 0 にすることができます。この行列による相似変換を「ギブンス回転 ( Givens rotation )」と言います。
ギブンス回転で 0 にすることができる非対角要素は二つのみです。しかし、この操作を繰り返すことで、全ての非対角要素も 0 にすることができます。しかも、この操作を繰り返しても固有値が変化することはありません。一回の操作で次のような相似変換を行なったとします。
このとき、A1 と A の固有値は変化しません。A1 に対して、直交行列 Q2 を使って相似変換をした結果を A2 とすると、A1 と A2 は固有値が変わらないので、A2 と A の固有値も等しくなります。以下、同様の操作を繰り返したとき、k 回目の操作に対して以下の漸化式が得られます。
同様に、Ak-1 = Qk-1TAk-2Qk-1、Ak-2 = Qk-2TAk-3Qk-2 ... なので、上式は次のように展開できます。
この結果が対角行列になれば、固有値は求められたことになります。また、Q1...Qk-2Qk-1Qk が A の固有ベクトルからなる行列になります。繰り返し相似変換をすることによって固有値を求める方法をヤコビ法と言い、ギブンス回転は相似変換を行なうための手法であるということになります。
ギブンス回転によって処理を行なった結果、他の非対角成分の中で値が変化するものがあり、値を 0 にする二つの行列に並んだ要素がそれにあたります。n 行 n 列の大きさの対称行列において、r 行 c 列めの要素を arc とした時、i 行 j 列と j 行 i 列の要素をギブンス回転によって 0 にした場合に影響を受ける要素は ari, arj, aic, ajc ( 但し、r,c = 1,2, ... n ) になり、前側の転置行列 QT によって aic, ajc、後ろ側の Q によって ari, arj が変化します。ギブンス回転後の r 行 c 列めの要素を a'rc とした時、
但し、r,c≠i,j
で求めることができます。これ以外の要素はギブンス回転によって変化しませんが、それでもある要素をゼロにしたときに他の要素がゼロでなくなるような場合が発生するため、あまり効率がいいやり方とは言えなくなります ( この様子をモグラ叩きに例えた方がいるそうです )。
ヤコビ法による固有値算出のためのサンプル・プログラムを以下に示します。
/* GetMaxValue : 非対角成分の中で絶対値が最大の値を求める a : 対象の対称行列 maxR, maxC : 最大値を持った要素の行列番号を取得する変数へのポインタ */ template< class T > void GetMaxValue ( const SymmetricMatrix< T >& a, typename SymmetricMatrix< T >::size_type* maxR, typename SymmetricMatrix< T >::size_type* maxC ) { typedef typename SymmetricMatrix< T >::size_type size_type; // 行列のサイズに対する型 size_type sz = a.size(); // 行列のサイズ if ( sz == 1 ) { *maxR = *maxC = 0; return; } *maxR = 0; *maxC = 1; // 求める最大値を最初の非対角成分で初期化 T maxValue = std::abs( a[*maxR][*maxC] ); for ( size_type r = 0 ; r < sz ; ++r ) { for ( size_type c = r + 1 ; c < sz ; ++c ) { T t = std::abs( a[r][c] ); if ( maxValue < t ) { *maxR = r; *maxC = c; maxValue = t; } } } } /* GivensRotation_ST : ギブンス回転による相似変換(非対角成分のもぐら叩き) mat : 対象の行列へのポインタ i, j : 消去対称となる要素の行列番号 g : γ sin, cos : sinθ, cosθ sc : sinθcosθ */ template< class T > void GivensRotation_ST ( SymmetricMatrix< T >* mat, typename SymmetricMatrix< T >::size_type i, typename SymmetricMatrix< T >::size_type j, T g, T sin, T cos, T sc ) { typedef typename SymmetricMatrix< T >::size_type size_type; // 対角成分 (i,i),(j,j) T d1 = ( (*mat)[i][i] * ( 1 + g ) + (*mat)[j][j] * ( 1 - g ) ) / 2 - 2 * (*mat)[i][j] * sc; T d2 = ( (*mat)[j][j] * ( 1 + g ) + (*mat)[i][i] * ( 1 - g ) ) / 2 + 2 * (*mat)[i][j] * sc; // 非対角成分 (i,j),(j,i) T d3 = ( (*mat)[i][j] * g ) + ( (*mat)[i][i] - (*mat)[j][j] ) * sc; (*mat)[i][i] = d1; (*mat)[j][j] = d2; (*mat)[i][j] = (*mat)[j][i] = d3; // その他の非対角成分 for ( size_type r = 0 ; r < mat->size() ; ++r ) { if ( r == i || r == j ) continue; d1 = (*mat)[r][i] * cos - (*mat)[r][j] * sin; d2 = (*mat)[r][i] * sin + (*mat)[r][j] * cos; (*mat)[r][i] = d1; (*mat)[r][j] = d2; } } /* GivensRotationMul_R : ギブンス回転用行列の積の計算(右側から掛ける) eigen : 対象の行列へのポインタ i, j : 消去対象となる要素の行列番号 sin, cos : sinθ,cosθ */ template< class T > void GivensRotationMul_R ( SquareMatrix< T >* eigen, typename SquareMatrix< T >::size_type i, typename SquareMatrix< T >::size_type j, T sin, T cos ) { typedef typename SquareMatrix< T >::size_type size_type; for ( size_type r = 0 ; r < eigen->size() ; ++r ) { T d1 = (*eigen)[r][i] * cos - (*eigen)[r][j] * sin; T d2 = (*eigen)[r][i] * sin + (*eigen)[r][j] * cos; (*eigen)[r][i] = d1; (*eigen)[r][j] = d2; } } /* Jacobi : ヤコビ法による行列 mat の固有値算出 求めた固有値は対角成分として残る。 eigen 固有ベクトルを求めるための行列へのポインタ(NULLなら無視) e 収束したかを判定するためのしきい値 maxCnt 収束しなかった場合の最大計算回数 */ template< class T > void Jacobi( SymmetricMatrix< T >* mat, SquareMatrix< T >* eigen, T e, unsigned int maxCnt ) { assert( mat != 0 && e >= 0 ); typedef typename SymmetricMatrix< T >::size_type size_type; unsigned int cnt = 0; // 処理回数 if ( eigen != 0 ) { eigen->assign( mat->size() ); for ( size_type i = 0 ; i < mat->size() ; ++i ) (*eigen)[i][i] = 1; } while ( cnt < maxCnt ) { size_type i, j; GetMaxValue( *mat, &i, &j ); if ( std::abs( (*mat)[i][j] ) < e ) break; T a = ( (*mat)[i][i] - (*mat)[j][j] ) / 2; // α : i, j 番目の対角成分の差の半分 T b = (*mat)[i][j] * -1; // β : 非対角成分の符号を反転した数 T g = std::abs( a ) / std::sqrt( a * a + b * b ); // γ : |a| / d( a, b ) T sin = std::sqrt( ( 1 - g ) / 2 ); // sinθ T cos = std::sqrt( ( 1 + g ) / 2 ); // cosθ T sc = std::sqrt( 1 - g * g ) / 2; // sinθcosθ if ( a * b < 0 ) { // sign(αβ)のチェック sin *= -1; sc *= -1; } GivensRotation_ST( mat, i, j, g, sin, cos, sc ); // ギブンス回転による相似変換(非対角成分のもぐら叩き) // 固有ベクトルの計算 if ( eigen != 0 ) { if ( cnt == 0 ) { (*eigen)[i][i] = (*eigen)[j][j] = cos; (*eigen)[i][j] = sin; (*eigen)[j][i] = -sin; } else { GivensRotationMul_R( eigen, i, j, sin, cos ); } } ++cnt; } // 処理が最大処理回数を超えたら例外を投げる if ( cnt >= maxCnt ) throw ExceptionExcessLimit( maxCnt ); }
計算式をそのまま当てはめただけなので、難しい部分はないと思います。得られたギブンス回転を使った相似変換は givensRotation_ST で行い、ここで非対角成分をゼロにする処理を行なっています。また、固有ベクトルの計算のため、ギブンス回転用の行列を順次掛け合わせる処理を givensRotationMul_R で行なっています。
行列を表すクラスとして、対称行列用の SymmetricMatrix クラスと正方行列用の SquareMatrix を利用しています。これらのクラスの具体的な内容については省略していますが、mat[r][c] によって r 行 c 列の要素にアクセスすることができることだけ理解しておけばここでは充分です。なお、SymmetricMatrix クラスでは、対角成分を軸に対称であることを利用して、保持すべき行列の要素を半分程度に抑えることができます。また、そのようにすることで対称であることが保証されることになります。
二次元ベクトル x = ( x, y )T を、対称行列 A を使って、x とノルムが等しいベクトル x' = ( x', 0 )T に変換することを考えます ( この時、|x'| = ( x2 + y2 )1/2 とします )。原点を O、点( x, y )を P、点( x', 0 )を Q とした時、三角形 OPQ は二等辺三角形になるので、頂角の二等分線は底辺 PQ の垂線二等分線になります。ここで、
最後は、H(v) = E - 2vvT / ||v||2 としています。この行列を「ハウスホルダー行列 ( Householder Matrix )」と呼び、ハウスホルダー行列による線形変換を「ハウスホルダー変換 ( Householder Transformation )」または「鏡映変換」と言います。
x = ( 4, 3 )T を例として同じ処理を行なうと、x' = ( 5, 0 )T の場合は v = ( -1, 3 )T となって、
| H(v) | = | | | 1, | 0 | | | - 2/10 | | | -1 | | | | | -1, | 3 | | | |
| | | 0, | 1 | | | | | 3 | | | ||||||||
| = | | | 1, | 0 | | | - 1/5 | | | 1, | -3 | | | |||||
| | | 0, | 1 | | | | | -3, | 9 | | | |||||||
| = | | | 4/5, | 3/5 | | | ||||||||||
| | | 3/5, | -4/5 | | | |||||||||||
x' = ( -5, 0 )T の場合は v = ( 9, 3 )T なので、
| H(v) | = | | | 1, | 0 | | | - 2/90 | | | 9 | | | | | 9, | 3 | | | |
| | | 0, | 1 | | | | | 3 | | | ||||||||
| = | | | 1, | 0 | | | - 1/45 | | | 81, | 27 | | | |||||
| | | 0, | 1 | | | | | 27, | 9 | | | |||||||
| = | | | -4/5, | -3/5 | | | ||||||||||
| | | -3/5, | 4/5 | | | |||||||||||
実際に、x を H(v) で変換すると、x' となることが確認できます。
一般に、ノルムが等しい二つのベクトル x, y は、v = x - y を法線ベクトルとする原点に交わる超平面に対して鏡像関係にあります。従って、H(v) は鏡映変換を行うことから直交行列であることになります。n 次元ベクトル空間でのハウスホルダー行列は、u = v / ||v|| = ( u1, u2, ... un ) とした時、次のように表されます。
| H = | | | 1 - 2u12, | -2u1u2, | ... | -2u1un | | |
| | | -2u2u1, | 1 - 2u22, | ... | -2u2un | | | |
| | | : | : | ... | : | | | |
| | | -2unu1, | -2unu2, | ... | 1 - 2un2 | | |
i 列めと j 列めのベクトルの内積は、i ≠ j のとき
| -2uiuj( 1 - 2ui2 ) -2ujui( 1 - 2uj2 ) + 4uiujΣk{1→n ; k≠i,j}( uk2 ) | = | 4uiujΣk{1→n}( uk2 ) - 4uiuj |
| = | 4uiuj||u||2 - 4uiuj = 0 |
i = jのとき
| ( 1 - 2ui2 )2 + 4ui2Σk{1→n ; k≠i}( uk2 ) | = | 4ui2Σk{1→n}( uk2 ) - 4ui2 + 1 |
| = | 4ui2||u||2 - 4ui2 + 1 = 1 |
なので、各列ベクトルは正規直交基底となり、確かに直交行列であることが証明できます。
ハウスホルダー変換を使うと、ベクトルの任意の成分だけを残してあとは全て 0 にするようなことができるので、これを利用すると上三角行列への変換ができます。具体的には、一列目の列ベクトルから順番にハウスホルダー変換を行い、その際、処理を進めるに従ってハウスホルダー行列の行列数を一つずつ減らしていきます。こうすると、すでに変換が完了した列ベクトルを変化させることなく処理することができます。
具体的な例を以下に示します。
| A = | | | 1, | -5, | 3 | | |
| | | 2, | 1, | 1 | | | |
| | | 2, | 0, | 2 | | |
x1 = (1,2,2)T に対して、x'1 = (-3,0,0)T, v1 = (4,2,2)T
| H(v1) = 1/3 | | | -1, | -2, | -2 | | |
| | | -2, | 2, | -1 | | | |
| | | -2, | -1, | 2 | | |
| H(v1)A | = 1/3 | | | -1, | -2, | -2 | || | 1, | -5, | 3 | | | |
| | | -2, | 2, | -1 | || | 2, | 1, | 1 | | | |||
| | | -2, | -1, | 2 | || | 2, | 0, | 2 | | | |||
| = 1/3 | | | -9, | 3, | -9 | | | ||||||
| | | 0, | 12, | -6 | | | |||||||
| | | 0, | 9, | -3 | | | |||||||
| = | | | -3, | 1, | -3 | | | = A1 | |||||
| | | 0, | 4, | -2 | | | |||||||
| | | 0, | 3, | -1 | | | |||||||
x2 = (4,3)T に対して、x'2 = (-5,0)T, v2 = (9,3)T
| H(v2) = | | | 1, | 0, | 0 | | |
| | | 0, | -4/5, | -3/5 | | | |
| | | 0, | -3/5, | 4/5 | | |
| H(v2)A1 = | | | 1, | 0, | 0 | || | -3, | 1, | -3 | | | |
| | | 0, | -4/5, | -3/5 | || | 0, | 4, | -2 | | | ||
| | | 0, | -3/5, | 4/5 | || | 0, | 3, | -1 | | | ||
| = | | | -3, | 1, | -3 | | | = R | ||||
| | | 0, | -5, | 11/5 | | | ||||||
| | | 0, | 0, | 2/5 | | | ||||||
H(v1)A = A1, H(v2)A1 = R より H(v2)H(v1)A = R になります。H(v2) と H(v1) はどちらも直交行列であり、その積も直交行列となることから、H(v2)H(v1) = Q とすると QA = R の形になり、両辺の左側から QT ( = Q-1 ) を掛けることで
つまり、ハウスホルダー変換によって、グラム・シュミットの直交化と同様に QR 分解を行なうことができます。
ハウスホルダー変換と、それを利用した QR 分解を行なうためのサンプル・プログラムを以下に示します。
/* CreateVec : データ列 x の鏡映変換(ハウスホルダー変換)を行い、変換後のベクトルのノルムの平方を返す ベクトル x とノルムが等しく、第一成分以外がゼロになるようなベクトル x' を求め、 v = x - x' に変換する(ハウスホルダー変換)。ノルム ||x|| ( = ||x'|| ) を返り値として返す。 */ template< class T > T CreateVec( std::vector< T >* x ) { T v = std::sqrt( std::inner_product( x->begin(), x->end(), x->begin(), T() ) ); // vec のノルム if ( x->front() > 0 ) x->front() += v; else x->front() -= v; return( std::inner_product( x->begin(), x->end(), x->begin(), T() ) ); } /* MultHouseholder : 行列 mat にハウスホルダー行列を掛ける H(v) = E - 2(v)(vT) / ||v|| E : 単位行列 v : 鏡映変換したベクトル , vT : vの転置ベクトル , ||v|| : vのノルム 行列 A に対し、H(v)・A を計算 対象範囲は col 以降の行とする(すでに変換した行は不要) norm は v のノルムである。 */ template< class T > void MultHouseholder ( SquareMatrix< T >* mat, typename SquareMatrix< T >::size_type col, const std::vector< T >& v, T norm ) { typedef typename SquareMatrix< T >::size_type size_type; typedef typename SquareMatrix< T >::const_iterator const_iterator; for ( size_type c = 0 ; c < mat->cols() ; ++c ) { // 計算対象の列ベクトルの要素をバッファにコピー const_iterator colIt = mat->column( c, col ); std::vector< T > buff( colIt, colIt.end() ); // すでに鏡映変換した行は処理不要 for ( size_type r = col ; r < mat->rows() ; ++r ) { T d = 0; for ( typename std::vector< T >::size_type i = 0 ; i < v.size() ; ++i ) d -= v[i] * buff[i]; d *= 2 * v[r - col] / norm; (*mat)[r][c] = buff[r - col] + d; } } } /* Householder_QR : ハウスホルダー法による行列 r の QR 変換 r 変換する正方行列(結果は上三角行列になる) q 直交行列を得るための行列(NULLならば無視) */ template< class T > void Householder_QR( SquareMatrix< T >* r, SquareMatrix< T >* q ) { assert( r != 0 ); typedef typename SquareMatrix< T >::size_type size_type; typedef typename SquareMatrix< T >::const_iterator const_iterator; if ( q != 0 ) q->assign( r->rows() ); for ( size_type c = 0 ; c < r->cols() - 1 ; ++c ) { // 対象の列ベクトルを鏡映変換 const_iterator colIt = r->column( c, c ); std::vector< T > v( colIt, colIt.end() ); T norm = CreateVec( &v ); MultHouseholder( r, c, v, norm ); if ( q == 0 ) continue; // 直交行列の計算 if ( c == 0 ) { for ( size_type j = 0 ; j < r->cols() ; ++j ) { (*q)[j][j] = 1 - 2 * v[j] * v[j] / norm; for ( size_type i = j + 1 ; i < r->rows() ; ++i ) (*q)[j][i] = (*q)[i][j] = - 2 * v[j] * v[i] / norm; } } else { MultHouseholder( q, c, v, norm ); } } if ( q != 0 ) q->transpose(); // 直交行列の転置 }
鏡映変換は CreateVecで行なっています。入力したベクトル x に対して、ノルムが等しく第一軸に沿うベクトル ( x'とします ) を求め、x - x' を計算して x にその要素を代入します。内容は非常にシンプルで、x のノルムを計算して、第一成分から加算または減算を行なうだけです。第一軸と沿うベクトルとの差を計算するので、第一成分以外の要素は変化しません。そのため、他の要素に対しては計算不要となります。第一成分に対してノルムを足すのか、それとも引くのかについては「どちらでもよい」ことになります。第一軸に沿うベクトルは、正負の方向それぞれに対して二つ存在するため、変換も二種類あることになります ( 前に示した計算例でも、二種類の変換を示しています )。しかし、変換後のベクトルに対するノルムが大きい方が、誤差を小さくすることができるため、x の第一要素が正ならば加算、負ならば減算するのが通常のやり方になります。最後に、求めたベクトルのノルムを計算し、その値を戻り値としています。
ハウスホルダー変換の要となる処理が MultHouseholder で、ここでハウスホルダー行列との積を算出しています。ベクトル v はすでに鏡映変換を行なったベクトルで、norm が v のノルムになります。計算処理は一列目からなのに対し、各要素の計算は col で指定した行から行ないます ( 理由は後述 )。最初に対象列ベクトルの要素をバッファにコピーして、あとはハウスホルダー行列の対象行ベクトルとの内積を順次計算するだけです。なお、ハウスホルダー行列の要素はベクトル v の要素から計算しているので、行列そのものは変数として持っていません。
列ベクトルのバッファへのコピーは、最初に正方行列 mat の列ベクトルの反復子 colIt をメンバ関数 column で取得して、colIt ( 先頭 ) から colIt.end() ( 末尾の次 ) までの範囲を指定して buff にコピーする流れになっています。column の第一引数は列番号を表し、第二引数は行番号 ( 何番目の要素からを先頭とするか ) を表しています。
c 列めの処理は、c 行め ( 対角成分 ) より下側の要素をゼロにするだけでよいので、ハウスホルダー行列は次のような形になります ( 前に示した例でもこの形の行列を使っています )。
| | | 1, | 0, | ... | 0, | 0, | ... | 0 | | |
| | | 0, | 1, | ... | 0, | 0, | ... | 0 | | |
| | | : | : | ... | : | : | ... | : | | |
| | | : | : | ... | uc,c, | uc,c+1, | ... | uc,n | | |
| | | : | : | ... | uc+1,c, | uc+1,c+1, | ... | uc+1,n | | |
| | | : | : | ... | : | : | ... | : | | |
| | | 0, | 0, | ... | un,c, | un,c+1, | ... | un,n | | |
ハウスホルダー変換をおこなう行列がすでに c 列めまで処理を行なって対角成分より下側がゼロである場合、上記行列との積を計算しても、c 列より左側及び c 行より上側の要素は変化しないので、計算処理は不要になります。よって、上三角行列を求めるためだけに利用するのであれば、行だけでなく列に対しても、col で指定した位置から計算を始めてよいことになります。しかし、MultHouseholder は直交行列を求める場合にも利用しており、その時は第一列めから計算をしないと正しい結果が得られません。
qr は、ハウスホルダー変換を利用して QR 分解を行うプログラムです。今までのサブルーチンを利用しているだけですが、直交行列の計算を行なっているところで若干補足すると、求めた直交行列と r の積から上三角行列が得られるので、逆行列を求めるために最後に転置を行う必要があります。
対称行列に対し、ハウスホルダー行列を使って相似変換を行うと、完全に対角化する一歩手前の状態まで変換することができます。n - 1 次元の列ベクトル ( a21, a31, ... an1 )T に対するハウスホルダー行列を H' とし、H' の一列目と一行目に単位ベクトル (1, 0, ... 0 )T を追加して、n 行 n 列の行列 H を作ったとき、
| HAHT | = | | | 1, | 0, | 0, | ... | 0 | || | a11, | a12, | a13, | ... | a1n | || | 1, | 0, | 0, | ... | 0 | | |
| | | 0, | u22, | u23, | ... | u2n | || | a21, | a22, | a23, | ... | a2n | || | 0, | u22, | u32, | ... | un2 | | | ||
| | | 0, | u32, | u33, | ... | u3n | || | a31, | a32, | a33, | ... | a3n | || | 0, | u23, | u33, | ... | un3 | | | ||
| | | : | : | : | ... | : | || | : | : | : | ... | : | || | : | : | : | ... | : | | | ||
| | | 0, | un2, | un3, | ... | unn | || | an1, | an2, | an3, | ... | ann | || | 0, | u2n, | u3n, | ... | unn | | | ||
積 HA について、r 行 c 列の成分を a'rc とすると、
a'rc = Σi{2→n}( uriaic ) ( r ≥ 2 )
a'rc = arc ( r = 1 )
さらに HT を掛けたとき、r 行 c 列の成分を a''rc とすると、
| a''rc | = | Σj{2→n}( a'rjujc ) |
| = | Σj{2→n}( ujcΣi{2→n}( uriaij ) ) | |
| = | Σj{2→n}( urjΣi{2→n}( uicaji ) ) |
ここで、H と A はともに対称行列なので、urj = ujr, uic = uci, aji = aij が成り立ち、
| a''rc | = | Σj{2→n}( ujrΣi{2→n}( uciaij ) ) |
| = | Σj{2→n}( a'cjujr ) | |
| = | a''cr |
よって、対称行列をハウスホルダー行列によって相似変換しても、結果は対称行列の形になります ( 補足 2 )。ハウスホルダー変換によって、一列目の列ベクトルに対して、三行め以降の要素はゼロになります。従って、一行目の行ベクトルに対しても、三列め以降の要素はゼロです。この操作を二行/二列め以降に対しても続けると、対角成分とその両隣の要素以外が全てゼロとなる行列を作ることができます。このような行列を「三重対角行列 ( Tridiagonal Matrix )」と言い、そのような行列への変換法を「三重対角化 ( Tridiagonalization )」と言います。三重対角行列から QR 分解を効率よく行う方法があります。
まずは三重対角行列を上三角行列にします。そのためには、対角成分よりすぐ下側にある要素だけをゼロにすればよいことになるので、前に示したギブンス回転を利用することにします。しかし、今回は相似変換ではなく、左側からのみ掛けるようにします。
| G(1,2,θ1)A | = | | | cosθ1, | sinθ1, | 0, | ... | 0 | || | a11, | a12, | 0, | ... | 0 | | |
| | | -sinθ1, | cosθ1, | 0, | ... | 0 | || | a21, | a22, | a23, | ... | 0 | | | ||
| | | 0, | 0, | 1, | ... | 0 | || | 0, | a32, | a33, | ... | 0 | | | ||
| | | : | : | : | ... | : | || | : | : | : | ... | : | | | ||
| | | 0, | 0, | 0, | ... | 1 | || | 0, | 0, | 0, | ... | ann | | | ||
| = | | | a11cosθ1 + a21sinθ1, | a12cosθ1 + a22sinθ1, | a23sinθ1, | ... | 0 | | | |
| | | -a11sinθ1 + a21cosθ1, | -a12sinθ1 + a22cosθ1, | a23cosθ1, | ... | 0 | | | ||
| | | 0, | a32, | a33, | ... | 0 | | | ||
| | | : | : | : | ... | : | | | ||
| | | 0, | 0, | 0, | ... | ann | | | ||
| = | | | a'11, | a'12, | a'13, | ... | 0 | | | |
| | | 0, | a'22, | a'23, | ... | 0 | | | ||
| | | 0, | a32, | a33, | ... | 0 | | | ||
| | | : | : | : | ... | : | | | ||
| | | 0, | 0, | 0, | ... | ann | | | ||
上記は、二行一列めの成分をゼロにするための処理を行なったときの様子を表しています。二行一列めの成分をゼロにするには、
となるように θ1 の値を取る必要があります。このとき、斜辺の長さは ( a212 + a112 )1/2 になるので、三角比から、sinθ1 と cosθ1 の値はそれぞれ
sinθ1 = a21 / ( a212 + a112 )1/2
cosθ1 = a11 / ( a212 + a112 )1/2
と計算できます。これらを使えば、変化した他の成分も計算を行なうことができます。上記では G(1,2,θ1) を使いましたが、次に三行二列めの成分をゼロにするためには G(2,3,θ2) を、以下、i + 1 行 i 列めの成分をゼロにするためには G( i, i+1, θi ) を掛ければよいことになります。
ギブンス回転だけを使っても QR 分解は可能で、左下側の成分から順番に右下の方向に進むように、ギブンス回転によって成分をゼロにすれば上三角行列を作ることができます ( an,1 → an-1,1 → an,2 → an-2,1 → an-1,2 → an-2,3 → ... )。しかし三重対角行に対する処理では、計算しなければならない成分は限られるので、その分高速な処理が期待できます。
今まで QR 分解を行なうための手法をいくつか紹介してきましたが、これは相似変換ではないので、Q と R のいずれも元の行列の固有値とは一致しなくなります。この手法だけでは固有値を求めることはできないので、もうひと工夫する必要があります。
行列 A を Q と R に分解したとします。
両辺の左側から QT を掛けると、
Q と R をひっくり返して掛け合わせた積を A' とします。
これに R = QTA を代入すると、
これは相似変換になるので、何回繰り返しても、A と A' の固有値は等しくなります。よって、処理を k 回行なったとき、行列 A が Ak に変換されたとすると、以下の漸化式が成り立ちます。
Ak = QkRk
| Ak+1 | = | RkQk |
| = | QkTAkQk |
上記操作を繰り返すことによって、Ak を上三角行列にすることができれば、上三角行列の対角成分はその行列の固有値に等しいので ( 補足 3 )、元の行列 A の固有値も求められたことになります。
Ak を QR 分解しても、Ak+1 を計算するとゼロにした成分は再びゼロでない値になります。しかし、前回よりはゼロに近い値になるので、やがてはゼロに収束することになります。具体的には、左下側の成分からゼロに収束し、対角成分のうち右下から順に真の固有値へ近づいていきます。
以上、三重対角行列化から QR 法までの具体的な処理の手順を以下にまとめます。
以下に、ハウスホルダー行列を使って三重対角行列を作成し、そこから QR 法によって上三角行列へ変換するためのサンプル・プログラムを示します。
/* Householder_ST : ハウスホルダー行列による行列 mat の相似変換 v は鏡映変換したベクトルで、ハウスホルダー行列の要素となる。 対象範囲は col 以降の行とする(すでに変換した行は不要) norm は v のノルムである。 */ template< class T > void Householder_ST ( SquareMatrix< T >* mat, typename SquareMatrix< T >::size_type col, const std::vector< T >& v, T norm ) { typedef typename SquareMatrix< T >::size_type size_type; SquareMatrix< T > buff( mat->size() ); /* 左側からの乗算(結果をbuffへ) */ // col行より上側の要素は変化しない for ( size_type r = 0 ; r < col ; ++r ) for ( size_type c = 0 ; c < mat->size() ; ++c ) buff[r][c] = (*mat)[r][c]; for ( size_type r = col ; r < mat->size() ; ++r ) { for ( size_type c = 0 ; c < mat->size() ; ++c ) { for ( size_type i = 0 ; i < v.size() ; ++i ) buff[r][c] -= v[i] * (*mat)[i + col][c]; buff[r][c] *= 2 * v[r - col] / norm; buff[r][c] += (*mat)[r][c]; } } /* 右側からの乗算(結果をmatへ) */ for ( size_type r = 0 ; r < mat->size() ; ++r ) { for ( size_type c = 0 ; c < col ; ++c ) (*mat)[r][c] = buff[r][c]; for ( size_type c = col ; c < mat->size() ; ++c ) { (*mat)[r][c] = 0; for ( size_type i = 0 ; i < v.size() ; ++i ) (*mat)[r][c] -= v[i] * buff[r][i + col]; (*mat)[r][c] *= 2 * v[c - col] / norm; (*mat)[r][c] += buff[r][c]; } } } /* Householder_TD : ハウスホルダー法による行列 r の三重対角行列への変換 q は直交行列を得るための行列 ( H(v)の積 ) */ template< class T > void Householder_TD ( SquareMatrix< T >* r, SquareMatrix< T >* q ) { assert( r != 0 ); typedef typename SquareMatrix< T >::size_type size_type; typedef typename SquareMatrix< T >::const_iterator const_iterator; if ( q != 0 ) { q->assign( r->size() ); for ( size_type i = 0 ; i < r->size() ; ++i ) (*q)[i][i] = 1; } if ( r->size() < 3 ) return; for ( size_type c = 0 ; c < r->size() - 2 ; ++c ) { // 対象の列ベクトルを鏡映変換 const_iterator colIt = r->column( c, c + 1 ); std::vector< T > v( colIt, colIt.end() ); T norm = CreateVec( &v ); // ハウスホルダー行列による相似変換 Householder_ST( r, c + 1, v, norm ); // 直交行列の計算 if ( q == 0 ) continue; if ( c == 0 ) { for ( size_type j = 0 ; j < r->size() - 1 ; ++j ) { (*q)[j + 1][j + 1] = 1 - 2 * v[j] * v[j] / norm; for ( size_type i = j + 1 ; i < r->size() - 1 ; ++i ) (*q)[j + 1][i + 1] = (*q)[i + 1][j + 1] = - 2 * v[j] * v[i] / norm; } } else { MultHouseholder( q, c + 1, v, norm ); } } } /* Householder_GR : ギブンス回転による三重対角行列 r の上三角行列化 q は直交行列( G(i,j,θ)の積 )、sz は処理範囲(行列数)をそれぞれ表す。 */ template< class T > void Householder_GR ( SquareMatrix< T >* r, SquareMatrix< T >* q, typename SquareMatrix< T >::size_type sz ) { assert( r != 0 ); typedef typename SquareMatrix< T >::size_type size_type; if ( q != 0 ) { q->assign( r->size() ); for ( size_type i = 0 ; i < r->size() ; ++i ) (*q)[i][i] = 1; } if ( r->size() < 2 ) return; for ( size_type i = 0 ; i < sz ; ++i ) { // 対角成分の下の成分がゼロなら何も処理しない(処理不要) if ( (*r)[i + 1][i] == 0 ) continue; T d = std::sqrt( std::pow( (*r)[i][i], 2.0 ) + std::pow( (*r)[i + 1][i], 2.0 ) ); T sin = (*r)[i + 1][i] / d; T cos = (*r)[i][i] / d; // ギブンス回転により r[i+1][i]をゼロにする for ( size_type j = 0 ; j < 2 ; ++j ) { T d1 = (*r)[i][i + j]; T d2 = (*r)[i + 1][i + j]; (*r)[i][i + j] = d1 * cos + d2 * sin; (*r)[i + 1][i + j] = -d1 * sin + d2 * cos; } if ( i + 2 < r->size() ) { d = (*r)[i + 1][i + 2]; (*r)[i][i + 2] = d * sin; (*r)[i + 1][i + 2] = d * cos; } // 直交行列の計算 if ( q == 0 ) continue; if ( i == 0 ) { (*q)[0][0] = (*q)[1][1] = cos; (*q)[0][1] = sin; (*q)[1][0] = -sin; } else { for ( size_type c = 0 ; c < r->size() ; ++c ) { T d1 = (*q)[i][c] * cos + (*q)[i + 1][c] * sin; T d2 = -(*q)[i][c] * sin + (*q)[i + 1][c] * cos; (*q)[i][c] = d1; (*q)[i + 1][c] = d2; } } } if ( q != 0 ) q->transpose(); // 直交行列の転値 } /* Householder_QR : 三重対角行列を作成して QR 変換により固有値・固有ベクトルを求める mat : 変換対象の対称行列 r : 変換後の上三角行列を格納する正方行列へのポインタ q : 変換後の直交行列を格納する正方行列へのポインタ e : 収束判定のためのしきい値 maxCnt : 収束しなかった場合の最大処理回数 */ template< class T > void Householder_QR ( const SymmetricMatrix< T >& mat, SquareMatrix< T >* r, SquareMatrix< T >* q, T e, unsigned int maxCnt ) { assert( &mat != 0 && r != 0 ); ErrLib::NNNum( e ); typedef typename SquareMatrix< T >::size_type size_type; mat.clone( r ); unsigned int cnt = 0; // 処理回数 Householder_TD( r, q ); if ( q != 0 ) q->transpose(); size_type sz = r->size() - 1; while ( cnt < maxCnt ) { SquareMatrix< T > qk; Householder_GR( r, &qk, sz ); *r *= qk; // RQを計算 if ( q != 0 ) *q *= qk; // 直交行列の計算 if ( std::abs( (*r)[sz][sz - 1] ) < e ) --sz; if ( sz == 0 ) break; ++cnt; } // 処理が最大処理回数を超えたら例外を投げる if ( cnt >= maxCnt ) throw ExceptionExcessLimit( maxCnt ); }
メイン・ルーチンは Householder_QR になります。最初に、Householder_TD を使って行列を三重対角行列へ変換します。Householder_TD の中では、一列めから順番に、ハウスホルダー行列を使って相似変換を行い、対角成分の下側と右側を残してあとはゼロに変換しています。この処理を Householder_ST が行ないます。
三重対角化が完了したら、ギブンス回転を使って上三角行列を作成していきます。この処理は Householder_GR が行なっています。右下側の対角成分に対し、その左側にある成分をチェックして、ゼロに近くなったら処理範囲を徐々に狭め、完全に上三角行列になったら処理完了です。
対角成分の左側にある成分がゼロに収束するに従い、対角成分との差が大きくなります。すると、ゼロにすべき要素がなかなかゼロに収束しにくくなります。そのため、固有値の中で絶対値が最小になる値の推測値をμとして、
とします。つまり、対角成分から μ を減算して、それから QR 分解することになります。このとき、
| A'k+1 | = | RkQk |
| = | QkTA'kQk | |
| = | QkT( Ak - μE )Qk | |
| = | QkTAkQk - μQkTEQk | |
| = | QkTAkQk - μE |
よって、
Ak+1 = QkTAkQk = A'k+1 + μE より
Ak+1 = RkQk + μE
従って、RkQk を計算したあとで対角成分に μ を加算すれば、漸化式は成り立ちます。ここで推測値 μ として、対象の行列 A の右下部分にある二行二列の行列に対する固有値を求め、その中から A の右下隅にある対角成分により近い方を利用することが多いようです。この方法を特に「ウィルキンソンの移動法 ( Wilkinson's Shift )」と呼ぶようです。
ウィルキンソンの移動法を利用した QR 変換のサンプル・プログラムを示します。
/* Householder_EV22 : 2x2行列の固有値を計算する double a,b,c,d : 行列の要素(それぞれ左上・右上・左下・右下) */ template< class T > T Householder_EV22( T a, T b, T c, T d ) { T d1 = a + d; T d2 = a * d - b * c; T a1 = ( d1 + std::sqrt( d1 * d1 - 4 * d2 ) ) / 2; T a2 = ( d1 - std::sqrt( d1 * d1 - 4 * d2 ) ) / 2; if ( std::abs( d - a1 ) < std::abs( d - a2 ) ) return( a1 ); else return( a2 ); } /* Householder_DoubleShiftQR : 原点シフト付きQR変換 mat : 変換対象の対称行列 r : 変換後の上三角行列を格納する正方行列へのポインタ q : 変換後の直交行列を格納する正方行列へのポインタ e : 収束判定のためのしきい値 maxCnt : 収束しなかった場合の最大処理回数 */ template< class T > void Householder_DoubleShiftQR ( const SymmetricMatrix< T >& mat, SquareMatrix< T >* r, SquareMatrix< T >* q, T e, unsigned int maxCnt ) { assert( &mat != 0 && r != 0 ); ErrLib::NNNum( e ); typedef typename SquareMatrix< T >::size_type size_type; mat.clone( r ); unsigned int cnt = 0; // 処理回数 Householder_TD( r, q ); if ( q != 0 ) q->transpose(); size_type sz = r->size() - 1; while ( cnt < maxCnt ) { SquareMatrix< T > qk; T u = Householder_EV22( (*r)[sz - 1][sz - 1], (*r)[sz - 1][sz], (*r)[sz][sz - 1], (*r)[sz][sz] ); for ( size_type i = 0 ; i <= sz ; ++i ) (*r)[i][i] -= u; Householder_GR( r, &qk, sz ); *r *= qk; // RQを計算 for ( size_type i = 0 ; i <= sz ; ++i ) (*r)[i][i] += u; if ( q != 0 ) *q *= qk; // 直交行列の計算 if ( std::abs( (*r)[sz][sz - 1] ) < e ) --sz; if ( sz == 0 ) break; ++cnt; } // 処理が最大処理回数を超えたら例外を投げる if ( cnt >= maxCnt ) throw ExceptionExcessLimit( maxCnt ); }
QR 変換を行う Householder_DoubleShiftQR は Householder_QR とほとんど同じ内容で、RQ を求める前後で、求めた μ を対角成分に加減算する処理が追加されただけです。μ を求める処理は Householder_EV22 が行い、ここでは二行二列の行列の固有値を求めています。二次方程式を解くだけなので、固有値は解の公式から簡単に求めることができます。解は二つ存在するので、右下隅の対角成分にあたる d との差を比較して、d により近い方を μ として利用します。
最後に、各サンプル・プログラムを使った固有値計算の処理量を調べてみます。「ヤコビ法」及び「ハウスホルダー + QR 法」とその改良版の「ウィルキンソンの移動法」による対称行列の固有値計算について、その処理回数 ( 収束までの回数 ) と処理時間を以下に示します。処理最大回数は 10000 回、収束判定用のしきい値を 1E-6 としました。それぞれの行列のサイズ・処理方法に対して 5 回試行し、その平均と標準偏差を示してあります。なお、固有値だけでなく固有ベクトルの算出も併せて行ったときの処理時間を計測しました。
| 行列のサイズ | ヤコビ法 | ハウスホルダー + QR 法 | ウィルキンソンの移動法 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 処理時間(sec) | 処理回数 | 成功した回数 | 処理時間(sec) | 処理回数 | 成功した回数 | 処理時間(sec) | 処理回数 | 成功した回数 | |||||||
| 平均 | 標準偏差 | 平均 | 標準偏差 | 平均 | 標準偏差 | 平均 | 標準偏差 | 平均 | 標準偏差 | 平均 | 標準偏差 | ||||
| 5 | 0.000006 | 0.000001 | 28 | 1 | 5 | 0.000496 | 0.000905 | 384 | 682 | 5 | 0.000014 | 0.000002 | 7 | 1 | 5 |
| 10 | 0.000066 | 0.000024 | 137 | 3 | 5 | 0.007415 | 0.009445 | 756 | 523 | 5 | 0.000109 | 0.000004 | 17 | 1 | 5 |
| 15 | 0.000154 | - | 328 | - | 1 | 0.029485 | 0.027030 | 1236 | 1297 | 4 | 0.000374 | 0.000011 | 26 | 1 | 5 |
| 20 | 0.000404 | - | 609 | - | 1 | 0.085951 | 0.062188 | 1691 | 1147 | 5 | 0.001650 | 0.000961 | 36 | 1 | 5 |
| 25 | - | - | - | - | 0 | 0.184369 | 0.154142 | 3549 | 3897 | 3 | 0.002058 | 0.000030 | 44 | 1 | 5 |
| 30 | - | - | - | - | 0 | 0.210077 | 0.085880 | 2835 | 1542 | 4 | 0.004100 | 0.000085 | 54 | 1 | 5 |
| 35 | - | - | - | - | 0 | 0.645136 | 0.355964 | 3627 | 924 | 4 | 0.008153 | 0.000244 | 62 | 2 | 5 |
| 40 | - | - | - | - | 0 | 1.35740 | 0.714998 | 4610 | 2505 | 2 | 0.022697 | 0.011633 | 70 | 2 | 5 |
| 45 | - | - | - | - | 0 | 2.40285 | - | 6132 | - | 1 | 0.025438 | 0.001022 | 81 | 2 | 5 |
| 50 | - | - | - | - | 0 | - | - | - | - | 0 | 0.052627 | 0.011479 | 88 | 2 | 5 |
| 60 | - | - | - | - | - | - | - | - | - | - | 0.151606 | 0.014178 | 105 | 2 | 5 |
| 70 | - | - | - | - | - | - | - | - | - | - | 0.173053 | 0.052095 | 121 | 2 | 5 |
| 80 | - | - | - | - | - | - | - | - | - | - | 0.233837 | 0.005553 | 137 | 2 | 5 |
| 90 | - | - | - | - | - | - | - | - | - | - | 0.34694 | 0.002928 | 155 | 2 | 5 |
| 100 | - | - | - | - | - | - | - | - | - | - | 0.64884 | 0.186371 | 171 | 2 | 5 |
| 120 | - | - | - | - | - | - | - | - | - | - | 0.773125 | 0.255435 | 203 | 4 | 5 |
| 140 | - | - | - | - | - | - | - | - | - | - | 1.33962 | 0.306924 | 236 | 3 | 5 |
| 160 | - | - | - | - | - | - | - | - | - | - | 2.70474 | 0.214812 | 267 | 6 | 5 |
| 180 | - | - | - | - | - | - | - | - | - | - | 3.62164 | 0.319654 | 301 | 4 | 5 |
| 200 | - | - | - | - | - | - | - | - | - | - | 5.75702 | 0.245213 | 328 | 3 | 5 |
各処理における処理回数・時間のグラフを以下に示します。横軸が行列のサイズを表し、縦軸の左側が処理時間 ( sec. )、右側が反復処理の回数を示しています。処理時間の目盛りは対数で表されていることに注意してください。
「ヤコビ法」は処理の単純さから反復処理の回数に対して処理時間が圧倒的に短いのですが、いわゆる "モグラ叩き" 方式であるため収束できる行列のサイズが 10 程度であり、小さなサイズの行列にしか対応できません。また「ハウスホルダー + QR 法」は処理回数が非常に多くなる傾向にあり、収束できる行列のサイズもせいぜい 30 程度が限界値となります。「ウィルキンソンの移動法」は処理回数が他と比べて非常に少なく、行列のサイズに応じて線形増加となるため非常に安定した性能が得られます。しかし、処理時間は行列のサイズが 2 倍になるのに対して 10 倍以上と指数関数的に増えています。内部で行列の積を計算しているため、処理時間は一気に増大する傾向にあります。
今まで、対称行列の固有値を求めるためのアルゴリズムをいくつか紹介しました。固有値を求めるには固有方程式を解く必要があり、行列数が n の正方行列に対する固有方程式は n 次方程式になるため、n の値が大きくなれば方程式を解くことができなくなります。そのため、相似変換を繰り返し行うことによって固有値を求めるヤコビ法やハウスホルダー法などが誕生しました。
しかし、固有方程式は n 次方程式であり、常に実数解を持つのかという疑問が生じます。実は、固有値として複素数となる場合もあります。例えば、次の行列
| A | = | | | 1, | -1 | | |
| = | | | 1, | 0 | | |
の固有値は ( 1 ± √3i ) / 2 で複素数になります。
幸いなことに、対称行列の固有値は全て実数になることが証明できます ( 補足 4 )。対称行列は非常に利用頻度が高い種類の行列であり、対称行列に対する固有値算出法を覚えておけば様々な場面で利用することができます。しかし、一般的な正方行列の固有値は複素数が含まれる場合があるため、今回のような方法で求めることができない場合も発生します。
今回は、対称行列の固有値を求める手法をいくつか紹介してきました。次の章では、これらのアルゴリズムを使って対称行列の固有値分解を行い、その結果を利用した手法をいくつか紹介する予定です。
ベクトルの内積とノルムは「正値性」「対称性」「線形性」を満たし、これらをまとめて「内積の公理」と言います。n 次元ベクトルに限らず、二つの元 u, v から実数 ( u, v ) を求める方法を定義したとき、それがこれら三つの公理を満たすならば、( u, v ) を内積と呼びます。従って、関数を使った次のような内積も定義することができます。
( f, g ) = Σi{1→n} f(xi)g(xi)
||f|| = ( Σi{1→n} f(xi)2 )1/2
区間 [ a, b ] 上の連続関数であれば、積分を使って次のような内積も定義できます。
( f, g ) = ∫{a→b} f(x)g(x) dx
||f|| = ( ∫{a→b} f(x)2 dx )1/2
内積やノルムに対しては、「コーシー = シュワルツの不等式」の他に、次の「三角不等式」も成り立ちます。
これらは「内積の公理」を満たせばどんなものに対しても成り立つので、例えば積分を使った内積に対しては、次の式が成り立ちます ( 見やすくするため、区間 [ a, b ] を省略して記述しています)。
- ( ∫f(x)2 dx )1/2( ∫g(x)2 dx )1/2 ≤ ∫f(x)g(x) dx ≤ ( ∫f(x)2 dx )1/2( ∫g(x)2 dx )1/2 ( コーシー = シュワルツの不等式 )
{ ∫( f(x) + g(x) )2 dx }1/2 ≤ ( ∫f(x)2 dx )1/2 + ( ∫g(x)2 dx )1/2 ( 三角不等式 )
内積とノルムを使って、二つのベクトルがなす角度を定義することができたように、関数に対しても同様の定義をすることができます。特に、内積がゼロになるならば、二つの関数は直交することになります。よって、 ( 正規 ) 直交基底となる関数を定義することも可能になります。
内積とノルムは、線形空間上で定義されるものです。そこで、線形空間の公理についてまとめておきます。
空でない集合 V が以下の性質を持つとき、これを「線形空間 ( Linear Space )」または「ベクトル空間 ( Vector Space )」という。
V 上の任意の元 u, v に対し、その和 u + v が V 上にただ一つ存在し、以下の性質を持つ。
V 上の任意の元 u と任意のスカラー λ に対し、スカラー積 λu が V 上にただ一つ存在し、以下の性質を持つ。
和の逆元に関する公理から、x = v - u と表します。つまり、元どうしの減算が定義されていることになります。すると、V 上の任意の元 u に対して u - u も V 上の元になり、これを零元として 0 で表します。V 上の任意の元 u に対し、零元との和 u + 0 は u と等しくなります。任意の元の和が同じ線形空間上にあり ( これを「加法に対して閉じている」といいます )、結合法則が成り立ち、逆元と零元が存在するとき、「加法に関して可換群 ( Commutative Group )になる」と表します。なお、可換群は「アーベル群 ( Abelian Group )」とも呼ばれます。
スカラーは四則演算が成り立つ集合であれば何でもよく、特にスカラーが実数の場合、その線形空間を「実線形空間」、複素数の場合は「複素線形空間」と呼びます。今回紹介した内容は、ほとんど全て「実線形空間」のみを考慮しています。
線形空間に対して内積とノルムが定義されているとき、その線形空間は「計量ベクトル空間 ( Metric Vector Space )」と呼ばれます。
今まで、内積の成分は実数のみを考えてきましたが、複素数を成分に持つことを考えた場合、「正値性」を満たすためには、ベクトルの内積を次のようにする必要があります。
( u, v ) = Σi{1→n}( uivi~ )
||u|| = ( u, u )1/2 = { Σi{1→n}( uiui~ ) }1/2
* vi~は viの共役複素数を表すものとする。
これを「エルミート内積」と言います。複素数に対してそのべき乗はやはり複素数になりますが、共役複素数との積はゼロまたは正の実数となるため、「正値性」を満たします。しかし、今度は「対称性」を満たさなくなるため、この公理を次のように変更します。
2'. 任意のベクトル u, v について ( u, v ) = ( v, u )~
* 右辺は内積の共役複素数を表している
このようにすると、複素数に対しても「対称性」が成り立つようになります。これを「エルミート対称性」と言います。エルミート対称性は、実数だけを考えた場合は対称性と一致します。複素線形空間に対してこのような内積とノルムが定義されたとき、これを「ユニタリ空間 ( Unitary Space )」と呼びます。
転置行列には次のような性質があります。
n 個の正方行列 A1, A2, ... An に対して
( A1A2...An-1An )T = AnTAn-1T...A2TA1T
証明は次のようになります。
任意のベクトル x, y に対して
( A1A2...An-1Anx, y ) = ( x, (A1A2...An-1An)Ty )
一方、次のような変換もできる。
| ( A1A2...An-1Anx, y ) | = | ( A2...An-1Anx, A1Ty ) |
| = | ( A3...An-1Anx, A2TA1Ty ) | |
| : | ||
| = | ( x, AnTAn-1T...A2TA1Ty ) | |
これが任意のベクトルで成り立つので ( A1A2...An-1An )T = AnTAn-1T...A2TA1Tとなる。
この式を利用すると、対称行列の積の転置は
| ( A1A2...An-1An )T | = | AnTAn-1T...A2TA1T |
| = | AnAn-1...A2A1 |
になります。ハウスホルダー行列は対称行列なので、対称行列 A をハウスホルダー行列 H で相似変換した行列 ( HAHT ) の転置は
| ( HAHT )T | = | HTATH |
| = | HAHT |
であり、HAHT も対称行列であることがわかります。
まず、三角行列の行列式は対角成分の積に等しいことを証明します。そのためには、行列式の定義を利用します。
行列数が n である行列の各列に対し、行番号が互いに異なる要素を取り出すことを考えます。この時、各列から選択した行番号からなる数列は、1 から n までの数列の順序を入れ替えたものであり ( これを順列と言います )、その選び方は n! 通りあります。順列は、二つの要素を入れ替えることを繰り返して作成することができるので、この入れ替え回数が偶数の場合を偶順列、奇数の場合を奇順列と区別します。それぞれの順列の番号に従って取り出した要素の積を計算し、偶順列の場合は加算、奇順列の場合は減算をします。こうして得られた結果が行列式になり、式に表すと次のようになります。
但し、A に対し、r 行 c 列目の要素を ar,c とし、σ(i1,i2,...in) は順列 i1, i2, ... in が偶順列のとき 1、奇順列のとき -1、それ以外は 0 を表すとします ( これを順列符号といいます )。
三角行列の場合、対角成分より上側または下側が全てゼロです。従って、各列ごとに対角成分を取り出したときの積以外は全てゼロになります。各列ごとに対角成分を選択したときは、行番号の入れ替えは発生していないため偶順列であり、よって、行列式は対角成分の積に等しいことになります。対角行列も同様の考え方により、対角成分の積が行列式になることがわかります。
三角行列の固有方程式も、三角行列の行列式を解く形になります。従って、求める固有値を λ とするとき、固有方程式は
となって、対角成分がそのまま固有値を表していることがわかります。
対称行列の固有ベクトルは互いに直交するので、対称行列の固有ベクトルを列ベクトルとする行列は直交行列となることはすでに説明した通りです。さらに、対称行列の固有値と固有ベクトルの成分は、全て実数となることも証明することができます。
証明の前に、共役複素数に関する性質について説明しておきます。
複素数 z に対し、z~ は z の共役複素数を表しているものとする。
z1 = a + bi, z2 = c + di とすると、
| z1・z2 | = | ( a + bi )( c + di ) |
| = | ( ac - bd ) + ( da + bc )i | |
| z1~・z2~ | = | ( a - bi )( c - di ) |
| = | ( ac - bd ) - ( da + bc )i |
よって、( z1・z2 )~ = z1~・z2~ であり、さらに上の操作を z に対して続けると ( z~ )n = ( zn )~、つまり、ある複素数に対し、その共役複素数のべき乗と、べき乗の共役複素数が等しいことになる。
また、任意の実数を r1, r2 として
| r1z1 + r2z2 | = | r1( a + bi ) + r2( c + di ) |
| = | ( ar1 + cr2 ) + ( br1 + dr2 )i | |
| r1z1~ + r2z2~ | = | r1( a - bi ) + r2( c - di ) |
| = | ( ar1 + cr2 ) - ( br1 + dr2 )i |
より、( r1z1 + r2z2 )~ = r1z1~ + r2z2~であり、この操作を続けると ( Σk{0→n}( rkzk ) )~ = Σk{0→n}( rkzk~ )、つまり和の共役複素数と、共役複素数の和は等しい。
対称行列は実数成分だけを持ちますが、複素数成分も持つ行列に対し、転置行列の成分を共役複素数に取り替えた行列を「随伴行列 ( Adjoint Matrix )」といい、随伴行列が等しくなる行列を「エルミート行列 ( Hermitian Matrix )」と呼びます。行列 A に対する随伴行列を A* としたとき、エルミート行列は
を満たすことになります。エルミート行列の成分が全て実数ならば、それは対称行列と等しくなります。
エルミート行列 A の固有値を λ、その固有ベクトルを u とすると、Au = λu が成り立ちます。Au と u の内積を計算すると、
ここでエルミート対称性の公理より ( Au, u ) = ( u, Au )~ なので、
但し、ここで任意の元 u, v に対して ( Au, v ) = ( u, A*v ) が成り立つことを利用しました。u の i 番目の成分を ui としたとき、( u, u ) = ( u, u )~ = Σi( uiui~ ) ≥ 0 なので λ = λ~ が成り立ち、これを満たすとき λ は実数となります。
ところで、( λu, u ) = ( u, λu )~ なので、ここから λ~( u, u )~ が示せそうに見えますが、これは成り立ちません。
( u, λu )~ = ( Σi( λ~uiui~ ) )~ = λ||u||2
λ~( u, u )~ = λ~( ( Σi( uiui~ ) )~ ) = λ~||u||2
となるため、( u, λu )~ ≠ λ~( u, u )~ です。これが成り立ってしまうと、任意の行列に対して固有値が実数となってしまいます。( λu, u ) = λ( u, u ) に対し、( u, λu ) = λ~( u, u ) となることに注意が必要です。
エルミート行列の固有値は全て実数であることが示せたので、対称行列の固有値もやはり全て実数となることになります。固有ベクトルは、固有値と行列の成分からなる係数を持った連立一次方程式であるため、固有値と行列の成分が実数であればその解も実数です。従って、対称行列の固有ベクトルの成分も実数であることになります。
上記の中で、( Au, v ) = ( u, A*v ) を利用していますが、これは、転置行列の性質 ( Au, v ) = ( u, ATv ) を証明するときと同じ方法で確認することができます。
| ( x, A*y ) | = | ( x, ( Σi{1→n}( ai1~yi ), Σi{1→n}( ai2~yi ), ... Σi{1→n}( ain~yi ) ) |
| = | x1( Σi{1→n}( ai1~yi ) )~ + x2( Σi{1→n}( ai2~yi ) )~ + ... + xn( Σi{1→n}( ain~yi ) )~ | |
| = | x1( a11y1~ + a21y2~ + ... an1yn~ ) + x2( a12y1~ + a22y2~ + ... an2yn~ ) + ... + xn( a1ny1~ + a2ny2~ + ... annyn~ ) | |
| = | y1~( a11x1 + a12x2 + ... a1nxn ) + y2~( a21x1 + a22x2 + ... a2nxn ) + ... + yn~( an1x1 + an2x2 + ... annxn ) | |
| = | y1~( Σi{1→n}( a1ixi ) ) + y2~( Σi{1→n}( a2ixi ) ) + ... + yn~( Σi{1→n}( anixi ) ) | |
| = | ( ( Σi{1→n}( a1ixi ), Σi{1→n}( a2ixi ), ... Σi{1→n}( anixi ) ), y ) | |
| = | ( Ax, y ) |
先ほど説明した、共役複素数に関する性質を利用していることに注意してください。
ところで、実数を係数に持つ n 次の方程式は、複素数解 z に対して共役な複素数 z~ を必ず解に持ちます。
実数を係数に持つ任意の方程式
において、複素数 z が解であるとする。この方程式に z~ を代入すると、
| f(z~) | = | Σk{0→n}( ak(z~)k ) |
| = | Σk{0→n}( ak(zk)~ ) | |
| = | ( Σk{0→n}( akzk ) )~ | |
| = | ( f(z) )~ = 0 |
よって、共役複素数 z~ も f(x) の解になる。
実数のみを成分とする行列 A の固有値の一つ λ が複素数であるとき、上記の結果からその共役複素数 λ~ も固有値となるため、固有ベクトルをそれぞれ u, u' とすると、
が成り立ちます。ここで、A の r 行 c 列の成分を arc、u の r 番目の成分を ur としたとき、Au = λu の r 行目の方程式は
両辺の共役複素数を取ると、
( Σc( arcur ) )~ = ( λur )~ より
Σc( arcur~ ) = λ~ur~
つまり、u' = u~ ということになり、共役複素数を固有値とする固有ベクトルは、同じ番号の成分もまた共役複素数になります。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |