数値演算法
(1) 整数の演算
前回紹介した「RSA 暗号」では巨大な数による計算が必要になります。しかし、サンプル・プログラムでは非常に小さな数値しか扱うことができませんでした。そこで、巨大な数値による演算処理を行うためのアルゴリズムを紹介したいと思います。今回はその前段階として、コンピュータ上での数値計算処理方法について紹介します。
1) 位取り記数法 ( Numeral System )
我々が普段利用している数は通常、0 から 9 までの十個の数字で構成されています。この数字単独では 0 から 9 までの数しか表現できないため、次に大きな整数を表す場合は桁を一つ上げて 10 と表現します。このような数の表記法を「位取り記数法 ( Numeral System )」といいます。
使用される数字の数を「基数 ( Radix )」または「底 ( Base )」といい、基数が N である位取り記数法を「N 進法」といいます。よって、0 から 9 で表現される位取り記数法の場合、基数は 10 であり「10 進法」になります。
次に示す表は、よく利用される位取り記数法を示しています。
表1-1. 位取り記数法の例
| 基数 | 記数法 |
|---|
| 2 | 2 進法 ( Binary ) |
| 8 | 8 進法 ( Octal ) |
| 12 | 12 進法 ( Dozenal ) |
| 16 | 16 進法 ( Hexadecimal ) |
| 60 | 60 進法 ( Sexagesimal ) |
12 進法や 60 進法は時刻の表記で利用されます。例えば、135 秒は 2 分 15 秒と表記できるので、60 進法と見ることができます ( 実際には "15 秒" と書いているので、厳密には 10 進法の表記になります )。2 進法・8 進法・16 進法はコンピュータで頻繁に利用される記数法です。
N 進法で表記された数を T = [C0C1C2 ... Cr]N と表すと次のように分解することができます。
| T | = | C0・[10]Nr + C1・[10]Nr-1 + C2・[10]Nr-2 + ... + Cr・[10]N0 |
| = | Σm{0→r}( Cm・[10]Nr-m ) ( 但し、0 ≤ Cm < [10]N ) |
[10]N = [N]10 ( つまり 10 進法での N ; 以下、[]で括られていない数値は 10 進数表記とします ) なので、10 進法に変換するには次の計算をすればいいことになります。
| T | = | C0・Nr + C1・Nr-1 + C2・Nr-2 + ... + Cr・N0 |
| = | Σm{0→r}( Cm・Nr-m ) |
例えば、5 進法で表記された数 [41033]5 を 10 進法に変換するには次の計算をすればいいことになります。
| [41033]5 | = | 4・54 + 1・53 + 0・52 + 3・51 + 3・50 |
| = | 4 x 625 + 1 x 125 + 0 x 25 + 3 x 5 + 3 x 1 = 2643 |
逆に、10 進法の 2643 を 5 進法で表記したい場合、10 = [20]5だから
| 2643 | = | 2・103 + 6・102 + 4・101 + 3・100 |
| = | [2]5・[20]53 + [11]5・[20]52 + [4]5・[20]51 + [3]5・[20]50 |
| = | [2]5・[13000]5 + [11]5・[400]5 + [4]5・[20]5 + [3]5 |
| = | [31000]5 + [4400]5 + [130]5 + [3]5 = [41033]5 |
と計算することができますが、10 進数に変換する場合に比べてかなり面倒です。これは、10 進数以外の表記法で計算することに慣れていないためであり、通常ならばこのような計算はしたくないものです。そのため、一般的には別の手法で求めることになります。
[C0C1C2 ... Cr]N = C0・[10]Nr + C1・[10]Nr-1 + C2・[10]Nr-2 + ... + Cr・[10]N0
を [10]N で割ると
商 q = C0・[10]Nr-1 + C1・[10]Nr-2 + C2・[10]Nr-3 + ... + Cr-1・[10]N0 = [C0C1C2 ... Cr-1]N
余り r = [Cr]N
になります。例えば 10 進法の 2643 を 10 で割ると、商は 264、余りは 3 になります。さらに 264 を 10 で割ると商は 26、余りは 4 になり、この操作を続けていくと下位の数を順に余りから取り出すことができます。これは基数がいくつになっても成り立つため、例えば 5 進数で表記する場合は 5 で割算をして余りを下位の方から順に並べていけばいいことになります。
| 2643 | / | 5 | = | 528 | ... 3 |
| 528 | / | 5 | = | 105 | ... 3 |
| 105 | / | 5 | = | 21 | ... 0 |
| 21 | / | 5 | = | 4 | ... 1 |
| 4 | / | 5 | = | 0 | ... 4 → [41033]5 |
基数を変換して文字列として返すサンプル・プログラムを以下に表示します。
std::string ChangeRadix( unsigned int num, unsigned int radix )
{
std::string ans;
do {
std::stringstream ss;
unsigned int r = num % radix;
num /= radix;
ss << "(" << r << ")";
ans = ss.str() + ans;
} while ( num != 0 );
return( ans );
}
数値から文字列への変換には STL ( Standard Template Library ) の stringstream を利用しています。標準出力への出力と同じような要領で文字列に対して任意の型のデータを出力することができます。処理の内容は先程説明したとおりで、数値の剰余を求めて上位側へ出力しているだけです。
当然のことながら、位取り記数法は単に表記方法を変更しているだけで数そのものは変わっていません。上記の例にある 2643 と [41033]5 は、数値そのものは全く同じです。また、10 進法で利用できるテクニックは他の基数の場合でも有用です。例えば、掛け算や割り算をする場合に利用される筆算は、基数が 10 でなくてもちゃんと使えます。
例) [1213]5 x [3223]5
1213
x) 3223
---------
4144 ← 1213 x 3
2431 ← 1213 x 2
2431 ← 1213 x 2
4144 ← 1213 x 3
-----------
10031104
[1213]5 = 183、 [3223]5 = 438 なので、10 進数では 183 x 438 = 80154 = [10031104]5 になり、10 進数で計算しても 5 進数を使っても結果は等しくなります。
2) 論理演算 ( Logical Operation )
プログラミングの世界では真偽値をよく利用します。if 文や while 文などで使われる条件文の戻り値は真偽値となり、条件を満たす場合は真 ( True )、満たさない場合は偽 ( False ) を返すことになります。C 言語では数値 0 を偽、それ以外を真として真偽値を表します。また、C++, Java, VB などは、bool や boolean といった専用の型を持っています。
論理演算は真偽値に対しての演算法で、この論理を初めて提唱した数学者である「ジョージ・ブール ( George Boole )」の名にちなんで「ブール演算 ( Boolean Operation )」とも呼ばれます。以下に、代表的な論理演算を示しておきます。
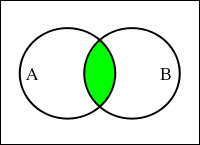
- ◆ 論理積(AND)
二つの真偽値がどちらも真ならば真を返し、それ以外は偽を返す。
表2-1. AND 演算
| A | B | A AND B |
|---|
| 真 | 真 | 真 |
| 真 | 偽 | 偽 |
| 偽 | 真 | 偽 |
| 偽 | 偽 | 偽 |
- ◆ 論理和(OR)
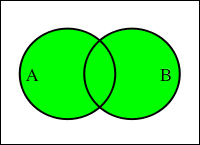
二つの真偽値の少なくともどちらかが真ならば真を返し、どちらも偽ならば偽を返す。
表2-2. OR 演算
| A | B | A OR B |
|---|
| 真 | 真 | 真 |
| 真 | 偽 | 真 |
| 偽 | 真 | 真 |
| 偽 | 偽 | 偽 |
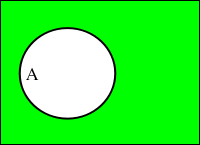
- ◆ 否定(NOT)
真偽値が真ならば偽、偽ならば真に反転する。
表2-3. NOT 演算
| A | NOT A |
|---|
| 真 | 偽 |
| 偽 | 真 |
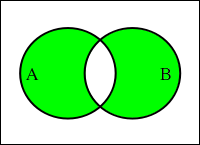
- ◆ 排他的論理和(XOR)
二つの真偽値のうちどちらか一方だけが真であれば真を返し、それ以外は偽を返す。
表2-4. XOR 演算
| A | B | A XOR B |
|---|
| 真 | 真 | 偽 |
| 真 | 偽 | 真 |
| 偽 | 真 | 真 |
| 偽 | 偽 | 偽 |
- ◆ 否定論理積(NAND)
論理積(AND)の否定(NOT)で、二つの真偽値がどちらも真ならば偽を返し、それ以外は真を返す。
表2-5. NAND 演算
| A | B | A NAND B |
|---|
| 真 | 真 | 偽 |
| 真 | 偽 | 真 |
| 偽 | 真 | 真 |
| 偽 | 偽 | 真 |
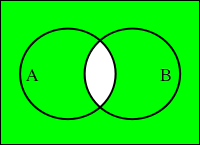
- ◆ 否定論理和(NOR)
論理和(OR)の否定(NOT)で、二つの真偽値の少なくともどちらかが真ならば偽を返し、どちらも偽ならば真を返す。
表2-6. NOR 演算
| A | B | A NOR B |
|---|
| 真 | 真 | 偽 |
| 真 | 偽 | 偽 |
| 偽 | 真 | 偽 |
| 偽 | 偽 | 真 |
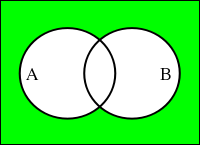
各論理演算で示されている図は「ベン図 ( Venn Diagram )」と呼ばれ、集合の関係を図示したものです。円は演算対象の集合を表し、緑色で塗りつぶされた箇所が演算結果となります。例えば、集合 A は「偶数の集合」を表し、集合 B は「3 の倍数の集合」を表しているとき、その論理積である「偶数かつ 3 の倍数 ( つまり 6 の倍数 ) の集合」は円の重なった部分に属しており、論理和である「偶数か 3 の倍数となる数の集合」はそれぞれの円全体に含まれていることになります。
アメリカの数学者「クロード・シャノン ( Claude Elwood Shannon )」は、スイッチのオンとオフをそれぞれ真・偽に対応させたとき、スイッチの直列回路が論理積、並列回路が論理和になることから、あらゆる論理演算がスイッチ回路で表現できることを示しました。現在のコンピュータが自動計算機として利用されるようになったことに、シャノンの業績が大きな影響を及ぼしているわけです。基本的な電子回路としては、AND 回路・OR 回路・NOT 回路があり、さらにこれらを組み合わせて NAND・NOR・XOR を実現するための回路を組み立てることもできます。
3) 二進数による四則演算
2 を基数とした場合、利用できる数は 0 と 1 しかありません。そのため数が大きくなると桁数は極端に大きくなります。例えば、
24 = [11000]2
387 = [110000011]2
28901 = [111000011100101]2
になります。二進数を使って手計算をしようというような方はおそらくいないと思いますが、コンピュータを使った計算処理では二進数による演算が行われています。
コンピュータ内部では、スイッチの ON / OFF を使って数値を表現しています。ON = 1、OFF = 0 とすると、これは二進数と考えることができます。コンピュータは電気回路の一種なので、四則演算も全て電気回路を使って実現しなければなりません。そのため、必然的に二進数による数値演算が利用されることになります。このことは、二進数による数値演算が論理演算だけで実現できることを意味しています。
例えば、二進数一桁の数値加算は以下の 4 通りあります。
| 0 + 0 = 00 |
| 0 + 1 = 01 |
| 1 + 0 = 01 |
| 1 + 1 = 10 |
一方、論理演算の論理積 ( AND ) と排他的論理和 ( XOR ) を使った演算結果は以下のようになります。
| 0 AND 0 = 0 |
| 0 AND 1 = 0 |
| 1 AND 0 = 0 |
| 1 AND 1 = 1 |
|
| 0 XOR 0 = 0 |
| 0 XOR 1 = 1 |
| 1 XOR 0 = 1 |
| 1 XOR 1 = 0 |
和の一桁目は排他的論理和、二桁目は論理積の結果とそれぞれ等しくなるため、これらの論理演算を使えば ( 一桁 + 一桁 ) の加算処理ができることになります。
void AddBin_1( bool i0, bool i1, bool& o0, bool& o1 )
{
o0 = i0 ^ i1;
o1 = i0 & i1;
}
これを任意の桁数に拡張する場合、繰り上がりが発生することを考慮する必要があります。下表は、入力データ i0・i1 の加算結果 ( o0・o1 ) に、さらに繰り上がり分 carry を加算した結果 ( o0'・o1' ) を示しています。
表3-1. 繰り上がりを考慮した加算処理
| i0 | i1 | o0 | o1 | carry | o0' | o1' |
|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 |
この場合、i0 と i1 で計算をした結果の一桁目 ( o0 ) をさらに carry と加算し、この加算結果の二桁目か、あるいは o1 のどちらかが 1 の場合、o1' を 1 とします。また、o0' は carry との加算結果の一桁目をそのまま代入します。
void AddBinWithCarry( bool i0, bool i1, bool carry, bool& o0, bool& o1 )
{
bool b0, b1;
AddBin_1( i0, i1, b0, b1 );
AddBin_1( b0, carry, o0, o1 );
o1 |= b1;
}
実際にはこのような回路を複数組み立てて、o1 を次の回路の入力データ carry として渡してやれば、任意の桁に対する加算処理ができます。以下に示したサンプル・プログラムは仮想的な加算回路です。このプログラムによって、32bit 整数値に対する加算処理を加算記号(+)を使わずに行うことができます。
unsigned int AddBin_n( unsigned int i0, unsigned int i1 )
{
const unsigned int UINT_BIT = CHAR_BIT * sizeof( unsigned int ) / sizeof( unsigned char );
unsigned int ans = 0;
bool o0;
bool o1 = false;
for ( unsigned int n = 0 ; n < UINT_BIT ; n++ ) {
bool b0 = i0 & 1;
bool b1 = i1 & 1;
AddBinWithCarry( b0, b1, o1, o0, o1 );
if ( o0 ) ans |= ( 1 << n );
i0 >>= 1;
i1 >>= 1;
}
return( ans );
}
二進数一桁の数値減算の場合、負の数が発生します。
| 0 - 0 = 0 |
| 0 - 1 = -1 |
| 1 - 0 = 1 |
| 1 - 1 = 0 |
そこで、結果が負になった場合は上位から桁を借りたと見なして表すことにします。具体的には、三桁目から繰り下げて計算したと考えると、
0 - 1 → 100 - 1 = 11
と表すことになります。よって、減算の結果は次のようになります。
| 0 - 0 = 00 |
| 0 - 1 = 11 |
| 1 - 0 = 01 |
| 1 - 1 = 00 |
一桁目は、加算処理の場合と同様に排他的論理和を使って表すことができます。しかし二桁目は少しややこしく、被減数のNOTと減数との論理積を計算して結果を得ます。
| ( NOT 0 ) AND 0 = 0 |
| ( NOT 0 ) AND 1 = 1 |
| ( NOT 1 ) AND 0 = 0 |
| ( NOT 1 ) AND 1 = 0 |
これを実装すると以下のようになります。
void SubBin_1( bool i0, bool i1, bool& o0, bool& o1 )
{
o0 = i0 ^ i1;
o1 = ( ! i0 ) & i1;
}
加算の時と同様にこれを任意の桁へ拡張する場合、今度は繰り下がりを考慮して演算する必要があります。下表は、入力データ i0・i1 の減算 ( i0 - i1 ) の結果 ( o0・o1 ) に、繰り下げ分 carry を減算した結果 ( o0'・o1' ) を示しています。
表3-2. 繰り下がりを考慮した減算処理
| i0 | i1 | o0 | o1 | carry | o0' | o1' |
|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 |
o0' は、o0 から carry を減算した結果の一桁目から得ることができます。o1' の取得方法は加算処理の場合とほぼ同じで、o0 から carry を減算した結果の二桁目か o1 のどちらかが 1 ならば値は 1 になります。
void SubBinWithCarry( bool i0, bool i1, bool carry, bool& o0, bool& o1 )
{
bool b0, b1;
SubBin_1( i0, i1, b0, b1 );
SubBin_1( b0, carry, o0, o1 );
o1 |= b1;
}
加算処理の時と同様に、32bit 整数値に対する減算処理を減算記号 ( - ) を使わずに行う仮想的な回路を示します。
unsigned int SubBin_n( unsigned int i0, unsigned int i1 )
{
const unsigned int UINT_BIT = CHAR_BIT * sizeof( unsigned int ) / sizeof( unsigned char );
unsigned int ans = 0;
bool o0;
bool o1 = false;
for ( unsigned int n = 0 ; n < UINT_BIT ; n++ ) {
bool b0 = i0 & 1;
bool b1 = i1 & 1;
SubBinWithCarry( b0, b1, o1, o0, o1 );
if ( o0 ) ans |= ( 1 << n );
i0 >>= 1;
i1 >>= 1;
}
return( ans );
}
一桁どうしの減算処理でも説明した通り、減算処理結果が負数になる場合は最上位ビットが 1 になります。絶対値の等しい正数と負数は互いに補数どうしの関係となっており、例えば 1 と -1 を 8 ビットで表すとそれぞれ [00000001]2、[11111111]2 になります ( 補数とは、ある数に対して加算することで桁が一つ上がる最小の数を意味します )。つまり、符号付き整数の -1 と、符号無し整数の 255 は、どちらも [11111111]2 という同じ値を持っていることになります。
加算と減算が完成すれば、乗算と除算もこれらを利用して作ることができます。
乗算処理を実現する最も簡単な方法は、乗数分だけ被乗数の加算処理を繰り返すというものですが、乗数が大きくなると処理時間が長くなり実用的ではありません。そこで、二進数での筆算をそのままプログラムで実現します。
例えば、135 x 251 を計算する場合、
135 = [10000111]2
251 = [11111011]2
なので、これを筆算で計算します。
10000111
x) 11111011
------------
10000111
10000111
10000111
10000111
10000111
10000111
10000111
-----------------
1000010001011101
筆算は、乗数 ( [11111011]2 ) から一桁ずつ取り出しては計算を行い、位を合わせておいて加算処理して結果を得る方法で計算します。二進数の場合、使う数値は 0 か 1 なので、各桁での乗算結果は必ず 0 か被乗数そのものになります。よって、加算処理を利用して次のように処理をすれば乗算処理ができます。
- 結果を取得する変数 ans を 0 で初期化する。
- ans を上位側に一つビットシフトする。
- 乗数の最上位ビット msb が立っていたら、ans に被乗数を加算する。
- 乗数を上位側に一つビットシフトする。
- 乗数のビット数分だけ、2 から 4 を繰り返す。
除算の場合も、筆算を利用して処理を行うことができます。例えば 251 / 13 を計算する場合、以下のように処理することになります。
_____10011_
1101 ) 11111011
1101
10101
1101
10001
1101
100
よって、減算処理を使って次のように処理すれば、除算処理が実現できます。
- 結果を取得する変数 q を 0 で初期化する。
- バッファ変数 r を 0 で初期化する。
- q を上位側に一つビットシフトする。
- r を上位側に一つビットシフトして、被除数の最上位ビット msb を r の最下位ビットに代入する。
- r が除数以上だったら、q に 1 を加え、r から除数を引く。
- 被除数のビット数分だけ、3 から 5 を繰り返す。
処理が完了すると、q からは商、r からは余りが得られます。
unsigned int MulBin( unsigned int u, unsigned int v )
{
const unsigned int UINT_BIT = CHAR_BIT * sizeof( unsigned int ) / sizeof( unsigned char );
const unsigned int USB_MASK = 1 << ( UINT_BIT - 1 );
unsigned int ans = 0;
for ( unsigned int n = 0 ; n < UINT_BIT ; n++ ) {
ans <<= 1;
if ( ( v & USB_MASK ) != 0 )
ans += u;
v <<= 1;
}
return( ans );
}
unsigned int DivBin( unsigned int u, unsigned int v, unsigned int& r )
{
const unsigned int UINT_BIT = CHAR_BIT * sizeof( unsigned int ) / sizeof( unsigned char );
const unsigned int USB_MASK = 1 << ( UINT_BIT - 1 );
unsigned int q = 0;
r = 0;
for ( unsigned int n = 0 ; n < UINT_BIT ; n++ ) {
q <<= 1;
r <<= 1;
if ( ( u & USB_MASK ) != 0 ) r++;
if ( r >= v ) {
q |= 1;
r -= v;
}
u <<= 1;
}
return( q );
}
今回は、コンピュータ上での数値演算処理の仕組みを紹介しました。次回はこの仕組みを応用して、任意の長さの整数、いわゆる多倍長整数を使った演算処理方法を説明したいと思います。
<参考文献>
- Oh!X 1992年9月号 X68000マシン後プログラミング 「整数演算のアルゴリズム」
- 「コンピュータのしくみ」 〜 名古屋工業大学 セラミックス基盤工学研究センター 井田 隆様 のページ 〜
- Wikipedia







![[Go Back]](../images/back1.png) 前に戻る
前に戻る![[Back to HOME]](../images/home1.png) タイトルに戻る
タイトルに戻る