乗算処理は、桁数の二乗に比例して処理速度が急激に増大します。これは、N 桁どうしの数値を乗算する場合、N x 1 桁の乗算処理を N 回繰り返すことから容易に理解できると思います。今回は、この処理回数を減らすことにより、乗算処理を高速化させるための手法について紹介したいと思います。
多倍長整数は、「位取り記数法」を利用して 16 ビットや 32 ビットのデータを一桁としたデータ構造を持っていました。この考え方を応用して、B 進 2N 桁の整数を、BN 進 2 桁の整数と見なします。ここで BN = p として 2N 桁の整数 u, v を表現すると、次のようになります。
但し 0 ≦ ui < p ; 0 ≦ vi < p ( i = 0, 1 )
この二数の積を w としたとき、
| w | = | uv |
| = | ( u1p + u0 )( v1p + v0 ) | |
| = | u1v1p2 + ( u1v0 + u0v1 )p + u0v0 |
と表すことができるため、N 桁の乗算処理を 4 回行い、シフト演算を使って桁をあわせる処理を行うことで計算ができます。しかし、このままでは処理回数に変化はありません。そこで、p の係数 u1v0 + u0v1 に着目して次のように式を変形します。
u1v1 と u0v0 はすでに計算済みなので、残る乗算処理は ( u1 - u0 )( v1 - v0 ) のみになります。u1 - u0 と v1 - v0 で減算処理が 2 回、結果の計算に加算・減算処理が 2 回と、計 4 回の加減算が増えることになりますが、その分乗算処理を 1 回減らすことができるため、普通に筆算処理を行うよりも処理速度は向上します。
ここで N が偶数であれば、N 桁の乗算処理にも同じ方法を使うことで乗算処理の回数を減らすことができます。さらにこの考え方を押し進めて、桁数が最初から 2 のべき乗になるようにしておけば、分割した数の乗算処理に対して再帰的に上記方法を使うことが可能となり、実際の乗算処理は 1 桁どうしの数のみでよくなります。
この手法を、発見者の名前を取って「Karatsuba法 ( Karatsuba Algorithm )」と呼びます。論文が発表されたのは、1962 年のことでした。
例として、1826 x 2199 を Karatsuba 法を用いて計算します。
1826 = 18 x 100 + 26 2199 = 21 x 100 + 99 1826 x 2199 = ( 18 x 100 + 26 )( 21 x 100 + 99 ) = 18 x 21 x 10000 + ( 18 x 99 + 26 x 21 ) x 100 + 26 x 99 18 x 99 + 26 x 21 = 18 x 21 + 26 x 99 - ( 18 - 26 )( 21 - 99 ) = 378 + 2574 - ( -8 x -78 ) = 2952 - 624 = 2328 1826 x 2199 = 378 x 10000 + 2328 x 100 + 2574 = 3780000 + 232800 + 2574 = 4015374
再帰的に処理を行った場合、例えば 18 x 21 に対して
18 x 21 = 1 x 2 x 100 + ( 1 x 1 + 8 x 2 ) + 8 x 1 = 2 x 100 + { 2 + 8 - ( 1 - 8 )( 2 - 1 ) } x 10 + 8 = 200 + 170 + 8 = 378
と同じ処理を繰り返して計算することができます。
Karatsuba法のサンプル・プログラムを以下に示します。
namespace BigNum { /* Unsigned::copy 部分コピー const Unsigned& num : 対象の Unsigned size_t s, e : コピーする要素の位置(開始・終了) this == &num の場合は処理しないことに注意 */ void Unsigned::copy( const Unsigned& num, size_t s, size_t e ) { if ( this == &num ) return; number_.clear(); if ( e - s + 1 > number_.capacity() ) number_.reserve( e - s + 1 ); while ( s <= e ) { if ( s >= num.size() ) break; push_upper( num.number_[s++] ); } if ( size() == 0 ) push_upper(); negZero(); } /* Unsigned::karaMul Karatsuba乗算 const Unsigned& v : 乗数 UnsignedBuff recLvl : 再帰処理を行う指数のしきい値(2^recLvlをサイズのしきい値とする) */ Unsigned& Unsigned::karaMul( const Unsigned& v, UnsignedBuff recLvl ) { if ( isNaN( v ) ) return( *this ); UnsignedBuff i = ( size() > v.size() ) ? size() : v.size(); // i以上で 2のべき乗になる数値を取得する UnsignedBuff sz = 2; while ( i > sz ) sz <<= 1; // recLvlから再帰を行うサイズのしきい値を計算する UnsignedBuff recSz = std::pow( 2, recLvl ); Unsigned u( *this ); karaMul_Main( u, v, *this, 0, sz, recSz ); return( *this ); } /* Unsigned::karaMul_Main Karatsuba乗算メインルーチン const Unsigned& u : 被乗数 const Unsigned& v : 乗数 Unsigned& ans : 結果を格納する多倍長整数 UnsignedBuff start : u,vの中の部分数列の開始位置 UnsignedBuff sz : u,vの中の部分数列のサイズ UnsignedBuff recSz : 再帰処理を行うサイズのしきい値 */ void Unsigned::karaMul_Main( const Unsigned& u, const Unsigned& v, Unsigned& ans, UnsignedBuff start, UnsignedBuff sz, UnsignedBuff recSz ) { if ( start >= u.number_.size() || start >= v.number_.size() ) { ans.clear(); return; } // 再帰レベル以下になったら通常の乗算処理 if ( sz <= recSz ) { if ( sz == 1 ) { ans.clear(); ans.number_[0] = u.number_[start]; ans.mulOneDigit( v.number_[start] ); } else { ans.copy( u, start, start + sz - 1 ); Unsigned v2( v, start, start + sz - 1 ); ans *= v2; } return; } // |u0 - u1|, |v0 - v1| を計算 sz >>= 1; Unsigned u01, v01; bool bu = u.partialSub( u01, start, sz ); bool bv = v.partialSub( v01, start, sz ); bool sign = ( bu == bv ) ? false : true; // (u0 - u1)(v0 - v1)の正負判定 // u0v0, u1v1, (u0 - u1)(v0 - v1) の積を計算 Unsigned uv0, uv1, uv01; karaMul_Main( u, v, uv0, start, sz, recSz ); karaMul_Main( u, v, uv1, start + sz, sz, recSz ); karaMul_Main( u01, v01, uv01, 0, sz, recSz ); // u1v0 + u0v1 の計算 ans = uv0; ans += uv1; if ( sign ) ans += uv01; else ans -= uv01; // u1v1とu0v0をシフトさせながら加算 uv1.ushift( sz * 2 ); ans.ushift( sz ); ans += uv0; ans += uv1; return; } /* Unsigned::partialSub 数列の一部を前半と後半に分割して減算処理を行う xxxxxxxxAAAAAAAABBBBBBBBxxxxxxxxxxxx -> |AAAAAAAA-BBBBBBBB| start start+sz Unsigned& u : 減算結果を格納する多倍長整数 UnsignedBuff start : 前半数列の開始位置 UnsignedBuff sz : 部分数列のサイズ 戻り値 : 前半部分の方が小さければTrueを返す */ bool Unsigned::partialSub( Unsigned& u, UnsignedBuff start, UnsignedBuff sz ) const { bool b = partialLess( start, sz ); if ( b ) { u.copy( *this, start + sz, start + sz * 2 - 1 ); u -= Unsigned( *this, start, start + sz - 1 ); } else { u.copy( *this, start, start + sz - 1 ); u -= Unsigned( *this, start + sz, start + sz * 2 - 1 ); } return( b ); } /* Unsigned::partialLess 数列の一部を前半と後半に分割して比較処理を行う xxxxxxxx+--------+--------+xxxxxxxxxxxx start start+sz UnsignedBuff start : 比較開始位置 UnsignedBuff sz : 比較する部分数列のサイズ 戻り値 : 前半部分の方が小さければTrueを返す */ bool Unsigned::partialLess( UnsignedBuff start, UnsignedBuff sz ) const { for ( UnsignedBuff i = sz ; i > 0 ; i-- ) { Digit l = ( start + i - 1 >= size() ) ? 0 : number_[start + i - 1]; Digit u = ( start + sz + i - 1 >= size() ) ? 0 : number_[start + sz + i - 1]; if ( l != u ) return( l < u ); } return( false ); } }
再帰処理を行うレベルは変数 recLvl で調節することができます。プログラム内で、recLvl を指数として 2 のべき乗を計算し、その結果が再帰処理を行うサイズのしきい値と定義されます。しきい値以下になったら通常の乗算処理を行ってその結果を返します。
再帰処理を行う場合、数列の一部分を抽出する必要があります。計算の度に部分数列をコピーするのは効率が悪いため、元の数列と、部分数列の先頭・末尾位置を引数として渡すようにしてあります。partialSub は部分数列専用の減算ルーチンで、部分数列の前半・後半部分で減算処理を行います。これは、プログラム中で u0 - u1 と v0 - v1 を計算するために利用します。計算結果は常に正数となるわけではないため、二数の大きさを比較して結果が必ず正数となるようにし、実際の符号は戻り値として返しています。
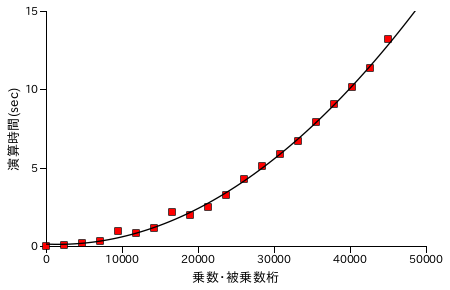
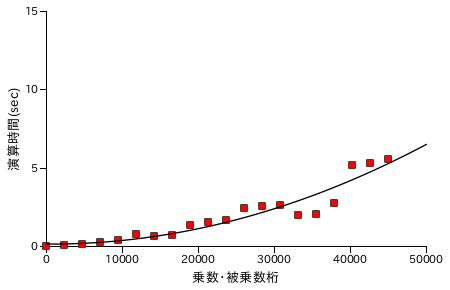
Karatsuba 法による乗算処理の性能評価結果を以下に示します。各グラフの X 軸は処理する数の桁数を表し、ほぼ同じ桁の数どうしを演算処理させています。また Y 軸は処理時間 ( sec. ) を表し、処理時間は同じ数値について演算を 25 回繰り返した合計時間になります。計測は Windows7 上の VirtualBox でゲスト OS を Xubuntu 16.04 LTS として行っています。CPU は Intel Core i7-2600 3.40GHz で、ゲスト OS 上ではコア数を 1 としています。
| 筆算処理 | recLvl = 5 | recLvl = 7 | recLvl = 9 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 被乗数桁数 | 乗数桁数 | 結果桁数 | 演算時間(sec) | 被乗数桁数 | 乗数桁数 | 結果桁数 | 演算時間(sec) | 被乗数桁数 | 乗数桁数 | 結果桁数 | 演算時間(sec) | 被乗数桁数 | 乗数桁数 | 結果桁数 | 演算時間(sec) |
| 5 | 5 | 10 | 0.000021 | 5 | 5 | 10 | 0.000036 | 5 | 5 | 10 | 0.000023 | 5 | 5 | 10 | 0.000039 |
| 2373 | 2373 | 4746 | 0.081552 | 2374 | 2373 | 4746 | 0.062302 | 2375 | 2372 | 4747 | 0.058622 | 2375 | 2373 | 4747 | 0.079374 |
| 4742 | 4741 | 9482 | 0.162331 | 4745 | 4741 | 9485 | 0.106685 | 4744 | 4743 | 9486 | 0.205522 | 4743 | 4743 | 9485 | 0.140728 |
| 7110 | 7109 | 14218 | 0.319659 | 7110 | 7109 | 14218 | 0.231172 | 7113 | 7110 | 14223 | 0.459370 | 7113 | 7112 | 14225 | 0.307907 |
| 9479 | 9479 | 18958 | 0.963838 | 9480 | 9479 | 18958 | 0.394850 | 9478 | 9476 | 18954 | 0.259869 | 9482 | 9477 | 18959 | 0.363773 |
| 11847 | 11844 | 23691 | 0.807104 | 11850 | 11848 | 23697 | 0.769301 | 11851 | 11848 | 23699 | 0.576953 | 11848 | 11846 | 23694 | 1.29939 |
| 14216 | 14215 | 28431 | 1.17271 | 14217 | 14214 | 28431 | 0.628833 | 14217 | 14217 | 28433 | 0.625489 | 14218 | 14215 | 28432 | 0.887644 |
| 16587 | 16583 | 33170 | 2.17764 | 16587 | 16581 | 33168 | 0.668772 | 16588 | 16586 | 33173 | 0.819879 | 16588 | 16585 | 33172 | 0.926788 |
| 18956 | 18950 | 37906 | 1.97341 | 18953 | 18953 | 37906 | 1.30767 | 18956 | 18952 | 37908 | 0.695926 | 18954 | 18951 | 37904 | 1.19530 |
| 21321 | 21321 | 42642 | 2.49744 | 21326 | 21322 | 42647 | 1.56087 | 21324 | 21324 | 42647 | 1.79989 | 21324 | 21322 | 42646 | 2.59476 |
| 23692 | 23691 | 47382 | 3.28202 | 23691 | 23689 | 47380 | 1.65630 | 23691 | 23691 | 47382 | 1.68554 | 23695 | 23692 | 47386 | 2.34473 |
| 26060 | 26057 | 52117 | 4.27776 | 26056 | 26055 | 52110 | 2.42245 | 26062 | 26058 | 52119 | 1.75813 | 26063 | 26062 | 52125 | 2.53149 |
| 28428 | 28428 | 56856 | 5.13220 | 28433 | 28430 | 56862 | 2.56622 | 28429 | 28429 | 56858 | 1.81126 | 28426 | 28424 | 56850 | 3.20492 |
| 30806 | 30792 | 61597 | 5.89680 | 30799 | 30798 | 61596 | 2.58775 | 30795 | 30794 | 61588 | 1.89857 | 30801 | 30794 | 61594 | 3.35070 |
| 33167 | 33162 | 66328 | 6.69753 | 33166 | 33163 | 66328 | 1.99392 | 33167 | 33163 | 66329 | 1.99513 | 33170 | 33166 | 66336 | 3.04059 |
| 35530 | 35528 | 71058 | 7.90779 | 35531 | 35527 | 71058 | 2.03343 | 35536 | 35533 | 71068 | 2.75324 | 35537 | 35531 | 71067 | 3.60135 |
| 37899 | 37898 | 75796 | 9.05008 | 37906 | 37900 | 75806 | 2.73571 | 37909 | 37902 | 75810 | 2.15128 | 37900 | 37896 | 75795 | 2.95120 |
| 40272 | 40271 | 80543 | 10.1587 | 40273 | 40270 | 80543 | 5.17328 | 40276 | 40272 | 80547 | 5.02242 | 40274 | 40269 | 80542 | 7.45715 |
| 2645 | 42635 | 85279 | 11.3702 | 42643 | 42635 | 85277 | 5.32442 | 42644 | 42639 | 85283 | 5.36077 | 42647 | 42634 | 85281 | 7.88211 |
| 45016 | 45006 | 90021 | 13.1765 | 45000 | 44998 | 89998 | 5.57535 | 45010 | 45004 | 90014 | 5.59056 | 45007 | 45002 | 90009 | 8.19759 |
| 筆算処理による乗算 | Karatsuba 法 ( recLvl = 5 ) |
|---|---|
 |  |
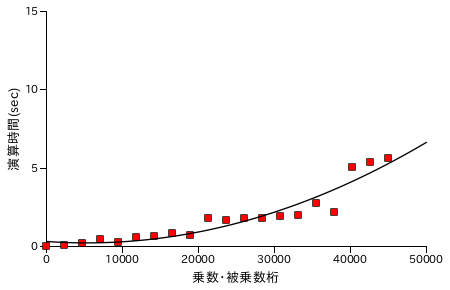
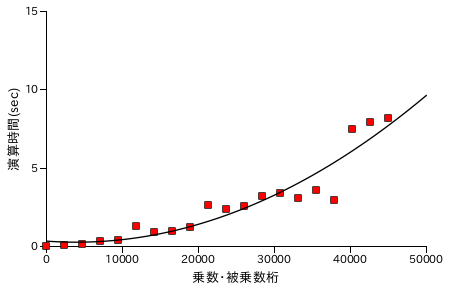
| Karatsuba 法 ( recLvl = 7 ) | Karatsuba 法 ( recLvl = 9 ) |
 |  |
筆算処理の場合と比較すると、処理時間は半分弱にまで短縮できていることが分かります。筆算処理の処理時間が桁数の二乗に比例して増大するのに対して、Karatsuba 法を使って再帰的に処理を行った場合は理論上、桁数の log23 ( ≅ 1.585 ) 乗まで抑えることができます。しかし、40000 桁あたりから処理時間が急激に増大しているため Karatsuba 法のグラフに対してもフィッティング曲線は次数 2 の多項式です。なお、処理時間が急激に増える箇所があるのは、しきい値を決めて再帰処理を行っているために演算回数が急激に上昇する箇所があることに由来すると考えられます。
recLvl に対する処理時間の推移を以下に示します。桁数は 10 万桁程度で、同じ数を 25 回演算した合計時間を示しています。
筆算処理と比較して、recLvl = 2 から処理時間は短くなっています。recLvl = 1 にすると、再帰処理の回数が増大してかえって処理時間は長くなるようです。だいたい、5 〜 6 あたりが最適値でしょうか。筆算処理と比較して 5 倍程度、処理能力は向上しています。
Karatsuba 法で示した二数の積の計算式を、もう一度以下に示します。
ここで p を変数 x と置き換えると、上式は以下のような二次方程式と考えることができます。
但し、
とします。各項の係数 wi の値を解くことができれば、w(p) は各係数を適当にシフトさせながら加算処理を行うことで求めることができます。Karatsuba 法では、係数 w1 の計算に w0 と w2 を利用することで、乗算処理を減らしました。
多項式の次数を大きくした場合を考えます。例えば、二数 u, v を三等分して二次式とした場合、
但し 0 ≦ ui < p ; 0 ≦ vi < p (i = 0,1,2)
と表すことができるので、その積 w(x) は、
| w(x) | = | ( u2x2 + u1x + u0 )( v2x2 + v1x + v0 ) |
| = | u2v2x4 + ( u2v1 + u1v2 )x3 + ( u2v0 + u1v1 + u0v2 )x2 + ( u1v0 + u0v1 )x + u0v0 | |
| = | w4x4 + w3x3 + w2x2 + w1x + w0 |
但し、
になります。係数 wi を求めるために上式の右辺を計算した場合、乗算しなければならない回数は 9 回となり、値を三等分しても意味がなくなってしまいます。そこで w(x) に対する式において、変数 x に -2, -1, 0, 1, 2 をそれぞれ代入してみます。
| w(-2) | = | 16w4 - 8w3 + 4w2 - 2w1 + w0 |
| w(-1) | = | w4 - w3 + w2 - w1 + w0 |
| w(0) | = | w0 |
| w(1) | = | w4 + w3 + w2 + w1 + w0 |
| w(2) | = | 16w4 + 8w3 + 4w2 + 2w1 + w0 |
これは w0 から w4 までを未知数とする連立方程式と見なすことができます。左辺の値は、u2x2 + u1x + u0 と v2x2 + v1x + v0 それぞれの式において変数 x に値を代入してから積を計算することによって求めることができ、この時の乗算処理回数は 5 回になります。元の二数 u,v の桁数が N 桁だったとき、w(x) の計算に使用する二数はおよそ N / 3 桁になるので、通常の乗算処理に必要な処理回数 N2 に対して、5 x ( N / 3 )2 = ( 5 / 9 )N2 と半分程度まで減らすことができます。Karatsuba 法が、一回の処理で 3 x ( N / 2 )2 = ( 3 / 4 )N2 に短縮できるのと比較すると、分割数を多くした方が処理回数を少なくすることができるわけです。ここで、さらに分割数を多くして、乗数と被乗数を N - 1 次式で表してみます。
| u(x) | = | uN-1xN-1 + uN-2xN-2 + ... + u1x + u0 |
| = | Σk{0→N-1}( ukxk ) | |
| v(x) | = | Σk{0→N-1}( vkxk ) |
但し 0 ≤ ui < p ; 0 ≤ vi < p ( i = 0,1 ... N-1 )
この時、二数の積 w(x) = Σk{0→2(N-1)}( wkxk ) の各係数 wk を未知数として 2N - 1 個の連立方程式が得られ、u(x) と v(x) に適当な値を代入して計算した結果がおよそ一桁だったと仮定した場合、乗算処理に必要な回数は約 2N - 1 までに短縮することができます。計算結果が全て一桁になることは実際にはあり得ませんが、それでも乗算時の桁数を大幅に下げることが可能になります。あとは、この連立方程式を効率よく解くことができればいいわけです。
上記の処理は結局、多項式の各係数を求めていることになります。このような処理を効率よく行うためのアルゴリズムとして「Toom-Cook 法 ( Toom-Cook Multiplication )」があります。まずは、アルゴリズムから紹介したいと思います。
これが第一段階の処理になります。ここではまだ係数を求めるには至っていないため、第二段階の処理が必要になります。
第二段階は複雑そうに見えますが、中身は二重ループ処理になっているだけです。内側のループは i 回繰り返され、i は 1 ずつ減算されているため、減算処理の回数は一回ずつ減っていくことに注意してください。
例として、10 進 4 桁の数 2901 と 5133 を、Toom-Cook 法で処理したいと思います。
u = 2901 = 2 x 103 + 9 * 102 + 0 x 10 + 1
v = 5133 = 5 x 103 + 1 * 102 + 3 x 10 + 3 より
u(x) = 2x3 + 9x2 + 0x + 1
v(x) = 5x3 + 1x2 + 3x + 3 とする。
この時、w(x) = u(x)v(x) は 6 次式となり、求めるべき係数は 7 つになる。
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| u(i) | 1 | 12 | 53 | 136 | 273 | 476 | 757 |
| v(i) | 3 | 12 | 53 | 156 | 351 | 668 | 1137 |
| w(i,0) | 3 | 144 | 2809 | 21216 | 95823 | 317968 | 860709 |
| w(i,1) | 141 | 2665 | 18407 | 74607 | 222145 | 542741 | |
| w(i,2) | 1262 | 7871 | 28100 | 73769 | 160298 | ||
| w(i,3) | 2203 | 6743 | 15223 | 28843 | |||
| w(i,4) | 1135 | 2120 | 3405 | ||||
| w(i,5) | 197 | 257 | |||||
| w(i,6) | 10 |
w(0,i) ( i = 0 〜 6 ) を使って第二段階の処理を行う。
| w(0,0) | w(0,1) | w(0,2) | w(0,3) | w(0,4) | w(0,5) | w(0,6) | d(0) | d(1) | d(2) | d(3) | d(4) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 141 | 1262 | 2203 | 1135 | 197 | 10 | 10 | 10 | 10 | 10 | 10 |
| 3 | 141 | 1262 | 2203 | 1135 | 47 | 10 | 147 | 107 | 77 | 57 | 47 |
| 3 | 141 | 1262 | 2203 | 15 | 47 | 10 | 547 | 226 | 72 | 15 | |
| 3 | 141 | 1262 | 38 | 15 | 47 | 10 | 562 | 110 | 38 | ||
| 3 | 141 | 28 | 38 | 15 | 47 | 10 | 138 | 28 | |||
| 3 | 3 | 28 | 38 | 15 | 47 | 10 | 3 |
よって、w(x) = 10x6 + 47x5 + 15x4 + 38x3 + 28x2 + 3x + 3 となり、w(10) = 10000000 + 4700000 + 150000 + 38000 + 2800 + 30 + 3 = 14890833
Toom-Cook 法のサンプル・プログラムを以下に示します。
namespace BigNum { /* Unsigned::toomCook Toom-Cook法による乗算 被乗数 uと乗数 vに対して u = Σ(ur * x^r) , v = Σ(vr * x^r) の形に分解し、それぞれの係数を求める const Unsigned& v : 乗数 UnsignedBuff r : 分割単位 - 1 (u,vを多項式と見たときの最大指数) */ Unsigned& Unsigned::toomCook( const Unsigned& v, UnsignedBuff r ) { if ( r == 0 ) { operator*=( v ); return( *this ); } if ( isNaN( v ) ) return( *this ); UnsignedBuff i = ( size() > v.size() ) ? size() : v.size(); r++; UnsignedBuff sz = i / r; // 分割後のサイズ if ( ( i % r ) != 0 ) sz++; // 値を分割して配列に代入 Unsigned uArray[r]; Unsigned vArray[r]; for ( i = 0 ; i < r ; i++ ) { uArray[i] = Unsigned( *this, i * sz, ( i + 1 ) * sz - 1 ); } for ( i = 0 ; i < r ; i++ ) { vArray[i] = Unsigned( v, i * sz, ( i + 1 ) * sz - 1 ); } // uvの指数を計算(=求めるべき係数の数) UnsignedBuff k = r * 2 + 1; // w(i) = u(i)v(i)を計算 vector< Unsigned > w; w.push_back( uArray[0] * vArray[0] ); for ( i = 1 ; i < k ; i++ ) { Unsigned u2( uArray[0] ); Unsigned v2( vArray[0] ); for ( UnsignedBuff j = 1 ; j < r ; j++ ) { Unsigned p( i ); p.pow( j ); u2 += uArray[j] * p; v2 += vArray[j] * p; } u2 *= v2; w.push_back( u2 ); } // ( w(i+1) - w(i) ) / i を計算 for ( i = 1 ; i < k ; i++ ) { vector< Unsigned > d; for ( UnsignedBuff j = i ; j < k ; j++ ) d.push_back( w[j] - w[j-1] ); for ( UnsignedBuff j = i ; j < k ; j++ ) { w[j] = d[j-i]; w[j] /= i; } } clear(); // 係数の計算 vector< Unsigned > d; for ( i = k - 2 ; i > 0 ; i-- ) d.push_back( w[k-1] ); for ( i = k - 2 ; i > 0 ; i-- ) { for ( UnsignedBuff j = 0 ; j < i ; j++ ) { d[j] *= i - j; w[i] -= d[j]; d[j] = w[i]; } } // 係数を使って結果を算出 for ( i = k ; i > 0 ; --i ) partialAdd( w[i - 1], ( i - 1 ) * sz ); return( *this ); } }
先ほど説明した処理の流れに沿った形になっているのでそれほど難しいところはないと思います。最後に呼び出している関数 partialAdd は部分的に加算処理をするためのもので、前章のサンプル・プログラム内で登場しています。
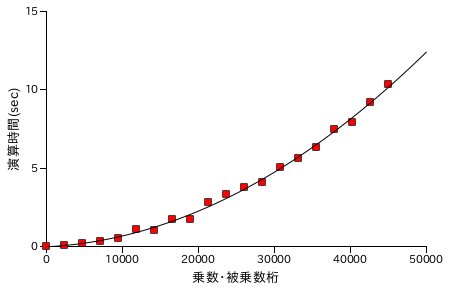
Karatsuba 法と同様に、Toom-Cook 法による乗算処理の性能評価結果を以下に示します。各グラフの X 軸は処理する数の桁数を表し、ほぼ同じ桁の数どうしを演算処理させています。また Y 軸は処理時間 ( sec. ) を表し、処理時間は同じ数値について演算を 25 回繰り返した合計時間になります。計測は Windows7 上の VirtualBox でゲスト OS を Xubuntu 16.04 LTS として行っています。CPU は Intel Core i7-2600 3.40GHz で、ゲスト OS 上ではコア数を 1 としています。
| 分割単位 2 | 分割単位 10 | 分割単位 16 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 被乗数桁数 | 乗数桁数 | 結果桁数 | 演算時間(sec) | 被乗数桁数 | 乗数桁数 | 結果桁数 | 演算時間(sec) | 被乗数桁数 | 乗数桁数 | 結果桁数 | 演算時間(sec) |
| 5 | 5 | 10 | 0.001737 | 5 | 5 | 10 | 0.045398 | 5 | 5 | 10 | 0.073798 |
| 2374 | 2373 | 4747 | 0.088116 | 2374 | 2373 | 4747 | 0.150084 | 2374 | 2373 | 4747 | 0.22038 |
| 4743 | 4743 | 9485 | 0.171667 | 4745 | 4742 | 9486 | 0.255045 | 4744 | 4744 | 9488 | 0.637321 |
| 7114 | 7112 | 14226 | 0.337664 | 7109 | 7108 | 14216 | 0.392355 | 7112 | 7112 | 14223 | 0.908824 |
| 9480 | 9479 | 18958 | 0.506623 | 9479 | 9478 | 18957 | 0.548437 | 9481 | 9477 | 18958 | 0.723668 |
| 11849 | 11848 | 23696 | 1.06708 | 11848 | 11848 | 23695 | 0.687584 | 11851 | 11846 | 23696 | 0.904597 |
| 14219 | 14217 | 28435 | 1.03544 | 14218 | 14216 | 28433 | 1.02949 | 14217 | 14217 | 28434 | 1.31089 |
| 16589 | 16580 | 33168 | 1.69822 | 16591 | 16586 | 33177 | 1.04457 | 16586 | 16585 | 33170 | 1.29101 |
| 18957 | 18956 | 37912 | 1.73489 | 18955 | 18952 | 37906 | 1.90878 | 18958 | 18949 | 37907 | 1.79107 |
| 21325 | 21324 | 42648 | 2.81449 | 21325 | 21321 | 42645 | 1.45298 | 21322 | 21319 | 42641 | 1.72331 |
| 23692 | 23691 | 47383 | 3.32285 | 23692 | 23689 | 47380 | 1.63567 | 23695 | 23692 | 47386 | 2.26623 |
| 26057 | 26057 | 52114 | 3.79106 | 26060 | 26058 | 52117 | 2.54994 | 26060 | 26057 | 52116 | 2.83283 |
| 28434 | 28428 | 56862 | 4.08191 | 28429 | 28425 | 56853 | 2.81353 | 28429 | 28429 | 56858 | 3.07073 |
| 30802 | 30792 | 61594 | 5.02249 | 30801 | 30799 | 61600 | 2.93562 | 30791 | 30790 | 61580 | 2.67334 |
| 33167 | 33159 | 66326 | 5.64314 | 33170 | 33165 | 66334 | 2.63251 | 33169 | 33169 | 66337 | 3.57780 |
| 35540 | 35534 | 71073 | 6.34679 | 35537 | 35533 | 71069 | 3.61923 | 35531 | 35531 | 71062 | 3.80327 |
| 37906 | 37901 | 75807 | 7.46538 | 37904 | 37899 | 75803 | 3.75717 | 37907 | 37900 | 75807 | 4.08856 |
| 40271 | 40267 | 80538 | 7.90257 | 40275 | 40268 | 80543 | 3.46710 | 40275 | 40275 | 80549 | 4.36678 |
| 42641 | 42638 | 85278 | 9.20287 | 42642 | 42636 | 85278 | 4.26450 | 42647 | 42638 | 85285 | 4.67242 |
| 45011 | 45008 | 90019 | 10.3309 | 45010 | 45008 | 90018 | 4.78654 | 45007 | 45005 | 90011 | 4.92400 |
| 筆算処理による乗算 | ToomCook法 ( 分割単位 2 ) |
|---|---|
 |  |
| ToomCook法 ( 分割単位 = 10 ) | ToomCook法 ( 分割単位 = 16 ) |
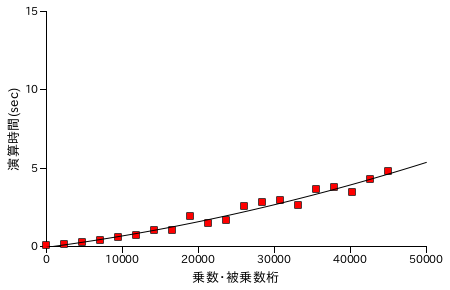 |  |
分割単位を多くするほど、フィッティング曲線は直線に近くなっていきます。約 45000 桁の数どうしの乗算について比較すると、Karatsuba 法が最短で 5.58 sec. なのに対し、Toom-Cook 法が 4.79 sec. なので大幅に時間が短縮されたというわけではありませんでした。
Toom-Cook 法でも 10 万桁程度の数どうしの乗算で分割単位による推移を確認したところ、以下のような結果になりました。
|
|
だいたい分割単位 15 程度で時間はほぼ一定となり、これ以上はしきい値を上げても効果はないようです。なお、分割単位をこのまま大きくしていくと筆算での乗算処理の処理速度に近づいてゆくことは容易に想像できるので、15 程度から徐々に演算時間は大きくなることが予想されます。
まず、n - 1 次の多項式 w(x) が、以下のように変形できたと仮定します。
| w(x) | = | sn-1x( x - 1 )( x - 2 )...[ x - ( n - 1 ) + 1 ] + sn-2x( x - 1 )( x - 2 )...[ x - ( n - 2 ) + 1 ] + ... + s2x(x-1) + s1x + s0 |
| = | Σk{0→n-1}( skP(x,k) ) |
但し、P(x,k) = x( x - 1 )( x - 2 )...( x - k + 1 ) = x! / ( x - k )!
P(x,k) は順列を求める式であり、x が自然数 n である場合、n 個の要素から k 個の要素を取り出して並べる方法の総数を表しています。
x が k より小さい自然数であるとき P(x,k) = 0 なので、x に 0 から n - 1 までの数を代入したときの値は、次のようになります。
| w(0) | = | P(0,0)s0 |
| w(1) | = | P(1,1)s1 + P(1,0)s0 |
| w(2) | = | P(2,2)s2 + P(2,1)s1 + P(2,0)s0 |
| w(3) | = | P(3,3)s3 + P(3,2)s2 + P(3,1)s1 + P(3,0)s0 |
| w(4) | = | P(4,4)s4 + P(4,3)s3 + P(4,2)s2 + P(4,1)s1 + P(4,0)s0 |
| : | ||
| w(n-2) | = | P(n-2,n-2)sn-2 + P(n-2,n-3)sn-3 + ... + P(n-2,1)s1 + P(n-2,0)s0 |
| w(n-1) | = | P(n-1,n-1)sn-1 + P(n-1,n-2)sn-2 + ... + P(n-1,2)s2 + P(n-1,1)s1 + P(n-1,0)s0 |
ここで、それぞれ隣り合った要素間の差 Δw(i) = w(i+1) - w(i) を計算してみます。
| Δw(0) | = | w(1) - w(0) | = | P(1,1)s1 + [ P(1,0) - P(0,0) ]s0 |
| Δw(1) | = | w(2) - w(1) | = | P(2,2)s2 + [ P(2,1) - P(1,1) ]s1 + [ P(2,0) - P(1,0) ]s0 |
| Δw(2) | = | w(3) - w(2) | = | P(3,3)s3 + [ P(3,2) - P(2,2) ]s2 + [ P(3,1) - P(2,1) ]s1 + [ P(3,0) - P(2,0) ]s0 |
| Δw(3) | = | w(4) - w(3) | = | P(4,4)s4 + [ P(4,3) - P(3,3) ]s3 + [ P(4,2) - P(3,2) ]s2 + [ P(4,1) - P(3,1) ]s1 + [ P(4,0) - P(3,0) ]s0 |
| : | ||||
| Δw(n-2) | = | w(n-1) - w(n-2) | = | P(n-1,n-1)sn-1 + [ P(n-1,n-2) - P(n-2,n-2) ]sn-2 + ... + [ P(n-1,1) - P(n-2,1) ]s1 + [ P(n-1,0) - P(n-2,0) ]s0 |
P(x,k) に対して、以下の等式が成り立ちます。
| P(x+1,k) - P(x,k) | = | ( x + 1 )x( x - 1 ) ... [ ( x + 1 ) - k + 1 ] - x( x - 1 )...( x - k + 1 ) |
| = | [ ( x + 1 ) - ( x - k + 1 ) ]x( x - 1 ) ... ( x - k + 2 ) | |
| = | kx( x - 1 ) ... [ x - ( k - 1 ) + 1 ] | |
| = | k・P(x,k-1) |
また、以下の関係式が成り立ちます。
| P(k,k) | = | k! / ( k - k )! |
| = | k(k-1)! / [ ( k - 1 ) - ( k - 1 ) ]! | |
| = | k・P(k-1,k-1) |
P(x,0) = 1 なので s0 の項は全て消え、先ほど計算した Δw(i) は上記の関係式を使って以下のようになります。
| Δw(0) | = | P(1,1)s1 |
| Δw(1) | = | 2P(1,1)s2 + P(1,0)s1 |
| Δw(2) | = | 3P(2,2)s3 + 2P(2,1)s2 + P(2,0)s1 |
| Δw(3) | = | 4P(3,3)s4 + 3P(3,2)s3 + 2P(3,1)s2 + P(3,0)s1 |
| : | ||
| Δw(n-2) | = | ( n - 1 )P(n-2,n-2)sn-1 + ( n - 2 )P(n-2,n-3)sn-2 + ... + 2P(n-2,1)s2 + P(n-2,0)s1 |
この結果から、s1 の値は Δw(0) / P(1,1) = Δw(0) より求めることができます。さらに Δ2w(i) = Δw(i+1) - Δw(i) を計算してみましょう。
| Δ2w(0) | = | 2P(1,1)s2 + [ P(1,0) - P(0,0) ]s1 |
| Δ2w(1) | = | 3P(2,2)s3 + 2[ P(2,1) - P(1,1) ]s2 + [ P(2,0) - P(1,0) ]s1 |
| Δ2w(2) | = | 4P(3,3)s4 + 3[ P(3,2) - P(2,2) ]s3 + 2[ P(3,1) - P(2,1) ]s2 + [ P(3,0) - P(2,0) ]s1 |
| : | ||
| Δ2w(n-2) | = | ( n - 1 )P(n-2,n-2)sn-1 + ( n - 2 )[ P(n-2,n-3) - P(n-3,n-3) ]sn-2 + ... + 2[ P(n-1,1) - P(n-2,1) ]s2 + [ P(n-1,0) - P(n-2,0) ]s1 |
↓
| Δ2w(0) | = | 2P(1,1)s2 |
| Δ2w(1) | = | (3x2)P(1,1)s3 + 2P(1,0)s2 |
| Δ2w(2) | = | (4x3)P(2,2)s4 + (3x2)P(2,1)s3 + 2P(2,0)s2 |
| : | ||
| Δ2w(n-2) | = | ( n - 1 )( n - 2 )P(n-3,n-3)sn-1 + ( n - 2 )( n - 3 )P(n-3,n-4)sn-2 + ... + 2P(n-2,0)s2 |
この結果により、s2 の値は Δ2w(0) / 2P(1,1) = Δ2w(0) / 2 で求められます。この操作は、全ての sk を求められるまで繰り返し実行することができ、結局各 sk は以下の式で求めることができることになります。
この処理を行うためのアルゴリズムが第一段階の部分になります。
ここで求められた係数 sk は P(x,k) に対するものなので、これを xk に対する係数に変換する必要があります。そこで、w(x) を次のように変形します。
これではわかりにくいと思いますので、四次式での例を以下に示します。
単純に、x から順に共通項を括ると、上記のような式ができます。
例に挙げた式中、一番内側にある括弧の中 s4(x - 3) + s3 を展開すると、
になります。s3 - 3s4 = d30 として、一つ外側の括弧を展開すると
今度は、d30 - 2s4 = d21、s2 - 2d30 = d20 として次を展開すると、
最後に d21 - s4 = d12、d20 - d21 = d11、s1 - d20 = d10 として展開すると、
になります。それぞれの処理において、
を展開したとき、p 次項の係数は
で計算することができます。n - k - 1 = 1 になったときの結果 d1p が求めるべき係数であり、上記操作を行うための処理が第二段階のアルゴリズムになるわけです。
乗算処理を高速化するためのアルゴリズムとして Booth の乗算アルゴリズム ( Booth's Multiplication Algorithm ) というものがあります。多倍長整数専用の乗算アルゴリズムという内容からは外れるため、番外編として紹介したいと思います。
処理の手順は、次のようになります。
実際の計算例を以下に示します。
例) 4 x -5 u = 4 = 0100 (uBit=4) v = -5 = 1011 (vBit=4) a : 0100 0000 0 s : 1100 0000 0 p : 0000 1011 0 ループ 1 回め p の末尾 2 ビット = 10 → p += s p : 1100 1011 0 右シフト p : 1110 0101 1 ループ 2 回め p の末尾 2 ビット = 11 → 何もしない p : 1110 0101 1 右シフト p : 1111 0010 1 ループ 3 回め p の末尾 2 ビット = 01 → p += a p : 0011 0010 1 右シフト p : 0001 1001 0 ループ 4 回め p の末尾 2 ビット = 10 → p += s p : 1101 1001 0 右シフト p : 1110 1100 1 最後にもう一度右シフト p : 1110 1100 = -20
何故このような方法で正しい結果が得られるのかについて、ある数 U に 14 を掛けることを例にして考えてみたいと思います。
14 は二進表記で 1110 になります。よって、
と表すことができます。しかし、1110 = 10000 - 10 なので、上式は次のように表すこともできます。
ビットの立った列があったとき、それが 2m + 2m-1 + ... + 2m-(n+1) + 2m-n であれば、2m+1 - 2m-n に変形することができます。これは、ビットの立った列が複数あった場合でも各列に対して独立に変形することが可能で、例えば 238 = 11101110 の場合、
| 11101110 | = | ( 27 + 26 + 25 ) + ( 23 + 22 + 21 ) |
| = | ( 28 - 25 ) + ( 24 - 21 ) |
と表せます。従って、加算・減算操作はそれぞれ、ビット列が "01", "10" になったところで行えばよいことになります。言わば、筆算処理の変型したバージョンと考えることができます。さらに、この手法は負数に対しても正常に機能するという特徴も持っています。
筆算処理を利用した場合は加算処理がビット列の長さ分必要になるのに対し、変更した形で処理を行うと、加算・減算処理が合わせて二回になるため、ビット列が長くなるほど演算回数を減らすことができます。しかし、1 が連続して並んでいないような場合は、逆に演算回数が増えてしまうという問題もあります。なお、この手法は、現在でも乗算器などで利用されているそうです。
以下に、Booth の乗算アルゴリズムを使った乗算処理のサンプル・プログラムを示します。
/* 有効ビット数をカウントする short s : 対象の数値 戻り値 : 有効ビット数 */ unsigned int countBit( short s ) { if ( s < 0 ) s *= -1; unsigned int bitCnt = 0; while ( s != 0 ) { s >>= 1; bitCnt++; } return( bitCnt + 1 ); } /* ブースの乗算処理 short u : 被乗数 short v : 乗数 戻り値 : 算術結果 u は15Bit(-16384〜16383) , v は16Bit(-32768〜32767)までとする。 範囲外だった場合は0を返す。 */ int boothMul( short u, short v ) { if ( u == 0 || v == 0 ) return( 0 ); if ( countBit( u ) > 15 ) return( 0 ); unsigned int vBit = countBit( v ); unsigned short vMask = ( 1 << ( vBit + 1 ) ) - 1; int a = u << ( vBit + 1 ); // add(加算) int s = (-u) << ( vBit + 1 ); // sub(減算) int p = ( v << 1 ) & vMask; // product(積) for ( unsigned int i = 0 ; i < vBit ; i++ ) { int bits = p & 3; // pの下位2Bits if ( bits == 1 ) p += a; else if ( bits == 2 ) p += s; p >>= 1; } return( p >> 1 ); }
多倍長整数の乗算処理において、もう一つの高速化手法として高速フーリエ変換があります。次回は、高速フーリエ変換を題材に進めたいと思います。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |