パターン認識の分野において、歴史上重要な役割を担ってきたものに「パーセプトロン ( Perceptron )」があります。パーセプトロンは「ローゼンブラット ( Frank Rosenblatt )」により 1962 年に公開された線形認識モデルの一つです。この章では、線形識別モデルの一般的な話から、その例としてパーセプトロンまでを紹介します。
「凝集型クラスタリング」の章でも説明したように、入力パターンの識別には「プロトタイプ ( Prototype )」と呼ばれる代表的な特徴ベクトルをあらかじめ用意しておいて、それを用いて行われます。そのようなお手本を用意せず、とりあえず近いものを集めるのがクラスタリングの考え方でした。今回はお手本があるので、最も近いお手本を選んでクラスタ分類するというのは自然なやり方です。
プロトタイプが属しているクラスタは「クラス ( Class )」と呼ばれます。入力パターンに最も近いプロトタイプが属しているクラスに分類する手法を「最近傍決定則 ( NN 法 ) ( Nearest Neighbor Rule ; NN Rule )」といいます。"最も近い" という概念を表す距離には通常ユークリッド距離が用いられます。より一般的に、入力パターンに最も近い k 個のプロトタイプを抽出してその中で最も多数を占めたクラスを選択する方法は「k-NN 法 ( k-nearest Neighbor Rule )」と呼ばれます。また、クラスあたりのプロトタイプの数についても選択肢があり、1 クラスあたり 1 プロトタイプの場合は「最小距離識別法 ( Minimum Distance Method )」と呼ぶこともあります。逆に収集した全てのパターンをプロトタイプとして使用する方法は「全数記憶方式 ( Complete Strage )」といいます。
早速、サンプル・プログラムを示したいと思います。
/* K_NN_Method : k-NN 法によるクラス分類 trainData : 教師ベクトル classNo : 各教師ベクトルに対応するクラス pattern : 入力パターン k : 最近傍の教師ベクトルとして抽出する数 reject : リジェクト値 戻り値 : 分類したクラス番号 */ int K_NN_Method( const vector< vector< double > >& trainData, const vector< int >& classNo, const vector< double >& pattern, unsigned int k, double reject ) { typedef vector< double >::size_type size_type; typedef map< int, unsigned int >::const_iterator MapCit; typedef multimap< double, int >::const_iterator MMapCit; L2Distance l2Distance; // 距離の近い順にソート multimap< double, int > distance; for ( size_type i = 0 ; i != trainData.size() ; ++i ) { distance.insert( std::pair< double, int > ( l2Distance( trainData[i].begin(), trainData[i].end(), pattern.begin() ), classNo[i] ) ); } // 距離の近いものから順に k 個取り出してクラスを取得 MMapCit cit = distance.begin(); map< int, unsigned int > count; for ( unsigned int i = 0 ; i < k ; ++i ) { if ( cit == distance.end() ) break; if ( cit->first >= reject ) break; if ( count.find( cit->second ) == count.end() ) count[cit->second] = 0; ++( count[cit->second] ); ++cit; } // 個数の最も大きいクラスを抽出 int ans = -1; unsigned int maxCnt = 0; for ( MapCit cit = count.begin() ; cit != count.end() ; ++cit ) { if ( maxCnt < cit->second ) { maxCnt = cit->second; ans = cit->first; } } return( ans ); }
距離としては「パターン認識 (1) 凝集型クラスタリング」でも紹介した「L2 ノルム ( L2Distance )」を利用しています。入力パターンと各プロトタイプとの距離を計算し、それをクラス番号と一緒にバッファに保持します。それを距離の小さい順に k 個選んでクラス番号を抽出し、最も数の多いクラス番号を戻り値として返します。
距離の小さい順にクラス番号を抽出するためにはバッファをソートする必要があります。このために STL ( Standard Template Library ) のコンテナ・クラス multimap を利用しています。map と multimap はキーと値をペアで登録するコンテナで、キー順にソートして登録されるため、あらかじめソートした状態でコンテナを用意したいような場合には便利です。map と multimap の違いは、前者がキーの重複を許さないのに対し、multimap はそれを許すという点です。
multimap 型のコンテナ distance は距離をキー、クラス番号を値として登録を行うため、登録後に先頭から k 個の要素を抽出すれば最近傍の k 個の要素に対するクラスが得られます。その中から数の多いクラス番号を取得する際にも map を利用しています。
1 クラスあたり 1 プロトタイプの 1-NN 法を定式化してみます。クラス数を C として、各クラスのプロトタイプを pj ( j = 1, 2, ... C ) とします。入力パターン x に対し、プロトタイプ pj との L2 ノルムは
と計算することができます。ここで || x ||2 は各プロトタイプに対して一定なので、ノルムを最小にすることは次の関数
を最大化することと同じ意味になります。
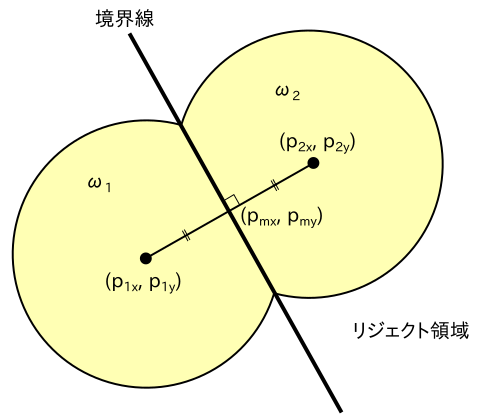
2 クラスの 1-NN 法について、プロトタイプとその判定領域を図に表したものを以下に示します。パターンの次元数は 2 となります。
 |
入力パターンがプロトタイプからあまりにもかけ離れている場合、どちらのクラスにも属さないと判断する方がよいことがあります。プロトタイプから一定の距離以上離れた領域は「リジェクト領域」と表しています。判定領域の境界線は、プロトタイプを結んだ線分の垂直二等分線になることが上図からわかります。この境界を表す関数を「識別関数 ( Discriminant Function )」といいます。上図の例では識別関数は y = w1( x - pmx ) + pmy の形で表されます。但し、
( pmx, pmy ) = ( ( p1x + p2x ) / 2, ( p1y + p2y ) / 2 )
w1 = -( p2x - p1x ) / ( p2y - p1y )
とします。この関数は ( x, y ) に関して線形なので「線形識別関数 ( Linear Discriminant Function )」といいます。
結局、上記内容を一般化すると
として gj(x') が最大となる j を選択することでパターン認識を行うことができます。ここで w'j は「重みベクトル ( Weight Vector )」、w'j0 は「バイアス・パラメータ ( Bias Parameter )」と呼ばれます。線形識別関数において、
w'j = pj
w'j0 = (-1/2)|| pj ||2
とすると、これは 1 クラスあたり 1 プロトタイプの 1-NN 法に相当します。
重みベクトルとバイアス・パラメータを一つにまとめて
wj = ( w'j0, w'jT )T = ( w'j0, w'j1, w'j2, ... w'jp )T
x = ( 1, x'T )T = ( 1, x'1, x'2, ... x'p )T
とすることで上式は
と簡単に表すことができます。このときの x を「拡張特徴ベクトル ( Augmented Feature Vector )」、wj を「拡張重みベクトル ( Augmented Weight Vector )」といいます。2 クラスならば
| g(x) | = | g1(x) - g2(x) |
| = | ( w1T - w2T )x | |
| = | wTx |
として g(x) > 0 ならばクラス 1、g(x) < 0 ならばクラス 2 を選択する形でも実現できます ( 補足 1 )。
g(x) = 0 は二つのクラスの境界となり、それは特徴ベクトル空間中の超平面に対応します。この超平面上の任意の点 x1, x2 について g(x1) = g(x2) = 0 なので
| g(x1) - g(x2) | = | wTx1 - wTx2 |
| = | wT( x1 - x2 ) | |
| = | 0 |
であり、w は境界面上の任意のベクトルに直交するので、境界面の方向を決定する法線ベクトルになります。また、超平面上の任意の点 x'1 に対して
なので
となります。w' と x'1 のなす角を θ とすると、左辺は
で、これは原点から境界面までの距離を表します。よって、バイアス・パラメータ w'0 は境界面の位置を決定するパラメータであることになります。
任意の点 x' について、境界面への直交射影 ( 境界面へ x' から垂線を下ろしたときの足 ) を x'⊥ とします。このとき、ある定数 r があって、
と表すことができます。この r は x' から境界面までの距離を表しています。両辺に w'T を掛けて w'0 を加えると
より
g(x'⊥) = 0 なので
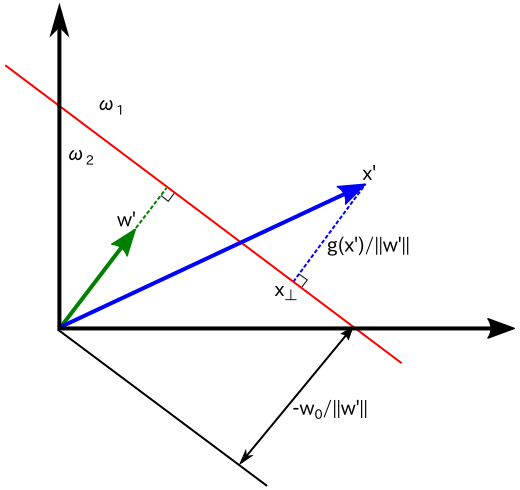
となり、g(x') の値より、x' から境界面までの距離を求めることができます。これらの関係を下図に示します。
 |
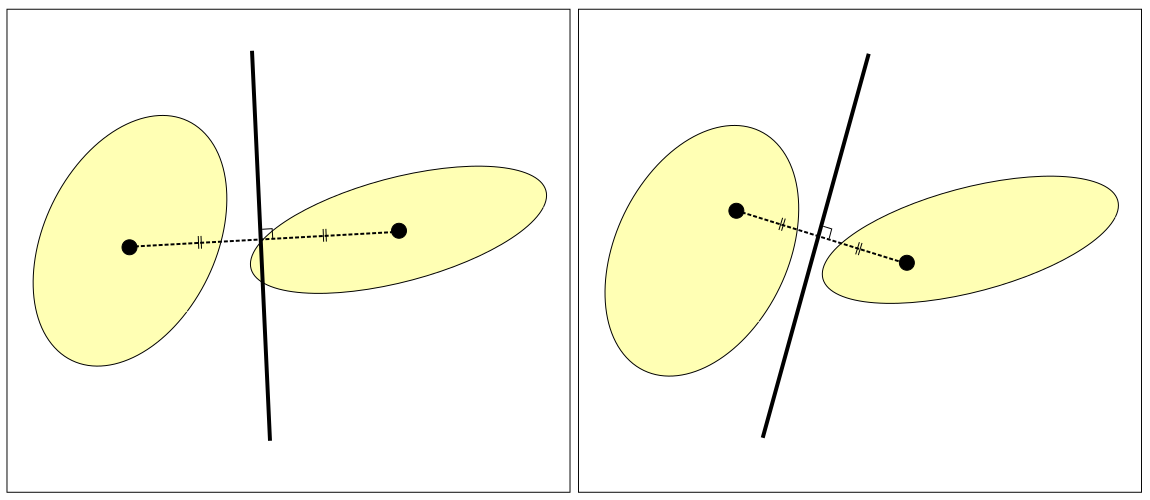
前節の NN 法ではプロトタイプがあらかじめ決まっているものとしてクラス分類を行っていました。プロトタイプとしては、収集したパターンの代表や、各クラスごとに重心を計算して利用する方法などが考えられます。しかし、これの方法ではクラスを正しく分割できない場合もあります。下に示した図の左側は、重心をプロトタイプとしたときに正しく分割できない例です。右側のようにプロトタイプを重心からずらすことにより正しく分割できるようになります。
 |
正しくクラス分割できるようにプロトタイプを求める処理を「学習 ( Learning )」といいます。線形識別関数では重みベクトル wj と入力ベクトル x の内積が最大となるような j を選択することでクラスを識別するのでした。従って、重みベクトルを学習によって求めることになります。重みベクトルを求めるために利用するパターンは「学習パターン ( Learning Pattern )」と呼ばれます。
n 個の要素からなる学習パターン Χ = { x1, x2, ... xn } に対して、i 番目の要素を入力したときの識別関数の出力値を gi ≡ ( g1( xi ), g2( xi ), ... gc( xi ), )T とします。但し、
で識別関数は線形であるとします。識別関数が出力する正しい ( 望ましい ) 値のことを「教師信号」といいます。gi に対応する教師信号からなるベクトル ( これを「教師ベクトル」といいます ) を ti = ( t1i, t2i, ... tci )T とすると、識別関数が最大値となる添字のクラスが選択されなければならないので、クラスを ω = { ω1, ω2, ... ωc } で表すと
となるように ti が設定されていなければなりません。
入力パターン xi に対する識別関数の出力値と教師信号の誤差を εki とすると、
であり、この二乗和 Ji は ( あとの計算を簡略化するため係数 1 / 2 を付けて )
| Ji | = | (1/2)Σk{1→c}( εki2 ) |
| = | (1/2)Σk{1→c}( [ gk( xi ) - tki ]2 ) | |
| = | (1/2)Σk{1→c}( ( wkTxi - tki )2 ) |
となって、wk の関数として表すことができます。さらに全ての入力パターンに対する二乗誤差 J は
| J | = | (1/2)Σi{1→n}( Ji ) |
| = | (1/2)Σi{1→n}( Σk{1→c}( [ gk( xi ) - tki ]2 ) ) | |
| = | (1/2)Σi{1→n}( Σk{1→c}( ( wkTxi - tki )2 ) ) |
となります。この二乗誤差 J が最小になるときの重みベクトル wk が最適な値であると考えると、重みベクトルの要素 wkl による J の偏微分値 ∂J / ∂wkl は
| ∂J / ∂wkl | = | ( ∂ / ∂wkl )(1/2)Σi{1→n}( Σk'{1→c}( ( Σl'{0→d}( wk'l'xil' ) - tk'i )2 ) ) |
| = | Σi{1→n}( ( Σl'{0→d}( wkl'xil' ) - tki )xil ) | |
| = | Σi{1→n}( ( wkTxi - tki )xil ) = 0 |
となるので、各項をさらに計算すると
| Σi{1→n}( wkTxixil ) | = | Σi{1→n}( Σl'{0→d}( wkl'xil'xil ) ) |
| = | Σl'{0→d}( wkl'Σi{1→n}( xil'xil ) ) | |
| = | Σl'{0→d}( wkl'x'lTx'l' ) | |
| = | x'lTΣl'{0→d}( wkl'x'l' ) | |
| = | x'lTXwk |
| Σi{1→n}( tkixil ) | = | x'lTt'k |
となります。但し、
x'l = ( x1l, x2l, ... xnl )T
t'k = ( tk1, tk2, ... tkn )T
X = ( x1, x2, ... xn )T
とします。
とすると、
より
という結果が得られますが、これは線形重回帰モデルで得られる正規方程式と全く同じ形になります。
正規方程式を解いて重みベクトルを求める場合、あらかじめ全ての学習パターンとその教師ベクトルを得た上で一括で学習することになります。このような学習は「バッチ学習」と呼ばれています。それに対し、一つずつ学習パターンと教師ベクトルを入力して学習させる手法は「オンライン学習」と呼んで区別されます。ここで、勾配法の原理を使い、パターンが示される度に以下の式で重みベクトルを修正することを考えます。
但し、ρ は刻み幅を表す正定数です。このような定数で更新する勾配法は「最急降下法 ( Steepest Descent Method ) 」といいます。
より更新式は
| w'k | = | wk - ρεkixi |
| = | wk - ρ( wkTxi - tki )xi |
となります。この学習方法を「Widrow-Hoff の学習規則 ( Widrow-Hoff Learning Rule )」といいます。
線形識別関数の重みベクトルを求めるための学習方法として有名なものに「パーセプトロン ( Perceptron )」があります。2 クラスにおけるパーセプトロンの学習規則は次のようなものになります。
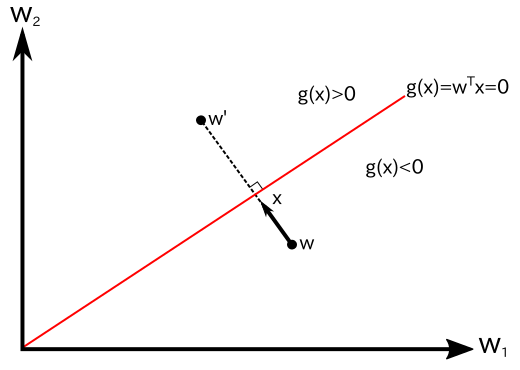
2 クラスで考えた場合、w を座標軸にとった空間において wTx = 0 ( この場合 xTw = 0 と書いたほうがいいかもしれません ) は原点を通り、x に垂直な超平面を表すことになります。この、w が張る空間のことを「重み空間 ( Weight Space )」といいます。従って、パーセプトロンにおける修正は、超平面に対して直交する方向に重みベクトル w を移動していることになります。クラス 1 のパターンをクラス 2 と誤判定した場合は、g(x) の値が本来は正であるべきが負であったことになるので、w に ρx を加算することで正となるように修正します。クラス 2 のパターンをクラス 1 と誤判定した場合はその逆を意味します。下図は、二次元重み空間におけるパーセプトロンによる重みベクトルの修正の様子を表したものです。
 |
ρ は正の定数で「学習率 ( Learining Rate )」といいます。この値が小さすぎると修正幅も小さくなり修正回数が増えてしまうことになります。また逆に大きすぎても振動しながら収束することになるので、適正な値を用いる必要があります。
重み空間において、クラスを区分する超平面 g(x) = wTx = 0 と x は直交しているので、重みベクトル w と超平面との距離を r、w と x のなす角を θ とすると、
と計算することができます。ある学習パターンに対して誤識別が生じた場合、重みベクトル w は超平面から r だけ誤った側に外れているので、これを誤差と考えることができます。従って、Widrow-Hoff の学習規則でオンライン学習を行ったように、
J0 = -wTx ( wTx < 0 なのに x ∈ ω1 だった場合 )
J0 = wTx ( wTx > 0 なのに x ∈ ω2 だった場合 )
J0 = 0 (正しく識別した時)
とします。ここで wTx / ||x|| の分母は w に関して定数なので除外して
としています。これを w で微分すると ∂J0 / ∂w = ±x であり、最急勾配法の式は
w' = w + ρx ( ω1 のパターンを ω2 と誤ったとき )
w' = w - ρx ( ω2 のパターンを ω1 と誤ったとき )
w' = w (正しく識別した時)
となって、パーセプトロンの学習規則における更新式に一致します。
2 クラスにおけるパーセプトロンによる学習のサンプル・プログラムを以下に示します。
namespace Perceptron
{
/*
Learning_2Class : パーセプトロン オンライン学習アルゴリズム(2クラス)
trainData : 入力ベクトル
ans : 教師データ
w : 重み係数
rho : 学習率
戻り値 : 重み係数の更新を行ったら true を返す
*/
bool Learning_2Class( const vector< double >& trainData, bool ans, vector< double >* w, double rho )
{
double wx = std::inner_product( w->begin(), w->end(), trainData.begin(), double() );
if ( ( wx > 0 && ( ! ans ) ) || ( wx < 0 && ans ) ) {
for ( size_t j = 0 ; j < trainData.size() ; ++j )
(*w)[j] += rho * trainData[j] * ( ( ans ) ? 1 : -1 );
return( true );
}
return( false );
}
/*
Learning_2Class_Batch : パーセプトロン バッチ学習アルゴリズム(2クラス)
trainData : 入力ベクトル
ans : 教師データ
w : 重み係数
rho : 学習率
戻り値 : なし
*/
void Learning_2Class_Batch( const vector< vector< double > >& trainData, const vector< bool >& ans, vector< double >* w, double rho )
{
bool trained;
do {
trained = false;
for ( size_t i = 0 ; i < trainData.size() ; ++i )
if ( Learning_2Class( trainData[i], ans[i], w, rho ) )
trained = true;
} while ( trained );
}
/*
Decision_2Class : パーセプトロン判定アルゴリズム(2クラス)
w : 重み係数
x : 入力パターン
戻り値 : 判定結果( true / false )
*/
bool Decision_2Class( const vector< double >& w, const vector< double >& x )
{
return( std::inner_product( w.begin(), w.end(), x.begin(), double() ) > 0 );
}
}
Learning_2Class は先に示したパーセプトロンのアルゴリズムの 2 から 3 までを行う関数で、それを呼び出す形で Learning_2Class_Batch がアルゴリズム全体を処理します。Learning_2Class がオンライン学習用関数、Learning_2Class_Batch がバッチ学習用関数ということになります。
パーセプトロンの学習規則は、学習パターンに対して線形識別関数が少なくとも一つ存在するとき、すなわち「線形分離可能 ( Linearly Separable )」であるときは必ず収束することが保証されています。これを「パーセプトロンの収束定理 ( Perceptron Convergence Theorem )」といいます( 補足 2 )。しかし、線形分離可能でない場合、解に到達せずに処理を無限に繰り返すことになります。処理最大回数を設けたり、その他の手法で処理を打ち切りたいような場合、Learning_2Class_Batch 側を変更するだけで実現することができます。
サンプル・プログラムを使ってテストデータで学習を行った結果を以下に示します。テストデータは、正規分布 N( 1, 0.3 ) と N( 2, 0.3 ) にそれぞれ従う 2 クラスのランダムな二次元の値とし、クラスごとに 20 個のプロトタイプを用意して学習しました。
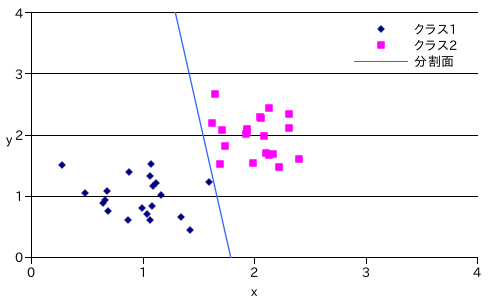 |
線形識別関数は次のような結果になりました。
線形識別関数は二つのクラスを分割していますが、最適な分割面とはいえません。分割面の引き方は無数にありますが、パーセプトロンによってその中から最適な分割面が選ばれるわけではないことに注意が必要です。
多クラスに拡張する場合、クラス j のパターンをクラス k と誤った時、
w'j = wj + ρx
w'k = wk - ρx
とすることで実現できます。
パーセプトロンは元々、動物の神経細胞 ( ニューロン ) が樹状突起という部分で複数の電気信号を受け取って、それがあるしきい値を超えたら信号を出力するという特徴をモデル化したものです。図で表すと以下のようになります。
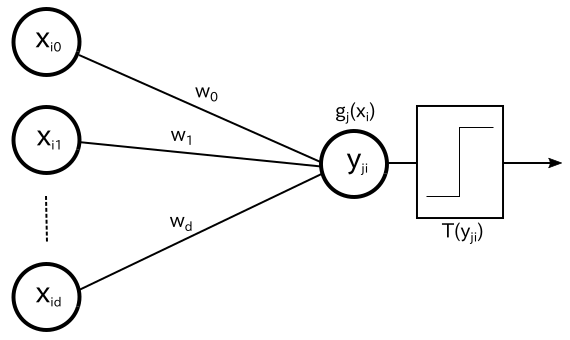 |
外部からの入力には重みベクトルによる重み付けがされます。その総和 yji = gj(xi) が「しきい値関数 ( Threshold Function )」T(yji) によって 1 または 0 の二値に変換されます。ここで、
| T(yji) | = | 1 ( yji > yki ; k ≠ j ) |
| = | 0 ( その他 ) |
と定義します。教師信号を
| tji | = | 1 ( xi ∈ ωj ) |
| = | 0 ( xi ∉ ωj ) |
とすると、パターン xi ∈ ωj を ωk と誤識別したとき
T(yji) = 0 ; tji = 1
T(yki) = 1 ; tki = 0
なので、Widrow-Hoff の更新式は
| w'j | = | wj - ρ[ T(yji) - tji ]xi |
| = | wj + ρxi | |
| w'k | = | wk - ρxi |
となります。識別結果が正しいときは、
gj(xi) = 1 ; tji = 1
gk(xi) = 0 ; tki = 0 ( k ≠ j )
より T(yki) - tki = 0 となるので更新はされません。この結果から、パーセプトロンは Widrow-Hoff の特別な場合とみることができます。
多クラスにおけるパーセプトロンによる学習のサンプル・プログラムを以下に示します。
namespace Perceptron
{
/*
Decision_MultiClass : パーセプトロン判定アルゴリズム(多クラス)
w : 重み係数
x : 入力パターン
戻り値 : 判定結果
*/
int Decision_MultiClass( const vector< vector< double > >& w, const vector< double >& x )
{
double max = std::numeric_limits< double >::min();
int maxIdx = -1;
for ( vector< vector< double > >::size_type i = 0 ; i < w.size() ; ++i ) {
double wx = std::inner_product( w[i].begin(), w[i].end(), x.begin(), double() );
if ( max < wx ) {
max = wx;
maxIdx = i;
}
}
return( maxIdx );
}
/*
Learning_MultiClass : パーセプトロン オンライン学習アルゴリズム(多クラス)
trainData : 入力ベクトル
ans : 教師データ
w : 重み係数
rho : 学習率
戻り値 : 重み係数を更新したら true を返す
*/
bool Learning_MultiClass( const vector< double >& trainData, int ans, vector< vector< double > >* w, double rho )
{
int maxIdx = Decision_MultiClass( *w, trainData );
if ( maxIdx != ans ) {
for ( size_t j = 0 ; j < trainData.size() ; ++j ) {
(*w)[ans][j] += rho * trainData[j];
(*w)[maxIdx][j] -= rho * trainData[j];
}
return( true );
}
return( false );
}
/*
Learning_MultiClass_Batch : パーセプトロン バッチ学習アルゴリズム(多クラス)
trainData : 入力ベクトル
ans : 教師データ
w : 重み係数
rho : 学習率
戻り値 : なし
*/
void Learning_MultiClass_Batch( const vector< vector< double > >& trainData, const vector< int >& ans, vector< vector< double > >* w, double rho )
{
bool trained;
do {
trained = false;
for ( size_t i = 0 ; i < trainData.size() ; ++i )
if ( Learning_MultiClass( trainData[i], ans[i], w, rho ) )
trained = true;
} while ( trained );
}
}
サンプル・プログラムを使ってテストデータで学習を行った結果を以下に示します。テストデータは、正規分布 N( 1, 0.3 ), N( 2, 0.3 ), N( 3, 0.3 ) にそれぞれ従う 3 クラスのランダムな二次元の値とし、クラスごとに 20 個のプロトタイプを用意して学習しました。
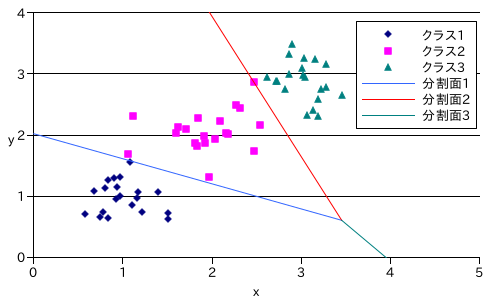 |
線形識別関数は次のようになりました。
g1( x, y ) = 50.5 - 11.0505x - 11.9846y
g2( x, y ) = 22 - 5.27534x + 2.11914y
g3( x, y ) = -69.5 + 19.3258x + 12.8655y
分割面はそれぞれ、g2( x, y ) - g1( x, y ), g3( x, y ) - g2( x, y ), g1( x, y ) - g3( x, y ) を計算することで得られます。また、分割面はちょうど一点で交わる様子も確認することができます。
パーセプトロンは「ローゼンブラット ( Frank Rosenblatt )」によりアナログ・ハードウェアとして実装され「Mark 1 Perceptron」と名付けられました。Mark 1 Perceptron は画像認識用の装置として実装され、20 x 20 のフォトセルからなる画素が入力されると電動可変抵抗により作られたニューロンにランダムに送られ学習します。
その後、パーセプトロンが線形分離可能なパターンしか学習できないことが判明すると、多層パーセプトロンに対しても同様の結果になるという誤解から機械学習への予算が大幅に削減され、1980 年代まで回復することはなかったそうです。今では、パーセプトロンを応用したニューラル・ネットワークによるアプリケーションが広く普及していることから、パーセプトロンが機械学習に与えた影響は非常に大きかったといえるでしょう。
C = 2 クラスの線形識別を C > 2 クラスへ拡張するには、2 クラスの線形識別を組み合わせることで実現します。これにはいくつかの方法があります。
C クラスの分類のために、特定のクラス ωj に入る点と入らない点に分類する 2 クラス用の線形識別を C - 1 個用意する方法を「1 対他分類器 ( One-Versus-The-Rest Classifier )」といいます。下図に 3 クラスでの 1 対他分類器の例を示します。ω1 とそれ以外、ω2 とそれ以外に分類する線形識別を二つ用意して、ω1, ω2 のいずれにも属さない領域を ω3 とします。この例の場合、ω1 と ω2 のいずれにも属するあいまいな領域が生じています。
 |
二つのクラスの全ての組み合わせに対して 2 クラス用の線形識別を C( C - 1 ) / 2 個用意する方法を「1 対 1 分類器 ( One-Versus-One Classifier )」といいます。下図に 3 クラスでの 1 対 1 分類器の例を示します。ω1 と ω2、ω2 と ω3、ω3 と ω1 に分類する線形識別を 3 つ用意して、例えば ω1 と ω2、ω3 と ω1 のいずれも ω1 に属する領域のクラスを 1 とします。この例の場合も、すべてに属するあいまいな領域が生じてしまいます。
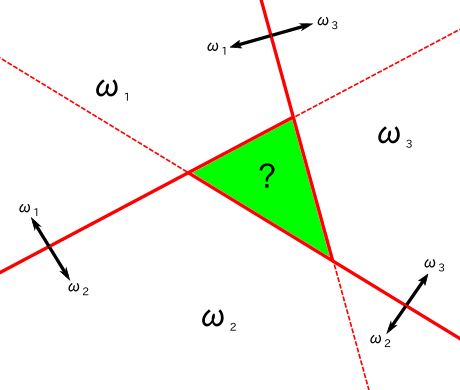 |
あいまいな領域が存在しないようにするためには、次のような C 個の線形関数で構成される単独の C クラス識別を利用します。
ここで wj は拡張重みベクトル、x は拡張特徴ベクトルです。すべての k ≠ j に対して gj(x) > gk(x) ならば、特徴ベクトル x はクラス j に割り当てられます。このとき、
であり、gjk(x) はクラス j とクラス k 間の境界面を表すことになります。
クラス j に属する任意の二点 x1, x2 をとり、直線で結んだとき、その線分上にある任意の点 x は
で表すことができます。このとき、
| gj(x) | = | wjTx |
| = | wjT( λx1 + ( 1 - λ )x2 ) | |
| = | λwjTx1 + ( 1 - λ )wjTx2 | |
| = | λgj(x1) + ( 1 - λ )gj(x2) |
であり、j 以外の全てのクラス k に対して gj(x1) > gk(x1), gj(x2) > gk(x2) なので gj(x) > gk(x) となって、x もクラス j に属することになります。よって、この識別器は常に一点で連結していて凸領域となっています。その様子を以下に図で示します。
 |
n 個の特徴ベクトル x1, x2, ... xn からなる学習パターンを用意します。各パターンはクラス ω1, ω2 のいずれかに属し、線形分離可能であるとします。このときの線形識別関数を g(xi) = wTxi とすると、線形分離可能なので、
g(xi) > 0 ( xi ∈ ω1 )
g(xi) < 0 ( xi ∈ ω2 )
となるような重みベクトル w が存在します。このとき、各特徴ベクトルに対して
| ti | = | 1 ( xi ∈ ω1 ) |
| = | -1 ( xi ∈ ω2 ) |
と教師信号を設定すると、
が成り立ちます。ここで、定数 α ( > 0 ) を両辺にかけると
より αw も解であることがになります。
パーセプトロンにて誤識別された学習パターンと教師信号のペアを ( e1, τ1 ), ( e2, τ2 ), ... ( ek, τk ) ( k ≤ n ) で表します。重みベクトルの初期値を w(0) とし、j 番目の誤識別パターン ej が発生したとき、重みベクトル w(j-1) は以下の式で w(j) に更新されます。
両辺から αw を引くと
両辺のノルムの二乗を計算すると
| ||w(j) - αw||2 | = | ||w(j-1) - αw||2 + 2ρτj( w(j-1) - αw )Tej + ρ2τj2||ej||2 |
| = | ||w(j-1) - αw||2 + 2ρτjw(j-1)Tej - 2ρατjwTej + ρ2τj2||ej||2 |
ej は誤識別したパターンなので、
が成り立ちます。従って、
という結果が得られます。ここで
β ≡ maxi{1→n}( ||tixi|| )
γ ≡ mini{1→n}( tiwTxi ) > 0
とすれば
となり、さらに α を
とすると、
| ||w(j) - αw||2 | ≤ | ||w(j-1) - αw||2 - ρ2β2 |
| ≤ | ||w(j-2) - αw||2 - 2ρ2β2 | |
| : | ||
| ≤ | ||w(0) - αw||2 - jρ2β2 |
が成り立ちます。左辺はゼロ以上なので、
より
となって、右辺は有限なので j も有限となり、必ず収束することが証明されます。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |