
前回は、回帰係数と共分散の最尤推定量の求め方から、両者のモデルが異なるということを紹介しました。この章ではさらに、回帰係数や相関係数の区間推定の方法について紹介したいと思います。
二つのデータ x, y のペアが複数個存在し、それをプロットしたものが直線と見なせるような場合、直線の傾きと切片に対する最尤推定量は最小二乗法から求められることを前の章で説明しました。当然、標本が変化すれば求められる推定量も変化するので、求めた値がどの程度信頼できるかを区間推定したり、さらにその結果を使って検定を行うことも必要になる場合があります。ここでは、最尤推定量として求めた傾きと切片が不偏推定量であること、また、それぞれの確率分布がどのようなものになるかを確認していきたいと思います。
確率変数 ( x, y ) において、x に対する y の回帰曲線が一次式 y = ax + b で表されるとき、N 個の観測値 ( xj, yj ) に対してランダムな誤差が εj が加わって
と表すことができて、誤差 εj が平均 0、分散 σ2 の正規分布 N( 0, σ2 ) に従うと仮定すれば、a, b の最尤推定量 a^, b^は
a^ = sxy / vx --- (1)
b^ = my - mx・sxy / vx = my - a^・mx --- (2)
となるのでした。ここで、mx, my はそれぞれ xj, yj の標本平均、vx は xj の標本分散、そして sxy は xj, yj の標本共分散を表しています。(1) 式の右辺に sxy = Σj{1→N}( ( xj - mx )( yj - my ) ) / N を代入すれば
| a^ | = | Σj{1→N}( ( xj - mx )( yj - my ) ) / Nvx |
| = | { Σj{1→N}( ( xj - mx )yj ) - myΣj{1→N}( xj - mx ) } / Nvx | |
| = | Σj{1→N}( { ( xj - mx ) / Nvx }yj ) |
Σj{1→N}( xj - mx ) = 0 になるので、途中で第二項めが消えて上記のような結果になります。(2)式に上で求めた a^ の式を代入すれば
| b^ | = | my - mxΣj{1→N}( { ( xj - mx ) / Nvx }yj ) |
| = | Σj{1→N}( yj / N ) - Σj{1→N}( { mx( xj - mx ) / Nvx }yj ) | |
| = | Σj{1→N}( [ 1 / N - { mx( xj - mx ) / Nvx } ]yj ) |
となって、 a^, b^ は yj による一次式で表すことができます。yj は、正規分布 N( 0, σ2 ) に従う確率変数 εj による一次式で表されるので、やはり正規分布に従います。従って、a^, b^ もまた正規分布に従うことになります。yj の期待値 E[yj] と分散 V[yj] は
E[yj] = E[axj + b + εj] = axj + b + E[εj] = axj + b
V[yj] = E[{ ( axj + b + εj ) - E[yj] }2] = E[εj2] = σ2
となるので、これを使って a^, b^ の期待値を求めると、
| E[a^] | = | E[ Σj{1→N}( { ( xj - mx ) / Nvx }yj ) ] |
| = | Σj{1→N}( E[ { ( xj - mx ) / Nvx }yj ] ) | |
| = | Σj{1→N}( { ( xj - mx ) / Nvx }E[yj] ) | |
| = | Σj{1→N}( ( xj - mx )( axj + b ) / Nvx ) | |
| = | ( a / Nvx )Σj{1→N}( xj( xj - mx ) ) + ( b / Nvx )Σj{1→N}( xj - mx ) | |
| = | ( a / Nvx )Σj{1→N}( xj( xj - mx ) ) |
ここでも Σj{1→N}( xj - mx ) = 0 を利用しています。さらにこれを使って、
| E[a^] | = | ( a / Nvx )Σj{1→N}( xj( xj - mx ) ) - ( amx / Nvx )Σj{1→N}( xj - mx ) |
| = | ( a / Nvx )Σj{1→N}( xj( xj - mx ) - mx( xj - mx ) ) | |
| = | ( a / vx )Σj{1→N}( ( xj - mx )2 / N ) = a |
と求められます。Σi( xi( xi - mx ) ) = Σi( ( xi - mx )2 ) = Nvx という公式はこの後も頻繁に利用するので注意してください。
b^ の期待値は、a^ を利用して
となるので、最尤推定量としての a^, b^ は不偏推定量でもあるということになります。分散 va = V[a^], vb = V[b^] は
| va = V[a^] | = | V[ Σj{1→N}( { ( xj - mx ) / Nvx }yj ) ] |
| = | Σj{1→N}( { ( xj - mx ) / Nvx }2V[yj] ) | |
| = | ( σ2 / Nvx2 )Σj{1→N}( ( xj - mx )2 / N ) | |
| = | σ2 / Nvx | |
| vb = V[b^] | = | V[ Σj{1→N}( [ 1 / N - { mx( xj - mx ) / Nvx } ]yj ) ] |
| = | Σj{1→N}( [ 1 / N - { mx( xj - mx ) / Nvx } ]2V[yj] ) | |
| = | ( σ2 / N2 )Σj{1→N}( 1 - 2{ mx( xj - mx ) / vx } + { mx( xj - mx ) / vx }2 ) | |
| = | ( σ2 / N )Σj{1→N}( 1 / N + ( mx2 / vx2 ){ ( xj - mx )2 / N } ) | |
| = | σ2 / N + ( σ2mx2 / Nvx2 )Σj{1→N}( ( xj - mx )2 / N ) | |
| = | ( 1 / N + mx2 / Nvx )σ2 |
ここで、独立な確率変数 xj ( j = 1, 2, ... N ) に対して V[ Σj{1→N}( kjxj ) ] = kj2Σj{1→N}( V[xj] ) が成り立つことを利用しています。以上の結果から、a^, b^ はそれぞれ正規分布 N( a, va ) = N( a, σ2 / Nvx ), N( b, vb ) = N( b, ( 1 / N + mx2 / Nvx )σ2 ) に従うことが分かります。
σ は未知の値ですが、yj と ( a^xj + b^ ) の差の平方和(つまり a, b の推定量 a^, b^ を使って求めた y の値と実測値としての y の差の平方和)に対してその期待値を求めると
| E[Σj{1→N}( { yj - ( a^xj + b^ ) }2 )] | |
| = | E[Σj{1→N}( { ( axj + b + εj ) - ( a^xj + b^ ) }2 )] |
| = | E[Σj{1→N}( { ( a - a^ )xj + ( b - b^ ) + εj }2 )] |
| = | E[Σj{1→N}( ( a - a^ )2xj2 + ( b - b^ )2 + εj2 + |
| 2( a - a^ )( b - b^ )xj + 2εj( a - a^ )xj + 2εj( b - b^ ) )] |
と計算できます。前半の項は
E[Σj{1→N}( ( a - a^ )2xj2 )] = Σj{1→N}( E[( a - a^ )2xj2] ) = Σj{1→N}( vaxj2 )
E[Σj{1→N}( ( b - b^ )2 )] = Nvb
E[Σj{1→N}( εj2 )] = Nσ2
と求めることができますが、後半の項は少し計算が面倒です。
より E[( a - a^ )( b - b^ )] を求めると
| E[( a - a^ )( b - b^ )] | = | E[ab] - E[ab^] - E[a^b] + E[a^b^] |
| = | E[a^b^] - ab |
| E[a^b^] | = | E[Σi{1→N}( { ( xi - mx ) / Nvx }yi )Σj{1→N}( [ 1 / N - { mx( xj - mx ) / Nvx } ]yj )] |
| = | E[Σi{1→N}( Σj{1→N}( { ( xi - mx )yi / Nvx }[ 1 / N - { mx( xj - mx ) / Nvx } ]yj ) )] | |
| = | Σi{1→N}( Σj{1→N}( [ ( xi - mx ) / N2vx - { ( xi - mx ) / Nvx }{ mx( xj - mx ) / Nvx } ]E[yiyj] ) ) |
となります。E[yiyj] は
| E[yiyj] | = | E[( axi + b + εi )( axj + b + εj )] |
| = | E[( axi + b )( axj + b ) + εi( axj + b ) + εj( axi + b ) + εiεj] | |
| = | ( axi + b )( axj + b ) + ( axj + b )E[εi] + ( axi + b )E[εj] + E[εiεj] | |
| = | ( axi + b )( axj + b ) ( i ≠ j ) | |
| = | ( axi + b )2 + σ2 ( i = j ) |
となるので、前半の項は
| Σi{1→N}( Σj{1→N}( { ( xi - mx ) / N2vx }E[yiyj] ) ) | |
| = | Σi{1→N}( Σj{1→N}( { ( xi - mx ) / N2vx }( axi + b )( axj + b ) ) + σ2( xi - mx ) / N2vx ) |
| = | Σi{1→N}( { ( xi - mx )( axi + b ) / N2vx }Σj{1→N}( axj + b ) ) |
| = | { ( aNmx + bN ) / N2vx }Σi{1→N}( ( xi - mx )( axi + b ) ) |
| = | { ( amx + b ) / Nvx }{ aΣi{1→N}( xi( xi - mx ) ) + bΣi{1→N}( xi - mx ) } |
| = | { a( amx + b ) / Nvx }Σi{1→N}( ( xi - mx )2 ) |
| = | a( amx + b ) |
後半の項は
| Σi{1→N}( Σj{1→N}( { ( xi - mx ) / Nvx }{ mx( xj - mx ) / Nvx }E[yiyj] ) ) | |
| = | ( mx / N2vx2 )Σi{1→N}( Σj{1→N}( ( xi - mx )( axi + b )( xj - mx )( axj + b ) ) + σ2( xi - mx )2 ) |
| = | ( mx / N2vx2 )Σi{1→N}( ( xi - mx )( axi + b ){ aΣj{1→N}( xj( xj - mx ) ) + bΣj{1→N}( xj - mx ) } + σ2( xi - mx )2 ) |
| = | ( mx / N2vx2 )Σi{1→N}( a( xi - mx )( axi + b ){ Σj{1→N}( ( xj - mx )2 ) } + σ2( xi - mx )2 ) |
| = | ( mx / N2vx2 )Σi{1→N}( aNvx( xi - mx )( axi + b ) + σ2( xi - mx )2 ) |
| = | ( mx / N2vx2 ){ a2NvxΣi{1→N}( xi( xi - mx ) ) + abNvxΣi{1→N}( xi - mx ) + σ2Σi{1→N}( ( xi - mx )2 ) } |
| = | ( mx / N2vx2 ){ a2NvxΣi{1→N}( ( xi - mx )2 ) + σ2Σi{1→N}( ( xi - mx )2 ) } |
| = | ( mx / N2vx2 ){ ( a2Nvx + σ2 )Nvx } |
| = | a2mx + mxσ2 / Nvx |
よって、
| E[( a - a^ )( b - b^ )] | = | E[a^b^] - ab |
| = | a( amx + b ) - ( a2mx + mxσ2 / Nvx ) - ab | |
| = | -mxσ2 / Nvx |
と求めることができて、Σj{1→N}( xj ) = Nmx だから
になります。また、
| E[Σj{1→N}( εj( a - a^ )xj )] | |
| = | E[Σj{1→N}( εj( a - Σi{1→N}( { ( xi - mx ) / Nvx }yi ) )xj )] |
| = | Σj{1→N}( axjE[εj] - E[εjΣi{1→N}( { ( xi - mx ) / Nvx }yi )xj] ) |
| = | -Σj{1→N}( E[Σi{1→N}( { ( xi - mx ) / Nvx }yi ) )εjxj] ) |
| = | -Σj{1→N}( xjΣi{1→N}( { ( xi - mx ) / Nvx }E[yiεj] ) ) |
| = | -Σj{1→N}( xj{ ( xj - mx ) / Nvx }σ2 ) |
| = | -( σ2 / Nvx )Σj{1→N}( ( xj - mx )2 ) |
| = | -( σ2 / Nvx )・Nvx = -σ2 |
ここで、
| E[yiεj] | = | E[( axi + b + εi )εj] |
| = | ( axi + b )E[εj] + E[εiεj] | |
| = | E[εi]E[εj] = 0 ( i ≠ j ) | |
| = | E[εi2] = σ2 ( i = j ) |
になることを利用しています。E[Σj{1→N}( εj( b - b^ ) )] については
| E[Σj{1→N}( εj( b - b^ ) )] | |
| = | E[Σj{1→N}( εj( b - Σi{1→N}( [ 1 / N - { mx( xi - mx ) / Nvx } ]yi ) ) )] |
| = | Σj{1→N}( bE[εj] - E[εjΣi{1→N}( [ 1 / N - { mx( xi - mx ) / Nvx } ]yi ) )] ) |
| = | -Σj{1→N}( Σi{1→N}( [ 1 / N - { mx( xi - mx ) / Nvx } ]E[εjyi] ) ) |
| = | -Σj{1→N}( [ 1 / N - { mx( xj - mx ) / Nvx } ]σ2 ) = -σ2 |
となるので、
| E[Σj{1→N}( { yj - ( a^xj + b^ ) }2 )] | |
| = | E[Σj{1→N}( ( a - a^ )2xj2 )] + E[Σj{1→N}( ( b - b^ )2 )] + E[Σj{1→N}( εj2 )] + |
| E[Σj{1→N}( 2( a - a^ )( b - b^ )xj )] + E[Σj{1→N}( 2εj( a - a^ )xj )] + E[Σj{1→N}( 2εj( b - b^ ) )] | |
| = | Σj{1→N}( vaxj2 ) + Nvb + Nσ2 - 2mx2σ2 / vx - 2σ2 - 2σ2 |
| = | ( σ2 / Nvx )Σj{1→N}( xj2 ) + N( 1 / N + mx2 / Nvx )σ2 + Nσ2 - 2mx2σ2 / vx - 4σ2 |
| = | ( σ2 + mx2σ2 / vx ) + ( σ2 + mx2σ2 / vx ) + Nσ2 - 2mx2σ2 / vx - 4σ2 |
| = | ( N - 2 )σ2 |
従って、vε = Σj{1→N}( { yj - ( a^xj + b^ ) }2 ) / ( N - 2 ) としたとき、vε は σ2 の不偏推定量となります。
a^, b^ はそれぞれ正規分布 N( a, va ) = N( a, σ2 / Nvx ), N( b, vb ) = N( b, ( 1 / N + mx2 / Nvx )σ2 ) に従うことから、( a^ - a ) / ( σ2 / Nvx )1/2 と ( b^ - b ) / ( 1 / N + mx2 / Nvx )σ2 )1/2 は標準正規分布 N( 0, 1 ) に従います。よって、
za = ( a^ - a ) / ( σ2 / Nvx )1/2
zb = ( b^ - b ) / { ( 1 / N + mx2 / Nvx )σ2 }1/2
より、za, zb が N( 0, 1 ) に従うことを利用して区間推定や検定を行うことができます。しかし、σ2 はたいてい未知の値であり、右辺を計算することが通常はできません。そこで、
ta = ( a^ - a ) / ( σ2 / Nvx )1/2( √vε / σ ) = ( a^ - a ) / ( vε / Nvx )1/2
tb = ( b^ - b ) / { ( 1 / N + mx2 / Nvx )σ2 }1/2( √vε / σ ) = ( b^ - b ) / { ( 1 / N + mx2 / Nvx )vε }1/2
とすると、ta, tb は自由度 N - 2 の t-分布に従うことが証明できます(補足1)。za, zb と ta, tb の違いを見ると、σ2 がその不偏推定量 vεに置き換わった形をしていることが分かります。これを利用することで、a, b に対する区間推定や検定を行うことができます。ta = tb = t として、上式を a, b について解くと
a = a^ - t( vε / Nvx )1/2
b = b^ - t{ ( 1 / N + mx2 / Nvx )vε }1/2
になります。しかし、t-分布は左右対称であり、a^ - a は a^ と a の大小関係で符号が変化するので、以下のように信頼区間を定義することになります。
a^ - t( vε / Nvx )1/2 ≤ a ≤ a^ + t( vε / Nvx )1/2
b^ - t{ ( 1 / N + mx2 / Nvx )vε }1/2 ≤ b ≤ b^ + t{ ( 1 / N + mx2 / Nvx )vε }1/2
回帰直線の傾きと切片に対して区間推定を行うためのサンプル・プログラムを以下に示します。
/* RegressionCoefficient : 回帰係数 */ class RegressionCoefficient { double _est_a; // 傾きの推定量 double _est_b; // 切片の推定量 unsigned int _cnt; // 標本数 double _mx; // x の平均 double _var_x; // x の分散 double _ve; // 誤差項の分散の不偏推定量 bool _isValid; // 正しく計算できたか? // 回帰直線の区間推定 bool regCoef_iEst( const ContDist& dist, double var, double b, pair<double,double>& interval_a, pair<double,double>& interval_b, double threshold ) const; public: /* コンストラクタ */ RegressionCoefficient( const vector<double>& x, const vector<double>& y ) { init( x, y ); } // 初期化処理 void init( const vector<double>& x, const vector<double>& y ); // 利用可能な状態か? bool isValid() const { return( _isValid ); } bool operator!() const { return( ! isValid() ); } // 回帰係数の推定値を返す double a() const { return( _est_a ); } // 傾き double b() const { return( _est_b ); } // 切片 /* 区間推定 */ // regCoef_iEst : 回帰直線の区間推定(誤差項の分散が既知の時) bool regCoef_iEst( double var, double b, pair<double,double>& interval_a, pair<double,double>& interval_b, double threshold ) const; // 回帰係数の区間推定(誤差項の分散が未知の場合) bool regCoef_iEst( double b, pair<double,double>& interval_a, pair<double,double>& interval_b, double threshold ) const; }; /* RegressionCoefficient::init 初期化処理 const vector<double> &x, &y : データ列 */ void RegressionCoefficient::init( const vector<double>& x, const vector<double>& y ) { _isValid = false; _cnt = x.size(); if ( y.size() != _cnt ) { cout << "The size of data ( x, y ) must be the same size." << endl; return; } if ( _cnt == 0 ) { cout << "The size of data must be greater than zero." << endl; return; } _var_x = sampleVariance( x ); // x の分散 double cov = sampleCovariance( x, y ); // 標本共分散 // x, y の平均 _mx = sampleAverage( x ); double my = sampleAverage( y ); // 回帰係数の推定値 _est_a = ( _var_x != 0 ) ? cov / _var_x : NAN; _est_b = ( isnan( _est_a ) ) ? NAN : my - _est_a * _mx; // 誤差項の分散の不偏推定量 vector<double> dy( _cnt ); for ( unsigned int i = 0 ; i < _cnt ; ++i ) dy[i] = pow( y[i] - _est_a * x[i] - _est_b, 2 ); _ve = sum( dy ) / (double)( _cnt - 2 ); _isValid = ! ( isnan( _est_a ) || isnan( _est_b ) ); } /* RegressionCoefficient::regCoef_iEst : 回帰直線の区間推定 const ContDist& dist : 確率密度関数(左右対称を前提) double var : 誤差項の分散 double b : 信頼度 pair<double,double> &interval_a, &interval_b : 求める信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... 利用不可, 信頼度が不正 */ bool RegressionCoefficient::regCoef_iEst( const ContDist& dist, double var, double b, pair<double,double>& interval_a, pair<double,double>& interval_b, double threshold ) const { if ( ! isValid() ) { cout << "It seems to fail to initialize." << endl; return( false ); } if ( b < 0 || b > 1 ) { cout << "Confidence value b must have the range [0,1]." << endl; return( false ); } double t = binSearch( dist, b / 2.0, threshold ); // 確率分布の片側信頼区間 double diff_a = t * sqrt( var / ( (double)_cnt * _var_x ) ); double diff_b = t * sqrt( var * ( 1 / (double)_cnt + pow( _mx, 2 ) / ( (double)_cnt * _var_x ) ) ); interval_a.first = _est_a - diff_a; interval_a.second = _est_a + diff_a; interval_b.first = _est_b - diff_b; interval_b.second = _est_b + diff_b; return( true ); } /* RegressionCoefficient::regCoef_iEst : 回帰直線の区間推定(誤差項の分散が既知の時) double var : 誤差項の分散 double b : 信頼度 pair<double,double> &interval_a, &interval_b : 求める信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... 利用不可, 信頼度が不正 */ bool RegressionCoefficient::regCoef_iEst( double var, double b, pair<double,double>& interval_a, pair<double,double>& interval_b, double threshold ) const { return( regCoef_iEst( NormalDistribution( 0, 1 ), var, b, interval_a, interval_b, threshold ) ); } /* RegressionCoefficient::regCoef_iEst : 回帰直線の区間推定(誤差項の分散が未知の時) double b : 信頼度 pair<double,double> &interval_a, &interval_b : 求める信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... 利用不可、データ数が 2 以下 */ bool RegressionCoefficient::regCoef_iEst( double b, pair<double,double>& interval_a, pair<double,double>& interval_b, double threshold ) const { // データ数は 3 以上必要 if ( _cnt < 3 ) { cout << "The size of data must be equal or greater than 3." << endl; return( false ); } return( regCoef_iEst( TDistribution( _cnt - 2 ), _ve, b, interval_a, interval_b, threshold ) ); }
RegressionCoefficient は回帰直線の推定量を保持するクラスです。コンストラクタ(実際には初期化処理用の init )の中で回帰直線の傾きと切片に対する推定量の他、区間推定に必要なパラメータをあらかじめ計算し、メンバ変数として保持しておきます。複数ある regCoef_iEst は全て回帰係数の区間推定を行うためのメンバ関数です。一番上側にある非公開のものは引数として渡された確率密度関数を使って信頼区間を求めています。確率密度関数としては、誤差項の分散が既知ならば標準正規分布が、未知ならば t-分布が利用されるので、原点を中心に左右対称であることを前提にコーディングされています。公開されたメンバ関数は二つあり、一つは標準正規分布を利用した区間推定で、誤差項の分散を引数として渡す必要があります。最後の一つは t-分布を利用したもので、誤差項の分散の不偏推定量を初期化処理で求め、ve として保持しているので、これを使って区間推定を行っています。その他に、求めた回帰係数の最尤(不偏)推定量を返す a, b などが用意されています。
回帰直線の推定ができれば、測定されていないデータの予測を行うことができるようになり、さらには予測値に対する区間推定を行うこともできます。回帰直線 y = ax + b の式が
と推定されていたとき、ある独立変数 x0 に対する従属変数の期待値を
によって推定するのは自然な考え方です。x0 に対する従属変数の期待値を μy0 としたとき、
が成り立ちますが、my0 の期待値は
になるので推定量 my0 は μy0 の不偏推定量であることになります。my0 の分散は
| E[( my0 - μy0 )2] | = | E[{ ( a^x0 + b^ ) - ( ax0 + b ) }2] |
| = | E[( a^ - a )2x02 + 2( a^ - a )( b^ - b )x0 + ( b^ - b )2] | |
| = | vax02 - 2mxσ2xj / Nvx + vb | |
| = | σ2x02 / Nvx - 2mxσ2x0 / Nvx + ( 1 / N + mx2 / Nvx )σ2 | |
| = | { 1 / N + ( x02 - 2mxx0 + mx2 ) / Nvx }σ2 | |
| = | { 1 / N + ( x0 - mx )2 / Nvx }σ2 |
になります。my0 は a^ と b^ の一次式で表され、a^ と b^ は正規分布に従うので my0 も正規分布に従います。そこで、
と正規化することで、mz0 は標準正規分布に従うことになります。しかし、σ は通常未知であることから、回帰係数の場合と同様に、σ をその不偏推定量 vε に置き換えた値
を定義し、mt0 が自由度 N - 2 の t-分布に従うことを利用して μy0 の区間推定や検定を行うことができます。
従属変数そのものを推定する場合、その推定量を y0 とすると、my0 との差 y0 - my0 の平均は
になります。y0 自身が a^ や b^ とは独立に正規分布 N( μy0, σ2 ) に従う確率変数であることから、y0 - my0 の分散は
となって、
とすれば、z0 は標準正規分布に、また
とすれば、t0 は自由度 N - 2 の t-分布に従い、これを利用して y0 の区間推定や検定を行うことができます。
μy0 や y0 の信頼区間の幅は、標本を固定すると ( x0 - mx ) の大きさに依存することになります。最も信頼区間が狭くなるのは x0 = mx のときで、x0 が mx から外れるほど ( x0 - mx )2 は大きくなり、その分信頼区間は大きく、ぼやけていくことになります。
従属変数に対して点・区間推定を行うためのサンプル・プログラムを以下に示します。
// 従属変数の推定値を返す double RegressionCoefficient::y( double x0 ) const { return( _est_a * x0 + _est_b ); } /* RegressionCoefficient::depVar_iEst : 従属変数(またはその期待値)の区間推定 const ContDist& dist : 確率密度関数(左右対称を前提) double var : 誤差項の分散 double b : 信頼度 double x0 : 独立変数 pair<double,double> &interval_y : 求める信頼区間 double expFlag : 期待値を求める場合は 1, そうでなければ 0 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... 利用不可, 信頼度が不正 */ bool RegressionCoefficient::depVar_iEst( const ContDist& dist, double var, double b, double x0, pair<double,double>& interval_y, double expFlag, double threshold ) const { if ( ! isValid() ) { cout << "It seems to fail to initialize." << endl; return( false ); } if ( b < 0 || b > 1 ) { cout << "Confidence value b must have the range [0,1]." << endl; return( false ); } double t = binSearch( dist, b / 2.0, threshold ); // 確率分布の片側信頼区間 double diff_y = t * sqrt( var * ( ( expFlag * (double)_cnt + 1 ) * _var_x + pow( x0 - _mx, 2 ) ) / ( (double)_cnt * _var_x ) ); interval_y.first = y( x0 ) - diff_y; interval_y.second = y( x0 ) + diff_y; return( true ); } /* depVarExp_iEst : 従属変数の期待値の区間推定(誤差項の分散が既知の時) double var : 誤差項の分散 double b : 信頼度 double x0 : 独立変数 pair<double,double>& interval_y : 求める信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... 利用不可, 信頼度が不正 */ bool RegressionCoefficient::depVarExp_iEst( double var, double b, double x0, pair<double,double>& interval_y, double threshold = DEFAULT_THRESHOLD ) const { return( depVar_iEst( NormalDistribution( 0, 1 ), var, b, x0, interval_y, 0, threshold ) ); } /* RegressionCoefficient::depVarExp_iEst : 従属変数の期待値の区間推定(誤差項の分散が未知の時) double b : 信頼度 double x0 : 独立変数 pair<double,double> &interval_y : 求める信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... 利用不可、データ数が 2 以下 */ bool RegressionCoefficient::depVarExp_iEst( double b, double x0, pair<double,double>& interval_y, double threshold ) const { // データ数は 3 以上必要 if ( _cnt < 3 ) { cout << "The size of data must be equal or greater than 3." << endl; return( false ); } return( depVar_iEst( TDistribution( _cnt - 2 ), _ve, b, x0, interval_y, 0, threshold ) ); } /* depVar_iEst : 従属変数の区間推定(誤差項の分散が既知の時) double var : 誤差項の分散 double b : 信頼度 double x0 : 独立変数 pair<double,double>& interval_y : 求める信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... 利用不可, 信頼度が不正 */ bool RegressionCoefficient::depVar_iEst( double var, double b, double x0, pair<double,double>& interval_y, double threshold = DEFAULT_THRESHOLD ) const { return( depVar_iEst( NormalDistribution( 0, 1 ), var, b, x0, interval_y, 1, threshold ) ); } /* RegressionCoefficient::depVar_iEst : 従属変数の区間推定(誤差項の分散が未知の時) double b : 信頼度 double x0 : 独立変数 pair<double,double> &interval_y : 求める信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... 利用不可、データ数が 2 以下 */ bool RegressionCoefficient::depVar_iEst( double b, double x0, pair<double,double>& interval_y, double threshold ) const { // データ数は 3 以上必要 if ( _cnt < 3 ) { cout << "The size of data must be equal or greater than 3." << endl; return( false ); } return( depVar_iEst( TDistribution( _cnt - 2 ), _ve, b, x0, interval_y, 1, threshold ) ); }
サンプル・プログラムは全て、RegressionCoefficient クラスのメンバ関数として実装されています。一番上側にある depVar_iEst 関数は従属変数およびその期待値の区間推定に利用する共通処理部になっています。従属変数とその期待値の区間推定の計算は、ほんの一部分しか差がないので、expFlag という引数を渡して式の切り替えを行っています。あとは、従属変数用の区間推定プログラム(depVar_iEst)と、その期待値用の区間推定プログラム(depVarExp_iEst)を、誤差項の分散が既知の場合と未知の場合の両方に対して用意すれば完成です。
独立変数と従属変数のペアから回帰曲線を推定する統計的手法を「回帰分析(Regression Analysis)」といいます。今まで説明してきた内容のほとんどは独立変数を一つのみに限定し、あてはめる式も一次式でした。この場合は「単回帰分析(Simple Linear Regression Analysis)」というのに対し、独立変数が複数になった場合は「重回帰分析(Multiple Linear Regression Analysis)」と呼ばれるものになります。また、線形モデル以外の回帰分析として「ロジスティック回帰(Logistic Regression)」という分析手法もあります。
回帰分析が役立つ場面は様々で、例えば求められた式を使い、通常では測定できない値を予測するなどといったことが考えられます。店舗ごとの商品の売上を調査し、それを店舗のある街の人口などと比較することで、新たな店舗で予想される売上を導き出すような場合、新店舗を展開する街の人口に合うデータは常にあるとは限りません。また、温度や処理時間などの条件をいくつかに振った上でその出来栄えを調べ、最適な条件を求めるようなとき、処理に時間がかかるのであれば条件の数は少ない方が調査時間を短くすることができます。このようなとき、回帰分析は有効な手段となります。
誤差が正規分布 N( 0, σ2 ) に従うとすれば、回帰係数の最尤推定量は正規分布に従うことを今まで見てきました。相関係数に対しても同様なことが成り立てばいいのですが、残念ながら、標本相関係数の確率分布は非常に複雑な式で表されます。しかし、もし、x と y の間に相関がなく、(母)相関係数がゼロならば、比較的単純な確率分布の式で表すことができます。そのために、回帰係数の確率分布を利用します。
は自由度 N - 2 の t-分布に従うのでした。(母)相関係数がゼロということは回帰直線の傾きの期待値はゼロであることを意味するので、a = 0 になります。従って上式は
になります。ここで vε は、
| vε | = | Σj{1→N}( { yj - ( a^xj + b^ ) }2 ) / ( N - 2 ) |
| = | Σj{1→N}( [ yj - { a^xj + ( my - a^・mx ) } ]2 ) / ( N - 2 ) | |
| = | Σj{1→N}( { ( yj - my ) - a^( xj - mx ) }2 ) / ( N - 2 ) | |
| = | { Σj{1→N}( ( yj - my )2 ) - 2a^Σj{1→N}( ( xj - mx )( yj - my ) ) + a^2Σj{1→N}( ( xj - mx )2 ) } / ( N - 2 ) | |
| = | ( Nvy - 2N( sxy / vx )sxy + ( sxy / vx )2Nvx ) / ( N - 2 ) | |
| = | { N / ( N - 2 ) }( vy - sxy2 / vx ) |
と変形することができます。但し、途中で a^ = sxy / vx, b^ = my - a^・mx を利用しています。標本相関係数 r = sxy / √vx√vy を使えば、上式はさらに
と表されます。a^ = sxy / vx なので、これも r を使って表すと
| a^ | = | sxy / vx |
| = | r・√vx・√vy / vx | |
| = | r・( vy / vx )1/2 |
となって、これらを ta に代入すれば
| ta | = | r・( vy / vx )1/2 / { Nvy( 1 - r2 ) / N( N - 2 )vx }1/2 |
| = | r( N - 2 )1/2 / ( 1 - r2 )1/2 |
と計算できます。よって、(母)相関係数 ρ = 0 ならば、t = r( N - 2 )1/2 / ( 1 - r2 )1/2 は自由度 N - 2 の t-分布に従うことになり、これを利用して r の区間推定を行うことができます。
(母)相関係数がゼロではない場合、一般的には近似式が用いられます。特によく知られているものに「フィッシャーの z 変換(Fisher's Z-transformation)」があります。
互いに独立な二変量変数 ( xi, yi ) ( i = 1, 2, ... N ) が、期待値 E[xi] = E[yi] = 0、分散 V[xi] = E[xi2] = σx2, V[yi] = E[yi2] = σy2 を持つある確率分布に従うと仮定します。また、xi と yi の共分散は E[xiyi] = σxy で表します。xi, yi の標本平均 mx, my を
mx = Σi{1→N}( xi ) / N
my = Σi{1→N}( yi ) / N
とし、標本分散 vx, vy を
vx = Σi{1→N}( ( xi - mx )2 ) / N = Σi{1→N}( xi2 ) / N - mx2
vy = Σi{1→N}( ( yi - my )2 ) / N = Σi{1→N}( yi2 ) / N - my2
また、標本共分散 sxy を
とします。標本平均の期待値は E[mx] = E[my] = 0、標本分散の期待値は σx2, σy2 とは等しくならず、不偏分散の期待値がこれらの値と等しくなるので E[vx] = ( N - 1 )σx2 / N, E[vy] = ( N - 1 )σy2 / N になります。標本共分散の期待値 E[sxy] は、
| E[sxy] | = | E[Σi{1→N}( xiyi ) / N - mxmy] |
| = | σxy - E[Σi{1→N}( xi )Σi{1→N}( yi )] / N2 | |
| = | σxy - E[Σi{1→N}( xiyi )] / N2 | |
| = | σxy - σxy / N = ( N - 1 )σxy / N |
になります。i ≠ j ならば E[xiyj] = E[xi]E[yj] = 0 なので、E[Σi{1→N}( xi )Σi{1→N}( yi )] = E[Σi{1→N}( xiyi )] が成り立ち、上記のような結果になります。標本共分散の期待値も σxy と等しくはならず、Nsxy / ( N - 1 ) が不偏推定量になります。
E[vx / σx2] = ( N - 1 ) / N なので、vx / σx2 の分散 V[vx / σx2] は
| V[vx / σx2] | = | E[( vx / σx2 )2] - { ( N - 1 ) / N }2 |
| = | E[{ Σi{1→N}( xi2 ) / N - mx2 }2 / σx4] - ( N - 1 )2 / N2 | |
| = | E[{ Σi{1→N}( ( xi / σx )2 ) }2 / N2 - 2( mx / σx )2Σi{1→N}( ( xi / σx )2 ) / N + ( mx / σx )4] - ( N - 1 )2 / N2 |
になります。ここで、ui = xi / σx と正規化を行えば、ui の標本平均は mu = mx / σx となるので、上式は
と表すことができます。また、E[ui2] = 1 が成り立つことも明らかです。期待値の中の各項を順番に計算すると、
| E[{ Σi{1→N}( ui2 ) }2 / N2] | |
| = | E[Σi{1→N}( ui4 ) + 2Σi{1→N-1}( Σj{i+1→N}( ui2uj2 ) )] / N2 |
| = | { Σi{1→N}( E[ui4] ) + 2Σi{1→N-1}( Σj{i+1→N}( E[ui2]E[uj2] ) ) } / N2 |
| = | { Σi{1→N}( E[ui4] ) + N( N - 1 ) } / N2 |
{ Σi{1→N}( ui2 ) }2 は、ui4 の項と ui2uj2 ( i ≠ j ) の項に分かれます。i, j の組み合わせは NC2 = N( N - 1 ) / 2 通りで、それぞれの係数は 2 となるので、E[ui2] = 1 より最後に示した結果が得られることになります。
| E[2mu2Σi{1→N}( ui2 ) / N] | |
| = | 2E[{ Σi{1→N}( ui ) / N }2Σi{1→N}( ui2 )] / N |
| = | 2E[{ Σi{1→N}( ui2 ) + 2Σi{1→N-1}( Σj{i+1→N}( uiuj ) ) }Σi{1→N}( ui2 )] / N3 |
| = | 2E[Σi{1→N}( ui2 )Σi{1→N}( ui2 )] / N3 |
| = | 2{ Σi{1→N}( E[ui4] ) + N( N - 1 ) } / N3 |
2Σi{1→N-1}( Σj{i+1→N}( uiuj ) ) と Σi{1→N}( ui2 ) の積は、ある変数 ui が必ず一次の項になるため、期待値は全てゼロになります。よって、Σi{1→N}( ui2 ) どうしの積だけが残り、最初に計算した式と全く同じ形で最後の結果が得られます。
| E[mu4] | |
| = | E[{ Σi{1→N}( ui ) / N }4] |
| = | { Σi{1→N}( E[ui4] ) + Σi{1→N-1}( Σj{i+1→N}( ( 4! / 2!・2! )E[ui2]E[uj2] ) ) } / N4 |
| = | { Σi{1→N}( E[ui4] ) + 3N( N - 1 ) } / N4 |
Σi{1→N}( ui ) の四乗和は、多項定理から ui4, (4!/3!)ui3uj, (4!/2!・2!)ui2uj2, (4!/2!)ui2ujuk, (4!)uiujukul の五種類の項に分けられます。ところが、この場合も一次の変数がある項は期待値がゼロになるので無視することができて、結局 ui4 と (4!/2!・2!)ui2uj2 の二つの項だけが残ります。
以上の結果から、V[vx / σx2] は
| V[vx / σx2] | = | { Σi{1→N}( E[ui4] ) + N( N - 1 ) } / N2 - 2{ Σi{1→N}( E[ui4] ) + N( N - 1 ) } / N3 + { Σi{1→N}( E[ui4] ) + 3N( N - 1 ) } / N4 - ( N - 1 )2 / N2 |
| = | Σi{1→N}( E[ui4] )( 1 / N2 - 2 / N3 + 1 / N4 ) + ( 1 - 1 / N ) - 2( 1 / N - 1 / N2 ) + 3( 1 / N2 - 1 / N3 ) - ( 1 - 2 / N + 1 / N2 ) | |
| = | Σi{1→N}( E[( xi / σx )4] )( 1 / N2 - 2 / N3 + 1 / N4 ) - 1 / N + 4 / N2 - 3 / N3 |
と求めることができます。ここで、ui の確率分布に対する条件をさらに絞って正規分布に従うものと仮定すれば、標準正規分布の尖度 E[ui4] = 3 になることから(「(7) 標本の抽出と要約」の「4) 積率(Moment)」参照)
| V[vx / σx2] | = | 3N( 1 / N2 - 2 / N3 + 1 / N4 ) - 1 / N + 4 / N2 - 3 / N3 |
| = | 2( N - 1 ) / N2 |
になります。以上、直接計算を行なってみましたが、最初から正規分布に従うと仮定していれば、χ2-分布の性質から Nvx / σ2 が自由度 N - 1 の χ2-分布に従い、その平均が N - 1、分散が 2( N - 1 ) となることを利用して
E[vx / σx2] = E[Nvx / σx2] / N = ( N - 1 ) / N
V[vx / σx2] = V[Nvx / σx2] / N2 = 2( N - 1 ) / N2
と簡単に結果を得ることができます。vy / σy2 に対する期待値と分散も全く同じ結果が得られます。以上の結果をまとめておきます。
E[vx / σx2] = E[vy / σy2] = ( N - 1 ) / N
V[vx / σx2] = V[vy / σy2] = 2( N - 1 ) / N2
今度は、標本共分散 sxy を xi, yi の母標準偏差 σx, σy で割った値 sxy / σxσy に対する分散 V[sxy / σxσy] を求めてみます。期待値は E[sxy / σxσy] = ( N - 1 )σxy / Nσxσy なので、
| V[sxy / σxσy] | = | E[( sxy / σxσy )2] - { ( N - 1 )σxy / Nσxσy }2 |
| = | E[{ Σi{1→N}( xiyi ) / N - mxmy }2] / σx2σy2 - { ( N - 1 )σxy / Nσxσy }2 | |
| = | E[{ Σi{1→N}( uivi ) }2 / N2 - 2mumvΣi{1→N}( uivi ) / N + mu2mv2] - { ( N - 1 )ρ / N }2 |
になります。ここでも、vi = yi / σy と正規化し、vi の標本平均を mv としています。また、σxy / σxσy は母相関係数を表すので、これを ρ としています。このとき、E[uivi] = E[xiyi] / σxσy = σxy / σxσy = ρ が成り立ちます。先程と同様に、期待値の中を項別に計算すると
| E[{ Σi{1→N}( uivi ) }2 / N2] | |
| = | E[Σi{1→N}( ( uivi )2 ) + 2Σi{1→N-1}( Σj{i+1→N}( uiviujvj ) )] / N2 |
| = | { Σi{1→N}( E[( uivi )2] ) + 2Σi{1→N-1}( Σj{i+1→N}( E[uivi]E[ujvj] ) ) } / N2 |
| = | { Σi{1→N}( E[( uivi )2] ) + N( N - 1 )ρ2 } / N2 |
{ Σi{1→N}( uivi ) }2 は、V[vx / σx2] の計算で { Σi{1→N}( ui2 ) }2 を求めたときと全く同じ考え方で計算することができます。
| E[2mumvΣi{1→N}( uivi ) / N] | |
| = | 2E[{ Σi{1→N}( ui ) / N }{ Σi{1→N}( vi ) / N }Σi{1→N}( uivi )] / N |
| = | 2E[{ Σi{1→N}( uivi ) + Σi{1→N}( Σj{j≠i,1→N}( uivj ) ) }Σi{1→N}( uivi )] / N3 |
| = | 2E[{ Σi{1→N}( uivi ) }2] / N3 |
| = | 2{ Σi{1→N}( E[( uivi )2] ) + N( N - 1 )ρ2 } / N3 |
Σi{1→N}( ui ) / N と Σi{1→N}( vi ) / N の積は、ui と vi の添字としてどちらも同じ変数 i を使っていますがこれらはそれぞれ 1 から N まで変化するので、実際には uivi と uivj ( i ≠ j ) の二つの項が存在します。しかし、uivj についてはこの後 uivi との積を求めても ui か vi のいずれかに一次の変数が必ず存在するので結果はゼロになります。よって、添字の一致する項だけが残り、Σi{1→N}( uivi ) になります。
| E[mu2mv2] | |
| = | E[{ Σi{1→N}( ui ) / N }2{ Σi{1→N}( vi ) / N }2] |
| = | E[{ Σi{1→N}( ui2 ) + 2Σi{1→N-1}( Σj{i+1→N}( uiuj ) ) }{ Σi{1→N}( vi2 ) + 2Σi{1→N-1}( Σj{i+1→N}( vivj ) ) }] / N4 |
| = | E[Σi{1→N}( ui2vi2 ) + Σi{1→N}( Σj{j≠i,1→N}( ui2vj2 ) ) + 4Σi{1→N-1}( Σj{i+1→N}( uiviujvj ) )] / N4 |
| = | { Σi{1→N}( E[( uivi )2] ) + N( N - 1 ) + 2N( N - 1 )ρ2 } / N4 |
Σi{1→N}( ui2 ) と 2Σi{1→N-1}( Σj{i+1→N}( vivj ) ) の積、Σi{1→N}( vi2 ) と 2Σi{1→N-1}( Σj{i+1→N}( uiuj ) ) の積はどちらも、すべての項で ui または vi が一次の変数があるので期待値がゼロになり、無視することができます。
ここで、先程と同様に、( ui , vi ) が標準正規分布に従うとして、E[( uivi )2] を求めます。二変量正規分布の確率密度関数 p( u, v ) は
になります。s = ( u + v ) / √2, t = ( u - v ) / √2 としたとき、∂s / ∂u = 1 / √2, ∂s / ∂v = 1 / √2, ∂t / ∂u = 1 / √2, ∂t / ∂v = -1 / √2 よりヤコビアンの絶対値は 1 になります。u = ( s + t ) / √2, v = ( s - t ) / √2 なので
u2 = ( s2 + 2st + t2 ) / 2
v2 = ( s2 - 2st + t2 ) / 2
uv = ( s2 - t2 ) / 2
となって、変数変換した確率密度関数 q( s, t ) は
| q( s, t ) | = | [ 1 / { 2π( 1 - ρ2 )1/2 } ] exp( -{ s2 - ρ( s2 - t2 ) + t2 } / 2( 1 - ρ2 ) ) |
| = | [ 1 / { 2π( 1 - ρ2 )1/2 } ] exp( -( 1 - ρ )s2 / 2( 1 - ρ2 ) ) exp( -( 1 + ρ )t2 / 2( 1 - ρ2 ) ) | |
| = | [ 1 / { 2π( 1 + ρ ) }1/2 ] exp( -s2 / 2( 1 + ρ ) ) [ 1 / { 2π( 1 - ρ ) }1/2 ]exp( -t2 / 2( 1 - ρ ) ) | |
| = | N( 0, 1 + ρ )・N( 0, 1 - ρ ) |
と互いに独立な変数へ変換することができます。このとき、E[( uv )2] は
| E[( uv )2] | = | E[( s2 - t2 )2 / 4] | |
| = | E[s4 - 2s2t2 + t4] / 4 |
なので、E[s4] は尖度を表し E[{ s / ( 1 + ρ )1/2 }4] = 3 より 3( 1 + ρ )2, E[t4] も同様に考えて 3( 1 - ρ )2 となり、E[s2t2] = E[s2]E[t2] より ( 1 + ρ )( 1 - ρ ) と求められることから
よって、各項は
| E[{ Σi{1→N}( uivi ) }2 / N2] | = | { N( 1 + 2ρ2 ) + N( N - 1 )ρ2 } / N2 |
| = | { 1 + ( N + 1 )ρ2 } / N |
| E[2mumvΣi{1→N}( uivi ) / N] | = | 2{ N( 1 + 2ρ2 ) + N( N - 1 )ρ2 } / N3 |
| = | 2{ 1 + ( N + 1 )ρ2 } / N2 |
| E[mu2mv2] | = | { N( 1 + 2ρ2 ) + N( N - 1 ) + 2N( N - 1 )ρ2 } / N4 |
| = | ( 1 + 2ρ2 ) / N2 |
と計算することができて、
| V[sxy / σxσy] | = | { 1 + ( N + 1 )ρ2 } / N - 2{ 1 + ( N + 1 )ρ2 } / N2 + ( 1 + 2ρ2 ) / N2 - { ( N - 1 )ρ / N }2 |
| = | ( 1 / N - 1 / N2 ) + ( 1 / N - 1 / N2 )ρ2 | |
| = | ( 1 + ρ2 )( N - 1 ) / N2 |
となります。
E[sxy / σxσy] = ( N - 1 )ρ / N
V[sxy / σxσy] = ( 1 + ρ2 )( N - 1 ) / N2
次に、vx / σx2 と vy / σy2 の共分散 S[vx / σx2, vy / σy2] = E[{ ( vx / σx2 ) - ( N - 1 ) / N }{ ( vy / σy2 ) - ( N - 1 ) / N }] を求めます。
| S[vx / σx2, vy / σy2] | = | E[{ ( vx / σx2 ) - ( N - 1 ) / N }{ ( vy / σy2 ) - ( N - 1 ) / N }] |
| = | E[( vx / σx2 )( vy / σy2 )] - { ( N - 1 ) / N }( E[vx / σx2] + E[vy / σy2] ) + { ( N - 1 ) / N }2 | |
| = | E[( vx / σx2 )( vy / σy2 )] - { ( N - 1 ) / N }2 | |
| = | E[{ Σi{1→N}( ui2 ) / N - mu2 }{ Σi{1→N}( vi2 ) / N - mv2 }] - { ( N - 1 ) / N }2 | |
| = | E[{ Σi{1→N}( ui2 )Σi{1→N}( vi2 ) / N2 - mv2Σi{1→N}( ui2 ) / N - mu2Σi{1→N}( vi2 ) / N + mu2mv2 }] - { ( N - 1 ) / N }2 |
より、期待値の中を項別に計算すると
| E[Σi{1→N}( ui2 )Σi{1→N}( vi2 ) / N2] | |
| = | E[Σi{1→N}( ( uivi )2 ) + Σi{1→N}( Σj{j≠i,1→N}( ui2vj2 ) )] / N2 |
| = | { Σi{1→N}( E[( uivi )2] ) + Σi{1→N}( Σj{j≠i,1→N}( E[ui2]E[vj2] ) ) } / N2 |
| = | { N( 1 + 2ρ2 ) + N( N - 1 ) } / N2 |
| = | ( 2ρ2 + N ) / N |
| E[mv2Σi{1→N}( ui2 ) / N] | |
| = | E[{ Σi{1→N}( vi ) / N }2Σi{1→N}( ui2 )] / N |
| = | E[{ Σi{1→N}( vi2 ) + 2Σi{1→N-1}( Σj{i+1→N}( vivj ) ) }Σi{1→N}( ui2 )] / N3 |
| = | E[Σi{1→N}( vi2 )Σi{1→N}( ui2 )] / N3 |
| = | ( 2ρ2 + N ) / N2 |
E[mu2Σi{1→N}( vi2 ) / N] も同様の方法で同じ値が得られます。E[mu2mv2] = ( 1 + 2ρ2 ) / N2 であることは前に示してあるので、
| S[vx / σx2, vy / σy2] | = | ( 2ρ2 + N ) / N - 2( 2ρ2 + N ) / N2 + ( 1 + 2ρ2 ) / N2 - { ( N - 1 ) / N }2 |
| = | 2ρ2( N - 1 ) / N2 |
になります。
S[vx / σx2, vy / σy2] = 2ρ2( N - 1 ) / N2
最後に、vx / σx2 と sxy / σxσy の共分散 S[vx / σx2, sxy / σxσy] = E[{ ( vx / σx2 ) - ( N - 1 ) / N }{ ( sxy / σxσy ) - ( N - 1 )ρ / N }] を求めます。
| S[vx / σx2, sxy / σxσy] | = | E[{ ( vx / σx2 ) - ( N - 1 ) / N }{ ( sxy / σxσy ) - ( N - 1 )ρ / N }] |
| = | E[( vx / σx2 )( sxy / σxσy )] - { ( N - 1 )ρ / N }E[vx / σx2] - { ( N - 1 ) / N }E[sxy / σxσy] ) + ρ{ ( N - 1 ) / N }2 | |
| = | E[( vx / σx2 )( sxy / σxσy )] - { ( N - 1 )ρ / N }{ ( N - 1 ) / N } - { ( N - 1 ) / N }{ ( N - 1 )ρ / N } + ρ{ ( N - 1 ) / N }2 | |
| = | E[{ Σi{1→N}( ui2 ) / N - mu2 }{ Σi{1→N}( uivi ) / N - mumv }] - ρ{ ( N - 1 ) / N }2 | |
| = | E[Σi{1→N}( ui2 )Σi{1→N}( uivi ) / N2 - mumvΣi{1→N}( ui2 ) / N - mu2Σi{1→N}( uivi ) / N + mu3mv] - ρ{ ( N - 1 ) / N }2 |
より、期待値の中を項別に計算すると
| E[Σi{1→N}( ui2 )Σi{1→N}( uivi ) / N2] | |
| = | E[Σi{1→N}( ui3vi ) + Σi{1→N}( Σj{j≠i,1→N}( ui2ujvj ) )] / N2 |
| = | { Σi{1→N}( E[ui3vi] ) + Σi{1→N}( Σj{j≠i,1→N}( E[ui2]E[ujvj] ) ) } / N2 |
| = | { Σi{1→N}( E[ui3vi] ) + N( N - 1 )ρ } / N2 |
| E[mumvΣi{1→N}( ui2 ) / N] | |
| = | E[{ Σi{1→N}( ui ) / N }{ Σi{1→N}( vi ) / N }Σi{1→N}( ui2 )] / N |
| = | E[Σi{1→N}( uivi )Σi{1→N}( ui2 )] / N3 |
| = | { Σi{1→N}( E[ui3vi] ) + N( N - 1 )ρ } / N3 |
| E[mu2Σi{1→N}( uivi ) / N] | |
| = | E[{ Σi{1→N}( ui ) / N }2Σi{1→N}( uivi )] / N |
| = | E[{ Σi{1→N}( ui2 ) + 2Σi{1→N-1}( Σj{i+1→N}( uiuj ) ) }Σi{1→N}( uivi )] / N3 |
| = | E[Σi{1→N}( ui2 )Σi{1→N}( uivi )] / N3 |
| = | { Σi{1→N}( E[ui3vi] ) + N( N - 1 )ρ } / N3 |
| E[mu3mv] | |
| = | E[{ Σi{1→N}( ui / N ) }3Σi{1→N}( vi / N )] |
| = | E[{ Σi{1→N}( ui3 ) + ( 3! / 2! )Σi{1→N}( Σj{j≠i,1→N}( ui2uj ) ) }Σi{1→N}( vi )] / N4 |
| = | E[Σi{1→N}( ui3vi ) + 3Σi{1→N}( Σj{j≠i,1→N}( ui2ujvj ) )] / N4 |
| = | { Σi{1→N}( E[ui3vi] ) + 3Σi{1→N}( Σj{j≠i,1→N}( E[ui2]E[ujvj] ) ) } / N4 |
| = | { Σi{1→N}( E[ui3vi] ) + 3N( N - 1 )ρ } / N4 |
E[mu3mv] だけ補足すると、{ Σi{1→N}( ui ) }3 は、i, j, k が全て相異なるとして ui3, ui2uj, uiujuk の三つの項に分かれ、ui3 と vi の積はそれぞれの要素の添字が一致したものだけが、ui2uj と vi の積は結果が ui2ujvj となる項だけが残ります。uiujuk と vi の積はどの組み合わせも一次となる変数 ui が残るので、全て期待値がゼロになり無視することができます。
u3v の期待値は、先程行った変数変換の結果を利用すると
| E[u3v] | = | E[( s + t )3( s - t )] / 4 |
| = | E[( s + t )2( s2 - t2 )] / 4 | |
| = | E[( s2 + 2st + t2 )( s2 - t2 )] / 4 | |
| = | E[( s4 + 2s3t - 2st3 - t4 )] / 4 | |
| = | { 3( 1 + ρ )2 - 3( 1 - ρ )2 } / 4 = 3ρ |
よって、
| S[vx / σx2, sxy / σxσy] | = | { 3Nρ + N( N - 1 )ρ } / N2 - { 3Nρ + N( N - 1 )ρ } / N3 - { 3Nρ + N( N - 1 )ρ } / N3 + { 3Nρ + 3N( N - 1 )ρ } / N4 - ρ{ ( N - 1 ) / N }2 |
| = | 2ρ( N - 1 ) / N2 |
となります。vy / σy2 と sxy / σxσy の共分散 S[vy / σy2, sxy / σxσy] も同様の値が得られることは明らかです。
S[vx / σx2, sxy / σxσy] = S[vy / σy2, sxy / σxσy] = 2ρ( N - 1 ) / N2
以上、三つの変数 vx / σx2, vy / σy2, sxy / σxσy に対し、それぞれの期待値、分散、共分散を全て求めました。これらはそれぞれ ( ui - mu )2, ( vi - mv )2, ( ui - mu )( vi - mv ) の標本平均を表します。よって中心極限定理により、N が十分に大きければこれらは漸近的に正規分布に従います。そこで、
と変数変換すれば、
E[u] = E[v] = √N( N - 1 ) / N = √N - 1 / √N ≅ √N
V[u] = V[v] = 2 - 2 / N ≅ 2
E[w] = √N( N - 1 )ρ / N = ρ√N - ρ / √N ≅ ρ√N
V[w] = ( 1 + ρ2 )( N - 1 ) / N ≅ 1 + ρ2
S[u, v] = 2ρ2( N - 1 ) / N ≅ 2ρ2
S[u, w] = S[v, w] = 2ρ( N - 1 ) / N ≅ 2ρ
となり、平均ベクトルが μ = √N( 1, 1, ρ ) で共分散行列 V が
| V = | | | 2, | 2ρ2, | 2ρ | | |
| | | 2ρ2, | 2, | 2ρ | | | |
| | | 2ρ, | 2ρ, | 1 + ρ2 | | |
の多変量正規分布に漸近的に従うことになります。
r( u, v, w ) = w / ( uv )1/2 としたとき、
| w / ( uv )1/2 | = | ( √Nsxy / σxσy ) / { ( √Nvx / σx2 )( √Nvy / σy2 ) }1/2 |
| = | sxy / ( vxvy )1/2 |
より r( u, v, w ) は標本相関係数を表します。u, v, w で偏微分すると
∂r / ∂u = ( -1 / 2 )wu-3/2v-1/2
∂r / ∂v = ( -1 / 2 )wu-1/2v-3/2
∂r / ∂w = u-1/2v-1/2
なので、μ = √N( 1, 1, ρ ) における r( u, v, w ) の増加量は ( -ρ / 2√N, -ρ / 2√N, 1 / √N ) になります。μ に十分近い場所においては r( u, v, w ) が超平面に近似できるとすれば、
になるので、平均と分散は近似的に
| E[r] | ≅ | E[-ρu / 2√N - ρv / 2√N + w / √N + ρ] |
| = | -ρ√N / 2√N - ρ√N / 2√N + ρ√N / √N + ρ = ρ | |
| V[r] | ≅ | E[ [ { -ρ( u - √N ) / 2√N - ρ( v - √N ) / 2√N + ( w - ρ√N ) / √N + ρ } - ρ ]2] |
| = | E[ ρ2( u - √N )2 / 4N + ρ2( v - √N )2 / 4N + ( w - ρ√N )2 / N + ρ2( u - √N )( v - √N ) / 2N - ρ( v - √N )( w - ρ√N ) / N - ρ( w - ρ√N )( u - √N ) / N] | |
| = | ρ2V[u] / 4N + ρ2V[v] / 4N + V[w] / N + ρ2S[u,v] / 2N - ρS[v,w] / N - ρS[w,u] / N | |
| = | { ρ2 / 2 + ρ2 / 2 + ( 1 + ρ2 ) + ρ4 - 2ρ2 - 2ρ2 } / N | |
| = | ( 1 - ρ2 )2 / N |
と求められ、r は ( u, v, w ) ≅ μ のとき正規分布 N( ρ, ( 1 - ρ2 )2 / N ) に近似することができます。大数の法則により、N が十分に大きければ ( u, v, w ) は μ に近似することができると考えられるので、N が十分に大きければ r は正規分布 N( ρ, ( 1 - ρ2 )2 / N ) に従うとすることができます。
最後に、z( r ) = ln( ( 1 + r ) / ( 1 - r ) ) / 2 として先程と同様な処理を行います。r で微分すると
| dz / dr | = | { ( 1 - r ) / ( 1 + r ) }{ 2 / ( 1 - r )2 } / 2 |
| = | 1 / ( 1 - r2 ) |
なので、r = ρ での z の増加量は 1 / ( 1 - ρ2 ) になり、r = ρ 付近では
と近似することができます。平均と分散は
| E[z] | ≅ | z( ρ ) = ln( ( 1 + ρ ) / ( 1 - ρ ) ) / 2 |
| V[z] | ≅ | E[ [ { ( r - ρ ) / ( 1 - ρ2 ) + z( ρ ) } - z( ρ ) ]2] |
| = | E[( r - ρ )2] / ( 1 - ρ2 )2 | |
| = | V[r] / ( 1 - ρ2 )2 = 1 / N |
となって、z は正規分布 N( z( ρ ), 1 / N ) に従うことになります。
実際には、z が N( z( ρ ), 1 / ( N - 3 ) ) に従うとした方が精度がよくなるようです。しかし、あくまでも近似式であり、特に母相関係数 ρ が ±1 に近づくほど標本相関係数 r は正規分布からかけ離れた分布を示すため、誤差はかなり大きくなっていきます。標本相関係数の正確な確率密度の式の一つとして次のようなものがあります。
この確率密度関数は無限級数を含むので値を正確に計算することはできませんが、ρ = 0 ならば
となるので、( N - 3 )! / 2N-3 を変形して
| ( N - 3 )! / 2N-3 | = | ( N - 3 )( N - 4 ) ... 3・2・1 / 2N-3 |
| = | { ( N - 3 ) / 2 }{ ( N - 4 ) / 2 } ... ( 3 / 2 )・( 2 / 2 )・( 1 / 2 ) | |
| = | [ ... ( 2k / 2 ) ... ( 2 / 2 ) ][ ... { ( 2k - 1 ) / 2 } ... ( 3 / 2 )・( 1 / 2 ) ] | |
| = | Γ( ( N - 1 ) / 2 )Γ( ( N - 2 ) / 2 ) / √π |
を代入すれば、
| f(r) | = | { ( 1 - r2 )(N-4)/2Γ( ( N - 1 ) / 2 ) } / √πΓ( ( N - 2 ) / 2 ) |
| = | ( 1 - r2 )(N-4)/2 / { Γ( 1 / 2 )Γ( ( N - 2 ) / 2 ) / Γ( ( N - 1 ) / 2 ) } | |
| = | ( 1 - r2 )(N-4)/2 / Β( 1 / 2, ( N - 2 ) / 2 ) |
t = r( N - 2 )1/2 / ( 1 - r2 )1/2 とすれば 1 / ( 1 - r2 ) = 1 + t2 / ( N - 2 ), dt = ( N - 2 )1/2( 1 - r2 )-3/2dr となって、
| f(t) | = | ( 1 - r2 )(N-4)/2 / { Β( 1 / 2, ( N - 2 ) / 2 )( N - 2 )1/2( 1 - r2 )-3/2 } |
| = | ( 1 + t2 / ( N - 2 ) ){(N-2)+1}/2 / { ( N - 2 )1/2Β( 1 / 2, ( N - 2 ) / 2 ) } |
と求めることができます。これは、最初に示した自由度 N - 2 の t-分布の確率密度関数そのものです。
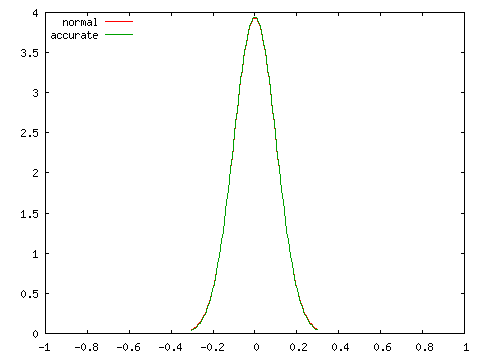
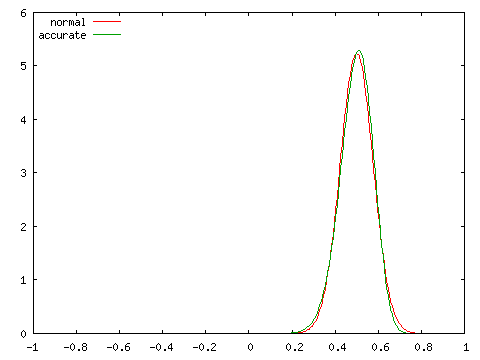
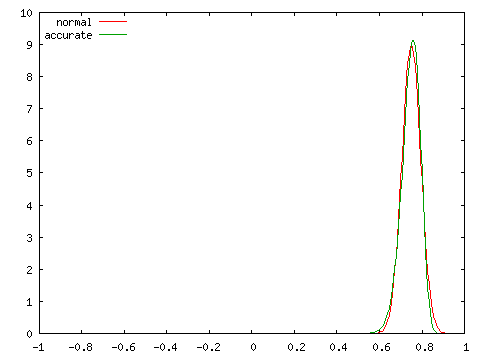
母相関係数 ρ = 0, 0.25, 0.5, 0.75 の四つの場合に対し、標本数 N = 100 としたときの標本相関係数の分布を正規分布 N( ρ, 1 / ( N - 3 ) ) と比較したグラフを以下に示します。
| 正規分布との比較 ( N = 100 ) | |
|---|---|
| ρ = 0 | ρ = 0.25 |
 |
 |
| ρ = 0.5 | ρ = 0.75 |
 |
 |
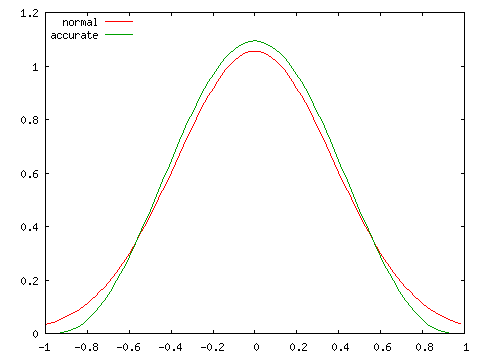
グラフにおいて、赤で示された曲線 (normal) が正規分布、緑で示された曲線 (accurate) が実際の分布を表しています。どの場合においても、両者は非常に近い分布を示しており、N = 100 程度であれば正規分布を使って非常によく近似できることが分かります。ところが、N = 10 として同じ条件での分布を調べると次のようになります。
| 正規分布との比較 ( N = 10 ) | |
|---|---|
| ρ = 0 | ρ = 0.25 |
 |
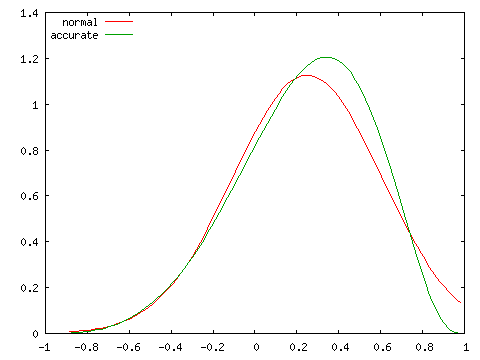 |
| ρ = 0.5 | ρ = 0.75 |
 |
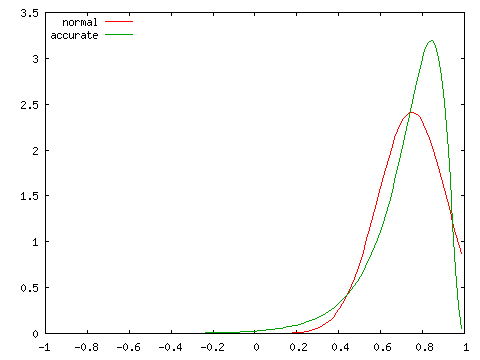 |
実際の分布は ρ が大きくなるほど偏りが大きくなり、左右対称な正規分布とは異なる分布となります。標本数が大きくなければ、正規分布による近似は精度のよい結果が得られないことになります。
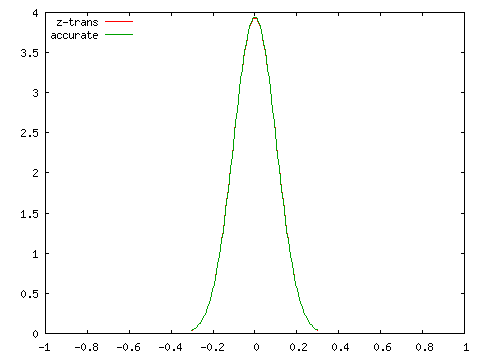
次に、フィッシャーの z-変換を利用した分布との比較を行った結果を示します。
| Fisherのz-変換値との比較 ( N = 100 ) | |
|---|---|
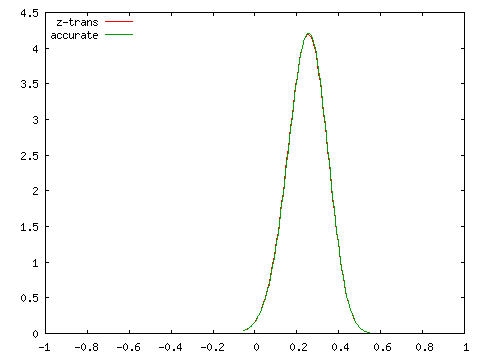
| ρ = 0 | ρ = 0.25 |
 |
 |
| ρ = 0.5 | ρ = 0.75 |
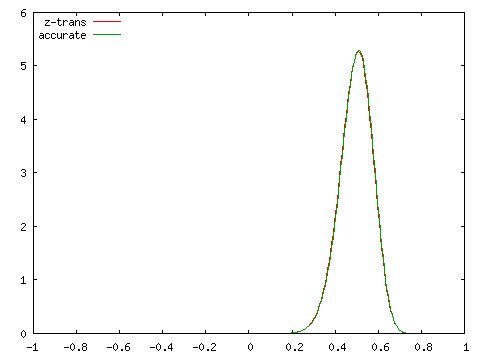 |
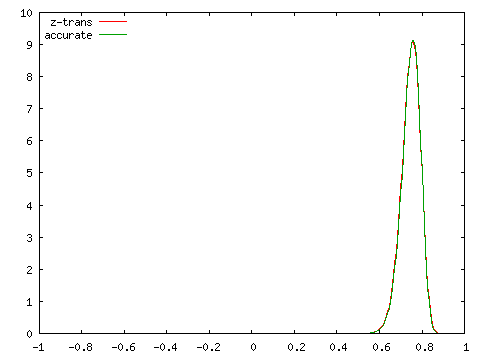 |
| Fisherのz-変換値との比較 ( N = 10 ) | |
|---|---|
| ρ = 0 | ρ = 0.25 |
 |
 |
| ρ = 0.5 | ρ = 0.75 |
 |
 |
こちらは標本数が小さくてもある程度の精度が保たれていることが分かります。
フィッシャーの z-変換を利用した相関係数の区間推定と、先ほど示した相関係数の確率分布を計算する処理のサンプル・プログラムを以下に示します。
/* corrCoef_iEst : 相関係数の区間推定 const vector<double> &x, &y : データ列 double b : 信頼度 double& r : 求めた標本相関係数 pair<double,double> &interval : 求める信頼区間 double threshold : binSearchでtを求める時のしきい値 戻り値 : True ... 成功 , False ... 利用不可, 信頼度が不正 */ bool corrCoef_iEst( const vector<double>& x, const vector<double>& y, double b, double& r, pair<double,double>& interval, double threshold ) { unsigned int n = x.size(); if ( n <= 3 ) { cout << "Data seems to be less than 3 ( It must be at least more than 4 )." << endl; return( false ); } if ( n != y.size() ) { cout << "Data x and y must be the same size." << endl; return( false ); } if ( b < 0 || b > 1 ) { cout << "Confidence value b must have the range [0,1]." << endl; return( false ); } // 標本相関係数 r = sampleCovariance( x, y ) / sqrt( sampleVariance( x ) * sampleVariance( y ) ); // r の z-変換 double z = log( ( 1 + r ) / ( 1 - r ) ) / 2; NormalDistribution nDist( 0, 1 / sqrt( n - 3 ) ); double t = binSearch( nDist, b / 2.0, threshold ); // 確率分布の片側信頼区間 interval.first = ( exp( ( z - t ) * 2 ) - 1 ) / ( exp( ( z - t ) * 2 ) + 1 ); interval.second = ( exp( ( z + t ) * 2 ) - 1 ) / ( exp( ( z + t ) * 2 ) + 1 ); return( true ); } /* accurateSCCProb : 標本相関係数の確率密度を求める double x : 確率変数 double n : 標本数 double rho : 母相関係数 戻り値 : 確率密度 */ double accurateSCCProb( double x, double n, double rho ) { // 定数項 double c = pow( 2, n - 3 ) * pow( 1 - pow( rho, 2 ), ( n - 1 ) / 2 ) * pow( 1 - pow( x, 2 ), ( n - 4 ) / 2 ) / ( M_PI * tgamma( n - 2 ) ); double a = 1; // 無限級数での pow( 2ρr, k ) / k! の値を保持する変数 double sum = 0; // 無限級数の計算結果 for ( int k = 0 ; ; ++k ) { // k 番目の項を計算 double d = a * pow( tgamma( ( n - 1 + (double)k ) / 2 ), 2 ); if ( fabs( d ) < 1E-6 ) break; sum += d; // a を更新 a *= 2 * rho * x / (double)( k + 1 ); } return( c * sum ); } /* sampleCorrelationCoefficientProb : 標本相関係数の確率分布を出力する 確率変数, 正規分布による近似値, Fisherの z-変換による近似値, 正確な確率密度の順で出力 double n : 標本数 double rho : 母相関係数 */ void sampleCorrelationCoefficientProb( unsigned int n, double rho ) { const unsigned int COUNT = 100; // 計算するデータ数 if ( n <= 3 ) return; if ( rho < 0 || rho > 1 ) return; double mu = log( ( 1 + rho ) / ( 1 - rho ) ) / 2; // rho の z-変換値 double sigma = sqrt( 1.0 / (double)( n - 3 ) ); // 正規分布に近似したときの標準偏差 NormalDistribution nDist( rho, ( 1 - pow( rho, 2 ) ) * sigma ); // 正規分布 NormalDistribution fisherDist( mu, sigma ); // z-変換値の分布 double min = ( rho - 3 * sigma < -1 ) ? -1 : rho - 3 * sigma; // 計算範囲の最小値 double max = ( rho + 3 * sigma > 1 ) ? 1 : rho + 3 * sigma; // 計算範囲の最大値 double delta = ( max - min ) / (double)COUNT; // 増分 cout << "#r Normal Fisher Accurate" << endl; for ( double r = min ; r < max ; r += delta ) { double d1 = nDist[r]; // 正規分布による近似値 double d2 = fisherDist[log( ( 1 + r ) / ( 1 - r ) ) / 2] / ( 1 - pow( r, 2 ) ); // Fisherの z-変換による近似値 double d3 = accurateSCCProb( r, n, rho ); // 正確な値 cout << r << " " << d1 << " " << d2 << " " << d3 << endl; } }
区間推定 (corrCoef_iEst) ではフィッシャーの z-変換を利用しています。標本相関係数 r を求め、それを母集団の相関係数として計算していますが、標本相関係数は不偏推定量ではないことに注意してください。本来ならば不偏推定量を利用した方が精度はよくなりますが、標本相関係数の不偏推定量は非常に複雑でややこしいので、ここでは標本相関係数をそのまま利用しています。なお、分散を 1 に正規化した場合、相関係数は共分散と等しくなります。標本共分散 sxy の不偏推定量は Nsxy / ( N - 1 ) なので、N - 1 で割った値を利用する場合もあるようです。
標本相関係数 r を z-変換した値 z(r) が、平均を母相関係数 ρ のz-変換値、分散を 1 / ( N - 3 ) とする正規分布 N( z(ρ), 1 / ( N - 3 ) ) に従うので、z - z(ρ) は正規分布 N( 0, 1 / ( N - 3 ) ) に従います。よって、z - z(ρ) の信頼区間 ( -t, t ) を求めれば、z(ρ) ± t が z の信頼区間として得られます。z-変換の逆変換は
なので、r の信頼区間 [ ta, tb ] は
ta = ( e2( z(ρ) - t ) - 1 ) / ( e2( z(ρ) - t ) + 1 )
tb = ( e2( z(ρ) + t ) - 1 ) / ( e2( z(ρ) + t ) + 1 )
で求めることができます。
相関係数の確率密度を求める関数 (accurateSCCProb) では無限級数の計算が必要になるので、プログラムでは k 番目の項があるしきい値以下になった段階で処理をストップすることで対応しています。計算式は複雑ですが、無限級数の扱いだけ注意すればそれほど難しいところはありません。なお、階乗 k! やガンマ関数の計算には、標準ライブラリ関数の tgamma を使っています。先頭の "t" は "true" を表し、これがガンマ関数を求めるための"真の"関数であることを示しています。この関数が用意される前から gamma という関数があり、こちらはガンマ関数の自然対数を返す関数なので、それと区別するための苦肉の策のようです。なお、
なので、例えば ( n - 3 )! を計算するためには tgamma( n - 2 ) としなければならないことに注意が必要です。
今回は、特に相関係数の部分で苦戦しました。まだ、いくつかやり残した部分もありますが、ある程度の区切りができたのでいったん公開したいと思います。相関係数をテーマとする論文や読み物は多岐に渡り、かなり奥が深い上に内容も難しいので、さらに理解ができた段階で別途更新していきたいと思います。
x が標準正規分布 N( 0, 1 ) に従い、y が自由度 N の χ2-分布 TN(y) に従うとき、x と y が独立ならば、t = x / ( y / N )1/2 は自由度 N の t-分布に従うのでした(「(6) 標本分布」の「3) t-分布(t-Distribution)」参照)。( a^ - a ) / ( σ2 / Nvx )1/2 と ( b^ - b ) / { ( 1 / N + mx2 / Nvx )σ2 }1/2 は標準正規分布に従うので、( N - 2 )vε / σ2 = Σj{1→N}( { yj - ( a^xj + b^ ) }2 ) / σ2 が自由度 N - 2 の χ2-分布 TN-2(y) に従うならば、
ta = ( a^ - a ) / ( σ2 / Nvx )1/2( √vε / σ ) = ( a^ - a ) / ( vε / Nvx )1/2
tb = ( b^ - b ) / { ( 1 / N + mx2 / Nvx )σ2 }1/2( √vε / σ ) = ( b^ - b ) / { ( 1 / N + mx2 / Nvx )vε }1/2
は自由度 N - 2 の t-分布に従うことになります。これを証明しましょう。( N - 2 )vε / σ2 は
と表され、zj = { yj - ( a^xj + b^ ) } / σ とすると、zj は平均
で、分散が
| V[zj] | = | V[{ yj - ( a^xj + b^ ) } / σ] |
| = | E[{ ( a - a^ )xj + ( b - b^ ) + εj }2] / σ2 | |
| = | { E[( a - a^ )2]xj2 + E[( b - b^ )2] + E[εj2] + | |
| 2E[( a - a^ )( b - b^ )]xj + 2E[( a - a^ )εj]xj + 2E[( b - b^ )εj] } / σ2 | ||
| = | [ vaxj2 + vb + σ2 - 2mxσ2xj / Nvx - 2xj{ ( xj - mx ) / Nvx }σ2 - 2[ 1 / N - { mx( xj - mx ) / Nvx } ]σ2 ] / σ2 | |
| = | [ σ2xj2 / Nvx + ( 1 / N + mx2 / Nvx )σ2 + σ2 - 2mxσ2xj / Nvx - 2xj{ ( xj - mx ) / Nvx }σ2 - 2[ 1 / N - { mx( xj - mx ) / Nvx } ]σ2 ] / σ2 | |
| = | -xj2 / Nvx + 2mxxj / Nvx - mx2 / Nvx + 1 - 1 / N | |
| = | -( xj - mx )2 / Nvx + 1 - 1 / N |
の正規分布に従います。また、zi と zj の共分散は
| E[zizj] | = | E[{ yi - ( a^xi + b^ ) }{ yj - ( a^xj + b^ ) } / σ2] |
| = | E[{ ( a - a^ )xi + ( b - b^ ) + εi }{ ( a - a^ )xj + ( b - b^ ) + εj }] / σ2 | |
| = | { E[( a - a^ )2]xixj + E[( b - b^ )2] + E[εiεj] + | |
| E[( a - a^ )( b - b^ )]( xi + xj ) + E[( a - a^ )εj]xi + E[( a - a^ )εi]xj + E[( b - b^ )( εi + εj )] } / σ2 | ||
| = | [ vaxixj + vb - mxσ2( xi + xj ) / Nvx - xi{ ( xj - mx ) / Nvx }σ2 - xj{ ( xi - mx ) / Nvx }σ2 - [ 1 / N - { mx( xi - mx ) / Nvx } ]σ2 - [ 1 / N - { mx( xj - mx ) / Nvx } ]σ2 ] / σ2 | |
| = | -xixj / Nvx - 1 / N - mx2 / Nvx + mxxi / Nvx + mxxj / Nvx | |
| = | -( xi - mx )( xj - mx ) / Nvx - 1 / N |
になります。そこで、r 行 c 列めの要素 arc を
とする行列 A を定義します。但し、δrc は「クロネッカーのデルタ」で r ≠ c のとき 0、r = c のとき 1 になります。すると、z = ( z1, z2, ... zN ) は平均ベクトルが 0 で共分散行列が A である多変量正規分布に従うことになります。これを以下 N( 0, A ) で表します。A は共分散行列であり、arc = acr となることも明らかなので対称行列になります。
A2 の r 行 c 列の要素を a2rc と表し、この値を求めると、
| a2rc | = | Σi{1→N}( { -( xr - mx )( xi - mx ) / Nvx + δri - 1 / N }{ -( xi - mx )( xc - mx ) / Nvx + δic - 1 / N } ) |
| = | Σi{1→N}( ( xr - mx )( xc - mx )( xi - mx )2 / N2vx2 + ( xr - mx )( xi - mx ) / N2vx + ( xi - mx )( xc - mx ) / N2vx + 1 / N2 | |
| - δri{ ( xi - mx )( xc - mx ) / Nvx + 1 / N } - δic{ ( xr - mx )( xi - mx ) / Nvx + 1 / N } + δriδic ) | ||
| = | ( xr - mx )( xc - mx ) / Nvx + 1 / N | |
| - { ( xr - mx )( xc - mx ) / Nvx + 1 / N } - { ( xr - mx )( xc - mx ) / Nvx + 1 / N } + δrc | ||
| = | -( xi - mx )( xj - mx ) / Nvx + δrc - 1 / N = arc |
となるので、A2 = A、つまり A は「べき等行列(Idempotent Matrix)」ということになります。A は対称行列なので、Aの固有ベクトルからなる直交行列を Q、固有値を対角成分とする行列を D としたとき、
と表すことができます(「固有値分解 - (2) カルーネン・レーベ展開」の「1) 対称行列と二次形式」参照)。A2 は
と求められるので(ここで QTQ = E(単位行列) であることを利用しています)、A2 = A から D2 = D であることになり、各対角成分 dii ( i = 1, 2, ... N ) に対して dii2 = dii となるので、対角成分すなわち固有値は 0 か 1 のどちらかであることになります。z' = QTz とすれば、
と求められるので(ここで、( x, Ax ) = ( ATx, x ) であることを利用しています)、D の対角成分が 1 の個数を r としたとき、z' 内の互いに独立な r 個の要素が標準正規分布に従うことが分かります。また、直交変換によって残り N - r 個の変数は消失します。これは、Az を N 個の線形方程式と見たときに r 個だけが独立で、残り N - r 個は線形従属であることを表しています。直交変換を行ってもノルムは変化しないので、||z|| = ||z'|| が成り立ちます。従って、||z||2 は標準正規分布に従う r 個の独立な確率変数の二乗和であり、この値は自由度 r の χ2-分布に従います(「(6) 標本分布」の「1) カイ二乗分布(Chi-square Distribution)」参照)。
r は行列 A の「階数(rank)」であり、行列の列ベクトル(または行ベクトル)の中で線形独立なものの個数を表します。行列 A の階数が一意に決まるのか、また、一意に決まったとしてその値を求められるのかについては、A がべき等行列であることから次の定理を利用することができます。
A の対角成分の和を求めると
| Σi{1→N}( aii ) | = | Σi{1→N}( -( xi - mx )2 / Nvx + δii - 1 / N ) |
| = | -1 + N - 1 = N - 2 |
よって、階数は常に N - 2 になり、||z||2 すなわち ( N - 2 )vε / σ2 は自由度 N - 2 の χ2-分布に従うことが証明されました。
ta, tb が自由度 N - 2 の t-分布に従うことを示すためにはもうひとつ、x にあたる ( a^ - a ) / ( σ2 / Nvx )1/2, ( b^ - b ) / { ( 1 / N + mx2 / Nvx )σ2 }1/2 と、y にあたる ( N - 2 )vε / σ2 = Σj{1→N}( { yj - ( a^xj + b^ ) }2 ) / σ2 が互いに独立であることを証明しなければなりません。二つの確率変数 x, y が互いに独立ならば、
すなわち共分散はゼロで x, y は相関がないことが成り立ちますが、逆は必ずしも成り立つわけではありません。しかし、確率変数が多変量正規分布に従う場合は逆も成り立ちます。二変量に限定して証明してみると、一般的な二変量正規分布は
で表されます。但し、μx, μy は x, y の平均、σx, σy は x, y の標準偏差、そして ρ は x, y の相関係数をそれぞれ表しています。確率変数 x = ( x1, x2, ... xN ) に対し、平均ベクトル μ = ( μ1, μ2, ... μN )、共分散行列を V とする多変量正規分布は
で表されるので、
| V = | | | σx2, | σxσyρ2 | | |
| | | σxσyρ2, | σy2 | | |
より二変量での具体的な式が得られます。ここで x, y の間に相関がなければ ρ = 0 なので、
| p( x, y ) | = | { 1 / 2πσxσy }exp( ( -1 / 2 ){ ( x - μx )2 / σx2 + ( y - μy )2 / σy2 } ) |
| = | { 1 / ( 2π )1/2σx }exp( -( x - μx )2 / 2σx2 ){ 1 / ( 2π )1/2σy }exp( -( y - μy )2 / 2σy2 ) |
と表されます。これは、二変量正規分布が一変量の正規分布の積で表されることを意味するので、x と y は互いに独立であることになります。変数の数を 3 以上にしても、相関係数が全てゼロになることから共分散行列が対角行列になり、結局一変量正規分布の積で表されることを示すことで証明ができます。
まず、xa = ( a^ - a ) / ( σ2 / Nvx )1/2 と zj = { yj - ( a^xj + b^ ) } / σ に対して、E[xazj] を求めてみます。xa, zj はどちらも平均ゼロの正規分布に従う確率変数です。
| E[xazj] | = | E[{ ( a^ - a ) / ( σ2 / Nvx )1/2 }[ { yj - ( a^xj + b^ ) } / σ ]] |
| = | E[( a^ - a ){ yj - ( a^xj + b^ ) }] / { σ2 / ( Nvx )1/2 } | |
| = | E[( a^ - a ){ ( a - a^ )xj + ( b - b^ ) + εj }] / { σ2 / ( Nvx )1/2 } | |
| = | { -E[( a^ - a )2]xj - E[( a^ - a )( b^ - b )] + E[( a^ - a )εj] } / { σ2 / ( Nvx )1/2 } | |
| = | [ -vaxj + mxσ2 / Nvx + { ( xj - mx ) / Nvx }σ2 ] / { σ2 / ( Nvx )1/2 } | |
| = | ( -σ2xj / Nvx + mxσ2 / Nvx + σ2xj / Nvx - mxσ2 / Nvx ) / { σ2 / ( Nvx )1/2 } | |
| = | 0 = E[xa]E[zj] |
となるので、(xa と zj が正規分布に従うことから) xa と zj は互いに独立です。確率変数 x, y が互いに独立であるとは同時分布 p( x, y ) が p(x) と p(y) の積で表されることだったので、p(zj) に対して uj = zj2 と変数変換をしても独立性は保たれます。さらに y = Σj{1→N}( uj ) と変数変換しても、全ての j に対して xa と uj は互いに独立なので、やはり xa , yの独立性は保たれます。
次に、xb = ( b^ - b ) / { ( 1 / N + mx2 / Nvx )σ2 }1/2 と zj = { yj - ( a^xj + b^ ) } / σ に対して、E[xbzj] を求めてみます。xb はやはり平均ゼロの正規分布に従う確率変数です。式が見やすくなるように、以下、xb = ( b^ - b ) / ( Aσ2 / N )1/2 で表します ( A = 1 + mx2 / vx になります )。
| E[xbzj] | = | E[{ ( b^ - b ) / ( Aσ2 / N )1/2 }[ { yj - ( a^xj + b^ ) } / σ ]] |
| = | E[( b^ - b ){ yj - ( a^xj + b^ ) }] / { σ2( A / N )1/2 } | |
| = | E[( b^ - b ){ ( a - a^ )xj + ( b - b^ ) + εj }] / { σ2( A / N )1/2 } | |
| = | { -E[( a^ - a )( b^ - b )]xj - E[( b^ - b )2] + E[( b^ - b )εj] } / { σ2( A / N )1/2 } | |
| = | [ mxσ2xj / Nvx - vb + [ 1 / N - { mx( xj - mx ) / Nvx } ]σ2 ] / { σ2( A / N )1/2 } | |
| = | [ mxxj / vx - ( 1 + mx2 / vx ) + { 1 - ( mxxj - mx2 ) / vx } ] / ( AN )1/2 | |
| = | 0 = E[xb]E[zj] |
よって、同様な考えによって xb と y も互いに独立であることが示され、これで ta, tb が自由度 N - 2 の t-分布に従うことが証明されました。
任意の M x Q 行列 A に対し、その列ベクトルを a1, a2, ... aQ とします。任意の M x P 行列 B に対して、
を満たす P 次元の列ベクトル fc が存在するとき、B の r 行 c 列めの要素を brc、ac の r 番めの要素を arc、fc の r 番目の要素を frc で表せば
| | | a1c | | | = | | | b11, | b12, | ... | b1P | | | | | f1c | | |
| | | a2c | | | | | b21, | b22, | ... | b2P | | | | | f2c | | | |
| | | : | | | | | : | : | ... | : | | | | | : | | | |
| | | aMc | | | | | bM1, | bM2, | ... | bMP | | | | | : | | | |
| | | : | | | ||||||||||
| | | fPc | | | ||||||||||
| = | | | b11f1c + b12f2c + ... + b1PfPc | | |
| | | b21f1c + b22f2c + ... + b2PfPc | | | |
| | | : | | | |
| | | bM1f1c + bM2f2c + ... + bMPfPc | | |
| = | f1c | | | b11 | | | + f2c | | | b12 | | | + ... + fPc | | | b1P | | |
| | | b21 | | | | | b22 | | | | | b2P | | | ||||
| | | : | | | | | : | | | | | : | | | ||||
| | | bM1 | | | | | bM2 | | | | | bMP | | |
と表すことができます。但し、b1, b2, ... bP は行列 B の列ベクトルを表します。これは、ac が B の列ベクトルの線形結合で表せることを示しています。全ての ac に対して fc が存在すれば、F = ( f1, f2, ... fQ ) となる行列が存在することになるので、A = BF となる行列 F が存在するならば、A の全ての列ベクトルが B の列ベクトルの線形結合で表されることになります。逆に、A の全ての列ベクトルが B の列ベクトルの線形結合で表されるならば、A = BF となる行列 F が存在することも、上記の内容を逆にたどることで示すことができます。
これらは、行ベクトルに対しても同様のことを示すことができます。すなわち、任意の Q x M 行列 A の行ベクトルを a'1, a'2, ... a'Q とし、任意の P x M 行列 B に対して、
を満たす P 次元の行ベクトル g'r が存在するとき、A = GB を満たす行列 G = ( g'1, g'2, ... g'Q )T が存在することになり、A の全ての行ベクトルが B の行ベクトルの線形結合で表されることが必要十分条件となります。
A の列ベクトルから、線形従属なものを除き、線形独立なベクトルだけを残した行列 B を新たにつくります。このとき、A の全ての列ベクトルが B の列ベクトルの線形結合で表されるので、A = BF となる行列 F が存在します。A の線形独立な列ベクトルの数を C とすれば、B の列数と F の行数は C になります。同様に、A の行ベクトルから線形独立なベクトルだけを残した行列 C を新たにつくったとき、A の全ての行ベクトルが C の行ベクトルの線形結合で表されるので、A = GC となる行列 G が存在します。A の線形独立な行ベクトルの数を R とすれば、G の列数と C の行数は R になります。
行列 F の行数は C なので、線形独立な行ベクトルの数は C 以下になります。また、A = BF ならば、A の全ての行ベクトルが F の行ベクトルの線形結合で表されるので、F の線形独立な行ベクトルの数は A のそれ以上になります。従って、行列 F の線形独立な行ベクトルの数を f とすれば、
が成り立ちます。同様に、行列 G の列数は R なので、線形独立な列ベクトルの数は R 以下になります。また、A = GC ならば、A の全ての列ベクトルが G の列ベクトルの線形結合で表されるので、G の線形独立な列ベクトルの数は A のそれ以上になります。従って、行列 G の線形独立な列ベクトルの数を g とすれば、
が成り立ちます。両者が成り立つためには C = R でなければなりません。これは、任意の行列の列ベクトルと行ベクトルに対し、その中の線形独立なものの数は等しいということを意味します。この数のことを「階数(Rank)」といい、行列 A の階数を一般的に rank(A) で表します。rank(A) は、A の中の線形独立な列(または行)ベクトルの数なので、A が M 行 N 列であるとき、先ほど示したように、 A = BC となる M x rank(A) の行列 B と、rank(A) x N の行列 C が必ず存在します。B と C の階数は、行数と列数を超える値には決してならないので、どちらも rank(A) 以下になります。ところが、A の全ての列ベクトルは B の列ベクトルの線形結合で、また A の全ての行ベクトルは C の行ベクトルの線形結合で表されるので、rank(A) は rank(B), rank(C) より大きくなることはなく、従って B と C の階数は rank(A) 以上になります。この両方を満たすためには、
となる必要があります。よって、次の定理が成り立ちます。
逆行列は、行列式がゼロではない(非特異な)正方行列に対してのみ存在します。しかし、正方行列ではない場合も制限付きで逆行列を定義することができます。任意の M x N 行列 A に対し、
となる N x M 行列 R を「右逆行列(Right Inverse)」といいます。但し、EM は M x M 単位行列を表します。同様に、
を満たす N x M 行列 L を「左逆行列(Left Inverse)」といいます。
rank( EM ) = M なので、rank(A) = M の場合のみ R が存在し、その階数も M になります。また、同様に L に対しても、rank(A) = N の場合のみ存在し、その階数は N になります。行列 A が正方行列ならば(つまり M = N ならば)、全ての列(または行)ベクトルが線形独立の場合のみ右逆行列と左逆行列の両方が存在することになります。このとき、
なので、
LAR = L(AR) = LEN = L
LAR = (LA)R = ENR = R
となり、L = R であることが示されます。
正方行列の対角成分の和のことを「トレース(Trace)」といい、正方行列 A に対するトレースは一般的に tr(A) で表されます。以下の公式は、容易に導くことができます。
M x N 行列 A と N x M 行列 B の積 AB は、M x M の正方行列になります。A, B の r 行 c 列めの要素をそれぞれ arc, brc としたとき、行列 AB のトレースは、行列 AB の i 番目の対角成分が Σj{1→N}( aijbji ) になることから
になります。積を計算する順番を逆転して、N x N 正方行列 BA を計算したとき、そのトレースは
になります。tr( BA ) の和の部分を分解・再構成すると
| tr( BA ) | = | Σi{1→N}( bi1a1i + bi2a2i + ... biMaMi ) |
| = | ( b11a11 + b12a21 + ... b1MaM1 ) + ( b21a12 + b22a22 + ... b2MaM2 ) + ... + ( bN1a1N + bN2a2N + ... bNMaMN ) | |
| = | ( a11b11 + a21b12 + ... aM1b1M ) + ( a12b21 + a22b22 + ... aM2b2M ) + ... + ( a1NbN1 + a2NbN2 + ... aMNbNM ) | |
| = | ( a11b11 + a12b21 + ... a1NbN1 ) + ( a21b12 + a22b22 + ... + a2NbN2 ) + ... + ( aM1b1M + aM2b2M + ... + aMNbNM ) | |
| = | Σi{1→M}( ai1b1i + ai2b2i + ... aiNbNi ) | |
| = | Σi{1→M}( Σj{1→N}( aijbji ) ) = tr( AB ) |
となって、両者の値は等しくなり、積の順番を交換してもトレースは変化しないことが証明できます。
以上の結果を利用して、以下の定理を証明します。
k ≠ 0 であるスカラーに対し、
を満たす正方行列 A について、
が成り立つ
A2 = kA という式を変形すると { (1/k)A }2 = (1/k)A となるので、(1/k)A はべき等行列であると仮定していることになります。このとき、A の階数がトレースから得られるということを上記定理は表しています。階数の計算は一般的に面倒で、通常は連立方程式を解くアルゴリズムを利用することになりますが、トレースの計算は非常に簡単にできるので、べき等行列に対しては階数が非常に求めやすいということになります。
A は当然正方行列なので、その行列数を N とします。また、A の階数を rank( A ) = r で表します。このとき、A = BC を満たす N x r の行列 B と r x N の行列 C が存在し、B, C の階数はどちらも r になります。このとき、
A2 = BCBC
kA = kBC = B(kEr)C ( Er : r x r 単位行列 )
と計算できて、両式の左辺は等しいので BCBC = B(kEr)C になります。B は N 行 r 列で階数が r なので左逆行列を持ちます。同様に、C は右逆行列を持つので、それぞれを左右から掛けることで CB = kEr という結果が得られます。従って、
より、tr( A ) = k・rank( A ) を示すことができます。特に k = 1 のとき、
すなわち A がべき等行列であり、この場合
が成り立つことになります。
6, 7 は相関係数に関する説明の中でいろいろと参考にしました。
 --- 統計学入門
--- 統計学入門
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |