 |
「分散分析法(ANOVA)」は、各集団の因子(装置ごとの製品処理時間やクラス別の学力テスト結果など)に対する「要因効果」、すなわち全体の平均と各集団における平均の差が、その要因(装置やクラス)だけに依存していることを前提条件としています。しかし、標本の抽出が無作為に行われていないような場合、他の要因によって集団間の差が生じてしまう可能性があります。この影響をできるだけ小さくすることを目的とした検定法として、今回は「共分散分析(ANCOVA)」を紹介します。
以前紹介した「線形重回帰モデル (Linear Multiple Regression Model)」では、独立変数が連続量であることを前提としていました。しかし、名義尺度の場合も「ダミー変数(Dummy Variable ; Indicator Variable)」を利用することで重回帰分析に含めることができます。
p 個の集団別に、一つの独立変数とその従属変数があると仮定します。i ( i = 1, 2, ... p ) 番目の集団が持つ独立・従属変数の個数を ni 個とし、その独立変数を xi,j ( j = 1, 2, ... ni ), 従属変数を yi,j とします。ここで、各集団を区別するための新たなダミー変数 δi を用意します。δi は、i 番目の集団に属する場合 1 で、それ以外は 0 とします。但し、δi は p - 1 番目の集団まで用意するものとし、p 番目の集団には適用しません。このとき、重回帰式は次のように表されます。
i 番目の集団に属するデータは、δi のみが 1 でその他はゼロになります。したがって、上式は
| yi,j | = | ( b0 + bi ) + axi,j + εi,j | ( i < p ) |
| = | b0 + axp,j + εp,j | ( i = p ) |
と表され、各集団ごとに、切片が異なり傾きは等しい回帰直線が得られることになります。
例として、性別によって二つの集団に分類し、年齢を独立変数、身長や体重を従属変数としたときの重回帰式を利用する場合を考えると、ダミー変数は一つだけでよく、男性のとき δ = 1 とするのならば、男性と女性に対する重回帰式は
y1,j = ( b0 + b1 ) + ax1,j + ε1,j ... (男性)
y2,j = b0 + ax2,j + ε2,j ... (女性)
になります。
上で示した式は、独立変数に対する従属変数の増加率がどの集団も変わらないということを前提としています。しかし、集団ごとに変化率が異なるようなデータが存在することは容易に想像できて、そのような場合にはこの重回帰式は採用できないので代わりに次のような式を利用します。
i 番目の集団に属するデータは次のようになります。
| yi,j | = | ( b0 + bi ) + ( a0 + ai )xi,j + εi,j | ( i < p ) |
| = | b0 + a0xp,j + εp,j | ( i = p ) |
よって、各集団によって bi だけ切片が変化し、ai だけ傾きが変化するような回帰直線が得られるという結果になります。
集団を分けず、ただ一つの独立変数だけで回帰式を計算すると、
となります。ここで、p - 1 個の集団ごとにダミー変数 δk を用意するということは、p - 1 本の軸を新たに用意して、各軸に垂直で、その軸の 0 と 1 を通る平面上にプロットを分ける操作に相当します。(実際には不可能ですが)ある軸以外は全てその軸の向いた方向に視線を移し、ただ一つの軸だけ斜め方向から見ると、ある集団のプロットだけ別の平面上にある様子を観察することができます。
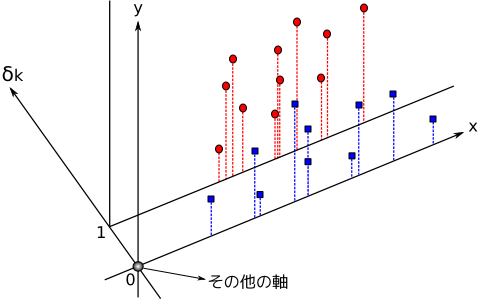
ダミー変数も独立変数の一つに変わりはないので、従来の重回帰分析法はそのまま流用することができます。また、通常の独立変数を二つ以上に増やすことももちろん可能です。
ここで次のような、(通常の)独立変数が一つもないダミー変数だけの回帰式を考えます。
i 番目の集団に対しては、重回帰式は
| yi,j | = | ( b0 + bi ) + εi,j | ( i < p ) |
| = | b0 + εi,j | ( i = p ) |
になります。重回帰式の回帰係数 bi ( i = 1, 2, ... p - 1 ) が全てゼロであると仮定すれば、回帰式から求められる予測値の不偏分散と、測定値と予測値の差(残差)の平方和から求められる不偏分散の比は F-分布に従います(*1-1)。すなわち、回帰式から求めた予測値を y^i,j、その平均を m^y、集団の数を p、i 番目の集団のデータ数を ni、全データ数を N ( = Σ{1→p}( ni ) ) とすれば、
予測値の不偏分散 v^y = Σi{1→p}( Σj{1→ni}( ( y^i,j - m^y )2 ) ) / ( p - 1 )
残差の不偏分散 vε = Σi{1→p}( Σj{1→ni}( ( yi,j - y^i,j )2 ) / ( N - p )
不偏分散の比 F0 = v^y / vε
より bi = 0 ( i = 1, 2, ... p - 1 ) という仮定のもとで F0 は自由度 ( p - 1, N - p ) の F-分布に従います。この仮説が棄却されるとき、いずれかの i に対して bi = 0 が成り立たないことになり、集団ごとの従属変数は一致しないことが示されるので、これは「一元配置分散分析法」そのものを意味します。つまり、分散分析は重回帰分析の一種と考えることができるわけです。
*1-1) 「(13) 回帰分析法」の「回帰係数の推定」に関する説明を参照
p 個の母集団 Ai ( i = 1, 2, ..., p ) から、独立変数 xi,j とその従属変数 yi,j ( j = 1, 2, ... ni ) が得られたとします。それぞれの母集団 Ai から得られた標本に対して、xi,j と yi,j に線形回帰モデルが適用できたとすれば、i 番目の集団に対して
と表すことができます。ai, bi は i 番目の集団に固有の回帰係数であり、εi,j は独立変数だけでは説明のできない誤差成分です。但し、εi,j は互いに独立で、正規分布 N( 0, σ2 ) に従うと仮定します。「最小二乗法」を使い、回帰係数の最尤推定量 a^i, b^i を求めると次のような値になるのでした(*2-1)。
a^i = sxy,i / vx,i
b^i = my,i - mx,i・sxy,i / vx,i
但し、mx,i, my,i は i 番目の集団の独立変数 xi,j と従属変数 yi,j の標本平均、vx,i, vy,i は xi,j と yi,j の標本分散、sxy,i は xi,j と yi,j の標本共分散をそれぞれ表しています。
この結果から、i 番目の集団に対する回帰式は
になります。これは各集団ごとの回帰式を表しています。
ここで、もし各集団の回帰係数 ai が等しいと仮定したとき、各集団ごとの回帰式で表される直線は全て平行で、切片だけが異なる状態になります。これを全体の回帰式として表すと、
になります。ここで、回帰直線の傾きは全て等しいと仮定したので a に統一し、ダミー変数として δk を追加しています。δk は k = i の場合だけ 1 となり、その他は全てゼロです。このとき、b0 は p 番目の集合の切片を、bk ( k = 1, 2, ... p - 1 ) は p 番目以外の集合の b0 との差異を表すので、i 番目の集合に対する回帰式は
| yi,j | = | ( b0 + bi ) + axi,j + εi,j | ( i < p ) |
| = | b0 + axi,j + εi,j | ( i = p ) |
となります。この回帰式の変数は p + 1 個になり、回帰式とデータの間の誤差を最小にするためには、
| J | = | Σi{1→p}( Σj{1→ni}( εi,j2 ) ) / 2 |
| = | Σi{1→p}( Σj{1→ni}( { yi,j - [ b0 + Σk{1→p-1}( bkδk ) + axi,j ] }2 ) ) / 2 | |
| = | Σi{1→p-1}( Σj{1→ni}( [ yi,j - ( b0 + bi + axi,j ) ]2 ) ) / 2 | |
| + Σj{1→np}( [ yp,j - ( b0 + axp,j ) ]2 ) ) / 2 |
を最小にすればいいのですが、ここで、b'p = b0、b'i = b0 + bi とすると、上式は以下のように変形することができます。
もう一度、b'i を bi に戻して、この式を係数で偏微分すれば、
| ∂J / ∂bi | = | - Σj{1→ni}( yi,j - ( bi + axi,j ) ) |
| = | - nimy,i + nibi + (nimx,i)a = 0 より |
bi + mx,ia = my,i --- (1)
| ∂J / ∂a | = | - Σi{1→p}( Σj{1→ni}( xi,j[ yi,j - ( bi + axi,j ) ] ) ) |
| = | - Σi{1→p}( Σj{1→ni}( xi,jyi,j ) ) + Σi{1→p}( (nimx,i)bi ) + aΣi{1→p}( Σj{1→ni}( xi,j2 ) ) = 0 より |
Σi{1→p}( (nimx,i)bi ) + aΣi{1→p}( Σj{1→ni}( xi,j2 ) ) = Σi{1→p}( Σj{1→ni}( xi,jyi,j ) ) --- (2)
より正規方程式が得られ、これを解けば回帰係数を求めることができます。
(1)式は p 個あり、それらの両辺に nimx,i を掛けて全式を加えると
になります。(1') と (2) を辺々引くと bi の項が消えて
という結果が得られます。ここで、左辺と右辺にある式は
| Σi{1→p}( Σj{1→ni}( xi,j2 ) ) - Σi{1→p}( nimx,i2 ) | |
| = | Σi{1→p}( Σj{1→ni}( ( xi,j - mx,i )2 ) ) |
| = | Σi{1→p}( nivx,i ) |
| Σi{1→p}( Σj{1→ni}( xi,jyi,j ) ) - Σi{1→p}( nimx,imy,i ) | |
| = | Σi{1→p}( Σj{1→ni}( ( xi,j - mx,i )( yi,j - my,i ) ) ) |
| = | Σi{1→p}( nisxy,i ) |
と変形できます。但し、vx,i と sxy,i は i 番目の集団に対する x の分散と x, y の共分散をそれぞれ表します。(二乗の平均) - (平均の二乗) = (分散)、(xyの平均) - (x,yの平均の積) = (共分散) となることを利用していることに注意してください。よって、
となって、これを (1) 式に代入すれば
より bi が求められるので、i 番目の集団に対する回帰式は
となります。もし、各集団の独立変数と従属変数の平均 mx,i, my,i が全て等しく mx, my となるならば、Σi{1→p}( nivx,i ) / N と Σi{1→p}( nisxy,i ) / N はそれぞれ全標本に対する x の分散、x, y の共分散を表すので、それらを vx, sxy と表せば上式は
となって、通常の単回帰式と等しくなります。
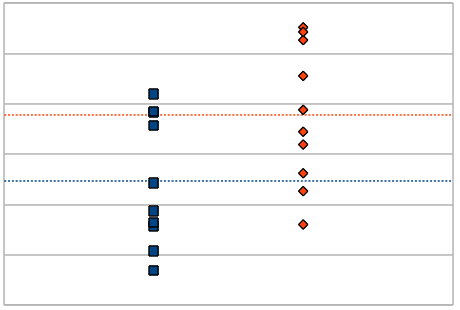
従属変数だけを使って各集団ごとの平均値に差異があるか検定する手法は「一元配置分散分析法」になるのでした。二つの集団に対して、検定を行いたい対象の値の分布をグラフに表すと、次のようなイメージになります。
グラフのラインは、各集団の平均 my,i を表しています。一見すると、右側の赤い点で示された分布の方が、平均値は大きいと判断できます。しかし、この値がある独立変数によって線形的に変化するとき、散布図で表すと次のように表される場合も考えられます。
すると、今度は左側の青い点で示された分布の回帰直線が上側になります。青い点の分布は独立変数の値が小さいため、その影響で従属変数の y の値も小さくなっていたことがこのグラフから読み取れます。このような、従属変数に対して影響を及ぼす独立変数のことを「共変数(Covariate)」といい、この影響を取り除かない限りは集団間の差異を調べることはできないということをこの例は示しています。
予測値 y^i,j とその平均 m^y の差の平方和 S^y は、
| S^y | = | Σi{1→p}( Σj{1→ni}( ( y^i,j - m^y )2 ) ) |
| = | Σi{1→p}( Σj{1→ni}( [ ( y^i,j - m^y,i ) + ( m^y,i - m^y ) ]2 ) ) | |
| = | Σi{1→p}( Σj{1→ni}( ( y^i,j - m^y,i )2 + 2( y^i,j - m^y,i )( m^y,i - m^y ) + ( m^y,i - m^y )2 ) ) | |
| = | Σi{1→p}( Σj{1→ni}( ( y^i,j - m^y,i )2 ) ) + Σi{1→p}( ni( m^y,i - m^y )2 ) |
と分解することができます。ここで、Σj{1→ni}( y^i,j - m^y,i ) = 0 であることを利用していることに注意してください。結果の第一項は、集団内における予測値とその平均の差の平方和を表しているので SC (クラス内(class)平方和) とし、第二項は、各集団の平均と全体の平均の差の平方和を意味するので SB (クラス間(between)平方和)で表すことにします。なお、m^y,i = my,i, m^y = my が成り立つことは容易に証明できます。よって、上式は
と表すこともできます。
観測値の平方和 Sy と残差の平方和 SE は
Sy = Σi{1→p}( Σj{1→ni}( ( yi,j - my )2 ) )
SE = Σi{1→p}( Σj{1→ni}( ( yi,j - y^i,j )2 ) )
で求めることができて、これらの間には Sy = S^y + SE の関係が成り立つので、全体をまとめると
となります。つまり、全体の誤差を、集団間の誤差・集団内の誤差・残差の三つに分解したことを意味します。SC は、
| SC | = | Σi{1→p}( Σj{1→ni}( ( y^i,j - m^y,i )2 ) ) |
| = | Σi{1→p}( Σj{1→ni}( { [ a( xi,j - mx,i ) + m^y,i ] - m^y,i }2 ) ) | |
| = | a2Σi{1→p}( Σj{1→ni}( ( xi,j - mx,i )2 ) ) | |
| = | [ Σi{1→p}( nisxy,i ) / Σi{1→p}( nivx,i ) ]2Σi{1→p}( nivx,i ) | |
| = | [ Σi{1→p}( nisxy,i ) ]2 / Σi{1→p}( nivx,i ) |
と変形することができます。どの集団も x と y の間に相関がなければ sxy,i = 0 なので(このとき、a = 0 でもあります)、SC = 0 より S^y は全て SB が占めることになり、通常の「一元配置分散分析法」を使ったときと同じ式になります。相関が強くなれば、誤差全体のなかで SC が占める割合は大きくなり、独立変数の従属変数の関係は強い、つまり共変数の影響が無視できないということを意味します。SB は、集団間に差異があるほど大きくなりますが、ここではまだ共変数の差異に起因するものが混在していることに注意してください。先ほど説明したように、独立変数の分布が異なるために従属変数にも差異が発生している可能性がまだ残っているので、SB を見ただけでは集団間の差異があるのか特定することはできません。
正規化した予測値の誤差の二乗和 S^y / σ2 は自由度 p の χ2-分布に従うのでした(*2-2)。また、a = 0 の仮定のもとで、正規化した集団間の誤差の二乗和 SB / σ2 は自由度 p - 1 の χ2-分布に従います(*2-3)。
最後の、正規化した集団内の誤差の二乗和 SC / σ2 は、全集団の y の平均が等しい場合は単回帰式に対する予測値の平方和そのものであり、a = 0 の仮定のもとでは自由度 1 の χ2-分布に従うことになります(*2-2)。この値は、各集団ごとに共分散を計算しているので集団間の差を取り除いたときの回帰式を表していて、下図のように集団ごとの平均を一点に合わせた上での回帰式と見ることができます。

これらを表にまとめると
| 平方和 | 自由度 | 不偏分散 | |
|---|---|---|---|
| 集団内 | SC = [ Σi{1→p}( nisxy,i ) ]2 / Σi{1→p}( nivx,i ) | 1 | vC = SC |
| 集団間 | SB = Σi{1→p}( ni( my,i - my )2 ) | p - 1 | vB = SB / ( p - 1 ) |
| 残差 | SE = Σi{1→p}( Σj{1→ni}( ( yi,j - y^i,j )2 ) ) | N - p - 1 | vE = SE / ( N - p - 1 ) |
| 全体 | Sy = Σi{1→p}( Σj{1→ni}( ( yij - my )2 ) ) | N - 1 |
となります。
*2-1) 「(11) 二標本の解析 - 1 -」の「2) 相関係数と回帰曲線」を参照
*2-2) 「(13) 回帰分析法」の「回帰係数の推定」を参照
*2-3) 「(14) 分散分析法(ANOVA)」の「補足1)」を参照
先ほど示したモデルは、各集団の回帰係数が等しいことを前提にしていました。しかし、場合によっては係数に差が生じる可能性も十分考えられます。そのときの重回帰式モデルは次のように表されるのでした。
i 番目の集団に対しては次のような式になります。
| yi,j | = | ( b0 + bi ) + ( a0 + ai )xi,j + εi,j | ( i < p ) |
| = | b0 + a0xp,j + εp,j | ( i = p ) |
この回帰式の変数は 2p 個になり、回帰式とデータの間の誤差を最小にするためには、
| J | = | Σi{1→p}( Σj{1→ni}( εi,j2 ) ) / 2 |
| = | Σi{1→p}( Σj{1→ni}( { yi,j - [ b0 + Σk{1→p-1}( bkδk ) + a0xi,j + Σk{1→p-1}( akδkxi,j ) ] }2 ) ) / 2 | |
| = | Σi{1→p-1}( Σj{1→ni}( { yi,j - [ ( b0 + bi ) + ( a0 + ai )xi,j ] }2 ) ) / 2 | |
| + Σj{1→np}( [ yp,j - ( b0 + a0xp,j ) ]2 ) ) / 2 |
を最小にすればいいのですが、ここで、b'p = b0、b'i = b0 + bi、a'p = a0、a'i = a0 + ai とすると、上式は以下のように変形することができます。
もう一度、bi = b'i, ai = a'i に戻して、この式を係数で偏微分すれば、
| ∂J / ∂bi | = | - Σj{1→ni}( yi,j - ( bi + aixi,j ) ) |
| = | - nimy,i + nibi + (nimx,i)ai = 0 より |
bi + mx,iai = my,i --- (1)
| ∂J / ∂ai | = | - Σj{1→ni}( xi,j[ yi,j - ( bi + aixi,j ) ] ) |
| = | - Σj{1→ni}( xi,jyi,j ) + (nimx,i)bi + aiΣj{1→ni}( xi,j2 ) = 0 より |
(nimx,i)bi + aiΣj{1→ni}( xi,j2 ) = Σj{1→ni}( xi,jyi,j ) --- (2)
から得られる正規方程式を解けばいいことになります。
(1) 式に nimx,i を掛けて (2) から辺々引くと bi の項が消えて
よって、
と求められます。これは、集団別に求めた回帰式での係数と等しい値です。bi の値は
なので、i 番目の集団に対する回帰式は
となり、集団ごとに回帰式を求めたときの結果に一致します。
i 番目の集団に対し、傾きを共通にしたときの回帰式は
なので、両者の違いは傾きだけで、どちらもその集団の平均 ( mx,i, my,i ) を通ります。各集団ごとに回帰式の傾きの差が大きくなるほど、二つの式から得られる予測値の差異は大きくなります。このときの、予測値 y^i,j とその平均 m^y の差の平方和 S^y は
| S^y | = | Σi{1→p}( Σj{1→ni}( ( y^i,j - m^y,i )2 ) ) + Σi{1→p}( ni( m^y,i - m^y )2 ) |
| = | Σi{1→p}( Σj{1→ni}( ( y^i,j - my,i )2 ) ) + Σi{1→p}( ni( my,i - my )2 ) | |
| = | SC' + SB |
で表され、SC' は
| SC' | = | Σi{1→p}( Σj{1→ni}( ( y^i,j - my,i )2 ) ) |
| = | Σi{1→p}( Σj{1→ni}( { [ ai( xi,j - mx,i ) + my,i ] - my,i }2 ) ) | |
| = | Σi{1→p}( ai2Σj{1→ni}( ( xi,j - mx,i )2 ) ) | |
| = | Σi{1→p}( ( sxy,i / vx,i )2nivx,i ) | |
| = | Σi{1→p}( nisxy,i2 / vx,i ) |
で表されます。傾きを共通にした場合と同様に、S^y は集団間の差異と集団内の差異の二つに分解されます。しかし、集団内の差異は、各集団の回帰直線の傾きが異なることによる差によって値が異なります。両者の差 SC' - SC は必ず非負となり(補足1)、その差は傾き、すなわち独立変数に対する従属変数の変化量のバラツキを表しています。従って、全ての集団において傾きが等しければ、SC' = SC で両者の差異はゼロになり、変化量のバラツキが大きくなるほど差も大きくなっていきます。これを交互作用により発生する差異 SI と表すと、
| Sy | = | SC' + SB + SE' |
| = | SC + SI + SB + SE' |
となり、SE = SE' + SI、つまり、回帰係数を共通とした場合の残差に対して、交互作用による差異をさらに抽出することができることになります。これらを全てまとめると、
と表すことができます。S^y / σ2 は、回帰係数が 2p 個あることから自由度 2p -1 の χ2-分布に従い(*3-1)、SB / σ2 は自由度 p - 1 の χ2-分布に従います(*3-2)。SC' / σ2 = ( SC + SI ) / σ2 は互いに独立な p 個の回帰式に対する予測値の平方和と考えられるので自由度 p の χ2-分布に従い、SC / σ2 が自由度 1 の χ2-分布に従うことから SI / σ2 は自由度を一つ失い p - 1 の χ2-分布に従うことになります。最後に、残差 SE に対しては SI 分の自由度を失い、SE / σ2 は自由度 N - 2p の χ2-分布に従うことになります。以上をまとめると、以下のような表になります。
| 平方和 | 自由度 | 不偏分散 | |
|---|---|---|---|
| 集団内 | SC = [ Σi{1→p}( nisxy,i ) ]2 / Σi{1→p}( nivx,i ) | 1 | vC = SC |
| 集団間 | SB = Σi{1→p}( ni( my,i - my )2 ) | p - 1 | vB = SB / ( p - 1 ) |
| 交互作用 | SI = Σi{1→p}( nisxy,i2 / vx,i ) - SC | p - 1 | vI = SI / ( p - 1 ) |
| 残差 | SE = Σi{1→p}( Σj{1→ni}( ( yi,j - y^i,j )2 ) ) | N - 2p | vE = SE / ( N - 2p ) |
| 全体 | Sy = Σi{1→p}( Σj{1→ni}( ( yij - my )2 ) ) | N - 1 |
SC は、回帰係数が集団ごとに変わらないという仮定のもとで、各データが回帰式にどれだけ近似できているかを表す指標になり、値が大きいほどよく近似できていることになります。SB は、集団ごとの差異を表す指標で、値が大きいほど集団間の差異が大きいことを示しますが、共変数の差異による影響もまだ残っています。SI は、回帰係数を共通したときの回帰式に対し、個別に回帰式を求めたときの差異を表し、値が小さいほど各集団の回帰係数は近いことを意味します。そして、これらでは説明できない残差部分が SE になります。
*3-1) 「(13) 回帰分析法」の「回帰係数の推定」を参照
*3-2) 「(14) 分散分析法(ANOVA)」の「補足1)」を参照
以上、名義尺度の線形重回帰モデルを、集団ごとに共通な係数を持つ場合と、各集団で異なる係数を持つ場合の二通りで考え、全体のバラツキを四つの種類、集団間 SB・集団内 SC・交互作用 SI・残差 SE に分離しました。vB, vC, vI, vE は、それぞれの平方和を自由度で割った不偏分散を表しています。ここで、回帰式の傾きがゼロである ( 独立変数と従属変数の間で相関がない ) という仮定のもとでは、vC, vI それぞれと vE の比率は、F-分布に従います。それをまとめた表を以下に示します。
| 平方和 | 自由度 | 不偏分散 | F値 | |
|---|---|---|---|---|
| 集団内 | SC = [ Σi{1→p}( nisxy,i ) ]2 / Σi{1→p}( nivx,i ) | 1 | vC = SC | FC = vC / vE |
| 集団間 | SB = Σi{1→p}( ni( my,i - my )2 ) | p - 1 | vB = SB / ( p - 1 ) | |
| 交互作用 | SI = Σi{1→p}( nisxy,i2 / vx,i ) - SC | p - 1 | vI = SI / ( p - 1 ) | FI = vI / vE |
| 残差 | SE = Σi{1→p}( Σj{1→ni}( ( yi,j - y^i,j )2 ) ) | N - 2p | vE = SE / ( N - 2p ) | |
| 全体 | Sy = Σi{1→p}( Σj{1→ni}( ( yij - my )2 ) ) | N - 1 |
FC の値が大きい場合、残差の影響が小さいことを意味するので、共通な傾きを持つ回帰式が独立変数と従属変数の関係をよく表していることになります。逆に値が小さければ残差の影響の方が大きいことになり、この場合、独立変数と従属変数の間に相関はないと考えられます。
次に FI の値に着目すると、この値が大きい時は、集団ごとに傾きを変化させた場合の回帰式が、共通な傾きを持つ回帰式から大きくずれていることを意味するので、独立変数に対する従属変数の変化量が各集団ごとで一定でないことになります。その場合、集団ごとの従属変数の差異は、共変数の取る値によって異なります。極端な例として、二つの集団において片方が正の傾き、もう一方が負の傾きを持てば、両直線の交点を境として従属変数の大小関係は逆転します。たまたま、共変数が交点に近い値ならば両者は差異がないと判断され、交点から両集団の共変数が同方向にシフトしていれば差異あり、異なる方向にあれば差異なしと判断される場合もあります。このような場合、集団ごとの特徴が異なることになるので、それぞれを個別に扱うなどの対処が必要となります。
FC も FI も値が小さければ、独立変数と従属変数の間に相関がなく、しかも傾きが共通(つまりどの集団も傾きはない)と考えられるので、この場合は通常の一元配置分散分析法を利用すれば充分であることになります。また、FI が大きければ各集団のごとの特徴が異なり、単純に比較することはできなくなります。FC が大きく、FI が小さい場合、各集団の独立変数と従属変数は、共通な傾きを持つ回帰式に従うと考えられ、共変数の影響を取り除けば集団間に差異があるかを調べることができます。
共変数の影響を取り除くためには x を全て一定に揃えればよいので、共変数が全体の平均 mx になるようにシフトすることを検討してみます。そのときの y は、yi,j から a( xi,j - mx ) を引くことで求められるので、調整後の ( xi,j, yi,j ) を ( x'i,j, y'i,j ) とすると、
x'i,j = mx
y'i,j = yi,j - a( xi,j - mx )
となります。ここで、a は各集団に共通な回帰係数を表していますが、x が全て等しい値を取ることから回帰直線は Y 軸に平行になるので、このとき a は不定になります。逆に言えば、a はどのような値も取りうることになります。
このとき、y'i,j の平均は
| Σi{1→p}( Σj{1→ni}( y'i,j ) ) | = | Σi{1→p}( Σj{1→ni}( yi,j - a( xi,j - mx ) ) ) |
| = | Nmy - a( Nmx - Nmx ) = Nmy |
より my になります。よって、y'i,j の平均差の平方和 Sy' は
| Sy' | = | Σi{1→p}( Σj{1→ni}( ( y'i,j - my )2 ) ) |
| = | Σi{1→p}( Σj{1→ni}( [ yi,j - a( xi,j - mx ) - my ]2 ) ) | |
| = | Σi{1→p}( Σj{1→ni}( [ ( yi,j - my ) - a( xi,j - mx ) ]2 ) ) | |
| = | Σi{1→p}( Σj{1→ni}( ( yi,j - my )2 - 2a( yi,j - my )( xi,j - mx ) + a2( xi,j - mx )2 ) ) | |
| = | Sy - 2aΣi{1→p}( Σj{1→ni}( ( yi,j - my )( xi,j - mx ) ) ) + a2Σi{1→p}( Σj{1→ni}( ( xi,j - mx )2 ) ) | |
| = | Sy - 2aNsxy + a2Nvx |
と求められます。但し、vx, sxy はそれぞれ、全データにおける x の分散と x,y の共分散を表します。Sy' が最小となるためには
が最小となればよいので、
| J | = | -2aNsxy + a2Nvx |
| = | Nvx( a - sxy / vx )2 - Nsxy2 / vx |
より a = sxy / vx のとき最小値 Sy - Nsxy2 / vx になります。この回帰係数は、全てのデータから回帰係数を求めた場合と一致し、Nsxy2 / vx はそのときの予測値と平均の平方和 Σi{1→p}( Σj{1→ni}( ( y^i,j - my )2 ) ) と等しくなります。つまり、共変数の影響を取り除くために共通の回帰係数を使って共変数を全データの平均に揃える場合、補正した従属変数の分散が最小となるようにするには回帰係数として全データから求めた回帰直線の傾きを使えばよく、Nsxy2 / vx = S0 とすると、
になります。ところで、上記計算の中では yi,j を使用していましたが、これを共通な回帰係数を用いたときの回帰式における予測値 y^i,j に置き換えても同様の結果が得られます。但しこの場合は Sy の代わりにその予測値 S^y = SB + SC を使うことになり、上記関係式は
になります。ここで、S^y' は
としたときの y^'i,j の平均差の平方和を表します。
S0 の自由度は線形回帰式の係数の個数と等しいので、このモデル式では 1 であり、正規化した S0 は a = 0 (つまり x,y の間に相関がない) という条件のもとで自由度 1 の χ2-分布に従うことになります。よって S^y' は自由度 1 + ( p - 1 ) - 1 = p - 1 の χ2-分布に従うことになります。
これらをまとめると、次のような共分散分析表(ANCOVA Table)になります。
| 平方和 | 自由度 | 不偏分散 | F値 | |
|---|---|---|---|---|
| 集団内 | SC = [ Σi{1→p}( nisxy,i ) ]2 / Σi{1→p}( nivx,i ) | 1 | vC = SC | FC = vC / vE |
| 集団間 | SB = Σi{1→p}( ni( my,i - my )2 ) | p - 1 | vB = SB / ( p - 1 ) | |
| 交互作用 | SI = Σi{1→p}( nisxy,i2 / vx,i ) - SC | p - 1 | vI = SI / ( p - 1 ) | FI = vI / vE |
| 補正した集団間差 | S^y' = SC + SB - Nsxy2 / vx | p - 1 | v^y' = S^y' / ( p - 1 ) | Fy' = v^y' / vE |
| 残差 | SE = Σi{1→p}( Σj{1→ni}( ( yi,j - y^i,j )2 ) ) | N - 2p | vE = SE / ( N - 2p ) | |
| 全体 | Sy = Σi{1→p}( Σj{1→ni}( ( yij - my )2 ) ) | N - 1 |
共分散分析を行うためのサンプル・プログラムを以下に示します。
/* KahanSum : Kahanの加算アルゴリズムを利用した和の計算 T x : 加算する値 T& sum : 今までの合計値 T& r : 今までの積み残し */ template<class T> void KahanSum( T x, T& sum, T& r ) { T y = x - r; // 計算値から積み残しを引いた値 T buff = sum + y; // 今までの合計値に yを加える r = ( buff - sum ) - y; // 積み残しを計算 sum = buff; } /* KahanSum : Kahanの加算アルゴリズムを利用した和の計算 const pair<T,T>& x : 加算する値 pair<T,T>& sum : 今までの合計値 pair<T,T>& r : 今までの積み残し UnaryFunc< pair<T,T> >& func : データ変換用関数オブジェクト */ template<class T> void KahanSum( const pair<T,T>& x, pair<T,T>& sum, pair<T,T>& r, UnaryFunc< pair<T,T> >& func ) { pair<T,T> y = func( x ); // 計算値 y.first -= r.first; // 計算値から積み残しを引いた値 y.second -= r.second; pair<T,T> buff( sum.first + y.first, sum.second + y.second ); // 今までの合計値に yを加える r.first = ( buff.first - sum.first ) - y.first; // 積み残しを計算 r.second = ( buff.second - sum.second ) - y.second; sum = buff; } /* sum : データの総和を求める(pair用) vector< pair<T,T> >& x : データ 誤差を軽減する方法は Kahanの加算アルゴリズムを利用 戻り値 : 求めた総和(データ数がゼロならゼロを返す) */ template<class T> pair<T,T> sum( const vector< pair<T,T> >& x ) { pair<T,T> ans( 0, 0 ); // 求める総和 pair<T,T> r( 0, 0 ); // 積み残し for ( unsigned int i = 0 ; i < x.size() ; ++i ) { KahanSum( x[i].first, ans.first, r.first ); KahanSum( x[i].second, ans.second, r.second ); } return( ans ); } /* sum : データを変換した上での総和を求める(pair用) vector< pair<T,T> >& x : データ UnaryFunc< pair<T,T> >& func : データ変換用関数オブジェクト 誤差を軽減する方法は Kahanの加算アルゴリズムを利用 戻り値 : 求めた総和(データ数がゼロならゼロを返す) */ template<class T> pair<T,T> sum( const vector< pair<T,T> >& x, UnaryFunc< pair<T,T> >& func ) { pair<T,T> ans( 0, 0 ); // 求める総和 pair<T,T> r( 0, 0 ); // 積み残し for ( unsigned int i = 0 ; i < x.size() ; ++i ) KahanSum( x[i], ans, r, func ); return( ans ); } /* sampleAverage : 標本平均を求める(pair用) vector< pair<T,T> >& x : データ 戻り値 : 求めた平均値(データ数がゼロならゼロを返す) */ template<class T> pair<T,T> sampleAverage( const vector< pair<T,T> >& x ) { pair<T,T> s = sum( x ); if ( x.size() > 0 ) { s.first /= (T)x.size(); s.second /= (T)x.size(); } return( s ); } /* sampleAverage : データを変換した上での標本平均を求める(pair用) vector< pair<T,T> >& x : データ UnaryFunc< pair<T,T> >& func : データ変換用関数オブジェクト 戻り値 : 求めた平均値(データ数がゼロならゼロを返す) */ template<class T> pair<T,T> sampleAverage( const vector< pair<T,T> >& x, UnaryFunc< pair<T,T> >& func ) { pair<T,T> s = sum( x, func ); if ( x.size() > 0 ) { s.first /= (T)x.size(); s.second /= (T)x.size(); } return( s ); } /* ProductSumXY : x, y の a との差の積和 const vector< pair<T,T> > &data : データ const pair<T,T> &a : a データの個数がゼロならゼロを返す 戻り値 : x, y の a との差の積和 */ template<class T> T ProductSumXY( const vector< pair<T,T> >& data, const pair<T,T>& a ) { unsigned int n = data.size(); if ( n == 0 ) return( 0 ); // ( x - a.x )( y - a.y ) を求める vector<T> xy( n ); for ( unsigned int i = 0 ; i < n ; ++i ) xy[i] = ( data[i].first - a.first ) * ( data[i].second - a.second ); return( sum( xy ) ); } /* ANCOVA : 共分散分析(ANalysis of COVAriance ; ANCOVA) const vector< vector< pair<double, double> > >& data : データ列 double a : 危険率 double threshold : binSearchで棄却域を求める時のしきい値 戻り値 : True ... 行間・列間変動・交互作用のいずれかの仮説が棄却 , False ... どの仮説も保留 または データが条件を満たさない */ bool ANCOVA( const vector< vector< pair<double, double> > >& data, double a, double threshold ) { vector<double> buff; unsigned int p = data.size(); // グループ数 vector< pair<double,double> > m_i( p, pair<double,double>( 0, 0 ) ); // グループごとの(X,Y)平均 pair<double,double> m( 0, 0 ); // 全体の平均 unsigned int n = 0; // 全データ数 for ( unsigned int i = 0 ; i < p ; ++i ) { m_i[i] = sum( data[i] ); n += data[i].size(); m.first += m_i[i].first; m.second += m_i[i].second; m_i[i].first /= (double)( data[i].size() ); m_i[i].second /= (double)( data[i].size() ); } m.first /= (double)n; m.second /= (double)n; vector< pair<double,double> > s_i( p, pair<double,double>( 0, 0 ) ); // グループごとのX,Yの平均差の平方和 vector<double> sxy_i( p, 0 ); // グループごとのX,Yの平均差の積 pair<double,double> sqSum( 0, 0 ); // 全体のX,Yの平均差の平方和 double sxy = 0; // 全体のx,yの平均差の積 for ( unsigned int i = 0 ; i < p ; ++i ) { Deviation< pair<double,double> > dev_i( m_i[i] ); Deviation< pair<double,double> > dev( m ); s_i[i] = sum( data[i], dev_i ); pair<double,double> s = sum( data[i], dev ); sqSum.first += s.first; sqSum.second += s.second; sxy_i[i] = ProductSumXY( data[i], m_i[i] ); sxy += ProductSumXY( data[i], m ); } // 平方和の計算 double sc = pow( sum( sxy_i ), 2 ) / sum( s_i ).first; buff.resize( p ); for ( unsigned int i = 0 ; i < m_i.size() ; ++i ) buff[i] = (double)( data[i].size() ) * pow( m_i[i].second - m.second, 2 ); double sb = sum( buff ); buff.resize( p ); for ( unsigned int i = 0 ; i < m_i.size() ; ++i ) buff[i] = pow( sxy_i[i], 2 ) / s_i[i].first; double si = sum( buff ) - sc; double se = sqSum.second - sb - sc - si; double sy_all = pow( sxy, 2 ) / sqSum.first; double sb_rev = sc + sb - sy_all; // F値の計算 double fc = sc * (double)( n - 2 * p ) / se; double fi = si * (double)( n - 2 * p ) / se * (double)( p - 1 ); double fb_rev = sb_rev * (double)( n - 2 * p ) / se * (double)( p - 1 ); // 集団別データ cout << "group(P) = " << p << ", data(N) = " << n << endl; double a0, b0; for ( unsigned int i = 0 ; i < p ; ++i ) { a0 = sxy_i[i] / s_i[i].first; b0 = m_i[i].second - m_i[i].first * a0; cout << "(" << i << ")\t: average (x,y) = (" << m_i[i].first << "," << m_i[i].second << ")" << endl; cout << "\t: sxx = " << s_i[i].first << ", sxy = " << sxy_i[i] << endl; cout << "\t: regression y = " << a0 << "x " << ( ( b0 >= 0 ) ? '+' : '-' ) << fabs(b0) << endl << endl; } a0 = sxy / sqSum.first; b0 = m.second - m.first * a0; cout << "all\t: average (x,y) = (" << m.first << "," << m.second << ")" << endl; cout << "\t: sxx = " << sqSum.first << ", sxy = " << sxy << endl; cout << "\t: regression y = " << a0 << "x " << ( ( b0 >= 0 ) ? '+' : '-' ) << fabs(b0) << endl << endl; // 共分散分析表 cout.precision(4); cout << "<< ANCOVA TABLE >>" << endl; cout << "\t\tSS\tDOF\tUnbiased Var.\tF-value" << endl; cout << "Covariate\t" << sc << "\t1\t" << sc << "\t\t" << fc << endl; cout << "Group\t\t" << sb << "\t" << p - 1 << "\t" << sb / (double)( p - 1 ) << endl << endl; cout << "Interaction\t" << si << "\t" << p - 1 << "\t" << si / (double)( p - 1 ) << "\t\t" << fi << endl; cout << "Group(rev)\t" << sb_rev << "\t" << p - 1 << "\t" << sb_rev << "\t\t" << fb_rev << endl; cout << "Error\t\t" << se << "\t" << n - 2 * p << "\t" << se / (double)( n - 2 * p ) << endl << endl; cout << "Total\t\t" << sqSum.second << "\t" << n - 1 << endl << endl; // 検定 FDistribution fDist1( 1, n - 2 * p ); double f1 = binSearch( fDist1, 1.0 - a, threshold ); double pc = 1.0 - fDist1.lower_p( fc ); cout << "Covariate : p-value = " << pc << " (F[>" << 1.0 - a << "] = " << f1 << ")" << endl; FDistribution fDistP_1( p - 1, n - 2 * p ); double fP_1 = binSearch( fDistP_1, 1.0 - a, threshold ); double pi = 1.0 - fDistP_1.lower_p( fi ); cout << "Interaction : p-value = " << pi << " (F[>" << 1.0 - a << "] = " << fP_1 << ")" << endl; double pb_rev = 1.0 - fDistP_1.lower_p( fb_rev ); cout << "Group(rev) : p-value = " << pb_rev << " (F[>" << 1.0 - a << "] = " << fP_1 << ")" << endl << endl; return( ( pc < a ) && ( pi >= a ) && ( pb_rev < a ) ); }
KahanSum は「Kahan の加算アルゴリズム」を利用した和の計算用サブ・ルーチンです。これを利用して、pair型を要素とする可変長配列 vector に対する総和計算用の sum と標本平均計算用の sampleAverage を用意しています。また、ProductSumXY は二要素 x, y のある値との差について積和を計算するための関数です。これらは全て、x, y の平均・分散(平均差の平方和)・共分散を計算するために利用します。
ANCOVA は共分散分析結果を出力するための関数で、内容は非常に長いですが、今まで説明した内容を順番に処理・出力しているだけなので難しい部分はないと思います。
下表に示すような架空のデータを使って、実際に共分散分析を行ってみたいと思います。
| Group | X | Y | Group | X | Y |
|---|---|---|---|---|---|
| 0 | 108.92 | 60.83 | 1 | 156.39 | 84.47 |
| 112.69 | 85.70 | 137.97 | 76.22 | ||
| 101.64 | 65.72 | 162.63 | 102.67 | ||
| 109.25 | 56.91 | 135.02 | 81.93 | ||
| 110.76 | 68.71 | 137.82 | 88.82 | ||
| 118.56 | 88.29 | 163.59 | 105.20 | ||
| 120.52 | 66.39 | 163.10 | 95.57 | ||
| 110.81 | 74.29 | 144.66 | 72.67 | ||
| 127.85 | 92.00 | 161.26 | 104.30 | ||
| 119.07 | 88.46 | 132.68 | 66.04 |
サンプル・プログラムを利用して出力した結果は次のようになります。
group(P) = 2, data(N) = 20
(0) : average (x,y) = (114.007,74.73)
: sxx = 504.359, sxy = 589.416
: regression y = 1.16864x -58.5034
(1) : average (x,y) = (149.512,87.789)
: sxx = 1527.02, sxy = 1363.01
: regression y = 0.892593x -45.6644
all : average (x,y) = (131.76,81.2595)
: sxx = 8334.41, sxy = 4270.73
: regression y = 0.512421x +13.7432
<< ANCOVA TABLE >>
SS DOF Unbiased Var. F-value
Covariate 1877 1 1877 22.69
Group 852.7 1 852.7
Interaction 28.89 1 28.89 0.3494
Group(rev) 540.8 1 540.8 6.54
Error 1323 16 82.69
Total 4081 19
Covariate : p-value = 0.0002114 (F[>0.95] = 4.494)
Interaction : p-value = 0.5627 (F[>0.95] = 4.494)
Group(rev) : p-value = 0.02109 (F[>0.95] = 4.494)
Covariate は集団内の平方和で、従属変数に対する共変数の影響度を表しています。残差との比率である F 値は非常に大きく、p 値も 0.0002 と非常に小さいことから、両者は強い相関を持つと断定することができます。Interaction は集団ごとの回帰係数の差異を表す指標で、この値は小さいため各集団の回帰係数は等しい、すなわち従属変数の変化量は同じであると判断できます。よって、Group(rev) すなわち共変数を全体の平均に補正したときの従属変数の平均差の平方和が意味を持ち、その残差との比率が 6.54 と比較的大きいことから、集団間の差異があると結論付けることができます。
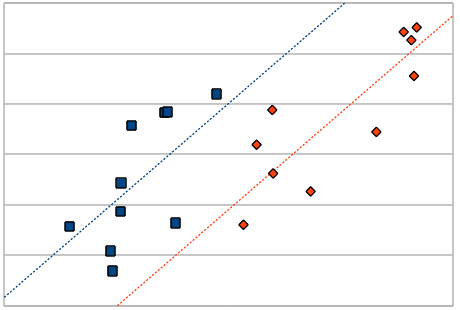
Group 0 と 1 において、y の平均はそれぞれ 74.73 と 87.79 なので、Group1 の方が y は大きい傾向にあるように見えます。しかし、共通な回帰係数を持つ場合の各集団の回帰式は、回帰係数 a が
なので、
Group0 : y = 0.9610( x - 114.007 ) + 74.73 = 0.9610x - 34.83
Group1 : y = 0.9610( x - 149.512 ) + 87.789 = 0.9610x - 55.89
と求められ、Group1 の切片は逆に小さくなります。よって、Group1 の平均が大きかったのは、共変数が Group0 よりも大きいことによるものであると判断することができます。このデータをグラフに表すと下図のようになります (これは「2) 傾きが共通な場合の回帰式」で示したグラフのデータそのものです)。
前回紹介した ANOVA と比べると、ANCOVA は知名度があまり高くないようです。統計解析用のパッケージソフトやフリーウェアなどを見ると、よく知られた有名なソフトなどはたいてい機能を持っているようなので、もう少し利用されてもいいような気がしますが、「共分散分析」で検索をすると心理学などで多く使われているようで、他の業種ではあまり活用されていないように感じました(これは調査不足が原因かもしれませんが)。しかし、ANOVA も ANCOVA も重回帰モデルをベースとしていることから同じ種類に属するものと考えれば、もっと活用されてもいいような気もします。
SI' - SI は次のような式で表されます。
| SI' - SI | = | Σi{1→p}( nisxy,i2 / vx,i ) - [ Σi{1→p}( nisxy,i ) ]2 / Σi{1→p}( nivx,i ) |
| = | Σi{1→p}( ( nisxy,i )2 / nivx,i ) - [ Σi{1→p}( nisxy,i ) ]2 / Σi{1→p}( nivx,i ) | |
| = | Σi{1→p}( Si2 / Vi ) - [ Σi{1→p}( Si ) ]2 / Σi{1→p}( Vi ) |
但し、Si = nisxy,i, Vi = nivx,i に途中で変数変換しています。第二項めは
と変形することができるので (ここで ΣV = Σi{1→p}( Vi ) と略記しています)、SI' - SI はさらに
| SI' - SI | = | Σi{1→p}( Si2 / Vi ) - [ Σi{1→p}( Si2 ) + 2Σi{1→p-1}( Σj{i+1→p}( SiSj ) ] / ΣV |
| = | Σi{1→p}( Si2 / Vi - Si2 / ΣV ) - 2Σi{1→p-1}( Σj{i+1→p}( SiSj ) / ΣV |
になります。ΣV > 0 なので、ΣV を掛けても不等号は変化せず、
| ΣV( SI' - SI ) | = | Σi{1→p}( ( ΣV - Vi )Si2 / Vi ) - 2Σi{1→p-1}( Σj{i+1→p}( SiSj ) |
| = | Σi{1→p}( Σj{1→p;j≠i}( Vj )Si2 / Vi ) - 2Σi{1→p-1}( Σj{i+1→p}( SiSj ) ) |
と計算することができます。ここで、第一項めは p( p - 1 ) 個の要素 VjSi2 / Vi ( i ≠ j ) からなる和であり、第二項めは ( p - 1 ) + ( p - 2 ) + ... + 1 = p( p - 1 ) / 2 個の要素 2SiSj ( i ≠ j ) からなる和であることに着目します。第一項めには VjSi2 / Vi に対して対称となる要素 ViSj2 / Vj が必ず存在します。全てのペアをまとめて和の形に再構成すれば、
となるので、
| ΣV( SI' - SI ) | = | Σi{1→p-1}( Σj{i+1→p}( ViSj2 / Vj + VjSi2 / Vi ) ) - 2Σi{1→p-1}( Σj{i+1→p}( SiSj ) ) |
| = | Σi{1→p-1}( Σj{i+1→p}( ViSj2 / Vj - 2SiSj + VjSi2 / Vi ) ) | |
| = | Σi{1→p-1}( Σj{i+1→p}( [ ( ViSj )2 - 2VjSiViSj + ( VjSi )2 ] / ViVj ) ) | |
| = | Σi{1→p-1}( Σj{i+1→p}( ( ViSj - VjSi )2 / ViVj ) ) ≥ 0 |
より、SI' - SI ≥ 0 が証明されます。
◆◇◆更新履歴◆◇◆
「4) 共分散分析 (ANalysis of COVAriance ; ANCOVA)」のサンプル・プログラムに誤りがあったため修正しました。
具体的には、補正した集団間差 ( pb_rev ) の計算に自由度 1 の F-分布 ( f1 )を使っていたというもので、正しくは自由度 p - 1 の F-分布 ( fP_1 ) を使う必要があります。
テスト結果では集団の数が 2 で p - 1 = 1 だったので結果的には正しい値になっていて、誤りに気づかなかったようです (2015-07-05)
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |