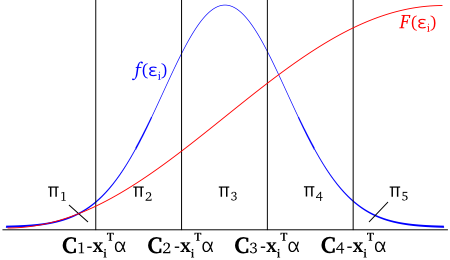
| 図 2-1. 潜在変数の確率密度 |
|---|
 |
前章では、二値確率変数に一般化線形モデルを適用し、ロジスティック・モデルをはじめとする二項分布を利用した回帰分析ができることと、さらに多項分布を適用して多値確率変数についても名義ロジスティック・モデルを使った回帰分析ができることを紹介しました。これらのモデルはすべて、「潜在変数 (Latent Variable)」と呼ばれる測定できない値を独立変数の線形式で表現できると仮定した上で構築することができます。この章では最初に潜在変数を使ったモデルについて検討し、それを利用して「順序ロジスティック・モデル (Ordered Logistic Regression)」の内容について紹介したいと思います。
二値変数 ( 1 / 0 ) が成功・失敗や選択・非選択を意味する時、どちらが採用されるのかが独立変数 xi によって左右されると仮定します。例えば、ある商品を購入するかどうかが性別や年齢、地域などによって影響を受けるとき、xi は性別(二値変数)、年齢(連続変数または順序変数)、地域(名義変数)を含むと考えることができます。i 番目の人が商品を購入する場合を U1i、購入しない場合を U0i として、それが性別 xi1、年齢 xi2、地域 xi3 の線形式
| U1i | = | α10 + α11xi1 + α12xi2 + α13xi3 + ε1i |
| = | xiTα1 + ε1i | |
| U0i | = | α00 + α01xi1 + α02xi2 + α03xi3 + ε0i |
| = | xiTα0 + ε0i |
で表されるとします。但し、αk = ( αk0, αk1, αk2, αk3 )T ( k = 0, 1 ) は回帰係数、xi = ( 1, xi1, xi2, xi3 )T は i 番目の人を表す独立変数ベクトルで、εki は xi で説明することのできない誤差成分とします。U0i < U1i のとき yi = 1、U0i > U1i のとき yi = 0 であるとしたとき、yi = 1 となる確率 P( yi = 1 ) は
| P( yi = 1 ) | = | P( U0i < U1i ) |
| = | P( xiTα0 + ε0i < xiTα1 + ε1i ) | |
| = | P( ε0i - ε1i < xiT( α1 - α0 ) ) | |
| ≡ | P( δi < xiTβ ) |
と表すことができます。δi はやはり xi では説明できない誤差成分であり、ある確率分布に従う確率変数と仮定します。確率分布が ( xiTβ によってパラメータは変化するものの ) i について全て共通であるとした時、それを F( xiTβ ) で表して
とすることができます。単純な例として、xi = ( 1, xi ) として
とした場合、P( yi = 1 ) = F( ( α11 - α01 )xi ) ≡ F( βxi ) となります。これは、Uki が傾きのみ異なるというモデルです。もし傾きが等しければ β = α11 - α01 = 0 であり、例えば εki が k について分散が一定となる正規分布 N( 0, σk2 ) に従うとしたとき、δi は正規分布 N( 0, σ02 + σ12 ) に従い、P( yi = 1 ) = P( δi < 0 ) より yi が 1 になる場合は五分五分になり、しかも xi には依存しなくなります。しかし β < 0 ならば、P( δi < βxi ) は xi が大きくなるほど低くなることになって yi = 1 になる回数は減るでしょうし、逆に β > 0 なら xi が大きくなるほど yi = 1 になる回数は多くなります。Uki を適当に変数変換することで、σ02 + σ12 = 1 として δi が標準正規分布 N( 0, 1 ) に従うとした時、P( δi < βxi ) は N( 0, 1 ) の累積分布関数
で表されます。π ≡ P( δi < βxi ) = P( yi = 1 ) とすれば π = Φ( βxi ) となって、
となります。一般化すれば
であり、これはプロビット・モデルそのものになります。
k が多値になったとき、その数を C とすれば、yi = k ( k = 1, 2, ... C ) となる場合を、l ≠ k である任意の l に対して Uki > Uli が成り立つときとすれば、
| P( yi = k | εki ) | = | P( ( U1i < Uki ) ∩ ( U2i < Uki ) ∩ ... ∩ ( Uk-1,i < Uki ) ∩ ( Uk+1,i < Uki ) ∩ ... ∩ ( UCi < Uki ) ) |
| = | P( ( xiTα1 + ε1i < xiTαk + εki ) ∩ ( xiTα2 + ε2i < xiTαk + εki ) ∩ ... | |
| ∩ ( xiTαk-1 + εk-1,i < xiTαk + εki ) ∩ ( xiTαk+1 + εk+1,i < xiTαk + εki ) ∩ ... | ||
| ∩ ( xiTαC + εCi < xiTαk + εki ) ) | ||
| = | P( ( ε1i < εki + xiT( αk - α1 ) ) ∩ ( ε2i < εki + xiT( αk - α2 ) ) ∩ ... | |
| ∩ ( εk-1,i < εki + xiT( αk - αk-1 ) ) ∩ ( εk+1,i < εki + xiT( αk - αk+1 ) ) ∩ ... | ||
| ∩ ( εCi < εki + xiT( αk - αC ) ) ) | ||
| ≡ | P( ( ε1i < εki + xiTβ1 ) ∩ ( ε2i < εki + xiTβ2 ) ∩ ... | |
| ∩ ( εk-1,i < εki + xiTβk-1 ) ∩ ( εk+1,i < εki + xiTβk+1 ) ∩ ... | ||
| ∩ ( εCi < εki + xiTβC ) ) | ||
となります。但し、P( yi = k | εki ) は εki を固定した時の条件付確率を意味します。
εli ( l = 1, 2, ... C ) は C 個あって、それぞれがある確率分布に従うと仮定することができます。ここで εli が「標準ガンベル分布 (Standard Gumbel Distribution)」
に独立に従うと仮定します。t = e-s ( s = -log t ) としたとき ds = -dt / t で、s → -∞ のとき t → ∞ なので、
| F(y) | = | ∫{-∞→y} exp( -s - e-s ) ds |
| = | ∫{∞→e-y} exp( log t )e-t( -1 / t ) dt | |
| = | ∫{e-y→∞} e-t dt | |
| = | [ -e-t ]∫{e-y→∞} | |
| = | exp( e-y ) |
となります。P( yi = k | εki ) は εki を固定した時の確率になるので、εki が取りうる範囲全体での周辺確率を求めるためには、Σj( Aj ) = Ω の条件下で
であることを利用して
を計算する必要があります。ここで
つまり εli < εki + xiTβl であるという事象が互いに独立であると仮定すれば、
| Πl{1→C;l≠k}( P( εli < εki + xiTβl ) )P( εki ) | |
| = | Πl{1→C;l≠k}( exp( exp( -εki - xiTβl ) ) )[ exp( -εki - exp( -εki ) ) ] |
| = | exp( Σl{1→C;l≠k}( exp( -εki - xiT( αk - αl ) ) ) - εki - exp( -εki ) ) |
| = | exp( -εki - exp( -εki )[ Σl{1→C;l≠k}( exp( xiT( αl - αk ) ) ) + 1 ] ) |
| ≡ | exp( -εki - Ki・exp( -εki ) ) |
と変形できます。但し、
とします。λi = log( Ki ) とすれば、与式は
となるので、t = εki - λi とすれば dεki = dt、t → ±∞ ( εki → ±∞ ) となることから、
| ∫{-∞→∞} exp( -εki - exp( -( εki - λi ) ) ) dεki | |
| = | ∫{-∞→∞} exp( -t - λi - e-t ) dt |
| = | exp( -λi )∫{-∞→∞} exp( -t - e-t ) dt |
| = | exp( -λi ) = 1 / Ki |
となります。但し、exp( -t - e-t ) が標準ガンベル分布であることから、その全積分が 1 であることを利用しています。Ki は
| Ki | = | Σl{1→C;l≠k}( exp( xiT( αl - αk ) ) ) + exp( 0 ) |
| = | Σl{1→C;l≠k}( exp( xiT( αl - αk ) ) ) + exp( xiT( αk - αk ) ) | |
| = | Σl{1→C}( exp( xiT( αl - αk ) ) ) | |
| = | Σl{1→C}( exp( xiTαl ) / exp( xiTαk ) ) | |
| = | Σl{1→C}( exp( xiTαl ) ) / exp( xiTαk ) |
と変形できるので、
であり、最終的に
という結果が得られます。
名義ロジスティック・モデルにおいて、カテゴリ k の発生確率を πk とし、基準カテゴリを k = 1 としてその比率を ρk = πk / π1 としたとき、
の関係式が成り立つのでした。ρ1 = π1 / π1 = 1 なので、上式は
とも表現できます。連結関数を対数関数として log( ρk ) = xiTαk となるような独立変数 xi があるとき、ρk = exp( xiTαk ) より
となります。これは先ほど求めた式と等しいことから、名義ロジスティックモデルは、潜在変数 Uki が最大となる時 yi = k となると仮定した時、誤差成分が標準ガンベル分布に従う場合の各カテゴリの確率密度を表しているという結果を得ることができます。
前述の結果から明らかなように、名義ロジスティックモデルの場合は εli < εki + xiTβl であるという事象が互いに独立であると仮定しています。つまり、カテゴリ k と l の間でこの不等号が成り立つことは、他のカテゴリから影響を受けないことを意味します。このとき得られる確率は
であることから、二つの確率の比 πk1 / πk2 は
となって、やはり他のカテゴリからの影響は受けません。これを「他の選択肢からの独立性 ( Independence of Irrelevant Alternatives ; IIA )」といい、場合によってはこの前提が問題になる可能性もあります。εki に標準ガンベル分布ではなく多変量正規分布を適用し、εi = ( ε1i, ε2i, ... εCi )T が平均ベクトル 0、共分散行列 V の多変量正規分布
に従うすれば、V の非対角成分がゼロでない限り εki は互いに独立ではなくなります。
| P( yi = k ) | = | P( ( U1i < Uki ) ∩ ( U2i < Uki ) ∩ ... ∩ ( Uk-1,i < Uki ) ∩ ( Uk+1,i < Uki ) ∩ ... ∩ ( UCi < Uki ) ) |
| = | P( ( ε1i - εki < xiT( αk - α1 ) ) ∩ ( ε2i - εki < xiT( αk - α2 ) ) ∩ ... | |
| ∩ ( εk-1,i - εki < xiT( αk - αk-1 ) ) ∩ ( εk+1,i - εki < xiT( αk - αk+1 ) ) ∩ ... | ||
| ∩ ( εCi - εki < xiT( αk - αC ) ) ) | ||
| ≡ | P( ( δ1i < xiTβ1 ) ∩ ( δ2i < xiTβ2 ) ∩ ... | |
| ∩ ( δk-1,i < xiTβk-1 ) ∩ ( δk+1,i < xiTβk+1 ) ∩ ... | ||
| ∩ ( δCi < xiTβC ) ) | ||
に対して、δi = ( δ1i, δ2i, ... δk-1,i, δk+1,i, ... δCi )T は平均ベクトルが 0 で、共分散行列 V' は次元が一つ減って C - 1 となります。この多変量正規分布 N( 0, V' ) を使って
というモデル式が得られます。これを「多項プロビット・モデル (Multinomial Probit Model ; MNP)」といいます。この値を求めるためには多変数関数に対して重積分を計算する必要があり、正規分布に対する原始関数 ( 関数 f(x) に対し、F'(x) = f(x) を満たす F(x) のこと ) は初等関数の形では存在しないため、カテゴリ数が多くなると計算が困難になります。そのため、多項プロビット・モデルの計算には「モンテカルロ法 (Monte Carlo Method)」などが利用されるようです。
ロジスティックモデルが、潜在変数モデルによるカテゴリの選択という考え方から導かれることを前節で示しました。ここで、カテゴリの選択が次のような形で表されると仮定します。
Ui = xiTα + εi に対し
yi = k のとき、Ck-1 < Ui < Ck
Ck ( k = 0, 1, ... C ) は区分点と呼ばれ、Ck-1 と Ck の間の領域に Ui が属するときに yi = k とします。但し、k1 < k2 ならば Ck1 < Ck2 で、C0 = -∞、CC = ∞ とします。Ui = xiTα + εi を代入して式を変形すると、
となるので、εi がある確率密度関数 f(εi) に従うとして
| πik = P( yi = k ) | = | P( Ck-1 - xiTα < εi < Ck - xiTα ) |
| = | ∫{Ck-1 - xiTα→Ck - xiTα} f(εi) dεi | |
| = | F( Ck - xiTα ) - F( Ck-1 - xiTα ) |
と表すことができます。但し、F(εi) は f(εi) に対する累積分布関数です。
f(εi) に、ロジスティック・モデルで利用した確率密度関数
f(εi) = exp( εi ) / [ 1 + exp( εi ) ]2
F(εi) = exp( εi ) / [ 1 + exp( εi ) ]
を適用すると、
であり、この式から、また上図からも明らかなように
F( Ui < Ck ) = Σl{1→k}( πil ) = exp( Ck - xiTα ) / [ 1 + exp( Ck - xiTα ) ]
F( Ui ≥ Ck ) = Σl{k+1→C}( πil ) = 1 - exp( Ck - xiTα ) / [ 1 + exp( Ck - xiTα ) ]
なので、
| F( Ui ≥ Ck ) / F( Ui < Ck ) | = | { 1 - exp( Ck - xiTα ) / [ 1 + exp( Ck - xiTα ) ] } / { exp( Ck - xiTα ) / [ 1 + exp( Ck - xiTα ) ] } |
| = | { [ 1 + exp( Ck - xiTα ) ] - exp( Ck - xiTα ) } / exp( Ck - xiTα ) | |
| = | 1 / exp( Ck - xiTα ) = exp( xiTα - Ck ) |
より
という結果が得られます。このとき、xiTα は各カテゴリに対して共通で、定数項となる Ck だけがカテゴリに依存することになります。xiTα に定数項が含まれているかどうかには無関係に、Ck を xiTα の内部に取り込んでも問題はないので、
として定数項以外はカテゴリに依存しないモデルを定義します。このようなモデルを「比例オッズ・モデル ( Proportional Odds Model )」といいます。
比例オッズモデルは、区分点によって分割した二つの確率密度の比が定数項以外はどのカテゴリも共通なので、独立変数による変化量はカテゴリごとに変化しないことを意味します。これが変化すると仮定した場合、モデル式は次のようになります。
違いは、回帰係数がカテゴリごとに異なるかどうかだけです。このようなモデルは「累積ロジット・モデル ( Cumulative Logit Model )」と呼ばれます。
名義ロジスティック・モデルの場合、各カテゴリについては順序がなく、潜在変数が最大となるカテゴリが選択されると解釈しました。それに対して、上に示したモデルはカテゴリが順序を持ち、潜在変数が位置する領域によってカテゴリが決まるという解釈になります。このようなモデルを用いた回帰分析を「順序ロジスティック回帰 (Ordered Logistic Regression)」といいます。
Ck-2 ≤ Ui ≤ Ck の範囲の中で Ck-1 ≤ Ui ≤ Ck となる条件付確率を p*ik ≡ P( yi = k | yi = k - 1 ∪ yi = k ) としたとき、
となります。p*ik にロジスティック・モデルで利用した累積分布関数
を適用すると、
p*ik = 1 - 1 / [ 1 + exp( Ck - xiTαk ) ] より
| exp( Ck - xiTαk ) | = | 1 / ( 1 - p*ik ) - 1 |
| = | ( πi,k-1 + πik ) / πi,k-1 - 1 | |
| = | πik / πi,k-1 | |
| Ck - xiTαk | = | log( πik / πi,k-1 ) |
という結果が得られます。左辺は Ck もまとめて線系結合 xiTαk の形に表すことができるので、
という、名義ロジスティックモデルによく似た式になります。これを「隣接カテゴリ・ロジット・モデル (Adjacent Category Logit Model)」といいます。「累積ロジット・モデル」や「比例オッズ・モデル」が区分点を境界として前後の累積確率密度の比率を扱うのに対し、「隣接カテゴリ・ロジット・モデル」は隣り合う二つのカテゴリの確率の比率を利用します。どちらも比率を使うところは同じですが、「隣接カテゴリ・ロジット・モデル」は二つのカテゴリ以外については考慮しないモデルであるという事ができます。
最後に、Ui ≤ Ck の範囲の中で Ck-1 ≤ Ui ≤ Ck となる条件付確率 p*ik ≡ P( yi = k | yi ∈ { 1, 2, ... k } ) に対して「隣接カテゴリ・ロジット・モデル」同様の操作を行います。
にロジスティック・モデルで利用した累積分布関数を適用して、
| exp( Ck - xiTαk ) | = | 1 / ( 1 - p*ik ) - 1 |
| = | Σl{1→k}( πil ) / Σl{1→k-1}( πil ) - 1 | |
| = | πik / Σl{1→k-1}( πil ) | |
| Ck - xiTαk | = | log( πik / Σl{1→k-1}( πil ) ) |
という結果となり、
というモデル式が得られます。条件付確率を
とすれば、モデル式は
となります。このモデル式は「連続比ロジット・モデル ( Continuation-Ratio Logit Model )」と呼ばれます。
多項分布を指数型分布族としたときの対数尤度 l は
で表されるのでした。但し、K = Σi{1→N}( log ni! - Σk'{1→C}( log yik'! ) ) は πi に依存しない定数項です。「累積ロジット・モデル」において、
とした時、
ρik = Σl{k+1→C}( πil ) / Σl{1→k}( πil ) = [ 1 - Σl{1→k}( πil ) ] / Σl{1→k}( πil ) より
Σl{1→k}( πil ) = 1 / ( 1 + ρik )
なので、πik は
πi1 = 1 / ( 1 + ρi1 )
πik = Σl{1→k}( πil ) - Σl{1→k-1}( πil ) = 1 / ( 1 + ρik ) - 1 / ( 1 + ρi,k-1 )
πiC = 1 - 1 / ( 1 + ρi, C-1 )
と表すことができます。対数尤度 l は
| l | = | Σi{1→N}( yi1log( 1 / ( 1 + ρi1 ) ) + yiClog( 1 - 1 / ( 1 + ρi,C-1 ) ) |
| + Σk'{2→C-1}( yik'log( 1 / ( 1 + ρik' ) - 1 / ( 1 + ρi,k'-1 ) ) ) ) + K | ||
| = | Σi{1→N}( yi1log( 1 / ( 1 + ρi1 ) ) + yiClog( ρi,C-1 / ( 1 + ρi,C-1 ) ) | |
| + Σk'{2→C-1}( yik'log( ( ρi,k'-1 - ρik' ) / ( 1 + ρik' )( 1 + ρi,k'-1 ) ) ) ) + K | ||
| = | Σi{1→N}( -yi1log( 1 + ρi1 ) + yiC[ log( ρi,C-1 ) - log( 1 + ρi,C-1 ) ] | |
| + Σk'{2→C-1}( yik'[ log( ρi,k'-1 - ρik' ) - log( 1 + ρik' ) - log( 1 + ρi,k'-1 ) ] ) ) + K | ||
| = | Σi{1→N}( -Σk'{1→C-1}( yik'log( 1 + ρik' ) ) - Σk'{2→C}( yik'log( 1 + ρi,k'-1 ) ) | |
| + Σk'{2→C-1}( yik'log( ρi,k'-1 - ρik' ) ) + yiClog( ρi,C-1 ) ) + K | ||
| = | Σi{1→N}( -Σk'{1→C-1}( ( yik' + yi,k'+1 )log( 1 + ρik' ) ) | |
| + Σk'{2→C-1}( yik'log( ρi,k'-1 - ρik' ) ) + yiClog( ρi,C-1 ) ) + K | ||
となり、これを αkj で偏微分すると ρik を持つ項だけが残るので
| |||||||||||||
| |||||||||||||
|
より
| ukj = ∂l / ∂αkj | = | Σi{1→N}( xij[ -( yik + yi,k+1 )ρik / ( 1 + ρik ) |
| + yi,k+1ρik / ( ρik - ρi,k+1 ) + yikρik / ( ρik - ρi,k-1 ) ] ) [ 1 < k < C - 1 ] | ||
| u1j = ∂l / ∂α1j | = | Σi{1→N}( xij[ -( yi1 + yi2 )ρi1 / ( 1 + ρi1 ) |
| + yi2ρi1 / ( ρi1 - ρi2 ) ] ) | ||
| uC-1,j = ∂l / ∂αC-1,j | = | Σi{1→N}( xij[ -( yi,C-1 + yiC )ρi,C-1 / ( 1 + ρi,C-1 ) |
| + yi,C-1ρi,C-1 / ( ρi,C-1 - ρi,C-2 ) + yiC ] ) | ||
とすることができます ( ρi0 → ∞、ρiC = 0 とすれば、三つの式は同一になります )。この式は、
| ρik / ( 1 + ρik ) | = | [ ( 1 + ρik ) - 1 ] / ( 1 + ρik ) |
| = | 1 - 1 / ( 1 + ρik ) |
| ρik / ( ρik - ρi,k±1 ) | = | [ ( ρik - ρi,k±1 ) + ρi,k±1 ] / ( ρik - ρi,k±1 ) |
| = | 1 + ρi,k±1 / ( ρik - ρi,k±1 ) |
より
| ukj | = | Σi{1→N}( xij{ -( yik + yi,k+1 )[ 1 - 1 / ( 1 + ρik ) ] |
| + yi,k+1[ 1 + ρi,k+1 / ( ρik - ρi,k+1 ) ] + yik[ 1 + ρi,k-1 / ( ρik - ρi,k-1 ) ] } ) | ||
| = | Σi{1→N}( xij[ ( yik + yi,k+1 ) / ( 1 + ρik ) | |
| + yi,k+1ρi,k+1 / ( ρik - ρi,k+1 ) + yikρi,k-1 / ( ρik - ρi,k-1 ) ] ) | ||
| u1j | = | Σi{1→N}( xij{ -( yi1 + yi2 )[ 1 - 1 / ( 1 + ρi1 ) ] + yi2[ 1 + ρi2 / ( ρi1 - ρi2 ) ] } ) |
| = | Σi{1→N}( xij[ ( yi1 + yi2 ) / ( 1 + ρi1 ) + yi2ρi2 / ( ρi1 - ρi2 ) - yi1 ] ) | |
| uC-1,j | = | Σi{1→N}( xij{ -( yi,C-1 + yiC )[ 1 - 1 / ( 1 + ρi,C-1 ) ] |
| + yi,C-1[ 1 + ρi,C-2 / ( ρi,C-1 - ρi,C-2 ) ] + yiC } ) | ||
| = | Σi{1→N}( xij[ ( yi,C-1 + yiC ) / ( 1 + ρi,C-1 ) + yi,C-1ρi,C-2 / ( ρi,C-1 - ρi,C-2 ) ] ) | |
と表すこともできます。これをもう一度 αk'j' で微分すると、値が残るのは k' = k, k - 1, k + 1 の場合のみであり、
| ( ∂ / ∂αkj' )[ 1 / ( ρik - ρi,k±1 ) ] | = | [ -1 / ( ρik - ρi,k±1 )2 ]( ∂ρik / ∂αkj' ) |
| = | -xij'ρik / ( ρik - ρi,k±1 )2 |
| ( ∂ / ∂αkj' )[ 1 / ( 1 + ρik ) ] | = | [ -1 / ( 1 + ρik )2 ]( ∂ρik / ∂αkj' ) |
| = | -xij'ρik / ( 1 + ρik )2 |
より
| ∂ukj / ∂αkj' | = | Σi{1→N}( xijxij'[ -( yik + yi,k+1 )ρik / ( 1 + ρik )2 |
| - yi,k+1ρikρi,k+1 / ( ρik - ρi,k+1 )2 - yikρikρi,k-1 / ( ρik - ρi,k-1 )2 ] ) | ||
| = | Σi{1→N}( xijxij'{ -yikρik[ ρi,k-1 / ( ρik - ρi,k-1 )2 + 1 / ( 1 + ρik )2 ] | |
| - yi,k+1ρik[ ρi,k+1 / ( ρik - ρi,k+1 )2 + 1 / ( 1 + ρik )2 ] } ) | ||
| ∂u1j / ∂α1j' | = | Σi{1→N}( xijxij'[ -( yi1 + yi2 )ρi1 / ( 1 + ρi1 )2 - yi2ρi1ρi2 / ( ρi1 - ρi2 )2 ] ) |
| ∂uC-1,j / ∂αC-1,j' | = | Σi{1→N}( xijxij'[ -( yi,C-1 + yiC )ρi,C-1 / ( 1 + ρi,C-1 )2 |
| - yi,C-1ρi,C-1ρi,C-2 / ( ρi,C-1 - ρi,C-2 )2 ] ) | ||
となり、また
| ( ∂ / ∂αk±1,j' )[ 1 / ( ρik - ρi,k±1 ) ] | = | [ 1 / ( ρik - ρi,k±1 )2 ]( ∂ρi,k±1 / ∂αk±1,j' ) |
| = | xij'ρi,k±1 / ( ρik - ρi,k±1 )2 |
より
| ∂ukj / ∂αk-1,j' | = | Σi{1→N}( xijxij'yikρikρi,k-1 / ( ρik - ρi,k-1 )2 ) |
| ∂ukj / ∂αk+1,j' | = | Σi{1→N}( xijxij'yi,k+1ρikρi,k+1 / ( ρik - ρi,k+1 )2 ) |
| ∂u1j / ∂α2j' | = | Σi{1→N}( xijxij'yi2ρi1ρi2 / ( ρi1 - ρi2 )2 ) |
| ∂uC-1,j / ∂αC-2,j' | = | Σi{1→N}( xijxij'yi,C-1ρi,C-1ρi,C-2 / ( ρi,C-1 - ρi,C-2 )2 ) |
となります ( この場合、k = 0, C - 1 の場合は特別扱いしなくてもよいことがわかります )。
α = ( α11, α12, ... α1p, α21, ... , αkj, ... αC-1,p )T
u( α ) = ( u11, u12, ... u1p, u21, ... , ukj, ... uC-1,p )T
とし、名義ロジスティック回帰のときと同様に、H の行と列を k が等しいものどうしを固める形で構成したとき、H を ( C - 1 ) x ( C - 1 ) 個の p x p 部分行列からなる分割行列 ( 行列をいくつかの部分行列に区切って表現した行列 ) とみれば、対角成分にあたる部分行列は k = k' の場合の式、対角成分をはさむ形で k' = k ± 1 の場合の式を使って分割行列を表し、それ以外はゼロ行列とすることで H を表すことができます。x'j = ( x1j, x2j, ... xNj )T とし、
| wikk | = | -yikρik[ ρi,k-1 / ( ρik - ρi,k-1 )2 + 1 / ( 1 + ρik )2 ] |
| - yi,k+1ρik[ ρi,k+1 / ( ρik - ρi,k+1 )2 + 1 / ( 1 + ρik )2 ] | ||
を対角要素とする対角行列を Wkk' とすれば、∂ukj / ∂αk'j' = x'jTWkk'x'j' で表されます。H を p x p 部分行列 ( ブロック ) に分けたとき、k 行 k' 列めのブロックは XTWkk'X で表され、分割行列は
| H = |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = |
|
となります。スコア法の漸化式
において、H の p x ( k - 1 ) + j 行目の行ベクトル hkjT は
なので、
| hkjTα | = | Σi{1→N}( Σk'{1→C-1}( Σj'{1→p}( ( ∂ukj / ∂αk'j' )αk'j' ) ) ) |
| = | Σi{1→N}( Σk'{k-1→k+1}( Σj'{1→p}( ( ∂ukj / ∂αk'j' )αk'j' ) ) ) | |
| = | Σi{1→N}( Σj'{1→p}( xijxij'yikρikρi,k-1αk-1,j' / ( ρik - ρi,k-1 )2 ) | |
| - Σj'{1→p}( xijxij'yikρikαkj'[ ρi,k-1 / ( ρik - ρi,k-1 )2 + 1 / ( 1 + ρik )2 ] ) | ||
| - Σj'{1→p}( xijxij'yi,k+1ρikαkj'[ ρi,k+1 / ( ρik - ρi,k+1 )2 + 1 / ( 1 + ρik )2 ] ) | ||
| + Σj'{1→p}( xijxij'yi,k+1ρikρi,k+1αk+1,j' / ( ρik - ρi,k+1 )2 ) ) | ||
| = | Σi{1→N}( xijyikρikρi,k-1Σj'{1→p}( xij'αk-1,j' ) / ( ρik - ρi,k-1 )2 | |
| - xijyikρikΣj'{1→p}( xij'αkj' )[ ρi,k-1 / ( ρik - ρi,k-1 )2 + 1 / ( 1 + ρik )2 ] | ||
| - xijyi,k+1ρikΣj'{1→p}( xij'αkj' )[ ρi,k+1 / ( ρik - ρi,k+1 )2 + 1 / ( 1 + ρik )2 ] | ||
| + xijyi,k+1ρikρi,k+1Σj'{1→p}( xij'αk+1,j' ) / ( ρik - ρi,k+1 )2 ) | ||
| = | Σi{1→N}( xijyikρikρi,k-1log( ρi,k-1 ) / ( ρik - ρi,k-1 )2 | |
| - xijyikρiklog( ρik )[ ρi,k-1 / ( ρik - ρi,k-1 )2 + 1 / ( 1 + ρik )2 ] | ||
| - xijyi,k+1ρiklog( ρik )[ ρi,k+1 / ( ρik - ρi,k+1 )2 + 1 / ( 1 + ρik )2 ] | ||
| + xijyi,k+1ρikρi,k+1log( ρi,k+1 ) / ( ρik - ρi,k+1 )2 ) | ||
| = | Σi{1→N}( xij{ -( yik + yi,k+1 )ρiklog( ρik ) / ( 1 + ρik )2 | |
| + yikρikρi,k-1[ log( ρi,k-1 ) - log( ρik ) ] / ( ρik - ρi,k-1 )2 | ||
| + yi,k+1ρikρi,k+1[ log( ρi,k+1 ) - log( ρik ) ] / ( ρik - ρi,k+1 )2 } ) | ||
| h1jTα | = | Σi{1→N}( Σk'{1→2}( Σj'{1→p}( ( ∂u1j / ∂αk'j' )αk'j' ) ) ) |
| = | Σi{1→N}( -Σj'{1→p}( xijxij'( yi1 + yi2 )ρi1α1j' / ( 1 + ρi1 )2 ) | |
| - Σj'{1→p}( xijxij'yi2ρi1ρi2α1j' / ( ρi1 - ρi2 )2 ) | ||
| + Σj'{1→p}( xijxij'yi2ρi1ρi2α2j' / ( ρi1 - ρi2 )2 ) ) | ||
| = | Σi{1→N}( -xij( yi1 + yi2 )ρi1Σj'{1→p}( xij'α1j' ) / ( 1 + ρi1 )2 | |
| - xijyi2ρi1ρi2Σj'{1→p}( xij'α1j' ) / ( ρi1 - ρi2 )2 | ||
| + xijyi2ρi1ρi2Σj'{1→p}( xij'α2j' ) / ( ρi1 - ρi2 )2 ) | ||
| = | Σi{1→N}( xij{ -( yi1 + yi2 )ρi1log( ρi1 ) / ( 1 + ρi1 )2 | |
| + yi2ρi1ρi2[ log( ρi2 ) - log( ρi1 ) ] / ( ρi1 - ρi2 )2 } ) | ||
| hC-1,jTα | = | Σi{1→N}( Σk'{C-2→C-1}( Σj'{1→p}( ( ∂uC-1,j / ∂αk'j' )αk'j' ) ) ) |
| = | Σi{1→N}( -Σj'{1→p}( xijxij'( yi,C-1 + yiC )ρi,C-1αC-1,j' / ( 1 + ρi,C-1 )2 ) | |
| - Σj'{1→p}( xijxij'yi,C-1ρi,C-1ρi,C-2αC-1,j' / ( ρi,C-1 - ρi,C-2 )2 ) | ||
| + Σj'{1→p}( xijxij'yi,C-1ρi,C-1ρi,C-2αC-2,j' / ( ρi,C-1 - ρi,C-2 )2 ) ) | ||
| = | Σi{1→N}( -xij( yi,C-1 + yiC )ρi,C-1Σj'{1→p}( xij'αC-1,j' ) / ( 1 + ρi,C-1 )2 | |
| - xijyi,C-1ρi,C-1ρi,C-2Σj'{1→p}( xij'αC-1,j' ) / ( ρi,C-1 - ρi,C-2 )2 | ||
| + xijyi,C-1ρi,C-1ρi,C-2Σj'{1→p}( xij'αC-2,j' ) / ( ρi,C-1 - ρi,C-2 )2 ) | ||
| = | Σi{1→N}( xij{ -( yi,C-1 + yiC )ρi,C-1log( ρi,C-1 ) / ( 1 + ρi,C-1 )2 | |
| + yi,C-1ρi,C-1ρi,C-2[ log( ρi,C-2 ) - log( ρi,C-1 ) ] / ( ρi,C-1 - ρi,C-2 )2 } ) | ||
となり、連立方程式の p x ( k - 1 ) + j 行目の式に対する右辺は
を求めることで得ることができます。hkjTα は k = 1, C - 1 の場合を特別扱いしていますが、実際には ρi0, ρiC を含む項を無視するようにすることで同じように処理することができることに注意して下さい。
「比例オッズ・モデル」の場合、
log( ρik ) = βk + α1xi1 + α2xi2 + ... + αpxip
| ρik | = | exp( βk + α1xi1 + α2xi2 + ... + αpxip ) |
| = | exp( βk )exp( α1xi1 + α2xi2 + ... + αpxip ) |
より
ρik - ρik' = [ exp( βk ) - exp( βk' ) ]exp( α1xi1 + α2xi2 + ... + αpxip )
log( ρik - ρik' ) = log( exp( βk ) - exp( βk' ) ) + α1xi1 + α2xi2 + ... + αpxip
となるので、
| ( ∂ / ∂αj )log( ρik - ρik' ) | = | ( ∂ / ∂αj )[ log( exp( βk ) - exp( βk' ) ) + α1xi1 + α2xi2 + ... + αpxip ] |
| = | xij | |
| ( ∂ / ∂βk )log( ρik - ρik' ) | = | ( ∂ / ∂βk )[ log( exp( βk ) - exp( βk' ) ) + α1xi1 + α2xi2 + ... + αpxip ] |
| = | exp( βk ) / [ exp( βk ) - exp( βk' ) ] | |
| = | exp( βk )exp( α1xi1 + α2xi2 + ... + αpxip ) | |
| / [ exp( βk ) - exp( βk' ) ]exp( α1xi1 + α2xi2 + ... + αpxip ) | ||
| = | exp( log( ρik ) ) / [ exp( log( ρik ) ) - exp( log( ρik' ) ) ] | |
| = | ρik / ( ρik - ρik' ) | |
| ( ∂ / ∂βk' )log( ρik - ρik' ) | = | -ρik' / ( ρik - ρik' ) |
| = | ρik' / ( ρik' - ρik ) | |
を利用すると、対数尤度 l の各項を αj, βk で偏微分した結果は
| |||||||||||
| |||||||||||
| |||||||||||
|
となり、対数尤度 l を、αj で偏微分した結果を uαj、βk で偏微分した結果を uβk とすると、それらの値は
| uαj = ∂l / ∂αj | = | Σi{1→N}( -Σk'{1→C-1}( xij( yik' + yi,k'+1 )ρik' / ( 1 + ρik' ) ) |
| + Σk'{1→C-1}( xijyi,k'+1 ) ) | ||
| = | Σi{1→N}( xijΣk'{1→C-1}( -( yik' + yi,k'+1 )[ 1 - 1 / ( 1 + ρik' ) ] + yi,k'+1 ) ) | |
| = | Σi{1→N}( xijΣk'{1→C-1}( ( yik' + yi,k'+1 ) / ( 1 + ρik' ) - yik' ) ) | |
| uβk = ∂l / ∂βk | = | Σi{1→N}( -( yik + yi,k+1 )ρik / ( 1 + ρik ) |
| + yi,k+1ρik / ( ρik - ρi,k+1 ) + yikρik / ( ρik - ρi,k-1 ) ) | ||
| = | Σi{1→N}( ( yik + yi,k+1 )[ 1 / ( 1 + ρik ) - 1 ] | |
| + yi,k+1[ 1 + ρi,k+1 / ( ρik - ρi,k+1 ) ] + yik[ 1 + ρi,k-1 / ( ρik - ρi,k-1 ) ] ) | ||
| = | Σi{1→N}( ( yik + yi,k+1 ) / ( 1 + ρik ) | |
| + yi,k+1ρi,k+1 / ( ρik - ρi,k+1 ) + yikρi,k-1 / ( ρik - ρi,k-1 ) ) | ||
| uβ1 = ∂l / ∂β1 | = | Σi{1→N}( -( yi1 + yi2 )ρi1 / ( 1 + ρi1 ) + yi2ρi1 / ( ρi1 - ρi2 ) ) |
| = | Σi{1→N}( -( yi1 + yi2 )[ 1 - 1 / ( 1 + ρi1 ) ] + yi2[ 1 + ρi2 / ( ρi1 - ρi2 ) ] ) | |
| = | Σi{1→N}( ( yi1 + yi2 ) / ( 1 + ρi1 ) + yi2ρi2 / ( ρi1 - ρi2 ) - yi1 ) | |
| uβ,C-1 = ∂l / ∂β,C-1 | = | Σi{1→N}( -( yi,C-1 + yiC )ρi,C-1 / ( 1 + ρi,C-1 ) |
| + yiC + yi,C-1ρi,C-1 / ( ρi,C-1 - ρi,C-2 ) ) | ||
| = | Σi{1→N}( -( yi,C-1 + yiC )[ 1 - 1 / ( 1 + ρi,C-1 ) ] | |
| + yiC + yi,C-1[ 1 + ρi,C-2 / ( ρi,C-1 - ρi,C-2 ) ] ) | ||
| = | Σi{1→N}( ( yi,C-1 + yiC ) / ( 1 + ρi,C-1 ) | |
| + yi,C-1ρi,C-2 / ( ρi,C-1 - ρi,C-2 ) ) | ||
となります ( ここでも ρi0 → ∞、ρiC = 0 とすれば、uβk において k = 0, C - 1 の場合も同じ式となります )。これらをさらに αj、βk、βk±1 で偏微分すると
| ( ∂ / ∂αj )[ 1 / ( 1 + ρik ) ] | = | [ -1 / ( 1 + ρik )2 ]( ∂ρik / ∂αj ) |
| = | -xijρik / ( 1 + ρik )2 | |
| ( ∂ / ∂βk )[ 1 / ( 1 + ρik ) ] | = | [ -1 / ( 1 + ρik )2 ]( ∂ρik / ∂βk ) |
| = | -ρik / ( 1 + ρik )2 |
より
| ∂uαj / ∂αj' | = | Σi{1→N}( xijxij'Σk'{1→C-1}( -( yik' + yi,k'+1 )ρik' / ( 1 + ρik' )2 ) ) |
| ∂uαj / ∂βk = ∂uβk / ∂αj | = | Σi{1→N}( -xij( yik + yi,k+1 )ρik / ( 1 + ρik )2 ) |
| ∂uβk / ∂βk | = | Σi{1→N}( -( yik + yi,k+1 )ρik / ( 1 + ρik )2 |
| - yi,k+1ρikρi,k+1 / ( ρik - ρi,k+1 )2 - yikρikρi,k-1 / ( ρik - ρi,k-1 )2 ) | ||
| ∂uβ1 / ∂β1 | = | Σi{1→N}( -( yi1 + yi2 )ρi1 / ( 1 + ρi1 )2 |
| - yi2ρi1ρi2 / ( ρi1 - ρi2 )2 ) | ||
| ∂uβ,C-1 / ∂βC-1 | = | Σi{1→N}( -( yi,C-1 + yiC )ρi,C-1 / ( 1 + ρi,C-1 )2 |
| - yi,C-1ρi,C-1ρi,C-2 / ( ρi,C-1 - ρi,C-2 )2 ) | ||
| ∂uβk / ∂βk-1 | = | Σi{1→N}( yikρikρi,k-1 / ( ρik - ρi,k-1 )2 ) |
| ∂uβk / ∂βk+1 | = | Σi{1→N}( yi,k+1ρikρi,k+1 / ( ρik - ρi,k+1 )2 ) |
という結果が得られ、これらが H の各成分を表します。
∂uβk / ∂βk' を k 行 k' 列の要素とする行列数 C - 1 の対称行列を H11、∂uαj / ∂αj' を j 行 j' 列の要素とする行列数 p の対称行列を H22、∂uαj / ∂βk を j 行 k 列の要素とする p 行 C - 1 列の行列を H21、H12 = H21T とすると、
| H = |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = |
|
となり、
α = ( β1, β2, ... βC-1, α1, α2, ... αp )T
u( α ) = ( uβ1, uβ2, ... uβ,C-1, uα1, uα2, ... uαp )T
としてスコア法の漸化式
を解けば α の最尤解が得られます。Hα(m-1) の r 行目の要素 hr は、1 ≤ r ≤ c - 1 において
で、c ≤ r ≤ c + p - 1 において
でそれぞれ求められます。一番目の式の最初の三つの項は
| ( ∂uβr / ∂βr-1 )βr-1 + ( ∂uβr / ∂βr )βr + ( ∂uβr / ∂βr+1 )βr+1 | |
| = | Σi{1→N}( [ -( yir + yi,r+1 )ρir / ( 1 + ρir )2 |
| - yi,r+1ρirρi,r+1 / ( ρir - ρi,r+1 )2 - yirρirρi,r-1 / ( ρir - ρi,r-1 )2 ]βr | |
| + βr-1yirρirρi,r-1 / ( ρir - ρi,r-1 )2 + βr+1yi,r+1ρirρi,r+1 / ( ρir - ρi,r+1 )2 ) | |
| = | Σi{1→N}( -βr( yir + yi,r+1 )ρir / ( 1 + ρir )2 |
| + yi,r+1ρirρi,r+1( βr+1 - βr ) / ( ρir - ρi,r+1 )2 + yirρirρi,r-1( βr-1 - βr ) / ( ρir - ρi,r-1 )2 ) |
と変形できますが、
| βr±1 - βr | = | βr±1 + Σj{1→p}( xijαj ) - βr - Σj{1→p}( xijαj ) |
| = | log( ρi,r±1 ) - log( ρir ) |
より、さらに
| ( ∂uβr / ∂βr-1 )βr-1 + ( ∂uβr / ∂βr )βr + ( ∂uβr / ∂βr+1 )βr+1 | |
| = | Σi{1→N}( -βr( yir + yi,r+1 )ρir / ( 1 + ρir )2 |
| + yi,r+1ρirρi,r+1[ log( ρi,r+1 ) - log( ρir ) ] / ( ρir - ρi,r+1 )2 | |
| + yirρirρi,r-1[ log( ρi,r-1 ) - log( ρir ) ] / ( ρir - ρi,r-1 )2 ) |
となります。また、
| Σj{1→p}( ( ∂uβr / ∂αj )αj ) | = | Σj{1→p}( Σi{1→N}( -xij( yir + yi,r+1 )ρir / ( 1 + ρir )2 )αj ) |
| = | Σi{1→N}( Σj{1→p}( -xijαj )( yir + yi,r+1 )ρir / ( 1 + ρir )2 ) |
より
| Σi{1→N}( -βr( yir + yi,r+1 )ρir / ( 1 + ρir )2 ) | |
| + Σi{1→N}( Σj{1→p}( -xijαj )( yir + yi,r+1 )ρir / ( 1 + ρir )2 ) | |
| = | Σi{1→N}( -[ βr + Σj{1→p}( xijαj ) ]( yir + yi,r+1 )ρir / ( 1 + ρir )2 ) |
| = | Σi{1→N}( -( yir + yi,r+1 )ρirlog( ρir ) / ( 1 + ρir )2 ) |
となるので、
| hr | = | Σi{1→N}( -( yir + yi,r+1 )ρirlog( ρir ) / ( 1 + ρir )2 |
| + yi,r+1ρirρi,r+1[ log( ρi,r+1 ) - log( ρir ) ] / ( ρir - ρi,r+1 )2 | ||
| + yirρirρi,r-1[ log( ρi,r-1 ) - log( ρir ) ] / ( ρir - ρi,r-1 )2 ) | ||
という結果が得られます。二番目の式は、
| hr | = | Σk{1→C-1}( Σi{1→N}( -xir( yik + yi,k+1 )ρik / ( 1 + ρik )2 )βk ) |
| + Σj{1→p}( Σi{1→N}( xirxijΣk{1→C-1}( -( yik + yi,k+1 )ρik / ( 1 + ρik )2 ) )αj ) | ||
| = | -Σi{1→N}( Σk{1→C-1}( xirβk( yik + yi,k+1 )ρik / ( 1 + ρik )2 ) ) | |
| - Σi{1→N}( Σk{1→C-1}( xirΣj{1→p}( xijαj )( yik + yi,k+1 )ρik / ( 1 + ρik )2 ) ) | ||
| = | -Σi{1→N}( xirΣk{1→C-1}( [ βk + Σj{1→p}( xijαj ) ]( yik + yi,k+1 )ρik / ( 1 + ρik )2 ) ) | |
| = | -Σi{1→N}( xirΣk{1→C-1}( ( yik + yi,k+1 )ρiklog( ρik ) / ( 1 + ρik )2 ) ) | |
と求められ、ここから u( α(m-1) ) を減算した値が連立方程式の右辺となります。
「累積ロジットモデル」を使ってロジスティック回帰を行うためのサンプル・プログラムを以下に示します。今回は非常に長いプログラムとなったので、いくつかに分割してあります。まずは、複数ある順序ロジスティックモデルを共通化するクラスの OrderedLogisticModel です。
/* OrderedLogisticModel : 順序ロジスティックモデル */ class OrderedLogisticModel { bool isValid_; // モデルは有効か protected: const vector< vector<double> >& x_; // 独立変数 const vector< vector<double> >& y_; // 従属変数(各カテゴリの発生回数) LinearEquationSystem<double> s_; // スコア法に利用する連立方程式 vector<double> a_; // 回帰係数 vector< vector<double> > rho_; // ρ値 // x は p_ 個のパラメータのベクトルからなる n_ 個のベクトル // y は c_ 個のパラメータのベクトルからなる n_ 個のベクトル unsigned int n_; // 独立変数ベクトルの数 unsigned int p_; // 独立変数ベクトルの要素数 unsigned int c_; // カテゴリ数 // π の初期化 ( y から計算する ) void initPi( vector< vector<double> >& pi ) const; // ρ の初期化 ( π から計算する ) virtual void initRho() = 0; // ρ から π を求める virtual void rho2Pi( vector< vector<double> >& pi ) const = 0; // 回帰係数の数を返す unsigned int coefSize() const { return( a_.size() ); } // 回帰係数の数をセットする void setCoefSize( unsigned int coefSz ) { if ( ! isValid() ) return; a_.resize( coefSz ); s_.resize( coefSz ); } public: // コンストラクタ OrderedLogisticModel( const vector< vector<double> >& x, const vector< vector<double> >& y ); virtual void coef2Rho() = 0; // 求めた係数から ρ を計算する virtual void calcCoefMatrix() = 0; // 係数行列を計算する virtual void calcRSide() = 0; // 連立方程式の右辺を計算する int solve( double threshold ); // 連立方程式を解いて、収束を調べる bool isValid() const { return( isValid_ ); } // モデルは有効か void printSize() const // 独立変数、その要素数(元の数)、カテゴリ数を出力 { if ( ! isValid() ) return; cout << "N = " << n_ << " ; p = " << p_ << " ; c = " << c_ << endl << endl; } void printX() const // 独立変数を出力 { if ( ! isValid() ) return; PrintMatrix( "x = ", x_ ); cout << endl; } void printY() const // 従属変数(各カテゴリの発生回数)を出力 { if ( ! isValid() ) return; PrintMatrix( "y = ", y_ ); cout << endl; } void printPi() const; // π を出力 void printRho() const // ρ を出力 { if ( ! isValid() ) return; PrintMatrix( "rho = ", rho_ ); cout << endl; } void printLES() const // 連立方程式を出力 { if ( ! isValid() ) return; s_.print(); cout << endl; } virtual void printVar() = 0; // 回帰係数に対する分散の出力 virtual void printEquation() const = 0; // 回帰式の出力 virtual string ident() const = 0; // モデル名 }; /* OrderedLogisticModel コンストラクタ const vector< vector<double> >& x : 独立変数 const vector< vector<double> >& y : 従属変数(各カテゴリの発生回数) unsigned int coefSz : 回帰係数の数 n は独立変数ベクトルの数 p は独立変数ベクトルの要素数 c はカテゴリの数 x は p 個のパラメータのベクトルからなる n 個のベクトル y は c 個のパラメータのベクトルからなる n 個のベクトル */ OrderedLogisticModel::OrderedLogisticModel( const vector< vector<double> >& x, const vector< vector<double> >& y ) : isValid_( false ), x_( x ), y_( y ), s_( 0 ) { // NULL のチェック if ( ! NullCheck( x_, "Independent Variable x" ) ) return; if ( ! NullCheck( y_, "Occurrence Count y" ) ) return; // 独立変数ベクトル x_i の数 n_ = x.size(); if ( n_ == 0 ) { cerr << "x has no data." << endl; return; } if ( ! SizeCheck( y_, "Occurrence Count y", n_, "Independent Variable x" ) ) return; // 独立変数ベクトルの要素数 p_ = x[0].size(); if ( ! SizeCheck_Loop( x_, "Independent Variable x", p_, "Independent Variable x[0]" ) ) return; // カテゴリ数 c_ = y[0].size(); if ( ! SizeCheck_Loop( y_, "Occurrence Count y", c_, "Occurrence Count y[0]" ) ) return; if ( c_ == 0 ) { cerr << "The size of categories is zero." << endl; return; } isValid_ = true; } /* OrderedLogisticModel::initPi : π の初期化 ( y から計算する ) vector< vector<double> >& pi : 計算結果を格納するベクトル */ void OrderedLogisticModel::initPi( vector< vector<double> >& pi ) const { if ( ! isValid() ) return; vector<double> ni( n_ ); // 各独立変数の総数 ( n ) for ( unsigned int i = 0 ; i < n_ ; ++i ) ni[i] = sum( y_[i] ); pi.assign( n_, vector<double>( c_ ) ); // 確率の当てはめ値 ( n x c ) // piは y_ik / ni_i で初期化 for ( unsigned int i = 0 ; i < n_ ; ++i ) for ( unsigned int k = 0 ; k < c_ ; ++k ) pi[i][k] = y_[i][k] / ni[i]; } /* ProportionalOddsModel::solve : 連立方程式を解いて、収束を調べる double threshold : 収束条件(全係数が threshold 以下なら処理終了) 戻り値 : >0 収束した ; =0 収束しない ; <0 計算に失敗 */ int OrderedLogisticModel::solve( double threshold ) { if ( ! isValid() ) return( -1 ); // 連立方程式の計算 if ( ! GaussianElimination( s_ ) ) { cerr << "Failed to calculate coefficients." << endl; return( -1 ); } // 各係数が収束しているかを確認する bool isMatched = true; for ( unsigned int i = 0 ; i < coefSize() ; ++i ) { if ( fabs( a_[i] - s_.ans( i ) ) >= threshold ) isMatched = false; a_[i] = s_.ans( i ); } return( ( isMatched ) ? 1 : 0 ); } /* OrderedLogisticModel::printPi : π の出力 */ void OrderedLogisticModel::printPi() const { if ( ! isValid() ) return; vector< vector<double> > pi; // π の計算結果 rho2Pi( pi ); PrintMatrix( "pi = ", pi ); cout << endl; }
OrderedLogisticModel は、順序ロジスティック回帰に登場する様々なモデルの基底クラスとして機能します。回帰式を求めるプログラムには、このインスタンスを渡すことになります。独立変数やその従属変数 (各カテゴリの発生回数) は、このインスタンスが保持して計算などに利用します。但し、連立方程式の係数や解の求め方や ρik の計算方法はモデルにより異なるので、純粋仮想関数として定義だけを行います ( initRho, rho2Pi, coef2Rho, calcCoefMatrix, calcRSide )。また、結果出力の書式がモデルによって異なる printVar と printEquation も定義のみで実装はされていません。
コンストラクタでは、渡されたデータのチェックとそのサイズの取得を行います。ここでデータに不備があった場合、メンバ変数 isValid_ を false にして、ほとんどの処理を無効とします。initPi は、渡された従属変数 y からカテゴリごとの確率 πik を求めるために使うメンバ関数で、ρik の初期値を計算する処理 ( initRho ) の中で一度だけ使用します。一度スコア法が始まったら ρik は回帰係数から求めることになり、その時に使う関数は coef2Rho です。また、πik は rho2Pi を使って ρik から求めます。残りの純粋仮想関数 calcCoefMatrix と calcRSide は連立方程式の左辺 (係数行列) と右辺を計算するためのメンバ関数です。この部分がモデルによって最も違いの大きな個所になります。
メンバ関数 solve は、連立方程式の計算と収束のチェックを行います。連立方程式の解法は「ガウスの消去法 (Gaussian elimination)」です。収束判断のためのしきい値 threshold は外部から渡すようにしています。求めた値と前の値の差分が全て threshold より小さければ solve は戻り値として 1 を返し、一つでも threshold より大きいものがあったら 0 を返します。また、連立方程式の計算に失敗したり、インスタンスが有効でなかったときは負数 -1 を返します。
* 今回のサンプル・プログラムは、前章で作成した名義ロジスティック回帰用のものをそのまま利用しています。しかし複数ある順序ロジスティックモデルごとに連立方程式の作成処理以外はほとんど同じプログラムを用意することになり非常に効率が悪く、それを回避するために計算処理とスコア法の処理を別々に分離しました。この分離の仕方がうまくできていないため、まだ検討の余地は残っています。時間があれば再度見直しをしたいところです。
次は、「比例オッズモデル」と「累積ロジットモデル」に当てはめて計算処理を行うためのクラス ( CumulativeLogitModel_Base, ProportionalOddsModel, CumulativeLogitModel ) を以下に示します。
/*------------------------------------------------------------------------------------------------ CumulativeLogitModel_Base : 累積ロジットモデルの基底クラス ------------------------------------------------------------------------------------------------*/ class CumulativeLogitModel_Base : public OrderedLogisticModel { protected: // ρ の初期化 ( π から計算する ) virtual void initRho(); // ρ から π を求める virtual void rho2Pi( vector< vector<double> >& pi ) const; public: // コンストラクタ CumulativeLogitModel_Base( const vector< vector<double> >& x, const vector< vector<double> >& y ) : OrderedLogisticModel( x, y ) { if ( isValid() ) initRho(); } }; /* CumulativeLogitModel_Base::initRho : ρ の初期化 ( y から計算する ) */ void CumulativeLogitModel_Base::initRho() { if ( ! isValid() ) return; // π の計算 ( y から求める ) vector< vector<double> > pi; initPi( pi ); rho_.assign( n_, vector<double>( c_ - 1 ) ); for ( unsigned int i = 0 ; i < n_ ; ++i ) { double sumPi = 0; // i までの累積確率 for ( unsigned int k = 0 ; k < c_ - 1 ; ++k ) { sumPi += pi[i][k]; if ( sumPi == 0 ) sumPi = 1E-9; // ゼロ除算防止 if ( sumPi > 1 ) sumPi = 1; rho_[i][k] = ( 1.0 - sumPi ) / sumPi; } } } /* CumulativeLogitModel_Base::rho2Pi : ρ から π を求める vector< vector<double> >& pi : 計算結果を格納するベクトル */ void CumulativeLogitModel_Base::rho2Pi( vector< vector<double> >& pi ) const { if ( ! isValid() ) return; pi.assign( n_, vector<double>( c_ ) ); // 確率の当てはめ値 ( n x c ) for ( unsigned int i = 0 ; i < n_ ; ++i ) { pi[i][0] = 1.0 / ( 1.0 + rho_[i][0] ); for ( unsigned int k = 1 ; k < c_ - 1 ; ++k ) pi[i][k] = 1.0 / ( 1.0 + rho_[i][k] ) - 1.0 / ( 1.0 + rho_[i][k - 1] ); if ( c_ > 1 ) pi[i][c_ - 1] = 1.0 - 1.0 / ( 1.0 + rho_[i][c_ - 2] ); } } /*------------------------------------------------------------------------------------------------ ProportionalOddsModel : 比例オッズモデル ------------------------------------------------------------------------------------------------*/ class ProportionalOddsModel : public CumulativeLogitModel_Base { void calcH11(); // H11 の計算 void calcH22(); // H22 の計算 void calcH12(); // H12(H21) の計算 public: // コンストラクタ ProportionalOddsModel( const vector< vector<double> >& x, const vector< vector<double> >& y ) : CumulativeLogitModel_Base( x, y ) { setCoefSize( c_ + p_ - 1 ); } virtual void coef2Rho(); // 求めた係数から ρ を計算する virtual void calcCoefMatrix(); // 係数行列を計算する virtual void calcRSide(); // 連立方程式の右辺を計算する virtual void printVar(); // 回帰係数に対する分散の出力 virtual void printEquation() const; // 回帰式の出力 // モデル名 virtual string ident() const { return( "Proportional Odds Model" ); } }; /* ProportionalOddsModel::coef2Rho : 求めた係数から ρ を計算する */ void ProportionalOddsModel::coef2Rho() { if ( ! isValid() ) return; for ( unsigned int i = 0 ; i < n_ ; ++i ) { for ( unsigned int k = 0 ; k < c_ - 1 ; ++k ) { double xi = a_[k]; for ( unsigned int j = 0 ; j < p_ ; ++j ) xi += a_[c_ - 1 + j] * x_[i][j]; rho_[i][k] = exp( xi ); } } } /* ProportionalOddsModel::calcH11 : H11 の計算 */ void ProportionalOddsModel::calcH11() { for ( unsigned int k = 0 ; k < c_ - 1 ; ++k ) { // 対角成分を計算 s_[k][k] = 0; for ( unsigned int i = 0 ; i < n_ ; ++i ) { s_[k][k] -= ( y_[i][k] + y_[i][k + 1] ) * rho_[i][k] / pow( 1.0 + rho_[i][k], 2 ); if ( k + 1 < c_ - 1 ) s_[k][k] -= y_[i][k + 1] * rho_[i][k] * rho_[i][k + 1] / pow( rho_[i][k] - rho_[i][k + 1], 2 ); if ( k > 0 ) s_[k][k] -= y_[i][k] * rho_[i][k] * rho_[i][k - 1] / pow( rho_[i][k] - rho_[i][k - 1], 2 ); } if ( k + 1 == c_ - 1 ) break; // 対角成分の右隣を計算 s_[k][k + 1] = 0; for ( unsigned int i = 0 ; i < n_ ; ++i ) s_[k][k + 1] += y_[i][k + 1] * rho_[i][k] * rho_[i][k + 1] / pow( rho_[i][k] - rho_[i][k + 1], 2 ); s_[k + 1][k] = s_[k][k + 1]; // 対称な成分にコピー // 残りはゼロで初期化 for ( unsigned int k2 = k + 2 ; k2 < c_ - 1 ; ++k2 ) s_[k][k2] = s_[k2][k] = 0; } } /* ProportionalOddsModel::calcH22 : H22 の計算 */ void ProportionalOddsModel::calcH22() { // k ごとの和の部分を先に計算 vector<double> sum( n_, 0 ); for ( unsigned int i = 0 ; i < n_ ; ++i ) for ( unsigned int k = 0 ; k < c_ - 1 ; ++k ) sum[i] += ( y_[i][k] + y_[i][k + 1] ) * rho_[i][k] / pow( 1.0 + rho_[i][k], 2 ); for ( unsigned int sr = c_ - 1 ; sr < coefSize() ; ++sr ) { // sr は係数行列の行番号 unsigned int jr = sr - ( c_ - 1 ); // x_ に対する行番号 for ( unsigned int sc = sr ; sc < coefSize() ; ++sc ) { // sc は係数行列の列番号(対角成分からスタート) unsigned int jc = sc - ( c_ - 1 ); // x_ に対する列番号 s_[sr][sc] = 0; for ( unsigned int i = 0 ; i < n_ ; ++i ) s_[sr][sc] -= x_[i][jr] * x_[i][jc] * sum[i]; // 対角成分(左下)はコピー if ( sc != sr ) s_[sc][sr] = s_[sr][sc]; } } } /* ProportionalOddsModel::calcH12 : H12(H21) の計算 */ void ProportionalOddsModel::calcH12() { // 計算は右上側(H12)に対して行う for ( unsigned int k = 0 ; k < c_ - 1 ; ++k ) { for ( unsigned int sc = c_ - 1 ; sc < coefSize() ; ++sc ) { unsigned int j = sc - ( c_ - 1 ); // x_ に対する列番号 s_[k][sc] = 0; for ( unsigned int i = 0 ; i < n_ ; ++i ) s_[k][sc] -= x_[i][j] * ( y_[i][k] + y_[i][k + 1] ) * rho_[i][k] / pow( 1.0 + rho_[i][k], 2 ); s_[sc][k] = s_[k][sc]; // 対角成分(左下)はコピー } } } /* ProportionalOddsModel::calcCoefMatrix : 係数行列を計算する */ void ProportionalOddsModel::calcCoefMatrix() { if ( ! isValid() ) return; calcH11(); // H11 の計算 calcH22(); // H22 の計算 calcH12(); // H12(H21) の計算 } /* ProportionalOddsModel::calcRSide : 連立方程式の右辺を計算する */ void ProportionalOddsModel::calcRSide() { if ( ! isValid() ) return; vector<double> u_sum( n_, 0 ); // 対数尤度の偏微分 u の計算に必要な項 vector<double> h_sum( n_, 0 ); // 係数行列と係数の積 Ha の計算に必要な項 for ( unsigned int i = 0 ; i < n_ ; ++i ) { for ( unsigned int k = 0 ; k < c_ - 1 ; ++k ) { u_sum[i] += ( y_[i][k] + y_[i][k + 1] ) / ( 1.0 + rho_[i][k] ) - y_[i][k]; h_sum[i] += ( y_[i][k] + y_[i][k + 1] ) * rho_[i][k] * log( rho_[i][k] ) / pow( 1.0 + rho_[i][k], 2 ); } } vector<double> u( coefSize(), 0 ); // u の値 vector<double> h( coefSize(), 0 ); // Ha の値 for ( unsigned int k = 0 ; k < c_ - 1 ; ++k ) { for ( unsigned int i = 0 ; i < n_ ; ++i ) { u[k] += ( y_[i][k] + y_[i][k + 1] ) / ( 1.0 + rho_[i][k] ); h[k] -= ( y_[i][k] + y_[i][k + 1] ) * rho_[i][k] * log( rho_[i][k] ) / pow( 1.0 + rho_[i][k], 2 ); if ( k + 1 < c_ - 1 ) { u[k] += y_[i][k + 1] * rho_[i][k + 1] / ( rho_[i][k] - rho_[i][k + 1] ); h[k] += y_[i][k + 1] * rho_[i][k] * rho_[i][k + 1] * ( log( rho_[i][k + 1] ) - log( rho_[i][k] ) ) / pow( rho_[i][k] - rho_[i][k + 1], 2 ); } if ( k > 0 ) { u[k] += y_[i][k] * rho_[i][k - 1] / ( rho_[i][k] - rho_[i][k - 1] ); h[k] += y_[i][k] * rho_[i][k] * rho_[i][k - 1] * ( log( rho_[i][k - 1] ) - log( rho_[i][k] ) ) / pow( rho_[i][k] - rho_[i][k - 1], 2 ); } else { u[k] -= y_[i][k]; } } } for ( unsigned int j = 0 ; j < p_ ; ++j ) { for ( unsigned int i = 0 ; i < n_ ; ++i ) { u[j + c_ - 1] += x_[i][j] * u_sum[i]; h[j + c_ - 1] -= x_[i][j] * h_sum[i]; } } for ( unsigned int k = 0 ; k < coefSize() ; ++k ) s_.ans( k ) = h[k] - u[k]; // 右辺 = Ha - u } /* ProportionalOddsModel::printVar : 回帰係数に対する分散の出力 */ void ProportionalOddsModel::printVar() { if ( ! isValid() ) return; // 係数行列の再計算(=フィッシャー情報行列) calcCoefMatrix(); LinearEquationSystem<double> inv( 0 ); // 連立方程式計算用インスタンスの逆行列 Inverse( s_, inv ); cout << "variance of b = ( " << -inv[0][0]; for ( unsigned int k = 1 ; k < c_ - 1 ; ++k ) cout << ", " << -inv[k][k]; cout << " )" << endl; cout << "variance of a = ( " << -inv[c_ - 1][c_ - 1]; for ( unsigned int j = c_ ; j < coefSize() ; ++j ) cout << ", " << -inv[j][j]; cout << " )" << endl << endl; } /* ProportionalOddsModel::printEquation : 回帰式の出力 */ void ProportionalOddsModel::printEquation() const { if ( ! isValid() ) return; vector<double> a2( a_.begin() + c_ - 1, a_.end() ); for ( unsigned int k = 0 ; k < c_ - 1 ; ++k ) { std::ostringstream oss; oss << "Regression equation : y[" << k << "] = " << a_[k] << " + "; PrintEquation( oss.str(), a2 ); } cout << endl; } /*------------------------------------------------------------------------------------------------ CumulativeLogitModel : 累積ロジットモデル ------------------------------------------------------------------------------------------------*/ class CumulativeLogitModel : public CumulativeLogitModel_Base { void calcCoefDiagBlock( unsigned int k ); void calcCoefNonDiagBlock( unsigned int k ); public: // コンストラクタ CumulativeLogitModel( const vector< vector<double> >& x, const vector< vector<double> >& y ) : CumulativeLogitModel_Base( x, y ) { setCoefSize( ( c_ - 1 ) * p_ ); } virtual void coef2Rho(); // 求めた係数から ρ を計算する virtual void calcCoefMatrix(); // 係数行列を計算する virtual void calcRSide(); // 連立方程式の右辺を計算する virtual void printVar(); // 回帰係数に対する分散の出力 virtual void printEquation() const; // 回帰式の出力 // モデル名 virtual string ident() const { return( "Cumulative Logit Model" ); } }; /* CumulativeLogitModel::coef2Rho : 求めた係数から ρ を計算する */ void CumulativeLogitModel::coef2Rho() { if ( ! isValid() ) return; for ( unsigned int i = 0 ; i < n_ ; ++i ) { for ( unsigned int k = 0 ; k < c_ - 1 ; ++k ) { double xi = a_[k * p_] * x_[i][0]; for ( unsigned int j = 1 ; j < p_ ; ++j ) xi += a_[k * p_ + j] * x_[i][j]; rho_[i][k] = exp( xi ); } } } /* CumulativeLogitModel::calcCoefDiagBlock : 係数行列の対角部分行列を計算する */ void CumulativeLogitModel::calcCoefDiagBlock( unsigned int k ) { // k に依存する部分を先に計算 vector<double> sum( n_, 0 ); for ( unsigned int i = 0 ; i < n_ ; ++i ) { sum[i] += ( y_[i][k] + y_[i][k + 1] ) * rho_[i][k] / pow( 1.0 + rho_[i][k], 2 ); if ( k + 1 < c_ - 1 ) sum[i] += y_[i][k + 1] * rho_[i][k] * rho_[i][k + 1] / pow( rho_[i][k] - rho_[i][k + 1], 2 ); if ( k > 0 ) sum[i] += y_[i][k] * rho_[i][k] * rho_[i][k - 1] / pow( rho_[i][k] - rho_[i][k - 1], 2 ); } for ( unsigned int jr = 0 ; jr < p_ ; ++jr ) { for ( unsigned int jc = 0 ; jc < p_ ; ++jc ) { s_[k * p_ + jr][k * p_ + jc] = 0; for ( unsigned int i = 0 ; i < n_ ; ++i ) s_[k * p_ + jr][k * p_ + jc] -= x_[i][jr] * x_[i][jc] * sum[i]; } } } /* CumulativeLogitModel::calcCoefNonDiagBlock : 係数行列の非対角部分行列(対角成分の右側)を計算する */ void CumulativeLogitModel::calcCoefNonDiagBlock( unsigned int k ) { // k に依存する部分を先に計算 vector<double> sum( n_, 0 ); for ( unsigned int i = 0 ; i < n_ ; ++i ) sum[i] += y_[i][k + 1] * rho_[i][k] * rho_[i][k + 1] / pow( rho_[i][k] - rho_[i][k + 1], 2 ); for ( unsigned int jr = 0 ; jr < p_ ; ++jr ) { for ( unsigned int jc = 0 ; jc < p_ ; ++jc ) { s_[k * p_ + jr][( k + 1 ) * p_ + jc] = 0; for ( unsigned int i = 0 ; i < n_ ; ++i ) s_[k * p_ + jr][( k + 1 ) * p_ + jc] += x_[i][jr] * x_[i][jc] * sum[i]; // 対称成分にコピー s_[( k + 1 ) * p_ + jc][k * p_ + jr] = s_[k * p_ + jr][( k + 1 ) * p_ + jc]; } } } /* CumulativeLogitModel::calcCoefMatrix : 係数行列を計算する */ void CumulativeLogitModel::calcCoefMatrix() { if ( ! isValid() ) return; for ( unsigned int k = 0 ; k < c_ - 1 ; ++k ) { calcCoefDiagBlock( k ); if ( k + 1 < c_ - 1 ) calcCoefNonDiagBlock( k ); } } /* CumulativeLogitModel::calcRSide : 連立方程式の右辺を計算する */ void CumulativeLogitModel::calcRSide() { if ( ! isValid() ) return; vector< vector<double> > u_sum( n_, vector<double>( c_ - 1 ) ); // 対数尤度の偏微分 u の計算に必要な項 vector< vector<double> > h_sum( n_, vector<double>( c_ - 1 ) ); // 係数行列と係数の積 Ha の計算に必要な項 // k に依存する部分を先に計算しておく for ( unsigned int k = 0 ; k < c_ - 1 ; ++k ) { for ( unsigned int i = 0 ; i < n_ ; ++i ) { h_sum[i][k] = -( y_[i][k] + y_[i][k + 1] ) * rho_[i][k] * log( rho_[i][k] ) / pow( 1.0 + rho_[i][k], 2 ); u_sum[i][k] = ( y_[i][k] + y_[i][k + 1] ) / ( 1.0 + rho_[i][k] ); if ( k > 0 ) { h_sum[i][k] += y_[i][k] * rho_[i][k] * rho_[i][k - 1] * ( log( rho_[i][k - 1] ) - log( rho_[i][k] ) ) / pow( rho_[i][k] - rho_[i][k - 1], 2 ); u_sum[i][k] += y_[i][k] * rho_[i][k - 1] / ( rho_[i][k] - rho_[i][k - 1] ); } else { u_sum[i][k] -= y_[i][k]; } if ( k + 1 < c_ - 1 ) { h_sum[i][k] += y_[i][k + 1] * rho_[i][k] * rho_[i][k + 1] * ( log( rho_[i][k + 1] ) - log( rho_[i][k] ) ) / pow( rho_[i][k] - rho_[i][k + 1], 2 ); u_sum[i][k] += y_[i][k + 1] * rho_[i][k + 1] / ( rho_[i][k] - rho_[i][k + 1] ); } } } for ( unsigned int k = 0 ; k < c_ - 1 ; ++k ) { for ( unsigned int j = 0 ; j < p_ ; ++j ) { s_.ans( k * p_ + j ) = 0; for ( unsigned int i = 0 ; i < n_ ; ++i ) s_.ans( k * p_ + j ) += x_[i][j] * ( h_sum[i][k] - u_sum[i][k] ); } } } /* CumulativeLogitModel::printVar : 回帰係数に対する分散の出力 */ void CumulativeLogitModel::printVar() { if ( ! isValid() ) return; // 係数行列の再計算(=フィッシャー情報行列) calcCoefMatrix(); LinearEquationSystem<double> inv( 0 ); // 連立方程式計算用インスタンスの逆行列 Inverse( s_, inv ); for ( unsigned int k = 0 ; k < c_ - 1 ; ++k ) { cout << "variance of a[" << k << "] = ( " << -inv[k * p_][k * p_]; for ( unsigned int j = 1 ; j < p_ ; ++j ) cout << ", " << -inv[k * p_ + j][k * p_ + j]; cout << " )" << endl; } cout << endl; } /* CumulativeLogitModel::printEquation : 回帰式の出力 */ void CumulativeLogitModel::printEquation() const { if ( ! isValid() ) return; for ( unsigned int k = 0 ; k < c_ - 1 ; ++k ) { vector<double> ak( a_.begin() + k * p_, a_.begin() + ( k + 1 ) * p_ ); std::ostringstream oss; oss << " y[" << k << "] = "; PrintEquation( oss.str(), ak ); } cout << endl; }
CumulativeLogitModel_Base クラスは「比例オッズモデル」と「累積ロジットモデル」に共通な、ρik と πik の間の変換をするメンバ関数 ( initRho, rho2Pi ) を実装した OrderedLogisticModel クラスの派生クラスで、ここからさらに比例オッズモデル ( ProportionalOddsModel ) と累積ロジットモデル ( CumulativeLogitModel ) を派生しています。それぞれの派生クラスで coef2Rho, calcCoefMatrix, calcRSide と出力用の未定義なメンバ関数を実装し、インスタンス化できるようにしています。この部分が非常に長いプログラムとなっていますが、そのほとんどは連立方程式の係数や右辺の計算処理です。注意すべき点としては、係数行列 H が対称行列であることを利用して、対角成分より右上だけを計算したら左下はコピーするようになっていることと、部分行列に分割できる場合はその単位ごとに処理を振り分けているというところが挙げられます。
なお、今回は「隣接カテゴリ・ロジット・モデル」と「連続比ロジット・モデル」の処理ルーチンは用意していません。
最後に、スコア法の処理を行うためのプログラムを示します。
/* OrderedLogisticRegression : 順序ロジスティック回帰 OrderedLogisticModel& model : 順序ロジスティックモデル bool verbose : 冗長モード(ON/OFF) unsigned int maxCount : 反復処理の最大回数 double threshold : 収束条件(全係数が threshold 以下なら処理終了) 戻り値 : 係数が得られた ... true ; データ異常・反復処理回数が最大値を超えた ... false */ bool OrderedLogisticRegression( OrderedLogisticModel& model, bool verbose, unsigned int maxCount, double threshold ) { cout << "*** " << model.ident() << " ***" << endl << endl; if ( ! model.isValid() ) { cerr << "The model is invalid." << endl; return( false ); } model.printSize(); if ( verbose ) { model.printX(); model.printY(); } unsigned int cnt; // 計算回数 for ( cnt = 0 ; cnt < maxCount ; ++cnt ) { if ( verbose ) { cout << "----- cnt = " << cnt << " -----" << endl << endl; model.printPi(); model.printRho(); } // 係数行列の計算 model.calcCoefMatrix(); // 右辺の計算 model.calcRSide(); if ( verbose ) { cout << "Equation System :" << endl; model.printLES(); } // 連立方程式の計算 int res = model.solve( threshold ); if ( res < 0 ) return( false ); if ( verbose ) model.printEquation(); if ( res > 0 ) break; // カテゴリごとの確率計算 model.coef2Rho(); } if ( cnt < maxCount ) { cout << "Estimated regression equation" << endl << endl; model.printEquation(); model.printVar(); cout << "Estimated probability" << endl; model.printPi(); } else { cout << "Failed to estimate regression coefficient" << endl << endl; } return( cnt < maxCount ); }
大半の処理はクラスの中に実装してしまったため、メイン・ルーチンは非常に単純になっています。変数のチェックや初期化は全て OrderedLogisticModel のインスタンス化で行われておりメイン・ルーチン側では不要になります。ループの中がスコア法の処理をしている部分で、漸化式 (連立方程式) を作成してはそれを解くことを解が収束するまで繰り返します。ρik は連立方程式の係数や右辺の計算で利用するので、coef2Rho を使って求めた係数からループの最後で再計算しています。
実際に利用するときは、以下のような形になります。
vector< vector<double> > x; // 定数項を含まない独立変数 vector< vector<double> > x2; // (必要なら)定数項を含む独立変数 vector< vector<double> > y; // 従属変数(各カテゴリの発生回数) /* x[i], x2[i] が独立変数ベクトルで、x[i][j], x2[i][j] がその要素になるように初期化 但し、x2[i] は(必要なら)定数項を含むのに対し、x[i] は定数項を含めないことに注意 同様に、y[i] が従属変数ベクトルで、y[i][j] がその要素になるように初期化 */ // 比例オッズモデル ProportionalOddsModel proModel( x, y ); OrderedLogisticRegression( proModel, true ); // 累積ロジットモデル CumulativeLogitModel cumModel( x2, y ); OrderedLogisticRegression( cumModel, true );
比例オッズモデルでは定数項とそれ以外の項を別々に扱っているため (さらに定数項は必須となります)、独立変数ベクトルに定数項 (常に 1 となる要素) は含める必要がないことに注意して下さい。
サンプル・プログラムを使い、前章の「名義ロジスティック回帰」で使ったサンプル・データを処理してみます。サンプル・データは、車の安全性や装備の嗜好に関するドライバーへの聞き取り調査結果の中で、エアコンとパワーステアリングをどれだけ重視するかを示した以下のようなものでした。
| 性別 | 年齢(歳) | 反応 | |||
|---|---|---|---|---|---|
| C/D | B | A | 計 | ||
| 女性 | 18-23 | 26 | 12 | 7 | 45 |
| 24-40 | 9 | 21 | 15 | 45 | |
| >40 | 5 | 14 | 41 | 60 | |
| 男性 | 18-23 | 40 | 17 | 8 | 65 |
| 24-40 | 17 | 15 | 12 | 44 | |
| >40 | 8 | 15 | 18 | 41 | |
| 計 | 105 | 94 | 101 | 300 | |
表の中の「反応」はどれだけ重視するかを評価した結果で、「C/D : あまり重要でない/重要でない」「B : 重要」「A : 非常に重要」となっています。前章と同様に、独立変数ベクトルは以下のようにします。
| xi1 | = | 1 | (男性) |
| = | 0 | (女性) | |
| xi2 | = | 1 | (年齢 24-40) |
| = | 0 | (それ以外) | |
| xi3 | = | 1 | (年齢 >40) |
| = | 0 | (それ以外) |
また、πi1 が「C/D : あまり重要でない/重要でない」、πi2 が「B : 重要」、πi3 が「A : 非常に重要」に対する発生確率であるとして、まずは「比例オッズモデル」を適用した以下の正規方程式で評価してみます。
log( ( πi2 + πi3 ) / πi1 ) = β1 + α1xi1 + α2xi2 + α3xi3
log( πi3 / ( πi1 + πi2 ) ) = β2 + α1xi1 + α2xi2 + α3xi3
結果は以下のようになります (出力を冗長にするため引数 verbose を ON にしています)。
*** Proportional Odds Model ***
N = 6 ; p = 3 ; c = 3
x = ( 0, 0, 0 )
( 0, 1, 0 )
( 0, 0, 1 )
( 1, 0, 0 )
( 1, 1, 0 )
( 1, 0, 1 )
y = ( 26, 12, 7 )
( 9, 21, 15 )
( 5, 14, 41 )
( 40, 17, 8 )
( 17, 15, 12 )
( 8, 15, 18 )
----- cnt = 0 -----
pi = ( 0.577778, 0.266667, 0.155556 )
( 0.2, 0.466667, 0.333333 )
( 0.0833333, 0.233333, 0.683333 )
( 0.615385, 0.261538, 0.123077 )
( 0.386364, 0.340909, 0.272727 )
( 0.195122, 0.365854, 0.439024 )
rho = ( 0.730769, 0.184211 )
( 4, 0.5 )
( 11, 2.15789 )
( 0.625, 0.140351 )
( 1.58824, 0.375 )
( 4.125, 0.782609 )
Equation System :
(-70.0509)x0 + (29.8394)x1 + (-24.69)x2 + (-12.3868)x3 + (-5.06352)x4 = -56.4671
(29.8394)x0 + (-68.4175)x1 + (-16.1809)x2 + (-13.3554)x3 + (-20.0287)x4 = 60.1093
(-24.69)x0 + (-16.1809)x1 + (-40.8709)x2 + (-12.9421)x3 + (-11.7394)x4 = 10.2556
(-12.3868)x0 + (-13.3554)x1 + (-12.9421)x2 + (-25.7421)x3 + (0)x4 = 0.633849
(-5.06352)x0 + (-20.0287)x1 + (-11.7394)x2 + (0)x3 + (-25.0922)x4 = -15.7605
Regression equation : y[0] = -0.0488767 + -0.566897x0 + 1.13082x1 + 2.20617x2
Regression equation : y[1] = -1.63239 + -0.566897x0 + 1.13082x1 + 2.20617x2
----- cnt = 1 -----
pi = ( 0.512217, 0.32428, 0.163503 )
( 0.253139, 0.36969, 0.377171 )
( 0.103652, 0.256713, 0.639635 )
( 0.649257, 0.250929, 0.0998146 )
( 0.374013, 0.370294, 0.255694 )
( 0.169328, 0.328951, 0.50172 )
rho = ( 0.952299, 0.195462 )
( 2.95039, 0.605577 )
( 8.64768, 1.77496 )
( 0.540222, 0.110882 )
( 1.67371, 0.343533 )
( 4.90568, 1.00691 )
Equation System :
(-71.1851)x0 + (30.5463)x1 + (-23.7073)x2 + (-13.1639)x3 + (-5.00035)x4 = -60.0371
(30.5463)x0 + (-69.9141)x1 + (-15.6347)x2 + (-13.5954)x3 + (-20.9275)x4 = 61.051
(-23.7073)x0 + (-15.6347)x1 + (-39.342)x2 + (-12.6306)x3 + (-11.485)x4 = 9.44813
(-13.1639)x0 + (-13.5954)x1 + (-12.6306)x2 + (-26.7592)x3 + (0)x4 = -0.343875
(-5.00035)x0 + (-20.9275)x1 + (-11.485)x2 + (0)x3 + (-25.9279)x4 = -16.4114
Regression equation : y[0] = -0.0436196 + -0.57613x0 + 1.14689x1 + 2.23208x2
Regression equation : y[1] = -1.6546 + -0.57613x0 + 1.14689x1 + 2.23208x2
----- cnt = 2 -----
pi = ( 0.510903, 0.328609, 0.160488 )
( 0.249128, 0.375142, 0.37573 )
( 0.100791, 0.258721, 0.640487 )
( 0.650162, 0.252814, 0.0970245 )
( 0.371185, 0.376036, 0.252779 )
( 0.166265, 0.333398, 0.500337 )
rho = ( 0.957318, 0.191168 )
( 3.014, 0.60187 )
( 8.92148, 1.78154 )
( 0.538079, 0.10745 )
( 1.69408, 0.338293 )
( 5.01449, 1.00135 )
Equation System :
(-69.7585)x0 + (29.3071)x1 + (-23.622)x2 + (-13.0809)x3 + (-4.9103)x4 = -57.8209
(29.3071)x0 + (-68.5156)x1 + (-15.5401)x2 + (-13.5439)x3 + (-20.9145)x4 = 58.8434
(-23.622)x0 + (-15.5401)x1 + (-39.1621)x2 + (-12.5688)x3 + (-11.4383)x4 = 9.35985
(-13.0809)x0 + (-13.5439)x1 + (-12.5688)x2 + (-26.6248)x3 + (0)x4 = -0.314511
(-4.9103)x0 + (-20.9145)x1 + (-11.4383)x2 + (0)x3 + (-25.8248)x4 = -16.235
Regression equation : y[0] = -0.0435382 + -0.576222x0 + 1.1471x1 + 2.23246x2
Regression equation : y[1] = -1.65498 + -0.576222x0 + 1.1471x1 + 2.23246x2
Estimated regression equation
Regression equation : y[0] = -0.0435382 + -0.576222x0 + 1.1471x1 + 2.23246x2
Regression equation : y[1] = -1.65498 + -0.576222x0 + 1.1471x1 + 2.23246x2
variance of b = ( 0.0539472, 0.0653297 )
variance of a = ( 0.0511567, 0.0770636, 0.0849555 )
Estimated probability
pi = ( 0.510903, 0.328609, 0.160488 )
( 0.249128, 0.375142, 0.37573 )
( 0.100791, 0.258721, 0.640487 )
( 0.650162, 0.252814, 0.0970245 )
( 0.371185, 0.376036, 0.252779 )
( 0.166265, 0.333398, 0.500337 )
名義ロジスティックモデルの場合と同様に、推定確率 πik から最大対数尤度 lα を求めてみます。lα は、以下の式に πik を代入すれば求めることができるのでした。但し、式の中に定数項は含めていません (*2-1)。
計算した結果は lα = -290.65 になり、最大モデルの対数尤度が lmax = -288.38、最小モデルの対数尤度が lmin = -329.27 と求められることから、対数尤度統計量 D と尤度比カイ二乗統計量 C は次のようになります。
D = 2 x ( lmax - lα ) = 4.53
C = 2 x ( lα - lmin ) = 77.25
また、擬似 R2 値は
となり、名義ロジスティックの場合と比較するとかなり近い結果が得られていることがわかります。名義ロジスティックモデルの場合、回帰係数の数は 8 だったのに対し、比例オッズモデルでは 5 つと、より少ないパラメータで同等の結果が得られています。また、今回のデータはカテゴリに対して順序を持っていることから、それを考慮した比例オッズモデルの方が名義ロジスティックモデルよりも望ましいと判断することができます。
次に、累積ロジットモデルを適用した結果を以下に示します。
*** Cumulative Logit Model ***
N = 6 ; p = 4 ; c = 3
x = ( 1, 0, 0, 0 )
( 1, 0, 1, 0 )
( 1, 0, 0, 1 )
( 1, 1, 0, 0 )
( 1, 1, 1, 0 )
( 1, 1, 0, 1 )
y = ( 26, 12, 7 )
( 9, 21, 15 )
( 5, 14, 41 )
( 40, 17, 8 )
( 17, 15, 12 )
( 8, 15, 18 )
----- cnt = 0 -----
pi = ( 0.577778, 0.266667, 0.155556 )
( 0.2, 0.466667, 0.333333 )
( 0.0833333, 0.233333, 0.683333 )
( 0.615385, 0.261538, 0.123077 )
( 0.386364, 0.340909, 0.272727 )
( 0.195122, 0.365854, 0.439024 )
rho = ( 0.730769, 0.184211 )
( 4, 0.5 )
( 11, 2.15789 )
( 0.625, 0.140351 )
( 1.58824, 0.375 )
( 4.125, 0.782609 )
Equation System :
(-70.0509)x0 + (-41.4428)x1 + (-21.8848)x2 + (-13.6486)x3 + (29.8394)x4 + (16.7527)x5 + (9.49799)x6 + (8.58506)x7 = -56.4671
(-41.4428)x0 + (-41.4428)x1 + (-13.6562)x2 + (-7.9467)x3 + (16.7527)x4 + (16.7527)x5 + (6.06942)x6 + (4.33456)x7 = -27.7359
(-21.8848)x0 + (-13.6562)x1 + (-21.8848)x2 + (0)x3 + (9.49799)x4 + (6.06942)x5 + (9.49799)x6 + (0)x7 = -26.0545
(-13.6486)x0 + (-7.9467)x1 + (0)x2 + (-13.6486)x3 + (8.58506)x4 + (4.33456)x5 + (0)x6 + (8.58506)x7 = -22.7268
(29.8394)x0 + (16.7527)x1 + (9.49799)x2 + (8.58506)x3 + (-68.4175)x4 + (-32.9337)x5 + (-22.8534)x6 + (-28.6138)x7 = 60.1093
(16.7527)x0 + (16.7527)x1 + (6.06942)x2 + (4.33456)x3 + (-32.9337)x4 + (-32.9337)x5 + (-11.4248)x6 + (-12.4619)x7 = 37.9915
(9.49799)x0 + (6.06942)x1 + (9.49799)x2 + (0)x3 + (-22.8534)x4 + (-11.4248)x5 + (-22.8534)x6 + (0)x7 = 26.6883
(8.58506)x0 + (4.33456)x1 + (0)x2 + (8.58506)x3 + (-28.6138)x4 + (-12.4619)x5 + (0)x6 + (-28.6138)x7 = 6.96634
y[0] = -0.0645247x0 + -0.583242x1 + 1.21903x2 + 2.2479x3
y[1] = -1.52196x0 + -0.565755x1 + 0.961902x2 + 2.09162x3
----- cnt = 1 -----
pi = ( 0.516126, 0.304701, 0.179174 )
( 0.239667, 0.396798, 0.363535 )
( 0.101253, 0.26006, 0.638687 )
( 0.656507, 0.233196, 0.110297 )
( 0.360945, 0.39412, 0.244935 )
( 0.167963, 0.331059, 0.500978 )
rho = ( 0.937513, 0.218285 )
( 3.17246, 0.571178 )
( 8.87623, 1.76768 )
( 0.523213, 0.123971 )
( 1.77051, 0.32439 )
( 4.9537, 1.00392 )
Equation System :
(-70.6723)x0 + (-39.2684)x1 + (-22.5911)x2 + (-14.072)x3 + (30.537)x4 + (15.819)x5 + (9.74311)x6 + (9.1287)x7 = -59.4201
(-39.2684)x0 + (-39.2684)x1 + (-11.5008)x2 + (-7.99589)x3 + (15.819)x4 + (15.819)x5 + (4.11955)x6 + (4.78162)x7 = -25.9091
(-22.5911)x0 + (-11.5008)x1 + (-22.5911)x2 + (0)x3 + (9.74311)x4 + (4.11955)x5 + (9.74311)x6 + (0)x7 = -27.8773
(-14.072)x0 + (-7.99589)x1 + (0)x2 + (-14.072)x3 + (9.1287)x4 + (4.78162)x5 + (0)x6 + (9.1287)x7 = -23.6467
(30.537)x0 + (15.819)x1 + (9.74311)x2 + (9.1287)x3 + (-70.0498)x4 + (-31.5157)x5 + (-23.0661)x6 + (-30.0708)x7 = 61.2723
(15.819)x0 + (15.819)x1 + (4.11955)x2 + (4.78162)x3 + (-31.5157)x4 + (-31.5157)x5 + (-9.11298)x6 + (-13.0316)x7 = 35.6552
(9.74311)x0 + (4.11955)x1 + (9.74311)x2 + (0)x3 + (-23.0661)x4 + (-9.11298)x5 + (-23.0661)x6 + (0)x7 = 27.5962
(9.1287)x0 + (4.78162)x1 + (0)x2 + (9.1287)x3 + (-30.0708)x4 + (-13.0316)x5 + (0)x6 + (-30.0708)x7 = 7.33885
y[0] = -0.0643347x0 + -0.590596x1 + 1.24593x2 + 2.2599x3
y[1] = -1.52615x0 + -0.572171x1 + 0.949439x2 + 2.10266x3
----- cnt = 2 -----
pi = ( 0.516078, 0.305365, 0.178557 )
( 0.234766, 0.405545, 0.359689 )
( 0.10015, 0.259587, 0.640264 )
( 0.658121, 0.232619, 0.10926 )
( 0.356406, 0.402901, 0.240693 )
( 0.167289, 0.331627, 0.501084 )
rho = ( 0.937691, 0.21737 )
( 3.25957, 0.561741 )
( 8.98505, 1.77981 )
( 0.519478, 0.122662 )
( 1.80579, 0.31699 )
( 4.97769, 1.00435 )
Equation System :
(-69.7736)x0 + (-38.8721)x1 + (-21.8865)x2 + (-13.9787)x3 + (29.8126)x4 + (15.5031)x5 + (9.15683)x6 + (9.06244)x7 = -58.0475
(-38.8721)x0 + (-38.8721)x1 + (-11.2139)x2 + (-7.95394)x3 + (15.5031)x4 + (15.5031)x5 + (3.87375)x6 + (4.74997)x7 = -25.3591
(-21.8865)x0 + (-11.2139)x1 + (-21.8865)x2 + (0)x3 + (9.15683)x4 + (3.87375)x5 + (9.15683)x6 + (0)x7 = -26.7497
(-13.9787)x0 + (-7.95394)x1 + (0)x2 + (-13.9787)x3 + (9.06244)x4 + (4.74997)x5 + (0)x6 + (9.06244)x7 = -23.487
(29.8126)x0 + (15.5031)x1 + (9.15683)x2 + (9.06244)x3 + (-69.1762)x4 + (-31.1206)x5 + (-22.3826)x6 + (-29.9803)x7 = 59.9194
(15.5031)x0 + (15.5031)x1 + (3.87375)x2 + (4.74997)x3 + (-31.1206)x4 + (-31.1206)x5 + (-8.80826)x6 + (-12.9999)x7 = 35.0174
(9.15683)x0 + (3.87375)x1 + (9.15683)x2 + (0)x3 + (-22.3826)x4 + (-8.80826)x5 + (-22.3826)x6 + (0)x7 = 26.4939
(9.06244)x0 + (4.74997)x1 + (0)x2 + (9.06244)x3 + (-29.9803)x4 + (-12.9999)x5 + (0)x6 + (-29.9803)x7 = 7.24619
y[0] = -0.064276x0 + -0.59071x1 + 1.24641x2 + 2.25992x3
y[1] = -1.52613x0 + -0.572248x1 + 0.949028x2 + 2.10268x3
----- cnt = 3 -----
pi = ( 0.516063, 0.305376, 0.17856 )
( 0.234669, 0.405731, 0.359599 )
( 0.100142, 0.259586, 0.640272 )
( 0.658133, 0.232612, 0.109254 )
( 0.356309, 0.403083, 0.240607 )
( 0.167293, 0.331632, 0.501075 )
rho = ( 0.937746, 0.217375 )
( 3.26131, 0.561522 )
( 8.9858, 1.77988 )
( 0.519449, 0.122655 )
( 1.80655, 0.316842 )
( 4.97754, 1.00431 )
Equation System :
(-69.7585)x0 + (-38.8661)x1 + (-21.8723)x2 + (-13.9783)x3 + (29.8001)x4 + (15.4981)x5 + (9.145)x6 + (9.06208)x7 = -58.0234
(-38.8661)x0 + (-38.8661)x1 + (-11.2081)x2 + (-7.95394)x3 + (15.4981)x4 + (15.4981)x5 + (3.86884)x6 + (4.74991)x7 = -25.3501
(-21.8723)x0 + (-11.2081)x1 + (-21.8723)x2 + (0)x3 + (9.145)x4 + (3.86884)x5 + (9.145)x6 + (0)x7 = -26.7267
(-13.9783)x0 + (-7.95394)x1 + (0)x2 + (-13.9783)x3 + (9.06208)x4 + (4.74991)x5 + (0)x6 + (9.06208)x7 = -23.4863
(29.8001)x0 + (15.4981)x1 + (9.145)x2 + (9.06208)x3 + (-69.1614)x4 + (-31.1143)x5 + (-22.3687)x6 + (-29.9798)x7 = 59.8957
(15.4981)x0 + (15.4981)x1 + (3.86884)x2 + (4.74991)x3 + (-31.1143)x4 + (-31.1143)x5 + (-8.80216)x6 + (-12.9999)x7 = 35.0071
(9.145)x0 + (3.86884)x1 + (9.145)x2 + (0)x3 + (-22.3687)x4 + (-8.80216)x5 + (-22.3687)x6 + (0)x7 = 26.4713
(9.06208)x0 + (4.74991)x1 + (0)x2 + (9.06208)x3 + (-29.9798)x4 + (-12.9999)x5 + (0)x6 + (-29.9798)x7 = 7.24569
y[0] = -0.0642759x0 + -0.59071x1 + 1.24641x2 + 2.25992x3
y[1] = -1.52613x0 + -0.572248x1 + 0.949028x2 + 2.10268x3
Estimated regression equation
y[0] = -0.0642759x0 + -0.59071x1 + 1.24641x2 + 2.25992x3
y[1] = -1.52613x0 + -0.572248x1 + 0.949028x2 + 2.10268x3
variance of a[0] = ( 0.0617995, 0.0714562, 0.0938823, 0.127779 )
variance of a[1] = ( 0.0988298, 0.0728118, 0.133176, 0.120376 )
Estimated probability
pi = ( 0.516063, 0.305376, 0.17856 )
( 0.234669, 0.405731, 0.359599 )
( 0.100142, 0.259586, 0.640272 )
( 0.658133, 0.232612, 0.109254 )
( 0.356309, 0.403083, 0.240607 )
( 0.167293, 0.331632, 0.501075 )
このときの最大対数尤度は lα = -290.30 となり、比例オッズモデルとほとんど変わらない結果となりました。回帰方程式を見ても、定数項以外の係数の差はそれほど大きくないことがわかります。これは、
ということを意味しますが、πi1 が小さくなれば第一項が大きくなるため、第二項がそれに比例して大きくなるためには πi3 が大きくなる必要があります。その度合いが x に依存しないということは、性別や年齢に関係なく、重要でないと判断している人が少なければ重要と判断している人が相対的に増える (その逆も成り立つ) ことになり、男性だけは重要性の判断が両極端に分かれている、などといったことはないということを示しています。確かに、πi1 が小さいほど πi3 は大きく、逆に πi1 が大きいほど πi3 は小さくなる傾向を結果から読み取ることができます。このような傾向は常に発生するとは限らず、データによって「累積ロジットモデル」の方が当てはめがよい場合も当然ありえます。また、カテゴリに順序性がなければ名義ロジスティックモデルが最もよい選択となり、ここは場合に応じて使い分ける必要があります。
*2-1) 「確率・統計 (19) ロジスティック回帰」の「脚注 3-1」参照。
今回はかなり苦戦してようやくここまでまとめ上げることができました (いや、前回もかなり苦戦したけど)。いろいろな文献を Web 上から探しまわっていたのですが、その中で非常に参考になったサイトを参考文献に記載しています。これらがなければこのドキュメントは完成しなかったと思います。本当に感謝しています。願わくば、このドキュメントも他の方の参考になることを期待してます。
しかし、正規方程式の解き方は結局自力でやりました。最後に頼れるのは自分自身ということでしょうか。いや、おそらくもっとスマートな解法があるのだと思います。
「極値分布 ( Generalized Extreme Value (GEV) Distribution )」とは、次のような累積分布関数で表される確率密度関数です。
但し、1 + ξ[ ( x - μ ) / σ ] > 0 である必要があります。μ は「位置母数(Location Parameter)」、σ は「尺度母数(Scale Parameter)」、ξ は「形状母数(Shape Parameter)」と呼ばれるパラメータで、この中の形状母数の値によって三つのタイプに分類されます。
lim{N→∞}( ( 1 + 1 / N )N ) = e より lim{N/α→∞}( ( 1 + α / N )-N ) = lim{N/α→∞}( [ ( 1 + α / N )(N/α) ]-α ) = e-α であることを利用すると、ξ = 1 / N として N → ∞ としたとき
となります。これを「タイプ I の極値分布 (Type I Extreme Value Distribution)」または「ガンベル分布 (Gumbel Distribution)」といいます。特に、μ = 0、σ = 1 の場合は「標準ガンベル分布 (Standard Gumbel Distribution)」と呼ばれます。確率密度関数 f( x ; μ, σ ) は、
| f = dF / dx | = | exp( -exp( -( x - μ ) / σ ) )・[ -exp( -( x - μ ) / σ ) ]・( -1 / σ ) |
| = | exp( -( x - μ ) / σ - exp( -( x - μ ) / σ ) ) / σ |
となります。
ξ = 1 / α ( 但し α > 0 ) とすると、
| F( x ; μ, σ, α ) | = | exp( -[ 1 + ( x - μ ) / ασ ]-α ) |
| = | exp( -{ [ x - ( μ - ασ ) ] / ασ }-α ) |
となるので、ασ を σ に、μ - ασ を μ に改めて置き換えると
となります (但し x < μ では 0 とします)。これを「タイプ II の極値分布 (Type II Extreme Value Distribution)」または「フレシェ分布 (Fréchet Distribution)」といいます。
最後に ξ = -1 / α ( 但し α > 0 ) とすると、
となり (但し x > μ では 1 とします)、これを「タイプ III の極値分布 (Type III Extreme Value Distribution)」または「ワイブル分布 (Weibull Distribution)」といいます。
極値分布の確率密度関数の一般式は、
| f( x ; μ, σ, ξ ) | = | exp( -{ 1 + ξ[ ( x - μ ) / σ ] }-1/ξ )・( 1 / ξ ){ 1 + ξ[ ( x - μ ) / σ ] }-1/ξ-1・( ξ / σ ) |
| = | ( 1 / σ ){ 1 + ξ[ ( x - μ ) / σ ] }-1/ξ-1exp( -{ 1 + ξ[ ( x - μ ) / σ ] }-1/ξ ) |
であり、フレシェ型とワイブル型はこの式に当てはまりますが、ガンブル型はこれではなく先ほど示した式が当てはまります。
◆◇◆更新履歴◆◇◆
「累積ロジットモデル」のサンプル・プログラムに誤りがあり、処理結果もおかしくなっていたため修正をしました。
具体的には、計算前のゼロ初期化が抜けていたという初歩的なミスです。
幸い、結果が大きく外れるというほどではありませんでしたが、処理ログの連立方程式が明らかに対称になっていないことにもっと早く気付くべきでした。失礼しました (2016/05/03)。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |