
「線形重回帰モデル式 ( Linear Multiple Regression Model )」は、身長や体重といった量的な独立変数・従属変数に対して適用することができます。しかし、例えば性別や装置IDなどのような質的なデータに対しても、ダミー変数を用いることによって線形重回帰モデルを利用することができます。これらは、「分散分析法 ( ANalysis Of VAriance ; ANOVA )」と呼ばれる手法になります。
「数量化法 ( Quantification Method )」は、質的データを使った統計解析手法です。この章では、数量化法に含まれる各種の手法について紹介します。
「一元配置分散分析法 ( One-way ANOVA )」は、ダミー変数 δj を用いて次のような線形重回帰式で表すことができます。
ダミー変数 δj は、一つの式の中でただ一つだけ 1 で、他の変数は全て 0 になります。但し、p 番目のカテゴリに属する場合は全てのダミー変数は 0 です。
これは、例えば j 番目のカテゴリに属しているならば、
であり、j = p のときは
となることを意味します。
このモデル式は、要因アイテムがただ一つだけですが、ダミー変数を追加すれば、複数の要因アイテムに対しても線形重回帰式を定義することができます。
| Yi | = | α11δi11 + α12δi12 + ... + α1C1δi1C1 + ... + α21δi21 + ... + αjkδijk + ... + αRCRδiRCR + εi |
| = | Σj{1→R}( Σk{1→Cj}( αjkδijk ) ) + εi | |
| ≡ | δTα + εi |
但し、
δi = ( δi11, δi12, ... δi1C1, δi21, ... δijk, ... δiRCR )T
α = ( α11, α12, ... α1C1, α21, ... αjk, ... αRCR )T
とします。δiT を i 行目の行ベクトルとするデザイン行列を Δ としたとき、この回帰式に対する正規方程式は ΔTΔα = ΔTy となります (*1-1)。
| ΔTΔ | = | ( δ1, δ2 , ... δN ) | | | δ1T | | |
| | | δ2T | | | |||
| | | : | | | |||
| | | δNT | | | |||
| = | Σi{1→N}( δiδiT ) | ||||
であり、
| δiδiT | = |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = |
|
なので、行列 ΔTΔ の各成分は
で表されます。ここで、j, k は行に対して、u, v は列に対して変化しない添字です。よって、j 番目のアイテムの k 番目のカテゴリーに対する正規方程式の左辺は
となります。右辺の ΔTy は ( δ1, δ2 , ... δN )T と ( y1, y2, ... yN )T の内積であることから Σi{1→N}( δiyi ) なので、正規方程式は
で求めることができます。
あとはこの正規方程式を解くことで最適な係数を得ることができますが、ここで問題が一つあります。ダミー変数は通常、各アイテムごとに、要素一つに対してただ一つのカテゴリに決まります。例えば、性別に対して男と女の両方が 1 になることはありませんし、階級に分割する場合、普通なら一つの階級に決まります。
そのため、各要素において、一つのアイテムに対して次のような制約が生じます。
このとき
| Σk{1→Cj}( Σi{1→N}( δijkδiuv ) ) | = | Σi{1→N}( δiuvΣk{1→Cj}( δijk ) ) |
| = | Σi{1→N}( δiuv ) ≡ nuv |
| Σk{1→Cj}( Σi{1→N}( δijkyi ) ) | = | Σi{1→N}( yiΣk{1→Cj}( δijk ) ) |
| = | Σi{1→N}( yi ) ≡ Sy |
となります。nuv は u 番目のアイテムが v 番目のカテゴリである要素の数、Sy は従属変数の合計であり、どちらも定数です。そして、上式の上側は左辺の αuv に対する係数、下側は右辺の値です。
つまり、正規方程式の中のアイテムごとの式を辺々加えた結果は、すべてのアイテムについて等しくなることを、この結果は示しています。そのため、正規方程式は線形従属の形となり ( 具体的には、R - 1 個少ない自由度になります )、このままでは解を得ることができません。
あるアイテムの全カテゴリの係数から任意の定数を減算し、他のアイテムの全カテゴリの係数に同じ値の定数を加算しても、予測値の値に変化はありません。これは、それぞれのアイテム内でただ一つのカテゴリに対する係数だけがそのまま予測値に加算されることを考えれば明らかです。つまり、各アイテムの係数の原点は任意であることを意味するので、解は一意には決まらないことになります。
そこで、アイテムごとの最初のカテゴリ ( v = 1 ) や最後のカテゴリ ( v = Cu ) をゼロとし、対応する u 番目のアイテムの v 番目の式を消すことで、線形独立の形にします。この処理を行うことで、ようやく正規方程式を解くことが可能になります。
参考文献にあるサンプルデータを使って具体的に解いてみましょう。
| 学生No. | 大学での数学 | 高校での数学 | 高校での国語 |
|---|---|---|---|
| 1 | 56 | C | C |
| 2 | 23 | C | B |
| 3 | 59 | B | B |
| 4 | 74 | A | A |
| 5 | 49 | C | B |
| 6 | 43 | C | B |
| 7 | 39 | B | A |
| 8 | 51 | A | B |
| 9 | 37 | C | B |
| 10 | 61 | A | A |
| 11 | 43 | C | B |
| 12 | 51 | B | A |
| 13 | 61 | C | C |
| 14 | 99 | A | A |
| 15 | 23 | C | C |
| 16 | 56 | B | C |
| 17 | 49 | C | C |
| 18 | 49 | A | A |
| 19 | 75 | B | A |
| 20 | 20 | C | A |
上記データについて、大学での数学は量的なデータですが、高校での数学・国語は階級なので、これらにはダミー変数を用いる必要があります。高校での数学・国語の階級から、大学での数学の点数を予測することを考えます。ダミー変数に置き換えると、次のような形に表すことができます。
| 学生No. | 大学での数学 | 高校での数学 | 高校での国語 | ||||
|---|---|---|---|---|---|---|---|
| A | B | C | A | B | C | ||
| 1 | 56 | 1 | 1 | ||||
| 2 | 23 | 1 | 1 | ||||
| 3 | 59 | 1 | 1 | ||||
| 4 | 74 | 1 | 1 | ||||
| 5 | 49 | 1 | 1 | ||||
| 6 | 43 | 1 | 1 | ||||
| 7 | 39 | 1 | 1 | ||||
| 8 | 51 | 1 | 1 | ||||
| 9 | 37 | 1 | 1 | ||||
| 10 | 61 | 1 | 1 | ||||
| 11 | 43 | 1 | 1 | ||||
| 12 | 51 | 1 | 1 | ||||
| 13 | 61 | 1 | 1 | ||||
| 14 | 99 | 1 | 1 | ||||
| 15 | 23 | 1 | 1 | ||||
| 16 | 56 | 1 | 1 | ||||
| 17 | 49 | 1 | 1 | ||||
| 18 | 49 | 1 | 1 | ||||
| 19 | 75 | 1 | 1 | ||||
| 20 | 20 | 1 | 1 | ||||
まずは正規方程式の左辺の係数 Σi{1→N}( δijkδiuv ) を求めます。これは、j 番目のアイテムの k 番目のカテゴリと、u 番目のアイテムの v 番目のカテゴリが両方とも 1 の要素数を数えることで得られます。
| uv | |||||||
|---|---|---|---|---|---|---|---|
| 11 | 12 | 13 | 21 | 22 | 23 | ||
| jk | 11 | 5 | |||||
| 12 | 0 | 5 | |||||
| 13 | 0 | 0 | 10 | ||||
| 21 | 4 | 3 | 1 | 8 | |||
| 22 | 1 | 1 | 5 | 0 | 7 | ||
| 23 | 0 | 1 | 4 | 0 | 0 | 5 | |
明らかに Σi{1→N}( δijkδiuv ) = Σi{1→N}( δiuvδijk ) なので、表は対称行列の形となります。そのため、上の表において右上側の要素は記入していません。
次に Σi{1→N}( δijkyi ) の値を計算します。
| Σi{1→N}( δijkyi ) | ||
|---|---|---|
| jk | 11 | 334 |
| 12 | 280 | |
| 13 | 404 | |
| 21 | 468 | |
| 22 | 305 | |
| 23 | 245 | |
以上の結果から、正規方程式は次のようになります。
| 5α11 | + | 4α21 | + | α22 | = | 334 | ||||||
| 5α12 | + | 3α21 | + | α22 | + | α23 | = | 280 | ||||
| 10α13 | + | α21 | + | 5α22 | + | 4α23 | = | 404 | ||||
| 4α11 | + | 3α12 | + | α13 | + | 8α21 | = | 468 | ||||
| α11 | + | α12 | + | 5α13 | + | 7α22 | = | 305 | ||||
| α12 | + | 4α13 | + | 5α23 | = | 245 |
正規方程式の上の 3 式を辺々加えたものと、下の 3 式を辺々加えたものは等しくなります。従って、このままでは連立方程式を解くことができません。そこで、α21 = 0 とおいて、対応する 4 番目の式を削除します。
| 5α11 | + | α22 | = | 334 | ||||||||
| 5α12 | + | α22 | + | α23 | = | 280 | ||||||
| 10α13 | + | 5α22 | + | 4α23 | = | 404 | ||||||
| α11 | + | α12 | + | 5α13 | + | 7α22 | = | 305 | ||||
| α12 | + | 4α13 | + | 5α23 | = | 245 |
これを解くと次のような結果になります。
| α11 | 66.87 |
|---|---|
| α12 | 54.41 |
| α13 | 37.26 |
| α21 | 0 |
| α22 | -0.3720 |
| α23 | 8.307 |
各アイテム内のカテゴリの係数に対する原点は任意だったので、解釈しやすくするために標準化することを考えます。予測値は、次式で計算することができます。
予測値の総和は、上記の値を N 個加算した結果になります。特に、j 番目のアイテムが予測値に寄与する分は
| Σi{1→N}( Σk{1→Cj}( αjkδijk ) ) | = | Σk{1→Cj}( αjkΣi{1→N}( δijk ) ) |
| = | Σk{1→Cj}( αjknjk ) |
で求めることができます。この値がゼロになるように αjk を調整します。
サンプルデータにおいて、njk の値は次のようになります。
| n11 | 5 |
|---|---|
| n12 | 5 |
| n13 | 10 |
| n21 | 8 |
| n22 | 7 |
| n23 | 5 |
Σk{1→C1}( α1kn1k ) = 0 にするためには、調整分を x とおくと
を満たせばいいので、これを解いて
となります。j = 2 についても同様に解けば、標準化した係数 α*jkは次のようになります。
| α*11 | 17.92 |
|---|---|
| α*12 | 5.46 |
| α*13 | -11.69 |
| α*21 | -1.95 |
| α*22 | -2.32 |
| α*23 | 6.36 |
しかし、標準化した係数で予測値を求めた場合、その総計は明らかにゼロになります。各アイテムごとに求めた調整分を xj とすると、
より
| Σi{1→N}( Σj{1→R}( Σk{1→Cj}( αjkδijk ) ) ) | = | -Σi{1→N}( Σj{1→R}( Σk{1→Cj}( xjδijk ) ) ) |
| = | -Σj{1→R}( xjΣk{1→Cj}( Σi{1→N}( δijk ) ) ) | |
| = | -Σj{1→R}( xjΣk{1→Cj}( njk ) ) ) | |
| = | -NΣj{1→R}( xj ) |
よって
となります。左辺はアイテムごとの調整分を合計したもので、予測値を計算する際にこの分だけ余分に見積もられることになります。その値が右辺と等しいことになり、これは予測値の平均の符号を反転した値を意味しています。よって、元の予測値に戻すには右辺の値を減算 ( つまり予測値の平均を加算 ) すればいいわけです。ところで、予測値の平均と実測値の平均は等しいので (*1-2)、実際の計算では実測値の平均を加算しても問題ありません。
学生 No.1 の高校での数学と国語の評価はどちらも C なので、予測値は
になります。ところが、標準化した方を使うと
であり、負数になってしまいます。実測値の平均値は 50.90 なので、これを加えると 45.57 になり、元の予測値と等しくなります。
求めた結果の評価方法としては、アイテム内の係数に対する範囲 ( range )
がよく用いられます。この値が大きいほど、カテゴリによる係数の変化は大きいことになるので、予測値への影響も大きいということになります。
また、求めた係数から、アイテム j に対する量的な値 xi(j) を次式で計算することができます。
この値を使い、回帰分析法の場合と同じように「重相関係数 ( Multiple Correlation Coefficient )」や「偏相関係数 ( Partial Correlation Coefficient )」を定義することができます。xi(j) と従属変数 y の間の共分散を syj ( = sjy )、xi(j) と xi(u) の間の共分散を sju ( = suj )、xi(j) の分散を sjj、y の分散を syy とし、次のような行列 S を定義します。
| | | syy, | sy1, | sy2 | ... | syR | | | |
| | | s1y, | s11, | s12 | ... | s1R | | | |
| | | s2y, | s21, | s22 | ... | s2R | | | |
| | | : | : | : | ... | : | | | |
| S = | | sRy, | sR1, | sR2 | ... | sRR | | |
S の逆行列を求め、その要素を syy, syj, sju などと表したとき、重相関係数 R は
偏相関係数 ryj・1,2,...,j-1,j+1,...p は
で表わされます( 補足1 )。
| sjj | = | Σi{1→N}( xi(j)2 ) / N - [ Σi{1→N}( xi(j) ) / N ]2 |
| = | Σi{1→N}( [ Σk{1→Cj}( αjkδijk ) ]2 ) / N - [ Σi{1→N}( Σk{1→Cj}( αjkδijk ) ) / N ]2 |
より、[ Σk{1→Cj}( αjkδijk ) ]2 は、ただ一つの k に対して δijk = 1 となるので、そのときの k を u としたとき αju2 になります。これを i = 1 から N まで加算するから、
です。同様に考えて
だから、
となります。また、
| syj | = | Σi{1→N}( xi(j)yi ) / N - [ Σi{1→N}( xi(j) ) / N ][ Σi{1→N}( yi / N ) ] |
| = | Σi{1→N}( yiΣk{1→Cj}( αjkδijk ) ) / N - my[ Σk{1→Cj}( αjknjk ) / N ] | |
| = | Σk{1→Cj}( αjkΣi{1→N}( yiδijk ) ) / N - my[ Σk{1→Cj}( αjknjk ) / N ] |
但し、my は yi の平均値です。最後に
| sju | = | Σi{1→N}( xi(j)xi(u) ) / N - [ Σi{1→N}( xi(j) ) / N ][ Σi{1→N}( xi(u) / N ) ] |
| = | Σi{1→N}( [ Σk{1→Cj}( αjkδijk ) ][ Σv{1→Cu}( αuvδiuv ) ] ) / N - [ Σk{1→Cj}( αjknjk ) / N ][ Σv{1→Cu}( αuvnuv ) / N ] | |
| = | Σi{1→N}( Σk{1→Cj}( Σv{1→Cu}( αjkαuvδijkδiuv ) ) ) / N - [ Σk{1→Cj}( αjknjk ) / N ][ Σv{1→Cu}( αuvnuv ) / N ] | |
| = | Σk{1→Cj}( Σv{1→Cu}( αjkαuvΣi{1→N}( δijkδiuv ) ) ) / N - [ Σk{1→Cj}( αjknjk ) / N ][ Σv{1→Cu}( αuvnuv ) / N ] |
と求められ、この結果を元に重相関係数や偏相関係数を計算することができます。
先程の例を使って、実際に重相関係数と偏相関係数を計算してみます。行列 S は次のような値になります。
| | | 336.59, | 139.57, | -2.9916 | | |
| | | 139.57, | 156.07, | -16.502 | | |
| S = | | -2.9916, | -16.502, | 13.510 | | |
逆行列は次の通りです。
| | | 0.00500, | -0.00500, | -0.00500 | | |
| | | -0.00500, | 0.0124, | 0.0140 | | |
| S = | | -0.00500, | 0.0140, | 0.00900 | | |
よって、
R = [ 1 - 1 / ( 336.59 x 0.00500 ) ]1/2 = 0.637
ry1・2 = -( -0.00500 ) / ( 0.00500 x 0.0124 )1/2 = 0.635
ry2・1 = -( -0.00500 ) / ( 0.00500 x 0.00900 )1/2 = 0.236
という結果が得られます。
数量化 I 類のサンプル・プログラムを以下に示します。
template< class X > using item_type = std::map< X, unsigned int >; // アイテムの型 template< class X > using list_type = std::vector< item_type< X > >; // アイテムリストの型 using stat_type = double; // 数量の型 using size_type = size_t; // 添字の型 /* GetCategory : カテゴリ毎のリストを作成する [ s, e ) : カテゴリデータ category : 生成するカテゴリリストへのポインタ */ template< class In, class X > void GetCategory( In s, In e, item_type< X, unsigned int >* category ) { for ( ; s != e ; ++s ) { auto i = category->find( *s ); if ( i == category->end() ) category->insert( std::make_pair( *s, 1 ) ); else ++( i->second ); // カテゴリに属する要素数をカウント } } /* GetCategoryList : カテゴリ毎のリストを作成する x : アイテムごとのカテゴリデータ ( 列:アイテム 行:要素 ) category : 生成するカテゴリリストへのポインタ */ template< class X > void GetCategoryList( const Matrix< X >& x, list_type< X, unsigned int >* category ) { using size_type = typename Matrix< X >::size_type; for ( size_type c = 0 ; c < x.cols() ; ++c ) { category->push_back( item_type< X, unsigned int >() ); auto& map = category->back(); GetCategory( x.column( c ), x.column( c ).end(), &map ); } } /* GetDupMatched : 指定した二つのアイテム・カテゴリを両方持つ要素の数をカウントする x : アイテムごとのカテゴリデータ ( 列:アイテム 行:要素 ) j, u : アイテムの番号 ( x の列番号 ) k, v : カテゴリ 戻り値 : 計算したカウント */ template< class X > stat_type GetDupMatched( const Matrix< X >& x, typename Matrix< X >::size_type j, const X& k, typename Matrix< X >::size_type u, const X& v ) { using size_type = typename Matrix< X >::size_type; // 同一アイテム内で異なるカテゴリが重複する事はない if ( j == u && k != v ) return( 0 ); stat_type total = 0; for ( size_type r = 0 ; r < x.rows() ; ++r ) if ( x[r][j] == k && x[r][u] == v ) total += 1; return( total ); } /* GetMatchedYSum : 指定したアイテム・カテゴリを持つ要素の従属変数の和を求める x : アイテムごとのカテゴリデータ ( 列:アイテム 行:要素 ) ys : 従属変数のリストの先頭 j : アイテムの番号 ( x の列番号 ) k : カテゴリ 戻り値 : 計算した和 */ template< class X, class In > stat_type GetMatchedYSum( const Matrix< X >& x, In ys, typename Matrix< X >::size_type j, const X& k ) { using size_type = typename Matrix< X >::size_type; stat_type total = 0; for ( size_type r = 0 ; r < x.rows() ; ++r ) { if ( x[r][j] == k ) total += *ys; ++ys; } return( total ); } /* CreateLES : 数量化 I 類用の正規方程式の係数計算 x : アイテムごとのカテゴリデータ ( 列:アイテム 行:要素 ) ys : 従属変数のリストの先頭 category : カテゴリのリスト coef : 生成する係数行列へのポインタ a : 生成する解ベクトルへのポインタ */ template< class X, class In > void CreateLES( const Matrix< X >& x, In ys, const list_type< X, unsigned int >& category, SquareMatrix< stat_type >* coef, std::vector< stat_type >* a ) { using SM = SquareMatrix< stat_type >; using List = list_type< X, unsigned int >; SM buff; // 線形独立の形にする前の係数行列 // カテゴリの総数を求める typename List::size_type total = 0; for ( auto i = category.begin() ; i != category.end() ; ++i ) total += i->size(); // 配列・行列のリサイズ buff.assign( total, total ); a->resize( total - category.size() + 1 ); coef->assign( total - category.size() + 1, total - category.size() + 1 ); // 係数の計算 SM::size_type startR = 0; SM::size_type c = 0; for ( typename List::size_type j = 0 ; j < category.size() ; ++j ) { for ( auto k = category[j].begin() ; k != category[j].end() ; ++k ) { SM::size_type r = startR; typename List::size_type u = j; for ( auto v = k ; v != category[j].end() ; ++v ) { buff[r][c] = buff[c][r] = GetDupMatched( x, j, k->first, u, v->first ); ++r; } while ( ++u < category.size() ) { for ( auto v = category[u].begin() ; v != category[u].end() ; ++v ) { buff[r][c] = buff[c][r] = GetDupMatched( x, j, k->first, u, v->first ); ++r; } } ++c; ++startR; } } // 解ベクトルの計算 auto ai = a->begin(); for ( typename List::size_type j = 0 ; j < category.size() ; ++j ) { for ( auto k = category[j].begin() ; k != category[j].end() ; ++k ) { if ( j > 0 && k == category[j].begin() ) continue; // 各アイテムの最初のカテゴリは除外(最初のアイテムを除く) *ai++ = GetMatchedYSum( x, ys, j, k->first ); } } // 線形独立の形になるように行列を削除する std::set< SM::size_type > ignoreRC; // 削除する行列番号 SM::size_type i = 0; for ( typename List::size_type j = 0 ; j + 1 < category.size() ; ++j ) { i += category[j].size(); ignoreRC.insert( i ); } SM::size_type oR = 0; // 出力行 for ( SM::size_type r = 0 ; r < total ; ++r ) { if ( ignoreRC.find( r ) != ignoreRC.end() ) continue; SM::size_type oC = 0; // 出力列 for ( SM::size_type c = 0 ; c < total ; ++c ) { if ( ignoreRC.find( c ) != ignoreRC.end() ) continue; (*coef)[oR][oC] = buff[r][c]; ++oC; } ++oR; } } /* NormalizeCoef : 係数の標準化 x : アイテムごとのカテゴリデータ ( 列:アイテム 行:要素 ) category : カテゴリのリスト a : 標準化する係数 */ template< class X > void NormalizeCoef( const Matrix< X >& x, const list_type< X, unsigned int >& category, list_type< X, stat_type >* a ) { using size_type = typename list_type< X, unsigned int >::size_type; for ( size_type j = 0 ; j < category.size() ; ++j ) { // 減算する値の計算 Δ = Σ( a_jk * n_jk ) / N stat_type delta = 0; auto& aj = (*a)[j]; for ( auto k = category[j].begin() ; k != category[j].end() ; ++k ) delta += aj[k->first] * k->second; delta /= x.rows(); // 標準化 for ( auto k = category[j].begin() ; k != category[j].end() ; ++k ) aj[k->first] -= delta; } } /* CalcSjj : x の分散値を求める x : アイテムごとのカテゴリデータ ( 列:アイテム 行:要素 ) j : アイテム番号 category : カテゴリのリスト aj : 対象アイテムの係数 戻り値 : 求めた分散値 */ template< class X > stat_type CalcSjj( const Matrix< X >& x, typename Matrix< X >::size_type j, const list_type< X, unsigned int >& category, const item_type< X, stat_type >& aj ) { stat_type t1 = 0; stat_type t2 = 0; for ( auto k = category[j].begin() ; k != category[j].end() ; ++k ) { auto ajk = aj.find( k->first ); t1 += std::pow( ajk->second, 2 ) * k->second; // Σ( a_jk * a_jk * n_jk ) t2 += ajk->second * k->second; // Σ( a_jk * n_jk ) } return( ( t1 - std::pow( t2, 2 ) / x.rows() ) / x.rows() ); } /* CalcSyj : x と y の共分散を求める x : アイテムごとのカテゴリデータ ( 列:アイテム 行:要素 ) j : アイテム番号 category : カテゴリのリスト ys : y のリストの先頭 my : y の平均値 aj : 対象アイテムの係数 戻り値 : 求めた共分散値 */ template< class X, class In > stat_type CalcSyj( const Matrix< X >& x, typename Matrix< X >::size_type j, const list_type< X, unsigned int >& category, In ys, stat_type my, const item_type< X, stat_type >& aj ) { stat_type t1 = 0; stat_type t2 = 0; for ( auto k = category[j].begin() ; k != category[j].end() ; ++k ) { auto ajk = aj.find( k->first ); t1 += ajk->second * GetMatchedYSum( x, ys, j, k->first ); // Σ( a_jk * Σy_iδ_ijk ) t2 += ajk->second * k->second; // Σ( a_jk * n_jk ) } return( ( t1 - my * t2 ) / x.rows() ); } /* CalcSju : x 同士の共分散を求める x : アイテムごとのカテゴリデータ ( 列:アイテム 行:要素 ) j, u : アイテム番号 category : カテゴリのリスト aj, au : 対象アイテムの係数 戻り値 : 求めた共分散値 */ template< class X > stat_type CalcSju( const Matrix< X >& x, typename Matrix< X >::size_type j, typename Matrix< X >::size_type u, const list_type< X, unsigned int >& category, const item_type< X, stat_type >& aj, const item_type< X, stat_type >& au ) { const auto& cj = category[j]; const auto& cu = category[u]; stat_type t1 = 0; for ( auto cjk = cj.begin() ; cjk != cj.end() ; ++cjk ) { for ( auto cuv = cu.begin() ; cuv != cu.end() ; ++cuv ) { auto ajk = aj.find( cjk->first ); auto auv = au.find( cuv->first ); // Σ( a_jk * a_uv * Σ( δ_ijk * δ_iuv ) ) t1 += ajk->second * auv->second * GetDupMatched( x, j, cjk->first, u, cuv->first ); } } stat_type t2 = 0; for ( auto cjk = cj.begin() ; cjk != cj.end() ; ++cjk ) { auto ajk = aj.find( cjk->first ); t2 += ajk->second * cjk->second; // Σ( a_jk * n_jk ) } stat_type t3 = 0; for ( auto cuv = cu.begin() ; cuv != cu.end() ; ++cuv ) { auto auv = au.find( cuv->first ); t3 += auv->second * cuv->second; // Σ( a_uv * n_uv ) } return( ( t1 - t2 * t3 / x.rows() ) / x.rows() ); } /* CreateCovariance : 共分散行列の計算 x : アイテムごとのカテゴリデータ ( 列:アイテム 行:要素 ) category : カテゴリのリスト ys, ye : y の先頭と終端の次の位置 my : y の平均値 a : 係数 s : 共分散行列を保持する変数のポインタ */ template< class X, class In > void CreateCovariance( const Matrix< X >& x, const list_type< X, unsigned int >& category, In ys, In ye, stat_type my, const list_type< X, stat_type >& a, SquareMatrix< stat_type >* s ) { using size_type = SquareMatrix< stat_type >::size_type; s->assign( x.cols() + 1 ); // syy の計算 (*s)[0][0] = Statistics::SampleVariance< stat_type >( ys, ye ); // sjj の計算 for ( size_type j = 1 ; j < s->rows() ; ++j ) (*s)[j][j] = CalcSjj( x, j - 1, category, a[j - 1] ); // syj の計算 for ( size_type j = 1 ; j < s->rows() ; ++j ) (*s)[j][0] = (*s)[0][j] = CalcSyj( x, j - 1, category, ys, my, a[j - 1] ); // sju の計算 for ( size_type j = 1 ; j < s->rows() ; ++j ) for ( size_type u = j + 1 ; u < s->rows() ; ++u ) (*s)[j][u] = (*s)[u][j] = CalcSju( x, j - 1, u - 1, category, a[j - 1], a[u - 1] ); } /* 数量化 I 類 */ template< class X > class Quantification1 { using x_item_type = item_type< X, unsigned int >; // 独立変数用のアイテムの型 using x_list_type = list_type< X, unsigned int >; // 独立変数用のアイテムリストの型 using a_item_type = item_type< X, stat_type >; // カテゴリごとの係数の型 using a_list_type = list_type< X, stat_type >; // 全アイテムの係数リストの型 a_list_type a_; // 係数 x_list_type category_; // カテゴリリスト stat_type my_; // y の平均値 SquareMatrix< stat_type > s_; // 共分散行列 SquareMatrix< stat_type > invS_; // 共分散行列の逆行列 public: /* 独立変数と従属変数を指定して構築 独立変数ベクトル(X)は、一行に一つのベクトルの要素が、列ごとに各ベクトルが並んだ行列で表される。 ベクトルの数(標本数)は従属変数(Y)の要素数で決まる。そのため、X行列の行数とYの要素数は一致 させる必要がある。 独立ベクトルの各要素はカテゴリ(分類)データとして扱われ、内部で同一データごとに集計される。 データの型は文字列・数値データのいずれも利用できるが、浮動小数点数などは少しでも値が異なれば 違うデータとして扱われるため注意すること。 x : 独立変数(X)を保持する行列 ys, ye : 従属変数(Y)のデータ列先頭と末尾の次 solver : 連立方程式を求めるソルバー */ template< class In, class Solver > Quantification1( const Matrix< X >& x, In ys, In ye, Solver solver ); /* アイテム数を返す */ size_type itemSize() const { return( category_.size() ); } /* 指定したアイテムのカテゴリ数を返す */ size_type categorySize( size_type item ) const { return( category_.at( item ).size() ); } /* 回帰係数 ( 数量 ) を返す アイテム数や、各アイテムのカテゴリ数より大きな添字を指定した場合は std::out_of_range 例外を投げる。 item : アイテムの番号 category : カテゴリの番号 */ stat_type a( size_type item, const X& category ) const; /* カテゴリ名を返す アイテム数や、各アイテムのカテゴリ数より大きな添字を指定した場合は std::out_of_range 例外を投げる。 item : アイテムの番号 category : カテゴリの番号 */ X category( size_type item, size_type category ) const; /* 従属変数の予測値を返す xs, xe : 独立変数の先頭と末尾の次の位置 */ template< class In > stat_type expY( In xs, In xe ) const; /* 重相関係数を返す */ stat_type mcc() const { return( std::sqrt( 1.0 - 1.0 / ( s_[0][0] * invS_[0][0] ) ) ); } /* 指定したアイテム番号と y の間の偏相関係数を返す */ stat_type partialCC( size_type item ) const; }; /* Quantification1 コンストラクタ x : アイテムごとのカテゴリデータ ( 列:アイテム 行:要素 ) ys, ye : y の先頭と終端の次の位置 solver : 連立方程式を解くためのソルバ */ template< class X > template< class In, class Solver > Quantification1< X >::Quantification1( const Matrix< X >& x, In ys, In ye, Solver solver ) { ErrLib::CheckLinearModel( x, ys, ye ); // カテゴリリストの作成 GetCategoryList( x, &category_ ); // y の平均値を求める my_ = Statistics::Mean< stat_type >( ys, ye ); // 正規方程式の作成 SquareMatrix< stat_type > coef; std::vector< stat_type > aBuff; CreateLES( x, ys, category_, &coef, &aBuff ); // 係数の計算 solver( coef, aBuff.begin() ); // 足りない係数(ゼロとおいた係数)を加える auto j = category_.begin(); auto a = aBuff.begin(); a_.push_back( a_item_type() ); for ( auto k = j->begin() ; k != j->end() ; ++k ) ( a_.back() )[k->first] = *a++; for ( ++j ; j != category_.end() ; ++j ) { auto k = j->begin(); a_.push_back( a_item_type() ); ( a_.back() )[k->first] = 0; for ( ++k ; k != j->end() ; ++k ) ( a_.back() )[k->first] = *a++; } // 係数の標準化 NormalizeCoef( x, category_, &a_ ); // 共分散行列の計算 CreateCovariance( x, category_, ys, ye, my_, a_, &s_ ); MathLib::InverseMatrix( s_, &invS_, solver ); } /* Quantification1< X >::a : 指定したアイテム番号・カテゴリに対する係数 ( 数量 ) を返す item : アイテム番号 category : カテゴリ */ template< class X > typename Quantification1< X >::stat_type Quantification1< X >::a( size_type item, const X& category ) const { const std::string FUNC_NAME = "Quantification1< X >::a"; // アイテム番号が範囲外なら out_of_range 例外を投げる if ( item >= category_.size() ) throw std::out_of_range( FUNC_NAME + " : item index is out of range" ); // カテゴリが見つからなかったら out_of_range 例外を投げる auto i = a_[item].find( category ); if ( i == a_[item].end() ) throw std::out_of_range( FUNC_NAME + " : category not found" ); return( i->second ); } /* Quantification1< X >::category : 指定したアイテム・カテゴリ番号のカテゴリの値を返す item : アイテム番号 category : カテゴリ番号 戻り値 : カテゴリの値 */ template< class X > X Quantification1< X >::category( size_type item, size_type category ) const { const std::string FUNC_NAME = "Quantification1< X >::category"; // 範囲外なら out_of_range 例外を投げる if ( item >= category_.size() ) throw std::out_of_range( FUNC_NAME + " : item index is out of range" ); if ( category >= category_[item].size() ) throw std::out_of_range( FUNC_NAME + " : category index is out of range" ); const auto& categoryList = category_[item]; auto ans = categoryList.begin(); std::advance( ans, category ); return( ans->first ); } /* Quantification1< X >::expY : 予測値を返す xs xe : 独立変数の開始と終了の次の位置 戻り値 : 予測値 */ template< class X > template< class In > typename Quantification1< X >::stat_type Quantification1< X >::expY( In xs, In xe ) const { const std::string FUNC_NAME = "Quantification1< X >::expY"; ErrLib::CheckArrayLength( xs, xe, itemSize() ); stat_type ans = my_; for ( size_type item = 0 ; xs != xe ; ++xs, ++item ) { auto ajk = a_[item].find( *xs ); if ( ajk == a_[item].end() ) throw std::out_of_range( FUNC_NAME + " : category not found" ); ans += ajk->second; } return( ans ); } /* Quantification1< X >::partialCC : 指定したアイテム番号と y の間の偏相関係数を返す item : アイテム番号 */ template< class X > typename Quantification1< X >::stat_type Quantification1< X >::partialCC( size_type item ) const { const std::string FUNC_NAME = "Quantification1< X >::partialCC"; // アイテム番号が範囲外なら out_of_range 例外を投げる if ( item >= category_.size() ) throw std::out_of_range( FUNC_NAME + " : item index is out of range" ); return( -invS_[0][item + 1] / std::sqrt( invS_[0][0] * invS_[item + 1][item + 1] ) ); }
サンプル・プログラムの中では、行列が多く利用されています。この行列を表現するためのクラスが Matrix ですが、具体的な実装については省略しています。二次元配列と同様に x[r][c] で r 行 c 列の要素にアクセスできる他、列ベクトルの先頭と末尾の反復子は x.column( c ), x.column( c ).end() で取得が可能で、行や列のサイズを得るためのメンバ関数は x.rows(), x.cols() となっています。
行列には SquareMatrix というクラスも使われていますが、これは正方行列であり、行と列のサイズが等しいという制約がある以外は基本的に Matrix と同じインターフェースを持つクラスです。
item_type という型は、アイテム毎のカテゴリと該当する要素数 njk を格納するためのコンテナで、STL ( Standard Template Library ) にある連相配列の map を利用します。このコンテナにデータを登録するための関数が GetCategory で、各要素ごとのカテゴリをチェックして初めて検出した場合は新規登録し、すでに登録済のカテゴリならカウントをひとつ増加させます。アイテム毎のカテゴリを配列にしたのが list_type で、この中では可変長配列である vector が使われています。
関数 GetDupMatched は指定した二つのカテゴリを持った要素数をカウントするために利用し、この関数によって Σi{1→N}( δijkδiuv ) が得られることになります。また、GetMatchedYSum は指定したカテゴリを持った要素の従属変数 yi の和を計算するための関数で、Σi{1→N}( δijkyi ) を得るために利用します。
CreateLES は正規方程式の係数行列を求めるための関数です。先に示した計算式に従って値を求めるだけの単純な処理ですが、前述の通り、正規方程式はそのままでは線形独立の形にならないため、線形独立となるように行・列の削除を行っていることに注意してください。
係数を求めた後、Σk{1→Cj}( αjknjk ) = 0 になるように係数を標準化するための関数が NormalizeCoef です。ここまでの関数を利用することで、係数を得ることができます。
重相関係数や偏相関係数を計算するためには、係数を用いて xi(j) を求め、さらに xi(j) や yi の分散や共分散を求める必要があります。そのための関数が CalcSjj、CalcSyj、CalcSju であり、さらにその計算結果を使って共分散行列 S を構築するための関数が CreateCovariance になります。
今まで紹介した関数を使って数量化 I 類を処理するためのクラスが Quantification1 です。計算処理はコンストラクタの中で行い、処理後にメンバ関数を使って各種パラメータを出力する形で作成されています。コンストラクタ内で、最初に引数のチェックをするため ErrLib::CheckLinearModel 関数が呼び出されていますが、この関数の実装内容はサンプル・プログラム内では省略しています。行列の x と配列の [ ys, ye ) の要素数は一致している必要があるので、この関数を使ってチェックを行い、もし一致していなければ例外を投げる仕様になっています。
*1-1) この形の正規方程式の求め方は「確率・統計 (18) 一般化線形モデル」の中の「3) スコア統計量 ( Score Statistic )」で詳しく紹介しています。
*1-2) 全要素についての、実測値と予測値の差分の和は 0 になるので、実測値と予測値の平均は等しいことになります。詳細については「確率・統計 (13) 回帰分析法」の「2) 重相関係数 ( Multiple Correlation Coefficient )」をご覧ください。
「数量化 I 類」では、従属変数が量的なデータなのに対し、「数量化 II 類 ( Quantification Class 2 )」では従属変数も質的なデータを扱います。つまり、質的な独立変数から、従属変数の中のどのカテゴリに属するのかを決定する手法といえます。
従属変数が K 個のカテゴリに分かれて存在するとします。各要素がそれぞれのカテゴリごとに分類され、その i 番目のカテゴリの要素数が ni 個 ( i = 1, 2, ... K ) あるとき、i 番目のカテゴリに属する p 番目の要素が、独立変数の中の j 番目のアイテムの k 番目のカテゴリに属しているかどうかを表わすダミー変数を δip(jk) とします。
「数量化 I 類」の場合と同様に、各要素に対する量的データ Yip が、係数 ajk とダミー変数 δip(jk) を使って線形結合の形で表わせると仮定します。
このとき、全平均 mY とカテゴリ毎の平均 mYi は下式のように表わされます。
| mY | = | Σi{1→K}( Σp{1→ni}( Yip ) ) / N |
| = | Σi{1→K}( Σp{1→ni}( Σj{1→R}( Σk{1→Cj}( ajkδip(jk) ) ) ) ) / N | |
| = | Σj{1→R}( Σk{1→Cj}( ajkΣi{1→K}( Σp{1→ni}( δip(jk) ) ) ) ) / N | |
| = | Σj{1→R}( Σk{1→Cj}( ajknjk ) ) / N |
| mYi | = | Σp{1→ni}( Yip ) / ni |
| = | Σp{1→ni}( Σj{1→R}( Σk{1→Cj}( ajkδip(jk) ) ) ) / ni | |
| = | Σj{1→R}( Σk{1→Cj}( ajkΣp{1→ni}( δip(jk) ) ) ) / ni | |
| = | Σj{1→R}( Σk{1→Cj}( ajknijk ) ) / ni |
但し、
は、独立変数の j 番目のアイテムのカテゴリが k である要素の数を、
は、i 番目のカテゴリに属する要素の中で、独立変数の j 番目のアイテムのカテゴリが k である要素の数をそれぞれ表します。また、N は要素の総数になります。
これらを使って、全平均と各要素の差分の平方和 ( 全体の変動 ) ST、全平均とカテゴリ別平均の差分の平方和 ( 各カテゴリ間の変動 ) SC それぞれを計算します。
| ST | = | Σi{1→K}( Σp{1→ni}( ( Yip - mY )2 ) ) |
| = | Σi{1→K}( Σp{1→ni}( [ Σj{1→R}( Σk{1→Cj}( ajkδip(jk) ) ) - Σj{1→R}( Σk{1→Cj}( ajknjk ) ) / N ]2 ) ) | |
| = | Σi{1→K}( Σp{1→ni}( { Σj{1→R}( Σk{1→Cj}( [ δip(jk) - njk / N ]ajk ) ) }2 ) ) | |
| = | Σi{1→K}( Σp{1→ni}( Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( [ δip(jk) - njk / N ][ δip(uv) - nuv / N ]ajkauv ) ) ) ) ) ) | |
| = | Σi{1→K}( Σp{1→ni}( Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( [ δip(jk)δip(uv) - δip(jk)( nuv / N ) - ( njk / N )δip(uv) + njknuv / N2 ]ajkauv ) ) ) ) ) ) | |
| = | Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( [ Σi{1→K}( Σp{1→ni}( δip(jk)δip(uv) ) ) - ( nuv / N )Σi{1→K}( Σp{1→ni}( δip(jk) ) ) - ( njk / N )Σi{1→K}( Σp{1→ni}( δip(uv) ) ) + Σi{1→K}( Σp{1→ni}( njknuv / N2 ) ) ]ajkauv ) ) ) ) | |
| = | Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( [ Σi{1→K}( Σp{1→ni}( δip(jk)δip(uv) ) ) - ( nuv / N )njk - ( njk / N )nuv + njknuv / N ]ajkauv ) ) ) ) | |
| = | Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( [ Σi{1→K}( Σp{1→ni}( δip(jk)δip(uv) ) ) - njknuv / N ]ajkauv ) ) ) ) |
| SC | = | Σi{1→K}( ( mYi - mY )2ni ) |
| = | Σi{1→K}( [ Σj{1→R}( Σk{1→Cj}( ajknijk ) ) / ni - Σj{1→R}( Σk{1→Cj}( ajknjk ) ) / N ]2ni ) | |
| = | Σi{1→K}( { Σj{1→R}( Σk{1→Cj}( [ nijk / ni - njk / N ]ajk ) ) }2ni ) | |
| = | Σi{1→K}( Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( [ nijkniuv / ( ni )2 - ( nijk / ni )( nuv / N ) - ( njk / N )( niuv / ni ) + njknuv / N2 ]ajkauv ) ) ) )ni ) | |
| = | Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( [ Σi{1→K}( nijkniuv / ni ) - ( nuv / N )Σi{1→K}( nijk ) - ( njk / N )Σi{1→K}( niuv ) + njknuvΣi{1→K}( ni ) / N2 ]ajkauv ) ) ) ) | |
| = | Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( [ Σi{1→K}( nijkniuv / ni ) - ( nuv / N )njk - ( njk / N )nuv + njknuv / N ]ajkauv ) ) ) ) | |
| = | Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( [ Σi{1→K}( nijkniuv / ni ) - njknuv / N ]ajkauv ) ) ) ) |
各要素とカテゴリ別平均の差分の平方和 ( カテゴリ内の変動 ) SE は次式で計算できます。
このとき、
が成り立つのでした (*2-1)。つまり、全体の変動は、カテゴリ間の変動とカテゴリ内の変動に分解できることを意味しています。両辺を ST で割って
つまり、SC / ST と SE / ST の和は一定です。各カテゴリができるだけ判別しやすいようにするためには、SC / ST の方ができるだけ大きくなればいいので、この値を η2 として、η2 が最大になるような ajk を求めます。
f( jk, uv ) = Σi{1→K}( Σp{1→ni}( δip(jk)δip(uv) ) ) - njknuv / N
g( jk, uv ) = Σi{1→K}( nijkniuv / ni ) - njknuv / N
とおくと、
| η2 | = | Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( g( jk, uv )ajkauv ) ) ) ) / |
| Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( f( jk, uv )ajkauv ) ) ) ) | ||
と表すことができるので、これを ast で偏微分すると、f( jk, uv ) = f( uv, jk ), g( jk, uv ) = g( uv, jk ) であることに注意して
(∂/∂ast)Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( g( jk, uv )ajkauv ) ) ) ) = 2Σj{1→R}( Σk{1→Cj}( g( jk, st )ajk ) )
(∂/∂ast)Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( f( jk, uv )ajkauv ) ) ) ) = 2Σj{1→R}( Σk{1→Cj}( f( jk, st )ajk ) )
となることから
| ∂η2 / ∂ast | = | [ 2Σj{1→R}( Σk{1→Cj}( g( jk, st )ajk ) )Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( f( jk, uv )ajkauv ) ) ) ) - |
| Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( g( jk, uv )ajkauv ) ) ) )2Σj{1→R}( Σk{1→Cj}( f( jk, st )ajk ) ) ] / | ||
| [ Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( f( jk, uv )ajkauv ) ) ) ) ]2 | ||
| = | 2[ Σj{1→R}( Σk{1→Cj}( g( jk, st )ajk ) ) - η2Σj{1→R}( Σk{1→Cj}( f( jk, st )ajk ) ) ] / | |
| Σj{1→R}( Σk{1→Cj}( Σu{1→R}( Σv{1→Cu}( f( jk, uv )ajkauv ) ) ) ) | ||
となります。よって、∂η2 / ∂ast = 0 になるためには
である必要があります。
数量化 I 類の場合と同様に、上式で表される連立方程式には従属性が存在します。まず
| Σt{1→Cs}( f( jk, st ) ) | |
| = | Σt{1→Cs}( Σi{1→K}( Σp{1→ni}( δip(jk)δip(st) ) ) - njknst / N ) |
| = | Σi{1→K}( Σp{1→ni}( δip(jk)Σt{1→Cs}( δip(st) ) ) ) - njkΣt{1→Cs}( nst ) / N |
| = | Σi{1→K}( Σp{1→ni}( δip(jk) ) ) - njkN / N |
| = | njk - njk = 0 |
また、
| Σt{1→Cs}( g( jk, st ) ) | |
| = | Σt{1→Cs}( Σi{1→K}( nijknist / ni ) - njknst / N ) |
| = | Σi{1→K}( nijkΣt{1→Cs}( nist ) / ni ) - njk |
| = | Σi{1→K}( nijkni / ni ) - njk |
| = | njk - njk = 0 |
以上の結果から、同一アイテム内のカテゴリに対する式を辺々加えると、全ての係数はゼロになることになります。そのため、例えば各アイテムの 1 番目のカテゴリに対する係数をゼロとおいて、対応する式を削除することで従属性をなくす必要があります。
f( jk, st ), g( jk, st ) が、各アイテムごとに 1 から R まで、さらに j 番目のアイテム内ではカテゴリごとに ( 1 番目を除外して ) 2 から Cj まで順番に並んだ行列をそれぞれ F, G とします。このとき、jk と st のどちらを行、列方向にしても結果は同じであり、F, G は対称行列になることに注意してください。F, G を利用すると、正規方程式は次式で表されます。
上式は一般固有値問題と呼ばれます。F は対称行列なので、固有値分解によって QDQT で表されます。但し、Q は直交行列、D は固有値を対角成分とする対角行列です。
| D1/2 | = | | | √λ1, | 0, | ... | 0 | | |
| | | 0, | √λ2, | ... | 0 | | | ||
| | | : | : | ... | : | | | ||
| | | 0, | 0, | ... | √λM | | | ||
とすれば、QD1/2(D1/2)TQT なので、QD1/2 = P とおけば、
となって、正規方程式は
と変形できます。Q は直交行列、D1/2 は対角行列なので、固有値にゼロが含まれなければ P は逆行列を持ちます。従って、
さらに変形して
すなわち、P-1G(PT)-1 の固有値問題を解くことで η2 が固有値として求められ、その固有ベクトルは PTa なので
として固有ベクトル b を求め、
から a を求めることができます。
文献にあるデータを使って、具体的に計算してみましょう。
| 独立変数 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 従属変数 | A1 | A2 | A3 | ||||||
| B1 | B2 | B3 | B1 | B2 | B3 | B1 | B2 | B3 | |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 2 | 0 | 0 |
| 2 | 8 | 5 | 1 | 9 | 1 | 3 | 8 | 6 | 3 |
| 3 | 2 | 5 | 7 | 0 | 6 | 5 | 0 | 4 | 5 |
| 4 | 0 | 0 | 2 | 0 | 2 | 2 | 0 | 0 | 2 |
表の横方向には独立変数に対してアイテム ( A, B ) とそれぞれのカテゴリ ( 1, 2, 3 ) が並び、縦方向には従属変数に対してカテゴリ ( 1, 2, 3, 4 ) が並んでいます。例えば、従属変数のカテゴリ 2 に対して、独立変数のアイテム A, B のカテゴリがどちらも 1 である要素の数は 8 になります。
この表を、各要素に対して該当するカテゴリにフラグを立てた形で表すと、従属変数のカテゴリが 1 の要素については次のように表すことができます。
| A1 | A2 | A3 | B1 | B2 | B3 |
|---|---|---|---|---|---|
| 1 | 1 | ||||
| 1 | 1 | ||||
| 1 | 1 | ||||
| 1 | 1 |
f( jk, uv ) の一つとして f( A1, B1 ) を求めてみます。
Σi{1→K}( Σp{1→ni}( δip(A1)δip(B1) ) ) = 0 + 8 + 2 + 0 = 10
nA1nB1 / N = 30 x 30 / 90 = 10
なので、両者の差は 0 になります。同様に計算すると、
| | | 20, | -10, | -10, | 0, | 0, | 0 | | |
| | | -10, | 20, | -10, | 0, | 0, | 0 | | |
| | | -10, | -10, | 20, | 0, | 0, | 0 | | |
| | | 0, | 0, | 0, | 20, | -10, | -10 | | |
| | | 0, | 0, | 0, | -10, | 20, | -10 | | |
| F = | | 0, | 0, | 0, | -10, | -10, | 20 | | |
次に g( jk, uv ) の一つとして g( A1, B1 ) を求めてみます。
なので、g( A1, B1 ) = 8.778 - 10 = -1.22193 になります。同様に計算して
| | | 0.71925, | -0.33422, | -0.38503, | -1.22193, | 0.49465, | 0.72727 | | |
| | | -0.33422, | 0.39973, | -0.06551, | -0.46658, | -0.10160, | 0.56818 | | |
| | | -0.38503, | -0.06551, | 0.45053, | 1.68850, | -0.39305, | -1.29545 | | |
| | | -1.22193, | -0.46658, | 1.68850, | 6.57219, | -1.54947, | -5.02273 | | |
| | | 0.49465, | -0.10160, | -0.39305, | -1.54947, | 0.64037, | 0.90909 | | |
| G = | | 0.72727, | 0.56818, | -1.29545, | -5.02273, | 0.90909, | 4.11364 | | |
この結果を元に、各アイテムの第一カテゴリにあたる行・列を削除した上で一般固有値問題を解くと、最大固有値 η2 = 0.38368、対応する固有ベクトルは ( -0.014739, -0.060725, 0.16860, 0.24452 ) になります。
第一カテゴリの係数を 0 として追加し、Σk{1→Cj}( njkajk ) = 0 になるように標準化すると、係数は ( 0.025155, 0.010416, -0.035571, -0.13771, 0.030896, 0.10681 ) になります。
結果の評価には、数量化 I 類の場合と同様で、係数の範囲 ( range ) や「重相関係数 ( Multiple Correlation Coefficient )」「偏相関係数 ( Partial Correlation Coefficient )」を利用します。xi(jk) の求め方は数量化 I 類の場合と同じなので、sjj や sju は数量化 I 類の時と同じ式を利用することができます。しかし、数量化 II 類の場合は従属変数が数量ではないので、先に示した下式を利用します。
ここで同一カテゴリ内の y は全て等しいと仮定した場合、カテゴリごとの y を bi として
で計算できます。すると Yip の分散 syy は
| syy | = | Σi{1→K}( Σp{1→ni}( bi2 ) ) / N - [ Σi{1→K}( Σp{1→ni}( bi ) ) / N ]2 |
| = | Σi{1→K}( nibi2 ) / N - [ Σi{1→K}( nibi ) / N ]2 |
xi(jk) との共分散 syj は、
| syj | = | Σi{1→K}( Σp{1→ni}( biΣk{1→Cj}( ajkδip(jk) ) ) ) / N |
| - [ Σi{1→K}( Σp{1→ni}( bi ) ) / N ][ Σi{1→K}( Σp{1→ni}( Σk{1→Cj}( ajkδip(jk) ) ) ) / N ] | ||
より
| Σi{1→K}( Σp{1→ni}( biΣk{1→Cj}( ajkδip(jk) ) ) ) | |
| = | Σk{1→Cj}( ajkΣi{1→K}( biΣp{1→ni}( δip(jk) ) ) ) |
| = | Σk{1→Cj}( ajkΣi{1→K}( binijk ) ) |
| Σi{1→K}( Σp{1→ni}( bi ) ) | |
| = | Σi{1→K}( bini ) |
| Σi{1→K}( Σp{1→ni}( Σk{1→Cj}( ajkδip(jk) ) ) ) | |
| = | Σk{1→Cj}( ajkΣi{1→K}( Σp{1→ni}( δip(jk) ) ) ) |
| = | Σk{1→Cj}( ajknjk ) |
なので
| syj | = | Σk{1→Cj}( ajkΣi{1→K}( binijk ) ) / N |
| - [ Σi{1→K}( bini ) ][ Σk{1→Cj}( ajknjk ) ] / N2 | ||
となります。
先ほどのサンプルデータから行列 S を求めると、次のようになります。
| | | 0.0042631, | 0.00025662, | 0.0040065 | | |
| | | 0.00025662, | 0.00066884, | 0.00000 | | |
| | | 0.0040065, | 0.00000, | 0.010442 | | |
逆行列は
| | | 380.60, | -146.03, | -146.03 | | |
| | | -146.03, | 1551.2, | 56.027 | | |
| | | -146.03, | 56.027, | 151.79 | | |
なので、重相関係数は
また、偏相関係数は
ry1・2 = -( -146.03 ) / ( 1551.2 x 380.60 )1/2 = 0.19005
ry2・1 = -( -146.03 ) / ( 151.79 x 380.60 )1/2 = 0.60754
となります。
数量化 II 類のサンプル・プログラムを以下に示します。
/* CalcNijk : あるカテゴリに属する要素の中で、指定したアイテム・カテゴリの独立変数を持つものをカウントする x : 独立変数 ys : 従属変数の開始位置 j : 対象のアイテム番号 cjk : 対象のカテゴリ y : 要素の対象カテゴリ 戻り値 : カウントした結果 */ template< class X, class In > stat_type CalcNijk( const Matrix< X >& x, In ys, typename Matrix< X >::size_type j, const X& cjk, typename std::iterator_traits< In >::value_type y ) { using size_type = typename Matrix< X >::size_type; stat_type total = 0; for ( size_type r = 0 ; r < x.rows() ; ++r ) { if ( *ys++ != y ) continue; if ( x[r][j] == cjk ) total += 1; } return( total ); } /* CalcFjk_uv : f( jk, uv ) の計算 x : 独立変数 j, u : 対象のアイテム番号 k, v : 対象のカテゴリ反復子 戻り値 : f( jk, uv ) の値 */ template< class X > stat_type CalcFjk_uv( const Matrix< X >& x, typename list_type< X, unsigned int >::size_type j, typename item_type< X, unsigned int >::const_iterator k, typename list_type< X, unsigned int >::size_type u, typename item_type< X, unsigned int >::const_iterator v ) { stat_type t1 = GetDupMatched( x, j, k->first, u, v->first ); // Σ( δ_ijk * δ_iuv ) stat_type t2 = k->second * v->second / x.rows(); // n_jk * n_uv / N return( t1 - t2 ); } /* CalcGjk_uv : g( jk, uv ) の計算 x : 独立変数 ys : 従属変数の開始位置 j, u : 対象のアイテム番号 k, v : 対象のカテゴリ反復子 y : 要素のカテゴリリスト 戻り値 : g( jk, uv ) の値 */ template< class X, class In > stat_type CalcGjk_uv( const Matrix< X >& x, In ys, typename list_type< X, unsigned int >::size_type j, typename item_type< X, unsigned int >::const_iterator k, typename list_type< X, unsigned int >::size_type u, typename item_type< X, unsigned int >::const_iterator v, const item_type< typename std::iterator_traits< In >::value_type, unsigned int >& y ) { stat_type t1 = 0; for ( auto i = y.begin() ; i != y.end() ; ++i ) { stat_type n_ijk = CalcNijk( x, ys, j, k->first, i->first ); stat_type n_iuv = CalcNijk( x, ys, u, v->first, i->first ); t1 += n_ijk * n_iuv / i->second; // Σ( n_ijk * n_iuv / n_i ) } stat_type t2 = k->second * v->second / x.rows(); // n_jk * n_uv / N return( t1 - t2 ); } /* CreateMatrix : 行列 F, G の計算 x : 独立変数 ys : 従属変数の開始位置 xCategory : カテゴリリスト(独立変数用) yCategory : カテゴリリスト(従属変数用) f : 行列 F へのポインタ g : 行列 G へのポインタ */ template< class X, class In > void CreateMatrix( const Matrix< X >& x, In ys, const list_type< X, unsigned int >& xCategory, const item_type< typename std::iterator_traits< In >::value_type, unsigned int >& yCategory, SymmetricMatrix< stat_type >* f, SymmetricMatrix< stat_type >* g ) { using SM = SymmetricMatrix< stat_type >; using List = list_type< X, unsigned int >; SM fBuff, gBuff; // 線形独立の形にする前の係数行列 // カテゴリの総数を求める typename List::size_type total = 0; for ( auto i = xCategory.begin() ; i != xCategory.end() ; ++i ) total += i->size(); // 行列のリサイズ fBuff.assign( total, total ); gBuff.assign( total, total ); f->assign( total - xCategory.size(), total - xCategory.size() ); g->assign( total - xCategory.size(), total - xCategory.size() ); // 行列の要素を求める typename List::size_type j = 0; auto k = xCategory[j].begin(); for ( SM::size_type r = 0 ; r < fBuff.rows() ; ++r ) { typename List::size_type u = j; auto v = k; for ( SM::size_type c = r ; c < fBuff.cols() ; ++c ) { fBuff[r][c] = CalcFjk_uv( x, j, k, u, v ); gBuff[r][c] = CalcGjk_uv( x, ys, j, k, u, v, yCategory ); if ( ++v == xCategory[u].end() ) { ++u; v = xCategory[u].begin(); } } if ( ++k == xCategory[j].end() ) { ++j; k = xCategory[j].begin(); } } // 線形独立の形になるように行列を削除する std::set< SM::size_type > ignoreRC; // 削除する行列番号 SM::size_type i = 0; for ( typename List::size_type j = 0 ; j < xCategory.size() ; ++j ) { ignoreRC.insert( i ); i += xCategory[j].size(); } SM::size_type oR = 0; // 出力行 for ( SM::size_type r = 0 ; r < total ; ++r ) { if ( ignoreRC.find( r ) != ignoreRC.end() ) continue; SM::size_type oC = oR; // 出力列 for ( SM::size_type c = r ; c < total ; ++c ) { if ( ignoreRC.find( c ) != ignoreRC.end() ) continue; (*f)[oR][oC] = fBuff[r][c]; (*g)[oR][oC] = gBuff[r][c]; ++oC; } ++oR; } } /* GeneralEigenvalueProblem : 一般固有値問題 ( G - λF )a = 0 を解く f : 行列 F g : 行列 G r : 固有値を保持する行列へのポインタ (対角成分が固有値になる) q : 固有ベクトルを保持する行列へのポインタ e : 収束判定のためのしきい値 maxCnt : 収束しなかった場合の最大処理回数 solver : 連立方程式の計算オブジェクト ( 逆行列計算用 ) */ template< class Solver > void GeneralEigenvalueProblem( const SymmetricMatrix< stat_type >& f, const SymmetricMatrix< stat_type >& g, SquareMatrix< stat_type >* r, SquareMatrix< stat_type >* q, stat_type e, unsigned int maxCnt, Solver solver ) { // F を固有値分解 try { EigenLib::Householder_DoubleShiftQR( f, r, q, e, maxCnt ); } catch( ExceptionExcessLimit& ee ) { SymmetricMatrix< stat_type > eigen( f ); EigenLib::Jacobi( &eigen, q, e, maxCnt ); *r = eigen; } // P = Q√R の計算 SquareMatrix< stat_type > p; p.assign( r->rows() ); for ( SquareMatrix< stat_type >::size_type i = 0 ; i < r->rows() ; ++i ) for ( SquareMatrix< stat_type >::size_type j = 0 ; j < q->rows() ; ++j ) p[j][i] = (*q)[j][i] * std::sqrt( (*r)[i][i] ); // P の転置行列 SquareMatrix< stat_type > pt( p ); pt.transpose(); // P, Pt の逆行列 SquareMatrix< stat_type > invP, invPt; MathLib::InverseMatrix( p, &invP, solver ); MathLib::InverseMatrix( pt, &invPt, solver ); // P^-1GPt^-1 の計算 SquareMatrix< stat_type > buff; MatrixLib::mult( invP, g, &buff ); MatrixLib::mult( buff, invPt, &buff ); SymmetricMatrix< stat_type > pmGPtm; pmGPtm.assign( buff.size() ); for ( SymmetricMatrix< stat_type >::size_type i = 0 ; i < buff.rows() ; ++i ) for ( SymmetricMatrix< stat_type >::size_type j = i ; j < buff.cols() ; ++j ) pmGPtm[i][j] = buff[i][j]; // P^-1GPt^-1 を固有値分解 try { EigenLib::Householder_DoubleShiftQR( pmGPtm, r, q, e, maxCnt ); } catch( ExceptionExcessLimit& ee ) { EigenLib::Jacobi( &pmGPtm, q, e, maxCnt ); *r = pmGPtm; } for ( SquareMatrix< stat_type >::size_type j = 0 ; j < q->cols() ; ++j ) MatrixLib::multMV( invPt, q->column( j ), q->column( j ) ); } /* CalcBi : 従属変数のカテゴリごとに Y の平均を求める x : 独立変数 ys : 従属変数の開始位置 yCategory : カテゴリリスト(従属変数用) a : 求めた係数 bi : Y の平均を保持する配列へのポインタ */ template< class X, class In > void CalcBi( const Matrix< X >& x, In ys, const item_type< typename std::iterator_traits< In >::value_type, unsigned int >& yCategory, const list_type< X, stat_type >& a, item_type< typename std::iterator_traits< In >::value_type, stat_type >* bi ) { // bi の初期化 for ( auto i = yCategory.begin() ; i != yCategory.end() ; ++i ) bi->insert( std::make_pair( i->first, 0 ) ); // Y の和をカテゴリごとに求める for ( typename Matrix< X >::size_type c = 0 ; c < x.cols() ; ++c ) { const auto& ac = a[c]; In y = ys; for ( typename Matrix< X >::size_type r = 0 ; r < x.rows() ; ++r ) { auto i = ac.find( x[r][c] ); (*bi)[*y++] += i->second; } } // カテゴリごとの個数で割って平均とする for ( auto i = bi->begin() ; i != bi->end() ; ++i ) { auto y = yCategory.find( i->first ); i->second /= y->second; } } /* CalcSyy : y の分散値を求める ( 数量化 II 類専用 ) x : 独立変数 xCategory : カテゴリリスト(独立変数用) ys : 従属変数の開始位置 yCategory : カテゴリリスト(従属変数用) a : 求めた係数値 bi : 従属変数のカテゴリごとの y の平均 */ template< class X, class In > stat_type CalcSyy( const Matrix< X >& x, const list_type< X, unsigned int >& xCategory, In ys, const item_type< typename std::iterator_traits< In >::value_type, unsigned int >& yCategory, const list_type< X, stat_type >& a, const item_type< typename std::iterator_traits< In >::value_type, stat_type >& bi ) { stat_type t1 = 0; stat_type t2 = 0; for ( auto i = bi.begin() ; i != bi.end() ; ++i ) { auto j = yCategory.find( i->first ); t1 += std::pow( i->second, 2 ) * j->second; // n_i * b_i * b_i t2 += i->second * j->second; // n_i * b_i } return( ( t1 - std::pow( t2, 2 ) / x.rows() ) / x.rows() ); } /* CalcSyj : x と y の共分散を求める x : アイテムごとのカテゴリデータ ( 列:アイテム 行:要素 ) j : アイテム番号 xCategory : カテゴリのリスト ( 独立変数用 ) ys : y のリストの先頭 yCategory : カテゴリのリスト ( 従属変数用 ) aj : 対象アイテムの係数 bi : 従属変数のカテゴリごとの y の平均 */ template< class X, class In > stat_type CalcSyj( const Matrix< X >& x, typename Matrix< X >::size_type j, const list_type< X, unsigned int >& xCategory, In ys, const item_type< typename std::iterator_traits< In >::value_type, unsigned int >& yCategory, const item_type< X, stat_type >& aj, const item_type< typename std::iterator_traits< In >::value_type, stat_type >& bi ) { stat_type t1 = 0; stat_type t2 = 0; for ( auto k = xCategory[j].begin() ; k != xCategory[j].end() ; ++k ) { stat_type sum = 0; for ( auto i = bi.begin() ; i != bi.end() ; ++i ) sum += i->second * CalcNijk( x, ys, j, k->first, i->first ); auto ajk = aj.find( k->first ); t1 += sum * ajk->second; // ΣkΣi( a_jk * b_i * n_ijk ) t2 += ajk->second * k->second; // Σk( a_jk * n_jk ) } stat_type t3 = 0; for ( auto i = yCategory.begin() ; i != yCategory.end() ; ++i ) { t3 += ( bi.find( i->first ) )->second * i->second; // Σi( n_i * b_i ) } return( ( t1 - t2 * t3 / x.rows() ) / x.rows() ); } /* CreateCovariance : 共分散行列の計算 x : アイテムごとのカテゴリデータ ( 列:アイテム 行:要素 ) xCategory : カテゴリのリスト ( 独立変数用 ) ys : y のリストの先頭 yCategory : カテゴリのリスト ( 従属変数用 ) a : 求めた係数 bi : 従属変数のカテゴリごとの y の平均 s : 共分散行列を保持する変数のポインタ */ template< class X, class In > void CreateCovariance( const Matrix< X >& x, const list_type< X, unsigned int >& xCategory, In ys, const item_type< typename std::iterator_traits< In >::value_type, unsigned int >& yCategory, const list_type< X, stat_type >& a, const item_type< typename std::iterator_traits< In >::value_type, stat_type >& bi, SquareMatrix< stat_type >* s ) { using size_type = SquareMatrix< stat_type >::size_type; s->assign( x.cols() + 1 ); // syy の計算 (*s)[0][0] = CalcSyy( x, xCategory, ys, yCategory, a, bi ); // sjj の計算 for ( size_type j = 1 ; j < s->rows() ; ++j ) (*s)[j][j] = CalcSjj( x, j - 1, xCategory, a[j - 1] ); // syj の計算 for ( size_type j = 1 ; j < s->rows() ; ++j ) (*s)[j][0] = (*s)[0][j] = CalcSyj( x, j - 1, xCategory, ys, yCategory, a[j - 1], bi ); // sju の計算 for ( size_type j = 1 ; j < s->rows() ; ++j ) for ( size_type u = j + 1 ; u < s->rows() ; ++u ) (*s)[j][u] = (*s)[u][j] = CalcSju( x, j - 1, u - 1, xCategory, a[j - 1], a[u - 1] ); } /* 数量化 II 類 */ template< class X, class Y > class Quantification2 { using x_item_type = item_type< X, unsigned int >; // 独立変数用のアイテムの型 using x_list_type = list_type< X, unsigned int >; // 独立変数用のアイテムリストの型 using y_type = item_type< Y, unsigned int >; // 従属変数用のカテゴリリストの型 using bi_type = item_type< Y, stat_type >; // カテゴリごとの y 値の型 using a_item_type = item_type< X, stat_type >; // カテゴリごとの係数の型 using a_list_type = list_type< X, stat_type >; // 全アイテムの係数リストの型 a_list_type a_; // 係数 x_list_type xCategory_; // x のアイテムリスト y_type yCategory_; // y のカテゴリリスト bi_type bi_; // 予測値(yに対する数量) SquareMatrix< stat_type > s_; // 共分散行列 SquareMatrix< stat_type > invS_; // 共分散行列の逆行列 public: /* 独立変数と従属変数を指定して構築 独立変数ベクトル(X)は、一行に一つのベクトルの要素が、列ごとに各ベクトルが並んだ行列で表される。 ベクトルの数(標本数)は従属変数(Y)の要素数で決まる。そのため、X行列の行数とYの要素数は一致 させる必要がある。 独立ベクトルの各要素はカテゴリ(分類)データとして扱われ、内部で同一データごとに集計される。 データの型は文字列・数値データのいずれも利用できるが、浮動小数点数などは少しでも値が異なれば 違うデータとして扱われるため注意すること。 x : 独立変数(X)を保持する行列 ys, ye : 従属変数(Y)のデータ列先頭と末尾の次 solver : 連立方程式を求めるソルバー */ template< class In, class Solver > Quantification2( const Matrix< X >& x, In ys, In ye, Solver solver ); /* アイテム数を返す */ size_type itemSize() const { return( xCategory_.size() ); } /* 指定したアイテムのカテゴリ数を返す アイテム番号が範囲外だった場合、例外 std::out_of_range を投げる。 */ size_type categorySize( size_type item ) const { return( xCategory_.at( item ).size() ); } /* 回帰係数(数量)を返す アイテム数や、各アイテムのカテゴリ数より大きな添字を指定した場合は std::out_of_range 例外を投げる。 item : アイテムの番号 category : カテゴリ */ stat_type a( size_type item, const X& category ) const; /* 指定したアイテム・カテゴリ番号のカテゴリの値を返す item : アイテム番号 category : カテゴリ番号 */ X category( size_type item, size_type category ) const; /* 指定した独立変数から予測値(数量)を求める s, e : 独立変数の開始と末尾の次の位置 */ template< class In > stat_type expY( In s, In e ) const; /* 指定した独立変数から判別を行う s, e : 独立変数の開始と末尾の次の位置 */ template< class In > Y discriminant( In s, In e ) const; /* 重相関係数を返す */ stat_type mcc() const { return( std::sqrt( 1.0 - 1.0 / ( s_[0][0] * invS_[0][0] ) ) ); } /* 指定したアイテム番号と y の間の偏相関係数を返す */ stat_type partialCC( size_type item ) const; }; /* Quantification2 コンストラクタ x : アイテムごとのカテゴリデータ ( 列:アイテム 行:要素 ) ys, ye : y の先頭と終端の次の位置 solver : 連立方程式を解くためのソルバ */ template< class X, class Y > template< class In, class Solver > Quantification2< X, Y >::Quantification2( const Matrix< X >& x, In ys, In ye, Solver solver ) { const stat_type THRESHOLD = 1E-6; const unsigned int MAX_CNT = 10000; const std::string FUNC_NAME = "Quantification2 constructor"; ErrLib::CheckLinearModel( x, ys, ye ); GetCategoryList( x, &xCategory_ ); GetCategory( ys, ye, &yCategory_ ); SymmetricMatrix< stat_type > f, g; CreateMatrix( x, ys, xCategory_, yCategory_, &f, &g ); SquareMatrix< stat_type > r, q; GeneralEigenvalueProblem( f, g, &r, &q, THRESHOLD, MAX_CNT, solver ); // 最大固有値の固有ベクトルを抽出する if ( r.size() == 0 ) throw std::runtime_error( "No eigenvalue found" ); stat_type maxEigenValue = r[0][0]; SquareMatrix< stat_type >::size_type maxEigenVector = 0; for ( SquareMatrix< stat_type >::size_type i = 1 ; i < r.size() ; ++i ) { if ( maxEigenValue < r[i][i] ) { maxEigenValue = r[i][i]; maxEigenVector = i; } } SquareMatrix< stat_type >::const_iterator c = q.column( maxEigenVector ); for ( auto i = xCategory_.begin() ; i != xCategory_.end() ; ++i ) { auto j = i->begin(); a_.push_back( a_item_type() ); ( a_.back() )[j->first] = 0; for ( ++j ; j != i->end() ; ++j ) ( a_.back() )[j->first] = *c++; } // 係数の標準化 NormalizeCoef( x, xCategory_, &a_ ); CalcBi( x, ys, yCategory_, a_, &bi_ ); CreateCovariance( x, xCategory_, ys, yCategory_, a_, bi_, &s_ ); MathLib::InverseMatrix( s_, &invS_, solver ); } /* Quantification2< X, Y >::a : 指定したアイテム番号・カテゴリに対する係数 ( 数量 ) を返す item : アイテム番号 category : カテゴリ */ template< class X, class Y > typename Quantification2< X, Y >::stat_type Quantification2< X, Y >::a( size_type item, const X& category ) const { const std::string FUNC_NAME = "Quantification2< X, Y >::a"; // アイテム番号が範囲外なら out_of_range 例外を投げる if ( item >= xCategory_.size() ) throw std::out_of_range( FUNC_NAME + " : item index is out of range" ); // カテゴリが見つからなかったら out_of_range 例外を投げる auto i = a_[item].find( category ); if ( i == a_[item].end() ) throw std::out_of_range( FUNC_NAME + " : category not found" ); return( i->second ); } /* Quantification2< X, Y >::category : 指定したアイテム・カテゴリ番号のカテゴリの値を返す item : アイテム番号 category : カテゴリ番号 戻り値 : カテゴリの値 */ template< class X, class Y > X Quantification2< X, Y >::category( size_type item, size_type category ) const { const std::string FUNC_NAME = "Quantification2< X, Y >::category"; // 範囲外なら out_of_range 例外を投げる if ( item >= xCategory_.size() ) throw std::out_of_range( FUNC_NAME + " : item index is out of range" ); if ( category >= xCategory_[item].size() ) throw std::out_of_range( FUNC_NAME + " : category index is out of range" ); const auto& categoryList = xCategory_[item]; auto ans = categoryList.begin(); std::advance( ans, category ); return( ans->first ); } /* Quantification2< X, Y >::expY : 独立変数から y の予測値を返す s, e : 独立変数の先頭と末尾の次の位置 */ template< class X, class Y > template< class In > typename Quantification2< X, Y >::stat_type Quantification2< X, Y >::expY( In s, In e ) const { const std::string FUNC_NAME = "Quantification2< X, Y >::expY"; ErrLib::CheckArrayLength( s, e, a_.size() ); stat_type y = 0; for ( typename a_list_type::size_type j = 0 ; j < a_.size() ; ++j ) { const auto& aj = a_[j]; const auto& ajk = aj.find( *s++ ); if ( ajk == aj.end() ) throw std::out_of_range( FUNC_NAME + " : category not found" ); y += ajk->second; } return( y ); } /* Quantification2< X, Y >::discriminant : 独立変数から y のカテゴリを判別する s, e : 独立変数の先頭と末尾の次の位置 */ template< class X, class Y > template< class In > Y Quantification2< X, Y >::discriminant( In s, In e ) const { const std::string FUNC_NAME = "Quantification2< X, Y >::discriminant"; // y の予測値に最も近い bi を探す stat_type ey = expY( s, e ); auto minIndex = bi_.begin(); if ( minIndex == bi_.end() ) return( ProbDist::nan() ); stat_type minDiff = std::abs( minIndex->second - ey ); auto i = minIndex; while ( ++i != bi_.end() ) { stat_type diff = std::abs( i->second - ey ); if ( minDiff > diff ) { minDiff = diff; minIndex = i; } } return( minIndex->first ); } /* Quantification2< X, Y >::partialCC : 指定したアイテム番号と y の間の偏相関係数を返す item : アイテム番号 */ template< class X, class Y > typename Quantification2< X, Y >::stat_type Quantification2< X, Y >::partialCC( size_type item ) const { const std::string FUNC_NAME = "Quantification2< X, Y >::partialCC"; // アイテム番号が範囲外なら out_of_range 例外を投げる if ( item >= xCategory_.size() ) throw std::out_of_range( FUNC_NAME + " : item index is out of range" ); return( -invS_[0][item + 1] / std::sqrt( invS_[0][0] * invS_[item + 1][item + 1] ) ); }
CalcFjk_uv と CalcGjk_uv は、f( jk, uv )、g( jk, uv ) を計算するための関数です。CalcFjk_uv の中で使われている関数 GetDupMatched は、二つのアイテム・カテゴリ両方を持つ要素をカウントするためのもので、数量化法 I で実装されていました。CalcGjk_uv で使われている関数 CalcNijk は、指定したアイテム番号とカテゴリの要素数をカウントするためのものですが、カウントの対象が一つの ( 従属変数に対する ) カテゴリに属する要素に限定されます。
行列 F, G の計算には CreateMatrix を使います。この関数で、CalcFjk_uv と CalcGjk_uv を使って行列の要素を計算し、線形独立の形になるように行・列の削除を行います。あとは一般固有値問題 ( G - λF )a = 0 を解くだけですが、このための関数が GeneralEigenvalueProblem です。固有値分解には、Householder_DoubleShiftQR と Jacobi を使い、Householder_DoubleShiftQR での処理に失敗したら Jacobi に切り替えるようになっています。この二つの関数の実装については、「固有値問題 (1) 対称行列の固有値」の「4) ヤコビ法 ( Jacobi Eigenvalue Algorithm )」「5) ハウスホルダー変換 ( Householder Transformation )」「6) 三重対角行列とQR法」のサンプル・プログラムをご覧ください。また、逆行列の計算は関数 InverseMatrix で処理しますが、その中では連立方程式の解法が利用されています。具体的な実装方法については「数値演算法 (7) 連立方程式を解く」の中の「3) 連立方程式による逆行列の計算」で紹介されています。その他にも、行列同士の乗算に mult、行列とベクトルの乗算に multMV が使われていますが、これらの実装は省略されています。また、SquareMatrix のメンバ関数として tranpose が使われていますが、これは行列を転置するためのものです。
行列 F, G は対称行列です。そのため、対称行列を表現するためのクラス SymmetricMatrix を利用しています。このクラスは、対称行列であるという制約がある以外は基本的に Matrix と同じインターフェースを持ちます。要素の代入を右上側半分しか行わない場面がありますが、対称行列なので左下側の代入が省略できます。
CalcBi は bi を、CalcSyy と CalcSyj はそれぞれ bi を使って y の分散値と x、y の共分散を求めるための関数です。x の分散や、x 同士の共分散は、数量化法 I のサンプル・プログラムにある CalcSjj、CalcSju がそのまま流用できます。これらを使って共分散行列を求めるための関数が CreateCovarience です。
数量化 II 類を処理するためのクラス Quantification2 は、数量化法 I 専用のクラス Quantification1 と同様に、計算処理はコンストラクタの中で全て行い、後でパラメータを出力する形になっています。
今までは、各アイテム・カテゴリ毎に係数を一つだけ求めました。しかし、一つだけでは十分に判別できない場合、係数を複数にすることは簡単にできます。まず、分散比 η2 を最大にする代わりに、複数の分散比 η(p)2 の積を最大にすることを考えます。
η(p)2 は互いに無相関だと仮定すれば、上記の値を ast(q) で偏微分したとき
であり、η(p)2 ≠ 0 なので
ということになります。結局、一般固有値問題を解いた後、固有値の大きいものから順番に対応する固有ベクトルを抽出することで、複数の係数を取得することが可能ということになります。
*2-1) ST = SC + SE の証明は「確率・統計 (14) 分散分析法 ( ANOVA )」の中の「1) 一元配置分散分析法 ( One-way ANalysis Of VAriance ; One-way ANOVA )」にあります。
今までの数量化法は、数量かカテゴリかの違いはありましたが、従属変数を持ったデータに対する解析法でした。しかし「数量化 III 類 ( Quantification Class 3 ) )」では従属変数を持たないデータを扱います。
下表のように、横にカテゴリ、縦に要素を並べ、各要素がカテゴリに反応した場合に 1、そうでない場合に 0 と表すことにします。
| カテゴリ | |||||
|---|---|---|---|---|---|
| 1 | 2 | ... | R | ||
| 要 素 | 1 | 1 | 0 | ... | 0 |
| 2 | 0 | 1 | ... | 1 | |
| : | : | : | ... | : | |
| n | 1 | 1 | ... | 0 | |
要素やカテゴリを適当に並べ替えて、反応するカテゴリの種類が近い要素、あるいは反応した要素のパターンが近いカテゴリをできるだけ近くに配置することを考えます。そのためには、1 であるセルが、表の中で対角線上に並ぶようにすればよいと考えられます。しかし、それを手作業で行うのは大変ですし、作業者によってバラツキも生じてしまうでしょう。これを定量的に評価するために、要素 i に数量 xi、カテゴリ j に数量 yj を導入し、反応するカテゴリの種類が近い要素、あるいは反応した要素のパターンが近いカテゴリに対してそれぞれ値の近い xi, yj を与えるものとします。そのためには、対角線上に 1 があるように並べ替えた表の中で、上から下へ順番に xi に小さい値から大きい値 ( あるいはその逆 )、左から右に順番に yj に小さい値から大きい値 ( あるいはその逆 ) を与えれば実現できます。そのような ( x, y ) の組は相関係数 r が大きくなるため、r を最大にするような xi, yj を考えればよいということになります。
そこで、
| δij | = | 1 ( 要素 i がカテゴリ j に反応したとき ) |
| = | 0 ( その他のとき ) |
と定義したダミー変数を使い
| r | = | [ Σi{1→n}( Σj{1→R}( δij( xi - mx )( yj - my ) ) ) / N ] / |
| [ Σi{1→n}( fi( xi - mx )2 ) / N ]1/2[ Σj{1→R}( gj( yj - my )2 ) / N ]1/2 | ||
を最大化することを考えます。但し、
fi = Σj{1→R}( δij )
gj = Σi{1→n}( δij )
はそれぞれ、要素 i が反応するカテゴリの数、カテゴリ j に反応する要素の数を表しています。このとき、
が成り立ちます。また、mx, my はそれぞれ xi, yj の平均を表します。
r は xi, yj の原点には依存しません。従って、mx = 0, my = 0 とおいても一般性を失うことはありません。よって、
| r | = | [ Σi{1→n}( Σj{1→R}( δijxiyj ) ) / N ] / |
| [ Σi{1→n}( fixi2 ) / N ]1/2[ Σj{1→R}( gjyj2 ) / N ]1/2 | ||
となります。さらに、r は xi, yj の分散値にも依存しないので、分散を 1 に標準化することができます。よって、
Σi{1→n}( fixi2 ) / N = 1
Σj{1→R}( gjyj2 ) / N = 1
という制約条件の下で
を最大化することを考えればよく、「ラグランジュの未定乗数法 ( Lagrange Multiplier )」を利用することができます。
ラグランジュの未定乗数 λ, μ を用いて
を最大化します。xi, yj で偏微分して
∂F / ∂xi = Σj{1→R}( δijyj ) / N - λfixi / N = 0 --- (1)
∂F / ∂yj = Σi{1→n}( δijxi ) / N - μgjyj / N = 0 --- (2)
式 (1) に xi を辺々掛けて、i について和をとると
式 (2) に yj を辺々掛けて、j について和をとると
なので、λ = μ = Q という結果が得られます。
式 (1) より
を式 (2) に代入すると
Σi{1→n}( δij[ Σv{1→R}( δivyv ) / λfi ] ) / N - μgjyj / N = 0 より
Σi{1→n}( Σv{1→R}( δijδivyv / figj ) ) - Q2yj = 0 --- (3)
また、式 (2) より
を式 (1) に代入すると
Σj{1→R}( δij[ Σu{1→n}( δujxu ) / μgj ] ) / N - λfixi / N = 0 より
Σj{1→R}( Σu{1→n}( δijδujxu / figj ) ) - Q2xi = 0 --- (4)
となります。式 (3) の両辺に √gj を掛けて、
あるいは、式 (4) の両辺に √fi を掛けて、
と変形すれば、上式は対称行列を係数行列とする固有値問題になるので、ヤコビ法やハウスホルダー変換などを使って Q2 の最大値と、そのときの √gjyj あるいは √fixi を求めることができます。
固有値問題は二つありますが、実際には片方だけを計算すれば、式 (1) (2) を使ってもう片方を計算することができます。従って、固有値問題は次元の小さい方を解けば十分です。
ここで一つ問題があります。Q2 = 1, yj = c ( 0 以外の定数 ) ( j = 1, 2, ... R ) としたとき、式 (3) の左辺は
| Σi{1→n}( Σv{1→R}( δijδivc / figj ) ) - c | |
| = | ( c / gj )Σi{1→n}( ( δij / fi )Σv{1→R}( δiv ) ) - c |
| = | ( c / gj )Σi{1→n}( ( δij / fi )fi ) - c |
| = | ( c / gj )Σi{1→n}( δij ) - c |
| = | ( c / gj )gj - c |
| = | c - c = 0 |
となって式 (3) を満たします。従って、解の一つになるのですが、my = c ≠ 0 なので、条件を満たさない解になります。Q は相関係数だったので、0 ≤ Q2 ≤ 1 であり、1 は最大値になります。よって、求めた固有値の中で最大値は省く必要があります。これは、式 (4) に対しても同様です。
2 番目以降の固有値に対する固有ベクトルの平均はゼロになるのでしょうか。固有ベクトルは互いに直交するので、その内積はゼロになります。固有値 1 に対する固有ベクトルは c( √g1, √g2, ... √gR )T になり、その他の固有値に対する固有ベクトル ( √g1y1, √g2y2, ... √gRyR )T との内積は cΣj( gjyj ) = cmy となりますが、先程説明したようにこの値はゼロです。従って、平均は必ずゼロになります。
数量化 II 類の場合と同じように、複数の数量 xi(p), yj(p) ( p = 1, 2, ... ) を定義することが可能です。この場合、最大化する対象は数量 xi(p), yj(p) の相関係数 r(p) の積 Πp( r(p) ) となります。これを xi(p), yj(p) で偏微分すれば、p ごとに式 (1) (2) が得られ、結局は固有値の大きいものから順に固有ベクトルを取り出せば目的の数量を得ることができます。
参考文献のサンプル・データで例を示します。
| カテゴリ 性別・年齢層 | fi | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) 男 〜15 | (2) 男 16〜20 | (3) 男 21〜30 | (4) 男 31〜40 | (5) 男 41〜 | (6) 女 〜15 | (7) 女 16〜20 | (8) 女 21〜30 | (9) 女 31〜40 | (10) 女 41〜 | |||
要 素 食 品 | 1.ごはん | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 10 |
| 2.カレーライス | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 7 | |
| 3.ひやむぎ | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 3 | |
| 4.やきそば | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 8 | |
| 5.みそ汁 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 9 | |
| 6.すきやき | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 10 | |
| 7.コロッケ | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 4 | |
| 8.ハム | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 7 | |
| 9.さしみ | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 8 | |
| 10.うなぎの蒲焼 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 6 | |
| 11.卵やき | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 10 | |
| 12.ゆで卵 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 10 | |
| 13.おでん | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 8 | |
| 14.八宝菜 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 6 | |
| 15.冷奴 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 8 | |
| gj | 10 | 13 | 12 | 12 | 10 | 11 | 12 | 11 | 12 | 11 | 114 | |
上表のデータは、15 種類の食品が性別・年齢によって分けられた 10 個の層に対して好まれているかどうかを 1 / 0 で表わしたもので、各層について、好むと回答した数が平均よりも高ければ 1 、そうでなければ 0 としています。また、処理に使う fi と gj も併せて集計してあります。
カテゴリ数の方が要素数よりも少ないので、(3') の固有値問題を解くことにします。行列 { δijδiv / fi√gj√gv } を計算すると、次のような結果になります。
| | | 0.135238, | 0.118612, | 0.089222, | 0.087592, | 0.069167, | 0.113053, | 0.096830, | 0.075596, | 0.085419, | 0.065948 | | |
| | | 0.118612, | 0.131807, | 0.107165, | 0.105735, | 0.092335, | 0.108446, | 0.113837, | 0.096500, | 0.103829, | 0.088038 | | |
| | | 0.089222, | 0.107165, | 0.125430, | 0.113525, | 0.084694, | 0.080235, | 0.111541, | 0.104067, | 0.111541, | 0.095259 | | |
| | | 0.087592, | 0.105735, | 0.113525, | 0.123942, | 0.096105, | 0.078680, | 0.099636, | 0.102512, | 0.110053, | 0.106139 | | |
| | | 0.069167, | 0.092335, | 0.084694, | 0.096105, | 0.138611, | 0.092433, | 0.069480, | 0.084487, | 0.080891, | 0.132161 | | |
| | | 0.113053, | 0.108446, | 0.080235, | 0.078680, | 0.092433, | 0.148196, | 0.101994, | 0.082179, | 0.091114, | 0.088131 | | |
| | | 0.096830, | 0.113837, | 0.111541, | 0.099636, | 0.069480, | 0.101994, | 0.132374, | 0.104067, | 0.111541, | 0.080753 | | |
| | | 0.075596, | 0.096500, | 0.104067, | 0.102512, | 0.084487, | 0.082179, | 0.104067, | 0.120058, | 0.114947, | 0.095707 | | |
| | | 0.085419, | 0.103829, | 0.111541, | 0.110053, | 0.080891, | 0.091114, | 0.111541, | 0.114947, | 0.121958, | 0.091633 | | |
| | | 0.065948, | 0.088038, | 0.095259, | 0.106139, | 0.132161, | 0.088131, | 0.080753, | 0.095707, | 0.091633, | 0.141162 | | |
1 を除いた固有値は、大きい値から順に 0.126567, 0.096762, 0.041525, 0.019640, ... と続きます。最初の二つが特に大きいので、それらの固有ベクトルを抽出すると
( 0.449189, 0.226261, 0.010423, -0.133918, -0.527264, 0.244481, 0.277567, -0.068292, 0.043993, -0.554591 )T
( -0.318164, -0.098637, 0.330615, 0.233589, -0.363430, -0.561543, 0.219098, 0.323172, 0.318239, -0.155048 )T
となり、y1, y2 は
y1 = ( 0.142046, 0.062754, 0.003009, -0.038659, -0.166735, 0.073714, 0.080127, -0.020591, 0.012700, -0.167216 )T
y2 = ( -0.100612, -0.027357, 0.095440, 0.067431, -0.114927, -0.169312, 0.063248, 0.097440, 0.091868, -0.046749 )T
と求められます。この値を使って x1, x2 を求めれば
x1 = ( -0.014895, 0.399288, -0.685373, 0.311197, -0.141250, -0.014895, 0.708398, 0.378895, -0.231707, -0.217014, -0.014895, -0.014895, -0.100725, -0.172017, -0.231707 )T
x2 = ( -0.044985, 0.074875 ,-1.140215, 0.152626, 0.065549, -0.044985, -0.604664, 0.030571, 0.292466, -0.218359, -0.044985, -0.044985, -0.261231, 0.635030, 0.292466 )T
となり、x1 または y1 を横軸、x2 または y2 を縦軸にとってグラフで図示すると、次のような結果になります。
 |
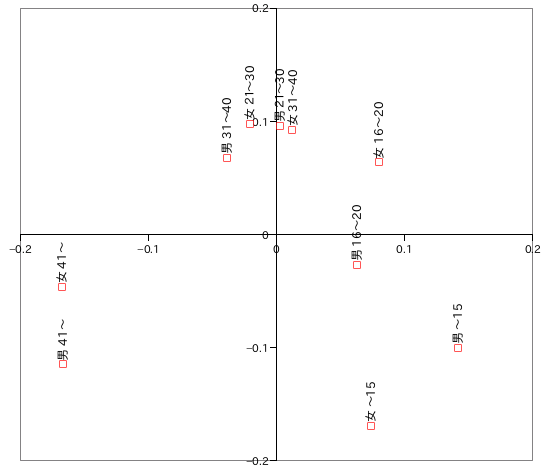 |
性別・年齢層のグラフでは、年齢層の等しい男女のプロットが近くに位置することから、性別よりも年齢の違いに大きく左右されることが分かります。横軸の正の側に年齢の若いプロットが、負の側に年齢の高いプロットが位置しているため、第一成分は年齢が低くなるほど値が大きくなっています。また、縦軸は主に 21 〜 40 の年齢層で高い値を示していることから、第二成分は中間層の年齢に対して高くなる値を意味することになります。
食品別のグラフを見ると、横軸の値はひやむぎが低く、コロッケが高いという結果になっています。つまり、ひやむぎは高齢層に人気があり、逆にコロッケは低年齢層に人気があることを示しています。中間層に人気の高い食品は第一成分がゼロ付近に集中しており、特に中間層のみに人気のある八宝菜は縦軸において最大値となっています。
男性だけに人気のあるうなぎの蒲焼は特徴的な値を示していません。このことからも、性差は数量にはほとんど反映されていないことが分かります。
数量化 III 類のサンプル・プログラムを以下に示します。
/* CalcFi : 要素 i が反応するカテゴリの数 fi を求める data : 対象データ fi : 求めた fi を保持する配列へのポインタ */ void CalcFi( const Matrix< bool >& data, std::vector< stat_type >* fi ) { fi->clear(); for ( Matrix< bool >::size_type i = 0 ; i < data.rows() ; ++i ) { stat_type total = 0; for ( Matrix< bool >::size_type j = 0 ; j < data.cols() ; ++j ) if ( data[i][j] ) total += 1; fi->push_back( total ); } } /* CalcGj : カテゴリ j に反応した要素の数 gj を求める data : 対象データ gj : 求めた gj を保持する配列へのポインタ */ void CalcGj( const Matrix< bool >& data, std::vector< stat_type >* gj ) { gj->clear(); for ( Matrix< bool >::size_type j = 0 ; j < data.cols() ; ++j ) { stat_type total = 0; for ( Matrix< bool >::size_type i = 0 ; i < data.rows() ; ++i ) if ( data[i][j] ) total += 1; gj->push_back( total ); } } /* CreateMatrixJ : yj に対する固有値問題の対称行列を計算する data : 対象データ fi : 要素 i が反応するカテゴリの数 gj : カテゴリ j に反応した要素の数 mat : 求めた行列を保持する変数へのポインタ */ void CreateMatrixJ( const Matrix< bool >& data, const std::vector< stat_type >& fi, const std::vector< stat_type >& gj, SymmetricMatrix< stat_type >* mat ) { mat->assign( data.cols() ); for ( Matrix< bool >::size_type j = 0 ; j < data.cols() ; ++j ) { for ( Matrix< bool >::size_type v = j ; v < data.cols() ; ++v ) { (*mat)[j][v] = 0; for ( Matrix< bool >::size_type i = 0 ; i < data.rows() ; ++i ) { if ( data[i][j] && data[i][v] ) (*mat)[j][v] += 1.0 / ( fi[i] * std::sqrt( gj[j] ) * std::sqrt( gj[v] ) ); } } } } /* CreateMatrixI : xi に対する固有値問題の対称行列を計算する data : 対象データ fi : 要素 i が反応するカテゴリの数 gj : カテゴリ j に反応した要素の数 mat : 求めた行列を保持する変数へのポインタ */ void CreateMatrixI( const Matrix< bool >& data, const std::vector< stat_type >& fi, const std::vector< stat_type >& gj, SymmetricMatrix< stat_type >* mat ) { mat->assign( data.rows() ); for ( Matrix< bool >::size_type i = 0 ; i < data.rows() ; ++i ) { for ( Matrix< bool >::size_type u = i ; u < data.rows() ; ++u ) { (*mat)[i][u] = 0; for ( Matrix< bool >::size_type j = 0 ; j < data.cols() ; ++j ) { if ( data[i][j] && data[u][j] ) (*mat)[i][u] += 1.0 / ( gj[j] * std::sqrt( fi[i] ) * std::sqrt( fi[u] ) ); } } } } /* 数量化 III 類 */ class Quantification3 { std::vector< std::vector< stat_type > > xi_; // 各要素の数量 std::vector< std::vector< stat_type > > yj_; // 各カテゴリの数量 std::vector< stat_type > lambda_; // 固有値 public: /* 各要素のカテゴリに対する反応を指定して構築 引数 data は、一行に一つの要素のカテゴリに対する反応が、一列に一つのカテゴリの要素ごとの反応が並んだ行列で表される。 data : 各要素のカテゴリ毎の反応を保持する行列 */ Quantification3( const Matrix< bool >& data ); /* 要素数を返す */ size_type dataSize() const; /* カテゴリ数を返す */ size_type categorySize() const; /* 固有値の数を返す */ size_type lambdaSize() const { return( lambda_.size() ); } /* 指定した要素の数量を返す 固有値数・要素数より大きな添字を指定した場合は std::out_of_range 例外を投げる。 k : 固有値の順位 ( 降順 ) i : 要素の番号 */ stat_type x( size_type k, size_type i ) const { return( xi_.at( k ).at( i ) ); } /* 指定したカテゴリの数量を返す 固有値数・カテゴリ数より大きな添字を指定した場合は std::out_of_range 例外を投げる。 k : 固有値の順位 ( 降順 ) j : カテゴリの番号 */ stat_type y( size_type k, size_type j ) const { return( yj_.at( k ).at( j ) ); } /* 指定した順位の固有値を返す 固有値の数より大きな添字を指定した場合は std::out_of_range 例外を投げる。 k : 固有値の順位 ( 降順 ) */ stat_type lambda( size_type k ) const { return( lambda_.at( k ) ); } }; /* Quantification3 コンストラクタ : データ data を指定して構築 */ Quantification3::Quantification3( const Matrix< bool >& data ) { const stat_type THRESHOLD = 1E-6; // 固有値計算用しきい値 const unsigned int MAX_CNT = 10000; // 固有値計算用最大反復回数 // fi, gj の計算 vector< stat_type > fi, gj; CalcFi( data, &fi ); CalcGj( data, &gj ); // 固有値分解を行う行列の計算 SymmetricMatrix< stat_type > mat; if ( data.cols() < data.rows() ) CreateMatrixJ( data, fi, gj, &mat ); else CreateMatrixI( data, fi, gj, &mat ); // 固有値分解 SquareMatrix< stat_type > r, q; try { EigenLib::Householder_DoubleShiftQR( mat, &r, &q, THRESHOLD, MAX_CNT ); } catch( ExceptionExcessLimit& ee ) { SymmetricMatrix< stat_type > eigen( mat ); EigenLib::Jacobi( &eigen, &q, THRESHOLD, MAX_CNT ); r = eigen; } // 固有値の取得 std::multimap< stat_type, SquareMatrix< stat_type >::size_type, std::greater< stat_type > > l; // 固有値用バッファ for ( SquareMatrix< stat_type >::size_type i = 0 ; i < r.rows() ; ++i ) l.insert( std::make_pair( r[i][i], i ) ); l.erase( l.begin() ); // 最大値(=1)は無効解なので除外 // xi, yj の取得 if ( data.cols() < data.rows() ) { for ( auto lp = l.begin() ; lp != l.end() ; ++lp ) { lambda_.push_back( lp->first ); yj_.push_back( vector< stat_type >( q.column( lp->second ), q.column( lp->second ).end() ) ); xi_.push_back( vector< stat_type >( fi.size(), 0 ) ); auto& y = yj_.back(); auto& x = xi_.back(); for ( vector< stat_type >::size_type j = 0 ; j < gj.size() ; ++j ) y[j] /= std::sqrt( gj[j] ); for ( vector< stat_type >::size_type i = 0 ; i < fi.size() ; ++i ) { for ( vector< stat_type >::size_type j = 0 ; j < gj.size() ; ++j ) if ( data[i][j] ) x[i] += y[j] / fi[i]; x[i] /= lp->first; } } } else { for ( auto lp = l.begin() ; lp != l.end() ; ++lp ) { lambda_.push_back( lp->first ); xi_.push_back( vector< stat_type >( q.column( lp->second ), q.column( lp->second ).end() ) ); yj_.push_back( vector< stat_type >( gj.size(), 0 ) ); auto& x = xi_.back(); auto& y = yj_.back(); for ( vector< stat_type >::size_type i = 0 ; i < fi.size() ; ++i ) x[i] /= std::sqrt( fi[i] ); for ( vector< stat_type >::size_type j = 0 ; j < gj.size() ; ++j ) for ( vector< stat_type >::size_type i = 0 ; i < fi.size() ; ++i ) { if ( data[i][j] ) y[j] += x[i] / gj[j]; y[j] /= lp->first; } } } } /* Quantification3::dataSize : 要素数を返す */ Quantification3::size_type Quantification3::dataSize() const { if ( xi_.size() == 0 ) return( 0 ); return( xi_[0].size() ); } /* Quantification3::categorySize : カテゴリ数を返す */ Quantification3::size_type Quantification3::categorySize() const { if ( yj_.size() == 0 ) return( 0 ); return( yj_[0].size() ); }
ここでも必要な処理は全てコンストラクタ内で行っています。最初に fi と gj を求め、その結果を使って固有値問題の式を生成します。このとき、データのカテゴリと要素でどちらの方が数が多いかを見て、xi と yj のどちらの固有値問題を計算するかを判定しています。あとは固有値問題を計算して固有値を取得し、固有値の大きいものから順に固有ベクトルを使って xi, yj を求めます。
今、N 個のデータがあり、それぞれのデータの間に親近性が定義できるとします。親近性は、データの類似度を表す指標で、値が大きいほど親近性は高いと見なされます。「数量化 IV 類 ( Quantification Class 4 )」は、この親近性を用いてデータの類似度をユークリッド距離で表わすための手法です。
データ i, j の間の親近性を eij とします。N 個のデータに対しては、eij は NP2 = N( N - 1 ) 個になります ( ユークリッド距離のように eij = eji が成り立つなら、数は半分の NC2 = N( N - 1 ) / 2 個になります )。それぞれのデータに対して数量 xi = ( xi1, xi2, ... xim )T を導入し、| xi - xj |2 が、eij を表すように決めたいとします。すなわち、親近性が小さい場合はデータが遠ざかるように、逆に大きい場合はデータが近くなるようにするわけです。そのためには、{ -eij } と { | xi - xj |2 } の内積
が大きくなるような xi を求めれば、非親和性とデータ間の距離が似通ったベクトルになることを意味するので、よいことになります。
そこで、Q を最大化するような xi を求めるのですが、求めた xi を定数倍 c ( > 1 ) すれば、明らかに Q → c2Q > Q なので、Q はいくらでも大きくできることになります。そこで制約条件として
を追加します。
「ラグランジュの未定乗数法 ( Lagrange Multiplier )」を利用して
| F | ≡ | -Σi{1→N}( Σj{1→N;j≠i}( eij| xi - xj |2 ) ) |
| - Σk{1→m}( λk{ Σi{1→N}( xik2 ) / N - [ Σi{1→N}( xik ) / N ]2 - 1 } ) | ||
| = | -Σi{1→N}( Σj{1→N;j≠i}( eijΣk{1→m}( xik - xjk )2 ) ) | |
| - Σk{1→m}( λk{ Σi{1→N}( xik2 ) / N - [ Σi{1→N}( xik ) / N ]2 - 1 } ) | ||
とおき、F を xuv で偏微分すると
| ∂F / ∂xuv | = | -Σj{1→N;j≠u}( 2euj( xuv - xjv ) - 2eju( xjv - xuv ) ) - λv[ 2xuv / N - 2Σi{1→N}( xiv ) / N2 ] |
| = | -Σj{1→N;j≠u}( 2( euj + eju )( xuv - xjv ) ) - λv[ 2xuv / N - 2Σi{1→N}( xiv ) / N2 ] |
xi の原点は任意 ( xik に定数を加えても F の値は不変 ) なので、Σi{1→N}( xiv ) = 0 が成り立つように取るとすれば、∂F / ∂xuv = 0 のとき
が成り立ちます。
とすれば明らかに huj = hju が成り立ち、上式は
-Σj{1→N;j≠u}( huj( xuv - xjv ) ) - λvxuv / N = 0
Σj{1→N;j≠u}( hujxjv ) - ( λv/ N + Σj{1→N;j≠u}( huj ) )xuv = 0
と変形することができます。huu( xuv -xuv ) = 0 なので、j = u の項を加えても Q の値には影響しません。よって、huu の値は任意にすることができて、
とおけば、先程の式が
となるので、huj を u 行 j 列の要素とする対称行列 H の固有値問題で表すことができます。
上式に xuv を掛けて辺々加えると
ここで
とおくと
| Qk | ≡ | -Σi{1→N}( Σj{1→N}( eij( xik - xjk )2 ) ) |
| = | -Σi{1→N}( Σj{1→N}( eijxik2 ) ) - Σi{1→N}( Σj{1→N}( eijxjk2 ) ) + Σi{1→N}( Σj{1→N}( eijxikxjk ) ) + Σi{1→N}( Σj{1→N}( eijxjkxik ) ) | |
| = | -Σi{1→N}( Σj{1→N}( eijxik2 ) ) - Σi{1→N}( Σj{1→N}( ejixik2 ) ) + Σi{1→N}( Σj{1→N}( eijxikxjk ) ) + Σi{1→N}( Σj{1→N}( ejixikxjk ) ) | |
| = | -Σi{1→N}( Σj{1→N}( hijxik2 ) ) + Σi{1→N}( Σj{1→N}( hijxikxjk ) ) | |
| = | -Σi{1→N}( xik2Σj{1→N}( hij ) ) + Σi{1→N}( Σj{1→N}( hijxikxjk ) ) |
Σj{1→N}( hij ) = 0 だったので、
すなわち
より
さらに
| V( xv ) | = | Σu{1→N}( xuv2 ) / N - [ Σu{1→N}( xuv ) / N ]2 |
| = | Σu{1→N}( xuv2 ) / N = 1 より |
Σu{1→N}( xuv2 ) = N
なので
となります。よって、固有値問題で得られた固有ベクトルを固有値の大きい順に抽出すれば、Q = Σk( Qk ) が最大になるような数量が得られることになります。
数量化 III 類で使用したサンプル・データを、数量化 IV 類で処理してみましょう。親近性を、各カテゴリ層での 0 / 1 の値が不一致である数の符号を反転したもの、すなわち
とします。この時、親近性からなる行列は
| | | 0, | -3, | -7, | -2, | -1, | 0, | -6, | -3, | -2, | -4, | 0, | 0, | -2, | -4, | -2 | | |
| | | -3, | 0, | -8, | -1, | -4, | -3, | -3, | -2, | -5, | -7, | -3, | -3, | -5, | -5, | -5 | | |
| | | -7, | -8, | 0, | -9, | -6, | -7, | -5, | -8, | -7, | -5, | -7, | -7, | -5, | -7, | -7 | | |
| | | -2, | -1, | -9, | 0, | -3, | -2, | -4, | -1, | -4, | -6, | -2, | -2, | -4, | -4, | -4 | | |
| | | -1, | -4, | -6, | -3, | 0, | -1, | -7, | -4, | -1, | -5, | -1, | -1, | -3, | -3, | -1 | | |
| | | 0, | -3, | -7, | -2, | -1, | 0, | -6, | -3, | -2, | -4, | 0, | 0, | -2, | -4, | -2 | | |
| | | -6, | -3, | -5, | -4, | -7, | -6, | 0, | -3, | -8, | -6, | -6, | -6, | -6, | -8, | -8 | | |
| | | -3, | -2, | -8, | -1, | -4, | -3, | -3, | 0, | -5, | -5, | -3, | -3, | -5, | -5, | -5 | | |
| | | -2, | -5, | -7, | -4, | -1, | -2, | -8, | -5, | 0, | -4, | -2, | -2, | -4, | -2, | 0 | | |
| | | -4, | -7, | -5, | -6, | -5, | -4, | -6, | -5, | -4, | 0, | -4, | -4, | -4, | -6, | -4 | | |
| | | 0, | -3, | -7, | -2, | -1, | 0, | -6, | -3, | -2, | -4, | 0, | 0, | -2, | -4, | -2 | | |
| | | 0, | -3, | -7, | -2, | -1, | 0, | -6, | -3, | -2, | -4, | 0, | 0, | -2, | -4, | -2 | | |
| | | -2, | -5, | -5, | -4, | -3, | -2, | -6, | -5, | -4, | -4, | -2, | -2, | 0, | -6, | -4 | | |
| | | -4, | -5, | -7, | -4, | -3, | -4, | -8, | -5, | -2, | -6, | -4, | -4, | -6, | 0, | -2 | | |
| | | -2, | -5, | -7, | -4, | -1, | -2, | -8, | -5, | 0, | -4, | -2, | -2, | -4, | -2, | 0 | | |
と求められます。eij = eji よりこの行列は対称行列なので、H は非対角成分の要素を 2 倍して、行 ( または列 ) の要素の和の符号を反転したものを、その行 ( または列 ) の対角成分の要素にすれば得られます。H の固有値問題を解けば、固有値は大きい順に
になるので、最初の 2 つを選んでその固有ベクトルを抽出すると
( -0.079130, -0.104865, 0.953769, -0.120448, -0.065043, -0.079130, 0.047037, -0.100454, -0.083071, -0.004688, -0.079130, -0.079130, -0.030532, -0.092115, -0.083071 )T
( 0.063815, -0.072336, 0.102411, -0.013120, 0.097818, 0.063815, -0.931893, -0.062208, 0.141163, 0.092004, 0.063815, 0.063815, 0.068069, 0.181669, 0.141163 )T
という結果が得られ、これを図示すると次のようになります。
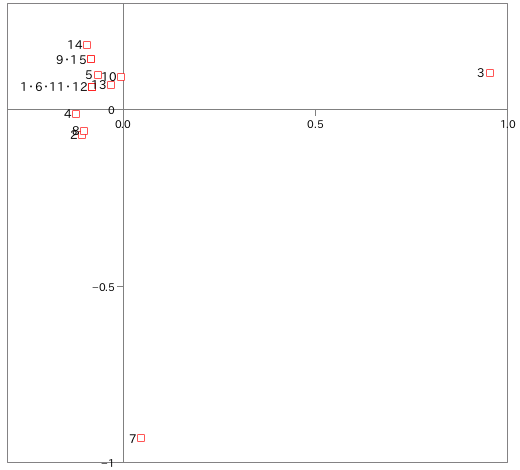 | 1.ごはん |
| 2.カレーライス | |
| 3.ひやむぎ | |
| 4.やきそば | |
| 5.みそ汁 | |
| 6.すきやき | |
| 7.コロッケ | |
| 8.ハム | |
| 9.さしみ | |
| 10.うなぎの蒲焼 | |
| 11.卵やき | |
| 12.ゆで卵 | |
| 13.おでん | |
| 14.八宝菜 | |
| 15.冷奴 |
横軸方向にはひやむぎが、縦軸方向にはコロッケが、それぞれ特徴的な値を示しています。これは、数量化 III 類の結果とも合致しています。
数量化 IV 類のサンプル・プログラムを以下に示します。
/* CreateH : 親近性からなる行列 E から H を作成する e : 親近性からなる行列 E h : 作成した行列 H を保持する変数へのポインタ */ void CreateH( const SquareMatrix< stat_type >& e, SymmetricMatrix< stat_type >* h ) { h->assign( e.size() ); // 非対角成分の計算 for ( SquareMatrix< stat_type >::size_type r = 0 ; r < e.size() ; ++r ) { for ( SquareMatrix< stat_type >::size_type c = r + 1 ; c < e.size() ; ++c ) { ( *h )[r][c] = e[r][c] + e[c][r]; } } // 対角成分の計算 for ( SquareMatrix< stat_type >::size_type r = 0 ; r < e.size() ; ++r ) { stat_type total = 0; for ( SquareMatrix< stat_type >::size_type c = 0 ; c < e.size() ; ++c ) { if ( c == r ) continue; total += ( *h )[r][c]; } ( *h )[r][r] = -total; } } /* 数量化 IV 類 */ class Quantification4 { std::vector< std::vector< stat_type > > xi_; // 各要素の数量 std::vector< stat_type > lambda_; // 固有値 public: /* 親近性を指定して構築 */ Quantification4( const SquareMatrix< stat_type >& e ); /* 要素数を返す */ size_type dataSize() const; /* 固有値の数を返す */ size_type lambdaSize() const { return( lambda_.size() ); } /* 指定した数量を返す 固有値数・要素数より大きな添字を指定した場合は std::out_of_range 例外を投げる。 k : 固有値の順位 ( 降順 ) i : 要素の番号 */ stat_type x( size_type k, size_type i ) const { return( xi_.at( k ).at( i ) ); } /* 指定した順位の固有値を返す 固有値の数より大きな添字を指定した場合は std::out_of_range 例外を投げる。 k 固有値の順位 ( 降順 ) */ stat_type lambda( size_type k ) const { return( lambda_.at( k ) ); } }; /* Quantification4 コンストラクタ : 親近性からなる行列 E を指定して構築 e : 親近性からなる行列 E */ Quantification4::Quantification4( const SquareMatrix< stat_type >& e ) { const stat_type THRESHOLD = 1E-6; // 固有値計算用しきい値 const unsigned int MAX_CNT = 10000; // 固有値計算用最大反復回数 // 行列 H の作成 SymmetricMatrix< stat_type > h; CreateH( e, &h ); // 固有値分解 SquareMatrix< stat_type > r, q; try { EigenLib::Householder_DoubleShiftQR( h, &r, &q, THRESHOLD, MAX_CNT ); } catch( ExceptionExcessLimit& ee ) { SymmetricMatrix< stat_type > eigen( h ); EigenLib::Jacobi( &eigen, &q, THRESHOLD, MAX_CNT ); r = eigen; } // 固有値の取得 multimap< stat_type, SquareMatrix< stat_type >::size_type, std::greater< stat_type > > l; // 固有値用バッファ for ( SquareMatrix< stat_type >::size_type i = 0 ; i < r.rows() ; ++i ) l.insert( std::make_pair( r[i][i], i ) ); // 数量の取得 for ( auto lp = l.begin() ; lp != l.end() ; ++lp ) { lambda_.push_back( lp->first ); xi_.push_back( vector< stat_type >( q.column( lp->second ), q.column( lp->second ).end() ) ); } } /* Quantification4::dataSize : 要素数を返す */ Quantification4::size_type Quantification4::dataSize() const { if ( xi_.size() == 0 ) return( 0 ); return( xi_[0].size() ); }
プログラムは非常に単純で、親近性 eij を i 行 j 列の要素とする行列 E から行列 H を計算し、固有値分解を行うだけの内容になっています。固有値や固有ベクトルもそのまま利用するだけなので、今までのような複雑な計算も必要ありません。最も大変なのは親近性を求める処理の方かも知れません。親近性にも様々な求め方があり、中には交換法則 eij = eji を満たさない場合もあるでしょう。
今まで紹介した数量化法の固有値問題は全て固有値が平方数であり、正値となることが保証されていました。しかし今回は、親近性の値によって固有値が負数になる場合もあります。これを避けるため、行列 H の非対角成分が全て負数となるように、任意の eij について eij - c < 0 となるような c > 0 を選び、あらかじめ減算しておいてから処理を行うことがよく行われます。このようにすると固有値は変化しますが、固有ベクトルは変化しません ( 補足 2 )。
「偏相関係数 ( Partial Correlation Coefficient )」については、「確率・統計 (13) 回帰分析法」の中の「3) 偏相関係数」でも紹介しています。xk と y を他の p - 1 個の独立変数から予測する、次のような重回帰モデル式を考えます。
y = a0 + Σj{1→p;j≠k}( ajxj )
xk = b0 + Σj{1→p;j≠k}( bjxj )
それぞれの重回帰モデルに対して、回帰係数の推定量 a^j, b^j を求めたとき、予測値からの誤差は
ui = yi - [ a^0 + Σj{1→p;j≠k}( a^jxj,i ) ]
vi = xk,i - [ b^0 + Σj{1→p;j≠k}( b^jxj,i ) ]
になります。この二つの値の相関係数
を「偏相関係数」というのでした。上式を計算するためには、重回帰分析を二度行う必要がありますが、実は「余因子 ( Cofactor )」を利用することでも計算が可能です。
「余因子」も、「数値演算法 (4) 高速フーリエ変換」の「1) 連立方程式を使った解法」で少し紹介していますが、ここではさらに深く掘り下げてみましょう。
次の公式を「余因子展開 ( Cofactor Expansion )」といいます。
detA = Σi{1→N}( ( -1 )r+i・ari・detAri )
detA = Σi{1→N}( ( -1 )i+c・aic・detAic )
Arc は、元の行列 A から r 行と c 列を除いた行列を表します。( -1 )r+c・detArc を、行列 A の要素 arc に関する「余因子」といい、除いた行列の交差する位置にある要素を「余因子」に掛ける操作を行または列が 1 から N になるまで行い、その和を求めた結果が A の行列式に等しくなることを上式は示しています。
行列式は、次の三つの性質を持ちます。
行列式の定義は、各行 ( または各列 ) から要素をひとつずつ取り出して積を計算し、その和を求めることによって得られます。但し、各行からは異なる列番号 ( 各列の場合は異なる行番号 ) から要素を取り出す必要があります。行列の大きさが N の場合、その取り出し方は、1 から N までの数値の並べ方に等しいので、N! 通りになります。また、順列は二つの要素を入れ替えること ( 互換 ) によって得られますが、この互換が奇数回だったら、積の値の符号を反転しなければなりません ( *N1-1 )。
この定義の内容から、三つの性質が成り立つことがわかります。一つの行または列が c 倍されたとき、その要素は各順列の中に必ず一つだけ含まれますから、行列式が c 倍になるのは明らかです。また、行ベクトルを分解したとき、それぞれの行列式の中にある順列のちょうど同じ位置だけが分解した値になり、他の位置は全く同じ値になります。よって、分配法則から成り立つことが理解できます。
二つの行または列を入れ替えたとき、行列式の中の順列にある二つの要素が交換された形になります。つまり、互換の回数が奇数回から偶数回、逆に偶数回から奇数回に変化するのと同じことになり、結果として符号が逆転することになるわけです。大きさが 2 の行列
| a, b | | c, d |
の行列式は ad - bc ですが、行を入れ替えた行列
| c, d | | a, b |
の行列式は cb - da となり、それぞれの積の符号が逆転するので、全体の和の符号も逆転することから考えると分かりやすいと思います。
| | | 1, | 2, | 3, | 4 | | |
| | | 2, | 3, | 4, | 1 | | |
| | | 3, | 4, | 1, | 2 | | |
| | | 4, | 1, | 2, | 3 | | |
という行列を例として「余因子展開」の成り立つことを示してみましょう。まず、第 1 列が
| | | 1 | | | | | 0 | | | | | 0 | | | | | 0 | | |
| | | 0 | | | | | 1 | | | | | 0 | | | | | 0 | | |
| | | 0 | | | | | 0 | | | | | 1 | | | | | 0 | | |
| 1| | 0 | | | +2| | 0 | | | +3| | 0 | | | +4| | 1 | | |
と分解できることから、性質の 1, 2 より行列式は次のように表すことができます。
| | | 1, | 2, | 3, | 4 | | | | | 0, | 2, | 3, | 4 | | | | | 0, | 2, | 3, | 4 | | | | | 0, | 2, | 3, | 4 | | |
| | | 0, | 3, | 4, | 1 | | | | | 1, | 3, | 4, | 1 | | | | | 0, | 3, | 4, | 1 | | | | | 0, | 3, | 4, | 1 | | |
| | | 0, | 4, | 1, | 2 | | | | | 0, | 4, | 1, | 2 | | | | | 1, | 4, | 1, | 2 | | | | | 0, | 4, | 1, | 2 | | |
| 1| | 0, | 1, | 2, | 3 | | | +2| | 0, | 1, | 2, | 3 | | | +3| | 0, | 1, | 2, | 3 | | | +4| | 1, | 1, | 2, | 3 | | |
さらに行を順番に入れ替えて、左上が 1 の要素になるようにすると、性質 3 より符号が変わり、次のように表すことができます。
| | | 1, | 2, | 3, | 4 | | | | | 1, | 3, | 4, | 1 | | | | | 1, | 4, | 1, | 2 | | | | | 1, | 1, | 2, | 3 | | |
| | | 0, | 3, | 4, | 1 | | | | | 0, | 2, | 3, | 4 | | | | | 0, | 2, | 3, | 4 | | | | | 0, | 2, | 3, | 4 | | |
| | | 0, | 4, | 1, | 2 | | | | | 0, | 4, | 1, | 2 | | | | | 0, | 3, | 4, | 1 | | | | | 0, | 3, | 4, | 1 | | |
| 1| | 0, | 1, | 2, | 3 | | | -2| | 0, | 1, | 2, | 3 | | | +3| | 0, | 1, | 2, | 3 | | | -4| | 0, | 4, | 1, | 2 | | |
行列式は、各行から一つずつ要素を選んで積を作るのでした。上の 4 つの行列は、第一列の要素が先頭を除いて全てゼロなので、先頭以外の要素を選んだ場合は和に反映されません。よって、第一列からは先頭の要素が選ばれた場合だけが有効になり、あとは右下の 3 x 3 の部分の順列から行列式が決まります。つまり、4 x 4 行列の行列式が、3 x 3 の部分行列の行列式に等しいことになります。
以上の操作を一般化したのが、先ほど示した「余因子展開」の式になります。
行列 A の要素 arc に関する余因子を Arc と表し、r 行 c 列の要素として Acr ( rc ではないことに注意 ) を持つ行列を A~ としたとき、この行列を「余因子行列 ( Adjugate Matrix )」といいます。このとき、次の関係が成り立ちます。
上式にある δrc は「クロネッカのデルタ (Kronecker Delta)」と呼ばれ、r = c のとき 1、それ以外は 0 になります。
r = c のとき、上式は「余因子展開」と同じ式になり、
で成り立つことが分かります。r ≠ c の場合、
なので、ちょうど A の c 行の要素が r 行の要素に置き換わった行列の「余因子展開」に等しくなります。つまり、r 行と c 行が等しい行列の行列式に等しいことになりますが、行ベクトルが線形従属であることになるので、その値はゼロです ( *N1-2 )。
上式を行列で表すと
但し、E は単位行列です。以上のことから、逆行列 A-1 と余因子行列 A~ の関係式として次の結果が得られます。
連立方程式は、行列を使って次のように表すことができます。
連立方程式の解ベクトル x を、余因子行列を使って表すと、
で、各要素は
となりますが、この式の分子はちょうど、A の i 列を b で置き換えた行列の余因子展開と等しくなります。つまり、連立方程式の解は、次のように表すことができます。
| (i) | ||||||||
| | | a11, | a12, | ... | b1 | ... | a1N | | | |
| | | a21, | a22, | ... | b2 | ... | a2N | | | |
| | | : | : | ... | : | ... | : | | | |
| | | aN1, | aN2, | ... | bN | ... | aNN | | | |
| xi = | --------------------------- | |||||||
| | | a11, | a12, | ... | a1i | ... | a1N | | | |
| | | a21, | a22, | ... | a2i | ... | a2N | | | |
| | | : | : | ... | : | ... | : | | | |
| | | aN1, | aN2, | ... | aNi | ... | aNN | | | |
上式の分子は、係数行列 A の第 i 列を b で置き換えた行列の行列式です。この式を「クラメルの公式 ( Cramer's Rule )」といいます。
重回帰モデルにおいて、正規方程式の係数行列は独立変数からなる共分散行列でした。また、右辺のベクトルは独立変数と従属変数の共分散となっていました。共分散行列の 1 行目と 1 列目に、従属変数 y と独立変数 xi の共分散を追加した行列を考えます ( 対角成分は、従属変数の分散とします )。つまり、右辺のベクトルを 1 行目と 1 列目に追加した行列となります。
| | | syy, | sy1, | sy2 | ... | syp | | | |
| | | s1y, | s11, | s12 | ... | s1p | | | |
| | | s2y, | s21, | s22 | ... | s2p | | | |
| | | : | : | : | ... | : | | | |
| S = | | spy, | ap1, | sp2 | ... | spp | | |
上記の行列について、syy は従属変数 y の分散、syc は c 番目の独立変数 xc と従属変数 y の共分散、そして src は r 番目と c 番目の独立変数の共分散をそれぞれ表わしています。共分散の定義から明らかに
syi = siy ( i = 1, 2, ... p )
src = scr ( r, c = 1, 2, ... p )
が成り立つので、S は対称行列になります。
クラメルの公式と見比べてみると、分母は係数行列の行列式なので、行列 S の syy に関する余因子 S11 に等しいことが分かります ( S11 = ( -1 )1+1・detS11 = detS11 なので、符号に変化はないことに注意してください )。分子の方は少し複雑ですが、行列 S の 1 行目を削除し、i 番目の独立変数 xi がある i + 1 列目を削除した上で、1 列目を隣の列と交換する操作を i - 1 回繰り返すと、S1(i+1) と同じ行列になります。
S1(i+1) = ( -1 )i+2・detS1(i+1)
(分子) = ( -1 )i-1・detS1(i+1)
なので、符号が反転することになり、まとめると
となり、係数を余因子を使って表わすことができます。
偏相関係数に話を戻すと、二つの重回帰モデルの係数は、余因子を使って次のように表すことができます。
| a^j | = | -S(k+1)(k+1),1(j+1) / S(k+1)(k+1),11 ( j < k ) |
| = | -S(k+1)(k+1),1j / S(k+1)(k+1),11 ( j > k ) | |
| b^j | = | -S11,kj / S11,kk |
Aji,vu は、最初に j 行 i 列を削除して余因子を計算し、次に v 行 u 列を削除して余因子を計算した結果です。余因子展開より
なので、
| Aji | = | ( -1 )j+idetAji |
| = | Σv{1→p}( ( -1 )j+i+v+u・avu・detAji,vu ) |
となり、
とおけば、
が成り立ちます。ここで気を付けなければならないのは、2 回目に余因子を計算する時に削除する行列の位置です。1 度行と列を削除しているので、j < v, i < u の場合、削除する行・列は、削除前の行列において一つ大きい添字の要素になります。aj の式が j と k の大小関係によって異なるのは、このためです。
実際に、a^j と b^j を求めてみましょう。a^j において、j < k のとき
| a^j = |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | ( -1 )j-1detS(k+1)(k+1),1(j+1) / ( -1 )-(k+1)-(k+1)-1-1S(k+1)(k+1),11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | ( -1 )j-1( -1 )-(k+1)-(k+1)-1-(j+1)S(k+1)(k+1),1(j+1) / S(k+1)(k+1),11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | -S(k+1)(k+1),1(j+1) / S(k+1)(k+1),11 |
j > k のとき
| a^j = |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | ( -1 )j-2detS(k+1)(k+1),1j / ( -1 )-(k+1)-(k+1)-1-1S(k+1)(k+1),11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | ( -1 )j-2( -1 )-(k+1)-(k+1)-1-jS(k+1)(k+1),1j / S(k+1)(k+1),11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | -S(k+1)(k+1),1j / S(k+1)(k+1),11 |
となります。また、b^j は、j < k のとき
| b^j = |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | ( -1 )k-j-1detS11,kj / ( -1 )-(k+1)-(k+1)-1-1S(k+1)(k+1),11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | ( -1 )k-j-1( -1 )-1-1-k-jS11,kj / S(k+1)(k+1),11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | -S11,kj / S(k+1)(k+1),11 |
j > k のとき
| b^j = |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | ( -1 )j-k-1detS11,kj / ( -1 )-(k+1)-(k+1)-1-1S(k+1)(k+1),11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | ( -1 )j-k-1( -1 )-1-1-k-jS11,kj / S(k+1)(k+1),11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | -S11,kj / S(k+1)(k+1),11 |
と求められます。
この係数を使い、偏相関係数を計算します。
は、ui, vi の平均をそれぞれ mu, mv としたとき、mu = 0, mv = 0 が成り立つことを利用して削除していますが、ここではあえてこれらの値を復活させます。yi の平均を my、xj,i の平均を mj として、
| mu | = | Σi{1→N}( yi - [ a^0 + Σj{1→p;j≠k}( a^jxj,i ) ] ) / N |
| = | Σi{1→N}( yi ) / N - [ Na^0 + Σj{1→p;j≠k}( a^jΣi{1→N}( xj,i ) ) ] / N | |
| = | my - [ a^0 + Σj{1→p;j≠k}( a^jmj ) ] | |
| mv | = | Σi{1→N}( xk,i - [ b^0 + Σj{1→p;j≠k}( b^jxj,i ) ] ) / N |
| = | Σi{1→N}( xk,i ) / N - [ Nb^0 + Σj{1→p;j≠k}( b^jΣi{1→N}( xj,i ) ) ] / N | |
| = | mk - [ b^0 + Σj{1→p;j≠k}( b^jmj ) ] |
となることから、
| Σi{1→N}( ( ui - mu )2 ) / N | = | Σi{1→N}( { { yi - [ a^0 + Σj{1→p;j≠k}( a^jxj,i ) ] } - { my - [ a^0 + Σj{1→p;j≠k}( a^jmj ) ] } }2 ) / N |
| = | Σi{1→N}( [ ( yi - my ) - Σj{1→p;j≠k}( a^j( xj,i - mj ) ) ]2 ) / N | |
| = | Σi{1→N}( ( yi - my )2 - 2Σj{1→p;j≠k}( a^j( yi - my )( xj,i - mj ) ) + [ Σj{1→p;j≠k}( a^j( xj,i - mj ) ) ]2 ) / N | |
| = | Σi{1→N}( ( yi - my )2 ) / N - 2Σj{1→p;j≠k}( a^jΣi{1→N}( ( yi - my )( xj,i - mj ) ) / N ) | |
| + Σu{1→p;u≠k}( a^uΣj{1→p;j≠k}( a^jΣi{1→N}( ( xu,i - mu )( xj,i - mj ) ) / N ) ) | ||
| = | syy - 2Σj{1→p;j≠k}( a^jsyj ) + Σu{1→p;u≠k}( a^uΣj{1→p;j≠k}( a^jsuj ) ) | |
| Σi{1→N}( ( vi - mv )2 ) / N | = | Σi{1→N}( { { xk,i - [ b^0 + Σj{1→p;j≠k}( b^jxj,i ) ] } - { mk - [ b^0 + Σj{1→p;j≠k}( b^jmj ) ] } }2 ) / N |
| = | skk - 2Σj{1→p;j≠k}( b^jskj ) + Σu{1→p;u≠k}( b^uΣj{1→p;j≠k}( b^jsuj ) ) |
| Σi{1→N}( ( ui - mu )( vi - mv ) ) / N | = | Σi{1→N}( [ ( yi - my ) - Σj{1→p;j≠k}( a^j( xj,i - mj ) ) ][ ( xk,i - mk ) - Σj{1→p;j≠k}( b^j( xj,i - mj ) ) ] ) / N |
| = | syk - Σj{1→p;j≠k}( b^jsyj ) - Σj{1→p;j≠k}( a^jsjk ) + Σu{1→p;u≠k}( a^uΣj{1→p;j≠k}( b^jsuj ) ) |
と計算することができます。但し、syy, sjj はそれぞれ yi, xj,i の分散、syj, suj はそれぞれ yi と xj,i、xu,i と xj,i の共分散を表します。
まずは厄介な入れ子構造の和 Σu{1→p;u≠k}( a^uΣj{1→p;j≠k}( a^jsuj ) ) を計算します。
| Σj{1→p;j≠k}( a^jsuj ) - suy | = | Σj{1→p;j≠k}( a^jΣi{1→N}( ( xu,i - mu )( xj,i - mj ) ) / N ) - Σi{1→N}( ( xu,i - mu )( yi - my ) ) / N |
| = | Σi{1→N}( ( xu,i - mu )[ Σj{1→p;j≠k}( a^j( xj,i - mj ) ) - ( yi - my ) ] ) / N | |
| = | Σi{1→N}( ( xu,i - mu ){ [ Σj{1→p;j≠k}( a^jxj,i ) - yi ] - [ Σj{1→p;j≠k}( a^jmj ) - my ] } ) / N |
| Σj{1→p;j≠k}( a^jmj ) - my | = | Σj{1→p;j≠k}( a^jΣi{1→N}( xj,i ) / N ) - Σi{1→N}( yi ) / N |
| = | Σi{1→N}( Σj{1→p;j≠k}( a^jxj,i ) - yi ) / N |
和の中は従属変数の予測値と実測値の差分を表しているので、これを εi とおくと、
| Σj{1→p;j≠k}( a^jsuj ) - suy | = | Σi{1→N}( ( xu,i - mu )εi - Σi{1→N}( εi ) / N ) / N |
| = | Σi{1→N}( xu,iεi ) / N - muΣi{1→N}( εi ) / N - Σi{1→N}( Σi{1→N}( εi ) ) / N2 |
になります。Σi{1→N}( εi ) = 0、Σi{1→N}( xu,iεi ) = 0 なので ( *N1-3 )、上式は 0 になり、
という結果が得られます。同様の考え方により
Σu{1→p;u≠k}( b^uΣj{1→p;j≠k}( b^jsuj ) ) = Σu{1→p;u≠k}( b^usuk )
Σu{1→p;u≠k}( a^uΣj{1→p;j≠k}( b^jsuj ) ) = Σu{1→p;u≠k}( a^usuk )
となることから、
Σi{1→N}( ( ui - mu )2 ) / N = syy - Σj{1→p;j≠k}( a^jsyj )
Σi{1→N}( ( vi - mv )2 ) / N = skk - Σj{1→p;j≠k}( b^jskj )
Σi{1→N}( ( ui - mu )( vi - mv ) ) / N = syk - Σj{1→p;j≠k}( b^jsyj )
と非常にシンプルな式になります。
ですが、余因子展開の式から
なので
| Σj{1→p;j≠k}( a^jsyj ) | = | ( S(k+1)(k+1),11syy - S(k+1)(k+1) ) / S(k+1)(k+1),11 |
| = | syy - S(k+1)(k+1) / S(k+1)(k+1),11 |
と計算できて
という結果が得られます。同様の方法で
となりますが、Σi{1→N}( ( ui - mu )( vi - mv ) ) / N については少し注意が必要です。
より、Σj{1→p;j≠k}( -S11,kjsyj ) が余因子展開の形になっていればいいのですが、残念ながら syj は 1 行目なので、余因子が示す k 行目とは一致しません。そこで、1 回目に削除する行と、2 回目に削除する行を入れ替えて、S11,kj から S(k+1)1,1j にするのです。削除する行が k 行から k + 1 行に変わっているのは、1 行目を削除してから k 行目を削除した場合、入れ替え後も同じ行を削除するためには k + 1 行目を削除して 1 行目を削除しなければならないからです。この時、
| S11,kj | = | ( -1 )1+1+k+jdetS11,kj |
| = | ( -1 )k+jdetS(k+1)1,1j | |
| = | ( -1 )k+j( -1 )-(k+1)-1-1-jS(k+1)1,1j | |
| = | -S(k+1)1,1j |
となって、符号が逆転します。従って、
| Σi{1→N}( ( ui - mu )( vi - mv ) ) / N | = | syk - Σj{1→p;j≠k}( -S11,kjsyj ) / S(k+1)(k+1),11 |
| = | syk - Σj{1→p;j≠k}( S(k+1)1,1jsyj ) / S(k+1)(k+1),11 | |
| = | syk - [ Σj{1→p}( S(k+1)1,1jsyj ) - S(k+1)1,1ksyk ] / S(k+1)(k+1),11 | |
| = | syk - [ S(k+1)1 - S(k+1)1,1ksyk ] / S(k+1)(k+1),11 | |
| = | syk - S(k+1)1 / S(k+1)(k+1),11 + S(k+1)1,1ksyk / S(k+1)(k+1),11 | |
| = | syk - S(k+1)1 / S(k+1)(k+1),11 - S11,kksyk / S(k+1)(k+1),11 |
最後に
| S11,kk | = | ( -1 )1+1+k+kdetS11,kk |
| = | detS(k+1)(k+1),11 | |
| = | ( -1 )-(k+1)-(k+1)-1-1S(k+1)(k+1),11 | |
| = | S(k+1)(k+1),11 |
なので、
となります。以上の結果から、偏相関係数は
| ryk・1,2,...,k-1,k+1,...p | = | ( -S(k+1)1 / S(k+1)(k+1),11 ) / [ ( S(k+1)(k+1) / S(k+1)(k+1),11 )( S11 / S(k+1)(k+1),11 ) ]1/2 |
| = | -S(k+1)1 / S(k+1)(k+1)1/2S111/2 |
と求められます。
S(k+1)1, S(k+1)(k+1), S11 はそれぞれ、S の余因子行列の 1 行 k + 1 列、k + 1 行 k + 1 列、1 行 1 列の成分です。detS で割れば、逆行列 S-1 の成分に置き換えることができるので、逆行列の要素を、添え字を上付きにしたもので表わすと、
となります。余因子の計算には行列式を求める必要があり、逆行列を利用する場合は逆行列の計算が必要です。行列式の計算には、LU 分解を利用すると高速に処理することが可能です。また、逆行列を計算するには連立方程式の解法を利用することになります。
重相関係数も同様に、行列 S と、その逆行列や余因子を使って計算することができます。
重相関係数 ryy^ の計算式は次の通りです。
ここで m^y は予測値 y^i の標本平均、sy^y^ は予測値の標本分散、my は観測値 yi の標本平均、syy は観測値の標本分散、そして yi と y^i の共分散を syy^とします。重相関係数は、yi と y^i の標本相関係数を意味することになります。
| syy^ | = | Σi{1→N}( ( yi - my )( y^i - m^y ) ) / N |
| = | Σi{1→N}( ( yi - my ){ [ a0 + Σj{1→p}( ajxj,i ) ] - Σl{1→N}( a0 + Σj{1→p}( ajxj,i ) ) / N } ) / N | |
| = | Σi{1→N}( ( yi - my ){ [ a0 + Σj{1→p}( ajxj,i ) ] - [ a0 + Σj{1→p}( ajmj ) ] } ) / N | |
| = | Σj{1→p}( ajΣi( ( yi - my )( xj,i - mj ) ) ) / N | |
| = | Σj{1→p}( ajsyj ) |
同様の計算方法により
偏相関係数の場合と同様に考えて、
となって、syy^ = sy^y^ が成り立ちます。従って、
という結果が得られます。この式は、「確率・統計 (13) 回帰分析法」の中の「2) 重相関係数(Multiple Correlation Coefficient)」でも示しています。
ですが、
なので、
よって
| ryy^ | = | { [ ( syyS11 - detS ) / S11 ] / syy }1/2 |
| = | ( 1 - detS / syyS11 )1/2 |
また、S の逆行列の 1 行 1 列成分を syy とおけば、
より
という結果が得られます。
*N1-1) 詳細は「確率・統計 (5) 正規分布」の中の「補足4) 行列の積の行列式」でも紹介しているので、参考にして下さい。
*N1-2) 線形従属については「数値演算法 (8) 連立方程式を解く -2-」の中の「5) 固有値と固有ベクトル」でも紹介しています。同じ行・列があれば、片側でもう片側を表すことができるのは明らかなので、線形従属になるのは当然のことです。
同じ行・列が存在する場合、行列式がゼロになる証明は他にもあります。行または列を入れ替えると行列式の符号が反転するのでした。しかし、同じ行・列を入れ替えても行列式の値は変わりません。符号が反転しても値が変わらない値はゼロしかないので、同じ行・列が存在する行列の行列式はゼロになるわけです。
*N1-3) Σi{1→N}( εi ) = 0、Σi{1→N}( xu,iεi ) = 0 になることの証明は、「確率・統計 (13) 回帰分析法」の中の「2) 重相関係数(Multiple Correlation Coefficient)」で紹介してあります。
eij → eij - c ( i ≠ j ) としたとき、hij → hij - 2c になります。また、この結果から対角成分は hii → hii + 2( N - 1 )c に変化します ( N は行列数 )。
このとき、行列 H は次のように表すことができます。
但し、1 は全成分が 1 の N x N 正方行列、E は N x N 単位行列です。
この行列に H の固有ベクトル x を掛けると
| ( H -2c1 + 2cNE )x | = | Hx - 2c1x + 2cNx |
| = | Qx + 2cNx - 2c1x |
となりますが、x の第 i 成分を xi とすると
と求められ、Σi{1→N}( xi ) = 0 になるように原点を定めていたため 1x = 0 という結果になります。従って、
となって、固有値は 2cN だけ大きくなり、固有ベクトルは変化しないことが証明されました。
固有値が大きくなるので、負数が正数になるのは分かりますが、どうして非対角成分を負数にすると必ず正数になることが保証されるのでしょうか。
0 でない任意のベクトル x に対して xTAx > 0 が成り立つ対称行列 A を「正定値対称行列」と言います。以前、正定値対称行列を固有値が全て正である対称行列として紹介したことがありますが、これらは同値関係にあります。また、任意のベクトルに対して xTAx ≥ 0 が成り立つなら「半正定値対称行列」であり、固有値は全て非負となります。
ベクトル x の第 i 成分を xi、行列 H の i 行 j 列の要素を hij としたとき、
となります。行列 H は対称行列であり、対角成分は同じ行 ( または列 ) の非対角成分の和の符号を逆転したものなので、
| Σj( Σi( hijxixj ) ) | = | Σj( hjjxj2 + Σi{i≠j}( hijxixj ) ) |
| = | Σj( -Σi{i≠j}( hijxj2 ) + Σi{i≠j}( hijxixj ) ) | |
| = | Σj( Σi{i≠j}( hij( xi - xj )xj ) ) |
と変形することができます。この式を展開してみると、
| Σj( Σi{i≠j}( hij( xi - xj )xj ) ) | = | h21( x2 - x1 )x1 | + | h31( x3 - x1 )x1 | + ... + | hN1( xN - x1 )x1 | ||
| h12( x1 - x2 )x2 | + | h32( x3 - x2 )x2 | + ... + | hN2( xN - x2 )x2 | ||||
| : | : | : | : | |||||
| h1N( x1 - xN )xN | + | h2N( x2 - xN )xN | + | h3N( x3 - xN )xN | + ... | |||
となりますが、H は対称行列だったので、hij = hji です。そこで、hij と hji を係数に持つ項同士を加算すると
| hij( xi - xj )xj + hji( xj - xi )xi | = | hij( xi - xj )xj - hij( xi - xj )xi |
| = | -hij( xi - xj )2 |
となるので、hij < 0 ならば、(上式) ≥ 0 が成り立ちます。展開式を見れば明らかなように、hij に対して hji を持つ項は必ず存在するので、結果として xTHx ≥ 0 となり、H は半正定値であることが証明されます。
正定値対称行列の対角成分は全て正値になります。正定値対称行列 A は 0 でない任意のベクトル x に対して xTAx > 0 だったので、特に i 番目の成分だけ 1 で他は 0 であるベクトル ei についてもそれが成り立ちます。A の i 行 j 列の成分を aij としたとき、
| eiTAei | = | ( ai1, ai2, ... aiN )ei |
| = | aii |
より aii > 0 となり、対角成分は全て正値であることが証明されます。
正定値対称行列 A が固有値分解によって QTDQ に対角化できるとしたとき、
| xTAx | = | xTQTDQx |
| = | ( Qx )TD( Qx ) > 0 |
なので、D はやはり正定値対称行列であり、固有値は A と等しく、その固有ベクトルは Qx となります。つまり、D の対角成分は正値であることになりますが、これは A の固有値でもあるため、正定値対称行列の固有値は正値であることが証明されます。
以上のことから、H の非対角成分を負値にすれば、固有値は必ず正になることが示されます。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |