「確率」という言葉は日常でもよく使われ、特に競馬・競輪や宝くじといったギャンブルではよく耳にします。簡単に言えば「ものごとの起こりやすさ」とか「ある現象が起こる比率」などと説明すれば何となく理解できるのではないかと思います。しかし、これが「確率論」という数学の世界になると、全ての事象に対する起こりやすさを数値によって表すことになるので、例えば「明日は多分晴れるでしょう」というのが「80 % の確率で晴れるでしょう」ということになって、「じゃあ、75 % の確率といった時とどの程度違うのか」と質問されても、普通は答えることができないと思います。今回は、この捕えどころのない「確率」について取り上げようと思います。
確率論は、17 世紀のヨーロッパに始まったというのが定説となっています。有名なのが、「シュバリエ・ド・メレ(Chevalier de Mere)」からの質問に対する「ブレーズ・パスカル(Blaise Pascal)」と「ピエール・ド・フェルマー(Pierre de Fermat)」との書簡のやり取りで、これが確率論の起源となったとされています。メレの出した問題の中で有名なのが以下の二つです。
一番目の問題の中で、メレはどのように確率が等しいと考えたのでしょうか。まず、サイコロを一つ投げた場合、1 〜 6 のいずれかの目が出るので、その中で 6 の目となるのは 1 / 6 の確率であり、それを 4 回繰り返せば、4 x ( 1 / 6 ) = 2 / 3 の確率で 6 の目が出るというのは自然な考え方であるように見えます。同様に、サイコロを二つ投げたときは、1 - 1 〜 6 - 6 の 36 通りの組み合わせの目が出るはずだから、その中で 6 - 6 のゾロ目になるのは 1 / 36 の確率で、それを 24 回繰り返せば 24 x ( 1 / 36 ) = 2 / 3 となり、両者は等しい確率で発生すると考えたわけです。しかし、これは誤った考え方であることをパスカルは指摘しました。
一つのサイコロを四回投げたとき発生する場合の数は 1 〜 6 の数を 4 つ並べる場合の数と等しいので、それは重複順列 6Π4 = 64 = 1296 通りになります。その中で 6 の目が全くない場合の数は 1 〜 5 の数を 4 つ並べる場合の数と等しいので、5Π4 = 54 = 625 通りです。よって、一回でも 6 の目が出る場合は 1296 - 625 = 671 で、全く出ない場合と比べて少しだけ有利であることになります。
それに対して、二つのサイコロを 24 回投げるときの場合の数は、1 - 1 〜 6 - 6 の 36 通りの組み合わせを 24 個並べる場合の数となって、36Π24 = 3624 ≒ 2.245 x 1037 通りという巨大な数になります。6 - 6 のゾロ目にならない場合の数は 35 通りであり、これを 24 個並べる場合の数は 35Π24 = 3524 ≒ 1.142 x 1037 通り。よって、一回でも 6 - 6 のゾロ目になる場合の数はおよそ 2.245 x 1037 - 1.142 x 1037 = 1.103 x 1037 通りで、今度は全く出ない場合より不利になってしまいます。
ある事象が発生する場合の数を全て数え上げ、それを他の事象の発生回数と比較すると、どちらの方がより多く発生しやすいかを類推することができます。また、全ての発生し得る場合の数を数えてそれとの比率を求めれば、発生する度合いを定量的に比較することが可能になります。このような考察から、確率論が誕生しました。
パスカルの時代からさらに 100 年以上経過して、「ピエール = シモン・ラプラス(Pierre-Simon Laplace)」が著した「確率論の解析理論」によって古典確率論が確立されたといわれています。その中での確率の定義は、次のようなものになります。
前の章で紹介したポーカー・ゲームでは、52 枚のカードから 5 枚のカードを選ぶときの組み合わせが 2598960 通りあって、その中で「ロイヤル・ストレート・フラッシュ」はわずか 4 通りしかないので、カードの中から 5 枚のカードを選択したとき「ロイヤル・ストレート・フラッシュ」になる確率は
百分率で表すと 0.0001539 % という非常に小さな値になります。また「ワン・ペア」は 1098240 通り、「ノー・ペア」は 1302540 通りなので、発生する確率は「ノー・ペア」の方が高くなり、それぞれ
ワン・ペア 1098240 / 2598960 = 0.4226
ノー・ペア 1302540 / 2598960 = 0.5012
と計算できます。起こりうる事象全てのうちいずれかが発生する確率は N / N = 1 で、これが全事象に対する確率になります。よって、確率が 0.5 を超える場合、何度も操作を繰り返す中でその事象が半分以上は発生することになり、上の結果から「ノー・ペア」がそのような事象に該当することになります。二つの事象が「同時に」発生することがなければ、それぞれが r1 個、r2 個であれば、どちらかが発生する確率は
と計算することができます。「ワン・ペア」と「ノー・ペア」は同時には発生しないので、いずれかが起こる確率は二つの確率の和 0.9238 となり、ほとんどは「ワン・ペア」か「ノー・ペア」になることを意味しています。
賭け事では「公平さ」が要求されるので、どの場合も「同等に確からしい」とするのは非常に自然な考え方です。しかし、この考え方が常に通用するとは限らず、例えば立方体ではない歪んだサイコロを使えば全ての目が「同等である」とは言えなくなります。もっと具体的な例として、野球のトーナメント戦を行った場合に、全てのチームの強さが「同等である」ことはまずあり得ないので、ここでもラプラスの確率の定義は利用できないことになります。確率の考え方が様々な問題に応用されるに従い、その定義もさらに厳密なものへと変化していきます。
何らかの「もの」の集まりのことを「集合(Set)」といいます。「もの」のことは「元 (または要素 ; Element)」と呼ばれ、その対象はどんなものでも構いません。集合自体を元として持つ集合も考えられ、そのような集合は「集合族(Family of Sets)」といって区別される場合もあります。
元 x がある集合 A に含まれるとき、
と表します。また、集合 B の元が全て 集合 A に含まれる場合、
と書きます。このとき、B は A の「部分集合(Subset)」になります。集合の包含関係については、以下の式が成り立ちます。
1 は、集合 A と B が等しいことを証明する場合によく利用されます。つまり、A ⊃ B を証明した後で B ⊃ A を証明すれば、二つの集合が等しいことが示されることになります。また、2 は三段論法( 命題 A → B と B → C が成り立つならば A → C )を集合で表したものになります。
集合は、元を列挙して表す「外延的記法(Extensional Definition)」と、条件や性質などを記述して表す「内包的記法(Intensional Definition)」の二種類があります。例えば、絶対値が 3 より小さい整数の集合を A で表す場合、
外延的記法 : A = { -2, -1, 0, 1, 2 }
内包的記法 : A = { n | n は整数, |n| < 3 }
のように書くことができます。
数を集合として表した特別な記号として以下のようなものがあり、数学の専門書などでよく利用されています。
実数の書き方だけややこしくなっていますが、二進数表現で無限に連なる 0, 1 の数列として表されることを表現しています。有理数の場合、ある有限値 m ≥ 0 に対して |k| > m の範囲においては 0 または 1 だけが連なった数列となる場合が考えられ、この場合は有限小数となります。また、 0 と 1 から成る同じパターンの数列が続く場合は循環小数であることになります。無理数の場合はどこまでいってもランダムに 0 と 1 が発生します。有限小数の例を以下に示します。
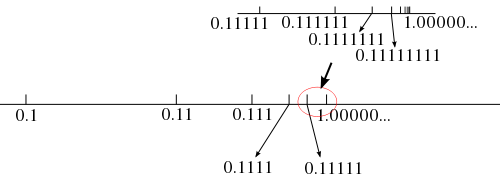
0.11111111 ..... 1.00000000 .....
上記二つの数は表し方が違うだけで同じ数値になります。実際、x = 0.11111111... とすれば、
2x = 1.11111111...
-) x = 0.11111111...
-------------------------
x = 1.00000000...
となります。よって 0 と 1 のどちらが連なった形になっても、それは有限小数となります。循環小数としては、次のような例があります。
0.00011001100...
"0011" のパターンが続くこの 2 進数は、10進数での 0.1 を表しています。このように、数値を表記するときの基数 ( n 進数表記での n のこと ) によって、有理数は有限小数にも循環小数にもなります。
0.11111111... と 1.00000000... が等しいという事実は、実数というものが全てつながってできている(連続している)ということを表現していることにもなります。この二つの数値が有限な数列からできていれば、その間にはやはり無数の数が存在するので、それぞれはつながってはいません。しかし、これが無限列になると、両者はいくらでも近づくことができて、極限としては等しくなります。これが「実数の連続性」と呼ばれるものです。
数の集合において C ⊃ R ⊃ Q ⊃ Z ⊃ N が成り立つことは容易に理解できると思います。また、先ほど示した、絶対値が 3 より小さい整数の集合 A の記法において、内包的記法は次のように表すこともできます。
または、n ∈ Z を左側にまとめて記述して次のように略記する書き方もよく見られます。
集合に対して演算を定義することができます。二つの集合 A, B に対して、その合併を「和集合(Union)」といって、A ∪ B で表します。A ∪ B の中には、A と B の両方の元が混在することになります。
また、共通部分からなる集合は「積集合(Intersection)」といって、A ∩ B で表します。
集合 A に対して、A に含まれない元からなる集合を A の「補集合(Absolute Complement Set)」といって、Ac で表します。
ある集合の中から、別の集合と共通の元を除いて得られる集合を「差集合(Relative Complement Set)」といいます。B から 集合 A と共通の元を除いた差集合は B - A または B \ A と表されます(日本語環境では後者の演算子が ¥ と表記されているかもしれませんが、正しくはバックスラッシュです)。
B - A は、Ac を使って次のように表すこともできます。
全ての元を持った集合はよく Ω で表されます。それに対して、元を全く持たない空の集合を「空集合(Empty Set)」と呼んで、一般に ∅ で表します。任意の集合 A に対し、補集合 Ac と空集合 ∅ の間には次の演算が成り立ちます。
A ∩ Ac = ∅
A ∪ Ac = Ω
差集合と補集合の関係式において B = Ω とすれば、
になるので、補集合とは集合全体との差集合でもあります。差集合を「相対的な補集合(Relative Complement Set)」、補集合を「絶対的な補集合(Absolute Complement Set)」と表現するのはこのためです。
| 和集合 A ∪ B | 積集合 A ∩ B | 補集合 Ac | 差集合 B - A |
|---|---|---|---|
 |
 |
 |
 |
和集合と積集合は、二つ以上の集合においても同様に考えることができます。n 個の集合 Ak ( k = 1, 2, ... n ) に対する和集合と積集合は、
∪k{1→n}( Ak )
∩k{1→n}( Ak )
と表すことにします。「可算無限回」の演算では n が ∞ になり、さらに「連続体濃度」の和・積となった場合は、さらに一般化して
∪α( Aα )
∩α( Aα )
と表すことにします(無限集合については後述)。
和集合と積集合においては、結合則と分配則が成り立ちます。
結合則
( A ∪ B ) ∪ C = A ∪ ( B ∪ C )
( A ∩ B ) ∩ C = A ∩ ( B ∩ C )
分配則
( ∪α( Aα ) ) ∩ B = ∪α( Aα ∩ B )
( ∩α( Aα ) ) ∪ B = ∩α( Aα ∪ B )
結合則は成り立つことが明らかですが、分配則は簡単には理解できないので、順を追って証明してみます。まず、任意の元 x に対して
が成り立つとしたとき、x は Aα の和集合と B の両方に含まれていることを意味しています。つまり x ∈ Aα ∩ B となるような α が存在することになって、x ∈ ∪α( Aα ∩ B ) となります。よって、( ∪α( Aα ) ) ∩ B の任意の元が ∪α( Aα ∩ B ) に含まれることになって
が成り立ちます。逆に、任意の元 y に対して
ということは、y が Aα と B の共通集合の中のいずれかに含まれていることを意味しています。つまり、y ∈ Aα ∩ B となるような α が存在することになり、y ∈ ∪α( Aα ) かつ y ∈ B が成り立つので、∪α( Aα ∩ B ) の任意の元が ∪α( Aα ) と B の共通集合に含まれることになって
となり、両者は等しいことが示されます。次に、任意の元 x に対して
となるときは、x が、Aα の共通部分か B のいずれかに含まれていることを意味しています。このとき、x は任意の α に対して必ず Aα ∪ B の中に含まれることになって、x ∈ ∩α( Aα ∪ B ) となるので、
が成り立ちます。逆に任意の元 y に対して
となるときは、任意の α に対して、y が Aα か B のいずれかに含まれることを意味するので、y は必ず Aα の共通集合 か B のいずれかに存在することになって、y ∈ ∩α( Aα ) ∪ B が成り立ちます。よって、
となって、全ての分配則が証明されたことになります。
和集合、積集合、補集合の間の関係式として、有名な「ド・モルガンの法則(De Morgan's Laws)」があります。
( ∪α( Aα ) )c = ∩α( Aαc )
( ∩α( Aα ) )c = ∪α( Aαc )
任意の元 x に対して x ∈ ( ∪α( Aα ) )c のとき、全ての α に対して x ∉ Aα つまり x ∈ Aαc であり、x ∈ ∩α( Aαc ) が成り立ちます。また、逆に任意の y に対して y ∈ ∩α( Aαc ) のとき、全ての α に対して y ∈ Aαc つまり y ∉ Aα であり、全ての Aα に含まれないことになるので、その和集合 ∪α( Aα ) にも含まれず、y ∈ ( ∪α( Aα ) )c となります。よって、最初の等式が証明されました。この等式の両辺の補集合も等しいことになるので、
左辺は ∪α( Aα ) になるので、左右を逆転すると
Bα = Aαc とすれば
となって、これは二番目の式を表すことになるので、これで全ての等式が証明されたことになります。
ある集合の部分集合すべてを抽出してそれを元とする集合族のことを「べき集合(Power Set)」といいます。例えば、集合 A = { x, y, z } について、その部分集合は
なので、これらを元とする集合族はべき集合であり、P(A) と表します。元の個数を n としたとき、考えられる部分集合の個数は 2n になります。上の例では、A の元の数 3 に対して部分集合の数は 8 = 23 となっています。A に元 a を追加すると、元の数 1 の部分集合 {a} と、元の数 2 の部分集合 {x,a}, {y,a}, {z,a}、元の数 3 の部分集合 {x,y,a}, {y,z,a}, {z,x,a} が追加され、最後に Ω として {x,y,z,a} が追加されます。ちょうど、P(A) の元となる集合に a を追加したものが P(A) の新たな元となるので、元の数は二倍に増えることになるわけです。
ここまでは、元の個数が有限か無限かをあまり考慮していませんでした。元の個数が有限な集合 A に対して、その部分集合 S の元個数は必ず A 以下になり、等しくなるのは A = S の場合だけです。例えば、1 から 100 までの自然数からなる集合 A に対して偶数だけからなる部分集合 E を考えたとき、元の個数を |A| で表せば
なので、|A| > |E| になります。しかし、これを自然数全体で考えると、次のように自然数と偶数を一対一に対応させることができてしまいます(このような対応の規則を「写像(Map)」といい、全ての元が一対一に対応できる写像は「全単射(Bijection)」になります)。
| 自然数 | 1, | 2, | 3, | ... | N, | ... |
| 偶数 | 2, | 4, | 6, | ... | 2N, | ... |
個数が無限になると、古代ギリシャ時代以来自明と思われていた「全体は部分より大きい」という公理に反する結果が得られてしまうことになります。最初にこのことに気付いたのは「ガリレオ・ガリレイ(Galileo Galilei)」とされており、著作の「新科学対話」の中で、自然数と平方数が一対一に対応できることが述べられています。しかしガリレオは、無限を考える場合はどちらが大きいかを論じることはできないとして、それ以上の考察はやめてしまいます。当時の一般的な考えかたとしては、無限というものが有限である人間の考えを超越したものであって、それを論じることは「うさんくさい」ものとされていたようです。
ニュートンやライプニッツなどによって微分積分法が利用されるようになると、無限に対する扱いは避けて通ることのできないものになります。その中で、最初に無限集合の確立を行ったのが「ゲオルグ・カントール(Georg Cantor)」で、彼によって「集合論(Set Theory)」が誕生しました。
先ほどの例で示した自然数と偶数の対応のように、自然数と一対一に対応できる集合のことをカントールは「可算無限集合(Countably Infinite Set)」と呼びました。つまり、一つずつ数えることのできる集合という意味になります。自然数の部分集合の中で、偶数や奇数、平方数、立法数、素数などは一対一対応が可能であり、全て可算無限集合になります。また、整数の場合は
| 自然数 | 0, | 1, | 2, | 3, | 4, | ... | 2N-1, | 2N, | ... |
| 整数 | 0, | 1, | -1, | 2, | -2, | ... | N, | -N, | ... |
とすれば対応が可能です。有理数の場合、自然数の二つの組から分数で表現できるので、
| 1/1, | 2/1, | 3/1, | ... | N/1, | ... |
| 1/2, | 2/2, | 3/2, | ... | N/2, | ... |
| 1/3, | 2/3, | 3/3, | ... | N/3, | ... |
| : | : | : | : | ||
| 1/N, | 2/N, | 3/N, | ... | N/N, | ... |
| : | : | : | : |
と平面上に並べた上で、左上の 1/1 からスタートして 2/1 → 1/2 → 1/3 → 2/2 → ... とジグザグに進めながら自然数と対応を付けることができます。そうなると、実数についても対応を付けることが可能なように思えますが、カントールは「対角線論法」と呼ばれる手法を使って対応付けができないことを証明しました。
まず、実数の範囲を 0 < x ≦ 1 として、その中にある全ての実数を並べてみます。但し、有限小数の場合は、末尾にゼロが続くとします。
| 0. | x00 | x01 | x02 | x03 | ... |
| 0. | x10 | x11 | x12 | x13 | ... |
| 0. | x20 | x21 | x22 | x23 | ... |
| : | : | : | : | : |
xrc の中には 0 から 9 までのいずれかの数値が入ります。上から順番に自然数と対応が付けられたと仮定したとき、yn として xnn とは異なる値を取って実数 0.y0y1y2 ... を作ると、y0 は x00 とは異なるように選んだため、上の表の一行目にある数値とは異なり、y1 は x11 と異なるように選んだため、上の表の二行目にある数値とも違う値になります。つまり、作成された値は表の中のどの値とも一致せず、最初の仮定に反することになります。同じ無限であるにもかかわらず、自然数と実数ではその大きさが異なるという不思議な結果が得られたことになります。
二つの集合が一対一に対応できたとき、それらは同じ「濃度(または基数 ; Cardinal Number)」を持つといいます。有限集合であれば、それは元の個数を意味することになります。カントールは、無限集合の場合の濃度を「超限基数」と呼び、可算無限集合の超限基数を「アレフ・ゼロ(Aleph Null)」と名付けました。ここで、可算無限集合 M のべき集合 P(M) を考えると、M のひとつの元からなる部分集合の濃度は |M| と等しいので、複数の元からなる部分集合の分だけ |M| より |P(M)| の方が大きいことになります。べき集合の元の数は 2|M| で表されるので、アレフ・ゼロを ℵ0 として、可算無限集合のべき集合の濃度を 2ℵ0 と定義します。
可算無限集合として Z を利用して、その部分集合の元の位置が 1 で残りが 0 となる二進無限小数と対応付けを行います。負数は小数点以下、ゼロと正数は整数部分を表すとすると、例えば
{} → 0
{ 0 } → 1
{ -1, 0, 1 } → 11.1
{ -3, -4, -6 } → 0.001101
{ 2, -1 } → 100.1
と対応付けができます。このとき、対応付けされた数値と P(Z) は一対一対応となり、しかもその数値は実数全体の集合 R を表しているため、Rの濃度は 2ℵ0 と等しいことになります。ここでカントールは 2ℵ0 = ℵ1 として、ℵ0 と ℵ1 の間に超限基数は存在しないことを証明しようとしました。これが有名な「連続体仮説(Continuum Hypothesis ; CH)」です。これを一般化すると、ℵn-1 の濃度を持つ集合のべき集合の濃度を ℵn として、2ℵn-1 = ℵn と表すことができ、これを「一般連続体仮説(Generalized Continuum Hypothesis ; GCH)」といいます。なお、実数の濃度 ℵ1 は「連続体濃度」と呼ばれます。
カントールは、連続体仮説を証明することは結局できませんでした。彼の生み出した理論はあまりにも斬新だったため、当時の数学界で大きな力を持っていた数学者「レオポルト・クロネッカー(Leopold Kronecker)」をはじめとして他の数学者からの激しい攻撃にさらされ、また連続体仮説の証明ができないことへの苛立ちもあって、次第に精神を病んでしまう結果となってしまいます。最終的に、連続体仮説の証明に決着を付けたのは「クルト・ゲーデル(Kurt Godel)」と「ポール・コーエン(Paul Cohen)」の二人で、まずはゲーデルが、連続体仮説の否定を証明することは「できない」ことを、次いでコーエンが連続体仮説の証明も「できない」ことを証明しました。つまり、現在の数学の公理では連続体仮説の証明は不可能ということになります。
ところで、連続体濃度を持つ実数と一対一に対応するものはあるでしょうか? 自然数と偶数は一対一に対応し、部分と全体が同じ濃度を持つことが示されたように、実数の部分集合も実数全体と一対一に対応することを簡単に示すことができます。例えば、次のような関数を考えます。
この関数は、定義域 ( 0, 1 ) に対して値域が実数全体となるので、( 0, 1 ) の区間の実数と実数全体が一対一に対応していることになります。また、0 < x < 1, 0 < y < 1 の範囲の矩形上の任意の点は
と表せるので、これを
とすれば、矩形上の点を全て ( 0, 1 ) の区間の実数と一対一対応させることができます (逆もまた可能であることに注意して下さい。つまり、数直線上の任意の点に対して偶数番目と奇数番目の数字に分離することで、平面上の一つの点にすることができるので、一対一対応であることになります)。これは任意の次数の実数空間 Rn でも成り立ってしまうので、次数に関係なく空間上の点を数直線上に一対一対応させることができることになります。
「現代確率論」は、ロシアの数学者「アンドレイ・コルモゴロフ(Andrey Nikolaevich Kolmogorov)」により確立されたとされ、そこでは起こりうる対象の集合を定義するところから始まります。
まず、何らかの「試行(Trial)」を行ったときに起こりうる対象全てからなる集合を「標本空間(Sample Space)」といい、一般に Ω で表されます。また、Ω の中の元を「標本点(Sample Point)」といいます。Ω の部分集合のことを「事象(Event)」といい、よく A, B, C などの大文字のアルファベットで表されます。例えば、サイコロを一回投げる試行を行ったときのサイコロの目は 1 から 6 までのいずれかなので、標本点は 1, 2, 3, 4, 5, 6 の 6 つ存在します。よって、
になります。この中で、偶数の目となる元は 2, 4, 6 なので、偶数の目となる事象を E で表すと
になります。
Ω の部分集合を元とする集合族に対し、次の三つの条件を満たす集合族 β を「完全加法族 (または σ-加法族 ; Sigma-algebra)」といいます。
完全加法族は全ての元から成る集合 Ω を含み、ある元 A に対してはその補集合 Ac も含んでいて、さらに任意の元の和集合(合併)も全て含んだ集合族になります。
例えば先程の例において、O = Ec = { 1, 3, 5 } として β = { ∅, E, O, Ω } とすれば、上記条件を満たすことになります。三番目の和集合に関する定義が有限回の和であればこの集合族は「有限加法族」になり、これが無限回の場合に「完全加法族」と表されます。但し、ここでの無限回とは「可算回」である必要があって、それ以上の濃度にはなりません。
Ω に対する補集合 ∅ を含むことから必ず ∅ ∈ β が成り立ちます。また、Ai ∈ β ならば Aic ∈ β であり、∪i{1→∞}( Aic ) ∈ β となって、その補集合に対しても ( ∪i{1→∞}( Aic ) )c ∈ β が成り立ちます。ド・モルガンの法則から ( ∪i{1→∞}( Aic ) )c = ∩i{1→∞}( ( Aic )c ) = ∩i{1→∞}( Ai ) となるので、
も成り立つことになります。つまり、任意の元の積集合(共通部分)も全て含むことになって、かなり大きな集合族になることが想像できると思います。
Ω より定義された完全加法族や有限加法族 β を定義域とする実数値関数 μ(A) ( A ∈ β ) が次の条件を満たすとします。
このとき、μ(A) を事象 A の「確率(Probability)」といい、標本点からなる全集合 Ω と、Ω から定義された加法族 β を合わせたもの ( Ω, β, μ ) を「確率空間(Probability Space)」といいます。Ai ∩ Aj = ∅ とは、二つの集合が互いに交わらない(共通な元が存在しない)ことを意味しているので、その和集合は ∪ ではなく Σ を使って
と表す場合もあります。
サイコロを一回投げる試行で確率を考えると、サイコロの目を事象 Ai ( i = 1,2,3,4,5,6 ) とすれば、μ(Ai) がそれぞれの目の出る確率を表し、また Ω = Σi{1→6}( Ai ) より
になります。ここで、サイコロの目の出る確率が全て等しいとすれば、μ(A1) = μ(A2) = μ(A3) = μ(A4) = μ(A5) = μ(A6) なので、これを μ とすれば
となって μ = 1 / 6 になります。偶数の目の出る事象は E = A2 + A4 + A6 だから、その確率は 1 / 2 と計算することができます。これは、ラプラスの算術的確率を現代確率論の形で定義し直したものになります。サイコロを二回投げる試行の場合、標本空間は
となって、標本点の個数は ( 1, 1 ) から ( 6, 6 ) までの重複順列の数 62 = 36 個になります。これらを事象 Aij = { ( ai, aj ) } として全てが等しい確率になるとすれば、μ(Aij) = 1 / 36 になります。すると同じ目になる事象は Aii ( i = 1 〜 6 ) なので 6 個であり、その和は 1/6 です。一般化して N 回投げる場合の標本空間は、
となるので、その個数は 6N 個になって、各々の事象を A(i1,i2,...iN) = { ( a1, a2, ... aN ) } で表して全てが等しい確率になるとすれば、μ( A(i1,i2,...iN) ) = 1 / 6N になります。N 回の試行で全ての目が等しくなる場合はその中の 6 個しかないので、その確率は 6 x ( 1 / 6N ) = 1 / 6N - 1 と計算することができます。
単純なモデルとして、試行の結果、二つの事象が発生する場合を考えてみます。例えば「コインを投げて表が出る/裏が出る」や「宝くじに当たる/はずれる」などのような場合、前者はどちらの事象もほぼ等しく、後者ははずれる場合の方が圧倒的に多いと予想できます。片方の事象を A としたとき、もう一方は A の補集合であり、その事象は A の「余事象(Complementary Event)」と呼ばれます。これを A~ で表すと、Ω = A + A~ なので
です。μ(A) = p ( 0 ≦ p ≦ 1 ) としたとき、μ(A~) = 1 - p になります。元 A を 1、A~ を 0 で表して、これを N 回繰り返す場合の標本空間は、先程のサイコロの例と同様な形で
と表すことができます。このような試行のことを「ベルヌーイ試行(Bernoulli Trial)」といい、その標本点である、0 と 1 からなる数列を「ベルヌーイ列(Bernoulli Sequence)」といいます。ここで、N 回の試行は互いに独立であるという条件が付加されます。独立とは、試行の結果に対して互いに影響を及ぼさないことを表していて、コインやサイコロをを投げた結果はその前後の結果には影響されないので独立な試行と考えても問題ないのに対して、ジャンケンなどは次に何を出すかをその前後の状況から判断して決めるのが普通なので、独立でない試行の例になります。このような試行から誕生したものとして「二項分布(Binomial Distribution)」と呼ばれる代表的な確率分布があります。
確率 μ は加法族 β を定義域とする実数値関数なので、β の各元を数値で表すことができれば通常よく利用される関数の形となって非常に便利になります。そこで、次のような確率空間 ( Ω, β, μ ) を考えます。
確率空間 - 1 -
Ω = Z
β = 「Ω ( つまり Z ) から成る完全加法族」
任意の n ∈ Z に対して p(n) ≧ 0 かつ Σn{-∞→∞}( p(n) ) = 1
μ(A) = Σn{n∈A}( p(n) )
確率空間 - 2 -
Ω = R
β = 「Ω ( つまり R ) から成る完全加法族」
任意の x ∈ R に対して ρ(x) ≧ 0 かつ ∫{-∞→∞} ρ(x) dx = 1
μ(A) = ∫{x∈A} ρ(x) dx
上記定義の中の p(n) や ρ(x) を「確率密度(Probability Density)」または「確率分布(Probability Distribution)」といい、1 は「離散分布(Discrete Distribution)」、2 は「連続分布(Continuous Distribution)」を表します。ここで、Σn{n∈A}( p(n) ) と ∫{x∈A} ρ(x) dx は事象 A の範囲にある n, x について和や積分を行うということを表しています。これを多変数に拡張した場合、次のようになります。
確率空間 - 1' -
Ω = Zn
β = 「Ω ( つまり Zn ) から成る完全加法族」
任意の m = ( m1, m2, ... mn ) ∈ Zn に対して p(m) ≧ 0 かつ Σm1{-∞→∞}Σm2{-∞→∞}...Σmn{-∞→∞}( p(m) ) = 1
μ(A) = Σm{m∈A}( p(m) )
確率空間 - 2' -
Ω = Rn
β = 「Ω ( つまり Rn ) から成る完全加法族」
任意の x = ( x1, x2, ... xn ) ∈ Rn に対して ρ(x) ≧ 0 かつ ∫{-∞→∞}∫{-∞→∞}...∫{-∞→∞} ρ(x) dx1dx2...dxn = 1
μ(A) = ∫{x∈A} ρ(x) dx
離散分布も連続分布も、β は完全加法族であって本質的には変わらず、離散分布では可算個の点に対して μ を定義しているのに対して連続分布では可算個の区間に対して μ を定義していることになります。従って、確率分布に関する性質はどちらに対しても同等であるといえます(補足1)。
ベルヌーイ列に対する確率空間において、a1 から aN までの和を n とすれば、n は 0 から N までの値を取ることになって、それは A が発生した(コインの表が出た、宝くじに当たった)回数を表すことになります。Ω 上の標本点 ω = ( a1, a2, ... aN ) に対して、x(ω) = Σk{1→N}( ak ) とすると、例えば A が全く発生しなかった場合は ω = ( 0, 0, ... 0 ) のみなので、x(ω) = 0 となる標本点はこの場合のみになります。x(ω) = n となる事象を An とすれば
と表されます。このように、集合に対して値を定義して、その大小によって確率の議論を行うことができるようにしたもの x(ω) を「確率変数(Random Variable)」といいます。この例のように確率変数を定義すれば、確率分布は先程紹介した Ω = Z 上での離散分布の形で表されることになるわけです。しかし、このように定義した確率変数 x(ω) がある範囲にあるとき、その条件を満たす ω の集合もまた加法族 β に含まれなければなりません。従って、x(ω) は次のような条件を満たす必要があります。
r1, r2 ∈ R で、r1 < r2 のとき、R1 = { ω | x(ω) ≦ r1 } も R2 = { ω | x(ω) ≦ r2 } も β に含まれることになるので、R1c ∩ R2 = { ω | r1 < x(ω) ≦ r2 } もまた β に含まれます。よって、上記の条件によって、任意の範囲の確率変数に対する確率が計算できることが保証できるわけです(もちろん、離散分布の場合は Z 上で同様な定義をすることになります)。
100 本中 1 本だけ当たりのあるくじがあって、当たれば一万円もらえるとします。くじを引くのにいくら支払うことにすれば、公平だといえるでしょうか。例えば、一回一万円も取られるのなら、だれもそんなくじを引きたいとは思わないし、逆に十円であれば、100 本のくじが売れても千円の利益にしかならず、その中に一本は当たりがある割合となるので今度はくじを売る方が必ず損をすることになります。
くじを引く側も用意する側も損得がないような公平な状態を考えると、この例では一回 100 円としておけば、一人で 100 回引けば一回は当たることが期待できるし、くじを売る方も損はしなくなります(利益もないですが)。このような値を期待値(Expected Value)といいます。
そこで、次のように定義した値を期待値とします。
E[f] = ∫{x∈Ω} f(x)ρ(x) dx [連続分布]
E[f] = Σ{x∈Ω}( f(x)p(x) ) [離散分布]
例えば、サイコロを投げて出た目の数に応じて次のようにお金がもらえるとします。
| サイコロの目 | 金額(円) |
|---|---|
| 1 | 130 |
| 2 | 40 |
| 3 | 30 |
| 4 | 110 |
| 5 | 120 |
| 6 | 140 |
サイコロの目 x に対して f(x) をもらえるお金とすれば、p(x) = 1 / 6 ( x = 1,2,3,4,5,6 ) なので、期待値は
になります。100 円払ってサイコロを投げ、出た目の数に応じて上記表に従ってお金がもらえるとした場合、100 円より多くもらえる確率は 2/3 で半分以上なので、一見すると繰り返すうちに得をしていくように見えます。サイコロの目が全て等しい確率で発生するとすれば、サイコロを投げる試行を何回も繰り返すうちにそれぞれの目の出た回数はほぼ等しくなることが予想されます。すると、試行一回あたりで手に入れることのできた金額は期待値に近づいていくことがイメージできると思います。その結果が 95 円になるので、この勝負を繰り返すほど損をするということをこの結果は表しています。
確率変数 x を f(x) として、x に対する期待値のことを特別に「平均値(Average)」といい、通常は μ で表されます。
μ = E[x] = ∫{x∈Ω} x・ρ(x) dx [連続分布]
μ = E[x] = Σ{x∈Ω}( x・p(x) ) [離散分布]
平均値は、確率変数に対する期待値を意味しています。しかし、確率変数は集合に対して何らかの値を定義したものなので、先程の例で示した金額をそのまま確率変数としてしまっても差し支えはないわけで、その意味で期待値と平均を同義語としている文献もよく見かけます。ここでは、確率変数 x に対してさらに別の関数 f(x) を定義した場合は期待値と表すようにします。
サイコロの目の平均があまり意味を持つとは思えないので、あるクラスで行った試験の結果に対して平均を算出してみます。そのクラスは全部で 20 人で、試験は 10 点満点だとします。
| 得点 | 人数 | 確率 |
|---|---|---|
| 0 | 1 | 0.05 |
| 1 | 0 | 0.00 |
| 2 | 2 | 0.10 |
| 3 | 1 | 0.05 |
| 4 | 0 | 0.00 |
| 5 | 1 | 0.05 |
| 6 | 4 | 0.20 |
| 7 | 7 | 0.35 |
| 8 | 3 | 0.15 |
| 9 | 0 | 0.00 |
| 10 | 1 | 0.05 |
確率は、クラス全体の数を N、k 点を取った人数を rk として rk / N で計算しています。この時の平均は
で、だいたい 6 点程度であることになります。ところで、上式の最左辺は、
であって、Σk{1→10}( k・rk ) は全ての得点の総和を表しています。従って、得点の合計を計算してからクラスの人数で割っても同じ結果が得られます。この平均のことを「算術平均(Arithmetic Mean)」ともいいますが、いわゆる平均値の計算にはこの手法がよく利用されています。これは、得点の分布が確率 rk / N に従っていると仮定した上での平均値を表していることになります。
f(x) = ( x - a )2 としたときの期待値を「a のまわりの分散(Variance)」といって、σa2 で表されます。特に、a = μ (平均値) ならば単に「分散」といい、σ2 で表します。また、σ のことを「標準偏差(Standard Deviation)」といいます。
( x - a )2 は、x が a から離れている度合いを表しています。その期待値が分散になるので、これは分布全体が a を中心にどれだけばらついているかを表す指標となります。分散が大きければばらつきが大きく、逆に分散が小さければばらつきも小さくなるわけです。例えば、先の例で示したクラス内の試験の結果において分散が大きい場合、クラス内のレベルにばらつきがあることになるし、製品のテスト結果にばらつきが大きければ、品質的にあまりいい状態であるとはいえないことになります。このように、分散を調べることも品質などを調べる上で非常に重要なことになります。
ところで、σa2 と σ2 の差を計算すると、
| σa2 - σ2 | = | ∫{x∈Ω} ( x - a )2ρ(x) dx - ∫{x∈Ω} ( x - μ )2ρ(x) dx |
| = | ∫{x∈Ω} { ( x - a )2 - ( x - μ )2 }ρ(x) dx | |
| = | ∫{x∈Ω} { 2( μ - a )x - ( μ2 - a2 ) }ρ(x) dx | |
| = | 2( μ - a )∫{x∈Ω} x・ρ(x) dx - ( μ2 - a2 )∫{x∈Ω}ρ(x) dx |
ここで、∫{x∈Ω} x・ρ(x) dx = μ、∫{x∈Ω}ρ(x) dx = 1 なので、
| σa2 - σ2 | = | 2μ( μ - a ) - ( μ2 - a2 ) |
| = | μ2 - 2μa + a2 | |
| = | ( μ - a )2 ≧ 0 |
よって、σa2 ≧ σ2 (等号は μ = a のとき)が成り立ち、平均のまわりの分散は最小値を取ることになります。平均とは、そのまわりの分散、つまりばらつきが最小となる値を意味するわけです。
平均値のような集計値は「要約統計量」とも呼ばれ、ある分布を代表する値になります。先程のテストの例においては、最も人数の多かった点は 7 点であり、これを代表値にするやり方も考えられます。これは「最頻値(Mode)」と呼ばれる要約統計量です。また、得点順に並べてちょうど中央にあたる点数(この場合も 7 点になります)を代表にする場合もあり、これは「中央値(Median)」といいます。その中で、ばらつきを最小とする代表値として利用されるのが平均値であることになります。それぞれは代表としての資格を持っていて、どれを利用するかは場合によって異なります。
ところで、期待値が得られない(発散するなど)ような確率分布が存在します。有名なものとして「聖ペテルブルクのパラドックス(St. Petersburg Paradox)」があります。
裏表どちらも等確率で発生するような、偏りのないコインを投げる試行を何度も繰り返し、表が出たところで終了するような場合を考えます。この時の事象は、
なので、各事象の元の数を確率変数 n とすれば、p(n) = 1 / 2n とすることができます。つまり、n 回投げて初めて表が出る確率が 1 / 2n となるわけです。この時、全事象に対する確率は
なので、確率分布として成り立つことがわかります。ここで、n 回コインを投げて初めて表が出たら、2n 円もらえるとしたとき、もらえる金額の期待値は
つまり無限大となります。しかし、期待値が無限大になるからと言って、例えば一億円を掛けて勝負するような人はいないと思います。この場合、少なくとも 26 回以上は裏が出ないと勝負に勝つことはできず、その確率は 1 / 227 = 7.45 x 10-9 という途方もなく小さな数になります。
平均値が得られない確率分布もあります。「標準コーシー分布(Standard Cauchy Distribution)」は次のような式で表される確率分布です。
このとき、任意の x について ρ(x) ≧ 0 が成り立ち、
において x = tanθ とすれば、dx = ( 1 / cos2θ )dθ で x → -∞ のとき θ → -π / 2、x → ∞ のとき θ → π / 2 なので、
| ∫{-∞→∞} ρ(x) dx | = | ∫{-π/2→π/2} 1 / πcos2θ( 1 + tan2θ ) dθ |
| = | ∫{-π/2→π/2} 1 / π( cos2θ + sin2θ ) dθ | |
| = | ∫{-π/2→π/2} 1 / π dθ | |
| = | [θ / π]{-π/2→π/2} = 1 |
で、確率分布の条件を満たしています。この分布の平均を求めると
において t = 1 + x2 とすれば、dt = 2x dx となり、x → 0 のとき t → 1 で、x → ±∞ のどちらも t → ∞ なので、積分範囲を -∞ 〜 0 と 0 〜 ∞ の二つに分けて
| ∫{-∞→∞} x・ρ(x) dx | = | ∫{∞→1} 1 / 2πt dt + ∫{1→∞} 1 / 2πt dt |
| = | [(1/2π)ln( t )]{∞→1} + [(1/2π)ln( t )]{1→∞} | |
| = | -lim{t1→∞}( (1/2π)ln( t1 ) ) + lim{t2→∞}( (1/2π)ln( t2 ) ) | |
| = | (1/2π)lim{t1→∞,t2→∞}( ln( t2 / t1 ) ) |
この場合、t1 と t2 の関係によってこの極限はどのような値にもなり得るので、平均は不定となり、決まった値は得られないことになります ( ∞ - ∞ は値が決められないという典型的な例です )。
期待値については、加法性が成り立ちます。f(x), g(x) の期待値の和 αE[f] + βE[g] (α, βは定数) は、離散分布ならば
| αE[f] + βE[g] | = | αΣ{x∈Ω}( f(x)p(x) ) + βΣ{x∈Ω}( g(x)p(x) ) |
| = | Σ{x∈Ω}( αf(x)p(x) + βg(x)p(x) ) | |
| = | Σ{x∈Ω}( { αf(x) + βg(x) }p(x) ) | |
| = | E[αf + βg] |
となって、積分の加法性から連続分布でも同様な結果が得られます。これを利用して平均値と分散の関係式を求めてみます。
| σ2 | = | E[(x - μ)2] |
| = | E[x2 - 2μx + μ2] | |
| = | E[x2] - 2μE[x] + μ2E[1] | |
| = | E[x2] - 2μ2 + μ2 ( E[x] = μ, E[1] = 1 より ) | |
| = | E[x2] - μ2 |
E[x2] は "二乗の平均" を表しているので、上式は
であることを示しています。
ある確率分布の平均や分散を計算するとき、「積率母関数(Moment Generating Function)」を利用すると便利な場合があります。
この式の両辺を微分すると、連続分布においては
| g'(θ) | = | (d/dθ)∫{x∈Ω} eθxρ(x) dx |
| = | ∫{x∈Ω} (d/dθ)eθxρ(x) dx | |
| = | ∫{x∈Ω} xeθxρ(x) dx |
よって、
もう一度微分すると
| g(2)(θ) | = | (d/dθ)∫{x∈Ω} xeθxρ(x) dx |
| = | ∫{x∈Ω} x2eθxρ(x) dx |
よって、
これを繰り返せば、次の一般式が得られます。
これは、離散分布の場合でも成り立ちます。
namespace Statistics
{
// 一次元確率分布用インターフェース
class ProbDist
{
public:
virtual double average() const = 0; // 平均値
virtual double variance() const = 0; // 分散
};
// 離散分布用インターフェース
class DiscDist : public ProbDist
{
public:
// 確率変数 n に対する確率密度を返す
virtual double operator[]( int n ) const = 0;
// 区間 [s,e] における確率を返す
double p( int s, int e ) const;
};
/*
DiscDist::p : 区間 [s,e] における確率を返す
int s,e : 区間
s > e の場合は反転して計算する
戻り値 : 確率
*/
double DiscDist::p( int s, int e ) const
{
if ( s > e ) { int i = s; s = e; e = i; }
double sum = 0;
for ( ; s <= e ; ++s )
sum += (*this)[s];
return( sum );
}
// 連続分布用インターフェース
class ContDist : public ProbDist
{
public:
// 確率変数 a における確率密度を返す
virtual double operator[]( double a ) const = 0;
// 区間 (-∞,a] における確率を返す
virtual double lower_p( double a ) const = 0;
// 区間 [a,b] における確率を返す
virtual double p( double a, double b ) const
{ return( ( a > b ) ? p( a ) - p( b ) : p( b ) - p( a ) ); }
};
/*
average : 平均値 μ = Σ xρ(x)を求める
const DiscDist& prob : 確率分布
int n1, n2 : 計算する範囲(分布の範囲)
誤差を軽減する方法は Kahanの加算アルゴリズムを利用
戻り値 : 平均値
*/
double average( const DiscDist& prob, int n1, int n2 )
{
double ans = 0;
double r = 0; // 積み残し
if ( n1 > n2 ) { int n = n1; n1 = n2; n2 = n; }
for ( int i = n1 ; i <= n2; ++i ) {
double y = (double)i * prob[i] - r; // 計算値から積み残しを引いた値
double buff = ans + y; // 今までの合計値に y を加える
r = ( buff - ans ) - y; // 積み残しを計算
ans = buff;
}
return( ans );
}
/*
variance : aのまわりの分散 v = Σ (x-a)^2ρ(x)を求める
double a : aの値
const DiscDist& prob : 確率分布
int n1, n2 : 計算する範囲(分布の範囲)
誤差を軽減する方法は Kahanの加算アルゴリズムを利用
戻り値 : 分散
*/
double variance( double a, const DiscDist& prob, int n1, int n2 )
{
double ans = 0;
double r = 0; // 積み残し
if ( n1 > n2 ) { int n = n1; n1 = n2; n2 = n; }
for ( int i = n1 ; i <= n2 ; ++i ) {
double y = pow( (double)i - a, 2 ) * prob[i] - r; // 計算値から積み残しを引いた値
double buff = ans + y; // 今までの合計値に y を加える
r = ( buff - ans ) - y; // 積み残しを計算
ans = buff;
}
return( ans );
}
// サイコロを一回投げる試行に対する確率分布
class Dice : public DiscDist
{
public:
// 確率変数 n に対する確率密度を返す
double operator[]( int n ) const
{ return( ( n < 1 || n > 6 ) ? 0 : 1.0 / 6.0 ); }
double average() const // 平均値
{ return( Statistics::average( *this, 1, 6 ) ); }
double variance() const // 分散
{ return( Statistics::variance( average(), *this, 1, 6 ) ); }
};
// 標準コーシー分布
class StdCauchyDist : public ContDist
{
public:
// 確率変数 a における確率密度を返す
double operator[]( double a ) const
{ return( 1.0 / ( M_PI * ( 1.0 + a * a ) ) ); }
// 区間 (-∞,a] における確率を返す
double lower_p( double a ) const
{ return( atan( a ) / M_PI ); }
// 区間 [a,b] における確率を返す
double p( double a, double b ) const
{ return( ( ( b > a ) ? atan( b ) - atan( a ) : atan( a ) - atan( b ) ) / M_PI ); }
double average() const { return( NAN ); } // 平均値
double variance() const { return( NAN ); } // 分散
};
}
まず、一変数での確率分布を定義するためのインターフェースとして ProbDist を用意して、その派生クラスとして離散・連続分布に対する確率分布用クラス DiscDist と ContDist を作成しています。メンバ関数として、確率密度を返す operator[] と、平均・分散を返す average、variance が定義されています。また、連続分布に対しては、指定した確率変数以下の区間における確率を返すメンバ関数 lower_p と、指定した区間の確率を返すメンバ関数 p が用意されています。
連続分布において、ある確率変数になる確率は常にゼロになります。連続分布における事象 A ⊂ R の確率は μ(A) = ∫{x∈A} ρ(x) dx で、事象 A が連続であれば、ある閉区間 [ a, b ] の範囲の確率として
と表せます。よって、a = b のとき、μ( [ a, a ] ) = ∫{a→a} ρ(x) dx = 0 になります。逆にこのことから、閉区間 [ a, b ] と 開区間 ( a, b ) の確率は等しいことになります。
離散分布の平均値と分散を求める関数 ( average と variance ) が別に用意されていて、離散分布と和を求める範囲を引数として渡せば結果を得ることができます。分布の範囲は計算する側では分からないので、呼び出し側が指定するようにしてあります。
誤差を軽減するため、「カハンの加算アルゴリズム(Kahan Summation Algorithm)」を利用しています。これは、切り捨てられた値を積み残し分として保持しておいて、ある程度積み残しが大きくなったら結果に反映されるようになっています。実際の値を使うと動作がよく分かります。積み残し r = 0 の状態で、有効桁数が 6 桁として、ans = 1.23456 に 0.00123456 を加算すると、
double y = 0.00123456 - r = 0.00123456 double buff = ans + y = 1.23456 + 0.00123456 = 1.23579 // 0.00000456 は切り捨て r = ( buff - ans ) - y = ( 1.23579 - 1.23456 ) - 0.00123456 = 0.00123 - 0.00123456 = -0.00000456 // 切り捨て分が符号だけ反転して得られる ans = buff;
さらに 0.00234567 が加算されると、
double y = 0.00234567 - r = 0.00234567 + 0.00000456 = 0.00235023 double buff = ans + y = 1.23579 + 0.00235023 = 1.23814 // 0.00000023 は切り捨て r = ( buff - ans ) - y = ( 1.23814 - 1.23579 ) - 0.00235023 = 0.00235 - 0.00235023 = -0.00000023 // 切り捨て分が符号だけ反転して得られる ans = buff;
こうして、切り捨てられた値が r に蓄積され、ある程度積み残しが大きくなれば結果に反映されることになります。なお、この方法は、コンパイラの最適化や、浮動小数点レジスタとメモリとの精度の差(レジスタの方が精度が高い場合が多い)によって正常に動作しない場合もあるようです。
具体例として、サイコロを一回投げる試行と標準コーシー分布を作成してあります。コーシー分布については平均・分散がないので、NaN を返すようにしてあります。
今回は、抽象的な話題ばかりになったので、次回はもう少し具体的な確率分布を紹介していきたいと思います。このあたりの話題は非常に奥が深く、その全てを紹介するには範囲が広すぎて、自分が消化しきれていないところも多々あります。確率論に関してはいろいろな書籍があって、ネット上でも話題が豊富にありますので、興味のある方は調べてみることをお勧めします。
確率論の書籍などを見ると必ず「測度論」「ルベーグ積分」「ボレル集合」などの言葉が見られます。今までの説明の中にはこれらの言葉は一切使っていませんが、確率論を勉強する上で「測度論」や「ルベーグ積分」は切り離せない話題であるようです。しかし、実際に統計学などで用いられる確率分布においては、これらを理解していなければ分からないようなものは見たことがないので、本文の中ではバッサリと省略してあります(自分もまだ勉強中で、完全に理解していないというのも理由の一つです)。
断面が六角形の鉛筆を使って、サイコロの代わりとした経験はあるでしょうか? 表面に 1 〜 6 までの数字を書いておけば、サイコロと同じように使うことができます。全ての面が等しい確率を持つとすれば、サイコロの場合と同様に、それぞれの数字になる確率は 1 / 6 になります。正多面体は五種類しかなく、面の数の最大は 20 なので、それ以上の数を持ったサイコロを作ることはできませんが、鉛筆なら断面を正多角形の形にすることで、100 面でも 200 面でも(理論上は)可能です。
断面を円形にして、その面に 0 ≤ x < 1 の範囲の実数 ( 半開区間[ 0, 1 ) ) を全て書いたとします。この時、確率空間を
Ω = [ 0, 1 )
β = Ω から成る完全加法族
任意の x ∈ Ω に対して ρ(x) ≧ 0 かつ ∫{x∈Ω} ρ(x) dx = 1
μ(A) = ∫{x∈A} ρ(x) dx
と定義すると、β はいろいろな決め方が考えられます。例えば、β = { ∅, Ω } とすれば β は有限加法族となりますが、μ(∅) = 0 と μ(Ω) = 1 だけ定義できても意味はないので役に立つモデルとはなりません。β を [ 0, 1 ) の範囲の全実数を使って完全加法族を定義すると、β の元 Aα = ∪i{1→∞}( xi ) が定義できますが、これは Ω の可算個の元の和集合であり、Ω の濃度は 2ℵ0 なので、直感的に考えても μ(Aα) = 0, μ(Aαc) = 1 となって、やはり意味のないモデルとなってしまいます(これは、例えばサイコロが有理数を示す確率がゼロであることを表しています)。
区間 [ 0, 1 ) において数列 { a0 = 0, a1, ... an, ... } が定義できて an → 1 ( n → ∞ ) ならば、Ω の元として { In = [ an-1, an ) } ( n = 1, 2, ... ) を考えることで、β を { In } の部分集合全体から成る完全加法族とすることができます。このとき、β は { In } と ∅, Ω を含み、さらに任意の In の和集合を全て含んだ集合族となるので、Im ∩ In = ∅ ( m ≠ n ) より、{ In } に対して確率 μ( In ) が定義できれば
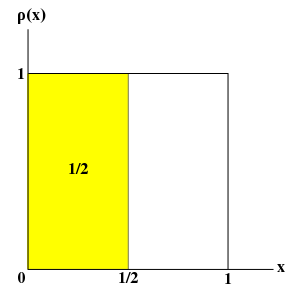
となって、確率空間が完成することになります。ak = k / n とすれば、In は全て 1 / n の幅を持つことになります。各区間に対する確率が等しいと仮定すると、ρ(x) = 1 とすれば ∫{0→1} ρ(x) dx = 1 が成り立ち、例えば μ( In ≤ 1/2 ) = ∫{0→1/2} ρ(x) dx = 1 / 2 と表すことができます。ここで、n → ∞ においては In はある実数に収束し、その時 μ( In ) → 0 になるので、サイコロがちょうどある実数を示す確率はゼロであり、連続分布では区間で確率を定義することになります。
集合 Ω に対し、その部分集合を使って次の公理を満たすように開集合を定義したとき、その開集合族を「位相(Topology)」といい、位相を伴った集合を「位相空間(Topological Space)」と呼んで、位相を τ としたとき、位相空間を ( Ω, τ ) で表します。
任意の元が必ず開集合のどれかに属し、その和集合が開集合なので、Ω が開集合になることが導かれます。また、有限個の積集合を「ゼロ個」も含めて解釈すれば、空集合が開集合になることも導かれるので、上記の公理の一番上は他の公理から得ることができます。
位相空間の開集合全てを含む完全加法族の中で最小のものを「ボレル集合族(Borel Family of Sets)」といいます。完全加法族では補集合も含めますが、位相空間においては開集合に対する補集合を閉集合とします。よって、ボレル集合族は開集合と閉集合の全てを含み、さらにその和集合や積集合も全て含めた大きな集合族になります。
先程の確率空間で定義した { In } は位相としての公理を満たします。任意個の和集合は事象を表し、その補集合もまた In の和集合になります(よって、開集合は閉集合でもあることになります)。積集合は全て空集合になるので、ボレル集合族には Ω, ∅, 任意の In の和集合を全て含むことになります。
ところで、先程の確率空間では全ての区間において等しい確率を持つと仮定しましたが、これを次のような確率密度に置き換えてみます。
任意の q ∈ Q ∩ [ 0, 1 ), r ∈ ( R - Q ) ∩ [ 0, 1 )に対して
μ( q ) = a, μ( r ) = b ( 但し 0 ≤ a ≤ 1, 0 ≤ b ≤ 1 )
つまり、μ(x) は [ 0, 1 ) の範囲の有理数と無理数で確率密度が異なるような関数になります。サイコロに細工をして(例えば有理数部分だけに凹みを付けて)、確率が等しくないようにしたと考えてみて下さい。ここで、a と b の値はまだ未知数で、∫{x∈Ω} ρ(x) dx = 1 が成り立つようにしなければなりません。しかし、この積分を求めることは不可能です。積分が成り立つためには、区分ごとの面積を矩形で表したときの上限と下限が極限において等しくなる必要があります (数値積分法 - 1 - の 定積分の定義 参照)。しかし、どのように区間を分けてもその中には有理数と無理数が存在するので、上限と下限は a または b のいずれかになって、等しくなることはないからです。
定積分法として学校で一般的に教えられているのは「リーマン積分(Riemann Integral)」と呼ばれる積分法です。定積分法自体は古代ギリシャ時代から使われていましたが、厳密に定義を行ったのは「リーマン予想(Riemann Hypothesis)」で有名な「ベルンハルト・リーマン(Bernhard Riemann)」で、その名を取って名付けられています。同様に、考案者「アンリ・ルベーグ(Henri Lebesgue)」の名を取って名付けられた積分法に「ルベーグ積分(Lebesgue Integral)」というものがあり、この積分法を使うと先程の積分値を求めることができます。
まず、「測度(Measure)」というものを定義します。
| 1. | 実数直線上の閉区間 I = [ a, b ] の長さを測度といい、m(I) = b - a で表す |
| 2. | a = b ならば m(I) = 0 つまり、点の測度はゼロとする |
| 3. | m( ( a, b ) ) = m ( [ a, b ) ) = m( ( a, b ] ) = m( [ a, b ] ) = b - a m( ( a, a ) ) = m(∅) = 0 |
| 4. | 平行移動しても測度は不変 m( [ a + h, b + h ] ) = m( [ a, b ] ) = b - a |
| 5. | 可算個の半開区間 In = [ in-1, in ) に対して I = ∪n{1→∞}( In ), Im ∩ In = ∅ ( m ≠ n ) ならば m(I) = Σn{1→∞}( m(In) ) (完全加法性) |
今までも実数直線上の区間の長さを使って積分などを行い面積を求めていたので、上記内容はイメージできると思います。点の測度(長さ)はゼロとしたので、両端点が同じであれば閉区間・開区間・半開区間は全て同じ測度を持ち、平行移動に対して不変であることも簡単に納得できます。
点の測度をゼロとしたということは、その和集合の測度もゼロになります。すると、点の集合からなる区間の測度もゼロになるように見えますが、実数直線上のある区間内に存在する点は可算個ではない(連続体濃度になる)ので、そのように考えることはできません。最後の完全加法性の定義は、あくまでも可算個の半開区間に対する和集合に対する測度の求め方を表していることに注意して下さい。しかし、いずれにしても、可算個の点の和集合の測度はゼロになりそうに思えるので、完全加法性を使って証明してみます。
[ 0, 1 ) 上の可算個の点列 { xn } ( n = 1, 2, ... ) を昇順に並べる。まず、y1 = x1 として、y1 を含む閉区間 I1 = [ y1 - ε / 2, y1 + ε / 2 ] をとると、
になる。次に、I1 に含まれない最小の元を { xn } から取り、それを y2 として、I2 = [ y2 - ε2 / 2, y2 + ε2 / 2 ] を I1 ∩ I2 = ∅ かつ ε2 ≤ ε / 2 が成り立つようにとると、
以下、Ik-1 まで閉区間を決めたとして、∪m{1→k-1}( Im ) に含まれない最小の元を { xn } から取り、それを yk として、Ik = [ yk - εk / 2, yk + εk / 2 ] を Ik-1 ∩ Ik = ∅ かつ εk ≤ ε / 2k-1 が成り立つようにとると、
になる。{ xn } の測度を m(I) とすると、完全加法性の定義から
| m(I) | = | Σn{1→∞}( m(In) ) |
| = | Σn{1→∞}( εn ) | |
| ≤ | Σn{1→∞}( ε / 2n-1 ) = 2ε |
ここで、ε はいくらでも小さくすることができるので、m(I) はゼロとなる。
可算個の点列として有理数を選べば、有理数からなる集合の測度はゼロです。測度は平行移動に対して不変なので、実数直線上の全区間に対しても有理数からなる集合の測度はゼロになってしまうわけです。このような集合を「零集合(Null Empty Set)」といいます。
区間 [ 0, 1 ) での有理数の集合の測度はゼロであり、逆に無理数の測度は 1 になります。すると、∫{x∈Ω} ρ(x) dx = ∫{x∈無理数 かつ x∈Ω} b dx = b となって、b = 1 であることになります ( a は定義できません )。
リーマン積分可能であればルベーグ積分可能ですが、その逆は成り立ちません。厳密には、ρ(x) はルベーグ積分が可能でなるという条件が付くのですが、通常はリーマン積分だけで理解ができるので、統計解析に関する書籍ではこのあたりの話はほんの少しだけ書かれて大半は省略されています。しかし「少しだけ」書かれていることで余計に理解ができなくなる場合があることも事実で、ここまで習得するのもかなり長い道のりでした。興味のある方は、末尾に参考とした書籍や URL を書いておきますので参考にしてみて下さい。
lower_p( b ) - lower_p( a ) で p( a, b ) の値を求めることができます。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |