「正規分布(Normal Distribution)」は別名を「ガウス分布(Gaussian Distribution)」といい、ガウスが論文の中で、「最小二乗法」の正確さが正規分布によって説明できることを示したことからこの名が付けられています。この分布は、統計学において最も基本となる分布の一つであり、またその応用範囲も非常に広いことから最もよく知られた確率分布でもあります。この章では、正規分布とその性質について紹介したいと思います。
下式のように表される関数を「ガウス関数(Gaussian Function)」といいます。
これは、画像処理の「ガボール・フィルタ」や「顕著性マップ」でも紹介しているように、画像処理や信号処理などでもよく利用される重要な関数です。
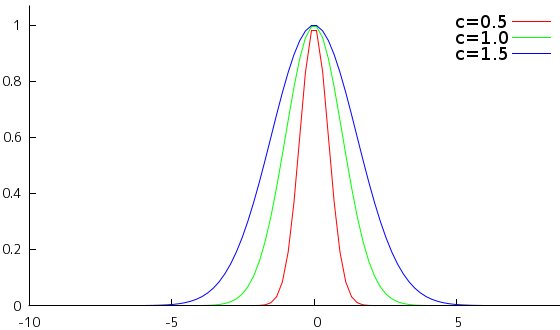
上に示したグラフは、a = 1, b = 0 としたときの、c = 0.5, 1.0, 1.5 に対するガウス関数のグラフを示しています。ガウス関数は、x = b を中心とした左右対称な偶関数で、釣鐘の形に似ていることから「鐘形曲線(Bell Curve)」とも呼ばれます。
a = 1, b = 0, c = 1 / √2 としたとき、g(x) = exp( -x2 ) の形になり、その実数全体での積分は「ガウス積分(Gaussian Integral)」と呼ばれ、
になります。よって、任意のガウス関数の積分は、t = ( x - b ) / √2c ( 但し、c > 0 ) とすれば dt = ( 1 / √2c )dx なので、
| ∫{-∞→∞} a exp( -( x - b )2 / 2c2 ) dx | = | a ∫{-∞→∞} exp( -t2 ) √2c dt |
| = | ac( 2π )1/2 |
で求めることができます。また、ガウス関数は偶関数なので、
が成り立ちます。そこで、t = x2 と変数変換すると、dt = 2x dx となるので、
| ∫{0→∞} exp( -x2 ) dx | = | ∫{0→∞} e-t ( 1 / 2 )t-1/2 dt |
| = | ( 1 / 2 ) Γ( 1 / 2 ) |
と求められます。ここで、Γ( x ) は「ガンマ関数(Gamma Function)」 ∫{0→∞} tx-1 e-t dt を表します。上式の値が √π / 2 となるので、
が成り立ちます。
ガウス関数のフーリエ変換は、
| G(ω) | = | ∫{-∞→∞} a exp( -( x - b )2 / 2c2 ) exp( -iωx ) dx |
| = | a ∫{-∞→∞} exp( -{ x2 - 2( b - ic2ω )x + b2 } / 2c2 ) dx | |
| = | a ∫{-∞→∞} exp( -[ { x - ( b - ic2ω ) }2 - ( b - ic2ω )2 + b2 ] / 2c2 ) dx | |
| = | a ∫{-∞→∞} exp( -[ { x - ( b - ic2ω ) }2 + 2ibc2ω + ( c2ω )2 ] / 2c2 ) dx | |
| = | a exp( -ibω - ( cω )2 / 2 ) ∫{-∞→∞} exp( -{ x - ( b - ic2ω ) }2 / 2c2 ) dx |
ここで、t = x - ( b - ic2ω ) とすれば、dt = dx となって、
| G(ω) | = | a exp( -ibω - ( cω )2 / 2 ) ∫{-∞→∞} exp( -t2 / 2c2 ) dt |
| = | ac( 2π )1/2 e-ibω exp( -ω2 / 2( 1 / c )2 ) |
になります。フーリエ変換は複素関数の積分なので、実際にはもう少しややこしい部分もありますが、そのあたりは上記では省略しています。詳細は、「ガボール・フィルタ」の章の「補足1) ガボール・フィルタのフーリエ変換」をご覧ください。ここで重要なのは、ガウス関数のフーリエ変換が、b = 0 の時はガウス関数になるということです。また、パラメータ c は逆数の関係となることも上記結果から分かります。
二つのガウス関数の積もガウス関数になります。gi(x) = ai exp( -( x - bi )2 / 2ci2 ) ( i = 1, 2 ) とすれば、
| g1(x)・g2(x) | = | { a1 exp( -( x - b1 )2 / 2c12 ) }{ a2 exp( -( x - b2 )2 / 2c22 ) } |
| = | a1a2 exp( -( x - b1 )2 / 2c12 - ( x - b2 )2 / 2c22 ) | |
| = | a1a2 exp( -{ ( c12 + c22 )x2 - 2( b1c22 + b2c12 )x + ( b12c22 + b22c12 ) } / 2c12c22 ) |
ここで、
A = a1a2
C = c12c22 / ( c12 + c22 )
B = ( b1c22 + b2c12 ) / ( c12 + c22 )
D = ( b12c22 + b22c12 ) / ( c12 + c22 )
とすれば、
| g1(x)・g2(x) | = | A exp( -( x2 - 2Bx + D ) / 2C ) |
| = | A exp( { -( x - B )2 + B2 - D } / 2C ) | |
| = | A exp( ( B2 - D ) / 2C ) exp( -( x - B )2 / 2C ) |
となるので、ガウス関数の形になります。特に、b1 = b2 = 0 ならば B = D = 0 なので、
| g1(x)・g2(x) | = | A exp( -x2 / 2C ) |
| = | a1a2 exp( -( c12 + c22 )x2 / 2c12c22 ) |
と表すことができます。ところで、二つの関数の畳み込み積分をフーリエ変換した結果は、それぞれの関数をフーリエ変換した結果の積と等しくなります。
これを「畳み込み積分定理(Convolution Theorem)」といいます。詳細は「サンプル補間」の「5) 補間関数と畳み込み積分」に示してありますが、この性質を利用して、畳み込み積分によって信号の「フィルタ」を行うことができます。この等式に、ガウス関数 gi(x) = ai exp( -x2 / 2ci2 ) ( i = 1, 2 ) を当てはめてみます。
| ∫{-∞→∞} g1(x) * g2(x)・e-iωx dx | = | G1(ω)・G2(ω) |
| = | a1c1( 2π )1/2 exp( -c12ω2 / 2 )・a2c2( 2π )1/2 exp( -c22ω2 / 2 ) | |
| = | 2πa1a2c1c2 exp( -( c12 + c22 )ω2 / 2 ) |
上記から、ガウス関数どうしの畳み込み積分をフーリエ変換してもその結果はガウス関数になることが分かります。ところが、ガウス関数自体をフーリエ変換してもガウス関数のままなので、ガウス関数どうしの畳み込み積分もまたガウス関数であることを意味し、そのパラメータを ac, bc = 0, cc とすれば、
| ∫{-∞→∞} g1(x) * g2(x)・e-iωx dx | = | 2πa1a2c1c2 exp( -( c12 + c22 )ω2 / 2 ) |
| = | accc( 2π )1/2 exp( -cc2ω2 / 2 ) |
より cc = ( c12 + c22 )1/2, ac = a1a2c1c2( 2π / ( c12 + c22 ) )1/2 になります。従って、ガウス関数どうしの畳み込み積分は
と表されます。
ガウス関数 a exp( -( x - b )2 / 2c2 ) の実数全体での積分値は ac( 2π )1/2 となるので、a = 1 / ( 2πc2 )1/2 とすれば積分値は 1 となります。また、ガウス関数は任意の実数 x に対して正値となるので、これを確率密度関数として扱うことが可能です。そこで、
と定義される確率分布を「正規分布(Normal Distribution)」といいます。正規分布の積率母関数は
| g(θ) = E[eθx] | = | ( 1 / ( 2πc2 )1/2 ) ∫{-∞→∞} eθx exp( -( x - b )2 / 2c2 ) dx |
| = | ( 1 / ( 2πc2 )1/2 ) ∫{-∞→∞} exp( { -x2 + 2( c2θ + b )x - b2 } / 2c2 ) dx | |
| = | ( 1 / ( 2πc2 )1/2 ) ∫{-∞→∞} exp( [ -{ x - ( c2θ + b ) }2 + ( c2θ + b )2 - b2 ] / 2c2 ) dx | |
| = | ( 1 / ( 2πc2 )1/2 ) exp( { ( cθ )2 + 2bθ } / 2 ) ∫{-∞→∞} exp( -{ x - ( c2θ + b ) }2 / 2c2 ) dx | |
| = | ( 1 / ( 2πc2 )1/2 ) exp( { ( cθ )2 + 2bθ } / 2 ) ( 2πc2 )1/2 | |
| = | exp( { ( cθ )2 + 2bθ } / 2 ) |
g(θ) を微分すると、
なので、正規分布の平均値 μ は
になります。二階導関数 g(2)(θ) は、
となるので、
よって、分散 σ2 は
つまり、パラメータ b は平均を、c は標準偏差をそれぞれ表していたことになります。そこで、式のパラメータを変えて、
のことを、平均 μ、分散 σ2 の正規分布と呼びます。特に、μ = 0, σ = 1 となる正規分布
は「標準正規分布(Standard Normal Distribution)」といいます。
正規分布の性質についてまとめておきます。
正規分布 N( μ, σ2 ) = ( 1 / ( 2πσ2 )1/2 ) exp( -( x - μ )2 / 2σ2 )
平均 : μ、分散 : σ2
ガウス関数が持つ性質は正規分布にも当然あって、μ を中心として左右対称な偶関数で釣鐘の形に似ているところや、N( 0, σ2 ) のフーリエ変換が N( 0, 1 / σ2 ) になるなどの特徴を持っています。また、N( μ, σ2 ) において [ μ - σ, μ + σ ] の区間の確率は 68.26 %、[ μ - 2σ, μ + 2σ ] の区間の確率は 95.44 %、[ μ - 3σ, μ + 3σ ] の区間の確率は 99.74 % となることもよく利用される性質です。
/* NormalDistribution : 正規分布 */ class NormalDistribution : public ContDist { double _mu; // 平均 double _var; // 分散 public: /* コンストラクタ double mu : 平均 double sigma : 標準偏差 */ NormalDistribution( double mu, double sigma ) : _mu( mu ), _var( pow( sigma, 2 ) ) {} // 確率変数 a における確率密度を返す double operator[]( double x ) const { return( exp( -pow( x - _mu, 2 ) / ( 2 * _var ) ) / sqrt( 2 * M_PI * _var ) ); } // 区間 (-∞,a] における確率を返す double lower_p( double a ) const; // 区間 [a,b] における確率を返す double p( double a, double b ) const; double average() const { return( _mu ); } // 平均値 double variance() const { return( _var ); } // 分散 }; /* NormalDistribution::lower_p : 区間 (-∞,a] における確率を返す double a : 区間の上限 戻り値 : 確率 */ double NormalDistribution::lower_p( double a ) const { a = ( a - _mu ) / sqrt( 2 * _var ); double p = erf( fabs( a ) ) / 2.0; if ( a < 0 ) p = 0.5 - p; else p += 0.5; return( p ); } /* NormalDistribution::p : 区間 [a,b] における確率を返す double a, b : 確率を求める区間 戻り値 : 確率 */ double NormalDistribution::p( double a, double b ) const { if ( a == b ) return( 0 ); if ( a > b ) { double d = a; a = b; b = d; } a = ( a - _mu ) / sqrt( 2 * _var ); b = ( b - _mu ) / sqrt( 2 * _var ); if ( a > 0 && b > 0 ) { return( ( erf( b ) - erf( a ) ) / 2 ); } else if ( a < 0 && b > 0 ) { return( ( erf( b ) + erf( -a ) ) / 2 ); } else { return( ( erf( -a ) - erf( -b ) ) / 2 ); } }
コンストラクタでは、平均値 mu と標準偏差 sigma を指定するようにしてあります。標準偏差として負数を指定しても、メンバ変数は分散(_var)として平方値を計算するので、必ず正数になります。よって、sigma が正数かどうかはチェックしていません。
確率を求めるためには、ガウス関数を有限な範囲で積分する必要がありますが、ガウス関数の不定積分を求めることはできないので、通常は「数値積分法」を利用して積分値を求めることになります。しかし、C 言語や C++ では通常、erf という関数が用意されています。これは「誤差関数(Error Function)」と呼ばれる特殊関数の値を求めるための関数で、次のような式で表されます。
これは、標準正規分布の [ -x, x ] の範囲の積分値を意味しています。任意の正規分布の [ a, b ] の範囲の積分値は、erf(x) を使って次のように表すことができます。
| ∫{a→b} ( 1 / ( 2πσ2 )1/2 ) exp( -( t - μ )2 / 2σ2 ) dt | = | ( √2σ / ( 2πσ2 )1/2 ) ∫{( a - μ ) / √2σ→( b - μ ) / √2σ} exp( -u2 ) du |
| = | ( 1 / √π ){ ∫{( a - μ ) / √2σ→0} exp( -u2 ) du + ∫{0→( b - μ ) / √2σ} exp( -u2 ) du | |
| = | ( 1 / √π )( √π / 2 ){ erf( ( b - μ ) / √2σ ) - erf( ( a - μ ) / √2σ ) } | |
| = | { erf( ( b - μ ) / √2σ ) - erf( ( a - μ ) / √2σ ) } / 2 |
u(t) = ( t - μ ) / √2σ と変数変換すると、du = ( 1 / √2σ ) dt, u(a) = ( a - μ ) / √2σ, u(b) = ( b - μ ) / √2σ となるので上式のように変形することができます。erf(x) は [ -x, x ] の範囲の積分値を意味しており、μ を中心として偶関数の形になるため、それぞれの値は最終的に 2 で徐算される形になっています。
正規分布は、二項分布の試行回数 N が充分大きい場合の近似として紹介されたのが最初とされています。その後、「ルジャンドル(Adrien-Marie Legendre)」や「ガウス(Johann Carl Friedrich Gauss)」によって、測定誤差の分布が正規分布に従うとする考え方から「最小二乗法(Least Squares Method)」が誕生しました。
二項分布の近似が正規分布であることを導いたきっかけを作ったのは「ド・モアブル(Abraham de Moivre)」、その考え方を発展させたのは「ピエール = シモン・ラプラス(Pierre-Simon Laplace)」とされています。この考え方をさらに発展して後に述べる「中心極限定理(Central Limit Theorem)」が証明され、正規分布は非常に重要な確率分布としての地位を確立することになります。正規分布誕生の背景には、この 4 名の数学者による貢献があったことは疑いようのない事実とされています。
二項分布の正規分布による近似は「ド・モアブル = ラプラスの定理(De Moivre-Laplace Theorem)」と呼ばれています。
二項分布 BN,p(r) = NCrprqN-r = { N! / r!( N - r )! } prqN-r において、t = ( r - μ ) / σ (但し、μ = Np, σ2 = Npq) とすると、dt = ( 1 / σ )dr となって、t によって変数変換された分布を B(t) とすれば B(t)dt = BN,p(r)dr が成り立つので
| B(t) | = | σ BN,p(r) |
| = | ( Npq )1/2 { N! / r!( N - r )! } prqN-r | |
| = | { N! N1/2 / r!( N - r )! } pr+1/2qN-r+1/2 |
ここで、「スターリングの公式(Stirling's Formula)」より
が成り立つので、
| B(t) | ≅ | { ( 2πN )1/2( N / e )N N1/2 / ( 2πr )1/2( r / e )r { 2π( N - r ) }1/2{ ( N - r ) / e }N-r } pr+1/2qN-r+1/2 |
| = | { NN+1 e-N / ( 2π )1/2 rr+1/2 e-r ( N - r )N-r+1/2 e-N+r } pr+1/2qN-r+1/2 | |
| = | ( 1 / 2π )1/2{ Nr+1/2・NN-r+1/2・pr+1/2・qN-r+1/2 / rr+1/2 ( N - r )N-r+1/2 } | |
| = | ( 1 / 2π )1/2 ( Np / r )r+1/2 { Nq / ( N - r ) }N-r+1/2 |
ここで、t = ( r - μ ) / σ を r について解くと
よって、
また、
より
になります。これらを代入すると、
L(t) = -ln( ( 2π )1/2B(t) ) とすると、
| L(t) | = | ln ( { 1 + ( q / Np )1/2t }Np+( Npq )1/2t+1/2 { 1 - ( p / Nq )1/2t }Nq-( Npq )1/2t+1/2 ) |
| = | { Np+( Npq )1/2t+1/2 } ln( 1 + ( q / Np )1/2t ) + { Nq-( Npq )1/2t+1/2 } ln( 1 - ( p / Nq )1/2t ) |
ここで、f(x) = ln( 1 + x ) のマクローリン展開は、f(n)(x) = (-1)n-1 ( n - 1 )! ( 1 + x )-n より
になります。x が充分小さくて、3 次以降の高次項を無視すれば、ln( 1 + x ) ≅ x - x2 / 2 とすることができて、N が充分に大きければ ( q / Np )1/2t と ( p / Nq )1/2t は充分小さいと考えることができるので、
| L(t) | ≅ | { Np + ( Npq )1/2t + 1 / 2 } { ( q / Np )1/2t - ( q / Np )t2 / 2 } + { Nq - ( Npq )1/2t + 1 / 2 } { -( p / Nq )1/2t - ( p / Nq )t2 / 2 } |
| = | ( Npq )1/2t - qt2 / 2 + qt2 - ( q3 / Np )1/2t3 / 2 + ( q / Np )1/2t / 2 - ( q / Np )t2 / 4 | |
| - ( Npq )1/2t - pt2 / 2 + pt2 + ( p3 / Nq )1/2t3 / 2 - ( p / Nq )1/2t / 2 - ( p / Nq )t2 / 4 |
ここでも、N が充分に大きければ、N を分母に持つ項は無視できるほど小さくなって
| L(t) | ≅ | ( Npq )1/2t - qt2 / 2 + qt2 - ( Npq )1/2t - pt2 / 2 + pt2 |
| = | ( p + q )t2 / 2 = t2 / 2 |
よって、
これは、標準正規分布の式そのものになります。B(t) = σ BN,p(r) なので、
| BN,p(r) | = | ( 1 / σ ) B(t) |
| ≅ | ( 1 / 2πσ2 )1/2 exp( -t2 / 2 ) | |
| = | ( 1 / 2πσ2 )1/2 exp( -( r - μ )2 / 2σ2 ) |
よって、N が充分に大きければ、二項分布は正規分布に近似することができます。
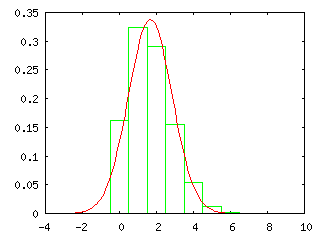
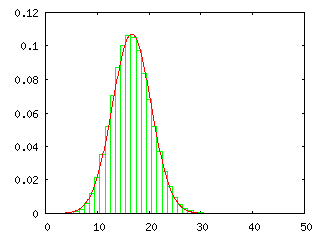
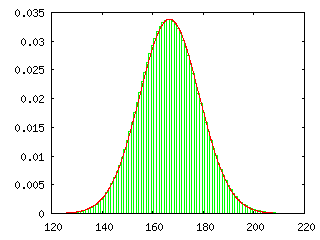
下のグラフは、二項分布 BN,p(r) = NCrprqN-r と正規分布 N( Np, Npq ) = ( 1 / ( 2πNpq )1/2 ) exp( -( x - Np )2 / 2Npq ) ( p = 1 / 6, q = 5 / 6 ) を実際に重ね合わせた結果を示しています。左側から順に試行回数 N を 10, 100, 1000 回としていますが、N = 10 の時点ですでによく似た分布となっていることがわかります。二項分布では階乗の計算が必要なので、まともに計算しようとすると計算がかなり大変です。スターリングの公式(Stirling's Formula)を利用すればある程度簡単に計算できるようになりますが、それよりも正規分布の式を利用した方が簡単に確率密度の近似値が得られます。下の結果を見ると、試行回数が 100 回程度になれば、ある程度の精度を持った近似値が得られることになります。
| N = 10 | N = 100 | N = 1000 |
|---|---|---|
 |
 |
 |
二項分布 BN,p(r) = NCrprqN-r において、確率変数 r を t = r / N に置き換えると、平均は p、分散は pq / N になることを、前章の「確率変数の変換」で紹介しました。N → ∞ のとき、分散はゼロに収束するため、その分布は「ディラックのデルタ関数(Dirac's Delta Function)」になります。
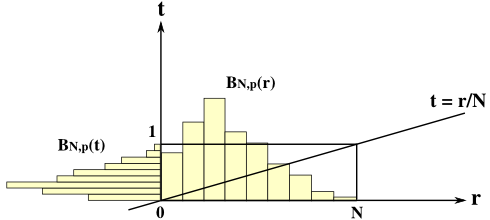
確率変数の範囲は 1 / N から N / N = 1 の間になることから、N → ∞ では [0,1] となり、その区間内の t = p に全ての分布が集中したような形になります。つまり、少ない試行回数では事象が起こる回数が平均 Np から外れる場合があっても、試行をたくさん繰り返せば、事象が起こる回数は Np にいくらでも近づいていくことになります。
二項分布は、一回の試行が起こる確率を p としたとき、N 回の試行で r 回発生する確率を表していました。一回の試行に注目すると、事象が起こる確率が p ( 0 ≤ p ≤ 1 ) で、起こらない確率が 1 - p になるので、事象を A とすれば、P(A) = p, P(A~) = 1 - p, P(Ω) = P(A) + P(A~) = 1 となって、これは確率空間として成り立っています。この確率分布は「ベルヌーイ分布(Bernoulli Distribution)」と呼ばれています。
ベルヌーイ分布の確率変数を x(A) = 1, x(A~) = 0 としたとき、試行を N 回繰り返したときの標本点を「ベルヌーイ列(Bernoulli Sequence)」といって
と表されることを「確率空間」の章で紹介しました。あるベルヌーイ列 a = ( a1, a2, ... aN ) は N 次元空間上にある超立方体上の各頂点を表していて、その同時確率を P(a) としたとき、
とすれば、異なる番号 i, j について ai と aj がどちらも 1 になる確率は、ai が 1 になる確率と aj が 1 になる確率の積で表されるので、それぞれの番号の事象は互いに独立となるのでした。つまり、ai が 1 になる事象を Ai と表せば、
になります(詳細は「多変数の確率分布」の末尾を参照)。また、それぞれの変数が独立していることは、ベルヌーイ列の中で事象が起こった回数が Σi{1→N}ai、起こらなかった回数が N - Σi{1→N}ai で、P(a) は事象が起こる確率 p と 起こらない確率 1 - p のそれぞれを回数分だけ掛けたものであることからも分かります。
さらに、事象が発生する回数が等しい標本点の確率の和に対する分布を求めたものが二項分布 BN,p(r) となり、確率変数 r を t = r / N に変換することは、和を総試行回数で割ることを意味していることから、これはベルヌーイ分布に従う試行を N 回繰り返したときの平均に対する分布と考えることができます。このとき、試行回数を増やすほど分散はゼロに近づき、分布は平均に近づいていきます。これを「大数の法則(Law of Large Numbers)」といいます。
下に示したグラフは、サイコロを投げたときに 1 の目が出た回数を試行回数で割った数、つまり全体の中で 1 の目が出た割合が、試行回数が増えるごとにどのように変化していくかを表したものです。サイコロを投げる試行は 100000 回繰り返していますが、実際に 100000 回もサイコロを投げて試すのはあまりにも時間がかかるので、乱数を利用したシミュレーションによって求めています。1 の目が出た割合は、試行回数が増えるにしたがって 1 / 6 ( グラフ上の赤いライン ; ≅ 0.167 ) に近づいていく様子がこの結果から分かります。

また、下のグラフは、ある試行回数分だけサイコロを投げて、1 の目が出る回数の全体との比率を求める操作を、試行回数を増やしながら繰り返した結果を示したもので、横軸は総試行回数を表しています。上側に示したグラフが一回の操作として、それを総試行回数を変えながら何度も繰り返すわけです。

総試行回数が少ない間は非常にバラツキが大きかったのが、試行回数が増えるにしたがって平均を中心として徐々に集まってくる様子がわかります。「ド・モアブル = ラプラスの定理(De Moivre-Laplace Theorem)」より、これを縦方向に輪切りにしたときの断面は、平均に近いほど点が密集した状態になり、ヒストグラムで表せばその形状は正規分布にかなり近い状態となるはずです。試行回数が無限に大きくなったときは分散がゼロに収束し、分布はディラックのデルタ関数になることから、正規分布も同様に、分散がゼロに収束したときはディラックのデルタ関数になります。
サイコロを投げたときに 1 の目が出る確率を私たちは 1 / 6 と定義しますが、これは、サイコロを何回も投げると全体の 1 / 6 は 1 の目になることを経験的に知っているためにそうしているわけで、本当に 1 の目が出る確率が 1 / 6 であることが証明できるわけではありません。逆に、サイコロを投げたときに 1 の目が出る確率を 1 / 6 と定義して二項分布に当てはめてみると、事象が起こる( 1 の目が出る)回数は試行を繰り返すほど全体の 1 / 6 に近づいていき、それが実際に測定した結果とよく合うようになるわけです。二項分布というモデルをサイコロを投げる事象に当てはめてみると、1 の目が出る回数の平均が 1 / 6 に収束していくことから、サイコロを 1 回投げたときに 1 の目が出る確率を 1 / 6 と考えると都合がいいわけで、最初から 1 / 6 であることが決まっているわけではないということに注意して下さい。
ベルヌーイ分布だけでなく、任意の確率分布に従う試行を繰り返した場合はどうなるのでしょうか。それを検討する前に、「チェビシェフの不等式(Chebyshev's Inequality)」を紹介します。
確率密度関数 p(x) の平均が μ であるとき、分散 σ2 の求め方は次のようになります。
この積分を、任意の定数 k を使って | x - μ | ≥ k と | x - μ | < k の二つに分けると
となりますが、第一項は | x - μ | ≥ k なので常に ( x - μ )2 ≥ k2 が成り立ち、
| σ2 | ≥ | ∫{| x - μ | ≥ k} k2p(x) dx + ∫{| x - μ | < k} ( x - μ )2p(x) dx |
| = | k2∫{| x - μ | ≥ k} p(x) dx + ∫{| x - μ | < k} ( x - μ )2p(x) dx |
第二項めは正なのでこれを取り除けば
になります。∫{| x - μ | ≥ k} p(x) dx は | x - μ | ≥ k の範囲の確率を表すので、これを P( | x - μ | ≥ k ) と表せば、
よって、
この不等式を「チェビシェフの不等式(Chebyshev's Inequality)」といいます(補足1)。
任意の確率分布上にある独立した確率変数 x1, x2, ... xN が、以下の条件を満たすとします。
各確率変数の期待値が等しい : E[x1] = E[x2] = ... = E[xN] = μ
分散が有限である(発散しない) : V(xi) = E[( xi - μ )2] < ∞ ( i = 1, 2, ... N )
まず、m = ( x1 + x2 + ... + xN ) / N とすれば、和の期待値は期待値の和になるので (前章の「相関係数」を参照)、各確率変数が独立なことから、
| E[m] | = | E[ ( x1 + x2 + ... + xN ) / N ] |
| = | Σi{1→N}( E[ xi / N ] ) | |
| = | Σi{1→N}( E[xi] / N ) | |
| = | Σi{1→N}( μ ) / N = μ |
V(m) = E[( m - μ )2] = E[m2] - μ2 より、
を使って
| E[m2] | = | Σi{1→N}( ∫{-∞→∞}...∫{-∞→∞} ( xi2 + Σj{1→N;j≠i}( xixj ) ) p1( x1 )...pN( xN ) dx1...dxN ) / N2 |
| = | Σi{1→N}( ∫{-∞→∞} xi2pi( xi ) dxi + Σj{1→N;j≠i}( ∫{-∞→∞} xi pi( xi ) dxi ∫{-∞→∞} xj pj( xj ) dxj ) ) / N2 | |
| = | Σi{1→N}( E[xi2] + Σj{1→N;j≠i}( E[xi]E[xj] ) ) / N2 | |
| = | Σi{1→N}( E[xi2] + ( N - 1 )μ2 ) / N2 | |
| = | Σi{1→N}( E[xi2] - μ2 ) / N2 + μ2 | |
| = | Σi{1→N}( V( xi ) / N2 ) + μ2 |
よって、
ここで、各 V( xi ) は発散しないので、この中の最大値を σ2 とすれば、
チェビシェフの不等式より、任意の ε に対して
m = ( x1 + x2 + ... + xN ) / N, E[m] = μ だったので、
つまり、任意の ε に対して、N をいくらでも大きくすることで P( | ( x1 + x2 + ... + xN ) / N - μ | ≥ ε ) をゼロに収束させることができます。
分布の状態を調べたいとき、その対象となる集団を「母集団(Statistical Population)」といいます。例えば、日本人の成人男女に対して身長と体重の分布を調べたいとすれば、日本全土にいる(または海外に在住している人も含めて)全ての成人男女が母集団となります。しかし、全ての人の身長と体重を計測して分布を作ろうのは非常に大変でコストも掛かるので、代わりに母手段の中から一部のデータを抽出して分布の状態を推定します。このとき抽出したデータを「標本(Sample)」といいます。母集団がある確率分布に従うとき、その分布の名称を先頭に付けます。例えば、正規分布に従うのであれば、「正規母集団」といいます。
m = ( x1 + x2 + ... + xN ) / N は「標本平均(Sample Mean)」または「算術平均(Arithmetic Mean)」と呼ばれ、母集団から任意の数だけ抽出した標本値の総和を標本数で割った値を意味します。大数の法則は、各標本の母集団の分布がどのようなものであれ、平均が等しくて分散が有限でさえあれば、その中から抽出した標本の標本平均は、標本数を多くするほど母集団の平均に近づいていくことを表しているわけです。
「ド・モアブル = ラプラスの定理(De Moivre-Laplace Theorem)」によって、二項分布にて試行回数を大きくすれば、正規分布に近づいていくことが示されました。二項分布は、ベルヌーイ分布に従う独立した確率変数の総和に対する分布であり、それが正規分布に近づいていくことになるので、ベルヌーイ試行を繰り返して総和を求める操作を何回も行って、その結果を元に分布を書いていくと、それが正規分布になると考えることもできます。また、総和ではなく標本平均を使えば、正規分布の平均はベルヌーイ分布で事象が起こる確率に一致します。大数の法則によって、ベルヌーイ分布だけでなく任意の確率分布についても標本平均が母集団の平均に近づいていくことが示されましたが、任意の確率分布に対してその標本平均を求める操作を繰り返し、その結果を元に分布を書いてみると、分布の形状はどのようになるのでしょうか。
大数の法則の場合より少し条件を厳しくして、同一の確率分布上にある独立した確率変数 x = ( x1, x2, ... xN ) について、E[xi] = μ、V(xi) = E[( xi - μ )2] = σ2 ( i = 1, 2, ... N ) が成り立つとします。
としたとき、yi の積率母関数を gi(θ) とすると
| gi(θ) | = | E[exp( θyi )] |
| = | E[exp( θ( xi - μ ) / σ )] | |
| = | ∫{-∞→∞}...∫{-∞→∞} exp( θ( xi - μ ) / σ ) p(x1)...p(xN) dx1...dxN | |
| = | ∫{-∞→∞} exp( θ( xi - μ ) / σ )p(xi) ) dxi | |
| = | E[exp( θ( xi - μ ) / σ )] |
になります。gi(θ) を微分すると、
| gi'(θ) | = | ∫{-∞→∞} ( d / dθ ) exp( θ( xi - μ ) / σ )p(xi) dxi |
| = | ∫{-∞→∞} { ( xi - μ ) / σ } exp( θ( xi - μ ) / σ )p(xi) dxi |
よって、
| gi'(0) | = | ∫{-∞→∞} { ( xi - μ ) / σ } p(xi) dxi |
| = | ( E[xi] - μ ) / σ = 0 |
もう一度微分して、
| gi(2)(θ) | = | ∫{-∞→∞} ( d / dθ ) { ( xi - μ ) / σ } exp( θ( xi - μ ) / σ )p(xi) dxi |
| = | ∫{-∞→∞} { ( xi - μ ) / σ }2 exp( θ( xi - μ ) / σ )p(xi) dxi |
より、
| gi(2)(0) | = | ∫{-∞→∞} { ( xi - μ ) / σ }2 p(xi) dxi |
| = | σ2 / σ2 = 1 |
となります。gi(0) = E[1] = 1 なので、g(θ) の マクローリン級数(Maclaurin Series) は
| gi(θ) | = | g(0) + g'(0)θ + g(2)(0)θ2 / 2 + ... |
| = | 1 + θ2 / 2 + ... |
となって、θ がゼロに非常に近ければ、三次以降の項を無視して
になります。ここで、
としたとき、y の積率母関数を g(θ) とすると、
| g(θ) | = | E[eθy] |
| = | E[exp( θΣi{1→N}( yi / √N ) )] | |
| = | E[Πi{1→N}( exp( θyi / √N ) )] |
ここで、xi が互いに独立なことから exp( θyi / √N ) も互いに独立となるので、積の期待値は期待値の積で表すことができて
| g(θ) | = | Πi{1→N}( E[exp( θyi / √N )] ) |
| = | Πi{1→N}( gi(θ / √N) ) |
gi(θ) ≅ 1 + θ2 / 2 より、gi(θ / √N) ≅ 1 + ( θ / √N )2 / 2 = 1 + θ2 / 2N となるので
| g(θ) | ≅ | ( 1 + θ2 / 2N )N |
| = | { 1 + 1 / ( 2N / θ2 ) }( 2N / θ2 )・( θ2 / 2 ) |
ネイピア数の定義から ( 1 + 1 / N )N → e ( N → ∞ ) なので、
になります。ところで、標準正規分布 N( 0, 1 ) = { 1 / sqrt( 2π ) }exp( t2 / 2 ) の積率母関数は exp( θ2 / 2 ) なので、先ほど求めた g(θ) はゼロの近傍において標準正規分布のそれと近似していることになります。このことは、確率分布の形も近似していることを意味することになり(補足2)、
として y の確率密度 p(y) を考えたとき、N が大きくなるに従ってそれは標準正規分布に近づいていくことを意味します。すなわち、
m = Σi{1→N}( xi ) / N としたとき
y = Σi{1→N}( ( xi - μ ) / σ√N ) = ( m - μ )√N / σ
dy = ( √N / σ )dm
となるので、p(y) を q(m) に変換したときは、p(y)dy = q(m)dm より
| q(m) | = | ( √N / σ ){ 1 / sqrt( 2π ) }exp( { ( m - μ )√N / σ }2 / 2 ) |
| = | { 1 / sqrt( 2πσ2 / N ) }exp( { ( m - μ ) / ( 2σ2 / N ) ) | |
| = | N( μ, σ2 / N ) |
すなわち、m の確率分布は N が大きければ N( μ, σ2 / N ) に近づきます。
平均 μ、分散 σ2 を持つ確率分布に従う母集団から互いに独立な標本を N 個抽出する操作を何回も繰り返したとき、その標本平均からなる分布は N( μ, σ2 / N ) に近似されるということがこれで示されたことになります。これを「中心極限定理(Central Limit Theorem)」といい、この定理から、正規分布が非常に重要な確率分布であることが理解できると思います。
大数の法則から、標本平均は N が大きくなるに従って母集団の平均に収束していきます。従って、中心極限定理においても N が大きくなれば分散はゼロに収束していき、その極限において正規分布はディラックのデルタ関数になります。大数の法則では標本平均が期待値に近づくことから、このことを「確率収束(Convergence in Probability)」といい、中心極限定理では分布が正規分布に近づくことから「分布収束(Converge in Distribution)」または「弱収束(Converge Weakly)」、「法則収束(Converge in Law)」などと呼ばれます。
ここで重要なのは、母集団がどんな確率分布に従っていようとも、平均と分散さえあれば、標本平均を求める操作を繰り返したときにその分布が正規分布に従うという事実です。また、標本平均を求める時に、その標本数が多いほど母集団の平均に近い値が得られます。このことは、統計学における様々な手法の骨組みとなっています。
本当に、中心極限定理が成り立つのか、実際に任意の確率分布から確率変数の標本平均を求め、その分布を調べてみた結果を以下に示します。
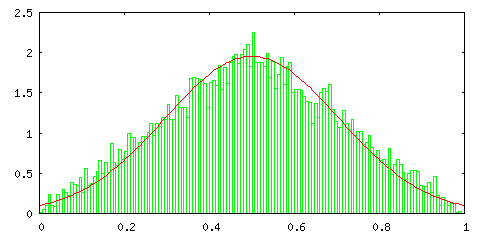
まずは、[0,1] の範囲の一様乱数を使ってその標本平均を計算し、ヒストグラムで表してみます。これは、一様分布 p0,1(x) から確率変数を抽出して標本平均を求めた結果を意味しています (補足3)。確率変数の取り得る範囲は [0,1] で、標本計算の算出は 10000 回繰り返して、150 個の階級に分けて度数を求め、そのヒストグラムを出力しています。赤線は比較のための正規分布 N( μ σ2 / [サンプル数] ) を示したもので、μ と σ2 はそれぞれ一様分布の平均と標準偏差なので、μ = 1 / 2, σ2 = 1 / 12 になります。また、正規分布と大きさをそろえるため、ヒストグラムの度数は次のような計算をしてあります。
標本平均の算出回数で割るのは全体の比率に換算するため、[階級の数] / [確率変数の取り得る範囲] を掛けるのは離散値を連続値(面積)に置き換えるためです。
| サンプル数 = 1 | サンプル数 = 2 |
|---|---|
 |
 |
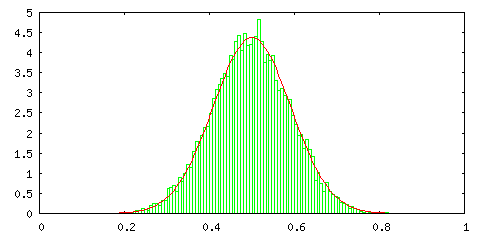
| サンプル数 = 10 | サンプル数 = 100 |
 |
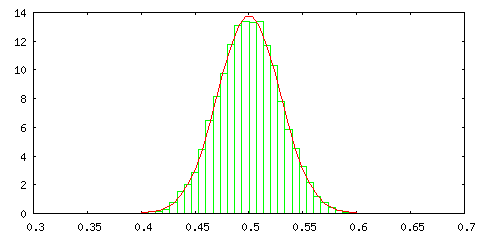 |
サンプル数は、標本平均算出時のデータ数を表しているので、サンプル数 1 とは抽出したデータそのままの状態であることを表しています。結果を見る限り、二つのサンプルで平均を取るだけでも分布は中央に集中し、サンプル数 10 の場合は正規分布にほとんど一致することが分かります。サンプル数が 100 になると、分布は中心に集中するようになり、分散がかなり小さくなる様子も確認できます。
上記計算を行うときに利用した一様乱数は、ライブラリ関数として用意されている rand() を利用して生成しています。この乱数はどの値も等しい確率で発生するため(つまり一様分布に従う乱数です)、ある確率分布に従った乱数を用意する場合、例えば、正規分布に従う乱数を用意しようとした場合は平均付近にある確率変数の方がより多く発生するように発生頻度を調整する必要があります。乱数の発生アルゴリズムは、これだけでもかなり大きなテーマになりますが、ここでは「逆変換法(Inverse Transformation Method)」と「棄却法(Rejection Method)」を紹介しておきます。
確率変数 t に対して確率密度関数 p(t) が定義されているとき、t ≤ x の範囲の確率は ∫{-∞→x} p(t) dt で求めることができます。x を変数とみなせば、これは x までの確率の累積を表しているので、これを「累積分布関数(Cumulative Distribution Function)」といい、以下 F(x) と表します。累積分布関数は非減少関数で、lim{x→-∞} F(x) = 0、lim{x→∞} F(x) = 1 が成り立ちます。つまり、通常は右上がりの曲線で、[ 0, 1 ] の値域を持った関数であるということになります。
ある F(x) = p に対する x の値は必ず一意に決まります。F(x) の傾きが大きな箇所は、x の変化に対して p の値は大きく変わることを意味するので、逆にいえば p の変化に対して x の変化量は小さいということになります。傾きの小さい箇所ではその逆が成り立ちます。これは、p のある一定範囲 [ p, p + Δp ] に対し、傾きが大きなところが小さなところよりも x が密に集まっていると考えることもできます。従って、一様乱数 p に対して x = F-1(p) を求める操作を繰り返して新たな乱数 x を集めると、それは、F(x) の傾きが大きな箇所に値が集中した乱数を得られることを意味します。このように、累積分布関数の逆関数を使ってある確率分布に従った乱数を得る方法を「逆変換法(Inverse Transformation Method)」といいます。
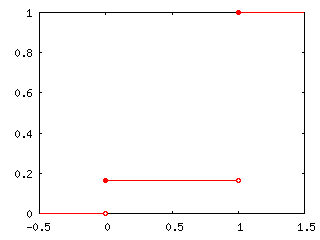
例えば、ベルヌーイ分布 P(1) = Pr, P(0) = 1 - Pr ならば、
| F(x) | = | 0 | ( x < 0 ) |
| = | 1 - Pr | ( 0 ≤ x < 1 ) | |
| = | 1 | ( x ≥ 1 ) |
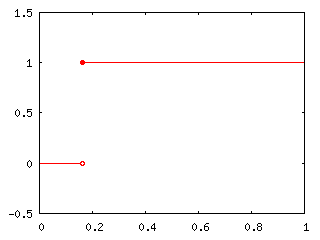
なので、逆関数 F-1(p) は
| F-1(p) | = | 0 | ( 0 ≤ p < 1 - Pr ) |
| = | 1 | ( 1 - Pr ≤ p ≤ 1 ) |
と定義できます。また、指数分布 Pλ(t) = λe-λt の場合、
| F(x) | = | ∫{0→x} λe-λt dt |
| = | [ -e-λt ]{0→x} | |
| = | -e-λx + 1 |
より
であり、標準コーシー分布 P(t) = 1 / π( 1 + t2 ) の場合は、t = tanθ とすれば dt = ( 1 / cos2θ )dθ で、t → -∞ のとき θ → -π / 2、t → x のとき θ → tan-1x なので、
| F(x) | = | ∫{-∞→x} 1 / π( 1 + t2 ) dt |
| = | ∫{-π/2→tan-1x} { 1 / π( 1 + tan2θ ) }( 1 / cos2θ )dθ | |
| = | ∫{-π/2→tan-1x} 1 / π( cos2θ + sin2θ ) dθ | |
| = | [ θ / π ]{-π/2→tan-1x} | |
| = | tan-1x / π + 1/2 |
となって、
と求めることができます。
| F(x) | F-1(p) | |
|---|---|---|
| ベ ル ヌ | イ 分 布 |
 |
 |
| 指 数 分 布 |
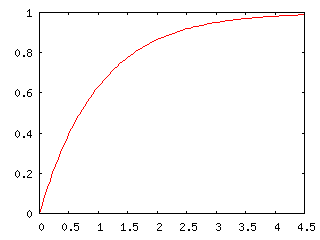 |
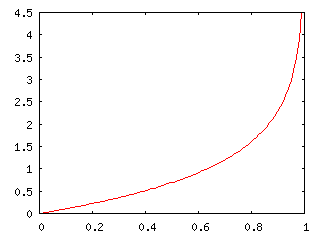 |
| 標 準 コ | シ | 分 布 |
 |
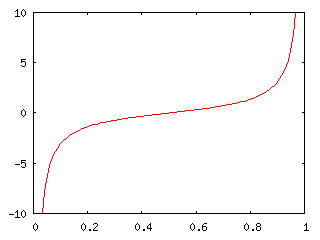 |
逆変換法を利用するには、累積分布関数とその逆関数を求める必要があります。つまり、対象の確率密度関数に対して不定積分とその逆関数が必須となりますが、それらが求められないような関数も存在します。例えば正規分布は不定積分が得られないため、逆変換法を用いるにはそれなりの工夫が必要です。そこで、どんな確率密度関数にも利用できる汎用的な手法として「棄却法(Rejection Method)」があります。
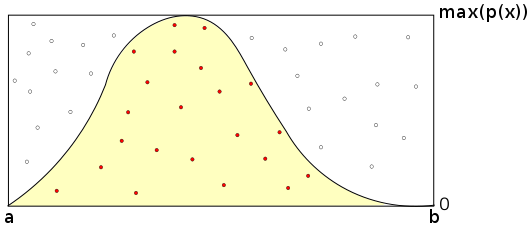
まず最初に、[ 0, 1 ] の範囲の値を持った二つの一様乱数 x, y を用意します。そのうちの一つ x を、次のような式を使って、対象の確率分布が取り得る範囲の値に置き換えます。
上式において、[ a, b ] が確率分布の定義域を表します。ここで、( -∞, b ], [ a, ∞ ), ( -∞, ∞ ) のような場合(正規分布など)は、分布の面積が 1 に十分近くなるような範囲を使うようにします。このようにした求めた x' に対する確率密度 p(x') を求め、その値を y' = y * [確率密度の最大値 ; max( p(x) )] と比較して、
ならばその乱数を採用し、そうでなければ棄却して再度処理を行います。これは、確率分布を含む、横軸 [ a, b ]、縦軸 [ 0, max( p(x) ) ] の矩形にある点 ( x' y' ) が確率分布の範囲内にあれば乱数として採用するという考え方です。範囲外にある場合は処理をやり直さなけばならず効率が悪いのですが、どのような確率分布に対しても利用できるので、汎用性は非常に高い方法になります。
逆変換法と棄却法を利用した乱数生成用サンプル・プログラムを以下に示します。
/* CumulativeDistributionFunction : 累積分布関数(逆関数) */ class CumulativeDistributionFunction { public: virtual double operator()( double p ) const = 0; }; /* CDF_Bernoulli : ベルヌーイ分布の累積分布関数(逆関数) */ class CDF_Bernoulli : public CumulativeDistributionFunction { double _pr; // 事象が起こる確率 public: CDF_Bernoulli( double pr ) : _pr( pr ) {} double operator()( double p ) const { return( ( p < 0 || p > 1 ) ? NAN : ( ( p < 1 - _pr ) ? 0 : 1 ) ); } }; /* CDF_Exp : 指数分布の累積分布関数(逆関数) */ class CDF_Exp : public CumulativeDistributionFunction { double _lambda; // λ public: CDF_Exp( double lambda ) : _lambda( lambda ) {} double operator()( double p ) const { return( ( p < 0 || p > 1 || _lambda <= 0 ) ? NAN : -log( 1 - p ) / _lambda ); } }; /* CDF_StdCauchy : 標準コーシー分布の累積分布関数(逆関数) */ class CDF_StdCauchy : public CumulativeDistributionFunction { public: double operator()( double p ) const { return( ( p < 0 || p > 1 ) ? NAN : tan( ( p - 0.5 ) * M_PI ) ); } }; /* RandomNumber : 一様乱数の生成 */ class RandomNumber { public: // [0,1]の間の一様乱数を返す virtual double operator()() const { return( (double)rand() / (double)RAND_MAX ); } }; /* InverseTransformationMethod : 逆変換法による乱数の生成 */ class InverseTransformationMethod : public RandomNumber { // 対象の確率密度関数の累積分布関数(逆関数) CumulativeDistributionFunction& _cdf; public: InverseTransformationMethod( CumulativeDistributionFunction& cdf ) : _cdf( cdf ) {} // [0,1]の間の一様乱数を返す double operator()() const { return( _cdf( RandomNumber::operator()() ) ); } }; /* RejectionMethod : 棄却法による乱数の生成 */ class RejectionMethod : public RandomNumber { // 対象の確率密度関数(連続分布) ContDist& _dist; // [_a,_b] : 確率変数の定義域 double _a; double _b; double _m; // 確率密度の最大値 public: RejectionMethod( ContDist& dist, double a, double b, double m ); // [0,1]の間の一様乱数を返す double operator()() const; }; /* RejectionMethod コンストラクタ : 棄却法による乱数の生成 ContDist& dist : 確率密度関数(連続分布) double a, b : 確率変数の定義域 double m : 確率密度の最大値 */ RejectionMethod::RejectionMethod( ContDist& dist, double a, double b, double m ) : _dist( dist ), _m( m ) { _a = ( a > b ) ? b : a; _b = ( a > b ) ? a : b; } /* RejectionMethod::operator() : 棄却法による確率分布に従った乱数の生成 戻り値 : 生成した乱数 */ double RejectionMethod::operator()() const { double x, y; do { x = (double)rand() * ( _b - _a ) / (double)RAND_MAX + _a; y = (double)rand() * _m / (double)RAND_MAX; } while ( y >= _dist[x] ); return( x ); }
CumulativeDistributionFunction は累積分布関数の逆関数を定義するための基底クラスで、逆変換法に利用されます。このクラスから派生して、各確率密度関数専用の累積分布逆関数を構築するわけです。サンプル・プログラムでは、ベルヌーイ分布・指数分布・標準コーシー分布に対する累積分布逆関数を用意しています。
一様乱数の生成用に RandomNumber クラスが用意されています。また、RandomNumber クラスから派生する形で逆変換法用の InverseTransformationMethod クラスと棄却法用の RejectionMethod クラスがあり、これらを使って任意の方法で乱数が得られるようにしてあります。
上述の乱数生成プログラムを利用してその標本平均を求め、ヒストグラムを生成するためのサンプル・プログラムを以下に示します。
/* Histogram : ヒストグラム階級 */ class Histogram { vector<unsigned int> _freq; // 度数 double _min; // 階級の最小値 double _range; // 階級一つあたりの幅 public: /* コンストラクタ double d1, d2 : 分布の範囲 unsigned int freqCnt : 階級の数 */ Histogram( double d1, double d2, unsigned int freqCnt ); // 分布への追加 bool add( double d ); // 分布の初期化 void clear( unsigned int freqCnt ) { _freq.assign( freqCnt, 0 ); } // 度数を返す unsigned int operator[]( unsigned int i ) const { return( ( i < size() ) ? _freq[i] : 0 ); } // 階級の値を返す(中央値) double median( unsigned int i ) const { return( ( i < size() ) ? _min + _range * ( (double)i + 0.5 ) : NAN ); } // 度数の数を返す unsigned int size() const { return( _freq.size() ); } }; /* Histogram コンストラクタ : ヒストグラム階級 double d1, d2 : 分布の範囲 unsigned int freqCnt : 階級の数 */ Histogram::Histogram( double d1, double d2, unsigned int freqCnt ) { if ( d1 > d2 ) { double d = d1; d1 = d2; d2 = d; } clear( freqCnt ); _min = d1; _range = ( d2 - d1 ) / (double)freqCnt; } /* Histogram::add : 分布への追加 double d : 対象の値 戻り値 : True ... 登録成功 , False ... 登録失敗(分布の範囲外など) */ bool Histogram::add( double d ) { if ( d < _min ) return( false ); if ( _range <= 0 ) return( false ); d = ( d - _min ) / _range; if ( d > (double)UINT_MAX ) return( false ); unsigned int i = d; if ( i < size() ) ++( _freq[i] ); return( i < size() ); } /* sum : データの総和を求める vector<T>& x : データ 誤差を軽減する方法は Kahan の加算アルゴリズムを利用 戻り値 : 求めた総和(データ数がゼロならゼロを返す) */ template<class T> T sum( const vector<T>& x ) { T ans = 0; T r = 0; // 積み残し for ( unsigned int i = 0 ; i < x.size() ; ++i ) { T y = x[i] - r; // 計算値から積み残しを引いた値 T buff = ans + y; // 今までの合計値に y を加える r = ( buff - ans ) - y; // 積み残しを計算 ans = buff; } return( ans ); } template double sum( const vector<double>& x ); /* sampleAverage : 標本平均を求める vector<T>& x : データ 戻り値 : 求めた標本平均(データ数がゼロならゼロを返す) */ template<class T> T sampleAverage( const vector<T>& x ) { T s = sum( x ); if ( x.size() > 0 ) s /= (T)x.size(); return( s ); } template double sampleAverage( const vector<double>& x ); /* createHistogram : 標本平均を算出して分布を作成する const RandomNumber& rand : 乱数生成クラス unsigned int sampleCnt : 平均算出時の標本の数 unsigned int procCnt : 算出の回数(度数の合計) Histogram& histogram : ヒストグラム用クラス */ void createHistogram( const RandomNumber& rand, unsigned int sampleCnt, unsigned int procCnt, Histogram& histogram ) { struct timespec tp; // クロック時間(乱数シード設定用) vector<double> rndData( sampleCnt ); // 乱数を登録する配列 // 乱数の初期化 clock_gettime( CLOCK_REALTIME, &tp ); srand( tp.tv_nsec ); for ( unsigned int pc = 0 ; pc < procCnt ; ++pc ) { for( unsigned int i = 0 ; i < rndData.size() ; ++i ) rndData[i] = rand(); double avg = sampleAverage( rndData ); histogram.add( avg ); } } /*** 出力サンプル ***/ unsigned int classCnt = 150; // 階級の数 unsigned int procCnt = 10000; // 標本平均の算出回数 unsigned int sampleCnt = 10; // 標本平均の標本数 /* 標準コーシー分布(逆変換法)の場合 */ double histMin = -5; double histMax = 5; Histogram histogram( histMin, histMax, classCnt ); // 度数 CDF_StdCauchy cdfStdCauchy; InverseTransformationMethod itm( cdfStdCauchy ); createHistogram( itm, sampleCnt, procCnt, histogram ); // データの出力 for ( unsigned int i = 0 ; i < histogram.size() ; ++i ) cout << histogram.median( i ) << " " << histogram[i] * (double)classCnt / ( ( histMax - histMin ) * (double)procCnt ) << endl; /* 指数分布(棄却法)の場合 */ double histMin = 0; double histMax = 5; Histogram histogram( histMin, histMax, classCnt ); // 度数 // 確率変数の範囲 double a = 0; double b = 100; double max = 1.0; // 確率密度の最大値 ExponentialDistribution ed( 1 ); RejectionMethod rnd( ed, a, b, max ); createHistogram( rnd, sampleCnt, procCnt, histogram ); // データの出力 for ( unsigned int i = 0 ; i < cls.size() ; ++i ) cout << histogram.median( i ) << " " << histogram[i] * (double)classCnt / ( ( histMax - histMin ) * (double)procCnt ) << endl;
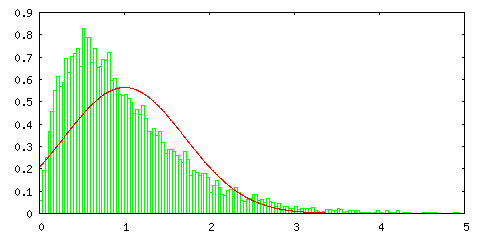
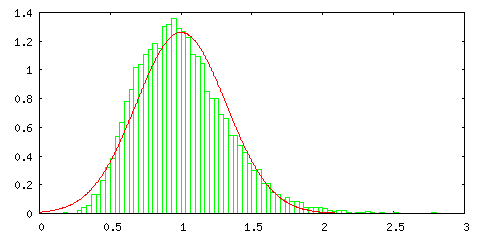
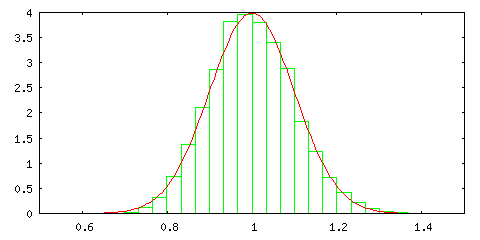
次のグラフは、以前紹介した指数分布 Pλ=1(t) = e-t に対して一様分布の場合と同様の処理を行った結果です。
逆変換法
| サンプル数 = 1 | サンプル数 = 2 |
|---|---|
 |
 |
| サンプル数 = 10 | サンプル数 = 100 |
 |
 |
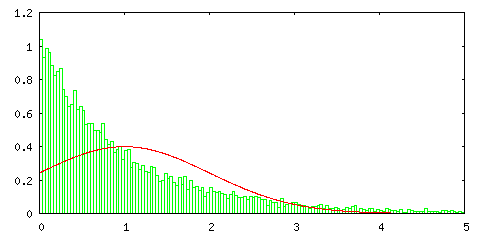
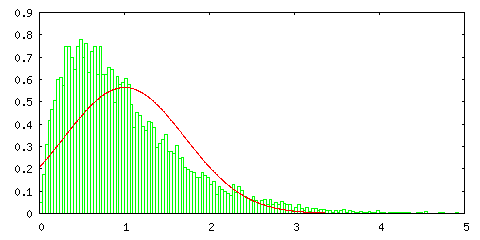
棄却法 ( 確率変数の範囲 [ 0, 1000 ] )
| サンプル数 = 1 | サンプル数 = 2 |
|---|---|
 |
 |
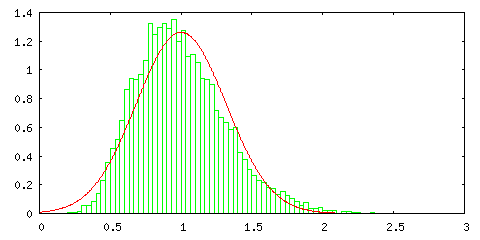
| サンプル数 = 10 | サンプル数 = 100 |
 |
 |
指数分布はかなり偏った形であり、サンプル数が 1 の場合は正規分布とは全く一致しないのですが、サンプル数が増えるとその形は左右対称に近づき、正規分布の形に近づいていく様子が分かります。指数分布の確率変数の範囲は [ 0, ∞ ) ですが、棄却法では変数の範囲を大きく取るほど処理に時間がかかるので、ここでは [ 0, 1000 ] の範囲で処理しています。
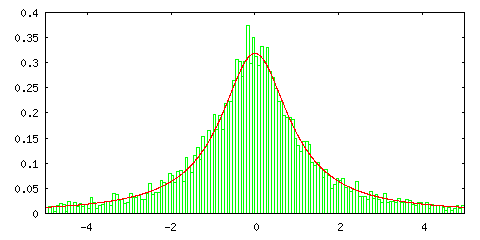
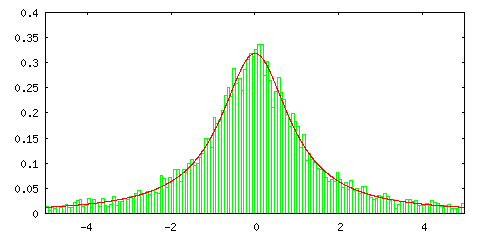
ところが、逆変換法を使って標準コーシー分布の標本平均の分布を見ると次のようになります。
逆変換法
| サンプル数 = 1 | サンプル数 = 2 |
|---|---|
 |
 |
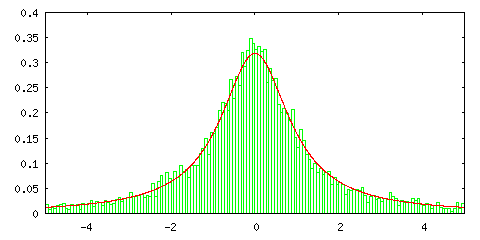
| サンプル数 = 10 | サンプル数 = 100 |
 |
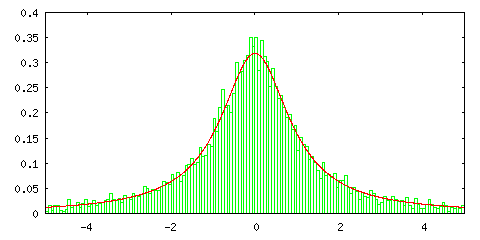 |
グラフの中の赤い線は正規分布ではなく標準コーシー分布を表します。サンプル数 1 の場合に一致するのは当然として、サンプル数を増やしても分布の形状に変化がないことがこの結果から分かります。標準コーシー分布は平均が存在しない確率密度関数でした (「(2) 確率空間」の「4) 期待値」参照 )。また、平均がなければ分散も定義できません。このような確率密度関数に対しては中心極限定理は成り立たないということを表しています。標準コーシー分布の場合は、標本平均の分布もまた標準コーシー分布に従うことになります。
中心極限定理によって、任意の確率分布に従う母集団の標本平均は正規分布に従うことが分かりました。任意の確率分布として正規分布を用いても当然成り立つので、N( μ, σ2 ) に従う母集団から N 個の標本による平均を計算する操作を繰り返すと、その平均は N( μ, σ2 / N ) に従います。よって、母集団からサンプリングしてデータを調査する場合、その数が多い方が信頼性は上がることになります。
任意の分布について、その平均と分散が存在するとき、それぞれの分布から標本を抽出して一次結合の形で表したとします。このとき、その値はどのような分布になるでしょうか。確率変数 x1, x2, ... xN がそれぞれ平均 μi, 分散 σi2 の分布に従うとします。このとき、
の平均 μy は、
になります。また、各確率変数が互いに独立ならば、分散 σy2 は、
になります。これらは、前章の「相関係数」で示した和や積の期待値に関する法則や、先ほどの大数の法則の証明で行った、標本平均の平均や分散を求めるやり方を利用することで証明することができます。まず、
| E[y] | = | E[a0 + a1x1 + a2x2 + ... + aNxN] |
| = | E[a0] + E[a1x1] + E[a2x2] + ... + E[aNxN] | |
| = | a0E[1] + a1E[x1] + a2E[x2] + ... + aNE[xN] | |
| = | a0 + a1μ1 + a2μ2 + ... + aNμN |
となるので、平均については成り立つことが証明されました(このとき、各確率変数の独立性には無関係に成り立つことに注意して下さい)。分散は
| E[( y - μy )2] | = | E[{ ( a0 + a1x1 + a2x2 + ... + aNxN ) - ( a0 + a1μ1 + a2μ2 + ... + aNμN ) }2] |
| = | E[{ a1( x1 - μ1 ) + a2( x2 - μ2 ) + ... + aN( xN - μN ) }2] | |
| = | E[Σi{1→N}( ai2( xi - μi )2 ) + Σi{1→N}Σj{1→N;j≠i}( aiaj( xi - μi )( xj - μj ) )] | |
| = | Σi{1→N}( E[ai2( xi - μi )2] ) + Σi{1→N}Σj{1→N;j≠i}( aiajE[xi - μi]E[xj - μj] ) |
第二項は E[xi - μi] = 0 になるので消えて( xi と xj が互いに独立なので、共分散を表す E[( xi - μi )( xj - μj )] がゼロになることからも示すことができます )、
| E[( y - μy )2] | = | Σi{1→N}( ai2E[( xi - μi )2] ) |
| = | Σi{1→N}( ai2σi2 ) |
分散に関しても同様に成り立つことが分かります(和の場合とは異なり、積の場合は各確率変数の独立性が前提となります)。また、この結果から、標本平均の期待値は Σi{1→N}( μi ) / N で、その分散は Σi{1→N}( σi2 ) / N2 になることを示すことができます。従って、各確率変数の平均と分散が等しくそれぞれ μ と σ2 になるならば、標本平均の期待値は μ、分散は σ2 / N になります。
さらに、互いに独立な確率変数 x1, x2, ... xN がそれぞれ平均 μi, 分散 σi2 の正規分布 N( μi, σi2 ) に従うとします。このとき、y = a0 + Σi{1→N}( aixi ) は、平均 μy = a0 + Σi{1→N}( aiμi )、分散 σy2 = Σi{1→N}( ai2σi2 ) の正規分布 N( μy, σy2 ) に従います。
y の積率母関数を gy(θ) とすると、
| gy(θ) = E[eθy] | = | E[exp( θ( a0 + Σi{1→N}( aixi ) ) )] ) |
| = | E[exp( a0θ ) Πi{1→N}( exp( aixiθ ) )] | |
| = | exp( a0θ ) Πi{1→N}( E[exp( aixiθ )] ) |
各確率変数が N( μi, σi2 ) に従うので、
| E[exp( aixiθ )] | = | ∫{-∞→∞} exp( aixiθ )・{ 1 / sqrt( 2π )σi } exp( -( xi - μi )2 / 2σi2 ) dxi |
| = | { 1 / sqrt( 2π )σi } ∫{-∞→∞} exp( aixiθ - ( xi - μi )2 / 2σi2 ) dxi | |
| = | { 1 / sqrt( 2π )σi } ∫{-∞→∞} exp( - { xi2 - 2( aiσi2θ + μi )xi + μi2 } / 2σi2 ) dxi | |
| = | { 1 / sqrt( 2π )σi } ∫{-∞→∞} exp( - [ { xi - ( aiσi2θ + μi ) }2 - ( aiσi2θ + μi )2 + μi2 ] / 2σi2 ) dxi | |
| = | { 1 / sqrt( 2π )σi } ∫{-∞→∞} exp( -{ xi - ( aiσi2θ + μi ) }2 / 2σi2 ) exp( { ( aiσi2θ )2 + 2aiμiσi2θ } / 2σi2 ) dxi | |
| = | { 1 / sqrt( 2π )σi } sqrt( 2π )σi exp( aiμiθ + ( aiσiθ )2 / 2 ) | |
| = | exp( aiμiθ + ( aiσiθ )2 / 2 ) |
よって、
| gy(θ) | = | exp( a0θ ) Πi{1→N}( exp( aiμiθ + ( aiσiθ )2 / 2 ) ) |
| = | exp( a0θ + Σi{1→N}( aiμiθ + ( aiσiθ )2 / 2 ) ) | |
| = | exp( { a0 + Σi{1→N}( aiμi ) }θ + Σi{1→N}( ( aiσi )2 / 2 )θ2 ) |
これは、N( a0 + Σi{1→N}( aiμi ), Σi{1→N}( ( aiσi )2 ) ) の正規分布に対する積率母関数に一致することから、y の分布は N( a0 + Σi{1→N}( aiμi ), Σi{1→N}( ( aiσi )2 ) ) であることになります。
それぞれが独立な確率変数の一次結合の分布は、その平均と分散も各分布のそれらの一次結合になることが分かりました。特に、上記の中で a0 = 0, a1 = a2 = ... = aN = 1 / N とすれば確率変数の標本平均に対する分布を意味することになり、その分布の平均は「各確率変数の持つ分布の平均」を平均した値に、分散は「各確率変数の持つ分布の分散」の平均をさらに N で割った値に等しくなります。「各確率変数の持つ分布の平均」が全て等しければ、分布の平均は「各確率変数の持つ分布の平均」に等しくなり、「各確率変数の持つ分布の分散」が全て有限値ならば、その最大値を σM としたとき分布の分散は σM / N 以下になるので、N が大きくなるほど分散は小さくなり、やがてゼロに収束します。これが「大数の法則」でした。さらに、N が充分大きければ、このときの分布の形が正規分布に近くなるというのが「中心極限定理」の内容でした。
ベルヌーイ分布に従う互いに独立な確率変数 { xi } ( i = 1, 2, ... N ; xi = 0 または 1 ) において、各確率変数の和 Σi{1→N}( xi ) に対する分布を考えるとそれは二項分布で、全ての確率変数に対して P( xi = 1 ) = p, P( xi = 0 ) = 1 - p とすれば、その平均は p、分散は p( 1 - p ) となるので、二項分布の平均は Np、分散は Np( 1 - p ) となります。また、各確率変数の和 Σi{1→N}( xi ) / N に対する分布の平均は p、分散は p( 1 - p ) / N になって、N が充分に大きければ分布は正規分布に近い形になります。これが「ド・モアブル = ラプラスの定理」で、「中心極限定理」の特別な場合と考えることができます。
今までは標本平均の性質について紹介してきました。繰り返しになりますが、ある分布に従う確率変数から任意に標本を抽出してそれらの平均を求める操作を繰り返して、その結果を元に分布を作成してみると、それがどのようになるかを見てきたわけです。ここで、抽出した標本の分散を求めてその分布を見た時、その形状がどのようになっているかを調べてみたいと思います。
まずは、標本の分散を定義しておく必要があります。確率密度 p(x) の平均と分散は
μ = ∫{-∞→∞} x・p(x) dx
σ2 = ∫{-∞→∞} ( x - μ )2p(x) dx
と定義されていました。離散分布の場合は
μ = Σr{-∞→∞}( r・p(r) )
σ2 = Σr{-∞→∞}( ( r - μ )2p(r) )
になります。このような分布から独立な N 個の標本 x1, x2, ... xN を抽出したとき、その標本平均は
で定義されていましたが、それに対して標本分散を
とします。これは、各標本が生じる確率が均等に 1 / N であるとしたとき、離散分布の分散を求める式と一致します。但し、平均として μ ではなく標本平均の m が使われていることに注意して下さい。この式を次のように変形していきます。
| s2 | = | Σi{1→N}( ( xi - m )2 ) / N |
| = | Σi{1→N}( { ( xi - μ ) + ( μ - m ) }2 ) / N | |
| = | Σi{1→N}( ( xi - μ )2 + 2( xi - μ )( μ - m ) + ( μ - m )2 ) / N | |
| = | Σi{1→N}( ( xi - μ )2 ) / N + ( 2 / N )Σi{1→N}( ( xi - μ )( μ - m ) ) + ( μ - m )2 |
上式の第二項は
| ( 2 / N )Σi{1→N}( ( xi - μ )( μ - m ) ) | |
| = | 2( μ - m ){ Σi{1→N}( xi ) / N - Σi{1→N}( μ ) / N } |
| = | 2( μ - m )( m - μ ) |
| = | -2( μ - m )2 |
となるので、
になります。s2 の期待値 E[s2] は、
| E[s2] | = | E[ Σi{1→N}( ( xi - μ )2 ) / N - ( μ - m )2 ] |
| = | Σi{1→N}( E[( xi - μ )2] ) / N - E[( μ - m )2] |
で求めることができますが、E[( xi - μ )2] = σ2 であり、E[( μ - m )2] は標本平均の分散を意味するので σ2 / N となって、
| E[s2] | = | Σi{1→N}( σ2 ) / N - σ2 / N |
| = | σ2 - σ2 / N | |
| = | { ( N - 1 ) / N }σ2 |
になります。つまり、標本平均の期待値は母集団の平均に等しかったのに対して、標本分散の期待値は母集団の分散とは一致しないことになります。
未知の分布の母集団から標本を抽出し、その標本平均を求めたとき、標本の数が十分であれば、その結果を母集団の平均として利用することができます。標本平均の期待値が母集団の平均に等しいので、標本平均で母集団の平均を推定するわけです。しかし、標本分散の期待値は母集団の分散とは一致しないので、標本分散を求めた後でその結果に N / ( N - 1 ) を掛けて母集団の分散を推定することがよく行われます。
としたとき、u2 は「不偏分散(Unbiased Variance)」になります。一般に、ある要約値(平均や分散など)の期待値が母集団と一致するとき、その値を「不偏推定量」といいます。よって、標本平均 m は母集団の平均 μ の、また不偏分散 u2 は母集団の分散 σ2 の不偏推定量であるということになります。
今までは、確率変数の和や標本平均に対する分布を見てきたので、次に同時分布がどのようになるかを調べてみたいと思います。まず、独立な二つの確率変数 x, y がそれぞれ正規分布 N( μx, σx2 ), N( μy, σy2 ) に従うとき、それぞれの確率変数は独立なので、同時分布は二つの正規分布の積で表され、
| p( x, y ) | = | N( μx, σx2 )・N( μy, σy2 ) |
| = | { 1 / ( 2πσx2 )1/2 }exp( -( x - μx )2 / 2σx2 )・{ 1 / ( 2πσy2 )1/2 }exp( -( y - μy )2 / 2σy2 ) | |
| = | ( 1 / 2πσxσy )exp( -{ ( x - μx )2 / 2σx2 + ( y - μy )2 / 2σy2 } ) |
さらに多変量になって、独立した確率変数 x = ( x1, x2, ... xN )T ( T は転置行列であることを表すので、ベクトルに対してはそれが列ベクトルであることを表します) がそれぞれ正規分布 N( μi, σi2 ) ( i = 1, 2, ..., N ) に従うとすれば、
になります。μ = ( μ1, μ2, ... μN )T とすると、
であり、さらに対角行列 D を
| D | = | | | σ12, | 0, | ... | 0 | | |
| | | 0, | σ22, | ... | 0 | | | ||
| | | : | : | ... | : | | | ||
| | | 0, | 0, | ... | σN2 | | |
とすれば、行列式 |D| = Πi{1→N}( σi2 ) で、逆行列 D-1 は
| D-1 | = | | | 1 / σ12, | 0, | ... | 0 | | |
| | | 0, | 1 / σ22, | ... | 0 | | | ||
| | | : | : | ... | : | | | ||
| | | 0, | 0, | ... | 1 / σN2 | | |
なので、
となって、ネイピア数に対する指数部分は次のように変形することができます。
但し、( x, y ) は二つのベクトル x, y の内積を表します。従って、
と表すことができます。ここで、以前紹介した「固有値分解」を利用すると、D の対角成分を固有値とする任意の対称行列 V に対し、その固有ベクトルから成る直交行列 Q を使って、
と表すことができます。V の固有値の一つを λ、その固有ベクトルを u としたとき、
が成り立つので、両辺に左側から V-1 を掛けて
V-1Vu = λV-1u より
V-1u = ( 1 / λ )u
となります。これが任意の固有値と固有ベクトルで成り立つので、対称行列 V とその逆行列 V-1 は固有ベクトルが等しく、固有値は逆数の関係にあります。すなわち、
が成り立ちます。これを D-1 について解くと
になります。但し、直交行列 Q の逆行列が転置行列 QT に等しくなることを利用しています。これを内積の部分に代入すると、
| ( x - μ, D-1( x - μ ) ) | = | ( x - μ, QTV-1Q( x - μ ) ) |
| = | ( Q( x - μ ), V-1Q( x - μ ) ) |
最後の等式は ( x, VTy ) = ( Vx, y ) を利用しています。ここで、Q( x - μ ) = Qx - Qμ = x' - μ' とすれば、上記の結果は ( x' - μ', V-1( x' - μ' ) ) と表され、最後に |D| = |V| が成り立つことから多変量正規分布は
のように表すことができます。上記内容の詳細については、「(1)対称行列の固有値」の「3) 直交行列」に記述してあります。
ここで、x' - μ' = Q( x - μ ) がどのようなベクトルを表すかを考えると、x - μ とは各分布の平均を表すベクトル μ が原点となるように x を平行移動したもので、さらにそれに Q を掛けたものを意味します。しかし、Q は直交行列であり、Qによって変換されたベクトルは長さが変化せず、各ベクトルのなす角度も変化しません。これは ( Ax, y ) = ( x, ATy ) と QTQ = QQT = E を使えば次のように簡単に証明ができます。
||Qx||2 = ( Qx, Qx ) = ( x, QTQx ) = ( x, x ) = ||x||2
( Qx, Qy ) = |Qx||Qy|cosθ = |x||y|cosθ = ( x, y )
これはちょうど、ベクトル自体は動かさずに座標自体を回転(または鏡映)させた状態を思い浮かべることができます。
Q を次のように具体的な要素を使って表します。
| Q | = | | | u11, | u12, | ... | u1N | | |
| | | u21, | u22, | ... | u2N | | | ||
| | | : | : | ... | : | | | ||
| | | uN1, | uN2, | ... | uNN | | | ||
このとき、V = QDQT を直接計算すると、
| QD | = | | | u11, | u12, | ... | u1N | || | σ12, | 0, | ... | 0 | | |
| | | u21, | u22, | ... | u2N | || | 0, | σ22, | ... | 0 | | | ||
| | | : | : | ... | : | || | : | : | ... | : | | | ||
| | | uN1, | uN2, | ... | uNN | || | 0, | 0, | ... | σN2 | | | ||
| = | | | u11 σ12, | u12 σ22, | ... | u1N σN2 | | | |
| | | u21 σ12, | u22 σ22, | ... | u2N σN2 | | | ||
| | | : | : | ... | : | | | ||
| | | uN1 σ12, | uN2 σ22, | ... | uNN σN2 | | | ||
より、
| V | = | | | u11 σ12, | u12 σ22, | ... | u1N σN2 | || | u11, | u21, | ... | uN1 | | |
| | | u21 σ12, | u22 σ22, | ... | u2N σN2 | || | u12, | u22, | ... | uN2 | | | ||
| | | : | : | ... | : | || | : | : | ... | : | | | ||
| | | uN1 σ12, | uN2 σ22, | ... | uNN σN2 | || | u1N, | u2N, | ... | uNN | | | ||
| = | | | Σi{1→N}( u1i2σi2 ), | Σi{1→N}( u1iu2i σi2 ), | ... | Σi{1→N}( u1iuNi σi2 ) | | | |
| | | Σi{1→N}( u2iu1i σi2 ), | Σi{1→N}( u2i2σi2 ), | ... | Σi{1→N}( u2iuNi σi2 ) | | | ||
| | | : | : | ... | : | | | ||
| | | Σi{1→N}( uNiu1i σi2 ), | Σi{1→N}( uNiu2i σi2 ), | ... | Σi{1→N}( uNi2σi2 ) | | | ||
この V-1 の要素が何を意味するかについては、各確率変数の共分散を求めることで分かります。x' - μ' の r 番目と c 番目の確率変数から成る共分散 γrc は
なので、x' - μ' = Q( x - μ ) と変数変換した時、
より、
となって、ヤコビ行列は直交行列 Q そのものになることを意味します。よって、直交行列の行列式は ±1 になることから、ヤコビアンの絶対値は 1 になります(補足4)。ネイピア数の指数部分にある内積は固有値分解の式から、
なので、
| γrc | = | { 1 / ( 2π )N/2|V|1/2 } ∫...∫ Σi{1→N}( uri( xi - μi ) ) Σi{1→N}( uci( xi - μi ) ) exp( -Σi{1→N}( ( xi - μi )2 / 2σi2 ) ) dx |
| = | { 1 / ( 2π )N/2Πi{1→N}( σi ) } ∫...∫ Σi{1→N}( uri( xi - μi ) ) Σi{1→N}( uci( xi - μi ) ) exp( -Σi{1→N}( ( xi - μi )2 / 2σi2 ) ) dx |
ここで、
| Σi{1→N}( uri( xi - μi ) ) Σi{1→N}( uci( xi - μi ) ) | |
| = | Σi{1→N}( Σj{1→N;i≠j}( uriucj( xi - μi )( xj - μj ) ) ) + Σi{1→N}( uriuci( xi - μi )2 ) |
となるので、共分散 γrc は uriucj( xi - μi )( xj - μj ) と uriuci( xi - μi )2 の期待値の和で表されることになります。ところが、確率密度関数は
となるので、各項の計算結果は、i ≠ j のとき
| ∫...∫ uriucj( xi - μi )( xj - μj ) Πi{1→N}( exp( -( xi - μi )2 / 2σi2 ) ) dx | |
| = | uriucj ∫ ( xi - μi ) exp( -( xi - μi )2 / 2σi2 ) dxi ∫ ( xj - μj ) exp( -( xj - μj )2 / 2σj2 ) dxj Πm{1→N;m≠i;m≠j}( ∫ exp( -( xm - μm )2 / 2σm2 ) dxm ) |
で、∫ ( xi - μi ) exp( -( xi - μi )2 / 2σi2 ) dxi = 0 なので、上式の計算結果もゼロとなります。i = j のときは
| uriuci ∫ ( xi - μi )2 exp( -( xi - μi )2 / 2σi2 ) dxi Πj{1→N;j≠i}( ∫ exp( -( xj - μj )2 / 2σj2 ) dxj ) | |
| = | uriuci ( 2πσi2 )1/2・σi2 Πj{1→N;j≠i}( ( 2πσj2 )1/2 ) |
| = | uriuci σi2 Πj{1→N}( ( 2πσj2 )1/2 ) |
なので、結局 γrc は
| γrc | = | { 1 / ( 2π )N/2Πj{1→N}( σj ) } Σi{1→N}( uriuci σi2 Πj{1→N}( ( 2πσj2 )1/2 ) ) |
| = | { 1 / ( 2π )N/2Πj{1→N}( σj ) } ( 2π )N/2 Πj{1→N}( σj ) Σi{1→N}( uriuci σi2 ) | |
| = | Σi{1→N}( uriuci σi2 ) |
になり、γrc は V の r 行 c 列の要素と等しくなります。よって、V は共分散行列であることになります。
もう一度整理すると、γrc = γcr が成り立つことから共分散行列は対称行列であり、その固有値は分散で必ず正値となるので、正値対称行列になります。共分散行列の固有値分解によって、確率変数を要素とするベクトルは共分散行列の固有ベクトルから作られる直交行列により回転・鏡映変換されて、互いに独立になるように確率密度関数が変化します。ちょうど、最初に説明した変換を逆方向に処理することになって、共分散行列はこのとき、分散を対角成分とする対角行列に変化します。共分散がゼロになることからも、各確率変数が独立であることがわかります。このような変換を「主軸変換」といい、それによって各確率変数を互いに独立な形で表したものを「主成分(Principal Component)」、主成分を利用してデータを解析する手法を「主成分分析(Principal Component Analysis ; PCA)」というのでした。多変量正規分布は N 次元空間上で楕円体の形となり、平均からなる点 μ 上での確率密度が最も高くなります。二次元の場合、切り口が楕円となるような下図の状態になります。下図では三次元で表していますが、平面上の楕円の中で密度の濃淡がある状態を考えれば、多次元での状態もイメージできるのではないかと思います。
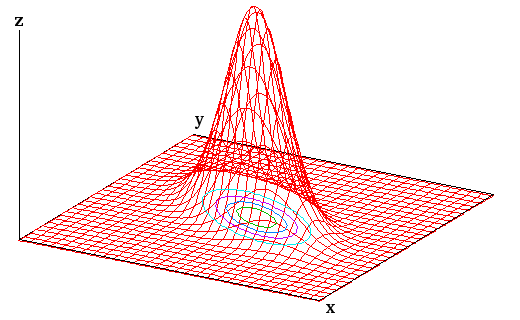
なお、二次形式の係数行列が正値対称行列ならば、その形は必ず楕円体になりますが、そうでなければ方物型や双曲型で表される場合もあります。上述の通り、分散が正値であることから多変量正規分布は必ず楕円体で表されるので、方物型や双曲型の場合は考える必要はありません。但し、分散がゼロとなるような確率変数が存在すれば、ある主軸方向に対して完全に潰れた、超平面上だけに分布が広がった状態になり、行列式もゼロになることから逆行列自体が存在しなくなるので、主軸変換を行うことはできなくなります。
多変量正規分布に関するもう一つの重要な手法に「最小二乗法(Least Squares)」があります。互いに独立で、正規分布 N( μ, σ2 ) に従う確率変数 x = ( x1, x2, ... xN ) に対する同時分布は
なので、p(x) が最大となるとき、σ が一定であれば、J = Σi{1→N}( ( xi - μ )2 ) が最小になればいいことになります。xi - μ とは平均との差を表しているので、これを ε とすれば
が最小になれば p(x) が最大になります。
ここで、ある入力値 x に対する出力データ y が y = f(x) の関係にあったとします。しかし、測定時の誤差などによって yi の測定値は f(xi) + εi となっていたとき、測定値から y = f(x) として最適な解を求めるためには、誤差が発生する同時分布の確率密度が最大になるような f(x) を計算すればよいと考えることができます。従って、εi = yi - f(xi) より
が最小となるような f(x) の式を求めることで、最適な解を求めることができると考えられます。このような手法を「最小二乗法(Least Squares)」といいます。x と y の関係が y = ax + b となるのであれば、
なので、これが最小となるような ( a, b ) の組を求めればよいことになります。最小二乗法については「(2) カルーネン・レーベ展開」の「最小二乗法(Least Squares)」でも紹介しています。なお、誤差が正規分布に従うということがその前提条件となっていることから、正規分布のことを「誤差の分布」ともいいます。
今回は「正規分布」から始めて「大数の法則」や「中心極限定理」などを紹介しました。この正規分布から発展した確率分布は様々なものがあり、それらが統計学の中で非常に重要な役割を担っています。次回は、そのような分布を紹介したいと思います。
文献によっては、次の不等式を「チェビシェフの不等式」として紹介している場合もあります。
分散に対する積分を、任意の定数 k を使って | x - μ | ≥ kσ と | x - μ | < kσ の二つに分ければ、同様の操作によって上式を得ることができます。
より、第一項は | x - μ | ≥ kσ なので常に ( x - μ )2 ≥ ( kσ )2 が成り立ち、
| σ2 | ≥ | ∫{| x - μ | ≥ kσ} ( kσ )2p(x) dx + ∫{| x - μ | < kσ} ( x - μ )2p(x) dx |
| = | ( kσ )2∫{| x - μ | ≥ kσ} p(x) dx + ∫{| x - μ | < kσ} ( x - μ )2p(x) dx |
第二項めは正なのでこれを取り除けば
∫{| x - μ | ≥ kσ} p(x) dx は | x - μ | ≥ kσ の範囲の確率を表すので、これを P( | ( x - μ ) / σ | ≥ k ) と表せば、
よって、
が得られます。自分が参考にした文献「確率・統計入門」(小針あき宏 著) ではこちらの形で紹介されています。( x - μ ) / σ は「標準得点(Standard Score)」と呼ばれ、分布の広がり方(バラツキ)による値の大小を正規化することで、分布の中の相対位置を分布の形状によらずに見ることができます。チェビシェフの不等式は、どのような確率密度関数においても、平均と分散が存在すれば、標準得点が k 以上になるような確率は必ず 1 / k2 以下になることを示しています。
ちなみに同文献では、この不等式にさんざん「悪たれ」をついています。というのも、不等式を証明する中で第二項を取り除いている部分について、(分布の)どまん中のふくらみの部分を'正だから'という一言の下に切り捨てご免にしている
とした上で、まさに殿様のようなぜい沢をした不等式
と書いています。まあ、これは単なる冗談で(だと思うのですが)、「大数の法則」の話のところでちゃんと役立つということを示しています。しかし、こんなことが書かれた入門書というのは他にはないんじゃないでしょうか。
確率分布は、公理さえ満たせばどんなものも自由に考えられるので、例えば、
| p(x) | = | 1 ( -a - 1 / 2 ≤ x ≤ -a または a ≤ x ≤ a + 1 / 2 ; 但し a ≥ 0 ) |
| = | 0 ( それ以外 ) |
のようなものも確率分布になります。この分布の平均は
で、分散は
です。平均の付近の確率密度はゼロなので、このような場合は第二項は逆に小さくなるはずです。しかし、それでもチェビシェフの不等式は成り立って、
となるはずです。そこで、k = a のときを考えると、P( | x | ≥ a ) = 1 ですが、
となって、任意の a に対してちゃんと成り立っています。
確率変数 x1, x2, ... の積率母関数がゼロの近傍で一致するとき、それらの確率変数の確率分布も一致するということが知られています。確率分布が等しければ積率母関数が等しいことは理解できますが、その逆も成り立つことになります。
積率母関数は
で表されます。積率母関数が等しい時に確率分布が一意に決まるのであれば、この逆変換 g(θ) → p(x) があることになります。実は、積率母関数の式によく似たものに「フーリエ変換(Fourier Transform)」があります。
F(ω) = ∫{-∞→∞} f(t)e-iωt dt
f(t) = ( 1 / 2π )∫{-∞→∞} F(ω)eiωt dω
上側がフーリエ変換で、下側がフーリエ逆変換です。この二つの式があるため、信号 f(t) と F(ω) は一対一に対応するわけです。しかし、フーリエ変換はネイピア数の指数が虚数なので、全く同じというわけではありません。そこで、このフーリエ変換をさらに一般化した「ラプラス変換(Laplace Transform)」が登場することになります。
L(s) = ∫{-∞→∞} f(t)e-st dt
f(t) = ( 1 / 2πi )∫{σ-i∞→σ+i∞} L(s)est ds
s は複素数 s = σ + iω を表します。フーリエ変換とよく似た形ですが、実際 s を分解してラプラス変換式を書き直すと
になるので、f(t)e-σt = g(t) とすればフーリエ変換と同じ式になります。つまり、ラプラス変換は f(t) に e-σt を掛けた上でフーリエ変換を行う操作と考えることもできます。フーリエ変換を行うためにはその積分値が存在しなければならないのですが、f(t) が t → ∞ で発散するような場合は積分値は収束しないので、f(t) を収束する形にしてフーリエ変換可能な状態にするわけです。しかし、今度は t → -∞ で発散することになるので、積分範囲を [ T, ∞ ) ( 通常 T = 0 ) として利用することが多いようです。この時の式は
になるので、こちらは「片側ラプラス変換(One-sided Laplace Transform)」、前に紹介した側は「両側ラプラス変換(Two-sided Laplace Transform)」と呼ばれ、片側ラプラス変換の方がよく利用されるようです。
ラプラス変換は微分方程式の解法などにその威力を発揮します。ここではそのあたりの説明は省略して、ラプラス変換に逆変換が存在し、f(t) と L(s) が一対一に対応することだけを紹介しておきます。ω = 0 のときのラプラス変換は積率母関数の式そのものなので、積率母関数にも逆変換が存在して、確率分布と一対一に対応していることになります。
一様分布は、次のような確率密度を持つ確率密度関数です。
| pa,b(x) | = | 1 / ( b - a ) | ( a ≤ x ≤ b ) |
| = | 0 | ( x < a または x > b ) |
離散分布の場合は、次のようになります。
| pk,N(r) | = | 1 / N | ( k ≤ r ≤ k + N - 1 ) |
| = | 0 | ( r < k または r > k + N - 1 ) |
離散分布の場合は、サイコロの出る目の確率などのモデルになっているので、今までにも何度か登場している確率密度関数です。平均値 μ は
| μ = E[x] | = | ∫{-∞→∞} x・pa,b(x) dx |
| = | ∫{a→b} x / ( b - a ) dx | |
| = | [ x2 / 2( b - a ) ]{a→b} | |
| = | ( b2 - a2 ) / 2( b - a ) | |
| = | ( b - a )( b + a ) / 2( b - a ) | |
| = | ( b + a ) / 2 |
分散 σ2 は
| σ2 | = | E[x2] - μ2 |
| = | ∫{-∞→∞} x2・pa,b(x) dx - { ( b + a ) / 2 }2 | |
| = | ∫{a→b} x2 / ( b - a ) dx - ( b2 + 2ab + a2 ) / 4 | |
| = | [ x3 / 3( b - a ) ]{a→b} - ( b2 + 2ab + a2 ) / 4 | |
| = | ( b3 - a3 ) / 3( b - a ) - ( b2 + 2ab + a2 ) / 4 | |
| = | ( b - a )( b2 + ab + a2 ) / 3( b - a ) - ( b2 + 2ab + a2 ) / 4 | |
| = | { 4( b2 + ab + a2 ) - 3( b2 + 2ab + a2 ) } / 12 | |
| = | ( b2 - 2ab + a2 ) / 12 | |
| = | ( b - a )2 / 12 |
になります。a = k, b = k + N - 1 としたとき、離散分布も同様の式になります。
| 一様分布(連続) pa,b(x) | = | 1 / ( b - a ) | ( a ≤ x ≤ b ) |
| = | 0 | ( x < a または x > b ) | |
| 一様分布(離散) pk,N(r) | = | 1 / N | ( k ≤ r ≤ k + N - 1 ) |
| = | 0 | ( r < k または r > k + N - 1 ) |
平均 : ( b + a ) / 2、分散 : ( b - a )2 / 12
一様分布用のクラスを以下に示します。
/* UniformDistribution : 一様分布 */ class UniformDistribution : public ContDist { // 確率変数の定義域 double _a; double _b; public: /* コンストラクタ double a, b : 確率変数の定義域 */ UniformDistribution( double a, double b ) { _a = ( a > b ) ? b : a; _b = ( a > b ) ? a : b; } // 確率変数 x における確率密度を返す double operator[]( double x ) const; // 区間 (-∞,a] における確率を返す double lower_p( double a ) const; double average() const // 平均値 { return( ( _a == _b ) ? NAN : ( _a + _b ) / 2.0 ); } double variance() const // 分散 { return( ( _a == _b ) ? NAN : pow( _b - _a, 2 ) / 12.0 ); } }; /* UniformDistribution::operator[] : 確率変数 x における確率密度を返す double x : 確率変数 戻り値 : 確率密度 */ double UniformDistribution::operator[]( double x ) const { if ( x < _a || x > _b ) return( 0 ); return( ( _a == _b ) ? FP_INFINITE : 1.0 / ( _b - _a ) ); } /* UniformDistribution::lower_p : 区間 (-∞,a] における確率を返す double a : 区間の上限 戻り値 : 確率 */ double UniformDistribution::lower_p( double a ) const { if ( a <= _a ) return( 0 ); if ( a >= _b ) return( 1 ); return( ( a - _a ) / ( _b - _a ) ); }
大きさ N の正方行列 A と B に対して
が成り立ちます。この証明は結構厄介で、行列式の定義を利用する必要があるので、まずはその定義内容から確認します。
行列式の計算は、各行(または各列)から要素をひとつずつ取り出して積を計算し、計算した積の和を求めることによって得られますが、積の計算は各行から異なる列番号(各列の場合は異なる行番号)の要素を取って行います。例えば、大きさ 3 の正方行列では、1 〜 3 列の要素に対して 1,2,3 行目、1,3,2 行目、2,1,3 行目、2,3,1 行目、3,1,2 行目、3,2,1 行目の要素の積を計算するので、その解は 6 つになります。大きさ N の場合、1 〜 N の数値を並べる順列は N! 通りになり、積は N! 個になります。
次にこの積の和を求めるのですが、順列の内容によって積の符号は変わります。順列は、二つの要素を入れ替えることを繰り返すことで作ることができます。この入れ替えのことを互換といい、例えば m と n の互換は ( m n ) と表します。例えば、1,3,2 は ( 2 3 ) で作られ、2,3,1 は ( 1 2 ) と ( 1 3 ) で作られます。互換を偶数回行った場合は偶置換(入れ替えが発生しなかった場合も含みます)、奇数回のときは奇置換といい、奇置換を行った場合は積を負数とすると定義されるので、大きさ 3 の正方行列では 1,2,3 行目、2,3,1 行目、3,1,2 行目が偶置換、1,3,2 行目、2,1,3 行目、3,2,1 行目が奇置換になって、行列の r 行 c 列の要素を arc で表せば、大きさ 3 の正方行列の場合、結局次のような式で表されます。
大きさ N の正方行列に対する行列式は、以下のように表現しておきます。
(i1 i2 ... iN) が順列を、ar,c が r 行 c 列の要素を表します。σ(i1 i2 ... iN) は、順列 (i1 i2 ... iN) が偶置換ならば 1、奇置換ならば -1 になるとします(これを「順列符号」といいます)。
AB の r 行 c 列の要素は、A, B の r 行 c 列の要素をそれぞれ arc, brc としたとき、
になります。よって、|AB| は
と表すことができます。Πr,c{r=1→N;c=i1→iN}( Σk{1→N}( arkbkc ) ) の部分を展開してみると、
| Πr,c{r=1→N;c=i1→iN}( Σk{1→N}( arkbkc ) ) | |
| = | Πr,c{r=1→N;c=i1→iN}( ar1b1c + ar2b2c + ... + arNbNc ) |
| = | ( a11b1,i1 + a12b2,i1 + ... + a1NbN,i1 )( a21b1,i2 + a22b2,i2 + ... + a2NbN,i2 ) |
| ... ( aN1b1,iN + aN2b2,iN + ... + aNNbN,iN ) | |
| = | ( a11b1,i1・a21b1,i2・...・aN1b1,iN ) + ( a12b2,i1・a21b1,i2・...・aN1b1,iN ) + ... + ( a1NbN,i1・a21b1,i2・...・aN1b1,iN ) |
| + ( a11b1,i1・a22b2,i2・...・aN1b1,iN ) + ( a12b2,i1・a22b2,i2・...・aN1b1,iN ) + ... + ( a1NbN,i1・a22b2,i2・...・aN1b1,iN ) | |
| : | |
| + ( a11b1,i1・a2NbN,i2・...・aN1b1,iN ) + ( a12b2,i1・a2NbN,i2・...・aN1b1,iN ) + ... + ( a1NbN,i1・a2NbN,i2・...・aN1b1,iN ) | |
| : | |
| + ( a11b1,i1・a2NbN,i2・...・aNNbN,iN ) + ( a12b2,i1・a2NbN,i2・...・aNNbN,iN ) + ... + ( a1NbN,i1・a2NbN,i2・...・aNNbN,iN ) |
各項は Πk{1→N}( akj(k)bj(k),i(k) ) = Πk{1→N}( akj(k) )・Πk{1→N}( bj(k),i(k) ) となります。この中で、i(k) は i1 〜 iN の添え字が k となったものを表します。また、j(k) は 1 〜 N での任意の数字で、重複を許す( k1 ≠ k2 のとき j(k1) = j(k2) となる場合がある )ので、項の数は NN という膨大な数になります。
しかし、k1 ≠ k2 かつ j(k1) = j(k2) となるとき、ある順列符号 σ(i1 i2 ... iN) の中で i(k1) と i(k2) を入れ替えたものは符号が入れ替わり、しかも Πk{1→N}( akj(k)bj(k),i(k) ) は ( j(k) が等しく、全ての i(k) に対する積を計算しているのだから ) 等しくなるので、互いに打ち消しあうことになります。よって、j(k) が重複しない項だけを考えればよく、j(k) も順列として扱うことができるので、
になります。ところで、arc は r が 1 〜 N の値を取るとき、c が j1 から jN に並べ替えられた状態で、これを ( 1 2 .. N ) → ( j1 j2 ... jN ) と表せば、brc は ( j1 j2 ... jN ) → ( i1 i2 ... iN ) になります。( 1 2 .. N ) → ( j1 j2 ... jN ) での互換の数と ( j1 j2 ... jN ) → ( i1 i2 ... iN ) での互換の数の和が σ(i1 i2 ... iN) に等しくなるので、( j1 j2 ... jN ) → ( i1 i2 ... iN ) を、j1 〜 jN が 1 〜 N になるように並べ替えた上でもう一度 ( 1 2 .. N ) → ( l1 l2 ... lN ) と定義し直した時(それでも互換の数は変わらないので)、
が成り立ちます。従って、
| |AB| | = | Σ(l1 l2 ... lN)( Σ(j1 j2 ... jN)( σ(j1 j2 ... jN)・σ(l1 l2 ... lN) Πr,c{r=1→N;c=j1→jN}( arc )・Πr,c{r=1→N;c=l1→lN}( brc ) ) ) | |
| = | Σ(l1 l2 ... lN)( σ(l1 l2 ... lN) Πr,c{r=1→N;c=l1→lN}( brc ) Σ(j1 j2 ... jN)( σ(j1 j2 ... jN) Πr,c{r=1→N;c=j1→jN}( arc ) ) ) | ||
| = | Σ(j1 j2 ... jN)( σ(j1 j2 ... jN) Πr,c{r=1→N;c=j1→jN}( arc ) ) Σ(l1 l2 ... lN)( σ(l1 l2 ... lN) Πr,c{r=1→N;c=l1→lN}( brc ) ) |
一方、|A| と |B| は
|A| = Σ(j1 j2 ... jN)( σ(j1 j2 ... jN) Πr,c{r=1→N;c=j1→jN}( arc ) )
|B| = Σ(l1 l2 ... lN)( σ(l1 l2 ... lN) Πr,c{r=1→N;c=l1→lN}( brc ) )
なので、|AB| = |A||B| が成り立つことになります。実際に、二行二列の行列
| A | = | | | a11, | a12 | | |
| | | a21, | a22 | | | ||
| B | = | | | b11, | b12 | | |
| | | b21, | b22 | | |
で確かめてみると、AB の r 行 c 列目の要素は ar1b1c + ar2b2c なので、
| |AB| | = | ( a11b11 + a12b21 )( a21b12 + a22b22 ) |
| - ( a21b11 + a22b21 )( a11b12 + a12b22 ) | ||
| = | a11b11a21b12 + a11b11a22b22 + a12b21a21b12 + a12b21a22b22 | |
| - a21b11a11b12 - a21b11a12b22 - a22b21a11b12 - a22b21a12b22 | ||
| = | a11a21b11b12 - a11a21b11b12 + a12a22b21b22 - a12a22b21b22 | |
| + a11a22b11b22 + a12a21b12b21 - a12a21b11b22 - a11a22b12b21 | ||
| = | 1・a11a22・1・b11b22 + (-1)・a12a21・(-1)・b12b21 + (-1)・a12a21・1・b11b22 + 1・a11a22・(-1)・b12b21 | |
| = | 1・a11a22{ 1・b11b22 + (-1)・b12b21 } + (-1)・a12a21{ (-1)・b12b21 + 1・b11b22 } | |
| = | { 1・a11a22 + (-1)・a12a21 }{ 1・b11b22 + (-1)・b12b21 } | |
| = | |A||B| |
になります。途中の計算で、行番号順に並べた時に、列番号が逆転していれば -1 を掛けていることに注意して下さい。これが順列符号を表しています。
この定理が証明できれば、直交行列の行列式を求めることは簡単です。直交行列は QQT = E が成り立ち、E の行列式は 1 なので、|Q||QT| = 1 になります。行列式の定義から、転置行列の行列式は元の行列のそれと等しくなります。従って、|Q| = |QT| が成り立ち、これを満たすには行列式が 1 か -1 である必要があります。従って、|Q| は 1 か -1 のいずれかです。
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |