
前章では、「中心極限定理」によって標本平均が正規分布に従うということ、また「大数の法則」によって標本数を増やすほど標本平均は真の平均に近づいてゆくことを紹介しました。例えば、サイコロを何回も投げた時に 1 の目が出る回数は、試行回数を増やすほど平均が 1 / 6 に近づき、その分布は正規分布に近づいていきます。「大数の法則」は経験上「当然」であるように見えますが、平均と分散を持った確率分布に従う事象ならば標本平均が正規分布に近似できる「中心極限定理」は驚くべき結果であって、正規分布が統計学の中で重要な位置を占めている理由の一つとなっています。「中心極限定理」は、標本平均の誤差が正規分布となることを意味していることにもなるので、正規分布は「誤差の分布」とも呼ばれます。
今回は、標本平均だけではなく、標本分散などの他の統計量の確率分布がどのようになるかを見ていきたいと思います。
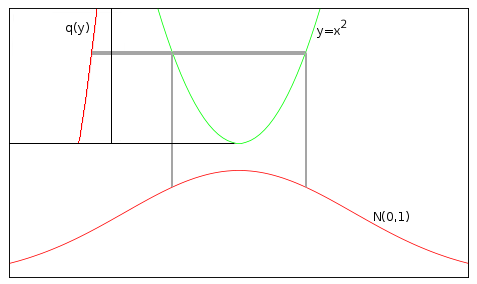
まずは、確率変数 x が標準正規分布 p(x) = N( 0, 1 ) に従うとき、y = x2 がどのような分布に従うのかを求めてみます。まず、求める分布を q(y) としたとき、y = x2 の逆関数は二価関数なので、q(y)dy = 2p(x)dx となります。また、dy = 2xdx なので、
| q(y) | = | 2p(x) / 2x |
| = | { 1 / sqrt( 2π ) }x-1exp( -x2 / 2 ) | |
| = | { 1 / sqrt( 2π ) }y-1/2e-y/2 ( 但し、y > 0 ) |
になります。
つぎに、独立した確率変数 yi ( yi = xi2 ; i = 1,2, ... N ) の和 Σi{1→N}( yi ) の確率分布を考えると、独立な確率分布の和の分布は「畳み込み積分(Convolution)」で表されるので(「(4) 多変数の確率分布」の「3) 確率変数の変換」参照)、N 個の確率変数の和の分布を TN( y ) とすれば、
が成り立つはずです。実際、N = 2 のときは
| T1( y1 )T1( y2 ) | = | { 1 / sqrt( 2π ) }y1-1/2exp( -y1 / 2 )・{ 1 / sqrt( 2π ) }y2-1/2exp( -y2 / 2 ) |
| = | ( 1 / 2π )( y1y2 )-1/2exp( -( y1 + y2 ) / 2 ) |
で、( u, v ) = ( y1 + y2, y2 ) とすれば、y1 = u - v, y2 = v より、ヤコビアンは
となって、
が得られます。u に対する周辺分布が T2( u ) なので、
| T2( u ) | = | ∫{-∞→∞} ( 1 / 2π ){ v( u - v ) }-1/2exp( -u / 2 ) dv |
| = | ∫{-∞→∞} ( 1 / sqrt( 2π ) )( u - v )-1/2exp( -( u - v ) / 2 )・( 1 / sqrt( 2π ) )v-1/2exp( -v / 2 ) dv | |
| = | T1( u ) * T1( u ) |
となって、畳み込み積分で表すことができます。実際に上式を解いてみると、まず、y1 = u - v > 0、y2 = v > 0 より 0 < v < u なので積分の範囲は ( 0, u ) となって、v = usin2θ とすれば dv = 2usinθcosθdθ、v → 0 のとき θ → 0、v → u のとき θ → π / 2 なので、
| T2( u ) | = | ( 1 / 2π )exp( -u / 2 )∫{0→u} { v( u - v ) }-1/2 dv |
| = | ( 1 / 2π )exp( -u / 2 )∫{0→π/2} { usin2θ( u - usin2θ ) }-1/2・2usinθcosθdθ | |
| = | ( 1 / 2π )exp( -u / 2 )∫{0→π/2} ( u2sin2θcos2θ )-1/2・2usinθcosθdθ | |
| = | ( 1 / 2π )exp( -u / 2 )[2θ]{0→π/2} | |
| = | exp( -u / 2 ) / 2 |
になります。さらに T3( y ) は
| T3( y ) | = | T2( y ) * T1( y ) |
| = | ∫{-∞→∞} T2( y - t )T1( t ) dt | |
| = | ∫{0→y} { exp( -( y - t ) / 2 ) / 2 }・( 1 / sqrt( 2π ) )t-1/2exp( -t / 2 ) dt | |
| = | { 1 / 2sqrt( 2π ) }exp( -y / 2 ) ∫{0→y} t-1/2 dt | |
| = | { 1 / 2sqrt( 2π ) }exp( -y / 2 ) [2t1/2]{0→y} | |
| = | { 1 / sqrt( 2π ) }y1/2exp( -y / 2 ) |
T4( y ) は
| T4( y ) | = | T3( y ) * T1( y ) |
| = | ∫{-∞→∞} T3( y - t )T1( t ) dt | |
| = | ∫{0→y} { 1 / sqrt( 2π ) }( y - t )1/2exp( -( y - t ) / 2 )・( 1 / sqrt( 2π ) )t-1/2exp( -t / 2 ) dt | |
| = | ( 1 / 2π )exp( -y / 2 ) ∫{0→y} ( y - t )1/2t-1/2 dt |
t = ysin2θ とすれば dt = 2ysinθcosθdθ、t → 0 のとき θ → 0、t → y のとき θ → π / 2 なので、
| T4( y ) | = | ( 1 / 2π )exp( -y / 2 ) ∫{0→π/2} ( y - ysin2θ )1/2( ysin2θ )-1/2 2ysinθcosθ dθ |
| = | ( 1 / 2π )exp( -y / 2 ) ∫{0→π/2} 2ycos2θ dθ |
cos2θ = 2cos2θ - 1 より cos2θ = ( cos2θ + 1 ) / 2 なので、
| T4( y ) | = | ( 1 / 2π )exp( -y / 2 )y ∫{0→π/2} cos2θ + 1 dθ |
| = | ( 1 / 2π )exp( -y / 2 )y [sin2θ / 2 + θ]{0→π/2} | |
| = | ( 1 / 4 )y・exp( -y / 2 ) |
と求めていくことができます。N に対する TN( y ) の式を下表にまとめておきます。
| N | TN( y ) |
|---|---|
| 1 | { 1 / sqrt( 2π ) }y-1/2e-y/2 |
| 2 | e-y/2 / 2 |
| 3 | { 1 / sqrt( 2π ) }y1/2e-y/2 |
| 4 | ( 1 / 4 )y・e-y/2 |
| 5 | ( 1 / 3sqrt( 2π ) )y3/2e-y/2 |
| 6 | ( 1 / 16 )y2e-y/2 |
| 7 | ( 1 / 15sqrt( 2π ) )y5/2e-y/2 |
| 8 | ( 1 / 96 )y3e-y/2 |
上記結果を見ると、e-y/2 に変化はなく、y のべき乗は N に対して y( N - 2 ) / 2 と表せそうです。係数のところが複雑ですが、例えば N が 3, 5, 7 と変化した時に 1 / 3, 1 / 5 と小さくなったり、4, 6, 8 と変化した時には 1 / 4, 1 / 6 と小さくなったりと、変化に一定の法則がありそうです。また、sqrt( 2π ) があるのは N が奇数のみであるという特徴もあります。実際、これらを一般化した式は存在し、次のようになります。
これを、自由度 N の「χ2(カイ二乗)-分布(Chi-square Distribution)」といいます。上記説明から、y = ΣN{1→N}( xi2 ) は 自由度 N の χ2-分布に従うことになります。
上式の中の Γ( N / 2 ) は「ガンマ関数」と呼ばれる次のような式になります。
ガンマ関数の主な性質として以下のようなものがあります。
ガンマ関数は階乗 n! を正の実数(実際には実部が正の複素数)まで拡張した関数であり、n が正の整数であれば階乗と一致します。従って、Γ( N / 2 ) は、N が偶数のときは階乗 ( N / 2 - 1 )! 【 ( N / 2 )! ではないことに注意 】になり、奇数の場合は
| Γ( N / 2 ) | = | ( N / 2 - 1 )Γ( N / 2 - 1 ) |
| = | ( N / 2 - 1 )( N / 2 - 2 )Γ( N / 2 - 2 ) | |
| : | ||
| = | ( N / 2 - 1 )( N / 2 - 2 ) ... ( 1 / 2 )Γ( 1 / 2 ) | |
| = | ( N / 2 - 1 )( N / 2 - 2 ) ... ( 1 / 2 )√π |
と計算することができます。
χ2-分布の全範囲の積分値は
| ∫{-∞→∞} TN( x ) dx | = | { 1 / 2N/2Γ( N / 2 ) } ∫{0→∞} x( N - 2 ) / 2 e-x/2 dx |
| = | { 1 / 2N/2Γ( N / 2 ) }・2N/2-1 ∫{0→∞} ( x / 2 )N/2-1 e-x/2 dx | |
| = | { 1 / 2N/2Γ( N / 2 ) }・2N/2-1 ∫{0→∞} tN/2-1 e-t・2 dt | |
| = | { 2N/2-1 / 2N/2Γ( N / 2 ) }・2Γ( N / 2 ) = 1 |
なので、確率分布として成り立っていることが分かります(ガンマ関数は常に正なので、TN( x ) ≥ 0 も成り立っています)。また、累積分布関数 F(x) は
| ∫{0→x} TN( t ) dt | = | { 1 / 2N/2Γ( N / 2 ) } ∫{0→x} t( N - 2 ) / 2 e-t/2 dt | |
| = | { 1 / 2N/2Γ( N / 2 ) }・2N/2 ∫{0→x/2} uN/2-1 e-u du | [ u = t / 2 で変数変換 ] | |
| = | γ( N / 2, x / 2 ) / Γ( N / 2 ) |
と表すことができます。ここで、γ( N / 2, x / 2 ) は「(第一種)不完全ガンマ関数 ( (Lower) Incomplete Gamma Function )」と呼ばれる以下の形をした関数になります。
ガンマ関数における積分範囲を ( 0, x ] に限定した形であり、逆に [ x, ∞ ) に限定したものは「(第二種)不完全ガンマ関数 ( (Upper) Incomplete Gamma Function )」と呼ばれます。
自由度 N の χ2-分布の積率母関数は
| g(θ) = E[eθx] | = | { 1 / 2N/2Γ( N / 2 ) } ∫{0→∞} eθxx( N - 2 ) / 2e-x/2 dx |
| = | { 1 / 2N/2Γ( N / 2 ) } ∫{0→∞} x( N - 2 ) / 2e( θ - 1/2 )x dx | |
| = | { 1 / 2N/2Γ( N / 2 ) } ( 1/2 - θ )-N/2 + 1∫{0→∞} { ( 1/2 - θ )x }N/2 - 1e-( 1/2 - θ )x dx |
t = ( 1/2 - θ )x とすれば dt = ( 1/2 - θ )dx となって、
| g(θ) | = | { 1 / 2N/2Γ( N / 2 ) } ( 1/2 - θ )-N/2 + 1∫{0→∞} tN/2 - 1e-t ( 1/2 - θ )-1 dt |
| = | { ( 1/2 - θ )-N/2 / 2N/2Γ( N / 2 ) } Γ( N / 2 ) | |
| = | ( 1/2 - θ )-N/2 / 2N/2 |
g(θ) を微分すると
なので、平均は
になります。もう一度微分して
となるので、E[x2] は
| E[x2] = g(2)(0) | = | ( -N / 2 )( -N / 2 - 1 )( 1 / 2 )-N/2 - 2・( 1 / 2 )N/2 |
| = | ( N / 2 )( N / 2 + 1 )・4 | |
| = | N( N + 2 ) |
よって、分散 σ2 は
になります。
以上まとめると、次のようになります。
自由度 N の χ2-分布 TN( x ) = { 1 / 2N/2Γ( N / 2 ) } x( N - 2 ) / 2 e-x/2 ( x > 0 )
平均 : N、分散 : 2N
/* ChiSquareDistribution : カイ二乗分布 */ class ChiSquareDistribution : public ContDist { unsigned int _n; // 自由度 // 不完全ガンマ関数の計算 static double iGamma( unsigned int n, double x ); public: /* コンストラクタ unsigned int n : 自由度 */ ChiSquareDistribution( unsigned int n ) : _n( n ) {} // 確率変数 x における確率密度を返す double operator[]( double x ) const; // 区間 (-∞,a] における確率を返す double lower_p( double a ) const; double average() const { return( ( _n > 0 ) ? _n : NAN ); } // 平均値 double variance() const { return( ( _n > 0 ) ? 2 * _n : NAN ); } // 分散 }; /* ChiSquareDistribution::iGamma : 不完全ガンマ関数 Γ( n / 2, x ) の計算 Γ( n / 2, x ) = ∫{0→x} t^(n/2) e^-t dt unsigned int n : 変数 n double x : 積分範囲 戻り値 : 確率密度 */ double ChiSquareDistribution::iGamma( unsigned int n, double x ) { if ( n == 1 ) { return( sqrt( M_PI ) * erf( sqrt( x ) ) ); } else if ( n == 2 ) { return( 1.0 - exp( -x ) ); } else if ( n > 2 ) { double a = (double)n / 2.0 - 1.0; return( a * iGamma( n - 2, x ) - pow( x, a ) * exp( -x ) ); } return( 0 ); } /* ChiSquareDistribution::operator[] : 確率変数 x における確率密度を返す double x : 確率変数 戻り値 : 確率密度 */ double ChiSquareDistribution::operator[]( double x ) const { if ( _n == 0 ) return( NAN ); if ( x == 0 && _n == 1 ) return( INFINITY ); if ( x < 0 ) return( 0 ); double n_2 = (double)_n / 2.0; return( pow( x, ( (double)_n - 2.0 ) / 2.0 ) * exp( -x / 2.0 ) / ( pow( 2, n_2 ) * tgamma( n_2 ) ) ); } /* ChiSquareDistribution::lower_p : 区間 (-∞,a] における確率を返す double a : 区間の上限 戻り値 : 確率 */ double ChiSquareDistribution::lower_p( double a ) const { if ( _n == 0 ) return( NAN ); if ( a <= 0 ) return( 0 ); return( iGamma( _n, a / 2.0 ) / tgamma( (double)_n / 2.0 ) ); }
χ2-分布の任意範囲の確率を計算するためには不完全ガンマ関数の計算が必要です。不完全ガンマ関数に対して部分積分法を用いると、以下の漸化式が成り立ちます。
| γ( α + 1, x ) | = | ∫{0→x} tα e-t dt |
| = | [-tα e-t]{0→x} + ∫{0→x} αtα-1 e-t dt | |
| = | αγ( α, x ) - xα e-x |
χ2-分布で利用する不完全ガンマ関数は α = N / 2 の形を取るので、漸化式を使って α = 1 または 1 / 2 にすることができて、
| γ( 1, x ) | = | ∫{0→x} e-t dt |
| = | [-e-t]{0→x} | |
| = | 1 - e-x |
| γ( 1 / 2, x ) | = | ∫{0→x} t-1/2 e-t dt | |
| = | ∫{0→√x} u-1 exp( -u2 ) 2u du | [ t = u2 で変数変換 ] | |
| = | 2∫{0→√x} exp( -u2 ) du | ||
| = | √π erf( √x ) |
と求めることができます。ここで、erf( x ) は正規分布のところでも紹介した「誤差関数(Error Function)」で、以下のような式になります。この関数で、標準正規分布の [ -x, x ] の範囲の確率を求めることができるので、ライブラリ関数として標準で用意されています。
不完全ガンマ関数を利用して、任意の値 α に対する [ 0, α ] の範囲の確率を求めることができるので、α < β に対して F(α), F(β) がそれぞれ [ 0, α ], [ 0, β ] の範囲の確率であるとすれば、F(β) - F(α) が [ α, β ] の範囲の確率を表すことになります。
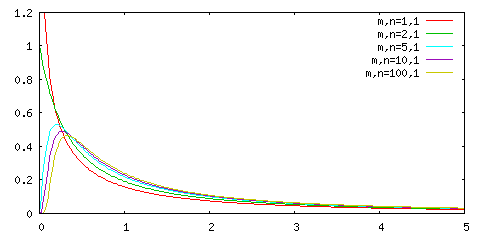
下図は、自由度 N = 1, 2, 5, 10 に対するχ2-分布を示したものです。自由度が大きくなるほど、分布の高さは低く、横に広がった形に変化していきます。また、大きく偏った形から次第に左右対称な形に近づいていきます。
z = ( x - N ) / ( 2N )1/2 としたとき、dz = dx / ( 2N )1/2 より q(z) = p(x)dx/dz = ( 2N )1/2p(x) なので、自由度 N の χ2-分布は
になります。スターリングの公式
は、ガンマ関数にも適用することができて(補足1)、
となるので、これを代入すると
| TN( z ) | ≅ | [ ( 2N )1/2 / 2N/2{ 2π( N / 2 - 1 ) }1/2{ ( N / 2 - 1 ) / e }N/2-1 ] { ( 2N )1/2z + N }( N - 2 ) / 2 exp( -{ ( 2N )1/2z + N } / 2 ) |
| = | [ ( 2N )1/2{ ( 2N )1/2z + N }( N - 2 ) / 2 / 2N/2{ 2π( N / 2 - 1 ) }1/2( N / 2 - 1 )N/2-1 ] exp( ( N / 2 - 1 ) - { ( 2N )1/2z + N } / 2 ) | |
| = | 21/2N1/2N( N - 2 ) / 2{ ( 2 / N )1/2z + 1 }( N - 2 ) / 22-N/2( 2π )-1/2( N / 2 - 1 )-1/2( N / 2 - 1 )-N/2+1 exp( -( N / 2 )1/2z - 1 ) | |
| = | ( 2π )-1/22-N/2+1/2NN/2-1/2( N / 2 - 1 )-N/2+1/2{ ( 2 / N )1/2z + 1 }( N - 2 ) / 2 exp( -( N / 2 )1/2z - 1 ) | |
| = | ( 2π )-1/2( 1 - 2 / N )-N/2+1/2{ ( 2 / N )1/2z + 1 }( N - 2 ) / 2 exp( -( N / 2 )1/2z - 1 ) |
ここで、
| ( 1 - 2 / N )-N/2+1/2 | = | { 1 + 1 / ( -N / 2 ) }-N/2( 1 - 2 / N )1/2 |
| → | e ( N → ∞ ) |
になります。また、f(x) = ln( x + 1 ) のマクローリン級数(Maclaurin Series) は
| ln( x + 1 ) | = | f(0) + f'(0)x + f(2)(0)x2 / 2! + ... |
| = | x - x2 / 2 + ... |
なので、x が充分に小さい場合は x + 1 ≅ exp( x - x2 / 2 ) と近似することができます。これを利用すると、N が充分に大きければ
| { ( 2 / N )1/2z + 1 }( N - 2 ) / 2 | ≅ | exp( ( 2 / N )1/2z - { ( 2 / N )1/2z }2 / 2 )( N - 2 ) / 2 |
| = | exp( ( N / 2 - 1 )( 2 / N )1/2z - ( N / 2 - 1 ){ ( 2 / N )1/2z }2 / 2 ) | |
| = | exp( { ( N / 2 )1/2 - ( 2 / N )1/2 }z - { 1 - ( 2 / N ) }z2 / 2 ) |
よって、
| TN( z ) | ≅ | ( 2π )-1/2 e・exp( { ( N / 2 )1/2 - ( 2 / N )1/2 }z - { 1 - ( 2 / N ) }z2 / 2 ) exp( -( N / 2 )1/2z - 1 ) |
| = | ( 2π )-1/2 exp( { -( 2 / N )1/2 }z - { 1 - ( 2 / N ) }z2 / 2 ) | |
| ≅ | ( 2π )-1/2 exp( -z2 / 2 ) |
従って、z = ( x - N ) / ( 2N )1/2 としたとき、χ2-分布は N が大きくなるに従って標準正規分布に近づいていきます。
平均 μ、分散 σ2 を持つ同一確率分布上にある独立した確率変数 x = ( x1, x2, ... xN ) に対して、
yi = ( xi - μ ) / σ
y = Σi{1→N}( yi / √N )
としたとき、N が大きくなるに従って、y は標準正規分布に近づいていきます。これを「中心極限定理(Central Limit Theorem)」というのでした。これは自由度 1 の χ2-分布に対しても成り立つので、x = Σi{1→N}( xi ) とすると、μ = 1、σ = √2 より
| y | = | Σi{1→N}( ( xi - μ ) / σ√N ) |
| = | ( x - N ) / ( 2N )1/2 |
となります。y が標準正規分布に従うことは先ほど示しましたが、中心極限定理からもこれは明らかであるということになります。
ところで、正規分布 N( μ, σ2 ) から N 個の標本 x1, x2, ... xN を抽出して
としたとき、
とすれば、ti は標準正規分布に従うので、y = Σi{1→N}( ti2 ) は自由度 N の χ2-分布に従うことになります。ところが、平均を母平均 μ から標本平均 m に置き換えて、y を
とすると、これは自由度 N - 1 の χ2-分布に従います。xi - μ は N 個の独立な変数であったのに対し、
の関係式によって、最後の変数は独立ではなくなってしまいます。すなわち、その変数を xN - m とすれば、
となるので、{ xi - m } は「線形従属(Linear Dependence)」になります(補足2)。
また、正規分布 N( μ σ2 ) からランダムに抽出した N 個の標本を使って標本平均 m を求めると、m はやはり正規分布 N( μ σ2 / N ) に従います。よって、標本平均 m を 1 個抽出して
を求めると、y は自由度 1 の χ2-分布に従うことになります。
χ2-分布のその他の性質として「再生性(Reproductive Property)」があります。再生性とは、ある確率分布に従う確率変数の和が、また同じ確率分布に従うことで、例えば正規分布は再生性を持った確率分布です(「(5) 正規分布」の「4) 標本平均と標本分散」参照 )。
独立な確率変数 xm、xn がそれぞれ自由度 M、N の χ2-分布に従うとしたとき、x = xm + xn の確率分布 p(x) は
になります。ところが、χ2-分布の性質から
が成り立つので、
となって、p(x) = TM+N( x ) が成り立ちます(補足3)。
二つの独立した確率変数 t, u が、それぞれ自由度 M, N の χ2-分布に従うとき、
がどのような分布になるかを調べてみます。まずは t、u を変数とする同時分布を φ( t, u ) とすると、t、u は独立なので、
で表すことができます。φ( t, u ) の変数 t、u を
x = ( t / M ) / ( u / N ) = Nt / Mu
y = Mu
と変数変換すると、
t = Mux / N = xy / N
u = y / M
となるので、ヤコビアンは
| det( J( x, y ) ) | = | ( ∂t / ∂x )・( ∂u / ∂y ) - ( ∂t / ∂y )・( ∂u / ∂x ) |
| = | ( y / N )・( 1 / M ) - ( x / N )・0 | |
| = | y / MN | |
| = | u / N |
になります。従って、変数変換した分布を f( x, y ) とすれば、
| f( x, y ) | = | φ( t, u )| det( J( x, y ) ) | |
| = | TM( t ) TN( u ) ( u / N ) |
f( x, y ) を y について ( -∞, ∞ ) の範囲で積分したものが x に対する周辺分布となるので、これを fx( x ) としたとき、
と表すことができます。y = Mu より dy = Mdu なので、
| fx( x ) | = | ∫{-∞→∞} f( x, y ) Mdu |
| = | ∫{-∞→∞} TM( t ) TN( u ) ( u / N ) Mdu | |
| = | ∫{-∞→∞} TM( Mux / N ) TN( u ) ( Mu / N ) du |
これが、求めたい分布になります。fx( x ) を f(x) に置き換えて、χ2-分布の式を代入すると次のようになります。
| f(x) | = | ∫{-∞→∞} [ { 1 / 2M/2 Γ( M / 2 ) } ( Mux / N )(M-2)/2 exp( -( Mux / N ) / 2 ) ] |
| [ { 1 / 2N/2 Γ( N / 2 ) } u(N-2)/2 exp( -u / 2 ) ] ( Mu / N ) du | ||
| = | { 1 / 2M/2 Γ( M / 2 ) 2N/2 Γ( N / 2 ) } ( Mx / N )(M-2)/2 ( M / N ) | |
| ∫{-∞→∞} { u(M-2)/2 exp( -( Mux / N ) / 2 ) } { u(N-2)/2 exp( -u / 2 ) } u du | ||
| = | { ( M / N )M/2 / 2(M+N)/2 Γ( M / 2 ) Γ( N / 2 ) } xM/2-1 | |
| ∫{-∞→∞} u(M+N)/2-1 exp( -u( Mx / N + 1 ) / 2 ) du |
I = ∫{-∞→∞} u(M+N)/2-1 exp( -u( Mx / N + 1 ) / 2 ) du として、t = u( Mx / N + 1 ) / 2 とすれば dt = du( Mx / N + 1 ) / 2 となって、
| I | = | ∫{-∞→∞} u(M+N)/2-1 exp( -u( Mx / N + 1 ) / 2 ) du |
| = | ∫{-∞→∞} { ( Mx / N + 1 ) / 2t }1-(M+N)/2 e-t { ( Mx / N + 1 ) / 2 }-1 dt | |
| = | { ( Mx / N + 1 ) / 2 }-(M+N)/2 ∫{-∞→∞} t(M+N)/2-1 e-t dt | |
| = | 2(M+N)/2 Γ( ( M + N ) / 2 ) / ( Mx / N + 1 )(M+N)/2 |
よって、
| f(x) = | Γ( ( M + N ) / 2 ) ( M / N )M/2 xM/2-1 |
| / Γ( M / 2 ) Γ( N / 2 ) ( Mx / N + 1 )(M+N)/2 |
「ベータ関数(Beta Function)」を利用すると、
が成り立つので、ガンマ関数をベータ関数に置き換え、最後に N(M+N)/2 を分母と分子に掛ければ
になります。この分布を自由度 ( M, N ) の「F-分布(F-distribution)」といいます。但し、x ≤ 0 では χ2-分布 TN(x) = 0 なので、最初の定義から x ≤ 0 では f(x) = 0 になります。
以下、F-分布を次のように表します。
分布は x > 0 の範囲のみにあるので、F-分布の全事象の積分値は
で計算できます。ここで、y = x / { x + ( N / M ) } とすると、
| 1 - y | = | 1 - x / { x + ( N / M ) } |
| = | [ { x + ( N / M ) } - x ] / { x + ( N / M ) } | |
| = | ( N / M ) / { x + ( N / M ) } |
| dy/dx | = | 1 / { x + ( N / M ) } - x / { x + ( N / M ) }2 |
| = | [ { x + ( N / M ) } - x ] / { x + ( N / M ) }2 | |
| = | ( N / M ) / { x + ( N / M ) }2 | |
| = | ( 1 - y )2 / ( N / M ) |
で、x → 0 のとき y → 0、x → ∞ のとき y → 1 となるので、
| ∫{0→∞} GM,N(x) dx | = | { MM/2 NN/2 / Β( M / 2, N / 2 ) } ∫{0→∞} M-(M+N)/2{ x / ( x + N / M ) }M/2-1{ 1 / ( x + N / M ) }N/2+1 dx |
| = | { ( N / M )N/2 / Β( M / 2, N / 2 ) } ∫{0→1} yM/2-1( N / M )-N/2-1( 1 - y )N/2+1 ( N / M )( 1 - y )-2 dy | |
| = | { 1 / Β( M / 2, N / 2 ) } ∫{0→1} yM/2-1( 1 - y )N/2-1 dy |
∫{0→1} yM/2-1( 1 - y )N/2-1 dy = Β( M / 2, N / 2 ) なので積分値は 1 になります。また、ベータ関数は常に正の値を取るので、定義から GM,N(x) ≥ 0 であり、確率分布として成り立っていることが分かります。もっとも、F-分布は、χ2-分布の積による同時分布から周辺分布を求めた結果なので、確率分布となっていることは明らかです。
上記結果を利用すると、累積分布関数 F(x) は
| F(x) | = | ∫{0→x} GM,N(t) dt |
| = | { 1 / Β( M / 2, N / 2 ) } ∫{0→x/{x+(N/M)}} yM/2-1( 1 - y )N/2-1 dy | |
| = | Βx/{x+(N/M)}( M / 2, N / 2 ) / Β( M / 2, N / 2 ) | |
| = | Ix/{x+(N/M)}( M / 2, N / 2 ) |
で表されます。ここで、Βx( α, β ) は「不完全ベータ関数(Incomplete Beta Function)」を表し、
で定義されます。また、Ix( α, β ) は「正規化不完全ベータ関数(Regularized Incomplete Beta Function)」を表し、
になります。
平均値 μ は
| μ = E[x] | = | ∫{0→∞} x・GM,N(x) dx |
| = | { MM/2 NN/2 / Β( M / 2, N / 2 ) } ∫{0→∞} M-(M+N)/2{ x / ( x + N / M ) }M/2{ 1 / ( x + N / M ) }N/2 dx | |
| = | { ( N / M )N/2 / Β( M / 2, N / 2 ) } ∫{0→1} yM/2( N / M )-N/2( 1 - y )N/2 ( N / M )( 1 - y )-2 dy | |
| = | { ( N / M ) / Β( M / 2, N / 2 ) } ∫{0→1} yM/2( 1 - y )N/2-2 dy | |
| = | ( N / M ) Β( M / 2 + 1, N / 2 - 1 ) / Β( M / 2, N / 2 ) |
ベータ関数の性質から
Β( M / 2 + 1, N / 2 - 1 ) = Γ( M / 2 + 1 )Γ( N / 2 - 1 ) / Γ( M / 2 + N / 2 )
Β( M / 2, N / 2 ) = Γ( M / 2 )Γ( N / 2 ) / Γ( M / 2 + N / 2 )
さらに、ガンマ関数の性質から
Γ( M / 2 + 1 ) = ( M / 2 ) Γ( M / 2 )
Γ( N / 2 ) = ( N / 2 - 1 ) Γ( N / 2 - 1 )
が成り立つので
| μ | = | ( N / M ) ( M / 2 ) Γ( M / 2 ) Γ( N / 2 - 1 ) / Γ( M / 2 ) ( N / 2 - 1 ) Γ( N / 2 - 1 ) |
| = | N / ( N - 2 ) |
と得られます。しかし、これは N > 2 の場合に成り立ちます。というのも、
が収束するためには N / 2 - 1 > 0 となる必要があるからです。N ≤ 2 の場合、平均は存在しません。簡単な例として M = N = 2 の場合を考えると
| ∫{0→1} y / ( 1 - y ) dy | = | ∫{0→1} 1 / ( 1 - y ) - 1 dy |
| = | [ -ln( 1 - y ) - y ]{0→1} | |
| = | ( ∞ - 1 ) - ( 0 - 0 ) = ∞ |
となって、積分値は発散してしまいます(補足4)。
E[x2] も同様に
| E[x2] | = | ∫{0→∞} x2・GM,N(x) dx |
| = | { MM/2 NN/2 / Β( M / 2, N / 2 ) } ∫{0→∞} M-(M+N)/2{ x / ( x + N / M ) }M/2+1{ 1 / ( x + N / M ) }N/2-1 dx | |
| = | { ( N / M )N/2 / Β( M / 2, N / 2 ) } ∫{0→1} yM/2+1( N / M )-N/2+1( 1 - y )N/2-1 ( N / M )( 1 - y )-2 dy | |
| = | { ( N / M )2 / Β( M / 2, N / 2 ) } ∫{0→1} yM/2+1( 1 - y )N/2-3 dy | |
| = | ( N / M )2 Β( M / 2 + 2, N / 2 - 2 ) / Β( M / 2, N / 2 ) | |
| = | ( N / M )2 Γ( M / 2 + 2 ) Γ( N / 2 - 2 ) / Γ( M / 2 ) Γ( N / 2 ) | |
| = | ( N / M )2 ( M / 2 + 1 )( M / 2 ) Γ( M / 2 ) Γ( N / 2 - 2 ) / Γ( M / 2 ) ( N / 2 - 1 )( N / 2 - 2 ) Γ( N / 2 - 2 ) | |
| = | N2( M + 2 ) / M( N - 2 )( N - 4 ) |
と計算できるので、分散 σ2 は
| σ2 = E[x2] - μ2 | = | N2( M + 2 ) / M( N - 2 )( N - 4 ) - { N / ( N - 2 ) }2 |
| = | { N2( M + 2 )( N - 2 ) - MN2( N - 4 ) } / M( N - 2 )2( N - 4 ) | |
| = | N2( MN - 2M + 2N - 4 - MN + 4M ) / M( N - 2 )2( N - 4 ) | |
| = | 2N2( M + N - 2 ) / M( N - 2 )2( N - 4 ) |
になります。但し、ここでも N > 4 の場合に成り立つという制約が付きます。
以上まとめると、次のようになります。
自由度 M, N の F-分布 GM,N( x ) = MM/2 NN/2 xM/2-1 / Β( M / 2, N / 2 ) ( Mx + N )(M+N)/2
平均 : N / ( N - 2 ) ( 但し N > 2 )、分散 : 2N2( M + N - 2 ) / M( N - 2 )2( N - 4 ) ( 但し N > 4 )
/* sinPowerInteg : sin関数のべき乗の積分値計算 In(x) = ∫{0→arcsin(√x)} sinθ^n dθ unsigned int n : べき乗の指数 double x : 積分範囲 */ double sinPowerInteg( unsigned int n, double x ) { if ( x < 0 || x > 1 ) return( NAN ); if ( n == 0 ) { return( asin( sqrt( x ) ) ); } else if ( n == 1 ) { return( 1.0 - sqrt( 1 - x ) ); } else { double d = -pow( x, ( (double)n - 1.0 ) / 2.0 ) * sqrt( 1 - x ) / (double)n; return( d + ( (double)n - 1.0 ) * sinPowerInteg( n - 2, x ) / (double)n ); } } /* iBeta : 不完全ベータ関数の計算 Bx( m / 2, n / 2 ) = ∫{0→x} t^(m/2-1) ( 1 - t )^(n/2-1) dt unsigned int m, n : 不完全ベータ関数のパラメータ(a=m/2,b=n/2) double x : 積分範囲 */ double iBeta( unsigned int m, unsigned int n, double x ) { if ( x < 0 || x > 1 ) return( NAN ); if ( m == 0 || n == 0 ) return( NAN ); double a = (double)m / 2.0; double b = (double)n / 2.0; if ( n == 1 ) { return( sinPowerInteg( m - 1, x ) * 2 ); } else if ( n == 2 ) { return( pow( x, a ) / a ); } else { return( ( b - 1 ) * iBeta( m + 2, n - 2, x ) / a + pow( x, a ) * pow( 1 - x, b - 1 ) / a ); } } /* FDistribution : F-分布 */ class FDistribution : public ContDist { unsigned int _m; // 自由度 M unsigned int _n; // 自由度 N public: /* コンストラクタ unsigned int m, n : 自由度 */ FDistribution( unsigned int m, unsigned int n ) : _m( m ), _n( n ) {} // 確率変数 x における確率密度を返す double operator[]( double x ) const; // 区間 (-∞,a] における確率を返す double lower_p( double a ) const; double average() const { return( ( _n > 2 ) ? _n / ( _n - 2 ) : NAN ); } // 平均値 double variance() const; // 分散 }; /* FDistribution::operator[] : 確率変数 x における確率密度を返す double x : 確率変数 戻り値 : 確率密度 */ double FDistribution::operator[]( double x ) const { if ( _m == 0 || _n == 0 ) return( NAN ); if ( x == 0 && _m == 1 ) return( INFINITY ); if ( x == 0 && _m == 2 ) return( 2.0 * tgamma( (double)_n / 2.0 + 1 ) / ( (double)_n * tgamma( (double)_n / 2.0 ) ) ); if ( x <= 0 ) return( 0 ); double a = (double)_m / 2.0; double b = (double)_n / 2.0; double s = (double)( _m + _n ) / 2.0; double beta = tgamma( a ) * tgamma( b ) / tgamma( s ); return( pow( _m, a ) * pow( _n, b ) * pow( x, a - 1 ) / ( beta * pow( (double)_m * x + (double)_n, s ) ) ); } /* FDistribution::lower_p : 区間 (-∞,a] における確率を返す double a : 区間の上限 戻り値 : 確率 */ double FDistribution::lower_p( double a ) const { if ( _m == 0 || _n == 0 ) return( NAN ); if ( a <= 0 ) return( 0 ); double beta = tgamma( (double)_m / 2.0 ) * tgamma( (double)_n / 2.0 ) / tgamma( (double)( _m + _n ) / 2.0 ); if ( _m >= _n ) return( iBeta( _m, _n, a / ( a + (double)_n / (double)_m ) ) / beta ); else return( 1.0 - iBeta( _n, _m, 1.0 - a / ( a + (double)_n / (double)_m ) ) / beta ); } /* FDistribution::variance : 分散を返す 戻り値 : 分散 */ double FDistribution::variance() const { if ( _n <= 4 ) return( NAN ); double m = _m; double n = _n; return( 2 * pow( n, 2 ) * ( m + n - 2 ) / ( m * pow( n - 2, 2 ) * ( n - 4 ) ) ); }
F-分布の任意範囲の確率を計算するためには不完全ベータ関数の計算が必要です。不完全ベータ関数に対して部分積分法を用いると、以下の漸化式が成り立ちます。
| Βx( α, β ) | = | ∫{0→x} tα-1 ( 1 - t )β-1 dt |
| = | [( 1 / α )tα ( 1 - t )β-1]{0→x} - ∫{0→x} ( 1 / α )tα { -( β - 1 )( 1 - t )β-2 } dt | |
| = | { ( β - 1 ) / α }Βx( α + 1, β - 1 ) + ( 1 / α )xα ( 1 - x )β-1 |
漸化式によって β = 1 または 1 / 2 にすることができて、
| Βx( α, 1 ) | = | ∫{0→x} tα-1 dt |
| = | [( 1 / α )tα]{0→x} | |
| = | xα / α |
| Βx( α, 1 / 2 ) | = | ∫{0→x} tα-1 ( 1 - t )-1/2 dt |
| = | ∫{0→sin-1√x} sin2(α-1)θ ( 1 - sin2θ )-1/2 2sinθcosθ dθ | |
| = | 2∫{0→sin-1√x} sin2α-1θ dθ |
但し、Βx( α, 1 / 2 ) では t = sin2θ で変数変換して導いています。さらに α = M / 2 ならば
となるので、積分値の部分を IM-1、y = sin-1√x とすると、
| IM-1 | = | ∫{0→y} sinM-1θ dθ |
| = | [ -sinM-2θcosθ ]{0→y} + ∫{0→y} ( M - 2 )sinM-3θcos2θ dθ | |
| = | [ -sinM-2θcosθ ]{0→y} + ( M - 2 )∫{0→y} sinM-3θ - sinM-1θ dθ | |
| = | -sinM-2ycosy + ( M - 2 )( IM-3 - IM-1 ) |
より、
| IM-1 | = | -sinM-2ycosy / M + { ( M - 2 ) / ( M - 1 ) } IM-3 |
| = | -x(M-2)/2( 1 - x )1/2 / ( M - 1 ) + { ( M - 2 ) / ( M - 1 ) } IM-3 |
のような漸化式が得られます。最終的には M - 1 は 0 か 1 になって、
| I0 | = | ∫{0→y} dθ = sin-1√x |
| I1 | = | ∫{0→y} sinθ dθ |
| = | [ -cosθ ]{0→y} | |
| = | 1 - ( 1 - x )1/2 |
より、不完全ベータ関数を解くことができます。
α < β のとき、α と β を交換して Βx( β, α ) として計算した方が早く処理ができます。残念ながら、ベータ関数とは異なり、不完全ベータ関数の場合は Βx( α, β ) ≠ Βx( β, α ) なので、単純に交換して処理するだけでは正しい結果は得られません。Βx( α, β ) と Βx( β, α ) の関係式は次のように得られます。
において、u = 1 - t とすると、du = -dt、t → 0 のとき u → 1、t → x のとき u → 1 - x になるので、
| Βx( α, β ) | = | ∫{1-x→1} uβ-1 ( 1 - u )α-1 du |
| = | ∫{0→1} uβ-1 ( 1 - u )α-1 du - ∫{0→1-x} uβ-1 ( 1 - u )α-1 du | |
| = | Β( β, α ) - Β1-x( β, α ) [ = Β( α, β ) - Β1-x( β, α ) ] |
よって、α < β の場合は Β1-x( β, α ) を計算した上でその結果を Β( α, β ) から減算することで同じ結果が得られます。求めたいのは正規化された不完全ベータ関数 Ix( α, β ) なので、
と計算すればよいことになります。
F-分布のグラフは次のような形になります。
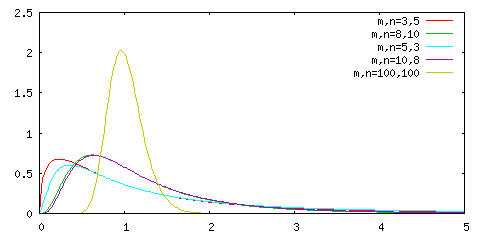
N または M を 1 に固定した上で、もう一方の自由度を変化させた時の F-分布のグラフを下図に示します。
| F-分布 ( N = 1 ) | F-分布 ( M = 1 ) |
|---|---|
 |
 |
分散の等しい二つの正規母集団 N( μ1, σ2 ), N( μ2, σ2 ) からそれぞれ大きさ M, N の標本 ( x11, x12, ... x1M ) と ( x21, x22, ... x2N ) をランダムに抽出して、標本平均 m1, m2 と標本分散 s12, s22 を得たとします。このとき、
χ12 = Σi{1→M}( x1i - m1 )2 / σ2 = Ms12 / σ2
χ22 = Σi{1→N}( x2i - m2 )2 / σ2 = Ns22 / σ2
はそれぞれ、自由度 M - 1, N - 1 の χ2-分布に従うのでした。ここで、N( μ1, σ2 ), N( μ2, σ2 )の分散の不偏推定量をそれぞれ u12, u22 としたとき、
u12 = { M / ( M - 1 ) }s12
u22 = { N / ( N - 1 ) }s22
になるので、これらの比 y = u12 / u22 を計算すると、
| y | = | u12 / u22 |
| = | { M / ( M - 1 ) }s12 / { N / ( N - 1 ) }s22 | |
| = | { M / ( M - 1 ) }( χ12σ2 / M ) / { N / ( N - 1 ) }( χ22σ2 / N ) | |
| = | { χ12 / ( M - 1 ) } / { χ22 / ( N - 1 ) } |
となって、y は自由度 ( M - 1, N - 1 ) の F-分布に従うことになります。
次に、上記と同じ条件で抽出した標本の平均と母集団の平均との差 m1 - μ1 と m2 - μ2 を求めると、これらはそれぞれ正規分布 N( 0, σ2 / M ), N( 0, σ2 / N ) に従うことになります。正規分布に従う確率変数の和の分布は、それらの分布の平均・分散の和を平均・分散とする正規分布に従うので(「(5) 正規分布」の「4) 標本平均と標本分散」参照)、( m1 - μ1 ) - ( m2 - μ2 ) は N( 0, ( 1 / M + 1 / N )σ2 ) に従い、χ2-分布の性質から
は自由度 1 の χ2-分布に従うことになります。また、Ms12 / σ2, Ns22 / σ2 はそれぞれ自由度 M - 1, N - 1 の χ2-分布に従い、この二つの確率変数の和
は χ2-分布の再生性から自由度 M + N - 2 の χ2-分布に従います。従って、
| χ12 / { χ22 / ( M + N - 2 ) } | = | [ { ( m1 - μ1 ) - ( m2 - μ2 ) }2 / ( 1 / M + 1 / N )σ2 ] / [ ( Ms12 + Ms22 ) / σ2( M + N - 2 ) ] |
| = | [ ( M + N - 2 ){ ( m1 - m2 ) - ( μ1 - μ2 ) }2 ] / [ ( 1 / M + 1 / N )( Ms12 + Ns22 ) ] |
は自由度 ( 1, M + N - 2 ) の F-分布に従うことになります。
また、正規母集団 N( μ, σ2 ) から N 個の標本を抽出して得られた標本平均 m を使って、
と定義すると、χ12 は自由度 1 の χ2-分布に従うのでした。同じ N 個の標本に対して標本分散 s2 を求めると、
は自由度 N - 1 の χ2-分布に従うので、
は自由度 ( 1, N - 1 ) の F-分布に従うことになります。この値を計算してみると、
| χ12 / { χ22 / ( N - 1 ) } | = | { ( m - μ )2 / ( σ2 / N ) } / { Ns2 / ( N - 1 )σ2 } |
| = | N( m - μ )2 / { Ns2 / ( N - 1 ) } |
{ Ns2 / ( N - 1 ) } は不偏分散を表すので u2 とすれば、
となって、N( m - μ )2 / u2 が自由度 ( 1, N - 1 ) の F-分布に従うことになります。
最後に、確率変数 x が自由度 ( M, N ) の F-分布に従うとき、1 / x がどのような分布に従うかを調べてみます。y = 1 / x とした時、dy = -dx / x2 なので、y が従う分布を p(y) とすれば p(y)dy = GM,N(x)dx より
| p(y) | = | GM,N(x)・| dx / dy | |
| = | { MM/2 NN/2 xM/2-1 / Β( M / 2, N / 2 ) ( Mx + N )(M+N)/2 }・( x2 ) | |
| = | MM/2 NN/2 ( 1 / y )M/2+1 / Β( M / 2, N / 2 ) ( M / y + N )(M+N)/2 | |
| = | MM/2 NN/2 yN/2-1 / Β( N / 2, M / 2 ) ( Ny + M )(M+N)/2 | |
| = | GN,M(y) |
よって、1 / x は自由度 ( N, M ) の F-分布に従うことになります。dx / dy の符号を勝手に外してもいいのかということになりますが、例えば y = x と y = -x のどちらで変換しても分布が変わらないのに、後者では分布が負の方向に反転したような形になってしまいます。x の分布 p(x) の微小領域 dx における確率が y の分布 q(y) の微小領域 dy の確率と等しくなるわけなので、ここでは dx と dy のどちらも正でなければならず、絶対値で考える必要があるわけです。
二項分布 BN,p(r) に従う確率変数 r において、r が 0 から k までの値を取る確率は Σr{0→k} BN,p(r) で求められます。また、逆に r が k + 1 から N までの値を取る確率は Σr{k+1→N} BN,p(r) を計算すれば得られます。意外なことに、これらの値は F-分布を利用して求めることができてしまいます。
まず、
を部分積分によって展開していくと、
| ∫{p→1} xr( 1 - x )N-r-1 dx | = | [ { -1 / ( N - r ) } xr( 1 - x )N-r ]{p→1} + { r / ( N - r ) }∫{p→1} xr-1( 1 - x )N-r dx |
| = | { 1 / ( N - r ) } pr( 1 - p )N-r + { r / ( N - r ) }∫{p→1} xr-1( 1 - x )N-r dx | |
| ∫{p→1} xr-1( 1 - x )N-r dx | = | { 1 / ( N - r + 1 ) } pr-1( 1 - p )N-r+1 + { ( r - 1 ) / ( N - r + 1 ) }∫{p→1} xr-2( 1 - x )N-r+1 dx |
| : | : | |
| ∫{p→1} xr-k( 1 - x )N-r+k-1 dx | = | { 1 / ( N - r + k ) } pr-k( 1 - p )N-r+k + { ( r - k ) / ( N - r + k ) }∫{p→1} xr-k-1( 1 - x )N-r+k dx |
| : | : | |
| ∫{p→1} x( 1 - x )N-2 dx | = | { 1 / ( N - 1 ) } p( 1 - p )N-1 + { 1 / ( N - 1 ) }∫{p→1} ( 1 - x )N-1 dx |
| = | { 1 / ( N - 1 ) } p( 1 - p )N-1 - { 1 / N( N - 1 ) }[ ( 1 - x )N ]{p→1} | |
| = | { 1 / ( N - 1 ) } p( 1 - p )N-1 + { 1 / N( N - 1 ) }( 1 - p )N |
よって、
| ∫{p→1} xr( 1 - x )N-r-1 dx | = | { 1 / ( N - r ) } pr( 1 - p )N-r |
| + { r / ( N - r )( N - r + 1 ) } pr-1( 1 - p )N-r+1 | ||
| : | ||
| + { r( r - 1 )...( r - k + 1 ) / ( N - r )( N - r + 1 )...( N - r + k ) } pr-k( 1 - p )N-r+k | ||
| : | ||
| + { r( r - 1 )...2 / ( N - r )( N - r + 1 )...( N - 1 ) } p( 1 - p )N-1 | ||
| + { r( r - 1 )...2 / ( N - r )( N - r + 1 )...N }( 1 - p )N | ||
| = | { r!( N - r - 1 )! / r!( N - r )! } pr( 1 - p )N-r | |
| + { r!( N - r - 1 )! / ( r - 1 )!( N - r + 1 )! } pr-1( 1 - p )N-r+1 | ||
| : | ||
| + { r!( N - r - 1 )! / ( r - k )!( N - r + k )! } pr-k( 1 - p )N-r+k | ||
| : | ||
| + { r!( N - r - 1 )! / 1!( N - 1 )! } p( 1 - p )N-1 | ||
| + { r!( N - r - 1 )! / 0! N! }( 1 - p )N |
各項に対して N! / r!( N - r - 1 )! を掛けると
| { N! / r!( N - r - 1 )! }{ r!( N - r - 1 )! / ( r - k )!( N - r + k )! } pr-k( 1 - p )N-r+k | |
| = | { N! / ( r - k )!( N - r + k )! } pr-k( 1 - p )N-r+k |
| = | NCr-k pr-k( 1 - p )N-r+k |
となるので、
| { N! / r!( N - r - 1 )! }∫{p→1} xr( 1 - x )N-r-1 dx | = | Σk{0→r}( NCr-k pr-k( 1 - p )N-r+k ) | |
| = | Σi{r→0}( NCi piqN-i ) [ r-k = i に変換 ] | ||
| = | Σi{0→r}( BN,p( i ) ) |
が成り立ちます。但し、q = 1 - p としています。これで、二項分布の 0 から r までの和が積分によって計算できることが示されたわけです。上式の左辺の係数 N! / r!( N - r - 1 )! をガンマ関数で表すと
となるので、r + 1 = m / 2、N - r = n / 2 とおくと、N + 1 = ( m + n ) / 2 となって、
次に、積分の部分を x = my / ( my + n ) で変数変換すると、y = nx / m( 1 - x ), dx = { mn / ( my + n )2 }dy で x → p のとき y → np / mq、x → 1 のとき y → +∞ になるので、
| ∫{p→1} xr( 1 - x )N-r-1 dx | = | ∫{p→1} xm/2-1( 1 - x )n/2-1 dx | |
| = | ∫{np/mq→∞} { my / ( my + n ) }m/2-1{ 1 - my / ( my + n ) }n/2-1 { mn / ( my + n )2 } dy | ||
| = | ∫{np/mq→∞} mm/2 nn/2 ym/2-1 / ( my + n )m/2+n/2 dy |
となって、この式を代入すれば
| Σi{0→r}( BN,p( i ) ) | = | ∫{np/mq→∞} mm/2 nn/2 ym/2-1 / Β( m / 2, n / 2 ) ( my + n )m/2+n/2 dy | |
| = | ∫{np/mq→∞} Gm,n( y ) dy |
となります。また、1 - Σi{0→r}( BN,p( i ) ) = Σi{r+1→N}( BN,p( i ) ) なので、
が成り立ちます。
F-分布の "F" は、イギリスの統計学者「ロナルド・フィッシャー(Sir Ronald Aylmer Fisher)」のイニシャルを表しているらしいのですが、本当のところは不明です。また、F-分布は別名「スネデカーの F-分布(Snedecor's F-distribution)」や「フィッシャー - スネデカー分布(Fisher-Snedecor Distribution)」などと呼ばれることもあるようです。"スネデカー"とは統計学者の「ジョージ・スネデカー(George W. Snedecor」のことで、おそらく分布を最初に発表したのがスネデカーではないかと思いますが、本当のところは調べきれませんでした。
今度は、x が標準正規分布 N( 0, 1 ) に従い、y が自由度 N の χ2-分布 TN(y) に従うとします。x と y が独立ならば、同時分布 p( x, y ) は
| p( x, y ) | = | { 1 / (2π)1/2 } exp( -x2 / 2 ) { 1 / 2N/2 Γ( N / 2 ) } y(N-2)/2 exp( -y / 2 ) |
| = | { 1 / √π 2(N+1)/2 Γ( N / 2 ) } y(N-2)/2 exp( -( x2 + y ) / 2 ) [ y > 0 ] |
y ≤ 0 のときは p( x, y ) = 0 になります。ここで、t = x / ( y / N )1/2、u = y / N と変数変換すれば、x = t√u、y = Nu となって、ヤコビアン det(J) は
| det(J) | = | (∂x/∂t)(∂y/∂u) - (∂x/∂u)(∂y/∂t) |
| = | √u・N - ( t / 2√u )・0 = N√u |
となるので、q( t, u ) = p( x, y )|det(J)| より
| q( t, u ) | = | { 1 / √π 2(N+1)/2 Γ( N / 2 ) } ( Nu )(N-2)/2 exp( -{ ( t√u )2 + Nu } / 2 ) N√u |
| = | { NN/2 / √π 2(N+1)/2 Γ( N / 2 ) } u(N-1)/2 exp( -( t2 + N )u / 2 ) |
但し、y > 0 より u > 0 のときのみ成り立ちます( u ≤ 0 なら y ≤ 0 なので、q( t, u ) = 0 です)。t に対する周辺分布を fN(t) とすると、
| fN(t) | = | ∫{-∞→∞} q( t, u ) du |
| = | { NN/2 / √π 2(N+1)/2 Γ( N / 2 ) } ∫{0→∞} u(N-1)/2 exp( -( t2 + N )u / 2 ) du |
v = ( t2 + N )u / 2 と変数変換すると、
| ∫{0→∞} u(N-1)/2 exp( -( t2 + N )u / 2 ) du | = | ∫{0→∞} { 2v / ( t2 + N ) }(N-1)/2 e-v { 2 / ( t2 + N ) } dv |
| = | { 2 / ( t2 + N ) }(N+1)/2 ∫{0→∞} v(N-1)/2 e-v dv | |
| = | { 2 / ( t2 + N ) }(N+1)/2 Γ( ( N + 1 ) / 2 ) |
なので、
| fN(t) | = | { NN/2 / √π 2(N+1)/2 Γ( N / 2 ) } { 2 / ( t2 + N ) }(N+1)/2 Γ( ( N + 1 ) / 2 ) |
| = | { NN/2 / N(N+1)/2( 1 + t2 / N )(N+1)/2 } { Γ( ( N + 1 ) / 2 ) / √πΓ( N / 2 ) } | |
| = | { 1 / √N( 1 + t2 / N )(N+1)/2 } { Γ( ( N + 1 ) / 2 ) / √πΓ( N / 2 ) } |
Γ( 1 / 2 ) = √π なので、
となって、
が得られます。これを自由度 N の「t-分布(t-distribution)」といいます。
x は標準正規分布に従うので、x2 は自由度 1 の χ2-分布に従うことになります。よって、
とすれば、s は自由度 ( 1, N ) の F-分布に従います。ところが、t = x / ( y / N )1/2 だったので t2 = s という関係式が成り立ちます。従って、t が自由度 N の t-分布に従うならば、s = t2 は自由度 ( 1, N ) の F-分布に従うことになります。
分布は t = 0 を中心に左右対象となるため、t-分布の全事象の積分値は
で求められます。u = ( 1 + t2 / N )-1 とすれば
となって、t → 0 のとき u → 1、t → ∞ のとき u → 0 なので
| ∫{-∞→∞} fN(t) dt | = | { 2 / √NΒ( 1 / 2, N / 2 ) } ∫{1→0} u(N+1)/2 ( -1 / 2 )u-2{ ( 1 - u ) / Nu }-1/2 du |
| = | { 1 / Β( 1 / 2, N / 2 ) } ∫{0→1} uN/2-1( 1 - u )-1/2 du | |
| = | { 1 / Β( 1 / 2, N / 2 ) } Β( N / 2, 1 / 2 ) = 1 |
となります。累積分布関数 F(t) は、x < 0 ならば t = -{ N( 1 - u ) / u }1/2 となることに注意して
ここで、( 1 + x2 / N )-1 = α とすれば
但し、Βα( N / 2, 1 / 2 ) は不完全ベータ関数、Iα( N / 2, 1 / 2 ) はその正規化されたものを表しています。x ≥ 0 ならば
| ∫{-∞→x} fN(t) dt | = | ∫{-∞→0} fN(t) dt + ∫{0→x} fN(t) dt |
| = | 1 / 2 - { 1 / 2Β( 1 / 2, N / 2 ) } ∫{1→( 1 + x2 / N )-1} uN/2-1( 1 - u )-1/2 du | |
| = | 1 / 2 + { 1 / 2Β( 1 / 2, N / 2 ) } { ∫{0→1} uN/2-1( 1 - u )-1/2 du - ∫{0→( 1 + x2 / N )-1} uN/2-1( 1 - u )-1/2 du } | |
| = | 1 / 2 + { 1 / 2Β( 1 / 2, N / 2 ) } { Β( N / 2, 1 / 2 ) - Βα( N / 2, 1 / 2 ) } | |
| = | 1 - Βα( N / 2, 1 / 2 ) / 2Β( 1 / 2, N / 2 ) | |
| = | 1 - Iα( N / 2, 1 / 2 ) / 2 |
となりますが、具体的には [ x, ∞ ) を計算する代わりに ( -∞, -x ] を計算して全体からその値を減算しているのと同じことになります。
分布の形状から平均 μ は 0 になります。実際に計算すると、
| μ = E[t] | = | ∫{-∞→∞} t・fN(t) dt |
| = | { 1 / √NΒ( 1 / 2, N / 2 ) } { ∫{-∞→0} t・( 1 + t2 / N )-(N+1)/2 dt + ∫{0→∞} t・( 1 + t2 / N )-(N+1)/2 dt } |
より、全事象の積分と同様に u = ( 1 + t2 / N )-1 とすれば
| ∫{-∞→0} t・( 1 + t2 / N )-(N+1)/2 dt | = | ∫{0→1} { N( 1 - u ) / u }1/2 u(N+1)/2 ( -1 / 2 )u-2{ ( 1 - u ) / Nu }-1/2 du |
| = | ( -N / 2 ) ∫{0→1} uN/2-3/2 du | |
| = | ( -N / 2 ) [ { 2 / ( N - 1 ) }u(N-1)/2 ]{0→1} | |
| = | -{ N / ( N - 1 ) } | |
| ∫{0→∞} t・( 1 + t2 / N )-(N+1)/2 dt | = | N / ( N - 1 ) |
なので、平均はゼロになります。しかし、これは N = 1 の時には成り立たず、( -∞, 0 ] の範囲は ∞、[ 0, ∞ ) の範囲は -∞ となって、平均は得られません。N = 1 の場合の t-分布は次のような式になります。
| f1(t) | = | { 1 / Β( 1 / 2, 1 / 2 ) } ( 1 + t2 )-1 |
| = | { Γ(1) / Γ( 1 / 2 ) Γ( 1 / 2 ) } { 1 / ( 1 + t2 ) } | |
| = | 1 / π( 1 + t2 ) |
これは「標準コーシー分布」の式であり、平均の存在しない確率分布の代表です。
分散 σ2 は次のように計算できます。
| σ2 = E[t2] - μ2 | = | ∫{-∞→∞} t2・fN(t) dt |
| = | { 2 / √NΒ( 1 / 2, N / 2 ) } ∫{0→∞} t2( 1 + t2 / N )-(N+1)/2 dt | |
| = | { 2 / √NΒ( 1 / 2, N / 2 ) } ∫{1→0} { N( 1 - u ) / u } u(N+1)/2 ( -1 / 2 )u-2{ ( 1 - u ) / Nu }-1/2 du | |
| = | { N / Β( 1 / 2, N / 2 ) } ∫{0→1} uN/2-2 ( 1 - u )1/2 du | |
| = | N Β( 3 / 2, N / 2 - 1 ) / Β( 1 / 2, N / 2 ) |
ベータ関数をガンマ関数に分解して変形すると、
| Β( 3 / 2, N / 2 - 1 ) | = | Γ( 3 / 2 ) Γ( N / 2 - 1 ) / Γ( ( N + 1 ) / 2 ) |
| = | √π Γ( N / 2 - 1 ) / 2Γ( ( N + 1 ) / 2 ) | |
| 1 / Β( 1 / 2, N / 2 ) | = | Γ( ( N + 1 ) / 2 ) / Γ( 1 / 2 ) Γ( N / 2 ) |
| = | Γ( ( N + 1 ) / 2 ) / √π ( N / 2 - 1 )Γ( N / 2 - 1 ) |
となるので、
しかし、ここでも N = 1 の場合は当然成り立たず、N = 2 のときは、
より v2 = 1 - u とすれば du = -2vdv で、u → 0 のとき v → 1、u → 1 のとき v → 0 なので、
| ∫{0→1} u-1 ( 1 - u )1/2 du | = | ∫{1→0} ( 1 / 1 - v2 )・v ( -2v ) dv |
| = | 2∫{0→1} v2 / ( 1 - v2 ) dv | |
| = | 2∫{0→1} 1 / ( 1 + v )( 1 - v ) - 1 dv | |
| = | ∫{0→1} 1 / ( 1 + v ) + 1 / ( 1 - v ) - 2 dv | |
| = | [ ln( 1 + v ) - ln( 1 - v ) - 2v ]{0→1} = +∞ |
つまり、N = 2 のときは分散は発散してしまいます。
以上まとめると、次のようになります。
自由度 N の t-分布 fN( t ) = { 1 / √NΒ( 1 / 2, N / 2 ) } ( 1 + t2 / N )-(N+1)/2
平均 : 0 ( 但し N > 1 )、分散 : N / ( N - 2 ) ( 但し N > 2 )
t-分布のサンプル・プログラムを以下に示します。
/* TDistribution : t-分布 */ class TDistribution : public ContDist { unsigned int _n; // 自由度 N public: /* コンストラクタ unsigned int n : 自由度 */ TDistribution( unsigned int n ) : _n( n ) {} // 確率変数 x における確率密度を返す double operator[]( double x ) const; // 区間 (-∞,a] における確率を返す double lower_p( double a ) const; double average() const { return( ( _n > 1 ) ? 0 : NAN ); } // 平均値 double variance() const // 分散 { return( ( _n > 2 ) ? (double)_n / (double)( _n - 2 ) : ( ( _n == 2 ) ? INFINITY : NAN ) ); } }; /* TDistribution::operator[] : 確率変数 x における確率密度を返す double x : 確率変数 戻り値 : 確率密度 */ double TDistribution::operator[]( double x ) const { if ( _n == 0 ) return( NAN ); double beta = tgamma( (double)( _n + 1 ) / 2.0 ) / ( tgamma( (double)_n / 2.0 ) * sqrt( M_PI ) ); return( beta / ( sqrt( _n ) * pow( 1 + pow( x, 2 ) / (double)_n, (double)( _n + 1 ) / 2.0 ) ) ); } /* TDistribution::lower_p : 区間 (-∞,a] における確率を返す double a : 区間の上限 戻り値 : 確率 */ double TDistribution::lower_p( double a ) const { if ( _n == 0 ) return( NAN ); double beta = 2 * ( tgamma( (double)_n / 2.0 ) * sqrt( M_PI ) ) / tgamma( (double)( _n + 1 ) / 2.0 ); double p = iBeta( _n, 1, (double)_n / ( (double)_n + pow( a, 2 ) ) ) / beta; if ( a > 0 ) p = 1.0 - p; return( p ); }
不完全ベータ関数を求めるところは、F-分布で利用したヘルパ関数の iBeta をそのまま利用しています。
t-分布は下図に示すような分布になります。
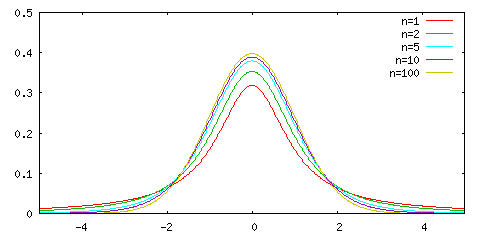
見ると正規分布に非常によく似ていることがわかります。実際、Β( 1 / 2, N / 2 ) においてスターリングの公式を利用すると N が十分大きければ
| Β( 1 / 2, N / 2 ) | = | Γ( 1 / 2 ) Γ( N / 2 ) / Γ( ( N + 1 ) / 2 ) |
| ≅ | √π { 2π( N / 2 - 1 ) }1/2{ ( N / 2 - 1 ) / e }N/2-1 / { 2π( ( N - 1 ) / 2 ) }1/2{ ( ( N - 1 ) / 2 ) / e }(N-1)/2 | |
| = | √π ( N / 2 - 1 )(N-1)/2 e-N/2+1 / ( N / 2 - 1 / 2 )N/2 e-(N-1)/2 | |
| = | √π e1/2 ( N / 2 )-N/2 ( 1 - 1 / N )-N/2 / ( N / 2 )-(N-1)/2 { 1 - 1 / ( N/2 ) }-(N-1)/2 | |
| ≅ | √π e1/2 e1/2 / ( N / 2 )1/2 e{ 1 - 1 / ( N/2 ) }1/2 | |
| = | √π / ( N / 2 - 1 )1/2 |
よって、
| fN(t) | = | { 1 / √N Β( 1 / 2, N / 2 ) } ( 1 + t2 / N )-(N+1)/2 |
| ≅ | { ( N / 2 - 1 )1/2 / √N√π } { ( 1 + t2 / N )N/t2 }-(N+1)t2/2N | |
| ≅ | { ( 1 / 2 - 1 / N )1/2 / √π } e-(1+1/N)t2/2 | |
| ≅ | { 1 / ( 2π )1/2 } e-t2/2 |
従って、N が大きい場合は標準正規分布に近似されることになります。
正規母集団 N( μ, σ2 ) から大きさ N の標本 x = ( x1, x2, ... xN ) を抽出して
t = ( m - μ )√N / u
但し、m = Σi{1→N}( xi ) / N、u2 = Σi{1→N}( xi - m )2 / ( N - 1 )
とします。このとき、t は自由度 N - 1 の t-分布に従います。これを証明してみましょう。
m は標本平均で、正規分布 N( μ, σ2 / N ) に従うので、( m - μ ) / ( σ / √N ) は標準正規分布に従います。これを y とすれば、
となるので、{ z / ( N - 1 ) }1/2 = u / σ としたときに z が自由度 N - 1 の χ2-分布に従うことが示されれば、t が自由度 N - 1 の t-分布に従うことが証明されたことになります。この式を z について解くと
| z | = | ( N - 1 )u2 / σ2 |
| = | Σi{1→N}( xi - m )2 / σ2 |
となって、χ2-分布の性質から z は自由度 N - 1 の χ2-分布に従います。よって、t は自由度 N - 1 の t-分布に従うことが示されました。
t-分布は、「ウィリアム・ゴセット(William Sealy Gosset)」によって「平均値の誤差の確率分布(The probable error of a mean)」という論文の中で 1908 年に発表されたのが最初です。当時、ゴセットの務めていたビール醸造会社のギネス社(あのギネス・ブックで有名な会社です)が社員による論文の発表を禁止していたため、ゴセットは「スチューデント(Student)」というペンネームを使って論文を発表していました。そのため、t-分布は「スチューデントのt-分布(Student's t-distribution)」という名でも知られています。
今回は、χ2-分布、F-分布、t-分布の三つの確率分布を中心に紹介しました。どの分布の確率密度関数もかなり複雑でしたが、統計学における推定や検定の問題の基礎となる分布としてどれも重要なものです。統計解析用のソフトウェアは、有名な R をはじめ様々なものがあり、Excel などにも関数として用意されているので、仕事などで使われている方もいらっしゃると思います。様々な統計解析に対してどのようにデータ処理をすればよいか、ある程度はその手法が決まっていてルーチンワークで作業することが多いと思いますが、その基礎となる考え方を理解すると、今までとは違った観点からデータを扱えるようになることも期待できます。そのためにも、今回紹介した分布の意味するところを理解することは重要だと考えています。
ガンマ関数 Γ( x + 1 ) を次のように表します。
右辺の積分に対して t = x( 1 + u ) で変数変換を行うと、dt = x・du で、t → 0 のとき u → -1、t → ∞ のとき u → ∞ なので、
| Γ( x + 1 ) | = | ∫{-1→∞} { x( 1 + u ) }x e-x(1+u) x・du |
| = | xx+1 e-x ∫{-1→∞} ex・ln( 1 + u ) e-xu du | |
| = | xx+1 e-x ∫{-1→∞} exp( -x{ u - ln( 1 + u ) } ) du |
積分の範囲を [ -1, -ε ), [ -ε, ε ), [ ε, ∞ ) の三つに分割します。但し、ε はゼロに非常に近い任意の正数とします。すると、x が充分に大きければ積分値は [ -ε, ε ) に集中するので、
と近似することができます。u は非常に小さいので、f(u) = ln( 1 + u ) の マクローリン級数(Maclaurin Series) から
| f(u) = ln( 1 + u ) | = | f(0) + f'(0)u + f(2)(0)u2 / 2! + ... |
| = | u - u2 / 2 + ... | |
| ≅ | u - u2 / 2 |
と三次以降の項を無視して近似することができます。よって、
| Γ( x + 1 ) | ≅ | xx+1 e-x ∫{-ε→ε} exp( -x{ u - ( u - u2 / 2 ) } ) du |
| ≅ | xx+1 e-x ∫{-ε→ε} exp( -xu2 / 2 ) du | |
| ≅ | xx+1 e-x ∫{-∞→∞} exp( -xu2 / 2 ) du |
積分範囲を ( -∞, ∞ ) に戻していますが、[ -ε, ε ) 以外の値はほとんどゼロで無視できることから、全範囲で積分しても近似できることを意味しています。この積分はガウス積分 ∫{-∞→∞} exp( -u2 ) du = √π と変数変換を利用すれば ( 2π / x )1/2 になるので、
| Γ( x + 1 ) | ≅ | xx+1 e-x ( 2π / x )1/2 |
| = | ( 2πx )1/2( x / e )x |
これはスターリングの公式そのものです。
確率変数 x = ( x1, x2, ... xN ) が全て互いに独立で、標準正規分布 N( 0 , 1 ) に従うと仮定します。このとき、x に対する同時分布 p(x) は
| p(x) | = | Πi{1→N}( { 1 / (2π)1/2 }exp( -xi2 / 2 ) ) |
| = | { 1 / (2π)N/2 }( exp( -Σi{1→N}( xi2 ) / 2 ) ) | |
| = | { 1 / (2π)N/2 }( exp( -||x||2 / 2 ) ) |
になります。任意の直交行列 Q によって、
と変換した時、z = ( z1, z2, ... zN ) は x を回転または鏡映した形になり、そのノルムは変わりません。つまり、
が成り立つことになります。変数を x から z に変換した時、z = Qx を実際に計算すると
| z = Qx | = | | | u11, | u12, | ... | u1N | || | x1 | | | = | | | u11x1 + u12x2 + ... + u1NxN | | |
| | | u21, | u22, | ... | u2N | || | x2 | | | | | u21x1 + u22x2 + ... + u2NxN | | | |||
| | | : | : | ... | : | || | : | | | | | : | | | |||
| | | uN1, | uN2, | ... | uNN | || | xN | | | | | uN1x1 + uN2x2 + ... + uNNxN | | |
より zi = ui1x1 + ui2x2 + ... + uiNxN なので、∂zi / ∂xj = uij となって、ヤコビ行列は Q と等しくなります。したがって、ヤコビアンの絶対値は |det( Q )| = 1 になり(「(5) 正規分布」の「補足 4) 行列の積の行列式」参照)、z に対する同時分布が q(z) ならば p(x) = q(z) となって、||z|| = ||x|| より
| q(z) | = | { 1 / (2π)N/2 }( exp( -||z||2 / 2 ) ) |
| = | Πi{1→N}( { 1 / (2π)1/2 }exp( -zi2 / 2 ) ) |
つまり、z = ( z1, z2, ... zN ) は互いに独立で、標準正規分布 N( 0, 1 ) に従うことを示しています。
直交行列 Q の N 行目の行ベクトルを uN = ( 1 / √N, 1 / √N, ... 1 / √N ) としても、
なので、Q は直交行列として成り立っています。このとき、
になります。但し、m は標本平均で m = Σi{1→N}( xi / N ) とします。y = Σi{1→N}( ( xi - m )2 ) とすれば、
| y | = | Σi{1→N}( ( xi - m )2 ) |
| = | Σi{1→N}( xi2 - 2mxi + m2 ) | |
| = | ||x||2 - 2mΣi{1→N}( xi ) + Nm2 | |
| = | ||z||2 - Nm2 | |
| = | ( z12 + z22 + ... + zN2 ) - zN2 | |
| = | z12 + z22 + ... + zN-12 |
になり、zi は N( 0, 1 ) に従うので、y は自由度 N - 1 の χ2-分布に従うことになります。
次に、x が正規分布 N( μ, σ2 ) に従う時を考えると、
とすれば zi は N( 0 , 1 ) に従うことになります。mz = Σi{1→N}( zi / N ) とすれば
| mz | = | Σi{1→N}( zi / N ) |
| = | Σi{1→N}( ( xi - μ ) / Nσ ) | |
| = | ( mx - μ ) / σ |
但し、mx = Σi{1→N}( xi / N ) とします。このとき、
| ( xi - mx ) / σ | = | ( xi - μ ) / σ + ( μ - mx ) / σ |
| = | zi - mz |
なので、y = Σi{1→N}( ( xi - mx )2 ) / σ2 とすれば
| y | = | Σi{1→N}( ( xi - mx )2 ) / σ2 |
| = | Σi{1→N}( ( zi - mz )2 ) |
になって、Σi{1→N}( ( zi - mz )2 ) は自由度 N - 1 の χ2-分布に従うので、y = Σi{1→N}( ( xi - mx )2 ) / σ2 も同様に自由度 N - 1 の χ2-分布に従うことになります。
畳み込み積分(または合成積 ; Convolution)は、画像のサンプル補間の中で「5) 補間関数と畳み込み積分」として紹介しています。入力信号に対する出力が時間に応じて線形的に変化するとき、出力信号の重ね合わせが畳み込み積分の形になり、次のような式で表されます。
f(x) * g(x) のことを ( f * g )(x) と表したり、変数 x を省略して単に f * g と表す場合もあります。
畳み込み積分は、通常の積と同様に以下の性質を持っています。
交換律 f * g = g * f
結合律 ( f * g ) * h = f * ( g * h )
分配律 f * ( g + h ) = f * g + f * h
交換律の場合、畳み込み積分において u = x - t と変数変換すれば t → ∞ のとき u → -∞、t → -∞ のとき u → ∞、du = -dt になるので
| f * g | = | ∫{-∞→∞} f(x - t) g(t) dt |
| = | ∫{∞→-∞} f(u) g(x - u) -du | |
| = | ∫{-∞→∞} g(x - u) f(u) du = g * f |
と証明することができます。結合律は、
| ( f * g ) * h | = | ∫{-∞→∞} ( f * g )(x - t) h(t) dt |
| = | ∫{-∞→∞} ( ∫{-∞→∞} f(x - t - u) g(u) du ) h(t) dt | |
| = | ∫{-∞→∞} ∫{-∞→∞} f(x - t - u) g(u) h(t) du dt |
として v = t + u と変数変換すれば、
| ( f * g ) * h | = | ∫{-∞→∞} ∫{-∞→∞} f(x - v) g(v - t) h(t) dv dt |
| = | ∫{-∞→∞} f(x - v) ( ∫{-∞→∞} g(v - t) h(t) dt ) dv | |
| = | ∫{-∞→∞} f(x - v) ( g * h )( v ) dv = f * ( g * h ) |
最後の分配律は、積分の加法性から簡単に示すことができます。以上の性質と χ2-分布の性質
から、TM * TN は
| TM * TN | = | TM * ( TN-1 * T1 ) |
| = | TM * ( T1 * TN-1 ) | |
| = | ( TM * T1 ) * TN-1 | |
| = | TM+1 * TN-1 |
となって、これを繰り返すことで TM * TN = TM+N を示すことができます。
ベータ関数 Β( α, β ) = ∫{0→1} tα-1( 1 - t )β-1 dt の被積分関数 tα-1( 1 - t )β-1 は、α ≥ 1 かつ β ≥ 1 ならば [ 0, 1 ] の範囲で有限なので、積分値も収束します。ところが、0 < α < 1 のときは t → 0 のとき、0 < β < 1 のときは t → 1 のときに、被積分関数は発散します。にもかかわらず、積分値は収束することを示すことができます。
まずは、ベータ関数の積分範囲を二つに分割します。
( 0, 1/2 ] の範囲において、tα-1( 1 - t )β-1 dt ≤ Mtα-1 を満たす定数 M が存在します。また、[ 1/2, 1 ) の範囲において、tα-1( 1 - t )β-1 dt ≤ N( 1 - t )β-1 を満たす定数 N が存在するので、結局 0 < α < 1 で ∫{0→1/2} tα-1 dt が、0 < β < 1 で ∫{1/2→1} ( 1 - t )β-1 dt が収束することが証明できればいいことになります。ところが、∫{1/2→1} ( 1 - t )β-1 dt において 1 - t = u とすれば t → 1/2 のとき u → 1/2、t → 1 のとき u → 0、du = -dt となって、
となるので、結局 ∫{0→1/2} tα-1 dt が収束することだけを示せばよいことになります。まず、0 < ε < 1/2 として ∫{ε→1/2} tα-1 dt を計算すると、
| ∫{ε→1/2} tα-1 dt | = | [ ( 1 / α )tα ]{ε→1/2} |
| = | ( 1 / α )( 1 / 2 )α - ( 1 / α )εα ≤ 1 / 2αα |
となります。よって、∫{0→1/2} tα-1 dt は収束することが示され、ベータ関数もまた収束することになります。ところが、α < 0 の場合、εα は発散してしまうので、ベータ関数も収束しなくなってしまいます。
ガンマ関数が収束することは以前証明しています。ベータ関数とガンマ関数の間には
の関係が成り立っているので、任意の α に対して Γ(α) > 0 であることから、Β( α, β ) が収束することは自明であるともいえます。
◆◇◆更新履歴◆◇◆
(誤)[ ( M + N - 2 ){ ( m1 - μ1 ) + ( m2 - μ2 ) }2 ] / [ ( 1 / M + 1 / N )( Ms12 + Ns22 ) ] は自由度 ( 1, M + N - 2 ) の F-分布に従う
(正)[ ( M + N - 2 ){ ( m1 - m2 ) - ( μ1 - μ2 ) }2 ] / [ ( 1 / M + 1 / N )( Ms12 + Ns22 ) ] は自由度 ( 1, M + N - 2 ) の F-分布に従う
![[Go Back]](../images/back1.png) 前に戻る 前に戻る |
![[Back to HOME]](../images/home1.png) タイトルに戻る タイトルに戻る |