確率・統計
(4) 多変数の確率分布
前回は、試行回数や事象の発生回数などを確率変数としたときの分布の具体例を紹介しました。しかし、確率分布が集合や集合族上で定義されている以上、その集合から定義できる確率変数が常に一つのみであるとは限らず、場合によっては複数の確率変数を用いた確率空間を考える必要もあります。ここでは、そのような多変数の確率分布について紹介したいと思います。
赤と白の二つの玉が箱の中にたくさんあり、各々の玉には A と B のいずれかの文字が書かれていたとします。箱から玉を一つ取り出した時、それが赤い玉である確率を P(R)、白い玉である確率を P(W) とすると、
P(R) + P(W) = P(Ω) = 1
が成り立ちます。また、箱から玉を一つ取り出した時、その玉に A と書かれている確率を P(A)、B と書かれている確率を P(B) とすると、同様に
P(A) + P(B) = P(Ω) = 1
が成り立ちます。赤い玉で A と書かれている確率を P(RA)、B と書かれている確率を P(RB)、白い玉も同様に考えて P(WA)、P(WB) とすれば、
P(RA) + P(RB) + P(WA) + P(WB) = P(Ω) = 1
が成り立つことも理解できると思います。この時、
P(RA) + P(RB) = P(R)
P(WA) + P(WB) = P(W)
P(RA) + P(WA) = P(A)
P(RB) + P(WB) = P(B)
という関係になっています。ここで、玉に書かれている文字がテープで隠されていたとします。箱から取り出した玉が赤い玉であったとき、それに A と書かれているかどうかをどのように評価すればいいでしょうか。
例えば、P(R) = P(W) = P(A) = P(B) = 0.5 だったとします。つまり、赤と白の玉が出る確率は五分五分、A と B が出る確率も五分五分ということになります。ここで、P(RA) = P(WB) = 0.4、P(RB) = P(WA) = 0.1 ならば、赤い玉の場合は A の出る確率の方が、また白い玉なら B の出る確率の方がそれぞれ高いので、箱から取り出した玉が赤い場合は、それに書かれている文字が A であると判断した方が有利になります。ここで、赤い玉が出た場合に限定して A の出る確率を P(A|R) とすると、
P(A|R) = P(RA) / P(A) = 0.4 / 0.5 = 0.8
と計算することができます。同様に、赤い玉が出た場合に限定して B の出る確率を P(B|R)、白い玉に限定した場合を P(A|W)、P(B|W) とすれば、
P(B|R) = P(RB) / P(B) = 0.1 / 0.5 = 0.2
P(A|W) = P(WA) / P(A) = 0.1 / 0.5 = 0.2
P(B|W) = P(WB) / P(B) = 0.4 / 0.5 = 0.8
になります。各々の確率を矩形で表現すると、P(R) と P(W) は同面積で、全体の矩形の大きさを 1 とすればどちらも 0.5 となります。また、P(RA) と P(WB) はそれぞれ全体の 40%、P(RB) と P(WA) はそれぞれ全体の 10% を占めます。ここで赤い玉の出る確率が占める面積を 1 と考えたとき、その中で A の出る確率は 0.8 を占めることになります。
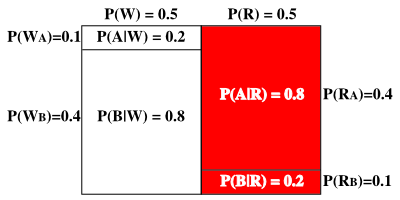
ある事象 B に限定したとき事象 A が起こる確率を「条件付確率(Conditiomal Probability)」といい、P(A|B) で表します。先程の例から考えると、これは 事象 B を全事象に置き換えた場合に事象 A と事象 B がどちらも発生した確率 P(A∩B) を求めることになるので、
P(A|B) = P(A∩B) / P(B)
が成り立ちます。但し、P(B) ≠ 0 である必要があります。
先ほど説明したように、赤と白の玉が出る確率は五分五分、A と B が出る確率も五分五分であるにもかかわらず、赤い玉が出た時は A の出る確率の方が高くなります。よって、その場合は「A である」と答えた方が有利です。逆に、誰かに玉を取り出してもらい、その玉に書かれている文字を読み上げてもらうとします。A であることが分かった場合、それが赤である条件付確率 P(R|A) は
P(R|A) = P(RA) / P(A) = 0.4 / 0.5 = 0.8
なので、「赤である」と答えた方が有利になります。
事象 B に限定して事象 A が発生する条件付確率 P(A|B) が、事象 B に限定せずに事象 A が発生する確率 P(A) と等しい場合、
P(A|B) = P(A∩B) / P(B) = P(A)
より
P(A∩B) = P(A)・P(B)
が成り立ちます。また、この等式が成り立てば、P(B|A) に対しても
P(B|A) = P(A∩B) / P(A) = P(B)
であることが分かります。これは、事象 B が起こるという現象が事象 A の発生に何の影響も及ぼさない、事象 A, B は互いに独立であるということを意味しています。
各試行が独立であるとして、N 回の試行を繰り返す標本点を「ベルヌーイ列」といって、
Ω = { ( a1, a2, ... aN ) | ai = 0, 1 ( i = 1, 2, ... N ) }
と定義しました。この中で、事象が i 番目に起こったときの事象を Ai (0 ≤ i ≤ N) としたとき、それ以外の点では 0 か 1 のいずれかを取るので、
Ai = { ( a1, a2, ... ai = 1, ... aN ) | ak = 0, 1 ( k = 1, 2, ... i - 1, i + 1, ... N ) }
と表すことができます。「二項分布」では、事象が r 回発生したときの標本点の確率を
p( Σi{1→N}( xi ) = r ) = prqN-r
と定義しました。i 番目 ( 0 ≤ i ≤ r ) の試行が必ず「成功」している場合、残りの r - 1 回分が N - 1 回の試行の中で「成功」したことになるので、その場合の数は N-1Cr-1 です。r が 1 から N まで変化したとき、i 番目の試行が必ず「成功」する確率 P(Ai) は
| P(Ai) | = | Σr{1→N}( N-1Cr-1 prqN-r ) |
| = | pΣr{1→N}( N-1Cr-1 pr-1qN-r ) |
| = | p( p + q )N-1 = p |
i, j 番目のどちらも「成功」していた場合の確率 P(Ai∩Aj) は、残りの r - 2 回分が N - 2 回の試行の中で「成功」したことになるので
| P(Ai∩Aj) | = | Σr{2→N}( N-2Cr-2 prqN-r ) |
| = | p2Σr{2→N}( N-2Cr-2 pr-2qN-r ) |
| = | p2( p + q )N-2 = p2 |
| = | P(Ai)・P(Aj) |
になり、何回目に成功したかということは互いに影響を及ぼさない、すなわち独立であるということになります。二項分布で定義した標本点の確率は、この独立性を保証するためのモデルの一つと考えることができます。
今までは、事象に対する確率変数を一つとして確率分布を紹介してきました。しかし、確率密度が集合や集合族の上で定義される以上、複数の変数を扱うことも可能なので、例えば確率空間 ( Ω, β, μ ) に対して
Ω' = Z2 ; ( m, n ) ∈ Z2
β' = 「Z2 から成る完全加法族」
p( ( m, n ) ∈ A ) = μ( { ω | m(ω), n(ω) ∈ A } ) ( A ∈ β )
となるような新たな確率空間 ( Ω', β', p ) が定義できれば、p は 2 つの変数 m, n を確率変数とする確率密度関数になり、
p( ( m, n ) ∈ A ) = ΣmΣn{ ( m, n ) ∈ A }( p( m, n ) )
と計算することができれば、事象 A に対する確率を求めることができます。連続分布に対しても同様な考えかたによって、
p( ( x, y ) ∈ A ) = ∫∫{ ( x, y ) ∈ A } p( x, y ) dxdy
が定義できれば確率を求めることができます。これはちょうど、xy 平面上に広がる確率変数に対して確率分布が広がっていて、その分布の和 (または体積) は 1 になることをイメージすれば分かりやすいと思います。具体的なイメージが難しくなるものの、確率変数の数をさらに増やして多変数での確率密度関数を考えることも可能です。このように、複数の確率変数がある場合に、それらが同時にある値となるときの確率を表すことから、多変数の確率分布は「同時分布」または「結合分布(Joint Probability Distribution)」と呼ばれています。ちなみに、「同時分布」に対する英訳が見当たらないため「結合分布」の方が一般的なようですが、個人的には「同時に起こる確率」という意味で「同時分布」の方がその内容をよく表しているように思います。

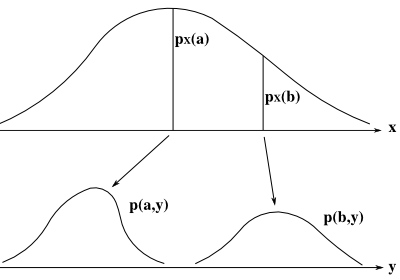
2 変数から成る分布を xy 平面に垂直で y 軸に平行な平面で切った切り口の形状を見ると、これは x をある値に固定したときの y に関する確率分布を表しています。同様に、xy 平面に垂直で x 軸に平行な平面で切った切り口の形状は、y をある値に固定したときの x に関する確率分布を表します。x または y を固定したときの分布についての和または面積
px(x) = ∫{-∞→∞} p( x, y ) dy
py(y) = ∫{-∞→∞} p( x, y ) dx
を「周辺分布(Marginal Distribution)」といいます。これは、一つの変数がある値を取るとき、その他の変数に関する確率密度全体について和を求めたときの確率分布になります。例えば、あるグループにおける身長と体重の分布に対して、体重に関係なく身長だけで分布を表せば、それが周辺分布となります。身長に関係なく体重の分布を表した場合も同様です。周辺分布は一変数の分布を表し、変数を固定したとき、その中で他の変数に対する分布として分解していくと元の多変数の分布に戻ります。また、多変数の分布における確率密度の和(または体積)は 1 になり、それを、一変数を固定して合計したものが周辺分布になるので、周辺分布の和や面積も 1 になり、上式において、
∫{-∞→∞} px(x) dx = 1
∫{-∞→∞} py(y) dy = 1
が成り立ちます。
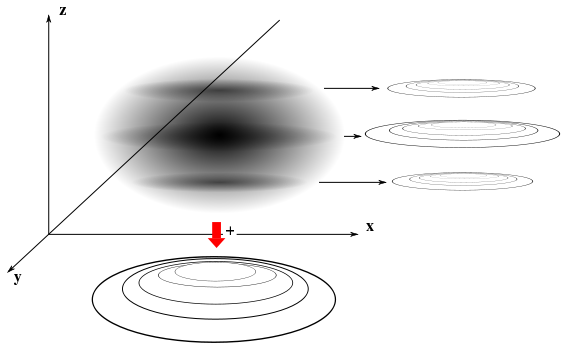
周辺分布自体が多変数になる場合を考えることもできます。例えば、3 変数の確率分布 p( x, y, z ) に対して
pxy( x, y ) = ∫{-∞→∞} p( x, y, z ) dz
とすれば、2 変数の周辺分布になります。これはちょうど、3 次元空間上で密度の濃淡で表現された確率分布があって、それを xy 平面に平行な平面で輪切りにした上で、それぞれの断面の値を合計した分布を得ることになります。
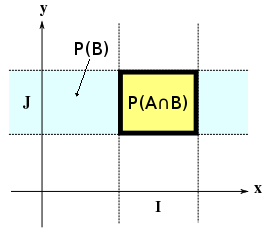
全事象 Ω の中で、x(ωx) ∈ I, y(ωy) ∈ J ( I, J は R のボレル集合 ) を満たす ωx, ωy の集合から成る事象をそれぞれ A, B とします。二つの事象 A, B の積集合 A ∩ B は、x(ω) ∈ I かつ y(ω) ∈ J となるような ω を要素とする部分集合を考えればいいので、R2 上の直積集合 I x J について
A ∩ B = { ω ∈ Ω | ( x(ω), y(ω) ) ∈ I x J }
と表せます。よって、( x(ω), y(ω) ) に対する確率密度関数を p( x, y ) とすると、
| P( A ∩ B ) | = | P( ( x(ω), y(ω) ) ∈ I x J ) |
| = | ∫∫{(x,y)∈IxJ} p( x, y ) dxdy |
| = | ∫{y∈J} ( ∫{x∈I} p( x, y ) dx ) dy |
になります。P(B) は x(ω) ∈ R, y(ω) ∈ J を満たす ω から成る事象に対する確率なので、x に関しては制限がないことを意味することになって、
P(B) = ∫{y∈J} ( ∫{-∞→∞} p( x, y ) dx ) dy = ∫{y∈J} py( y ) dy
P(A|B) = P(A∩B) / P(B) より
P(A|B) = ∫{y∈J} ( ∫{x∈I} p( x, y ) dx ) dy / ∫{y∈J} py( y ) dy
と表すことができます。ここで、y を定数 k とすれば、上式は x のみの関数として表せて
P(A|y = k) = ∫{x∈I} p( x, k ) / py( k ) dx
になります。そこで、
p(x|y) = p( x, y ) / py( y )
を、x の y に関する条件付確率密度といいます。右辺を x ∈ R において積分すると、∫{-∞→∞} p( x, y ) dx = py( y ) よりその結果は 1 になります。従って、p(x|y) は、y を固定したときに x に関する全ての和または面積が 1 になるように周辺分布で割ったものと考えることができます。
ここで、2 変数の確率密度関数 p( x, y ) が、それぞれの変数 x, y の関数の積で表される場合を考えます。
p( x, y ) = f(x)・g(y)
このときの周辺分布は
px(x) = ∫{-∞→∞} f(x)・g(y) dy = c・f(x) ( c = ∫{-∞→∞} g(y) dy )
py(y) = ∫{-∞→∞} f(x)・g(y) dx = d・g(y) ( d = ∫{-∞→∞} f(x) dx )
になります。ところが、∫{-∞→∞} px(x) dx = 1 なので、
∫{-∞→∞} px(x) dx = ∫{-∞→∞} c・f(x) dx = 1
d = ∫{-∞→∞} f(x) dx より
c・d = 1
が成り立ちます。よって、
px(x)・py(y) = c・f(x)・d・g(y) = f(x)・g(y) = p( x, y )
となって、p( x, y ) が周辺分布の積で表されることになります。一般的に、N 変数に対して二つの関数の積に分解することができれば、同様の方法によって
p(x) = px1(x1)・px2(x2)
と表すことができます。但し、x1 と x2 の中の変数を全て集めたものが x になるとします。
2 変数の場合に話を戻すと、p( x, y ) = px(x)・py(y) ならば、
p(x|y) = px(x)・py(y) / py(y) = px(x)
と表すことができます。y = y0 としたとき、py(y0) は定数となって、
p( x, y0 ) = px(x)・py(y0) = K0・px(x) ( K0 = py(y0) )
つまり、平面上に広がる分布の山を x = x0 で切った分布と、別の変数 x = x1 で切った分布は、定数値が異なるだけで、y の値によって変化する分布の形状は同じになることを示しています。このとき、変数 x と y は独立であるといいます。例えば、ある学力テストの点数と身長とは互いに無関係で、身長が高くなるほどテストの点が高くなったり、逆に低くなるとは通常考えないと思います。よって、テストの点数に対する分布は身長に関係なくどれも同じで、身長を考慮しない、全体に対する分布の形状と等しいと考えるのが自然です。このような場合、身長とテストの点数を変数とする確率密度関数は、身長についての関数とテストの点数についての関数の積で表すことができます。しかし、身長と体重の分布や、テストの点の中で数学と英語の点数についての分布を考えるような場合、分布の形状は変化することが予想できます。このようなとき、二つの変数は独立ではないということになるわけです。
簡単な例を挙げます。3 回の試行を繰り返す「ベルヌーイ列」
Ω = { ( a1, a2, a3 ) | ai = 0, 1 ( i = 1, 2, 3 ) }
が表す標本点を実際に書き出してみると、
Ω = {
( 0, 0, 0 ),
( 1, 0, 0 ), ( 0, 1, 0 ), ( 0, 0, 1 ),
( 1, 1, 0 ), ( 1, 0, 1 ), ( 0, 1, 1 ),
( 1, 1, 1 )
}
で、これらは三次元空間において、原点を頂点の一つとする体積 1 の立方体の各頂点になります。分かりやすくなるように ( a1, a2, a3 ) = ( x, y, z ) として、各頂点の持つ確率は P( x, y, z ) = px+y+z( 1 - p )3-(x+y+z) とします。ここで、x 軸方向に並んだ標本点( ( y, z ) が等しい点 ) の確率の和を Pyz( y, z ) とすると、
Pyz( 0, 0 ) = P( 0, 0, 0 ) + P( 1, 0, 0 ) = p0( 1 - p )3 + p1( 1 - p )2 = ( 1 - p )2{ ( 1 - p ) + p } = ( 1 - p )2
Pyz( 1, 0 ) = P( 0, 1, 0 ) + P( 1, 1, 0 ) = p1( 1 - p )2 + p2( 1 - p )1 = ( 1 - p ){ p( 1 - p ) + p2 } = p( 1 - p )
Pyz( 0, 1 ) = P( 0, 0, 1 ) + P( 1, 0, 1 ) = p1( 1 - p )2 + p2( 1 - p )1 = p( 1 - p )
Pyz( 1, 1 ) = P( 0, 1, 1 ) + P( 1, 1, 1 ) = p2( 1 - p )1 + p3( 1 - p )0 = p2
になります。これはちょうど、立方体を yz 平面上に押しつぶして正方形にしたときに重なった標本点について和を求めたことになり、x の値に関係なく y と z が取る値に対する周辺分布を表しています。さらに、y 軸上に並んだ標本点( z が等しい点 ) について和を求め、それを Pz( z ) とすると、
Pz( 0 ) = Pyz( 0, 0 ) + Pyz( 1, 0 ) = ( 1 - p )2 + p( 1 - p ) = ( 1 - p ){ ( 1 - p ) + p } = 1 - p
Pz( 1 ) = Pyz( 0, 1 ) + Pyz( 1, 1 ) = p( 1 - p ) + p2 = p
となって、1 回のベルヌーイ試行における確率と等しくなります。これは、x と y の値に関係なく z が 0 または 1 となった場合の周辺分布を示しています。Px( x ) や Py( y ) も同じ値になり、その独立性から
P( x, y, z ) = Px( x )・Pyz( y, z ) = Px( x )・Py( y )・Pz( z )
が成り立ちます。例えば、
P( 1, 0, 1 ) = p2( 1 - p )
Px( 1 )・Pyz( 0, 1 ) = p・p( 1 - p ) = p2( 1 - p )
Px( 1 )・Py( 0 )・Pz( 1 ) = p( 1 - p )p = p2( 1 - p )
と求めることができます。
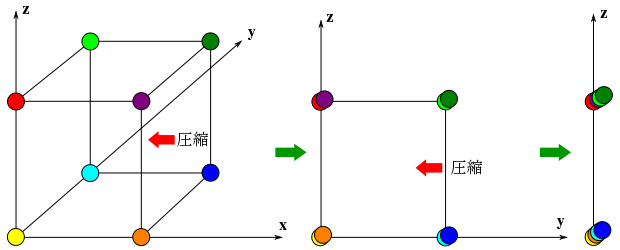
ある集合族に対する確率変数の決め方は一意ではないので、ある事象を数値で判断する場合に最適なパラメータを選択することがある程度できます。例えば、二項分布においては事象の起こった回数(成功数)で確率を調べる代わりに全試行回数との比率(成功率)を用いることもできます。確率変数を変換したとき、その分布はどのようになるでしょうか。
Ω = R 上の任意の確率分布 p(x) に対して、関数 y = f(x) によって確率変数 x を y に対する分布 q(y) へ変換するとき、x 軸上の微小区間 [ x, x + dx ] に対する確率 p(x)dx は y 軸上の微小区間 [ y, y + dy ] = [ f(x), f(x + dx) ] に対する確率 q(y)dy ( = q(f(x))dy ) と等しくなるように分布が移されることになるので、
p(x)dx = q(y)dy より
q(y) = p(x)・| dx / dy | = p(x)・| f-1(y) / dy |
が成り立ちます。p(x) も q(y) も確率密度なので正値をとることから、dx / dy と f-1(y) / dy は絶対値をとって必ず正値とする必要があります。
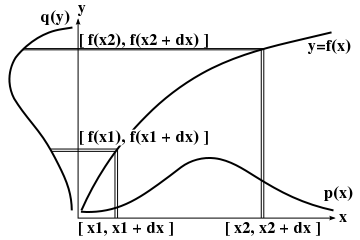
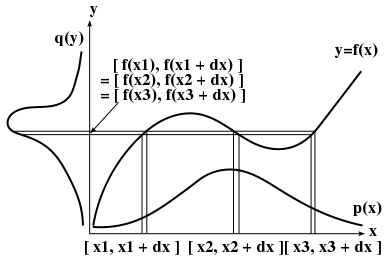
また、上記の場合は逆関数 x-1(y) が y に対して一意に決まる必要があって、そうでない場合、任意の y に対する複数の x 値 xi = fi-1(y) に対して
q(y) = Σi( p(x)・| dxi / dy | ) = Σi( p(x)・| fi-1(y) / dy | )
とする必要があります。
例えば、確率分布 p(x) を y = ax + b に対する分布 q(y) に変換すると、
q(y) = p(x)・| dx / dy | = p(x) / |a|
となります。また、p(x) と q(y) の平均と分散をそれぞれ μx, σx2 及び μy, σy2 とすれば、q(y)dy = p(x)dx より
| μy = ∫ yq(y) dy | = | ∫ ( ax + b )p(x) dx |
| = | a∫ xp(x) dx + b∫ p(x) dx |
| = | aμx + b |
| σy2 | = | ∫ ( y - μy )2q(y) dy |
| = | ∫ a2( x - μx )2p(x) dx |
| = | a2σx2 |
という関係式を得ることができます(積分の範囲 {-∞→∞} は省略して書いています)。
二項分布 BN,p(r) = NCrprqN-r において、確率変数 r を t = r / N に置き換えれば、dr / dt = N より
BN,p(t) = NNCNtpNtqN(1-t)
また、平均と分散は
μt = μr / N = p
σt2 = σr2 / N2 = pq / N
になります。
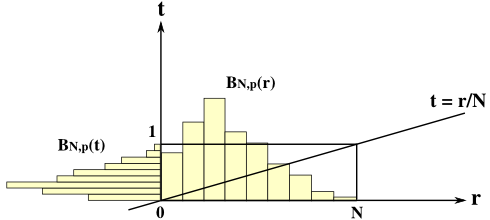
N → ∞ としたとき、t = r / N → 0 であり、変換された分布の幅 [ 0, 1 ] に対して相対的に N が大きくなることからその比率はゼロに近づいていきます。このとき、平均は p であり、分散は pq / N → 0 ( N → ∞ ) なので、分布は p の周囲に集まり、最終的には幅がゼロになってしまします。幅がゼロでもその積分は 1 になることから、これは次に示すような関数 δp(t) になります。
| δp(t) | = | 0 ( t ≠ p ) |
| = | ∞ ( t = p ) |
∫{-∞→∞} δp(t) dt = 1
∫{-∞→∞} δp(t)f(t) dt = f(p)
これを「ディラックのデルタ関数(Dirac's Delta Function)」といいます。δp(t) は x = p のときだけ「無限大」という値を持ちますが、通常はこのような関数はないため、超関数(Generalized Function)と呼ばれる、関数をより一般化した概念になります。
多変数の確率密度に対しても同様な考え方で確率変数を変化させることができます。N 個の確率変数 x = ( x1, x2, ... xN ) を持つ確率分布 p(x) を y = ( y1, y2, ... yN ) に対する分布 q(y) に変換するとき、微小区間 Ii = [ x, xi + dxi ] ( i = 1,2, ... N ) から成る直積集合 I = I1 x I2 x ... x IN 上の確率 p(x)dx1dx2...dxN = p(x)dx が、微小区間 Ji = [ y, yi + dyi ] ( i = 1,2, ... N ) から成る直積集合 J = J1 x J2 x ... x JN 上の確率 q(y)dy1dy2...dyN = q(y)dy と等しいとすれば、
q(y)dy = p(x)dx
になります。ここで、重積分における変数変換で利用される「ヤコビアン(Jacobian)」 det( J(y) ) を使って
dx = | det( J(y) ) |dy
より、
q(y) = p(x)| det( J(y) ) |
但し、det( J(y) ) ≠ 0 である必要があります。J(y) は「ヤコビ行列(Jacobian matrix)」と呼ばれる次のような行列を表し、ヤコビアンはその行列式です。
| J(y) | = | | | dx1/dy1 | , | dx1/dy2 | , ... , | dx1/dyn | | |
| | | dx2/dy1 | , | dx2/dy2 | , ... , | dx2/dyn | | |
| | | : | , | : | , ... , | : | | |
| | | dxn/dy1 | , | dxn/dy2 | , ... , | dxn/dyn | | |
2 変数の確率分布 p( x, y ) に対して、( u, v ) = ( x + y, y ) として変数変換を行ったとき、x = u - v, y = v より
det( J( u, v ) ) = ∂x/∂u・∂y/∂v - ∂x/∂v・∂y/∂u = 1
なので、変数変換後の確率分布を q( u, v ) としたとき、
q( u, v ) = p( x, y ) = p( u - v, v )
が成り立ちます。この周辺分布 qU(u) は
qu(u) = ∫{-∞→∞} q( u, v ) dv
になりますが、x と y が独立なら
q( u, v ) = p( x, y ) = px(x)py(y)
なので、
qu(u) = ∫{-∞→∞} px( u - v )py(v) dv
これは「畳み込み積分(Convolution)」と同じ式であり、px(u) * py(u) と表すことができます。u = x + y の形に表したということは、片側の確率変数を二つの変数の和に置き換えたことを意味します。その周辺分布を考えるということは和の分布に置き換えるということで、その場合の式が畳み込み積分の形を取ることになります。
ベルヌーイ試行の確率 φ(x) を、
φ(1) = p
φ(0) = q = 1 - p
φ(x) = 0 ( x ≠ 0 かつ x ≠ 1 )
と表したとき、独立した二つのベルヌーイ試行によるベルヌーイ列の要素を ( x1, x2 ) で表せば、それは ( 0, 0 ), ( 1, 0 ), ( 0, 1 ), ( 1, 1 ) のいずれかになり、r = x1 + x2 としたとき、r は 0 から 2 までの値を取ることができます。このとき、r に対する確率密度は畳み込み積分 φ(r) * φ(r) で求められ、これを φ2(r) とすると、
| φ2(r) | = | Σt{0→1}( φ( r - t )φ( t ) ) |
| = | φ( r )φ( 0 ) + φ( r - 1 )φ( 1 ) |
より
φ2(2) = φ( 2 )φ( 0 ) + φ( 1 )φ( 1 ) = p2
φ2(1) = φ( 1 )φ( 0 ) + φ( 0 )φ( 1 ) = 2pq
φ2(0) = φ( 0 )φ( 0 ) + φ( -1 )φ( 1 ) = q2
さらに三つのベルヌーイ試行に対して r に対する確率密度を φ3(r) とすれば、これは φ2(r) * φ(r) で求められ、
| φ3(r) | = | Σt{0→1}( φ2( r - t )φ( t ) ) |
| = | φ2( r )φ( 0 ) + φ2( r - 1 )φ( 1 ) |
より
φ3(3) = φ2( 3 )φ( 0 ) + φ2( 2 )φ( 1 ) = p3
φ3(2) = φ2( 2 )φ( 0 ) + φ2( 1 )φ( 1 ) = 3p2q
φ3(1) = φ2( 1 )φ( 0 ) + φ2( 0 )φ( 1 ) = 3pq2
φ3(0) = φ2( 0 )φ( 0 ) + φ2( -1 )φ( 1 ) = q3
になります。これは二項分布を表しており、その確率密度関数は nCr prqn-r ですが、上記の結果は二項分布の式と一致しています。そこで、φn-1( r ) = n-1Cr prqn-1-r とすれば、φn( r ) = φn-1(r) * φ(r) は
| φn(r) | = | Σt{0→1}( φn-1( r - t )φ( t ) ) |
| = | φn-1( r )φ( 0 ) + φn-1( r - 1 )φ( 1 ) |
| = | qn-1Cr prqn-1-r + pn-1Cr-1 pr-1qn-1-(r-1) |
| = | ( n-1Cr + n-1Cr-1 ) prqn-r |
| = | nCr prqn-r ( 「組み合わせ」の公式 nCr = n-1Cr + n-1Cr-1 より ) |
となるので、二項分布は n 個のベルヌーイ試行の畳み込み積分として表せることになります。
一変数の場合と同じように、N 変数を持つ確率密度関数 p(x) ( x = ( x1, x2, ... xN ) ) と可積分関数 f(x) が与えられたとき、その期待値 E[f] を
E[f] = ∫...∫{x∈RN} f(x)p(x) dx
と定義します。ここで、関数 f が x の i 番目の成分 xi だけを変数として持っている場合、
| E[f] | = | ∫...∫{x∈RN} f(xi)p(x) dx |
| = | ∫{-∞→∞} f(xi) ( ∫{-∞→∞}...∫{-∞→∞} p(x) dx1dx2...dxi-1dxi+1...dxN ) dxi |
ここで、∫{-∞→∞}...∫{-∞→∞} p(x) dx1dx2...dxi-1dxi+1...dxN は周辺分布を表しているので pi(xi) とおけば、
E[f] = ∫{-∞→∞} f(xi) pi(xi) dxi
になります。確率密度関数が多変数であっても、関数 f が一変数であれば、一変数の周辺分布を利用した積分に置き換えることができることになります。特に、f(xi) = xi ならば、
E[xi] = ∫{-∞→∞} xi pi(xi) dxi = μi
として、一変数の場合と同様に平均値 μi を定義することができます。また、( xi - μi )2 の期待値は
E[( xi - μi )2] = ∫{-∞→∞} ( xi - μi )2 pi(xi) dxi = σi2
となるので、分散 σi2 が定義できることになります。
f(x) が各確率変数を持った関数の和の形、すなわち f(x) = f1(x1) + f2(x2) + ... + fn(xn) の形をとる関数に対する期待値は、
| E[f] | = | ∫{-∞→∞}...∫{-∞→∞} f(x) p(x) dx1...dxn |
| = | ∫{-∞→∞}...∫{-∞→∞} { f1(x1) + f2(x2) + ... + fn(xn) } p(x) dx1...dxn |
| = | Σi{1→n}( ∫{-∞→∞} fi(xi) pi(xi) dxi ) |
| = | Σi{1→n}( E[fi] ) |
となるので、和に対する期待値は期待値の和で表せることを意味します。また、確率変数 x = ( x1, x2, ... xn ) が全て互いに独立で、p(x) = p1(x1)p2(x2)...pn(xn) の形に表すことができる場合、f(x) = f1(x1)f2(x2)...fn(xn) の形をとる関数に対する期待値は、
| E[f] | = | ∫{-∞→∞}...∫{-∞→∞} f(x) p(x) dx1...dxn |
| = | ∫{-∞→∞}...∫{-∞→∞} f1(x1)f2(x2)...fn(xn) p1(x1)p2(x2)...pn(xn) dx1...dxn |
| = | ∫{-∞→∞}...∫{-∞→∞} f1(x1)p1(x1) f2(x2)p2(x2) ... fn(xn)pn(xn) dx1...dxn |
| = | Πi{1→n}( ∫{-∞→∞} fi(xi) pi(xi) dxi ) |
| = | Πi{1→n}( E[fi] ) |
となって、確率変数が全て互いに独立であれば、積に対する期待値は期待値の積で表せることになります。
任意の N 次元ベクトル x = ( x1, x2, ... xN ) と、N 変数の確率密度関数の平均値から成るベクトル μ = ( μ1, μ2, ... μN ) の差を δ = ( x1 - μ1, x2 - μ2, ... xN - μN ) としたとき、δTδ は N 行 N 列の正方行列となって、その r 行 c 列目の要素 arc は
arc = ( xr - μr )( xc - μc )
になります。x を確率変数とする確率分布 p(x) の arc に対する期待値を γrc とすると、
γrc = E[arc] = ∫{-∞→∞}...∫{-∞→∞} ( xr - μr )( xc - μc ) p(x) dx
となり、この値を「共分散(Covariance)」、共分散を要素とする行列を「共分散行列(Covariance Matrix)」といいます。共分散行列に関しては「主成分分析」でも紹介していますが、そこでは各ベクトルの要素から直接、平均と共分散を求めています。ここでは N 次元ベクトル上の各要素が離散値から連続量となって、ある確率分布に従うとしたときの式であると考えると分かりやすいと思います。
xr と xc を変数とする周辺分布を prc( xr, xc ) としたとき、共分散 γrc は
γrc = ∫{-∞→∞}∫{-∞→∞} ( xr - μr )( xc - μc ) prc( xr, xc ) dxrdxc
になります。r = c ならば周辺分布は一変数のみとなって、分散と一致します。また、上式は
| γrc | = | ∫{-∞→∞}∫{-∞→∞} ( xrxc - μcxr - μrxc + μrμc ) prc( xr, xc ) dxrdxc |
| = | ∫{-∞→∞}∫{-∞→∞} xrxcprc( xr, xc ) dxrdxc - μc∫{-∞→∞}xr ( ∫{-∞→∞} prc( xr, xc ) dxc ) dxr |
| | - μr∫{-∞→∞}xc ( ∫{-∞→∞} prc( xr, xc ) dxr ) dxc
+ μrμc∫{-∞→∞}∫{-∞→∞} prc( xr, xc ) dxrdxc |
| = | ∫{-∞→∞}∫{-∞→∞} xrxcprc( xr, xc ) dxrdxc - μc∫{-∞→∞}xr pr(xr) dxr - μr∫{-∞→∞}xc pc(xc) dxc + μrμc |
| = | ∫{-∞→∞}∫{-∞→∞} xrxcprc( xr, xc ) dxrdxc - μcμr - μrμc + μrμc |
| = | ∫{-∞→∞}∫{-∞→∞} xrxcprc( xr, xc ) dxrdxc - μrμc |
となって、∫{-∞→∞}∫{-∞→∞} xrxcprc( xr, xc ) dxrdxc = E[xrxc]、μrμc = E[xr]E[xc] だから、
γrc = E[xrxc] - E[xr]E[xc]
が成り立ちます。
共分散は、確率変数が表す値の単位に影響を受けます。例えば、身長と体重の分布を使って共分散を求めた時、身長を cm と m のどちらで表すか、また体重を kg と g のどちらで表すか、などによって共分散は変化します。各データにおける共分散の大小を比較したいような場合にこれでは困るので、それぞれの分散の平方根(標準偏差)の積で徐算することで正規化処理を行います。
ρrc = γrc / σrσc
この値 ρrc を「相関係数(Correlation Coefficient)」といいます。具体的に書くと
ρrc = ∫∫ ( xr - μr )( xc - μc ) prc( xr, xc ) dxrdxc / [ { ∫∫ ( xr - μr )2 prc( xr, xc ) dxrdxc }1/2・{ ∫∫ ( xc - μc )2 prc( xr, xc ) dxrdxc }1/2 ]
但し、積分する区間 ( {-∞→∞} ) の記述は省略しています。prc は確率密度関数なので、任意の ( xr, xc ) に対して prc( xr, xc ) ≥ 0 が保証されています。従って、
fr( xr, xc ) = ( xr - μr ) { prc( xr, xc ) }1/2
fc( xr, xc ) = ( xc - μc ) { prc( xr, xc ) }1/2
とすれば上式は
ρrc = ∫∫ frfc dxrdxc / [ { ∫∫ fr2 dxrdxc }1/2・{ ∫∫ fc2 dxrdxc }1/2 ]
ここで、fr, fc の引数をさらに省略して記述しています。( fr, fc ) = ∫∫ frfc dxrdxc とすれば、( fr, fc ) は内積の公理を満たすので、「コーシー = シュワルツの不等式(Cauchy-Schwarz Inequality)」から
- { ∫∫ fr2 dxrdxc }1/2・{ ∫∫ fc2 dxrdxc }1/2 ≤ ∫∫ frfc dxrdxc ≤ { ∫∫ fr2 dxrdxc }1/2・{ ∫∫ fc2 dxrdxc }1/2
よって、
-1 ≤ ρrc ≤ 1
つまり、相関係数の絶対値は 1 以下になります。もし、xr と xc が独立ならば、prc( xr, xc ) = pr(xr)pc(xc) となるので、
| γrc | = | ∫{-∞→∞}∫{-∞→∞} ( xr - μr )( xc - μc ) pr(xr)pc(xc) dxrdxc |
| = | ∫{-∞→∞} ( xr - μr )pr(xr) dxr ∫{-∞→∞} ( xc - μc )pc(xc) dxc |
| = | { ∫{-∞→∞} xrpr(xr) dxr - μr∫{-∞→∞} pr(xr) dxr }{ ∫{-∞→∞} xcpc(xc) dxc - μc∫{-∞→∞} pc(xc) dxc } |
| = | ( μr - μr )( μc - μc ) = 0 |
よって、共分散も相関係数もゼロになります。|ρrc| = 1 ならばどうなるかというと、これは |γrc| = σrσc を意味するので、この両辺を二乗した上で少し変形すると
γrc2 - σr2σc2 = 0
これを、二次方程式
σr2t2 + 2γrct + σc2 = 0
の判別式とみなせば t は重根となって、
( σrt + σc )2 = 0
になります。上に示した二次方程式は、σr2 = ∫∫ ( xr - μr )2 prc dxrdxc, σc2 = ∫∫ ( xc - μc )2 prc dxrdxc, γrc = ∫∫ ( xr - μr )( xc - μc ) prc dxrdxc より (以下、積分する区間 ( {-∞→∞} ) の記述は省略します。また、prc はもちろん prc( xr, xc ) のことです)
| ∫∫ t2( xr - μr )2 prc dxrdxc + ∫∫ 2t( xr - μr )( xc - μc ) prc dxrdxc + ∫∫ ( xc - μc )2 prc dxrdxc |
| = | ∫∫ [ { ( xr - μr )t }2 + 2( xr - μr )( xc - μc )t + ( xc - μc )2 ] prc dxrdxc |
| = | ∫∫ { ( xr - μr )t + ( xc - μc ) }2 prc dxrdxc |
| = | E[ { ( xr - μr )t + ( xc - μc ) }2 ] |
になるので、|ρrc| = 1 のとき、{ ( xr - μr )t + ( xc - μc ) }2 の期待値がゼロになるような実数 t を持つことができます。E[ { ( xr - μr )t + ( xc - μc ) }2 ] ≥ 0 なので、これがゼロになるためには prc = 0 でない限り
( xr - μr )t + ( xc - μc ) = 0
の形を取る必要があり、このとき xr と xc は一次関数の形で表されます。
|ρrc| < 1 のとき、上で示した判別式は負数であり、二次方程式は実数解を持つことができません。よって E[ { ( xr - μr )t + ( xc - μc ) }2 ] ≠ 0 であり、xr と xc は一次関数の形になりえないことを意味します。逆に、xr = axc + b の形を取るとき、
| μr | = | ∫{-∞→∞} xr pr(xr) dxr |
| = | ∫{-∞→∞} xr ( ∫{-∞→∞} prc( xr, xc ) dxc ) dxr |
| = | ∫{-∞→∞} ( axc + b ) ( ∫{-∞→∞} prc dxr ) dxc |
| = | ∫{-∞→∞} ( axc + b ) pc(xc) dxc |
| = | aμc + b |
また、分散は
| σr2 | = | ∫{-∞→∞} ( xr - μr )2 pr(xr) dxr |
| = | ∫{-∞→∞} { ( axc + b ) - ( aμc + b ) }2 pc(xc) dxc |
| = | a2∫{-∞→∞} ( xc - μc )2 pc(xc) dxc |
| = | a2σc2 |
なので、共分散 γrc は
| γrc | = | ∫{-∞→∞}∫{-∞→∞} ( xr - μr )( xc - μc ) prc( xr, xc ) dxrdxc |
| = | ∫{-∞→∞}∫{-∞→∞} { ( axc + b ) - ( aμc + b ) }( xc - μc ) prc( xr, xc ) dxrdxc |
| = | ∫{-∞→∞}∫{-∞→∞} a( xc - μc )2 prc( xr, xc ) dxrdxc |
| = | aσc2 |
よって、相関係数 ρrc は、
|ρrc| = | γrc / σrσc | = | aσc2 / |a|σcσc | = 1
になります。2 変数が互いに影響を及ぼさない独立した状態ならば、相関係数はゼロになり、一次関数の形で表される場合は 1 になります。2 変数を xy座標上にプロットすると、直線に近似できるような状態であれば、相関係数の値は大きくなっていくことになるので、グラフを見てデータの相関を読み取るようなことができます。これを「散布図(Scatter Plot ; Scattergraph)」といいます。
y の x に関する条件付確率密度は次のように表されるのでした。
p(y|x) = p( x, y ) / px( x )
ここで、x は定数、y は変数になっています。この分布の平均を μy|x とすると、
μy|x = ∫{-∞→∞} y・p(y|x) dy
となって、今度は x のみを含む関数として見ることができるようになります。この関数を μy(x) として、グラフ上にプロットしたものを x に対する y の「回帰曲線(Regression Curve)」といいます。
x と y が独立なら、
p(y|x) = p( x, y ) / px( x ) = px( x )py( y ) / px( x ) = py( y )
なので、
μy(x) = ∫{-∞→∞} y・py( y ) dy = μy
つまり、x の値に関係なく一定となります。μy(x) は、x の値を変化させた時の y の平均を表しているので、x と y が独立であれば x がどのように変化しても平均が変化することはないことを意味しています。もちろん μx(y) も同様に変化はしません。
次に、回帰曲線が一次関数 Y = aX + b の形をとる場合を考えてみます。このとき、
μy(x) = ∫{-∞→∞} y・p(y|x) dy = ax + b ... (1)
となります。この右辺の期待値は
| E[ax + b] | = | ∫{-∞→∞}∫{-∞→∞} ( ax + b )p( x, y ) dxdy |
| = | ∫{-∞→∞} ( ax + b )( ∫{-∞→∞} p( x, y ) dy ) dx |
| = | ∫{-∞→∞} ( ax + b )px( x ) dx |
| = | aμx + b |
となりますが、μy(x) は x を固定したときの y の期待値を表しているので、さらにその期待値を求めた結果は
E[μy(x)] = ∫{-∞→∞} μy(x) dx = μy
であり、
μy = aμx + b ... (2)
となります。(1) と (2) を辺々引くと
∫{-∞→∞} y・p(y|x) dy - μy = a( x - μx )
∫{-∞→∞} p(y|x) dy = 1 なので、上式の左辺は
∫{-∞→∞} y・p(y|x) dy - ∫{-∞→∞} μy・p(y|x) dy = ∫{-∞→∞} ( y - μy )・p(y|x) dy
よって、
∫{-∞→∞} ( y - μy )・p(y|x) dy = a( x - μx ) ... (3)
次に、E[a( x - μx )2] = aσx2 を計算すると、
aσx2 = ∫{-∞→∞} a( x - μx )2・px( x ) dx
ここに、(3)式を代入すると
| aσx2 | = | ∫{-∞→∞} ( x - μx ) ( ∫{-∞→∞} ( y - μy )・p(y|x) dy )・px( x ) dx |
| = | ∫{-∞→∞} ∫{-∞→∞} ( x - μx )( y - μy )・p(y|x)・px( x ) dxdy |
| = | ∫{-∞→∞} ∫{-∞→∞} ( x - μx )( y - μy )・p( x, y ) dxdy |
| = | γxy |
よって、
a = γxy / σx2 = ρσy / σx
また、(2) 式より
b = μy - aμx = μy - ρ( σy / σx )μx
よって回帰曲線の式は
( Y - μy ) / σy = ρ( X - μx ) / σx
になります。( X - μx ) / σx や ( Y - μy ) / σy は「標準得点(Standard Score)」と呼ばれ、ばらつき(分散)の大小によって平均との差の意味が異なるのを調整する、言わば正規化処理です。相関係数のところでも説明したように、平均との差はデータの単位によって異なるため、このような正規化が行われます。すると、それぞれの標準得点を Zx, Zy とすれば、
Zy = ρZx
という非常にシンプルな式で表すことができます。
回帰曲線が直線であるということは、二変数の分布が直線の付近に集中しているということになります。どの程度集中しているかは分散の大きさによって変化しますが、正規化したとき、その傾きは相関係数 ρ と等しくなります。μx(y) を一次関数として考えても全く同じ流れで Zx = ρZy すなわち Zy = ( 1 / ρ )Zx という式が得られます。この違いは、x を固定したときの y の平均を考えるのか、それとも y を固定したときの x の平均を考えるのかによって発生します。
二変数の確率密度関数に対する共分散行列は
となりますが、変数を正規化すると μZx = μZy = 0, σZx2 = σZy2 = 1 となり、
γZxZy = E[( Zx - μZx )( Zy - μZy )] = E[ZxZy]
なので、
| V | = | | | 1, | γZxZy | | |
| | | | γZxZy, | 1 | | |
| = | | | 1, | E[ZxZy] | | |
| | | | E[ZxZy], | 1 | | |
になります。σZx2 = σZy2 = 1 より、γZxZy は相関係数と等しいので、以降 γZxZy を ρ として、固有方程式は
| det( | λE - V | ) | =det( | | | λ - 1, | -ρ | | | ) |
| | | -ρ, | λ - 1 | | |
| = | ( λ - 1 )2 - ρ2 |
| = | λ2 - 2λ + ( 1 - ρ2 ) |
よって、固有値 λ は
λ = 1 ± ρ
固有ベクトルは
| | ( 1 ± ρ )E - V | | | | | x | | = | | | ±ρ, | -ρ, | || | x | | = 0 |
| | | | y | | | | | -ρ, | ±ρ, | || | y | | |
より、一つの解として
( x, y ) = ( ±1 / √2, 1 / √2 )
が得られます。よって、V の固有値分解は
| | | 1 / √2, | 1 / √2 | | | | 1, | ρ | | | | 1 / √2, | -1 / √2 | | | = | | | 1 + ρ, | 0 | | |
| | | -1 / √2, | 1 / √2 | | | | ρ, | 1 | | | | 1 / √2, | 1 / √2 | | | | | | 0, | 1 - ρ | | |
であり、二次形式の標準形は
| | | x' | | | = | | | 1 / √2, | 1 / √2 | || | x | | | = | | | x / √2 + y / √2 | | |
| | | y' | | | | | | -1 / √2, | 1 / √2 | || | y | | | | | | -x / √2 + y / √2 | | |
としたとき、
f = ( 1 + ρ )x'2 + ( 1 - ρ )y'2
になります。
変数を正規化したとき、回帰曲線が直線だった場合はその傾きは 1 / ρ になりました。それに対し、主軸変換を行った場合の主軸の傾きは ±1 となり、両者の値は異なります。どちらも分布の平均 ( μx, μy ) を通る直線を表しているのにも関らず、その傾きに違いが発生するのは、そもそも求め方に違いがあるのが理由なのですが、両者はよく混同されているようです。両者の違いについては別途紹介をしたいと思いますが、ここでは両者が異なるモデルから成るということを強調しておきます。ちなみに、回帰曲線を利用した手法として「最小二乗法」、相関係数や共分散を利用した手法として「主成分分析」が代表として挙げられます。
多変数の確率分布を定義する上でのインターフェースを以下に示します。
namespace Statistics
{
class MultiProbDist
{
public:
virtual double average( unsigned int i ) const = 0;
virtual double variance( unsigned int i ) const = 0;
virtual double covariance( unsigned int i, unsigned int j ) const = 0;
virtual unsigned int size() const = 0;
};
class MultiDiscDist : public MultiProbDist
{
double getProb( vector<int>& p, const vector<int>& s, const vector<int>& e, unsigned int curIdx ) const;
public:
virtual double operator[]( const vector<int>& n ) const = 0;
double p( vector<int> s, vector<int> e ) const;
};
class MultiContDist : public MultiProbDist
{
public:
virtual double operator[]( const vector<double>& a ) const = 0;
virtual double p( const vector<double>& a, const vector<double>& b ) const = 0;
};
double MultiDiscDist::getProb( vector<int>& p, const vector<int>& s, const vector<int>& e, unsigned int curIdx ) const
{
double d = 0;
for ( p[curIdx] = s[curIdx] ; p[curIdx] <= e[curIdx] ; ++( p[curIdx] ) ) {
if ( curIdx == size() - 1 ) {
d += (*this)[p];
} else {
d += getProb( p, s, e, curIdx + 1 );
}
}
return( d );
}
double MultiDiscDist::p( vector<int> s, vector<int> e ) const
{
unsigned int n = size();
if ( s.size() != n || e.size() != n ) return( NAN );
for ( unsigned int i = 0 ; i < n ; ++i ) {
if ( s[i] > e[i] )
{ int j = s[i]; s[i] = e[i]; e[i] = j; }
}
vector<int> p( n );
return( getProb( p, s, e, 0 ) );
}
}
一変数の場合と異なり、多変数では平均と分散は確率変数の番号を指定する形を取ります。また、共分散を求めるためのメンバ関数も用意します。相関係数は、共分散を標準偏差で割れば求めることができるので、専用のメンバ関数は省略しています。
指定した範囲の確率を求めるためのメンバ関数 p が用意されています。引数として、各確率変数の開始位置を示す s と、終了位置を示す e を渡すようにしてあります。連続分布に対しては、各確率分布の中で定義を行うのに対し、離散分布では operator[] を使って各確率変数に対する確率密度を順番に計算し、その和を求める処理をあらかじめ実装しています。各区間を指定する方法を取っているため、その範囲は、二変数なら矩形、三変数なら直方体の形になって、任意の範囲に対して(例えば二変数において三角形の範囲となるように)指定することはできません。
多変数の確率分布の代表として「多項分布(Multinomial Distribution)」を紹介します。
二項定理の展開式を利用して二項分布が確率分布として成り立っていることが証明できたように、多項定理を利用すると「多項分布」という確率分布を導くことができます。多項定理は、任意の数の項を持つ多項式のべき乗を展開したときの式に関する定理で、次のような公式で表されます。
多項定理
( x1 + x2 + ... + xk )n = Σr1,r2, ... rk{ r1 + r2 + ... + rk = n }( ( n! / r1!・r2!・...・rk! )・x1r1・x2r2・...・xkrk )
上の公式は、展開式の各項 x1r1・x2r2・...・xkrk に対する係数が n! / r1!・r2!・...・rk! であることを示しています。また、各項の次数 ( r1 から rk までの和 ) は必ずべき乗の数 n と等しくなります。例えば、( x + y + z )3 を展開したとき、項としては次の 10 通りが存在します。
x3, y3, z3, x2y, zx2, xy2, y2z, z2x, yz2, xyz
また、この中の項 x2y に対する係数は 3! / 2!・1!・0! = 3 と求めることができます。
x1 + x2 + ... + xk = 1 であれば、公式の左辺は 1 になります。よって、展開式の各項がある事象に対する確率密度を表すと考えれば、これは確率分布としての条件を満たしていることになります。この確率分布は次のような式で表すことができます。
Pn,p( r ) = P( r1, r2, ... rk ) = ( n! / r1!・r2!・...・rk! ) p1r1・p2r2・...・pkrk
但し r1 + r2 + ... + rk = n、p1 + p2 + ... + pk = 1
さて、多項定理を使って先に確率分布の定義を行いましたが、これはどのような状態を表しているでしょうか。
一回の試行 E に対し、k 個の事象 ( E1, E2, ... Ek ) の中の一つだけが必ず起こるとして、それぞれの事象が発生する確率は p1, p2, ... pk だったとします。この試行 E を n 回 繰り返したとき、その標本空間 Ω は
Ω = { ( r1, r2, ... rn ) | ri = 1, 2, ... k ( i = 1, 2, ... n ) }
と表すことができます。ここで、二項分布のときと同様に、各事象が発生した回数に着目して、各事象 Ei がそれぞれ ri 回発生した場合の標本点に対する確率を次のように定義します。
p( r1, r2, ... rk ) = p1r1・p2r2・...・pkrk
但し r1 + r2 + ... + rk = n、p1 + p2 + ... + pk = 1
ここでも二項分布と同様に、各試行が独立で、各事象が発生する箇所に関係なく、回数が同じであれば確率も同じであると仮定しています。各事象 Ei がそれぞれ ri 回発生するとき、その合計が n 回になるような並べ方は「重複順列」の式より n! / r1・r2・...・rk 個だから、多項分布の式が導かれたことになります。
i 番目の事象 Ei の発生回数に対する周辺分布は、ri = r、Σj{j≠i}( rj ) = n - r となるような分布を意味していることになるのでそれは二項分布であり、平均 μi = E[ri] = npi に、また ri に対する分散も σi2 = npi( 1 - pi ) になります。
二組の確率変数 xi, xj に対する共分散 γij は、
| γij | = | E[( ri - μi )( rj - μj )] |
| = | Σ...Σ( ( ri - μi )( rj - μj )P( r1, r2, ... rk ) ) |
で計算できます。ri, rj 以外の確率変数をひとまとめにした周辺分布は
Pij( ri, rj, n - ri - rj ) = { n! / ri! rj! ( n - ri - rj )! }・piri・pjrj・( 1 - pi - pj )n - ri - rj
になるので、これを
Pij( i, j, n ) = { n! / i!・j!・( n - i - j )! }・pi・qj・( 1 - p - q )n-i-j
と表すことにします。このとき、共分散は
| γij | = | Σi{0→n}( Σj{0→n-i}( ( i - np )( j - nq ) Pij( i, j, n ) ) |
| = | Σi{0→n}( Σj{0→n-i}( ( i - np )( j - nq ) { n! / i!・j!・( n - i - j )! }・pi・qj・( 1 - p - q )n-i-j ) ) |
| = | Σi{0→n}( ( i - np ){ n! / i!・( n - i )! }・pi Σj{0→n-i}( ( j - nq ) { ( n - i )! / j!・( n - i - j )! }・qj・( 1 - p - q )n-i-j ) ) |
| = | Σi{0→n}( ( i - np ) nCi pi Σj{0→n-i}( ( j - nq ) n-iCj qj・( 1 - p - q )n-i-j ) ) |
ここで、
| Si | = | Σj{0→n-i}( ( j - nq ) n-iCj qj・( 1 - p - q )n-i-j ) |
| = | Σj{0→m}( ( j - nq ) mCj qj・( 1 - p - q )m-j ) |
とすると、
| Si | = | Σj{0→m}( ( j - nq ) mCj qj・( 1 - p - q )m-j ) |
| = | Σj{0→m}( j・mCj qj・( 1 - p - q )m-j ) - nqΣj{0→m}( mCj qj・( 1 - p - q )m-j ) |
ここで、第一項は二項分布の平均を求める方法を利用して mq ( 1 - p )m-1 となるので ( 補足 2 の (1)式 )
| Si | = | mq ( 1 - p )m-1 - nq( 1 - p )m |
| = | -q{ n( 1 - p ) - m }( 1 - p )m-1 |
| = | -q{ n - np - ( n - i ) }( 1 - p )n-i-1 |
| = | -q( i - np )( 1 - p )n-i-1 |
よって、
| γij | = | Σi{0→n}( ( i - np ) nCi pi { -q( i - np )( 1 - p )n-i-1 } ) |
| = | -{ q / ( 1 - p ) } Σi{0→n}( ( i - np )2 nCi pi・( 1 - p )n-i ) |
ところが、和の部分は二項分布での分散を表しているので np( 1 - p ) となって、
γij = -{ q / ( 1 - p ) }・np( 1 - p ) = -npq
と求めることができます。
以上をまとめると、
多項分布 Pn,p(r) = ( n! / r1!・r2!・...・rk! ) p1r1・p2r2・...・pkrk
平均 : μi = npi、分散 : σi2 = npi( 1 - pi )
共分散 : γij = -npipj
多項分布の変数は k 個ありますが、その中のひとつは ri = n - Σj{j≠i}( rj ) という制限を持っているので k - 1 次元上の分布となります。よって、k = 2 ならばそれは一次元分布となり、二項分布と一致することになります。実際、二項分布 Bn,p(r) = nCrprqn-r において n - r = s とすれば、r + s = n, p + q = 1 であり、
Bn,p(r) = ( n! / r!・( n - r )! )prqn-r = ( n! / r!・s! )prqs
なので、多項分布の式と一致します。Bm,p1,p2(r) = mCrp1rp2m-r ( 但し、p1 + p2 < 1 ) の m を変数として、Σr{0→m}( Bm,p1,p2(r) ) = SBp1,p2(m) としたとき、「SBp1,p2(m) が二項分布 nCmp3m( 1 - p3 )n-m に従うとすれば、Bm,p1,p2(r) は多項分布である」と考えることもできます。このとき、p1 + p2 + p3 = 1 となり、p1 + p2 < 1 なので、Bm,p1,p2(r) は事象の発生回数の合計が m となるときの条件付確率を表し、その和は 1 以下です。また、各々の m に対する Bm,p1,p2(r) の和 SBp1,p2(m) の分布は多項分布の周辺分布なので、その和を求めたときはじめて 1 になるわけです。そこで、
q1 = p1 / ( p1 + p2 )
q2 = p2 / ( p1 + p2 )
と表せば q1 + q2 = 1 となるので、Bm,q1,q2(r) = mCrq1rq2m-r は二項分布となります。
多項分布用クラスのサンプル・プログラムを以下に示します。
class MultinomialDistribution : public MultiDiscDist
{
vector<double> _p;
unsigned int _n;
static double fact( double n );
public:
MultinomialDistribution( const vector<double>& p, unsigned int n )
: _n( n ) { _p.assign( p.begin(), p.end() ); }
double operator[]( const vector<int>& r ) const;
double average( unsigned int i ) const
{ return( ( i >= size() ) ? NAN : (double)_n * _p[i] ); }
double variance( unsigned int i ) const
{ return( ( i >= size() ) ? NAN : (double)_n * _p[i] * ( 1.0 - _p[i] ) ); }
double covariance( unsigned int i, unsigned int j ) const;
unsigned int size() const { return( _p.size() ); }
};
double MultinomialDistribution::fact( double n )
{
if ( n <= 1 ) return( 1 );
return( n * fact( n - 1 ) );
}
double MultinomialDistribution::operator[]( const vector<int>& r ) const
{
if ( _p.size() != r.size() ) return( NAN );
if ( r.size() == 0 ) return( NAN );
unsigned int n = 0;
for ( unsigned int i = 0 ; i < r.size() ; ++i ) {
if ( _p[i] < 0 ) return( NAN );
if ( r[i] < 0 ) return( 0 );
n += r[i];
}
if ( n != _n ) return( 0 );
double fact_r = fact( r[0] );
double p = pow( _p[0], r[0] );
for ( unsigned int i = 1 ; i < r.size() ; ++i ) {
if ( _p[i] == 0 && r[i] != 0 ) return( 0 );
fact_r *= fact( (double)r[i] );
p *= pow( _p[i], r[i] );
}
return( fact( _n ) * p / fact_r );
}
double MultinomialDistribution::covariance( unsigned int i, unsigned int j ) const
{
if ( i >= size() || j >= size() ) return( NAN );
return( - (double)( size() ) * _p[i] * _p[j] );
}
コンストラクタでは、各試行の発生する確率と、試行の総回数の二つを引数として渡します。ここで、全事象の確率の和が 1 であることはチェックを行っていません。従って、利用する側で事前にチェックをしておく必要があります。
メンバ関数 operator[] に各事象の発生した回数をやはり可変長配列の形で渡すことで、その場合の確率密度を返します。この時、配列の要素数は事象の数と完全に一致している必要があります。また、発生回数の総和は、コンストラクタで渡したものと一致する必要があり、そうでなければ戻り値としてゼロが返されます。多項分布の場合、各試行の回数の総和が定数であるという制限がありますが、実際には試行の総回数を制限しなくても、各試行回数から総和を計算することで計算自体はできるので、呼び出し側で総和が定数となるように気を付ければ、インスタンス化のときに試行の総回数を引数として渡すようなことは不要です。しかし、基底クラスの MultiDiscDist で用意したメンバ関数 p を利用して確率の総和を正しく求めることができるように、このような仕様にしています。
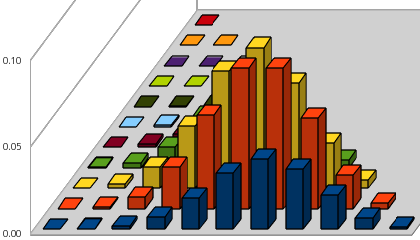
下図は、サイコロを投げたときに 1 の目が出た事象を E1、偶数の目が出た事象を E2、その他の場合を E3 として、サイコロを投げる試行を 10 回繰り返したときのの分布の状態を表しています。それぞれの事象 Ei の確率 pi は { p1, p2, p3 } = { 1 / 6, 1 / 2, 1 / 3 } であり、グラフ内において、底平面上の縦軸が E1 の発生回数 r1、横軸が E2 の発生回数 r2 となります。従って、一番手前にある青色の分布は、r1 = 0 の場合の、r2 に対する分布を示していることになります。この分布を表す式は
10Cr2 p2r2p310 - r2
となり、この和は、E1 の発生回数に対する二項分布を考えたとき、その発生回数がゼロとなる確率を表します。
|
| E2の発生回数 |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 合計 |
|---|
E1
の
発
生
回
数 | 10 | 0.00000 | | | | | | | | | | | 0.00000 |
|---|
| 9 | 0.00000 | 0.00000 | | | | | | | | | | 0.00000 |
|---|
| 8 | 0.00000 | 0.00001 | 0.00001 | | | | | | | | | 0.00002 |
|---|
| 7 | 0.00002 | 0.00007 | 0.00011 | 0.00005 | | | | | | | | 0.00025 |
|---|
| 6 | 0.00006 | 0.00033 | 0.00075 | 0.00075 | 0.00028 | | | | | | | 0.00217 |
|---|
| 5 | 0.00013 | 0.00100 | 0.00300 | 0.00450 | 0.00338 | 0.00101 | | | | | | 0.01302 |
|---|
| 4 | 0.00022 | 0.00200 | 0.00750 | 0.01500 | 0.01688 | 0.01013 | 0.00253 | | | | | 0.05427 |
|---|
| 3 | 0.00025 | 0.00267 | 0.01200 | 0.03001 | 0.04501 | 0.04051 | 0.02025 | 0.00434 | | | | 0.15505 |
|---|
| 2 | 0.00019 | 0.00229 | 0.01200 | 0.03601 | 0.06752 | 0.08102 | 0.06076 | 0.02604 | 0.00488 | | | 0.29071 |
|---|
| 1 | 0.00008 | 0.00114 | 0.00686 | 0.02401 | 0.05401 | 0.08102 | 0.08102 | 0.05208 | 0.01953 | 0.00326 | | 0.32301 |
|---|
| 0 | 0.00002 | 0.00025 | 0.00171 | 0.00686 | 0.01800 | 0.03241 | 0.04051 | 0.03472 | 0.01953 | 0.00651 | 0.00098 | 0.16151 |
|---|
| 合計 | 0.00098 | 0.00977 | 0.04395 | 0.11719 | 0.20508 | 0.24609 | 0.20508 | 0.11719 | 0.04395 | 0.00977 | 0.00098 |
|---|
|
最も確率密度の高い事象は { r1, r2, r3 } = { 1, 5, 4 }, { 1, 6, 3 }, { 2, 5, 3 } であり、各事象に対する期待値が { 1.67, 5.00, 3.33 } と計算できる事実とも一致します。
7) 負の多項分布(Negative Multinomial Distribution)
多項分布は、二項分布 Bn,p(r) の n を変数と考えて、その確率の和がまた二項分布になるとすることで得られることを前節で説明しました。この操作は各独立事象の発生する確率の和が 1 になるまで何回でも続けることができて、その結果もある事象に対する二項分布の形になります。
ここで、多項分布の中の事象の一つ E0 は「どの事象も発生しなかった場合」と見なします。E0 を除く事象の個数を k としたとき、多項分布は
| Pn,p( r ) | = | ( n! / r0!r1!r2! ... rk! ) p0r0p1r1p2r2 ... pkrk |
| = | { ( Σi{1→k}( ri ) + r0 )!・p0r0 / r0! } Πi{1→k}( piri / ri! ) |
と表されます。ここで、全試行回数を n に固定する代わりに、E0 の発生回数が r0 = s に達するまで試行を繰り返す操作を考えると、最後は必ず E0 が起こるという制約のため、組み合わせは ( n - 1 )! / ( s - 1 )!r1!r2! ... rk! となって、
Ps,p( r ) = { ( Σi{1→k}( ri ) + s - 1 )!・p0s / ( s - 1 )! } Πi{1→k}( piri / ri! )
と表すことができます。これを「負の多項分布(Negative Multinomial Distribution)」といいます。上式において、各確率変数 ri は自然数 Z 上の任意の値を取ります。Σi{1→k}( ri ) = r となる場合の周辺分布は
| Ps,p(r|r) | = | { ( r + s - 1 )!・p0s / ( s - 1 )! } Πi{1→k}( piri / ri! ) |
| = | { ( r + s - 1 )! / r!・( s - 1 )! }p0s { r! / r1!r2!...rk! } p1r1p2r2...pkrk |
| = | r+s-1Cr p0s { r! / r1!r2!...rk! } p1r1p2r2...pkrk |
になるので、その分布の和は r+s-1Cr p0s ( p1 + p2 + ... + pk )r = r+s-1Cr p0s ( 1 - p0 )r であり、負の二項分布と一致します。よって、その総和も 1 となり、確率分布として成り立っていることになります。
周辺分布 Ps,p(r|r) に対してさらに ri だけを変数とする周辺分布を考えると、それは二項分布に似た形をとり
Ps,p(ri|r) = r+s-1Cr p0s rCri piri( 1 - p0 - pi )r-ri
よって、確率変数 ri に対する平均は
| μi | = | Σr{0→∞}( Σri{0→r}( ri・Ps,p(ri|r) ) ) |
| = | Σr{0→∞}( r+s-1Cr p0s Σri{0→r}( ri・rCri piri( 1 - p0 - pi )r-ri ) ) |
| = | Σr{0→∞}( r+s-1Cr p0s r・pi ( 1 - p0 )r-1 ) [ 補足 2 (1)式 より ] |
| = | { pi / ( 1 - p0 ) }・Σr{0→∞}( r・r+s-1Cr p0s ( 1 - p0 )r ) |
| = | { pi / ( 1 - p0 ) }・{ s( 1 - p0 ) / p0 } = s・pi / p0 |
Σr{0→∞}( r・r+s-1Cr p0s ( 1 - p0 )r ) は負の二項分布における平均を表すので s( 1 - p0 ) / p0 であり、上式のように求めることができます。
また、ri に対する分散は
| σi2 | = | Σr{0→∞}( Σri{0→r}( ri2・Ps,p(ri|r) ) ) - μi2 |
| = | Σr{0→∞}( r+s-1Cr p0s Σri{0→r}( ri2rCri piri( 1 - p0 - pi )r-ri ) ) - μi2 |
| = | Σr{0→∞}( r+s-1Cr p0s { r( r - 1 )pi2( pi + 1 - p0 - pi )r-2 + rpi( pi + 1 - p0 - pi )r-1 } ) - μi2 |
| = | Σr{0→∞}( r+s-1Cr p0s {
rpi( 1 - p0 )r-1 + r( r - 1 )pi2( 1 - p0 )r-2
} ) - μi2 |
| = | { pi / ( 1 - p0 ) }Σr{0→∞}( r・r+s-1Cr p0s ( 1 - p0 )r ) + { pi / ( 1 - p0 ) }2Σr{0→∞}( r( r - 1 )・r+s-1Cr p0s ( 1 - p0 )r ) - μi2 |
第一項は μi そのものであり、第二項は補足 2 (5)式を使って求められるので、
| σi2 | = | μi + { pi / ( 1 - p0 ) }2[ s( s + 1 )( 1 - p0 )2 p0k { 1 - ( 1 - p0 ) }-(k+2) ] - μi2 |
| = | ( s・pi / p0 ) + { s( s + 1 )pi2 / p02 } - ( s・pi / p0 )2 |
| = | ( s・pi / p0 ) + ( s・pi2 / p02 ) |
になります。
共分散は、ri = i, rj = j, pi = p, pj = q で表して
Ps,p(i,j|r) = r+s-1Cr p0s { r! / i!j!( r - i - j )! } pi qj( 1 - p0 - p - q )r-i-j
とすれば
| E[ij] | = | Σr{0→∞}( Σi{0→r}( Σj{0→r-i}( i・j・Ps,p(i,j|r) ) ) ) |
| = | Σr{0→∞}( r+s-1Cr p0s Σi{0→r}( Σj{0→r-i}( i・j・{ r! / i!j!( r - i - j )! } pi qj( 1 - p0 - p - q )r-i-j ) ) ) |
| = | Σr{0→∞}( r+s-1Cr p0s Σi{0→r}( i・{ r! / i!・( r - i )! } pi |
| | Σj{0→r-i}( j・{ ( r - i )! / j!・( r - i - j )! } qj( 1 - p0 - p - q )r-i-j ) ) ) |
| = | Σr{0→∞}( r+s-1Cr p0s Σi{0→r}( i・rCi pi Σj{0→r-i}( j・r-iCj qj( 1 - p0 - p - q )r-i-j ) ) ) |
Σj{0→r-i}( j・r-iCj qj( 1 - p0 - p - q )r-i-j ) = q( r - i )( 1 - p0 - p )r-i ( 補足 2 (1)式 ) より、
| E[ij] | = | Σr{0→∞}( r+s-1Cr p0s Σi{0→r}( qi( r - i )・rCi pi ( 1 - p0 - p )r-i-1 ) ) |
| = | Σr{0→∞}( r+s-1Cr p0s Σi{0→r}( qi( r - i )・{ r! / i!・( r - i )! } pi ( 1 - p0 - p )r-i-1 ) ) |
| = | Σr{0→∞}( r+s-1Cr p0s pqr( r - 1 ) Σi{1→r-1}( { ( r - 2 )! / ( i - 1 )!( r - i - 1 )! } pi-1 ( 1 - p0 - p )r-i-1 ) ) |
| = | Σr{0→∞}( r+s-1Cr p0s pqr( r - 1 ) Σi{1→r-1}( r-2Ci-1 pi-1 ( 1 - p0 - p )r-i-1 ) ) |
二項定理より Σi{1→r-1}( r-2Ci-1 pi-1 ( 1 - p0 - p )r-i-1 ) = ( 1 - p0 )r-2 なので、
| E[ij] | = | Σr{0→∞}( r+s-1Cr p0s pqr( r - 1 )( 1 - p0 )r-2 ) |
| = | { pq / ( 1 - p0 )2 } Σr{0→∞}( { r( r - 1 ) r+s-1Cr p0s( 1 - p0 )r ) |
Σr{0→∞}( { r( r - 1 ) r+s-1Cr p0s( 1 - p0 )r ) = s( s + 1 )( 1 - p0 )2 p0s { 1 - ( 1 - p0 ) }-(s+2) = s( s + 1 )( 1 - p0 )2 / p02 ( 補足 2 (5)式 ) より
| E[ij] | = | { pq / ( 1 - p0 )2 }{ s( s + 1 )( 1 - p0 )2 / p02 } |
| = | s( s + 1 )( pq / p02 ) |
最後に、γij = E[ij] - E[i]E[j] より
| γij | = | s( s + 1 )( pq / p02 ) - ( sp / p0 )( sq / p0 ) |
| = | spq / p02 |
以上、まとめると
負の多項分布 Ps,p( r ) = { ( Σi{1→k}( ri ) + s - 1 )!・p0s / ( s - 1 )! } Πi{1→k}( piri / ri! )
平均 : μi = s・pi / p0、分散 : σi2 = ( s・pi / p0 ) + ( s・pi2 / p02 )
共分散 : γij = spq / p02
になります。
負の多項分布用クラスのサンプル・プログラムを以下に示します。
class NegativeMultinomialDistribution : public MultiDiscDist
{
vector<double> _p;
double _p0;
unsigned int _s;
static double fact( double n );
public:
NegativeMultinomialDistribution( const vector<double>& p, unsigned int s );
double operator[]( const vector<int>& r ) const;
double average( unsigned int i ) const
{ return( ( i >= size() || _p0 == 0 ) ? NAN : (double)_s * _p[i] / _p0 ); }
double variance( unsigned int i ) const
{ return( ( i >= size() || _p0 == 0 ) ? NAN : (double)_s * _p[i] / _p0 + (double)_s * pow( _p[i] / _p0, 2 ) ); }
double covariance( unsigned int i, unsigned int j ) const;
unsigned int size() const { return( _p.size() ); }
};
NegativeMultinomialDistribution::NegativeMultinomialDistribution( const vector<double>& p, unsigned int s )
: _s( s )
{
_p.assign( p.begin(), p.end() );
_p0 = 1.0;
for ( unsigned int i = 0 ; i < _p.size() ; ++i )
_p0 -= _p[i];
}
double NegativeMultinomialDistribution::fact( double n )
{
if ( n <= 1 ) return( 1 );
return( n * fact( n - 1 ) );
}
double NegativeMultinomialDistribution::operator[]( const vector<int>& r ) const
{
if ( _p.size() != r.size() ) return( NAN );
if ( r.size() == 0 ) return( NAN );
if ( _p0 <= 0 ) return( NAN );
if ( _s == 0 ) return( NAN );
unsigned int n = 0;
for ( unsigned int i = 0 ; i < r.size() ; ++i ) {
if ( _p[i] < 0 ) return( NAN );
if ( r[i] < 0 ) return( 0 );
n += r[i];
}
double p = pow( _p0, _s );
double rFact = fact( _s - 1 );
for ( unsigned int i = 0 ; i < r.size() ; ++i ) {
p *= pow( _p[i], r[i] );
rFact *= fact( r[i] );
}
return( fact( n + _s - 1 ) * p / rFact );
}
double NegativeMultinomialDistribution::covariance( unsigned int i, unsigned int j ) const
{
if ( i >= size() || j >= size() ) return( NAN );
return( _s * _p[i] * _p[j] / pow( _p0, 2 ) );
}
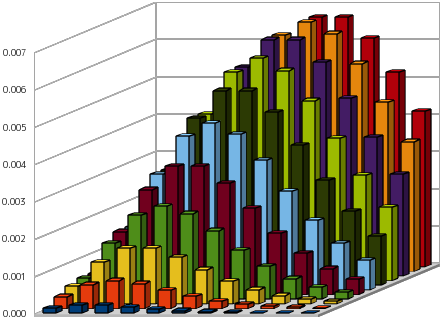
下図は、多項分布と同様に、サイコロを投げたときに 1 の目が出た事象を E1、偶数の目が出た事象を E2、その他の場合を E3 として、サイコロを投げる試行を繰り返したときのの分布状態を示したものですが、ここでは E1 がある回数に達した段階で試行をストップした場合を表しています。それぞれの事象 Ei の確率 pi は { p1, p2, p3 } = { 1 / 6, 1 / 2, 1 / 3 } であり、グラフ内において、底平面上の縦軸が E2 の発生回数 r2、横軸が E3 の発生回数 r3 となります。
E1 が 5 回に達した段階で試行をストップした場合
|
| E3の発生回数 |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 合計 |
|---|
E2
の
発
生
回
数 | 10 | 1.26E-04 | 6.29E-04 | 1.68E-03 | 3.17E-03 | 4.75E-03 | 6.02E-03 | 6.68E-03 | 6.68E-03 | 6.13E-03 | 5.22E-03 | 4.18E-03 | 4.53E-02 |
|---|
| 9 | 1.80E-04 | 8.38E-04 | 2.10E-03 | 3.72E-03 | 5.28E-03 | 6.33E-03 | 6.68E-03 | 6.37E-03 | 5.57E-03 | 4.54E-03 | 3.48E-03 | 4.51E-02 |
|---|
| 8 | 2.49E-04 | 1.08E-03 | 2.51E-03 | 4.19E-03 | 5.59E-03 | 6.33E-03 | 6.33E-03 | 5.73E-03 | 4.77E-03 | 3.71E-03 | 2.72E-03 | 4.32E-02 |
|---|
| 7 | 3.32E-04 | 1.33E-03 | 2.87E-03 | 4.47E-03 | 5.59E-03 | 5.96E-03 | 5.63E-03 | 4.82E-03 | 3.82E-03 | 2.83E-03 | 1.98E-03 | 3.96E-02 |
|---|
| 6 | 4.22E-04 | 1.55E-03 | 3.09E-03 | 4.47E-03 | 5.21E-03 | 5.21E-03 | 4.64E-03 | 3.75E-03 | 2.81E-03 | 1.98E-03 | 1.32E-03 | 3.45E-02 |
|---|
| 5 | 5.06E-04 | 1.69E-03 | 3.09E-03 | 4.13E-03 | 4.47E-03 | 4.17E-03 | 3.48E-03 | 2.65E-03 | 1.88E-03 | 1.25E-03 | 7.92E-04 | 2.81E-02 |
|---|
| 4 | 5.63E-04 | 1.69E-03 | 2.81E-03 | 3.44E-03 | 3.44E-03 | 2.98E-03 | 2.32E-03 | 1.66E-03 | 1.10E-03 | 6.95E-04 | 4.17E-04 | 2.11E-02 |
|---|
| 3 | 5.63E-04 | 1.50E-03 | 2.25E-03 | 2.50E-03 | 2.29E-03 | 1.83E-03 | 1.32E-03 | 8.83E-04 | 5.52E-04 | 3.27E-04 | 1.85E-04 | 1.42E-02 |
|---|
| 2 | 4.82E-04 | 1.13E-03 | 1.50E-03 | 1.50E-03 | 1.25E-03 | 9.17E-04 | 6.11E-04 | 3.78E-04 | 2.21E-04 | 1.23E-04 | 6.54E-05 | 8.17E-03 |
|---|
| 1 | 3.22E-04 | 6.43E-04 | 7.50E-04 | 6.67E-04 | 5.00E-04 | 3.33E-04 | 2.04E-04 | 1.16E-04 | 6.31E-05 | 3.27E-05 | 1.64E-05 | 3.65E-03 |
|---|
| 0 | 1.29E-04 | 2.14E-04 | 2.14E-04 | 1.67E-04 | 1.11E-04 | 6.67E-05 | 3.70E-05 | 1.94E-05 | 9.70E-06 | 4.67E-06 | 2.18E-06 | 9.75E-04 |
|---|
| 合計 | 3.87E-03 | 1.23E-02 | 2.29E-02 | 3.24E-02 | 3.85E-02 | 4.02E-02 | 3.79E-02 | 3.31E-02 | 2.69E-02 | 2.07E-02 | 1.52E-02 |
|---|
|
E1 が 1 回に達した段階で試行をストップした場合

|
| E3の発生回数 |
|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 合計 |
|---|
E2
の
発
生
回
数 | 10 | 1.63E-04 | 5.97E-04 | 1.19E-03 | 1.72E-03 | 2.01E-03 | 2.01E-03 | 1.79E-03 | 1.45E-03 | 1.09E-03 | 7.64E-04 | 5.09E-04 | 1.33E-02
|
|---|
| 9 | 3.26E-04 | 1.09E-03 | 1.99E-03 | 2.65E-03 | 2.87E-03 | 2.68E-03 | 2.23E-03 | 1.70E-03 | 1.21E-03 | 8.04E-04 | 5.09E-04 | 1.81E-02 |
|---|
| 8 | 6.51E-04 | 1.95E-03 | 3.26E-03 | 3.98E-03 | 3.98E-03 | 3.45E-03 | 2.68E-03 | 1.92E-03 | 1.28E-03 | 8.04E-04 | 4.82E-04 | 2.44E-02 |
|---|
| 7 | 1.30E-03 | 3.47E-03 | 5.21E-03 | 5.79E-03 | 5.30E-03 | 4.24E-03 | 3.06E-03 | 2.04E-03 | 1.28E-03 | 7.57E-04 | 4.29E-04 | 3.29E-02 |
|---|
| 6 | 2.60E-03 | 6.08E-03 | 8.10E-03 | 8.10E-03 | 6.75E-03 | 4.95E-03 | 3.30E-03 | 2.04E-03 | 1.19E-03 | 6.62E-04 | 3.53E-04 | 4.41E-02 |
|---|
| 5 | 5.21E-03 | 1.04E-02 | 1.22E-02 | 1.08E-02 | 8.10E-03 | 5.40E-03 | 3.30E-03 | 1.89E-03 | 1.02E-03 | 5.30E-04 | 2.65E-04 | 5.91E-02 |
|---|
| 4 | 1.04E-02 | 1.74E-02 | 1.74E-02 | 1.35E-02 | 9.00E-03 | 5.40E-03 | 3.00E-03 | 1.57E-03 | 7.86E-04 | 3.78E-04 | 1.77E-04 | 7.90E-02 |
|---|
| 3 | 2.08E-02 | 2.78E-02 | 2.31E-02 | 1.54E-02 | 9.00E-03 | 4.80E-03 | 2.40E-03 | 1.14E-03 | 5.24E-04 | 2.33E-04 | 1.01E-04 | 1.05E-01 |
|---|
| 2 | 4.17E-02 | 4.17E-02 | 2.78E-02 | 1.54E-02 | 7.72E-03 | 3.60E-03 | 1.60E-03 | 6.86E-04 | 2.86E-04 | 1.16E-04 | 4.66E-05 | 1.41E-01 |
|---|
| 1 | 8.33E-02 | 5.56E-02 | 2.78E-02 | 1.23E-02 | 5.14E-03 | 2.06E-03 | 8.00E-04 | 3.05E-04 | 1.14E-04 | 4.23E-05 | 1.55E-05 | 1.87E-01 |
|---|
| 0 | 1.67E-01 | 5.56E-02 | 1.85E-02 | 6.17E-03 | 2.06E-03 | 6.86E-04 | 2.29E-04 | 7.62E-05 | 2.54E-05 | 8.47E-06 | 2.82E-06 | 2.50E-01 |
|---|
| 合計 | 3.33E-01 | 2.22E-01 | 1.46E-01 | 9.59E-02 | 6.19E-02 | 3.93E-02 | 2.44E-02 | 1.48E-02 | 8.79E-03 | 5.10E-03 | 2.89E-03 |
|---|
|
E1 はサイコロの目が 1 になる事象なので、サイコロの目が 1 になるまでサイコロを投げる試行を繰り返して、その時偶数が出た回数を縦軸、それ以外が出た回数を横軸に取ったのが上で示したグラフになります。サイコロの目が一回でも出たら試行をストップするというのは幾何分布と同じということになって、同時確率としては 1 の目が最初に出る( E2 も E3 もともにゼロである)ときの確率が最も高くなっています。
複数の事象に対して確率を考える場合、一つだけ考えればよかったときと比べると問題は難しくなります。この場合、各事象の独立性や周辺分布を利用することで問題を単純化することができます。また、各変数間の関係を調べる方法として、相関係数や回帰曲線などが利用できることについても説明を行いました。
今回は、「多項分布」と「負の多項分布」の二つを多変数確率密度の例として紹介しましたが、これらは他の確率密度関数、例えばポアソン分布や正規分布などを複数組み合わせた場合を考えることもできます。特に、各変数が独立ならば、その同時分布は周辺分布の積として表されるので、そのような例は簡単に作ることができます。
次回は、連続分布の代表である「正規分布」を中心に紹介したいと思います。
二つの集合 A, B からそれぞれ元 a ∈ A, b ∈ B を取り出し、新たな集合 { a, b } を作ります。このような集合を「対(Pair)」といい、特に並べる順番を持ったものは「順序対(Ordered Pair)」になります。よって、二つの順序対 { a, b } と { c, d } が等しいのは、a = c かつ b = d のときに限ることになります(順序を持たなければ、a = d かつ b = c のような場合も成り立つことになります)。以降、順序対を ( a, b ) と表します。
順序対 ( a, b ) 全体の集合を「直積集合(Cartesian Product)」といい、A x B で表します。
A x B = { ( a, b ) | a ∈ A, b ∈ B }
n 個の集合 A1, A2, ... An の直積集合 A1 x A2 x ... x An = Πi{1→n}( Ai ) も同様に、
Πi{1→n}( Ai ) = { ( a1, a2, ... an ) | ai ∈ Ai ( i = 1, 2, ... n ) }
と定義されます。
一つの集合 A に対して 直積集合 A x A を作ることも可能です。このような直積集合を「デカルト冪(Cartesian Power)」といいます。実数 R からなるデカルト冪 Rn がその代表で、R2 は平面、R3 は空間を表すのによく利用されます。
前章で、「二項分布」と「負の二項分布」の平均・分散は積率母関数を利用して求めましたが、これらは二項定理を使って直接求めることもできます。二項分布の平均を
μB = Σr{0→n}( r・nCr prqn-r )
で表せば、
| μB | = | Σr{0→n}( r・nCr prqn-r ) |
| = | Σr{0→n}( r・{ n! / r!・( n - r )! } prqn-r ) |
| = | np Σr{1→n}( { ( n - 1 )! / ( r - 1 )!・( n - r )! } pr-1qn-r ) |
| = | np Σr{1→n}( n-1Cr-1 pr-1qn-r ) |
| = | np ( p + q )n-1 ... (1) |
となって、p + q = 1 ならば μB = np になります。また、
| Σr{0→n}( r( r - 1 )・nCr prqn-r ) |
| = | Σr{0→n}( r( r - 1 )・{ n! / r!・( n - r )! } prqn-r ) |
| = | n( n - 1 )p2 Σr{2→n}( { ( n - 2 )! / ( r - 2 )!・( n - r )! } pr-2qn-r ) |
| = | n( n - 1 )p2 Σr{2→n}( n-2Cr-2 pr-2qn-r ) |
| = | n( n - 1 )p2( p + q )n-2 ... (2) |
となりますが、同時に
| Σr{0→n}( r( r - 1 )・nCr prqn-r ) |
| = | Σr{0→n}( r2・nCr prqn-r ) - Σr{0→n}( r・nCr prqn-r ) |
| = | Σr{0→n}( r2・nCr prqn-r ) - μB |
でもあるので、二項分布の分散を σB2 とすれば
| σB2 | = | Σr{0→n}( r2・nCr prqn-r ) - μB2 |
| = | n( n - 1 )p2( p + q )n-2 + np( p + q )n-1 - n2p2 ( p + q )2n-2 |
| = | { n2p2 - np2 + np( p + q ) - n2p2( p + q )n }( p + q )n-2 |
| = | { n2p2 + npq - n2p2( p + q )n }( p + q )n-2 ... (3) |
ここで、p + q = 1 とすれば
σB2 = n2p2 + npq - n2p2 = npq
になります。これらは p + q = 1 でなくても成り立つので、「多項分布」や「負の多項分布」の期待値を求める時に利用しています。
負の二項分布の場合、平均を
μNB = Σr{0→∞}( r・r+k-1Cr pkqr )
とすれば、
| μNB | = | Σr{0→∞}( r・r+k-1Cr pkqr ) |
| = | Σr{0→∞}( r・{ ( r + k - 1 )! / r!・( k - 1 )! } pkqr ) |
| = | kq Σr{1→∞}( { ( r + k - 1 )! / ( r - 1 )!・k! } pkqr-1 ) |
| = | kq Σr{1→∞}( C( ( r - 1 ) + ( k + 1 ) - 1, r - 1 ) pkqr-1 ) |
| = | kq pk Σr{1→∞}( C( -( k + 1 ), r - 1 ) ( -q )r-1 ) |
| = | kq pk ( 1 - q )-(k+1) ... (4) |
p + q = 1 とすれば、
μNB = kq / p
と求めることができます。但し、途中で負の二項係数に関する以下の等式
C( -a, r ) = (-1)rC( a + r - 1, r )
と、一般の二項定理
( 1 + x )a = Σr{0→∞}( C( a, r ) xr )
を利用しています。また、二項分布の場合と同様にして
| Σr{0→∞}( r( r - 1 )・r+k-1Cr pkqr ) |
| = | Σr{0→∞}( r( r - 1 )・{ ( r + k - 1 )! / r!・( k - 1 )! } pkqr ) |
| = | k( k + 1 )q2 Σr{2→∞}( { ( r + k - 1 )! / ( r - 2 )!・( k + 1 )! } pkqr-2 ) |
| = | k( k + 1 )q2 Σr{2→∞}( C( ( r - 2 ) + ( k + 2 ) - 1, r - 2 ) pkqr-2 ) |
| = | k( k + 1 )q2 pk Σr{2→∞}( C( -( k + 2 ), r - 2 ) ( -q )r-2 ) |
| = | k( k + 1 )q2 pk ( 1 - q )-(k+2) ... (5) |
より、分散を σNB2 として
| σNB2 | = | Σr{0→∞}( r2・r+k-1Cr pkqr ) - μNB2 |
| = | k( k + 1 )q2 pk ( 1 - q )-(k+2) + kq pk ( 1 - q )-(k+1) - k2q2 p2k ( 1 - q )-2(k+1) |
| = | kq pk ( 1 - q )-(k+2) { ( k + 1 )q + ( 1 - q ) - kq pk ( 1 - q )-k } |
| = | kq pk ( 1 - q )-(k+2) { kq + 1 - kq pk ( 1 - q )-k } ... (6) |
よって、p + q = 1 ならば
| σNB2 | = | k( 1 - p ) pk p-(k+2) ( kq + 1 - kq pk p-k ) |
| = | k( 1 - p ) / p2 |
になります。
<参考文献>
- 「確率・統計入門」 小針あき宏著 (岩波書店)
- 「統計数学入門」 本間鶴千代著 (森北出版)
- Wikipedia













![[Go Back]](../images/back1.png) 前に戻る
前に戻る![[Back to HOME]](../images/home1.png) タイトルに戻る
タイトルに戻る